Abstract
Modulation of carrier concentration in strongly correlated oxides offers the unique opportunity to induce different phases in the same material, which dramatically change their physical properties, providing novel concepts in oxide electronic devices with engineered functionalities. This work reports on the electric manipulation of the superconducting to insulator phase transition in YBa2Cu3O7−δ thin films by electrochemical oxygen doping. Both normal state resistance and the superconducting critical temperature can be reversibly manipulated in confined active volumes of the film by gate-tunable oxygen diffusion. Vertical and lateral oxygen mobility may be finely modulated, at the micro- and nano-scale, by tuning the applied bias voltage and operating temperature thus providing the basis for the design of homogeneous and flexible transistor-like devices with loss-less superconducting drain–source channels. We analyze the experimental results in light of a theoretical model, which incorporates thermally activated and electrically driven volume oxygen diffusion.
Keywords: electrochemical oxygen doping, strongly correlated oxides, metal−insulator transition, reversible switching, high-temperature superconductors
1. Introduction
Strong electronic correlations present in several complex transition metal oxides are responsible for the extraordinary physical phenomena, such as Mott insulation, multiferroicity, superconductivity, or colossal magnetoresistance effects that they exhibit.1,2 Metal–insulator transitions (MITs) between different electronic phases can be induced by several external perturbations, such as pressure, temperature, strain, or electric field,3−7 delivering unique opportunities to manipulate these complex oxides for multiple electronic device applications.
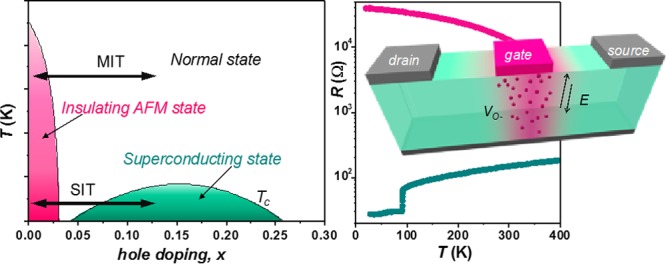
Specially, band filling-controlled Mott MIT in strongly correlated materials can induce very large resistance variations with a small change of the carrier concentration, which can also be driven by an electric field.8−10 Thus, these materials have demonstrated high performance and reliable bipolar field-induced resistive switching behavior,11−13 making them promising candidates for next-generation nonvolatile resistive memory devices.8,9,12,14−16 Electronic devices exploiting Mott MIT known as “Mottronics”, may open up new possibilities and functionalities for fast and energy efficient future electronics.17−19 Particularly interesting are strongly correlated high-temperature superconducting cuprates, in which besides their nonvolatile resistive switching behavior at the normal state,13,20−22 a superconducting–insulating transition (SIT) can be induced by hole doping their CuO2 planes. Under-doped parent compounds are antiferromagnetic insulators and they become superconductors at optimum doping levels, with a transition temperature (Tc) following a superconducting dome with roughly parabolic dependence,23 as schematically shown in Figure 1a. Therefore, cuprates offer the unique opportunity to locally switch ON and OFF its outstanding macroscopic quantum coherence superconducting state, through an optimal modulation of their carrier concentration.
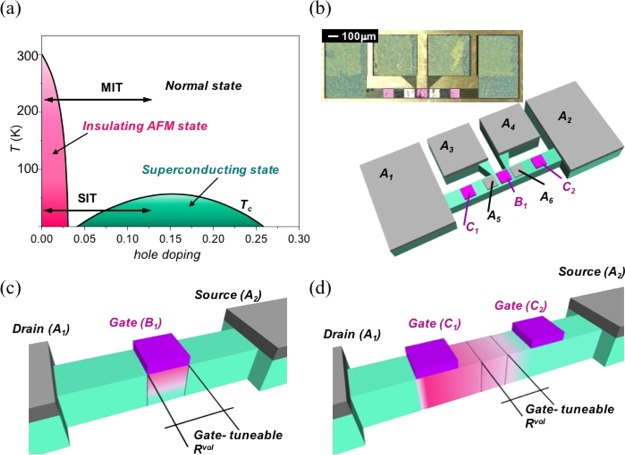
Figure 1.
(a) Phase diagram of high-temperature superconducting cuprates with the MIT and SIT indicated. (b) Schematic illustration a YBCO multielectrode device. Inset shows an optical picture of the patterned device with the different silver electrodes (false color). (c,d) Schematic representation of vertical and lateral transistor-like devices.
In this context, the possibility to reversibly tune the critical temperature (Tc) in high-temperature superconductors, by means of an electric field as an external control parameter, is clearly an active area of research in condensed matter physics.10,24 Great progress has been made by inducing electrostatic doping through a ferroelectric polarization or by using a dielectric or electrolyte gating.25−31 However, ultrathin superconducting layers and large electric fields must be used to observe significant carrier modulation. Besides pure electrostatic doping effects, it has been observed that electrolyte gating may also induce oxygen vacancies which may proliferate longer distances (∼10–30 nm).5,30,32,57 Thus, electrochemical doping through oxygen diffusion represents an interesting alternative to manipulate the carrier density of these materials, if this can be driven by an electric field. The detailed mechanisms underlying the generation of an electrochemical MIT in metal oxides is still unclear though it has been associated to local migration of oxygen vacancies, generally produced by confined filaments or homogenously distributed interface effects.11,16 In the case of metallic perovskite oxide thin films, volume phase resistive switching effects have been observed, inducing homogeneous metal insulating phase changes spanning the whole film thickness of about 10 nm.13,33
Here, we propose an original system based on the reversible modulation of nonvolatile superconducting–insulator volume phase transition through oxygen diffusion, that offers several technological and scientific breakthroughs compared with superconducting devices based on pure electrostatic doping. The transition achieved with the proposed approach is not just confined at the vicinity of the interface between the superconductor and the gate but allows a nonvolatile homogenous bulk modulation of the carrier density in gate-tuneable active volumes. A volumetric reversible SIT, which may be directly driven from the superconducting state, appears as a very appealing mechanism for the design of homogeneous and reliable superconducting transistor-like devices. In addition, completely reversible phase transitions may be tuned by directly using a metallic gate, without the need of an electrostatic or ferroelectric layer, thus simplifying very much the device design.
Transport and micro-Raman experiments performed in specially designed multiterminal devices show that lateral and vertical oxygen motion may be finely modulated at the micro- and nano-scale, providing the basis for gate-controlled systems with flexible configurations for reconfigurable logic applications and neuromorphic computing. A systematic analysis has been performed to quantitatively evaluate and discern the switching effects localized at the interface from those modifying the electric properties of the bulk. On this basis, we developed a theoretical simulation of volume oxygen dynamics, beyond the actual theoretical studies based on the formation of conductive filaments or the modulation of a Schottky depletion layer,34−39 yielding good agreement with transport and micro-Raman experiments. Superconducting transistors and memory devices working with a loss-free channel can be produced, compatible with other superconducting components for a high-end cryogenic supercomputer, which by virtue of their inherent energy-efficiency, offer an excellent opportunity to overcome silicon counterparts with radical reduction of power consumption and improved performances.40 Moreover, the potentiality of nano-engineering the superconducting order parameter of YBa2Cu3O7−δ (YBCO) films offers the possibility to investigate novel Fluxtronics device functionalities based on the controlled motion of flux quanta.29,41,42
2. Methods
2.1. Device Fabrication
Single crystalline epitaxial (001) oriented YBCO films of different thickness (50–250 nm) were grown by chemical solution deposition and pulsed laser deposition on 5 mm × 5 mm (001)-LaAlO3 single-crystal substrates. High-quality samples were obtained with critical temperature Tc ≈ 90–92 K and self-field critical current density Jcsf(77 K) = 4–5 MA cm–2.43,44 Large 250 nm thick silver contacts for four-point resistance measurements (500 μm × 500 μm) were grown on top of YBCO films by sputtering and post annealed at 450 °C in oxygen atmosphere to assure good contact resistances (∼μΩ cm2). Films were then patterned using standard photolithography in bridges of 1000 μm length, 10–30 μm width, allowing for variable four-point contact transport measurements. During the patterning process, sample degradation may occur thus reducing the initial critical temperature to Tc ≈ 82–85 K. Still, in devices patterned with carefully chosen parameters Tc values of ∼90 K were preserved. After patterning, 100 nm thick contact pads, used as gate electrodes, were grown by sputtering. Equivalent switching performances were obtained by using either silver, gold, or silver/chromium electrodes, thus excluding any effect of silver diffusion in the switching behavior.
Figure 1b shows a schematic representation of multiterminal devices patterned, specially designed to allow measuring the volume resistance of the bridge in a four-point transport configuration, while applying voltage pulses from additional gate electrodes. For four-point contact measurements, we used A contacts, by applying a small current between A1 and A2 and reading the A3–A4 or A5–A6 voltages. The switching effect in the YBCO devices was induced in a two-terminal geometry, by using gate electrodes in a top–top configuration [pink electrodes (C1, C2 and B1) in Figure 1b]. Two different transistor-like structures, named VERT-gate (Figure 1c) and LAT-gate devices (Figure 1d), were considered. The name is chosen in this way because, as it will be discussed, in the first case we will explore the vertical oxygen diffusion through the film (along the YBCO c-axis), whereas in the second case, configuration will be used to detect mainly the lateral oxygen motion along the YBCO a–b planes. Specifically, we will use the following structures:
2.1.1. VERT-Gate Transistor-like Devices
Volume resistance between drain and source is modulated by applying voltage pulses in a gate (B1), using an external contact (A1). We evaluate the gate-tuneable volume located below the gate, Rvol, measured in four-point configuration.
2.1.2. LAT-Gate Transistor-like Devices
Volume resistance between drain and source is modulated by applying voltage pulses between two lateral gate electrodes (C1–C2). We evaluate a gate-tuneable volume located between the gates, Rvol, measured in four-point configuration. The devices measured in this configuration were covered with a 10 nm CeO2 buffer layer grown by atomic layer deposition on top of the YBCO,22 acting as a protective layer and making unnecessary any oxygen exchange with the atmosphere.45
2.2. Device Characterization
I–V and R(T) curves were measured using a two-point configuration with an external source measure unit (Keithley 2604B). In the first case, we use voltage pulses of 10 s with a compliance current of 0.1 A. Two-terminal resistance versus temperature measurements were performed with a dc current 0.01 mA. Temperature-dependent volume resistance, Rvol(T), were measured in a four-point configuration, by applying an ac current of 0.01 mA in a Quantum Design physical properties measurement system with variable temperature range (5–400 K). Micro-Raman measurements were carried out using the 5145 Å line of an argon-ion laser at room temperature with a Jobin-Yvon T-64000 Raman spectrometer attached to an Olympus microscope and equipped with a liquid-nitrogen cooled charge coupled device detector. The laser power density onto the sample was maintained below 10 kW/cm2 to avoid degradation or excessive heating.
2.3. Theoretical Approach
Simulation of the oxygen diffusion process has been modeled by using the partial differential equation solver developed by COMSOL. The model has been conceived in a simple way by using two driving forces based on two different interactions: on the one hand, conventional diffusion of one species (oxygen) in a vacancy field in a thermally activated framework, which is reflected in the dependence of the diffusion coefficient with the temperature and on the other hand, the electrical nature of the oxygen ions, movable along the material, allows electrically driven ionic diffusion based on an electric field produced by the application of an external bias voltage and the local electrodynamical properties of the material. The metallic behavior or the system allows a local charge balance to be achieved by mixed valance states thus assuring charge neutrality in the system.
Simulations were performed in a twofold rectangular domain with a width x (parallel to the a–b planes) and thickness y (parallel to the c-axis), being (x ∈ [0,520] μm and y ∈ [0,10] μm). Two 40 μm long top contacts were located at 35 μm of both ends to polarize the sample. The right contact was grounded while a bias voltage was applied to the left one. The simulation domain does not include the electrode region. A parabolic-like distributed contact surface conductivity has been considered (see Table 1) to soften the contact discontinuity at the pad edges.
Table 1. Parameters Used in the Simulation.
| effective variation of oxygen concentration | c = 0–6.26 × 1027 ions/m3 |
| initial oxygen concentration | c0 = 3.6 × 1027 ions/m3 |
| electronic conductivity | σx = 102 S/m; c < 3.01 × 1027 ions/m3 |
| σx = 1.54 × 10–22 (c – 3.01 × 1027) + 102 S/m; (3.01 < c < 6.26) × 1027 ions/m3 | |
| σx = 10σy | |
| diffusion Tensor | Dx = 10–7 m2/s |
| Dy = 10–13 m2/s | |
| contact surface conductivity | 107/[(x – x0)2+ 10] S/m; x0 = contact center |
The fundamental assumptions considered in the model are listed as follows.
-
i.
We assume a diffusion equation in a continuous medium approximation. The diffusion coefficient has been considered anisotropic, with a ratio Dx/Dy = 106 (see Table 1),46 which qualitatively describes the experimentally observed anisotropy in the oxygen diffusion along the CuO2 planes and across of them, independent of the diffusion mechanism.
-
ii.
The concentration of oxygen ions in conditions to be diffused has been established considering the maximum and minimum YBCO oxygen stoichiometry, 7 and 6, with δ ∈ [0,1]. The concentration values were estimated with the volume of the limiting structures, orthorhombic and tetragonal, being 4.03 × 1028 and 3.41 × 1028 ions/m3, respectively. Then, assuming that only the oxygen in excess to the tetragonal composition can contribute to the oxygen diffusion, the effective change in the oxygen carrier concentration should be between c = 0 and c = 6.26 × 1027 ions/m3. The pristine state has been considered homogeneous along the sample with a concentration of c0 = 3.6 × 1027 ions/m3.
-
iii.
We assume a redistribution of oxygen vacancies within the system, with no external oxygen exchange.
-
iv.
The material is considered as an electronic conductor with an electric resistivity directly correlated with the local oxygen concentration. The local conductivity has been defined as an oxygen dependent linear function, which phenomenologically describe the conductivity change between the optimally doped and under-doped states (see Table 1).47,48
-
v.
The electric field is defined according to the Ohm constitutive equation as a function of the local current density, J, and the electronic conductivity, σ, neglecting de contribution of the ionic conduction. The electronic carrier concentration distributes in a way to maintain the local charge compensation.
-
vi.
Both electronic conductivity, σ, and diffusion coefficient, D, have been considered anisotropic with higher values along the a–b planes (x-axis) (see Table 1).
Equation 1 shows the time evolution of the oxygen concentration in each point of the domain
| 1 |
where ċ is the time derivative of the concentration, D is the diffusion tensor, z the charge number of oxygen ions, u is the Nernst–Einstein ratio (u = D/RT), and F is the Faraday number. The electric potential is deduced from the constitutive and the charge conservation equations as
| 2 |
where J is the electric current density, σ is the electronic conductivity, and q is the electronic charge density.
3. Results and Discussion
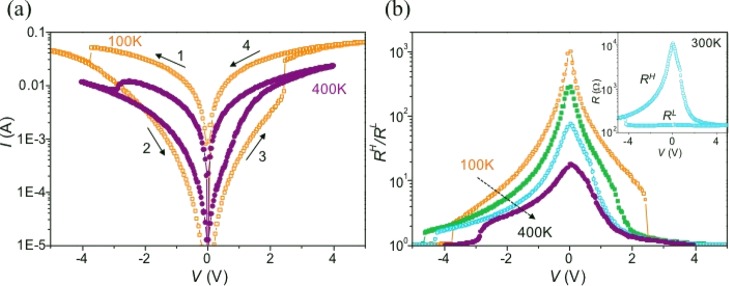
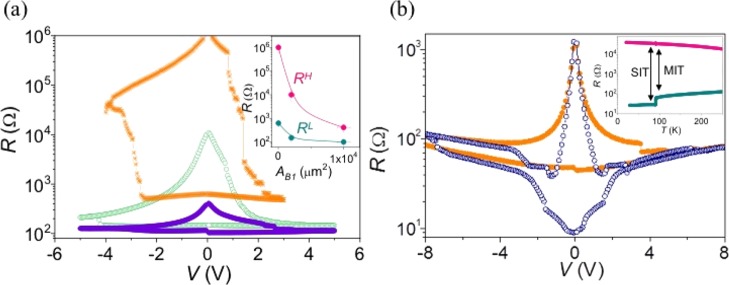
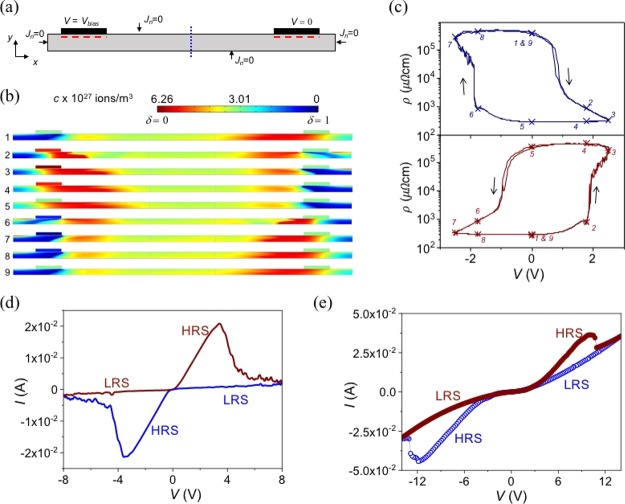
Figure 2a shows typical I–V curves, in a semilogarithm current scale, obtained for a 250 nm thick, 30 μm wide bridge by using a VERT-gate electrode configuration. Hysteresis loops were measured by sweeping the voltage between ±5 V at 100 and 400 K. Nonvolatile bipolar resistive switching is found in both cases, where the switching direction depends on the polarity of the applied field. Starting from a pristine low resistance state (LRS), a transition to the high resistance state (HRS) occurs when applying a negative voltage (1). The nonvolatile HRS is maintained by reducing the bias voltage to 0 V (2). The system is switched back to the LRS in a subsequent positive voltage sweep (3) and maintained at this LRS by reducing again the bias voltage to 0 V (4). We checked in any case that a positive bias sweep in the pristine optimally doped LRS does not induce any switching hysteresis because no more oxygen can be introduced into the structure.
Figure 2.
(a) Semilog I–V characteristics measured in a 250 nm thick, 30 μm wide YBCO VERT-gate device by using electrode B1, at 100 and 400 K. Arrows and numbers show the voltage sweep direction. (b) High–low resistance ratio, RH/RL, determined at different temperatures as a function of the bias voltage. Inset shows the resistance hysteresis loop measured at 300 K.
The general aspect of the hysteresis loops obtained at different temperatures shows similar features, with large resistance changes induced by using modest gate voltages. Nevertheless, the resistance hysteresis is clearly enlarged and the change in the resistive state is more abrupt at low temperatures. Although data shows the general trend of decreasing the switching voltage by increasing the temperature (see Figure 2b), in agreement with a higher oxygen mobility, we found considerable variation of this parameter at low temperature, where a very abrupt current change is observed. At all temperatures, we find an asymmetric behavior, where the voltage needed to drive the system from the HRS to the LRS is always lower than the one required to go from the LRS to the HRS. This asymmetry in the switching voltages, found in all of the devices tested (and also observed in the I–V curves shown in Figure 5b), can be explained with our theoretical model, which will be discussed in detail below. The voltage dependence of the resistance values obtained at 300 K in the HRS and LRS (RH and RL), is given in the inset of Figure 2b, where a very large ratio of almost 2 orders of magnitude is found at low voltages. The conduction mechanism through the metal–oxide interface in the two resistance states has been evaluated by analyzing the d(ln(I))/d(ln(V)) versus V1/2 (see Supporting Information S1). The derivative term shows a constant value equal to 1 which corresponds to an Ohmic conduction for the LRS, with a small deviation at high voltages at 100 K. The HRS, however, shows a complex behavior, which cannot be described with any single electrode or bulk, limited mechanism.49,50 The enhancement of RH/RL obtained by decreasing the temperature is explained by considering the temperature dependence of RH and RL, as shown in Figure 3a. The LRS displays the metallic behavior expected for an optimally doped YBCO film, with a superconducting transition at 90 K. Resistance values have been obtained by applying a current of 0.01 mA in a two-point configuration. In this way, the resistance measured below Tc corresponds to the contact resistance. The switching drives the system to a semiconducting state through a MIT, showing an enhancement of the resistance at 300 K of more than 2 orders of magnitude with respect to the optimally doped state (indicated with an arrow in Figure 3a). This change in the normal state resistivity corresponds to a high oxygen-deficient YBCO being in the under-doped regime with δ > 0.65.47,48 Thus, the different temperature dependence of the resistance (decrease/increase of the resistance with the temperature in the HRS/LRS, respectively) fully determines the experimentally observed temperature dependence of the I–V hysteresis loops and the current and resistance values obtained. According to this, for the device shown in Figure 3a, the resistance ratio is reduced to less than 2 orders of magnitude as the temperature increases to 400 K, although the switching behavior is maintained. Nevertheless, as we will see in the following, for practical applications requiring such high temperatures, this ratio may be improved by reducing the size of the gate electrode. Figure 4a shows the R–V curves obtained for several devices with different size of the top contact B1, where one can clearly observe that the hysteresis is strongly increased by decreasing the electrode area. As a general trend, the switching voltage decreases in the devices with small contact area, displaying much abrupt changes of the resistance states. The inset of Figure 4a shows that both HRS and LRS values decrease with the area. Area dependence resistance values are consistent with a switching effect homogeneously distributed underneath the electrode, excluding thus a local filamentary switching mechanism. Additionally, intermediate resistance states, with different oxygen doping, can be obtained with multiple-branch minor hysteresis loops, as observed in other oxide perovskites (see Supporting Information S2),33,45,51,52 robust nonvolatile multiple resistance states may be obtained (see retention data shown in Supporting Information S3), leading to multilevel memory performance, which offers much promise for high-density data storage in memory devices and potential applications in neuromorphic computing.
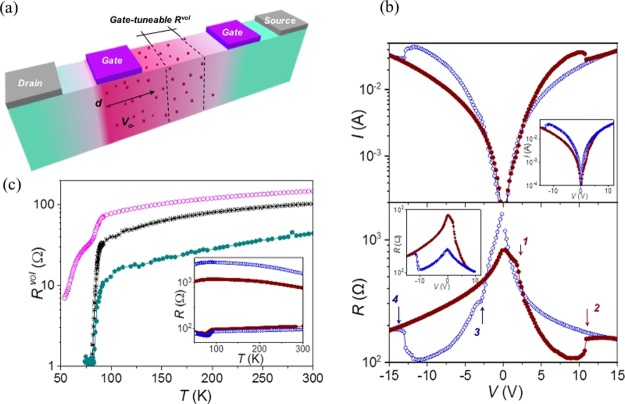
Figure 5.
(a) Schematic illustration of the lateral oxygen diffusion in a LAT-gate device after switching the gate electrode C1 at the HRS. (b) Semilog I–V (top) and two-terminal resistance (bottom) characteristics of a YBCO film measured for a 100 nm thick, 30 μm wide LAT-gate device, at 300 K, with symmetric voltage pulses, inducing switching of both gate electrodes C1 and C2. Closed and open symbols show sweeps performed by increasing and decreasing the voltage, respectively. Solid arrows and numbers show the voltage values that induce complementary transitions from HRS to LRS, VH→L (points 1, 3) and from LRS to HRS, VL→H (points 2 and 4). Inset shows the same measurements performed with asymmetric voltage pulses to switch just one of the gate electrodes. (c) Temperature dependence of Rvol at the pristine state (stars) and after positive (open symbols) and negative (closed symbols) voltage pulses of 15 V. Inset shows the two-point resistance measured below C1 and C2 after positive (open symbols) and negative (closed symbols) voltage pulses.
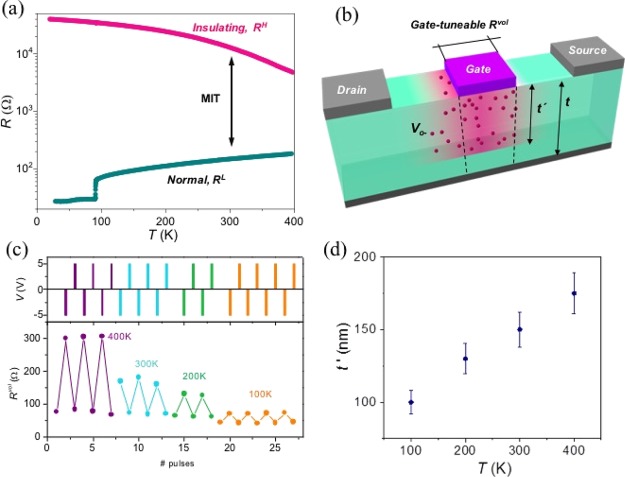
Figure 3.
(a) Temperature dependence of RH and RL obtained for the same device shown in Figure 2. (b) Schematic illustration of oxygen vacancy formation, VO–, in a VERT-gate device after driving the top contact B1 at the HRS. (c) Voltage pulses at different temperatures, and Rvol evolution. (d) Effective thickness, t′, homogenously switched below the gate electrode B1 at different temperatures.
Figure 4.
(a) Typical semilog R–V characteristics measured in VERT-gate device, at 300 K varying the area of the gate electrode B1, AB1 = 104, 2 × 103, and 25 μm2, orange stars, green open circles, and purple closed circles, respectively. Inset shows the evolution of HRS and LRS, obtained at 0.1 V, as a function of the contact area. (b) Resistance hysteresis loops obtained at 100 and 80 K for a 250 nm thick, 100 μm wide VERT-gate device. Inset shows the temperature dependence of the HRS and LRS obtained with the MIT at 100 K (closed symbols) and the SIT at 80 K (open symbols) indicated.
In the following, we will evaluate the oxygen distribution within the devices and we will show that the induced MIT is a bulk effect not limited to the vicinity of the metal–oxide interface, reaching an active volume of the device. The size of the active region that has been switched below the gate electrode B1 has been evaluated by using a transistor-like configuration (schematically shown in Figure 1c) in which we measure the local gate-tuneable volume resistance underneath the contact, Rvol, by applying a current through a drain–source channel. It is important to note that we intentionally chose this four-point configuration to evaluate the vertical oxygen diffusion through the film, although both lateral and vertical oxygen motion may be induced in view of the electric field vector generated. Figure 3b schematically shows the expected oxygen diffusion induced after applying a negative bias voltage at B1. Oxygen ions migrate away from the electrode thus generating oxygen vacancies, VO–, which would drive the active volume depicted in pink at the HRS. Dashed lines limit volume considered in the measurement of the Rvol, determined by applying a current of 0.01 mA in a four-point configuration. Figure 3c shows the transistor-like behavior, evaluated by measuring the change in Rvol, after a series of negative and positive pulses of ±5 V applied on B1, at different temperatures. A large reversible variation of Rvol is found indicating that we strongly modify the electric properties of the bulk through a volume electrochemical oxygen doping. Assuming that a homogenous switching below the gate and considering that the resistivity of the HRS is much higher than that of the LRS (as observed in Figure 3a), the ratio of the volume bridge resistance can be determined as
| 3 |
where Rvol(HRS) and Rvol(LRS) are the bridge resistance measured at the HRS and LRS and t and t′ are the thickness of the bridge and the transformed thickness below the contact, respectively (see Figure 3b). For this particular device with t = 250 nm, the obtained active switched thickness t′ as a function of the temperature is shown in Figure 3d. It is worth noting that the volume of the bulk transited to the HRS increases with the temperature in agreement with a higher oxygen mobility that extends the field-induced oxygen migration to larger distances. Similar measurements performed in a 50 nm thick VERT-gate YBCO device showed a ratio Rvol(HRS)/Rvol(LRS) ≈ 102 at 300 K (see Supporting Information S3), indicating that the whole bridge thickness was transformed to a high under-doped insulating state. Thus, with a proper device design, we are able to homogenously and reversibly tune a superconducting channel or part of it, ON and OFF, by means of an electric field as external control parameter.
Besides the large resistance variations induced above Tc [driving the system from the metallic to the insulating state (MIT)], resistive switching effects can be even induced directly at the superconducting (SC) state by means of a direct SIT generated below Tc (see inset of Figure 4b). Resistance hysteresis loops measured just above and below Tc (100 and 80 K) for a 250 nm thick, 100 μm wide VERT-gate YBCO device are shown in Figure 4b. We observe that in both cases a reversible transition from the LRS to the HRS can be induced, though the R(V) curves below Tc exhibit a rather complex behavior, with an additional enhancement of RH/RL thanks to the SC transition of the LRS. In this case, the value of RL corresponds to the contact resistance.
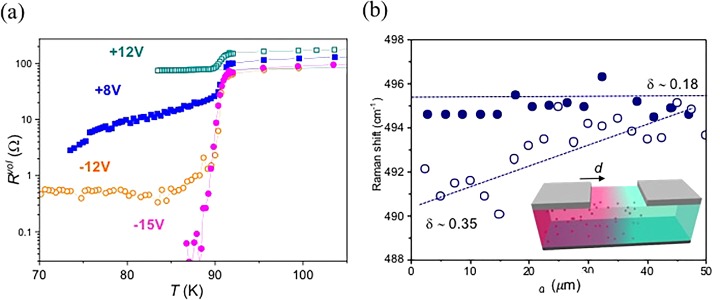
With the aim to push a bit further the enormous potential of cuprates in electrochemical oxygen doping-based devices, we explored the possibility to field-induced lateral oxygen diffusion. The key point is to use the intrinsic anisotropic oxygen mobility of cuprates in a top–top gate configuration, to promote lateral oxygen motion as indicated in Figure 5a. It is well-known that in YBCO the oxygen diffusion coefficient along the CuO2 planes (a–b planes) is much larger than across them (c-axis), with a ratio Dab/Dc ≈ 106.46 We conducted switching experiments in a 100 nm thick, 30 μm wide LAT-gate device by applying voltage pulses between side contacts (C1–C2 in Figures 1d and 5a). Figure 5b shows the I–V and R–V characteristics obtained by applying symmetric voltage pulses of ±15 V. A complementary switching behavior is observed in which reversible transitions of both active gate electrodes occur,34,53 that is for a given polarity, one of the electrodes is driven to the HRS, whereas the other is driven to the LRS. The complex shape of the hysteresis loops is well described by considering that upon the application of a voltage pulse with a positive polarity, the contact with a negative bias switches to the LRS (point 1), whereas the other, with positive bias, switch to the HRS (point 2). The behavior is interchanged with a pulse of the opposite polarity (points 3 and 4). The resistive state below each contact has been checked by measuring the two-point resistance through A1–C1 and A2–C2, after applying positive and negative gate polarities. Inset of Figure 5c shows that certainly one contact is at the LRS and the other at the HRS state after applying a pulse of a given polarity, while their behaviors are switched at the opposite polarity. In all of the devices tested, the transition to the LRS occurred at lower voltages than that to the HRS (VHRS→LRS ≈ 4 V and VLRS→HRS ≈ 12 V for the device shown in Figure 5). This asymmetry in the switching voltages, also observed in the I–V curves shown in Figure 2a, can be understood in the framework of the theoretical model proposed, which will be discussed in detail below. Thus, by reducing the maximum applied voltage in one of the polarities to a value lower than VLRS→HRS, we can confine the switching effect in just one of the two contacts. Insets in Figure 5 show minor loops performed in the device with a maximum applied positive voltage V < VLRS→HRS preventing the transition to the HRS of the contact with positive bias, that always stays at the LRS. The transistor-like behavior of the structure has been evaluated by measuring the temperature dependence of Rvol, at the volume depicted with dashed lines in Figure 5a, at different resistance states; pristine and after ±15 V applied to the gate electrodes (Figure 5c). A reversible change in the critical transition temperature (Tc) of more than 40 K is observed, indicating that oxygen have been reversibly diffused, hundreds of microns far from the switching contacts. It is important to remark that both lateral and vertical oxygen diffusion is evaluated in these devices and thus the modulation of Rvol will strongly depend on the volume of the drain–source channel considered. In this case, the HRS shows a partial transition and shoulder at ∼80 K, which reveals that not all of the tested volume has been homogeneously driven to the HRS. Figure 6a shows several Rvol(T) curves, measured in a region close to one of the gate switching electrodes, for a 100 nm thick, 30 μm wide LAT-gate device. Different transitions may be induced, depending on the applied gate voltage pulse. In all cases, a first transition at ∼90 K is observed, also indicating that there is still part of the volume that has not been completely switched to the HRS, with a contribution that is reduced as the voltage is increased.
Figure 6.
(a) Temperature dependence of Rvol after applying different voltage pulses (indicated as labels) in a LAT-gate device. (b) Frequency of the O(4) Ag YBCO Raman mode obtained at different points along a 50 μm long, 50 μm wide uniform track patterned in a YBCO film grown on a LaAlO3 substrate, at the pristine state (solid symbols) and after switching the left contact at the HRS (open symbols). Inset shows a schematic representation of the oxygen diffusion in the track. The phonon frequencies corresponding to the maximum and minimum δ-values determined are indicated with straight lines.
Further confirmation of the lateral oxygen motion in the films comes from micro-Raman experiments. In YBCO, a linear dependence of the oxygen content with the apical oxygen (O(4)) stretching bond along the c-axis phonon mode frequency, ωO(4) can be established.54,55Figure 6b shows the values of the phonon frequency measured at different points along a uniform YBCO channel with two lateral contacts, in its pristine state and after switching the left contact to the HRS (inset of Figure 6b). The values of the Raman shift decrease near the switched contact, confirming the formation of oxygen vacancies. The δ values depicted in the figure have been determined using eq 4, which is a simple empirical law calculated in ref (54) using experimental data points reported by different authors for Raman spectroscopy of oxygen-deficient YBCO samples excited by Ar-laser light (λ = 488 and 514 nm) in the out-of-plane scattering geometry. Considering this equation, we obtain a value of δ ≈ 0.35 in the region with less oxygen content.
| 4 |
To obtain a more detailed understanding of the role of oxygen dynamics on the resistive switching process, we performed numerical simulations by considering both the thermally activated diffusion and electrical field-induced oxygen mobility within the YBCO film (see the Theoretical Approach section). Figure 7a shows a schematic representation of the simulation domain, with top electric contacts at the sides and boundary conditions indicated. Figure 7b shows the evolution of the oxygen concentration, c, obtained by applying a bias voltage on the left contact with the right one grounded. We depict nine stages, taken every 2.5 ms, of a switching cycle which consist of biasing the sample with a sinusoidal driving voltage of ±2.5 V at a frequency of 50 Hz. Image #1 shows an initial stable configuration at 0 V in which the right contact is at the LRS and the left one at the HRS. By polarizing the left contact with a positive voltage (1.76 V at image #2), we observe a clear enhancement of oxygen concentration at the bottom of the left contact and oxygen vacancies that are generated at the right one. It is worth noting that due the material anisotropy imposed by the conductivity and diffusivity tensors, σ and D, and specially by the large domain aspect ratio, ionic carriers move anisotropically, creating a lateral oxygen diffusion of hundreds of microns away from the contacts, as experimentally observed. By further increasing the voltage up to 2.5 V (image #3), the HRS and LRS areas created close to the contacts are enlarged. These areas are preserved by decreasing the voltage to zero (images #4 and #5) indicating the nonvolatile nature of the process. By inverting the voltage polarity (image #6), oxygen vacancies are created at the left contact, whereas the oxygen concentration increases at the right one. Subsequent images (#7 and #8) show the evolution of the oxygen concentration with a negative voltage pulse until the starting position is recovered at 0 V (image #9). The enhancement/reduction of the oxygen concentration near the contacts occurs through the generation/annihilation of oxygen vacancies in the nearby region. The net change of the oxygen concentration in a given volume located along the bridge (away from the contacts) will strongly depend on the initial conditions of our system (contact resistance, initial oxygen doping, and lateral and vertical dimensions), offering high degree of freedom in device design. Figure 7c shows the evolution of a mean value of the resistance below each contact, determined considering a segment of 20 μm, placed 1 μm below the contact (red dashed lines in Figure 7a). The average resistance has been calculated by using the diagonal values of the conductivity tensor, determined according to the oxygen concentration at each point (see Theoretical Approach). The hysteresis curves correspond to stable switching characteristics, achieved after several loops, starting from an initial homogeneous oxygen concentration (see Supporting Information S5a). A complementary resistance switch is obtained, that is for a given polarity (positive voltage) the average resistance changes to the HRS below the right contact (bottom loop) and to the LRS below the left one (top loop). The behavior is interchanged with a pulse of the opposite polarity. Simulations also show that the transition from HRS to LRS occurs at lower voltage than that from LRS to HRS, which agrees with the experimental results. This asymmetry in the switching voltage, observed in all of the measured devices, is explained due to the fast motion of oxygen in the low conductivity regions where extremely large values of electric field are induced (see Supporting Information S5b). Figure 7d shows the simulated total I–V characteristics of the system, determined considering the whole cross section of the domain (blue dotted line in Figure 7a). Figure 7e shows the experimental I–V curves measured for the device described in Figure 5, which are in good agreement with the simulation.
Figure 7.
(a) Schematic representation of the simulation domain and boundary conditions. Jn is the electric current normal to the surface. Red dashed lines show the length of the integration segment chosen to calculate the hysteresis loops depicted in (b). Blue dotted line shows the cross section used to calculate the I–V characteristics depicted in (d). (b) Oxygen concentration at different stages of the switching process, after the application of a sinusoidal voltage pulse of amplitude 2.5 V with a frequency of 50 Hz at the left contact with the right one grounded (see text). Images are acquired every 2.5 ms. Colors in the contact taps depict the applied bias voltage (red positive and blue negative). Colors in the bar show the oxygen concentration (excess from the tetragonal phase with δ = 1) depicted in the scale. (c) Evolution of the resistance in a segment below the left (top) and right (bottom) contacts (see text). Numbers indicate the different switching stages shown in (b). (d) I–V hysteresis behavior simulated considering the whole domain cross section. Red and blue show curves obtained by increasing and decreasing the voltage, respectively. (e) I–V hysteresis characteristics shown in Figure 5b in a linear scale. Closed red and open blue symbols show the sweeps performed by increasing and decreasing the voltage, respectively.
A quantitative evaluation of the lateral distance of oxygen diffusion in our LAT-gate devices has been performed by reversibly switching one of the contacts (C1), using the minimum voltage sweep rates available in our experimental system (τ ≈ 100 ms) and checking that the volume resistance of the central bridge (located d = 300 μm apart of C1) is reversibly changed. With these values, we determine a lower limit of the effective oxygen diffusion coefficient Dab*, stimulated by the presence of an electric field, Dab ≈ d2/τ ≈ 10–2 cm2/s at room temperature. This value is up to 10 orders of magnitude higher than the reported values for thermally activated oxygen diffusion in YBCO single crystals.56 Such a high value can be understood considering the extremely large gradients of electric field (E > 105 V m–1) generated between the HRS and LRS regions (see Supporting Information S5b). Assuming the obtained lower limit value of the electric field-induced oxygen diffusion, the estimated speed for switching of oxygen vacancies, along the a–b planes, in a device of hundreds of nanometers would be ∼10 ns, which is in the range of what is required for high performance, high-speed memory devices.
4. Conclusion
We show the potential of reversible, nonvolatile electrochemical oxygen doping for a systematic tuning of the carrier density in YBCO films, which in turn is substantial and shows robust effects in the bulk critical temperature and electric properties at the normal state. We evidence a direct gating of superconducting–insulator transition in precise active volumes of the film, as a very appealing tool for the design of transistor-like superconducting devices, which may operate both at room temperature or exploit their superconducting nature. The possibility to homogeneously change the oxygen doping in confined regions of the bulk opens new opportunities for the study of complex phases appearing in the doping phase diagram of cuprates.
Acknowledgments
We acknowledge the financial support from Spanish Ministry of Economy and Competitiveness through the Severo Ochoa Programme for Centres of Excellence in R&D (SEV-2015-0496), CONSOLIDER Excellence Network (MAT2015-68994-REDC), COACHSUPENERGY project (MAT2014-51778-C2-1-R), co-financed by the European Regional Development Fund. We also thank the support from the European Union for NanoSC Cost Action (MP1201), NANOCOHYBRI (CA 16218) and ERC-2014-ADG-669504, and from the Catalan Government with 2014-SGR-753 and Xarmae. A.F.-R. and J.C.G.-R. thank Spanish Ministry of Economy for his FPI Spanish grants (BES-2016-077310, BES-2012-053814).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsami.8b08042.
Analysis of the conduction mechanism occurring at the HRS and LRS; multiple resistance states induced by applying minor hysteresis loops; retention characteristics of multilevel resistance states; nonvolatile transition to the insulating phase induced in the whole thickness of a superconducting channel; simulated hysteresis loops starting from an initial homogeneous oxygen doping and their evolution to stable switching characteristics; and simulation of the electric field distribution at different stages of the switching process (PDF)
Author Present Address
§ Electrochemical Materials Laboratory Massachusetts Institute of Technology, Cambridge, MA 02139, USA.
The authors declare no competing financial interest.
This paper was published on the Web on August 28, 2018. An additional reference was added to the paper, and the corrected version was reposted on September 12, 2018.
Supplementary Material
References
- Morosan E.; Natelson D.; Nevidomskyy A. H.; Si Q. Strongly Correlated Materials. Adv. Mater. 2012, 24, 4896–4923. 10.1002/adma.201202018. [DOI] [PubMed] [Google Scholar]
- Bibes M.; Villegas J. E.; Barthélémy A. Ultrathin Oxide Films and Interfaces for Electronics and Spintronics. Adv. Phys. 2011, 60, 5–84. 10.1080/00018732.2010.534865. [DOI] [Google Scholar]
- Limelette P.; Georges A.; Jerome D.; Wzietek P.; Metcalf P.; Honig J. M. Universality and Critical Behavior at the Mott Transition. Science 2003, 302, 89–92. 10.1126/science.1088386. [DOI] [PubMed] [Google Scholar]
- Morrison V. R.; Chatelain R. P.; Tiwari K. L.; Hendaoui A.; Bruhács A.; Chaker M.; Siwick B. J. A photoinduced metal-like phase of monoclinic VO2revealed by ultrafast electron diffraction. Science 2014, 346, 445–448. 10.1126/science.1253779. [DOI] [PubMed] [Google Scholar]
- Jeong J.; Aetukuri N.; Graf T.; Schladt T. D.; Samant M. G.; Parkin S. S. P. Suppression of Metal-Insulator Transition in VO2 by Electric Field-Induced Oxygen Vacancy Formation. Science 2013, 339, 1402–1405. 10.1126/science.1230512. [DOI] [PubMed] [Google Scholar]
- Scherwitzl R.; Gariglio S.; Gabay M.; Zubko P.; Gibert M.; Triscone J.-M. Metal-Insulator Transition in Ultrathin LaNiO3 Films. Phys. Rev. Lett. 2011, 106, 246403. 10.1103/physrevlett.106.246403. [DOI] [PubMed] [Google Scholar]
- Aetukuri N. B.; Gray A. X.; Drouard M.; Cossale M.; Gao L.; Reid A. H.; Kukreja R.; Ohldag H.; Jenkins C. A.; Arenholz E.; Roche K. P.; Dürr H. A.; Samant M. G.; Parkin S. S. P. Control of the Metal-Insulator Transition in Vanadium Dioxide by Modifying Orbital Occupancy. Nat. Phys. 2013, 9, 661–666. 10.1038/nphys2733. [DOI] [Google Scholar]
- Zhou Y.; Ramanathan S. Correlated Electron Materials and Field Effect Transistors for Logic: A Review. Crit. Rev. Solid State Mater. Sci. 2013, 38, 286–317. 10.1080/10408436.2012.719131. [DOI] [Google Scholar]
- Janod E.; Tranchant J.; Corraze B.; Querré M.; Stoliar P.; Rozenberg M.; Cren T.; Roditchev D.; Phuoc V. T.; Besland M.-P.; Cario L. Resistive Switching in Mott Insulators and Correlated Systems. Adv. Funct. Mater. 2015, 25, 6287–6305. 10.1002/adfm.201500823. [DOI] [Google Scholar]
- Ahn C. H.; Triscone J.-M.; Mannhart J. Electric Field Effect in Correlated Oxide Systems. Nature 2003, 424, 1015–1018. 10.1038/nature01878. [DOI] [PubMed] [Google Scholar]
- Waser R.; Dittmann R.; Staikov G.; Szot K. Redox-Based Resistive Switching Memories - Nanoionic Mechanisms, Prospects, and Challenges. Adv. Mater. 2009, 21, 2632–2663. 10.1002/adma.200900375. [DOI] [PubMed] [Google Scholar]
- Lee H. S.; Choi S. G.; Park H.-H.; Rozenberg M. J. A New Route to the Mott-Hubbard Metal-Insulator Transition: Strong Correlation Effects in Pr0.7Ca0.3MnO3. Sci. Rep. 2013, 3, 1704. 10.1038/srep01704. [DOI] [Google Scholar]
- Gonzalez-Rosillo J. C.; Ortega-Hernandez R.; Jareño-Cerulla J.; Miranda E.; Suñe J.; Granados X.; Obradors X.; Palau A.; Puig T. Volume Resistive Switching in Metallic Perovskite Oxides Driven by the Metal-Insulator Transition. J. Electroceram. 2017, 39, 185–196. 10.1007/s10832-017-0101-2. [DOI] [Google Scholar]
- Yang J. J.; Strukov D. B.; Stewart D. R. Memristive Devices for Computing. Nat. Nanotechnol. 2013, 8, 13–24. 10.1038/nnano.2012.240. [DOI] [PubMed] [Google Scholar]
- Yan Z. B.; Liu J.-M. Resistance Switching Memory in Perovskite Oxides. Ann. Phys. 2015, 358, 206–224. 10.1016/j.aop.2015.03.028. [DOI] [Google Scholar]
- Sawa A. Resistive Switching in Transition Metal Oxides. Mater. Today 2008, 11, 28–36. 10.1016/s1369-7021(08)70119-6. [DOI] [Google Scholar]
- Inoue I. H.; Rozenberg M. J. Taming the Mott Transition for a Novel Mott Transistor. Adv. Funct. Mater. 2008, 18, 2289–2292. 10.1002/adfm.200800558. [DOI] [Google Scholar]
- Stoliar P.; Cario L.; Janod E.; Corraze B.; Guillot-Deudon C.; Salmon-Bourmand S.; Guiot V.; Tranchant J.; Rozenberg M. Universal Electric-Field-Driven Resistive Transition in Narrow-Gap Mott Insulators. Adv. Mater. 2013, 25, 3222–3226. 10.1002/adma.201301113. [DOI] [PubMed] [Google Scholar]
- Hwang H. Y.; Iwasa Y.; Kawasaki M.; Keimer B.; Nagaosa N.; Tokura Y. Emergent Phenomena at Oxide Interfaces. Nat. Mater. 2012, 11, 103–113. 10.1038/nmat3223. [DOI] [PubMed] [Google Scholar]
- Acha C.; Rozenberg M. J. Non-volatile resistive switching in the dielectric superconductor YBa2Cu3O7−δ. J. Phys. Condens. Matter 2009, 21, 045702. 10.1088/0953-8984/21/4/045702. [DOI] [PubMed] [Google Scholar]
- Tomasek M.; Plecenik T.; Truchly M.; Noskovic J.; Roch T.; Zahoran M.; Chromik S.; Spankova M.; Kus P.; Plecenik A. Temperature dependence of the resistance switching effect studied on the metal/YBa2Cu3O6+x planar junctions. J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom. 2011, 29, 01AD04. 10.1116/1.3521408. [DOI] [Google Scholar]
- Coll M.; Palau A.; Gonzalez-Rosillo J. C.; Gazquez J.; Obradors X.; Puig T. Integration of atomic layer deposition CeO2 thin films with functional complex oxides and 3D patterns. Thin Solid Films 2014, 553, 7–12. 10.1016/j.tsf.2013.08.131. [DOI] [Google Scholar]
- Keimer B.; Kivelson S. A.; Norman M. R.; Uchida S.; Zaanen J. From Quantum Matter to High-Temperature Superconductivity in Copper Oxides. Nature 2015, 518, 179–186. 10.1038/nature14165. [DOI] [PubMed] [Google Scholar]
- Ahn C. H.; Bhattacharya A.; Di Ventra M.; Eckstein J. N.; Frisbie C. D.; Gershenson M. E.; Goldman A. M.; Inoue I. H.; Mannhart J.; Millis A. J.; Morpurgo A. F.; Natelson D.; Triscone J.-M. Electrostatic Modification of Novel Materials. Rev. Mod. Phys. 2006, 78, 1185–1212. 10.1103/revmodphys.78.1185. [DOI] [Google Scholar]
- Leng X.; Garcia-Barriocanal J.; Bose S.; Lee Y.; Goldman A. M. Electrostatic Control of the Evolution from a Superconducting Phase to an Insulating Phase in Ultrathin YBa2Cu3O7-x Films. Phys. Rev. Lett. 2011, 107, 027001. 10.1103/physrevlett.107.027001. [DOI] [PubMed] [Google Scholar]
- Dhoot A. S.; Wimbush S. C.; Benseman T.; MacManus-Driscoll J. L.; Cooper J. R.; Friend R. H. Increased Tc in Electrolyte-Gated Cuprates. Adv. Mater. 2010, 22, 2529–2533. 10.1002/adma.200904024. [DOI] [PubMed] [Google Scholar]
- Ahn C. H.; Gariglio S.; Paruch P.; Tybell T.; Antognazza L.; Triscone J. M. Electrostatic Modulation of Superconductivity in Ultrathin GdBa2Cu3O7-x Films. Science 1999, 284, 1152–1155. 10.1126/science.284.5417.1152. [DOI] [PubMed] [Google Scholar]
- Takahashi K. S.; Gabay M.; Jaccard D.; Shibuya K.; Ohnishi T.; Lippmaa M.; Triscone J.-M. Local Switching of Two-Dimensional Superconductivity Using the Ferroelectric Field Effect. Nature 2006, 441, 195–198. 10.1038/nature04731. [DOI] [PubMed] [Google Scholar]
- Crassous A.; Bernard R.; Fusil S.; Bouzehouane K.; Le Bourdais D.; Enouz-Vedrenne S.; Briatico J.; Bibes M.; Barthelemy A.; Villegas J. E. Nanoscale Electrostatic Manipulation of Magnetic Flux Quanta in Ferroelectric/Superconductor BiFeO3/YBa2Cu3O7-d Heterostructures. Phys. Rev. Lett. 2011, 107, 247002. 10.1103/physrevlett.107.247002. [DOI] [PubMed] [Google Scholar]
- Perez-Muñoz A. M.; Schio P.; Poloni R.; Fernandez-Martinez A.; Rivera-Calzada A.; Cezar J. C.; Salas-Colera E.; Castro G. R.; Kinney J.; Leon C.; Santamaria J.; Garcia-Barriocanal J.; Goldman A. M. In operandoevidence of deoxygenation in ionic liquid gating of YBa2Cu3O7-X. Proc. Natl. Acad. Sci. U.S.A. 2017, 114, 215–220. 10.1073/pnas.1613006114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dubuis G.; Yacoby Y.; Zhou H.; He X.; Bollinger A. T.; Pavuna D.; Pindak R.; Bozovic I. Oxygen Displacement in Cuprates under Ionic Liquid Field-Effect Gating. Sci. Rep. 2016, 6, 32378. 10.1038/srep32378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walter J.; Yu G.; Yu B.; Grutter A.; Kirby B.; Borchers J.; Zhang Z.; Zhou H.; Birol T.; Greven M.; Leighton C. Ion-Gel-Gating-Induced Oxygen Vacancy Formation in Epitaxial La0.5Sr0.5CoO3-d Films from in Operando X-Ray and Neutron Scattering. Phys. Rev. Mater. 2017, 1, 071403(R) 10.1103/physrevmaterials.1.071403. [DOI] [Google Scholar]
- Baumans X. D. A.; et al. Healing Effect of Controlled Anti-Electromigration on Conventional and High-Tc Superconducting Nanowires. Small 2017, 13, 1700384. 10.1002/smll.201700384. [DOI] [PubMed] [Google Scholar]
- Moreno C.; Munuera C.; Valencia S.; Kronast F.; Obradors X.; Ocal C. Reversible Resistive Switching and Multilevel Recording in La0.7Sr0.3MnO3Thin Films for Low Cost Nonvolatile Memories. Nano Lett. 2010, 10, 3828–3835. 10.1021/nl1008162. [DOI] [PubMed] [Google Scholar]
- Nardi F.; Balatti S.; Larentis S.; Gilmer D. C.; Ielmini D. Complementary Switching in Oxide-Based Bipolar Resistive-Switching Random Memory. IEEE Trans. Electron Devices 2013, 60, 70–77. 10.1109/ted.2012.2226728. [DOI] [Google Scholar]
- Marchewka A.; Roesgen B.; Skaja K.; Du H.; Jia C.-L.; Mayer J.; Rana V.; Waser R.; Menzel S. Nanoionic Resistive Switching Memories: On the Physical Nature of the Dynamic Reset Process. Adv. Electron. Mater. 2016, 2, 1500233. 10.1002/aelm.201500233. [DOI] [Google Scholar]
- Marchewka A.; Waser R.; Menzel S.. Physical Simulation of Dynamic Resistive Switching in Metal Oxides Using a Schottky Contact Barrier Model. International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Washington, DC, 2015; pp 297–300.
- Marchewka A.; Waser R.; Menzel S.. 2D Axisymmetric Dynamic Drift-Diffusion Model for Numerical Simulation of Resistive Switching Phenomena in Metal Oxides. International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Nuremberg, 2016; pp 145–148.
- Larentis S.; Nardi F.; Balatti S.; Gilmer D. C.; Ielmini D. Resistive Switching by Voltage-Driven Ion Migration in Bipolar RRAM-Part II: Modeling. IEEE Trans. Electron Devices 2012, 59, 2468–2475. 10.1109/ted.2012.2202320. [DOI] [Google Scholar]
- Aoki Y.; Wiemann C.; Feyer V.; Kim H.-S.; Schneider C. M.; Ill-Yo H.; Martin M. Bulk Mixed Ion Electron Conduction in Amorphous Gallium Oxide Causes Memristive Behaviour. Nat. Commun. 2014, 5, 3473. 10.1038/ncomms4473. [DOI] [PubMed] [Google Scholar]
- Holmes D. S.; Ripple A. L.; Manheimer M. A. Energy-Efficient Superconducting Computing-Power Budgets and Requirements. IEEE Trans. Appl. Supercond. 2013, 23, 1701610. 10.1109/tasc.2013.2244634. [DOI] [Google Scholar]
- Reichhardt C. Vortices Wiggled and Dragged. Nat. Phys. 2009, 5, 15–16. 10.1038/nphys1169. [DOI] [Google Scholar]
- Veshchunov I. S.; Magrini W.; Mironov S. V.; Godin A. G.; Trebbia J.-B.; Buzdin A. I.; Tamarat P.; Lounis B. Optical Manipulation of Single Flux Quanta. Nat. Commun. 2016, 7, 12801. 10.1038/ncomms12801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Obradors X.; Puig T.; Ricart S.; Coll M.; Gazquez J.; Palau A.; Granados X. Growth, nanostructure and vortex pinning in superconducting YBa2Cu3O7thin films based on trifluoroacetate solutions. Supercond. Sci. Technol. 2012, 25, 123001. 10.1088/0953-2048/25/12/123001. [DOI] [Google Scholar]
- Singh R. K.; Kumar D. Pulsed laser deposition and characterization of high-Tc YBa2Cu3O7 – x superconducting thin films. Mater. Sci. Eng., R 1998, 22, 113–185. 10.1016/s0927-796x(97)00019-3. [DOI] [Google Scholar]
- Ortega-Hernandez R.; Coll M.; Gonzalez-Rosillo J.; Palau A.; Obradors X.; Miranda E.; Puig T.; Suñe J. Resistive switching in CeO2/La0.8Sr0.2MnO3 bilayer for non-volatile memory applications. Microelectron. Eng. 2015, 147, 37–40. 10.1016/j.mee.2015.04.042. [DOI] [Google Scholar]
- Rothman S. J.; Routbort J. L.; Welp U.; Baker J. E. Anisotropy of oxygen tracer diffusion in single-crystalYBa2Cu3O7−δ. Phys. Rev. B: Condens. Matter Mater. Phys. 1991, 44, 2326–2333. 10.1103/physrevb.44.2326. [DOI] [PubMed] [Google Scholar]
- Wuyts B.; Moshchalkov V. V.; Bruynseraede Y. Resistivity and Hall effect of metallic oxygen-deficientYBa2Cu3Oxfilms in the normal state. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 53, 9418–9432. 10.1103/physrevb.53.9418. [DOI] [PubMed] [Google Scholar]
- Semba K.; Matsuda A. Superconductor-to-Insulator Transition and Transport Properties of UnderdopedYBa2Cu3OyCrystals. Phys. Rev. Lett. 2001, 86, 496–499. 10.1103/physrevlett.86.496. [DOI] [PubMed] [Google Scholar]
- Acha C.; Schulman A.; Boudard M.; Daoudi K.; Tsuchiya T. Transport Mechanism through Metal-Cobaltite Interfaces. Appl. Phys. Lett. 2016, 109, 011603. 10.1063/1.4955204. [DOI] [Google Scholar]
- Chiu F.-C. A Review on Conduction Mechanisms in Dielectric Films. Adv. Mater. Sci. Eng. 2014, 2014, 1–18. 10.1155/2014/578168. [DOI] [Google Scholar]
- Lau H. K.; Leung C. W. Nonvolatile Multilevel Memory Effect by Resistive Switching in Manganite Thin Films. J. Appl. Phys. 2008, 104, 123705. 10.1063/1.3043801. [DOI] [Google Scholar]
- Oligschlaeger R.; Waser R.; Meyer R.; Karthäuser S.; Dittmann R. Resistive switching and data reliability of epitaxial (Ba,Sr)TiO3 thin films. Appl. Phys. Lett. 2006, 88, 042901. 10.1063/1.2162860. [DOI] [Google Scholar]
- Linn E.; Rosezin R.; Kügeler C.; Waser R. Complementary Resistive Switches for Passive Nanocrossbar Memories. Nat. Mater. 2010, 9, 403–406. 10.1038/nmat2748. [DOI] [PubMed] [Google Scholar]
- Feile R. Lattice vibrations in high-Tc superconductors: Optical spectroscopy and lattice dynamics. Phys. C 1989, 159, 1–32. 10.1016/0921-4534(89)90099-3. [DOI] [Google Scholar]
- Barboy I.; Camerlingo C.; Bar I.; Bareli G.; Jung G. Micro-Raman spectroscopy of laser processed YBa2Cu3O7-δ thin films. J. Appl. Phys. 2011, 110, 033912. 10.1063/1.3602111. [DOI] [Google Scholar]
- Michaelis A.; Irene E. A.; Auciello O.; Krauss A. R. A study of oxygen diffusion in and out of YBa2Cu3O7−δ thin films. J. Appl. Phys. 1998, 83, 7736–7743. 10.1063/1.367947. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.