Native State of Complement Protein C3d Analysed via Hydrogen Exchange and Conformational Sampling

Abstract

Hydrogen/deuterium exchange detected by mass spectrometry (HDXMS) provides valuable information on protein structure and dynamics. Although HDX-MS data is often interpreted using crystal structures, it was suggested that conformational ensembles produced by molecular dynamics simulations yield more accurate interpretations. In this paper, we analyse the complement protein C3d by performing an HDX-MS experiment, and evaluate several interpretation methodologies using an existing prediction model to derive HDX-MS data from protein structure. To interpret and refine C3d’s HDX-MS data, we look for a conformation (or conformational ensemble) of C3d that allows computationally replicating this data. We confirm that crystal structures are not a good choice and suggest that conformational ensembles produced by molecular dynamics simulations might not always be satisfactory either. Finally, we show that coarse-grained conformational sampling of C3d produces a conformation from which its HDX-MS data can be replicated and refined.

1. Introduction

Hydrogen/deuterium exchange detected by mass spectrometry (HDX-MS) is an extremely valuable technique for analysing various aspects of proteins (Engen et al., 2011). It has been used to study protein structure and conformational changes, as well as protein folding and interactions (Pirrone et al., 2015). The hydrogen/deuterium exchange undergone by a protein is influenced by its structure. Although HDX-MS cannot produce a precise three-dimensional model of a protein, it can provide useful structural information (Huang and Chen, 2014). Additionally, since HDX-MS experiments involve monitoring proteins in solution over time, they can generate insights on protein dynamics (Wei et al., 2013). HDXMS also has the advantage of not suffering from the same restrictions as other structural biology techniques: it requires only small quantities of protein sample, and it is not limited by protein size (Jaswal, 2013). As such, HDX-MS has proven infinitely valuable to study systems as challenging as, for example, membrane proteins (Konermann et al., 2011).

HDX-MS has greatly impacted the study of plasma proteins that undergo dynamic structural transitions to exert their functional spectrum, such as members of the complement cascade and other innate immune pathways (Schuster et al., 2007). In the complement system, HDX-MS has proven particularly valuable to examine the various conformational changes of the central component C3. C3 is the point of convergence for all complement activation routes, the driving force of complement response amplification, and a major source of immune effectors. Over the years, HDX-MS studies have helped elucidate the mechanisms that define the perpetual solution activation of C3 via hydrolysis (Winters et al., 2005), and the major conformational transition of C3 to the potent opsonin C3b upon activation by convertases (Schuster et al., 2008). HDX-MS has also helped characterize the structural effects of point mutations in patients with a form of functional C3 deficiency (Sfyroera et al., 2015), and of a bacterial immune evasion protein that allosterically inhibits C3b activity (Chen et al., 2010). HDX-MS was among the few structural methods that could be applied to these large plasma proteins, which typically exceed 150 kDa; it has provided important insight that was not readily available from X-ray crystallography.

Despite the usefulness of HDX-MS experiments, it has sometimes proven challenging to interpret the data they produce, namely deuterium-uptake kinetic curves for various peptides extracted from a protein (see Section 4.1.1). Such a kinetic curve is often reduced to a single number: the peptide’s average protection factor (Jaswal, 2013), which quantifies the extent to which this part of the protein is protected from exchange (which is, in turn, thought to be influenced by the protein’s structure). Typically, these average protection factors are visualized on a protein heat map (Huang and Chen, 2014) built using a structural model reported in the Protein Data Bank (PDB). However, it has been argued that the correspondence between experimental HDX-MS data and such structural models is often not satisfactory, especially for models resulting from X-ray crystallography studies (Radou et al., 2014). The reason is that, contrary to crystal structures, HDX-MS data reflects the inherent variability of a protein’s native state, which emanates from the protein’s equilibrium fluctuations. Therefore, it was suggested that experimental HDX-MS data could be better interpreted using a conformational ensemble produced by a molecular dynamics (MD) simulation (Best and Vendruscolo, 2006). This technique has been used to validate experimental HDX-MS data and refine it from the peptide to the residue level (Radou et al., 2014).

In this work, we analyse the native state of the complement protein C3d through HDX-MS, using the aforementioned methodology and similar ones. A fragment of the central complement component C3, the opsonin C3d has recently gained attention as immune effector, biomarker, drug targeting structure, and potential therapeutic target itself. Upon complement activation by various triggers, C3 gets cleaved by convertases, yielding opsonins, such as C3d, that exert important biological functions (Ricklin et al., 2016). Whereas C3d has long been known to help induce adaptive immune responses by binding to CD21 on B cells (Carroll and Isenman, 2012), newer studies have identified C3d as ligand for the integrin receptor CD11b/CD18 (Bajic et al., 2013), and have indicated its role in the phagocytic uptake of opsonized particles (Lin et al., 2015). Owing to the fact that C3d is the final opsonin stage and remains covalently bound to cells that experienced complement attack, it has evolved into an important surface biomarker in the diagnosis of complement-mediated clinical conditions, such as antibody-mediated rejection during transplantation (Stites et al., 2015). Furthermore, its newly discovered roles in innate and adaptive immune effector functions put C3d into the spotlight as potential therapeutic target. C3d-binding entities based on antibodies or small molecules are therefore being developed and investigated (Gorham et al., 2015; Thurman et al., 2013). Though important as an individual opsonin, C3d also corresponds to the thioester-containing domain (TED) in C3, C3b and iC3b. This domain fulfils important functions during the activation of C3 and serves as binding site for natural ligands and immune evasion proteins alike (Chen et al., 2010; Hammel et al., 2007; Haspel et al., 2008). Therefore, gaining additional structural information about this important opsonin and immune mediator, expanding on early crystal structures of C3d (Nagar et al., 1998), is highly important. At the same time, its comparatively small size within the family of C3 opsonins facilitates the establishment of experimental and computational analyses for the purpose of this study.

In this paper, we report on an HDX-MS experiment we have performed to gather data about C3d’s native state (see Section 2.1). To interpret this experimental HDX-MS data in relation to C3d’s structure, we needed to find a conformation (or a conformational ensemble) of C3d from which this data could be first computationally replicated. For that, we had to choose an HDX prediction model (i.e., a theoretical model defining how to derive HDX data from a protein’s structure) among those available in the literature. We selected a theoretical model built on a phenomenological approximation of the protection factors of a protein’s residues (see Section 4.1.2) (Best and Vendruscolo, 2006; Vendruscolo et al., 2003). Using this model, we compare various strategies to obtain a conformation (or a conformational ensemble) of C3d from which its experimental HDX-MS data can be computationally replicated (see Sections 2.2 to 2.5).

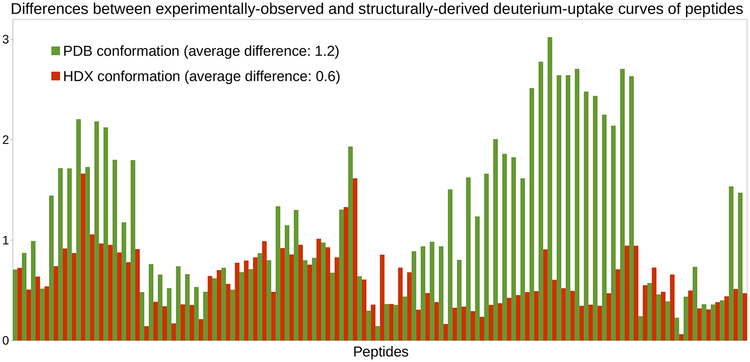
• First, we point out that computationally deriving HDX-MS data from C3d’s crystal structure does not produce good estimates of its experimental HDX-MS data. This confirms that, as noted in (Radou et al., 2014), using only a crystal structure may be limiting when interpreting HDX-MS data in certain applications.

• Second, we show that better estimates of C3d’s experimental HDX-MS data are obtained when computationally deriving HDX-MS data from conformations or conformational ensembles produced by MD simulations. However, as we observe only small improvements and a clear lack of consistency, we argue that using MD conformations might not always be an accurate way to interpret HDX-MS data either. We also explain why increasing the temperature in an MD simulation to broaden conformational sampling does not improve results.

• Third, we suggest that using coarse-grained conformational sampling might be a better strategy to obtain conformations that allow computationally replicating experimental HDX-MS data. By exploring C3d’s native state with such a method, we obtain a conformation, referred to as the “HDX conformation”, yielding the best estimates of C3d’s experimental HDX-MS data.

Finally, we analyse the HDX conformation of C3d, and we elaborate on what it reveals about C3d’s native state (see Section 2.6). We also use this HDX conformation to refine C3d’s experimental HDX-MS data from the peptide level to the residue level, and we discuss the usefulness of this data (see Section 2.7).

2. Results and Discussion

The three-dimensional structure of C3d was resolved by X-ray crystallography almost two decades ago (Nagar et al., 1998). In our work, we use a similar description of C3d’s structure produced by a more recent X-ray crystallography study of C3d in complex with the extracellular fibrinogen-binding protein (Efb) (Hammel et al., 2007); it can be found in the PDB under ID 2GOX. In this crystal structure, C3d contains 297 residues, where residue 1 corresponds to residue 991 of the full complement protein C3.

C3d can be described as a single-domain α−protein containing twelve α−helices and five 3₁₀−helices. We refer to these helices using the notations introduced in (Nagar et al., 1998). Overall, the helices of C3d are organized into an α−α barrel: an inner barrel of helices enclosed within an outer barrel of helices. Most consecutive helices alternate between the inner barrel and the outer barrel; the remaining helices are not located on the side but at the ends of the barrel. The inner barrel is composed of six parallel α−helices: α₁ (Glu22 to Thr41), α₃ (Thr86 to Leu102), α₅ (Lys149 to Ala164), α₈ (Ser196 to Met209), α₁₀ (Gln236 to Leu253), and α₁₂ (Ser278 to Asp295). The outer barrel contains six parallel helices running anti-parallel to those of the inner barrel; they comprise one 3₁₀−helix, T₁ (Ala7 to Leu13), and five α−helices: α₂ (Leu49 to Arg70), α₄ (Ser107 to Lys121), α₇ (Ser174 to Asn189), α₉ (Pro215 to Thr223), and α₁₁ (Phe256 to Gln269). The remaining helices are rather short; they include one α−helix, α₆ (Asp166 to Gln171), and four 3_10-helices: T₂ (Gln43 to Phe47), T₃ (Gln137 to Ile140), T₄ (Gly142 to Arg144), and T₅ (Tyr190 to Asn192).

The ends of the barrel differ significantly: one is a convex surface containing the thioster region involved in cell-surface attachment; the other is a concave surface containing a large acidic pocket (Nagar et al., 1998). It has been observed that Efb binds to C3d on one side of this acidic pocket (Hammel et al., 2007; Haspel et al., 2008). Various ligands of C3d are known to bind in the same region, while complement receptor 2 (CR2) binds over the whole acidic pocket (Gorham et al., 2015). Finally, note that C3d also features a disulfide bridge between Cys111 and Cys168.

2.1. HDX-MS Experiment on C3d

As part of this work, following the methodology presented in Section 4.2.1, we performed an HDX-MS experiment on C3d, alone in solution. Therefore, the data produced by this experiment is expected to characterize C3d’s native state. This HDX-MS experiment produced deuterium-uptake curves for 86 peptides extracted from C3d (see Table 1). Only six amino acids of C3d are not included in any peptide: Phe156, Glu187–Tyr190 and Leu248. Therefore, the HDX-MS experiment achieved a coverage of 98% of the protein. The redundancy of the data, through the presence of overlapping peptides is also good: 87% of amino acids are included in more than one peptide, 62% in more than two peptides, and 41% in more than three.

Table 1.

HDX-MS data experimentally-obtained for C3d. Results are reported as percentage of deuterium uptake (i.e., ratio of effective deuterium uptake over maximal deuterium uptake) at seven time points for the 86 peptides extracted from C3d. The first two and last three peptides are not used in the attempts to computationally reproduce this data.

	time points (min)
	0.17	0.5	1.7	5	17	50	167
[1–16]	67	76	86	95	97	99	100
[1–25]	64	70	80	90	97	100	100
[26–40]	6	6	7	10	16	28	46
[26–43]	8	11	16	22	30	40	55
[28–43]	12	15	20	26	33	41	51
[33–40]	9	9	9	10	13	19	34
[33–43]	14	20	29	40	50	55	64
[34–43]	15	23	34	46	57	64	73
[35–43]	15	24	35	48	60	66	74
[36–43]	18	27	42	58	72	78	85
[41–58]	68	69	71	74	79	84	90
[44–56]	78	79	81	82	85	90	94
[44–57]	73	74	75	77	83	90	96
[44–58]	65	66	67	69	74	83	90
[50–57]	35	36	40	44	51	58	71
[50–58]	43	45	46	49	57	68	79
[57–68]	6	7	10	15	21	29	51
[58–66]	7	7	7	8	12	16	50
[58–67]	4	5	5	6	8	13	48
[58–68]	6	8	11	17	22	31	56
[59–66]	6	6	7	8	10	24	48
[59–67]	5	5	5	6	9	14	48
[59–68]	6	8	11	17	23	31	56
[67–75]	25	26	30	41	60	85	99
[67–76]	20	21	25	35	56	78	97
[67–78]	14	17	22	35	52	71	92
[68–75]	28	29	34	44	67	85	98
[68–76]	24	25	29	40	61	82	96
[69–75]	32	34	38	50	73	89	99
[69–76]	26	28	31	42	65	84	99
[78–89]	39	45	51	53	55	61	70
[79–88]	46	54	61	62	65	72	83
[79–91]	34	40	45	46	50	54	63
[80–91]	28	34	39	41	44	50	59
[91–98]	3	3	3	4	4	4	5
[91–99]	1	1	2	2	2	2	5
[92–98]	3	3	4	4	4	4	4
[92–102]	19	23	30	34	35	39	47
[103–110]	69	76	86	93	96	98	98
[103–113]	52	59	72	79	84	89	95
[113–119]	3	3	3	3	4	4	4
[117–128]	9	10	11	14	24	39	63
[120–128]	15	15	17	18	22	32	56
[120–139]	31	35	42	53	64	72	80
[129–137]	32	38	47	60	73	80	82
[129–139]	37	43	54	71	83	90	92
[140–150]	65	67	75	82	90	95	97
[140–153]	53	55	60	69	83	95	98
[140–155]	47	48	53	62	75	86	89
[157–166]	17	18	20	25	39	54	70
[157–169]	26	32	40	47	58	70	81
[159–166]	19	20	23	30	45	62	79
[159–169]	33	40	49	56	67	79	88
[159–170]	34	40	49	58	67	79	88
[159–185]	44	51	59	65	73	80	85
[170–184]	45	53	64	72	79	82	85
[170–185]	43	50	60	66	73	76	80
[170–186]	41	48	56	65	70	73	77
[171–184]	45	51	61	71	75	79	83
[191–200]	69	75	81	86	91	94	96
[194–203]	41	51	56	69	77	81	83
[201–217]	39	44	56	69	78	87	94
[201–220]	33	38	51	63	73	81	86
[202–220]	33	39	54	66	75	83	88
[204–217]	41	46	58	70	79	88	94
[204–220]	34	40	54	66	76	85	89
[207–217]	48	53	68	82	87	92	94
[207–220]	38	45	61	73	81	86	88
[210–220]	36	43	62	73	79	83	84
[221–241]	63	76	90	97	98	99	99
[221–242]	60	72	86	92	94	96	98
[242–247]	3	4	4	4	4	5	5
[249–268]	18	21	26	30	34	41	54
[251–265]	28	33	37	39	44	52	67
[252–268]	20	24	28	33	40	47	61
[256–265]	8	13	16	20	29	41	62
[256–268]	6	9	14	20	28	37	54
[256–280]	47	52	56	61	65	70	78
[257–268]	4	5	8	15	24	32	50
[258–268]	3	4	8	14	19	25	44
[260–268]	3	4	7	13	18	24	43
[269–280]	93	96	97	97	97	97	98
[269–283]	71	74	77	81	83	86	93
[284–297]	23	29	33	35	38	42	48
[287–297]	35	46	51	52	55	61	68
[290–297]	55	73	81	83	87	94	99

Traditionally, this data would be interpreted by (i) converting the deuterium-uptake curves into average protection factors of peptides, and (ii) visualizing these average protection factors as a heat map using a crystal structure (if available). The first drawback of this approach is the loss of information it causes (from a kinetic curve to a single number). Second, it can be difficult to deal with overlapping peptides whose data may not be consistent. Finally, as suggested in (Radou et al., 2014), there exist more meaningful ways to analyse experimentally-observed HDX-MS data, such as refining this data from the peptide to the residue level. However, this requires using a protein conformation or a conformational ensemble from which the experimental HDX-MS data can be first computationally replicated. This also necessitates an HDX prediction model that allows deriving HDX-MS data from protein structure, such as the one presented in Section 4.1.2.

In the context of our work, to refine and interpret C3d’s experimental HDX-MS data, we first have to reproduce the deuterium-uptake data reported in Table 1. For that, we need to find a conformation (or a conformational ensemble) from which this data can be accurately derived. Note that, as the N-terminus and C-terminus are known to undergo significant levels of back-exchange, our confidence in the HDX-MS data gathered for the corresponding peptides is rather low. Therefore, the first two and last three peptides (italicized in Table 1) are not considered in the attempt to reproduce C3d’s HDX-MS data, which leaves us with 81 peptides to perform this analysis.

2.2. HDX Data Derived from the Crystal Structure of C3d

We started by trying to reproduce C3d’s experimental HDX-MS data, using its crystal structure, the HDX prediction model described in Section 4.1.2, and the methodology presented in Section 4.2.2. Although it was suggested that using a crystal structure to reproduce HDX-MS data may not be the most accurate way of doing so (Radou et al., 2014), our objective was to obtain a baseline against which other strategies could be compared. We subsequently refer to the crystal structure of C3d reported in the PDB (under ID 2GOX) as its “PDB conformation.”

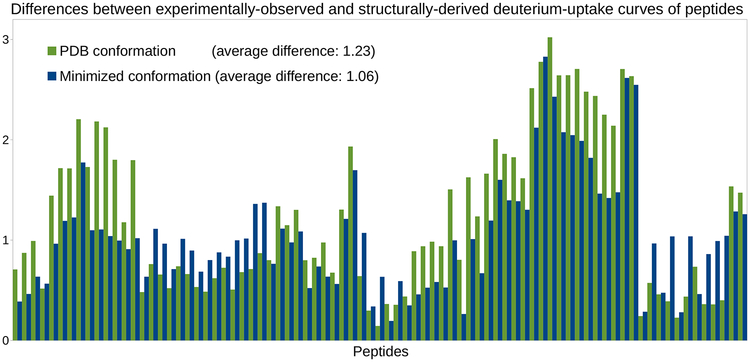
Our results show that the HDX-MS data which is computationally derived from the PDB conformation of C3d does not fit well the experimentally-observed data (see Figure 1). The average difference between the structurally-derived and experimentally-observed HDX-MS data across all peptides is 1.23 (see Section 4.2.2). Discrepancies are especially significant on the right-hand side of the chart, which corresponds to peptides of C3d comprising the region between residues Met191 and Ala242. This region includes helices T₅, α₈ and α₉, the beginning of helix α₁₀, as well as the loops between them. It is located on the side of the α−α barrel and does not cover areas of C3d with known major biological activity. Therefore, the discrepancies observed in this region cannot be linked, a priori, to any biologically-relevant conformational change in C3d.

Figure 1.

Deriving HDX-MS data from two conformations of C3d. Histograms of differences (for the 81 peptides extracted from C3d) obtained when assessing the goodness-of-fit between the experimental HDX-MS data obtained for C3d and the HDX-MS data derived from the PDB conformation of C3d, or from a minimized version of this conformation.

The fact that a PDB conformation does not typically provide good estimates of experimental HDX-MS data is due to the very nature of HDX-MS experiments, which monitor proteins in solution, contrary to X-ray crystallography. Since HDX-MS data reflects the inherent flexibility of a protein, a single conformation was not expected to provide good estimates (Vendruscolo et al., 2003). Therefore, it was suggested that HDX-MS data could be accurately reproduced only as an average over an ensemble of conformations representing the native state of a protein, such as an ensemble extracted from an MD simulation (Best and Vendruscolo, 2006).

2.3. HDX Data Derived from MD Simulations of C3d

Following the methodology described in Section 4.2.3, we performed three MD simulations of C3d (which were 100 ns long) to try and obtain better estimates of its experimental HDX-MS data. The premise of this experiment is that an MD simulation can produce a richer representation of a protein’s native state than a crystal structure, by sampling the protein’s equilibrium fluctuations.

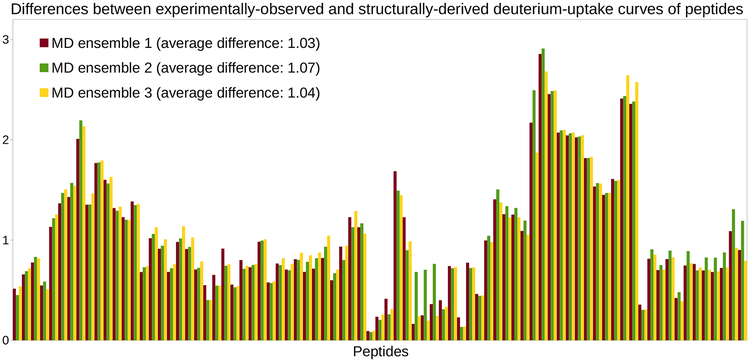
Our results confirm that using a conformational ensemble extracted from an MD simulation allows deriving HDX-MS data that fits the experimental data better than when using the PDB conformation. Aggregating the histogram of differences obtained for each MD ensemble (see Figure 2) yields an average difference of about 1.05 (as compared to 1.23 with the PDB conformation). However, Figure 2 shows that there are significant discrepancies between the HDX-MS data sets derived from the three MD ensembles: for numerous peptides, the deuterium-uptake curves derived from these ensembles are not consistent. This is due to the fact that the sampling performed by MD significantly differs across simulations. Therefore, this raises questions about using MD to characterize the variability of a protein’s native state, as captured through an HDX-MS experiment. Previous studies, such as (Radou et al., 2014), have usually based their analysis on a single MD simulation. Our experiment shows that results obtained this way might not always be reproducible.

Figure 2.

Deriving HDX-MS data from MD simulations of C3d. Histograms of differences (for the 81 peptides extracted from C3d) obtained when assessing the goodness-of-fit between the experimentally-observed HDX-MS data and the HDX-MS data derived from ensembles of conformations extracted from three MD simulations of C3d.

Another important fact that raises questions about using MD conformational ensembles to replicate experimental HDX-MS data is that a single conformation might provide better estimates than the whole ensemble. For example, the conformation obtained at the end of the energy minimization step of MD (see Section 4.2.3) provides reasonable estimates. Indeed, aggregating the histogram of differences obtained with this “minimized conformation” (see Figure 1) yields an average difference of 1.06, which is similar to the averages obtained with the MD ensembles (1.03, 1.07 and 1.04, respectively).

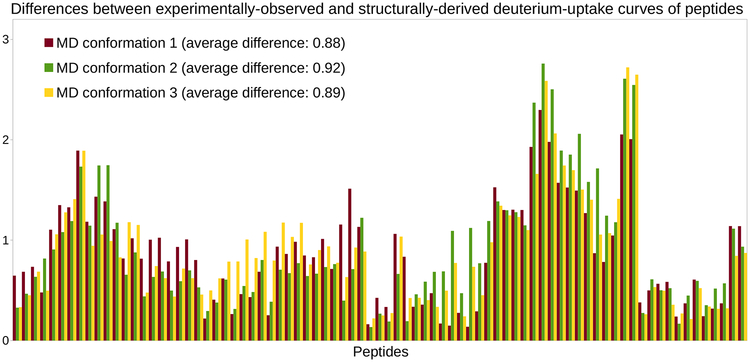
This prompted us to determine which conformations within the three MD ensembles would provide the best estimates of C3d’s experimental HDX-MS data. For that, we applied the HDX prediction model to each conformation in these ensembles, instead of computing averages. In each MD ensemble, we selected the conformation providing the best estimates. These MD conformations produce even better estimates than the minimized conformation of C3d. Aggregating the histograms of differences obtained with these MD conformations (see Figure 3) yields average differences between 0.88 and 0.92. Despite such consistency in terms of average difference, Figure 3 shows that the HDX-MS data sets derived from the three MD conformations are far from being consistent. Indeed, discrepancies between histograms are even worse than when using the full MD ensembles.

Figure 3.

Deriving HDX-MS data from MD conformations of C3d. Histograms of differences (for the 81 peptides of C3d) obtained when assessing the goodness-of-fit between the experimentally-observed HDX-MS data and the HDX-MS data derived from single conformations extracted from three MD simulations of C3d.

Although we observe a slight improvement in HDX prediction, as compared to what C3d’s crystal structure produced, it is still not good enough to consider that the experimental HDX-MS data has been replicated. Errors in HDX prediction are especially high on the right-hand side of the chart, which corresponds to region [Met191–Ala242] of C3d. To investigate whether these errors were due to this region being more flexible than other parts of C3d, we examined the B factors reported in the PDB. No correlation was found between B factors and errors in HDX prediction. We also performed a normal mode analysis of C3d, using ProDy (Bakan et al., 2011). No correlation was found between normal modes and errors in HDX prediction.

The extent of discrepancies between experimentally-observed and structurally-derived HDX-MS data initially prompted us to think that they might have captured significant conformational differences corresponding to distinct states of C3d. This would have been surprising, as C3d is not known to be very flexible (Haspel et al., 2008). In fact, we show in what follows that these discrepancies do not correspond to structural differences. We believe that the failure to replicate C3d’s experimental HDX-MS data using MD conformations (or conformational ensembles) is a consequence of MD not sampling C3d’s native state thoroughly enough. Note that this issue remained, even after extending one of the MD simulations from 100 ns to 300 ns.

2.4. HDX Data Derived from High-Temperature MD Simulations of C3d

The computational cost of MD makes it often impractical to run a simulation for long enough to produce a thorough exploration of a protein’s native state. Various methods have been proposed to improve performance, such as temperature-accelerated replica exchange, umbrella sampling, metadynamics, or accelerated MD (Feixas et al., 2014; Rocchia et al., 2012). As our objective was not to evaluate these methods, we decided to try and broaden the scope of MD’s conformational exploration by simply increasing the temperature.

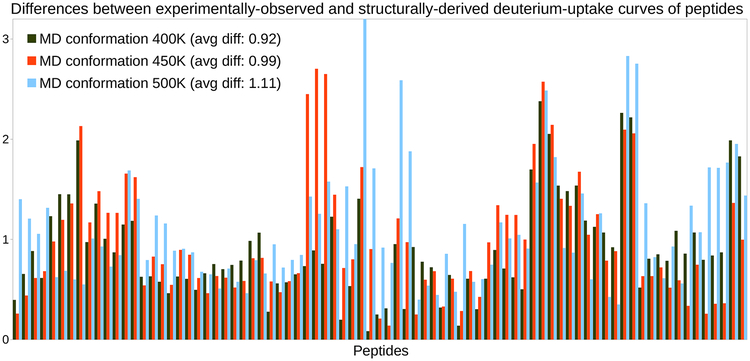
We performed four additional MD simulations of C3d, following our previous methodology (see Section 4.2.3), except for the temperature of the production stage. In this experiment, we used four different temperatures: 350 K, 400 K, 450 K, and 500 K (instead of 300 K, as in the previous experiment). From each produced trajectory, which was 200 ns long, we extracted a set of 1000 conformations at regular time steps. We then determined, in each set, which conformation provided the best estimates of C3d’s experimental HDXMS data.

Increasing the temperature to 350 K did not produce anything different from the previous MD simulations. Therefore, we report only the results achieved by the three other MD simulations (see Figure 4). From these results, it appears that increasing the temperature is not beneficial: the average differences obtained with the MD simulations at 400 K, 450 K and 500 K are 0.92, 0.99 and 1.11 respectively. An interesting outcome of this experiment is that the histograms of differences are significantly different from those of previous MD simulations (compare Figures 3 and 4). This shows that increasing temperature had the intended effect of broadening the sampling of C3d’s conformational space. This is confirmed by data on the radius of gyration, Rg, of various conformations of C3d: for the PDB conformation, Rg = 18 Å; the largest radius observed in regular MD simulations is Rg = 18.7 Å; the largest radius observed in high-temperature MD simulations is Rg = 19Å at 400 K, Rg = 19.6Å at 450 K, and Rg = 22.2Å at 500 K.

Figure 4.

Deriving HDX-MS data from high-temperature MD simulations of C3d. Histograms of differences obtained when assessing the goodness-of-fit between the experimentally-observed HDX-MS data and the HDX-MS data derived from single conformations extracted from MD simulations of C3d at 400 K, 450 K and 500 K respectively.

To sum up, increasing the temperature in MD can broaden the sampling of a protein’s conformational space. However, in this case, it did not yield a conformation from which good estimates of C3d’s experimental HDX-MS data could be derived. One reason is that, when temperature is too high, the protein starts unfolding and conformations are generated outside the native state. We recognize that increasing temperature is not the most efficient way to improve MD’s performance, and that more sophisticated variants of MD (Feixas et al., 2014; Rocchia et al., 2012) could be successful in producing a good HDX predictor for C3d. However, in this study, we chose to follow a different approach because we believe that coarse-grained conformational sampling can be a valuable alternative to all-atom simulations, such as classical (molecular mechanics) MD.

2.5. HDX Data Derived from Coarse-Grained Conformational Sampling of C3d

We argue, here, that using “coarse-grained” conformational sampling can help broaden the exploration of C3d’s conformational space in a beneficial way. Note that we use the term “coarse-grained” in its most general sense. In this context, numerous coarse-grained computational tools can be considered: MD-like methods using coarse-grained force fields (Davtyan et al., 2012), Monte-Carlo-based simulations (Boomsma et al., 2013; Sim et al., 2012), methods using elastic network models (López-Blanco and Chacón, 2016), or robotics-inspired conformational sampling methods (Al-Bluwi et al., 2012; Devaurs et al., 2013, 2015; Gipson et al., 2012), among others. Here, we use a computational tool called SIMS (Gipson et al., 2013), which combines a robotics-inspired conformational sampling method with the Rosetta modelling software (Das and Baker, 2008) (see Section 4.2.4).

We refer to the conformation produced by this experiment (cf. Section 4.2.4) as the “HDX conformation” of C3d. Indeed, this conformation provides very good estimates of C3d’s experimental HDX-MS data (see Figure 5). The average difference between experimentally-observed and structurally-derived deuterium-uptake curves across all peptides is only 0.6. Therefore, we can consider that deriving HDX-MS data from this conformation allows replicating C3d’s experimentally-observed HDX-MS data. This is the first step toward interpreting and refining this experimental data.

Figure 5.

Deriving HDX-MS data from coarse-grained conformational sampling of C3d. Histograms of differences obtained when assessing the goodness-of-fit between the experimentally-observed HDX-MS data of C3d and the HDX-MS data derived from its PDB conformation or its HDX conformation (i.e., the conformation produced by coarse-grained conformational sampling).

2.6. Examination of the HDX Conformation of C3d

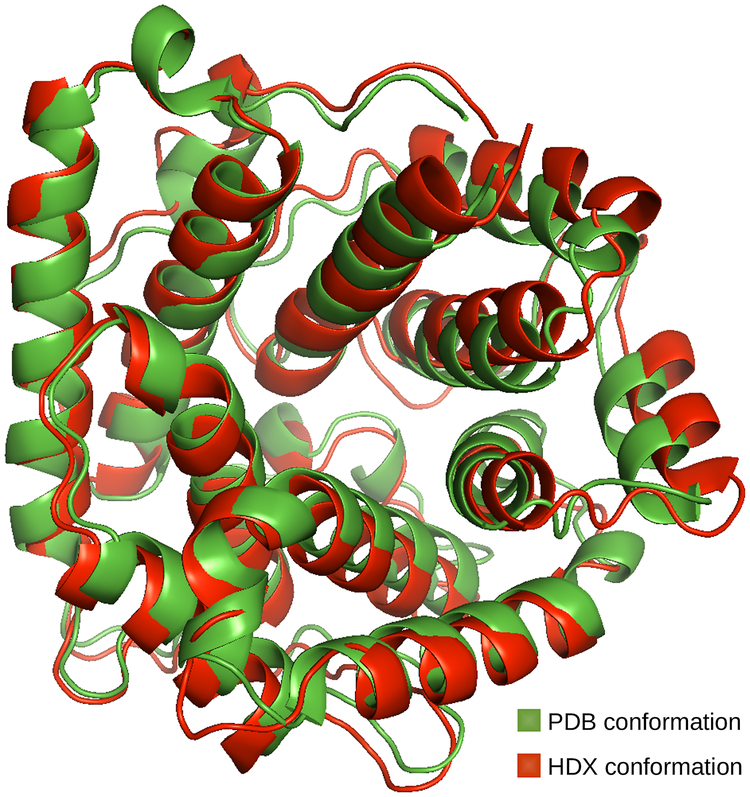
The HDX conformation of C3d, which allows replicating its experimental HDX-MS data, is very similar to the PDB conformation (see Figure 6). All the helices forming the α−α barrel are conserved in the HDX conformation, although some are slightly different: α₁ is extended from [Glu22–Thr41] to [Gly21–Thr41], α₅ is shortened from [Lys149–Ala164] to [Asp150–Ala164], α₇ is shortened from [Ser174–Asn189] to [Leu175–Asn189], α₁₀ is shortened from [Gln236–Leu253] to [Tyr238–Leu253], α₁₂ is shortened from [Ser278–Asp295] to [Thr279–Asp295], and T₁ is shortened from [Ala7–Leu13] to [Ala7–Lys11]. The disulfide bridge between Cys111 and Cys168 is also conserved. On the other hand, two small helices have disappeared (T₄ and T₅), and α₆ has been shortened from [Asp166– Gln171] to [Asp166–Glu169]. Another difference is that the α−α barrel of the HDX conformation (Rg = 19 Å) is slightly wider than the α−α barrel of the PDB conformation (Rg = 18 Å). However, we do not consider these to be significant differences.

Figure 6.

PDB and HDX conformations of C3d depicted using the ribbon model.

The HDX conformation is also similar to other crystal structures obtained for C3d itself (Bajic et al., 2013; Morgan et al., 2011; Nagar et al., 1998; van den Elsen and Isenman, 2011) or for other molecules that contain C3d as their TED (see Section 1), such as C3 (Janssen et al., 2005). This confirms that this C3d state is rather stable, in the sense that it displays little conformational variability. Indeed, comparatively to other areas of C3, and particularly its a-chain, the C3d/TED domain has typically been considered stable. The strong similarity between the HDX conformation of C3d and its crystal structures demonstrates that they all are reasonably good representations of the three-dimensional structure of C3d in solution. Therefore, these conformations may be suitable to interpret experimental data, such as results of ligand interaction analyses, which may benefit functional studies and drug development efforts.

Despite the similarity between the HDX conformation of C3d and its crystal structures, small differences exist, mostly in terms of width of the α−α barrel. We wish to stress that the HDX conformation should only be regarded as an averaged representation of C3d’s flexibility, as captured in its experimental HDX-MS data. In other words, we do not consider this conformation to be a better representation of C3d’s native state than its crystal structures. Indeed, the HDX conformation does not appear to be energetically stable. First, after performing an energy minimization of the HDX conformation, we obtained a conformation whose energy is higher than the minimized version of the PDB conformation. Second, after running an MD simulation starting from the HDX conformation, we observed that, except at the very beginning, all generated conformations were more similar to the PDB conformation than to the HDX conformation, in terms of width of the α−α barrel.

Since the experimental HDX-MS data reflects the inherent variability of a protein’s native state, a conformational ensemble describing this state would provide a better HDX prediction than a single conformation. We still believe this to be true, but only if the ensemble is a good representation of this state. Our results show that this could not be achieved for C3d by simply using MD. On the other hand, coarse-grained conformational sampling provided us with a conformation yielding good HDX predictions. Predictions could be even better if this method was used to generate conformational ensembles, but evaluating these ensembles would be too computationally-expensive. In practice, it is reasonable enough to use a single conformation for HDX prediction, instead of a conformational ensemble. The only caveat is that this conformation should not be regarded as a better representation of a protein’s native state than a conformational ensemble. It should only be considered as a mean to interpret and refine experimental HDX-MS data.

2.7. Refinement of C3d’s HDX-MS Experimental Data

A clear benefit of using the HDX prediction model we chose and a protein conformation to replicate experimental HDX-MS data is that it allows refining this data from the peptide level to the residue level. Indeed, in this HDX prediction model, the HDX-MS data is first derived from the protein’s structure at the residue level, and then aggregated at the peptide level (see Section 4.1.2). Therefore, this method provides residue-level HDX-MS information at no experimental or computational cost. Another technique was proposed to obtain residue-level information, but it requires collecting experimental HDX-MS data with high levels of redundancy, in terms of overlapping peptides (Kan et al., 2013). On the other hand, the method we use can be applied to any experimental dataset, irrespective of the level of redundancy.

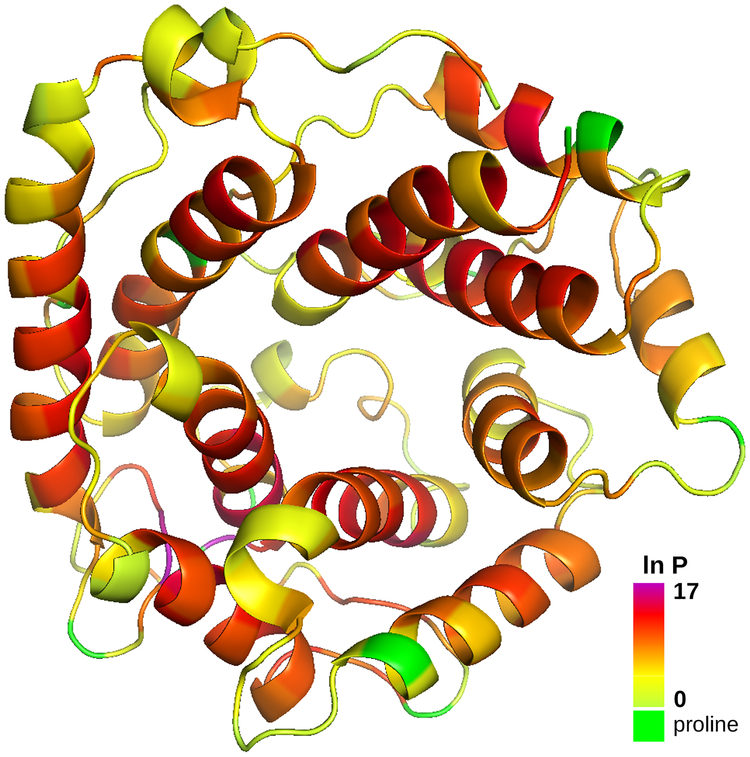
Using the HDX prediction model and the HDX conformation of C3d, we refined the peptide-level HDX-MS data reported in Table 1 into a list of protection factors for C3d’s residues. These protection factors are visualized on the HDX conformation of C3d as a heat map (see Figure 7). This is a clear improvement over the classical methodology producing such heat maps at the peptide level (Huang and Chen, 2014). Some observations derived from Figure 7 were expected: for example, helices generally benefit from higher protection factors than loop regions. On the other hand, local packing density induces an unexpected result: the highest protection factors are observed within two loop regions (Ala75, Phe76 and Ser85).

Figure 7.

Heat-map visualization of the protection factors of C3d’s residues. Protection factors are derived from, and depicted on, the HDX conformation of C3d. Prolines are coloured in green. Other residues are coloured using a spectrum corresponding to the range of protection values.

Obtaining residue-level HDX-MS data is considered highly valuable for most HDX-based applications, including ligand interaction studies. If an HDX-MS experiment is performed on a complex involving C3d and one of its ligands, refining the experimentally-observed data at the residue level and comparing it to the data obtained for C3d alone can help characterize the interaction interface or even locate key residues maintaining the complex. Moreover, comparing residue-level HDX-MS data obtained for complexes involving distinct ligands can help explain potential differences in binding affinity and engineer more potent binders during rational drug design. This may be particularly important to alleviate the possible absence of suitable co-crystal structures, or to increase the throughput in screening and hit validation.

3. Conclusions

In this paper, we have analysed the native state of the complement protein C3d. Although several crystal structures of C3d are available (Hammel et al., 2007; Nagar et al., 1998), little is known about its inherent variability in solution. To gather data that could help bridge this gap, we performed an HDX-MS experiment on C3d. As a result, we obtained deuterium-uptake curves for 86 peptides extracted from C3d. To interpret this experimental data in relation to C3d’s structure, it is imperative to have a conformation (or a conformational ensemble) of C3d from which this data can be replicated. As a crystal structure might not be the most accurate predictor for experimental HDX-MS data (Radou et al., 2014), we used various conformational sampling techniques to generate alternative conformations of C3d.

Although using a conformational ensemble produced by an MD simulation was thought to be an appropriate way to reproduce experimentally-obtained HDX-MS data (Radou et al., 2014), our study shows that this might not always be true. First, we observe that a single conformation of such ensemble can be a better HDX predictor than the whole ensemble. Second, at least in the case of C3d, there seems to be a lack of consistency between the HDX predictions obtained with different MD simulations. Third, using MD conformations yields HDX predictions that are only slightly better than when using C3d’s crystal structure. All this indicates that MD might not produce a representation of a protein’s native state that can capture its inherent variability in the same way as HDX-MS data does. This is particularly surprising for C3d because, comparatively to other regions of C3, the C3d/TED has typically been considered very stable.

As an alternative to MD simulations, we suggest using coarse-grained conformational sampling to obtain good HDX predictors. At least for the model protein C3d, such sampling could generate a conformation from which the best estimates of C3d’s experimental HDXMS data could be derived. As a result, this HDX conformation can be used to interpret the experimental data and refine it from the peptide to the residue level. Although not necessarily a better representation of C3d’s native state than crystal structures or MD-derived conformational ensembles, the HDX conformation can be regarded as an average representation of the variability of C3d’s native state that is captured in its experimental HDX-MS data. Therefore, this conformation contains valuable information that may guide structural studies or help identifying hitherto unrecognised areas of structural dynamics.

The similarity between the HDX conformation we have obtained for C3d and its crystal structures confirms the stability of its native state: it seems to display little conformational variability. Therefore, in practice, C3d’s crystal structures can be regarded as good-enough representations of its three-dimensional structure in solution. Combining this structure with the residue-level HDX-MS data we have obtained for C3d could prove extremely valuable for ligand interaction studies, with potential implications for rational drug design.

As part of our future work, we plan to investigate whether the results reported in this paper can be generalized to yield a comprehensive HDX prediction and refinement methodology. More specifically, we will examine whether coarse-grained conformational sampling is generally better than MD at producing conformations that are good HDX predictors. We will evaluate our methodology on several proteins. We envision several applications for an accurate HDX prediction method. First, it would allow evaluating the consistency between crystallographic and HDX-MS data, in cases where it is not certain whether both datasets correspond to the same protein state. Second, if a protein’s native state is described in the PDB, and if only HDX-MS data is available for another (non-native) protein state, it would be possible to obtain a structural model of this non-native state. Finally, the possibility to refine HDX-MS data from the peptide to the residue level will benefit all the applications of the HDX-MS technique itself (Pirrone et al., 2015).

4. Methods

In the Methodological Background, we outline general concepts underpinning the HDX-MS experimental technique, and we introduce the HDX prediction model chosen for this study. Then, in the Experimental Methods, we present the specific details of our experimental and computational methodology.

4.1. Methodological Background

4.1.1. Hydrogen/Deuterium Exchange Detected by Mass Spectrometry (HDX-MS)

Hydrogen/Deuterium exchange (HDX) is a chemical phenomenon in which hydrogen atoms of proteins are exchanged with deuterium atoms in the surrounding solvent (Engen et al., 2011). As the mass of deuterium is about twice the mass of hydrogen, HDX can be monitored by Mass Spectrometry (MS): the amount of deuterium incorporated in a protein, which is referred to as deuterium uptake, corresponds to an increase in mass. In HDX-MS experiments, only the exchange of amide hydrogens (i.e., hydrogens attached to backbone nitrogens) is monitored (Engen et al., 2011). Therefore, HDX-MS experiments are interpreted on the basis of a single measurement per amino acid, for all amino acids of a protein, except for proline residues and for the N-terminus because they do not possess an amide N–H group.

The HDX rates of amino acids can vary up to several orders of magnitude, depending on pH and temperature (Brier and Engen, 2008). The HDX rate of an amino acid in an unstructured peptide is only affected by its neighbours; this “intrinsic” HDX rate, denoted by k^int, can be predicted (Bai et al., 1993; Connelly et al., 1993). The HDX rate of an amino acid in a protein is influenced by additional factors, such as solvent accessibility and protein structure; this HDX rate, denoted by k^obs, is the one that is observed experimentally (Wei et al., 2013). The extent to which amide hydrogens of a protein are protected from being exchanged can be quantified by defining the protection factor of every amino acid i as $P_i=k_i^{\text{int}}/k_i^{\text{obs}}$.

At the beginning of an HDX-MS experiment, the protein is equilibrated in H₂O at room temperature under physiological conditions (pH close to 7). To start the HDX reaction, the protein is then diluted with excess D₂O. At several time points, the reaction is quenched in a solution sample by bringing the pH down to 2.5, and the temperature down to 0°C. Proteins in the sample are digested using pepsin, which is active at acidic pH and generates numerous peptides typically 6–20 amino acids long. The sample is then introduced into a chromatography system that separates the peptides and sends them into a mass spectrometer. The MS analysis identifies the peptides and quantifies their deuterium uptake. As this analysis is repeated at several time points, an HDX-MS experiment produces deuterium-uptake kinetic curves for various peptides (Huang and Chen, 2014). Additionally, as the maximum number of deuterium atoms that can be incorporated by a peptide is known, results are usually reported as fraction of deuterium uptake, instead of “absolute” deuterium uptake.

An important aspect of HDX-MS experiments is that, because sample analysis is performed in H₂O solution, some deuterium atoms incorporated by the peptides are exchanged back to hydrogens. This phenomenon, known as back-exchange, can be detrimental if deuterium in amide groups start reverting to hydrogen. This is why digestion and MS analysis have to be performed rapidly. As back-exchange of amide groups cannot be totally avoided, it has to be accounted for in the analysis of deuterium-uptake curves: if the HDX rate of a peptide is considered as the average rate of its amino acids, the first two amino acids in the chain have to be ignored because they systematically undergo back-exchange (Huang and Chen, 2014; Konermann et al., 2011).

4.1.2. Hydrogen/Deuterium Exchange Derived from Protein Structure

The levels of HDX undergone by different parts of a protein are known to be influenced by the protein’s three-dimensional structure. Several theoretical models have been proposed to define a relationship between a protein’s conformation and HDX data, but none of them has been widely accepted by the scientific community (Skinner et al., 2012). Among these models, we chose to use the one that performed best in a recent comparative study (Skinner et al., 2012). This model relies on the definition of a phenomenological expression approximating the protection factors of the protein’s residues (Vendruscolo et al., 2003). Since its conception, this model has been applied in several studies (Best and Vendruscolo, 2006; Gsponer et al., 2006; Kieseritzky et al., 2006; Radou et al., 2014; Tartaglia et al., 2007).

The theoretical model is based on the assumption that protection from HDX arises from the involvement of amide groups in hydrogen bonds and from the packing density of atoms around amides. More specifically, given a conformation C, the protection factor of residue i, P_i(C), can be derived from the phenomenological expression

$$\text{ln\hspace{0.17em}}{P}_i\left(C\right)={\beta }^{\text{h}}{N}_i^{\text{h}}\left(C\right)+{\beta }^{\text{c}}{N}_i^{\text{c}}\left(C\right)$$ (1)

where $N_i^{\text{h}}\left(C\right)$ is the number of hydrogen bonds involving the amide group of residue i, and $N_i^{\text{c}}\left(C\right)$ is the number of atom contacts (quantifying packing density) involving residue i. Parameters β^h and β^c have been estimated by fitting experimentally-determined HDX data of various proteins: β^h = 2 and β^c = 0.35 (Best and Vendruscolo, 2006). The number of hydrogen bonds, $N_i^{\text{h}}\left(C\right)$, is defined as the number of main-chain oxygens in any residue (excluding residues i − 2,…, i + 2) within a cutoff distance of 2.4Å from the amide hydrogen of residue i. The number of atom contacts, $N_i^{\text{c}}\left(C\right)$, is the number of heavy atoms (i.e., non-hydrogens) in any residue (excluding residues i − 2,…, i + 2) within a cutoff distance of 6.5Å from the amide hydrogen of residue i. Note that, instead of being derived from a single conformation, protection factors can be computed as ensemble averages over a set of conformations, such as a conformational ensemble produced by an MD or Monte Carlo simulation (Best and Vendruscolo, 2006; Vendruscolo et al., 2003).

Using the protection factors derived from (1), one can generate deuterium-uptake curves of peptides that can be compared to experimentally-obtained HDX-MS data. For that, we first assume that a residue’s deuterium uptake follows pseudo-first-order kinetics (Brier and Engen, 2008; Huang and Chen, 2014; Konermann et al., 2011). Since $P_i=k_i^{\text{int}}/k_i^{\text{obs}}$, the fraction of deuterium incorporated by residue i at time t is thus

$$d_i\left(t\right)=1-\text{exp}\left(-k_i^{\text{obs}}t\right)=1-\text{exp}\left(-\left(k_i^{\text{int}}/P_i\right)t\right)$$ (2)

where $k_i^{\text{int}}$ rates are known. Then, the deuterium uptake of peptide j can be considered as an average over the residues it contains (Radou et al., 2014). Note that we systematically exclude from the average the first two amino acids of the peptide because of back-exchange.

4.2. Experimental Methods

4.2.1. HDX-MS Experiment

Human purified C3d (0.25 mg/mL) was expressed in E. coli, as described in other work (Hammel et al., 2007). Deuterium oxide (99.9 atom % D; 151882) was obtained from Aldrich (St. Louis, MO). Tris(2-carboxyethyl)-ohosphine hydrochloride (TCEP-HCl; 20491) and immobilized pepsin (20343) were from Thermo Scientific (Rockford, IL). Guanidine hydrochloride (> 99.5% purity; BP178–500), acetonitrile (99.9%; A998) and formic acid (> 99.5% purity; A117) were purchased from Fisher (Fair Lawn, NJ).

C3d’s peptides (2 pmol) were analysed in data-dependent acquisition (DDA) mode. Precursor ions were acquired in the m/z 300–1500 Da range using a top 3 method and MS/MS scans of the fragment ions were acquired in the m/z 100–1200 Da range. The total cycle time was 3.8 sec and ions selected for fragmentation were excluded for 20 sec. UPLC parameters were as described below. Peptide identification took place in ProteinLynx Global Server™ (version 3.0.2, Waters) using 10 ppm peptide tolerance and 0.8 Da fragment tolerance.

For the labelling experiment, 4 μL of purified C3d (0.2 μg/μL in PBS; 10 mM Na₂HPO₄, 1.8 mM KH₂PO₄, 2.7 mM KCl and 137 mM NaCl, pH 7.5) was mixed with 40 μL of deuterated PBS at 24±0.5°C. Samples were quenched at 10, 30, 100, 300, 1000, 3000 and 10000 sec using an equal volume (44 μL) of pre-chilled guanidinium hydrochloride-TCEP (3.2 M and 0.8 M, respectively) at a final pH 2.4. Samples were incubated on ice for 2 min prior to LC-MS analysis. Non-deuterated samples were prepared similarly in protiated PBS; fully-deuterated samples were prepared by incubating the protein for 48 h at 37±0.5°C. Samples were prepared and analysed in duplicate using a Synapt G2S ESI-QToF (Waters) mass spectrometer with MassLynx™ 4.1 (SCN 916, Waters). Spectra were acquired in the positive ion mode. Leu-Enk was co-infused as a lock spray standard. Chromatographic separation took place on a nano-Acquity UPLC system with HDX technology (Waters). Quenched samples were injected on an Acquity UPLC R BEH C18 VanGuard Pre-column (130 Å, 1.7 μm, 2.1×5 mm, Waters P/N 186003975). Peptides were generated upon online digestion (3 min at 300 μL/min using 0.23% v/v formic acid) of C3d using immobilized pepsin. They were separated on an Acquity UPLC R BEH C18 analytical column (130 Å, 1.7 μm, 1×100 mm; 186002346, Waters). Chromatographic parameters were: flow rate at 40 μL/min; solvents A (0.23% v/v formic acid) and B (0.23% v/v formic acid in acetonitrile). Solvent B was ramped from 3% to 10% in 0.2 min, to 38.5% in 19.8 min, to 90% in 2 min, and then kept at 90% for 2 min before re-equilibrating to initial conditions. Data processing took place in DynamX (version 2.0, Waters).

4.2.2. HDX Data Derived from Crystal Structures

Using the model described in Section 4.1.2, we derived HDX-MS data from the conformation of C3d reported in the PDB (i.e., 2GOX). More precisely, we calculated the fraction of deuterium uptake at all experimental time points for the 81 peptides retained for analysis (see Section 2.1). We then compared this data to the experimentally-obtained data reported in Table 1. To assess the goodness-of-fit between structurally-derived and experimentally-observed HDX-MS data, we constructed a histogram of differences by computing, for every peptide j, the error ${\displaystyle {\sum }_{t\in T}\left|D_j^{\text{der}}\left(t\right)-D_j^{\text{obs}}\left(t\right)\right|}$, where T is the list of experimental time points, $D_j^{\text{der}}\left(t\right)$ is the structurally-derived deuterium uptake at time t, and $D_j^{\text{obs}}\left(t\right)$ is the experimentally-observed deuterium uptake at time t. Note that this histogram can be aggregated into an average difference over all peptides.

4.2.3. HDX Data Derived from MD simulations

All MD simulations were performed with the GROMACS v4.6.5 package (Pronk et al., 2013) using the GROMOS96 (53a6) force field and the SPC water model. A cubic box was defined with at least 9Å of liquid layer around C3d’s structure (for a total of 15052 water molecules), with periodic boundary conditions. Sodium (Na⁺) and chloride (Cl⁻) counter-ions were added to neutralize the system, with a final concentration of 0.15 mol/L. The algorithms v-rescale (with tau-t = 0.1 ps) and parrinello-rhaman (with tau-p = 2 ps) were used for temperature and pressure coupling, respectively. A cutoff value of 1.2 nm was used for both the van der Waals and Coulomb interactions, with Fast Particle-Mesh Ewald electrostatics (PME).

The production stage of each MD simulation is preceded by (i) three steps of Energy Minimization (EM) and (ii) eight steps of Equilibration (EQ). The first EM step is conducted using the steepest-descent algorithm and position restraints on C3d’s heavy atoms (5000 kJ⁻¹mol⁻¹nm⁻¹), allowing relaxation of the solvent only. The second EM step involves the same algorithm, but no restraint. The third EM step uses the conjugate-gradient algorithm, without restraint, to further relax the protein. The EQ phase starts at a temperature of 310 K, which is maintained for 300 ps, applying position restraints on C3d’s heavy atoms (5000 kJ⁻¹mol⁻¹nm⁻¹). This step allows solvation layers to form without affecting C3d’s folding. Temperature is then reduced to 280 K, and position restraints are gradually reduced. This process is followed by a progressive temperature increase, up to 300 K. Together, these EQ steps constitute the first 500 ps of each MD simulation. During the production stage, the system is not subjected to any restraint, and temperature remains constant at 300 K.

All MD simulations were run on a single node of our local High-Throughput Computing cluster. Such node includes two octo-core Intel E5–2650v2 Ivy Bridge EP processors (2.6 GHz), for a total of 32 threads, sharing 32 GB of memory. The performance of an MD simulation of C3d on this architecture is approximately 29 ns/day. We initially ran three MD simulations of C3d and obtained trajectories of 100 ns in length, which is the length of the MD performed in (Radou et al., 2014). Then, we extended one of these simulations to 300 ns. Finally, we performed four additional MD simulations of 200 ns in length, using increasing temperatures for the production stage: 350 K, 400 K, 450 K, and 500 K. From each MD simulation, we extracted a set of 1000 conformations at regular time steps along the trajectory. Using the HDX prediction model described in Section 4.1.2, we derived HDX-MS data from each MD conformational ensemble. First, protection factors of residues were calculated as averages over the conformational ensembles. Then, within each ensemble, we determined which conformation would provide the best estimates of C3d’s experimental HDX-MS data.

4.2.4. HDX Data Derived from Coarse-Grained Conformational Sampling

In this work, we used a computational framework developed to explore a protein’s conformational space: Structured Intuitive Move Selector (SIMS) (Gipson et al., 2013). This framework integrates robotics-inspired sampling algorithms with the Rosetta modelling software (Das and Baker, 2008). SIMS follows a “coarse-grained” approach: the representation of a protein involves only backbone dihedral angles; this representation is manipulated in a multi-resolution fashion during sampling. Starting from the PDB conformation of a protein, SIMS can iteratively generate an ensemble of low-energy conformations by perturbing previously-generated conformations. Typical perturbations include dihedral angle rotation, loop closure and others. In this experiment, SIMS was run for five days on four threads of a 3.6 GHz Intel i7–4790 quad-core CPU. Then, from the produced conformational ensemble, we determined which conformation would provide the best estimates of C3d’s experimental HDX-MS data.