Abstract
Neutrophils display rapid and potent innate immune responses in various diseases. Tumor-associated neutrophils (TANs) however either induce or overcome immunosuppressive functions of the tumor microenvironment through complex tumor-stroma crosstalk. We developed a mathematical model to address the question of how phenotypic alterations between tumor suppressive N1 TANS, and tumor promoting N2 TANs affect nonlinear tumor growth in a complex tumor microenvironment. The model provides a visual display of the complex behavior of populations of TANs and tumors in response to various TGF-β and IFN-β stimuli. In addition, the effect of anti-tumor drug administration is incorporated in the model in an effort to achieve optimal anti-tumor efficacy. The simulation results from the mathematical model were in good agreement with experimental data. We found that the N2-to-N1 ratio (N21R) index is positively correlated with aggressive tumor growth, suggesting that this may be a good prognostic factor. We also found that the antitumor efficacy increases when the relative ratio (Dap) of delayed apoptotic cell death of N1 and N2 TANs is either very small or relatively large, providing a basis for therapeutically targeting prometastatic N2 TANs.
Introduction
Lung cancer is the leading cause of cancer mortality worldwide, with an approximate 1.6 million deaths each year [1]. The most common (∼85%) form of lung cancer in patients is non-small cell lung cancer (NSCLC), of which lung squamous cell carcinoma (LUSC) and lung adenocarcinoma (LUAD) are the most common subtypes [2]. Various groups of myeloid cells have been known to promote tumor development by direct inhibition of immune responses [3], as well as by secreting growth factors, angiogenic factors, or matrix-degrading enzymes [4, 5]. For example, tumor-associated macrophages (TAMs), also known as M2 macrophages [3], have been shown to promote tumor growth [6, 7]. There is growing evidence suggesting that neutrophils play a major role in tumor progression from establishment of tumor formation and throughout the progression to the malignant state [8–12]. For example, tumor associated neutrophils (TANs) have been associated with poor prognosis in many cancers including metastatic melanoma [13], bronchoalveolar carcinoma [14], and renal carcinoma [15]. Like TAMs, TANs infiltrate tumor tissue and can have two differential states in cancer progression [8, 9, 16]: (i) an antitumorigenic role (called N1) (ii) promoting tumor progression (called N2). How these two phenotypes are regulated is largely unknown but many experimental and clinical findings suggest the significant potential of therapeutic targeting of the prometastatic role of TANs [17].
TGF-β has been identified as a major cytokine within a tumor that skews neutrophil differentiation toward the N2 phenotype [16, 18, 19], while TGF-β blockade and type-1 IFN (α, β, ω) treatment are known to shift the balance toward the N1 phenotype [20, 21]. IFN-β in tumor microenvironment can directly suppress tumor growth [22] by interacting with p53 [23–25]. IFN treated neutrophils were shown to upregulate PD-L1 and suppress T-cell proliferation [26]. After binding to interferon receptor type 1, IFNAR1 and IFNAR2, Type 1 IFN-β signals through TYK2 and JAK1, which in turn phosphorylate STAT family members (STAT1, STAT2, STAT3, and others) and activate its downstream functions to stimulate anti-tumor activities [27]. For example, vesicular stomatitis virus expressing IFN-β was shown to enhance anti-tumor immune responses in a murine model of NSCLC [28]. It is well established that cancer associated fibroblasts (CAFs) can promote tumor growth, aggressive invasion, and metastasis through mutual interaction in the tumor microenvironment [29, 30]. Fibroblast-secreted IFN-β was also able to restrict expression of the p53 RNA stabilizer, WIG1, and bring down mutant p53 RNA levels, thus suggesting an alternative therapeutic agent for mutant p53 positive lung cancer patients [31]. There are multiple levels of crosstalk between neutrophils and many cells including other immune cells and Th17 cells [32]. Neutrophils may express many important factors such as IL-6, IL-17A, IL-17F and IFNγ [33]. How neutrophils are induced by a tumor is still poorly understood. It is well known that tumor cells interact with stromal cells such as fibroblasts, immune cells (neutrophils, macrophages, Th17, Tregs, T cells), and cytokines in the tumor microenvironment, and that these complex interactions play a critical role in tumor initiation, growth, angiogenesis, and metastasis. The mutual interactions between a tumor and immune system involving TANs are summarized in Fig 1 with references in Table 1.
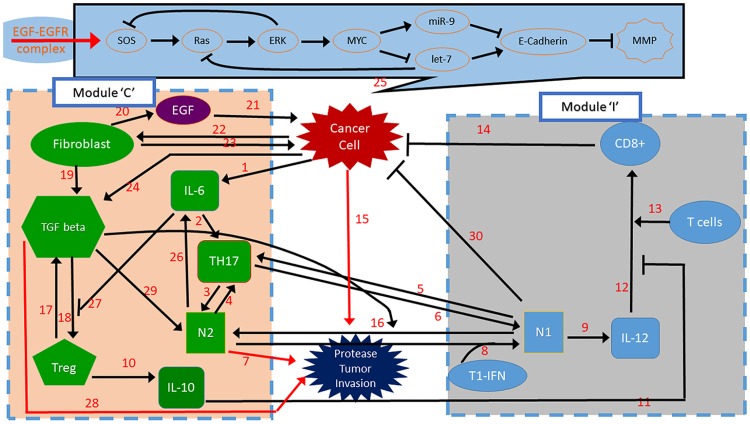
Fig 1. A schematic of tumor-microenvironment interaction.
(Top) A signaling pathway for lung cancer. (Bottom) Network of interactions between cells involved (cancer cells, fibroblasts, Th17 cells, N1 cells, N2 cells, CD8+ T cells, Tregs) and cytokines and growth factors (EGF, IL-6, IL-10, IL-12, MMPs, TGFβ). By convention, the kinetic interpretation of solid arrows and hammerheads in the interaction network represents induction (arrow) and inhibition (hammerhead), respectively. The module on the left and right will be represented by a module ‘C’ and ‘I’, respectively, in our simplified mathematical model. References for each interaction (number on the arrow or hammerhead) are provided in Table 1.
Table 1. Summary of interaction networks (Fig 1) in invasion processes in lung cancer development.
| # | Description | References |
|---|---|---|
| 1 | cancer cells secrete IL-6 | [157] |
| 2 | In combination with TGF-beta, IL-6 promotes the differentiation of Th17 cells by activating transcription factors including retinoic acid-related orphan receptor RORγt and RORα | [158–160] |
| 3 | IL17 can indirectly induce the recruitment of neutrophils. | [32, 102] |
| 4 | Neutrophils secrete chemokines that can mediate the recruitment of Th17 cells and. secrete IL-17 | [33, 102] |
| 5, 6 | IL17 can indirectly induce the recruitment of neutrophils | [32] |
| 7 | Neutrophils release TIMP-free MMP-9, MMP infiltration supplies MMP-9, Intravenous co-injection of mammary adenocarcinoma cells and neutrophils significantly raises lung metastases, N2 phenotype induces angiogenesis, invasion and metastasis, and maintain immunosuppression [161] | [161, 161–166] |
| 8 | Type I IFNs (or IFNbeta) induce anti-tumor polarization, N2 TAN, in mice and human | [20, 21] |
| 9 | Neutrophils secrete/induce IL-12 | [97, 99, 167] |
| 10, 11 | Tregs can inhibit tumor-specific CD8+ (54) and CD4+ (55) T cell effector functions through IL-10 | [168–173] |
| 12, 13 | N1 Neutrophils promote recruitment and activation of CD8(+) cells by producing cytokines (IL-12, TNFα, GM-CSF, VEGF) | [97] |
| 15, 23 | Cancer associated fibroblasts (CAFs) promote tumor growth, aggressive invasion, and metastasis | [29, 30] |
| 16 | TGF-β within the tumor microenvironment induces TAN with a pro tumor phenotype. TGF-β blockade results in the recruitment and activation of TANs with an anti tumor phenotype | [16, 18, 19] |
| 17 | Tregs can inhibit tumor-specific CD8+ (54) and CD4+ (55) T cell effector functions through TGFβ | [168–174] |
| 18 | TGF-β induces Foxp3+ T-reg from CD4+CD25 | [160, 161, 175–177] |
| 19 | CAF secretes TGF-β and VEGF for Treg induction | [177, 178] |
| 20, 21 | CAF secretes EGF, which in turn promotes tumor growth and invasion | [41, 47, 64, 152, 178, 179] |
| 22, 23 | Lung cancer cells recruit CAFs and CAFs induce tumor growth, chemoresistance, angiogenesis, metastasis | [178] |
| 24 | Cancer cells change tumor microenvironment by secreting TGF-β | [178] |
| 25 | RAS-let-7-miR-9 signaling network induce lung cell invasion | [180–187] |
| 26 | N2 TANs expressed TGFbeta and IL-6 | [8, 103, 104, 188] |
| 27 | IL-6 inhibits the generation of Treg cells and induces production of IL-17 | [160] |
| 28 | IL-6 enhanced epithelial cell EMT and stimulated tumor progression by enhancing TGFβ signaling. IL-6 and TGFβ plays a central role in regulation of the paracrine loop between these two cytokines in LSCLS, TGFβ exposure induces EMT in CSCs and non-CSCs | [189, 190] |
| 29 | “Neutrophils are driven by transforming growth factor-β (TGFβ) to acquire a polarized, pro-tumoural N2 phenotype (characterized by high levels of arginase expression).” | [33] |
| 30 | Neutrophils have cytotoxic mediators for tumor cell killing such as TNF-α, IL-1β, and IFNs | [161, 191] |
In this work, we employed the framework of the differential equation model in order to take into account the role of N1 and N2 TANs in the regulation of tumor-neutrophil interactions and tumor growth. Based on a schematic diagram in Fig 2, the model consists of a system of ordinary and delay differential equations involving the following variables:
TGF-β and IFN-β play a central role in the critical transition between N1 and N2 TANs, resulting in either tumor-promoting or tumor-suppressing microenvironment. We summarize in Fig 3 the fundamental, phenotypic spectrum underlying how the oncogenic and tumor suppressive properties of TANs arise in relation to TGF-β, IFN-β, and delayed apoptotic cell death mechanisms. This model is then used (i) to investigate how TGF-β and IFN-β regulate the balance between N1 and N2 phenotypes by complex mutual interactions, (ii) to investigate how up- or down-regulation of these N1 and N2 phenotypes affect tumor growth and anti-tumor efficacy in the absence and presence of delayed apoptotic cell death mechanisms, and (iii) to develop optimal strategies of the combination therapy with TGF-β inhibitor and IFN-β.
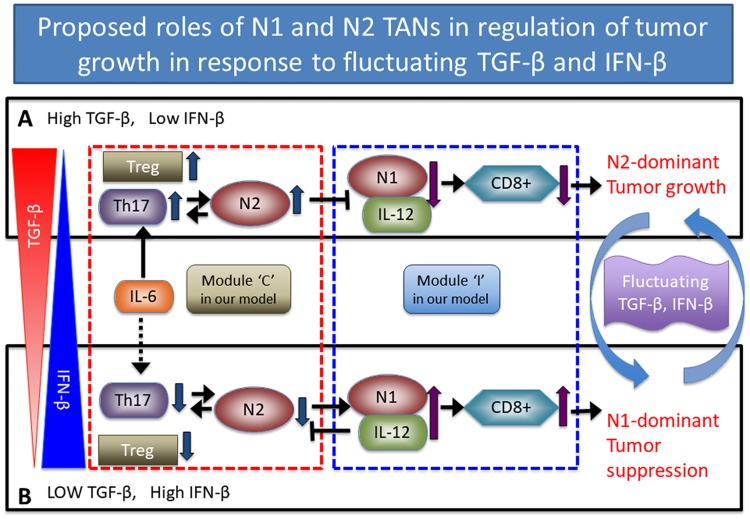
Fig 2. Proposed role of N1 and N2 complexes in the regulation of tumor growth and immune-suppression in response to fluctuating TGF-β and IFN-β.
The phenotypic balance between N1 and N2 complexes determines tumor growth or suppression in response to TGF-β (red triangle on the left) and IFN-β (blue triangle on the left). (A) High TGF-β levels and low IFN-β activities induce Treg infiltration which in turn leads to biochemical suppression of the overall anti-tumor immune activities of T cells. TGF-β also modifies the tumor microenvironment by transforming N1 into N2 TANs [8, 34] while IFN-β brings the N2 phenotype back to the N1 phenotype [8]. This N2-dominant microenvironment leads to enhanced tumor growth. (B) Low TGF-β levels and upregulation of IFN-β reduce the phenotypical transition from N1 to N2 TANs and leads to upregulation of immune activities of T cells and N1 TANs, leading to suppression of tumor growth. Schematic components of the N2/Th17/Treg complex and the N1/IL12/CD8+ complex are represented by modules ‘C’ (box with the red dotted line) and ‘I’ (box with the blue dotted line) in our theoretical framework. Blue arrows on the right indicate the switching behavior between a tumor-promoting mode in (A) and the tumor-suppressive state in (B) in response to fluctuating TGF-β and IFN-β levels.
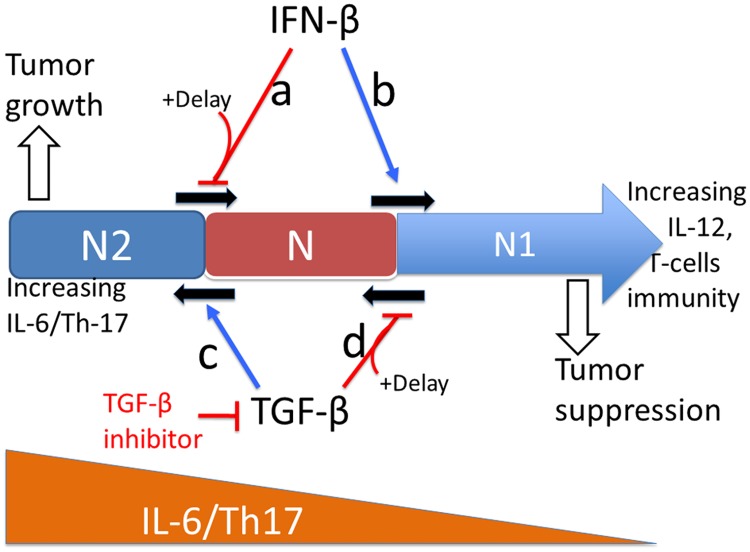
Fig 3. Tumor suppressive and tumor promoting roles of TGF-β and IFN-β respectively in the tumor microenvironment.
As the CD8+ cytokines (IL-12) increase, differentiation of N cells transits to the N1 phenotype. There are three ways that IFN-β, TGF-β inhibitor, and delayed apoptotic pathways can keep the system in the safe-guard immune N1 zone. (Cases a, b) Increasing IFN-β levels induces the transition from N2 to N1-zone (case b) [22–25, 35–37]. The delayed apoptotic cell death of N2 TANs suppresses entry into the transition phase (case a). (Cases c, d) As the IL-6 level is increased (to the left), the tumor-promoting phenotype, N2, becomes dominant and TGF-β promotes the exit from the transition zone to enter the N2-zone (case c) [35]. The TGF-β inhibitor can reverse the phenotype back to the N1 microenvironment [38]. The delayed apoptotic cell death of N1 TANs suppresses entry into the transition phase (case d).
Materials and methods
Mathematical model
N1 module and N2 complex
In this work, we assume: (i) High levels of TGF-β and IL-6 induce upregulation of the N2 complex [8, 34]. (ii) High IFN-β levels induce upregulation of the N1 phenotype [8]. (iii) Cells in the N1 and N2 complex have natural decay at rates μN1, μN2, respectively. (iv) Those factors in (i) and (ii) determines the critical transition between N1 and N2 complexes [35], determining either promotion or suppression of tumor growth.
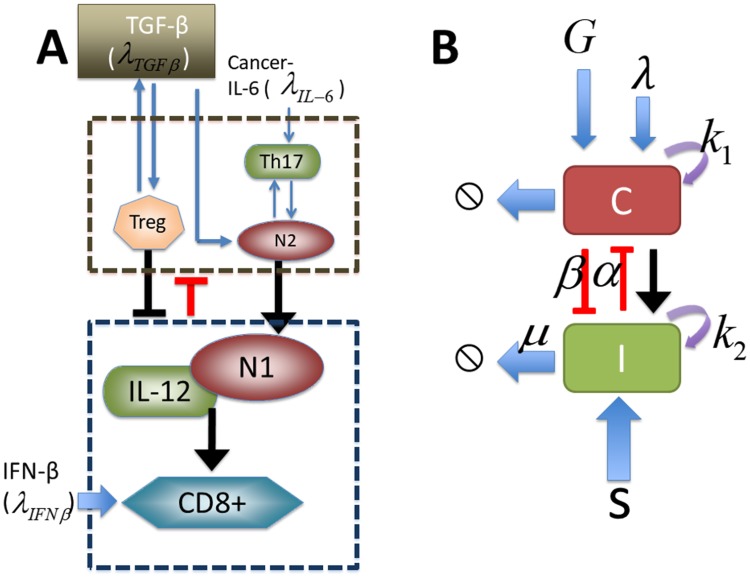
In order to incorporate the signaling network into a mathematical model we simplified the network shown in Fig 4A as follows: We merged the N2 regulatory network among Treg, Th17 and N2 cells into one component (N2 complex; brown dashed box in Fig 4A) while we merged the immune regulatory network of N1 cells, IL-12 and CD8+ (N1 complex; blue dashed box in Fig 4A) in a separate module. The mathematical model network is shown in Fig 4B. By convention, the kinetic interpretation of solid arrows and hammerheads in the signaling network represents induction (arrow) and inhibition (hammerhead), respectively.
Fig 4. A schematic of our mathematical model.
Let the variables N2(t) and N1(t) be activities of the N2 complex and N1 module, respectively, at time t. The scheme includes autocatalytic activities of the N2 complex (N2) and N1 complex (N1), removal of those key cells in the tumor microenvironment, mutual inhibition between those two modules, and clearance/decay of those complexes.
The mass balance (or conservation of mass) of a physical variable states that the rate of change of this quantity is the sum of contributing factors such as an input factor with the positive sign and an output factor with the negative sign. Therefore, the mass balance of the densities of the N2 module (N2) and N1 module (N1) leads to a system of ordinary differential equations (ODEs) as follows:
| (1) |
| (2) |
The first term in Eq (1) represents the signaling from N2-promoting molecules such as IL-6 and TGF-β. Similarly, the first term in Eq (2) represents the signaling from N1-promoting molecules such as IFN-β. The third terms in Eqs (1) and (2) indicate natural decay/consumption of N2 and N1 complexes, respectively. The second term in Eq (1) represents autocatalytic enhancement of the N2 module (numerator) with inhibition from the N1 module (denominator). The second term in Eq (2) is defined in a similar fashion. In more detail, f1(λIL−6, g) is a positive function that represents the signaling pathways from cancer-induced IL-6 (λIL−6) and cancer-induced TGF-β (g) to the N2 module, f2(s) is a function that represents the signaling pathways from IFN-β (s) to the N1 complex, a1, a2 are the autocatalytic enhancement parameters for the N2 and N1 modules, respectively, a3, a5 are the Hill-type inhibition saturation parameters from the counter part of N2 and N1 complex, respectively, a4 is the inhibition strength of the N2 complex by the N1 TANs, a6 is the inhibition strength of the N1 module by the N2 module, and finally μN2, μN1 are the clearance/death rate of N2 and N1 complexes, respectively.
As indicated in Eq (1), the signals λIL−6 and g increase the rate of N2 activation through the function f(λIL−6, g) in the first term, while N1-dependent inhibition of the N2 complex is expressed through the function F(N1) in the denominator of the second term. A simple requirement of these functions is that the function has to be an increasing function of the factor molecules. For example, the signaling function of the N2 complex (f1(λIL−6, g)) increases as the signaling of IL-6 (λIL−6) and TGF-β (g) increases, and the inhibition strength of the N2 complex by the N1 complex, F(N1), increases as the N1 population (N1) increases. In other words, for all non-negative λIL−6 and g, and for all non-negative N1. Similarly, the first term f2(s) on the right-hand side of Eq (2) represents an increase in N1 activity induced by the signal s, and N2-dependent suppression of N1 activity is explored through the function H(N2) in the denominator. The signaling function of the N1 complex (f2(s)) increases as the signaling of IFN-β (s) increases, and the inhibition strength of N1 complex by N2 complex, H(N2), increases as the N2 population (N2) increases. In other words, for all non-negative s, N2. Based on biological observations (Fig 4A), we assume that
| (3) |
where λTGF−β is the TGF-β-induced signal rate and λIFNβ is the IFN-β -induced signal rate.
After performing the following non-dimensionalization
| (4) |
from the dimensional Eqs (1)–(3), we obtain the associated dimensionless equations for N2 (C) and N1 (I) complexes with a set of essential control parameters:
| (5) |
| (6) |
Tumor volume (T(t))
As we discussed above, neutrophils play either tumorigenic or anti-tumorigenic roles in response to various biochemical signals such as TGF-β and IFN-β in a complex microenvironment. While N1 TANs kill tumor cells [8], N2 TANs promote tumor growth [8, 35]. Therefore, tumor growth and tumor cell killing are promoted or suppressed by relative balance between N1 and N2 TANs [8], which, in our model, is determined by dichotomous polarization of neutrophils (either N2 TANs (C) or N1 TANs (I)) in Eqs (3)–(6) in response to microenvironmental signals such as IL-6 (λ), TGF-β (G) and IFN-β (S). Gompetz growth, logistic growth, and other nonlinear growth curves have been suggested to fit to the experimental data on tumor growth [39]. Logistic growth in the absence and presence of growth factor-mediated enhancement of tumor growth has been observed in experiments [40–44] and mathematical models were successfully applied to predict these experimental results [7, 40–51]. We assume that (i) the tumor grows at a basic rate r in the absence of promotion of N2 TANs (C) and tumor cell killing by N1 TANs (I), following logistic growth, (ii) tumor growth is enhanced in a N2-mediated tumor microenvironment, (iii) anti-tumorigenic N1 TANs kill the tumor cell at a rate δ. In particular, the N2-mediated enhancement of tumor growth is modeled by a fraction of the N2 phenotype (C) relative to the N1 phenotype (I) in tumor microenvironment:
where K, γ1 are the inhibition parameters of N2-mediated growth.
The mass balance of the tumor volume (T) leads to an ordinary differential equation as follows:
| (7) |
where r is a growth rate of the tumor and T0 is the carrying capacity of the tumor population.
All simulations were performed using Matlab (Mathworks) for ordinary differential equations (ode45) and delay differential equations (dde23).
Parameter estimation
μN1, μN2: Neutrophil turnover in blood is quite rapid [52]. The half-life of neutrophils within the circulation (T1/2) was reported to be 3.2 hours in rabbits [53, 54], 11.4 hours in mice [55], and 7-10 hours in humans [56, 57]. On the other hand, the measured half-life in in vivo experiments [58] was measured to be longer: 90 h in vivo experiments [59], 20.3 in neutropenia patients [60], and 17.3 h in terminal cancer patients with glioblastoma and chronic lymphocytic leukemia [61]. For example, Andzinski et al. [62] recently reported that the life span of TANs can be remarkably prolonged in tumor microenvironment where IFN-β activity is suppressed [63]. Based on these biological observations in the tumor microenvironment, neutrophils in tumor tissue, we take the half-life of about T1/2 = 20 h. In general, we can obtain the decay rate of a variable when we know the half-life. In more detail, by solving a typical differential equation of the form with an initial condition y(0) = y0 and a delay rate λ, and comparing the solution y(t) = y0e−λt at t = T1/2, we can obtain the decay rate . This calculation then leads to . We also take μN1 = μN2.
μG: The decay rate of TGF-β was estimated to be 8.02 × 10−6 s−1 = 2.89 × 10−2 h−1 = 6.929 × 10−1 day−1 [7, 41, 47, 64]. Thus, dimensionless μG = 2.89 × 10−2 h−1/(0.035h−1) = 0.826.
μL (decay rate of TGF-β inhibitor): The half-life of galunisertib, TGF-β inhibitor, was measured to be 0.53 h in rat, 0.3 h in mice, 2.26h in dogs [65]. We take μL = 3 h, leading to μL = ln(2)/(3h) = 2.31 × 10−1 h−1. Thus, dimensionless μL = 2.31 × 10−1 h−1/(0.035h−1) = 6.6.
μS (decay rate of IFN-β): The serum half-life of IFN-β ranges from minutes to hours depending on biological conditions of its receptors in response to intravenous injection in mice [66]. The distribution and terminal half-lives were measured to be 5 min and 5 h in healthy male volunteers (N = 12) [67]. We take μS = 5 h, leading to μS = ln(2)/(5h) = 1.386 × 10−1 h−1. Thus, dimensionless μS = 1.386 × 10−1 h−1/(0.035h−1) = 3.96.
G*: The TGF-β level in the lung cancer microenvironment was measured to be in the range of 400 − 2, 000 pg/mL [38]. We take G* = 1, 000 pg/mL.
S*: Deng et al. [68] investigated the effect of STING-dependent cytosolic DNA sensing on the IFN-β-dependent anti-tumor efficacy with the control IFN-β concentration of 10 ng/mL and IFNγ value of 20 ng/mL. We take S* = 10 ng/mL.
Table 2 summarizes all the essential parameter values in the system (5)–(7).
Table 2. Parameters used in the model.
| Par | Description | Value | Refs |
|---|---|---|---|
| N1/N2 modules | |||
| λ | IL-6-induced signaling source of the N2 module | 0.01 | [103], Estimated |
| G | TGF-β-induced signaling source of the N2 module | 0-1.0 | [38] |
| k1 | autocatalytic production rate (N2 module) | 4.0 | Estimated |
| k3 | Hill-type coefficient | 1.0 | Estimated |
| α | Inhibition strength of the N2 module by the N1 module | 1.5 | Estimated |
| k2 | autocatalytic production rate (N1 module) | 4.0 | Estimated |
| k4 | Hill-type coefficient | 1.0 | Estimated |
| β | Inhibition strength of the N1 module by the N2 module | 1.0 | Estimated |
| S | IFN-β-induced signaling source of the N1 module | 0-1.0 | [68], Estimated |
| μ | Relative decay rate of N1 and N2 TANs | 1.0 | [60, 61] |
| thC | Threshold of the N2 module for tumor growth switch | 1.5 | Estimated |
| Tumor module | |||
| r | Tumor growth rate | 0.05 | [36] |
| K | Inhibition parameter of N2-mediated growth | 1.0 | [36], Estimated |
| γ1 | Inhibition parameter of N2-mediated growth | 0.1 | [36], Estimated |
| T0 | Carrying capacity of a tumor | 100 | [36], Estimated |
| δ | Killing rate of tumor cells by N1 TANs | 0.005 | [36], Estimated |
| Therapeutics | |||
| Gs | TGF-β source | 0.826 | Estimated |
| μG | Decay rate of TGF-β | 0.826 | [7, 41, 47, 64]. |
| γL | Clearance rate of TGF-β from TGF-β inhibitor binding | 100 | Estimated |
| Ls | Injection rate of TGF-β inhibitor | 13 | Estimated |
| μL | Decay rate of TGF-β inhibitor | 6.6 | [65] |
| SS | IFN-β injection rate | 1 -100 | [22–25, 36, 37] |
| μS | Decay rate of IFN-β | 3.96 | [67] |
| Reference values | |||
| G* | TGF-β Concentration | 1 ng/mL | [38] |
| S* | IFN-β Concentration | 10 ng/mL | [68] |
| T* | Tumor Volume | 100 mm3 | [36] |
Results
Dynamics of the model
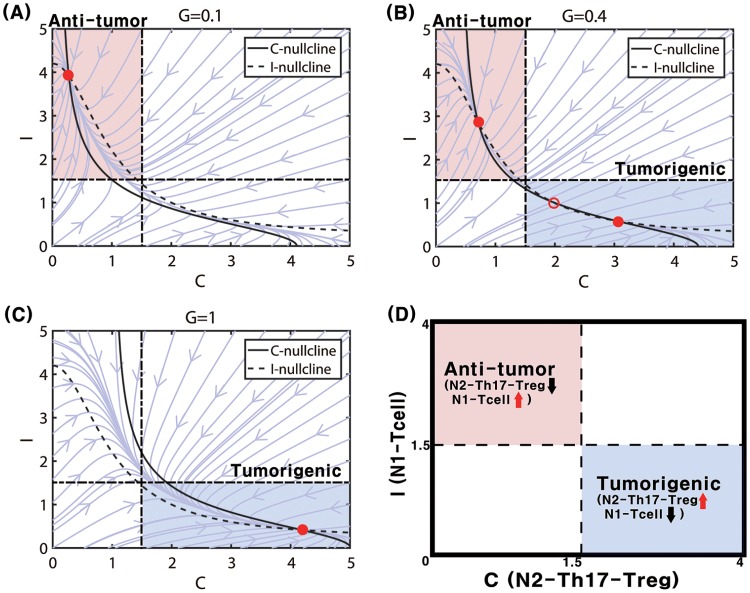
We first investigated the local dynamics of the system (5) and (6). By taking different initial values of N1 and N2 complexes and numerically solving Eqs (5) and (6), one can obtain solutions (C(t), I(t)) at time t and plot the relative locations of solutions in the C − I domain. In Fig 5 we illustrate three different flow patterns of the system (5) and (6) near the equilibrium point (steady state (SS); circles) in response to low (G = 0.1 in Fig 5A), intermediate (G = 0.4 in Fig 5B), and high (G = 1.0 in Fig 5C) TGF-β levels in the C − I phase diagram. We note that if the equilibrium point is stable, the solution converges to the stable SS (called attractor). On the other hand, when the equilibrium point is unstable, the solution does not converge to the unstable SS and the solution is repelled by the unstable SS (called repeller). By taking the thresholds, Cth (= 1.5) for the N2 level and Ith (=1.5) for the N1 level, we shall define the anti-tumorigenic () and tumorigenic () phases as follows:
Fig 5D illustrates the anti-tumorigenic (low activities of the N2 module, high activities of N1 TANs) and tumorigenic (high activities of the N2 complex, low activities of the N1 complex) in a C − I plane. A low TGF-β level (G = 0.1) induces only one stable SS (Fig 5A) where suppression of N2 activities and promotion of N1 activities induce the anti-tumorigenic status (). In this case, the environment eventually induces the anti-tumorigenic phenotype regardless of initial status of N1 and N2 complexes. In contrast, the increased activity of N2 TANs, and decreased activity of N1 TANs, leading to the tumorigenic phase (), are induced under a high TGF-β condition (G = 1.0; Fig 5C; one stable SS). In this case, the environment eventually induces the tumorigenic phenotype regardless of initial status of N1 and N2 complexes. For an intermediate level of TGF-β signals (G = 0.4), there exist three equilibria: two stable SS (two filled circles; one in and one in ) and one unstable SS (empty circle) in the middle. This leads to a bi-stable system shown in Fig 5B. In this case, the environment will induce either anti-tumorigenic or tumorigenic phenotype depending on the initial status of N1 and N2 complexes. From these observations, we anticipate to see a bifurcation curve, especially hysteresis, i.e., the N2 level with TGF-β signal parameter G.
Fig 5. Nonlinear dynamics.
Dynamics of the system (5) and (6) in the C-I phase plane in response to low (G = 0.1 in (A)), intermediate (G = 0.4 in (B)), and high (G = 1.0 in (C)) levels of TGF-β-induced transition signals. Steady states marked with circles (stable steady state = filled circle, unstable steady state = empty circle). (D) A schematic of anti-tumorigenic (C < Cth, I > Ith) and tumorigenic (C > Cth, I < Ith) regions in the C − I plane. S = 0.2 fixed. Other parameters are given in Table 2.
Effect of TGF-β on transitions between N1/N2 TANs and tumor growth
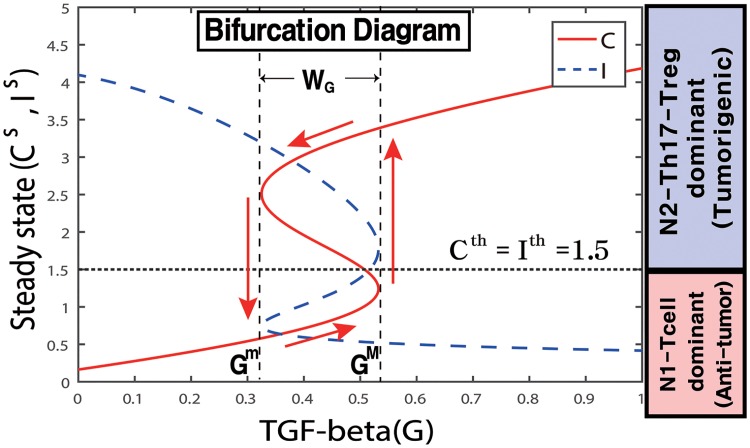
When the system (5) and (6) is in equilibrium, we can solve C as a function of the TGF-β signal (G). Fig 6 shows the graphs C = C(G) and I = I(G) as a hysteresis. While the upper and lower branches are stable, the middle branch is unstable (recall the G-dependent stability in Fig 5). If G is small, then the system is in the lower branch (C low, I high), leading to the anti-tumorigenic phase (). This situation continues to hold as G is increased until it reaches the right knee point of the curve (when G = 0.53). At this point, the N2 level jumps to the high branch, with an elevated level of N2 TANs, leading to the tumorigenic phase (). As G is decreased, the N2 level remains elevated, until G is decreased to the left knee point of the curve (when G = 0.33), at which time the N2 level jumps down to the lower branch, and the system returns to the cancer-free mode (). We conclude that the effect of G is history dependent: when G is at an intermediate level (0.33 = Gm < G < GM = 0.53; bi-stable mode in Fig 5B), the system induces the anti-tumor phase if G is in an increasing mode from the low G value, and leads to the tumor-promoting phase if G is in decreasing mode from the high G level. The bifurcation diagram in Fig 6 suggests that a state (G, C) with C > Cth = 1.5 will be moved by the dynamical system (5) and (6) into the upper stable steady state branch, resulting in prevailing -status. On the other hand, if C < Cth = 1.5, then (G, C) will stay in the lower stable state branch, leading to -status. The size of the bi-stability window (WG = [Gm, GM]) depends on other parameters and may even disappear for some parameter sets.
Fig 6. Bifurcation diagram.
High and low TGF-β signals (G) provide an on-off switch of N2 activation and determine the dichotomous behavior: cancer cell activation and benign status. Y-axis = steady state (SS) of levels of the N2 (C) and N1 (I) complex modules. WG = [Gm, GM] = a window of bi-stabilty. S = 0.2. Other parameters are given in Table 2.
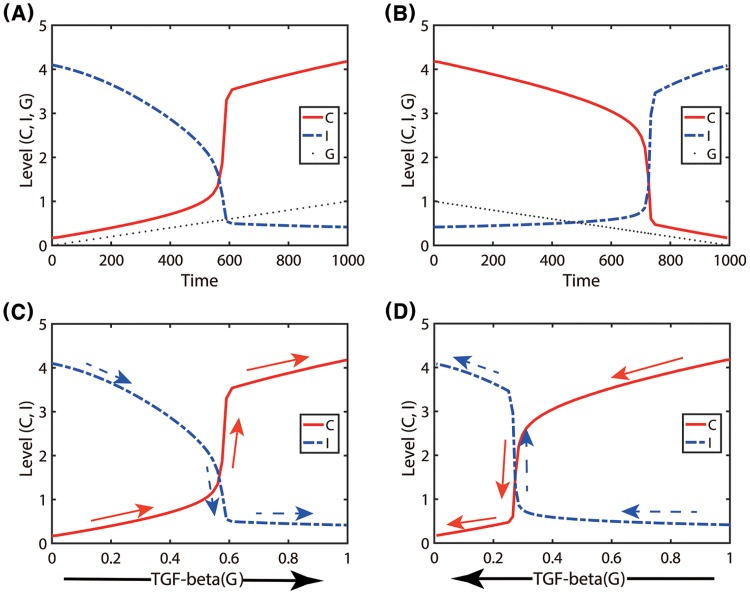
Fig 7A shows how main variables (C, I) in the system respond to the slowly increasing TGF-β level (G). The solution C(t) (solid red line) initially follows the -status along the lower branch of the bifurcation curve until the right knee point of the bifurcation curve and transits to the upper branch solution, leading to the -mode. This trajectory of the solutions (C, I) along G is illustrated in Fig 7C. This illustrates that when G is increasing from a low value, the system will stay longer in the -phase. On the other hand, when G is slowly decreased from a high value, the solution C(t) follows the upper branch of the bifurcation curve in Fig 6 until the left knee point and drops down to the lower branch, staying longer in the -phase including the bistability region WG (Fig 6). The corresponding trajectory of the solutions (C, I) along G is shown in Fig 7D.
Fig 7. Immune response of TANs to increasing or decreasing TGF-β.
(A, B) Time courses of the N2 (C, red solid curve) and N1 (I, blue dashed curve) levels as the TGF-β level (G; black dotted line) is slowly increased (from 0 to 1.0 in (A)) and slowly decreased (from 1.0 to 0.1 in (B)), respectively. (C, D) Change of C and I as a function of G corresponding to (A, B), respectively. Arrows indicate the moving direction of the solutions. S = 0.2. Other parameters are given in Table 2.
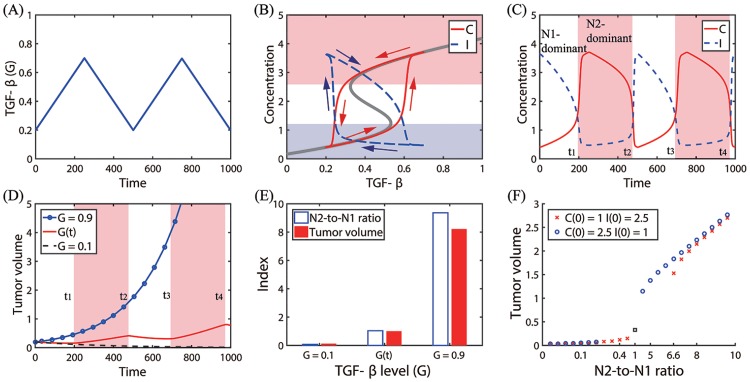
In Fig 8, we test the effect of fluctuating TGF-β on tumor growth. A time-dependent TGF-β level was assigned for a periodic supply of TGF-β in tumor microenvironment as follows (Fig 8A):
In response to the initial increasing TGF-β level, the trajectory of the solution C(t) follows the lower branches of the hysteresis bifurcation loop (thick gray curve) and jumps to the upper branch (Fig 8B). However, a decrease in G around t = 250 switches the moving direction of the solution and it follows the upper branch in the bi-stability region until it jumps down to the lower branch near the left knee of the hysteresis curve. This flow of the solution (G(t), C(t)) was marked in red arrows with initial position on the left lower corner (Fig 8B). The blue dashed curve and blue arrows represent the solution (G(t), I(t)) and its flow, respectively, in the opposite side (Fig 8B). The detailed time courses of solutions (C(t), I(t)) in response to the periodic G input are shown in Fig 8C. The specific N1/N2 phenotypic transitions occur at time t = t1, t2, t3, t4. For example, the initial N1-dominant -status (white region in Fig 8C) switches to a N2-dominant -mode (pink region in Fig 8C) in the tumor microenvironment at time t = t1 due to increasing TGF-β levels. The TAN phenotypic ratio, described by in the second term of Eq (7), and N1 TAN immunity on tumor cells, described by δIT in the third term of Eq (7), determine either promotion or suppression of tumor growth in the model. Fig 8D shows time courses of tumor volumes in response to either fixed or varying TGF-β: (i) high TGF-β (G = 0.9, blue circle), (ii) low TGF-β (G = 0.1, dashed), and (iii) fluctuating TGF-β levels given in Fig 8A. The high TGF-β level induces N2-dominant -phase (Fig 5C), therefore, leading to N2-mediated, faster tumor growth (blue circle). When G is low, the system induces the N1-dominant microenvironment (Fig 5A), resulting in N1-mediated, slower tumor growth (black dashed). On the other hand, fluctuating TGF-β induces alternating transitions between (white region) and (pink region) phases at t = t1, t2, t3, t4 (Fig 8C), which induces slow (white band in Fig 8D) or fast (pink band in Fig 8D) tumor growth in and -regions, respectively, and eventually leads to an intermediate tumor volume at final time (Fig 8D). These results are in good agreement with experimental observations where N1 TANs significantly reduced the size of a tumor relative to N2 TANs [8]. The N2-to-N1 ratio (N21R) index and tumor volume corresponding to these three cases are shown in Fig 8E. An increase in the TGF-β level leads to an increase in the N2-to-N1 ratio, which in turn increase the tumor size. In Fig 8F, we investigate the correlation between N21R and the tumor size. The tumor volume and N21R were calculated from tumor and TAN populations in response to various TGF-β stimuli (G = 0 − 0.9) with two different initial conditions: C(0) = 1, I(0) = 2.5 in red asterisk; C(0) = 2.5, I(0) = 1 in blue circle. The case of the fluctuating G(t) was marked in black square. As N21R is increased, the tumour volume is increased, leading to a positive correlation between N21R and the tumor size. The neutrophil-to-lymphocyte ratio (NLR) has been highly associated with cancer progression [69, 70], becoming biomarkers for various cancers including non-small-cell lung cancer [71, 72] and cervical cancer [73]. In our simulation, N21R is equivalent to NLR and may be suggested to be a prognostic factor.
Fig 8. Effect of fluctuating TGF-β on tumor growth.
(A) A time-dependent TGF-β level was assigned for a periodic supply of TGF-β in tumor microenvironment. (B) Trajectories of solutions ((G(t), C(t)) and (G(t), I(t))) in response to TGF-β in (A). The thick gray curve represents the upper and lower branches of steady states (C − G hysteresis bifurcation loop in Fig 6). Red and blue arrows = solution flow direction of C and I, respectively. (C) Time courses of concentrations of C and I in response to periodic G input in (A). The N2-dominant -regions were shaded in pink. (D) Time courses of tumor volumes in response to a fixed (G = 0.9 (blue circle); G = 0.1 (dashed)) and fluctuating TGF-β level. Fluctuating TGF-β levels induce transitions between N1- and N2-dominant phenotypes, leading to transient tumor growth at the transition times (t1, t2, t3, t4). (E) The N2-to-N1 ratio and tumor size for three TGF-β conditions in (D). (F) Positive correlations between the tumor volume and the N2-to-N1 ratio with two initial conditions (C(0) = 1, I(0) = 2.5 in red asterisk; C(0) = 2.5, I(0) = 1 in blue circle). Initial conditions in (A-E): C(0) = 0.4, I(0) = 3.6, G(0) = 0.2, T(0) = 0.2. Other parameters are given in Table 2.
See S1 Appendix for analysis of the model. We investigated effects of N1 immunity (δ) on cancer cell killing. Depending on various values of δ, the killing rate of cancer cells by N1 TANs, time courses of tumor volume in response to fluctuating TGF-β may show different patterns: monotonic increase, monotonic decrease, or alternation between growth and shrinkage.
Dynamic transition to N1-dominant TANs by normalizing the complex immune system
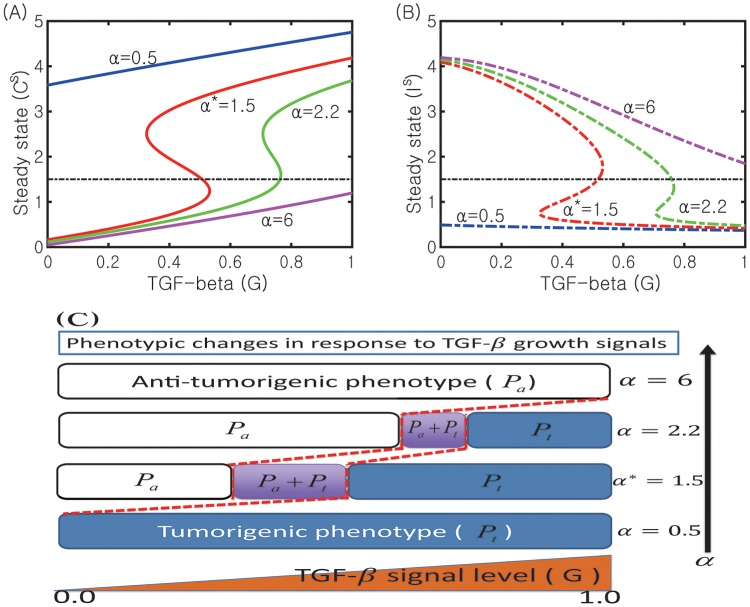
In Fig 9A, we show the sensitivity of G-dependent N2 states (Cs) to changes in inhibition strength of the N2 module by the N1 module (α = 0.5, 1.5, 2.2, 6.0). The corresponding N1 states (Is) are shown in Fig 9B. As α is increased, the bifurcation curve (Cs, G) shifts to the right. This increase in α also moves the bi-stability window (WG) to the right and leads to a decrease in the size of the window (|WG|). This indicates that the probability of switching to the anti-tumorigenic phase () is increased when α is increased. For example, the immune response is already in the -phase (C < Cth, I > Ith) when G = 0.6 in the case of the higher α value (α = 2.2; green curve in Fig 9A) while it is still in the phase (C > Cth, I < Ith) in the base case (α* = 1.5; red line in Fig 9A). On the other hand, the immune system would initiate the tumor-favoring progress even under low TGF-β conditions when α is decreased. For example, the system would be in the -phase for a low TGF-β signal (G = 0.1) when α is lowered (α = 0.5; blue curve in Fig 9A) while it should be in the -phase in the base case (α* = 1.5). We recall that, for the base case (α* = 1.5), the existence of the bi-stability regime WG illustrates that the TGF-β signal can regulate the forward transition from the -state to the -state and the recurrent process from the -state to the -state. However, when the N2 activity is highly enhanced with the decreased inhibition signal from the N1 complex (a decrease in α), the TGF-β signal may regulate only forward transition from the -state to the -state (one way switch) and a monotonic decrease in TGF-β signals does not push the immune system to the anti-tumorigenic phase. The phenotypic changes between - and -states for increased or decreased α are illustrated in Fig 9C. This mechanism of low α’s therefore provides a way of keeping the immune system in a tumorigenic phase. Functional plasticity associated with a decrease in α induces a critical immunosuppressive switch to promote aggressive tumor growth and cancer progression [35, 74].
Fig 9. Transition to the N1-dominant environment by increasing α.
(A, B) Bifurcation curves G − C (Cs in (A)) and G − I (Is in (B)) for various N2 inhibition strengths (α = 0.5, 1.5, 2.2, 6.0). (C) The corresponding phenotypic switches between tumorigenic and anti-tumorigenic phases when α is varied. Other parameters are fixed as in Table 2. The base case (α* = 1.5) was marked in star (*).
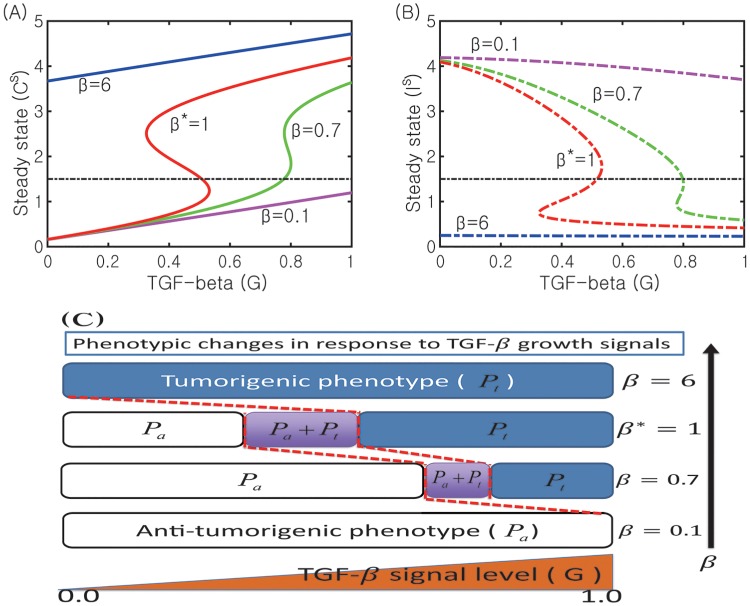
In Fig 10 we show the effect of the inhibition strength of N1 activities by the N2 module (β = 0.1, 0.7, 1.0*, 6.0) on the dynamics of the core control system. As β is increased, the bifurcation curves (G, C) shift to the left (Fig 10A). In contrast to the case of changes in α in Fig 9, this increase in β reverses its shifting direction i.e., it moves the bi-stability window (WG) to the left and leads to an increase in the size of the window (WG) despite disappearance of the bistable switch for larger β. Thus, an increase in β induces transient changes from a bistable- to a one-way-switch and to a mono-stability. This indicates that the probability of switching to the tumorigenic phase () is increased in response to fluctuating TGF-β levels (0 ≤ G ≤ 1.0) when β is increased. For example, the immune system is already in the tumorigenic phase (; C > Cth, I < Ith) in response to G = 0.12 in the case of higher β’s (for example, β = 6.0; blue curve in Fig 10A) while it should still be in the anti-tumorigenic phase (; C < Cth, I > Ith) in the base case (β* = 1.0; red line in Fig 10A). On the other hand, the immune system would activate the anti-tumorigenic machinery even under high TGF-β signal conditions when β is decreased. For example, the system would increase probability of switching to the anti-tumorigenic phase by lowering N2 levels for a high TGF-β level (G = 1.0) when β is lowered (β = 0.1; cyan curve in Fig 10A) while it should be in the tumorigenic phase in the base case (β* = 1.0). While a decrease in β reduces the size of the bi-stability window (|WG|), an increase in β reduces the size of the one-way switch window. When N2 activities are highly enhanced with the increased inhibition signal of the N1 module by the N2 complex (an increase in β) due to mutual antagonism between N2 and N1 modules, TGF-β signals may also regulate only forward transition from -state to -state (one way switch) and a monotone decrease in TGF-β signals does not push the immune system to the anti-tumorigenic phase. Therefore, this β-induced mechanism has a similar effect on keeping high N2 activities as that of a decrease in α, providing a way of keeping the immune system in a tumorigenic phase.
Fig 10. Effect of the inhibition parameter (β) on the transitions between N1 and N2 system.
(A, B) Bifurcation curves G − C (Cs in (A)) and G − I (Is in (B)) for for various N1 inhibition strengths (β = 0.1, 0.7, 1.0*, 6.0). (C) The corresponding phenotypic switches between tumorigenic and anti-tumorigenic phases when β is varied. Other parameters are fixed as in Table 2. The base case (β* = 1.0) was marked in star (*).
Therefore, these results provide a scientific basis for targeting suppressive effect of N2 TANs by normalizing immune activities (increase in α or decrease in β) within the tumor microenvironment or keeping a favorable balance of the N1/N2 TAN’s properties toward N1 TANs [35]. For example, blood normalization was suggested to be an alternative way of creating anti-tumor TAN microenvironment [75, 76].
Role of IFN-β signaling in regulation of the transition between N1- and N2-dominant system
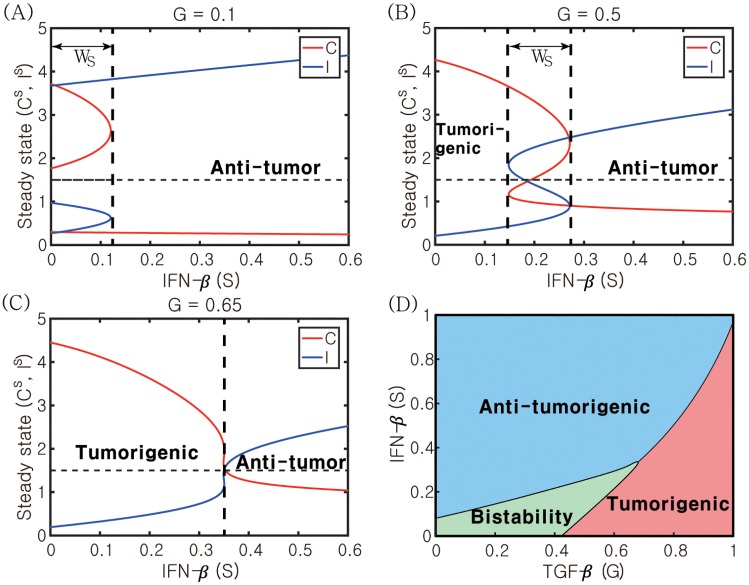
In Fig 11, we investigate the role of the IFN-β signaling pathway in the phenotypic balance of N2 and N1 complexes for various TGF-β levels (G = 0.1, 0.5, 0.65). When G is low, the system induces a bi-stable system for low IFN-β levels and N1-dominant phenotypes in response to intermediate and high IFN-β levels (Fig 11A). Therefore, the system is quite sensitive to relatively low IFN-β stimuli to induce the anti-tumor microenvironment. When G is increased to G = 0.5, the bistability window (Ws) in Fig 11A moves to the right and the system now can generate tumorigenic, bi-stable, and anti-tumorigenic status in response to low, intermediate, and high IFN-β levels, respectively. Therefore, the relative balance between TGF-β and IFN-β signaling determines the phenotypic preference (Fig 11B). On the other hand, in the presence of high levels of TGF-β (G = 0.65; Fig 11C), the bistability window disappears and the probability of inducing a N1-dominant microenvironment is decreased, shifting the balance toward the high N2-to-N1 ratio. Fig 11D summarizes the phenotypic representation of the system in response to various TGF-β and IFN-β stimuli. The majority of the bi-stable region resides in the lower left corner of the G − S plane. Therefore, the biochemical fluctuation of both TGF-β and IFN-β levels in the lower regime is likely to generate a selection process of either promoting or suppressing tumor growth based on the initial distribution and phenotypic status of TANs in tumor microenvironment.
Fig 11. Dynamic change in response to the IFN-β signal.
(A-C) Activities of N2- and N1-modules in response to IFN-β levels (S) when the TGF-β level is low (G = 0.1 in (A)), intermediate (G = 0.5 in (B)), and high (G = 0.65 in (C)). When the TGF-β level is low or intermediate, there exists a bi-stable window (WS = {S ∈ [0, 1]: Sm ≤ S ≤ SM}) where both and coexist. (D) For a constant IFN-β signaling, the system transits from - to -modes as the TGF-β level is increased. On the other hand, for a fixed TGF-β level, an increase in S induces a transition from -favoring mode to the -status. Other parameters are given in Table 2.
Sensitivity analysis
In the model developed in this paper, there are parameters for which no experimental data are known and they may affect the simulation results. We take all parameters in the model (r, K, γ1, T0, λ, δ, G, S, k1, k2, k3, k4, α, β, and μ) for sensitivity analysis. We investigated the sensitivity of the activities of N2 and N1 modules at t = 10, 100, 200 to these parameters. We have chosen a range for each of these parameters and divided each range into 10,000 intervals of uniform length. For each of the fifteen parameters of interest, a partial rank correlation coefficient (PRCC) value is calculated. PRCC values range between -1 and 1 with the sign determining whether an increase in the parameter value will decrease (-) or increase (+) activities of the N2 and N1 complex, and tumor size at a given time. The sensitivity analysis to be described below was carried out using the method from [77] and Matlab files available from the website of Denise Kirschner’s Lab: http://malthus.micro.med.umich.edu/lab/usadata/.
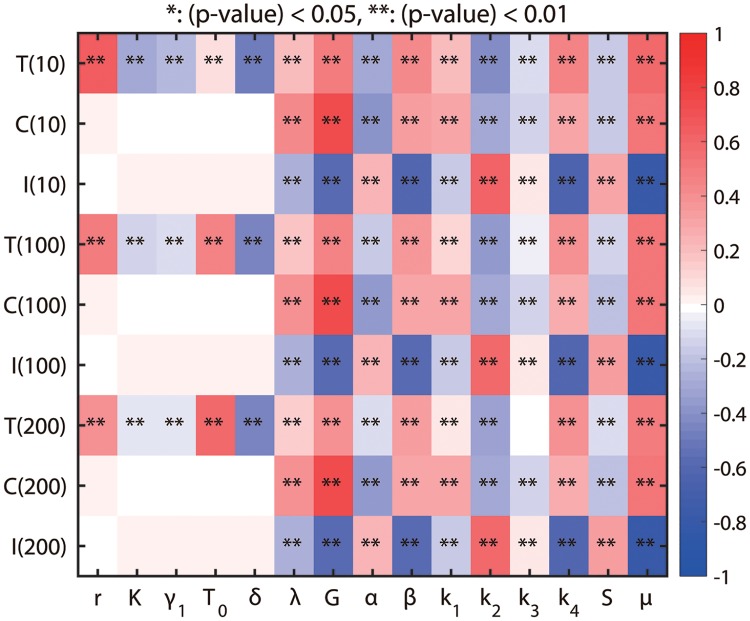
Fig 12 shows the sensitivity analysis results for the N2 level and N1 activity, and tumor volume at t = 10, 100, 200 for Eqs (5)–(7) i.e., we compute PRCC values for C, I, T at time t = 10, 100, 200. We calculate PRCC values and associated p-value for fifteen perturbed parameters (r, K, γ1, T0, δ, λ, G, S, k1, k2, k3, k4, α, β, μ). We conclude that the activity of the N2 complex at t = 200 is positively correlated to the parameters λ, G, μ but is very little correlated (and thus not sensitive) to r, K, γ1, T0, α, β, k1, k2, k3, k4, S. Thus, in particular, the N2 level will increase significantly if the TGF-β signal is increased. Due to mutual antagonism between N1- and N2-dominant system, it is expected to see opposite correlations between N1 activity and those parameters. Indeed, the N1-dominant system is positively correlated to the parameters k2, S but is negatively correlated to the parameters G, β, k4, μ, i.e., there would be significant reduction in the N1 expression level if the TGF-β signaling strength is increased. The tumor volume is positively correlated to the growth rate (r) and carrying capacity (T0) but is negatively correlated to the tumor killing rate by N1 TANs (δ).
Fig 12. Sensitivity analysis: General Latin Hypercube Sampling (LHS) scheme and partial rank Correlation Coefficient (PRCC) performed on the model.
The colors in each sub box indicates PRCC values of the N2 level and N1 activity for model parameters (r, K, γ1, T0, δ, λ, G, S, k1, k2, k3, k4, α, β, μ) at t = 10, 100, 200. The analysis was carried out using the method of [77] with sample size 10000.
Therapeutic approaches: Blocking the N2-dominant system by TGF-β inhibitors
In Fig 13 we investigate the anti-tumor effect of a TGF-β inhibitor on tumor growth. We introduce new variables: concentration of TGF-β (G), instead of a parameter, and TGF-β inhibitor concentration (L) whose dynamics are described as follows:
| (8) |
| (9) |
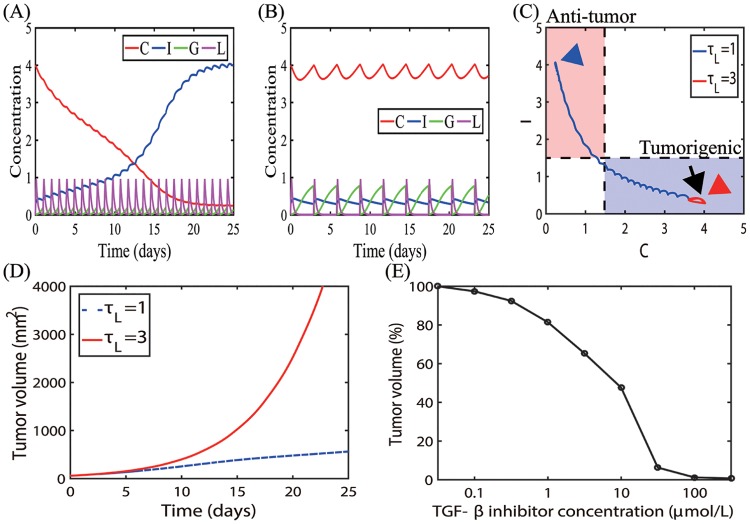
Here, Gs is the constant source of TGF-β, μG is the decay rate of TGF-β, γL is the degradation rate of TGF-β by its inhibitor, Ls is the external periodic source of the TGF-β inhibitor on the time intervals [ti, ti + hd], i = 1, …, Nl with the duration hd and the period τL (= ti+1 − ti, i = 1, …, NL − 1; hd < τL) between those intervals, NL is the number of injections, J[⋅] is the indicator function (giving 1 and 0 on the given condition), μL is the decay rate of the TGF-β inhibitor. Eqs (8) and (9) then are coupled with the original Eqs (5)–(7) to investigate the effect of TGF-β inhibitors on the transition behaviors between N1 and N2 phenotypes. In Fig 13(A) and 13(B), the dynamic system shows different mode changes as the TGF-β inhibitor was injected at the different periods (τL = 1, 3). A frequent injection of the inhibitor (τL = 1 in Fig 13A) induces a decrease in the TGF-β level (G < 0.4), resulting in the transition from the initial tumorigenic condition (black arrow in Fig 13C) to the anti-tumorigenic mode (blue arrowhead in Fig 13C). On the other hand, the TGF-β level still stays in the upper stable branch (Fig 6) in response to a less frequent injection schedule (τL = 3 in Fig 13B), keeping the system in the tumorigenic phase (red arrowhead in Fig 13C). These different cellular compositions in N1- or N2-dominant tumor microenvironment result in fast or slow tumor growth: slow and fast tumor growth in response to frequent (τL = 1) and less frequent (τL = 3) injection schedules, respectively (Fig 13D). Fig 13E shows the normalized tumor volume at final time (t = 25 days) for various TGF-β inhibitor levels (L0 = 0 − 100 μmol/L). As the loading dose is decreased, the anti-tumor efficacy is significantly decreased especially when its concentration is less than 10 μmol/L. These results are in good agreement with experimental data [38]. Serizawa et al. [38] found that gefitinib, a TGF-β inhibitor, can effectively kill non-small-cell lung cancer cells, PC-9 (cell lines without erlotinib, an EGFR inhibitor) and PC-9ER1/PC-9ER4 (cell lines with resistance to erlotinib) in in vitro experiments [38]. While the overall cell viabilities in these cell lines were significantly decreased in response to the increasing concentrations of gefitinib, the anti-tumor efficacy in low dose of gefitinib (∼0.1μmol/L) was higher and sensitive in PC-9 cell lines in the response curve. This implies that the higher dose TGF-β inhibitor needs to be injected into the tumor in order to maintain the same level of anti-tumor efficacy in the tumor microenvironment.
Fig 13. Therapeutic effect of TGF-β inhibitor injection.
(A, B) Time courses of activity levels of the N2 complex (C) and N1 complex (I), and concentrations of TGF-β (G) and TGF-β inhibitor (L) in response to a periodic injection of the TGF-β inhibitor with periods τL = 1 (A) and τL = 3 (B), respectively. (C) Dynamics of the core N1-N2 system in response to the frequent (τL = 1 in (A)) and less frequent (τL = 3 in (B)) injections of the TGF-β inhibitor in the C − I plane. (D) Time courses of tumor volume for two different injection protocols in (A, B). (E) Tumor volume (%) at final time (t = 25 days) in response to various TGF-β inhibitor levels (0, 0.02, 0.1, 0.3, 1.0, 3.0, 10, 20, 100 μmol/L). Initial conditions: C(0) = 4.0, I(0) = 0.3, G(0) = 0, L(0) = 0. Initial injection time: t1 = 0. All other parameters are fixed as in Table 2.
Therapeutic strategies by IFN-β injection
We investigate the effect of normalizing immune activities on tumor growth by injecting IFN-β. We consider the following conventional equations for time-dependent IFN-β administration:
| (10) |
where Ss is the injection dose of IFN-β, J(⋅) is the indicator function. The IFN-β is injected over the time interval [ti, ti + hs], i = 1, …, Ns for the time duration hs and a period τs (= ti+1 − ti, i = 1, …, Ns − 1), Ns is the number of the IFN-β injections.
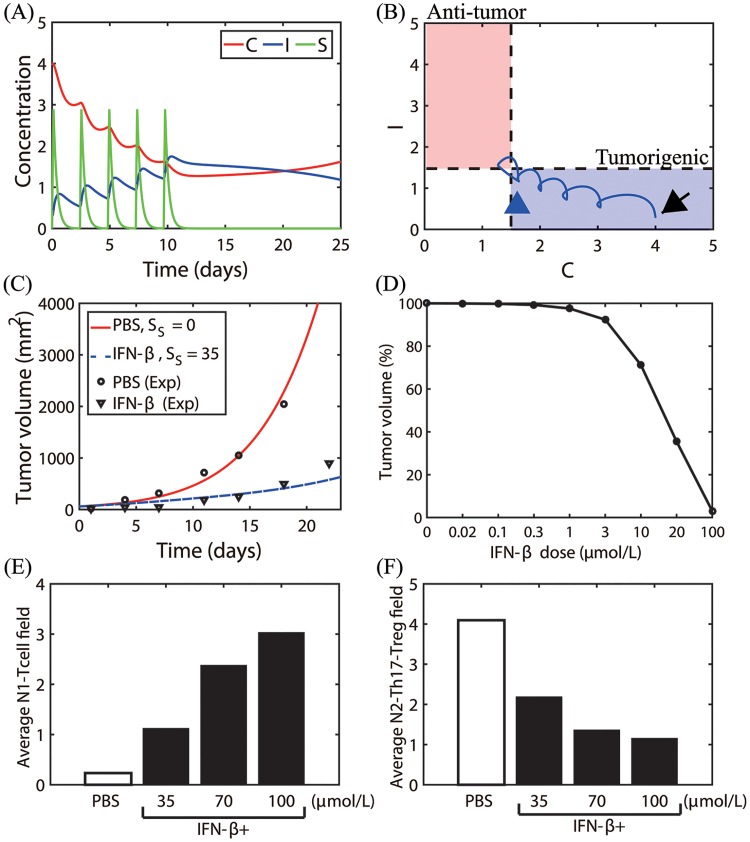
Fig 14A shows the time courses of N2 levels (C), N1 activity (I), and IFN-β level (S) in response to intratumoral injections of IFN-β. Fig 14B shows the corresponding trajectory of the solution (C(t), I(t)) in the C − I plane. Starting from an initial condition in the tumorigenic phase (black arrow in Fig 14B), the N2-dominant system responds to the injected IFN-β in a periodic fashion and slowly transits to the N1-dominant system (pink box in Fig 14B) by decreasing the N2 level and increasing N1 activity (blue arrowhead). Fig 14C shows time courses of tumor volume (mm2) in the absence (PBS; red solid curve, Ss = 0) and presence (blue dashed curve, Ss = 35) of intratumoral injection of IFN-β. IFN-β treatment significantly reduces the tumor size through repressing the N2-suppressing immune microenvironment (Fig 14B), which is in good agreement with experimental data. Note that even though the (C, I) returned back to the tumorigenic phase (blue arrowhead in Fig 14B) after the last IFN-β injection on day 9 (Fig 14A), the overall tumor growth is still very slow due to the earlier suppression of the N1-dominant environment, thus normalizing the immune activities against the tumor. The empty circles and triangles in Fig 14C represent experimental results for the LLC1 tumor cell line implanted in C57BL/6 mice in controls (PBS; empty circle) and after IFN-β injection (triangles) cases, respectively [36]. In Fig 14D, we show the dose-response curve of IFN-β at day 25 after a periodic intratumoral injection of IFN-β when G = 0.4. IFN-β therapy in combination with other anti-tumor drugs [36] has been suggested to be effective in reducing tumor growth [22–25] and stimulating the anti-tumor immune response [37]. Fig 14E shows the average N1-Tcell levels over the time interval [0–12 days] in the absence of IFN-β (PBS; white bar) and in response to various IFN-β doses (35,70,100 μmol/L; black bars). The corresponding average N2 populations are shown in Fig 14F. In experimental studies [28], the relative population of tumor-infiltrating CD8 T cells were significantly increased in tumor microenvironment in response to IFN-β treatment but the Treg population was reduced in non-small cell lung cancer. The model predicts a significant increase in the immune activities (Fig 14E) and dramatic decrease in Treg populations, which is consistent with the experimental results [28].
Fig 14. Therapeutic effect of IFN-β on tumor growth.
(A) Time courses of the N2 complex level (C), N1 complex activity (I), and concentration of IFN-β (S) in response to a periodic injection of IFN-β on 0, 3, 5, 7, 9 days. (B) Dynamics of the core N1-N2 system corresponding to (A) in the C − I plane. Black arrow = initial position, blue arrowhead = terminal point at t = 25 days. (C) Time courses of tumor volume in control (PBS) and IFN-β+ cases: Control (PBS) from the model (red solid line, Ss = 0), IFN-β injection case from the model (blue dashed line, Ss = 35), control (PBS) from experiments (empty circle), IFN-β injection case from experiments (triangle). (D) Tumor volume (%) at final time (t = 25 days) in response to various IFN-β injection levels (Ss = 0, 0.02, 0.1, 0.3, 1.0, 3.0, 10, 20, 100 μmol/L). (E, F) Tumor-infiltrating CD8 T cells and Tregs. Average field of N1-Tcell (E) and N2-Th17-Tregs (F) over the time interval [0–12 days], in the absence (PBS) and presence of IFN-β injections (35,70,100 μmol/L). Initial conditions: C(0) = 4.0, I(0) = 0.3, S(0) = 0. Initial injection time: t1 = 0. Parameters used: G = 0.4. All other parameters are fixed as in Table 2.
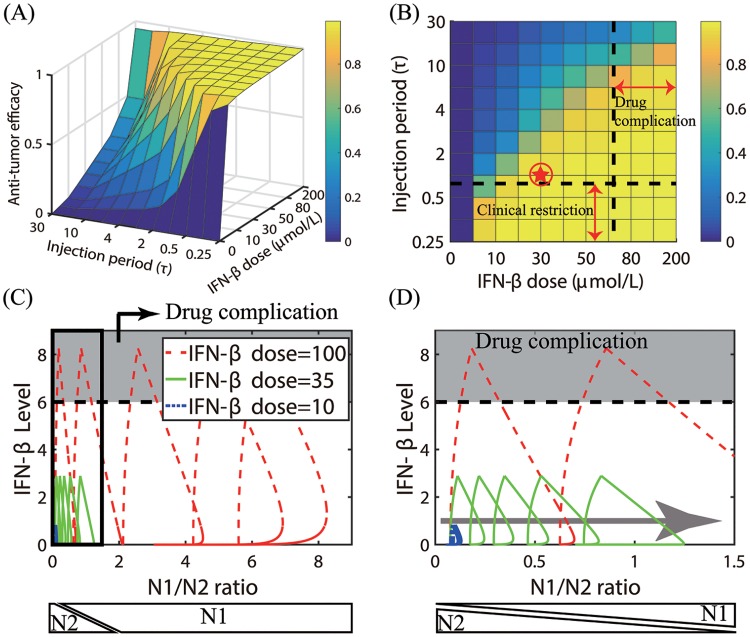
In Fig 15A, we show anti-tumor efficacy for various dose schedules and injection doses of IFN-β. For a fixed IFN-β dose, the low (or high) dosing frequency induces N2-dominant (or N1-dominant) tumor microenvironment and thus faster (or slower) tumor growth. For a fixed injection frequency, the system transits from the N2-dominant phase to the N1-dominant phase, thus slower tumor growth, as the injection dose amount (Ss) is increased as shown in Fig 14. The mathematical model predicts that the larger injection period (τs) and smaller dose (Ss) would result in the N2-mediated, faster tumor growth while the frequent injection schedule and larger doses would lead to the phenotypic switch to the N1-dominant microenvironment and the greater anti-tumor efficacy. Unfortunately, IFN therapy has been shown to be associated with side effects and significant toxicity in cancer, including neuropsychiatric, constitutional, hepatic, and hematologic effects [78], as well as in multiple sclerosis [79]. Therefore, clinicians would want to optimize the overall administration schedule in order to minimize the dose amount while still avoiding high dose therapy and maintaining sustainable clinical results. In other words, the dose level needs to be minimized in order to avoid drug complication region in Fig 15B. On the other hand, too frequent injections are not desirable due to an increase in administrative costs at a clinic, i.e., avoiding clinical restriction region in Fig 15B. In our simulations, the optimal treatment schedule can be obtained with an intermediate dose of 30 μmol/L and τs = 1 day (red circled asterisk in Fig 15B) as explained below. In Fig 15C we show the trajectories of solutions (Γ(t), S(t)) in the IFN-β-N1/N2 plane in response to the low (10 μmol/L, blue dashed line), intermediate (35 μmol/L, green solid line), and high (100 μmol/L, red dashed line) doses of IFN-β every day (τs = 1 day). Here, Γ(t)(= I(t)/C(t)) and S(t) are the N1/N2 ratio and IFN-β concentration, respectively, at time t. An enlarged subpanel (black box on the left) in Fig 15C is shown in Fig 15D. As the injection strength is increased (10→35→100), the N1/N2 ratio is increased and the tumor microenvironment transits from N2- to the N1-dominant system (gray arrow), leading to better anti-tumor efficacy (Fig 15A). High doses of IFN-β were shown to suppress tumor cell proliferation and promote cell death in both in vitro and in vivo experiments [80–82]. However, a high IFN-β dose also increases IFN-β levels, leading to drug complications or extensive associated toxicity (gray zone on the top) [83–86]. Therefore, the injection schedule should be designed to avoid the associated toxicity but still maximize the N1/N2 ratio for optimal clinical outcome.
Fig 15. Optimal anti-tumor strategies of IFN-β injection.
(A) Anti-tumor efficacy for various dose schedules (τs = 0.25, 0.33, 0.5, 1, 2, 3, 4, 5, 10, 15, 30 days) and injection doses of IFN-β (5, 10, 20, 30, 40, 50, 60, 80, 100, 200 μmol/L). (B) Illustration of anti-tumor efficacy for various schedules in (A) with practical restrictions at a clinic. The optimal dose and schedule are obtained for an intermediate IFN-β dose and an injection schedule without drug complication and under clinical restrictions (100 μmol/L, τs = 1 day; red asterisk). (C) Trajectories of solutions (Γ(t), S(t)) in the IFN-β-Γ plane in response to low (10 μmol/L, blue dashed line), intermediate (35 μmol/L, green solid line), and high (100 μmol/L, red dashed line) doses of IFN-β every day (τs = 1 day). Here, Γ(t)(= I(t)/C(t)) and S(t) are the N1/N2 ratio and IFN-β concentration, respectively, at time t. (D) Enlarged figure from a subpanel (black box on the left) in (C). As the injection strength is increased (10→35→100), the trajectory transits to the N1-dominant system (gray arrow). However, the high dose IFN-β may lead to drug complications or extensive associated toxicity (gray zone on the top) [83–86]. N1 and N2 phenotypes on the bottom of panels (C, D) are determined from the N1/N2 ratio.
Combination therapy
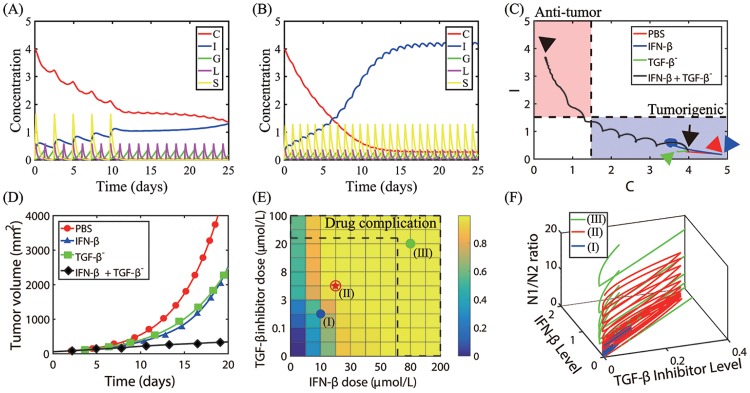
In this section, we investigate the effect of a combined therapy (TGF-β-inhibitor +IFN-β) therapy on tumor growth by solving Eqs (5)–(10). Fig 16A shows time courses of the activities of N2 (C) and N1 (I) modules, and concentrations of TGF-β (G), TGF-β inhibitor (L), and IFN-β (S) in response to a periodic injection of TGF-β inhibitor every day (τL = 1 day) and IFN-β on 0, 3, 5, 7, 9 days (Ls = 8, Ss = 20). Injections of both two drugs induce a decrease in C and increase in I, generating the N1-favoring microenvironment, thus suppressing tumor growth. When these drugs are administered more often (τL = 1 day, τs = 1 day), the system quickly switches from the N2-favoring system to the N1-dominant system even with lower doses (Ls = 5, Ss = 15; See Fig 16B). Fig 16C shows the trajectories of solutions (C(t), I(t)) in response to control (PBS, red) and injections of IFN-β alone (blue), TGF-β inhibitor alone (TGF-β−, green), and combination therapy (IFN-β + TGF-β inhibitor, black): Ls = 8, Ss = 20. While solutions in control (PBS) and single drug (either IFN-β or TGF-β inhibitor) stay in the tumorigenic phase (arrowheads (red, blue, green) in the blue box), the solution in the combination therapy (TGF-β inhibitor+IFN-β) moves to the anti-tumorigenic region (black arrowhead in the pink box). Thus, these dynamics illustrate how the combination therapy may induce the transition from the -phase to the -phase even when either TGF-β inhibitor or IFN-β therapy transits the system to the -mode. Time courses of the tumor volume corresponding to four cases in Fig 16C are shown in Fig 16D. Thus, the combination therapy leads to synergistic tumor killing effects via switching to the -phase (Fig 16C). Fig 16E shows anti-tumor efficacy of the combination therapy with various doses of IFN-β and TGF-β inhibitor at final time (t = 25 days). For a fixed dose level of either IFN-β or TGF-β inhibitor, the anti-tumor efficacy is increased in general. However, high doses of either IFN-β [78, 85–87] or TGF-β inhibitor [88, 89] alone can induce toxicity, resistance and side effects. Therefore, careful dosing strategies need to be developed in order to efficiently deliver IFN-β to a tumor and maximize anti-tumor efficacy while minimizing critical, systemic side effects [90, 91]. Therefore, double high doses of those two drugs may not be desirable due to economic costs as well as serious side effects. It has been shown that high doses of TGF-β inhibitors may lead to poor response to the combined 5-fluorouracil and IFNα-2b therapy in hepatocellular carcinoma patients [92]. The optimal drug dose schedule (red asterisk) can be obtained by avoiding drug complications (dotted region on the upper and right sides) and minimizing dose levels of both drugs while maintaining the overall high anti-tumor efficacy. Fig 16F shows the trajectories of solutions (L(t), S(t), Γ(t)) for the low (blue; (I) in Fig 16E), intermediate (red; (II) in Fig 16E), and high (green; (III) in Fig 16E) doses of both TGF-β inhibitor and IFN-β. Here, Γ(t) = I(t)/C(t) is the N1-to-N2 ratio. While the N1-to-N2 ratios in (II) and (III) are large, the N1-to-N2 ratio is small for low doses of IFN-β and TGF-β inhibitor (case (I)). Thus, the case (III) in Fig 16E is not desirable because of the high N1-to-N2 ratio.
Fig 16. Therapeutic effect of a combination therapy (TGF-β inhibitor + IFN-β) on tumor growth.
(A) Time courses of the N2 (C) and N1 complex (I) activity, and concentrations of TGF-β (G), TGF-β inhibitor (L), and IFN-β (S) in response to a periodic injection of TGF-β inhibitor every day (τL = 1 day) and IFN-β on 0, 3, 5, 7, 9 days. Ls = 8, Ss = 20. (B) Time courses of all variables (C, I, G, L, S) in response to a periodic injection of both TGF-β inhibitor and IFN-β every day. Ls = 5, Ss = 15. (C) Trajectories of solutions (C(t), I(t)) in response to control (PBS, red) and injections of IFN-β only (blue), TGF-β inhibitor only (TGF-β−, green), and combination therapy (IFN-β + TGF-β inhibitor, black). Black arrow = initial position, arrowheads = terminal points at t = 25 day for four cases. Ls = 8, Ss = 20. (D) Time courses of tumor volume corresponding to four cases in (C). The combination therapy leads to synergistic effect on killing tumor cells. (E) Anti-tumor efficacy of the combination therapy with various doses of IFN-β (0, 5, 10, 20, 30, 40, 50, 60, 80, 100, 200) and TGF-β inhibitor (0, 0.02, 0.1, 0.3, 3, 5, 8, 10, 20, 50, 100) at final time (t = 25 days). The optimal dose schedule (marked in red asterisk) is obtained by avoiding drug complications and minimizing dose levels while maintaining the high anti-tumor efficacy. (F) Trajectories of solutions (L(t), S(t), Γ(t)) for the low (blue; (I) in (E)), intermediate (red; (II) in (E)), and high (green; (III) in (E)) doses of both TGF-β inhibitor and IFN-β. Here, Γ(t) = I(t)/C(t) is the N1/N2 ratio. Initial conditions: C(0) = 4.0, I(0) = 0.3, G(0) = 0, L(0) = 0, S(0) = 0. Initial injection time: t1 = 0. All other parameters are fixed as in Table 2.
Effect of time delays
We investigated the effect of time delays on regulation of phenotypic switches and tumor growth. We prescribe time delays in the suppression terms of the N2 and N1 complex. There are many cellular and molecular factors that may affect delayed processes of signaling pathways, apoptosis, and inhibition of neutrophils in the microenvironment [62, 93–96]. This may also be caused by partial blocking of signaling pathways of these TANs by drugs. Recall that the transition probability between and -phases can be modified by the mutual inhibition strength of both N1 and N2 complex (α, β; Figs 9 and 10). Therefore, we modify Eqs (5) and (6) by introducing time delays in the inhibition terms as follows
| (11) |
| (12) |
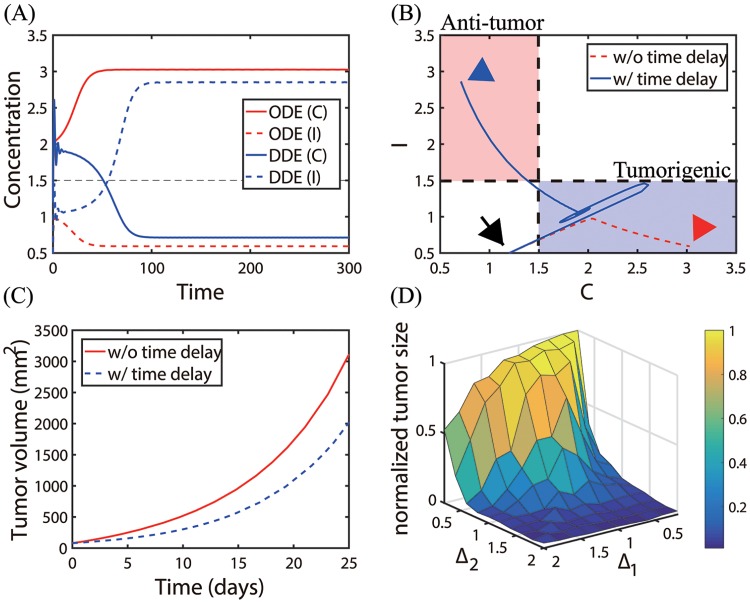
where Δ1, Δ2 are the time delays in the inhibitory pathway of the N2 module and suppression of N1 module, respectively (See Fig 4B). Fig 17A shows concentrations of two main variables (C, I) in the absence (ODE, red) and presence (DDE, blue) of time delays (Δ1, Δ2) = (1.0, 1.2) with initial condition: T(0) = 0.2, C(0) = 1.2, I(0) = 0.5. The corresponding trajectories of solutions (C(t), I(t)) without (red dotted) and with (solid blue) time delays are shown in Fig 17B. Starting with the same initial condition (black arrow), the system adapts to changes in the microenvironment by inducing tumorigenic status (C high, I low; blue box) and anti-tumorigenic mode (C low, I high; pink box) in the absence and presence of time delays, respectively. This delay-induced mode results in a decrease in the tumor size (Fig 17C). This illustrates that the time delays in suppressing N1 or N2 TANs may stimulate a homeostatic imbalance, resulting in either promotion or suppression of tumor growth. Fig 17D shows the normalized tumor volume at day 25 for various strengths of the two time delays (Δ1, Δ2). For a fixed Δ1, as Δ2 is increased, the inhibition strength of the N1 module is decreased and N1 TANs become a dominant phenotype, decreasing the tumor volume. For a fixed Δ2, the tumor size is a nonlinear function of Δ1, inducing a small tumor for either high or low Δ1 but assuming the maximum tumor size for an intermediate Δ1. These results illustrate the complex dynamics of the N1/N2 transitions and nonlinear tumor growth in the presence of time delays in mutual inhibitory properties.
Fig 17. Dynamics of the system with time delays (Δ1, Δ2) in inhibition of TANs.
(A) Time courses of concentrations of two main variables (C, I) in the absence (ODE, red) and presence (DDE, blue) of time delays (Δ1 = 1.0, Δ2 = 1.2). (B) Trajectories of solutions (C(t), I(t)) in the C − I plane corresponding to (A). Time delays can push the -phase to the -phase. (C) Time courses of the tumor volumes corresponding to (A, B). Time delays can slow down the tumor size by the N1 to N2 transition in (B). (D) Normalized tumor sizes for various strengths of the two time delays (Δ1, Δ2). Parameters: S = 0.2, G = 0.4. All other parameters are fixed as in Table 2. Initial condition: T(0) = 0.2, C(0) = 1.2, I(0) = 0.5.
Now, we investigate the effect of time delays in apoptosis of TANs by modifying Eqs (5) and (6) by introducing time delays in the decay term as follows
| (13) |
| (14) |
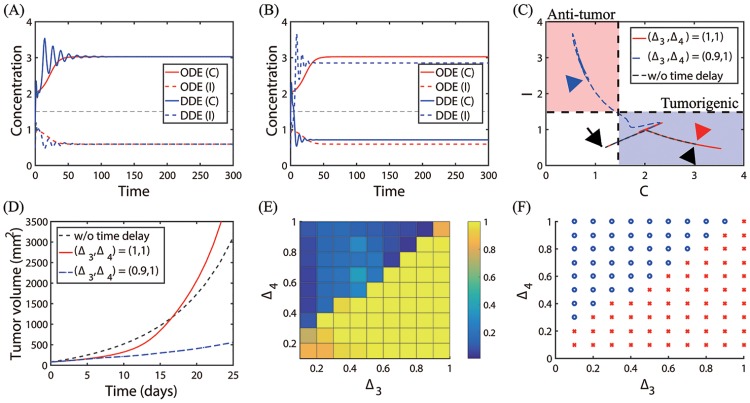
where Δ3, Δ4 are the time delays in apoptosis of N2 and N1 modules, respectively. Fig 18(A) and 18(B) show time courses of the N2- and N1-modules in the absence (ODE, red) and presence (DDE, blue) of time delays: (Δ3, Δ4) = (1, 1) in (A), (Δ3, Δ4) = (0.9, 1) in (B). Fig 18C shows trajectories of the corresponding solutions (C(t), I(t)) in the C − I plane. The initial position was marked in black arrow. While the presence of time delays (Δ3, Δ4) = (1, 1) induces initial fluctuations (Fig 18A), the solutions converge to the N2-dominant steady states of ODEs (red arrowhead in Fig 18C). However, a slightly different combination of time delays ((Δ3, Δ4) = (0.9, 1)) leads to a phenotypic transition from the N2-dominant mode to the N1-dominant phase (blue arrowhead in Fig 18C) despite the initial fluctuation of solutions (blue curves in Fig 18B). Delayed apoptotic cell death leads to different tumor growth dynamics. Fig 18D shows time courses of the tumor volumes corresponding to three cases in Fig 18C. In the presence of time delays (Δ3, Δ4) = (1, 1), the tumor grows slower than the control (case without time delays) initially but the delay-induced oscillations push the TAN system to the N2-dominant phenotype faster than the control case around t = 18 days, leading to the larger N2-to-N1 ratio and faster tumor growth (red curve in Fig 18D). On the other hand, in the presence of time delays (Δ3, Δ4) = (0.9, 1), the tumor grows slower than the control due to strong suppression of the N2 module and enhancement of the N1 module. Fig 18E shows the normalized tumor size at t = 25 days for various strengths of the two time delays (Δ3, Δ4 ∈ [0, 1]) with a uniform length of 0.1. A risk map of time delay-induced transition of TANs from N2 to N1 phenotypes in the Δ3 − Δ4 plane is shown in Fig 18F. For a fixed value of Δ3, an increase in Δ4 results in the higher chance of transition to the -phase, thus slower tumor growth. On the other hand, for a fixed value of Δ4, an increase in Δ3 leads to a higher probability of transition to the -phase and faster tumor growth. To characterize the complex dynamics of the apoptotic cell death mechanism, we introduce the following Δ4-to-Δ3 ratio:
When Dap is large, the delayed apoptotic process of N1 phenotypes and minimal delay in the apoptotic process of N2 phenotypes allow accumulation of more N1 TANs within the microenvironment, pushing the system to the -phase and effective inhibition of tumor growth. On the other hand, a large delay in the apoptosis of N2 TANs with a relatively small delay in the apoptosis of N1 TANs, (i.e., Dap ≪ 1), leads to significant accumulation of N2 TANs in the tumor microenvironment, leading to faster tumor growth.
Fig 18. Dynamics of the system with time delays (Δ3, Δ4) in apoptosis of TANs.
(A, B) Time courses of concentrations of two main variables (C, I) in the absence (ODE, red) and presence (DDE, blue) of time delays: Δ3 = 1, Δ4 = 1 in (A); Δ3 = 0.9, Δ4 = 1.0 in (B). (C) Trajectories of solutions (C(t), I(t)) without (black dotted) and with ((Δ3, Δ4) = (1, 1) red solid; (Δ3, Δ4) = (0.9, 1) blue dashed) time delays in (A-B). (D) Time courses of the tumor volumes corresponding to (C). (E) Normalized tumor sizes for various strengths of the two time delays (Δ3 and Δ4). (F) Risk map of the time delay-induced transition of TANs from N2 to N1 phenotypes in the Δ3 − Δ4 plane. Blue circle = switching to the N1-dominant system. Red asterisk = persisting N2-dominant mode. Parameters: S = 0.2, G = 0.4. All other parameters are fixed as in Table 2. Initial condition: T(0) = 0.2, C(0) = 1.2, I(0) = 0.5.
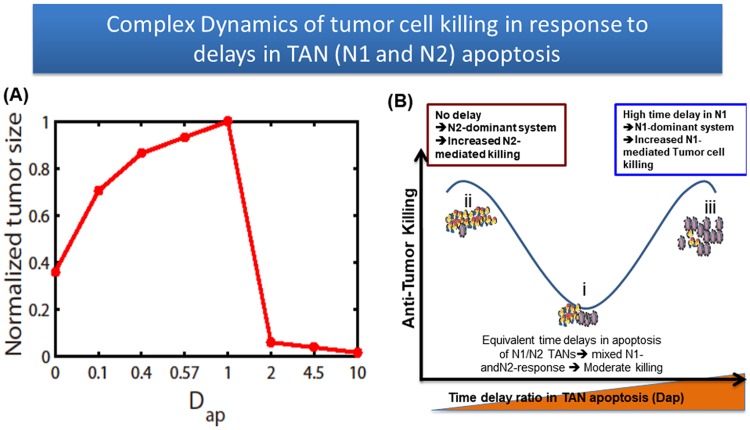
Fig 19A shows the tumor volume for various Dap at final time t = 25 day. As Dap is increased from the control value (Dap = 1), the tumor size is significantly decreased. On the other hand, a decrease in Dap also induces slower tumor growth, indicating the maximum tumor growth rate when Dap = 1. The absence of the time delays in apoptosis signaling also induces slower tumor growth. Fig 19B illustrates a dynamic antitumor killing model with the relative time delay function Dap as a key parameter. A relatively small delay ratio (Dap ≪ 1) (basic step i) induces phenotypic perturbations in N1- or N2-responses, which in turn decreases the N2-assisted tumor growth rate. On the other hand, the depletion of time delays in the apoptosis pathways of TANs (step ii) improved antitumor efficacy and suggests that the major antitumor response was likely due to the persistent N2-dominant microenvironment with quick clearance of TANs (Fig 18A). Our study also showed that complementing TANs with adjuvant N1 immunotherapy improved overall antitumor efficacy (step iii), through the facilitation of a robust N1-mediated tumor cell killing response beyond the limits of endogenous N2 TANs. In spite of a typical short half life of neutrophils, delayed apoptosis and accumulation of neutrophils in a tumor environment have been observed in other biological studies [93, 95, 96]. In particular, TANs often have a longer lifespan in the tumor microenvironment due to delayed apoptosis of TANs by modifying its signaling pathways involving FAS, ROS, active Caspase 3, 9, and Bcl-2 family [62]. Our mathematical model predicts that (i) Dap can be used as a reliable diagnostic measure for aggressiveness of tumor progression; (ii) Anti-tumor efficacy can be improved by increasing the apoptosis decay of N1 TANs or by blocking the accumulation of N2 TANs in tumor microenvironment. In particular, drugs targeting apoptosis pathways of N1 TANs can effectively be used to enhance N1 neutrophil activities to reduce the tumor size.
Fig 19. Effect of apoptosis delays of TANs in anti-tumor efficacy.
(A) Tumor volume for various time delay ratios of TAN apoptosis (Dap). (B) A model depicting the impact of Dap on anti-tumor efficacy.
Discussion
The immune system protects the host against various types of biological threats. However, it is well established that immune cells show functional plasticity in the context of cancer, and undergo phenotypic changes, promoting tumor growth and metastatic progression [74]. There have been substantial studies to pinpoint fundamental mechanisms through which TANs act on cancer progression [8, 17, 34], and especially via the coordination of chemotaxis-driven recruitment and activation of distinct immune cells to the tumor microenvironment [97–100] as well as immune suppression [74, 101, 102]. A groundbreaking work by Fridlender and colleagues [16] had illustrated that TGF-β in tumor microenvironment can generate a functional transition from the proinflammatory neutrophil phenotype (termed “N1”) to the anti-inflammatory phenotype (termed “N2”); [74]. IL-6 also contributes to the formation of the N2 microenvironment [103, 104]. Neutrophil-to-lymphocyte ratio (NLR) was highly associated with progression in many cancer types [69] and has been suggested to be a prognostic factor (or biomarker) for various cancers including colorectal cancer [105, 106], nasopharyngeal carcinoma [107], non-small-cell lung cancer [71], breast cancer [108, 109], hepatocellular carcinoma [110], and melanoma [13]. Recently, it was shown that lung adenocarcinomas can promote bone stromal activity and increase bone mass even without bone metastasis, which in turn enhances tumor growth by remotely supplying tumor-infiltrating neutrophils [111]. However, how the systemic host environment can communicate with a tumor at a remote site is poorly understood.
Since TGF-β was identified as a master player that skews differentiation toward the N2 phenotype [16, 18, 19], TGF-β inhibitors are suggested to shift the TAN balance toward the N1 phenotype [20, 21]. In cancer research, type I IFNs (α and β) are substantially studied and tried for cancer therapy due to their anti-tumor capabilities by acting directly on cancer cells and through immunoregulatory characteristic [112]. These Type I IFNs can induce cell cycle arrest and apoptosis in several models [112–114] by acting on several signaling pathways including upregulation of p53 transcription [24]. Type I IFNs are suggested to mediate initial recruitment, active proliferation, phenotypic differentiation, and activation of various immune cells [115–118]. Interestingly, recent evidence from animal models has implicated that IFN-β signaling pathways play a critical role in inducing antitumor response in chemotherapy [119] and radiotherapy [68, 120]. Therefore, it is not surprising to see IFN-β gene transfer in extensive studies, due to the ability of IFN-β to improve (or normalize) immunological response in the tumor microenvironment [121–125]. IFN-mediated neutrophils was shown to upregulate PD-L1 and suppress T-cell proliferation [26].
We have developed a mathematical model by a system of ODEs and DDEs to study the effect of regulatory cytokines (TGF-β, IFN-β) and delayed apoptotic cell death mechanism on transitions between N1- and N2-dominant system, the N1/N2 mutual antagonism, and their impact on tumor growth (Fig 3). Mathematical analysis showed the complex, nonlinear behaviors of phenotypic switches between N1- and N2-dominant phases in response to fluctuating TGF-β and IFN-β, and tumor growth patterns (Figs 6–11). In particular, the bi-stability of the N1/N2 system generates a selection process of either promoting or suppressing tumor growth based on the initial distribution and phenotypic status of TANs in a tumor microenvironment (Figs 6 and 11). The microenvironmental pressure of inhibiting the phenotypes also determines the phenotypic switches (Figs 9–10). We also developed therapeutic strategies to control this complex network of TANs for slowing down tumor growth (Figs 13–16). Even though high-dose IFNs were suggested to the only available therapy for relapse-free benefits and overall survival (OS) [126], the administration of high-dose IFN in cancer patients in stage IIb/III needs to be considered carefully [112]. High-dose IFN is not always considered as the first line of treatment option for melanoma patients due to a lack of substantial evidence supporting a long-term OS merit and the extensive associated toxicity [83–86]. Therefore, it is necessary to establish optimal dose and treatment duration of IFNs despite extensive clinical experience [112]. In this study, we investigated the optimal dose schedule of IFN-β in the absence or presence of an alternative drug, the TGF-β inhibitor (Fig 15). In our mathematical framework, the high N2-to-N1 ratio (equivalent to NLR) was highly associated with faster tumor growth and worse clinical outcomes (Fig 15). Experimental studies [22–25, 36, 38] are in good agreement with the conclusions of the mathematical model. The optimal strategies of reducing the tumor size with minimal side effects [78, 85–89] and maximal antitumor efficacy were explored by using the TGF-β inhibitor only, IFN-β only, and the combination (TGF-β inhibitor + IFN-β) therapy (Fig 16).
The life span of neutrophils is strictly regulated in order to maintain tissue homeostasis due to their potential toxicity [127]. These cells are quickly removed from circulation after leaving the bone marrow with a very short half life. However, several proinflammatory cytokines were reported to influence their longevity [128, 129]. There are also many cellular and molecular factors that may affect delays in signaling pathways, apoptosis, and inhibition of neutrophils in the given microenvironment [93–95]. For example, external (smoking and nicotine) and internal (ROS) factors were shown to delay neutrophil apoptosis by suppressing signaling pathways (InsP7, Akt, ROS) in lung diseases such as COPD and lung cancers [93, 95, 96]. Recently, it was also shown that ROS production is reduced in the absence of endogenous IFN-β, causing the delayed apoptosis of TANs [62]. Interestingly, a recent study showed that a radiation therapy (RT) can induce the polarization of N1 TANs and reactive oxygen species induced by RT damage tumor tissues, which overall improves anti-tumor efficacy [130]. These microenvironmental factors delay the inhibition and apoptosis of both types of TANs, inducing a complex imbalance between N1 and N2 phenotypes. The mathematical model predicted that various combinations of two time delays in inhibition of signaling pathways within those TANs will induce the relative imbalance between N1 and N2-dominant phases, leading to promotion or suppression of aggressive tumor growth (Fig 17).
We have shown that typical therapy can be exploited by manipulating the delay of apoptosis pathways of both types of TANs. By reducing the relative ratio of apoptosis delay of N1 and N2 TANs, or by increasing time delay of apoptotic pathways of N1 TANs, the efficacy of the antitumor treatment is increased. The mathematical model also predicts that the absence of time delays in apoptosis may allow a greater chance to induce N1 TANs in response to intermediate levels of TGF-β, thereby increasing antitumor efficacy (Fig 18). In particular, the model predicted that either strategy, i.e., induction of small (or none) delay of N2 TANs or large delay of N1 TANs, increased the survival rate (Fig 19), even though it is not clear which of the two strategies is clinically better. The answer should also depend on negative side effects associated with the delays of TANs (mixed N1/N2 immune response) and with the injection of apoptosis-targeting drugs (toxicity and inflammation). Our results provide a scientific basis for targeting suppressive effect of N2 TANs by normalizing immune activities (increase in α or decrease in β) within the tumor microenvironment or keeping a favorable balance of the N1/N2 TAN’s properties toward N1 TANs [35]. While blood normalization was suggested to be an alternative concept of creating an anti-tumor microenvironment including N1 TANs [75, 76], more innovative platforms of normalizing the immune system need to be invented.
In this work, we did not specifically consider many other microenvironmental players such as signaling networks [131], human neutrophil elastase as a therapeutic target in the absence [132, 133] and presence [134] of LPS, endogenous NK immune dynamics [40, 135], angiogenesis from blood vessels [136–138], ECM remodeling [139], or growth factors such as epidermal growth factor (EGF) [140, 141], and CSF-1 [7, 142]. These factors may play critical roles in cancer progression. For example, neutrophil elastin (NE) was shown to indirectly promote the tumor growth by stimulating the PI3K signaling pathways in lung cancer cells [143]. Neutrophil extracellular traps (NETs) were abundant in tumour sections and induce the transformation of B cells [144], contributing to cancer progression [145]. However, another study [146] suggested that the NETs suppressed tumor growth in colonic adenocarcinoma. It is possible that unforeseen microenvironmental factors could have an effect on our approach (governing equations and the many estimated values for mathematical and biological variables). For example, in our model, it is assumed that the tumor microenvironment neutrophils can switch freely from N1 to N2 TANs or from N2 to N1 TANs, given a specific biochemical stimulus. However in vivo there may be unknown biochemical limits to these transitions, such as factors that stabilize one state or another after it has been established. This could be the presence of NETs and associated pro-inflammatory factors. The exact role of this biochemical structural device in regulation of promotion [147–150] or suppression of tumor progression [146] still remains controversial. Our model, however, provides a starting point of the general framework of those key transitions between N1 and N2 TANs in response to known key players. We also plan to investigate the role of the possibly continuous spectrum of the N1 → N2 transition. Further investigation and experimental validation need to be done as more experimental data are available. A multi-scale mathematical model [64, 151–156] could be used to take into account inter and intra-cellular signaling regulation at the microscale level and integrating those to stromal cells and tumor cells at the cellular level. However, the mathematical model in this paper is a first step toward further understanding of lung cancer development in a tumor microenvironment and further experimental investigation. We hope to address these issues in future work.
Supporting information
(PDF)
Acknowledgments
This paper was supported by Konkuk University in 2015 (Yangjin Kim).
Data Availability
All relevant data are within the manuscript and its Supporting Information files.
Funding Statement
This work was supported by Konkuk University 2015 Research fund (www.konkuk.ac.kr, Y.J.). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Torre LA, Bray F, Siegel RL, Ferlay J, Lortet-Tieulent J, Jemal A. Global cancer statistics. CA Cancer J Clin. 2015;65(2):87–108. 10.3322/caac.21262 [DOI] [PubMed] [Google Scholar]
- 2. Molina JR, Yang P, Cassivi SD, Schild SE, Adjei AA. Non-small cell lung cancer: epidemiology, risk factors, treatment, and survivorship. Mayo Clin Proc. 2008;83(5):584–594. 10.4065/83.5.584 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Mantovani A, Sozzani S, Locati M, Allavena P, Sica A. Macrophage polarization: tumor-associated macrophages as a paradigm for polarized M2 mononuclear phagocytes. Trends Immunol. 2002;23(11):549–55. 10.1016/S1471-4906(02)02302-5 [DOI] [PubMed] [Google Scholar]
- 4. Balkwill F, Coussens LM. Cancer: an inflammatory link. Nature. 2004;431(7007):405–6. 10.1038/431405a [DOI] [PubMed] [Google Scholar]
- 5. Luo Y, Zhou H, Krueger J, Kaplan C, Lee SH, Dolman C, et al. Targeting tumor-associated macrophages as a novel strategy against breast cancer. J Clin Invest. 2006;116(8):2132–2141. 10.1172/JCI27648 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Yuan A, Hsiao YJ, Chen HY, Chen HW, Ho CC, Chen YY, et al. Opposite Effects of M1 and M2 Macrophage Subtypes on Lung Cancer Progression. Sci Rep. 2015;5:14273 10.1038/srep14273 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Kim Y, Jeon H, Othmer HG. The role of the tumor microenvironment in glioblastoma: A mathematical model. IEEE Trans Biomed Eng. 2017;64(3):519–527. 10.1109/TBME.2016.2637828 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Shaul ME, Levy L, Sun J, Mishalian I, Singhal S, Kapoor V, et al. Tumor-associated neutrophils display a distinct N1 profile following TGFbeta modulation: A transcriptomics analysis of pro- vs. antitumor TANs. Oncoimmunology. 2016;5(11). 10.1080/2162402X.2016.1232221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Hagerling C, Werb Z. Neutrophils: Critical components in experimental animal models of cancer. Semin Immunol. 2016;28(2):197–204. 10.1016/j.smim.2016.02.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Sionov RV, Fridlender ZG, Granot Z. The multifaceted roles neutrophils play in the tumor microenvironment. Cancer Microenviron. 2015;3:125–158. 10.1007/s12307-014-0147-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Swierczak A, Mouchemore KA, Hamilton JA, Anderson RL. Neutrophils: important contributors to tumor progression and metastasis. Cancer Metast Rev. 2015;34:735–751. 10.1007/s10555-015-9594-9 [DOI] [PubMed] [Google Scholar]
- 12. Liang W, Ferrara N. The complex role of neutrophils in tumor angiogenesis and metastasis. Cancer Immunol Res. 2016;4:83–91. 10.1158/2326-6066.CIR-15-0313 [DOI] [PubMed] [Google Scholar]
- 13. Schmidt H, Bastholt L, Geertsen P, Christensen IJ, Larsen S, Gehl J, et al. Elevated neutrophil and monocyte counts in peripheral blood are associated with poor survival in patients with metastatic melanoma: a prognostic model. Br J Cancer. 2005;93(3):273–8. 10.1038/sj.bjc.6602702 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Bellocq A, Antoine M, Flahault A, Philippe C, Crestani B, Bernaudin JF, et al. Neutrophil alveolitis in bronchioloalveolar carcinoma: induction by tumor-derived interleukin-8 and relation to clinical outcome. Am J Pathol. 1998;152(1):83–92. [PMC free article] [PubMed] [Google Scholar]
- 15. Atzpodien J, Reitz M. Peripheral blood neutrophils as independent immunologic predictor of response and long-term survival upon immunotherapy in metastatic renal-cell carcinom. Cancer Biother Radiopharm. 2008;23(1):129–34. 10.1089/cbr.2007.0429 [DOI] [PubMed] [Google Scholar]
- 16. Fridlender ZG, Sun J, Kim S, Kapoor V, Cheng G, Ling L, et al. Polarization of tumor-associated neutrophil phenotype by TGF-beta: N1 versus N2 TAN. Cancer Cell. 2009;16(3):183–194. 10.1016/j.ccr.2009.06.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Tuting T, de Visser KE. CANCER. How neutrophils promote metastasis. Science. 2016;352(6282):145–146. 10.1126/science.aaf7300 [DOI] [PubMed] [Google Scholar]
- 18. Saha S, Biswas SK. Tumor-Associated Neutrophils Show Phenotypic and Functional Divergence in Human Lung Cancer. Cancer Cell. 2016;30(1):11–13. 10.1016/j.ccell.2016.06.016 [DOI] [PubMed] [Google Scholar]
- 19. Shen L, Smith JM, Shen Z, Eriksson M, Sentman C, Wira CR. Inhibition of human neutrophil degranulation by transforming growth factor-beta1. Clin Exp Immunol. 2007;149:155–161. 10.1111/j.1365-2249.2007.03376.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Andzinski L, Kasnitz N, Stahnke S, Wu CF, Gereke M, von Kockritz-Blickwede M, et al. Type I IFNs induce anti-tumor polarization of tumor associated neutrophils in mice and human. Int J Cancer. 2016;138:1982–93. 10.1002/ijc.29945 [DOI] [PubMed] [Google Scholar]
- 21. Jablonska J, Leschner S, Westphal K, Lienenklaus S, Weiss S. Neutrophils responsive to endogenous IFN-beta regulate tumor angiogenesis and growth in a mouse tumor model. J Clin Invest. 2010;120(4):1151–64. 10.1172/JCI37223 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Studeny M, Marini FC, Dembinski JL, Zompetta C, Cabreira-Hansen M, Bekele BN, et al. Mesenchymal stem cells: potential precursors for tumor stroma and targeted-delivery vehicles for anticancer agents. J Natl Cancer Inst. 2004;96(21):1593–603. 10.1093/jnci/djh299 [DOI] [PubMed] [Google Scholar]
- 23. Chiantore MV, Vannucchi S, Accardi R, Tommasino M, Percario ZA, Vaccari G, et al. Interferon-β induces cellular senescence in cutaneous human papilloma virus-transformed human keratinocytes by affecting p53 transactivating activity. PLoS One. 2012;7(5):e36909 10.1371/journal.pone.0036909 [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 24. Takaoka A, Hayakawa S, Yanai H, Stoiber D, Negishi H, Kikuchi H, et al. Integration of interferon-alpha/beta signalling to p53 responses in tumour suppression and antiviral defence. Nature. 2003;424(6948):516–23. 10.1038/nature01850 [DOI] [PubMed] [Google Scholar]
- 25. Zhang F, Sriram S. Identification and characterization of the interferon-beta-mediated p53 signal pathway in human peripheral blood mononuclear cells. Immunology. 2009;128(1 Suppl):e905–18. 10.1111/j.1365-2567.2009.03104.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. de Kleijn S, Langereis JD, Leentjens J, Kox M, Netea MG, Koenderman L, et al. IFN-γ-stimulated neutrophils suppress lymphocyte proliferation through expression of PD-L1. PLoS One. 2013;8(8):e72249 10.1371/journal.pone.0072249 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Garcia-Diaz A, Shin DS, Moreno BH, Saco J, Escuin-Ordinas H, Rodriguez GA, et al. Interferon Receptor Signaling Pathways Regulating PD-L1 and PD-L2 Expression. Cell Rep. 2017;19(6):1189–1201. 10.1016/j.celrep.2017.04.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Patel MR, Jacobson BA, Ji Y, Drees J, Tang S, Xiong K, et al. Vesicular stomatitis virus expressing interferon-β is oncolytic and promotes antitumor immune responses in a syngeneic murine model of non-small cell lung cancer. Oncotarget. 2015;6(32):33165–77. 10.18632/oncotarget.5320 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Horie M, Saito A, Mikami Y, Ohshima M, Morishita Y, Nakajima J, et al. Characterization of human lung cancer-associated fibroblasts in three-dimensional in vitro co-culture model. Biochem Biophys Res Commun. 2012;423(1):158–63. 10.1016/j.bbrc.2012.05.104 [DOI] [PubMed] [Google Scholar]
- 30. Liao D, Luo Y, Markowitz D, Xiang R, Reisfeld RA. Cancer associated fibroblasts promote tumor growth and metastasis by modulating the tumor immune microenvironment in a 4T1 murine breast cancer model. PLoS One. 2009;4(11):e7965 10.1371/journal.pone.0007965 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Madar S, Harel E, Goldstein I, Stein Y, Kogan-Sakin I, Kamer I, et al. Mutant p53 attenuates the anti-tumorigenic activity of fibroblasts-secreted interferon beta. PLoS One. 2013;8(4):e61353 10.1371/journal.pone.0061353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Pelletier M, Maggi L, Micheletti A, Lazzeri E, Tamassia N, Costantini C, et al. Evidence for a cross-talk between human neutrophils and Th17 cells. Blood. 2010;115(2):335–43. 10.1182/blood-2009-04-216085 [DOI] [PubMed] [Google Scholar]
- 33. Mantovani A, Cassatella MA, Costantini C, Jaillon S. Neutrophils in the activation and regulation of innate and adaptive immunity. Nat Rev Immunol. 2011;11(8):519–31. 10.1038/nri3024 [DOI] [PubMed] [Google Scholar]
- 34. Powell DR, Huttenlocher A. Neutrophils in the Tumor Microenvironment. Trends Immunol. 2016;37(1):41–52. 10.1016/j.it.2015.11.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Shaul ME, Fridlender ZG. Cancer related circulating and tumor-associated neutrophils - subtypes, sources and function. FEBS J. 2018;Epub ahead of print. 10.1111/febs.14524 [DOI] [PubMed] [Google Scholar]
- 36. Catani JPP, Medrano RFV, Hunger A, Valle PD, Adjemian S, Zanatta DB, et al. Intratumoral Immunization by p19Arf and Interferon-beta Gene Transfer in a Heterotopic Mouse Model of Lung Carcinoma. Transl Oncol. 2016;9(6):565–574. 10.1016/j.tranon.2016.09.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Ghosh D, Parida P. Interferon Therapy in Lung Cancer: Current Perspectives. Current Cancer Therapy Reviews. 2016;12(4):237–245. 10.2174/1573394713666170316124158 [DOI] [Google Scholar]
- 38. Serizawa M, Takahashi T, Yamamoto N, Koh Y. Combined treatment with erlotinib and a transforming growth factor-β type I receptor inhibitor effectively suppresses the enhanced motility of erlotinib-resistant non-small-cell lung cancer cells. J Thorac oncol. 2013;8(3):259–69. 10.1097/JTO.0b013e318279e942 [DOI] [PubMed] [Google Scholar]
- 39. Demidenko E. Mixed Models: Theory and Applications with R. 2nd ed Wiley Series; 2013. [Google Scholar]
- 40. Kim Y, Yoo JY, Lee TJ, Liu J, Yu J, Caligiuri MA, et al. Complex role of NK cells in regulation of oncolytic virus-bortezomib therapy. Proc Natl Acad Sci USA. 2018;115(19):4927–4932. 10.1073/pnas.1715295115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Kim Y, Wallace J, Li F, Ostrowski M, Friedman A. Transformed epithelial cells and fibroblasts/myofibroblasts interaction in breast tumor: a mathematical model and experiments. J Math Biol. 2010;61(3):401–421. 10.1007/s00285-009-0307-2 [DOI] [PubMed] [Google Scholar]
- 42. Stein AM, Demuth T, Mobley D, Berens M, Sander LM. A mathematical model of glioblastoma tumor spheroid invasion in a three-dimensional in vitro experiment. Biophys J. 2007;92(1):356–65. 10.1529/biophysj.106.093468 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Enderling H, Anderson AR, Chaplain MA, Munro AJ, Vaidya JS. Mathematical modelling of radiotherapy strategies for early breast cancer. J Theor Biol. 2006;241(1):158–71. 10.1016/j.jtbi.2005.11.015 [DOI] [PubMed] [Google Scholar]
- 44. Weis JA, Miga MI, Yankeelov TE. Three-dimensional Image-based Mechanical Modeling for Predicting the Response of Breast Cancer to Neoadjuvant Therapy. Comput Methods Appl Mech Eng. 2017;314:494–512. 10.1016/j.cma.2016.08.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Enderling H, Chaplain MA, Anderson AR, Vaidya JS. A mathematical model of breast cancer development, local treatment and recurrence. J Theor Biol. 2007;246(2):245–59. 10.1016/j.jtbi.2006.12.010 [DOI] [PubMed] [Google Scholar]
- 46. Corwin D, Holdsworth C, Rockne RC, Trister AD, Mrugala MM, Rockhill JK, et al. Toward patient-specific, biologically optimized radiation therapy plans for the treatment of glioblastoma. PLoS One. 2013;8(11). 10.1371/journal.pone.0079115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Kim Y, Friedman A. Interaction of tumor with its microenvironment: A Mathematical Model. Bull Math Biol. 2010;72(5):1029–1068. 10.1007/s11538-009-9481-z [DOI] [PubMed] [Google Scholar]
- 48.Maini P. Modelling Aspects of Tumour Metabolism. Proc Int Cong Mathematicians. 2010;Indiana.
- 49. Kim Y, Lee HG, Dmitrieva N, Kim J, Kaur B, Friedman A. Choindroitinase ABC I-mediated enhancement of oncolytic virus spread and anti-tumor efficacy: A mathematical model. PLoS One. 2014;9(7):e102499 10.1371/journal.pone.0102499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Swanson KR, Alvord EC, Murray JD. Virtual resection of gliomas: Effect of extent of resection on recurrence. Math Comp Modelling. 2003;37:1177–1190. 10.1016/S0895-7177(03)00129-8 [DOI] [Google Scholar]
- 51. Kim Y, Roh S, Lawler S, Friedman A. miR451 and AMPK/MARK mutual antagonism in glioma cells migration and proliferation. PLoS One. 2011;6(12):e28293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. von Vietinghoff S, Ley K. Homeostatic regulation of blood neutrophil counts. J Immunol. 2008;181(8):5183–8. 10.4049/jimmunol.181.8.5183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Price TH, Dale DC. Neutrophil preservation: the effect of short-term storage on in vivo kinetics. J Clin Invest. 1977;59(3):475–80. 10.1172/JCI108662 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Rosenshein MS, Price TH DD. Neutropenia, inflammation, and the kinetics of transfused neutrophils in rabbits. J Clin Invest. 1979;64:580–585. 10.1172/JCI109496 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Basu S, Hodgson G, Katz M, Dunn AR. Evaluation of role of G-CSF in the production, survival, and release of neutrophils from bone marrow into circulation. Blood. 2002;100:854–861. 10.1182/blood.V100.3.854 [DOI] [PubMed] [Google Scholar]
- 56. Price TH, Chatta GS, Dale DC. Effect of recombinant granulocyte colony-stimulating factor on neutrophil kinetics in normal young and elderly humans. Blood. 1996;88:335–340. [PubMed] [Google Scholar]
- 57. Cartwright GE, Athens JW, Wintrobe MM. The Kinetics Of Granulopoiesis In Normal Man. Blood. 1964;24:780–803. [PubMed] [Google Scholar]
- 58. Tak T, Tesselaar K, Pillay J, Borghans JA, Koenderman L. What’s your age again? Determination of human neutrophil half-lives revisited. J Leukoc Biol. 2013;94(4):595–601. 10.1189/jlb.1112571 [DOI] [PubMed] [Google Scholar]
- 59. Pillay J, den Braber I, Vrisekoop N, Kwast LM, de Boer RJ, Borghans JA, et al. In vivo labeling with 2H2O reveals a human neutrophil lifespan of 5.4 days. Blood. 2010;116:625–627. 10.1182/blood-2010-01-259028 [DOI] [PubMed] [Google Scholar]
- 60. Dale DC, Liles WC, Llewellyn C, Rodger E, Price TH. Neutrophil transfusions: kinetics and functions of neutrophils mobilized with granulocyte-colony-stimulating factor and dexamethasone. Transfusion. 1998;38:713–721. 10.1046/j.1537-2995.1998.38898375509.x [DOI] [PubMed] [Google Scholar]
- 61. Steinbach KH, Schick P, Trepel F, Raffler H, Dohrmann J, Heilgeist G, et al. Estimation of kinetic parameters of neutrophilic, eosinophilic, and basophilic granulocytes in human blood. Blut. 1979;39:27–38. 10.1007/BF01008072 [DOI] [PubMed] [Google Scholar]
- 62. Andzinski L, Wu CF, Lienenklaus S, Kroger A, Weiss S, Jablonska J. Delayed apoptosis of tumor associated neutrophils in the absence of endogenous IFN-β. International Journal of Cancer. 2015;136(3):572–583. 10.1002/ijc.28957 [DOI] [PubMed] [Google Scholar]
- 63. Granot Z, Jablonska J. Distinct Functions of Neutrophil in Cancer and Its Regulation. Mediators Inflamm. 2015;2015(701067):1–11. 10.1155/2015/701067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Kim Y, Othmer HG. A hybrid model of tumor-stromal interactions in breast cancer. Bull Math Biol. 2013;75:1304–1350. 10.1007/s11538-012-9787-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Herbertz S, Sawyer JS, Stauber AJ, Gueorguieva I, Driscoll KE, Estrem ST, et al. Clinical development of galunisertib (LY2157299 monohydrate), a small molecule inhibitor of transforming growth factor-beta signaling pathway. Drug Design, Development and Therapy. 2015;9:4479–4499. 10.2147/DDDT.S86621 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. McKenna SD, Vergilis K, Arulanandam AR, Weiser WY, Nabioullin R, Tepper MA. Formation of human IFN-beta complex with the soluble type I interferon receptor IFNAR-2 leads to enhanced IFN stability, pharmacokinetics, and antitumor activity in xenografted SCID mice. J Interferon Cytokine Res. 2004;24(2):119–29. 10.1089/107999004322813363 [DOI] [PubMed] [Google Scholar]
- 67. Salmon P, Cotonnec JYL, Galazka A, Abdul-Ahad A, Darragh A. Pharmacokinetics and pharmacodynamics of recombinant human interferon-beta in healthy male volunteers. J Interferon Cytokine Res. 1996;16(10):759–64. 10.1089/jir.1996.16.759 [DOI] [PubMed] [Google Scholar]
- 68. Deng L, Liang H, Xu M, Yang X, Burnette B, Arina A, et al. STING-Dependent Cytosolic DNA Sensing Promotes Radiation-Induced Type I Interferon-Dependent Antitumor Immunity in Immunogenic Tumors. Immunity. 2014;41(5):843–52. 10.1016/j.immuni.2014.10.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Chen Y, Yan H, Wang Y, Shi Y, Dai G. Significance of baseline and change in neutrophil-to-lymphocyte ratio in predicting prognosis: a retrospective analysis in advanced pancreatic ductal adenocarcinoma. Sci Rep. 2017;7(1):753 10.1038/s41598-017-00859-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Zeren S, Yaylak F, Ozbay I, Bayhan Z. Relationship Between the Neutrophil to Lymphocyte Ratio and Parathyroid Adenoma Size in Patients With Primary Hyperparathyroidism. Int Surg. 2015;100(7–8):1185–9 [DOI] [PubMed] [Google Scholar]
- 71. Peng B, Wang YH, Liu YM, Ma LX. Prognostic significance of the neutrophil to lymphocyte ratio in patients with non-small cell lung cancer: a systemic review and meta-analysis. Int J Clin Exp Med. 2015;8(3):3098–106. [PMC free article] [PubMed] [Google Scholar]
- 72. Shimizu K, Okita R, Saisho S, Maeda A, Nojima Y, Nakata M. Preoperative neutrophil/lymphocyte ratio and prognostic nutritional index predict survival in patients with non-small cell lung cancer. World J Surg Oncol. 2015;13:291 10.1186/s12957-015-0710-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Huang QT, Man QQ, Hu J, Yang YL, Zhang YM, Wang W, et al. Prognostic significance of neutrophil-to-lymphocyte ratio in cervical cancer: A systematic review and meta-analysis of observational studies. Oncotarget. 2017;8(10):16755–16764. 10.18632/oncotarget.15157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Granot Z, Fridlender ZG. Plasticity beyond cancer cells and the immunosuppressive switch. Cancer Res. 2015;75(21):4441–5. 10.1158/0008-5472.CAN-15-1502 [DOI] [PubMed] [Google Scholar]
- 75. Gordon-Weeks AN, Lim SY, Yuzhalin AE, Jones K, Markelc B, Kim KJ, et al. Neutrophils promote hepatic metastasis growth through fibroblast growth factor 2-dependent angiogenesis in mice. Hepatology. 2017;65(6):1920–1935. 10.1002/hep.29088 [DOI] [PubMed] [Google Scholar]
- 76. Schaaf MB, Garg AD, Agostinis P. Defining the role of the tumor vasculature in antitumor immunity and immunotherapy. Cell Death Dis. 2018;9(2):115 10.1038/s41419-017-0061-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Marino S, Hogue IB, Ray CJ, Kirschner DE. A methodology for performing global uncertainty and sensitivity analysis in systems biology. Journal of Theoretical Biology. 2008;254(1):178–196. 10.1016/j.jtbi.2008.04.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Jonasch E, Haluska FG. Interferon in oncological practice: review of interferon biology, clinical applications, and toxicities. Oncologist. 2001;6(1):34–55. 10.1634/theoncologist.6-1-34 [DOI] [PubMed] [Google Scholar]
- 79. Tavakoli M, Manshadi SMP, Naderi N, Dehghan A, Azizi S. Unusual side effects of interferon Beta-1a in patient with multiple sclerosis. Mater Sociomed. 2012;24(3):203–5. 10.5455/msm.2012.24.203-205 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Essers MA, Offner S, Blanco-Bose WE, Waibler Z, Kalinke U, Duchosal MA, et al. IFNalpha activates dormant haematopoietic stem cells in vivo. Nature. 2009;458(7240):904–908. 10.1038/nature07815 [DOI] [PubMed] [Google Scholar]
- 81. Parker BS, Rautela J, Hertzog PJ. Antitumour actions of interferons: implications for cancer therapy. Nat Rev Cancer. 2016;16(3):131–144. 10.1038/nrc.2016.14 [DOI] [PubMed] [Google Scholar]
- 82. Brockwell NK, Owen KL, Zanker D, Spurling A, Rautela J, Duivenvoorden HM, et al. Neoadjuvant Interferons: Critical for Effective PD-1-Based Immunotherapy in TNBC. Cancer Immunol Res. 2017;5(10):871–884. 10.1158/2326-6066.CIR-17-0150 [DOI] [PubMed] [Google Scholar]
- 83. Lens MB, Dawes M. Interferon alfa therapy for malignant melanoma: a systematic review of randomized controlled trials. J Clin Oncol. 2002;20(7):1818–25. 10.1200/JCO.2002.07.070 [DOI] [PubMed] [Google Scholar]
- 84. Wheatley K, Ives N, Hancock B, Gore M, Eggermont A, Suciu S. Does adjuvant interferon-alpha for high-risk melanoma provide a worthwhile benefit? A meta-analysis of the randomised trials. Cancer Treat Rev. 2003;29(4):241–252. 10.1016/S0305-7372(03)00074-4 [DOI] [PubMed] [Google Scholar]
- 85. Kirkwood JM, Manola J, Ibrahim J, Sondak V, Ernstoff MS, Rao U. A pooled analysis of eastern cooperative oncology group and intergroup trials of adjuvant high-dose interferon for melanoma. Clin Cancer Res. 2004;10(5):1670–1677. 10.1158/1078-0432.CCR-1103-3 [DOI] [PubMed] [Google Scholar]
- 86. Bajetta E. Adjuvant use of interferon alpha 2b is not justified in patients with stage IIb/III melanoma. Nat Clin Pract Oncol. 2008;5(1):4–5. 10.1038/ncponc1007 [DOI] [PubMed] [Google Scholar]
- 87. Kingwell E, Evans C, Zhu F, Oger J, Hashimoto S, Tremlett H. Assessment of cancer risk with beta-interferon treatment for multiple sclerosis. J Neurol Neurosurg Psychiatry. 2014;85(10):1096–1102. 10.1136/jnnp-2013-307238 [DOI] [PubMed] [Google Scholar]
- 88. Connolly EC, Freimuth J, Akhurst RJ. Complexities of TGF-β targeted cancer therapy. International journal of biological sciences. 2012;8(7):964 10.7150/ijbs.4564 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89. Calone I, Souchelnytskyi S. Inhibition of TGFbeta signaling and its implications in anticancer treatments. Exp Oncol. 2012;34(1):9–16. [PubMed] [Google Scholar]
- 90. Doherty MR, Jackson MW. The Critical, Clinical Role of Interferon-Beta in Regulating Cancer Stem Cell Properties in Triple-Negative Breast Cancer. DNA Cell Biol. 2018;37(6):513–516. 10.1089/dna.2018.4247 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91. Ohshio Y, Teramoto K, Hashimoto M, Kitamura S, Hanaoka J, Kontani K. Inhibition of transforming growth factor-beta release from tumor cells reduces their motility associated with epithelial-mesenchymal transition. Oncol Rep. 2013;30(2):1000–1006. 10.3892/or.2013.2505 [DOI] [PubMed] [Google Scholar]
- 92. Okada Y, Wang T, Kasai K, Suzuki K, Takikawa Y. Regulation of transforming growth factor is involved in the efficacy of combined 5-fluorouracil and interferon alpha-2b therapy of advanced hepatocellular carcinoma. Cell Death Discov. 2018;4::42 10.1038/s41420-018-0040-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93. Xu Y, Li H, Bajrami B, Kwak H, Cao S, Liu P, et al. Cigarette smoke (CS) and nicotine delay neutrophil spontaneous death via suppressing production of diphosphoinositol pentakisphosphate. Proc Natl Acad Sci USA. 2013;110(19):7726–7731. 10.1073/pnas.1302906110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94. Kuijpers T, Lutter R. Inflammation and repeated infections in CGD: two sides of a coin. Cell Mol Life Sci. 2012;69(1):7–15. 10.1007/s00018-011-0834-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95. Kasahara Y, Iwai K, Yachie A, Ohta K, Konno A, Seki H, et al. Involvement of reactive oxygen intermediates in spontaneous and CD95 (Fas/APO-1)-mediated apoptosis of neutrophils. Blood. 1997;89(5):1748–1753. [PubMed] [Google Scholar]
- 96. Dibbert B, Weber M, Nikolaizik WH, Vogt P, Schoni MH, Blaser K, et al. Cytokine-mediated Bax deficiency and consequent delayed neutrophil apoptosis: a general mechanism to accumulate effector cells in inflammation. Proc Natl Acad Sci USA. 1999;96(23):13330–13335. 10.1073/pnas.96.23.13330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97. Scapini P, Lapinet-Vera JA, Gasperini S, Calzetti F, Bazzoni F, Cassatella MA. The neutrophil as a cellular source of chemokines. Immunol Rev. 2000;177:195–203. 10.1034/j.1600-065X.2000.17706.x [DOI] [PubMed] [Google Scholar]
- 98. Gabrilovich D, Nagaraj S. Myeloid-derived suppressor cells as regulators of the immune system. Nat Rev Immunol. 2009;9(3):162–174. 10.1038/nri2506 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99. Gregory AD, Houghton AM. Tumor-associated neutrophils: new targets for cancer therapy. Cancer Res. 2011;71(7):2411–6. 10.1158/0008-5472.CAN-10-2583 [DOI] [PubMed] [Google Scholar]
- 100. Tecchio C, Micheletti A, Cassatella MA. Neutrophil-derived cytokines: facts beyond expression. Front Immunol. 2014;5:508 10.3389/fimmu.2014.00508 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101. Sagiv JY, Michaeli J, Assi S, Mishalian I, Kisos H, Levy L, et al. Phenotypic diversity and plasticity in circulating neutrophil subpopulations in cancer. Cell Rep. 2015;10(4):562–73. 10.1016/j.celrep.2014.12.039 [DOI] [PubMed] [Google Scholar]
- 102. Coffelt SB, Kersten K, Doornebal CW, Weiden J, Vrijland K, Hau CS, et al. IL-17-producing γδ T cells and neutrophils conspire to promote breast cancer metastasis. Nature. 2015;522(7556):345–348. 10.1038/nature14282 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103. Yan B, Wei JJ, Yuan Y, Sun R, Li D, Luo J, et al. IL-6 cooperates with G-CSF to induce protumor function of neutrophils in bone marrow by enhancing STAT3 activation. J Immunol. 2013;190(11):5882–5893. 10.4049/jimmunol.1201881 [DOI] [PubMed] [Google Scholar]
- 104. Zhou L, Ivanov II, Spolski R, Min R, Shenderov K, Egawa T, et al. IL-6 programs TH-17 cell differentiation by promoting sequential engagement of the IL-21 and IL-23 pathways. Nat Immunol. 2007;8(9):967–974. 10.1038/ni1488 [DOI] [PubMed] [Google Scholar]
- 105. Malietzis G, Giacometti M, Kennedy RH, Athanasiou T, Aziz O, Jenkins JT. The emerging role of neutrophil to lymphocyte ratio in determining colorectal cancer treatment outcomes: a systematic review and meta-analysis. Ann Surg Oncol. 2014;21(12):3938–3946. 10.1245/s10434-014-3815-2 [DOI] [PubMed] [Google Scholar]
- 106. Walsh SR, Cook EJ, Goulder F, Justin TA, Keeling NJ. Neutrophil-lymphocyte ratio as a prognostic factor in colorectal cancer. J Surg Oncol. 2005;91(3):181–184. 10.1002/jso.20329 [DOI] [PubMed] [Google Scholar]
- 107. He JR, Shen GP, Ren ZF, Qin H, Cui C, Zhang Y, et al. Pretreatment levels of peripheral neutrophils and lymphocytes as independent prognostic factors in patients with nasopharyngeal carcinoma. Head Neck. 2012;34(12):1769–76. 10.1002/hed.22008 [DOI] [PubMed] [Google Scholar]
- 108. Krenn-Pilko S, Langsenlehner U, Thurner EM, Stojakovic T, Pichler M, Gerger A, et al. The elevated preoperative platelet-to-lymphocyte ratio predicts poor prognosis in breast cancer patients. Br J Cancer. 2014;110(10):2524–2530. 10.1038/bjc.2014.163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109. Pistelli M, Lisa MD, Ballatore Z, Caramanti M, Pagliacci A, Battelli N, et al. Pre-treatment neutrophil to lymphocyte ratio may be a useful tool in predicting survival in early triple negative breast cancer patients. BMC Cancer. 2015;15:195 10.1186/s12885-015-1204-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110. Halazun KJ, Hardy MA, Rana AA, Woodland DC, Luyten EJ, Mahadev S, et al. Negative impact of neutrophil-lymphocyte ratio on outcome after liver transplantation for hepatocellular carcinoma. Annals of Surgery. 2009;250(1):141–151. 10.1097/SLA.0b013e3181a77e59 [DOI] [PubMed] [Google Scholar]
- 111. Engblom C, Pfirschke C, Zilionis R, Martins JDS, Bos ASA, Courties G, et al. Osteoblasts remotely supply lung tumors with cancer-promoting SiglecFhigh neutrophils. Science. 2017;358(6367):eaal5081 10.1126/science.aal5081 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112. Bracarda S, Eggermont AM, Samuelsson J. Redefining the role of interferon in the treatment of malignant diseases. Eur J Cancer. 2010;46(2):284–97. 10.1016/j.ejca.2009.10.013 [DOI] [PubMed] [Google Scholar]
- 113. Chawla-Sarkar M, Lindner DJ, Liu YF, Williams BR, Sen GC, Silverman RH, et al. Apoptosis and interferons: role of interferon-stimulated genes as mediators of apoptosis. Apoptosis. 2003;8(3):237–249. 10.1023/A:1023668705040 [DOI] [PubMed] [Google Scholar]
- 114. Maeda S, Wada H, Naito Y, Nagano H, Simmons S, Kagawa Y, et al. Interferon-alpha acts on the S/G2/M phases to induce apoptosis in the G1 phase of an IFNAR2-expressing hepatocellular carcinoma cell line. J Biol Chem. 2014;289(34):23786–95. 10.1074/jbc.M114.551879 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115. Rogge L, D’Ambrosio D, Biffi M, Penna G, Minetti LJ, Presky DH, et al. The role of Stat4 in species-specific regulation of Th cell development by type I IFNs. J Immunol. 1998;161(12):6567–74. [PubMed] [Google Scholar]
- 116. Biron CA, Nguyen KB, Pien GC, Cousens LP, Salazar-Mather TP. Natural killer cells in antiviral defense: function and regulation by innate cytokines. Annu Rev Immunol. 1999;17:189–220. 10.1146/annurev.immunol.17.1.189 [DOI] [PubMed] [Google Scholar]
- 117. Salazar-Mather TP, Lewis CA, Biron CA. Type I interferons regulate inflammatory cell trafficking and macrophage inflammatory protein 1alpha delivery to the liver. J Clin Invest. 2002;110(3):321–30. 10.1172/JCI15376 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118. Blanco P, Palucka AK, Gill M, Pascual V, Banchereau J. Induction of dendritic cell differentiation by IFN-alpha in systemic lupus erythematosus. Science. 2001;294(5546):1540–1543. 10.1126/science.1064890 [DOI] [PubMed] [Google Scholar]
- 119. Sistigu A, Yamazaki T, Vacchelli E, Chaba K, Enot DP, Adam J, et al. Cancer cell-autonomous contribution of type I interferon signaling to the efficacy of chemotherapy. Nat Med. 2014;20(11):1301–1309. 10.1038/nm.3708 [DOI] [PubMed] [Google Scholar]
- 120. Lim JY, Gerber SA, Murphy SP, Lord EM. Type I interferons induced by radiation therapy mediate recruitment and effector function of CD8(+) T cells. Cancer Immunol Immunother. 2014;63(3):259–71. 10.1007/s00262-013-1506-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121. Oh SS, Moon C, Kim DH, Song H, Park S, Fu Y, et al. Adenovirally delivered IFN-β exerts antitumor effects through transient T-lymphocyte depletion and Ag-specific T-cell proliferation. Int J Mol Med. 2012;29(6):1153–1157. 10.3892/ijmm.2012.936 [DOI] [PubMed] [Google Scholar]
- 122. Huang H, Xiao T, Ji H, Liu XY. Interferon-beta-armed oncolytic adenovirus induces both apoptosis and necroptosis in cancer cells. Acta Biochim Biophys Sin(Shanghai). 2012;44:737–745. [DOI] [PubMed] [Google Scholar]
- 123. Park MY, Kim DR, Jung HW, Yoon HI, Lee JH, Lee CT. Genetic immunotherapy of lung cancer using conditionally replicating adenovirus and adenovirus-interferon-beta. Cancer Gene Ther. 2010;17(5):356–64. 10.1038/cgt.2009.78 [DOI] [PubMed] [Google Scholar]
- 124. Shih CS, Laurie N, Holzmacher J, Spence Y, Nathwani AC, Davidoff AM, et al. AAV-mediated local delivery of interferon-beta for the treatment of retinoblastoma in preclinical models. Neuromolecular Med. 2009;11(1):43–52. 10.1007/s12017-009-8059-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125. Wakabayashi T, Natsume A, Hashizume Y, Fujii M, Mizuno M, Yoshida J. A phase I clinical trial of interferon-beta gene therapy for high-grade glioma: novel findings from gene expression profiling and autopsy. J Gene Med. 2008;10(4):329–339. 10.1002/jgm.1160 [DOI] [PubMed] [Google Scholar]
- 126. Kirkwood JM, Tarhini AA, Moschos SJ, Panelli MC. Adjuvant therapy with high-dose interferon alpha 2b in patients with high-risk stage IIB/III melanoma. Nat Clin Pract Oncol. 2008;5(1):2–3. 10.1038/ncponc1004 [DOI] [PubMed] [Google Scholar]
- 127. Amulic B, Cazalet C, Hayes GL, Metzler KD, Zychlinsky A. Neutrophil function: from mechanisms to disease. Annu Rev Immunol. 2012;30:459–489. 10.1146/annurev-immunol-020711-074942 [DOI] [PubMed] [Google Scholar]
- 128. Gabelloni ML, Trevani AS, Sabatte J, Geffner J. Mechanisms regulating neutrophil survival and cell death. Semin Immunopathol. 2013;35(4):423–437. 10.1007/s00281-013-0364-x [DOI] [PubMed] [Google Scholar]
- 129. Ibrahim SA, Kulshrestha A, Katara GK, Beaman KD. Delayed neutrophil apoptosis is regulated by cancer associated a2 isoform vacuolar ATPase. J Immunol. 2017;198(1 Supplement):76.15. [Google Scholar]
- 130. Takeshima T, Pop LM, Laine A, Iyengar P, Hannan ESVR. Key role for neutrophils in radiation-induced antitumor immune responses: Potentiation with G-CSF. Proc Natl Acad Sci USA. 2016;113(40):11300–11305. 10.1073/pnas.1613187113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131. Grimes M, Hall B, Foltz L, Levy T, Rikova K, Gaiser J, et al. Integration of protein phosphorylation, acetylation, and methylation data sets to outline lung cancer signaling networks. Sci Signal. 2018;11(531). 10.1126/scisignal.aaq1087 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132. Moroy G, Alix AJ, Sapi J, Hornebeck W, Bourguet E. Neutrophil elastase as a target in lung cancer. Anticancer Agents Med Chem. 2012;12(6):565–79. 10.2174/187152012800617696 [DOI] [PubMed] [Google Scholar]
- 133. Gong L, Cumpian AM, Caetano MS, Ochoa CE, la Garza MMD, Lapid DJ, et al. Promoting effect of neutrophils on lung tumorigenesis is mediated by CXCR2 and neutrophil elastase. Mol Cancer. 2013;12(1):154 10.1186/1476-4598-12-154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134. Hattar K, Franz K, Ludwig M, Sibelius U, Wilhelm J, Lohmeyer J, et al. Interactions between neutrophils and non-small cell lung cancer cells: enhancement of tumor proliferation and inflammatory mediator synthesis. Cancer Immunol Immunother. 2014;63(12):1297–306. 10.1007/s00262-014-1606-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135. Aktas ON, Ozturk AB, Erman B, Erus S, Tanju S, Dilege S. Role of natural killer cells in lung cancer. J Cancer Res Clin Oncol. 2018;144(6):997–1003. 10.1007/s00432-018-2635-3 [DOI] [PubMed] [Google Scholar]
- 136. Revels SL, Lee JM. Anti-angiogenic therapy in nonsquamous non-small cell lung cancer (NSCLC) with tyrosine kinase inhibition (TKI) that targets the VEGF receptor (VEGFR): perspective on phase III clinical trials. J Thorac Dis. 2018;10(2):617–620. 10.21037/jtd.2018.01.105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137. Qu J, Zhang Y, Chen X, Yang H, Zhou C, Yang N. Newly developed anti-angiogenic therapy in non-small cell lung cancer. Oncotarget. 2017;9(11):10147–10163. 10.18632/oncotarget.23755 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138. Stratigos M, Matikas A, Voutsina A, Mavroudis D, Georgoulias V. Targeting angiogenesis in small cell lung cancer. Transl Lung Cancer Res. 2016;5(4):389–400. 10.21037/tlcr.2016.08.04 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139. Lee B, Konen J, Wilkinson S, Marcus AI, Jiang Y. Local alignment vectors reveal cancer cell-induced ECM fiber remodeling dynamics. Sci Rep. 2017;7:39498 10.1038/srep39498 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140. Siegelin MD, Borczuk AC. Epidermal growth factor receptor mutations in lung adenocarcinoma. Lab Invest. 2014;94(2):129–137. 10.1038/labinvest.2013.147 [DOI] [PubMed] [Google Scholar]
- 141. Liu X, Wang WP, Zhang C, Ma Z. Epidermal growth factor receptor (EGFR): A rising star in the era of precision medicine of lung cancer. Oncotarget. 2017;8(30):50209–50220. 10.18632/oncotarget.16854 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142. Pyonteck SM, Akkari L, Schuhmacher AJ, Bowman RL, Sevenich L, Quail DF, et al. CSF-1R inhibition alters macrophage polarization and blocks glioma progression. Nat Med. 2013;19(10):1264–72. 10.1038/nm.3337 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143. Houghton AM, Rzymkiewicz DM, Ji H, Gregory AD, Egea EE, Metz HE, et al. Neutrophil elastase-mediated degradation of IRS-1 accelerates lung tumor growth. Nat Med. 2010;16(2):219–223. 10.1038/nm.2084 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144. Sangaletti S, Tripodo C, Vitali C, Portararo P, Guarnotta C, Casalini P, et al. Defective stromal remodeling and neutrophil extracellular traps in lymphoid tissues favor the transition from autoimmunity to lymphoma. Cancer Discov. 2014;4(1):110–129. 10.1158/2159-8290.CD-13-0276 [DOI] [PubMed] [Google Scholar]
- 145. Uribe-Querol E, Rosales C. Neutrophils in Cancer: Two Sides of the Same Coin. J Immunol Res. 2015;2015::983698 10.1155/2015/983698 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146. Arelaki S, Arampatzioglou A, Kambas K, Papagoras C, Miltiades P, Angelidou I, et al. Gradient Infiltration of Neutrophil Extracellular Traps in Colon Cancer and Evidence for Their Involvement in Tumour Growth. PLoS One. 2016;11(5):e0154484 10.1371/journal.pone.0154484 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 147. Cools-Lartigue J, Spicer J, Najmeh S, Ferri L. Neutrophil extracellular traps in cancer progression. Cell Mol Life Sci. 2014;71(21):4179–94. 10.1007/s00018-014-1683-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148. Demers M, Wagner DD. Neutrophil extracellular traps: A new link to cancer-associated thrombosis and potential implications for tumor progression. Oncoimmunology. 2013;2(2):e22946 10.4161/onci.22946 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149. Wculek SK, Malanchi I. Neutrophils support lung colonization of metastasis-initiating breast cancer cells. Nature. 2015;528(7582):413–417. 10.1038/nature16140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150. Tohme S, Yazdani HO, Al-Khafaji AB, Chidi AP, Loughran P, Mowen K, et al. Neutrophil Extracellular Traps Promote the Development and Progression of Liver Metastases after Surgical Stress. Cancer Res. 2016;76(6):1367–1380. 10.1158/0008-5472.CAN-15-1591 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151. Kim Y, Stolarska M, Othmer HG. A hybrid model for tumor spheroid growth in vitro I: Theoretical development and early results. Math Models Methods in Appl Scis. 2007;17:1773–1798. 10.1142/S0218202507002479 [DOI] [Google Scholar]
- 152. Kim Y, Stolarska M, Othmer HG. The role of the microenvironment in tumor growth and invasion. Prog Biophys Mol Biol. 2011;106:353–379. 10.1016/j.pbiomolbio.2011.06.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153. Kim Y. Regulation of cell proliferation and migration in glioblastoma: New therapeutic approach. Frontiers in Molecular and Cellular Oncology. 2013;3:53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154. Kim Y, Roh S. A hybrid model for cell proliferation and migration in glioblastoma. Discrete and Continuous Dynamical Systems-B. 2013;18(4):969–1015. 10.3934/dcdsb.2013.18.969 [DOI] [Google Scholar]
- 155. Kim Y, Othmer H. Hybrid models of cell and tissue dynamics in tumor growth. Math Bios Eng. 2015;12(6):1141–1156. 10.3934/mbe.2015.12.1141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156. Kim Y, Powathil G, Kang H, Trucu D, Kim H, Lawler S, et al. Strategies of eradicating glioma cells: A multi-scale mathematical model with miR-451-AMPK-mTOR control. PLoS One. 2015;10(1):e0114370 10.1371/journal.pone.0114370 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157. Crestani B, Cornillet P, Dehoux M, Rolland C, Guenounou M, Aubier M. Alveolar type II epithelial cells produce interleukin-6 in vitro and in vivo. Regulation by alveolar macrophage secretory products. J Clin Invest. 1994;94(2):731–40. 10.1172/JCI117392 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158. Yao X, Huang J, Zhong H, Shen N, Faggioni R, Fung M, et al. Targeting interleukin-6 in inflammatory autoimmune diseases and cancers. Pharmacol Ther. 2014;141(2):125–39. 10.1016/j.pharmthera.2013.09.004 [DOI] [PubMed] [Google Scholar]
- 159. Veldhoen M, Hocking RJ, Atkins CJ, Locksley RM, Stockinger B. TGF-β in the context of an inflammatory cytokine milieu supports de novo differentiation of IL-17-producing T cells. Immunity. 2006;24(2):179–189. 10.1016/j.immuni.2006.01.001 [DOI] [PubMed] [Google Scholar]
- 160. Korn T, Bettelli E, Gao W, Awasthi A, Jäger A, Strom TB, et al. IL-21 initiates an alternative pathway to induce proinflammatory TH17 cells. Nature. 2007;448(7152):484–487. 10.1038/nature05970 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161. Piccard H, Muschel RJ, Opdenakker G. On the dual roles and polarized phenotypes of neutrophils in tumor development and progression. Crit Rev Oncol Hematol. 2012;82(3):296–309. 10.1016/j.critrevonc.2011.06.004 [DOI] [PubMed] [Google Scholar]
- 162. Ardi VC, Kupriyanova TA, Deryugina EI, Quigley JP. Human neutrophils uniquely release TIMP-free MMP-9 to provide a potent catalytic stimulator of angiogenesis. Proc Natl Acad Sci USA. 2007;104(51):20262–20267. 10.1073/pnas.0706438104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 163. Coussens LM, Tinkle CL, Hanahan D, Werb Z. MMP-9 supplied by bone marrow-derived cells contributes to skin carcinogenesis. Cell. 2000;103(3):481–90. 10.1016/S0092-8674(00)00139-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164. Acuff HB, Carter KJ, Fingleton B, Gorden DL, Matrisian LM. Matrix metalloproteinase-9 from bone marrow-derived cells contributes to survival but not growth of tumor cells in the lung microenvironment. Cancer Res. 2006;66(1):259–66. 10.1158/0008-5472.CAN-05-2502 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165. Masson V, d l Ballina LR, Munaut C, Wielockx B, Jost M, Maillard C, et al. Contribution of host MMP-2 and MMP-9 to promote tumor vascularization and invasion of malignant keratinocytes. FASEB J. 2005;19(2):234–6. 10.1096/fj.04-2140fje [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166. Welch DR, Schissel DJ, Howrey RP, Aeed PA. Tumor-elicited polymorphonuclear cells, in contrast to normal circulating polymorphonuclear cells, stimulate invasive and metastatic potentials of rat mammary adenocarcinoma cells. Proc Natl Acad Sci U S A. 1989;86(15):5859–63. 10.1073/pnas.86.15.5859 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167. Romani L, Mencacci A, Cenci E, Spaccapelo R, Sero GD, Nicoletti I, et al. Neutrophil production of IL-12 and IL-10 in candidiasis and efficacy of IL-12 therapy in neutropenic mice. J Immunol. 1997;158(11):5349–56. [PubMed] [Google Scholar]
- 168. Curiel TJ. Tregs and rethinking cancer immunotherapy. J Clin Invest. 2007;117(5):1167–117. 10.1172/JCI31202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169. Bach JF. Regulatory T cells under scrutiny. Nat Rev Immunol. 2003;3:189–198. 10.1038/nri1026 [DOI] [PubMed] [Google Scholar]
- 170. Shevach EM. CD4+ CD25+ suppressor T cells: more questions than answers. Nat Rev Immunol. 2002;2:389–400. 10.1038/nri821 [DOI] [PubMed] [Google Scholar]
- 171. Levings MK, Sangregorio R, Roncarolo MG. Human CD25(+)CD4(+) T regulatory cells suppress naive and memory T cell proliferation and can be expanded in vitro without loss of function. J Exp Med. 2001;193(11):1295–302. 10.1084/jem.193.11.1295 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172. Wang RF. Immune suppression by tumor-specific CD4+ regulatory T-cells in cancer. Semin Cancer Biol. 2006;16(1):73–9. 10.1016/j.semcancer.2005.07.009 [DOI] [PubMed] [Google Scholar]
- 173. Wang RF, Peng G, Wang HY. Regulatory T cells and Toll-like receptors in tumor immunity. Semin Immunol. 2006;18(2):136–42. 10.1016/j.smim.2006.01.008 [DOI] [PubMed] [Google Scholar]
- 174. Chen ML, Pittet MJ, Gorelik L, Flavell RA, Weissleder R, von Boehmer H, et al. Regulatory T cells suppress tumor-specific CD8 T cell cytotoxicity through TGF-beta signals in vivo. Proc Natl Acad Sci USA. 2005;102:419–424. 10.1073/pnas.0408197102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 175. Fu S, Zhang N, Yopp AC, Chen D, Mao M, Chen D, et al. TGF-beta induces Foxp3 + T-regulatory cells from CD4 + CD25 - precursors. Am J Transplant. 2004;4(10):1614–27. 10.1111/j.1600-6143.2004.00566.x [DOI] [PubMed] [Google Scholar]
- 176. Ni XY, Sui HX, Liu Y, Ke SZ, Wang YN, Gao FG. TGF-beta of lung cancer microenvironment upregulates B7H1 and GITRL expression in dendritic cells and is associated with regulatory T cell generation. Oncol Rep. 2012;28(2):615–21. 10.3892/or.2012.1822 [DOI] [PubMed] [Google Scholar]
- 177. Kinoshita T, Ishii G, Hiraoka N, Hirayama S, Yamauchi C, Aokage K, et al. Forkhead box P3 regulatory T cells coexisting with cancer associated fibroblasts are correlated with a poor outcome in lung adenocarcinoma. Cancer Sci. 2013;104(4):409–15. 10.1111/cas.12099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 178. Tao L, Huang G, Song H, Chen Y, Chen L. Cancer associated fibroblasts: An essential role in the tumor microenvironment. Oncol Lett. 2017;14(3):2611–2620. 10.3892/ol.2017.6497 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 179. Choe C, Shin YS, Kim C, Choi SJ, Lee J, Kim SY, et al. Crosstalk with cancer-associated fibroblasts induces resistance of non-small cell lung cancer cells to epidermal growth factor receptor tyrosine kinase inhibition. Onco Targets Ther. 2015;8:3665–3678. 10.2147/OTT.S89659 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 180. Wang Z, Lin S, Li JJ, Xu Z, Yao H, Zhu X, et al. MYC protein inhibits transcription of the microRNA cluster MC-let-7a-1—let-7d via noncanonical e-box. Journal of Biological Chemistry. 2011;286(46):39703–39714. 10.1074/jbc.M111.293126 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 181. Takamizawa J, Konishi H, Yanagisawa K, Tomida S, Osada H, Endoh H, et al. Reduced expression of the let-7 microRNAs in human lung cancers in association with shortened postoperative survival. Cancer Research. 2004;64(11):3753 10.1158/0008-5472.CAN-04-0637 [DOI] [PubMed] [Google Scholar]
- 182. Johnson SM, Grosshans H, Shingara J, Byrom M, Jarvis R, Cheng A, et al. RAS is regulated by the let-7 microRNA family. Cell. 2005;120(5):635–647. 10.1016/j.cell.2005.01.014 [DOI] [PubMed] [Google Scholar]
- 183. Mitselou A, Batistatou A, Nakanishi Y, Hirohashi S, Vougiouklakis T, Charalabopoulos K. Comparison of the dysadherin and E-cadherin expression in primary lung cancer and metastatic sites. Histology and Histopathology. 2010;25(10):1257–1267. 10.14670/HH-25.1257 [DOI] [PubMed] [Google Scholar]
- 184. Roberts P, Der C. Targeting the Raf-MEK-ERK mitogen-activated protein kinase cascade for the treatment of cancer. Oncogene. 2007;26(22):3291–3310. 10.1038/sj.onc.1210422 [DOI] [PubMed] [Google Scholar]
- 185. Zhao C, Du G, Skowronek K, Frohman MA, Bar-Sagi D. Phospholipase D2-generated phosphatidic acid couples EGFR stimulation to Ras activation by Sos. Nature Cell Biology. 2007;9(6):707–712. 10.1038/ncb1594 [DOI] [PubMed] [Google Scholar]
- 186. Brown KS, Hill CC, Calero GA, Myers CR, Lee KH, Sethna JP, et al. The statistical mechanics of complex signaling networks: nerve growth factor signaling. Physical Biology. 2004;1:184 10.1088/1478-3967/1/3/006 [DOI] [PubMed] [Google Scholar]
- 187. Huang S, Ren X, Wang L, Zhang L, Wu X. Lung-cancer chemoprevention by induction of synthetic lethality in mutant KRAS premalignant cells in vitro and in vivo. Cancer Prevention Research. 2011;4(5):666 10.1158/1940-6207.CAPR-10-0235 [DOI] [PubMed] [Google Scholar]
- 188. Bettelli E, Carrier Y, Gao W, Korn T, Strom TB, Oukka M, et al. Reciprocal developmental pathways for the generation of pathogenic effector TH17 and regulatory T cells. Nature. 2006;441(7090):235–238. 10.1038/nature04753 [DOI] [PubMed] [Google Scholar]
- 189. Abulaiti A, Shintani Y, Funaki S, Nakagiri T, Inoue M, Sawabata N, et al. Interaction between non-small-cell lung cancer cells and fibroblasts via enhancement of TGF-beta signaling by IL-6. Lung Cancer. 2013;82(2):204–13. 10.1016/j.lungcan.2013.08.008 [DOI] [PubMed] [Google Scholar]
- 190. Tirino V, Camerlingo R, Bifulco K, Irollo E, Montella R, Paino F, et al. TGF-β1 exposure induces epithelial to mesenchymal transition both in CSCs and non-CSCs of the A549 cell line, leading to an increase of migration ability in the CD133+ A549 cell fraction. Cell Death Dis. 2013;4:e620 10.1038/cddis.2013.144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 191. Borregaard N. Neutrophils, from marrow to microbes. Immunity. 2010;33:657–70. 10.1016/j.immuni.2010.11.011 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(PDF)
Data Availability Statement
All relevant data are within the manuscript and its Supporting Information files.