Improved Modeling of Halogenated Ligand-Protein Interactions using the Drude Polarizable and CHARMM Additive Empirical Force Fields

Abstract

Halogenated ligands can participate in nonbonding interactions with proteins via halogen bond (XB) or halogen-hydrogen bond donor (X-HBD) interactions. In the context of molecular dynamics (MD) simulations, the accuracy of the simulations depends strongly on the force field (FF) used. To assure good reproduction of XB and X-HBD interactions with proteins, we optimized the previously developed additive CHARMM36/CHARMM General force field (CGenFF) and Drude polarizable force field by including atom pair-specific Lennard-Jones parameters for aromatic halogen-protein interactions. The optimization targeted quantum mechanical interaction energy surfaces with the developed parameters then examined for their ability to reproduce experimental halogen-containing ligand-protein interactions in MD simulations. The calculated halogenated ligand interaction geometries were in good overall agreement with the experimental crystal data for both the polarizable and additive FFs, showing that these models can accurately treat both XB and X-HBD interactions. Analysis of the ligand-protein interactions shows significant contributions of polarizability to binding occurring in the Drude FF, with self-polarization energy making both favorable and unfavorable contributions to binding. Further analysis of the dipole moments from aqueous solution to protein indicates the polarizable FF accounts for subtle changes of the environment of the ligands that can impact binding. The present work demonstrates the utility of the updated additive CHARMM36/CGenFF and polarizable Drude FFs for the study of halogenated ligand-protein interactions in computer-aided drug design.

Graphical Abstract

Introduction

The inclusion of the halogens during ligand optimization represents an important aspect of drug design. This is due to the potential of halogens to improve selectivity and binding affinity as well as physiochemical properties related to bioavailability, thereby leading to better therapeutic agents.^1,2 These properties lead to a significant number of drug candidates and launched drugs containing halogens.³ In earlier drug design campaigns the lipophilic or hydrophobic contributions of halogen were mainly considered with respect to improving biological activity.^2,4 Recently, specific ligand-protein interactions involving halogens are being considered due to studies showing halogens to participate in halogen bonds (XB).^1,2,5 In addition, halogens may contribute to ligand binding via halogen-hydrogen bond donor (X-HBD) interactions that are potentially more favorable than halogen bonds as indicated by quantum mechanical (QM) calculations and survey data from the Protein Data Bank (PDB).⁶

In drug discovery, computer-aided drug design (CADD) is able to speed up the identification of lead compounds as well as facilitate their optimization.^8–11 Molecular dynamics (MD) simulation-based methods are often used to predict binding orientations and provide thermodynamic information, including the prediction of the absolute or relative binding affinity of ligands. In order to apply these approaches to halogen-containing compounds, well-developed force fields are required. Recent efforts have extended the widely used additive force fields to explicitly treat halogenated ligands, including extensions of CGenFF (CHARMM General Force Field),^12–16 OPLS (Optimized Potentials for Liquid Simulations),^17–20 and GAFF (Generalized AMBER Force Field).^21–24 In addition, polarizable force fields that explicitly treat electronic polarizability have been introduced,^25–27 including both the classical Drude^28–41 and AMOEBA force fields (FFs).^42–44 With the above additive and Drude polarizable FFs, improved treatment of halogens has involved attaching a charged virtual particle to the halogen to mimic the σ-hole in halogen and adequately reproduce XBs.^{13,20,23,24,45,46}

An important feature of halogens is their asymmetric van der Waals (vdW) surface associated with the shift of the electron density resulting in a shorter electron repulsion distance along the halogen linear to the C-X bond.⁴⁷ Moreover, a recent study indicates that the vdW contribution of halogens could significantly affect ligand-protein binding energies.⁴⁸ Accordingly, it is important for a force field to capture the asymmetric vdW surface of the halogen. In the region linear to C-X bond, this requires the electropositive σ-hole to have an effective smaller radius when interacting with nucleophilic atoms to allow for the shorter interaction distances, while the perpendicular peripheral region of halogens should have a larger effective radius, allowing for relatively longer interaction distances with electrophilic atoms.⁴⁷ However, to date only a few halogen FFs considered such features during parametrization.^47,49 In our recent halogen polarizable force field⁴⁹ based on the classical Drude oscillator model⁵⁰ the model was parametrized to reproduce the asymmetric vdW surface of halogens to more accurately treat both XB and X-HBD interactions. This was achieved by assigning atom pair-specific Lennard-Jones (LJ) parameters⁵¹ between the halogen Drude particles and hydrogens on hydrogen bond donors (i.e. an NBFIX term in CHARMM nomenclature^52–54). This term in combination with the inclusion of polarizability yielded improved modeling of halogen-water interactions as well as reproducing pure solvent properties and hydration free energies.

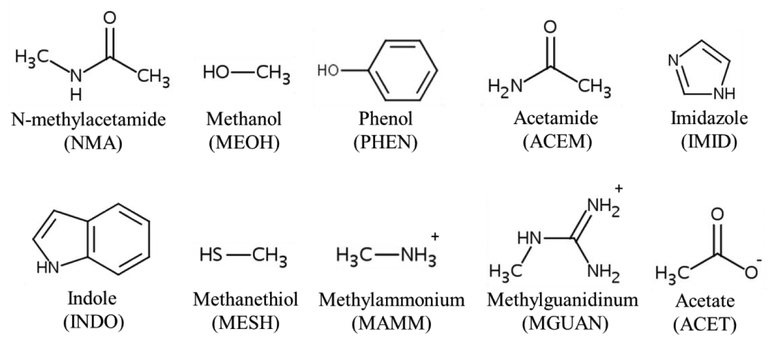
In this study, atom pair-specific LJ parameters on halogen Drude particles were extended to selected hydrogen bond donors and acceptors present in proteins and were optimized targeting representative small model compounds (Figure 1). The halogenated model compounds in this work focused on chlorobenzene (CHLB) and bromobenzene (BROB), as chlorine and bromine are often used during drug development. Iodobenzene was not considered as only 1.8 % of the organohalogens include iodine.³ These parameters were initially optimized targeting quantum mechanical (QM) interaction energy surfaces between halogen and protein model compounds. In addition, atom pair-specific LJ parameters were added to the additive CHARMM36/CGenFF FF to improve the agreement with the QM X-HBD interactions. The optimized atom pair-specific LJ parameters were then examined with respect to their ability to reproduce non-bonded interactions of halogen-containing ligands or a halogen-modified residue with the surrounding proteins occurring in crystallographic structures using MD simulations. With these parameters, the calculated halogenated-ligand/residue interaction geometries were in good overall agreement with the experimental data for both the polarizable and additive FFs. These results indicate that the developed polarizable and additive halogen force fields can accurately treat both XB and X-HBD interactions, thereby indicating their utility in computer-aided drug design.

Figure 1.

Abbreviations and 2D structures of the protein model compounds.

Computational methods

Quantum mechanical calculations

QM geometry optimizations were performed at the MP2 level of theory with the aug-cc-pVDZ basis set⁵⁵ for chlorobenzene (CHLB) and protein model compounds (Figure 1), including N-methylacetamide (NMA), methanol (MEOH), and phenol (PHEN), acetamide (ACEM), imidazole (IMID), indole (INDO), methanethiol (MESH), methylammonium (MAMM), methylguanidinum (MGUAN), and acetate (ACET). Bromobenzene (BROB) was optimized at the MP2 level of theory with the aug-cc-pVDZ-PP basis set.^56,57 All the QM geometry optimizations were performed using Gaussian03.⁵⁸

Single-point interaction energies for CHLB and BROB with the protein model compounds were obtained at the RIMP2 level of theory with the cc-pVQZ basis set⁵⁵ using PSI4.⁵⁹ The basis set superposition error (BSSE) was corrected using the counterpoise method.⁶⁰ In the interaction energy calculations, the intramolecular geometries of the two interacting molecules were kept rigid in their gas-phase QM optimized geometries. In calculating the QM interaction energies, when the halogen acts as a hydrogen bond acceptor (HBA), the hydrogen bond donor (HBD) hydrogen of each moiety was directed toward the halogen in both the perpendicular and linear orientations (Figure S2 and S4). When the halogen participates in a halogen bond interacting with a HBA, the HBA atom of each moiety was directed toward the halogen along C-X direction (linear orientation, Figure S3 and S5). The interaction energy profiles were calculated by varying the distance between the halogen and the interacting atom from 1.5 to 5.0 Å in intervals of 0.1 Å.

Molecular mechanical calculations

Additive force field calculations used the CHARMM General Force Field^53,54 for the small model compounds and the CHARMM36 protein model.⁵² We note that the present parameters will also be compatible with the earlier C22/CMAP^61,62 and more recent C36m parameters⁶³ as well as the remainder of the C36 macromolecular force field.^64–70 Polarizable calculations used the Drude-2013 protein force field⁷¹ with the parameters for the ligands built based on the published Drude polarizable parameters for small molecules^32,34,38 as well as the new halogen-protein non-bond parameters optimized in the present study. In addition, dihedral linkages in the ligands not previously optimized were refined as part of the present study (see Supporting Information Table S17). Molecular mechanics calculations were performed with the programs CHARMM^52–54 and NAMD⁷².

To calculate the interaction energies of the halogenated benzenes with the protein model compounds, the geometries in each interaction orientation were identical to those used in the QM calculations. In the additive model, the interaction energies were obtained by taking the energy difference between the CHLB/BROB-protein model compound complex and the CHLB/BROB/protein model compound monomers (e.g. equivalent to the interaction energy between the halogenated benzenes and protein model compound monomers). In the Drude model, relaxation of the Drude particles (i.e. self-consistent field (SCF) calculation) was performed via minimization by the steepest-descent (SD) and adopted-basis Newton-Raphson (ABNR) algorithms to reach a force gradient of 10⁻⁵ kcal·mol⁻¹·Å⁻¹ while the atomic positions were restrained with a force constant of 10⁷ kcal/mol/Ų. This was performed for the individual monomers (E_monomer) and then for the complex (E_complex) with the interaction energy calculated as E_inter = E_complex – (E_monomer1 + E_monomer2).

MD simulations were performed on eight systems including seven complexes that include halogenated ligands and one protein crystal with a halogenated lysine. Starting coordinates for all the protein-ligand complexes/modified protein were taken from the Protein Data Bank.⁶ Systems under study include human thrombin (PDB id: 2ZC9),⁷³ protein kinase (PDB id: 2UW8),⁷⁴ eukaryotic initiation factor 4E (PDB id: 4DT6),⁷⁵ human MutT Homolog1 (MTH1) protein (PDB id: 4N1T),⁷⁶ transcriptional activator protein LasR (PDB id: 3IX8),⁷⁷ PDZ domain with 4-bromobenzoic acid modified lysine (LYS9) (PDB id: 4NMV),⁷⁸ aminoacyl-tRNA synthetase (PDB id: 2AG6),⁷⁹ and phenazine biosynthesis protein (PDB id: 3JUM).⁸⁰ The protein coordinate and structure files were initially prepared in CHARMM additive formats using the PDB Reader module in the CHARMM-GUI.⁸¹ These additive coordinate and structure files were then submitted to the Drude Prepper module in the CHARMM-GUI⁸¹ to obtain files in Drude format.

For the polarizable Drude simulations the systems were solvated in a rectangular box with a 10 Å minimum distance between the edge of the box and the protein with the SWM4-NDP water⁸² and Na⁺ or Cl⁻ ions^83,84 were added to neutralize the systems as required. MD simulations were carried out using NAMD.⁷² The dual Langevin thermostat integrator was used with a 20 ps⁻¹ damping coefficient for Drude oscillators and a 5 ps⁻¹ damping coefficient for the atoms.⁸⁵ SHAKE was used to fix bonds involving hydrogen atoms.⁸⁶ Short-range LJ forces were switched to zero from 10–12 Å.⁸⁷ Electrostatic interactions were computed with the smooth particle mesh Ewald method with a real space cutoff of 12 Å, a kappa factor of 0.34 and a 6-order spline.^88,89 Each system was simulated under isothermal-isobaric (NPT) conditions at the temperature where the crystals were obtained, and the pressure was set at 1 atm using Langevin piston pressure control with a piston oscillation period of 200 fs and a relaxation time of 100 fs. A 100ps equilibration was performed with a 0.5 fs time step with all heavy atom restrained using a harmonic force constant of 1 kcal/mol·Å² followed by a 20 ns production simulation with a 1.0 fs time step. In the production simulations weak restraints were applied to the backbone Cα atoms of all residues that did not have one or more atoms within 8 Å of the ligand in the crystal structure using a harmonic force constant of 0.5 kcal/mol·Å². MD simulations were performed with and without the updated atom pair-specific LJ parameters (NBFIX in CHARMM nomenclature) for all the systems respectively based on the Drude model. All analyses were carried out using facilities within CHARMM,^52–54 and statistical analysis was based on three independent simulations using different random seeds to assign the initial velocities.

Additive MD simulations were performed following the same protocols as those for the Drude calculations with the following exceptions. The CHARMM36 force field⁹⁰ was used for the protein. Ligand topologies were generated using CGenFF^15,16 and water was treated using the CHARMM TIP3P model.⁹¹ LJ forces were force switched to zero from 10–12 Å.⁸⁷ Pressure control was based on a Nosé–Hoover Langevin piston algorithm.^92,93 A 100ps equilibration was performed with a 1.0 fs time step with all heavy atoms restrained using a harmonic force constant of 1 kcal/mol·Å², followed by a 20 ns production simulation with a 2.0 fs time step. As with the Drude production simulations weak restraints were applied to the backbone Cα atoms of all residues that did not have one or more atoms within 8 Å of the ligand in the crystal structure using a harmonic force constant of 0.5 kcal/mol·Å². Similarly, MD simulations were performed with and without the updated NBFIX parameters, respectively, based on the additive model. Note that in the previously released additive halogen force field,¹³ NBFIX parameters were included between only aromatic chlorine and the carbonyl oxygen on the protein backbone. In the present study, additional NBFIX parameters were applied between chlorine/bromine and other protein model compounds.

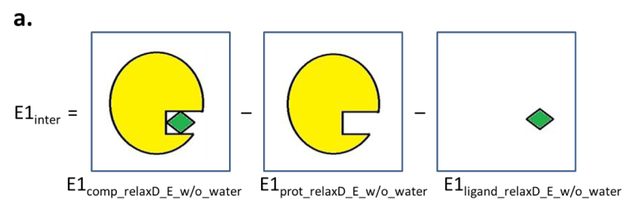
Interaction energies for the additive model were calculated using the “INTER” command in CHARMM that yields the sum of the LJ and electrostatic interactions between the interacting partners.^52–54 For the polarizable model, it is necessary to perform a SCF calculation on each of the individual interacting partners as well as on the full complex to allow for relaxation of the electronic degrees of freedom in analogy to the QM Born-Oppenheimer approximation. The SCF calculation in the Drude model was performed by allowing the Drude particles to relax to their local energy minima for the given fixed configuration of their parent nuclei. This was performed by constraining all real atoms (e.g. applying the “CONS FIX” command in CHARMM^52–54) and relaxing the Drude particles by minimizing them through the steepest-descent algorithm with a step size of 0.01 to a force gradient of 10⁻² kcal·mol⁻¹·Å⁻¹ followed by the adopted basis Newton-Raphson algorithm with a step size of 0.02 to a force gradient of 10⁻⁵ kcal·mol⁻¹·Å⁻¹. Energies of the systems were then calculated following removal of constraints on the real atoms. Interaction energies were then calculated using the following three methods (Figure 2).

Figure 2.

Schematic depictions of the interaction energy calculations based on methods a) 1, b) 2, and c) 3. Protein is colored in yellow, ligand in green, and water are labeled as “w”.

Method 1:

The relaxation of the Drude particles was performed after the water molecules were removed followed by calculation of the total energy of the complex (E1_comp__relaxD__E__w/o__water), the protein alone (E1_prot__relaxD__E__w/o__water) and the ligand alone (E1_ligand__relaxD__E__w/o__water). The interaction energy (E_inter1) was then calculated through equation 1:

$$\text{E}{1}_{\mathrm{i}\text{nter}}=\left({\text{E1}}_{\text{comp}\_\text{relaxD}\_\text{E}\_\text{w}/\text{o}\_\text{water}}\right)-\left({\text{E1}}_{\text{prot}\_\text{relaxD}\_\text{E}\_\text{w}/\text{o}\_\text{water}}\right)-\left({\text{E1}}_{\text{ligand}\_\text{relaxD}\_\text{E}\_\text{w}/\text{o}\_\text{water}}\right).$$ (Eq. 1)

Method 2:

The relaxation of the Drude particles was performed for the complex, protein-alone, and ligand-alone systems in the presence of the water (comp_relaxD_w/_water, prot_relaxD_w/_water, ligand_relaxD_w/_water, respectively). Then, the water molecules were removed for calculating the total energies of the complex (E2_comp__w/o__water), protein-alone (E2_prot__w/o__water) and ligand-alone (E2_ligand__w/o__water) systems, respectively, without additional relaxation of the Drude particles. The interaction energy (E2_inter) was calculated through equation 2:

$$\text{E}{2}_{\mathrm{i}\text{nter}}=\left({\text{E2}}_{\text{comp}\_\text{w}/\text{o}\_\text{water}}\right)-\left({\text{E2}}_{\text{prot}\_\text{w}/\text{o}\_\text{water}}\right)-\left({\text{E2}}_{\text{ligand}\_\text{w}/\text{o}\_\text{water}}\right).$$ (Eq. 2)

Method 3:

The relaxation of the Drude particles was performed for the complex and protein-alone systems in the presence of water, respectively, to obtain total energy for the complex (E3_comp__relaxD__w/__water) and protein alone (E3_prot__relaxD__w/__water). Water was not included in the relaxation of Drude particles in the ligand-alone systems for calculation of the ligand energies (E3_ligand__relaxD__w/o__water, which is equal to E1_ligand__relaxD__w/o__water). The interaction energy (E3_inter) was calculated through equation 3:

$$\text{E}{3}_{\mathrm{i}\text{nter}}=\left({\text{E3}}_{\text{comp}\_\text{relaxD}\_\text{w}/\_\text{water}}\right)-\left({\text{E3}}_{\text{prot}\_\text{relaxD}\_\text{w}/\_\text{water}}\right)-\left({\text{E3}}_{\text{ligand}\_\text{relaxD}\_\text{w}/\text{o}\_\text{water}}\right)$$ (Eq. 3)

To calculate the variation of dipole moments in different environments for the neutral ligands, the ligand conformations from the crystal structures were submitted to aqueous phase simulations for both the additive and Drude models in NAMD.⁷² Aqueous phase simulations were performed by solvating the ligands in a cubic water box with the box size determined by a 10 Å distance between the longest edge of the box and the ligand, with a harmonic force constant of 0.5 kcal/mol·Å² applied to the non-hydrogen atoms of the ligands. The rest of the parameters are the same as those performed in ligand-protein simulations for the additive and Drude models, respectively. A 10 ns NPT simulation of pure liquid water was performed using CHARMM^52–54 with a 19×19×19 Å cubic box of 216 water molecules of the SWM4-NDP water model,⁸² from which the mean dipole moment of water in the bulk phase was calculated based on the mean of the average dipole moment of each water molecule over the entire simulation. In addition, the root-mean-square fluctuations of the water dipole were calculated from the trajectory.

Results and Discussion

Halogens, such as chlorine, bromine and iodine, can act as hydrogen bond acceptors (HBA) to interact favorably with hydrogen bond donors (HBD) on proteins, referred to as X-HBD interactions, along with participating in halogen bonds (XB) with HBAs. XB interactions have also been referred to as X-HBA interactions.⁷ In the development of the halogen polarizable force field, good reproduction of both the QM X-HBD and XB water interactions was achieved by applying NBFIX parameters between the X-Drude particle and water hydrogen as well as X and water oxygen atoms.⁴⁹ Based on the same strategy, NBFIX parameters are optimized targeting QM interactions with protein model compounds with the goal of better X-HBD/XB interactions with protein residues. While comparing the QM results with the additive model, the agreement with QM X-HBD interactions was found not to be satisfactory, although the NBFIX between the chlorine and the carbonyl oxygen of the protein backbone model compound (NMA) was previously added. To improve the additive model, additional NBFIX parameters were also included and optimized. Finally, both the polarizable and additive force fields with optimized NBFIX parameters were applied in the MD simulations of protein-halogenated ligand (or modified residue) complexes to examine the ability of the resulting models in reproducing the halogenated-ligand geometries. A schematic illustration of the overall parametrization procedure is shown in Figure S1.

QM interaction energies with protein model compounds

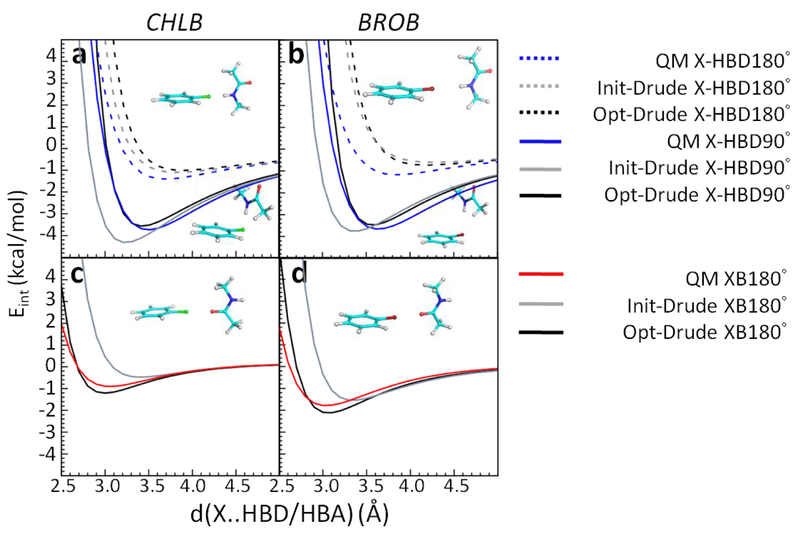
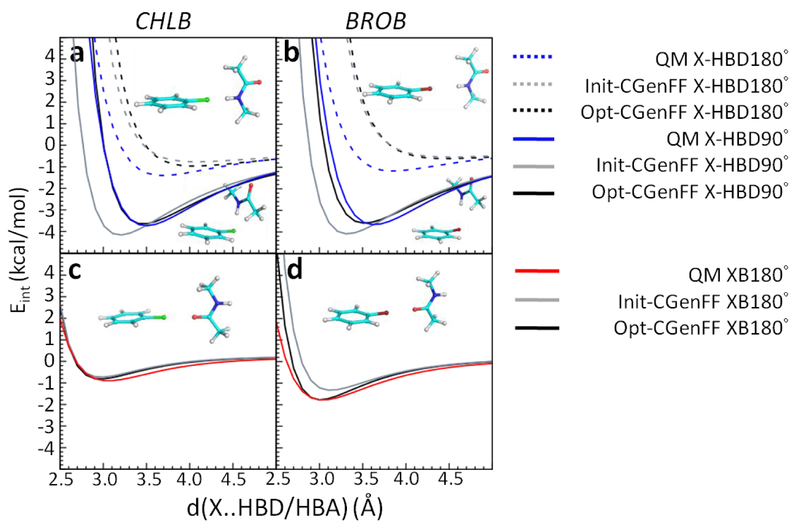
Optimization of atom pair-specific LJ parameters targeted both QM perpendicular X-HBD (X-HBD90°) and linear X-HBD/XB (X-HBD180° and XB180°) interaction energies with the protein model compounds. NMA served to model the protein backbone while other protein model compounds were used to model the side chains (Figure 1). Without the NBFIX parameters, the interaction energies with NMA displayed poor agreement with the QM target data in the Drude model (Figure 3, Init-Drude in gray). The X-HBD90° interaction energies between the halogens and NMA are too favorable with shorter interaction distances whereas the XB180° interaction energies are less favorable with longer interaction distances compared to the QM data. To overcome this disagreement, NBFIX terms between the halogen-Drude (X-Drude) and the hydrogen on amide NH in NMA as well as NBFIX between the X and carbonyl oxygen in NMA were added, resulting in better reproduction of both the X-HBD and XB (halogen bond) interactions (Figure 3, Opt-Drude in black). For the side-chain protein model compounds, the inclusion of NBFIX parameters yielded significant improvement in the balance of these interaction orientations (Figure S2–S3 for CHLB and Figure S4–S5 for BROB, Init-Drude in gray and Opt-Drude in black). Note that as the atom type of all polar hydrogens among the HBDs are the same,³⁹ the perpendicular X-HBD90° interactions among all the protein model compounds required compromise. The NBFIX parameters for the Drude model can be found in Table S15.

Figure 3.

Interaction energies between chlorobenzene (CHLB)/bromobenzene (BROB) and NMA acting as hydrogen bond donors (HBD) and a hydrogen bond acceptor (HBA). a-b are X-HBD90° and X-HBD180° interactions, c-d are XB180° interactions. QM results are in blue, initial Drude force field without NBFIX parameters (Init-Drude) are in gray, and optimized Drude force field with NBFIX parameters (Opt-Drude) are in black. Hydrogens are white, carbons are cyan, nitrogens are blue, oxygens are red, chlorines are green, and bromines are dark red.

In the additive model, the NBFIX between chlorine and carbonyl oxygen were already parametrized based on NMA¹³ such that XB180° interactions with NMA are quite good from the initial CHARMM36/CGenFF model (Figure 4c). However, the X-HBD90 ° interactions displayed too favorable interaction energies with shorter interaction distance (Figure 4a, Init-CGenFF in gray). To improve these interactions, the NBFIX approach was again taken. Considering that the atom type of the hydrogen is already shared with many other compounds, the NBFIX parameters are added for the X atom with the hydrogen-bond donor or acceptor non-hydrogen atoms (e.g. nitrogen or oxygen) of the model compounds (except MESH, explained below). With NBFIX parameters between the halogen and the nitrogen on the amide in NMA, the X-HBD90 ° interactions with NMA are significantly improved (Figure 4a–b, Opt-CGenFF in black). As for the interaction energies with the protein side-chain model compounds, most of the X-HBD90°/XB180° are in good agreement with QM data using the optimized NBFIX parameters (Figure S6–S9, Opt-CGenFF). With the MEOH/PHEN interactions, no NBFIX terms were required as the initial CGenFF parameters already achieved an acceptable balance of the various interactions, though some compromise of the X-HBD90 ° and XB180 ° interactions is present. With the charged species, ACET/MAMM/MGUAN, larger well-depth parameters were required to better reproduce the QM interaction energy surfaces. This use of larger well-depth parameters has been previously applied to molecules participating in interactions with significant electrostatic contributions.⁹⁴ Given that the hydrogen atom type on MESH is unique to thiol groups in the additive model, NBFIX parameters were applied between the halogen and hydrogen on MESH to improve X-HBD interactions. The NBFIX parameters for the additive model can be found in Table S16.

Figure 4.

Interaction energies between chlorobenzene (CHLB)/bromobenzene (BROB) and NMA acting as hydrogen bond donors (HBD) and a hydrogen bond acceptor (HBA). a-b are X-HBD90° and X-HBD180° interactions, c-d are XB180° interactions. QM results are in blue, initial additive CGenFF force field without NBFIX parameters (Init-CGenFF) are in gray, and optimized additive CGenFF force field with NBFIX parameters (Opt-CGenFF) are in black. Hydrogens are white, carbons are cyan, nitrogens are blue, oxygens are red, chlorines are green, and bromines are dark red.

A summary of the differences between QM and the Drude/additive minimum interaction energies and distances with the protein model compounds is shown in Table 1. The individual interaction energies and distances are shown in Table S1–S4. All the interaction energies computed using the NBFIX parameters (Opt-Drude and Opt-CGenFF) yield average difference (AVG), averaged unsigned errors (AUD), and root-mean-square differences (RMSD) generally smaller than those in the initial parameters that lacked the NBFIX parameters (Init-Drude and Init-CGenFF). The AVG of Cl-HBD interaction is somewhat larger in the Opt-Drude result compared to the Init-Drude; however, its AUD and RMS are smaller as are those for XB (X=Cl) or X-HBD/XB (X=Br) interactions. Although some of the HBD180° interactions, which are less favorable than the HBD90° or XB interactions, are still poorly treated both with and without the NBFIX parameters (Tables S1–S4), similar to those with water,⁴⁹ it is evident that including the NBFIX parameters for both the optimized Drude and additive models achieved substantial improvements in the balance of gas phase X-HBD/XB interaction orientations.

Table 1.

Statistical comparison of the Drude and CGenFF computed minimum interaction energies (E_min, kcal/mol) and distances (R, Å) with QM data for chlorobenzene (CHLB) or bromobenzene (BROB) interacting with the protein model compounds. Presented are average differences and standard errors. (AVG), absolute unsigned error (AUD), and root-mean-square differences (RMSD) without or with atom pair-specific LJ terms compared with their QM target data of halogen-hydrogen bond donor (X-HBD) interactions and halogen bond (XB) interactions or ALL. Individual interaction results are shown in Table S1–S4. The errors are the standard errors.

Mol.	Init-Drude		Opt-Drude		Init-CGenFF		Opt-CGenFF
CHLB	Emin	R	Emin	R	Emin	R	Emin	R
ALL
AVG	0.30 ± 0.14	0.0 ± 0.1	0.24 ± 0.11	0.0 ± 0.0	0.92 ± 0.33	0.1 ± 0.1	0.54 ± 0.20	0.1 ± 0.1
AUD	0.51	0.3	0.34	0.1	1.05	0.4	0.60	0.3
RMSD	0.73	0.3	0.57	0.2	1.84	0.5	1.12	0.4
Cl-HBD
AVG	0.21 ± 0.16	−0.1 ± 0.1	0.33 ± 0.13	0.0 ± 0.0	0.94 ± 0.40	0.1 ± 0.1	0.65 ± 0.27	0.1 ± 0.1
AUD	0.48	0.3	0.40	0.2	1.10	0.5	0.73	0.3
RMSD	0.70	0.3	0.65	0.2	1.89	0.5	1.29	0.4
XB, X=Cl
AVG	0.59 ± 0.27	0.3 ± 0.1	−0.04 ± 0.08	0.0 ± 0.0	0.89 ± 0.64	0.1 ± 0.1	0.21 ± 0.05	0.0 ± 0.0
AUD	0.59	0.3	0.16	0.1	0.89	0.2	0.21	0.1
RMSD	0.84	0.3	0.19	0.1	1.69	0.2	0.24	0.1
BROB	Emin	R	Emin	R	Emin	R	Emin	R
ALL
AVG	0.31 ± 0.08	0.2 ± 0.1	0.11 ± 0.06	0.2 ± 0.1	0.99 ± 0.35	0.3 ± 0.1	0.58 ± 0.22	0.3 ± 0.1
AUD	0.38	0.4	0.26	0.2	1.11	0.5	0.62	0.4
RMSD	0.48	0.6	0.32	0.3	1.95	0.7	1.20	0.5
Br-HBD
AVG	0.29 ± 0.10	0.2 ± 0.1	0.21 ± 0.06	0.2 ± 0.1	0.92 ± 0.39	0.4 ± 0.2	0.69 ± 0.28	0.4 ± 0.1
AUD	0.39	0.4	0.26	0.2	1.07	0.7	0.71	0.5
RMSD	0.50	0.5	0.33	0.3	1.84	0.8	1.36	0.6
XB, X=Br
AVG	0.36 ± 0.11	0.3 ± 0.1	−0.20 ± 0.10	0.1 ± 0.0	1.23 ± 0.85	0.2 ± 0.0	0.28 ± 0.16	0.0 ± 0.1
AUD	0.37	0.3	0.27	0.1	1.23	0.2	0.34	0.1
RMSD	0.43	0.3	0.30	0.1	2.26	0.2	0.46	0.1

MD simulations of ligand-protein crystal structures

Validation of the force field was performed by examining its ability to capture the halogenated ligand (or modified residue)-protein interactions with the aim of reproducing their binding geometries from MD simulations initiated from the crystal structures. In both the Drude and additive models, NBFIX parameters directly obtained from targeting QM CHLB- and BROB-protein model compounds interactions yielded good reproduction of the ligand-protein geometries as compared to the crystal structures, as described below. In the MD simulations weak harmonic restraints were applied to all Cα atoms on residues that did not have one or more atoms within 8 Å of the halogenated ligands or residue to limit deviations of the overall protein structures thereby assuring that the results from simulations were dominated by the ligand-protein interactions.

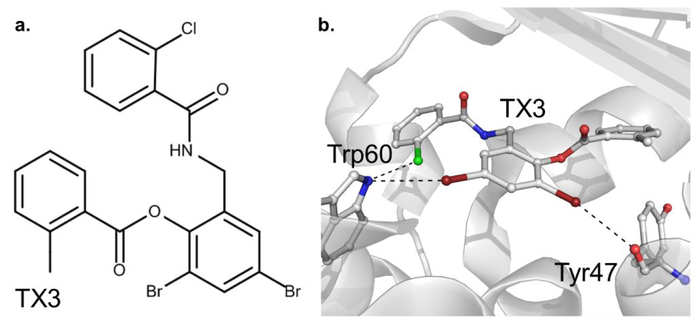
An example of one of the systems studied, the LasR ligand-protein complex,⁷⁷ is shown in Figure 5. The ligand contains both Cl and Br. The Cl and one Br participate in X-HBD interactions with the indole NH moiety of Trp60 in approximately perpendicular and linear orientations, respectively. The other Br participates in an XB interaction with the backbone O of Tyr47. Analysis of the remaining complexes in Figures S10 to S17 of the supporting information shows them to encompass a range of halogen-protein interactions as required to assure a diverse range of interactions were being tested.

Figure 5.

Illustration of X-HBD and XB interactions in the LasR protein-ligand complex (PDB id: 3IX8, 1.80 Å).⁷⁷ a. 2D representation of the halogenated ligand TX3. b. The ligand structure and the region of the protein in the vicinity of the ligand halogen atoms are shown. Chlorine is colored in green, bromine in dark red, nitrogen in blue, oxygen in red and carbon in white.

For quantitative analysis all the X-HBD or XB interactions from the crystal structures, the X…heavy atom distances within 4.5 Å were used as target data. These target data include the X…HBD and X…HBA distances and the C-X…HBD and C-X…HBA angles. Distances and angles from the MD trajectories were calculated to compare with those in the crystals. The deviations of the halogenated ligand (or modified residue) interaction geometries obtained from the MD simulations based on the developed force field parameters are summarized in Table 2, with detailed analysis for each crystal MD simulation presented in Tables S5–S12. With the human MutT Homolog1 (MTH1) protein (PDB id: 4N1T) the ligand geometry was poorly reproduced with both the initial Drude and CGenFF models;¹³ however, significantly better agreement with the crystal structure was achieved with the optimized additive and Drude models (see Table S8). Accordingly, the global analysis in Table 2 was performed both with and without those results.

Table 2.

Analysis of the angle (ϕ, deg) and distance (r, Å) deviations of the protein-ligand intermolecular simulated geometries compared to the crystal structures for all eight protein systems. Average differences (AVG) and standard error (SE), absolute unsigned error (AUD), root-mean-square differences (RMSD), and the number of each type of interaction (Count) were obtained from three independent simulations.

		All systems				All systems excluding PDB:4NIT
ALLa		Init-Drude	Opt-Drude	Init-CGenFF	Opt-CGenFF	Init-Drude	Opt-Drude	Init-CGenFF	Opt-CGenFF
AVG	ϕ	−9.59	−3.53	−9.13	−5.13	−2.19	−2.19	−4.43	−4.44
	r	0.57	0.21	0.63	0.17	0.33	0.18	0.20	0.16
SE	ϕ	3.77	1.49	2.71	1.45	1.24	1.51	1.23	1.60
	r	0.14	0.07	0.23	0.06	0.08	0.07	0.09	0.07
AUD	ϕ	12.34	7.09	8.74	7.09	5.15	6.05	6.14	6.88
	r	0.63	0.33	0.58	0.29	0.40	0.30	0.32	0.30
RMSD	ϕ	23.06	9.02	14.62	9.47	6.80	8.17	7.78	9.43
	r	0.95	0.44	1.21	0.37	0.52	0.42	0.51	0.38
Count			32				28
X-HBDb,c		Init-Drude	Opt-Drude	Init-CGenFF	Opt-CGenFF	Init-Drude	Opt-Drude	Init-CGenFF	Opt-CGenFF
AVG	ϕ	1.66	4.30	−4.82	−3.41
	r	0.40	0.18	0.23	0.12
SE	ϕ	0.97	1.76	3.22	3.20
	r	0.15	0.10	0.07	0.09
AUD	ϕ	2.64	5.37	8.56	7.00
	r	0.44	0.26	0.24	0.23
RMSD	ϕ	2.90	6.08	9.25	8.54
	r	0.55	0.31	0.29	0.26
Count			7
XBd		Init-Drude	Opt-Drude	Init-CGenFF	Opt-CGenFF	Init-Drude	Opt-Drude	Init-CgenFF	Opt-CGenFF
AVG	ϕ	−23.82	−10.54	−13.71	−4.14	−9.82	−9.93	−0.55	−2.55
	r	0.79	0.30	0.91	−0.08	0.23	0.17	−0.14	−0.16
SE	ϕ	14.21	2.36	13.21	2.43	3.20	2.95	1.42	2.37
	r	0.57	0.17	1.06	0.17	0.16	0.14	0.20	0.19
AUE	ϕ	23.82	10.54	14.70	5.27	9.82	9.93	1.79	3.97
	r	0.87	0.40	1.27	0.33	0.34	0.29	0.32	0.35
RMSD	ϕ	37.09	11.55	29.76	6.38	11.28	11.17	2.53	4.83
	r	1.39	0.46	2.30	0.35	0.36	0.29	0.37	0.37
Count			5				4

^aAll indicates all interactions based on all protein nitrogen and oxygen atoms within 4.5 Å of the ligand halogen atoms in the crystal structures.

^bX-HBD results limited to interaction geometries in Table S5–S12 where C-X..O/N_HBD angles from crystals are less than 120° and belong to HBD groups (i.e. Cl…N_SER in PDB id 2ZC9, Cl…N_TYR and Cl…O_SER in PDB id 4DT6, Br…N_HIS in PDB id 3JUM, Br…O_SER in PDB id 4NMV, BR…N_HIS and Br…O_TYR in PDB id 2AG6 of Table S5–S12).

^cAs there are no X-HBD interaction with PDB id: 4N1T, only one set of X-HBD interactions are presented.

^dXB results are limited to interaction geometries in Table S5–S12 where C-X..O/N_HBA angles from crystals are between 150–180° and belong to HBA groups (i.e. Cl…N_GLY in PDB id 2UW8, Cl…O_TRP and Cl…N_PHE in PDB id 4DT6, Br…O_TYR in PDB id 3IX8, Cl…O_THR in PDB id 4N1T of Table S5–S12).

When all the complexes and ligand-protein interactions are taken into account, both the optimized Drude and additive CHARMM36/CGenFF models yield substantial overall improvements in both the interaction distances and angles. Omission of the 4NIT system leads to the systematic improvement in the angles no longer being present, though the interaction distances are improved.

Analysis was also performed separately on X-HBD and XB interactions as defined by the criteria listed in the legend of Table 2. With the X-HBD interactions the distances are significantly better with the optimized Drude parameters while there is a degradation of the angles, though the standard errors of the angle differences are large. Optimization of additive CHARMM36/CGenFF leads to a systematic improvement in the treatment of the X-HBD interactions. With the XB interactions improvements occur with all interaction angles and distances with the optimized parameters when complex 4N1T is included in the analysis. When that structure is omitted, the optimized Drude model yield better agreement for the distances while the angles are similar and again show large standard errors. With the additive CHARMM36/CGenFF the optimized model performs slightly worse for the C-X…HBA angles while the distance differences are similar. The lack of differences is due, in part, to the presence of an NBFIX term in the initial CHARMM36/CGenFF model for the interaction of Cl with the peptide carbonyl O that is present in 5 of the complexes studied. Thus, the inclusion of atom pair-specific halogen-protein LJ parameters leads to improvements in the treatment of X-HBD interactions, especially with the distances in the Drude model. This trend was also present in the XB interactions for the Drude model though improvements did not occur with the additive CGenFF model. Notably, the inclusion of the optimized parameters avoided the extremely poor treatment of the 4N1T system.

To check if the deviations of the ligand-protein interactions were associated with shifts in the ligand or protein, conformational analysis was performed on the root-mean-square differences (RMSD) of the ligands and of the unrestrained, local protein backbone structure. In addition, root-mean-square fluctuation (RMSF) analysis of the local protein backbone structure was performed. Supporting information Table S13 shows only minimal conformational changes in the protein, with all RMSD values less than 1.0 Å. Larger differences are present for the ligands with the average RMSDs for both optimized FFs being below 1.5 Å. The largest RMSD values were obtained with the 4N1T system, with the significant improvement associated with the optimized parameters reflected in decreased RMSD values. Similar improvements were obtained with the 3JUM system. While within the standard errors, the Drude FF typically has larger RMSD values as compared to the additive FF. Contributing to this may be slightly larger fluctuations for the ligand with the optimized Drude model versus the additive, though the protein RMSF were similar (Table S14). These analyses indicate that more global structural or dynamical changes were not significantly impacting the Drude vs. additive results, which is expected given the use of harmonic restraints on protein Cα atoms remote from the ligands.

Ligand-Protein Interaction Energies

An accurate prediction of ligand-protein interaction energies is critical in the development of the scoring function in drug design.⁹⁵ Recent studies have shown that the electronic polarization contributes to the electrostatic interaction energy based on the QM/MM studies.^96–98 Accordingly, analysis was undertaken on the contribution of polarization to the interaction energy in the Drude model as such analysis, to our knowledge, has not yet been reported. Four approaches were used to calculate the protein-ligand interaction energies for the Drude model using the trajectories from the crystal MD simulations, which were compared to interaction energies obtained with the additive FF. In Table 3 the interaction energies using Drude-E1_inter~Drude-E3_inter methods that include the relaxation of the Drude particles are systematically more favorable than the additive values as well as Drude values without relaxation of the electronic degrees of freedom (i.e. Drude-E4_inter using INTER command in the CHARMM program^52–54) with the exception of 4DT6. These differences indicate that the treatment of the polarization effect contributes to the ligand-protein interaction energy as expected based on previous QM/MM studies.^96–98

Table 3.

Ligand–protein interaction energies based on the optimized additive and Drude polarizable force fields.

PDB	Opt-CGenFF		Opt-Drude
Metdodb	Einter	E1inter	E2inter	E3inter	E4inter
2ZC9	−59.1 ± 1.3	−106.1 ± 1.6	−104.5 ± 2.0	−177.1 ± 0.4	−66.4 ± 0.8
2UW8	−54.8 ± 0.6	−136.2 ± 7.22	−135.9 ± 6.1	−117.8 ± 2.2	−68.0 ± 2.1
4DT6	−119.9 ± 0.3	−195.3 ± 6.7	−192.6 ± 7.0	−344.6 ± 2.8	−85.5 ± 1.2
4N1T	−37.2 ± 0.6	−42.6 ± 2.9	−42.0 ± 3.1	−57.2 ± 2.5	−44.3 ± 3.0
31X8	−75.6 ± 0.2	−96.5 ± 0.1	−96.7 ± 0.2	−99.2 ± 0.2	−92.6 ± 0.4
2AG6	−53.8 ± 0.1	−77.0 ± 0.2	−71.6 ± 0.5	−146.9 ± 3.2	−74.6 ± 0.2
3JUM	−83.3 ± 6.8	−149.8 ± 3.2	−145.0 ± 2.4	−345.9 ± 10.9	−83.2 ± 4.0

^aErrors shown are standard errors based on three independent simulations for each system.

^bPolarizable E1_inter, E2_inter, and E3_inter are based on equations 1, 2 and 3, respectively (Figure 2). CGenFF E_inter and E4inter are directly calculated using INTER command in the CHARMM program.^52–54

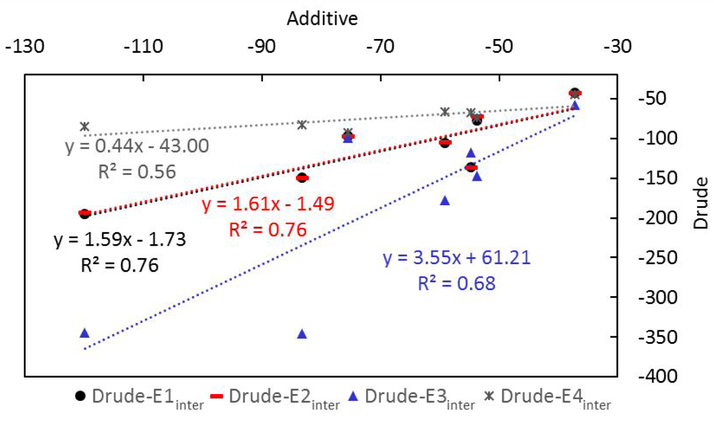
Comparison of the interaction energies calculated with the Drude model with those from the additive model shows the correlation to be relatively high (Figure 5). The negative y-intercepts show the Drude interactions to be more favorable than the additive values while the larger slopes suggest the polarizable interaction energies that include relaxation of the Drude may be more sensitive to the nature of the interactions with the Drude model than with the additive. Such an effect suggests that polarizable models may be more sensitive to ligand modifications, though explicit studies addressing this point are necessary. Interestingly, the Drude interaction energy without electronic relaxation, E4_inter, is less sensitive to the environment than the additive. This may be due to the overpolarization of the charges in the additive model designed to take into account the omission explicit treatment of electronic polarization⁹⁹ while such contributions are not present in the Drude model when the electronic degrees of freedom are not allowed to relax in the different environments. The results clearly indicate the importance of allowing the electronic degrees of freedom to relax when calculating interaction energies with the Drude or any polarizable force field.

Concerning the three Drude interaction energy methods that include relaxation of the electronic degrees of freedom, method 1 and 2 give similar results with method 3 differing significantly. The absence and inclusion of water when calculating the polarization response in methods 1 and 2, respectively, while yielding similar results suggest that the overall impact of the water environment is not significant (E1_inter and E2_inter in Table 3). When water is included as part of the protein and the complex during the interaction energy calculation (i.e. method 3), the energies are often more favorable, though exception exists with complexes 2UW8 and 3IX8 where they are slightly less favorable or similar, respectively (E3_inter in Table 3). This variation indicates the complex nature of the contribution of water to binding, another area that requires additional study. Given the similarity of the E1_inter or E2_inter methods and their high correlation with the additive interaction energy calculations (Figure 5), the present analyses suggest that the E1_inter or E2_inter methods are most appropriate for interaction energy analysis using the Drude or other polarizable force field.

An important contribution to binding comes from the electronic self-polarization energy when applying polarizable MM or QM methods. Analysis of the contribution of the electronic self-polarization energy (or self-energy) to the interaction energies varies widely (Table 4). These contributions go from large favorable to large unfavorable contributions, with those ranges of variations occurring for both between and within the individual systems. While interaction energies E1_inter and E2_inter are similar, the Drude self-energy contributions (E1_self and E2_self) are substantially anticorrelated (R=−0.72). This suggests differential impact of the aqueous environment on the protein versus ligand, though these contributions balance leading to the similar interaction energies (R=1.00). On the other hand, the self-energy contributions of E2_self and E3_self, in which the Drude particle relaxation includes contributions from water in both the ligand and the protein or just the protein, respectively, show good correlation (R=1.00). This similarity suggests that the impact of water is dominating the polarization of the protein over the ligand, a results that may be considered obvious given the relative size of the proteins and extent of exposure of the protein versus the ligand to the aqueous solvent.

Table 4.

Ligand–protein interaction self-energies (E_self) based on the optimized Drude polarizable force field.^a Errors shown are standard errors based on the three independent simulations for each system.

PDB	Opt-Drude-El	Opt-Drude-E2	Opt-Drude-E3
Metdod	E1self	E2self	E3self
2ZC9	−101.0 ± 2.7	−5.6 ± 7.6	15.7 ± 6.1
2UW8	−42.0 ± 12.0	−93.3 ± 11.4	−99.2 ± 11.6
4DT6	−126.2 ± 6.9	39.9 ± 12.0	51.0 ± 13.4
4N1T	2.2 ± 1.6	8.9 ± 5.5	13.1 ± 6.5
3IX8	−2.5 ± 0.8	−11.3 ± 2.5	−6.0 ± 2.3
2AG6	78.6 ± 15.7	9.2 ± 24.9	24.9 ± 35.2
3JUM	−237 ± 25.3	292.7 ± 21.8	334.0 ± 17.3

^aIn methods 1–3, each self-energy contribution from the complex, protein and ligand were obtained (e.g. E_{self, comp}, E_{self, prot}, and E_{self, ligand}). The self-energy for each component is calculated from the total bond energy minus the bond energy with the Drude particles omitted based on the geometry after Drude particles are relaxed in the SCF calculation. E_self is calculated as E_{self, comp} - E_{self, prot} - E_{self, ligand}. Self-energies from method 4 are zero, i.e. E_{self, comp} = E_{self, prot} + E_{self, ligand}, as no relaxation of Drude particles is performed.

Favorable self-energy contributions to ligand-protein interactions energies are somewhat counterintuitive. They indicate that the self-energies are larger (i.e. less favorable) in the monomers than in the complex, indicating that the effective electric field acting on the protein and ligand is smaller in the complex than in the individual monomers. Such an effect is due to the intramolecular contributions to the electric field along with condensed phase environment intermolecular contributions. These latter contributions lead to the anticorrelated nature of the E1_self and E2_self terms. It is interesting that despite this difference the E1_inter and E2_inter terms are similar. Given that the difference between the two calculations is the absence or presence of water in the SCF calculation, the similarity of the interactions energies suggest that the assumption of an isotropic polarization contribution inherent in additive models is not unreasonable.⁹⁹ However, it should be emphasized that the similarity between the E1_inter and E2_inter terms does not indicate that water is not contributing to the overall binding affinity of ligands to proteins. Indeed the significant difference in E3_inter versus E1_inter and E2_inter indicates a significant contribution of water itself. Additional studies are required to develop approaches to appropriately account for the contribution of water to binding in the context of both additive and polarizable force field.

Variation of the Dipole moments

To demonstrate the effect of the explicit treatment of polarization, including the response to different environments, dipole moments of the neutral ligands were obtained from a 20 ns MD simulations of the ligands in the aqueous phases and from the three 20 ns protein-ligand simulations (Table 5). In the aqueous phase simulations the ligand conformation was restrained to that present in the crystal structure to limit the analysis to the impact of the protein vs. aqueous environment on the dipole moments. Significantly larger changes in the dipole moments would also occur in most systems due to change in the ligand conformation, though such analysis requires full conformational sampling of the ligand in solution. The difference in the dipole moments of the full ligands vary from the aqueous phases to the protein with both the additive and polarizable models generally by 1 Debye or less, though with the polarizable FF there is a significant change of almost 3 Debye with 4NIT. Comparison of the RMS fluctuations shows generally higher values with the Drude model. This is anticipated as the fluctuations occurring with the additive force field are associated with changes in conformation of the ligands, as no change in electronic structure is possible, while both conformational and electronic effects contribute to the changes with the Drude model.

Table 5.

Dipole moments and RMS fluctuations (Debye) of each neutral ligand and their halogenated aromatic groups (Ar-X) in the aqueous solution and in the ligand-protein (w/Protein) simulations for the optimized Drude and additive force fields.

PDBID		Aqueous	w/Protein	Watera (Aqueous)	Waterb (w/Protein)
Full ligand
Additive
4N1T		5.14 ± 0.73	4.18 ± 1.63
31X8		6.63 ± 0.62	7.83 ± 0.50
2AG6		15.04 ± 0.33	14.91 ± 0.36
Drude				2.46 ± 0.16c
4N1T		7.17 ± 0.99	4.32 ± 1.06	2.46 ± 0.16	2.42 ± 0.19
31X8		9.70 ± 1.02	9.00 ± 0.60	2.48 ± 0.16	2.36 ± 0.22
2AG6		16.10 ± 0.88	15.96 ± 0.74	2.46 ± 0.16	2.44 ± 0.18
Halogenated aromatic group
Additive
PDBid	Ar-Xd
4N1T	CL	3.11 ± 0.07	3.11 ± 0.07
31X8	CL	2.29 ± 0.08	2.29 ± 0.07
	BR	2.50 ± 0.09	2.52 ± 0.09
2AG6	BR	0.73 ± 0.08	0.72 ± 0.08
Drude
PDBid	Ar-Xd
4N1T	CL	3.94 ± 0.46	3.50 ± 0.60
31X8	CL	3.46 ± 0.42	3.61 ± 0.29
	BR	3.08 ± 0.45	3.72 ± 0.35
2AG6	BR	1.17 ± 0.50	0.86 ± 0.41

^aDipole of waters within 3 Å of the full ligand are calculated.

^bDipole of waters within 3 Å of both the protein and the full ligand are calculated.

^cAverage and RMS fluctuations of the dipole moment of water in pure aqueous solution.

^dAr-X indicates which halogen is included. The halogenated aromatic group includes all the functional groups on the same aromatic ring.

Analysis was also performed on the halogenated aromatic moieties in the ligands. With the additive FF the dipoles are approximately the same in both environments. With the Drude FF changes of the dipole moment up to 0.5 Debye from the aqueous phase to the protein binding pocket are seen. In addition, the RMS fluctuations in the dipole moments are significantly larger than in the additive FF as the halogenated aromatic groups are relatively rigid such that the fluctuations of the dipoles are dominated by the electronic response.

The dipole moments of waters in the vicinity of the protein and ligand were also analyzed for the Drude model. In aqueous solution there is little change in the average dipoles or their fluctuations. However, in the presence of the proteins some larger differences are observed in both the average and RMS fluctuations, especially with 3IX8 and 2AG6. This difference is evident in probability distributions of the water dipoles shown in Figure S18 of the supporting information. Similar variations are seen in the water molecules around the charged ligands (Figure S19). The results for the ligands and water indicate that variations in dipole moments can occur in the ligands upon binding as well as with water in the vicinity of the bound ligand, though the presence and magnitude of the effect is system dependent.

Conclusion

Presented are optimized polarizable Drude and additive CHARMM36/CGenFF force field parameters for the interaction of halogen containing aromatic compounds with proteins. While developed in the context of proteins, the improvements will be applicable to analogous functional groups on other classes of macromolecules. The improvements were implemented using atom pair-specific LJ or NBFIX parameters. These NBFIX parameters were developed to improve the halogen-hydrogen bond donor and acceptor interactions by targeting QM interaction energies between chlorobenzene or bromobenzene and a series of protein model compounds for both the additive CHARMM and polarizable Drude FFs. The optimized parameters were then evaluated in their ability to reproduce the crystallographic geometry of halogenated ligands or a modified halogenated residue with the proteins. The optimized model shows significant improvements against the target QM data for both XB and X-HBD interactions, with those results yielding a moderate level of improvement in the interactions with proteins. We note that the initial CHARMM36/CGenFF model already included NBFIX terms for the interaction of Cl with the carbonyl O of NMA, such that improvements in this class of interaction, which are present in PDB files 2ZC9, 2UW8, 4DT6, 3IX8, and 2AG6, were expected to be minimal. With system 4N1T large deviations in the ligand-protein geometry occurred with both the original additive and Drude models, an issue that was overcome with the optimized parameters in both cases. While the halogen model compounds in this study are limited to chloro- and bromobenzene, the optimized NBFIX parameters are expected to be applicable to aromatic species substituted with multiple chlorine and bromine atoms, including combinations of the two halogens. Such transferability was demonstrated in our previous study where pure solvent properties for a range of halogenated derivatives were shown to reproduce the experimental values when using halogen nonbonded parameters developed based on halogenated benzene systems.⁴⁹

The results from MD simulation of the ligand-protein complexes are also useful for studying properties of the ligand in the presence of the protein with the Drude model. Methods to compute the ligand-protein interaction energies are illustrated and compared. Instead of simply calculating the energy contributed from atoms and Drude particles, a more physically correct way is to perform a self-consistent field calculation by allowing the Drude particles to relax to their local energy minima for the complex as well as the individual interacting partners. Application of this approach with all species in the absence and presence of water yield similar results, which are well correlated with interaction energy analysis performed using the additive model. Interestingly, the contribution of the electronic self-polarization energy is shown to both favor and disfavor the ligand-protein interaction energy, indicating the complex nature of the contribution of polarizability to ligand binding. Analysis of the dipole moments of ligands suggests that explicit treatment of induced polarization captures local variations in the environment of the ligands that impact their electronic structure, a phenomena that is not accounted by the mean-field approximation in the additive model.

In summary, an improved model of the interactions of halogenated aromatic ligands with proteins is presented. Improvements are made in both the additive CHARMM36/CGenFF and polarizable Drude force fields. It is anticipated that these improvements will facilitate investigations of ligand-protein interactions including efforts in the area of computer-aided drug design.

Figure 6.

Correlation of the interaction energies (kcal/mol) from the optimized additive and Drude force fields based on the data in Table 3. Drude-E1_inter, Drude-E2_inter, and Drude-E3_inter are based on equations 1, 2 and 3, respectively. Drude-E4_inter is directly calculated using INTER command in the CHARMM program.^52–54