Fixed- versus Variable-RBE Computations for Intensity Modulated Proton Therapy

Abstract

Purpose

To evaluate how using models of proton therapy that incorporate variable relative biological effectiveness (RBE) versus the current practice of using a fixed RBE of 1.1 affects dosimetric indices on treatment plans for large cohorts of patients treated with intensity modulated proton therapy (IMPT).

Methods and Materials

Treatment plans for 4 groups of patients who received IMPT for brain, head-and-neck, thoracic, or prostate cancer were selected. Dose distributions were recalculated in 4 ways: 1 with a fast-dose Monte Carlo calculator with fixed RBE and 3 with RBE calculated to 3 different models—McNamara, Wedenberg, and repair-misrepair-fixation. Differences among dosimetric indices (D02, D50, D98, and mean dose) for target volumes and organs at risk (OARs) on each plan were compared between the fixed-RBE and variable-RBE calculations.

Results

In analyses of all target volumes, for which the main concern is underprediction or RBE less than 1.1, none of the models predicted an RBE less than 1.05 for any of the cohorts. For OARs, the 2 models based on linear energy transfer, McNamara and Wedenberg, systematically predicted RBE >1.1 for most structures. For the mean dose of 25% of the plans for 2 OARs, they predict RBE equal to or larger than 1.4, 1.3, 1.3, and 1.2 for brain, head-and-neck, thorax, and prostate, respectively. Systematically lower increases in RBE are predicted by repair-misrepair-fixation, with a few cases (eg, femur) in which the RBE is less than 1.1 for all plans.

Conclusions

The variable-RBE models predict increased doses to various OARs, suggesting that strategies to reduce high-dose linear energy transfer in critical structures should be developed to minimize possible toxicity associated with IMPT.

Introduction

Interest in proton therapy has been triggered by the theoretical advantages of the dose distribution of protons over that of photons. Protons have a lower dose in the proximal edge and no exit dose because the energy of the proton can be tuned to stop within or just distal to the target. However, one of the challenges of proton therapy is to understand its relative biological effectiveness (RBE) with respect to photon therapy. Currently, for clinical applications the simplistic assumption is made that the RBE of protons (relative to photons) is a constant value of 1.1.1, 2, 3, 4, 5 However, the RBE is a complex function of radiation dose, dose per fraction, linear energy transfer (LET), biological endpoint, tissue or cell type (characterized normally by α/β), oxygenation, and other factors. Thus the biologically effective dose distributions seen on a treatment plan designed using a fixed RBE value of 1.1 may be significantly different from what is actually delivered to the patient, which can lead in turn to suboptimal treatments and unforeseen toxic effects. A recent preclinical study of head-and-neck human papillomavirus–positive oropharyngeal carcinoma cells suggested that using an RBE of 1.1 for daily 2-Gy fractions could lead to differences in dose ranging from 4.5% to 21% in clinical practice.⁶

A variety of models has been proposed to estimate variable proton RBE, and most use LET as a key factor. A few authors have evaluated the effect of such models in clinical cases. Tilly et al⁷ evaluated one plan of a hypopharynx cancer. Oden et al⁸ analyzed plans from 4 patients with prostate cancer, and Giovannini et al⁹ compared the predictions of 3 of the main radiobiological models for 2 clinical cases. Carabe et al¹⁰ compared 5 prostate tumors, 5 brain tumors, and 5 liver tumors for various fractionation schemes. A study of variable RBE effects of a cohort of 15 breast patients with plans robustly optimized was carried out by Oden et al.¹¹ Underwood et al¹² studied a cohort of 8 prostate patients and compared photon and proton therapy. They found that variable RBE generated significant hotspots and underlined the importance of solving the issue of proton RBE. Giantsoudi et al¹³ investigated at a cohort of 111 patients with medulloblastoma and compared variable RBE doses to RBE 1.1 doses, even though they performed Monte Carlo calculations only for 11 patients.

In this study we evaluate how using variable RBE according to 3 models affects dosimetric indices on treatment plans from 4 groups of at least 75 patients each, who received intensity modulated proton therapy (IMPT) for brain, head-and-neck, thoracic, or prostate cancer. We focused on the variation in the predictions over sizeable cohorts and IMPT because previous studies were reduced to a few patients, mainly treated with passive scattering proton therapy, for which the dose was calculated with Monte Carlo techniques.

Materials and methods

Patient data

Treatment plans for patients with brain, head-and-neck, thoracic, or prostate cancer treated with IMPT at University of Texas MD Anderson Cancer Center institution were selected from a patient database, as described elsewhere.¹⁴ Patient characteristics of the 4 cohorts are presented in Table 1. Each patient was represented with a voxelized volume based on computed tomography (CT) images, as described elsewhere.15, 16 Structures of interest were selected from among structures that had been contoured by physicians and were stored in a Digital Imaging and Communication in Medicine structure file. The analysis was restricted to primary plans. Target volumes considered in this study included gross target volume, clinical target volume, and internal target volume. Two basic methods were used for plan optimization: multiple field optimization (MFO) and single-field optimization (SFO). Dependence of the results with the optimization method was analyzed.

Table 1.

Features of treatment plans for the 4 patient cohorts

Characteristics	Brain	Head and neck	Thorax	Prostate
No. of patients	80	128	117	75
No. of patients with MFO	45	116	87	6
No. of beams
Average	2.9	3.0	2.8	2
Median	3	3	3	2
Range	2-4	2-5	1-4	1-3
Minimum range in patient (cm)
Average	2.9	0.6	4.2	14.7
Median	2.9	0.4	4.0	15.5
Range	0.2-7.1	0.3-7.4	0.2-11.5	5.2-18.8
Maximum range in patient (cm)
Average	14.9	17.2	18.5	25.1
Median	14.6	18.3	18.9	25.0
Range	9.2-20.8	4.8-23.7	7.4-28.6	22.3-28.6
Volume, cm3
Average	109	244	366	136
Median	71	218	240	91
Range	6-426	6-1083	13-2911	17-599
Prescription dose (Gy)
Average	53.0	63.8	59.8	69.1
Median	55.7	69.3	63.8	79.1
Range	14.4-78.4	15.6-75.4	18.0-78.4	24.0-80.8

Abbreviation: MFO = multiple field optimization.

Concerning beam arrangements, the prostate cases had a rather constant set with 2 opposed lateral beams. For other sites, some general patterns existed. For example, in thoracic patients with lung tumors, lateral beams were avoided. However, general beam arrangement patterns for the other 3 cohorts (brain, head-and-neck, and thorax) were not established. Nevertheless, to evaluate the dependence on the results with beam arrangement, the results were studied for single beams as a function of gantry angle for patients with no couch rotation.

The range of voxel size is 1.37 to 2.34 mm in the transverse plane and 1 to 3 mm in the inferior-superior axis.

Monte Carlo and RBE models

Calculations were done by using a fast Monte Carlo algorithm (FMC; also known as the fast dose calculator). The general concept of this algorithm15, 16, 17 and its application for comparisons of Monte Carlo calculations with those of a currently used treatment planning system are described elsewhere.¹⁴ FMC was set to run 100 million histories per beam, but the calculation was stopped when the average statistical uncertainty of the deposit energy for voxels with deposited energy larger than 10% of the maximum was less than 0.3%. The Monte Carlo algorithm calculates the dose and unrestricted dose-averaged LET, LET_d, for each voxel in the CT image representing the patient anatomy. The LET only includes primary and secondary protons, and it is calculated from stopping power tables obtained from GEANT4¹⁸ according to the third method in the study by Cortes-Giraldo and Carabe.¹⁹ Visual inspections revealed smooth LET distributions for areas with a dose 1% larger than the maximum dose.

The RBE for proton beams is defined as the ratio of the reference low-LET radiation (x-ray) dose D_x and the proton dose D with both doses producing the same biological effect. Three different models were implemented in the FMC algorithm, and all were based on the linear-quadratic (LQ) model with the assumption that each model represents all types of biological effects. The resulting general expression for RBE is given by:

$$RBE\equiv \frac{D_x}{D}\equiv -\frac{1}{2D}\left(\frac{{\alpha }_x}{{\beta }_x}\right)+\frac{1}{D}\sqrt{\frac{1}{4}{\left(\frac{{\alpha }_x}{{\beta }_x}\right)}^2+\frac{{\alpha }_p}{{\alpha }_x}\left(\frac{{\alpha }_x}{{\beta }_x}\right)D+\frac{{\beta }_p}{{\beta }_x}{D}^2}$$ (1)

where x indicates the reference radiation.²⁰ The LQ model parameters, α_x and β_x, depend on the type of tissue and the toxicity under consideration. Two models used in this analysis (described later) provide the parameters of the LQ for protons (α_P, β_P) as a function of LET_d and the ratio α_x/β_x, whereas a third model does not explicitly use LET as an input variable.

The McNamara (McN) model²¹ is represented by:

$$\frac{{\alpha }_p}{{\alpha }_x}=0.999064+\frac{0.35605}{{\alpha }_x/{\beta }_x}LE{T}_d;\frac{{\beta }_p}{{\beta }_x}={\left(1.1012-0.0038703\sqrt{{\alpha }_x/{\beta }_x}LE{T}_d\right)}^2$$ (2)

where LET is given in keV/μm α_x/β_x in Gy.

The Wedenberg (WDG) model²² is represented by:

$${\alpha }_p={\alpha }_x\left(1+\frac{c}{{\alpha }_x/{\beta }_x}LE{T}_d\right),{\beta }_p={\beta }_x$$ (3)

with c = 0.434 Gy μm keV^–1, resulting from a fit to a total of 10 different cell lines.

The repair-misrepair-fixation (RMF) model23, 24 is represented by:

$$\frac{{\alpha }_p}{{\alpha }_x}=RB{E}_{DSB}\left(1+\frac{2{\overline{z}}_{F}RB{E}_{DSB}}{{\alpha }_x/{\beta }_x}\right);\frac{{\beta }_p}{{\beta }_x}=RB{E}_{DSB}^2$$ (4)

where RBE_DSB depends on the relation between the number of DNA double-strand breaks (DSBs) from protons and from γ-rays from ⁶⁰Co, and Z_F is the frequency-mean specific energy in a cell nucleus. RBE_DSB and Z_F depend on the proton energy and were obtained from the Monte Carlo damage simulation system developed by Stewart et al.²⁵ The dose-averaged RBE_DSB and z_F RBE_DSB in each voxel were used as input for the RBE calculations for this model.

The value of α_x/β_x for target volumes was 10 Gy for all cohorts²⁶ except for prostate, for which it was 3.1 Gy.²⁴ Concerning organs at risk (OARs), a value of 2 Gy was used for brainstem, spinal cord, optic chiasm, and optic nerve, whereas for the rest of the OARs the value used was 3 Gy, whether they were found in the literature or not.²⁶

Analyses

Fixed-RBE (1.1) weighted dose (FRD) distributions were calculated along with variable-RBE-weighted doses (RWD) according to the 3 models used in this study. For each patient with thoracic cancer, CT averaged over 10 phases of a 4-dimensional CT, representing a breathing cycle, was used.

The typical FMC calculation time for 1 patient was approximately 5 to 10 minutes. Dose-volume histograms (DVHs) from the fixed-RBE-weighted dose and variable-RBE-weighted distributions were calculated with the same DVH algorithm for all dose distributions. The following dosimetric indices were also obtained to provide a quantitative comparison of DVHs for the various models: (1) the mean dose (mean) and (2) D02, D50, and D98—that is, the minimum dose covering 2%, 50%, and 98% of the considered structure. Similarly, for LET, the L02, L50, and mean LET were calculated, where L02 and L50 are the minimum LET covering 2% and 50% of the considered structure, respectively. For analysis of target volumes, only indices larger than 10 Gy were considered. As noted earlier, target volumes considered included the gross target volume, clinical target volume, and internal target volume. For OAR indices, only those with D50 larger than 5 Gy were considered.

Differences in the dosimetric indices between FRD and RWD results were analyzed by looking at the RBE for each dosimetric index, defined as: RBE_DXX = 1.1. RWD_DXX/FRD_DXX, where RWD_DXX and FRD_DXX are the values of index DXX for RWD and FRD, respectively. Subsets of OARs relevant to each site were selected from the following list: bladder, optic chiasm, cochlea, esophagus, femur, heart, larynx, lung, optic nerve, parotid, rectal wall, rectum, and spinal cord.

We present the results of this study with descriptive statistics in the form of box plots. Each box plots represents the distribution of a variable, such as D02, L50, or RBE_D02. Boxes have 3 horizontal lines: The bottom line represents the first quartile, the middle corresponds to the median, and the top depicts the third quartile. The top whisker corresponds to the position for which 98% of the entries in the distribution are below, whereas the bottom whisker depicts the point for which 98% are above. Each point above and below the whiskers represent one entry higher than the 98% or lower than the 2%.

We estimated the effect of the uncertainties in the α_x/β_x by analyzing the maximum change in the RBE for any LET and for a fraction dose of 2 Gy. We define the RBE relative change range ($\mathbf{R}\mathbf{B}{\mathbf{E}}_{\mathit{Min}}/\mathit{RB}{\mathit{E}}_{\mathit{def}},\mathit{RB}{\mathit{E}}_{\mathit{Max}}/\mathit{RB}{\mathit{E}}_{\mathit{def}}$) for a particular α_x/β_x range around a default value, where $\mathit{RB}{\mathit{E}}_{\mathit{Min}}\mathbf{a}\mathbf{n}\mathbf{d}\mathit{RB}{\mathit{E}}_{\mathit{Max}}$ are the minimum and maximum RBE obtained for any LET and α_x/β_x in the range considered and $\mathit{RB}{\mathit{E}}_{\mathit{def}}$ is the RBE obtained for the default α_x/β_x.

Results

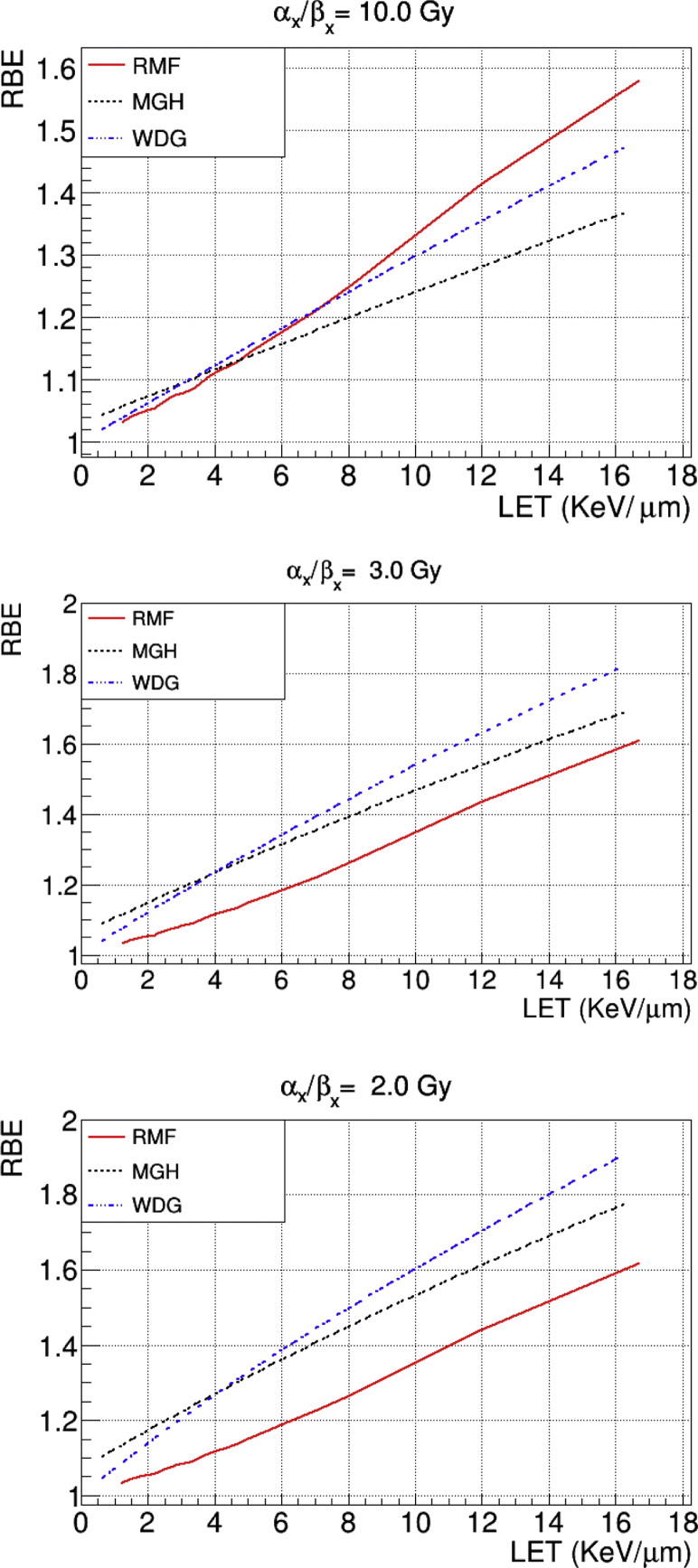
The RBE as a function of LET for α_x/β_x = 2, 3, and 10 Gy for the 3 models is presented in Figure 1. For α_x/β_x = 10 Gy the 3 models are close at low LET, with RMF yielding higher values for high LET. For α_x/β_x = 2 and 3 Gy, RMF is lower than the other 2 models for all LETs, whereas McN is higher than WDG for LET <4 keV/μm, and the opposite is the case above that threshold.

Figure 1.

Relative biological effectiveness (RBE) as a function of linear energy transfer (LET) for the McNamara (McN), Wedenberg (WDG), and repair-misrepair-fixation (RMF) for α_x/β_x = 2, 3, and 10 Gy.

RBE_D02, RBE_D50, RBE_Mean, and RBE_D98 for the target volumes were analyzed. The median for RBE_Mean and RBE_D50 were in the range of 1.08 to 1.12 for all models and targets. The lowest RBEs, or underprediction, for any index were greater than 1.05. Concerning D02, overdosage estimates of RBE larger than 1.25, especially for WDG and MCN, were found. Such overestimates may be clinically relevant if the excess dose is on or near critical structures. However, such an issue is addressed in this study when we look at the effects of variable RBE on OARs.

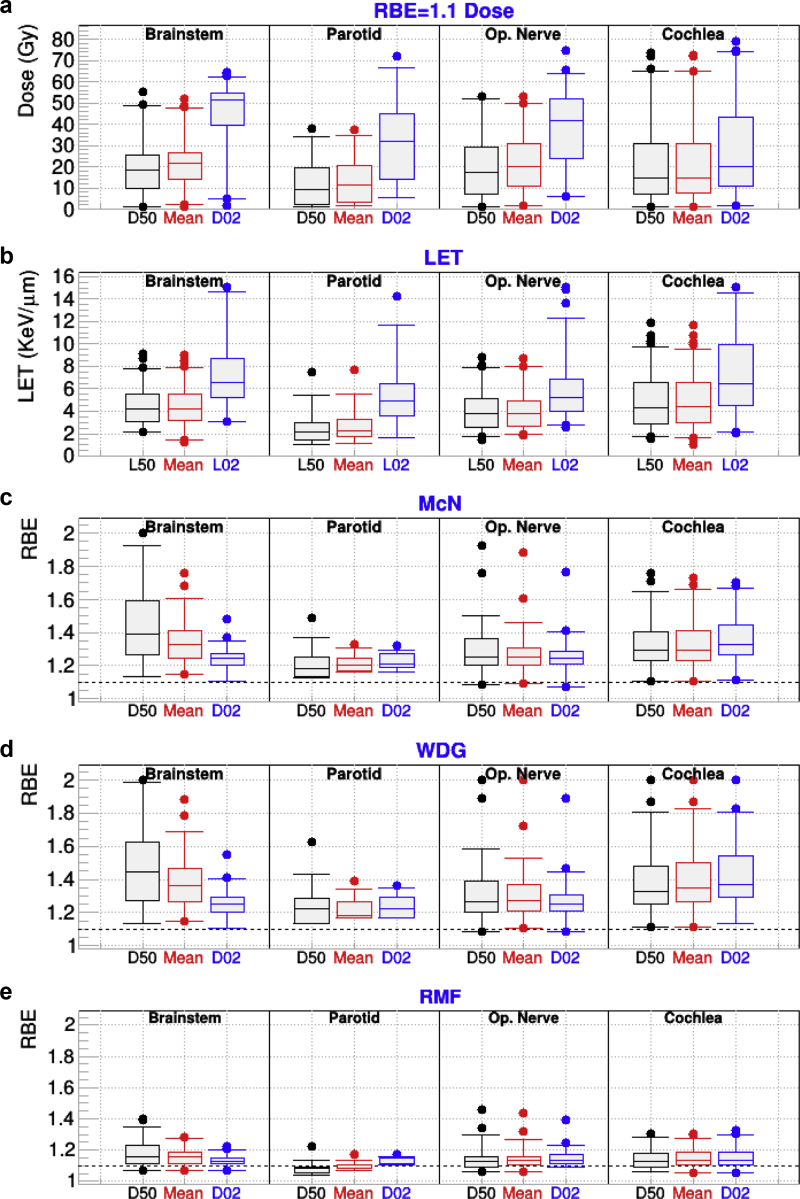
The top panel of Figure 2 shows D02, mean, and D50 for FRD and the bottom panel depicts L02, mean LET, and L50 for a few structures of interest for patients treated for brain cancer. In addition, RBE_D02, RBE_Mean, and RBE_D50 for the same structures for the 3-variable RBE models are also presented. As expected, all models, especially those based on LET (WDG and McN), predict RBE >1.1. For the RBE_D50 median (the value at the central box line), values as large as 1.4 are observed for the brainstem. For that structure, RBE_D50 and RBE_Mean tend to be higher than RBE_D02 because of the combination of a lower α_x/β_x = 2 Gy and low dose, which increases the RBE especially for D02. A few cases of RBE_D50 above RBE = 2 (not shown in the figure) were identified for WDG and McN, which were generated by a combination of high LET (8 keV/mm) and low dose (<10 Gy). Similarly, the outliers with higher RBE values for all models and structures are produced by less extreme cases of low dose and high LET. The outliers tend to be the same in all models. The increases for all indices for the optic nerve and the cochlea are larger and more dispersed than those for the parotid. This is attributed to the fact that those 2 organs have a small volume and are more sensitive to LET hot spots. It should also be noted that the RBE for the cochlea in McN and WDG are higher than those for the optic nerve, in spite of having assigned α_x/β_x = 2 Gy to the latter. We attribute that effect to the larger value for the mean LET for cochlea (5 keV/μm) than for optic nerve LET (4.1 keV/μm), whereas the opposite is the case for FRD. With the exception of the parotid, for which RBE₅₀ median is less than 1.1, the results for RMF have trends similar to those for MCN and WDG, although the magnitude is smaller, as expected from Figure 1.

Figure 2.

For patients who received intensity modulated proton therapy for brain cancer and for the indicated organs at risk: (a) minimum dose covering 2% and 50% of the targeted structures (D02 and D50) and mean dose calculated from fixed relative biological effectiveness (RBE) dose; (b) the minimum linear energy transfer (LET) covering 2% (L02) and 50% (L50) of the organ, along with the mean LET; (c-e) RBE_D50, RBE_Mean, and RBE_D02 for the McNamara (McN), Wedenberg (WDG), and repair-misrepair-fixation (RMF) models. Op = Optical.

Concerning the angle dependence in brainstem RBE_D02 for single beams, we found that anteroposterior beams produced larger RBE than posteroanterior beams. No clear angular dependence was found for other OARs. When comparing MFO and SFO, the excess over 1 for RBE_D50 MFO plans for the brainstem were found to be 50% larger than for SFO.

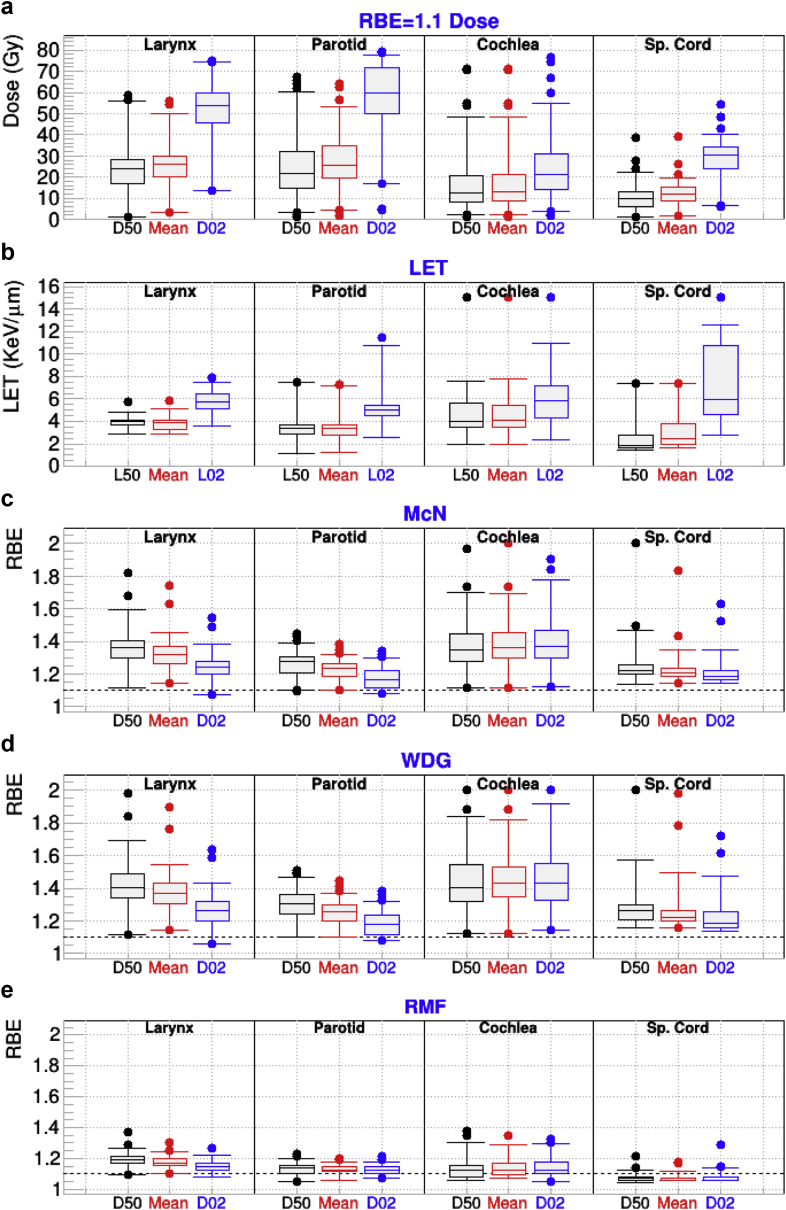
Figure 3 depicts FRD dosimetric and LET indices for a few OARs in the head-and-neck cancer group in the top 2 panels. In addition, RBE_D02, RBE_Mean, and RBE_D50 are shown in the lower 3 panels for RWD. Also, for this cohort, an RBE increase was found for all models and structures, with the exception of the spinal cord and RMF, in spite of having been assigned α_x/β_x = 2 Gy, which should produce larger increases than with a value of 3 as assigned to most OARs. Such a small absolute increase reflects the fact that the spinal cord in general has lower LET (median RBE_Mean = 2.5 ke V/μm) than other OARs. The largest differences for the mean were found for the cochlea for all models and indices, which is driven by slightly larger average LET values and lower average dose. The largest values for the top 2% overpredictions (top whisker in figures) were for the cochlea for WDG and McN, which we attribute to the small size of the OAR, as in brain patients. No clear dependence of these results on the beam angle was found for this cohort. Larynx RBE_D50 excess over 1 for all models was 30% larger for SFO than for MFO with P values < .01. The effect is opposite to that from the brainstem in the brain cohort.

Figure 3.

For patients who received intensity modulated proton therapy for head and neck cancer and for the indicated organs at risk: (a) minimum dose covering 2% and 50% of the targeted structures (D02 and D50) and mean dose calculated from fixed relative biological effectiveness (RBE) dose; (b) the minimum linear energy transfer (LET) covering 2% (L02) and 50% (L50) of the organ, along with the mean LET; (c-e) RBE_D50, RBE_Mean, and RBE_D02 for the McNamara (McN), Wedenberg (WDG), and repair-misrepair-fixation (RMF) models. Sp = spinal.

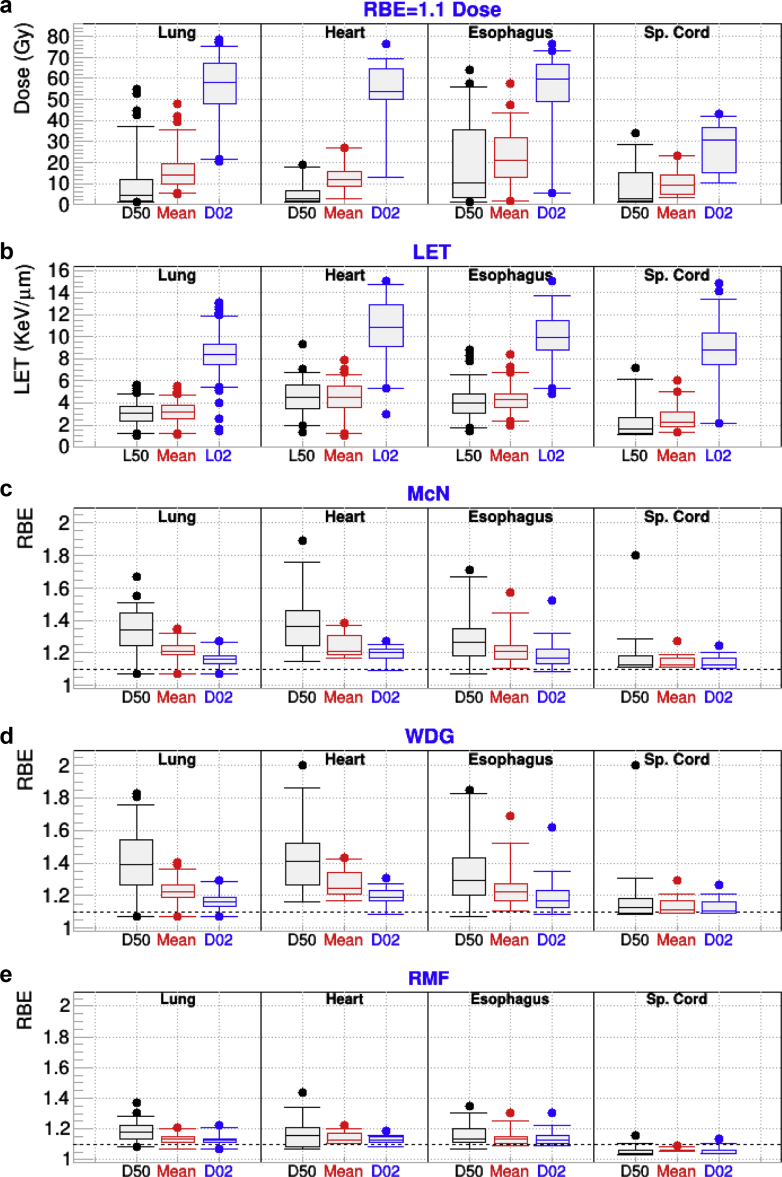
The FRD, LET, and index RBE results for the various models and the selected structures of interest in the thorax are presented in Figure 4. For this group, the average FRDs are lower than for other groups; however, some plans present mean FRD as high as 40 Gy for lung and esophagus. We also see hot LET spots (high L02 values) for all structure with LET values of 12 keV/μm or higher for all structures. A closer examination of plans with very large LET increases revealed that they were cases with those OARs close to the target. The largest increases in RBE were found for RBE_D50 with values of 1.4 or larger for the LET-based-models for all structures.

Figure 4.

For patients who received intensity modulated proton therapy for cancer in the thoracic region and for the indicated organs at risk: (a) minimum dose covering 2% and 50% of the targeted structures (D02 and D50) and mean dose calculated from fixed relative biological effectiveness (RBE) dose; (b) the minimum linear energy transfer (LET) covering 2% (L02) and 50% (L50) of the organ, along with the mean LET; (c-e) RBE_D50, RBE_Mean, and RBE_D02 for the McNamara (McN), Wedenberg (WDG), and repair-misrepair-fixation (RMF) models. Sp = spinal.

As for previous groups, the McN and WDG results are very similar, while RMF presents similar trends; however, they are systematically less pronounced. As in the case of head-and-neck the RMF predictions for the spinal cord are less than 1.1. Such behavior is attributed to the low value of LET (median L50 of 2 keV/mm) in that OAR.

An analysis of the RBE_D02 with beam angle indicated an increase for the spinal cord with posteroanterior beams. Such behavior may be attributed to the fact that posteroanterior beams have high energy and low LET when they traverse areas close to the spine. The opposite is to be expected from anteroposterior beams. For this cohort, there was no significant difference between MFO and SFO plans.

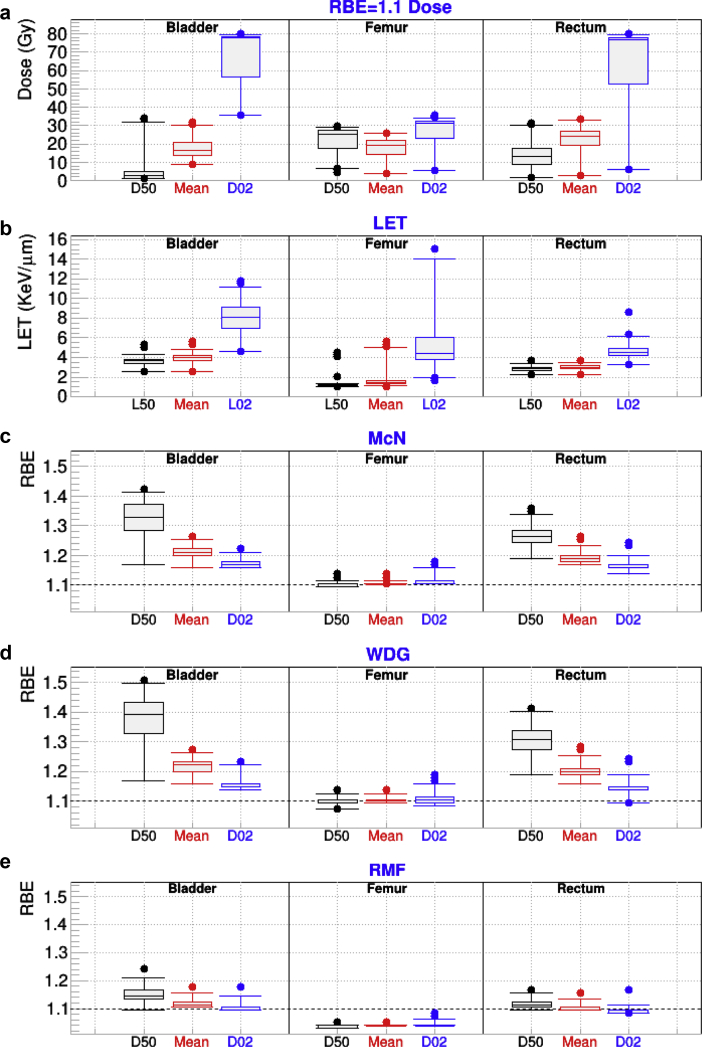
Figure 5 depicts similar data for the prostate plans. The median for the mean dose for the 3 OARs considered (bladder, rectum, and femur) was between 15 and 25 Gy. The median for the average LET was highest for the bladder (4 keV/μm) and rectum (3.5 keV/μm), whereas it was only around 1.6 keV/μm for the femur. Such a pattern is to be expected because the femur is not at the end of the proton range for most plans with 2 lateral opposed beams; thus, the LET is not large. In fact, RMF predicts an RBE <1.1 for all indices for that OAR because of such a low LET and the α_x/β_x = 3 Gy used. There are few plans for which the femur L02 is larger than 8 keV/μm. Those cases were identified as unusual plans with an additional anteroposterior beam. For all models, RBE_D50 > RBE_D02 for the bladder and rectum. Such a behavior is attributed to the fact that for each plan D50 < D02; the lower the dose (D50) the higher the LET, with both effects contributing to increasing the RBE.

Figure 5.

For patients who received intensity modulated proton therapy for cancer in the pelvic region and for the indicated organs at risk: (a) minimum dose covering 2% and 50% of the targeted structures (D02 and D50) and mean dose calculated from fixed relative biological effectiveness (RBE) dose; (b) the minimum linear energy transfer (LET) covering 2% (L02) and 50% (L50) of the organ, along with the mean LET; (c-e) RBE_D50, RBE_Mean, and RBE_D02 for the McNamara (McN), Wedenberg (WDG), and repair-misrepair-fixation (RMF) models.

For all cohorts, we found clear correlations among various models concerning plans with extreme values of RBE₅₀, RBE_Mean, and RBE₀₂. When a model predicted an unusual increase or decrease of an index, other models predicted similar variations within the values of the model.

Concerning uncertainties caused by the values of α_x/β_x, in structures with α_x/β_x = 2 Gy, the interval α_x/β_x = (0.5 Gy, 5 Gy) yielded relative RBE changes of (0.87, 1.09) for WDG, (0.86, 1.10) for MGH, and (0.98, 1.01) for RMF. For structures for which α_x/β_x = 3 Gy was used, if the interval α_x/β_x = (1 Gy, 6 Gy) is considered, the range of variation for RBE is (0.88, 1.11) for WDG, (0.87, 1.12) for MGH, and (0.98, 1.02) for RMF. Finally, for structures for which α_x/β_x = 10 Gy was used, if the interval α_x/β_x = (3 Gy, 20 Gy) is considered, the range of variation for RBE is (0.82, 1.28) for WDG (0.84, 1.30) for MGH, and (0.98, 1.03) for RMF.

Discussion

Various studies for small cohorts have found results that seem compatible with those presented in this study, even though precise comparisons are difficult because of the variety of models, treatment modalities, and α_x/β_x values used. Two passive scattering proton therapy (PSPT) studies7, 10 found dosimetric index increases for brain, head-and-neck, and prostate patients that are consistent with the IMPT results presented in this study. Moreover, Giantsoudi et al¹³ reported results for 11 central nervous system PSPTs with brainstem RBE in the range 1.1 to 1.3, which also seems compatible with our IMPT results.

For most dosimetric indices for the target volumes, the models considered in this study predict higher biologically effective dose values than those obtained with RBE = 1.1. The inclusion of a variable-RBE model may also introduce hot and cold spots in the target area, which could degrade the prescribed target coverage. The 3 models considered produce similar RBEs for the commonly used fraction dose of 2 Gy, α_x/β_x = 10 Gy, and low LET, whereas RMF predicted slightly higher values of RBE for high LET. That explains why the median values tend to be higher for RMF than for McN and WDG for brain, head-and-neck, and thorax cohorts, even though the dispersion of the values was larger for the latter models. The prostate case is the opposite for the median values because a value of α_x/β_x = 3 Gy was used, for which RMF predicts lower RBE for all LET values.

Concerning OARs, the inclusion of variable RBE also predicts higher values for dosimetric indices for most OARs. However, for OARs, unlike target volumes, we are mainly concerned with RBE larger than 1.1, which may lead to toxicity. For all plans the largest increases in RBE were identified for cases that combined large LET and low dose because both factors contribute to increase the RBE. For that reason, we often found the RBE_D50 to be larger than RBE_D02; even though the LET may be similar, the usually lower value for D50 increases the effective RBE. Another factor contributing to large RBE increases was fluctuations in dose and LET distributions in small structures, such as cochlea or optic nerves, which are particularly sensitive to such fluctuations.

The LET-based models (McN and WDG) systematically predict larger RBEs for OARs than the RMF model. When evaluating the risk of toxicity, we are interested in the worst-case scenario or the highest possible RBE. Therefore it does not seem necessary to include the RMF model for plan evaluations.

Optimization techniques have been reported that avoid placing high-LET protons in the vicinity of OARs, which is equivalent to avoiding large RBEs in critical OARs.27, 28, 29 The results presented in this study suggest the need for continued development of such IMPT optimization techniques to avoid potential toxicity as a result of higher biologically effective doses from high LET.

Conclusions

Increases in RBE to OARs were predicted by the models used in these analyses. Even though previous studies for PSPT had found similar trends in the dose variations, we have confirmed the trend for IMPT. Moreover, this is the largest study of which we are aware and was intended to evaluate RBE variation in a large cohort of patients. Our study presents the range of the variations in RBE related to dosimetric indices for a variety of clinical cases. The spread of the results provides an idea of the uncertainty in their predictions because of patient anatomy. Considering the presented results, we recommend the use of techniques to place high-LET dose away from OARs to minimize the risk of toxicity; we also recommend the inclusion of variable RBE models for plan evaluations.

In this article we have limited ourselves to study the effective RBE for various dosimetric indices. In general, for most structures and disease sites, the RBE found is not much larger than 1.1. However, RBE is >1.3 for a nonnegligible percentage of patients, which may have significant consequences with regard to toxicity. We plan further analyses of the data for this subset of patients to determine whether the larger deviations from prescribed target doses and normal tissue dose constraints are associated with local failure and toxicity. Although we do not report clinical outcomes here, unanticipated toxicity from proton therapy has been reported, which may be attributable to higher biologically effective dose than had been assumed based on use of a constant RBE of 1.1.