Abstract
Phosphatidylinositol (3–5)-trisphosphate (PtdInsP3) is known to propagate as waves on the plasma membrane and is related to the membrane-protrusive activities in Dictyostelium and mammalian cells. Although there have been a few attempts to study the three-dimensional (3D) dynamics of these processes, most studies have focused on the dynamics extracted from single focal planes. However, the relation between the dynamics and 3D cell shape remains elusive because of the lack of signaling information about the unobserved part of the membrane. Here, we show that PtdInsP3 wave dynamics are directly regulated by the 3D geometry (i.e., size and shape) of the plasma membrane. By introducing an analysis method that extracts the 3D spatiotemporal activities on the entire cell membrane, we show that PtdInsP3 waves self-regulate their dynamics within the confined membrane area. This leads to changes in speed, orientation, and pattern evolution, following the underlying excitability of the signal transduction system. Our findings emphasize the role of the plasma membrane topology in reaction-diffusion-driven biological systems and indicate its importance in other mammalian systems.
Introduction
Self-organized pattern formation is ubiquitous in nature, particularly under conditions far from thermal equilibrium. The key elements behind the pattern formation are spontaneous symmetry breaking and nonlinearity. Those key elements are also present in biological cells. In particular, signal transduction systems exhibit a variety of self-organized pattern formations, such as asymmetric protein distributions and wave propagations (1, 2, 3), which play pivotal biological roles in Escherichia coli (4), yeast (5), Caenorhabditis elegans (6), and chemotactic eukaryotic cells (7). During the symmetry breaking in these systems, states change from initially homogeneous to asymmetric, and they are sometimes accompanied by complex interplay between system geometry and spatiotemporal signaling (8). How spatiotemporal signaling is related to the geometry of cells remains elusive. An asymmetric state of cell signaling dynamics is usually formed on the plasma membrane, which has characteristics of a closed and boundary-less surface in three dimensions. Therefore it is essential to study the relationship between pattern formation and cell geometry, to investigate the entire plasma membrane as a system.
Similar questions have been addressed in both small- and large-scale systems. For small reaction-diffusion-type systems (9, 10, 11), chemical waves that propagate in a one-dimensional ring exhibit a modulation in speed and phase, depending on the system size (12, 13, 14). Similar behavior was also observed in large-scale systems, such as spatially constrained cardiac tissue preparates (15). But such a relation has been barely investigated in closed surfaces in three dimensions, such as cell membranes, because it is still methodologically challenging to extract and analyze pattern dynamics on the entire living cell surface. In this study, we present a method to extract and analyze pattern dynamics on entire cell membranes, using single Dictyostelium cells as the model system.
A variety of spontaneous and complex pattern formation has been reported in the chemotaxis signaling pathway of Dictyostelium cells. The reaction dynamics of Phosphatidylinositol (3–5)-trisphosphate (PtdInsP3) lipids play a pivotal role in gradient sensing of chemoattractant and actin polymerization (7). In the front region along a gradient, phosphoinositide 3-kinase produces PtdInsP3 from Phosphatidylinositol (4,5)-bisphosphate, whereas phosphatase and tensin homolog catalyzes the reverse reaction in the rear area, leading to an accumulation of PtdInsP3 in the cell front. However, such an asymmetric distribution of PtdInsP3 and filamentous actin can be generated even in the absence of a chemoattractant gradient (16, 17, 18, 19). A variety of self-organizing patterns have been observed on the membrane, such as propagating waves and standing waves along the cell periphery in single optical sections (i.e., along a closed line (20) and on the adhesive membrane area (18, 21, 22, 23)). These patterns have been shown to be generated by an excitable chemotactic signaling pathway (24, 25), and a modulation of the excitable system affects cell migration behaviors (22). The pattern orientation can be easily biased by external chemoattractant gradients (26, 27). Although the signaling pathways are well understood, it is still unclear how the formation of patterns on the membrane are linked to the geometry and size of the cell membrane.
Here, we approached this problem by developing an automated computational method to localize the cell membrane and extract the corresponding PtdInsP3 lipid dynamics on the entire three-dimensional (3D) plasma membrane using Delaunay triangulation. We found that differences in cell shape (i.e., size and adhesion-mediated membrane distortion) regulate the spatiotemporal PtdInsP3 dynamics. The propagation direction of PtdInsP3 domains is biased toward the longest pathway on the cell surface, and the speed of PtdInsP3 domains depends on the size of the membrane (e.g., the average domain speed increased with increasing cell size). Our findings imply a self-regulatory effect of domain dynamics that follow basic principles seen in other excitable media, such as cardiac tissue and Belousov-Zhabotinsky reactive medium. We successfully confirmed our findings by performing additional experiments on spatially constrained Dictyostelium cells that were embedded in narrow grooves of microchambers.
Materials and Methods
Cell preparation
Dictyostelium discoideum cells were used to observe spatiotemporal dynamics of PHAkt/PKB -EGFP. GFP-fused pleckstrin-homology domain of Akt/PKB (PHAkt/PKB) was expressed in wild-type AX-2 cells. Cells were cultured at 21°C in HL-5 medium and selected with 20 μg/mL G418 (28). Before observation, the cells were placed in glass bottom dishes (IWAKI, Tokyo, Japan) 27 mm in diameter and starved in development buffer (DB) (5 mM Na phosphate buffer, 2 mM MgSO4, and 0.2 mM CaCl2 (pH 6.3)) for 4.5 h, leading to chemotactic competency with respect to cAMP (20). The glass bottom dishes were used in the presence or the absence of polyethylenimine (PEI) at a concentration of 2.4 μg/mL in DB. The number of cells was maintained at less than 5 ± 105 cells to sufficiently separate neighboring cells. After starvation, the extracelluar fluid was exchanged and additionally 20 min incubated before observation with 1 mL DB supplemented with 20 μM latrunculin A (L5163-100UG; Sigma, St. Louis, MO), which inhibits actin polymerization and adenylylcyclase and 4 mM caffeine, which is responsible for intrinsic cAMP production. The latter is required to observe self-organizing patterns (20). All in all, 79 cells were observed on glass and 98 cells on PEI-coated glass. A microfluidic chamber with 5-μm-wide and 10-μm-deep grooves made of polydimethylsiloxane (PDMS) (Sylgard 184 Silicone Elastomer; Dow Corning, Midland, MI) were used. Only cells that were completely fixed between the grooves were observed and analyzed .
Cell observation
Fluorescence images were obtained by using an inverted microscope (IX81-ZDC2; Olympus, Tokyo, Japan) equipped with a motorized piezo stage and a spinning disc confocal unit (CSU-X1-A1; Yokogawa, Musashino, Japan) through a 60× oil immersion objective lens (numerical aperture 1.35; UPLSAPO 60XO; Olympus, Tokyo, Japan). PtdInsP3-GFP was excited by a 488-nm laser diode (50 mW). The images were passed through an emission filter (YOKO 520/35; Yokogawa) and captured simultaneously by a water-cooled electron-multiplying charge-coupled device camera (Evolve; Photometrics, Huntington Beach, CA). Time-lapse movies were acquired at 10-s intervals at a spatial resolution of dx = dy = 0.2666 μm and dz = 0.5 μm using z-streaming (MetaMorph 7.7.5; MetaMorph, Nashville, TN). Cells observed in the microfluidic chamber are acquired at a spatial resolution of dx = dy = 0.2222 μm and dz = 0.2 μm.
3D reconstruction of membrane topology and signals
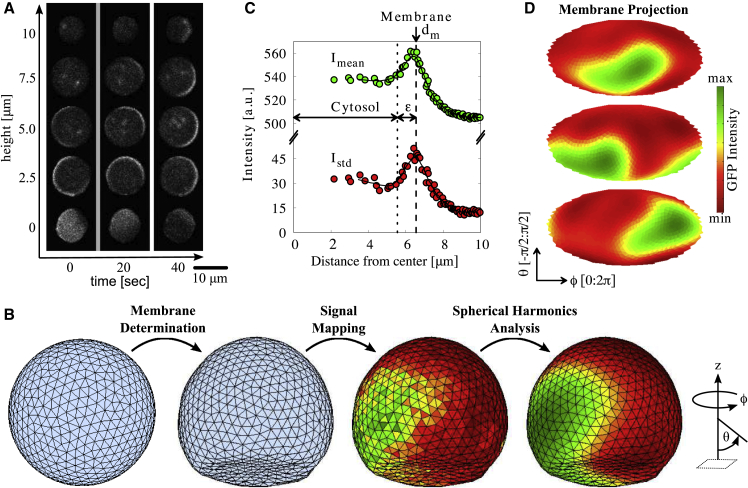
To map and analyze the entire Dictyostelium membrane topology and PtdInsP3 signaling dynamics, we considered the spatial information as a matrix consistent of all three spatial directions (x, y, and z) rather than analyzing recorded focal heights (x and y) independently. A spherical grid was generated and centered to that of the cell using a Delaunay triangulation routine in MATLAB (The MathWorks, Natick, MA) (29) (Fig. 1 B). The spatial coordinates were sorted to the tetrahedral-shaped grid elements, as Mm (x, y, z), considering the corners of each tetrahedron to be the center of the cell and the triangular membrane node. The intensity profile for each Mm is calculated as the time-averaged SD as a function of the distance from the center, d. The membrane position of a grid is determined at the position d = dm with the maximal intensity at dm. The number of nodes, mmax, is then iteratively determined as a function of the respective cell size so that the average area, Am, of all nodes at a given mesh was approximately 0.3 μm2. The number of grids ranged from mmax = 620 to 6632 nodes that correspond to the smallest and largest observed cell, respectively. Fig. 1 C shows an example of the time-averaged intensity profile Imean (green) and the temporal SD Istd (red) extracted from one tetrahedron (node). The dashed line shows the position of the membrane defined by the maximum in Istd that is set by definition as dm. We have chosen to use Istd instead of Imean to define the membrane position at each Mm because the fluorescence signals on the membrane and in cytosol can overlap leading to an underestimation of dm. Additionally, Istd is the more sensitive marker in case of cells that exhibit low PtdInsP3 activity. Thereafter, dm is smoothed among neighboring nodes using a triangular low-Gaussian kernel as follows:
| (1) |
Figure 1.
Signal analysis of PtdInsP3 waves on Dictyostelium membranes. (A) Snapshots of raw data at three time points and five different focal heights. (B) The mapping strategy of propagating waves on the entire cell membrane (viewpoint: ϕ = 360°, θ = −20°). (C) The intensity profile of a single mesh unit. The upper green and lower red data points show the time-averaged intensity (Imean) and SD (Istd) of the signaling as a function of the distance from the cell center, respectively. The membrane position dm is obtained by the local maximum of Istd. The mean cytosolic intensity is obtained by considering an offset ε = 1 μm from dm. (D) The corresponding Mollweide projection of the entire membrane after analysis of the data shown in (A). The second snapshot (t = 20 s) corresponds to the example illustrated in (B) after spherical harmonics analysis. The GFP-signal conservation between the mean cytosolic and mean membrane intensity as a function of time is shown in Fig. S1 (see also Video S1).
Finally, the membrane and cytosolic intensities for each node is extracted at a given time. An offset of ε = 1 μm is considered to separate the cytosolic intensities from the membrane intensity (see Fig. 1 C). The effect of bleaching is corrected considering a single exponential decay that fitted the data best. Fig. S1 shows the GFP-intensity conservation between the mean cytosolic and mean membrane intensity as a function of time for the cell illustrated in Fig. 1 B.
We used the spherical harmonic expansion to smoothen the intensity distribution for peek detection. The membrane intensity is expanded in the spherical harmonics as follows:
| (2) |
where the spherical harmonics is given by
| (3) |
with the Legendre polynomial . The membrane intensity is reconstructed by removing higher frequency modes as follows:
| (4) |
In this study, lmax = 3 is used that corresponds to the octupole moment. To determine the location of PtdInsP3 intensity domains, was used.
Mollweide projection
The Mollweide projection is a homolographic equal-area projection (30) (i.e., the area accuracy-based projection), which is generally used for visualizing global distributions (31), such as the cosmic microwave background and cerebral cortex (32). The transformation from spherical coordinates to cartesian coordinates (x, y) is performed through the following equations:
| (5) |
| (6) |
with the auxiliary angle γ given as
| (7) |
which can be solved iteratively by the Newton-Raphson method (30, 33). For simplicity, only the nodes of the 3D triangular grid have been projected, leading to a nonsmoothened periphery of the projection area (i.e., Fig. 1 D).
Wave peak and speed analysis
The wave domains were tracked and analyzed considering a time-independent threshold Ithresh = (Imax−Imin)/2. Wave speed on the membrane is calculated considering the displacement on the membrane between temporal subsequent peak positions as follows:
| (8) |
with , where n is the temporal index of the corresponding domains . The distance of simultaneously occurring waves is approximated as the shortest distance along the great circle on the membrane as follows:
| (9) |
with , , and , where the indexes correspond to the first and second peak at a given time step, respectively.
Results
3D reconstruction of membrane geometry and signals
Pattern formation in the PtdIns lipid signaling system of Dictyostelium cells was studied by measuring the distribution of PtdInsP3 using the EGFP-labeled PH-domain of Akt/PKB (PH-GFP) in 3D space with time as shown in Fig. 1 A. The cells were treated with 10 μM latrunculin A (an actin polymerization inhibitor) to avoid the effects of motile and protrusive activities of the actin cytoskeleton and with 4 mM caffeine to inhibit cell-to-cell interactions via secreted cAMP (20) (Materials and Methods). To extract the precise spatiotemporal pattern dynamics on the entire cell membrane, we employed a method that uses the signaling itself to specify the membrane position. Once the membrane is correctly localized, the patterns can be mapped (Materials and Methods). First, the position of the entire membrane is determined. Around the cell center, grids are generated on a closed surface, such as a spherical surface, using a Delaunay triangulation routine in MATLAB (29) (Fig. 1 B, left). Each grid element is identified by the azimuthal angle ϕ (latitude) and the polar angle θ (longitude) using spherical coordinates. We then considered the fluorescence intensity along the radial distance from the cell center (Fig. 1 C). Along the radial distance of a grid point, the cell membrane is located at the position at which the fluorescence variation is highest. This is possible because of the stable cell membrane position and the fact that the phosphorylation activity of Phosphatidylinositol (4,5)-bisphosphate to PtdInsP3 and vice versa is highest at the cell membrane. This procedure was independently performed for all grid elements so that the entire membrane position could be determined and reconstructed in three dimensions (Fig. 1 B, left arrow).
Next, the fluorescence intensities on the membrane and in the cytoplasm were determined for each grid element at a given time (Fig. 1 C). The PtdInsP3 signaling distribution on the entire membrane was visualized with a two-dimensional map using the Mollweide projection as shown in Fig. 1 D (see also Video S1). To extract the spatiotemporal dynamics, we performed spherical harmonic transformation at each time frame and removed higher-frequency modes (Fig. 1 B, right). Knowing the exact spatiotemporal information of the membrane geometry and signaling activity, we were able to correlate the spatiotemporal pattern dynamics and the membrane geometry.
(A) Three-dimensional (3D) view (ϕ = 360°, θ = −20°) and (B) two-dimensional Mollweide projection. Each frame corresponds to 10sec in realtime. The mesh size is mmax = 1544. The cell volume and adhesion radius is 0.95pL and 4.5μm, respectively. The line indicates the interface between adhesion and non-adhesion membrane areas.
PtdInsP3 domain formation in single focal planes
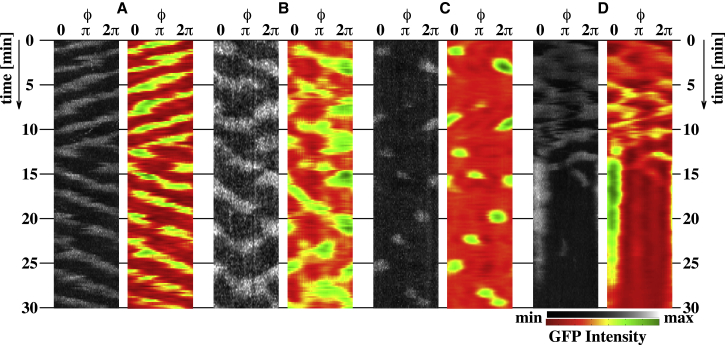
First, we studied the pattern dynamics along the cell periphery at a single focal plane to reproduce the phenomena reported previously (18, 20, 34). Typical examples are shown in Fig. 2. Fig. 2 A shows a traveling wave that changes propagation direction spontaneously, Fig. 2 B a more complex pattern of periodic wave generation and annihilation, and Fig. 2 C a localized domain pattern that appears and disappears at random positions. Chaotic wave dynamics that suddenly change to a stationary localized spot are shown in Fig. 2 D. Though these patterns have been shown in previous studies, they give only a glimpse of the complex dynamics on the entire membrane. To get deeper insights into the formation, dynamics, and influence of the membrane geometry, we use the introduced analysis method (see Fig. 1) to extract the pattern dynamics and cell shape in 3D space.
Figure 2.
PtdInsP3 dynamics of Dictyostelium cell membranes. (A) A propagating wave, (B) complex wave pattern, (C) transient spot pattern, and (D) stationary spot. (A–D) Two kymographs —raw (black-white) and analyzed (red-green) intensity data — that show the dynamics at the equatorial plane (θ ≈ 0°). To see this figure in color, go online.
Pattern dynamics on the entire membrane
The observation and analysis of PtdInsP3 dynamics on the entire membrane enables a more complete and precise view of the complex spatiotemporal dynamics that remain invisible in data from single focal planes. Fig. 3, A–D show the dynamics of the four cells shown in the kymographs of Fig. 2. The Mollweide projections show snapshots of representative dynamics on the entire membrane (Fig. 3, A–D, left; see also Videos S2, S3, S4, and S5). In Fig. 3 A (Video S2), the PtdInsP3 domains propagate along the equatorial cell periphery (horizontal direction), as is expected from the kymograph in Fig. 2 A. In contrast, the Mollweide projection in Fig. 3 B reveals persistently traveling waves in the longitudinal (vertical) direction despite the complex pattern dynamics found in the kymograph of a single section (Fig. 2 B; see also Video S3).
Figure 3.
Spatiotemporal dynamics on Dictyostelium cell membranes. (A–D) Three-dimensional (3D) dynamics of the examples shown in Fig. 2, respectively. (A) Longitudinal propagating waves (along periphery), (B) transversal propagating waves (bottom-top waves), (C) transient spot, and (D) stationary spot. Left: Five prototypical subsequent snapshots. The 3D kymographs show the entire membrane dynamics using the temporal integrated Mollweide projection over time (see Materials and Methods). Bottom Right: Time series of peak position given by longitude ϕ and latitude θ on the cell membrane and the corresponding intensity levels of PtdInsP3. Up to two domains are shown with red and green circles at a time. When one PtdInsP3 wave domain is present (e.g., red), the secondary wave domain is shown by the opposite color (e.g., green). The same domains are connected by a black line in time. In the time series plot of θ, the horizontal dotted lines mark the latitude θc of the interface between adhesive and nonadhesive areas. Gray shaded regions correspond to the snapshots illustrated in the left panel. (E and F) The probability distributions of θ in the cells shown in (A) and (B), respectively. (G) The shape of the cells shown in (A)–(D). To see this figure in color, go online.
Each frame corresponds to 10sec in realtime. The mesh size is mmax = 1892. The cell volume and adhesion radius is 1.25pL and 2.6μm, respectively. The line indicates the interface between adhesion and non-adhesion membrane areas.
Each frame corresponds to 10sec in realtime. The mesh size is mmax = 1388. The cell volume and adhesion radius is 0.89pL and 5.6μm, respectively. The line indicates the interface between adhesion and non-adhesion membrane areas.
Each frame corresponds to 10sec in realtime. The mesh size is mmax = 956. The cell volume and adhesion radius is 0.53pL and 4.4μm, respectively. The line indicates the interface between adhesion and non-adhesion membrane areas.
Each frame corresponds to 10sec in realtime. The mesh size is mmax = 1892. The cell volume and adhesion radius is 1.30pL and 5.1μm, respectively.
Next, we determined the precise spatiotemporal position of the domains from the local maximal PtdInsP3 intensity. We considered up to two domains at a time because more than two domains were rarely observed and thus are statistically insignificant. The domain positions in latitude ϕ and longitude θ are plotted as a function of time (Fig. 3, A–D, right). Fig. 3 A shows the domain motion in the equatorial direction, indicated by the smooth change in the latitude position ϕ with almost constant speed, whereas it was longitudinally constrained around (see Fig. 3 E). Fig. 3 B shows the domain motion in the longitudinal direction. A repetition of zig-zag-like dynamic was found for θ that was accompanied by phase jumps in ϕ when θ reached a cell pole. A comparison of the dynamics between these two cells reveals that the probability of the longitudinal direction θ is distributed more uniformly for the latter cell (Fig. 3, E and F).
The pattern dynamics illustrated in Fig. 3 C, corresponding to Fig. 2 C, show domains that appear and disappear without significant propagation (see also Video S4). The domain lifetime was about 1–2 min. The rate of new domain formation was roughly every 2–3 min. Occasionally, secondary waves formed on the opposite side of the cell membrane (see t ≈ 15, Fig. 3 C), indicating the existence of an inhibitory area around the first domain. This suppression of additional domains forming in the domain vicinity is commonly observed in excitable systems (35).
Although most of the cells exhibited dynamic PtdInsP3 domains, only a very small fraction of cells showed stationary domains. These were high PtdInsP3 intensity, locally stable PtdInsP3 domains that lasted in some cases for more than 20 min, even in the absence of any external stimulus, similarly as for dissipative Turing patterns (36, 37). A typical example is shown in Fig. 3 D (see also Video S5). The cell shows initially propagating waves that switch suddenly (t ≈ 13 min) to a stationary domain with a much higher PtdInsP3 intensity. Although the kymograph in Fig. 2 D indicates that the intensity of the domain fades out, the 3D analysis revealed that the domain drifts gradually to the bottom of the cell (Fig. 3 D).
Fig. 3 G illustrates the cross sections of cell shapes along the z axis for the four cells shown in Fig. 3, A–D. The first cell (A) has a large and spherical shape, whereas the other two cells (B and C) are distorted and thus have larger membrane areas that adhere to the substrate. In the following sections, we study how the domain dynamics correlate with the cell shape and size.
3D cell shape distribution
We studied ∼200 cells to investigate the influence of cell membrane shape on the PtdInsP3 domain dynamics. The cells were cultured on glass (Nglass = 79) or PEI-coated glass (NPEI = 98) to broaden the cell shape distribution (see Materials and Methods). Cell sizes vary from ∼6 to 26 μm in diameter and 20 to 80 μm in perimeter Ccell. All cells were circular symmetric in the xy section, and we characterized the cell shape by the adhesion area Aadh (μm2) relative to the entire membrane area Amem (μm2) as shape parameter ra = Aadh/Amem ranging from ∼5 to 30%. Without PEI, the shape distribution of ra has a peak around 0%, indicating that the cells tend to be spherical (Fig. S2 D). In contrast, the peak shifts to around 15% for cells cultured on PEI, indicating more distorted shapes. This is because PEI-coated glass leads to an increase in the cell-substrate adhesion strength (38) and thus to larger Aadh with a peak at about 30 μm2 compared to 0 μm2 on glass (Fig. S2 C).
Interaction of two domains on 3D cell surface
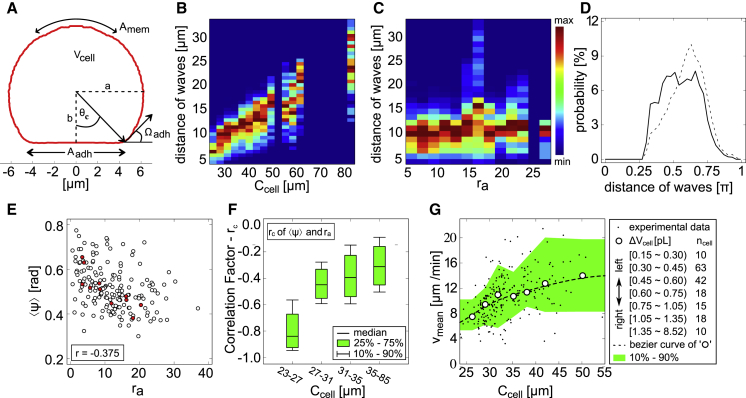
The number of observed domains on the cell membrane is usually one and occasionally two, which also indicates that the characteristic length of the domains is comparable to the cell perimeter. The absolute distance of simultaneously occurring domains on the membrane showed a linear correlation to Ccell (Fig. 4, A and B), whereas it did not show any significant dependence on the cell shape ra (Fig. 4 C). When a secondary PtdInsP3 domain appeared (Fig. 4 D, solid line), the angle distribution between those two domains was almost equally distributed (>0.3π). After the second domain appeared, the distance between these two domains increased, as seen in the change of the angle distribution (Fig. 4 D, dashed line). We observed a shift to larger distances with a peak at around 0.65π. This tendency is typical in excitable systems, where the distance between two propagating waves increases until the inhibitory interaction ceases or an equilibrium is set up.
Figure 4.
Correlation between PtdInsP3 domain dynamics and cell shape. (A) ϕ-integrated membrane profile of the cell illustrated in Fig. 2. Some of the extracted topological parameters are shown. (B and C) Absolute peak-to-peak distance of simultaneously occurring domains on the membrane as a function of the equatorial circumferences Ccell and the shape parameter ra = Aadh/Amem, respectively. (D) The probability angle distribution of secondary PtdInsP3 domains at the time of initiation (solid line) and thereafter (dashed line). (E) The average direction of domain motion as a function of ra for each individual cell. Red highlighted circles show cells whose circumferences are Ccell < 27 μm. (F) Correlation factor rc calculated from (E) as a function of Ccell. (G) The relationship between the mean speed of PtdInsP3 domains vmean and Ccell. Each black point corresponds to a single cell. White circles are averaged data for cells of similar volume Vcell, as listed in the legend box. The number of cells for each data point was set to be ncell ≥ 10 to maintain a minimal statistical significance. The dashed line shows the Bézier curve of the white circles. To see this figure in color, go online.
3D cell shape constraint dynamics of PtdInsP3 domains
Next, we studied PtdInsP3 domain dynamics on various membrane shapes. We first considered the average direction of domain motions for individual cells that is defined between 0 (horizontal direction) and π/2 (vertical direction). We found that is negatively correlated with the shape parameter ra with a correlation coefficient of (Fig. 4 E). Less distorted spherical cells (ra ≈ 0) are distributed around , indicating that the domain motion has no preferred direction. In contrast, as the cell shape gets more distorted (more flattened) with larger ra, the speed in the ϕ direction tends to be larger than the speed in the θ direction (Fig. S3 C), and the domain motion tends to be more oriented to horizontal directions ϕ. This negative correlation is more pronounced for smaller cells (Ccell < 27 μm) (Fig. 4, E and F). Thus, we conclude that the domain motion tends to orient to the horizontal direction in flattened cells.
Next, we considered the dependence of the domain speed vmean on the equatorial circumference Ccell for individual cells. As shown in Fig. 4 G, the speed tends to increase with the cell size. We sorted cells with comparable volume (ncell ≥ 10) and calculated the average domain speed vmean for the respective cells (Fig. 4 G, open circles). The obtained relationship between speed and cell size shows that vmean increases with the increase of Ccell. For sufficiently large Ccell, vmean approaches a plateau speed of ∼12 μm/s, indicating that the cell size is much larger than the domain size. Such a change in speed has been observed in other excitable systems when the intrinsic length of a pattern is modulated (39, 40). The speed and direction of PtdInsP3 domain motion is modulated in small cells because the intrinsic size of the domain is comparable or smaller than the length of cell surface area. In contrast, domain propagation in larger cells is less affected (i.e., the influence of the cell geometry is small). We can conclude that the membrane size and shape influence the formation, speed, and propagation direction of the PtdInsP3 domains (see also Fig. S3).
Additional constraints in cell shape modulate the direction of domain motion
To strengthen the conclusion of our findings, we further modified the cell shape using a microfluidic chamber keeping the 3D analysis of the domain dynamics. We cultured Dictyostelium cells in 5-μm-wide and 10-μm-deep grooves and consistently treated the cells with 20 μM latrunculin A and 4 mM caffeine as before (Materials and Methods). We considered cells with small volumes only (V < 0.3 pL, n = 6). We expected that the shape and limited area of the membranes strongly affect the PtdInsP3 domain dynamics. Fig. 5 A shows an example of such a cell. The cell forms an ellipsoidal shape that is flattened horizontally in contrast to cells that adhere to glass (i.e., x axis is shortest, whereas it is circular symmetric in the yz plane). In Fig. 5 B, we show the average direction of domain motion, as introduced in Fig. 4 E. As expected, we observed with this topological constraint that the PtdInsP3 domains propagate more dominantly along the longitudinal direction (Fig. 5, B and C) than in cells that adhere to glass (with and without PEI). This result gives another strong indication that the 3D cell shape affects the pattern formation of PtdInsP3 in Dictyostelium cells.
Figure 5.
PtdInsP3 dynamics of spatially confined Dictyostelium cells. (A) A three-dimensional (3D) map of a cell cultured in a narrow PDMS chamber. The color code depicts the radius of each grid element from the center of the cell. (B) Projections of typical longitudinal directed dynamics of a PtdInsP3 domain. (C) The median of the average direction of domain motion for small ellipsoidal cells (V < 0.3 pL, n = 6), small glass and PEI-adhered cells (V < 0.3 pL, n = 10), and all adhered cells (n = 177), respectively. The p-values were determined by two-sided Wilcoxon rank-sum test, ∗p < 0.0005 and ∗∗p < 0.00005. To see this figure in color, go online.
Discussion
Signaling dynamics of amoeboid cells have been studied in depth, revealing intracellular mechanisms of cell migration dynamics and protrusion formation of the membrane edge in Dictyostelium and other mammalian cells (7). In previous studies, only a fraction of the cell membrane was typically observed, which is insufficient to understand the complex multidimensional signaling dynamics. In this study, we developed a membrane extraction and signal mapping methodology that enables the correlation between PtdInsP3 signaling dynamics and cell morphology of the entire 3D plasma membrane. We found that cell size and shape affect the spatiotemporal pattern dynamics and that the speed of domain motion increases with increasing cell size, whereas in flattened cells, the direction of motion tends to be perpendicular to the flattened direction.
We performed stochastic simulations to see whether these cell topological constraint dynamics are reproducible in a reaction-diffusion-type system (Fig. S4). We adopted a previously proposed model of PtdInsP3 pattern formation (20, 34) on a 3D cell surface considering realistically distorted cell shapes, as observed experimentally (see Fig. S2). The cell surface is discretized by triangular grid elements without a numerical boundary, as done for the analysis of experimental data. Thus, the membrane geometry is reflected in the spatial distribution of triangular grid elements. In each grid element, the molecular numbers of chemical species are given by integers, which can change by the reactions and the diffusion between neighboring grid elements. The reaction scheme and the diffusion process were solved by using the τ-leap method (41, 42). Thus, the reaction-diffusion dynamics are constrained by the cell shape and the membrane geometry through the asymmetrical distribution of triangular grid elements along the vertical and horizontal direction. For details of the numerical simulation, see Supporting Materials and Methods. With that model, we were able to reproduce the main features as we observed experimentally. In particular, the speed of domain motion was increased as the cell size increased (Fig. S4 A; see also Fig. 4 G), whereas the direction of motion tended to be oriented along the horizontal direction (ϕ direction) (Fig. S4 B). We also observed that the bias in the propagation direction increased with an increase in the cell shape distortion (compare Figs. S3 C and S4 C) and that the simultaneously occurring domains on the membrane show a linear correlation to Ccell (compare Figs. 4 B and S4 D). Although the simulations capture the experimental findings well, the difference between theoretical and experimental results (Fig. S4 C) imply additional, still unknown effects in real Dictyostelium cells (see Fig. S4 C). A possible explanation of the discrepancy between experiments and simulations might be the additional influence of the membrane mechanics, which are not considered in the current model. For example, the higher membrane tension along the periphery of the adhesive part may lead to a local change in the membrane thickness (43) and thus may also change diffusion properties or other membrane curvature-sensitive properties (44).
From our results, we speculate that the PtdInsP3 domains tend to propagate in the direction of the longest possible propagation path. In the case of strongly distorted cells (large ra), this path is the equatorial circumference. In contrast, cells that are horizontally fixed in PDMS grooves have their longest propagation path along the vertical axis and thus dominantly show vertically directed wave dynamics. Because the membrane curvature along the equatorial circumference in flat cells is relatively high and the confined cells shown in Fig. 5 show high-curvature area along the vertical direction, the PtdInsP3 domain pattern may have a tendency to move along this high-curvature region. Considering that the leading edges of migrating Dictyostelium cells is a high-curvature area of flatter shape, such a tendency may be appropriate. Additional studies would be necessary to understand how different shapes of closed surfaces affect pattern dynamics.
Our observations reveal that PtdInsP3 domains can propagate in any direction depending on the shape of the 3D cell membrane. Single focal plane observation at the adhesion area has shown that pattern dynamics may appear as translational waves or self-sustaining rotational waves (18). In contrast, our results show that those two types of waves can be classified as the same type of wave with different propagation directions. Waves that propagate along the horizontal direction (ϕ direction) appear as self-sustaining rotational waves at the adhesion area (Figs. 2 A and 3 A), whereas translational waves at the adhesion area are self-sustaining rotational waves that propagate along the vertical direction (Figs. 2 B and 3 B).
Most cells exhibit waves with interchanging propagation directions during the course of observation. Changes in direction from clockwise to anticlockwise or vice versa are observed in the case of cells that show horizontal wave propagation dominantly (Fig. 2 A, ∼12 min). During this directional change, the domain often propagates vertically for a brief moment as indicated by the zig-zag pattern of the θ position (Fig. 3 A, ∼12 min). Whether this change is noise induced or mediated by other intrinsic dynamics remains to be elucidated in future investigations. However, we expect it is a general concept, because such dynamics are also seen in stochastic simulations (Fig. S4 E). Additionally, we remark that the wave domains continuously propagate at the interface between adhesion and nonadhesion membrane areas without the disappearance of domains or other noticeable effects (the interface line at θ = θc is indicated in Fig. 3, A–D; Videos S2, S3, S4, and S5). This implies that the interface plays no role in the pattern dynamics, contrary to a previous report (18).
Many cellular subsystems of Dictyostelium cells, such as the actin cytoskeleton (45) and the signaling pathway (24, 25), have been reported to exhibit excitable properties. The relationship between domain speed and cell size shown in Fig. 4, F and G can be interpreted in terms of the dispersion relation (velocity restitution) of excitable systems. Classically, the dispersion relation indicates that the speed of waves decreases when the distance between two subsequently activated waves decreases, as observed in spatially constrained Belousov-Zhabotinsky media, such as spherical surfaces (9) and rings (12, 13, 14), and cardiac tissue (46). Here, we consider the equatorial circumference instead of the wave distance because of the complexity of the two-dimensional closed membrane. Our findings suggest that the pattern dynamics adjust dynamically to changes in the surface size and shape of the membrane. In the case of small cells, the domains may fail to propagate, as shown in (Fig. 3 C) (47). In the case of motile cells, we expect a decrease in the propagation speed in sufficiently small membrane regions, such as in pseudopods, leading to a domain localization that may act as an activation area of other signaling pathways. How the heterogeneity in shape and size of biological systems controls the spatiotemporal pattern formation dynamics is an intriguing future topic for in-depth studies in biophysics.
The proposed 3D analysis method enables the realistic comparison of PtdInsP3 domain dynamics and membrane geometry. In this study, we take advantage of the simple geometry of actin polymerization inhibited Dictyostelium cells. A next challenge would be to apply this method to motile Dictyostelium cells. Additionally, other more complex cellular systems can be considered, such as cancer cells and rapidly beating heart cells by adding an analysis of the actin remodeling dynamics (48, 49).
Author Contributions
M.H. and T.S. designed research, performed data acquisition, analyzed data, and wrote the article. M.H. implemented the analysis routine.
Acknowledgments
We thank M.-L. Latteyer, M.-L. Lemloh, M. Tanaka, I. Weiss, and T. Bullmann for their fruitful discussions and helpful comments on the manuscript. We would also like to thank H. Miyoshi (Tokyo Metropolitan University), M. Nishimura, and M. Sugawara (Chiba University) for providing the microfluidic chambers and Y. Wada and M. Hayakawa for the experimental support.
M.H. thanks Japan Society for the Promotion of Science for the financial support (KAKENHI, grant no. 16K18525).
Editor: Mark Alber.
Footnotes
Supporting Materials and Methods, four figures, two tables, and five videos are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)34507-7.
Contributor Information
Marcel Hörning, Email: marcel.hoerning@bio.uni-stuttgart.de.
Tatsuo Shibata, Email: tatsuo.shibata@riken.jp.
Supporting Material
References
- 1.Jilkine A., Edelstein-Keshet L. A comparison of mathematical models for polarization of single eukaryotic cells in response to guided cues. PLoS Comput. Biol. 2011;7:e1001121. doi: 10.1371/journal.pcbi.1001121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Beta C., Kruse K. Intracellular oscillations and waves. Annu. Rev. Condens. Matter Phys. 2017;8:239–264. [Google Scholar]
- 3.Halatek J., Brauns F., Frey E. Self-organization principles of intracellular pattern formation. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2018;373 doi: 10.1098/rstb.2017.0107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Loose M., Kruse K., Schwille P. Protein self-organization: lessons from the min system. Annu. Rev. Biophys. 2011;40:315–336. doi: 10.1146/annurev-biophys-042910-155332. [DOI] [PubMed] [Google Scholar]
- 5.Slaughter B.D., Smith S.E., Li R. Symmetry breaking in the life cycle of the budding yeast. Cold Spring Harb. Perspect. Biol. 2009;1:a003384. doi: 10.1101/cshperspect.a003384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Goehring N.W., Grill S.W. Cell polarity: mechanochemical patterning. Trends Cell Biol. 2013;23:72–80. doi: 10.1016/j.tcb.2012.10.009. [DOI] [PubMed] [Google Scholar]
- 7.Devreotes P.N., Bhattacharya S., Miao Y. Excitable signal transduction networks in directed cell migration. Annu. Rev. Cell Dev. Biol. 2017;33:103–125. doi: 10.1146/annurev-cellbio-100616-060739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Howard J., Grill S.W., Bois J.S. Turing’s next steps: the mechanochemical basis of morphogenesis. Nat. Rev. Mol. Cell Biol. 2011;12:392–398. doi: 10.1038/nrm3120. [DOI] [PubMed] [Google Scholar]
- 9.Maselko J., Showalter K. Chemical waves on spherical surfaces. Nature. 1989;339:609–611. [Google Scholar]
- 10.Aihara R., Yoshikawa K. Size-dependent switching of the spatiotemporal structure between a traveling wave and global rhythm. J. Phys. Chem. A. 2001;105:8445–8448. [Google Scholar]
- 11.Kitahata H., Yoshikawa K. Spatio-temporal pattern formation with oscillatory chemical reaction and continuous photon flux on a micrometre scale. J. Phys. Condens. Matter. 2005;17:S4239–S4248. [Google Scholar]
- 12.Courtemanche M., Glass L., Keener J.P. Instabilities of a propagating pulse in a ring of excitable media. Phys. Rev. Lett. 1993;70:2182–2185. doi: 10.1103/PhysRevLett.70.2182. [DOI] [PubMed] [Google Scholar]
- 13.Nishiyama N. Experimental observation of dynamical behaviors of four, five and six oscillators in rings and nine oscillators in a branched network. Physica D. 1995;80:181–185. [Google Scholar]
- 14.Suematsu N.J., Sato T., Nakata S. Density wave propagation of a wave train in a closed excitable medium. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2011;84:046203. doi: 10.1103/PhysRevE.84.046203. [DOI] [PubMed] [Google Scholar]
- 15.Campanari L., You M.J., Shrier A. Varieties of reentrant dynamics. Chaos. 2017;27:041101. doi: 10.1063/1.4979602. [DOI] [PubMed] [Google Scholar]
- 16.Sasaki A.T., Janetopoulos C., Firtel R.A. G protein-independent Ras/PI3K/F-actin circuit regulates basic cell motility. J. Cell Biol. 2007;178:185–191. doi: 10.1083/jcb.200611138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Asano Y., Nagasaki A., Uyeda T.Q. Correlated waves of actin filaments and PIP3 in Dictyostelium cells. Cell Motil. Cytoskeleton. 2008;65:923–934. doi: 10.1002/cm.20314. [DOI] [PubMed] [Google Scholar]
- 18.Taniguchi D., Ishihara S., Sawai S. Phase geometries of two-dimensional excitable waves govern self-organized morphodynamics of amoeboid cells. Proc. Natl. Acad. Sci. USA. 2013;110:5016–5021. doi: 10.1073/pnas.1218025110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gerhardt M., Ecke M., Gerisch G. Actin and PIP3 waves in giant cells reveal the inherent length scale of an excited state. J. Cell Sci. 2014;127:4507–4517. doi: 10.1242/jcs.156000. [DOI] [PubMed] [Google Scholar]
- 20.Arai Y., Shibata T., Ueda M. Self-organization of the phosphatidylinositol lipids signaling system for random cell migration. Proc. Natl. Acad. Sci. USA. 2010;107:12399–12404. doi: 10.1073/pnas.0908278107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gerisch G., Schroth-Diez B., Ecke M. PIP3 waves and PTEN dynamics in the emergence of cell polarity. Biophys. J. 2012;103:1170–1178. doi: 10.1016/j.bpj.2012.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Miao Y., Bhattacharya S., Devreotes P.N. Altering the threshold of an excitable signal transduction network changes cell migratory modes. Nat. Cell Biol. 2017;19:329–340. doi: 10.1038/ncb3495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Helenius J., Ecke M., Gerisch G. Oscillatory switches of dorso-ventral polarity in cells confined between two surfaces. Biophys. J. 2018;115:150–162. doi: 10.1016/j.bpj.2018.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Huang C.H., Tang M., Devreotes P.N. An excitable signal integrator couples to an idling cytoskeletal oscillator to drive cell migration. Nat. Cell Biol. 2013;15:1307–1316. doi: 10.1038/ncb2859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Nishikawa M., Hörning M., Shibata T. Excitable signal transduction induces both spontaneous and directional cell asymmetries in the phosphatidylinositol lipid signaling system for eukaryotic chemotaxis. Biophys. J. 2014;106:723–734. doi: 10.1016/j.bpj.2013.12.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Xiong Y., Huang C.H., Devreotes P.N. Cells navigate with a local-excitation, global-inhibition-biased excitable network. Proc. Natl. Acad. Sci. USA. 2010;107:17079–17086. doi: 10.1073/pnas.1011271107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Shibata T., Nishikawa M., Ueda M. Intracellular encoding of spatiotemporal guidance cues in a self-organizing signaling system for chemotaxis in Dictyostelium cells. Biophys. J. 2013;105:2199–2209. doi: 10.1016/j.bpj.2013.09.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Watts D.J., Ashworth J.M. Growth of myxameobae of the cellular slime mould Dictyostelium discoideum in axenic culture. Biochem. J. 1970;119:171–174. doi: 10.1042/bj1190171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Persson P.-O., Strang G. A simple mesh generator in MATLAB. SIAM Rev. 2004;46:2004. [Google Scholar]
- 30.Weisstein, E. W. Mollweide Projection. From MathWorld–A Wolfram web resource (Wolfram MathWorld). http://mathworld.wolfram.com/MollweideProjection.html.
- 31.Feeman T. Equal area world maps: a case study. SIAM Rev. 2000;42:109–114. [Google Scholar]
- 32.Kang X., Herron T.J., Woods D.L. Hemispherically-unified surface maps of human cerebral cortex: reliability and hemispheric asymmetries. PLoS One. 2012;7:e45582. doi: 10.1371/journal.pone.0045582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Snyder J.P. U.S. Government Printing Office; Washington, D.C: 1987. Map Projections: A Working Manual: USGS Numbered Series 1395. [Google Scholar]
- 34.Shibata T., Nishikawa M., Ueda M. Modeling the self-organized phosphatidylinositol lipid signaling system in chemotactic cells using quantitative image analysis. J. Cell Sci. 2012;125:5138–5150. doi: 10.1242/jcs.108373. [DOI] [PubMed] [Google Scholar]
- 35.Hörning M., Isomura A., Yoshikawa K. Liberation of a pinned spiral wave by a single stimulus in excitable media. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;79:026218. doi: 10.1103/PhysRevE.79.026218. [DOI] [PubMed] [Google Scholar]
- 36.Turing A.M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1952;237:37–72. doi: 10.1098/rstb.2014.0218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Leppänen T., Karttunen M., Barrio R.A. Dimensionality effects in turing pattern formation. Int. J. Mod. Phys. B. 2003;17:5541–5553. [Google Scholar]
- 38.Miyanaga Y., Matsuoka S., Ueda M. Single-molecule imaging techniques to visualize chemotactic signaling events on the membrane of living Dictyostelium cells. Methods Mol. Biol. 2009;571:417–435. doi: 10.1007/978-1-60761-198-1_28. [DOI] [PubMed] [Google Scholar]
- 39.Cherry E.M., Fenton F.H. Suppression of alternans and conduction blocks despite steep APD restitution: electrotonic, memory, and conduction velocity restitution effects. Am. J. Physiol. Heart Circ. Physiol. 2004;286:H2332–H2341. doi: 10.1152/ajpheart.00747.2003. [DOI] [PubMed] [Google Scholar]
- 40.Hörning M. Termination of pinned vortices by high-frequency wave trains in heartlike excitable media with anisotropic fiber orientation. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2012;86:031912. doi: 10.1103/PhysRevE.86.031912. [DOI] [PubMed] [Google Scholar]
- 41.Gillespie D.T. Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 2001;115:1716–1733. [Google Scholar]
- 42.Cao Y., Gillespie D.T., Petzold L.R. Efficient step size selection for the tau-leaping simulation method. J. Chem. Phys. 2006;124:044109. doi: 10.1063/1.2159468. [DOI] [PubMed] [Google Scholar]
- 43.Reddy A.S., Warshaviak D.T., Chachisvilis M. Effect of membrane tension on the physical properties of DOPC lipid bilayer membrane. Biochim. Biophys. Acta. 2012;1818:2271–2281. doi: 10.1016/j.bbamem.2012.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gov N.S. Guided by curvature: shaping cells by coupling curved membrane proteins and cytoskeletal forces. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2018;373:20170115. doi: 10.1098/rstb.2017.0115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Weiner O.D., Marganski W.A., Kirschner M.W. An actin-based wave generator organizes cell motility. PLoS Biol. 2007;5:e221. doi: 10.1371/journal.pbio.0050221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Weiss J.N., Qu Z., Karma A. The dynamics of cardiac fibrillation. Circulation. 2005;112:1232–1240. doi: 10.1161/CIRCULATIONAHA.104.529545. [DOI] [PubMed] [Google Scholar]
- 47.Lindemans F.W., Denier Van der Gon J.J. Current thresholds and liminal size in excitation of heart muscle. Cardiovasc. Res. 1978;12:477–485. doi: 10.1093/cvr/12.8.477. [DOI] [PubMed] [Google Scholar]
- 48.Zemel A., Rehfeldt F., Safran S.A. Optimal matrix rigidity for stress fiber polarization in stem cells. Nat. Phys. 2010;6:468–473. doi: 10.1038/nphys1613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Hörning M., Nakahata M., Tanaka M. Dynamic mechano-regulation of myoblast cells on supramolecular hydrogels cross-linked by reversible host-guest interactions. Sci. Rep. 2017;7:7660. doi: 10.1038/s41598-017-07934-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(A) Three-dimensional (3D) view (ϕ = 360°, θ = −20°) and (B) two-dimensional Mollweide projection. Each frame corresponds to 10sec in realtime. The mesh size is mmax = 1544. The cell volume and adhesion radius is 0.95pL and 4.5μm, respectively. The line indicates the interface between adhesion and non-adhesion membrane areas.
Each frame corresponds to 10sec in realtime. The mesh size is mmax = 1892. The cell volume and adhesion radius is 1.25pL and 2.6μm, respectively. The line indicates the interface between adhesion and non-adhesion membrane areas.
Each frame corresponds to 10sec in realtime. The mesh size is mmax = 1388. The cell volume and adhesion radius is 0.89pL and 5.6μm, respectively. The line indicates the interface between adhesion and non-adhesion membrane areas.
Each frame corresponds to 10sec in realtime. The mesh size is mmax = 956. The cell volume and adhesion radius is 0.53pL and 4.4μm, respectively. The line indicates the interface between adhesion and non-adhesion membrane areas.
Each frame corresponds to 10sec in realtime. The mesh size is mmax = 1892. The cell volume and adhesion radius is 1.30pL and 5.1μm, respectively.