A Comparison of Knee Abduction Angles Measured by a 3D Anatomic Coordinate System Versus Videographic Analysis: Implications for Anterior Cruciate Ligament Injury

Abstract

Background:

Knee positions involved in noncontact anterior cruciate ligament (ACL) injury have been studied via analysis of injury videos. Positions of high ACL strain have been identified in vivo. These methods have supported different hypotheses regarding the role of knee abduction in ACL injury.

Purpose/Hypothesis:

The purpose of this study was to compare knee abduction angles measured by 2 methods: using a 3-dimensional (3D) coordinate system based on anatomic features of the bones versus simulated 2-dimensional (2D) videographic analysis. We hypothesized that knee abduction angles measured in a 2D videographic analysis would differ from those measured from 3D bone anatomic features and that videographic knee abduction angles would depend on flexion angle and on the position of the camera relative to the patient.

Study Design:

Descriptive laboratory study.

Methods:

Models of the femur and tibia were created from magnetic resonance images of 8 healthy male participants. The models were positioned to match biplanar fluoroscopic images obtained as participants posed in lunges of varying flexion angles (FLAs). Knee abduction angle was calculated from the positioned models in 2 ways: (1) varus-valgus angle (VVA), defined as the angle between the long axis of the tibia and the femoral transepicondylar axis by use of a 3D anatomic coordinate system; and (2) coronal plane angle (CPA), defined as the angle between the long axis of the tibia and the long axis of the femur projected onto the tibial coronal plane to simulate a 2D videographic analysis. We then simulated how changing the position of the camera relative to the participant would affect knee abduction angles.

Results:

During flexion, when CPA was calculated from a purely anterior or posterior view of the joint—an ideal scenario for measuring knee abduction from 2D videographic analysis—CPA was significantly different from VVA (P < .0001). CPA also varied substantially with the position of the camera relative to the participant.

Conclusion:

How closely CPA (derived from 2D videographic analysis) relates to VVA (derived from a 3D anatomic coordinate system) depends on FLA and camera orientation.

Clinical Relevance:

This study provides a novel comparison of knee abduction angles measured from 2D videographic analysis and those measured within a 3D anatomic coordinate system. Consideration of these findings is important when interpreting 2D videographic data regarding knee abduction angle in ACL injury.

Conflicting data exist regarding which knee motions increase the likelihood of noncontact anterior cruciate ligament (ACL) injury.³⁶ This may hinder efforts to enhance the efficacy of training programs targeted at injury prevention. To better understand how ACL injuries occur, joint motions occurring around the time of injury have been studied via analysis of injury videos.^{2,3,15,18,21,22,28} Alternatively, knee positions that result in ACL elongation and strain, therefore increasing the risk of injury, have been identified in vivo by use of 3-dimensional (3D) imaging techniques.^{16,24–26,31,32} These methods have supported differing hypotheses on how noncontact ACL injuries occur. Specifically, several videographic analyses have supported an injury mechanism involving aberrant knee abduction,^3,15,21,30 whereas 3D imaging studies indicate that the ACL is elongated with decreased flexion^31,32 and support the hypothesis that the ACL fails with the knee positioned at a low flexion angle (FLA).^9,10,36

A potential reason for these different hypotheses regarding ACL injury mechanism stems from differences in how knee abduction angle is measured. In a videographic analysis, knee abduction angles are commonly measured from 2-dimensional (2D) video frames, ideally with the camera perspective approximating an anterior or posterior coronal view of the knee.^3,15 Knee abduction angle is estimated by measuring the angle between a line drawn along the long axis of the femur to the center of the knee joint and a line from the same point on the knee to the center of the tibia at the ankle joint.³ This method of estimating knee abduction angle may depend on the angle between the camera and the patient. Alternatively, several in vivo studies have combined biplanar radiography with 3D joint models derived from magnetic resonance (MR) images to determine the relative position of the bones for a specified knee posture or motion.^24,31,32 Subsequently, knee abduction angles and ligament deformations are measured from a 3D coordinate system based on the anatomic features of the bones.¹⁴ The angles measured in this way are invariant to the perspective from which they are measured.

In the present study, we compared these methods of measuring knee abduction angle (measurement of joint angles through 2D videographic analysis versus use of a 3D coordinate system based on bone anatomic features). Because information about mechanism of injury has been derived from 2D videographic analysis, where an injured player’s orientation with respect to the camera is not controlled, we explored how knee abduction angles measured by means of both a 3D anatomic coordinate system and 2D videographic analysis change with FLA and with viewing angle. Specifically, we measured knee abduction angles in vivo using imaging while participants performed static lunges of varying FLA. We then simulated the knee abduction angle that would be measured in a 2D videographic analysis of the knee joint in the position determined by the imaging data. In a subsequent simulation, we explored the effect of the angle between the camera and the knee joint (the camera “viewing angle”) on the knee abduction angle determined from the simulated videographic analysis. We hypothesized that knee abduction angles measured in a 2D videographic analysis would differ from those measured via a 3D anatomic coordinate system and that videographic knee abduction angles would depend on FLA and on the position of the camera relative to the patient.

Methods

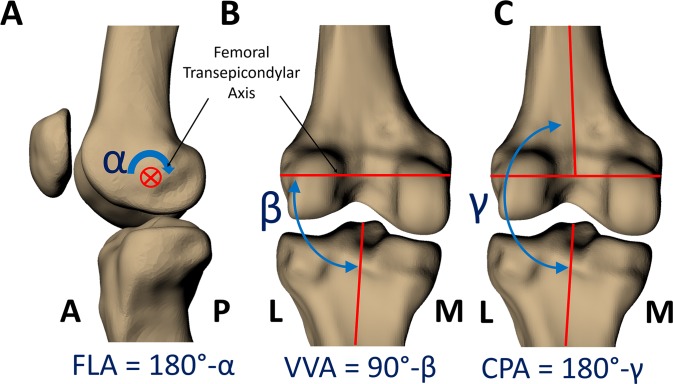
Eight male participants (mean age, 26.5 ± 5.5 years) with no history of lower extremity injury participated in this institutional review board–approved protocol. One knee from each participant underwent both MR imaging and biplanar fluoroscopic imaging, with the goal of determining the relative positions of the femur and tibia during lunges of varying FLA. The 3D models of the femur and tibia were created by outlining the bony contours in the MR images. The models of the femur and tibia were positioned to match the biplanar fluoroscopic images obtained for each lunge position (Figure 1), and knee joint angles were measured from the models in their matched positions. Specifically, FLA was confirmed, and knee abduction angles were measured in 2 ways (Figure 2). First, the varus-valgus angle (VVA; defined as the angle between the femoral transepicondylar axis and the long axis of the tibia^14,31) was calculated for each lunge position. Then, we simulated how knee abduction would be measured in a 2D videographic analysis by calculating the coronal plane angle (CPA, defined as the angle between the long axis of the tibia and the long axis of the femur projected onto the tibial coronal plane) for each lunge position. In an additional simulation, to explore how the angle between the camera and the participant affected the CPA, we rotated the coronal plane about several “viewing angles” (Figure 3).

Figure 1.

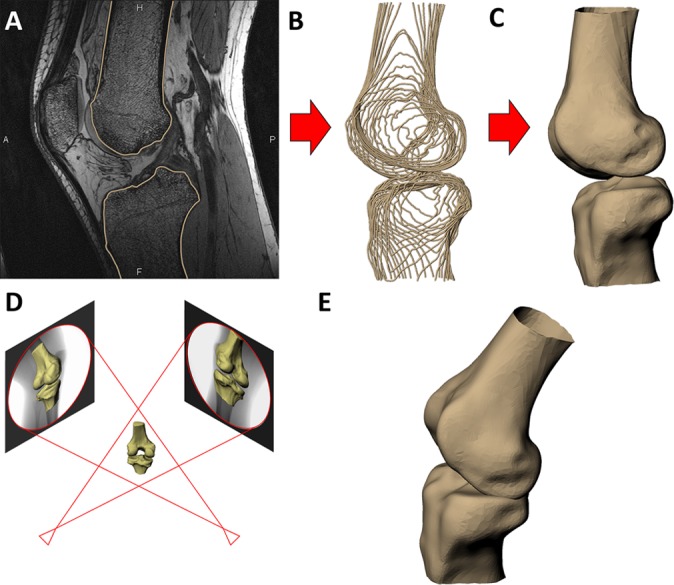
(A) The outer contours of the femur and tibia were outlined on each slice of the magnetic resonance images. (B) The contours were compiled into wireframe models. (C) Three-dimensional surface models were created from the wireframe models. (D) The models of the femur and tibia were positioned to match the biplanar fluoroscopic images. (E) The matched models then represented the in vivo positions of the bones as the participant performed the lunges.

Figure 2.

Joint angles were measured from the models through use of a standardized coordinate system. (A) The flexion angle (FLA) is the angle between the long axes of the femur and tibia measured about the femoral transepicondylar axis, subtracted from 180°. (B) The varus-valgus angle (VVA) is the angle between the long axis of the tibia and the femoral transepicondylar axis, subtracted from 90°. This measurement of VVA is based on the anatomic features of the bones and is invariant to the perspective from which it is measured. (C) The coronal plane angle (CPA) is the angle between the long axis of the tibia and the long axis of the femur projected onto the tibial coronal plane (defined by the tibial anteroposterior axis), subtracted from 180°. All angles were measured in degrees. For both VVA and CPA, a positive value indicates valgus alignment, and a negative value indicates varus alignment. A, anterior; L, lateral; M, medial; P, posterior.

Figure 3.

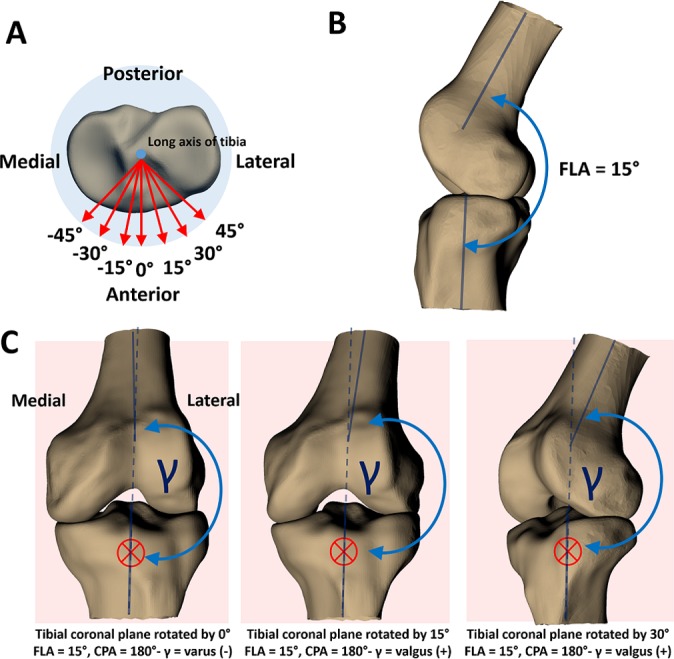
(A) The blue dot in the center of the tibial plateau represents the long axis of the tibia oriented perpendicular to the page. The red arrows represent the tibial anteroposterior axis, rotated by viewing angles of –45° to 45° in increments of 15°. These anteroposterior axes represent the unit-normal vectors to the coronal planes in which coronal plane angles (CPAs) are measured. The viewing angle of 0° represents a measurement of the CPA in the plane defined by the unrotated unit-normal vector of the tibial coronal plane (representing an anterior or posterior coronal view of the joint)—a best-case scenario for measuring knee abduction angle from 2D video frames. (B) The knee positioned at a flexion angle (FLA) of 15°. (C) Changing the viewing angle (rotating the anteroposterior axis that defines the tibial coronal plane) changes the CPA. The red crosses denote the coronal plane, oriented perpendicular to the page, and the dashed blue line represents the long axis of the tibia extended into the femur for reference. At a viewing angle of 0°, CPA is negative, indicating varus alignment. However, at a viewing angle of 15°, CPA is positive, indicating a valgus alignment. As viewing angle increases, alignment appears more valgus. The FLA is 15° in all of these scenarios; this effect would be more pronounced when the knee is positioned in more flexion.

Image Collection

One knee from each participant underwent MR imaging via a 3.0-T scanner (Trio Tim; Siemens Medical Solutions USA). Sagittal images were acquired from the participants while they were lying supine, through use of a double-echo steady-state sequence and an 8-channel knee coil (resolution, 0.3 × 0.3 × 1 mm; flip angle, 25°; repetition time, 17 ms; echo time, 6 ms).^27,31,35 Then, images of the knee were obtained from 2 orthogonal directions through use of biplanar fluoroscopes (BV Pulsera; Philips) while participants stood on a level platform and posed in single-legged static lunge positions of various FLAs.⁶ Each fluoroscopic image had a resolution of 1024 × 1024 pixels.² For each pose, participants were guided on how to position their knee with a goniometer.

Image Analysis

The bony contours of the femur and tibia were segmented from the MR images by use of solid-modeling software (Rhinoceros 4.0; Robert McNeel and Associates) (Figure 1A). These contours were compiled into wireframe (Figure 1B) and 3D surface models of the femur and tibia (Figure 1C) as previously described.^24,31,32 To model the relative positions of the femur and tibia during the single-legged static lunges, the fluoroscopic images were imported into the solid-modeling software program and positioned in 2 orthogonal planes. The 3D models of the femur and tibia were then moved in 6 degrees of freedom to match the biplanar fluoroscopic images (Figure 1D).⁶ Previous validation has shown that this method can measure in vivo 3D tibiofemoral kinematics within a resolution of 0.1 mm and 0.3°.^4,8

Measurement of Joint Angles

Before joint angles were measured from the bone models in their matched positions, a 3D coordinate system was defined for the femur and tibia.¹⁴ Cylinders were fit to the shafts of the femur and tibia to define their long axes. The transepicondylar axis of the femur was defined as the axis between the most medial and most lateral points of the femoral condyles. The mediolateral axis of the tibia was defined as the axis perpendicular to the long axis of the tibia and tangent to the posterior aspects of the tibial plateaus. Finally, an anteroposterior axis was set orthogonal to both the long and mediolateral axes of the tibia. The unit-normal vector describing the anteroposterior axis was used to define the coronal plane.

Joint angles were measured from the models in their matched positions (Figure 2).³¹ Specifically, we verified FLA for each lunge position and measured knee abduction angles in 2 ways: (1) by calculating the VVA and (2) by calculating the CPA, which was meant to simulate how a videographic analysis would estimate knee abduction angle. These angles were measured according to the following definitions:

• FLA (Figure 2A): the angle between the long axes of the femur and tibia measured about the femoral transepicondylar axis, subtracted from 180°.

• VVA (Figure 2B): the angle between the long axis of the tibia and the femoral transepicondylar axis measured from the lateral side of the joint, subtracted from 90°. A negative VVA indicates varus alignment (where the proximal end of the long axis of the tibia is angled toward the lateral side of the femoral transepicondylar axis). A positive VVA indicates valgus alignment (where the proximal end of the long axis of the tibia is angled toward the medial side of the transepicondylar axis).

• CPA (Figure 2C): the angle between the long axis of the tibia and long axis of the femur projected into the coronal plane (defined by the tibial anteroposterior axis), subtracted from 180°. A negative CPA indicates varus alignment, and a positive CPA represents a valgus alignment.

Effect of Viewing Angle on Knee Abduction Angle

To explore the effect of camera angle relative to the participant (the camera “viewing angle”) on knee abduction angle, the tibial anteroposterior axis (that defined the coronal plane) was rotated about the tibial long axis by several viewing angles (Figure 3A). In Figure 3A, the blue dot in the center of the tibial plateau represents the long axis of the tibia, oriented perpendicular to the page. The red arrows represent the unit-normal vectors to the coronal planes from which CPA is measured, rotated by viewing angles of –45° to 45° in increments of 15°. The viewing angle of 0° represents a measurement of the CPA in the plane defined by the nonrotated unit-normal tibial anteroposterior axis, which represents an anterior or posterior coronal view of the joint. This view is ideal for measuring knee abduction in a videographic analysis. Knee abduction angles were recalculated at each viewing angle.

Statistical Analysis

All measurements were interpolated from the data to represent values of each variable at FLAs between 0° and 90° in increments of 15°. The data were summarized by use of routine descriptive statistics (SAS, version 9.4; SAS Institute) with P < .05 indicating significance. A repeated-measures analysis of covariance (ANCOVA) was carried out through use of a linear mixed model to determine the effects of FLA (0° to 90° in 15° increments), viewing angle (–45° to 45° in 15° increments), and type of measurement (either VVA or CPA) on knee abduction angle. Mixed models were used to accommodate the experimental design, in which both covariates (FLA and viewing angle) and fixed factors (measurement type) were present. Where a significant interaction of measurement type with either FLA or viewing angle was found, separate ANCOVAs were performed for both VVA and CPA to determine differences in how FLA and viewing angle affected the measurement types. Subsequently, to compare CPA and VVA on an equal basis, a repeated-measures ANCOVA was run in which only data from a viewing angle of 0° were included, to remove the influence of viewing angle. The statistical tests are summarized in Table 1.

TABLE 1.

Summary of Statistics^a

Test	Outcome Variable	Dependent Variable	Covariates	Interaction Effects
Repeated-measures mixed-model ANCOVA	Knee abduction angle	Measurement type (CPA or VVA)	FLA, viewing angle	Measurement type × FLA Measurement type × viewing angle FLA × viewing angle
ANCOVA	CPA	Not applicable (ANCOVA)	FLA, viewing angle	None
ANCOVA	VVA	Not applicable (ANCOVA)	FLA, viewing angle	None
Repeated-measures mixed-model ANCOVA (only data from viewing angle = 0°)	Knee abduction angle	Measurement type (CPA or VVA)	FLA	None

^aANCOVA, analysis of covariance; CPA, coronal plane angle; FLA, flexion angle; VVA, varus-valgus angle.

Results

The overall repeated-measures ANCOVA revealed significant effects of FLA (P = .0017) and viewing angle (P < .0001) on knee abduction angle. At a viewing angle of 0°, both VVA and CPA increased with increasing FLA. Furthermore, the overall repeated-measures ANCOVA indicated a significant interaction between the viewing angle and the measurement type (VVA vs CPA, P < .0001), meaning that viewing angle affected CPA and VVA differently. Specifically, separate ANCOVAs for the 2 knee abduction measurement types showed that viewing angle was a significant covariate of CPA (P < .0001) but not of VVA (P ≤ .999). To this point, while VVA was invariant to viewing angle (Figure 4, solid red line), CPA changed dramatically with viewing angle, particularly with increasing FLA (Figure 4, dashed lines). Finally, the repeated-measures ANCOVA including only data from a viewing angle of 0°, representing a best-case scenario for measuring CPA from a 2D video frame, revealed that CPA (Figure 4, solid blue line) was significantly different from VVA (P < .0001), indicating that the 2 methods for quantifying knee abduction angle are not equivalent. At a viewing angle of 0°, the magnitude of the difference between CPA and VVA across FLA ranging from 0 to 75° was 12.5° ± 8.9° (mean ± SD).

Figure 4.

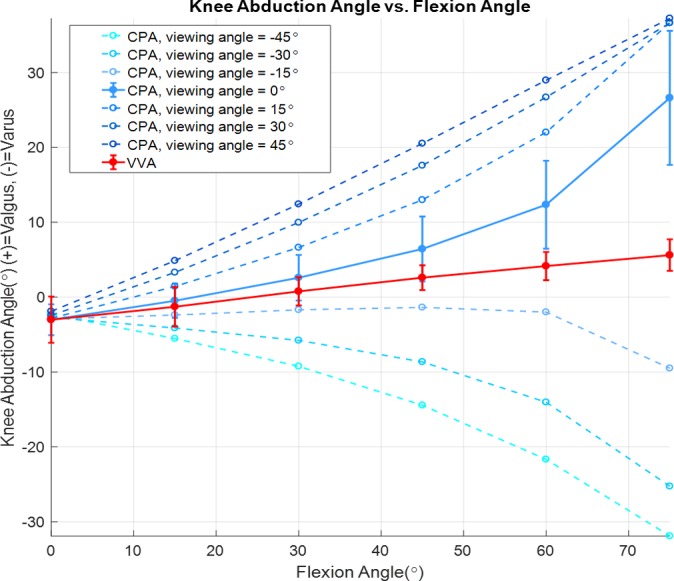
Knee abduction angles (varus-valgus angle [VVA] and coronal plane angle [CPA], vertical axis) were measured as a function of flexion angle (horizontal axis) for several viewing angles. Viewing angle significantly affected CPA (dashed blue lines, P < .0001), whereas VVA (solid red line) was invariant to viewing angle. CPA differed significantly from VVA when CPA was measured in the unrotated coronal plane (viewing angle of 0°, solid blue line), a best-case scenario for measuring knee abduction from 2D video frames. Values in the figure are means ± SDs.

Discussion

Analysis of videographic footage is used to provide information on knee positions at the time of ACL injury.⁵ Several of these studies have supported the hypothesis that aberrant knee abduction angle plays a crucial role in ACL rupture.^3,15,28 In contrast, 3D in vivo imaging studies suggest that the ACL is elongated at lower FLA and support the hypothesis that landing in extension is a highly relevant risk factor for ACL injury.^{24,25,31,32,36} To explore the hypotheses generated by these 2 techniques, we determined the relative positions of the femur and tibia for several lunge positions using in vivo imaging and then compared knee abduction angles obtained directly from the positioned models (VVA) using a 3D anatomically derived coordinate system with those angles measured from a simulated 2D videographic analysis (CPA) of the joint. We demonstrated that CPA differed from VVA when measured from an ideal anterior or posterior view of the joint (Figure 4, solid lines). Furthermore, because information about mechanism of injury was derived from 2D videographic analysis, where the injured player’s orientation with respect to the camera was not controlled, we demonstrated that differences between CPA and VVA became more pronounced with increasing FLA and when the angle between the camera and participant was not ideal (Figure 4, dashed blue lines). These findings are in congruence with a prior study that also showed that knee abduction measured in a 2D plane differed from knee abduction measured from 3D anatomic features and that 2D knee abduction measurements were elevated with increased knee flexion and hip internal rotation.³⁴

These findings may have important implications for the interpretation of 2D videographic studies that support a valgus collapse mechanism of ACL injury. Valgus collapse refers to medial buckling of the knee, characterized by increased knee abduction angles following ground contact.^28,30 For example, Boden et al³ showed that female athletes during ACL injury made impact with the ground in extension, with small knee abduction angles, and subsequently progressed into an average knee abduction angle of 38° several video frames after ground contact. In another study, injured female athletes progressed into a maximum knee abduction angle averaging close to 40°, compared with 20° in injured male athletes, at 250 milliseconds after initial ground contact.¹⁵ These studies suggested that the large increase in knee abduction angle present after ground contact plays a role in the mechanism of ACL rupture. However, the findings presented here suggest that the degree to which 2D videographic measurements of knee abduction angle relate to VVA depends on FLA and the perspective of the camera.

Because of the noted difficulty in obtaining 3D joint angles from single 2D video frames,²⁰ several videographic analysis studies have used a technique that involves matching skeletal models to multiple camera views, from which injury kinematics are estimated (3D videographic analysis).^18,19,22 A recent systematic review⁵ found that 3D videographic analysis studies report higher FLA and lower valgus angulation (knee abduction) relative to 2D videographic analyses at time points distant from initial ground contact but report similar FLA and valgus closer to initial ground contact when the knee is potentially less flexed. Using 3D videographic analysis, Koga et al¹⁸ described an injury motion pattern that included initially landing on a relatively straight knee (average FLA = 23°), progressing to an average FLA of 47° by 40 milliseconds later. Additionally, knee abduction angle was neutral at ground contact and progressed to an average of 12° at 40 milliseconds after ground contact. However, as in 2D videographic analysis, it remains unclear whether the reported increases in FLA and valgus occurred as a result of the injury or were involved in the injury mechanism itself. Notably, increased valgus was accompanied by increased FLA in the time period after ground contact.¹⁸ This finding is in line with the data presented here, which indicate that VVA increases with increasing FLA (Figure 4, solid red line). Furthermore, while 3D videographic analysis may offer improvements over 2D videographic analysis, the accuracy of 3D videographic analysis is dependent on the investigator’s ability to reliably match a skeletal model to a clothed individual,^18,22 and it may be difficult to assess the accuracy of this technique during injury scenarios.²²

The variance in CPA with viewing angle seen in the present study might have arisen because FLA was interpreted as knee abduction (see Figure 3C) when the 3D angles were projected in a 2D plane. In Figure 3C, we showed that with the knee positioned at a 15° FLA, a rotation of the viewing angle had a notable effect on CPA. This finding is particularly important, given that the selection criterion for the aforementioned 2D videographic studies was that the video frame approximated an anterior or posterior coronal view of the knee.^3,15 Furthermore, several studies have hypothesized that the point of ACL injury occurs closer in time to initial ground contact (around 40-50 ms)^18,21 than the points in time where the large increases in knee abduction were reported in aforementioned 2D videographic studies.^3,15 Thus, it is possible that the observation of valgus collapse in injury videos is influenced by the joint buckling into flexion after the ACL has ruptured,²⁸ which is being interpreted as valgus, rather than the mechanism of ACL rupture itself. Furthermore, during the complex motions involved with ACL ruptures, the effect of knee flexion being interpreted as valgus may be further exacerbated by internal-external knee or hip rotation.

In vivo imaging studies allow for quantification of the relationships between ligament deformations and joint angles, which are measured within a 3D coordinate system based on joint anatomic features.³⁴ Specifically, several in vivo imaging studies have measured ACL elongation resulting from various knee postures.^31,32,34 For example, Utturkar et al³⁴ found that in static knee positions, ACL length was maximized with the knee in extension and decreased when the knee was positioned in 30° of flexion. Taylor et al^31,32 reported that during dynamic activities, relative ACL strain was greatest when the knee was close to full extension, specifically during the midstance phase and just prior to heel strike during gait³¹ and just prior to ground contact in jump landing.³² Studies using arthroscopically implanted strain gauges also show that ACL strain is maximized when the knee is extended.^7,13,23 Furthermore, analyses of bone bruise patterns have indicated that large anterior tibial translations occur with the knee close to extension during an ACL injury.^17,29 Along with evidence from cadaveric studies that demonstrated anterior tibial translation and ACL strain due to simulated quadriceps loading with the knee positioned at a low flexion angle,^1,9–11,33 these studies support the theory that landing with an extended knee is a particularly relevant risk factor for ACL rupture. Despite these studies providing a mechanistic explanation for why landing in extension may cause the ACL to fail, such investigations cannot be performed during an injury scenario.

In this study, we quantified the relationship between FLA, camera viewing angle, and knee abduction angles using a simulation approach. Along these lines, additional work may examine the effect of hip rotation on the magnitude of perceived knee abduction when measurements are made in a 2D plane. A quasi-static lunge was selected for this study because it allowed us to measure knee abduction angles when the knee was flexed to various degrees. Furthermore, this was a controlled activity that was likely to be performed similarly across participants. By measuring knee abduction for various flexion angles, we showed that knee flexion can be interpreted as knee abduction when measured in a 2D plane. While the quasi-static lunge was not dynamic, the procedure of projecting a 3D coordinate system onto a 2D plane would not be influenced by type of activity. Future work regarding knee joint angles and ACL injury mechanisms will include measurements of knee kinematics and ACL elongation during dynamic activities, which will further elucidate the motions that result in increased ACL loading¹² and increased injury risk. Our study included a male-only cohort, but the procedure of projecting 3D angles onto a 2D plane is not likely to be influenced by the sex of the participant. However, future studies using this technique may include female participants.

Conclusion

The results of the present study show that knee abduction angles obtained via 2D videographic analysis (CPA) differ from knee abduction angles obtained with a 3D anatomic coordinate system (VVA). Furthermore, our data suggest that FLA and camera viewing angle should be considered when one is interpreting results from 2D video analysis studies.