Novel imaging phantom for accurate and robust measurement of brain atrophy rates using clinical MRI

Abstract

Brain volume loss, or atrophy, has been proven to be an important characteristic of neurological diseases such as Alzheimer's disease and multiple sclerosis. To use atrophy rate as a reliable clinical biomarker and to increase statistical power in clinical treatment trials, measurement variability needs to be minimized. Among other sources, systematic differences between different MR scanners are suspected to contribute to this variability. In this study we developed and performed initial validation tests of an MR-compatible phantom and analysis software for robust and reliable evaluation of the brain volume loss. The phantom contained three inflatable models of brain structures, i.e. cerebral hemisphere, putamen, and caudate nucleus. Software to reliably quantify volumes form the phantom images was also developed. To validate the method, the phantom was imaged using 3D T1-weighted protocols at three clinical 3T MR scanners from different vendors. Calculated volume change from MRI was compared with the known applied volume change using ICC and mean absolute difference. As assessed by the ICC, the agreement between our developed software and the applied volume change for different structures ranged from 0.999–1 for hemisphere, 0.976–0.998 for putamen, and 0.985–0.999 for caudate nucleus. The mean absolute differences between measured and applied volume change were 109–332 μL for hemisphere, 2.9–11.9 μL for putamen, and 2.2–10.1 μL for caudate nucleus. This method offers a reliable and robust measurement of volume change using MR images and could potentially be used to standardize clinical measurement of atrophy rates.

Highlights

• •We developed a method for standardizing measurements of volume change between different scanners.
• •The method makes use of an imaging phantom by which volume change can be applied in a highly controlled way.
• •The phantom structures resemble three brain structures, i.e. hemisphere, putamen and caudate nucleus.
• •The volume change was quantified from the phantom MR images using developed segmentation software.

1. Introduction

Neurodegeneration is a persistent problem in multiple sclerosis (MS) and some other diseases like Alzheimer's disease (AD). In MS, new treatments are being developed to slow down or prevent this neurodegeneration. An accessible in vivo surrogate of neurodegeneration is brain atrophy, i.e. brain volume loss, which can be measured using magnetic resonance imaging (MRI). However, measurement variability is substantial; among other factors, differences between MRI scanners introduce unwanted variability of atrophy measures. Studies in MS observed different volumes and volume changes for two different scanners using similar or even identical acquisition parameters (Durand-Dubief et al., 2012), differences in global brain tissue volumes and cortical thickness were found between three different 3-Tesla MR scanners (Biberacher et al., 2016), and even different whole-brain volumes between two scanners of the exact same type with identical imaging protocols (Takao et al., 2011).

Unwanted scanner or acquisition protocol dependent variability of atrophy rates directly affects the statistical power of multi-center treatment trials. Moreover, it hampers the use of monitoring of atrophy progression in individual patients in the clinical setting. This is especially problematic in diseases like MS in which the typical annual rate of brain volume loss is only about 0.5–1% (De Stefano et al., 2016).

In MRI, imaging phantoms have been widely used for quality control as well as for detecting geometrical distortions (Chen et al., 2004; Ihalainen et al., 2011; Vassiliou et al., 2016; Wang et al., 2004a, Wang et al., 2004b). To our knowledge, no application has yet been published in which imaging phantoms are used to standardize measurements of brain atrophy rates between scanners and acquisition protocols.

In this study we aimed to develop a phantom for standardizing measurements of volume change between different scanners. This works by scanning the phantom at each scanner/site independently, and derive a calibration function specific to the scanner and acquisition protocol used. Therefore, the resulting calibration is supposed to be scanner-specific which takes into account a couple of sources of variability such as hardware, field strength and pulse sequence type. The method makes use of an imaging phantom containing three inflatable structures to which volume change can be applied in a highly controlled way. The phantom structures resemble three brain structures, i.e. hemisphere, putamen and caudate nucleus. In this initial validation study, the phantom is imaged at various known set volume changes, and then for each structure the volume change is quantified from the phantom MR images using dedicated segmentation software.

2. Materials and methods

2.1. Phantom development

The MRI phantom contains inflatable structures equipped with a precise volume change system (Fig. 1). The phantom contains three brain structures: a cerebral hemisphere, putamen, and caudate nucleus. The hemisphere model was created by scanning a post-mortem healthy brain using a surface 3D scanner (Artec Spider, Arc 3D). The models of putamen and caudate nucleus were generated from MR images of healthy control subjects using FSL-FIRST (Patenaude et al., 2011). Using these models, molds of all three structures were 3D-printed by ZP151 powder (3D systems). Then, the molds were repeatedly dipped into pre-vulcanized latex rubber (pvs-elastica, FromX) to reach a homogenized thickness. Finally, the molds were dissolved in water and phantoms remained. All three structures were attached on a nylon plate for stabilization and embedded in a 3D-printed cylinder made by plexiglass. Syringes (Hamilton®, Switzerland) of 100 mL and 100 μL were incorporated with a custom-made stainless steel plunger with a finely bored syringe barrel to change the volume in the hemisphere and the small structures, respectively.

Fig. 1.

(a) Side-view and (b) top-view of the phantom, with (c) the volume change system and (d) the complete device. Each structure had inlet and outlet valves to fill them up with water and to make them air-free, respectively. Rigid tubes (VYGON) of inner and outer diameter of 1 mm and 2 mm, respectively, were used to connect structures to the volume change system. All structures are mounted in an oval-shaped 3D-printed housing (PA2200, EOS SLS).

2.2. MR imaging

To validate the method, the phantom was imaged at three different clinical 3 T MR scanners (GE, Toshiba and Philips) using a standard clinical 3D gradient echo sequence available at each scanner with voxel volumes 1–1.2 μL. To eliminate any signal originating from the latex material constituting the inflatable structures, the clinical protocol was adjusted by a suitable choice of echo time (TE) and repetition time (TR). Other parameters remained unchanged. For example, at each scanner, we used the k-space filters (Fermi at GE, NL2:7* k-space LSI (linear space invariant) only at Toshiba, and no filters at Philips) which were already used in the clinic to get the best image qualities. Scanner and pulse sequence parameters are given in Table 1. Typical phantom MR images on Toshiba are shown in Fig. 2.

Table 1.

Scanner and pulse sequence parameters for the three scanners used.

Vendor	GE	Philips	Toshiba
Model	MR750	Ingenuity	Titan
Field strength (T)	3	3	3
Coil type	8-channel head coil	8-channel head coil	32-channel head coil
Sequence type	FSPGR	FEE	FEE
TR (ms)	8.21	7.9	5.7
TE (ms)	3.2	4.5	2.4
Flip angle (degrees)	12	8	5
Acquisition matrix	256*256	256*256	256*256
Voxel size (mm)	1 × 1 × 1	1 × 1 × 1	1 × 1.2 × 1
Slab orientation	sagittal	sagittal	sagittal
Number of slices	140	140	140
Parallel imaging?	Yes	Yes	Yes

Fig. 2.

Representative MR images of the hemisphere, putamen, and caudate nucleus phantoms in (a) axial, (b) coronal and (c) sagittal plane as obtained on Toshiba Titan.

2.3. Volume change

In each scanning session, five volume changes were applied to each of the three structures as indicated in Table 2. The volume changes were applied as integer multiples of the full rotation of the precision screw controlling the syringe. They were chosen to range between about 1% - 5% of the volume of each structure. Because the caudate nucleus and putamen are of comparable size, the same amount of volume changes were applied to them. For the hemisphere, the applied volume changes were chosen much larger than for the two small structures. Note that the volumes of all three structures were increased simultaneously as indicated in Table 2, to maximize efficiency of scanning. For the analysis, step number five was taken as a reference volume to calculate the volume decrease towards baseline.

Table 2.

Applied volume changes of different structures at different steps.

Step	Caudate nucleus volume-change (μL)	Putamen volume-change (μL)	Hemisphere volume-change (mL)
Baseline	0	0	0
1	26.46	26.46	3.332
2	52.92	52.92	6.665
3	79.38	79.38	9.998
4	105.84	105.84	13.330
5	132.30	132.30	16.663

2.4. Image analysis

We developed a segmentation software to measure the volume changes from the MR images of the phantom. Note that the software operates on a single 3D image, and quantifies the water volume inside the structure of interest for that image. Volume changes between steps in a phantom measurement series are then quantified by subtracting the calculated volumes, rather than being quantified directly by our software.

Fig. 3 shows a diagram of the image analysis pipeline. The final output of the software is the volume of water inside the structure of interest, which is quantified by integrating the voxel-wise partial volume estimates of water across the interior of the structure, including its internal latex-water boundary voxels. First, the images were corrected for intensity non-uniformity using nonparametric non-uniform intensity normalization (N3) (Sled et al., 1998). A spline distance of 50 mm and a full width at half maximum (FWHM) value of 0.05 were used. The small FWHM value was chosen to favour accuracy over speed. Because some Gibbs ringing is present in our images, peak values were adjusted as follows. First, the mean and standard deviation of the water inside the hemisphere was calculated. Then inside the area that is considered to be surely water, voxels with intensity higher than the median plus 3 times the standard deviation were reduced to the square root above this cut-off level. Because latex and nylon give very low signal, we improved their contrast with the background by adding to the intensity of every voxel inside the housing (i.e., also including the water voxels) 0.5 times the mean intensity of the water inside the core of the hemisphere.

Fig. 3.

Diagram of the image analysis pipeline to estimate the volumes of the hemisphere, putamen and caudate nucleus. Briefly, the software includes correction for intensity non-uniformity using N3, Gibbs ringing artifact removal, introduction of an artificial (“virtual”) latex component to balance the classes in the subsequent FSL-FAST segmentation, and quantification of total internal volume of each structure from the PVE values obtained from FSL-FAST. Red-to-yellow color bar indicates the water PVE.

Next, images were prepared to perform FSL-FAST partial volume estimation. FSL-FAST models voxel intensities with 3 Gaussian distributions and noise. Without additional pre-processing, FSL-FAST may treat the nylon and latex material as noise because (i) only a small portion of voxels in the image contain nylon or latex and (ii) the intensity distribution of these voxels does not match a Gaussian distribution due to the relatively high number of partial volume voxels. Therefore, we added areas of voxels with the same intensity as the latex (“virtual latex”). In order not to influence the partial volume estimates (PVEs) in the boundary between water and real latex, we added this (virtual) extra latex well away from the real latex. Subsequently, FSL-FAST was run without bias field correction. Finally, to correctly estimate volumes, the class of the virtual latex was replaced with the water class.

2.5. Statistical analysis

To determine the reliability of our measured volume changes, measured volume changed were compared with the applied volume changes using interclass correlation coefficient (ICC) with the two-way mixed model for absolute agreement. Furthermore, mean absolute differences (MAD) between measured and applied volume changes were calculated across each phantom measurement series. For both statistics, SPSS software version 22 (IBM) was used.

3. Results

3.1. Phantom validation

A representative MR image of the phantom for a given volume is shown in Fig. 2. To validate the accuracy of the volume change system and the developed segmentation software, the true applied volume changes versus measured volume changes are plotted in Fig. 4. As seen in this figure, the measured data showed a perfect agreement with the applied volume changes.

Fig. 4.

Applied versus measured volume change at three different scanners for (top row) hemisphere, (middle row) caudate nucleus, and (bottom row) putamen. The green dotted line represents the identity line.

3.2. ICC and mean absolute differences

Table 3 reports the ICC for absolute agreement and MAD, for the three brain structures. ICC values indicate that agreement between applied and measured volume changes is excellent. The MAD data also shows that deviation of the measured volume changes from the mean change are relatively negligible compared to the applied volume changes.

Table 3.

ICC and MAD for all three brain structures.

	Hemisphere		Putamen		Caudate nucleus
	ICCa	MADb (mL)	ICC	MAD (μL)	ICC	MAD (μL)
GE	0.999	0.3322	0.998	2.9	0.999	2.2
Toshiba	1.000	0.1089	0.994	5.5	0.997	3.7
Philips	1.000	0.2612	0.976	11.9	0.985	10.1

^aICC = Interclass correlation coefficient.

^bMAD = Mean absolute difference; voxel sizes: 1 μL for GE and Philips and 1.2 μL for Toshiba.

4. Discussion

In this study we developed and validated a phantom and analysis software to induce and measure volume change of models of brain structures. The ICCs revealed a very strong agreement between our developed method and the applied volume change. Therefore, our method can potentially offer a reliable and robust tool to standardize measurements of volume change in clinical trials as well as in clinical settings.

Despite the importance of brain atrophy measurement in neurological conditions such as MS and AD, its clinical use at the individual subject level is hampered by the large measurement variability (Rocca et al., 2017). Among other sources of variability such as physiological effects, between-scanner and between-acquisition protocol differences are suspected to contribute importantly (Amiri et al., 2018). For example, volume differences were seen when using two different scanners with similar or even identical acquisition parameters (Durand-Dubief et al., 2012). In another study performed at three different 3-Tesla MR scanners, significant differences in total lesion volume, global brain tissue volumes and cortical thickness measures between the scanners were observed (Biberacher et al., 2016). Even when using identical imaging protocols, it was found that the whole brain volumes were significantly different between two scanners of the exact same type (Takao et al., 2011). Therefore, to increase statistical power in clinical trials and to establish atrophy measures as reliable clinical biomarkers, such scanner-induced effects should be minimized.

To date, some anthropomorphic brain phantoms have been described, e.g. by using agar gel and manganese chloride (Altermatt et al., 2017; Fujimoto et al., 2015),) or using polyvinyl alcohol (PVA) (Chen et al., 2012). The advantage of the method presented in this paper is that it would allow standardization of the volume change measurements within and between scanners and acquisition protocols. Moreover, this method can accurately and robustly provide a selected volume change to mimic e.g. the change typically observed in a certain disease.

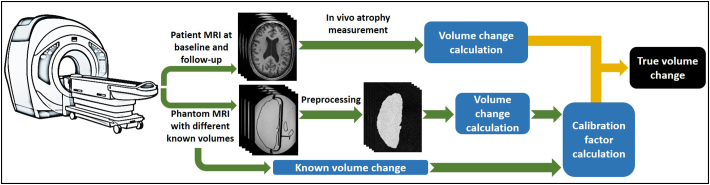
A limitation of this study was that we did not test our method in vivo. Therefore, an important next step in the development of the present method would be to investigate translation of this method to a clinical setting to validate it in patients. In our view, as schematically illustrated in Fig. 5, the translation to an in vivo setting requires additional steps such as (i) the phantom contrast-to-noise ratio (CNR) should mimic the in vivo CNR and (ii) the image analysis software used to obtain calibration functions from the phantom images should be similar to that used in the patient studies. This implementation includes acquiring scans of the phantom on the same day as patient scans while applying known volume changes to the phantom. This would lead to calibration factors not only per scanner and acquisition protocol, but also per day of patient visits. Future studies should investigate whether scanning the phantom on the same day is necessary. Furthermore, it would be interesting to use this method to test widely used brain volume analysis software to assess their accuracy, in a manner comparable to the work done by Chen et al. on their PVA phantom (Chen et al., 2012), and to possibly find standardization functions to correct for them. This would facilitate use of this method to standardize volume change measurements obtained on different scanners and analysed using specific analysis methods.

Fig. 5.

Scheme of the phantom clinical implementation for “true volume change” calculation.

It is known that analysis methods are another source of variability in volume measurements. A study tested reproducibility of the commonly used software package SIENA (Cover et al., 2011). They showed that the variability of atrophy measurement, obtained from scan and re-scan of the subjects without repositioning, was of considerable magnitude compared to the typical atrophy rates. Interestingly, use of 3-Tesla instead of 1.5-Tesla MRI did not reduce the error (Cover et al., 2014). It also has been shown that, for both FSL-FIRST and FreeSurfer, within-session reproducibility error for measuring 1-year hippocampal volume change was substantial (Mulder et al., 2014). A recent study (Cover et al., 2016) showed that reproducibility of 1-year volume change highly depends on the image analysis method, which affects the statistical power and required sample sizes in clinical trials. Therefore, next to the scanner-induced variabilities, the analysis software should also be considered as an important source of variability in measuring brain volume change in vivo. Even for in vivo measurements that are standardized according to the final proposed clinical method, such variability of the in vivo analysis software would remain an issue. Of note, the analysis software that we developed provides high accuracy in the measurement of the phantom volume change, thus adding only minimal error.

In conclusion, we demonstrated the feasibility of producing inflatable brain phantoms, and were able to adjust the volume of such a phantom in a controlled and precise way. Future studies should implement and validate the clinical application of this phantom for standardizing atrophy measurements.