Abstract.
Ovarian cancer has the lowest survival rate among all gynecologic cancers predominantly due to late diagnosis. Early detection of ovarian cancer can increase 5-year survival rates from 40% up to 92%, yet no reliable early detection techniques exist. Optical coherence tomography (OCT) is an emerging technique that provides depth-resolved, high-resolution images of biological tissue in real-time and demonstrates great potential for imaging of ovarian tissue. Mouse models are crucial to quantitatively assess the diagnostic potential of OCT for ovarian cancer imaging; however, due to small organ size, the ovaries must first be separated from the image background using the process of segmentation. Manual segmentation is time-intensive, as OCT yields three-dimensional data. Furthermore, speckle noise complicates OCT images, frustrating many processing techniques. While much work has investigated noise-reduction and automated segmentation for retinal OCT imaging, little has considered the application to the ovaries, which exhibit higher variance and inhomogeneity than the retina. To address these challenges, we evaluate a set of algorithms to segment OCT images of mouse ovaries. We examine five preprocessing techniques and seven segmentation algorithms. While all preprocessing methods improve segmentation, Gaussian filtering is most effective, showing an improvement of . Of the segmentation algorithms, active contours performs best, segmenting with an accuracy of compared with manual segmentation. Even so, further optimization could lead to maximizing the performance for segmenting OCT images of the ovaries.
Keywords: optical coherence tomography, image segmentation, image processing, ovarian cancer
1. Introduction
1.1. Burden of Ovarian Cancer
Despite concerted efforts to improve patient outcomes, ovarian cancer remains the deadliest gynecologic malignancy in the United States. While ovarian cancer is not exceedingly common, the disease maintains a high mortality rate, with median 5-year survival less than 45%.1 One cause of this is the fact that ovarian cancer can grow to a large size before causing signs or symptoms, leading to a high proportion of advanced disease at the time of detection. In fact, a large majority of patients have already experienced spread of their disease to local or distant tissues at initial diagnosis, resulting in a significantly poorer prognosis.2
This insidious pattern of disease progression has led to strong interest in the area of ovarian cancer screening, with the ultimate goal of identifying early-stage tumors, while the patient is still asymptomatic, allowing more effective treatment. Various screening modalities have been investigated to reduce the burden of the disease including physical examination, transvaginal ultrasound, and serum tumor marker measurement (most commonly Ca-125).3 Other screening tests and multimodal protocols have also been investigated; however, at this time, no routine screening is recommended in average-risk patients.4 As such, there remains a strong need for a high-quality, minimally invasive modality for effective detection of early-stage ovarian malignancies.
1.2. Optical Coherence Tomography
Optical coherence tomography (OCT) is an interferometric imaging technique first introduced in 19915 that yields depth-resolved, high-resolution images of tissue, providing information about the tomography and microstructure. Historically, OCT has been successfully applied to biological imaging in the human eye,6–8 the lung,9,10 the esophagus,11 the coronary artery,12,13 in addition to a number of other organs, including the ovaries.14–18 The physical principle of OCT systems is similar to that of ultrasound, except that OCT systems measure time-resolved backscattered light instead of sound waves.19 A complicating factor of OCT is the depth dependence of the system performance. Lateral resolution varies throughout the sample depth. In addition, the axial resolution degrades in deeper tissue as a result of breaking the assumption of single-scattering of light; furthermore, absorption by the tissue attenuates the signal. Ultimately, the image statistics vary as a function of depth, which can frustrate attempts at quantitative analysis. Despite these drawbacks, OCT is a widely applied and robust approach to characterizing tissue microstructure. In particular, OCT has shown great potential for disease diagnostics and tissue classification in the ovaries by imaging a wealth of microstructural features, including the stroma, epithelium, and collagen.14–17,20
A myriad of different image analysis techniques have recently been investigated in the scope of classifying tissue health based on OCT images. Some examples include structure and texture analysis,21–25 convolutional neural networks,13,26,27 and other machine-learning techniques.10,28,29 Quantitatively characterizing tissue with such approaches has shown great promise as a diagnostic aid. One important step to test and evaluate the suitability of different methods relies on mouse models, which are critical to provide a systematic control in which to observe biological variations. However, in the scope of ovarian OCT imaging, the mouse ovaries must first be separated from the image background due to the small organ size relative to a typical OCT system field of view. This process, known as image segmentation, allows the relevant image content to be extracted and analyzed, preventing corruption from background features. The need for segmentation is not unique to ovarian OCT imaging: segmentation is a common challenge in medical imaging.30,31 Unfortunately, pre-existing solutions are tuned to a given application and do not translate well between imaging modalities.32 Segmentation can be accomplished either manually or automatically. While accurate, manual segmentation is time-intensive, particularly when OCT yields three-dimensional (3-D) data. Also of importance, appropriate preprocessing is required to suppress noise to best segment the image. Much work has investigated noise-reduction and automated segmentation for retinal OCT imaging;33 however, little has considered the application to the ovaries, which exhibit higher structural variance and inherent inhomogeneity than the retina. Hence, to efficiently evaluate quantitative analysis methods for ovarian OCT imaging, finding an effective approach to automatic segmentation is critical. A robust segmentation algorithm would widely inform the field of OCT imaging as the application has expanded to organs, such as the esophagus,11 colon,34 and coronary artery,12 where segmentation is required to quantitatively assess tissue health.35,36 Here, we evaluate a set of preprocessing techniques and segmentation algorithms for the purpose of segmenting OCT images of the ovaries.
1.3. Image Segmentation Methods
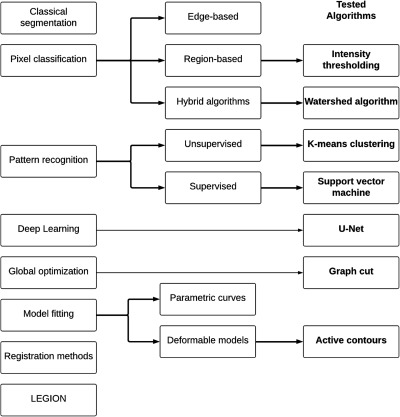
Many different approaches to segmentation have been proposed in the scope of medical image processing.30,32,33 These methods can be separated into different groups, depending on the underlying mathematics involved (Fig. 1). Classical segmentation techniques partition the image into nonoverlapping, continuous, segments based on the value of some features, such as brightness or texture.37–39 Pixel classification methods are an extension of classical approaches, albeit the constraint on region continuity is relaxed. Thresholding the image remains one of the simplest and most intuitive approaches to segmentation. In this case, a histogram is created to cluster pixels according to some feature, such as pixel intensity or a texture parameter. The thresholds are selected to partition the histogram, where the pixels residing in a given partition are assigned a label for segmentation. Depending on the feature represented in the histogram, thresholding can be used to segment based on edges or regions; other methods use a combination of the two and are referred to as hybrid algorithms.40 For example, the watershed algorithm is a widely used technique where regions of different classes are first seeded based on finding maxima in a distance-transform of the image; the regions are then grown until the sources meet.41 The resulting boundary between sources is taken then as the segmentation.
Fig. 1.
Image segmentation algorithms can be decomposed into different classes, depending on the mathematics involved. We test seven of the most commonly found techniques for medical image segmentation, each of which belongs to a different class of algorithm.
Pattern recognition algorithms can perform segmentation by identifying inherent structure in an image. These algorithms can either be supervised or unsupervised; in either case, the algorithm identifies patterns in the image, which are then used to partition the image area. Supervised approaches are first trained on a set of manually segmented images that are used as reference; examples include artificial neural networks and support vector machines (SVM).42,43 Recently, deep learning methods have found increasingly widespread application for segmentation and analysis. The most notable is the U-Net, which was developed specifically for biological image segmentation.44 Unsupervised methods, also known as clustering methods, do not need training data; however, properly initializing the algorithm parameters is essential for accuracy.45–47 Another class of segmentation algorithms is referred to as global optimization methods, which are based on energy minimization techniques. One such example is graph cutting, where the image is represented as an adjacency graph.48,49 In this graph, the vertices represent pixels of an image, and the weight between two vertices is the similarity between two given pixels. The graph is then partitioned by cutting the vertex connections to create different groups. The optimization minimizes the summation of the weights that are cut, which can be thought of as minimizing the energy in the system. Another form of energy-minimization is to fit a model to the image, which takes advantage of morphologic or structural characteristics. Examples of this include fitting deformable models and parametric curves to an image.50,51 Recently, one such technique known as the active contour model has found much success in medical image segmentation.52–54 An active contour model is applied by initializing a so-called snake, which is a two-dimensional (2-D) path within the image. This path can be constrained with different boundary conditions and the algorithm proceeds by fitting this path to the contours in the image. This deformable path is an energy minimizing spline influenced by image forces, defined to pull it toward object contours, which are balanced by internal forces that resist deformation. Active contours may be understood as a special case of the general technique of matching a deformable model to an image by means of energy minimization. While quite robust, the active contour approach does require knowledge of the desired contour shape beforehand to properly initialize the path.
Other classes of segmentation exist that are found less frequently in medical image analysis; for example, registration-based methods, such as ATLAS warping,55,56 other machine learning models including active appearance modeling,42,57,58 and a method known as locally excitatory globally inhibitory oscillator network (LEGION), which is based on a biologically plausible computational framework inspired by a biological oscillator network.59,60 In this paper, we test the performance of seven different segmentation techniques for segmenting OCT images of the ovaries: intensity thresholding, the watershed algorithm, -means clustering, graph cutting, an SVM, active contour modeling, and a deep neural network. While numerous other approaches to segmentation exist, these seven methods are a representative sample of the most widespread approaches to segmentation in medical imaging, covering a wide range of the different classes of segmentation.
2. Methods
2.1. Optical Coherence Tomography System
Three-dimensional OCT imaging was completed with a swept source OCT system (OCS1050SS, Thorlabs). The system operates in noncontact mode with a central wavelength of 1040 nm and spectral bandwidth of 80nm. The axial scan rate was 16 kHz, and the power on the sample was measured as 0.36 mW. The system was set to average four axial scans. The OCT system has transverse resolution and axial resolution in tissue. Imaging volume was and (voxel size of approximately ). The image volume was exported as a series of 2-D en face () images, or slices, and saved to disk as .tif image files.
2.2. Mouse Model
For this experiment, we used a mouse model of ovarian cancer and imaged mice of different ages, genotypes, and reproductive statuses. Females of the transgenic mouse model (TgMISIIR-TAg) spontaneously develop bilateral epithelial ovarian cancer.61,62 Both transgenic females and their wild type female littermates were imaged. Two reproductive status groups were obtained by dosing with 4-vinylcyclohexene diepoxide dissolved in sesame oil, which induces follicular atresia mimicking postmenopause63 or vehicle (sesame oil). We imaged mice at 4 and 8 weeks of age. In total, we acquired 70 images to analyze. By examining mice at different ages, reproductive status, and genotypes, we introduce biological variability into the dataset, thus creating a challenging segmentation problem.
2.3. Image Processing
2.3.1. Manual segmentation protocol
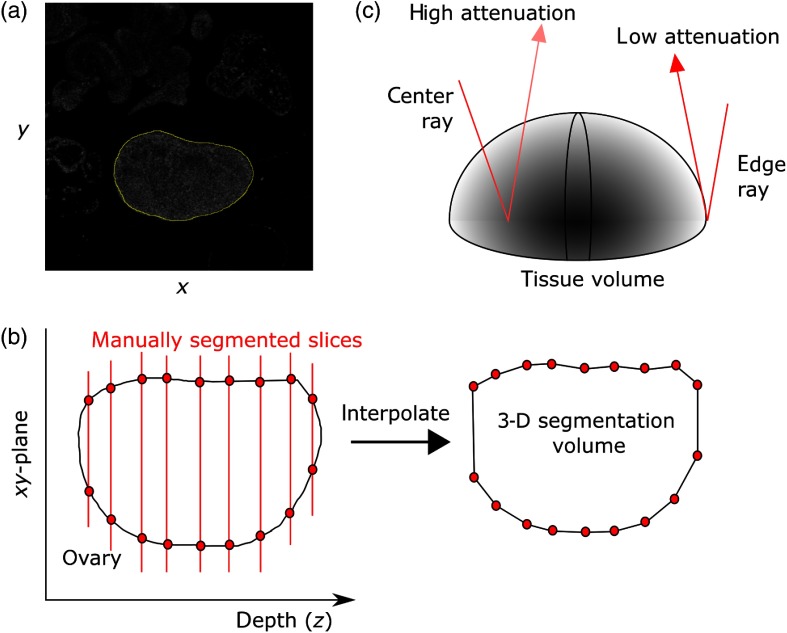
We established a ground truth set of segmentation masks by manually segmenting each image using the ImageJ program.64 To do so, a given 3-D image stack was loaded, where each en face slice in the stack represented a different depth. We located the first valid image by finding the most superficial image slice where the ovaries were visible and the image was not occluded by artifacts such as strong surface back reflections. A mask was then drawn around the ovaries using the create mask tool [Fig. 2(a)]. The result was a binary mask where the value was one within the drawn region of interest and zero elsewhere. The image was saved to disk, and the process was repeated every 10 slices until the average brightness within the ovary dropped below 20% of that recorded from the first valid image. Once this step was complete, the segmentation mask was linearly interpolated between each manually segmented slice to account for the sampling step of 10 slices [Fig. 2(b)].
Fig. 2.
(a) Individual slices of the OCT image stack were manually segmented using ImageJ. (b) This was repeated throughout the image depth and interpolated to yield the final segmented volume. (c) Due to the absorbing nature of tissue, as the imaging depth increases, the signal within the tissue is expected to decrease, while the signal at the edges will remain high.
We choose to segment every 10 slices to reduce the time required for a full segmentation ( to 120 slices). While this action may result in a decrease in accuracy, the shape of the organs evolves roughly linearly on a small scale; thus, the approximation by sampling every 10 slices (, less than two axial resolution units) is reasonable. We quantified the error introduced by interpolating the segmentation mask during manual segmentation. To do so, we manually segmented an ovary using every slice in the valid region. We then compared the accuracy of this result to the segmented mask created by interpolating between every 5, 10, and 20 slices using the performance metric defined in Sec. 2.3.4.
All images were segmented by a single observer; however, there is a degree of uncertainty as the observer must decide where the segmentation boundary is. To evaluate the error inherent in manual segmentation, a different individual segmented 25 randomly selected ovaries. We compared the randomness introduced by a given observer by computing the similarity between the two results. One factor that contributes to this observer error is the decreased signal through the imaging depth. As the imaging depth increases, we expect the signal within the center of the ovaries to decrease, as incident light propagates through more volume and absorbed more. Conversely, light striking the edge of the roughly spherical ovaries will remain high, as it undergoes relatively less attenuation [Fig. 2(c)].
2.3.2. Preprocessing techniques
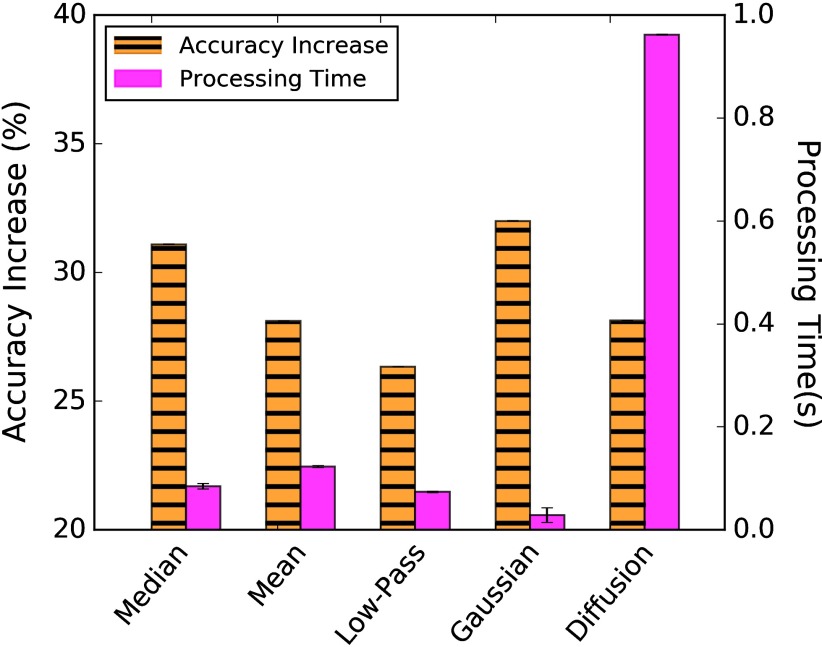
Preprocessing is an essential step of OCT image analysis due to the speckle noise intrinsic to all OCT images.65 The presence of speckle noise, among other sources of noise, reduces image quality and can prohibitively frustrate some analysis techniques, such as texture analysis22,29,66 and boundary identification.33 In the body of literature, nearly all OCT image analysis methods consist of a preprocessing step to suppress electronic and speckle noise. The most common approach is to apply a median filter; however, other filtering methods have been successfully applied, which may offer advantages in preserving spatial resolution or reducing processing time.33 Of these possibilities, we examine five representative preprocessing techniques for the reduction of speckle noise in OCT images (Fig. 3). These include mean and median filtering with a kernel size, as well as Gaussian filtering with a standard deviation of five pixels. Additionally, we applied nonlinear anisotropic filtering (50 iterations; gamma = 0.1) and low-pass filtering (thresholded at 50% frequency content).
Fig. 3.

(a) Five preprocessing techniques were investigated to suppress speckle noise in OCT images of the ovaries. (b) We tested mean, (c) median, (d) low-pass, (e) Gaussian filters, (f) in addition to anisotropic diffusion filtering. Each image here is a single en face slice.
The kernel size was selected to attenuate the effect of speckle in the image. Speckle caused by multiple scattered light and electronic noise is effectively one resolution unit in size;19 therefore, our kernel size was chosen as two resolution units in size to eliminate the speckle. Given the system specifications, two resolution units correspond to , leading to the selection of a 5-pixel kernel size. This kernel size, along with the parameters for the anisotropic diffusion filtering and low-pass filtering is consistent with what is found in the literature for applications with similar lateral resolution.5,7,67 To evaluate the performance of each preprocessing technique, we calculated the average segmentation accuracy (defined in Sec. 2.3.4) across a set of 10 randomly selected test images for the seven different segmentation approaches. We also conducted segmentation on the same set of 10 test images, no preprocessing. By averaging the results of the 10 images for each preprocessing approach and taking the ratio between the processed and unprocessed images for each segmentation approach, we compute the relative increase in performance. In addition, we recorded the computation time to compare the speed of each technique. We tested the statistical significance of the results using analysis of variance (ANOVA).
2.3.3. Segmentation algorithms
We tested the performance of seven different segmentation techniques: intensity thresholding, the watershed algorithm, -means clustering, graph cutting, an SVM, and a deep neural network. These seven methods are a representative sample of the most widespread approaches to segmentation in medical imaging. Each belongs to a different class of algorithm and are thus indicative of how appropriate a given class may be for segmenting OCT images of the ovaries. Many other approaches to segmentation exist; by examining the performance of this subset, the results will inform further studies that may focus on a specific class of segmentation algorithms to further optimize the performance. For each case, we first filtered the images using a Gaussian filter with a standard deviation of five pixels to suppress speckle noise, which we found led to the most accurate segmentation. We also scaled the means of each individual slice to be equal to correct for the signal decrease caused by attenuation. This preprocessing was applied to the entire dataset before any segmentation was attempted. We evaluate the accuracy of each algorithm throughout the depth of the imaging volume, investigating the maximum accuracy, processing time, average positive predictive value (PPV) and negative predictive value (NPV), as well as how well the algorithm maintains accuracy throughout the image depth.
All image processing, including preprocessing, was completed in Python using a computer with an Intel Core I-4710HQ CPU (2.50 GHz) and 16 GB DDR3L memory. Many segmentation algorithms are readily available in Python; the algorithms tested here can be implemented using the open-source scientific computing package Anaconda and other packages available on Github. The parameters for each segmentation algorithm were determined by optimizing the performance on the most superficial image slice on the set of 10 randomly selected images selected previously. Thresholding was performed by assigning all pixel values within a range as the ovary; in this case, the threshold range was between normalized pixel values of 0.3 and 0.7. For the watershed algorithm, we generated the initial seeds for each region by computing the distance transform of the image and finding the maximum value in a local window. The watershed algorithm was then used to segment the image into nine sections, where these nine sections were ordered according to the mean pixel brightness; we then discarded the two brightest and two darkest sections and merged the remaining five into the segmentation area. The choice to discard the brightest and darkest sections was determined by iteratively testing combinations of the sections; the most accurate segmentation was given by the central five sections.
Similarly, we used -means clustering with a compactness of 0.1 to segment into nine clusters, again where five clusters were merged to represent the ovaries using the same process as before. In this case, we constrained each of the clusters to be contiguous, ensuring that all pixels in a group were spatially connected. Next, we applied graph cutting using a normalized graph cut algorithm; first, the images were presegmented by being clustered into 30 groups. This presegmentation step is a traditional step in graph cutting, and the choice of 30 groups was found to improve the overall algorithm performance. Then, the adjacency graph was constructed, and the cut made with a maximum edge value of 0.15 and a threshold of 0.05. This results in between eight to 10 segmentation areas, depending on the image, which we again merged together according to the mean brightness.
We next trained an SVM by splitting the image data equally into training and testing sets, resulting in 35 images for each set, equally distributed among genotype, age, and treatment. For each pixel, a five-element feature vector was constructed by recording the slice depth, the pixel brightness, and the values of several local filters: a median filter (), mean filter (), and Gaussian filter (). We used a radial basis function kernel with a regularization parameter of 1.0. The SVM was then trained by fitting the array of feature vectors to the ground truth manual segmentation images for each of the training set. The model was then used to predict the outcome for the test set. Following the output from the SVM, we applied a binary closing operation followed by a median filter to reduce uncharacteristically bright and dim in the result. The accuracy was computed after applying the morphological operations. Note that this median filter was applied to the postprocessed image and is different than the initial preprocessing filter.
To test the ability of deep learning for segmentation, we implemented the convolutional neural network known as U-Net, which as been used with much success for biomedical image segmentation.44 The U-Net architecture resembles an autoencoder, where the network consists of the repeated application of two convolutional layers, followed by a rectified linear unit (ReLU) and a max pooling operation with a stride of 2. This contracts the arrays, reducing spatial information but increasing the information contained in the features. The arrays are then expanded by upsampling the feature map, followed by applying a upconvolution and a concatenation with the correspondingly cropped feature map from the contracting path, and two convolutions, each followed by an ReLU. The final layer is a convolution used to map each 64-component feature vector to the two possibe classes for binary segmentation. This is the standard architecture for the U-Net; additional details about the network architecture can be found in the literature. The same training and test sets used for the SVM are used here: 35 images in each set, distributed equally among genotype, age, and treatment. Of the training sets, 10 images are selected for validation. The network was trained for 20 epochs.
Finally, we fit an active contour model to conduct the segmentation. We initialized the snake by selecting the most superficial manually segmented image for a given image stack and using the manually defined segmentation boundary to define the initial contour. The segmentation then proceeds throughout the image stack by using the contour from the previous image as the new seed. Thus, this approach requires a single manual segmentation, which is then propagated throughout the depth of the image to yield the full 3-D segmented volume. We constrained the snake to be a closed curve and specified two additional parameters to characterize the snake evolution: a length parameter (alpha), for which higher values make the snake contract faster and a smoothness parameter (beta). For this study, alpha was chosen as 0.001 and beta was chosen as 0.5. These values were selected by logarithmically evaluating the parameter space and selecting those values that produced the highest accuracy.
2.3.4. Performance metric
A digital image is represented in a computer as a matrix of numbers, where the magnitude of each number represents the signal level. In the case of the OCT images in this study, the image is a 3-D matrix, where the size of each dimension is represented by the pixel count in the , , and directions. A single en face image indexes the 3-D matrix along the -axis, resulting in a 2-D matrix. Assessing the performance of the segmentation amounts to comparing the similarity between two separate 2-D matrices, one of which represents the ground truth, and the other represents the result of the segmentation. These matrices can subsequently be collapsed into a one-dimensional vector by concatenating the separate rows into a single array of numbers, which has a length given by the product of the number of pixels in the and directions. With this methodology, the similarity of two images is analogous to computing the similarity between two vectors.
Taking this approach to evaluate the performance of a given segmentation method, the resulting segmentation mask was compared with a ground truth mask obtained from manually segmenting the images. The comparison was made between the two binary masks that were generated during segmentation, where the mask has a value of one corresponding to a pixel containing the ovary and a value of zero otherwise. The images therefore can be thought of as vectors of ones and zeros. The accuracy was measured by correlating the two images, which is analogous to taking the dot product. Mathematically, this is expressed as
| (1) |
where is the accuracy, is the segmented image from the algorithm, and is the ground truth image. Scaling down by the vector magnitude of each image results in a value between one and zero, where one indicates that the images are identical. One implication of using this metric is that the weight associated with a true-positive result (correctly classifying an organ) is higher than that of a true negative (correctly classifying the background). Other performance metrics exist and can be used interchangeably; in this study, we select this definition for due to the computational simplicity and widespread familiarity.
To gain additional insight, we also use two standard performance metrics: the PPV and NPV, defined as
| (2) |
and
| (3) |
Other performance metrics exist and can be used interchangeably; in this study, we select these three metrics for a broad understanding of how well each algorithm performs and also for the widespread familiarity of each metric.
3. Results and Discussion
3.1. Manual Segmentation Error
We first tested the error introduced by interpolating the segmentation mask during manual segmentation. We find that the two masks yield an accuracy of 97.7% for sampling every 20 slices, 98.2% for sampling every 10 slices, and 98.3% for sampling every 5 slices. We also examined how the choice of observer can introduce randomness into the result. Comparing manual segmentations between two observers for 10 randomly selected images yielded a similarity of 97.6%; thus, the interpolation process does not introduce more error than what is inherent to the variation in the observer. We also observed that there was no appreciably decrease in accuracy when observers randomly sampled slices through the depth of an image. This error varied minimally () over the sample of 25 images, which indicates that the computed error is representative of the total population. Furthermore, the error between the segmentation algorithm results and the manually segmented slices compared with the interpolated slices had no observable difference. For each subsequent manual segmentation, we sampled every 10 slices.
3.2. Preprocessing Techniques
The average increase in accuracy when using different preprocessing techniques (as compared with no preprocessing), as well as the required processing time, is shown in Fig. 4. The results indicate that Gaussian filtering and median filtering produce the highest average improvement, with the Gaussian filtering increasing relative accuracy by 32% when compared with segmenting an unfiltered image. Considering processing time, the Gaussian filtering is also most rapid, completing in an average time of ; second is the low-pass filter with an average processing time of . Taking these results with the high statistical significance of the ANOVA testing (), we can conclude that Gaussian filtering is most suitable for preprocessing in our segmentation problem.
Fig. 4.
Average increase in segmentation accuracy (orange) and processing time (magenta) of different filtering techniques. The Gaussian filter performs best in both categories, while the median filter also exhibits high accuracy and rapid processing time.
3.3. Segmentation Algorithms
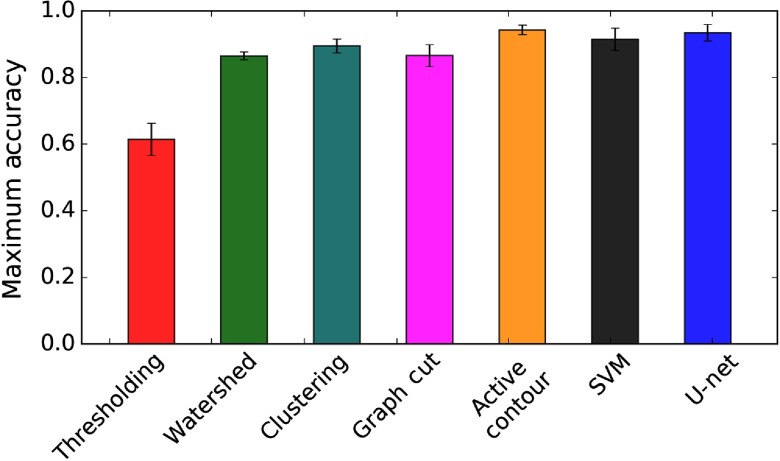
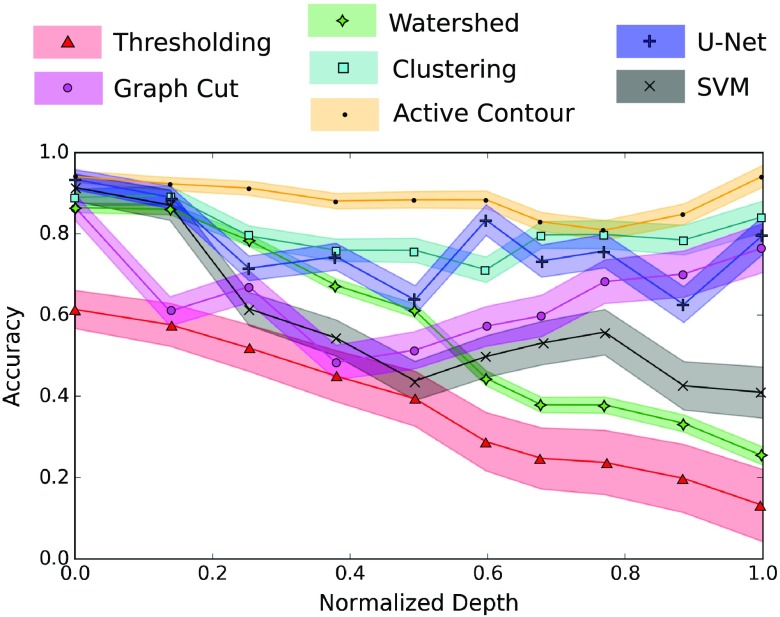
Figure 5 illustrates the results of applying the seven segmentation techniques, showing the maximum segmentation accuracy throughout the image depth. While each algorithm with the exception of intensity thresholding yields high maximum accuracy (), the active contour method performs best, with a maximum accuracy of on average (). Evaluating the performance as a function of image depth (Fig. 6), we see that clustering and active contour modeling remain the most effective, while the other approaches suffer from high variations in accuracy throughout the depth. In particular, the watershed algorithm, SVM, and thresholding all significantly degrade in performance as a function of depth.
Fig. 5.
Highest accuracy obtained by each algorithm for a single 2-D slice throughout the image depth. Active contour modeling performs the best, followed by -means clustering and the SVM.
Fig. 6.
Segmentation accuracy as a function of image depth. We see that an active contour model maintains high accuracy throughout the depth while thresholding; the watershed algorithm and the SVM degrade rapidly throughout the depth. Clustering and graph cutting perform reasonably well, but have a larger variation than active contours.
While clustering and graph cutting perform reasonably well, active contour modeling is most accurate. These results may be due to the high inhomogeneity of the image content for OCT images. Methods such as thresholding and the SVM classifier depend on pixel intensity; these vary throughout the image depth and across the area of the ovary due to nonuniform attenuation of light in the roughly spherical ovary; furthermore, much of the connective tissue has similar levels of intensity to the ovaries. Thus, intensity-based methods cannot discriminate well between these tissue types, nor do they adapt well to depth-dependent intensity. One potential solution could be to train the SVM or threshold based on local textural features, instead of intensity features. As the local region is likely to undergo similar changes throughout depth, much of the variance could be reduced; hence, characterizing the local texture would enable a more depth-independent feature. Furthermore, qualitatively inspecting the OCT images, we observe that the connective tissue exhibits different textural differences than the ovary; therefore, texture could be a more appropriate feature for segmentation than intensity.
While clustering and graph cutting consider pixel brightness as well, they also incorporate spatial information by weighting the pixels based on the location and enforcing connectivity between segmented regions. Thus, this additional information provides a constraint that makes the algorithm more resistant to the changes in image content as a function of depth. The watershed algorithm, which also includes regional information, does not enforce connectivity and therefore is also highly susceptible to the changes in depth. However, taken generally, we see that for the region-based techniques, the accuracy is more consistent throughout the image depth. This is not surprising, as the shape and contours of the organs will remain continuous throughout the depth, making these algorithms more robust to the variations in image content throughout the depth.
Using the U-Net for deep learning, we see a marked improvement over the traditional machine learning approach of the SVM. However, the results are not as strong as what has been observed for other biological segmentation applications of the U-Net. This could be due to the lack of sufficient training data. The results vary somewhat unpredictably throughout the depth; this may indicate that the features learned by the U-Net do not appear isotropically throughout the depth. With a more extensive dataset, these feature maps could be refined to produce a more accurate and consistent segmentation. Other potential solutions include using a generative model to simulate additional training data. These methods have frequently been used to supplement limited datasets, and this remains an objective for future research.
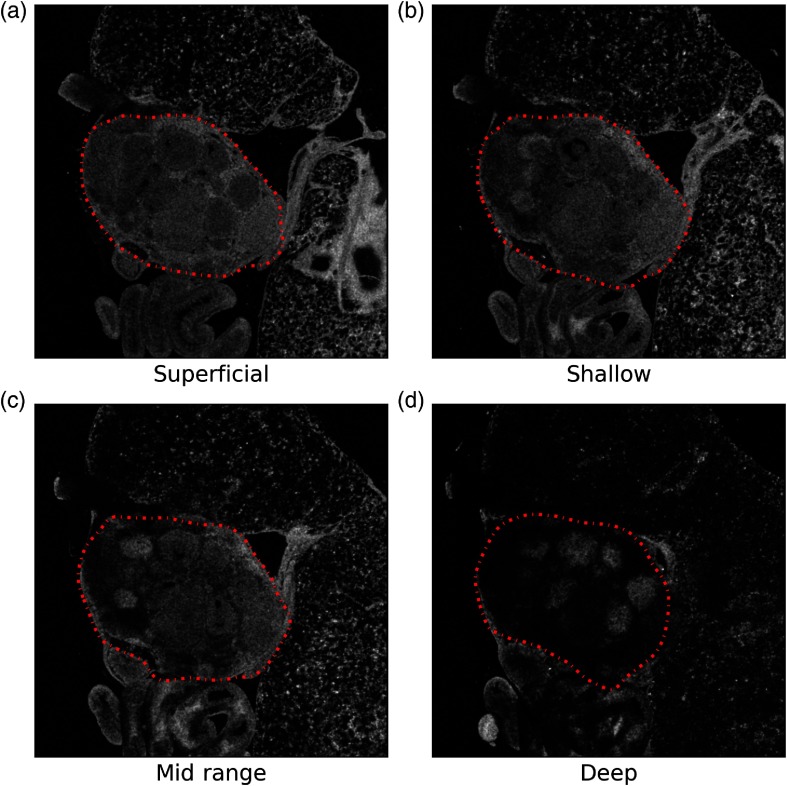
The active contour model further improves on the region-based techniques by seeding the algorithm with an initial segmentation boundary curve. With this starting point, the algorithm then deforms the boundary curve to fit the optimal shape, given the contents of the image. Considering that the shape of the ovary changes slowly throughout the image depth, propagating the segmentation boundary throughout the depth is highly effective by providing an initial condition very close to the final solution. As a result, we observe high accuracy throughout the entire image depth using this approach (Fig. 7). As expected, the signal within the tissue drops as the depth increases; however, the signal on the edges remains high, preserving the boundary. This may be the cause of the characteristic dip in accuracy observed in Fig. 6 for several of the segmentation approaches; the contrast at the organ boundary may decrease in the center of the imaging depth.
Fig. 7.
Propagating active contour snake throughout the tissue depth maintains high accuracy for delineating the segmentation boundary throughout the tissue depth, from (a) the most superficial slice to (b) shallow, (c) midrange, and (d) deep slices. The overall signal is attenuated as the depth increases, which introduces challenges with other segmentation techniques.
Observing the effectiveness of the active contour modeling, we then considered if the segmentation could be propagated throughout the image depth by sampling every slices, instead of using every slice. In this case, the sampled result could be interpolated using the same approach as with the manual segmentation. The processing time of the approach scales linearly with the number of slices; therefore, by increasing the sampling increment, we reduce the number of slices and hence the processing time. Figure 8 illustrates the effects of increasing the sampling increment. While the processing time decreases linearly, we also observe a roughly linear decrease in the average accuracy [Fig. 8(a)] for each segmented slice; furthermore, we must consider the additional error introduced through the interpolation between slices [Fig. 8(b)], which evolves linearly as well. Considering these factors, the processing time must be balanced with the desired accuracy to determine the optimal sampling depth. For example, if 88% average accuracy throughout the image depth is sufficient, a sampling depth of eight slices would be optimal.
Fig. 8.
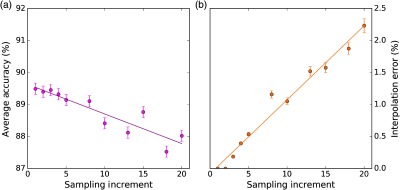
Increasing the sampling depth for propagating the active contour through (a) the image leads to a linear decrease in accuracy, (b) as well as an added interpolation error. The processing time for an image stack decreases with an increased sampling depth, suggesting that an optimal sampling depth can yield rapid processing time while maintaining high accuracy.
Summarizing the results in Table 1, we report that active contour modeling is the most accurate approach to segmenting OCT images of ovarian tissue. The results are encouraging, showing that accurate segmentation can be achieved throughout the image depth with minimal user interaction. In addition, considering that a manual segmentation required for each slice, the time required to segment the full image stack improves by approximately two orders of magnitude. Nevertheless, we identify several objectives for future investigation. First, while we find that active contours are most effective of the tested algorithms, other segmentation approaches exist, particularly in the realm of machine learning, such as neural networks and68 active appearance modeling.31 Machine learning continues to evolve and these algorithms could lead to more time-efficient and accurate segmentation. In addition, the feature vector used to train the SVM contains a relatively naive measure of the local image content by simply inspecting the local mean, median, and Gaussian average. Higher accuracies could be achieved by developing a more descriptive feature vector, such as one that incorporates texture analysis.69 Finally, with the 3-D of OCT data, traditional segmentation approaches are slow to process, as they consider each image in the stack iteratively. Extending these algorithms to apply to a 3-D image could both increase the accuracy while improving the processing time. While processing high-dimensional data is memory-intensive, recent advances in computing have lowered this barrier, making 3-D processing more feasible and an exciting frontier in image processing.
Table 1.
Summary of performance for each segmentation algorithm. Active contours provide both the highest maximum accuracy, as well as the most consistent accuracy throughout the depth of the tissue, as well as a rapid processing time. Note that the processing time for the SVM does not include training.
| Thresholding | Watershed | SVM | Graph cut | Clustering | Active contour | U-Net | |
|---|---|---|---|---|---|---|---|
| Maximum accuracy (%) | 62.4 | 86.4 | 89.5 | 86.5 | 89.4 | 94.8 | 93.4 |
| Depth variation (%) | 78.1 | 71.6 | 59.3 | 44.3 | 14.2 | 13.9 | 22.1 |
| Avg. PPV | 0.324 | 0.921 | 0.831 | 0.743 | 0.907 | 0.892 | 0.861 |
| Avg. NPV | 0.866 | 0.890 | 0.955 | 0.926 | 0.982 | 0.956 | 0.923 |
| Processing time (s) | 0.001 | 0.289 | 14.16 | 1.64 | 0.954 | 0.274 | 0.637 |
| Manual input | None | None | Training set | None | None | Initial contour | Training set |
4. Conclusions
We present the evaluation of seven different algorithms for the segmentation of OCT images of the ovaries in addition to examining five preprocessing techniques to reduce speckle noise. While all preprocessing methods improve segmentation, Gaussian filtering is most effective, showing an improvement of . Of the segmentation algorithms, active contour modeling performs best, segmenting with a similarity of compared with manual segmentation. The time required to perform the segmentation using this approach increases by approximately two orders of magnitude. The results suggest that active contour models are most suitable for segmenting 3-D image data that varies as a function of depth. While encouraging, extending these algorithms to process 3-D data, as opposed to a series of 2-D slices, could lead to higher accuracy and more efficient processing.
Acknowledgments
We would like to thank Dr. Sarah Bohndiek and Marcel Gehrung for technical discussion and feedback. This material was based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE-1143953. All animal procedures performed in this study were covered by a protocol approved by the University of Arizona Institutional Animal Care and Use Committee. This work was also funded by the National Institutes of Health/National Cancer Institute Grant No. 1R01CA195723, the University of Arizona Cancer Center, Grant No. 3P30CA023074. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation or National Institutes of Health.
Biographies
Travis W. Sawyer is a PhD student at the University of Arizona, expected to graduate in May 2022. He holds his BS degree in optical sciences and engineering from the University of Arizona and his MPhil degree in physics from the University of Cambridge. His research focuses on developing multimodal imaging systems for cancer surveillance and also image analysis.
Photini F. S. Rice holds an associate in applied science in medical technology and has American Society for Clinical Pathology certification. She worked 13 years as a medical technologist and technical consultant in a clinical laboratory, including achieving CLIA (Clinical Laboratory Improvement Amendments) certification for the laboratory. Currently, she is a senior research specialist at the University of Arizona with 7 years of experience in cardiovascular research and the past 10 years in cancer imaging.
David M. Sawyer is a PGY-2 diagnostic radiology resident at the University of Arizona/Banner University Medical Center—Tucson. He completed his MD degree from Tulane University in 2017, where he researched cerebrovascular disease. His current research interests include imaging of neurodegenerative disorders.
Jennifer W. Koevary is an assistant professor in biomedical engineering at the University of Arizona and chief operating officer at Avery Therapeutics. Her research interests are primarily in the areas of imaging for cancer detection and evaluation of therapeutic safety and efficacy. She is also interested in the use of engineered human tissues for drug toxicity screening and development of human tissues/organoids for clinical trials in a dish. She has provisional patents in these areas.
Jennifer K. Barton is a professor of optical sciences and biomedical engineering and also the director of the BIO5 institute at the University of Arizona. Her research interests are in translational biomedical optics, and the prevention and early detection of cancer. In particular, her work focuses on technology and application development of optical coherence tomography (OCT) and fluorescence spectroscopy (FS), and design/development of miniature endoscope-enabled imaging systems.
Disclosures
We have no conflicts of interest to disclose.
References
- 1.Barnholtz-Sloan J. S., et al. , “Ovarian cancer: changes in patterns at diagnosis and relative survival over the last three decades,” Am. J. Obstet. Gynecol. 189(4), 1120–1127 (2003). 10.1067/S0002-9378(03)00579-9 [DOI] [PubMed] [Google Scholar]
- 2.Maringe C., et al. , “Stage at diagnosis and ovarian cancer survival: evidence from the International Cancer Benchmarking Partnership,” Gynecol. Oncol. 127(1), 75–82 (2012). 10.1016/j.ygyno.2012.06.033 [DOI] [PubMed] [Google Scholar]
- 3.Carlson K. J., Skates S. J., Singer D. E., “Screening for ovarian cancer,” Ann. Intern. Med. 121, 124–132 (1994). 10.7326/0003-4819-121-2-199407150-00009 [DOI] [PubMed] [Google Scholar]
- 4.Moyer V. A., “Screening for ovarian cancer: U.S. preventive services task force reaffirmation recommendation statement,” Ann. Intern. Med. 157(12), 900–904 (2012). 10.7326/0003-4819-157-11-201212040-00539 [DOI] [PubMed] [Google Scholar]
- 5.Huang D., et al. , “Optical coherence tomography,” Science 254(5035), 1178–1181 (1991). 10.1126/science.1957169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Swanson E. A., et al. , “In vivo retinal imaging by optical coherence tomography,” Opt. Lett. 18(21), 1864–1866 (1993). 10.1364/OL.18.001864 [DOI] [PubMed] [Google Scholar]
- 7.Hee M. R., et al. , “Optical coherence tomography of the human retina,” Arch. Ophthalmol. 113(3), 325–332 (1995). 10.1001/archopht.1995.01100030081025 [DOI] [PubMed] [Google Scholar]
- 8.Abràmoff M., Garvin M. K., Sonka M., “Retinal imaging and image analysis,” IEEE Rev. Biomed. Eng. 3, 169–208 (2010). 10.1109/RBME.2010.2084567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tsuboi M., et al. , “Optical coherence tomography in the diagnosis of bronchial lesions,” Lung Cancer 49(3), 387–394 (2005). 10.1016/j.lungcan.2005.04.007 [DOI] [PubMed] [Google Scholar]
- 10.Otte S., et al. , “OCT A-Scan based lung tumor tissue classification with bidirectional long short term memory networks,” in IEEE Int. Workshop Mach. Learn. Signal Process. (MLSP), pp. 1–6 (2013). 10.1109/MLSP.2013.6661944 [DOI] [Google Scholar]
- 11.Lightdale C. J., “Optical coherence tomography in Barrett’s esophagus,” Gastrointest. Endosc. Clin. N. Am. 23(3), 549–563 (2013). 10.1016/j.giec.2013.03.007 [DOI] [PubMed] [Google Scholar]
- 12.Ferrante G., et al. , “Current applications of optical coherence tomography for coronary intervention,” Int. J. Cardiol. 165(1), 7–16 (2013). 10.1016/j.ijcard.2012.02.013 [DOI] [PubMed] [Google Scholar]
- 13.Abdolmanafi A., et al. , “Deep feature learning for automatic tissue classification of coronary artery using optical coherence tomography,” Biomed. Opt. Express 8(2), 1203–1220 (2017). 10.1364/BOE.8.001203 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Brewer M. A., et al. , “Imaging of the ovary,” Technol. Cancer Res. Treat. 3(6), 617–627 (2004). 10.1177/153303460400300612 [DOI] [PubMed] [Google Scholar]
- 15.Hariri L. P., et al. , “Simultaneous optical coherence tomography and laser induced fluorescence imaging in rat model of ovarian carcinogenesis,” Cancer Biol. Ther. 10(5), 438–447 (2010). 10.4161/cbt.10.5.12531 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang T., “An overview of optical coherence tomography for ovarian tissue imaging and characterization,” Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 7(1), 1–16 (2015). 10.1002/wnan.1306 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Watanabe Y., et al. , “Optical coherence tomography imaging for analysis of follicular development in ovarian tissue,” App. Opt. 54(19), 6111–6115 (2015). 10.1364/AO.54.006111 [DOI] [PubMed] [Google Scholar]
- 18.Takae S., et al. , “Accuracy and safety verification of ovarian reserve assessment technique for ovarian tissue transplantation using optical coherence tomography in mice ovary,” Sci. Rep. 7, 43550 (2017). 10.1038/srep43550 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schmitt J., “Optical coherence tomography (OCT): a review,” IEEE J. Sel. Top. Quantum Electron. 5(4), 1205–1215 (1999). 10.1109/2944.796348 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Welge W. A., et al. , “Diagnostic potential of multimodal imaging of ovarian tissue using optical coherence tomography and second-harmonic generation microscopy,” J. Med. Imaging 1, 025501 (2014). 10.1117/1.JMI.1.2.025501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pande P., et al. , “Automated classification of optical coherence tomography images for the diagnosis of oral malignancy in the hamster cheek pouch,” J. Biomed. Opt. 19(8), 086022 (2014). 10.1117/1.JBO.19.8.086022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gossage K. W., et al. , “Texture analysis of optical coherence tomography images: feasibility for tissue classification,” J. Biomed. Opt. 8(3), 570–575 (2003). 10.1117/1.1577575 [DOI] [PubMed] [Google Scholar]
- 23.Depeursinge A., et al. , “Three-dimensional solid texture analysis in biomedical imaging: review and opportunities,” Med. Image Anal. 18(1), 176–196 (2014). 10.1016/j.media.2013.10.005 [DOI] [PubMed] [Google Scholar]
- 24.Nandy S., Sanders M., Zhu Q., “Classification and analysis of human ovarian tissue using full field optical coherence tomography,” Biomed. Opt. Express 7(12), 5182–5187 (2016). 10.1364/BOE.7.005182 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.St-Pierre C., et al. , “Dimension reduction technique using a multilayered descriptor for high-precision classification of ovarian cancer tissue using optical coherence tomography,” J. Med. Imaging 4, 041306 (2017). 10.1117/1.JMI.4.4.041306 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Venhuizen F., et al. , “Robust total retina thickness segmentation in optical coherence tomography images using convolutional neural networks,” Biomed. Opt. Express 8(7), 3292–3316 (2017). 10.1364/BOE.8.003292 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Liu G. S., et al. , “ELHnet: a convolutional neural network for classifying cochlear endolymphatic hydrops imaged with optical coherence tomography,” Biomed. Opt. Express 8(10), 4579–4594 (2017). 10.1364/BOE.8.004579 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Burgansky-Eliash Z., et al. , “Optical coherence tomography machine learning classifiers for glaucoma detection: a preliminary study,” Invest. Ophthalmol. Visual Sci. 46(11), 4147–4152 (2005). 10.1167/iovs.05-0366 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Singh A. S. G., Schmoll T., Leitgeb R. A., “Segmentation of Doppler optical coherence tomography signatures using a support-vector machine,” Biomed. Opt. Express 2(5), 1328–1339 (2011). 10.1364/BOE.2.001328 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pham D. L., Xu C., Prince J. L., “Current methods in medical image segmentation,” Annu. Rev. Biomed. Eng. 2(1), 315–337 (2000). 10.1146/annurev.bioeng.2.1.315 [DOI] [PubMed] [Google Scholar]
- 31.Heimann T., Meinzer H.-P., “Statistical shape models for 3D medical image segmentation: a review,” Med. Imag. Anal. 13(4), 543–563 (2009). 10.1016/j.media.2009.05.004 [DOI] [PubMed] [Google Scholar]
- 32.DeBuc D. C., A Review of Algorithms for Segmentation of Retinal Image Data Using Optical Coherence Tomography, Ho P.-G., Ed., pp. 15–54, INTECH Open Access Publisher, Rijeka, Croatia: (2011). [Google Scholar]
- 33.Kafieh R., Rabbani H., Kermani S., “A review of algorithms for segmentation of optical coherence tomography from retina,” J. Med. Signals Sens. 3(1), 45–60 (2013). [PMC free article] [PubMed] [Google Scholar]
- 34.Brand S., et al. , “Optical coherence tomography in the gastrointestinal tract,” Endoscopy 32(10), 796–803 (2000). 10.1055/s-2000-7714 [DOI] [PubMed] [Google Scholar]
- 35.Wang Z., et al. , “Semiautomatic segmentation and quantification of calcified plaques in intracoronary optical coherence tomography images,” J. Biomed. Opt. 15(6), 061711 (2010). 10.1117/1.3506212 [DOI] [PubMed] [Google Scholar]
- 36.Zhang J., et al. , “Automatic and robust segmentation of endoscopic OCT images and optical staining,” Biomed. Opt. Express 8(5), 2697–2708 (2017). 10.1364/BOE.8.002697 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Haralick R. M., Shapiro L. G., “Image segmentation techniques,” Comput. Gr. Image Process. 29(1), 100–132 (1985). 10.1016/S0734-189X(85)90153-7 [DOI] [Google Scholar]
- 38.Gonzalez R., Woods R., Digital Image Processing, Prentice Hall, Upper Saddle River: (2002). [Google Scholar]
- 39.Pal N. R., Pal S. K., “A review on image segmentation techniques,” Pattern Recognit. 26(9), 1277–1294 (1993). 10.1016/0031-3203(93)90135-J [DOI] [Google Scholar]
- 40.Yezzi A., Tsai A., Willsky A., “A statistical approach to snakes for bimodal and trimodal imagery,” in Proc. Seventh IEEE Int. Conf. Comput. Vision, Vol. 2, p. 898 (1999). 10.1109/ICCV.1999.790317 [DOI] [Google Scholar]
- 41.Roerdink J., Meijster A., “The watershed transform: definitions, algorithms and parallelization strategies,” Fundam. Inf. 41(1–2), 187–228 (2000). 10.3233/FI-2000-411207 [DOI] [Google Scholar]
- 42.Alirezaie J., Jernigan M. E., Nahmias C., “Neural network-based segmentation of magnetic resonance images of the brain,” IEEE Trans. Nucl. Sci. 44(2), 194–198 (1997). 10.1109/23.568805 [DOI] [Google Scholar]
- 43.Wang S., Zhu W., Liang Z.-P., “Shape deformation: SVM regression and application to medical image segmentation,” in Proc. Eighth IEEE Int. Conf. Comput. Vision, Vol. 2, pp. 209–216 (2001). 10.1109/ICCV.2001.937626 [DOI] [Google Scholar]
- 44.Ronneberger O., Fischer P., Brox T., “U-Net: convolutional networks for biomedical image segmentation,” Lect. Notes Comput. Sci. 9351, 234–241 (2015). 10.1007/978-3-319-24574-4 [DOI] [Google Scholar]
- 45.Cheng K.-S., Lin J.-S., Mao C.-W., “The application of competitive hopfield neural network to medical image segmentation,” IEEE Trans. Med. Imaging 15(4), 560–567 (1996). 10.1109/42.511759 [DOI] [PubMed] [Google Scholar]
- 46.Ahmed M. N., et al. , “A modified fuzzy C-means algorithm for bias field estimation and segmentation of MRI data,” IEEE Trans. Med. Imaging 21(3), 193–199 (2002). 10.1109/42.996338 [DOI] [PubMed] [Google Scholar]
- 47.Wong R. C. K., et al. , “Visualization of subsurface blood vessels by color Doppler optical coherence tomography in rats: before and after hemostatic therapy,” Gastrointest. Endosc. 55(1), 88–95 (2002). 10.1067/mge.2002.120104 [DOI] [PubMed] [Google Scholar]
- 48.Ford L. R., Jr., Fulkerson D. R., “Maximal flow through a network,” Can. J. Math. 8, 399–404 (1956). 10.4153/CJM-1956-045-5 [DOI] [Google Scholar]
- 49.Felzenszwalb P. F., Huttenlocher D. P., “Efficient graph-based image segmentation,” Int. J. Comput. Vision 59(2), 167–181 (2004). 10.1023/B:VISI.0000022288.19776.77 [DOI] [Google Scholar]
- 50.Osher S., Sethian J. A., “Fronts propagating with curvature-dependent speed: algorithms based on Hamilton–Jacobi formulations,” J. Comput. Phys. 79(1), 12–49 (1988). 10.1016/0021-9991(88)90002-2 [DOI] [Google Scholar]
- 51.Mishra A., et al. , “Intra-retinal layer segmentation in optical coherence tomography images,” Opt. Express 17(26), 23719–23728 (2009). 10.1364/OE.17.023719 [DOI] [PubMed] [Google Scholar]
- 52.Kass M., Witkin A., Terzopoulos D., “Snakes: active contour models,” Int. J. Comput. Vision 1(4), 321–331 (1988). 10.1007/BF00133570 [DOI] [Google Scholar]
- 53.Ji Z., et al. , “Active contours driven by local likelihood image fitting energy for image segmentation,” J. Inf. Sci. 301, 285–304 (2015). 10.1016/j.ins.2015.01.006 [DOI] [Google Scholar]
- 54.Yazdanpanah A., et al. , “Segmentation of intra-retinal layers from optical coherence tomography images using an active contour approach,” IEEE Trans. Med. Imaging 30(2), 484–496 (2011). 10.1109/TMI.2010.2087390 [DOI] [PubMed] [Google Scholar]
- 55.Maintz J. B., Viergever M. A., “A survey of medical image registration,” Med. Imag. Anal. 2(1), 1–36 (1998). 10.1016/S1361-8415(01)80026-8 [DOI] [PubMed] [Google Scholar]
- 56.Chakravarty M. M., et al. , “Towards a validation of atlas warping techniques,” Med. Imag. Anal. 12(6), 713–726 (2008). 10.1016/j.media.2008.04.003 [DOI] [PubMed] [Google Scholar]
- 57.Cootes T., “Active appearance models,” IEEE Trans. Pattern Anal. Mach. Intell. 23(6), 681–685 (2001). 10.1109/34.927467 [DOI] [Google Scholar]
- 58.Lee C. S., et al. , “Deep-learning based, automated segmentation of macular edema in optical coherence tomography,” Biomed. Opt. Express 8(7), 3440–3448 (2017). 10.1364/BOE.8.003440 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Wang D., Terman D., “Locally excitatory globally inhibitory oscillator networks,” IEEE Trans. Neural Network Learn. Syst. 6(1), 283–286 (1995). 10.1109/72.363423 [DOI] [PubMed] [Google Scholar]
- 60.Wang D. L., Terman D., “Image segmentation based on oscillatory correlation,” Neural Comput. 9(4), 805–836 (1997). 10.1162/neco.1997.9.4.805 [DOI] [PubMed] [Google Scholar]
- 61.Connolly D. C., et al. , “Female mice chimeric for expression of the simian virus 40 TAg under control of the MISIIR promoter develop epithelial ovarian cancer,” Cancer Res. 63(6), 1389–1397 (2003). [PubMed] [Google Scholar]
- 62.Quinn B. A., et al. , “Development of a syngeneic mouse model of epithelial ovarian cancer,” J. Ovarian Res. 3(1), 24 (2010). 10.1186/1757-2215-3-24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Romero-Aleshire M. J., et al. , “Loss of ovarian function in the VCD mouse-model of menopause leads to insulin resistance and a rapid progression into the metabolic syndrome,” Am. J. Physiol. Regul. Integr. Comp. Physiol. 297(3), R587–R592 (2009). 10.1152/ajpregu.90762.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Rasband W., “ImageJ,” U. S. National Institutes of Health, Bethesda, Maryland, //imagej.nih.gov/ij/ (2012). [Google Scholar]
- 65.Schmitt J. M., Xiang S. H., Yung K. M., “Speckle in optical coherence tomography,” J. Biomed. Opt. 4(1), 95–105 (1999). 10.1117/1.429925 [DOI] [PubMed] [Google Scholar]
- 66.Lingley-Papadopoulos C. A., et al. , “Computer recognition of cancer in the urinary bladder using optical coherence tomography and texture analysis,” J. Biomed. Opt. 13(2), 024003 (2008). 10.1117/1.2904987 [DOI] [PubMed] [Google Scholar]
- 67.Podoleanu A. G., “Optical coherence tomography,” J. Microsc. 247(3), 209–219 (2012). 10.1111/j.1365-2818.2012.03619.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Jiang J., Trundle P., Ren J., “Medical image analysis with artificial neural networks,” Comput. Med. Imaging Graphics 34(8), 617–631 (2010). 10.1016/j.compmedimag.2010.07.003 [DOI] [PubMed] [Google Scholar]
- 69.Haralick R., Shanmugan K., Dinstein I., “Textural features for image classification,” IEEE Trans. Syst. Man Cybern. SMC-3, 610–621 (1973). 10.1109/TSMC.1973.4309314 [DOI] [Google Scholar]