Physical Layer Cryptographic Key Generation by Exploiting PMD of an Optical Fiber Link

Abstract

We present a symmetric physical layer based secret key generation scheme for Point-to-Point Optical Link (PPOL) communication by exploiting Polarization Mode Dispersion (PMD) as a random and inimitable channel characteristic. The randomness and security strength of generated cryptographic keys based on PMD is significantly high. In this paper, we present that random modulation of a probe signal caused by PMD in a high-speed data communication network (40Gb/s and 60Gb/s) is reciprocal with average Pearson correlation coefficient of 0.862, despite the presence of optical nonlinearities, dispersion, and noise in the system. 128-bit symmetric cryptographic key has been successfully generated using the proposed scheme. Moreover, PMD based encryption keys passed the National Institute of Standards and Technology (NIST) tests. We have shown through simulations with a 50km link that, with optimal key generation settings, symmetric keys can be generated with high randomness (high P-values for NIST randomness tests) and with sufficient generation rates (>50%). Furthermore, we considered an attack model of a non-invasive adversary intercepting at 10km into the link and found that the generated keys have high average key bit mismatch rates (>40%).

I. Introduction

OVER recent decades the accessibility and bandwidth demand of optical network has been increased tremendously. The Point-to-Point Optical Link (PPOL) has been employed in various applications ranging from Ethernet systems to telecommunications backbone infrastructure as well as military communication system. Optical Link incorporates Optical Fiber as high speed transmission channel. However, like any other communication channel, Optical fiber is vulnerable to many security threats, involving jamming, eavesdropping, interceptions, and infrastructure attacks. In optical networks an adversary can eavesdrop on an optical system in various way including physically tapping into the optical fiber [1], listening to residual crosstalk from an adjacent channel [2]. As the data rate of today’s communication networks goes beyond 40Gb/s, the implementation of the real time, low latency authentication and security of the data transmitted over optical fiber has become one of the most important areas of research. State-of-the-art data security (including fiber optic communication) is implemented by encrypting the data at the transmitter side and decrypting at the receiver side as shown in Fig 1. In general, cryptography requires one or more unique number known as keys.

Fig. 1.

Schematic for data encryption and decryption system

The cryptographic algorithm can be classified into two major categories [3]: Symmetric and Asymmetric. Symmetric algorithms (like AES, RC4, DES, etc.) use identical cryptographic keys for both encrypting the plaintext as well as decrypting cipher text [4]. Since symmetric algorithms do not require complex bit manipulations, they have low overhead and high performance [5]. However, the key needs to be shared between two or more parties participating in the communication. The secret key is to be transmitted to the receiver side before the information is to be transmitted. It is impractical to ensure that no one will be able to tap communication channels during key exchange unless the channel is secured via cryptography and authentication. Hence, the only secure method of key exchange would be to personally transport the keys directly to the transmitters. This is a major drawback of symmetric key encryption. On the other hand, asymmetric algorithms (like RSA, SSL, DSA etc.) do not involve a shared key for encryption and decryption, but public and private keys instead. However, higher computational power requirements, slow key generation process, more memory space requirements make asymmetric algorithms less suitable for time-critical and resource-limited applications. Thus, various research groups and organizations have proposed to establish a hybrid solution for cryptographic algorithms [6]. There are many research works on securing fiber-optic communication describing different approaches to establish secure network. However, most of them assumed that the adversary either does not have information of a secret parameter or does not have a sophisticated tool to replicate the key generation scheme. These are naive assumptions in today’s world. The most secure and solid alternative today is quantum optical-fiber cryptography, which provides impregnable security as assessed in [7], [8]. However, this quantum cryptography is an expensive and sophisticated solution suitable only for critical applications. Further, the secure quantum key distribution itself is a challenging task. Hence, a simple and efficient yet safe method for cryptographic key distribution is necessary. To address this problem, researchers have recently proposed to generate secret keys from the randomness of the physical environment [9]–[13].

The concept of the physical layer (PHY) based secret key generation is to exploit the randomly varying properties of the underlying physical layer. In the fiber-optic communication channel, the deployed optical fibers are considered as part of the physical layer (PHY). In [7] the author presented the use of quantum seals to test the integrity of the authenticity of a communication channel. The authors explained how a quantum physical layer senses tempering and how it communicates with the higher protocol layers to allow quantum seals to influence the security of data communication. Phase fluctuation in the optical fiber is exploited by using a large-scale Mach-Zehnder interferometer to generate and share keys in [10]. In [14], the authors showed that optical fiber communication encryption is possible based on four-wave mixing (FWM) in a very high non-linear bismuth-oxide fiber (Bi-NLF) and therefore requires specific fiber deployment. In [15], we showed that the stochastic nature of polarization mode dispersion in the optical fiber can be exploited to generate secret keys for cryptography. To summarize the previous work, most of the methods related to physical-layer based fiber optic security requires delicate and sophisticated system deployments which are complex and expensive. In addition to that, almost all of the previous works did not describe the key generation techniques established on their system modeling nor adequate analysis on secret key strength, key mismatch rates, and key entropy. In our research, we aim to implement a low cost, easily deployable symmetric cryptographic key generation technique based on uncompromisable physical randomness. Our goal is to solve the security challenges in resource-limited optical fiber links.

The preliminary analysis presented in [15] shows that the encryption keys based on PMD have high reciprocity and high entropy. In this paper, we describe the detailed system model to exploit the contingent nature of Polarization Mode Dispersion (PMD) using an optical switch and Randomly Spliced Polarization Maintaining Fibers (RSPMF). We characterize the required length of RSPMF for different data rates and explained some of their effects on the overall key generation scheme. In addition to that, we explain the security key generation scheme based on the proposed system model. We evaluated the effectiveness of the key generation scheme for 60Gb/s and 40Gb/s via mismatch rate analysis and state-of-the-art randomness tests created by the National Institute of Standards and Technology (NIST). From our analysis, we found optimal settings for our key generation scheme that maximizes the key randomness (98% test pass rate) and has a moderate key bit generation rate (60% on average). Key randomness tests prove the randomness of the PMD modulated signal. Further, based on key generation parameters, the generated keys are 40% different on average compared keys generated by a malicious non-invasive adversary.

II. System Modelling

A. Randomly Spliced Polarization Maintaining Fiber Model

The proposed key generation scheme is based on the random variation of Polarization Mode Dispersion. PMD is related to Differential Group Delay (DGD) caused by birefringence in the optical fiber in a long haul network, PMD =<Δτ>, where <Δτ> is the average value of DGD [16]. Birefringence varies along the fiber length and is totally nonstationary stochastic in nature. It arises from different internal and external stresses on the fiber including core asymmetry, non-uniform loading, bends, and twists. PMD is a random effect because it relies on the instantaneous weak birefringence state of the fiber link. Many experiments with the fiber of various lengths proved that PMD of a fiber link is proportional to the square root of the fiber length as in (1), where L is the length of the fiber.

$$PMD=PM{D}_{coefficient}\times \sqrt{L}$$ (1)

Commercially available SMF-28 fibers have PMD coefficient of $0.04ps/\sqrt{km}-0.1ps/\sqrt{km}$. Equation (1) reveals that, depending on the data rate, commercially available SMF-28 with PMD coefficient of $\approx 0.04ps/\sqrt{km}$, the PMD effect manifests itself over an extremely large distance as shown in Table I, column 2[16]. As a consequence, the cryptographic keys generated from the modulated bit streams based on commercial SMF-28 possess low entropy. To mimic the effect of Polarization Mode dispersion of a long-haul fiber network in a smaller(≤50km) dispersion compensated Point to Point Optical Link (PPOL), we incorporated two sections of randomly oriented RSPMF at both transceivers ends as in Fig. 4. Fig. 2(a) shows the transmitted pre-defined bit sequence and Fig 2(b) shows the received signal at a 50km distance with RSPMF (blue) and without RSPMF (red).

Table I.

Summary of maximum allowable transmission distances for fibers with PMD coefficient of $0.04ps/\sqrt{km}$ and required RSPMF lengths

Data rate (Gb/s)	PMD limited link length for SMF-28 (km)	Required RSPMF length (m)
10	6.25 × 104	> 45
20	1.5 × 104	> 22
40	0.4 × 104	> 10
60	0.16 × 104	>8

Fig. 4.

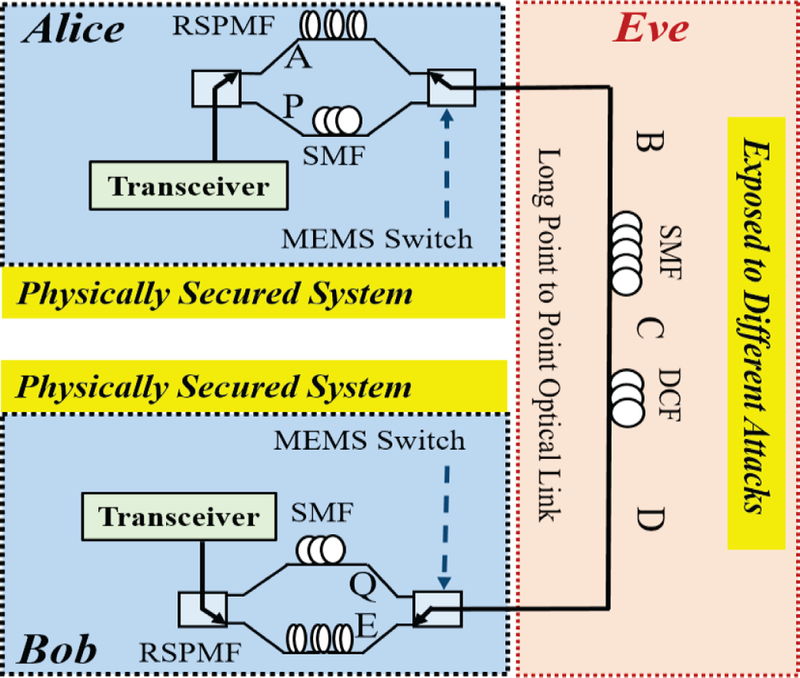
Proposed PMD based key generation scheme incorporating Randomly Spliced Polarization Maintaining Fibers (RSPMF). Alice and Bob are the two legitimate communication parties. The adversary (EVE) has access to the fiber network constitutes of SMF and Dispersion Compensated Fiber (DCF).

Fig. 2.

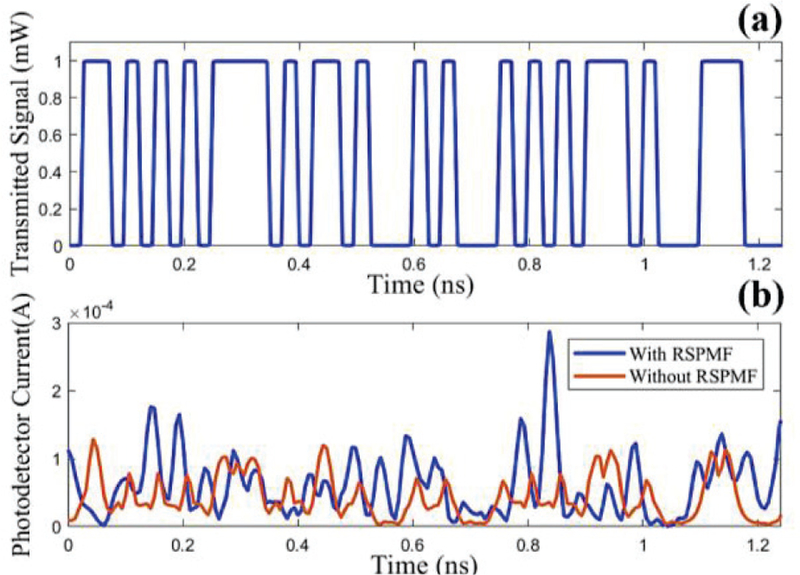
(a) Transmitted random optical Signal at 40Gbps, (b) received signal with and without RSPMF of a 50km PPOL (bottom).

It is evident from Fig. 2, the received signal in a 50km link without RSPMF has analogous amplitude variation as the pre- defined bit sequence. Therefore, the received signal cannot be exploited to generate cryptographic keys assuming that the attacker has the knowledge of the predefined bit sequence. The RSPMF is designed in such a way that the average value of DGD (PMD) exceeds the maximum allowable PMD of the link, that is Δτ ≥ 0.1T_B [16] where T_B is the bit period.

To demonstrate the concept, we selected Δτ ≈ 0.25T_B to achieve random amplitude modulation of the bit pattern. In our simulation, each PMF has beat length=1mm (from manufacturers specs) which implies Δn=0.0016. Given that DGD, Δτ ≈( Δn / c)L, the total RSPMF length to achieve the desired PMD effect for 60Gb/s, 40Gb/s, 20 Gb/s and 10 Gb/s are summarized in Table I. For example, in a 60Gb/s system, Δτ exceeds 4.16ps (≥0.25T_B) when the RSPMF length is ≥8m. It can be seen from Fig 2 (b) that RSPMF enhances PMD, therefore, causes stochastic amplitude modulation of the bit pattern due to pulse splitting and random walk-offs between two orthogonal polarization states. In addition to the total length of the RSPMF, the number of spliced segments plays a crucial role in PMD modulation. Theoretically, one segment splits the input pulse into two. As a result, n number of segments can split the pulse ≤ 2ⁿ Therefore, the higher the number of RSPMF segments the higher the random pulse modulation due to PMD. Fig. 3 shows the random amplitude modulation of the input pulse pattern cause by RSPMF consists of 1,3,6 segments respectively in a 60Gb/s communication link.

Fig. 3.

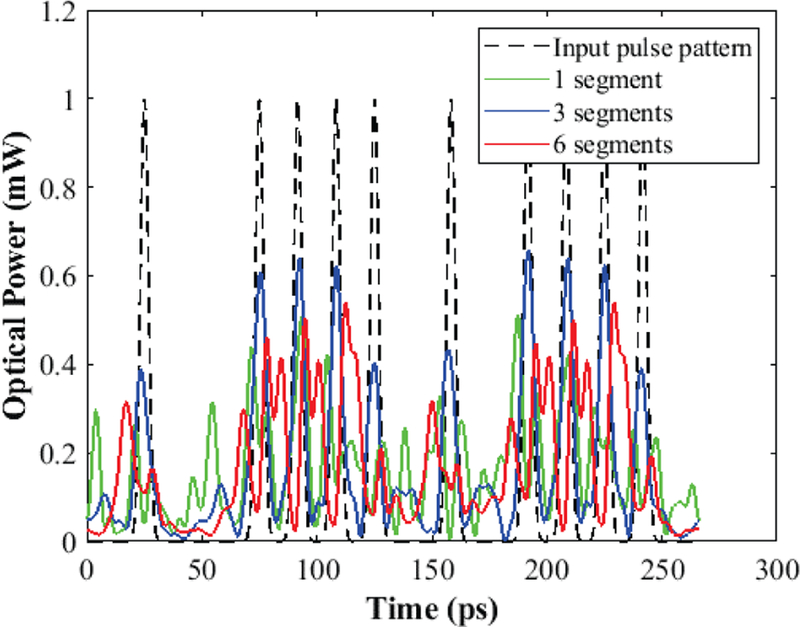
Effect of RSPMF segment number on the amplitude modulation of the optical pulse pattern due to PMD. The total length of RSPMF is 42m

The correlation among the modulated signals by RSPMF of different segments is given in Table II. It is evident that modulation of the input pulse by RSPMF of different segment number (1,3,6) are highly uncorrelated from each other. In our paper, to demonstrate the concept we chose 6 segments of PMF with randomly generated length between 8m and 16m to design each RSPMF of 42m. In total, we incorporated two RSPMF (one at each transceiver side), in the simulation model.

B. Total Optical Point to Point Link Model

To prove the concept and to assess the feasibility of our model we developed a point-to-point optical link simulation model as shown in Fig. 4. In this model, Alice and Bob are the two legitimate parties who want to communicate over a secured communication channel with symmetric cryptography. As mentioned earlier, symmetric encryption algorithms are faster and require less processing overhead compared to asymmetric algorithms. Using our presented method, Alice and Bob will be able to generate and exchange strong symmetric cryptographic keys to encode their plaintext without facing the key transportation challenges [17]

The proposed system works in two modes i.e. communication mode and key generation mode. The state of the link can switch between these two modes very fast with current technologies. For instance, by using commercially available fast optomechanical MEMS switches, the switching time between these two modes can be less than 0.5ms. In the key generation mode, the communication link between Alice and Bob is A-B-C-D-E in Fig. 4. The Differential Group Delay (DGD) between two Principal States of Polarization (PSP) will be higher and more stochastic due to the high PMD effect from the long SMF-28 fibers in between the transceivers and the RSPMF and SMF pigtails in this path. After the key establishment agreement between Alice and Bob, the system will go into communication mode and send signals via the P-B- C-D-Q path just as in a conventional point-to-point optical fiber link. In the key generation mode, the changes in the Differential Group Delay follow a Maxwell probability distribution as given in (2), where l, Δτ, q² are, fiber length, the average DGD and the variance of the Maxwell distribution, respectively [18]

$$P(\text{Δ}\tau ,l)=\frac{2\text{Δ}{\tau }^2}{\sqrt{2\Pi q^3}}exp\left[-\frac{\text{Δ}{\tau }^2}{2q^2}\right]$$ (2)

Due to the orthogonality of the input principle state of the polarization (PSP), any input polarization can be written as a vector sum of its components. Equation (3) states the output electric field vector in the time domain. In (3), r₊ and r_– are the complex projections, ${\epsilon }_{out+}\hspace{0.17em}\text{and}\hspace{0.17em}{\epsilon }_{out-}$ are unit vectors of the output PSP and ϕ± are the constant phases picked by the polarization modes, $\Delta \tau =\left|{\tau }_{+}-{\tau }_{-}\right|$ represents the DGD.

$$\overrightarrow{E_{out}(t)}=r_{+}\stackrel{\rightharpoonup }{{\epsilon }_{out+}}{e}^{j\varphi +}{E}_{in}(t+{\tau }_{+})+r_{-}\stackrel{\rightharpoonup }{{\epsilon }_{out-}}{e}^{j\varphi -}{E}_{in}(t+{\tau }_{-})$$ (3)

We adopted the renowned discrete waveplate model and used Jones matrix calculations [19], [20] to simulate our model in MATLAB and VPI Transmission maker. In our model, a long single-mode fiber is simulated as the concatenation of a large number of birefringent waveplates each having the same indices but different lengths and orientations. If we do not include polarization dependent loss, the frequency dependence of the Jones matrix, and temperature fluctuation, any waveplate can be represented by (4). Where S (θ ) denotes the rotation of the fast axis of the wave plate by θ degree from +x axis, L is the fiber length, n_fast and n_slow are the refractive indices for fast and slow modes, respectively.

$$\begin{gathered} M(\omega )=S(-\theta )e^{\frac{-j\omega L(n_{fast}+n_{slow})}{2c}}\times \\ \left[e^{\frac{-j\omega L(n_{fast}-n_{slow})}{2}}0;0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{e}^{\frac{j\omega L(n_{fast}-n_{slow})}{2}}\right]\times S(\theta ) \end{gathered}$$ (4)

In our simulations, we found that there is high reciprocity of the modulated probe signal in Alice’s and Bob’s channel. Across ten probe signals (1024 samples), the average Pearson correlation coefficient between Bob’s received samples and Alice’s received samples was 0.862 when the data rate was 60Gb/s and 0.868 when the data rate was 40Gb/s (1.0 is the maximum).

C. Attack Model

In our attack model, we assume two communicating parties, Alice and Bob and a non-invasive eavesdropping adversary, Eve. The adversary, Eve, does not have direct physical access to the transceiver systems, but may have access to a point along the communication link as shown in Fig. 4. As a result, Eve will not be able to observe the randomly spliced PMF, the probe signal, or input polarization state of the signal in the fiber that Bob observes from Alice and vice-versa. Moreover, in a later section, we will show that even if we assume Eve has information about these systems or features, Eve will not be able to generate the same keys as Alice and Bob due to the stochastic nature of the PMD, which distributes over the entire length of the fiber.

D. Physical-Layer Key Generation Scheme

The key generation scheme exploits the physical randomness from the PMD effect of the optical fiber link to generate symmetric secret keys for Alice and Bob. Alice and Bob initiate the key generation mechanism by sending predefined probe signal (bit sequence) to each other. These pre-defined signal pulses experience random polarization rotation, pulse splitting caused by pulse walk-offs between two orthogonal polarization states. The proposed scheme not only rely on Δτ, but also rely on the polarization rotations of the pulses. That leads to stochastic amplitude modulations due to the stochastic nature of PMD. The randomness is observed as the photodetector current and then sampled, processed and quantized independently by Alice and Bob. Since they experience the same physical channel, the amplitude modulation measured at the two ends of the fiber would be highly correlated. Moreover, two parties perform a mismatch removal step to generate symmetric cryptographic keys to reduce the mismatch rate. In a practical application, we anticipate that key generation algorithm will run a few times (≈10) in a day. It is evident that, the temperature, DGD of a deployed fiber varies significantly over a day due to hot spots [21]. A small change of polarization state and DGD at any hot spot of the link influences the overall experienced PMD effect and therefore, enable us to achieve random patterns more frequently than required.

D.1. Thresholds and Quantization:

The first step in the key generation scheme involves Alice and Bob independently splitting their sets of received samples X_Alice and X_Bob into subsets/groups notated as x_Alice,i ⊆ X_Alice and x_Bob,i ⊆X_Bob each of size G_size (the size of the last group may be less than or equal to G_size). Then, Alice and Bob take the average µ(x_id,i) and the standard deviation σ(x_id,i) of each group and from them compute an upper threshold Thr_upper(x_id,i) and a lower threshold Thrlower(x_id,i), where id ∈ {Alice, Bob}. The thresholds are defined as follows:

$$\begin{gathered} Th{r}_{upper}(x_{id,i})=\mu (x_{id,i})+\alpha \ast \sigma (x_{id,i}) \\ Th{r}_{lower}(x_{id,i})=\mu (x_{id,i})-\alpha \ast \sigma (x_{id,i}) \end{gathered}$$

Where α is a programmable parameter that we assume is constant. Nonetheless, it could be a unique value per threshold definition. This thresholding approach is the same as the one proposed by [22]. Per each subset x_id (_{i, j}), Alice and Bob will generate thresholds and iterate through each sample x_id (_{i, j}). They will either quantize the sample into a binary value for their corresponding secret key and store its index for a later step or discard the sample and index. Alice and Bob will have a set with the quantized and stored key bits denoted as K_id and the stored indexes denoted as J_id. The pseudocode for the simple key bit quantization of a sample is defined as follows:

$$\begin{gathered} if\hspace{0.17em}{x}_{id,(i,j)}\ge Th{r}_{upper}(x_{id,i})\hspace{0.17em}then\hspace{0.17em}{K}_{id}+\left\{1\right\};J_{id}+\left\{j\right\}; \\ else\hspace{0.17em}if\hspace{0.17em}{x}_{id,(i,j)}\le Th{r}_{lower}(x_{id,i})\hspace{0.17em}then\hspace{0.17em}{K}_{id}+\left\{0\right\};J_{id}+\left\{j\right\}; \\ else\hspace{0.17em}do\hspace{0.17em}nothing \end{gathered}$$

D.2. Index Exchange and Index Mismatch Removal:

After each group of samples are quantized into secret key bits, Alice and Bob will perform a secure mismatch removal step without revealing the secret key bits. This requires Alice and Bob to store the indices of the samples that were successfully quantized in their own sets, J_alice and J_bob respectively. Because of system noise and the choices for α and G_size, these sets may not match one another. Thus, Alice and Bob must exchange these sets (note that the actual values or key bits are not revealed in this manner) to compare their own sets with the received sets and remove indices that do not exist in the received sets. Only the quantized secret key bits corresponding to the indices that have not been removed can be used in the final keys. The following is the pseudocode for the index removal and exchange steps from the perspective of one of the parties:

$$\begin{gathered} Define\hspace{0.17em}id1,id2\hspace{0.17em}\hspace{0.17em}\in \hspace{0.17em}\left\{alice,bob\right\}s.t.id1\ne id2 \\ for\hspace{0.17em}each\hspace{0.17em}j\in J_{id1}: \\ if\hspace{0.17em}j\notin J_{id2}\hspace{0.17em}then\hspace{0.17em}{J}_{id1}=J_{id1}-\left\{j\right\}; \\ else\hspace{0.17em}do\hspace{0.17em}nothing \end{gathered}$$

D.3. Key Bit Generation Rate:

Per each group of samples x_id,i, there are M_i secret key bits generated after the quantization and mismatch removal steps, where M_i ≤ G_size. Thus, the key generation scheme will continue to generate secret key bits until it runs out of samples to quantize (N). The final number of generated secret key bits is notated as M, where M ≤ N. Then, according to the selected cryptographic scheme’s key length requirement L_K, the M secret key bits can be divided into M/L_K secret keys which will be stored and used for the current and future sessions. The high data and sampling rates (limited only by hardware) due to the optical fiber medium are highly suitable for this key generation technique because it makes up for the quantization method’s tendency to have low key bit generation rates. In radio channel communication, the data rates are strictly limited and constrain the effectiveness of the technique.

D.4. Generated Key Bit Mismatch Rate:

After the entire key generation process, we consider all the removed samples from the quantization step in Section C.1 as R_Q and the removed samples/bits from the index mismatch removal step as R_I. We call the ratio of R_Q to R_I, the quantization mismatch rate (QMR). Preferably, we would like to have a low QMR because a lower QMR implies a higher key bit generation rate. Unfortunately, the noise and choices for G_size and α can greatly affect the QMR. We would also like to evaluate the number of mismatching bits between Alice’s generated key and Bob’s generated key. These mismatching bits may be caused from extreme elements of noise that disturbed the reciprocity of the signals. We consider this as the final mismatch rate (FMR) which is equivalent to the Hamming distance (number of bits needed to be flipped for one key to be the same as another key) between Alice’s and Bob’s keys. Fig. 5 provides a visual overview of the key generation scheme.

Fig. 5.

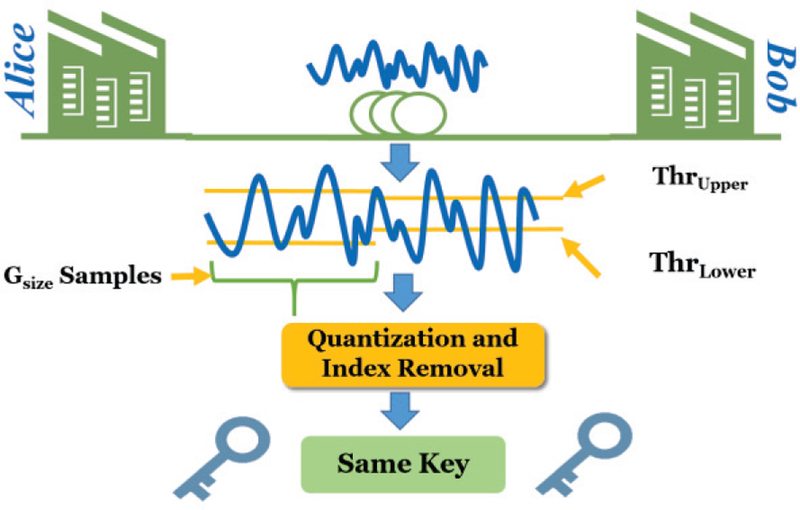
Key generation overview.

III. Simulation Results AND System Verification

A. Simulation Tools

Signal propagation through the system is modeled by a combination of commercial simulation tools including VPI transmission Maker and Matlab. We used the VPI transmission Maker to generate the probe signal’s bit sequence, to create the modulated NRZ optical signal, to detect the signal at the detector and to include Relative Intensity Noise (RIN), shot noise, thermal noise, etc. The propagation of the optical signal in both directions based on the split-step method is modeled in MATLAB. The reciprocity check and the key generation algorithm are implemented in MATLAB as well. In our simulation, input laser power= 1mW, link length=50km, wavelength=1550nm, PMD coefficient of $\text{SMF}=0.04ps/\sqrt{km}$, PMF’s beat length=1mm, SMF dispersion= 18 ps / nm⦁km, DCF dispersion= –100 ps / nm⦁km, Non Linear Index= 2.6 × 10^–20m² / W RSPMF segments=6, total length of RSPMF=42m, length of each randomly oriented segment= 8m-15m. We performed simulations according to different bit rates (40Gb/s, 60Gb/s) to check the reciprocity and entropy of the modulated signal due to high PMD. In this section, we also provide some results on our simulations using the system model in Section II. The rate of change of average DGD is considerably slower than the data transmission rate (40Gb/s, 60Gb/s). Hence, the channel response is considered as constant during predefined probe signal propagation. An example of the received signal thresholding for Alice and Bob at 60 Gb/s is shown in Fig. 6. A critical aspect of this section is to find settings that result in keys with strong randomness and moderately low mismatch rates.

Fig. 6.

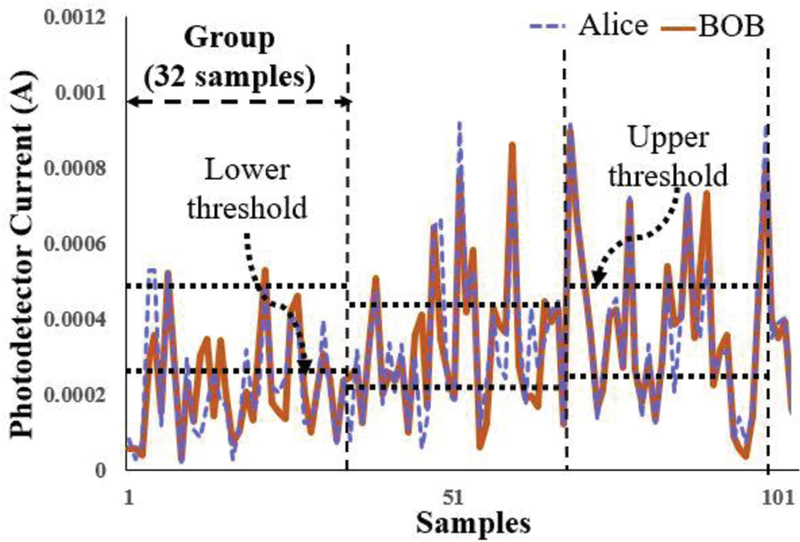
Sample thresholding for 60Gb/s PMD modulated data

B. Quantization and Final Mismatch Rate (FMR) Evaluation

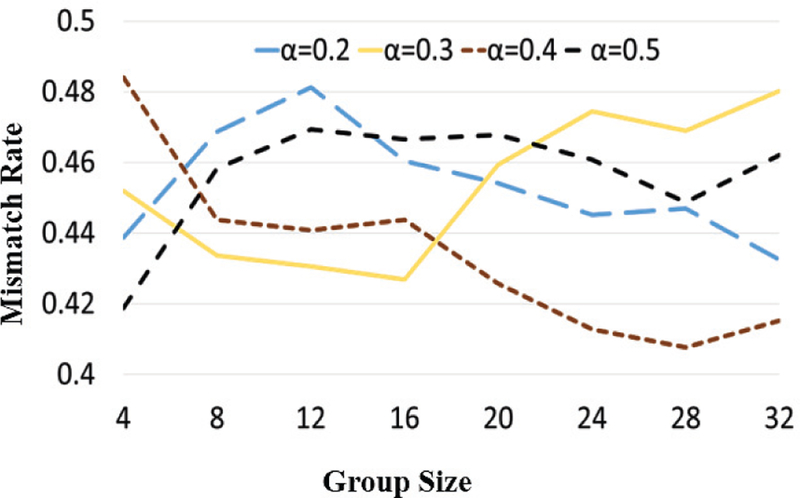
In the simulation, we exchanged 10 probe signals (each one with the same 1028-bit pattern) between Alice and Bob and ran the key generation algorithm with different settings. Fig. 7(a) and 7(b) show the quantization mismatch rates, QMR, according to the settings that we tested the key generation algorithm with for the 40Gb/s and 60Gb/s fiber links, respectively. As can be shown in Fig. 7, α and G_size deeply affect the mismatch rate. As α decreases, the mismatches greatly increase and as G_size increases, the mismatches tend to increase as well. However, around G_size ∈ [28, 32] the mismatch rates begin to plateau and decrease. Interestingly, one may observe that the quantization mismatch rates for α = 0.2 and α = 0.3 for the 40Gb/s rate simulation were quite similar (unlike in the 60 Gb/s rate simulation).

Fig. 7.

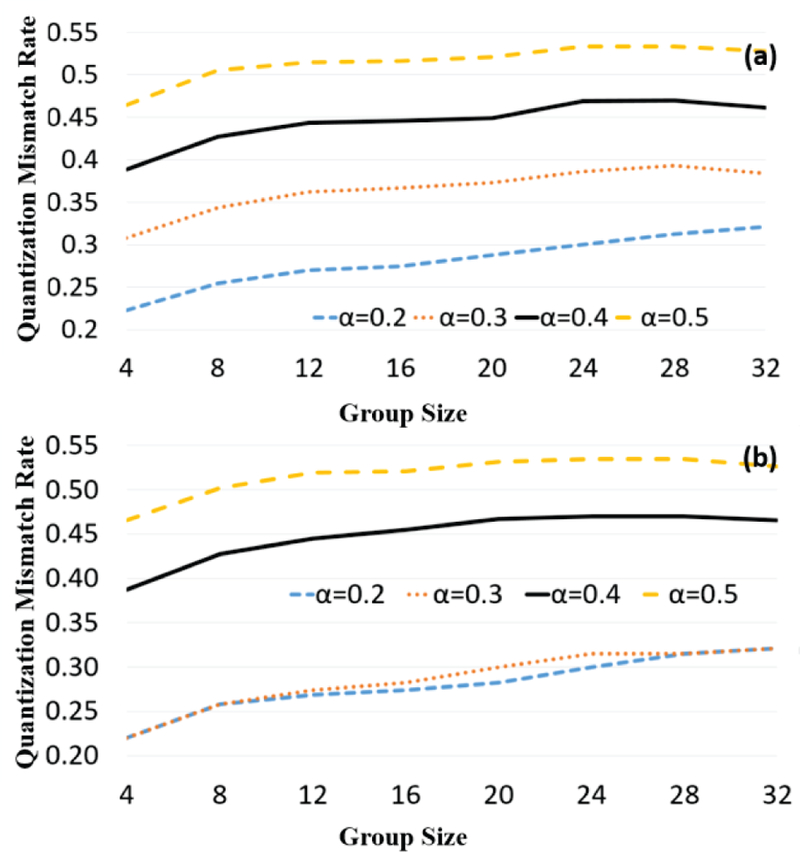
Alice-Bob quantization mismatch rates (QMR) from quantization and index exchange and removal steps for 40Gb/s (a) and 60Gb/s (b) rates when sampling offset = 1, L_K = 128 bits, α ∈ [.2, .5] with a step size of 0.1, and G_size ∈ [4, 32] with a step size of 4.

As shown in Fig. 8, we also found that for both the 40Gb/s and 60Gb/s rates, the FMR values were ≤10% (worst case). On average (across all settings), the FMR values were about 5%, except when G_size = 5. Despite having FMR values less than 10%, we do have a final key mismatch rate (# of mismatching keys / # of total keys) greater than 50% and less than 85% for each setting (besides α = 0.5). However, these values can be considered negligible considering how many 128-bit keys that can be generated per sent probe signal (approximately less than or equal to five keys per probe signal).

Fig. 8.

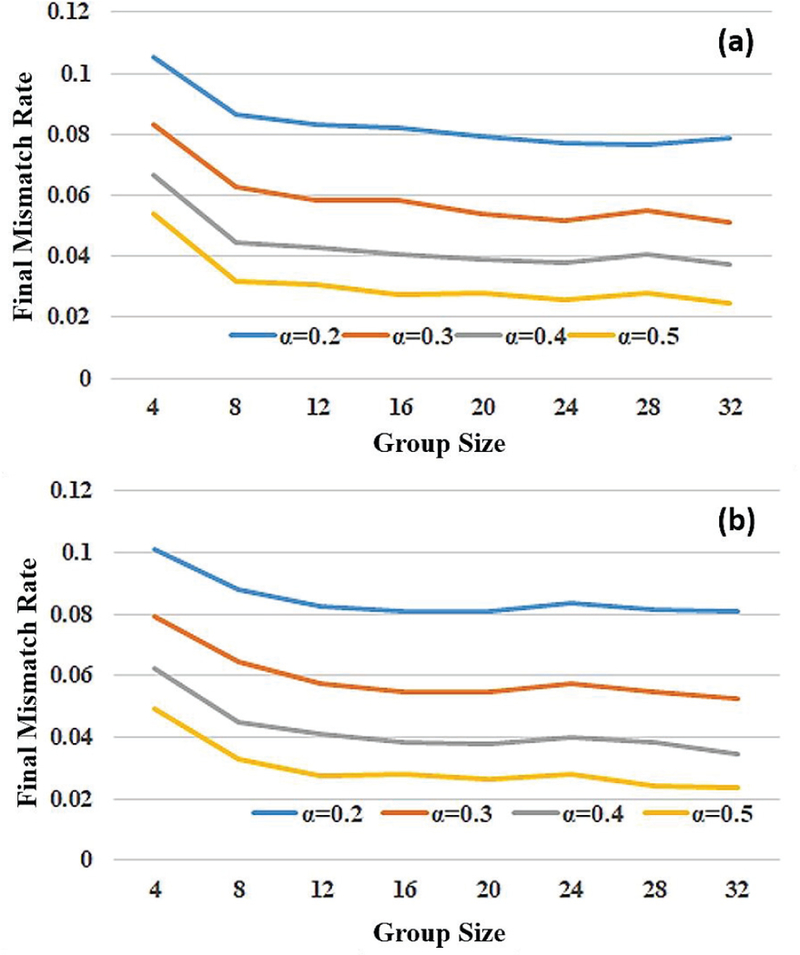
Final Mismatch Rate (FMR) between Alice and Bob for a 50km link (a) 40 Gb/s data rate (b) 60 Gb/s data rate

C. Randomness Evaluation

C.1. NIST Randomness Test Settings:

To evaluate the randomness (and equivalently, the security strength) of the generated secret keys, we opted to use the randomness tests provided by NIST [23]. Each test is designed to evaluate a bit sequence’s randomness via a specific pattern or an information theoretic metric. Since several NIST tests require certain lengths for their tests, we cannot use all the 16 tests because we are restricted by the key length L_K (some tests require 10⁶ bits or more per bit sequence). We apply tests with more relaxed constraints. We set the bit stream size N as same as L_K and for certain tests, we specify another value, block size M. The tests that we chose to use were: Frequency; Block Frequency; Cumulative Sums Forward and Backward; Runs; Longest Run; Discrete Fourier Transform; Approximate Entropy (AppEnt); and Serial Forward and Backward.

The block size (M) was set to: 128, 1, and 3 for the Frequency, Approximate Entropy, and Serial tests, respectively, where the rest of the tests did not have an adjustable block size. For each pair of α and G_size that we chose in the previous tests, we ran each NIST test over all of Alice’s generated 128-bit keys generated from the 10 exchanged probe signals between Alice and Bob. To pass a test, a 128-bit key (bit stream) must not have a predictive pattern and must have a P- value greater than the default 0.01 significance level (this also means that only 1% of the tests can fail). To derive the P-value, we use a standard normal distribution and a chi-square reference distribution.

C.2. Evaluation of Security Strength of Alice-Bob Generated Symmetric Keys:

In Table III and Table IV, per each key generation setting in Columns 1 and 2, we provide: the averaged P-values for the Approximate Entropy test in Column 3; the average number of passed tests for each setting in Column 4; the minimum number of tests required to pass (per test type) in Column 5; and finally, the total number of tests ran are in Column 6. Table III corresponds to the tests when the data rate is 40Gb/s and Table IV corresponds to the tests when the data rate is 60Gb/s. As seen in the tables, the results vary according to the choices of the data rate, G_size, and α. In general, from observations alone, it can be understood that the lower G_size and α are, the less the randomness. However, one benefit of having lower values for these settings is that there is a higher key bit generation rate. Thus, there is a possibility that there is a Pareto optimal solution for the key generation settings, the key randomness and the key bit generation rate.

Table III:

The results of the NIST randomness tests of a 50km fiber link for generated keys when the data rate is 40Gb/s

α	Gsize	AppEnt(p-value)	Avg. Passed Tests	Pass Req.	Total Tests
0.2	4	0.063	104.5	119	124
0.2	16	0.221	111.6	111	116
0.2	28	0.199	102.8	104	109
0.2	32	0.220	103	103	108
0.3	4	0.036	87.2	106	111
0.3	16	0.199	97.8	96	101
0.3	28	0.193	94.4	94	98
0.3	32	0.193	94.3	93	97
0.4	4	0.015	73.7	94	98
0.4	16	0.229	86.1	84	88
0.4	28	0.196	82.1	80	84
0.4	32	0.204	82.7	81	85
0.5	4	0.005	60.9	81	85
0.5	16	0.273	73.7	72	76
0.5	28	0.317	73	70	74
0.5	32	0.276	72.8	71	75

Table IV:

The results of the NIST randomness tests of a 50km fiber link for generated keys when the data rate is 60Gb/s.

α	Gsize	AppEnt(p-value)	Avg. Passed Tests	Pass Req.	Total Tests
0.2	4	0.081	104.9	119	124
0.2	16	0.215	112.1	116	111
0.2	28	0.215	103.9	107	109
0.2	32	0.207	104.5	103	108
0.3	4	0.028	85.8	105	110
0.3	16	0.204	88.6	96	101
0.3	28	0.202	94.1	93	97
0.3	32	0.189	94.4	94	98
0.4	4	0.014	71.1	93	97
0.4	16	0.182	85.7	84	88
0.4	28	0.196	81.5	80	84
0.4	32	0.173	83.9	82	86
0.5	4	0.005	61	81	85
0.5	16	0.212	75.6	73	77
0.5	28	0.205	72.2	70	74
0.5	32	0.241	72.4	71	75

Interestingly, the best solutions (in terms of randomness and decent key generation rates) occur when G_size = 28 or G_size = 32 for all values of α where the minimum number of tests were passed and there were moderately high entropy values (the average P-value was greater than 0.2 and individual P-values reached up to 0.7–0.9).

C.3. Evaluation of Security Strength in Presence of Noninvasive Attack by Eve:

Our security key generation scheme is based on the detected amplitude modulation of the probe signal that is caused by splitting, random walk-off and the mixing between two orthogonal polarization states which takes place statistically over the whole fiber length. It is seen from (3) that each pulse (E_in) of the probe signal splits into two in the presence of high birefringence segment. After passing n segments of RSPMF one single pulse can BE splitted successively up to 2ⁿ. The predefined signal consists of 1024 bits (pulses). Total number of pulses can be ≤ 41×10⁵. Random walk-offs and mixing of this large number of pulses over a long distance(≈50km) is totally stochastic. As a result, the probe signal experiences random intensity modulation. This modulation due to pulse splitting and mixing is highly sensitive to polarization changes due to hotspots[23], segment number of RSPMF, orientation among the segments, the total length of the RSPMF as well as input polarization state. For example, Fig. 9 shows the variation of the modulation due to three different input linear polarization states (0°,10° and 20°), keeping all other parameters of RSPMF and SMF same. It can be seen from Table V that the modulated signals are highly uncorrelated from each other. It is quite impossible for an attacker to know all these parameters and therefore, Eve will not be able to emulate the same bit pattern modulation even after possessing knowledge of the Jones matrix.

Fig. 9.

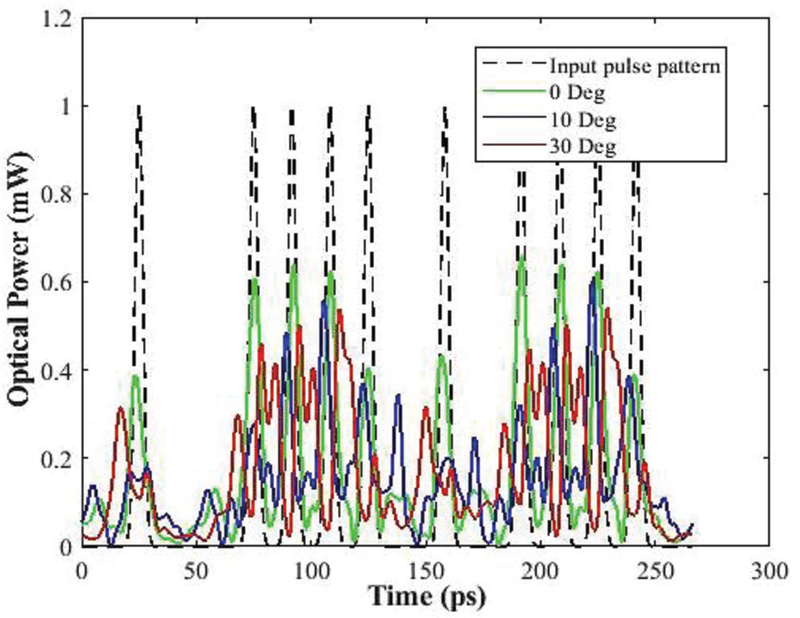
Random modulation of bit pattern due to different input polarization.

Table V.

Correlation among modulated signal for input polarization state.

Polarization angle	0o	10o	20o
0o	N/A
10o	0.550008	N/A
20o	0.068404	−0.05037	N/A

To further evaluate the security strength of the key generation scheme, we generated keys between Alice and Eve, where Eve is imagined to be eavesdropping messages sent across the fiber link around 10 km from Alice. Eve is assumed to be a non- invasive attacker who is purely interested in deriving the same symmetric keys as Alice and Bob to decrypt and eavesdrop on the secured channel. We compare the newly generated keys between Alice and Eve with the same keys generated between Alice and Bob as in the previous section. The results are summarized in Fig. 10 where the 128-bit keys generated between Alice-Bob and those between Alice-Eve are approximately 40–50% different from one another across all settings. This is a nontrivial mismatch rate range (keeping in mind that a single bit mismatch would cause encryption to fail) and indicates that there is almost no way that Eve can generate similar keys to Bob, unless they are virtually beside Bob (which is assumed to be impossible since Bob’s transceiver is assumed to be physically protected).

Fig. 10.

Averages of the final mismatch rates (FMR) between the keys that Alice and Bob generated (50km) and the keys that Eve generated (10km from Alice) at 60Gb/s.

Further research will involve developing a more extensive attack model with higher position granularity along the fiber link. Moreover, we will conduct real experiments to verify the practicality of the model and key generation technique

IV. Conclusion

We introduced and discussed a novel scheme for Point-to- Point Optical Link communication security to help resolve the high resource requirements and lack of a trustworthy source of high randomness of existing communication security solutions. The scheme includes a novel model and a physical layer symmetric cryptographic key generation technique. It focuses on exploiting the physical randomness manifested by the PMD effect. We showed that this randomness makes it extremely hard for an adversary to generate the same cryptographic keys as the communicating parties. We successfully generated 128- bit keys with low final mismatch rates (≤10%) which could easily be truncated for 64-bit and 32-bit keys if necessary. Moreover, we showed that the majority of the 128-bit keys passed NIST randomness tests. In our future work, a more advanced and optimal key generation algorithm will be developed.

Table II.

Correlation between the modulated bit pattern due to RSPMF

Segment Number	1	3	6
1	N/A
3	0.431808	N/A
6	0.225244	0.068404	N/A