Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2019 Jan 29.
Published in final edited form as: Cold Spring Harb Symp Quant Biol. 2017 Nov 28;82:57–70. doi: 10.1101/sqb.2017.82.033761

SpotLearn: Convolutional Neural Network for Detection of Fluorescence In Situ Hybridization (FISH) Signals in High-Throughput Imaging Approaches

Prabhakar R Gudla 1,2, Koh Nakayama 2,3, Gianluca Pegoraro 1,2, Tom Misteli 2
PMCID: PMC6350914  NIHMSID: NIHMS999233  PMID: 29183987

Abstract

DNA fluorescence in situ hybridization (FISH) is the technique of choice to map the position of genomic loci in three-dimensional (3D) space at the single allele level in the cell nucleus. High-throughput DNA FISH methods have recently been developed using complex libraries of fluorescently labeled synthetic oligonucleotides and automated fluorescence microscopy, enabling large-scale interrogation of genomic organization. Although the FISH signals generated by high-throughput methods can, in principle, be analyzed by traditional spot-detection algorithms, these approaches require user intervention to optimize each interrogated genomic locus, making analysis of tens or hundreds of genomic loci in a single experiment prohibitive. We report here the design and testing of two separate machine learning–based workflows for FISH signal detection in a high-throughput format. The two methods rely on random forest (RF) classification or convolutional neural networks (CNNs), respectively. Both workflows detect DNA FISH signals with high accuracy in three separate fluorescence microscopy channels for tens of independent genomic loci, without the need for manual parameter value setting on a per locus basis. In particular, the CNN workflow, which we named SpotLearn, is highly efficient and accurate in the detection of DNA FISH signals with low signal-to-noise ratio (SNR). We suggest that SpotLearn will be useful to accurately and robustly detect diverse DNA FISH signals in a high-throughput fashion, enabling the visualization and positioning of hundreds of genomic loci in a single experiment.

The genome is nonrandomly organized in the cell nucleus (Bonev and Cavalli 2016). Spatial genome organization occurs in a hierarchical fashion: Genomic loci with similar transcriptional activity and epigenetic profiles preferentially fold into domains, known as topologically associated domains (TADs); these, in turn, form larger domains, which are then further organized into chromosome territories. The three-dimensional (3D) organization of the genome allows the compaction of ~2 m of linear DNA in human cell nuclei with an ~10 μm diameter, and it provides a regulatory layer for key cellular pathways such as transcription, replication, and DNA damage and repair (Cavalli and Misteli 2013). Alterations in genome folding and organization have been linked to cancer (Flavahan et al. 2016) and developmental syndromes (Lupiáñez et al. 2015; Franke et al. 2016), highlighting the importance of 3D genome architecture in physiological and diseased states.

DNA fluorescence in situ hybridization (FISH) is one of the widely used tools of choice to study genome organization, because it directly visualizes the position of genomic loci in 3D space in the nucleus (Solovei et al. 2002). Traditional DNA FISH uses enzymatically labeled fluorescent probes, which hybridize in a sequence-specific manner to the genomic region of interest. In contrast to other biochemical techniques used to study genome organization, such as chromosome conformation capture (3C), DNA FISH allows visualization and measurement of actual physical distances between multiple genomic loci at the single-allele level. Despite this advantage, DNA FISH has mostly been used as a semiquantitative technique to validate a select few genomic interactions, mostly because of the need for laborious generation of fluorescent probes and the limited throughput of traditional fluorescence microscopy.

Two recent technical developments have helped overcome these limitations and enable large-scale FISH detection. The first is the substitution of enzymatically labeled DNA FISH probes with large libraries of chemically synthesized DNA oligos, a technique named Oligopaint (Beliveau et al. 2012, 2015; Joyce et al. 2012). Oligopaint allows the precise and flexible selection of computationally designed primary oligonucleotides binding to nonrepetitive genomic regions, increases the resolution of DNA FISH to as little as 5 kb, and, because of the use of combinatorial labeling schemes involving secondary fluorescent oligo DNA barcodes (Beliveau et al. 2015; Chen et al. 2015), increases the potential number of genomic loci that can be visualized to a few hundred in a single experiment (Wang et al. 2016). The second technical innovation is high-throughput imaging (HTI), which uses multiwell imaging plates, automated liquid handling, and high throughput 3D confocal fluorescence image acquisition to generate hundreds of thousands of images relative to thousands of cells for each of hundreds of experimental conditions (Pegoraro and Misteli 2017).

Despite these experimental advances, challenges remain to the reliable and automated detection and quantification of DNA FISH signals, which appear as diffraction-limited fluorescent spots in the nucleus. Several image-processing algorithms, such as difference of Gaussians (Bright and Steel 1987), multiscale wavelet-based (Olivo 1996), and radial symmetry (Parthasarathy 2012), detect spot-like objects in 2D fluorescence microscopy images. However, for efficient spot detection performance, the investigator needs to empirically determine appropriate sets of values for the algorithm parameters. The optimal parameter values vary with the signal-to-noise ratio (SNR) of the fluorescent spot signal, which itself varies between different DNA FISH probe sets and fluorophores in a single experiment. Although manual value optimization of spot detection parameters is feasible for one or a few DNA FISH probe sets, it is extremely laborious and subject to bias when used in the analysis of image data sets of hundreds of probes. These drawbacks, thus, negate the gains of using Oligopaint with HTI to visualize genomic organization on a large scale. In an effort to overcome this limitation, we have implemented two supervised machine learning–based analysis workflows for the high-throughput segmentation and classification of large and diverse sets of FISH signals generated by Oligopaint DNA FISH and high-throughput confocal imaging. The first method uses a manually optimized spot detection algorithm coupled with a supervised random forest (RF) classifier (Breiman 2001), whereas the second method is based on a different class of supervised machine learning (ML) algorithms, deep convolutional neural networks (CNNs) (Szegedy et al. 2016; Krizhevsky et al. 2017; Shelhamer et al. 2017). Here we describe and report on the performance of the RF- and CNN-based algorithms in DNA FISH spot detection and classification tasks. Our results indicate that SpotLearn will be readily adaptable to high throughput FISH data sets, thus allowing fully automated, single-allele analysis of genome organization using HTI.

MATERIALS AND METHODS

Cell Culture

MDA-MB-231 cells (ATCC, Cat. HTB-26) were maintained in DMEM medium, 10% FBS, penicillin 100 U/mL, streptomycin 100 μg/mL in a humidified incubator at 37°C and 5% CO2. Cells were seeded in CellCarrier-Ultra 384-well plates (PerkinElmer, Cat. 6057500) at a seeding density of 5000 cells per well. Cells were cultured for 72 h before direct fixation in the medium with 4% paraformaldehyde (PFA) in PBS.

Oligopaint DNA FISH

After fixation, cells were washed in PBS three times for 5 min, permeabilized with 0.5% saponin, 0.5% Triton X-100 for 20 min, washed in PBS three times for 3 min, treated with 0.1 N HCl for 15 min, washed in 2× SSC buffer once for 5 min, and then preincubated in 2× SSC/ 50% formamide for at least 30 min. The DNA oligo library including encoding probes were synthesized by Twist Bioscience and amplified according to a previously published protocol (Chen et al. 2015). The 5′-labeled (Alexa488, ATTO565, or Cy5) decoding probes were synthesized by Eurofin Genomics. Both the encoding oligo library and the fluorescent decoding oligos were added to cells in a 15 μL volume of hybridization buffer (50% formamide, 20% dextran sulfate, 1× Denhardt’s solution, 2× SSC) per well. The encoding oligo library was used at a final concentration of 330 nM in every well. Different three-way combinations of fluorescently labeled readout oligos were used in each well at a final concentration of 6.6 nM each. Cells and oligo DNA probes were denatured for 7 min at 85°C on a heating block, and then immediately transferred for a 16 h incubation at 37°C. After oligo DNA FISH probe hybridization, cells were washed with 2× SSC three times for 5 min at 42°C and three times for 5 min at 60°C. Finally, nuclei were stained with DAPI (4′6-diamidino-2phenylindole), washed in PBS three times for 3 mi, and stored in PBS at 4°C until imaging.

Experimental Layout

Cells were grown and stained with Oligopaint DNA FISH probes in three colors in 28 wells on a single 384-well plate as described above (training plate, Train-P1). The images from Train-P1 were used for training a supervised RF classifier (Ho 1998; Breiman 2001) for filtering mis-segmented and/or overlapping nuclei, optimizing parameters of the FISH spot detection algorithm, training a supervised RF classifier for filtering false-positive FISH spots from spot detection, and training and validation of supervised fully CNN-based spot segmentation algorithm. For testing, cells were grown and stained with Oligopaint DNA FISH in three colors in 48 wells (12 unique three-color probe sets, four wells as technical controls per probe set) on two separate 384-well plates on different days as described above (Testing Plates plate, Test-P1 and Test-P2). Test-P1 and Test-P2 were biological replicates. Three-color Oligopaint DNA FISH sets were designated with an “i-j-k” scheme, where “i” is an identifier for the gene locus labeled with Alexa488, “j” is an identifier for the gene locus labeled with ATTO565, and “k” is an identifier for the gene locus labeled with Cy5. The Oligopaint DNA FISH probe sets used for Test-P1 and Test-P2 were different from those used for Train-P1.

High-Throughput Image Acquisition

Images were acquired using an automated high-throughput spinning disk microscope (Yokogawa Cell Voyager 7000) to acquire four spectral channels: DAPI, Alexa-488, ATTO565, and Cy5. We used a 40× dry objective (0.95 NA), four excitation lasers (405, 488, 561, and 640 nm), a quad-band dichroic mirror for excitation, a fixed 568-nm dichroic mirror for detection, two 16-bit Andor Neo 5.5 sCMOS cameras (5.5 Mp; pixel binning, 2; field-of-view covering 1276 × 1076 pixels), and switchable matched bandpass filters for each channel in front of the cameras (DAPI, BP445/45; Alexa488, BP525/50; ATTO565, BP600/37; and Cy5, BP676/29). In addition, Z stacks of four images at every1.0μm were acquired for each channel in each field. In these imaging conditions, the pixel size was 323 nm. These channels were imaged in a sequential mode to minimize spectral potential bleed-through. We imaged six locations (fields of view) for each well. Identical acquisition settings were used for every well on the same plate—namely, laser intensity and exposure time on the CMOS cameras.

Nucleus Segmentation and Filtering

The nuclei from the maximum intensity projected DAPI channel were segmented using a seeded watershed algorithm (Vincent and Soille 1991). The preliminary segmentation boundaries from the seeded watershed were further refined using ultrametric contour maps (UCMs) to minimize oversegmentation (Arbelaez 2006). Briefly, UCMs achieve this by combining several types of low-level image information (e.g., gradients and intensity) to construct hierarchical representation of the image boundaries. Under this representation, boundary pixels along the nucleus periphery typically receive a higher score than other pixels associated with internal structures of the nucleus. Global thresholding (Otsu 1979; Sezgin 2004) of UCMs eliminates weaker, internal boundaries, and it minimizes oversegmentation.UCMs, however, cannot resolve boundaries between overlapping nuclei. To filter out overlapping nuclei from subsequent analysis, as well as any remaining oversegmented nuclei, we used a binary RF classifier (Good and Bad). To generate the training data for the RF classifier, we used an interactive KNIME (Berthold et al. 2008) workflow to annotate 441 segmented objects (class-Good, 304; class-Bad, 137) selected randomly from different wells of the training plate, Train-P1. Next, we extracted 14 morphometric features (e.g., circularity, solidity, area, perimeter, and major elongation) for each of the labeled object using the 2D geometric feature set from the KNIME Image Processing (KNIP) Feature Calculator Node (Dietz and Berthold 2016). The extracted features along with the class labels were used to train a RF classifier using KNIME’s Tree Ensemble Learner node. The goal of this supervised classifier was to filter out overlapping and mis-segmented objects from the nucleus segmentation.

Spot Detection and Filtering

DNA FISH signals in each spectral channel were segmented using the undecimated multiscale wavelet transform algorithm (UMSWT) (Olivo 1996; Olivo-Marin 2002). We used two wavelet scales for segmenting DNA FISH signals. The per-scale threshold parameters of the spot detection algorithm were manually adjusted so that DNA FISH signals in all three channels (Alexa488, ATTO565, and Cy5), which could be reliably detected with the same set of parameters. We found that the values of 2.0 and 1.0 for scale 0 and 1, respectively, gave the best results across all three FISH channels. These per-scale threshold parameters were intentionally set to lower values for detecting FISH signals with low SNR. Therefore, the spot detection algorithm also segmented background regions as potential FISH signals (false positives). To filter out these background regions we used a binary supervised RF classifier. To filter out false-positive FISH signals, we incorporated normalized spot intensity features in addition to the spot morphometric features. For generating the training data for random classifier per FISH channel, objects detected by the UMSWT spot detection algorithm were manually annotated as either correctly (class-GoodFISH) or incorrectly (class-BadFISH) segmented FISH spots. FISH images from training plate Train-P1 were used for generating this training data.

Fully CNN Model for FISH Spot Detection

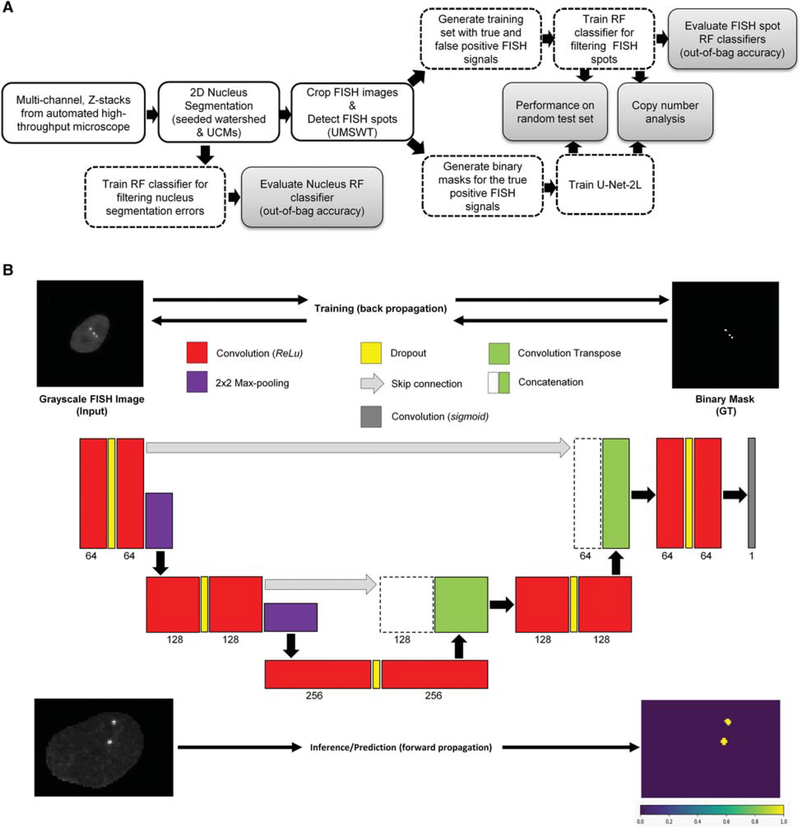
The fully CNN model is based on the U-Net autoencoder architecture (Ronneberger et al. 2015). All convolutional layers in our CNN model used a 3×3 kernel size and ReLU (Rectified Linear Unit) activation, except for the last layer, which used a sigmoid activation function to generate an output image containing pixel-level probability values. Convolutional layers were followed by a max-pooling (2×2 window size) layer for downsampling the input. The max-pooling layers were used to generate discriminating features at multiple scales/resolutions. We also introduced a dropout layer (dropout rate = 0.2) in between convolution layers within each CNN block to minimize overfitting (Srivastava et al. 2014). These minor modifications resulted in a model with a total of 402,625 training parameters. We used the modified Dice coefficient as the loss function (see Eq. 1) for optimizing the model.

For training (and validation) of the CNN we used 222 DNA FISH images and their corresponding binary masks of the DNA FISH signals collected from all three DNA FISH channels. These images were a subset of annotated spots data used for training the RF classifiers for spot filtering: Only those nuclei where all DNA FISH signals were annotated as GoodFISH were retained for CNN training. The CNN model was optimized using the Adam optimizer (KingmaandBa2014) with a learning rate of 10−5, a batch size of two images, and 5000 epochs with early stopping criteria (validation loss change of <10−7 across 500 epochs). The collection of 222 images and their corresponding binary masks were randomly split (90%–10%) to generate training (198) and validation (23) data sets. Note that the FISH images and the ground truth binary masks from the validation set are never used by the CNN model for optimizing the training parameters. The U-Net2L model was implemented as a stand-alone Python script (https://github.com/jocicmarko/ultrasound-nervesegmentation) and run on a HPC compute node with Nvidia Tesla K80 GPU.

Quantitative Assessment Methodology

We used the out-of-bag training accuracy calculations to assess the performance of the RF classifiers. For these classifiers, out-of-bag accuracy on the training sets is a good approximation of testing accuracy for similar sets of the same size. The training set was generated using the data (nuclei and spots) from training plate, Train-P1. We used the modified Dice coefficient (Dice 1945; Sørensen 1948; Zijdenbos et al. 1994) as the loss function for the CNN model:

ModifiedDicecoefficient=−loss(CNN)=2*(G∩P)+1(G∪P)+1∈[0,1], (1)

where G is the ground truth binary image of DNA FISH signals in the input grayscale image, and P is the predicted probability image of each pixel belonging to a DNA FISH signal. The symbols ∩ and ∪ denote intersection and union operations, respectively. The smoothing factor 1 in both the numerator and denominator helps the CNN model to handle the special case of input grayscale DNA FISH image not having any segmented objects.

To quantitatively compare the two FISH spot detection methods (RFandCNN), we generated ground truth images (binary masks) corresponding to FISH signals from a randomly sampled FISH images in Test-P2. The ground truth images were generated for all three FISH channels (Alexa488, ATTO565, andCy5) and are used to enumerate the total number of true positives (TP, FISH signal correctly detected as a spot), false positives (FP, background signal detected as FISH spot), and false negatives/missing spot(s) (FN, FISH signal not detected as spot) for both ML-based spot detection methods. We then calculated the following performance metrics for both methods:

Accuracy=TPTP+FP+FN,Precision=TPTP+FP,Recall=TPTP+FN,F-score=2×Precision×RecallPrecision+Recall.

We validated the robustness of both spot detection approaches by comparing the number of FISH signals identified in each cell (copy number) per probe set in separate technical and biological replicates.

Implementation

We implemented all image analysis and ML classification workflows in the Konstanz Information Miner, KNIME (Berthold et al. 2008), Analytics Platform (version 3.2.1, 64-bit) using compatible KNIME Image Processing Nodes (KNIP, version 1.5.2.201610061254) (Berthold et al. 2008; Dietz and Berthold 2016). All the KNIME image analysis workflows were run on dedicated computing nodes from a high-performance batch cluster (Biowulf, National Institutes of Health) either interactively or in a batch mode. The computing nodes had the following specifications: 64-Bit RedHat Enterprise Linux 6.9 (Santiago), 28 cores (56 threads) Intel X2680 processor, 256 GB RAM, 4 Nvidia Tesla K80 GPUs (12 GB VRAM), and 800 GB of Solid State Storage. The CNN-based spot segmentation algorithm (U-Net-2L) was implemented as a Python script (Python version, 2.7.13, 64-bit) using Keras (version 2.0.5) with the Tensorflow backend (GPU-enabled, version 1.1.0, 64-bit). The trained CNN model was used in the KNIME workflow for spot segmentation using the Python Scripting KNIME node.

Code Availability

All the KNIME workflows, the training and validating data, and the models are available via GitHub repository at https://github.com/CBIIT/Misteli-Lab-CCR-NCI/tree/master/Gudla_CSH_2017.

RESULTS

Complex Oligopaint Libraries of Probes Generate Diverse FISH Signals

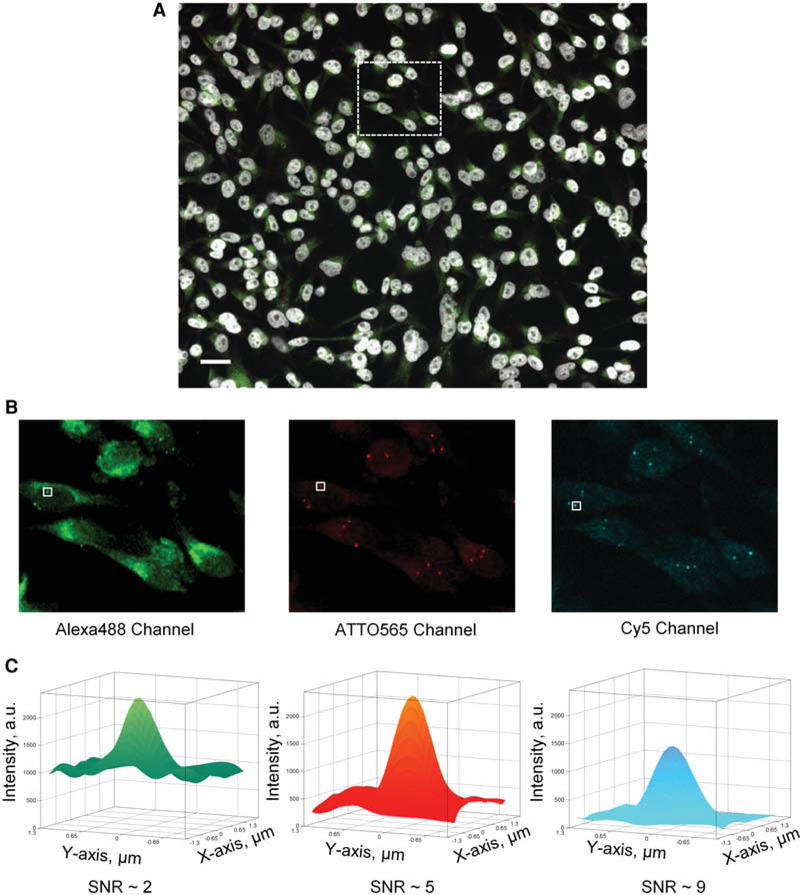
Our laboratory has extensively used enzymatically labeled fluorescent DNA FISH probes and traditional spot detection algorithms for HTI applications (Burman et al. 2015; Shacharet al. 2015; Finn et al. 2017). In these cases, although the number of experimental conditions reached up to approximately 700 wells per experiment (Shachar et al. 2015), the number of different genomic loci labeled in any single experiment never exceeded 21 (Finn et al. 2017), making it feasible to empirically determine the most appropriate sets of spot detection parameters on a per genomic locus basis. Oligopaint DNA FISH (Beliveau et al. 2012, 2015; Joyce et al. 2012), on the other hand, allows one to label and detect hundreds of different genomic loci in a single experiment on one or more 384-well plates by using combinatorial hybridization of pools of chemically synthesized oligo probes to genomic targets, together with fluorescently labeled decoding oligo probes (Fig. 1A,B; Chen et al. 2015; Moffitt et al. 2016; Wang et al. 2016). While developing HTI assays for the detection of tens of genomic loci in the same experiment, we observed that FISH signals generated by Oligopaint probe sets targeting different genomic regions can have considerably different SNRs, ranging from ~2 to 9 (Fig. 1C). Consequently, manual parameter setting of traditional spot detection algorithms for potentially hundreds of different genomic targets did not seem to be either a practical or a robust solution to this computational problem. To tackle this issue, we tested and compared the performance of two independent supervised ML approaches for the rapid and robust detection of DNA FISH spots from high-throughput fluorescence microscopy images (Fig. 2A,B).

Figure 1.

Figure 1.

Open in a new tab

(A) Representative maximum intensity projection images of MDA-MB-231 cells from one of the 48 wells with a unique Oligopaint DNA FISH set from test plate Test-P2. The DAPI-stained nuclei (blue channel) are displayed in grayscale, whereas the Alexa488 (green channel), ATTO565 (red channel), and Cy5 (far-red channel) channels are displayed using green, red, and cyan lookup tables, respectively. Scale bar, 10 μm. (B) Three Oligopaint DNA FISH channels corresponding to the region enclosed by the dashed box in A. (C) Representative surface rendering of the DNA FISH signals intensity identified by the solid-white colored boxes in B. The surface plots were generated by interpolating the raw DNA FISH signal intensities (Z-axis, arbitrary units) of 8 × 8 pixels region centered around the brightest pixel of the DNA FISH spot (1 pixel = 0.325 μm). The DNA FISH signal intensity for the Alexa488-labeled genomic locus had higher background around 1000 arbitrary units (a.u.) with peak signal of ~2000 a.u., thus leading to a signal-to(background/)noise ratio (SNR) of ~2. The ATTO565- and Cy5-labeled DNA had lower background, 400 and 160 a.u., respectively, and SNR of 5 and 9, respectively.

Figure 2.

Figure 2.

Open in a new tab

(A) Schematic of the image analysis workflow for detecting DNA FISH signals from high-throughput microscope images (blue-shaded block). The top branch after the spot detection block corresponds to a first approach for detecting and filtering DNA FISH signal using a random forest (RF) classifier, whereas the bottom branch corresponds to a second approach using fully CNN (U-Net-2L). UCMs, ultrametric contour maps; RF, random forest(s); UMSWT, undecimated multiscale wavelet transform. (B) The U-Net-2L architecture used for DNA FISH signal segmentation. During the training phase, the CNN model uses a grayscale DNA FISH image (top left) along with binary mask (GT; top right) corresponding to DNA FISH signals for optimizing the model parameters using error back-propagation. The numbers below each layer in the CNN correspond to the number of convolution filters and the height of each layer is proportional to the height of the input image(s). During the prediction (inference) phase, for a given grayscale DNA FISH image (bottom left) the CNN model predicts the probability of each pixel belonging to a DNA FISH signal (bottom right). Red boxes represent the 2D convolutional layer with 3 × 3 filter size and ReLU activation; purple boxes represent the maximum-pooling layers using 2 × 2 window size; green boxes represent the up-convolutional (convolutional transpose) layer; yellow boxes correspond to dropout layers; the gray box corresponds to a 1 × 1 convolution layer with sigmoid activation function for generating probability for each pixel belonging to a DNA FISH signal; green boxes along with dashed boxes represent concatenation layer to merge information from different resolutions/ scales.

Random Forest Filtering for Nuclear Segmentation

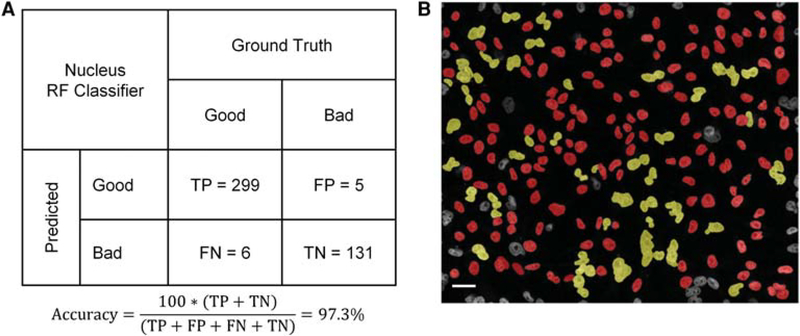
As a first step in the image analysis workflow, both spot detection methods rely on supervised RF (for details, see Materials and Methods) for nuclear segmentation using the DAPI channel images as input (Fig. 2A). We trained the RF binary classifier to distinguish bona fide segmented nuclei from debris and segmentation errors by using 441 user-annotated images of segmented nuclei from the training plate Train-P1 and achieved an out-of-bag classification accuracy of 97.3% (Fig. 3A,B; see Materials and Methods for details). The trained RF classifier was then tested on a larger data set of images originating from two biological replicate plates, Test-P1 and Test-P2, containing 48 wells each stained with DAPI and Oligopaint DNA FISH probe sets in three colors targeting 12 genomic loci. The workflow detected 23,235 and 21,208 nuclei from Test-P1 and Test-P2, respectively. The run time of the complete workflow for each plate, including reading the multichannel 3D stacks of images, was ~2400 sec (60 sec per well) on a 56-core compute node (see Materials and Methods for details). The workflow detected 493 ± 52 (mean ± SD) and 442 ± 39 (mean ± SD) nuclei per well in testing plates Test-P1 and Test-P2, respectively (Supplemental Fig. S1). We conclude that the RF classifier for nuclear segmentation can classify nuclei with high accuracy.

Figure 3.

Figure 3.

Open in a new tab

(A) Confusion matrix for calculating the out-of-bag accuracy for the random forest (RF) classifier for filtering out mis-segmented nuclei from the DAPI channel. TP, true positives; FP, false positives; FN, false negatives; TN, true negatives. (B) A representative example of classes (class-Good and class-Bad) assigned by RF classifier to the segmented objects in the DAPI channel using seeded watershed with ultrametric contour maps. Red and yellow colors represent class-Good and class-Bad nuclei, respectively. Nuclei along the edge of the field of view are filtered out before applying the RF classifier. Scale bar, 10 μm.

Training Strategy and Initial Testing for the Performance of Two Different ML-Aided Spot Detection Algorithms

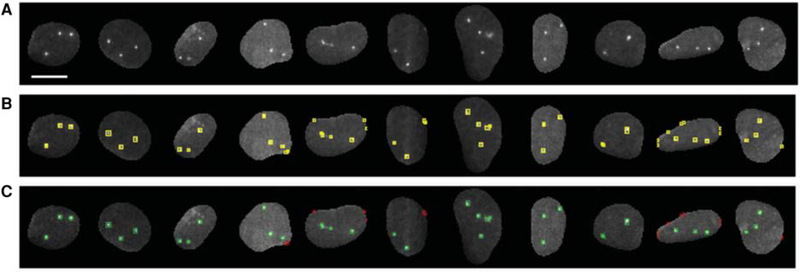
We then used the nuclear masks generated in the previous step as the search region for a traditional wavelet-based spot detection algorithm (UMSWT; see Materials and Methods for details) in images for all three DNA FISH channels (Fig. 4A). The parameters for spot detection were set for low object detection stringency to provide both positive (real FISH signals) and negative (background) examples for subsequent classifier training (Fig. 4B). In these conditions, the spot detection algorithm generated 619, 110, and 459 spot segmentation masks for the Alexa488, ATTO565, Cy5 channels, respectively. These sets were then user-annotated in two classes depending on whether they contained a real FISH signal (GoodFISH) or not (BadFISH), to generate a ground truth set for the ML algorithms (Fig. 4C).

Figure 4.

Figure 4.

Open in a new tab

(A) Representative examples of DNA FISH images used for generating the training set(s) for (a) spot filtering using random forest classifier(s) and (b) binary masks for CNN spot segmentation. Scale bar, 10 μm. (B) Spots detected by the wavelet-based method with low stringency detection parameters. Each detected object in the nucleus is labeled with a yellow color bounding box. (C) Detected objects after user annotation using an interactive KNIME workflow. Spots labeled class-goodFISH and class-badFISH by the user are shown in green and red colors, respectively. Nuclei in which all the DNA FISH signals were labeled as class-goodFISH were used for generating the binary masks for CNN.

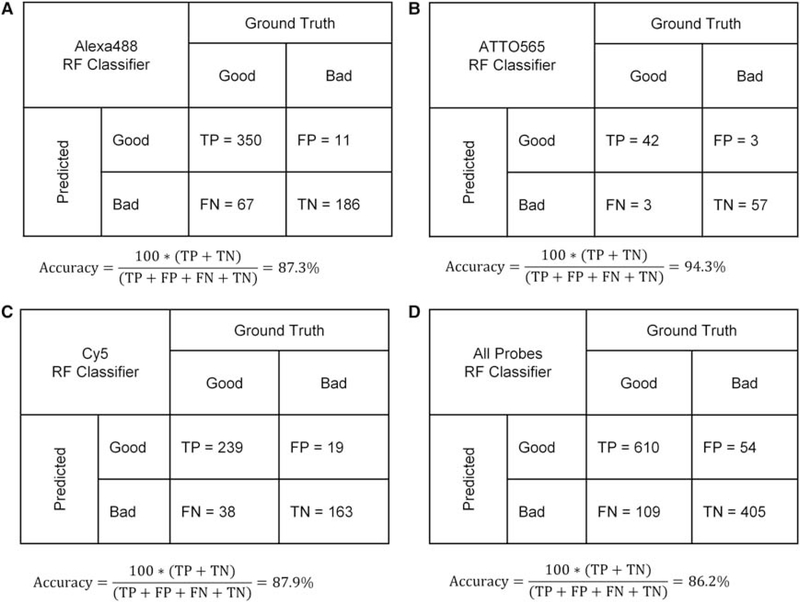
In the first of the two spot detection workflows (Fig. 2A), three separate supervised RF binary classifiers were trained using the spot masks images from the Alexa488, ATTO565, and Cy5 channels to filter out false positives (i.e., background regions detected as FISH signals). These RF classifiers used a predetermined set of spot morphology and intensity features, which were user-specified and extracted by a traditional image processing algorithm that was a part of the upstream image analysis workflow. The extracted features for the annotated objects were used to learn a binary classification scheme for FISH signals based on the GoodFISH or BadFISH labels provided by userannotation.Theout-of-bag accuracy for the spot detection using the RF classifiers in the Alexa488, ATTO565, and Cy5 was 87.3%, 94.3%, and 87.5%, respectively (Fig. 5A–C). Training a single RF classifier using an ensemble of spots from the three different DNA FISH fluorescent channels did not improve the overall out-of-bag accuracy (86.2%; Fig. 5D). We then tested the trained RF classifiers for spot classification using the two test plates (Test-P1 and Test-P2), which constitute two independent biological replicates and were previously unseen by the RF models. As a result, the three RF spot classifiers detected a total of 38,796 (59,854), 61,1121 (57,341), and 56,488 (51,750) DNA FISH spots in the Alexa488, ATTO565, and Cy5 channels from the Test-P1 (Test-P2) plates, respectively, which contain four replicate wells and 12 separate three-color probe sets each. The total run times were 2.0 and 2.5 h for each plate on a 56-core compute node (approximately 10 nuclei per second) and included FISH spot detection, spot feature extraction, and RF filtering. The spot detection, feature calculation, and filtering out false positives steps using the RF classifiers took ~18–22 min per 10,000 nuclei (i.e., 8–10 nuclei per second).

Figure 5.

Figure 5.

Open in a new tab

Confusion matrices for calculating the out-of-bag accuracy for random forest (RF) classifier(s) for filtering out background signals in the (A) Alexa488 channel, (B) ATTO565 channel, and (C) Cy5 channel. (D) Confusion matrix for the RF classifier trained with images from all the DNA FISH channels. TP, true positives; FP, false positives; FN, false negatives; TN, true negatives.

The second approach for FISH spot detection was based on the CNN architecture originally named U-Net (Ronne-berger et al. 2015), with the important distinction that it used only two downsampling and upsampling blocks, resulting in a shallow convolution network (U-Net-2L) (Fig. 2B). This allowed the use of smaller training data sets and to optimize only 402,625 parameters when compared with state-of-the-art deep learning architectures for semantic segmentation of objects from digital images (Jegou et al. 2017). The main difference for this CNN model, as opposed to the RF classifiers for spot filtering described above, is that it assigns each pixel in DNA FISH images a probability value between 0 and 1 of belonging to a FISH signal. The CNN achieves this result by autonomously extracting an optimized set of image features directly from the FISH images of the training set for pixel-level classification. We trained the CNN for approximately 3000 epochs using an ensemble data set of DNA FISH images in three channels and their corresponding candidate spot masks previously generated by the wavelet-based spot detection algorithm. These were the same spot candidate regions previously used to train the RF classifiers (Plate Train-P1). We assessed the accuracy of the CNN in segmenting DNA FISH spots by calculating the Dice coefficient (a measure of pixel classification accuracy; see Materials and Methods for details). The calculated Dice coefficient values for the trained CNN model were 0.993 for the training data (198 FISH images) and 0.913 for the validation data (23 FISH images), indicating that it can classify pixels as spots with high classification accuracy (Supplemental Fig. S2). Furthermore, and similar to previous observations on RF classifiers, we tested the CNN method to detect FISH signals from 48 wells in the Test-P1 and Test-P2 plates. For this task, we implemented an image analysis workflow that, when compared with the RF filtering approach, used the CNN method to replace (i) the wavelet-based spot detection, (ii) the feature calculation of detected spots, and (iii) the RF predictor for filtering out false-positive spots. Using this workflow, we identified a total of 63,100 (53,698), 69,244 (64,025), and 72,549 (66,260) Alexa488, ATTO565, and Cy5-labeled FISH spots from Test-P1 (Test-P2) images, respectively. The total runtime for CNN FISH detection was ~15min for each plate on a 56-core, HPC compute node with 4 Tesla K80 GPUs (approximately 80 nuclei per second) of which the CNN spot detection was only ~42 sec for 10,000nuclei (i.e., 230 nuclei per second). These results indicate that the CNN classifier is 25–30-fold faster than the RF at detecting spots when compared with the RF models.

Comparison between RF and CNN for FISH Spot Detection Accuracy

Having determined the feasibility and computational speed of applying either the RF or the CNN methods for detection of FISH signals in three spectral channels on two independent test plates, we conducted a side-by-side comparison of their accuracy in the identification and classification of FISH spots not present in the training data set (Train-P1). To this end, we first randomly selected 184, 186, and 153 cropped nuclear Alexa488, ATTO565, and Cy5 images, respectively, from Test-P2 plate (Fig. 6A–C, top rows), and spot regions generated by the wavelet-based spot detection algorithm were manually annotated as belonging to the GoodFISH or BadFISH classes as previously described (Fig. 6A–6C, second row). Finally, spots were detected using either the RF filter method (Fig. 6A–C, third row) or the CNN method (Fig. 6A–C, fourth row).

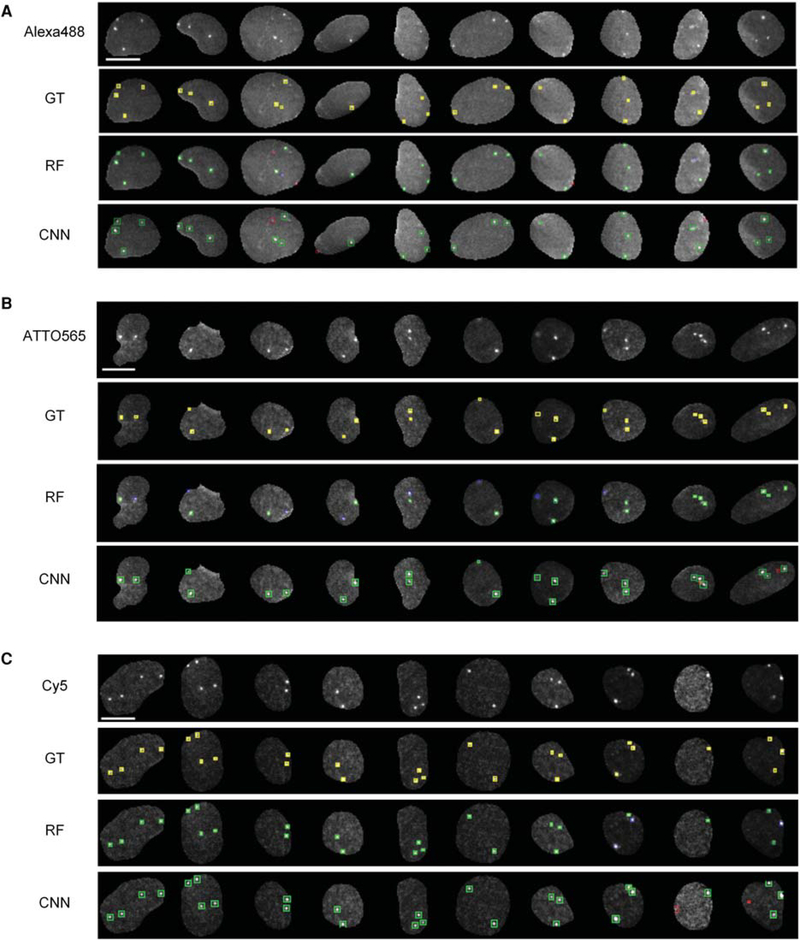
Figure 6.

Figure 6.

Open in a new tab

Illustrative examples of DNA FISH spot detection by random forest (RF) and CNN methods on a random set of nuclei from test plate Test-P2. (A–C) Representative images with Alexa488, ATTO565, and Cy5-labeled DNA FISH (rows: Alexa488, ATTO565, Cy5). “GT” rows correspond to ground truth FISH regions (yellow color) identified by a user. “RF” rows correspond to DNA FISH spot regions after applying RF filtering to remove background regions, green colored spot regions represent true DNA FISH signals (true positives), red colored spot regions represent background signals even after RF filtering (false positives), and blue colored spot regions represent true DNA FISH signals that did not get detected (false negatives). CNN rows correspond to DNA FISH spots detected by the U-NET-2L spot detection method. The color scheme of the spot regions in CNN rows is identical to in the RF rows. Scale bar, 10 μm.

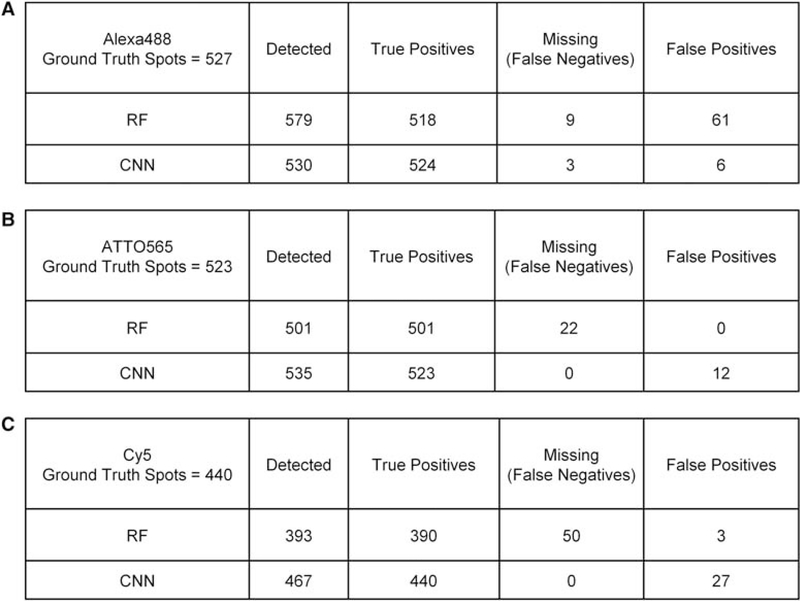
A quantitative assessment of the results of this comparison showed that for the Alexa488 images, in which the FISH signals were dimmer (SNR ∼ 2), the RF method detected 579 FISH spots. Of these, 518 were true positives, whereas the RF method failed to detect nine bona fide DNA FISH spots. Altogether, testing the RF model on this subset of annotated spots from the Test-P2 plate resulted in an accuracy of 88.1%, precision of 89.5%, recall of 98.3%, and F-score of 93.7% (Fig. 7A; see Materials and Methods for details). On the same set of images, the CNN method detected a total of 530 spots, of which 524 (out of 527) were true positives and failed to detect only three DNA FISH signals, thus resulting in an accuracy of 98.3%, precision of 98.9%, recall of 99.4%, and F-score of 99.1% (Fig. 7A). For the random set of ATTO565 images, in which the DNA FISH signals had a higher SNR (~5) than did the Alexa488 signals, the RF classifier detected 501 spots out of 523 (ground truth) without any false positives, but failed to detect 22 bona fide DNA FISH spots (false negatives) (Fig. 7B). The CNN classifier detected all the 523 spots (true positives) from the ground truth along with 12 false positives. Thus, the performance metrics for the RF versus the CNN spot detection methods on the ATTO565 images were, respectively: accuracy 95.80% versus 97.76%, precision 100% versus 97.78%, recall 95.79% versus 100%, and F-score 97.85% versus 98.87% (Fig. 7B). The performance of the two methods on Cy5-labeled DNA FISH signals images followed a similar trend as for ATTO565. In fact, out of 153 Cy5 images (SNR ~ 9) containing 440 FISH spots, the RF method detected 393 FISH spots of which only three were false positives and failed to detect 50 true FISH spots (false negatives). Most of the false negatives were due to corresponding RF classifier filtering out detected spots by the wavelet-based spot detection algorithm (data not show). This resulted in accuracy of 88.03%, precision of 99.24%, recall of 88.64%, and F-score of 93.64% (Fig. 7C). In contrast, the CNN method (Fig. 7C) detected all the 440 true positives, but also detected 27 false positives, thus, leading to performance metrics of 94.22% accuracy, 94.21% precision, 100% recall, and 97.02% F-score.

Figure 7.

Figure 7.

Open in a new tab

Summary of DNA FISH signal detection, using (a) random forest (RF) filtering on spots identified by the wavelet-based method and (b) CNN, on randomly selected set of DNA FISH images from test plate Test-P2. (A) Results for 184 Alexa488-labeled DNA FISH images with 527 spots. (B) Results for 186 ATTO565-labeled DNA FISH images with 523 spots. (C) Results for 153 Cy5-labeled DNA FISH images with 440 spots.

Altogether, these results suggest that both the RF and the CNN methods can detect FISH signals originating from diverse genomic loci and in three different spectral channels with high accuracy and precision, especially when the SNR of the FISH signals is high (≥5). The CNN method, however, outperformed the RF-based spot classifier based on quantitative metrics on images with weaker FISH signal (SNR ~ 2).

Distribution of the Oligopaint DNA FISH Signals Sets as Detected by RF and CNN Models

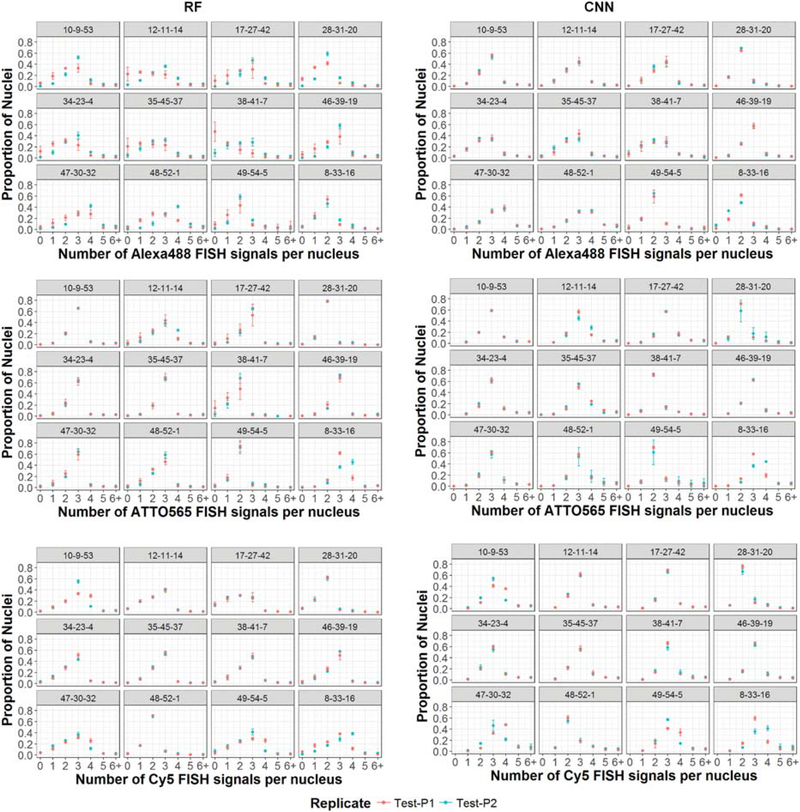
To further compare the performance of the RFand CNN spot detection algorithms on different sets of Oligopaint DNA FISH probes, we measured the number of DNA FISH signals per nucleus in Alexa488, ATTO565, and Cy5 FISH images obtained from the two biological replicate plates Test-P1 and Test-P2 (Fig. 8). The cells used in this study, MDA-MB-231, are hypotriploid and contain a total of 59 to 66 highly rearranged chromosomes, with an autosomal chromosome copy number ranging from 2 to 4, depending on the chromosome (American Tissue Culture Collection 2012). The copy number profile generated by the RF and CNN spot detection algorithms for each OligoPaint DNA FISH probe set directed against a particular genomic target was concordant for all probes in all channels (Fig. 8). As expected from MDA-MB-231 karyotype analysis, most genomic loci probed here with Oligopaint and detected either with RF or with CNN in the ATTO565 or Cy5 channels, and to a lesser extent in the Alexa488 channel, showed a sharp peak, in at least 50% of the nuclei, at either 2(e.g., locus 49 in the Alexa488 channel, locus 31 in the ATTO565 channel, and locus 1 in the Cy5 channel; Fig. 8) or 3 FISH spots per nucleus (e.g., locus 49 in the Alexa488 channel, locus 39 in the ATTO565 channel, or locus 19 in the Cy5 channel; Fig. 8). Importantly, the standard deviation among technical replicates was low(Fig. 8), and the measurements on the two biological replicates (Test-P1 and Test-P2) were highly concordant (Fig. 8). We conclude that both RF and CNN are robust spot detection algorithms that can be trained once on an ensemble of different Oligopaint DNA FISH probe sets and then reused in multiple independent biological replicates to visualize multiple genomic loci with high accuracy without the need for a manual search of the best detection parameters.

Figure 8.

Figure 8.

Open in a new tab

Plots comparing the number of DNA FISH signals (copy number) detected per nucleus in MDA-MB-231 cells between biological replicates. The results for 36 genomic loci labeled using 12 unique combinations of Alexa488-, ATTO565-, and Cy5-labeled DNA Oligopaint probes are displayed in the first, second, and third row, respectively. DNA FISH probe sets were designated with an “i-j-k” scheme, where “i” is an identifier for the gene locus labeled with Alexa488, “j” is an identifier for the gene locus labeled with ATTO565, and “k” is an identifier for the gene locus labeled with Cy5. The left column shows the copy number histograms using the RF classifier for spot filtering, and the corresponding results from CNN-based spot-detection method (U-Net-2L) are in the right column. Each dot in the histogram represents the mean proportion of nuclei with the detected copy number calculated over the four technical replicates. The bars represent the standard deviation (SD) of the mean across the technical replicates.

DISCUSSION

We present here two ML-based image analysis work-flows that can be used to detect multiple FISH signals from three fluorescence microscopy channels at high throughput with diverse SNR. More importantly, the workflows do not require manual parameter tweaking for each individual genomic loci tested (Figs. 4–7). Because the RF and CNN spot classifiers presented here are supervised ML methods, the main effort for the user is in the manual annotation of sets of DNA FISH channels images to create a ground truth data set of spots regions of interest to train the spot ML classifiers. Given that spot-like features generally are limited to small image regions (e.g., 10×10 pixels) we reduced this burden by selecting an RF model for spot classification task and a shallow CNN autoencoder model (U-Net-2L) for spot segmentation. This resulted in a smaller number of model parameters to train and in smaller training data sets for efficient performance. In addition, we greatly facilitated manual annotation of the FISH images by using a wavelet-based spot detection algorithm with nonstringent detection parameters, to automatically generate a diverse set of spot segmentation masks that can be directly used by the user for training ML methods. Overall this resulted in a manual annotation time of the order of 30–60 min. This initial investment dramatically reduces the time needed for downstream image analysis setup when compared with manual tweaking of traditional spot detection parameters, and we expect that ML methods for spot detection will greatly reduce this bottleneck in the analysis of image data sets including tens or hundreds of different genomic loci tagged with fluorescently labeled Oligopaint DNA FISH probes. Furthermore, it is likely that these ML spot detection methods explore a much larger parameter optimization space when compared with manual parameter tweaking of traditional spot detection methods and will likely result in higher spot detection accuracy. Finally, given the robustness of these ML approaches to reproducibly detect spots from images generated in different technical and biological replicates (Fig. 8), we expect that, provided that the experimental conditions remain the same, it will be possible to apply these models to different experiments performed on different days without the need for retraining, thus making it a “train once and reuse multiple times” approach for DNA FISH spot detection.

Although both the more traditional RF classifier and the CNN model show comparable high performance in terms of spot segmentation accuracy (Figs. 4–7), we expect that the CNN model will be the approach of choice because it performs better than RF in both high- and low-SNR conditions (Fig. 7). More importantly, the CNN approach eliminates the need for computationally intensive image feature calculations, takes advantage of highly efficient GPU hardware acceleration for spot segmentation, and leads to a 25–30-fold increase in the spot detection speed. This last feature is essential to process large data sets of images generated by high-throughput microscopes (up to 105 images per 24 h). For these reasons, the CNN model, which we named SpotLearn, is an ideal choice for ML-mediated spot detection of Oligopaint DNA FISH signals. We expect that SpotLearn could be further improved by tuning the hyperparameters of the model—namely, the number of filters in the convolutional layers, the filter activation functions, the number of downsampling and upsampling levels—and by including batch normalization (Ioffe and Szegedy 2015). In addition, it might be possible to improve the SpotLearn model accuracy and to further strengthen it against overfitting by performing K-fold cross-validation by training K SpotLearn models on training-validation data sets (He et al. 2016). Finally, it might also be worthwhile to explore data augmentation strategies (vertical and horizontal flips and shifting) for increasing the size of the data training sets (Huang et al. 2017). More generally, it should also be possible to use SpotLearn for a range of cellular and biomolecular imaging applications requiring spot detection as an intermediate step. For instance, SpotLearn could be used in lieu of traditional spot detection algorithms for detecting single molecules in super-resolution and localization microscopy (Betzig et al. 2006; Smith et al. 2010; Liu et al. 2017) and for detecting nascent RNA transcripts in live cell images (Larson et al. 2011). Altogether, we anticipate that SpotLearn will become an important tool for the detection of genomic loci in a high-throughput fashion and in the study of the 3D genome organization.

Supplementary Material

Supplemental Information

ACKNOWLEDGMENTS

We thank the High-Performance Computing Group, CIT, National Institutes of Health for their computational hardware and support. This research was supported by funding from the Intramural Research Program of the National Institutes of Health (NIH), National Cancer Institute, and Center for Cancer Research.

Footnotes

Supplemental material is available for this article at symposium.cshlp.org.

This is a work of the US Government.

REFERENCES

  1. American Tissue Culture Collection. 2012. SOP: Thawing, propagation and cryopreservation of NCI-PBCF-HTB26 (MDA-MB-231). Version 1.5 https://physics.cancer.gov/docs/bioresource/breast/NCI-PBCF-HTB26_MDA-MB-231_SOP-508.pdf.
  2. Arbelaez P 2006. Boundary extraction in natural images using ultrametric contour maps. In Conference on Computer Vision and Pattern Recognition Workshop, pp. 182–189. [Google Scholar]
  3. Beliveau BJ, Joyce EF, Apostolopoulos N, Yilmaz F, Fonseka CY, McCole RB, Chang Y, Li JB, Senaratne TN, Williams BR, et al. 2012. Versatile design and synthesis platform for visualizing genomes with Oligopaint FISH probes. Proc Natl Acad Sci 109: 21301–21306. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Beliveau BJ, Boettiger AN, Avendaño MS, Jungmann R, McCole RB, Joyce EF, Kim-Kiselak C, Bantignies F, Fonseka CY, Erceg J, et al. 2015. Single-molecule super-resolution imaging of chromosomes and in situ haplotype visualization using Oligopaint FISH probes. Nat Commun 6: 7147. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Berthold MR, Cebron N, Dill F, Gabriel TR, Kötter T, Meinl T, Ohl P, Sieb C, Thiel K, Wiswedel B. 2008. KNIME: The Konstanz information miner In Data analysis, machine learning and applications, studies in classification, data analysis, and knowledge organization, pp. 319–326. Springer, Berlin. [Google Scholar]
  6. Betzig E, Patterson GH, Sougrat R, Lindwasser OW, Olenych S, Bonifacino JS, Davidson MW, Lippincott-Schwartz J, Hess HF. 2006. Imaging intracellular fluorescent proteins at nanometer resolution. Science 313: 1642–1645. [DOI] [PubMed] [Google Scholar]
  7. Bonev B, Cavalli G. 2016. Organization and function of the 3D genome. Nat Rev Genet 17: 661–678. [DOI] [PubMed] [Google Scholar]
  8. Breiman L 2001. Random forests. Mach Learn 45: 5–32. [Google Scholar]
  9. Bright DS, Steel EB. 1987. Two-dimensional top hat filter for extracting spots and spheres from digital images. J Microsc 146: 191–200. [Google Scholar]
  10. Burman B, Zhang ZZ, Pegoraro G, Lieb JD, Misteli T. 2015. Histone modifications predispose genome regions to breakage and translocation. Genes Dev 29: 1393–1402. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Cavalli G, Misteli T. 2013. Functional implications of genome topology. Nat Struct Mol Biol 20: 290–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Chen KH, Boettiger AN, Moffitt JR, Wang S, Zhuang X. 2015. RNA imaging. Spatially resolved, highly multiplexed RNA profiling in single cells. Science 348: aaa6090. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Dice LR. 1945. Measures of the amount of ecologic association between species. Ecology 26: 297–302. [Google Scholar]
  14. Dietz C, Berthold MR. 2016. KNIME for open-source bioimage analysis: A tutorial. Adv Anat Embryol Cell Biol 219: 179–197. [DOI] [PubMed] [Google Scholar]
  15. Finn E, Pegoraro G, Brandao HB, Valton A-L, Oomen ME, Dekker J, Mirny L, Misteli T. 2017. Heterogeneity and intrinsic variation in spatial genome organization. bioRxiv doi: 10.1101/171801 (accessed August 28, 2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Flavahan WA, Drier Y, Liau BB, Gillespie SM, Venteicher AS, Stemmer-Rachamimov AO, Suvà ML, Bernstein BE. 2016. Insulator dysfunction and oncogene activation in IDH mutant gliomas. Nature 529: 110–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Franke M, Ibrahim DM, Andrey G, Schwarzer W, Heinrich V, Schöpflin R, Kraft K, Kempfer R, Jerković I, Chan W-L, et al. 2016. Formation of new chromatin domains determines pathogenicity of genomic duplications. Nature 538: 265–269. [DOI] [PubMed] [Google Scholar]
  18. He K, Zhang X, Ren S, Sun J. 2016. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 770–778. IEEE, Piscataway, NJ. [Google Scholar]
  19. Ho TK. 1998. The random subspace method for constructing decision forests. IEEE Trans Pattern Anal Mach Intell 20: 832–844. [Google Scholar]
  20. Huang Z, Pan Z, Lei B. 2017. Transfer learning with deep convolutional neural network for SAR target classification with limited labeled data. Remot Sens 9: 907. [Google Scholar]
  21. Ioffe S, Szegedy C. 2015. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In International Conference on Machine Learning, pp. 448–456. [Google Scholar]
  22. Jegou S, Drozdzal M, Vazquez D, Romero A, Bengio Y. 2017. The one hundred layers tiramisu: Fully convolutional Dense-Nets for semantic segmentation. In 2017 IEEE Conference on Computer Vision and Pattern Recognition WorkshopsCVPRW) 10.1109/cvprw.2017.156. [DOI] [Google Scholar]
  23. Joyce EF, Williams BR, Xie T, Wu C-T. 2012. Identification of genes that promote or antagonize somatic homolog pairing using a high-throughput FISH–based screen. PLoS Genet 8: e1002667. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kingma DP, Ba J. 2014. Adam: A method for stochastic optimization. arXiv [csLG]. http://arxiv.org/abs/1412.6980. [Google Scholar]
  25. Krizhevsky A, Sutskever I, Hinton GE. 2017. ImageNet classification with deep convolutional neural networks. Commun ACM 60: 84–90. [Google Scholar]
  26. Larson DR, Zenklusen D, Wu B, Chao JA, Singer RH. 2011. Real-time observation of transcription initiation and elongation on an endogenous yeast gene. Science 332: 475–478. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Liu S, Mlodzianoski MJ, Hu Z, Ren Y, McElmurry K, Suter DM, Huang F. 2017. sCMOS noise-correction algorithm for microscopy images. Nat Methods 14: 760–761. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Lupiáñez DG, Kraft K, Heinrich V, Krawitz P, Brancati F, Klopocki E, Horn D, Kayserili H, Opitz JM, Laxova R, et al. 2015. Disruptions of topological chromatin domains cause pathogenic rewiring of gene-enhancer interactions. Cell 161: 1012–1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Moffitt JR, Hao J, Wang G, Chen KH, Babcock HP, Zhuang X. 2016. High-throughput single-cell gene-expression profiling with multiplexed error-robust fluorescence in situ hybridization. Proc Natl Acad Sci 113: 11046–11051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Olivo J-C. 1996. Automatic detection of spots in biological images by a wavelet-based selective filtering technique. In Proceedings of 3rd IEEE International Conference on Image Processing, pp. I:311–I:314. IEEE, Piscataway, NJ. [Google Scholar]
  31. Olivo-Marin J-C. 2002. Extraction of spots in biological images using multiscale products. Pattern Recognit 35: 1989–1996. [Google Scholar]
  32. Otsu N 1979. A threshold selection method from gray-level histograms. IEEE Trans Syst Man Cybern 9: 62–66. [Google Scholar]
  33. Parthasarathy R 2012. Rapid, accurate particle tracking by calculation of radial symmetry centers. Nat Methods 9: 724–726. [DOI] [PubMed] [Google Scholar]
  34. Pegoraro G, Misteli T. 2017. High-throughput imaging for the discovery of cellular mechanisms of disease. Trends Genet 33: 604–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Ronneberger O, Fischer P, Brox T. 2015. U-Net: Convolutional networks for biomedical image segmentation. In Lecture notes in computer science, pp. 234–241. [Google Scholar]
  36. Sezgin M 2004. Survey over image thresholding techniques and quantitative performance evaluation. J Electron Imaging. http://electronicimaging.spiedigitallibrary.org/article.aspx?articleid=1098183. [Google Scholar]
  37. Shachar S, Voss TC, Pegoraro G, Sciascia N, Misteli T. 2015. Identification of gene positioning factors using high-through put imaging mapping. Cell 162: 911–923. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Shelhamer E, Long J, Darrell T. 2017. Fully convolutional networks for semantic segmentation. IEEE Trans Pattern Anal Mach Intell 39: 640–651. [DOI] [PubMed] [Google Scholar]
  39. Smith CS, Joseph N, Rieger B, Lidke KA. 2010. Fast, singlemolecule localization that achieves theoretically minimum uncertainty. Nat Methods 7: 373–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Solovei I, Cavallo A, Schermelleh L, Jaunin F, Scasselati C, Cmarko D, Cremer C, Fakan S, Cremer T. 2002. Spatial preservation of nuclear chromatin architecture during three-dimensional fluorescence in situ hybridization (3D-FISH). Exp Cell Res 276: 10–23. [DOI] [PubMed] [Google Scholar]
  41. Sørensen T 1948. [A method of establishing groups of equal amplitude in plant sociology based on similarity of species and its application to analyses of the vegetation on Danish commons]. Biol Skr 5: 1–34. [Google Scholar]
  42. Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. 2014. Dropout: A simple way to prevent neural networks from overfitting. J Mach Learn Res 15: 1929–1958. [Google Scholar]
  43. Szegedy C, Vanhoucke V, Ioffe S, Shlens J, Wojna Z. 2016. Rethinking the inception architecture for computer vision. In 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 10.1109/cvpr.2016.308. [DOI] [Google Scholar]
  44. Vincent L, Soille P. 1991. Watersheds in digital spaces: An efficient algorithm based on immersion simulations. IEEE Trans Pattern Anal Mach Intell 13: 583–598. [Google Scholar]
  45. Wang S, Su J-H, Beliveau BJ, Bintu B, Moffitt JR, Wu C-T, Zhuang X. 2016. Spatial organization of chromatin domains and compartments in single chromosomes. Science 353: 598–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Zijdenbos AP, Dawant BM, Margolin RA, Palmer AC. 1994. Morphometric analysis of white matter lesions in MR images: Method and validation. IEEE Trans Med Imaging 13: 716–724. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Information
NIHMS999233-supplement-Supplemental_Information.pdf (281.9KB, pdf)

RESOURCES