Accounting for Label Uncertainty in Machine Learning for Detection of Acute Respiratory Distress Syndrome

Abstract

When training a machine learning algorithm for a supervised-learning task in some clinical applications, uncertainty in the correct labels of some patients may adversely affect the performance of the algorithm. For example, even clinical experts may have less confidence when assigning a medical diagnosis to some patients because of ambiguity in the patient’s case or imperfect reliability of the diagnostic criteria. As a result, some cases used in algorithm training may be mis-labeled, adversely affecting the algorithm’s performance. However, experts may also be able to quantify their diagnostic uncertainty in these cases. We present a robust method implemented with Support Vector Machines to account for such clinical diagnostic uncertainty when training an algorithm to detect patients who develop the acute respiratory distress syndrome (ARDS). ARDS is a syndrome of the critically ill that is diagnosed using clinical criteria known to be imperfect. We represent uncertainty in the diagnosis of ARDS as a graded weight of confidence associated with each training label. We also performed a novel time-series sampling method to address the problem of inter-correlation among the longitudinal clinical data from each patient used in model training to limit overfitting. Preliminary results show that we can achieve meaningful improvement in the performance of algorithm to detect patients with ARDS on a hold-out sample, when we compare our method that accounts for the uncertainty of training labels with a conventional SVM algorithm.

I. Introduction

The Acute Respiratory Distress Syndrome (ARDS) is a critical illness syndrome affecting 200,000 patients in United States each year [1]. While the mortality rate of patients with ARDS is 30%, multiple evidence-based management strategies can be provided to patients with ARDS to improve their outcomes [2]. However, recent evidence suggests that patients with ARDS are not recognized when they develop this syndrome, and consequently, do not receive the evidence-based therapies proven to reduce mortality [3]. The inability of healthcare providers to process the massive streams of clinical data generated while caring for these patients has been specifically cited as a potential reason for poor ARDS recognition [4]. Algorithms that analyze electronic health record (EHR) data and alert providers when patients develop signs of ARDS have been proposed as a potential way to improve early ARDS detection [5, 6].

At present, simple rule-based electronic algorithms have been described that analyze EHR data to screen patients for ARDS [7, 8]. Current systems search the text of radiology reports for language consistent with ARDS to identify patients. For these systems to be successful, however, chest imaging must be obtained at the time when ARDS develops and a radiologist must accurately interpret the radiology image in a timely manner using language that could be interpreted as consistent with ARDS. These dependencies are problematic for successful implementation in clinical practice. Systems that rely solely on routinely collected clinical data to identify at risk patients could alert clinicians to those patients who warrant further evaluation, specifically triggering chest imaging for timely ARDS diagnosis.

An additional challenge in the development of an ARDS detection algorithm is the creation of reference patient cohorts to train the algorithm. ARDS is a clinical diagnosis that requires a nuanced interpretation of each patient’s clinical data by clinical experts. Some patients are difficult to classify with available clinical data even for highly trained experts [9]. Previous research has shown how errors in the labeling of ARDS and non-ARDS patients can substantially degrade clinical study results [10]. One potential solution is to allow clinical experts to classify patients as equivocal when a diagnosis of ARDS is uncertain. Using this approach, researchers have previously shown that known ARDS risk factors have stronger associations with ARDS development when equivocal patients were excluded [11].

When training an algorithm to detect ARDS, rather than excluding patients with diagnostic uncertainty, an alternative approach is to use this additional infonnation about diagnostic certainty during training, which could lead to more efficiently learning and better generalize to new patient cases. Learning with uncertainty is a recent machine learning paradigm that may be well suited for the task of training an ARDS detection algorithm [12]. The standard machine-learning classification task is to learn a function f(x) : X → Y, which maps input training data x ∈ X to class y ∈ Y, where X represents a feature space of each patient’s covariates and Y is the classification label. The model is trained on well-defined input data of labeled training examples. However, in certain clinical applications, there may be uncertainty in the training labels themselves that could adversely affect model training. In the example of ARDS, there may be challenging cases where the physician has difficulty determining a patient’s diagnosis due to clinical ambiguity. As a result, this uncertainty and subsequent mislabeling of training data could adversely affect model training.

Varying methods have been proposed to address the issue of training with label uncertainty. Frenay and Verleysen considered uncertainty as a stochastic process of noise in the label and proposed a statistical taxonomy of definitions for various label noise typically presented in classification with machine learning [13]. Natarajan et al addressed the challenges of learning with noisy labels and developed an algorithm for risk minimization under certain conditions using an unbiased estimator and logistic regression to account for labels independently corrupted by random noise [14]. Duan and Wu proposed the concept of flipping probability used to model inaccurate labels in real-world applications [15] and suggested several methods to optimize for noise tolerance. Vembu and Zilles developed an iterative learning scheme to address label uncertainty, which they recognize as disagreement among annotators in generation of classification labels [16].

Although these methods propose novel solutions to address label uncertainty, many of them are theoretical and were not tested on real-world data (primarily benchmarked on artificially generated data and referenced datasets) or simply consider uncertainty in the label as random noise. Such an approach may not be well suited for biomedical or clinical applications where a clinical expert might also be able to provide a level of confidence in a patient’s label.In the current study, when clinical experts reviewed each patients’ clinical data to determine whether they developed ARDS, they also provide their level of confidence in the diagnosis. This uncertainty rating was represented as the confidence of the label’s annotation. Using a support vector machines learning model, the confidence weighting of the label is used as additional information in the training process. This approach is a form of instance-weighted SVM, although instead of learning weights based on characteristics of the data [17], or weights based on the class label [18], we use a clinical expert’s confidence in the diagnosis weights during SVM training. This approach incorporates a more realistic representation of uncertainty in real-world applications, avoids discarding uncertain data, and balances the influence of such uncertain inputs in the learning algorithm.

The current study also addresses the problem of using highly correlated longitudinal clinical data in machine-learning model training, which is often ignored in applications of machine learning in biomedical domains. With the increased use of electronic health records, clinical data are often available in a longitudinal format, where specific metrics of health (e.g. vital signs, or laboratory values) are measured intermittently over time. Analysis of such data requires additional consideration of the stochastic dependency and time-series nature of these data [19], and they should not be considered independent and identically distributed (i.i.d.) [20], as the data is obviously not. By ignoring the inter-dependency of the time-series data and the i.i.d assumption, training may result in a biased model that overfits to the available data and yield unrealistically large values of specificity, sensitivity, and AUROC [21, 22]. Methods exist to deal with correlated data in traditional machine learning, such as using a Markov switching process model [23], or partially linear regression model [24] for longitudinal time-series data analysis or a correlation-based fast filter method [25] for choosing among highly correlated features in the model selection process. Beyond the scope of generalized machine learning problems, additional methods to analyze time series properties exist in many domain-specific applications, such as stock market prediction with support vector machine and case-based reasoning [26], or time-delay neural networks [27] and dynamic time warping [28] for speech recognition.

Several techniques, such as dynamic sampling within Markov chain Monte Carlo methods [29] and Bayesian Changepoint Detection [30], are established for analyzing the dependency structure of multivariate time series data. However, methods addressing stochastic dependency are largely underdeveloped for applications on longitudinal clinical data. We address the problem by viewing patients’ time-series data as a mixing process and consider the data structure as a stationary process with exponentially weakening dependency, and sample instances in a strategic manner to minimize intercorrelation. This approach provides a way to measure the decay in correlation [31] among data on an individual patient over time, and informs a novel sampling strategy to minimize the correlation among data sampled from the same patient for model training.

II. Methods

A. Data Generation

The patient cohort included consecutive adult patients hospitalized in January of 2016 with moderate hypoxia, defined as requiring more than 3 L of supplemental oxygen by nasal cannula for at least 2 hours. The cohort was enriched with additional patients who developed acute hypoxic respiratory failure (PaO₂/FiO₂ ratio of < 300 mm Hg while receiving invasive mechanical ventilation) in February and March of 2016 who are higher risk for developing ARDS. In total, 401 patients were used to develop the ARDS detection algorithm.

A group of expert clinicians reviewed all patients for the development of ARDS based on the Berlin definition [32]. As ARDS is a clinical diagnosis without a simple gold standard, we were unable to benchmark expert performance. However, because the inter-rater reliability of ARDS diagnosis is known to be only moderate in patients with acute hypoxic respiratory failure [33], these patients were reviewed independently by 3 experts, and their ratings were averaged. In addition to determining whether the diagnosis was present (yes or no) and record the time of ARDS onset among positive cases, the experts were also asked to provide their confidence level in the diagnosis label (high, moderate, low, equivocal). This 4-point confidence scale was carefully tested on the experts prior to use in this study, and felt to reasonably capture the range of uncertain that they might have when reviewing patient cases. Their diagnosis label and confidence level could then be converted to a 1-8 scale, as illustrated in Figure 1, where 1 = no ARDS with high confidence, 8 = ARDS with high confidence.

Fig. 1:

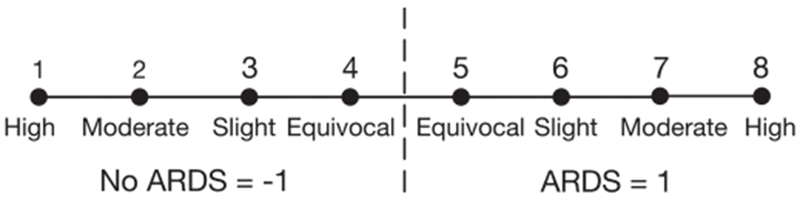
Accounting for uncertainty in a classification label using a clinical expert’s confidence in the diagnosis of ARDS. Critical care trained clinicians were asked to independently review patients’ EHR data and determine if any individuals in the cohort had ARDS, while also rating their confidence of the diagnosis using the following scale: equivocal, slight, moderate, or high.

In patients who developed ARDS, data collected before the time of onset were labeled as no ARDS, while data collected after the time of onset were labeled as ARDS. In total, 48 of the patients in the cohort were diagnosed with ARDS with a confidence of 5 or higher after expert review.

Time-stamped vital signs and laboratory values were extracted from each patient’s Electronic Health Record (EHR) from the first six days of hospitalization and included as clinical features (covariates) to train the ARDS algorithm. Only routinely acquired vital signs and laboratory values with potential for association with ARDS were included, based on guidance from clinical experts. Further details of the clinical variables in the model could be made available upon request. This approach minimized the total number of features in the model to 24 variables commonly used in clinical practice and statistical feature selection techniques were not utilized prior to model training. Patients were observed every 2 hours with previous data carried forward until a new value was recorded. If clinical data was missing on a patient because the vital sign or laboratory tests was not performed, it was imputed as a normal value. This is standard approach when developing clinical predictions models and assumes data is not collected because the treating clinician had a low suspicion that it would be abnormal [34, 35].

B. Sampling from Longitudinal Data and Inter-Correlation

Longitudinal patient data with repeated measurements over time have strong inter-dependency between each instance for a given patient. Ignoring these dependencies during training may lead to a biased estimator and a flawed learning model.

Inter-dependency among longitudinal data has been previously conceptualized as a system under mixing conditions [23]. For a given stochastic process, mixing indicates asymptotically independency implying that for a stationary process X, the dependency between X(t₁) and X(t₂) becomes negligible as |t₁ − t₂| increases towards infinity [36]. This mixing structure, while assuming that the dependency weakens in time, often exponentially, allows local dependency among the data points, and as such matches the reality of the majority of time-series processed in medicine as well as many other applications [37].

In order to address the interdependency of the data, we assumed that each patient’s time-series data used to develop the ARDS detection algorithm was a mixing stochastic process and we sampled data according to the quantitative assessment of the correlation decay among the data points. This approach limits the degree of inter-correlation on the data points sampled within the same patient and allows a more realistic assessment of model accuracy and reliability.

To implement this sampling strategy, we first calculated pairwise correlation distance matrices to represent dependency over the span of each patient’s time-series data. Given an m-by-n matrix for each patient’s data, where m is the number of times the patient was observed, and each observation is treated as 1-by-n row vectors, the correlation distance between vectors X_a and X_b for a single pair of observations is defined as:

$$d_{ab}=1-\frac{(X_a-{\tilde{X}}_a){(X_b-{\tilde{X}}_b)}^{\prime }}{\sqrt{(X_a-{\tilde{X}}_a){(X_a-{\tilde{X}}_a)}^{\prime }}\sqrt{(X_b-{\tilde{X}}_b){(X_b-{\tilde{X}}_b)}^{\prime }}}$$

where:

$${\tilde{X}}_a=\frac{1}{n}\sum _j{X}_{aj}\text{and}{\tilde{X}}_b=\frac{1}{n}\sum _j{X}_{bj}$$

Using this correlation distance formula, an m-by-m correlation distance matrix can be derived for all observations on the patient, taken pairwise.

The sampling procedure begins by examining the correlation distances between X_t and 〈X_t〉 was generated, where X_t corresponds to an instance at the start of a patient’s time-series data and 〈X_t〉 is the span of all subsequent time-points. Then a sampling threshold η is set, which represents the point in which the inter-dependency between data becomes more limited. We chose the threshold value of η to be $\frac{1}{\sqrt{2}}$, based on literature that suggests values of approximately $\frac{1}{\sqrt{2}}$ as an estimate of the width of a correlation-type function [38]. We also explored other values of η to understand their effect on the model building process. Figure 2 shows the effect of different sampling thresholds on model performance, including the difference in model accuracy in the training to testing set and AUROC of the testing set. This empirical analysis confirmed that optimal results are achieved when the sampling threshold is approximately 0.7 and supports the literature suggested value of $\frac{1}{\sqrt{2}}$.

Fig. 2:

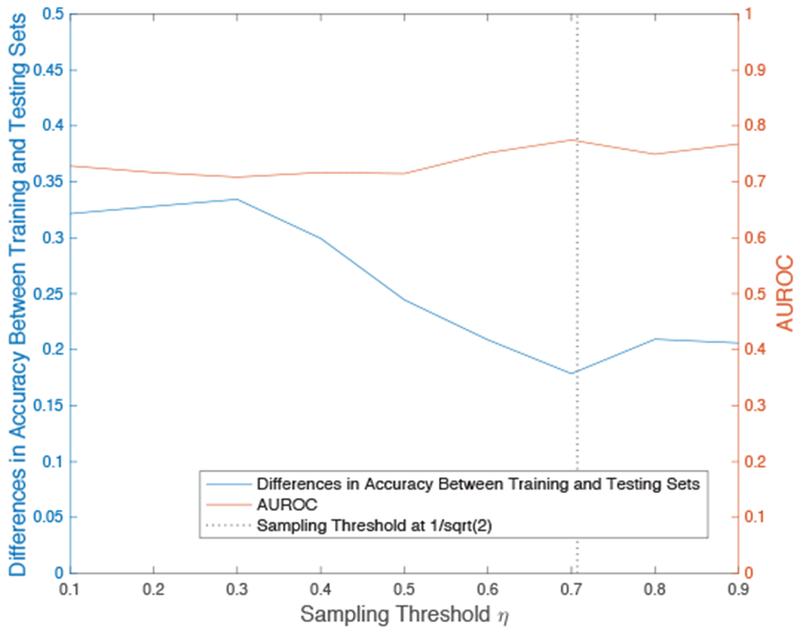
Effects of different sampling thresholds on prediction generalizability with SVM. With our sampling strategy, SVM performs very well on the training data at any threshold. We indicate the loss in training accuracy when the same model makes a prediction on a hold-out testing set to properly assess the effects of changing the sampling threshold and empirically determine the value for optimal results.

During the data sampling process for each patient, X_t is selected as the start of a patient’s time-series data. A pairwise correlation distance matrix is then calculated between X_t and 〈X_t〉, and a data point X_t1 is sampled as the first instance with a correlation distance of below η from 〈X_t〉. This selected point X_t1 and subsequent time points beyond X_t1, 〈X_t1〉, are used to re-calculate a new pairwise correlation distance matrix. A data point X_t2 is then selected in a similar manner as X_t1 from data points in 〈X_t1〉 with a correlation distance below the threshold of η. The sampling method is repeated until no further instances of 〈X_tn〉 are below the threshold from X_tn.

For this specific dataset, we did not utilize the sampling strategy described above for patient instances with the classification label of ARDS = 1. After inspection of the data, we observed the correlation decay to behave differently according to the label, with the data remained highly correlated over time when ARDS = 1 while correlation decay occurring when ARDS = −1. Therefore, this sampling approach was only performed on the data when ARDS = −1 while all instances were sampled when ARDS = 1. This approach effectively samples all positive examples while undersampling negative examples, which was also necessary given the significant class imbalance of the two labels [39]. The sampling strategy is shown in pseudocode as Algorithm 1 and the average decay of correlation from all patients is shown in Figure 5 with error bars representing standard error of the mean.

Fig. 5:

Average decay of correlation from all patients. Error bars represent standard error of the mean and each point represents correlation in relation to time (hours) from the initial observation sampled on each patient.

C. Formulation of SVM with Label Uncertainty

We implement the following formulation of Support Vector Machine [40] to account for label uncertainty in the classification model in the following manner:

$$\underset{w,\xi }{{\displaystyle \min }}\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{z}_i{\xi }_i$$

subject to:

$$\{\begin{array}{cc}{y}_i(w^T{x}_i+b)\ge 1-{\xi }_i,& i=1,\mathrm{...},N\\ {\xi }_i\ge 0& \end{array}$$ (1)

Algorithm 1:

Pseudocode for our algorithm to sample time-series data and reduce inter-dependency.

	Input : All available time-series data 〈Xt〉 from each patient.
1	for each patient do
2	partition data into separate bins according to the classification label;
3	if size of either bins is ≤ 4 then sample all available data;
4
5	else
6	1) select Xt at the start of the time-series data and sample this instance;
7	2) calculate the pairwise correlation distance from Xt to 〈Xt〉;
8	3) sample the first row in 〈Xt〉 with a correlation distance < η and set as the new Xt;
9	repeat
10	1) set 〈Xt〉 as all points subsequent to Xt;
11	2) calculate the pairwise correlation distance matrix from Xt to 〈Xt〉;
12	3) sample the first row where the correlation distance is < η and set as the new Xt;
13	until pairwise distance of Xt to 〈Xt〉 > η;
14	end
15	end
	Output: Partial data {Xt,Xt1,Xt2, … ,Xtn} with reduced inter-correlation from each patient.

where:

$$z_i=(|l_i-\alpha |-\beta )\ast \gamma +\delta$$

This formulation incorporates the slack variable ξ_i to permit some misclassification and also includes the penalty parameter C to establish soft-margin decision boundaries because ARDS and non-ARDS examples are not linearly separable. In this implementation, support vectors that are based on patients’ data with high label confidence are given more weight and influence in the SVM decision boundary. Uncertainty in the label (l_i), as shown in Figure 1, is incorporated within (z_i) to directly influence the box constraint (C). The formula for z_i combines two linear transformations for uncertainty in the label annotation (l_i) and generate a scalable weight to that specific observation. In this application, we set α = 4.5, β = 3.0, γ = 20, and δ = 90, which scales l_i, with a range of 1-8, into the weighting z_i, with a range between 40-100 in increments of 20. As a result, labels with high confidence (eg. l_i = 1 or 8) receive the weight z_i = 100, while equivocal labels (eg. l_i = 4 or 5) receive the weight z_i = 40. z_i is then normalized to 1. This formula for z_i adjusts sample weighting based on l_i and rescales the C parameter as C_i for each observation in a patient’s data structure so that the classifier puts more emphasis on points with high confidence.

To ensure that our proposed sampling strategy and threshold still maintains for SVM with label uncertainty, we repeat the previous analysis to show the effect of different sampling thresholds on prediction generalizability. Figure 3 confirms that optimal results are achieved when the sampling threshold is approximately 0.7, which supports the previous analysis and the literature suggested value of $\frac{1}{\sqrt{2}}$.

Fig. 3:

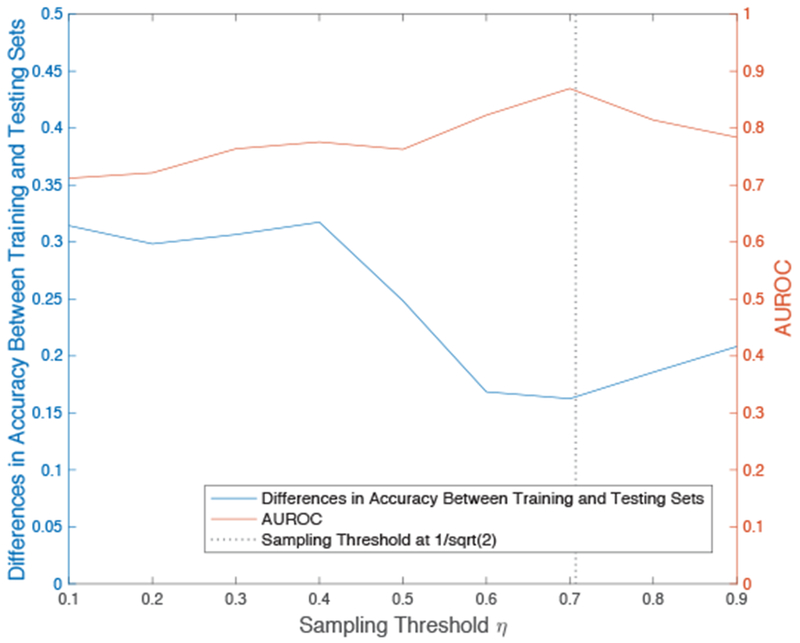
Effects of different sampling thresholds on prediction generalizability with SVM and label uncertainty. We confirm that the sampling strategy and threshold effects observed in Figure 2 is maintained when the SVM model is formulated to account for label uncertainty.

D. Model Building, Cross-Validation and Model Testing

In this study, the primary learning algorithms we compare are linear SVM with and without label uncertainty. Prior to building these models, the data was first normalized to prevent features with large dynamic ranges from dominating the separating hyperplane. Then the training data was sampled using the proposed sampling method described previously to minimize correlation between data points on the same patient. Prior to sampling, the training set contained 13,722 total instances, 736 of which were positive. After sampling, there were 1,893 total instances, 736 of which were positive.

5-fold cross validation was performed on the training data to find the optimal value of the hyper-parameter C using grid search [41] over C ∈ {0.001,0.01,0.1,1,10,100,1000}. We then re-trained the model on the entire training set using this optimal C parameter. This updated model was then used to classify patients in the hold-out dataset using all their data (i.e. no sampling was performed on the holdout data). The model predictions for each patient in the holdout sample, i.e. ARDS = 1 or −1, are then compared against the label assigned by the majority of experts reviewing the patient. We also compare the performance of our proposed SVM method with Logistic Regression and Random Forest (using the same subsampled training/testing bins and 5-fold cross validation partitions) to determine if the achieved results are equivalent or superior to other state-of-the-art methods.

A simplified protocol of this analysis, including data pre-processing, sampling from the training data to limit inter-correlation, hyper-parameter optimization with 5-fold cross-validation, and hold-out testing is shown in the flowchart of Figure 4.

Fig. 4:

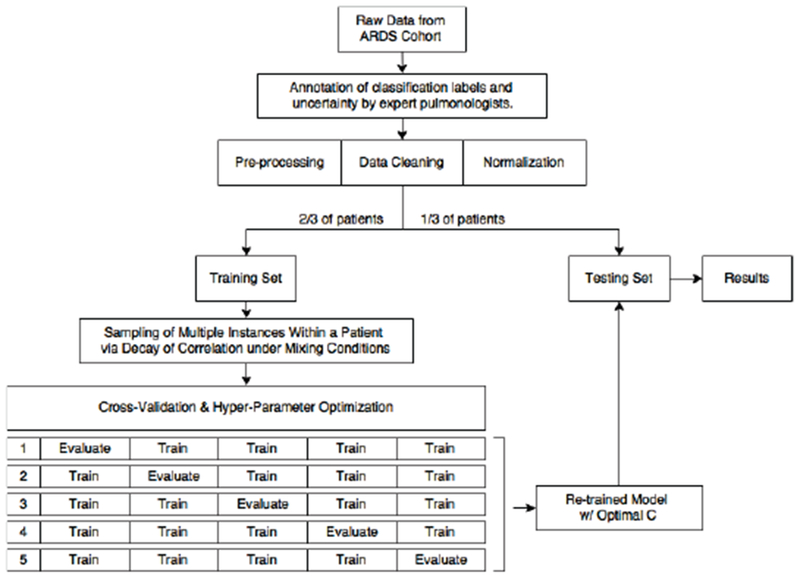
Flowchart of this study’s protocol with 5-fold cross-validation and hyper-parameter optimization using grid search. All samples from the same patient are kept exclusively in either the training or testing set. Hyper-parameter optimization was implemented for separately each model (with and without label uncertainty weight) to give an accurate assessment of performance.

III. Results

A total of 401 patient cases were available from the study cohort. Within this dataset, 48 were positive for ARDS and the remaining 353 were negative. Two-thirds of the patients were used in the model training process while the remaining one-third were kept as a hold-out set for testing. All samples from the same patients are kept exclusively in either the training or testing set (not both) to avoid bias in the data.

The average correlation decay for each patient’s data is shown in Figure 5. On average, the correlation between X_t and 〈X_t〉 drops below η at a distance in time of around 22 hours. Figure 6 shows the decay of correlation to be different when the data was analyzed separately according to the classification label: decay of correlation is observed when ARDS = −1 but not observed when ARDS = 1. Therefore, the sampling under η approach was performed on the data when ARDS = −1, which reduce the number of negative examples for model training. Due to the lower number examples, and lack of correlation decay when ARDS = 1, sampling was not performed as it would have further exacerbated the class imbalance.

Fig. 6:

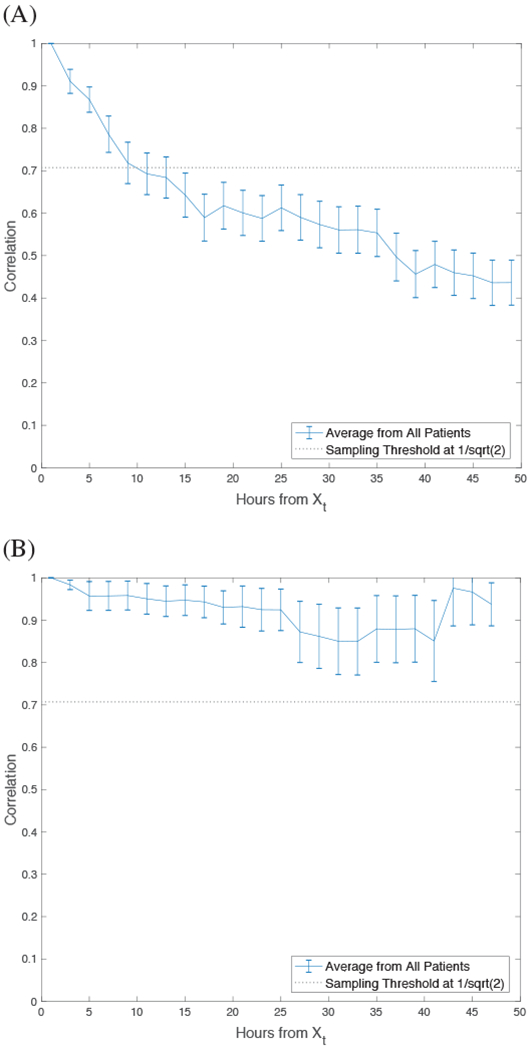
Average decay of correlation from all patients during (A) negative diagnosis of ARDS and (B) positive diagnosis of ARDS. Error bars represent standard error of the mean and each point represents correlation in relation to time (hours) from the initial observation sampled on each patient.

When the SVM was trained to account for uncertainty in the label, we observed over 10% improvement of AUROC (0.8548 versus 0.7542) compared to the conventional SVM learning algorithm (Figure 7) when judged in the holdout sample. When the algorithms were benchmarked at a sensitivity of 95% and 90% (to ensure few ARDS cases are missed), the SVM model that accounted for label uncertainty also had improved specificity and outperforms the standard model (Table 1). These sensitivity levels were set to high levels because it is important clinically for a model to have a high sensitivity and not miss cases of ARDS.

Fig. 7:

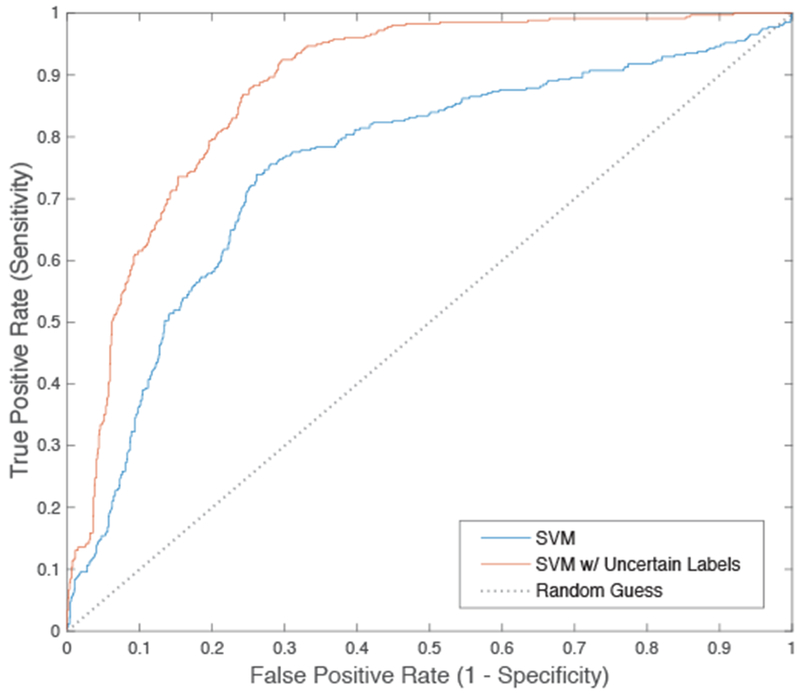
ROC curve comparing SVM with and without label uncertainty. Performance metrics are reported in Table 1.

TABLE I:

Performance of Logistic Regression, Random Forrest, SVM, SVM with a class-weighted cost function, and SVM with label uncertainty.

	Sampling Based on the Proposed Correlation Decay Method				Random Sampling for Balanced (2:1) Training Data		No Sampling
	Accuracy	AUROC	Specificity at 95% Sensitivity	Specificity at 90% Sensitivity	Accuracy	AUROC	Accuracy	AUROC
Logistic Regression	0.7263	0.7265	0.3007	0.4267	0.6982	0.6979	0.6621	0.6454
Random Forest	0.7434	0.7488	0.3392	0.4751	0.7111	0.7254	0.6873	0.6903
SVM	0.7492	0.7542	0.3797	0.5114	0.7253	0.7361	0.6920	0.7152
SVM w/ Class-Weighted Cost Function	0.7804	0.8113	0.4571	0.5918	0.7478	0.7703	0.7094	0.7122
SVM w/ Uncertain Labels	0.8157	0.8548	0.5285	0.6450	0.7698	0.7989	0.7188	0.7431

We benchmarked our proposed SVM method utilizing uncertainty in the label to SVM with a misclassification cost function proportional to the weight of imbalance in the datasets and other standard classification models, such as Random Forest and Logistic Regression, in Table 1. We also compared our sampling strategy to an alternative method that utilizes random sampling on negative examples to yield a 2:1 negative to positive ratio from each patient to provide a more balanced dataset. In addition, we also examined performance without sampling (using all available data).

IV. Discussion

We present a robust machine learning algorithm to detect Acute Respiratory Distress Syndrome among hospitalized patients using routinely collected electronic health record data. We report an increase of 10% in AUROC in a hold-out data set when label uncertainty is incorporated in the learning process as a weight on classification penalty, when compared to a conventional SVM learning model.

Our proposed SVM model was trained by incorporating a clinical expert’s uncertainty in each patient’s classification label as a constraining weight of confidence on the SVM’s box constraint. Rather than treating label uncertainty as simple stochastic noise, this approach leverages information about the degree of uncertainty of each label, as provided by clinical experts, to improve the efficiency of model training. Our implementation of label weighting (z_i) directly influences the C parameter and rescales the cost of misclassification according to uncertainty associated with each label (l_i). Support vectors that are based on the data from patients with high label confidence are given more influence in the SVM decision boundary while instances with more uncertainty are assigned less weight when determining the SVM hyperplane. In future works, alternative mappings between the label uncertainty (l_i) provided by clinical experts and label weighting (z_i) used to find the SVM decision boundary should also be explored.

In addition, we performed a novel time-series sampling method, guided by the theory of mixing in stochastic processes, to limit the amount of correlation among data points on the same patient over time. Due to the time-series structure of a patient’s longitudinal health data, each instance is not independent from another. We explored whether the data could be represented under mixing conditions and implemented a novel sampling strategy for minimizing inter-correlation among data points in the training data. For the data to be represented under mixing conditions, the correlation between data on the same patient should decay over time such that C_F,G(n) → 0 as n → ∞. A plot of the correlation function of the data in Figure 6 supported this assumption overall, but not for the data with a classification label of ARDS = 1.

It may not be appropriate to assume all data types can be represented under mixing conditions, therefore, plotting the correlation function of the data is essential prior to utilizing the sampling algorithm. When patients were diagnosed with ARDS, we found their data to have very high inter-correlation with little observable decay indicating a strong mixing process. Therefore, the proposed sampling method would have been unsuccessful in reducing inter-correlation and would yield very little data instances available for training. This finding made sense when interpreted from a clinical point of view. When a patient is admitted to the emergency room for pulmonary injury (eg. sepsis) and has not yet reached the critical stage of ARDS, their condition rapidly changes as a result of clinical intervention or decline of health, resulting in less stability and inter-correlation in the recorded data. If the patient develops ARDS, less rapid change in the data would be observed since ARDS is recognized as the final pathway of pulmonary damage [42].

Since there were significantly more negative than positive examples, we decided against using the sampling strategy when ARDS = 1, which ensured a more balanced number of positive and negative examples in the training data. As minimal correlation decay was observed among the data when ARDS = 1, implementing the sampling strategy for those data instances would have led to further imbalance among positive and negative examples, and limited the model’s ability to learn a good decision boundary. Our sampling approach utilized a pairwise correlation distance matrix to quantify dependency within the data structure. There are many ways to quantify the measurement of dependency between X_t to 〈X_t〉. Bradley et al provides a comprehensive list of mathematical definitions for dependency coefficients to define these mixing conditions [43] and measure decay of correlations [31]. In the future work, we will perform a more comprehensive examination of the data structure using formalized definitions of mixing, such as quantifying dependency with the α-mixing coefficient.

Our sampling method outperforms using all available data (no sampling) from the EHR by producing a much balanced dataset for training and minimizing dependencies in each patient’s time series data, making it closer to the state of being i.i.d. We also compared our sampling algorithm to randomly sampling on negative examples to yield a 2:1 negative to positive ratio from each patient. This random sampling method also provides a balanced dataset for training, and as a result, we observed an increase in accuracy and AUROC from all algorithms when compared to training without sampling. However, compared to our proposed sampling strategy, random sampling doesn’t achieve as high performance metrics because it does not account for correlation and may be sampling repeated measurements with strong dependencies, and therefore is not as robust as our method.

This study used a linear SVM for the ARDS model. In preliminary work not shown, we found that an SVM with a non-linear kernel (RBF) had less consistent results. Although the SVM with RBF kernel generally outperformed linear SVM on training dataset, it had inferior performance (accuracy and AUROC) on the hold-out set. Even with 5-fold cross-validation and grid-search hyper-parameter optimization (of C and gamma), we found the performance of the SVM with RBF kernel to be lower on the test set, and standard deviation of the results (after multiple random train-test splits) to be 2-3 fold larger than the linear SVM. We speculate that overfitting possibly occurred because of lower sample size and the number of variables used as features for machine learning. Because linear SVM was more robust, we chose to focus on using label uncertainty in the modeling process using only linear SVM.

With more clinical data, it would be worthwhile to investigate whether incorporating both label uncertainty and a non-linear SVM model would lead to improved model performance. The electronic health record may contain additional data that could be added to our model. Evaluating the performance of the training approach that considers label uncertainty in a higher dimensional space would be of value; however, to limit the possibility of overfitting with our current small dataset size, we have focused on using features that are routinely used for clinical evaluation of ARDS in the current study.

In additional future work, we plan to re-formulate the SVM model to account for both label uncertainty and privileged information to improve algorithm training [44]. Learning with privileged information (LUPI) also utilizes information available only in the training stage to help establish decision boundaries. Privileged information, which is information available during training but not when the model is deployed in real-time, may also be frequently available when developing machine-learning algorithms for healthcare applications and could also be relevant for ARDS detection.

We believe our paper makes a significant contribution towards solving traditional classification problems in the context of biomedical and clinical applications. In medicine, there is almost always a degree of uncertainty when assigning a patient to a medical diagnosis. Yet, that diagnosis label may then be used as the classification label or predictive outcome during a machine learning task. Typically, the diagnostic uncertainty associated with the label is not considered during model building. We show how an expert clinicians’ confidence in a diagnosis label can be used as vital information in the model training process. Exploiting the known diagnostic uncertainty within a medical domain is a generalizable approach that could be used in many medical applications. For example, sepsis is a clinical condition where early recognition is import for optimal patient care. However, diagnostic uncertainty is common [45], limiting ability to develop robust algorithms for sepsis detection. Incorporating label uncertainty when training an algorithm for sepsis detection may improve algorithm performance in a manner similar to ARDS.

It would also likely be of value to further develop approaches to incorporate label uncertainty into other machine learning frameworks besides SVM, such as random forest and neural networks. Since uncertainty in medical diagnosis occurs so commonly in clinical practice, accounting for label uncertainty with these learning algorithms may be highly applicable in other healthcare applications.

V. Conclusion

This paper introduces and tests a method of implementing uncertainty in the classification label in machine learning for detection of ARDS. It also describes a novel sampling strategy to reduce inter-correlation among longitudinal clinical data to prevent the creation of a biased model. using these novel approaches, we successfully trained an ARDS classification algorithm with significantly increased performance compared to a standard approach.