Investigating site-level longitudinal effects of population health interventions: Gay-Straight Alliances and school safety

Abstract

There is limited research on evaluating nonrandomized population health interventions. We aimed to introduce a new approach for assessing site-level longitudinal effects of population health interventions (SLEPHI) by innovatively applying multiple group multilevel (MG-ML) modeling to repeated cycles of cross-sectional data collected from different individuals of the same sites at different times, a design commonly employed in public health research. For illustration, we used this SLEPHI method to examine the influence of Gay-Straight Alliances (GSAs) on school-level perceived safety among lesbian, gay, and bisexual (LGB) and heterosexual (HET) adolescents. Individual-level data of perceived school safety came from 1625 LGB students (67.4% female; mean age, 15.7 years) and 37,597 HET students (50.2% female; mean age, 15.4 years) attending Grades 7–12 in 135 schools, which participated in 3 British Columbia Adolescent Health Surveys (BCAHS: 2003, 2008, 2013) in Canada. School-level data of GSA length since established were collected by telephone in 2008 and 2014. Nested MG-ML models suggested that after accounting for secular trend, cohort effects, measurement error, measurement equivalence, and student age, GSA length linearly related to increased school-level perceived safety among LGB students (b = 1.57, SE = 0.21, p < .001, β = 0.32) and also among HET students (β = 0.34 in 2003 & 2013, β = 0.32 in 2008) although statistical differences between years for HET youth were likely due to the large sample size. By conducting MG-ML analysis on repeated cross-sectional surveys, this SLEPHI method accounted for many confounding factors and followed schools for a longer period than most longitudinal designs can follow individuals. Therefore, we drew a stronger conclusion than previous observational research about GSAs and LGB students’ well-being. The SLEPHI method can be widely applied to other repeated cycles of cross-sectional data in public health research.

Highlights

• •We created a new method to evaluate nonrandomized population health interventions.
• •The SLEPHI method can draw causal inferences from repeated cross-sectional data.
• •GSA length is linked to increased school-level safety among LGB and heterosexual students over time.

1. Introduction

There has been a recent move toward “evidence-based public health” to evaluate the effectiveness and efficacy of all types of interventions beyond randomized controlled trials (RCTs) (Victora, Habicht, & Bryce, 2004). It has long been recognized that despite being the gold standard in establishing causal effects of treatments and interventions, RCTs are not always feasible. In practice, many interventions occur at the population or group level in sites such as community centers or schools without systematic planning, in contrast to RCTs in which randomized interventions can occur at the individual or group level. The causal influence of these nonrandomized population interventions is difficult to draw, because differences in the outcome is confounded by background factors, including secular trends (time-dependent changes in the outcome), cohort effects (cohort-dependent changes in the outcome), measurement errors, and measurement equivalence. Yet another challenge in conducting RCTs is to follow the same individuals over a long time, which is not always possible because of the resources longitudinal research requires.

This study introduces a new approach to evaluate nonrandomized population interventions, namely the “Site-level Longitudinal Effects of Population Health Interventions” (SLEPHI) method. Specifically, we innovatively applied multiple group multilevel (MG-ML) modeling (Asparouhov & Muthén, 2012a) to repeated cycles of cross-sectional school-based survey data, a sampling approach commonly used in public health research. The MG-ML analysis can estimate site-level intervention effects while adjusting for secular trends, cohort effects, measurement errors, and measurement equivalence. In addition, it is more feasible and cost-effective to follow the same sites over a long period of time and collect cross-sectional data from different individuals than to follow the same individuals for the same length of time in longitudinal designs. This SLEPHI method attempts to identify linear or nonlinear changes observed within sites initiating the intervention at varying times, compared to linear or nonlinear changes observed over the same repeated times in sites without the intervention. The research questions that this new application of MG-ML analysis aims to answer are: What is the relation between length of time since initiation of intervention and site-level health outcomes? And how does this relation vary by cycles of data collection in different individuals nested within the same sites?

1.1. Design of the SLEPHI method

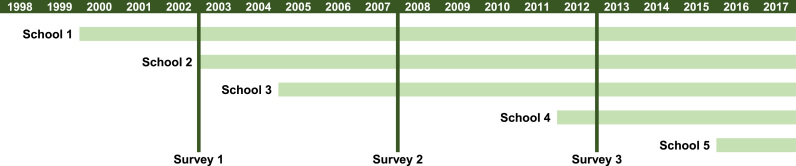
The SLEPHI method relies on repeated cycles of cross-sectional data collected in different individuals nested in the same sites over different times, a design commonly employed in public health research. An example of this design is found in Fig. 1: Different students are recruited in schools that repeatedly participate in a student health survey every few years. The schools implemented the same population intervention—in this study Gay-Straight Alliances (GSAs)—but may have started that intervention in different years. Within each survey cycle, therefore, the length of time of intervention may vary across schools: For example, at Survey 2 in Fig. 1, the lengths of intervention in Schools 1–5 were 8, 5, 3, 0, and 0 years, respectively.

Fig. 1.

A Design Appropriate for the “Site-level Longitudinal Effects of Population Health Interventions” (SLEPHI) Method Note. Different individuals are recruited at different time points from the same schools. Horizontal bars illustrate the same population health intervention implemented in 5 schools. For example, School 1 implemented the intervention in the year 2000. Vertical lines illustrate 3 student health surveys (in 2003, 2008, and 2013), in which all 5 schools participated. Within each survey, the intervention lengths vary across schools. For example, at Survey 2, the lengths of intervention in Schools 1–5 were 8, 5, 3, 0, and 0 years, respectively. As a rough guide, at least 50 sites (schools) are recommended to ensure statistical power (Maas & Hox, 2005). In addition, no more than 10 cycles of cross-sectional data (surveys) should be included (Asparouhov & Muthén, 2012a).

More generally, there are four prerequisites for a design to be suitable for the SLEPHI method: (1) repeated cycles of cross-sectional data are collected within each site at roughly the same time points, while the maximum number of cycles should be limited to 10 (Asparouhov & Muthén, 2012a); (2) the same sites (N > 50) (Maas & Hox, 2005) are followed over time in all repeated cycles, but different individuals are sampled from the sites at different cycles; (3) the start dates of the population intervention can vary across sites and are not controlled by the researcher, as a natural experiment; and (4) the lengths of intervention vary by site within each cycle of cross-sectional data collection. These design features allow the site-level intervention effects to be examined within each cycle of data collection and compared across different cycles.

Compared to a one-time cross-sectional correlational design, the SLEPHI method is superior in two ways: First, when the sample includes comparison sites receiving no intervention at any cycle of data collection (e.g., School 5 in Fig. 1), site-level secular trends in the health outcomes can be tracked. Second, by comparing the site-level health outcomes across cycles, differences across sampling cohorts can be examined. In this way, the cohort characteristics (e.g., distribution of different sexual-orientation groups) do not need to remain the same over time, and the effects of varying cohort characteristics on the health outcome can be compared across the sampling cohorts by incorporating cohort-varying site-level and individual-level covariates into the statistical model (see Section 1.2). Therefore, the SLEPHI method monitors both secular trends and cohort effects, thus enhancing causal inferences in observational research.

The SLEPHI method also differs from conventional longitudinal designs (Laursen, Little, & Card, 2011), including cohort sequential design (Prinzie & Onghena, 2005), in which the same individuals (or cohorts of individuals) are followed over time. Longitudinal designs are limited in assessing long-term population intervention effects when data are collected in clusters that have a rapid population renewal rate. For example, students recruited from high schools typically graduate within four years, thereby limiting the longitudinal inference to four years (if students are not followed after graduation). In contrast, in the SLEPHI method, different individuals are sampled from the same sites at different time points, while the sites themselves are followed over a flexible length of time. Because in practice it is easier to follow the same sites than the same individuals for a long time, the SLEPHI method can be used to evaluate long-term population interventions at the site-level. Despite all these advantages, the SLEPHI method requires a different analytic technique than regular longitudinal analysis (Laursen et al., 2011, Prinzie and Onghena, 2005), which we describe in the next section.

1.2. The MG-ML analytical approach

Various analytical approaches have been developed to try to evaluate changes in populations (rather than individuals) over time after population-level interventions. For example, the difference-in-differences (DiD) analytical approach has been developed and used relatively recently to evaluate policy changes in observational studies (Dimick and Ryan, 2014, Raifman et al., 2017, Rajaram et al., 2014). The DiD approach uses linear regression models to compare the difference between treatment and control groups in the differences of the health outcome assessed during the pre-intervention period vs. the post-intervention period (thereby “difference-in-differences”). Compared to the conventional pre-post design, the DiD approach is capable of ruling out secular trends by adding a parallel comparison group that is assessed at the same pre- and post-intervention periods as the treatment group. The DiD approach is also advantageous because it uses simple statistics (linear regression models). However, the DiD analysis has limitations that render it inappropriate for the kind of data available in the SLEPHI design. Conceptually, the DiD approach regards intervention as a binary term (with or without intervention), which ignores the possibility that the intervention effects may be additive or nonlinear over time. Statistically, the DiD analysis assumes homoscedasticity, which is often violated by having different participants at different measurement times (i.e., cohort effects). The DiD analysis further assumes independence of residuals, which is also violated by autocorrelations in the outcome measure and by data clustering within sites. Violation of these assumptions, if not properly addressed, can bias site-level estimates, leading to an increased Type I error rate (Bertrand et al., 2004, Ryan et al., 2015). Moreover, the DiD analysis cannot handle potential measurement errors or measurement nonequivalence across repeated measures, which may further bias findings.

Another recent approach to examine site-level interventions has been interrupted time series (ITS) analysis (Bernal et al., 2017, Kontopantelis et al., 2015, Penfold and Zhang, 2013). The ITS analysis applies regression modeling on time series data to examine changes in the level and slope of the outcome, from before to after the intervention. While the ITS analysis addresses one limitation of the DiD approach by conceptualizing the intervention effect as time-varying, it shares DiD’s other limitations, such as biased estimates from autocorrelation, data clustering, and measurement errors and measurement nonequivalence (unless complex statistical adjustments are made; see Bernal et al., 2017). More importantly, the ITS analysis requires repeated data from at least eight time points both before and after the intervention (Penfold & Zhang, 2013). For survey data that are collected every few years, this is an impossible approach, as too much time will pass before interventions could be evaluated for SLEPHI designs.

To overcome the limitations of the DiD and ITS analyses, we recommend using the MG-ML analysis for the SLEPHI method (Asparouhov & Muthén, 2012a). The MG-ML analysis is a type of multilevel structural equation modeling (Asparouhov and Muthen, 2008, Hox, 2013). In MG-ML analysis, repeated measures (e.g., survey cycles) are specified as multiple “known groups” in a mixture model. Meanwhile, in each measure, individuals (e.g., students) are nested within sites (e.g., schools), hence the data have a 2-level clustered structure. Typically, the site, rather than the individual, is the level of inference interest. That is, the site-level outcome, estimated from the individuals clustered in each site, is treated as the dependent variable. Site-level information, such as length of intervention, can be included to predict the health outcome. Thus, the MG-ML analysis allows researchers to examine cohort effects and track secular trends, while accounting for measurement errors and ensuring that measurement scores are comparable over time. In this study, we apply the MG-ML analysis to real-world data collected in repeated cross-sectional surveys to demonstrate these advantages of the SLEPHI method.

1.3. The current study

We adopted the SLEPHI method to examine the effect of Gay-Straight Alliances (GSAs) on school-level perceived safety in lesbian, gay, and bisexual (LGB) and heterosexual students. LGB adolescents experience significant health disparities compared to their heterosexual counterparts (Institute of Medicine, 2011), which has been largely attributed to experiences of victimization, bullying, and discrimination at school (Chesir-Teran and Hughes, 2009, Espelage et al., 2008, Poteat, 2008). To build a safe and supportive school environment for sexual and gender minority students and their straight allies, many schools in North America have established school-based student clubs such as GSAs (Genders & Sexualities Alliance Network | trans and queer youth uniting for racial and gender justice,, MyGSA.ca,). Previous research has suggested that the presence of GSAs in schools are linked to better student mental health and safer school climates (Poteat et al., 2013, Saewyc et al., 2014, Toomey et al., 2012), yet most of these studies have relied on single cross-sectional survey designs, limiting the ability to draw causal inferences. A prospective panel study (Ioverno, Belser, Baiocco, Grossman, & Russell, 2016) focused on changes experienced by LGBQ students actually participating in the GSA, as well as those whose schools implemented a GSA even if they did not participate, but they were only followed for a short period of time (two years). The results suggested that LGBQ students who do not participate in the GSA may still experience benefits through changing school climate in schools that implement a GSA. However, that study was relatively small, not population-based, and participants were not from the same schools. The study also did not examine potential experiences of heterosexual allies participating in GSAs, or heterosexual bystanders who attend schools with GSAs, although previous cross-sectional research in Canada suggests heterosexual students in schools with GSAs may also report lower odds of discrimination and suicidality (Saewyc et al., 2014).

In this study, we used the SLEPHI method by first combining student reports of perceived school safety from three survey years administered in the same schools but among different students. In addition, we recorded the year of GSA establishment in each school, to create a school-level predictor of GSA length, thus creating a 2-level dataset combining individual-level and school-level information. We conducted MG-ML analysis to examine the relation between GSA length and school-level perceived safety among LGB students, within and across the three survey cycles, and repeated the same analyses separately for the much larger sample of heterosexual students from the same schools. We hypothesized that after accounting for participant characteristics (e.g., age), cohort differences, secular trend, measurement errors, and measurement equivalence, the longer a GSA had been in place in a school, the higher the school-level perceived safety that would be reported by LGB students. We expected there to be similar, but likely attenuated, results for heterosexual students.

2. Methods

2.1. Participants

Participants included 1,625 self-identified LGB students (67.4% female) and 37,597 self-identified exclusively heterosexual students (50.2% female) attending grades 7–12 in 135 public schools across the western Canadian province of British Columbia. Only schools that consistently participated in the BCAHS in 2003, 2008, and 2013 were included in the study. The BCAHS randomly sampled classrooms by grade and geographic region to represent enrolled students across the province. Detailed sampling methodology is described elsewhere (Green, 2004, Saewyc and Green, 2009; Saewyc, Stewart & Green, 2014). Consent was obtained from parents and/or from students (with parental notification) according to procedures approved by each school district. The overall response rates of the 2003, 2008, and 2013 BCAHS were 76%, 66%, and 70%, respectively. Participant characteristics of the current sample are presented in Table 1.

Table 1.

Sample Characteristics of the British Columbia Adolescent Health Survey, 2003–2013.

Characteristic	2003	2008	2013
LGB students	(n= 481)	(n= 521)	(n= 623)
Heterosexual students	(n= 15,014)	(n= 12,164)	(n= 11,322)
Age, years, mean (SD)
LGB	15.8 (1.5)	15.7 (1.5)	15.7 (1.5)
Heterosexual	15.5 (1.6)	15.4 (1.5)	15.4 (1.5)
Female, No. (%)
LGB	338 (70.3)	341 (65.7)	413 (66.7)
Heterosexual	7,153 (47.7)	6,006 (49.4)	5,451 (48.2)
Race/ethnicity, No. (%)
LGB European	332 (69.0)	312 (59.9)	380 (61.0)
LGB all others	149 (31.0)	209 (40.1)	243 (39.0)
Heterosexual European	9,905 (66.0)	7,244 (59.6)	7,059 (62.3)
Heterosexual all others	5,109 (34.0)	4,920 (40.4)	4,263 (37.7)
Sexual orientation, No. (%)
Lesbian/gay	92 (0.6)	122 (1.0)	162 (1.4)
Bisexual	389 (2.5)	399 (3.1)	461 (3.9)
Heterosexual	15,014 (96.9)	12,164 (95.9)	11,322 (94.8)
Years of living in Canada, No. (%)
LGB 5 years or shorter	47 (9.8)	44 (8.6)	67 (11.1)
LGB 6 years or longer	434 (90.2)	465 (91.4)	538 (88.9)
Heterosexual 5 years or shorter	921 (6.1)	771 (6.5)	844 (7.6)
Heterosexual 6 years or longer	14,082 (93.9)	11,091 (93.5)	10,298 (92.4)
Schools	(n= 135)	(n= 135)	(n= 135)
Length of GSA presence till survey cycle, No. (%)
0 year	115 (92.7)	85 (68.5)	60 (48.4)
1 year	2 (1.6)	8 (6.5)	4 (3.2)
2 years	3 (2.4)	8 (6.5)	5 (4.0)
3 years	2 (1.6)	3 (2.4)	4 (3.2)
4 years	2 (1.6)	6 (4.8)	7 (5.6)
5 years	0 (0.0)	5 (4.0)	5 (4.0)
6 years	0 (0.0)	2 (1.6)	8 (6.5)
7 years	0 (0.0)	3 (2.4)	8 (6.5)
8 years	0 (0.0)	2 (1.6)	3 (2.4)
9 years	0 (0.0)	2 (1.6)	6 (4.8)
10 years	0 (0.0)	0 (0.0)	5 (4.0)
11 years	0 (0.0)	0 (0.0)	2 (1.6)
12 years	0 (0.0)	0 (0.0)	3 (2.4)
13 years	0 (0.0)	0 (0.0)	2 (1.6)
14 years	0 (0.0)	0 (0.0)	2 (1.6)

Note. Some numbers do not add up to the column totals of participants or schools, due to missing data. Valid column percentages are presented. GSA = Gay-Straight Alliance.

2.2. Measures

2.2.1. Perceived school safety

In the 2003, 2008, and 2013 BCAHS, students reported how often they felt safe in 6 school settings: classrooms, washrooms, hallway, cafeteria, library, and outside on school property during school hours. Participant rated perceived safety on a 3-point Likert scale in 2003 and 2008 (0 = never or rarely, 2 = usually or always) and on a 5-point Likert scale in 2013 (0 = never, 4 = always). These responses were recoded such that 0 = never or rarely felt safe and 1 = sometimes, usually, or always felt safe for all 3 survey cycles. The 6 items demonstrated good internal consistency with Cronbach’s αs > .90.

2.2.2. Length of GSA presence

In 2008 and 2014, research assistants contacted administrators of participating schools in the BCAHS via telephone for the year of GSA establishment. Information from both data collections was merged into one record for each school. Of the 124 schools that provided data, 7.3% established a GSA before 2003, 24.2% between 2004 and 2007, 20.1% between 2008 and 2012, and 48.4% in or after 2013. To calculate the length of GSA presence at each survey cycle, the year of GSA establishment was subtracted from the year of survey cycle (Table 1).

2.3. MG-ML model specification

We adopted latent response variable (LRV) Y* approach (Muthén & Asparouhov, 2002) to formulate the measurement model for the six binary items. The LRV formulation assumes a continuous normal latent response variable Y* underlying individuals’ dichotomous choice of each item y. That is, an observed y is the manifestation of Y* through the threshold parameter τ. The value of τ is a cut-off on the continuum of Y* such that an individual’s y = 1 if Y* ≤ τ and y = 2 if Y* > τ. A measurement model is then fit to the tetrachoric correlation matrix of the 6 latent response variables Y*. The measurement model is given as,

$${\mathbf{Y}}^{*}=\mathbf{\mu }+\mathbf{\Lambda }\mathrm{F}+\mathbf{u}$$ (1)

where Y* denotes a 6 × 1 vector of scores on the latent response variables Y*; F is a latent common factor score; Λ is a 6 × 1 vector of factor loadings; and u is a 6 × 1 vector of residual scores of Y*.

The data in the current study had a 2-level structure: cross-sectional students at level-1 were nested within longitudinal schools at level-2. To account for data clustering, Y* in Eq. (1) is split into two parts:

$${\mathbf{Y}}^{*}={\mathbf{Y}}_{\mathbf{W}}^{*}+{\mathbf{Y}}_{\mathbf{B}}^{*}$$ (2)

$${\mathbf{Y}}_{\mathbf{W}}^{*}={\mathbf{\mu }}_{\mathbf{W}}+{\mathbf{\Lambda }}_{\mathbf{W}}{\mathrm{F}}_{\mathrm{W}}+{\mathbf{u}}_{\mathbf{W}}$$ (3)

$${\mathbf{Y}}_{\mathbf{B}}^{*}={\mathbf{\mu }}_{\mathbf{B}}+{\mathbf{\Lambda }}_{\mathbf{B}}{\mathrm{F}}_{\mathrm{B}}+{\mathbf{u}}_{\mathbf{B}}$$ (4)

where Y*_W and Y*_B represent latent response variables at the individual-level (“W” for “within”) in Mplus notations (Asparouhov & Muthén, 2012a) and the school-level (“B” for “between”), respectively. F_W and F_B are the latent common factors and Λ_W and Λ_B are factor loadings at the individual-level and the school-level, respectively.

Although all of the parameters in Eqs. (3), (4) can be freely estimated in principle, certain constraints are needed for model identification. In this study, we fixed the loading of the first latent response variable to 1 for factor scale identification. We held the loadings on the school-level equal to those on the individual-level, so that the school-level factor F_B can be interpreted (Asparouhov & Muthén, 2012a). Moreover, the loadings were constrained equal across groups (survey cycles) so that the school-level factor F_B was calibrated on a common scale, and hence comparable across the groups (survey cycles). The intercepts μ_W and μ_B were not estimated because we chose the thresholds parameterization for the LRV formulation, where either μ or τ, but not both, can be estimated for model identification (Muthén & Asparouhov, 2002). Hence, the τ parameters were freely estimated, but only at the school-level following Mplus specification (Asparouhov & Muthén, 2012a). Finally, the residual variances of u were only estimated at the school-level following Mplus specification (Asparouhov & Muthén, 2012a).

To investigate the influence of GSA implementation on school-level perceived safety, GSA length and the possible quadratic form, were included as predictors for F_B:

$${\mathrm{F}}_{\mathrm{B}}={\mathrm{\gamma }}_{0g}+{\mathrm{\gamma }}_{1g}{(\mathrm{GSA\; length})}_{\mathit{jg}}+{\mathrm{\gamma }}_{2g}{(\mathrm{GSA\; length})}_{\mathit{jg}}^2+{\mathrm{\epsilon }}_{\mathit{jg}}$$ (5)

where γ_0g denotes the grand mean of the school-level common factor score (F_B) of perceived school safety in survey cycle g, which was fixed to 0 for the 2003 cycle for model identification and freely estimated for the 2008 and 2013 survey cycles. γ_1g and γ_2g respectively denote the slopes of the linear and quadratic terms of GSA length on the school-level common factor score (F_B) in survey cycle g. ε_jg is the residual of F_B for school j in survey cycle g, which is assumed to follow a normal distribution across schools; these residuals were freely estimated among survey cycles. Finally, covariances of F_B were freely estimated among the survey cycles (Asparouhov & Muthén, 2012a).

Both individual-level and school-level covariates can be added to Eq. (2). In this study, no school-level covariates were added due to a lack of appropriate measures. At the individual-level, we included one covariate, age, as an example:

$${\mathrm{F}}_{\mathrm{W}}={\mathrm{\beta }}_{1g}{(\mathrm{Age})}_{\mathit{ijg}}+{\mathrm{\epsilon }}_{\mathit{ijg}}$$ (6)

where β_1g is a slope of age on the individual-level common factor score (F_W) of perceived school safety and was freely estimated for each cycle g. ε_ijg denotes the individual-level residual for individual i in school j in survey cycle g, which is assumed to follow a normal distribution and was constrained equal across survey cycles, because the error differences were specified to be freely estimated at the school-level. Note that the random intercept β_0jg is not included and a fixed (instead of random) slope β_1g is used for simplicity.

First-order maximum likelihood (MLF) estimator was used to facilitate model convergence (Asparouhov & Muthén, 2012b), with the convergence criterion for the EM algorithm set to 0.1 following Mplus specification (Asparouhov & Muthén, 2012a). In addition, Markov Chain Monte Carlo integration was used, with the number of integration points set to 10,000. Missing data (at both the individual-level and the school-level) were handled using listwise deletion, resulting in 8.7% of individual participants removed from the MG-ML models. Full information maximum likelihood was not used because it was not compatible with MG-ML models (Asparouhov & Muthén, 2012a). A series of nested models were built, with variations in γ_1g, γ_2g, and β_1g (see Table 2). Model fit was compared using chi-square tests. See Electronic Supplementary Material for annotated Mplus (Muthén & Muthén, 1998) inputs.

Table 2.

Model fit comparisons for nested multi-group multilevel models among lesbian, gay, and bisexual adolescents in the British Columbia Adolescent Health Survey, 2003–2013^a.

Model	Specification	-2LL	df	AIC	BIC	aBIC	|Δχ2|	|Δdf|	p
1	γ11 = γ12 = γ13; γ2g = 0	7219.15	34	7287.15	7467.44	7359.43	––	––	––
2	γ1g freely estimated; γ2g = 0	7226.18	36	7298.18	7489.07	7374.71	7.03	2	.030
3	γ11 = γ12 = γ13; γ2g freely estimated	7226.97	37	7300.97	7497.16	7379.62	7.82	3	.050
4	β1g = 0; γ11 = γ12 = γ13; γ2g = 0	7345.65	31	7407.65	7572.21	7473.73	126.50	3	< .001

Note. -2LL = -2 × Log-likelihood; df = degrees of freedom; AIC = Akaike information criterion; BIC = Bayesian information criterion; aBIC = Bayesian information criterion adjusted for sample size.

^aModels 2, 3, and 4 are compared to Model 1. Model 1 is the best fitting model, given the smallest values of -2LL, AIC, BIC, and aBIC.

3. Results

Annotated Mplus (Muthén & Muthén, 1998) outputs are available in the Electronic Supplementary Material. Across all three survey cycles, the proportions of LGB and (heterosexual) students reporting never or rarely feeling safe were: in the classroom, 7.0% (2.0%); in the washroom, 14.1% (5.4%); in the hallways, 13.5% (4.3%); in the library 7.2% (2.2%); in the cafeteria, 13.6% (4.4%); and outside on school property during school hours 15.5% (5.7%).

A series of nested MG-ML models were built to find the best fitted model for LGB students first (Table 2). The first model accounted for age, constrained the slope of GSA length equal across the three survey cycles, and excluded the quadratic term of GSA length. The second model, which had the same specification as Model 1 except for freely estimating the slope of GSA length across survey cycles, resulted in a significant decrease in model fit, |Δχ²(2)| = 7.03, p = .030 (Table 2). The third model built on Model 1 to freely estimate the quadratic effect of GSA length, which also resulted in decreased model fit, |Δχ²(3)| = 7.82, p = .050 (Table 2). Finally, removing the age covariate from Model 1 still significantly decreased the model fit, |Δχ²(3)| = 126.50, p < .001 (Table 2). Therefore, Model 1 was accepted as the final model (Table 2), suggesting a linear relation between GSA length and school-level perceived safety among LGB students, which did not significantly differ among the three survey cycles.

Results of Model 1 are presented in Table 3. We found that increased GSA length significantly predicted increased school-level perceived safety among LGB students (b = 1.57, SE = 0.21, p < .001). When school-level perceived safety was standardized, the corresponding estimate was 0.32; that is, for every one more year since the GSA was established, there was a 0.32 SD increase in standardized school-level perceived safety among LGB students, supporting our main hypothesis.

Table 3.

Final multi-group multilevel model for perceived school safety among lesbian, gay, and bisexual adolescents in the British Columbia Adolescent Health Survey, 2003–2013^a.

Parameter		b	SE	p
Intercept
	γ01	0.00 (reference)	–	–
	γ02	-0.98	0.68	.146
	γ03	0.81	0.77	.291
Age
	β11	0.58	0.22	.007
	β12	0.93	0.26	< .001
	β13	0.80	0.20	< .001
GSA length
	γ1g	1.57	0.21	< .001

Note. SE = standard error.

^aPerceived school safety: 0 = never or rarely felt safe, 1 = sometimes, usually, or always felt safe. Estimates from Model 1 in Table 2 are presented. The last digit of parameter subscripts represents survey cycle g: 1 = 2003 British Columbia Adolescent Health Survey (BCAHS), 2 = 2008 BCAHS, 3 = 2013 BCAHS. γ₁₁ = γ₁₂ = γ₁₃. Factor structures (Λ_W and Λ_B), thresholds (τ_B), residual variances and covariances are omitted from the table for simplicity. See Electronic Supplementary material for all parameter estimates.

We then conducted the same SLEPHI analyses for heterosexual students (Table 4). The findings were slightly different from those from the LGB sample: specifically, GSA length was positively associated with school-level perceived safety in the 2003 survey cycle (b = 3.68, SE = 0.02, p < .001, β = 0.34), in the 2008 survey cycle (b = 1.00, SE = 0.03, p < .001, β = 0.32), and in the 2013 survey cycle (b = 4.73, SE = 0.03, p < .001, β = 0.34), but the strengths of association differed slightly but significantly across survey cycles. These findings suggest that a 1-year increase in length since GSA was started was related to a 0.34-SD increase in school-level perceived safety among heterosexual students in 2003 and 2013, and a 0.32-SD increase in perceived safety in 2008, after accounting for secular trend, cohort differences, age, measurement error and measurement nonequivalence, and data clustering (see Table 5 for the final model). This supported our second hypothesis. The slight but statistically significant difference in the strengths of the GSA effect may be due to the large heterosexual sample size.

Table 4.

Model fit comparisons for nested multi-group multilevel models among heterosexual adolescents in the British Columbia Adolescent Health Survey, 2003–2013^a.

Model	Specification	-2LL	df	AIC	BIC	aBIC	|Δχ2|	|Δdf|	p
1	γ11= γ12= γ13; γ2g=0	152,182.36	34	152,250.37	152,540.54	152,432.49	–	–	–
2	γ1g freely estimated; γ2g= 0	151,660.39	36	151,732.39	152,039.64	151,925.23	521.97	2	< .001
3	γ1g and γ2g freely estimated	152,001.17	39	152,079.17	152,412.03	152,288.09	340.78	3	< .001
4	β1g=0; γ1g freely estimated; γ2g=0	152,051.19	33	152,117.19	152,399.00	152,294.13	390.80	3	< .001

Note. -2LL = -2 × Log-likelihood; df = degrees of freedom; AIC = Akaike information criterion; BIC = Bayesian information criterion; aBIC = Bayesian information criterion adjusted for sample size.

^aModel 2 is compared to Model 1; Models 3 and 4 are compared to Model 2. Model 2 is the best fitting model, given the smallest values of -2LL, AIC, BIC, and aBIC.

Table 5.

Final multi-group multilevel model for perceived school safety among heterosexual adolescents in the British Columbia Adolescent Health Survey, 2003–2013^a.

Parameter		b	SE	p
Intercept
	γ01	0.00 (reference)	–	–
	γ02	0.37	0.01	< .001
	γ03	1.18	0.02	< .001
Age
	β11	0.08	0.00	< .001
	β12	0.19	0.01	< .001
	β13	-0.04	0.01	< .001
GSA length
	γ11	3.68	0.02	< .001
	γ12	1.00	0.03	< .001
	γ13	4.73	0.03	< .001

Note. SE = standard error.

^aPerceived school safety: 0 = never or rarely felt safe, 1 = sometimes, usually, or always felt safe. Estimates from Model 1 in Table 2 are presented. The last digit of parameter subscripts represents survey cycle g: 1 = 2003 British Columbia Adolescent Health Survey (BCAHS), 2 = 2008 BCAHS, 3 = 2013 BCAHS. γ₁₁ = γ₁₂ = γ₁₃. Factor structures (Λ_W and Λ_B), thresholds (τ_B), residual variances and covariances are omitted from the table for simplicity.

4. Discussion

Using the SLEPHI method, we found GSA length related positively to school-level perceived safety among LGB students, suggesting that LGB students on average feel safer in schools the longer a GSA has been present; so too, do heterosexual students. Importantly, this effect held after accounting for secular trend (by freely estimating intercepts in different survey cycles), cohort differences (by comparing the slopes of GSA length among survey cycles), demographic variables (by using age as an example), measurement error and measurement nonequivalence (by incorporating a measurement model and fixing it equal across survey cycles), and data dependence due to clustering (by using a multilevel framework). Moreover, this linear increment remained robust even after 14 years of GSA presence (the longest GSA length in our data), lending support to the long-term protective effect of GSAs.

The current findings are consistent with findings from prior cross-sectional studies, which have found GSAs in high schools are associated with increased perceived school safety, decreased bullying and victimization, and better mental health among sexual minority students (Heck et al., 2014, Poteat et al., 2015, Saewyc et al., 2014, Toomey and Russell, 2013, Toomey et al., 2011, Walls et al., 2010) and among heterosexual students (Poteat et al., 2013, Saewyc et al., 2014). However, our study strengthens these correlational inferences by suggesting the link between GSA presence and students’ well-being is not confounded by measurement issues, secular trend, or cohort differences. A recent prospective panel study further reported that GSA presence predicted increased perceived school safety and decreased homophobic bullying in sexual and gender minority youth in the next school year, and that new GSAs also predicted increased perceived school safety (Ioverno et al., 2016). Together, findings based on various research designs in different samples have converged to imply a causal protective effect of GSAs in high schools on the well-being of sexual and gender minority youth.

The similar findings for heterosexual youth in schools with GSAs provide further support for the potential benefit of GSAs on school climate for all students, not just sexual minority students, and results do suggest increasing trends over time as well. This may be welcome news for schools trying to address concerns that the benefits of GSAs for the small proportion of LGB students in schools might be outweighed by potential for harm to heterosexual students. Our findings suggest no harm, and to the extent that perceived safety in school is linked to better educational and health outcomes for students, clear benefits for all students.

We also observed a novel finding, that longer GSA presence in a school was linearly related to increased school-level perceived safety among LGB and heterosexual students. Therefore, LGB students in a school with eight years’ GSA presence may on average feel safer than LGB students in a school with four years’ GSA presence, by 4 × 0.32 = 1.28 SDs on a z-distribution. Moreover, this finding appeared to hold for different LGB student cohorts in the same school with continuing GSA presence, suggesting that GSAs may have a long-term positive effect on overall school climate. Given the effect sizes for heterosexual youth were nearly identical, and they are a much larger proportion of the overall school population, the effect sizes noted in these analyses suggest GSAs may exert a wide spread, long-term effect within schools on safety. Future research may usefully examine potential mechanisms for this long-term effect. For example, in one study, the number of years an adult advisor served in the GSA was related to positive youth development (Poteat et al., 2015). Having the same advisors over a long time may pass down beneficial traditions, discard unhelpful practices, and develop new initiatives in a GSA. The continuing presence of a GSA in a school may also benefit students by providing training and support to teachers and administrators on safe-school practices, monitoring school climate, establishing effective feedback systems, and generating a positive cascading effect from senior to junior students (Russell et al., 2016, Russell et al., 2010). Future research could also explore other potential effects of GSAs noted in previous cross-sectional studies using this new SLEPHI application, to identify whether similar longitudinal site-level effects are identified.

Regarding method advancement, this study illustrates a novel application of MG-ML analysis on existing datasets routinely collected in public health research. Compared to other methods for population health intervention evaluations, MG-ML modeling is better adapted to accounting for heteroscedasticity and interdependence of standard errors, which often leads to increased false rejections (Bertrand et al., 2004, Ryan et al., 2015). The MG-ML can also adjust for measurement errors and ensure measurement equivalence, resulting in more accurate estimates. Moreover, the SLEPHI method can examine changes in site-level health outcomes in a longer time frame and with fewer follow-ups, thereby reducing research costs compared to conventional longitudinal designs that follow the same individuals or cohorts of individuals over time. It also makes effective use of large-scale data collected for monitoring purposes, providing an efficient further use of existing data. In short, this sophisticated SLEPHI method is adaptable for evaluating nonrandomized population interventions.

4.1. Limitations

The findings of the current study may be limited by the exclusion of schools that did not consistently participate in all repeated cycles of data collection. It is not possible to impute individual-level missing data when there is whole-school-level attrition, because there is no information available about the missing students, including the number of students in the missing schools. For the current study, school-level attrition may be less problematic, due to the large number of available schools. However, when applying the SLEPHI method to other datasets, we encourage researchers to consider the implications of site-level attrition, especially on sample representativeness and generalizability of the findings.

Another limitation of this study concerns the exclusion of other possible individual-level covariates. We selected age as an example individual-level covariate because it was significantly related to school safety. When we added in more individual-level covariates (e.g., sexual orientation identity, gender), the models did not converge, possibly due to limited statistical power associated with the small number of LGB students within some schools in a survey cycle. Therefore, when applying the SLEPHI method, it is important to keep a reasonable, carefully theorized number of covariates to retain statistical power, as in other multilevel models, especially when the within-cluster sample sizes are small.

Finally, the current study did not include school-level covariates in the MG-ML analysis, therefore it is unknown if the effect of GSA on school-level perceived safety among LGB students was confounded by time-invariant and time-varying factors at the school level. While some countries may have data sources that provide detailed school-level information at each survey cycle going back 10 years or more, these type of data are not universally available with all large-scale school surveys. From a practical perspective, obtaining site-level information long after the fact can be challenging or impossible. From a statistical perspective, however, we recommend against including too many site-level covariates, as in the framework of multilevel modeling, especially when the number of sites is small.

Likewise, publicly available repeating cross-sectional data sources may exclude the identifiable information about schools due to administrative regulations and ethical concerns about data privacy. In our case, the data source (the McCreary Centre Society) merged the cross-sectional surveys into a single file with an assigned school code (removing the school identifying information from the file). We provided the McCreary Centre Society with the information about GSA length from the results of our telephone data collection, by school name, and they merged that information into the data without the identifiers, so that we could conduct analyses with school-level information. We also signed confidentiality undertakings that committed us to reporting in aggregate, and not identifying particular schools in any of our analyses. This is one strategy to ensure the confidentiality of the data while allowing analyses to determine site-level longitudinal effects of policies or programs implemented in sites. We would therefore encourage survey custodians to develop secure plans such as the one we used to share site-level information, in order for researchers to more adequately evaluate the efficacy of population health interventions.

4.2. Implications and conclusion

This SLEPHI method has broad application in public health research for evaluating nonrandomized population interventions on site-level health outcomes. For example, it could be used to examine trends in school-level mental health among students after schools sequentially establish an anti-bullying policy; to monitor hospital-level changes in patient outcomes after hospitals roll out new case-mix workload policies across a health region; to compare state-level health access records before and after health insurance expansions occurred at different times in different states.

In conclusion, by using the SLEPHI method, we were able to draw stronger inferences than prior cross-sectional studies on the protective role of GSAs on LGB and heterosexual students’ well-being. This innovative method can be applied to assess the effectiveness of other nonrandomized population health interventions.

Ethics approval

Ethics approval was obtained from the Behavioural Research Ethics Board of the University of British Columbia.

Conflicts of interest

The authors have no conflicts of interest to declare.

Appendix A. Supplementary material

Supplementary material