Sparse Canonical Correlation Analysis Applied to fMRI and Genetic Data Fusion

Abstract

Fusion of functional magnetic resonance imaging (fMRI) and genetic information is becoming increasingly important in biomarker discovery. These studies can contain vastly different types of information occupying different measurement spaces and in order to draw significant inferences and make meaningful predictions about genetic influence on brain activity; methodologies need to be developed that can accommodate the acute differences in data structures. One powerful, and occasionally overlooked, method of data fusion is canonical correlation analysis (CCA). Since the data modalities in question potentially contain millions of variables in each measurement, conventional CCA is not suitable for this task. This paper explores applying a sparse CCA algorithm to fMRI and genetic data fusion.

I. INTRODUCTION

Increased interest in fusion of fMRI and genetic information has driven several recent research inquiries [1]. While fMRI techniques can provide a narrow range of activations, genetic information can vary widely depending upon the type of measurement being made. For example, single nucleotide polymorphism (SNP) measurements can span millions of sites and when coupled with fMRI data the researcher is presented with a significant data mining challenge. Only a small number of potentially interrelated sites may be connected to brain function.. Unconstrained CCA [2] approaches suffer from the high dimensionality; since there are far more sites than the number of observations, collinearity becomes an issue leading to unstable estimates and results which cannot be generalized.

Another type of genetic measurement, copy number variation (CNV), which has shown significant promise as a biomarker in several diseases [3], presents a different set of challenges. The dimensionality of CNV measurements are dramatically reduced from SNP studies, with values representing insertions and deletions in the DNA sequence covering kilo to mega bases. Even with this dramatic data reduction; there typically are still fewer observations than CNV regions of interest leading again to collinearity issues. Coupled with this, the quantization of CNV data does not immediately lend itself to some prevalent blind data reduction and analysis techniques like independent component analysis [4]. A different analysis framework which can satisfy the collinearity issues as well as accommodate quantized data is needed.

The problem of collinearity can be mitigated by use of sparse loadings in the CCA algorithm. In recent years, several researchers have produced penalized or sparse versions of CCA. In [5], a penalized matrix decomposition is introduced using a LASSO penalty [6], to compute a rank-K approximation of a matrix. This approach is very similar to the one adopted in [7] where a sparse singular value decomposition (SVD) is used to compute the sparse CCA loadings and variates. In [8], the elastic net [9] is applied constrained CCA. While these approaches all attempt to solve the collinearity problem, typically applied to gene association studies, they do not necessarily produce sparse variates. In [10] the collinearity issues are ignored and problem of producing sparse variates is considered using an alternating least squares approach. While this paper is principally concerned with collinearity issues, it should be noted there are some cases where sparse variates are of interest, particularly in interpreting results.

This paper investigates adapting one of the penalized CCA formulations, dubbed sparse CCA (SCCA), to fMRI and genetic data fusion. First, the SCCA algorithm is introduced and issues with its formulation are explained. Next the algorithm is applied to simulated linked fMRI and genetic data sets to demonstrate its applicability to this type of data fusion. The algorithm’s performance under varying conditions is discussed along with some directions for improvement and continuing work.

II. SPARSE CCA

Consider two sets of variables, X of size n x p and Y of size n x q. Where n is the number of observations and p and q are the number of variables in each set. The goal of the CCA algorithm is to find a linear combination of variables from X and Y which are maximally correlated. Explicitly this can be written as

$$\underset{u,v}{\max }{u}^T{X}^{T}Yv,$$ (1)

subject to

$$u^T{X}^{T}Xu\le 1,v^T{Y}^{T}Yv\le 1$$ (2)

The optimal weight vectors, u and v have a closed form solution involving the eigenvectors of the covariance matrices Σ_XX, Σ_{Y Y} and the cross covariance matrix Σ_XY [11]. Practically these can be found by computing the left and right singular vectors of

$$K={\sum }_{XX}^{-\frac{1}{2}}{\sum }_{XY}{\sum }_{YY}^{-\frac{1}{2}}.$$ (3)

For very high dimensional data (p, q >> n), collinearity between variables becomes a problem in the standard CCA analysis. Furthermore, in many cases only a small number of available variables may be related across sets. Even in cases where p and q are on the order of n, collinearity may still be an issue, due to intrinsic dependencies in the variables. This problem can be remedied in part by adding penalty terms to the weight vectors in Eq.(2)

$$P_1(u)\le c_u,P_2(v)\le c_v.$$ (4)

Here, P₁ and P₂ are chosen to be convex penalty functions. Since the goal is to produce sparse weight vectors, it is appropriate to use the LASSO penalty so that

$$P_1(u)=\sum _{i=1}^p\left|u_i\right|,$$ (5)

where P₂(v) takes on a similar form. The resulting optimization problem using the LASSO constraints can be optimized using a soft thresholding update rule for both weight vectors

$$\begin{gathered} u_{i+1}=K{v}_i \\ {u}_{i+1}={\left(\left|u_{i+1}\right|-\frac{1}{2}{\lambda }_u\right)}_{+}Sign\left(u_{i+1}\right) \\ {v}_{i+1}=K^T{u}_{i+1} \\ {v}_{i+1}={\left(\left|v_{i+1}\right|-\frac{1}{2}{\lambda }_v\right)}_{+}Sign\left(v_{i+1}\right) \end{gathered}$$ (6)

where the weight vector is first found using a typical SVD power iteration and then soft-thresholded to satisfy the LASSO constraint. The initial vectors can be chosen at random and the sparsity parameters λ_u and λ_v can be chosen using cross-validation or by utilizing prior information.

While a sparse SVD or penalized matrix decomposition solves the problem of removing collinear variables from the canonical variates, in practice there is still another problem that must be addressed. Eq.(3) requires the computation of ${\sum }_{XX}^{-1}$ and ${\sum }_{YY}^{-1}$; these matrices may be singular in many cases, especially when there is a high degree of collinearity. Regularization is often used as a solution to ill-posed inverse problems [12]. A more extreme form is used here which considers diag (Σ_XX) and diag (Σ_{Y Y} ) as estimates of the actual covariance and cross covariance matrices.

III. SIMULATIONS

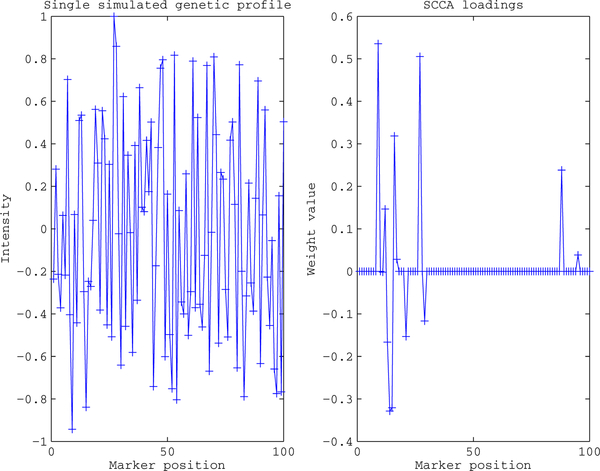
To explore the effectiveness of applying SCCA to fMRI and genetic data fusion several simulations were carried out. First, two sets of cross correlated variables were generated using a latent model similar to [7]. The variables were generated so that the traditional canonical correlation between sets was 0.5 and each set was then embedded into a larger data set of independent variables. The independent fMRI variables were generated using an fMRI image collected during an auditory task. One hundred fifty cross correlated variables were embedded into the contrast image at points of high activation and unit variance noise was added to create fifty realizations. One realization is shown in Fig.(1(a)), the embedded variables can be seen in the regions of slightly higher intensity. The second set of thirty cross correlated variables was embedded into a larger data set consisting of 10000 Gaussian independent variables to simulate the gene signal; the first one hundred variables are shown in Fig.(2).

Figure 1.

Sample simulated fMRI and associated SCCA weights on 16 axial slices. Fifty simulated fMRI images were generated to conduct a group simulation. Notice the locations of slightly higher intensity in the fMRI data, these are the cross set correlated variables. The SCCA weights appear at the locations that cross set correlated variables were inserted into the fMRI data set.

Figure 2.

Sample simulated profile and resulting SCCA weights. The set of 30 cross correlated variables was embedded at the beginning in a set of 10000 independent variables, for ease of visualization only the first 100 variables are shown. The cross set correlated variables are located in the first 30 marker positions. Notice the majority of the nonzero SCCA weights appear in that marker range.

The SCCA algorithm was then run on the two sets of variables with λ_fMRI ranging between 0.005 and 0.05 and λ_gene between 0.01 and 0.1. Parameter values higher than 0.1 resulted in no variables being selected. Using k-fold cross-validation, λ_fMRI = 0.015 and λ_gene = 0.065 were selected corresponding to a maximum variate correlation averaged over cross-validation steps of 0.4130. For each step of the cross-validation a $\frac{k-1}{k}$ portion of the data is used to identify canonical variates using a set of sparseness parameters from the selected range. The correlation between the obtained canonical variates is then evaluated on the remaining testing sample of data. These correlations are averaged over k steps with the optimal combination of sparseness parameters corresponding to the highest average correlation.

The resulting SCCA fMRI weight component is shown in Fig.(1(b)). In each realization there were 1500 embedded voxels corresponding to the cross correlated variables, the SCCA component contains 1281 voxels corresponding to the original embedded variables and an additional 124 voxels corresponding to unrelated variables. The SCCA gene weight component is shown in Fig.(2), only the first 100 positions are shown for ease of visualization. In each realization there were 30 embedded variables, the SCCA weight component contains 10 nonzero weights corresponding to these variables and 2 corresponding to the independent variables.

To investigate the effect of quantization on the SCCA algorithm Fig.(4) shows an integer valued data set similar to what is found with CNV data. The same SCCA procedure was applied, with λ_fMRI = 0.016 and λ_gene = 0.3 chosen after cross-validation. 100 CNV variables were simulated at integer values between zero and four in the gene data set to correspond to the low dimensionality of CNV studies. The number of variables remained unchanged in the fMRI set. As before the SCCA fMRI component picks up most of the embedded variables seen in Fig.(3(a)) with 1283 voxels corresponding to the embedded variables and 111 corresponding to the separate independent variables. Similarly, Fig.(4) shows the SCCA weights for the simulated CNV data. The nonzero weights almost all correspond to the original 30 embedded variables.

Figure 4.

Sample simulated CNV profile and resulting SCCA loadings. The cross set correlated variables are located in the first 30 marker positions, the resulting nonzero SCCA weights appear predominately at these positions.

Figure 3.

Simulated fMRI weights on 16 axial slices for simulated CNV data. The cross set correlated variables are embedded at the same locations, using the same generative model. The majority of the embedded variables appear with nonzero weights after the SCCA algorithm is run.

The noise variance was increased in the fMRI data set to 1.5 times of the embedded variable’s variance. A sample realization is shown in Fig.(5(a)), the cross correlated variables were embedded in the same positions but the noise variance is much higher making it difficult to see them. The SCCA algorithm was then run on the two sets with λ_fMRI and λ_gene in the same range as before. Again using cross-validation, λ_fMRI = 0.008 and λ_gene = 0.062 were selected corresponding to a maximum variate correlation averaged over cross-validation steps of 0.2230. The SCCA fMRI component is shown in Fig.(5(b)) and gene component is shown in Fig.(6). In either case the nonzero weights do not correspond to the cross correlated variables. This indicates the the algorithm is vulnerable to high noise or the correlation structure of the embedded variables is not sufficient for identification when unrelated variables have a larger variance.

Figure 5.

Here the unrelated variables variance is increased. The cross set correlated variables are embedded at the same locations, however, the SCCA weights do not account for the embedded variables. Some weights correspond to cross set correlated variables, however several variables are not represented and several weights correspond to variables that are not cross set correlated.

Figure 6.

Sample simulated profile and resulting SCCA loadings in high noise. The cross set correlated variables are located in the first 30 marker positions, however the resulting nonzero SCCA weights are no longer appearing in the cross set correlated variables.

These results are encouraging in the sense that the SCCA algorithm is able to deal with high dimensional data sets of different measurements under appropriate conditions. Fig.(1) and Fig.(2) show that the SCCA algorithm is able to recover the majority of the embedded variables with only a few unrelated variables having nonzero weights. If there is some prior information available about the expected number of influential variables in each set, the effect can be mitigated by further adjusting the sparsity parameters λ_fMRI and λ_gene. The algorithm was able to recover the embedded variables in the simulated CNV case as well. It should be noted that the sparsity parameters depend on the dimensionality of the data, so for lower dimensional data the associated sparsity parameter must be larger in magnitude. The high variance case of Fig.(5) and Fig.(6) demonstrates the algorithm’s weakness in cases where the independent variables’ variance is much higher than the embedded variables’ variance. While this is certainly a limitation, fMRI and genetic studies are usually designed to produce areas of high activation in the brain which are believed to be linked to a genetic data set. This situation precludes cases where the unrelated variables swamp the cross correlated set.

IV. CONCLUSION

CCA is a powerful tool that can be used for data fusion. However, fMRI and genetic studies provide a particularly difficult set of problems in the form of two things. First, the high dimensionality of the data sets in question causes collinearity between variables resulting in improper associations. Second, the sparse nature of some genetic data, namely CNV studies, coupled with collinearity issues makes conventional CCA unsuited for this type of fusion. However, the SCCA algorithm built around a penalized singular value decomposition can accommodate collinearity issues as well as integer valued data.

These preliminary simulations are encouraging in their ability to recover associations between high dimensional data sets. There are, however, some limitations that need to be addressed as well further investigations that need be made. First, the selection of the optimal sparsity parameters is often a difficult task, relying heavily upon cross-validation. Aside from adopting a general rule of thumb for the sparsity parameters, an alternative selection method based up minimum description length principles may prove to be more robust. Next, while these simulations are illustrative of the SCCA algorithm’s power in these types fMRI and genetic information problems, a better latent variable model needs to be developed that can more accurately simulate real world fMRI activations. Finally, the effects of the independent variable variance need to be further explained and a better determination of what fMRI tasks and genetic measurements SCCA is applicable to.