Heterogeneous retreat and ice melt of Thwaites Glacier, West Antarctica

The heterogeneous retreat of Thwaites glacier indicates complexities of ice melt processes taking place at the grounding zone.

Abstract

The glaciers flowing into the Amundsen Sea Embayment, West Antarctica, have undergone acceleration and grounding line retreat over the past few decades that may yield an irreversible mass loss. Using a constellation of satellites, we detect the evolution of ice velocity, ice thinning, and grounding line retreat of Thwaites Glacier from 1992 to 2017. The results reveal a complex pattern of retreat and ice melt, with sectors retreating at 0.8 km/year and floating ice melting at 200 m/year, while others retreat at 0.3 km/year with ice melting 10 times slower. We interpret the results in terms of buoyancy/slope-driven seawater intrusion along preferential channels at tidal frequencies leading to more efficient melt in newly formed cavities. Such complexities in ice-ocean interaction are not currently represented in coupled ice sheet/ocean models.

INTRODUCTION

The Antarctic Ice Sheet is changing rapidly and contributing notably to global sea level rise (1, 2). With 1.2-m potential sea level equivalent, the Amundsen Sea Embayment (ASE) sector of West Antarctica is a dominant contributor to sea level rise at present and for decades to come (3–5). Thwaites Glacier accounts for one-third of the mass loss from the ASE (6). The fast-flowing main trunk of Thwaites accelerated by 0.8 km/year, or 33%, between 1973 and 1996, and another 33% between 2006 and 2013 (7). Between 1970–2003 and 2010–2013, ice discharge increased at a rate of 2.2 Gt/year², and the rate quadrupled in 2003–2010 (9.5 Gt/year²). More recently, parts of the glacier have been observed to thin as much as 4 m/year (8).

As bed topography beneath Thwaites is several hundreds of meters below sea level at the grounding line and is getting deeper inland (retrograde bed slope), this sector may be prone to rapid retreat (9, 10). Several studies have suggested that the glacier is already in a stage of collapse and the retreat is unstoppable (3, 4, 11). The rate of grounding line retreat is controlled by bed topography, dynamic ice thinning, and ice shelf melt by warm, salty circumpolar deep water (CDW), with ice shelf melt playing a critical role (12). The grounding line retreated at 0.6 to 0.9 km/year between 1996 and 2011 along the glacier sides and the main trunk, respectively (Fig. 1) (4). There has been no adequate interferometric synthetic aperture radar (InSAR) data after 2011 to observe the grounding line retreat (13, 14).

Fig. 1. Thwaites Glacier, West Antarctica.

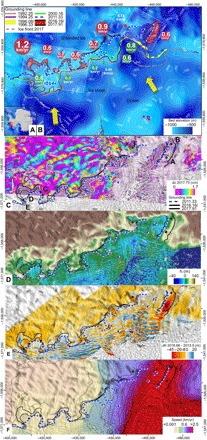
(A) Map of Antarctica with Thwaites Glacier (red box). (B) Shaded-relief bed topography (blue) with 50-m contour levels (white) (16), grounding lines color-coded from 1992 to 2017, and retreat rates for 1992–2011 (green circle) versus 2011–2017 (red circle) in kilometer per year. Thick yellow arrows indicate CDW pathways (32). White boxes indicate outline of figs. S1 and S2 (C) DInSAR data for 11 to 12 and 27 to 28 April 2016, with grounding lines in 2011, 2016, and 2017 showing vertical displacement, dz, in 17-mm increments color-coded from purple to green, yellow, red, and purple again. Points A to F are used in Fig. 2. (D) Height of the ice surface above flotation, h_f, in meters. (E) Change in ice surface elevation, dh, between decimal years 2013.5 and 2016.66 color-coded from red (lowering) to blue (rising). (F) Ice surface speed in 2016–2017 color-coded from brown (low) to green, purple, and red (greater than 2.5 km/year), with contour levels of 200 m/year in dotted black.

RESULTS

Here, we use 12 one-day repeat InSAR observations from the COSMO-SkyMed (CSK) constellation to survey Thwaites at an unprecedented level of temporal details from 2016 to 2017 (15). We combine the CSK DInSAR data with 120 time-tagged TanDEM-X (TDX) digital elevation models (DEMs) covering the time period 2010–2017. The DInSAR data reveal the time-evolving position of the grounding line from tidal cycles to multiple years. The TDX DEMs quantify changes in surface elevation caused by ice dynamics and surface mass balance on grounded ice and, additionally, by ocean-induced ice shelf melt on floating ice.

In the rapidly moving main trunk of Thwaites (Fig. 1 and fig. S1), the grounding line migrates at tidal scales over a zone 2.5 km wide in 2016–2017 versus 0.5 km wide in 1996. A larger migration zone is explained by the flatter bed topography at the 2016–2017 grounding line (16) versus 1996, similar to what is observed on Pine Island Glacier (15). The average retreat rate in 2011–2017 is 3.6 ± 1.2 km/year or 0.6 ± 0.2 km/year, which is 20% less than in 1992–2011 (0.8 km/year). Several areas of local grounding vanished since 2011. Their presence revealed a shallow water column, with the ice shelf scraping over a rough bed (17–19). Their disappearance indicates rapid ice thinning and ungrounding. Within the 2016–2017 grounding zone, we detect ephemeral pinning points, a few kilometers in diameter, where the ice shelf alternatively scrapes over the bed and lifts off the bed (fig. S1). Ephemeral points disappear with time, indicating vigorous formation of new cavities.

To the east, ice retreat peaks at 1.2 km/year in 2011–2017 in the “butterfly” extension of the Thwaites Eastern Ice Shelf (TEIS) (location D in Fig. 1) versus 0.6 km/year in 1992–2011, i.e., a doubling in retreat rate. The retreat is accompanied by the disappearance of pinning points (fig. S2). Elsewhere, the 2011–2017 retreat varies from 0.3 to 0.6 km/year, similar to 1992–2011, and the grounding zone is 0.5 km wide, consistent with a steeper bed that limits tidal migration.

On grounded ice, we detect widespread thinning of 3 to 7 m/year across the glacier width at locations A to E (Fig. 2). This high thinning is caused not by a change in surface mass balance, which is less than 1 m/year (20), but by dynamic thinning (Fig. 3) (8, 13). At locations A to F, ungrounding of the ice around year 2014 results in a sharp increase in thinning, which we attribute to the vigorous melting of ice exposed to warm, salty CDW. At A, after accounting for dynamic thinning and converting the change in ice shelf surface elevation above mean sea level into ice shelf thickness, we calculate an ice shelf melt rate of 207 m/year in 2014–2017, which is the highest ice shelf melt rate on record in Antarctica (movies S1 and S2) (21). At B, we calculate an accretion of 12 m/year instead, which we explain later. At D and E, ice melts at 34 to 52 m/year, comparable to the highest melt rate on Smith Glacier (13), while at F, ice melts at 10 m/year along a narrow corridor.

Fig. 2. Changes in ice surface elevation, h, of Thwaites Glacier.

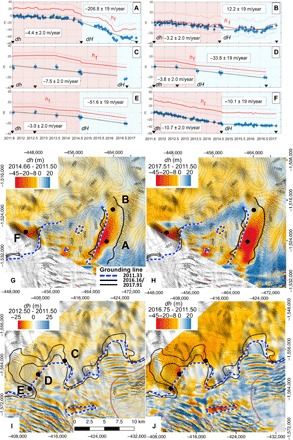
(A to F) from TDX data (blue dots) for the time period 2011–2017 over grounded ice (red domain, dh/dt) at locations A to F, with height above floatation, h_f (red lines), and 1σ uncertainty (dashed red lines), converted into change in ice thickness, H, over floating ice (blue domain, dH/dt) in meters per year. Black triangles are TDX dates in (G) to (J). (G and H) Main trunk. (I and J) TEIS. Grounding line position is thin black for 2016–2017 and white dashed blue for 2011.

Fig. 3. Ice thickness change of Thwaites Glacier.

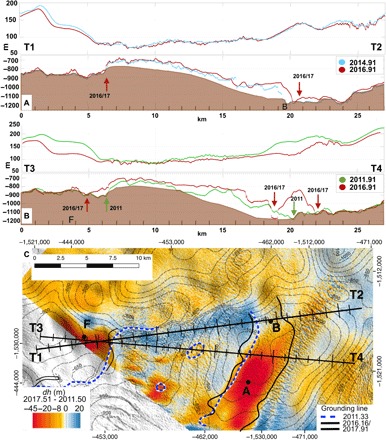
(A) Ice surface elevation from Airborne Topographic Mapper and ice bottom from MCoRDS radar depth sounder in 2011, 2014, and 2016, color-coded green, blue, and brown, respectively, along profiles T1-T2 and (B) T3-T4 with bed elevation (brown) from (16). Grounding line positions deduced from the MCoRDS data are marked with arrows, with the same color coding. (C) Change in TDX ice surface elevation, h, from June 2011 to 2017, with 50-m contour line in bed elevation and tick marks every 1 km.

Along two profiles surveyed by MCoRDS radar depth sounder (22), we obtain direct measurements of ice thickness from 2011–2016 (Fig. 3). On profile T3-T4, we confirm the formation of a cavity 4 km wide by 350 m in height between 2011 and 2016. The 10-km-long cavity contained 14 billion tons of ice. The average melt rate along T3-T4 agrees with that calculated from TDX (figs. S4 and S5). The MCoRDS data confirm the disappearance of an ice rise at km 12, a 2-km retreat in 5 years at A, and grounding line retreat at F. Along T1-T2, ice thinning is less pronounced but cumulates to 100 m at km 17 to 21, i.e. the new cavity is shallow. The inferred melt rate is opposite in sign with that indicated by TDX, which we explain as follows. This area lies in the glacier bending zone, which is a zone a few kilometers wide (23) where ice is deflected several meters below floatation (Fig. 1E) because of the viscoelastic bending stresses of ice in ocean waters. As the grounding line retreats, so is the bending zone, which allows ice seaward of the grounding line to rebound by several meters to floatation. As a result, the surface of the ice is rising, but the total thickness is decreasing. At A, the ice shelf melt is large enough to mask the hydrostatic adjustment and the bending zone is also narrow. In the more confined B area, the bending zone is wider (4) and the hydrostatic adjustment is large and masks the net decrease in ice thickness at the surface (fig. S5).

DISCUSSION

The rapid migration of ice at A is unexpected because the bed is prograde at that location (Fig. 1), i.e., bed elevation rises in the inland direction, which should be conducive to a slower retreat rate for a given rate of ice thinning (2, 5, 10). The migration at B is slower, with a lower rate of ice shelf thinning, yet the bed slope at that location is nearly flat or retrograde, which should favor more rapid retreat for a given thinning rate. The newly formed cavity at B is thin, however, which does not favor warm CDW intrusion from geostrophic flow and efficient vertical mixing (19, 24) and explains the low ice shelf melt rates. In contrast, the prograde bed at A favors an efficient opening of a new ice shelf cavity, stronger CDW intrusion, and efficient mixing, with melt rates 20 times higher than those at B. Ice shelf melt at A exceeds values used in numerical ice sheet/ocean models by factors of 2 to 3 (3, 13). At B, the melt rate is low versus numerical simulations. We also find that melt intensity along the newly ungrounded ice at A is linearly correlated with the slope of the ice draft along the direction perpendicular to the gradient in melt, consistent with the plume theory (fig. S6) (24). At B, no such correlation exists. Geostrophic and buoyancy/slope-driven flows are not efficient in the thin cavity near B, which is likely dominated by tidal mixing (25).

At D, the TDX data reveal the formation of a subglacial channel before ungrounding, followed by rapid melting along the sides near C and E. The D channel is initially 1.2 ± 0.2 km wide (Fig. 2J). As there is no change in speed along the channel, hence no dynamic thinning, ice thinning reflects melt by the ocean (26). Along the sides, ice shelf melt is high along prograde slopes—as for A—and low along retrograde slopes—as for B—where cavity formation is less efficient. These observations reveal a process of ice melt via channel intrusion that is different from the diffusive process taking place in the grounding zone near A.

The ice shelf melt rates discussed in Figs. 1 to 3 are calculated using a Eulerian framework, i.e., at a fixed location in space, to capture ice shelf melt rates as ice ungrounds. We also calculated the melt rates in a Lagrangian framework, where ice blocks are tracked with time and corrected for flow divergence. The Lagrangian calculation does not apply on land, on areas partially grounded, or where ice is depressed below floatation and rebounds during the retreat. Away from these zones, we confirm ice shelf melt rates up to 50 m/year on the butterfly and up to 200 m/year near the main trunk, with large spatial variations (fig. S7).

Our observations contrast with the traditional view on ice-ocean interaction at grounding lines. First, preferential melt channels 1 to 2 km wide and newly formed cavities less than 100 m in height would require ocean models to operate at the subkilometer horizontal scale and sub–100 m vertical scale to replicate the melt processes that form the cavities, which is a challenge. Second, the fact that peak melt rates in the main trunk are two to three times higher than those in models limits the ability of models to reproduce ice retreat at those locations. Third, in the main trunk of Thwaites, ocean-induced ice melt occurs over a 2.5-km-wide grounding zone, whereas numerical ice sheet models use fixed grounding lines, i.e., not affected by tidal mixing (3, 5, 10–12), with zero melt applied at the grounding line. Our results reveal the existence of wide grounding zones, with a distinct melt regime, narrow cavities, and nonzero ice melt over the entire grounding zone. Last, ice shelf melt rates may be lower along retrograde slopes than those along prograde slopes, another observation to explore in detail with ice-ocean models. We conclude that the cavity shape, including bed slope, bumps, and hollows in the bed, influences the access of ocean heat to the glacier and ocean-induced melt rates.

We detect the highest rates of retreat at the heads of major channels of CDW transport toward the main trunk and TEIS (Fig. 1) (27), with slow retreat in between (E to F), where ice is grounded on a ridge. Recent numerical models (12) replicate the faster retreat of TEIS versus the rest of the glacier and the mean retreat rate of 0.8 km/year since 1992; hence, model skills and boundary conditions have improved considerably. The recent models, however, do not replicate the fast retreat rate along the main trunk of Thwaites, in part because the ice shelf buttressing in that region is limited. In that zone, we report heterogeneous melt, up to 200 m/year, with large tidal migration of the grounding line and significant ice melts over the entire zone of tidal migration. This configuration calls into question the concept of a fixed grounding line with zero melt because models using melt at the grounding line predict more rapid retreat. Detailed studies of the grounding zone and its specific regime of ice melt will therefore be critical to explore in more detail using numerical models, remote sensing data, and in situ observations to improve our characterization of the retreat of Thwaites Glacier near its grounding line, its rate of mass loss, and, in turn, projections of its contribution to global sea level rise in decades to come.

MATERIALS AND METHODS

TDX DEM in Antarctica

TDX DEMs have a spatial resolution of 12 m by 12 m at the equator. The absolute vertical accuracy, defined as the uncertainty in height of a point with respect to the World Geodetic System (WGS) 84 ellipsoid caused by random and uncorrected systematic errors, is better than 10 m. The relative height accuracy, defined as the uncertainty between two height estimates caused by random errors, is smaller than 2 m over a 1° × 1° geocell in latitude/longitude (28). The horizontal accuracy, defined as the uncertainty in horizontal position of a point with respect to the WGS84 ellipsoid, is better than 10 m. ICESat-1 laser altimeter data, namely, GLAS/ICESat L2 Global Land Surface Altimetry Data, version 34, GLA14, was used to calibrate the TDX product. Several criteria were used to extract the most reliable pixels. Outliers above 100 m were discarded. Using a laser-specific weighting function, the 10 best ICESat points per 50-km TDX scene were selected and TDX pixels within the ICESat resolution cell were averaged. In addition, the SD of the TDX DEM within the footprint must be less than 1 m. One issue is the unknown penetration depth of X-band radar signals into snow depending on ice structure, dielectric properties, and incidence angle. This issue was solved by selecting areas with homogeneous backscattering characteristics and presumably homogeneous penetration depths based on a Radarsat-1 image mosaic of Antarctica. For each area, a constant offset between ICESat and TDX was calculated. Starting from these fixed blocks, all Antarctica acquisitions were adjusted and calibrated following an inner-to-outer direction.

We generated a time series of time-tagged DEMs using the global TDX product (28) for geocoding and calibration. The SAR processing chain comprises three main steps: (i) spaceborne monostatic TerraSAR-X processing, (ii) bistatic TDX processing, (iii) interferometric combination of images, (iv) phase unwrapping, and (v) phase-to-height conversion and geocoding to a latitude/longitude grid. Movie S1 shows a time series of TDX DEM differences over Thwaites Glacier, West Antarctica. The time-tagged TDX DEM difference accuracy is of the order of 2 m (28). Using Airborne Topographic Mapper (ATM) data over grounded ice, we found a relative height accuracy of 4 m (fig. S4).

CSK grounding line measurements

We surveyed the Thwaites Glacier grounding zone using CSK SAR acquisition. CSK is a constellation of four low Earth orbit satellites each carrying an X band SAR antenna (3.1 cm wavelength) enabling a finer resolution (3 m) and a better sampling rate (up to 176.25 MHz) of ground displacements. Each satellite had a repeat cycle of 16 days. Shorter repeats were achieved using the constellation. The shortest interferometric time period between two successive acquisitions was 1 day when using satellites CSK2 and CSK3, which we used here. CSK SAR data were assembled by concatenating 9 × CSK STRIPMAP-HIMAGE consecutive overlapping frames, each covering a 40 km by 40 km swath, at a 3-m resolution in both the azimuth (along-track) and range (cross-track) directions. The incidence angle averaged 26.27° across the swath. We analyzed scenes in a single-look complex format. Polarization of the electromagnetic waves is HH (horizontal transmit and receive). We used an orbit co-registration and pixel offsets to maximize coherence in image pairs. We applied a multilooking of 8 in both range and azimuth directions to improve phase coherence. We used 18 images (9 CSK pairs) acquired between February 2016 and September 2017 to produce pixel offset velocity maps and differential interferograms (DInSAR), revealing changes in ice velocity and vertical tidal displacements (figs. S1 to S3). We did not combine image pairs 48 days apart to avoid contaminating the DInSAR results with long-term changes in horizontal velocity. We generated velocity maps and analyzed the results to verify this hypothesis a posteriori (fig. S3). The precision with which we detected grounding lines also depends on the amplitude of the tidal signal. A larger differential tidal signal is preferable for delineating grounding lines. In total, 60% of our DInSAR pairs include small differential tidal displacements; hence, they are not used in the final analysis (figs. S1 and S2). Because the baseline separation between CSK2 and CSK3 is large, we also need to remove the topographic component of the interferometric phase. To do this, we used the time-tagged TDX DEM acquired closest in time with the CSK data (15). Using multiple grounding line measurements, we identified a grounding zone, i.e., an area over which the grounding line migrates back and forth with changes in oceanic tide (fig. S1).

Bed topography and height above flotation

We used a bed topography from mass conservation (16) that combines ice thickness derived from an airborne radar depth sounder (22) with InSAR-derived ice velocity maps (29) and RACMO2.3 surface mass balance data (20). Combined analysis of DInSAR data and bed elevation allowed us to interpret grounding line migration. The TEIS grounding zone is located inland of a set of topographic bumps, on a reverse slope of about 3%, i.e., leaving no resistance for future retreat. Bed elevation, h_b, was combined with surface elevation above mean sea level, h, to deduce ice thickness, H = h − h_b, and calculate a height above flotation, h_f, as

$${\mathit{h}}_{\mathrm{f}}=\mathit{h}-\mathit{H}(1-\frac{{\mathrm{\rho }}_{\mathrm{i}}}{{\mathrm{\rho }}_{\mathrm{w}}})$$ (1)

where ρ_i is the density of ice (917 kg/m³) and ρ_w is the density of seawater (1028 kg/m³). The relative error in h_f is 14 m based on an uncertainty of 2 m for h, 100 m in H, 0.6% in water density, and 1% in ice density (Fig. 1E). Movie S2 shows a time series of h_f on Thwaites Glacier, West Antarctica.

Ice shelf melt rate

Time series of surface elevation, h, allowed us to calculate ice shelf melt rates, m. We calculated the height of the ice above floatation, h_f. We identified when the glacier reaches h_f = 0 m (Fig. 2A) in the time series and calculated the slope of the change in elevation before that transition, dh/dt_PRE, and after that transition, dh/dt_POST, i.e., the date of ungrounding of ice. dh/dt_PRE is the average thinning rate on grounded ice, which is caused principally by dynamic thinning, and reflects a total change in thickness (because the bed elevation is not changing with time during that time period). dh/dt_POST is the average thinning rate on floating ice, which includes dynamic thinning and also ice shelf melt. The ice shelf melt rate, m_b, was deduced from

$$\frac{\mathit{d}\mathit{h}}{\mathit{d}{\mathit{t}}_{\text{PRE}}}=\nabla (\mathit{u}\cdot \mathit{h})+{\mathit{m}}_{\mathrm{s}}$$ (2)

$$\frac{\mathit{d}\mathit{h}}{\mathit{d}{\mathit{t}}_{\text{POST}}}=\raisebox{1ex}{$[\nabla (\mathit{u}\cdot \mathit{h})+{\mathit{m}}_{\mathrm{s}}+{\mathit{m}}_{\mathrm{b}}]$}\!\left/ \!\raisebox{-1ex}{$\mathit{f}$}\right.$$ (3)

$${\mathit{m}}_{\mathrm{b}}=\mathit{f}\frac{\mathit{d}\mathit{h}}{\mathit{d}{\mathit{t}}_{\text{POST}}}-\frac{\mathit{d}\mathit{h}}{\mathit{d}{\mathit{t}}_{\text{PRE}}}$$ (4)

where m_s and m_b are the melt rates (positive is melt, and negative is accretion) at the surface and base of the ice, respectively; h is the ice surface elevation above mean sea level; u is the depth-averaged velocity; and f = 9.61 is a flotation factor deduced from densities of ice and seawater. We assumed that the rate of dynamic thinning, ${\frac{\mathit{d}\mathit{h}}{\mathit{d}\mathit{t}}}_{\text{PRE}}$, varies smoothly along the flow; hence, it is nearly the same above and below the grounding line, which is justified a priori because changes in ice velocity take place over spatial scales of 10 to 100 km. We also assumed that ice shelf melt is smoothly varying near the grounding line, which is an approximation, so the change in surface elevation may be assumed to be varying almost linearly with time (Fig. 2, A to F). This Eulerian framework, based on the change in elevation with time at a fixed point in space, identifies the temporal change in ice melt at a given location; hence, it reveals how rapidly a piece of ice melts as the grounding line retreats and ice ungrounds and is exposed to warm ocean waters. One drawback of this method is that it produces noisy results, where heterogeneities in ice thickness are advected downstream, for instance, seaward of the grounding line due to the presence of deep bottom crevasses traveling with the main flow.

In a Lagrangian framework (see below), we tracked a piece of ice with time and calculated its rate of ice melt after correction for flow divergence. The heterogeneities in ice shelf melt were removed, but the method did not apply on grounded ice; hence, we could not use the Lagrangian framework to calculate how ice melt changes with time as ice ungrounds. In our analysis, we only used a Eulerian framework for that reason and we noted that caution must be exercised when interpreting the results within a few kilometers seaward of the grounding line due to the rebound of ice to hydrostatic equilibrium as the bending zone migrates.

Using ATM surface elevation and MCoRDS depth-sounding radar-derived thickness, we obtained direct information about changes in ice thickness along profiles T1-T2 and T3-T4 from years 2011, 2014, and 2016. We compared ATM versus TDX surface elevation acquired closest in time. We found a difference with an SD of 4 m (fig. S4). We compared MCoRDS direct thickness changes with thickness changes inferred using TDX DEMs closest in time to the MCoRDS data. We found an agreement at the 4-m level along the grounded part of T3-T4 in 2014–2016 (fig. S5). Near the grounding line of T1-T2 for the 2014–2016 data and along T3-T4 for the 2011–2014 data, ATM/MCoRDS showed peak changes of 150 and 20 m, respectively, whereas TDX DEMs indicated 50- and 300-m thickening, respectively (fig. S5). As explained in the main text, we attributed this discrepancy to the rebound of ice from below floatation to at floatation as the grounding line retreats, i.e., the bending zone retreats, and ice exits the bending zone to become freely floating. Direct measurements of ice thickness confirmed that ice melted from the bottom despite the observed uplift in surface elevation.

Lagrangian framework

The Lagrangian approach calculates the change in ice thickness by tracking parcels of floating ice with time and correcting for flow divergence. We assumed that the ice parcel had a uniform rate of motion and was in hydrostatic equilibrium. The change in ice surface elevation, h, is given by the conservation of mass as

$$\mathit{D}\mathit{h}/\mathit{D}\mathit{t}+\mathit{h}(\nabla \cdot \mathit{u})={\mathit{m}}_{\mathrm{s}}$$ (5)

where h is the surface change, u is the surface velocity, ∇ is the del operator, (∇ ∙ u) is the divergence in ice velocity, and m_s is the change in surface elevation caused by basal melt. In Eq. 5, we implicitly assumed that ice was in hydrostatic equilibrium and the surface accumulation and melt were negligible.

Assuming ice to be in steady state, the rate of basal melt, m_b, was then deduced from m_s as

$${\mathit{m}}_{\mathrm{b}}={\mathrm{\rho }}_{\text{sw}}{\mathit{m}}_{\mathrm{s}}/({\mathrm{\rho }}_{\mathit{i}}-{\mathrm{\rho }}_{\text{sw}})$$ (6)

where ρ_i = 918 kg m⁻³ and ρ_sw = 1029 kg m⁻³ are, respectively, ice and seawater densities. We used 12-m resolution TDX DEMs to produce yearly melt maps along the main trunk of Thwaites and the butterfly zone of TEIS. We used a chip size of 30 pixels with step of 16 pixels to obtain 360-m resolution maps. Annual velocity maps from (30) were used to correct for the ice flux divergence. We needed to correct the DEM tides because every meter of tide converts into a 9.6-m change in thickness over floating ice. We used the CATS2.0 tidal model (31). Table S1 lists the values used for tidal correction. Figure S7 shows annual melt rate maps, revealing ice shelf melt rates up to 50 m/year on the butterfly and up to 200 m/year near the main trunk, with large spatial variations in between.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/1/eaau3433/DC1

Table S1. Tidal corrections used with the Lagrangian framework to calculate ice shelf melt rate, derived using the CATS tidal model at the time of passage of the TDX satellites.

Fig. S1. CSK DInSAR data over the main trunk of Thwaites Glacier.

Fig. S2. CSK DInSAR data of the TEIS.

Fig. S3. Speed map over Thwaites Glacier.

Fig. S4. TDX surface deformation accuracy analysis.

Fig. S5.TDX inferred thickness change accuracy analysis.

Fig. S6. Relationship between ice shelf melt rate and the ice shelf draft slope.

Fig. S7. Annual ice shelf melt rates.

Movie S1. TDX time series of surface elevation.

Movie S2. TDX time series of changes in height above flotation.