MPGAfold in Dengue Secondary Structure Prediction

Abstract

This chapter presents the computational prediction of the secondary structures within the 5′ and 3′ untrans lated regions of the dengue virus serotype 2 (DENV2), with the focus on the conformational prediction of the two dumbbell-like structures, 5′ DB and 3′ DB, found in the core region of the 3′ untranslated region of DENV2. For secondary structure prediction purposes we used a 719 nt-long subgenomic RNA construct from DENV2, which we refer to as the minigenome. The construct combines the 5′-most 226 nt from the 5′ UTR and a fragment of the capsid coding region with the last 42 nt from the non-structural protein NS5 coding region and the 451 nt of the 3′ UTR. This minigenome has been shown to contain the elements needed for translation, as well as negative strand RNA synthesis. We present the Massively Parallel Genetic Algorithm MPGAfold, a non-deterministic algorithm, that was used to predict the secondary structures of the DENV2 719 nt long minigenome construct, as well as our computational workbench called StructureLab that was used to interactively explore the solution spaces produced by MPGAfold. The MPGAfold algorithm is first introduced at the conceptual level. Then specific parameters guiding its performance are discussed and illustrated with a representative selection of the results from the study. Plots of the solution spaces generated by MPGAfold illustrate the algorithm, while selected secondary structures focus on variable formation of the dumbbell structures and other identified structural motifs. They also serve as illustrations of some of the capabilities of the StructureLab workbench. Results of the computational structure determination calculations are discussed and compared to the experimental data.

1. Introduction

The dengue virus (DENV) is a mosquito-borne flavivirus (MBFV) from the family Flaviviridae [1]. In humans it causes dengue fever, and in approximately 10 % of the most severe cases dengue hemorrhagic fever and dengue shock syndrome, which are life-threatening [2–4]. Flaviviruses include three subgroups: DENV (dengue serotypes DENV1 through 4), Yellow fever virus, and Japanese enceph alitis virus (JEV) [5, 6]. The DENV viral genome is a single positive-stranded RNA, approximately 11,000 nucleotides long (10,723 nt for the DENV2 New Guinea strain C used in this study, GenBank# M29095 [7]). It is depicted schematically in Fig. 1a. Its 5′ end is capped (type I cap), while the 3′ end is not polyadenylated [8]. The short 5′ and 3′ untranslated regions (UTRs) contain conserved cis-acting secondary structure elements needed for translation and replication [9–18]. The UTRs precede and follow one long open reading frame coding for a polyprotein, ultimately processed into three structural proteins (C—capsid, M—membrane, and E—envelope) and seven non-structural proteins (NS1, NS2a, NS2b, NS3, NS4a, NS4b, NS5). For more information see the reviews [8, 19, 20] and references therein. In the current replication model, the viral replicase complex assembles in cytoplasmic membrane compartments. Inside it the negative RNA strand is synthesized starting from the 3′ end of the viral genome RNA (positive strand). The negative strand is then used as a template for transcription into the positive genomic RNA strand [21] (also see reviews in refs. 1, 22).

Fig. 1.

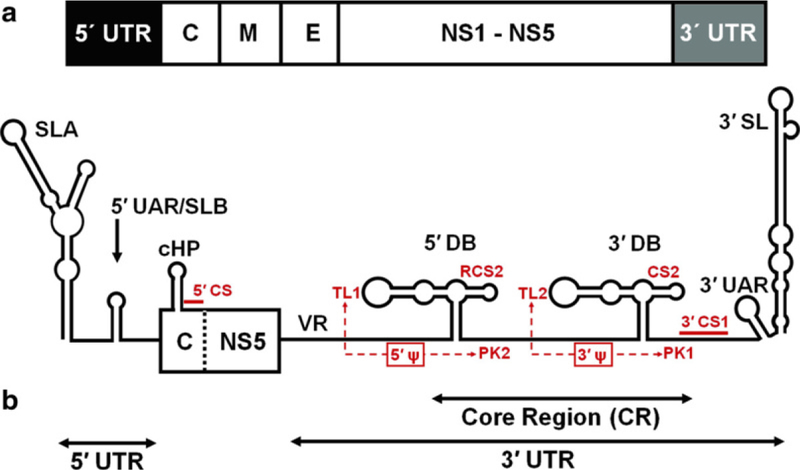
(a) A schematic view of the DENV2 genomic RNA and the minigenome construct used for computational structure prediction. (a) Full genome regions are labeled as follows: UTRs—untranslated regions; C—capsid, M—membrane, and E—envelope structural protein coding regions; NS1-NS5 non-structural proteins coding regions. DENV2 New Guinea strain C (GenBank# M29095) is 10,723nt long. (b) The schematic representation of the 719nt long minigenome construct of DENV2, which was used in the computational structure predictions performed with the aid of the MPGAfold program. The minigenome includes the 5′ UTR, the C region fragment, the end of the NS5 and the 3′ UTR (VR indicates the variable region). Small red labels indicate sequence motifs of interest discussed in the text and involved in the predicted secondary structures and inferred pseudoknots (5′ Ψ and 3′ Ψ). Refer to the text for more details (Color figure online)

Approximately 100nt long, the 5′ UTRs of flaviviruses form stable secondary structures [13, 23, 24] that include two stem-loop structures, SLA and SLB (Fig. 1b). This un-translated region is important for binding the NS5 protein, which includes the viral RNA-dependent RNA polymerase (RdRp) in its C terminal region [13]. Another identified functional secondary structure called capsidcoding region hairpin (cHP) is located downstream of the 5′ UTR (Fig. 1b) and plays a role in the initiation of translation [25, 26], as well as DENV and WNV replication [25, 26]. Another motif known as the 5′−3′ DAR (“downstream of AUG region”) is also required for viral RNA replication [27–29]. While the 3′ UTRs of flaviviruses show a lot of heterogeneity in their sequences and sizes, they also contain conserved sequences that are required for replication [9–11, 13, 15–18, 30]. The 3′ UTRs have a variable region (VR), the core region (CR), and the terminal stem-loop (3′ SL) region (Fig. 1b). The terminal stem-loop is formed within approximately the last 100 nucleotides [31, 32], the region that plays a significant role in replication [30, 33–36]. The core region, CR, includes the 3′ cyclization sequence (3′ CS1), which is complementary to the 5′ cyclization sequence (5′ CS) located within the capsid coding region (Fig. 1b). A long-range interaction between these two complementary RNA sequences results in circularization of the genome [11, 37] that has been shown to be essential for RNA synthesis in vitro [18, 38] and for replication of subgenomic replicons or infectious clones [9, 15, 16, 39, 40]. Two other complementary sequence fragments referred to as 5′ and 3′ UARs (upstream AUG) are found in the terminal regions of the genomic RNA, and they can form a long-distance UAR interaction. These are also required for cyclization and replication [10, 11, 41]. Relative to the CS/ CS1 sequences, the 5′ and 3′end UAR sequences are located closer to both ends of the genomic RNA; the 5′ UAR upstream of the 5′ CS, and the 3′ UAR downstream of the 3′ CS1 (Fig. 1b). The core region maintains a high degree of sequence conservation among the mosquito-borne flaviviruses, and it is believed to fold into well- defined secondary structures local to the region [42, 43]. Also within the CR and upstream of the 3′ CS1, another conserved sequence, called CS2, is found in all three subgroups in the mosquito-borne flaviviruses. The repeat conserved sequence 2 (RCS2), on the other hand, is found only in DENV and JEV subgroups [37] (Fig. 1b). The CS2 and RCS2 sequences are part of two nearly identical secondary structures, referred to as the dumbbell-like structures (DBs) that can form in DENV (Fig. 1b). The hairpin loops at the end of the longer arms of the 5′ and 3′ DBs contain identical sequences (5′-GAAGCUGUA-3′) [42]. Different DENV serotypes conserve the inner five nucleotides in these loops (5′- GCUGU-3′), referred to as TL1 in the 5′ DB and TL2 in the 3′ DB (Fig. 1b). Also conserved are two complementary sequences, PK2 (5′-GCAGC-3′) and PK1 (5′-ACAGC-3′), downstream of the 5′ and 3′ dumbells, respectively. This conservation of sequence motifs suggests potential base pair interactions resulting in pseudoknot structures 5′Ψ and 3′Ψ, involving the 5′DB (sequences TL1/PK2) and the 3′ DB (sequences TL2/PK1) [42].

This chapter focuses on the computational tools we have developed and applied to the study of the core region within the 3′-untranslated region (UTR) of the dengue virus by focusing on the functional roles of the two dumbbell structures in the CR region and the TL and PK sequences [29]. For secondary structure prediction and analysis, we used our programs, the Massively Parallel Genetic Algorithm, MPGAfold, and StructureLab [44–52] to fold a 719 nt subgenomic RNA construct from the DENV2 (New Guinea C strain). The construct contained the 5′-most 226 nt (5′ UTR and a fragment of the capsid coding region C), the last 42 nt from the non-structural protein NS5 coding region including the translation termination codon, and the 451nt of the 3′ UTR [29]. It has been shown to contain the elements needed for translation [12, 25, 26, 53] and negative strand RNA synthesis in vitro [18, 38, 54, 55]. We refer to this construct as the minige-nome. Combination of the experimental and computational data in our study showed that all four sequence motifs (TL1, PK2, TL2, PK1) played a crucial role in replication. On the other hand, the experimental results suggested that TL1/PK2 and TL2/PK1 played differential roles in translation. The structure prediction results generated by MPGAfold indicated differences in the stabilities of the two DBs and frequency of their occurrence in the sets of predicted structures [29]. These results offer a potential explanation of the fact that the TL1 and TL2 are not functionally identical despite having identical sequences within the two DBs.

2. Materials: Software Packages

Two of several software packages developed by our group were used to elucidate the secondary structure of the dengue minige-nome. These programs, MPGAfold and StructureLab, are presented below with specific examples of how they were used in the dengue study. Together with many other downloadable programs and Web servers, the tools mentioned in this chapter are publicly available on our Web site: www.ccrnp.ncifcrf.gov/users/bshapiro/software.html and webserver_index.html.

3. Methods for RNA Secondary Structure Prediction and Analysis

3.1. RNASecondary Structure Representations

The primary structure of an RNA molecule is its sequence that can be represented as a string built from an alphabet of just four lettersA, G, C, U. These letters correspond to the nucleic acid bases,Adenine, Guanine, Cytosine and Uracil. The bases tend to interact with each other preferentially via hydrogen bonds to form Watson-Crick base pairs (G-C and A-U) and a wobble base pair G-U. These interactions are additionally stabilized by base stacking interactions. Many other base interactions that occur less frequently in nature are possible and were classified by Westhof and Leontis [56]. However, to keep the introduction brief, they will not be discussed here.

Figure 2 illustrates how a generic RNA secondary structure with its different types of motifs, can be represented. In the drawing, the crosshatched lines correspond to base pairs forming stems, which are 2D equivalents of three-dimensional helices. The unpaired positions in the drawing form loop regions and are labeled according to their motif type. Labels M, I, B, and H indicate multibranch, internal, bulge, and hairpin loops respectively. The same topology can be represented (encoded) in the form of a region table, also shown in Fig. 2. The region table explicitly lists all the secondary structure stems, sorted based on their 5′ positions. For example, the first stem, represented by the triple (1 100 6) is a stem whose 5′ position is 1, its 3′ position is 100 and its size is 6 In this compact representation the unpaired regions of the structure are not listed explicitly and have to be derived as a complement of the paired regions for a given sequence. Other representations can also be used that are more explicit (the CT file format or the parenthesis notation employed by the mfold and RNAfold servers [57, 58]).

Fig. 2.

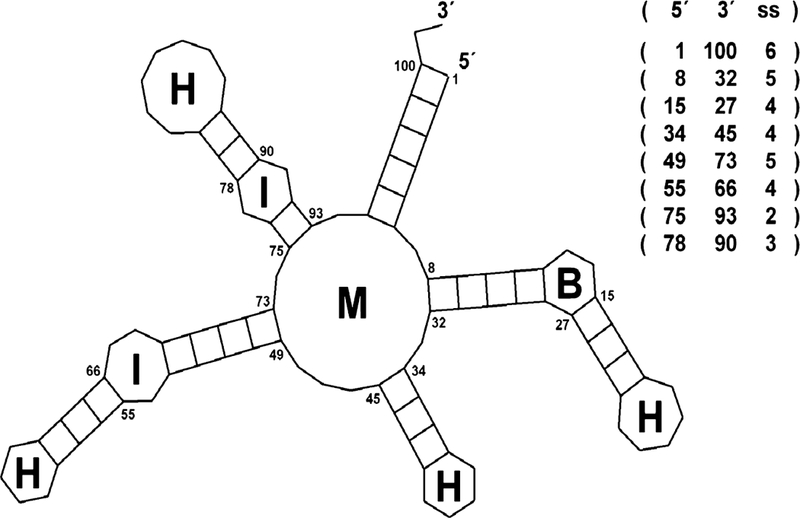
An RNA secondary structure represented as a 2D drawing and a corresponding region table. Commonly found morphological features are labeled as follows: M—multi-branch loop, I—internal loop, B—bulge loop, and H—hairpin loop. Base-paired regions, listed explicitly in the region table, are represented are rectangles with cross-links corresponding to the number of base pairs in each region

Regardless of its representation the relative stability of the secondary structure can be characterized by its free energy, the more negative the free energy the more stable the structure. Base-paired and additionally stabilized by base pair stacking, stem regions tend to add to the overall stability of the structure, while the loops generally decrease it. Additional stabilizing contributions can be made by stem stackings and higher order interactions, which, however, are poorly characterized in terms of their free energy contributions. Several free energy rule sets, with different degrees of context sensitivity, have been adopted for use in free energy calculations of an RNA secondary structure, the latest allowing for stem stacking calculations (efn2) [59] (also see reviews [60, 61]).

3.2. MassivelyParallel Genetic Algorithm (MPGAfold)

Many algorithms have been developed for predicting RNA secondary structure. Broadly speaking, these fall into two main categories which may be defined as deterministic and or stochastic, e.g., genetic algorithm-based. The algorithm that was applied in this case was MPGAfold, a massively parallel genetic algorithm for secondary structure prediction that was developed by our group [45, 48–52].

3.2.1. Genetic Algorithm Fundamentals

Originally presented by John Holland [62], genetic algorithms (GAs) are optimization procedures that can be used to search large solution spaces for “best” or near optimal results that are achievable within the limits of the parameters describing the problem and the objective function. MPGAfold is based on the principles of GAs. In the process of RNA secondary structure determination, the objective function MPGAfold uses is the free energy of the RNA secondary structure. Thus the algorithm searches for an RNA fold such that its free energy is optimal or near the optimal for the given input sequence and a set of energy rules. The term “fitness” is used alternatively to free energy, with the better of higher fitness corresponding to lower free energy of a secondary structure. A key feature and strength of the algorithm is its Boltzman-like preference for the most probable solutions, rather than exclusively the lowest energy ones. This is a non-deterministic algorithm that must be run repeatedly in order to determine the consensus solution of multiple runs. This feature also implies that one or more frequent alternative secondary structures can be revealed in multiple runs, a feature that we used in the dengue minigenome study. The alphabet of MPGAfold, i.e., the set of fundamental building blocks used in the optimization procedure is comprised of all theoretically possible, contiguous, fully base-paired stems (i.e., equivalents of perfectly base-paired helical fragments). This set of stems, called the stem pool, is pre-computed from the given input sequence in a procedure preceding the optimization phase. As it is explained later, in the actual algorithm runs these stems may be shortened by a peel-back operator that (optionally) resolves conflicts between overlapping stems. An expansion of the basic alphabet adds to the stem pool motifs that consist of two neighboring stems separated by small bulge or internal loops of sizes 1 × 1, 1 × 2, and 2 × 2 (i.e., loops with combinations of one to two nucleotides in their 5′ and/or 3′ sides). In the optimization phase of the algorithm the GA applies operations of mutation, recombination, and selection to the maturing structures from the current (parent) population in order to generate new secondary structures that constitute the next population generation (children). These are discussed in more detail in the next paragraph. The process is repeated until the improvements to the fitness (free energy) of the population of the structures maturing in parallel fall below a selected criterion. Secondary structures, one in each virtual processing element reside on a rectangular or square grid representing a population (see Fig. 3). The most often employed population sizes range from as low as 2K (1K = 1,024) to as high as 128K with a power of 2 increments. The population size is chosen as a function of the input sequence length, with the longer sequences usually subjected to MPGAfold runs over a broader range of sizes (i.e., runs are performed at several population levels, which is discussed below). Each population element in the grid, which consists of an RNA secondary structure, is connected vertically, horizontally and diagonally with its eight neighbors (i.e., N, S, E, W, NE, NW, SE, and SW, to employ the direction of the compass). From the functional point of view, the grid can be viewed as a toroid. In other words, its top and bottom as well as left and right boundaries are wrapped so that all population elements have eight neighbors and there are no boundaries. For example, the Left/West neighbor of a population element on the conceptual left edge of the grid will be an element on the right edge of the grid. Figure 3 illustrates a 5-by-5 square section of a larger grid of the population elements. MPGAfold has been implemented to run on a parallel cluster computer, distributing the population across a set of power of 2 CPUs, and its speed scales up almost linearly with the doubling of processors (or halving of the population size) [51].

Fig. 3.

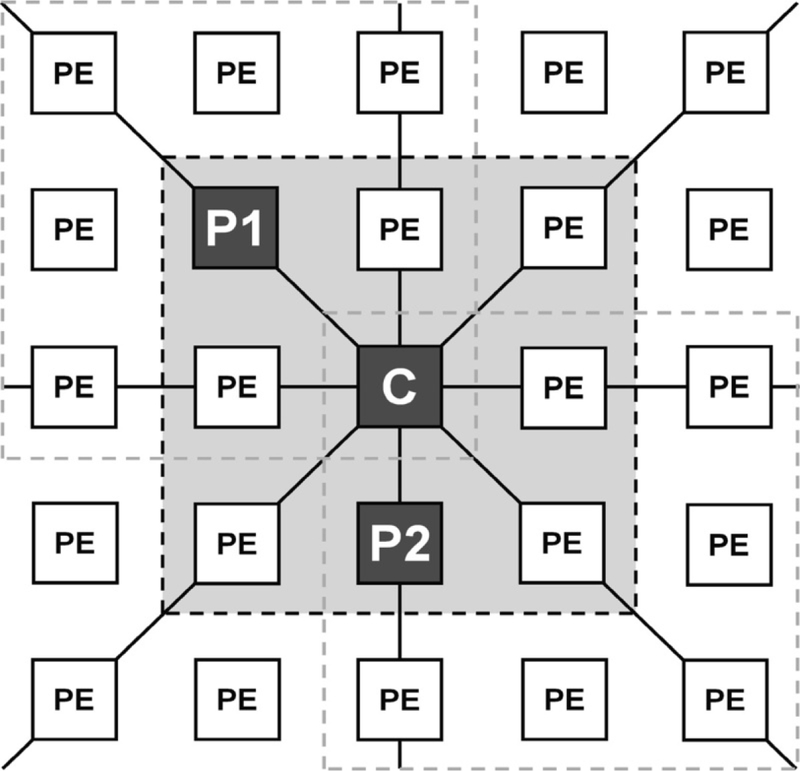
A schematic illustration of a fragment of the grid of population elements (PEs) employed by the Massively Parallel Genetic Algorithm (MPGAfold). Only the full 8-way connectivity of the central element (C) in the central nine element neighborhood (3-by-3 neighborhood with the light-gray background) is shown. Labels P1, P2 and C in the central neighborhood indicate two current generation parent structures and the next generation child structure. New child structures are generated in parallel for all the central elements of all the overlapping 3-by-3 neighborhoods, three of which are delineated with the dashed lines. The full population grid is connected toroidally, i.e., the top PEs connect with the bottom, and the left with the right. At every generation MPGAfold replaces all the current structures (in all the PEs) with the child structures, calculated for all the overlapping 3-by-3 neighborhoods

3.2.2. MPGAfold Operators

MPGAfold fundamental operations are mutation, recombination, and selection. Mutation randomly draws stems or the small stem motifs (i.e., the fundamental building block, as was explained in the previous section) from the stem pool and adds them to existing structures, replacing or partly opening (via the so-called peel-back) any conflicting stems already part of the structure. Mutations are a precursor step to each recombination operation. In the process of recombination each population element and its eight nearest neighbors from a 3-by-3 neighborhood (the central box in Fig. 3) are placed in an array, sorted in the decreasing fitness order (i.e., from the lowest free energy to the highest). A sampling biased toward selection of the best fit structures chooses two parent structures, and their stems are distributed to two child structures, which have been initialized with stems from mutations. Both mutations and recombinations employ a probabilistic stem peel-back scheme that resolves structural conflicts (overlapping stem fragments) between the stems being added to a structure and the ones already a part it. Peel-back shortens stems (effectively removing some of their base pairs) in order to fit them into the rest of the structure. This mechanism has two advantages. First, it effectively increases the resolution of the algorithm by allowing stems to be peeled-back to a single base pair. Second, it keeps the stem pool smaller and stem pool sampling more effective by including in it only the stems of maximum size. Finally, in the selection operation the free energies of the two child structures are computed, and the lower free energy structure (better fit) is selected to replace the center element in the 3-by-3 neighborhood.

3.2.3. MPGAfold Output

The three GA operators described above are applied iteratively in parallel across the entire population grid. Initially, the entire population may contain all new secondary structures after calculations of the new generation of structures. MPGAfold employs an annealing mutation scheme that gradually lowers the mutation rate. As a consequence of this and the natural maturation, i.e., fitness improvements in individual structures and the whole population on average, the population stabilizes. This may mean convergence by a vast majority of the population elements to the same secondary structure or a situation in which multiple secondary structure populations remain at equilibrium with respect to each other. Once this population stabilization is detected, the algorithm run is terminated. MPGAfold can output either the population-wide consensus (population histogram peak) structure or the best fit (lowest free energy) structure. In some runs these two may be the same, but most often they are not. A histogram of the free energy values is calculated for an evolving population at every generation, and the structures corresponding to the peak value or the lowest energy value can be output for every generation of a run as well. Thus, MPGAfold provides a wealth of information on the intermediate as well as the final structures in multiple runs. In the dengue study presented here we collected both kinds of data.

3.2.4. Transient or Intermediate Structures

The significant transient structures (dominant for a significant fraction of generations of the whole run) that the algorithm outputs during each of many runs at the constant population level (grid size) can also be captured as the final population consensus structures in the runs with lower population sizes. The algorithm has been demonstrated to capture RNA secondary structures that are representative of significant intermediates in runs with varying population sizes [45, 63–66]. A folding RNA sequence may form intermediate conformations that are themselves functional alternatives to the better fit final states or play an important role in the folding pathway of the RNA helping it to reach its final state. At lower population levels, the algorithm has a tendency to converge to less fit population consensus structures, which are indicative of these significant inter mediates. In the runs at higher population levels, the maturing structures will transition through potentially several intermediates on their path to the best fit, low free energy final states.

3.2.5. H-Type Pseudoknots

By using stems as the fundamental building blocks, MPGAfold can relatively easily generate structures including general pseudoknots. The key limitation on taking full advantage of this ability to generate general secondary structure topologies is the limited knowledge of the energies of complex pseudoknots, which makes it impossible to evaluate fitness of such structures using the same objective function applied to secondary structures without pseudoknots. For this reason the algorithm currently considers only the H-type pseudoknots for which the free energies can be calculated. H-type pseudoknots allow base pairs to form between the nucleo tides of simple hairpin loops and those of single stranded regions immediately upstream or downstream of them. It is worth noting that a scheme of 3D geometric constraints guiding prediction of general pseudoknotted structures has been successfully implemented in our CyloFold algorithm [67]. Potentially, it could be included in MPGAfold, by adopting a kind of a hybrid objective function. (See the CyloFold Web server:http://cylofold.abcc.ncifcrf.gov).

3.2.6. Other MPGAfold Capabilities

The MPGAfold program is also capable of co-transcriptional folding and can be monitored and queried during execution with the aid of a satellite visualization module [47, 51].

RNA is transcribed by the sequential addition of nucleotides to its 3′ end. RNA folding can be influenced by this elongation because of different folding pathways (intermediate structures) resulting from the changing sequence length. Final co-transcriptional folding conformations may differ from the full- length sequence folding, such as in quench-cooling experiments. MPGAfold offers an option of folding with sequence elongation. This is implemented by gradually increasing the size of the sampled stem pool space in correspondence to the increments in the input sequence’s 3′ position. In other words, the rate of elongation determines how fast stems with the increasing 3′ positions can be drawn from the stem pool by the mutation and recombination operators. The rate of elongation is parameterized (e.g., increments by n nucleotides for every m algorithmic generations) to fine-tune its impact on the maturation of a predicted structure [45, 66]. However, the elongation rate adjustments were not designed to reflect the experimentally known transcription rates. The standard operators of the algorithm determine how quickly the newly available stems propagate throughout the evolving population or become parts of the population-wide consensus structures. An opposite feature of the algorithm allows for sequence shortening (from the 3′ end), which may be useful in the cases of post- transcriptional processing leading to refolding. This feature proved to be critically important in our study of the host-killing/ suppression-of-killing (hok/sok) mechanism of E. coli plasmid R1 [45]. Employment of such an option requires multi-phase runs, which can be performed by MPGAfold. In the first phase the regular full length or the elongated sequence is folded. In the subsequent phase(s) the initial GA population is randomly seeded with selected secondary structures and the algorithm is run with other options, such as the 3′ end truncation from the full (starting point) sequence length until the foreshortened sequence length is reached. Then the algorithm is allowed to terminate normally. Other options available in MPGAfold allow for the imposition of constraints in cases where outside knowledge is available (e.g., structure probing data). Selected stems can be “forced” to be part of solutions or be designated as “sticky,” in which case they are designated to be passed to the next generation from parent structures to their progeny. However, the resulting child structures are subject to the standard selection process, which means that the “sticky” stems persist only as natural parts of best fit structures.

MPGAfold can be run in batch mode or in conjunction with an interactive Visualizer program, which acts as a Graphical User Interface (GUI). Two-dimensional interactive maps of the population grid are displayed and can be manipulated while the algorithm is running. In this way runs can be paused and structural information queried at any stage. Color-coded maps allow for the monitoring of population energy distributions, formation of pseudoknots, and the presence and persistence of user-defined stems. Finally, MPGAfold can be run in synchronization with the Visualizer and StructureLab (see the next section), in which case StructureLab can draw individual RNA secondary structures selected by the user from the population displays [47].

3.2.7. Non-deterministic Nature of MPGAfold and Its Benefits

The non-deterministic nature of MPGAfold means that for the same input sequence no two runs will follow exactly the same folding intermediate states and are not guaranteed to converge to the same final structure. For the same reason the performance of the algorithm cannot be described as a function of the input sequence. Multiple runs for the same input sequence or for several sequences of the same length may result in highly variable inumbers of generations required by the algorithm to converge to the final answers. Careful analysis of such differences in the MPGAfold output can help indicate—in a coarse way—multiple folding pathways and stable intermediates of potential biological significance. In the studies referenced here biologically significant conformations were identified as population consensus structures, both in the case of the intermediate and the final states [45, 65, 66].

3.3. StructureLab

StructureLab is a graphical data mining program developed in our lab and employed in the dengue minigenome study. The program helps to interactively explore large numbers of RNA conformations produced by secondary structure prediction programs [44, 46, 47]. These may include MPGAfold described above, or any of the DPA-based programs, such as the Vienna package RNAfold [57, 68, 69], Mfold [58, 59], or RNAstructure [59, 60, 70]. Also, see the reviews [60, 61]. The design and functional features of StructureLab have been presented in-depth before [44, 46, 47]. In this chapter we are going to review briefly one of the StructureLab tools, called StemTrace that was employed extensively in this dengue minigenome folding study.

3.3.1. StemTrace

StemTrace presents a set of secondary structures (MPGAfold or DPA output data) in the form of an interactive, two-dimensional plot of all the stems found in the input secondary structures. Each entry along the horizontal axis (X axis) represents an RNA secondary structure, while entries along the vertical axis (Y axis) represent all stems found in at least one of the plotted structures. A stem is defined as a unique triplet of values corresponding to the 5′-start position of a stem, its 3′-stop position, and the number of base pairs (i.e., the stem size). Conceptually, a vertical line intersecting all the Y-axis entries for a given x-position corresponds to a stem table describing one RNA secondary structure. Stem entries on the Y-axis is can be ordered either by their first appearance in the solution space (i.e., order in which they are generated by an algorithm), which is the default option, or by a user-selected sort criterion (e.g., increasing 5′-start positions of the stems, stem size, or the 5′−3′ distance). Stems appearing repeatedly in the predicted secondary structures, each plotted as a pixel will form horizontal bands appearing at specific y-positions. The bands are color-coded on a 10 color bin scale, to help identify frequency of occurrence of individual stems within the displayed (input) set of structures. The user can interact with StemTrace plots by “pointing and clicking” over any graphed positions. Depending on which mouse button is pressed, one stem or information about a full structure can be retrieved, and, optionally, it can be drawn as a secondary structure (thanks to the integration of multiple tools within StructureLab).

The flexibility with which StemTrace can represent the secondary structure solution space is well suited to the many types of output that can be generated by MPGAfold. A StemTrace plot can depict an ensemble of RNA secondary structures predicted for a single input sequence in multiple runs (Fig. 4) thus giving insight into the consensus structure or consensus structural motifs. Results for several sequences in a family that can be reasonably aligned (with interactive corrections informed by structural considerations) [44, 47] can be plotted together to aid in searching for common structural features. StemTrace can also depict the process of conformation maturation in one MPGAfold run (see Fig. 5). Each of these application examples is briefly discussed below.

Fig. 4.

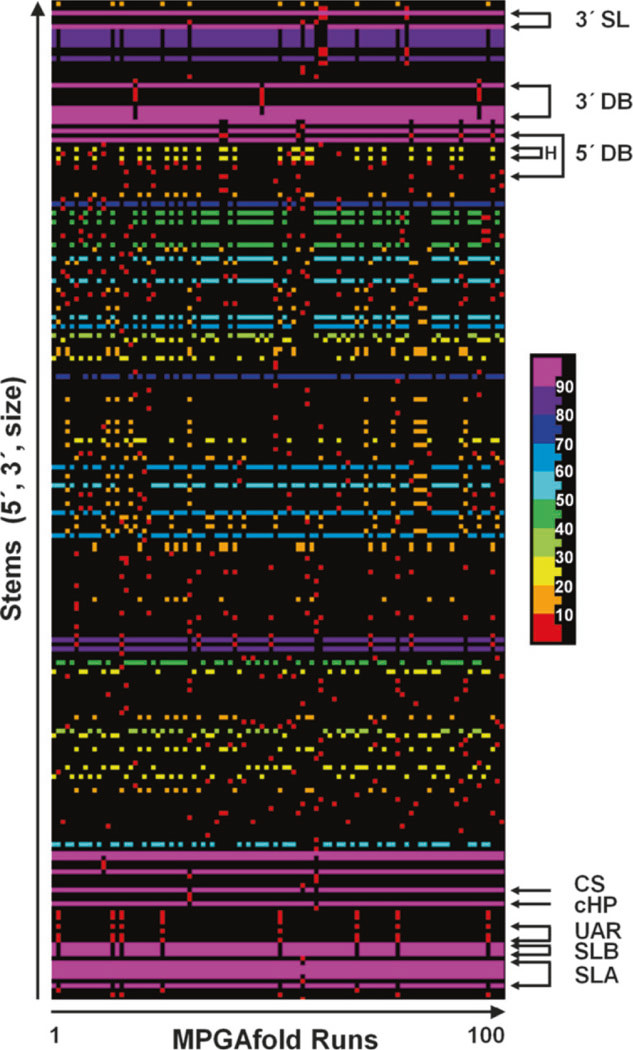
A Stem Trace graph of the final results of 100 runs of MPGAfold with a population of 16K (16,384 structures maturing in parallel). All the stems found in the final structures, defined by unique triples (5′ pos., 3′ pos., stem size), are plotted on the vertical axis and sorted in the increasing order of their 5′ positions. Entries along the horizontal axis correspond to the final results of each MPGAfold run. The color-coding of individual stems in the structures shown is based on their frequencies of occurrence in the ensemble of the final predicted (final results of 100 runs). The 10 bin color scale is shown to the right of the plot. The stems from the structural motifs drawn and labeled in the same way in Figs. 6 and 7 are indicated with arrows and labels. The Stem Trace plot shows clearly the difference in the frequency of the full 3′ DB and the 5′ DB structures (refer to Fig. 6b), as well as the higher frequency of the 5′ DB head than the full 5′ DB (labeled as H above and 5′ DBH in Fig. 7b). Another result worth noting is the 8 % frequency of the UAR structures among the predicted conformations

Fig. 5.

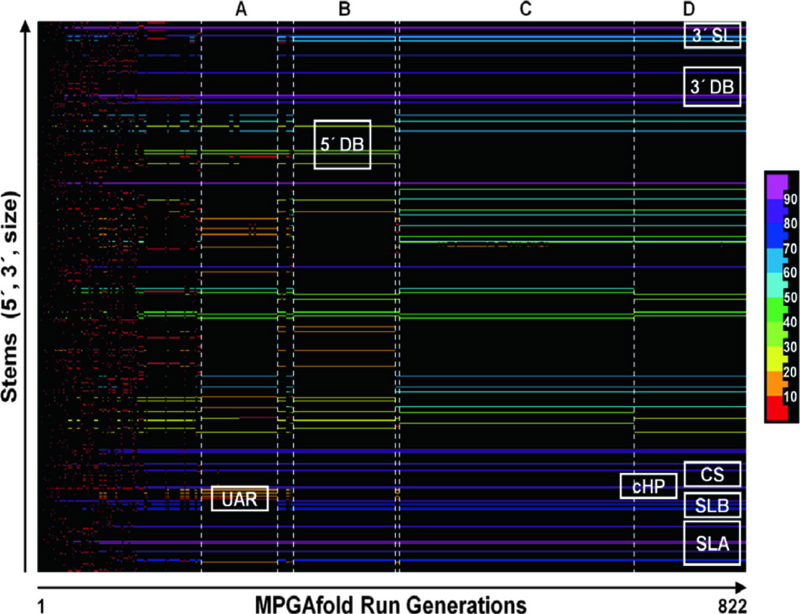
A Stem Trace plot of one full MPGAfold run corresponding to the final result of the 86th run at the 16K population level, shown in Fig. 4. The color-coding of individual stems is based on their frequencies of occurrence in the 822 generations of this run. The 10 bin color scale is shown to the right of the plot. Letters A through D above the plot indicate key conformations that became dominant (population histogram peak structures) after the initial phase of rapid maturation and frequent conformation changes. A: Two secondary structure variants (−210.7 and −212.5 kcal/mol) with the long distance UAR structures, 5′ DBH and 3′ DB, overall similar to that shown in Fig. 7b. B: A secondary structure with both full dumbbells, but without the UAR interactions (−216.7 kcal mol). C and D: Variants of the secondary structures without the 5′ DB, but with the 3′ DB (−222.0 kcal/mol for C and −225.5 kcal/mol for D), both similar to the structure shown in Fig. 6a. In addition to the 3′ DB, all other key structural motifs (SLA, SLB, cHP, CS, and 3′ SL) form early in this MPGAfold run and are present in the above described transitional conformations. The short transient states between conformers A and B and conformers B and C contain the UAR and 5′ DBH motifs, with the second transient conformer reaching the free energy level of −218.1 kcal/mol

3.3.2. Plotting the Final Structures from Multiple MPGAfold Runs

In this case a StemTrace plot could represent, for example, 100 final consensus structures generated in 100 independent folding runs ofthe same input sequence (Fig. 4). Results can be thresholded based on the frequency of occurrence of individual stems. Such filtering, combined with the 2D drawing option provided by other integrated StructureLab tools, allows the user to quickly depict a consensus structure.

3.3.3. Plotting the Final Structures for a Family of Related Sequences

Solutions for each input sequence are plotted in separate blocks of runs along the X-axis (e.g., 25 at a time) and visually outlined with thin vertical separators. The Y-axis position for stems from different sequences of the family can be adjusted based on the sequence alignment to account for the difference (insertions and deletions), yielding one common Y-axis range. The most often used and simpler variant of this representation is applied to a series of multiple solution sets for the same input sequence, for which the secondary structures were run at different MPGAfold population (grid size) levels. In this case, no sequence alignment corrections are necessary.

3.3.4. Plotting the Evolution of an RNA Secondary Structure Generated in a Single MPGAfold Run

This helps to gain more insight into the folding states (rough pathway) (Fig. 5). The early structure entries (low x-values) correspond to RNA secondary structures in the early stages of development. As one examines the RNA structures captured along the X-axis, they become more mature with more stems and decreasing free energies. Middle of the run results begin to display longer persistence of specific population histogram peak structures, measured in the number of generations. Usually in the final phase of an MPGAfold run StemTrace plots depict one persistent set of stems, indicating that the population of solutions has converged to one stable structure.

3.4. MPGAfold Parameter Settings and Simulation Run Protocols

MPGAfold requires the Local Area Multicomputer/Message Passing Interface (LAM/MPI-2) environment. It can be run as a Unix shell process or a batch job handled by a queuing system. In either case the key command invoking the program is the same. An example of a parallel run on 8 CPUs would look as follows: prompt>mpirun-np8/path/GA.1.2.2/x86_64/GA.dir/bin/ga_mpi-fga_param_file.com

The sample path may be installation-specific and in the example shown here and in the selected fragments of the parameters file (“ga_param_file.com”), shown below, is based on our setup.

The MPGAfold distribution package, which is available from our laboratory upon request (see www.ccrnp.ncifcrf.gov/users/bshapiro/software.html ; contact shapirbr@mail.nih.gov), provides sample shell scripts that make the above call and perform some housekeeping operations. A sample parameters file is also provided. MPGAfold recognizes nearly 100 parameters, most of which have either been used to tune its performance and should be changed very carefully, or specify less often used options. A subset of the parameters is listed below in the form of an input file, with the hash marks indicating comments (explanations and examples).

# SELECTED INPUT PARAMETERS most often modified by the user 
#
# PROCESSORS and GA POPULATION (Note: PhysicalPEs must not exceed the
# number of processors (NUM) specified in the call: mpirun -np NUM … PhysicalPEs = 8
totalVirtualPEs = 16384
#
# NUMBER of runs, offset for output file names, and limit of generations per run
startRun = 1 
stopRun = 100
outputStart =1
numGen = 1000
#
# INPUT and OUTPUT file specifications. 
sequenceFile = /home/username/DEN719/dengue-719.seq
OutputPath = /home/username/DEN719/gaout. dir/
FilePrefix = DEN719–16K
# Solution output type (ex: output population histogram peak structures)
dumpSolFlag = true
dumpSolType = peak 
#
# ENERGY rule set to be used (binary format tables provided with MPGAfold,
# including the H-type pseudoknot energies and stem-stacking energies - efn2) 
energyRule = 4
energyTableFile = /bin/GA.1.2.2/x86_64/GA.dir/ene/rule_4/energyRule_4.ene 
pkenergyTableFile = /bin/GA.1.2.2/x86_64/GA.dir/ene/rule_pk/pkenergy.ene
# Rule set 4 option 
efn2Flag = true
efn2energyTableFile = /bin/GA.1.2.2/x86_64/GA.clir/ene/rule_efn2/energyRule_efn2.ene
#
# SELECTED ALGORITHM PARAMETERS  
#
# RNGteeed = 0 - ncnGteterministic runs; other seed number - repeatable runs (keeping
# all other parameters unchanged)
RNGseed = 0
# Algorithm termination criterion (Z score) and window size (interval of generations)
# over which the score is calculated. 
convergenceCriterion = 0.0001 
windowWidth = 50
#
# CORRELATED STEMS parameters - expand the stem pool sampling process so that
# motifs consisting of stems separated by the loops specified below are selected as a unit 
motifFlag = true
loop1by1 = true 
loop1by2and2by1 = true 
loop2by2 = true
# Bulge motif Flag & Max bulge size in a motif 
loopbulge = true
bulgemotifsize = 2
#
# STEM FORCING or BIASING - allows for lists of stems to be included
# unconditionally (forced) or conditionally (inherited, if yielding best fit child)
# forceStemFile = /home/username/DEN719/UAR.stems
# stickyStemFile = /home/username/DENV719/DB5.sstem
#
# TRACING - track presence of user-specified stems in population
# (can also be visualized in the interactive runs).
# traceFile = /home/username/project/stems-to-trace-file.trace
# dumpTraceHits = true
#
# FOLDING with SEQUENCE ELONGATION parameters
# (ex: starting with a 30 nt-long fragment, add 2 nts at every GA generation) 
sequentialFoldFlag = false
# startSeqMax = 30
# ntsPerExtend = 2
# gensPerNuc = 1
#
# CROSSOVER, MUTATION and POPULATION SEEDING
# (parameters for probabilistic structure conflict resolution by peelback) 
peelToFitProb = 0.70
doCrossPeelToFit = true 
doMutPeelToFit = true
doNumfillPeelToFIt = false
#
# DISPLAY parameters for interactive runs (to be used with GUI front end) 
displayFlag = false 
pkDisplayFlag = false

MPGAfold outputs a list of parameters specified by the user and defaulted to by the program into a file name based on the FilePrefix parameter value and with extension “params,” which documents a run. A typical set of output files is enumerated below for a batch job generating a set of data from 100 individual MPGAfold runs. Other output may depend on the type and amount of data requested by the user via specific parameters, such as stem tracing, based on parameters traceFile and dumpTraceHits (i.e., keeping track of requested stems in the population throughout the run).

1. DEN719–16K8P-100sol.reg—output file with (concatenated) region tables of the final structures (histogram peak in this case). This kind of file was used to plot the solution space shown in Fig. 4.

2. DEN719–16K8P-100sol.ene—output file listing the free energies of the structures from the DEN719–16IK8P-100sol. reg file.

3. DEN719–16K8P-99.reg—one of the 100 output files (corresponding to the 99th run in this example), each containing region tables representing MPGAfold output at every generation on one run (see Fig. 5).

4. DEN719–16K.ene.hist_99—one of the 100 output files listing the population histogram at the end of every run; numbers of structures at all free energy levels observed in the population at the end of each run. This information may be helpful in deciding whether to run the algorithm at a higher population level, which in general tends to increase fitness of the dominant structures.

5. DEN719–16K8P-best-100sol.reg/ene—two files (region tables and energy data) analogous to the output files described in points 1 and 2, but with output reflecting the best fit structures encountered in the genetic algorithm populations that might not have reached the dominant status by the end of a run. Similarly useful as the population histogram information.

6. DEN719–16K.min/max/avg_99—one of the 100 output files listing minimum/maximum/average free energy in each generation of each run. This is auxiliary information useful in monitoring the energy landscape explored in the folds of a sequence.

7. DEN719–16K.convg_99—file tracking convergence of the population to a dominant solution at every generation of a run (99th run in this example). Output lists percentage of structures with the dominant free energy value and the Z-score (ratio of standard deviation to average population energy) within the convergence window (specified by the user as the windowWidth parameter).

8. DEN719–16K.efn2sol_99—an output file with stem stacking information for the final structures in runs utilizing efn2 calculations. The same information can be alternatively obtained from the secondary structure drawing and energy calculating applications within the StructureLab package.

To see a brief description of all MPGAfold parameters, one can issue the following help command:

prompt> mpirun -np 8 /path/GA.1.2.2/x86_64/GA.dir/bin/ ga_mpi -h

StemTrace was used to explore the generated solution spaces, as shown in Figs. 4 and 5, draw sample secondary structures presented in Figs. 6 and 7, and collect statistics on the motifs of interest present in final structures. Simple Unix shell scripts were used to collect the transient structure statistics from the individual runs (considering the observed minor variants, such as the CS long distance interactions 10 or 11 base pairs in length).

Fig. 6.

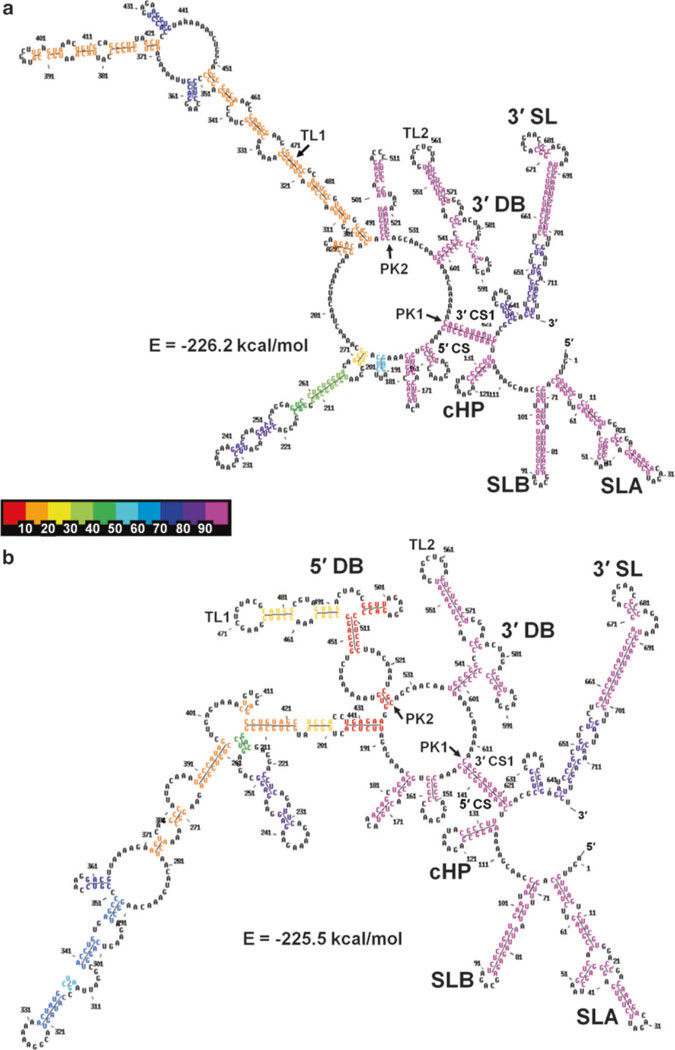
MPGAfold-predicted secondary structures of the DENV2 minigenome construct (719nt). (a) A best fit and most frequent structure from the 16K population level runs (−226.2 kcal/mol, run 15). It contains only the 3′ DB structural motif. (b) The 5′ DB motif was found in lower fitness (−225.5 kcal/mol, run 55), metastable structures. The color-coding of individual stems in the structures shown is based on their frequencies of occurrence in the ensemble of the final predicted (final results of 100 runs). The 10 bin color scale is shown in- between the panels, increasing from left to right in 10 % increments. As the two colors of the 5′ DB stems in (b) indicate, the TL1 arm of this DB, referred to as the 5′ DB head motif (5′ DBH) was predicted to be a part of more final structures (26 %, yellow) than the full 5′ DB (6 %, red) in the 16Kpopulation level runs

Fig.7.

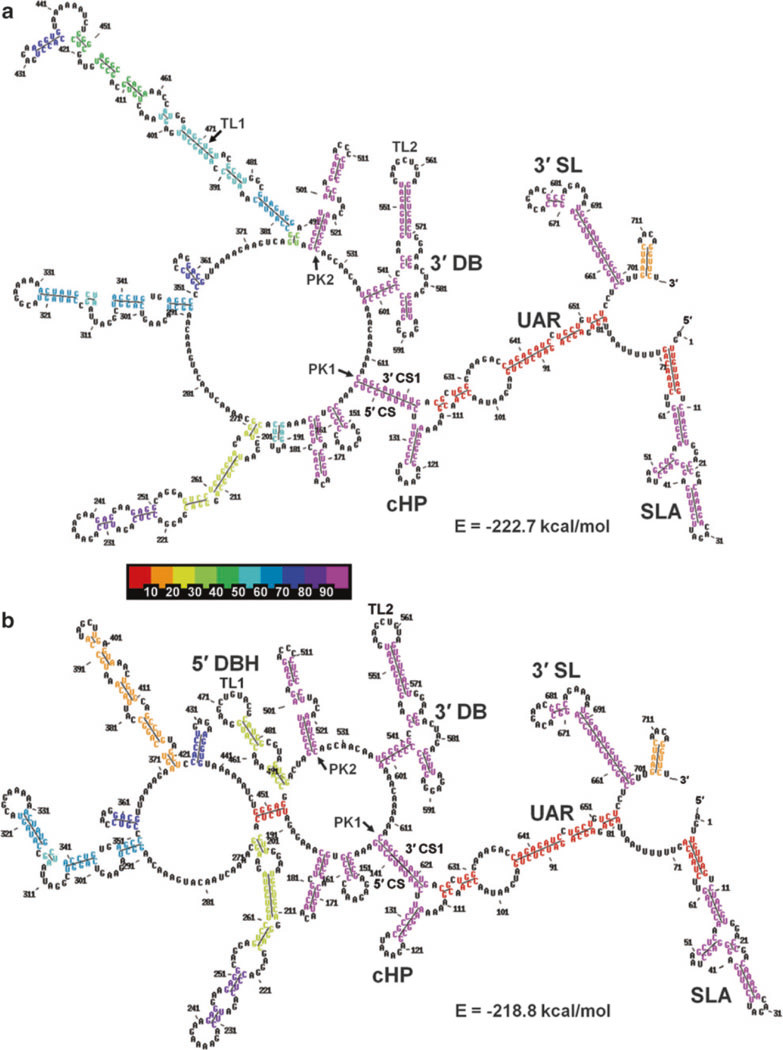
MPGAfold-predicted secondary structures of the DENV2 minigenome construct (719nt) that include the long-distance 5′−3′ UAR interactions predicted in 16K population level runs. (a) The best fit structure containing the long-distance UAR interactions (−222.7 kcal/mol, run 14) contains only the 3′ full DB. (b) The best-fit structure combining the UAR and the elements of the 5′ DB (head motif, 5′ DBH) has a lower fitness (−218.86 kcal/mol, run 68). The color-coding of individual stems in the structures shown is based on their frequencies of occurrence in the ensemble of the final predicted (final results of 100 runs). The 10 bin color scale is shown in-between the panels

3.5. MPGAfold- Predicted Secondary Structures of the Dengue Minigenome

MPGAfold was used to predict the secondary structure of the 719 nt subgenomic RNA from the DENV2 (minigenome). We employed energy calculations with and without the efn2 coaxial stem-stacking energy calculations (parameter energyRule = 4) [59]. The results illustrated in the figures included in this chapter are based on the efn2 results, and the differences in the prediction runs performed without the efn2 calculations are briefly discussed below. Of particular interest was the core region of the 3′UTR of the dengue virus, with the two dumbbell structures (5′ DB and 3′ DB), and the impact of experimentally tested mutations on dumb-bell formation. Given MPGAfold’s ability to identify energetically suboptimal metastable conformations, the analysis of the results included results of runs at multiple population levels and intermediate conformations in individual runs (see Fig. 5). The results presented here are derived from 100 independent MPGAfold runs at a 16,384 population level. For more information refer to our 2011 publication (and its supplemental information) in the Journal of Biological Chemistry [29].

3.6. Results of MPGAfold Runs with efn2 Calculations

MPGAfold was run with 100 repeats for each sequence/MPGAfold population combination, in order not to miss any potentially low frequency motifs. Theoretically, structural motifs that may occur in 5–10 % of the runs could be found only once or be missed completely in the solution spaces with only 20 repeats, for example. Also, the secondary structures predicted by MPGAfold for the dengue minigenome construct exhibit a fairly flat energy landscape, and the higher number of runs could help in a more thorough exploration of the potential conformations.

The best-fit final state structures in the range of −225.6 to −226.2 kcal/mol (and up to −227.1 kcal/mol in the 32K population runs, results not shown) contain the full 3′ DB, and the CS long-distance interaction. However, the 5′ DB is replaced in them by alternative long-distance interactions, and the long distance and UAR interactions are missing (Fig. 6a). The best fit structure including the full 5′ DB motif together with the 3′ DB reached the free energy level of −225.5 kcal/mol (Fig. 6b). Finally, structures combining the 3′ DB, CS and UAR reach the best fitness of −222.7 kcal/mol (Fig. 7a, run 14 in Fig. 4), while a structure adding the head motif of the 5′ DB to the above reaches a fitness of −218.8 kcal/mol (run 68 in Fig. 4). Structures combining the full 5′ DB and UAR were found only as intermediates in individual MPGAfold runs, the best-fit of them reaching −216.3 kcal/mol (run 61 in Fig. 4). Among the final structures predicted in 100 MPGAfold runs at a 16K population level, the 3′ DB is found in 97 % of runs. The frequency of occurrence of the 5′ DB among the final structures is, on the other hand, only 6 %, while the 5′ DBH submotif is found in 26 % of the solutions. However, searching all the individual 16K population level runs for additional transient structures containing the 5′ DB brings the frequency to 68 % of the runs and 94 % for the 5′ DBH. These numbers increase to 73 and 99 % for the 5′ DB and 5′ DBH, respectively, in the 32 K population level runs confirming a very strong, if transient, presence of the 5′ DB and its sub-motifs. It should also be considered that the best fit secondary structure with both full DBs is less than 1 % less fit than the best fit structures without the 5′ DB. Because both dumbbells can potentially form pseudoknot interactions between their TL and downstream PK sequences, these additional stabilizing interactions could change the energy landscape and allow the 5′ DB to “survive” until the end of the MPGAfold runs. At this stage we cannot calculate these pseudoknot energy contributions, because the TL1/PK2 and TL2/PK1 interactions are not of the H-type.

Full long distance UAR motifs (three individual stems) were predicted in 8 out of the 100 MPGAfold final solutions at a 16K population level (Fig. 4). Because the structures containing the UAR motif are more suboptimal than structures with the other monitored motifs, the UAR disappeared from the final solutions of the 32K population level runs, but it remained present in the intermediate structures at a relatively steady rate (35 % in 16K runs and 33 % in 32K runs).

3.7. Resultsof MPGAfold Co-transcriptional Runs Without the efn2 Calculations

In our earlier studies of the Hepatitis delta virus (HDV) we showed potential benefits of running MPGAfold in the co-transcriptional folding mode (folding with elongation) and without the efn2 calculations [65, 66]. Therefore we also tested these options with the DENV2 minigenome.

The mini genome construct was run 100 times without the efn2 component of the free energy calculations, both in full length folds and with sequence elongation (with 2nt added to the sequence per one GA generation).

Full length fold final structures contained a much higher percentage (54 %) of the full UAR, mostly because this motif was predicted to be part of the energetically best-fit structures. However, the frequency of the full 5′ DB (3 %) and 5′ DBH (11 %) went down among the final structures and the transient structures.

Despite the different fitness (free energy) rankings of the conformer types (structures with different combinations of the monitored motifs), the results of the co-transcriptional folding runs without the efn2 calculation at the 16K population level were very similar to the full length folding runs with efn2 calculations. The frequency of the full 5′ DBs was slightly increased (14 %), but the long-distance CYC motif frequency decreased (60 %) most probably due to the algorithmically delayed selection of the stems containing the 3′ CS1 sequence from the stem pool (as explained earlier in the “Other MPGAfold capabilities” section). Full UAR motifs were predicted with a comparable frequency in the final solutions (10 %). Overall, despite the changed free energy landscape, the difference in the frequencies of the key motifs was not altered significantly, and the unequal frequency of the occurrence of the difference in the 5′ and 3′ dumbbells was indicated by both folding options.

4. Summary

Our MPGAfold was used to predict the secondary structure of the 719 nt-long subgenomic RNA from the DENV2. The results agree with the experimental data with respect to the 5′ UTR and 3′ UTR structures SLA, SLB, 3′ SL and the cyclization long distance motif (CS/CS1). The other known long-distance interactions forming the UAR motif (and DAR) are predicted with a lower frequency in the lower fit (higher free energy) conformations, but are a constant feature in the intermediate structures in all the solution spaces. The analysis of MPGAfold results focused on the structures forming within the core region of the 3′ UTR. The results indicate that the minigenome RNA can fold into two dumbbell structures (5′ and 3′ DBs), but with different frequencies of occurrence for each dumb bell. Among the final structures predicted in multiple MPGAfold runs the 3′ DB is found in nearly all the runs at 16K (and 32K) population levels. In contrast, the frequency of occurrence of the 5′ DB and the 5′ DBH submotif is dramatically lower among the final structures. However, among the transient structures the 5′ DB, and even more so the 5′ DBH, are present in the majority of runs. The predicted variable frequency of occurrence of the two dumbbell structures offers a potential explanation of the fact that the TL1 and TL2 sequence motifs in the heads of the two dumbbells are not functionally identical despite having identical sequences within the two DBs. One has to keep in mind, however, that these structures have the propensity to form two potential pseudoknots between identical terminal loop sequences TL1 and TL2 and their complementary pseudoknot motifs, PK2 and PK1. It may be that the 5′ DB is stabilized by the TL1/PK2 pseudoknot interaction, the energy of which we cannot evaluate now in MPGAfold because it is not an H-type pseudoknot, and the additionally stabilized 5′ DB is an integral structural feature of the dengue virus structure, which may open under certain conditions. On the other hand, due to an overlap of the PK1 sequence with the strong cyclization motif (CYC), the other potential pseudoknot TL2/PK1 may not form, leaving the more stable 3′ DB with the TL2 sequence free to inter act. It is also conceivable that one or both of the dumbbell structures act as function-dependent structural switches. This idea would also be consistent with the experimental results indicating that the cis-acting RNA elements in the core region of DENV2 RNA, including the two DBs, are required for both RNA replication, as well as optimal translation. Recent SHAPE-based results [71] provide specific indications of the base pair interactions present in the minigenome, verifying the existence of the dumbbells and shedding further light on structural implications involved in the 3′ UTR.