Single-neuron correlates of error monitoring and post-error adjustments in human medial frontal cortex

Abstract

Humans can self-monitor errors without explicit feedback, resulting in behavioral adjustments on subsequent trials such as post-error slowing (PES). The error-related negativity (ERN) is a well-established macroscopic scalp EEG correlate of error self-monitoring, but its neural origins and relationship to PES remain unknown. We recorded in the frontal cortex of patients performing a Stroop task and found neurons that track self-monitored errors and error history in dorsal anterior cingulate cortex (dACC) and pre-supplementary motor area (pre-SMA). Both the intracranial ERN (iERN) and error neuron responses appeared first in pre-SMA, and ~50 ms later in dACC. Error neuron responses were correlated with iERN amplitude on individual trials. In dACC, such error neuron-iERN synchrony and responses of error-history neurons predicted the magnitude of PES. These data reveal a human single-neuron correlate of the ERN and suggest that dACC synthesizes error information to recruit behavioral control through coordinated neural activity.

eTOC Blurb

Fu et al. identified a single-neuron correlate of self-monitoring of errors in the human medial frontal cortex. Error neurons responded first in pre-SMA, followed by dACC. The activity of error neurons predicted the amplitude of the error-related negativity trial-by-trial.

Introduction

A fundamental feature of behavior is the ability to optimize performance based on outcomes (Ullsperger et al., 2014). In humans, performance failure can be monitored not only by explicit external feedback, but also through self-monitoring in the absence of such feedback. Successful detection of errors then initiates behavioral adjustments across various timescales. These include within-trial adjustment such as on-line error avoidance (leading to ‘covert errors’) (Bonini et al., 2014) and immediate correction of the response (Rabbitt, 1966), next-trial adjustment that requires cognitive control such as delaying an impending action (Laming, 1979, Ridderinkhof et al., 2004, Ullsperger et al., 2014), as well as more deliberate adjustments that span several trials to maximize potential rewards (Frank et al., 2005, Quilodran et al., 2008, Shima and Tanji, 1998).

Previous work on identifying the neural substrates for the different components of this behavioral feedback-control loop has revealed that the medial frontal cortex (MFC), which includes the dorsal anterior cingulate cortex (dACC, sometimes also referred to as anterior midcingulate cortex (Vogt et al., 2003)) and the pre-supplementary motor area (pre-SMA), serves a critical role for both monitoring and control (Ullsperger et al., 2014). While self-monitored errors are robustly signaled by the error-related negativity (ERN) (Gehring et al., 1993, Burle et al., 2008, Godlove et al., 2011, Falkenstein et al., 1991), no single-neuron correlates of this process have yet been reported in humans.

A second large topic concerns the changes in cognitive control that ensue either as a consequence of ongoing prediction of action outcomes, or subsequent to having detected an outcome such as an error. The MFC is also crucially involved in these processes (Kolling et al., 2016, Rushworth and Behrens, 2008, Kerns et al., 2004, Behrens et al., 2007, Brown and Braver, 2005, Shenhav et al., 2013, Sheth et al., 2012, Alexander and Brown, 2011). Such control can either trigger switching to a different action based on its estimated value, or influence the production of an action, such as delaying an action or adjusting the force with which an action is executed (Gehring et al., 1993, Ullsperger et al., 2014). As an example for the former, MFC neurons encode plans to switch to the alternative action triggered by a reduction of reward (Shima and Tanji, 1998, Williams et al., 2004, Kennerley et al., 2006). Similarly, MFC neurons signal the need to switch saccade directions in response to an externally cued rule change (Isoda and Hikosaka, 2007). Lesioning or pharmacological manipulation of the MFC disrupt such reward history-dependent alternative action selection (Shima and Tanji, 1998, Kennerley et al., 2006), illustrating a critical role for the MFC in explore – exploit decisions.

Less is known about the MFC’s involvement in control of action production triggered by monitored outcomes (mentioned above as the second type of behavioral adjustments). In the case externally cued response inhibition, electrical stimulation of the supplementary eye field or pre-SMA has been shown to delay saccades in service of avoiding errors (Stuphorn and Schall, 2006, Isoda and Hikosaka, 2007). These studies provide crucial causal evidence that MFC can influence action production, but the neuronal mechanisms that bridge monitoring to such control and the possible roles of other brain regions in this process remain unclear. Self-monitored errors, on the other hand, have a typical behavioral consequence: they can delay successive actions, a phenomenon known as the post-error slowing (‘PES’) (Ullsperger et al., 2014). Functional imaging studies have revealed the complex neural mechanism that may underlie PES with MFC being the central node of this control network. In this framework, the need for PES is signaled by MFC after detection of an error. PES involves inhibitory activity in the cortico-subthalamic pathways (Danielmeier et al., 2011, Aron and Poldrack, 2006, Aron et al., 2007), as well as adaptations in motor cortex (Danielmeier et al., 2011) and sensory processing and integration regions (Purcell and Kiani, 2016, Ullsperger and Danielmeier, 2016, King et al., 2010). This argument is principally supported by the finding that BOLD activation in dACC is correlated with the magnitude of PES (Kerns et al., 2004). In addition, in rodents, pharmacological inactivation of MFC abolishes PES (Narayanan et al., 2013).

A natural hypothesis thus links the detection of self-generated errors, as reflected in the ERN, with changes in cognitive control, as exhibited behaviorally in PES, predicting that the two measures should be correlated. However, several EEG studies have failed to find a significant relationship between PES and ERN (Gehring and Fencsik, 2001, Nieuwenhuis et al., 2001, Hajcak et al., 2003). Curiously, while BOLD activity in MFC predicts PES, the ERN does not. Based on these discrepancies in the literature, we tested a more detailed mechanistic hypothesis that might reconcile them. The ERN is thought to be produced by the summation of postsynaptic potentials within MFC and may thus, in part, reflect inputs to this region (Holroyd and Coles, 2002, Luck, 2014). One possibility explaining the aforementioned discrepancies is that the inputs to the MFC that produce the ERN only carry information about error monitoring, but not about the engagement of control. The computations within MFC that underlie cognitive control, while not reflected in the ERN, might instead be evident in oscillatory components in the LFP (Siegel et al., 2012, Pesaran et al., 2018) or in correlations between spike rates of neurons and the LFP (Nir et al., 2007). Such correlated neuronal activity could also explain why BOLD signals are associated with PES (Niessing et al., 2005).

Results

Task and behavior

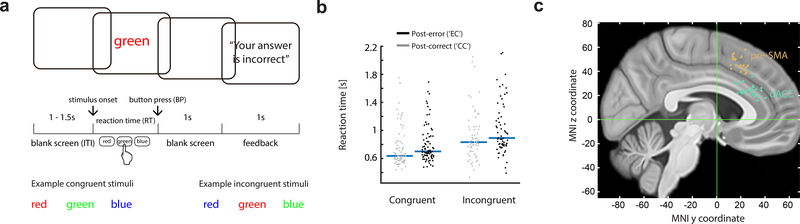
Subjects performed a color-naming Stroop task, which required subjects to name the color of words while ignoring their semantic meaning (Fig. 1a). RTs were longer on word-color incongruent trials than word-color congruent trials (the “Stroop effect”; 224.9 ± 19.2 ms difference, mean ± s.e.m. across sessions, F (1, 84) = 116.6, p < 0.001, mixed-effects one-way ANOVA). Subjects responded incorrectly (‘error trials’) in 7.2 ± 0.5 % (± s.e.m) of all trials. On correct trials that follow an error (‘EC’ trials), responses were significantly slower than on correct trials that follow another correct trial (‘CC’ trials) (Fig. 1b, amount of post-error slowing (‘PES’): 64.3 ± 11.0 ms, mean ± s.e.m. across sessions, mixed-effect one-way ANOVA, F (1,184) = 23.4, p < 0.001). To quantify PES for individual trials in the analysis below, we used sequences of ‘CCEC’ trials (see methods; median RT difference = 33ms, p = 0.0016, z = 3.154; signed rank test).

Figure 1. Task, behavior, and electrode localization.

(a)Task structure.

(b)Behavior. Each dot represents the mean RT of ‘EC’ or ‘EC’ trials of a session.

(c)Recording locations, projected onto the x=5 mm slice. Each dot represents the location of a micro-wire bundle in a patient.

See also Figure S1.

Single-neuron correlates of error self-monitoring

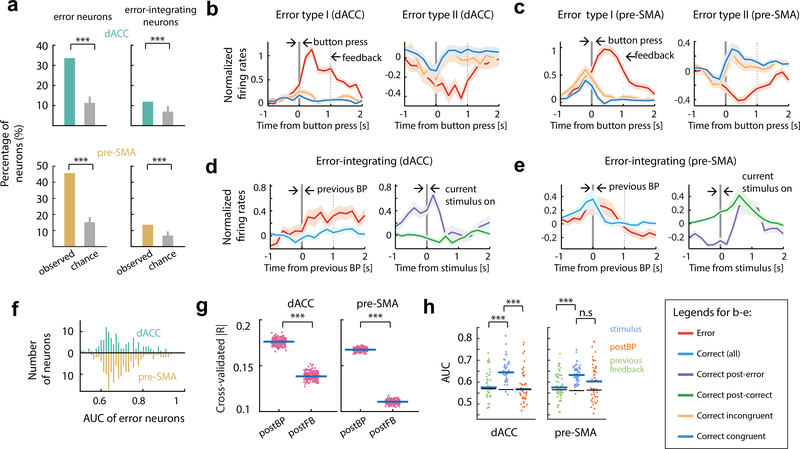
We isolated 1171 single units from dACC (n = 399) and pre-SMA (n = 431) across 29 patients (Fig. 1c, Table S1; see also Fig. S1a-c and Fig. S1d-i). Some neurons were in sessions with fewer than seven error trials and thus were excluded from the analyses that involve errors (number of neurons included in dACC is n = 399 and in pre-SMA is n = 431). Error neurons were identified using a Poisson regression model. Spike rates in a one-second epoch starting immediately after the action (button press) were regressed against trial labels (‘error’ or ‘correct’) and RTs. 34% (N = 134) of dACC and 46% (N = 198) of pre-SMA neurons signaled errors (see Fig. 2a-d, Fig. 3a, Fig. 3b-c, Fig. S2c-d and Table S2). We classified error neurons based on whether they had higher (“Type I”, error > correct, n = 99 and 118 in dACC and pre-SMA, respectively; see Fig. 2a,c and Fig. 3b,c, left) or lower (“Type II”, error < correct, n = 35 and 80 in dACC and pre-SMA, respectively, Fig. 2b,d and Fig. 3b,c, right) spike rates for error than correct trials. The responses of error neurons on individual trials differed reliably between error and correct trials as evaluated using receiver operating characteristic analysis (see methods and Fig. 3f): AUC values were, on average, 0.61 and 0.60 for dACC and pre-SMA, respectively (significantly greater than 0.5 with p < 10⁻¹⁰, t(133) = 12.86 and p < 10⁻¹⁰, t(197) = 18.5, respectively; t-test). AUC values of error neurons did not differ significantly between dACC and pre-SMA (Fig. 3f; p = 0.52, t(330) = 0.64, t-test).

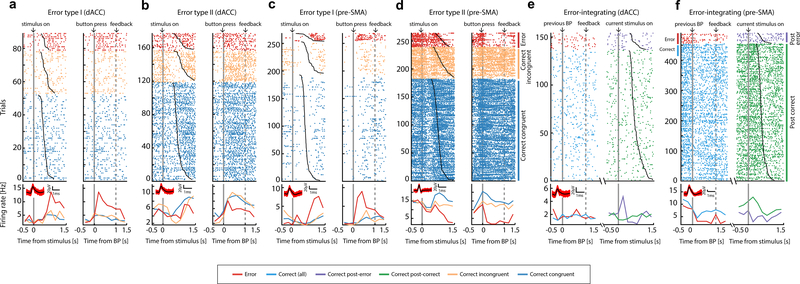
Figure 2. Examples of error and error-integrating neurons.

(a-d) Error neurons (e-f) Error-integrating neurons. (a-f) Raster (top) and mean spike rates (bottom) aligned at stimulus onset (left) and button press (right; ‘BP’) for (a-d); aligned to previous-trial button press (left) and to current-trial stimulus onset (right) for (e-f). Trials are sorted by reaction time (black line overlaying raster plots) and trial type (color; from top to bottom, error, correct incongruent, correct congruent for (a-d); ‘eC’ and ‘cC’ trials for (e-f)). Solid gray bars, time points for alignments. Broken gray bars, onset of feedback. Insets show the waveforms associated with each neuron and the corresponding scale bars.

Figure 3. Temporal profile of error and error-integrating neurons.

(a)Percentage of significant error and error-integrating neurons in dACC and pre-SMA. Gray bar is null distribution (mean and 95% confidence interval).

(b)Average standardized spike rates for all dACC error neurons, aligned at button press (t=0, gray bar). Broken bars, 1s after button press. Shading is ± s.e.m. across neurons.

(c)Same as (b), but for pre-SMA error neurons.

(d)Average standardized spike rates as a function of time for dACC error-integrating neurons, aligned at preceding-trial button press (left) or current-trial stimulus onset (right).

(e)Same as (d) but for the pre-SMA.

(f)ROC analysis. Error signal can be reliably decoded at the single-trial level (Type I and Type II pooled).

(g)Statistics for (b-c). Error neurons distinguished between error and correct trials more strongly after button press compared to after onset of feedback. Shown are cross-validated partial correlation coefficients across all error neurons (Type I and II pooled). Each data point represents the mean effect size across all error neurons in one cross-validation run.

(h)Statistics for (d-e). ROC analysis of the response of error-integrating neurons in three different time windows. The spike rates of error-integrating neurons differentiated between ‘eC’ and ‘cC’ trials in the peri-stimulus time window (blue; [−500ms 500ms] relative to stimulus onset) significantly better than those in the post-feedback period in differentiating between error and correct trials. Error bars, ± s.e.m. across neurons. Broken horizontal lines, the 97.5^th percentile of the null distribution.

‘*’, ‘**’, and ‘***’ mark statistical comparisons with p value <0.05, ≤0.01, or ≤0.001, respectively. ‘n.s’ marks not significant (p>0.05). BP=button press.

The majority of errors (67%) occurred on incongruent trials. Spike rates of error neurons on the error trials (within the post-action epoch; Fig. S2a) did not correlate with RT (Fig. S3a-b; for Type I error neurons, p > 0.4, t(98) = 0.86 in dACC, p > 0.5, t(117) = −0.41 in pre-SMA; for Type II error neurons, p > 0.5, t(34) = −0.54 in dACC and p > 0.5, t(79) = −0.63 in pre-SMA; t-test) and did not distinguish significantly between congruent and incongruent errors (Fig. S4a,c, see Fig. S4b,d for statistics). We thus pooled congruent and incongruent error trials in all subsequent analyses. Unlike the responses of error neurons, RTs were significantly longer on incongruent compared to congruent error trials (Fig. S4g; p < 0.001, t(57) = 4.03, paired t-test), arguing that errors were not due to lapses in stimulus processing.

While the neuronal error signal persisted into the post-feedback epoch (which appeared 1 sec after button press; Fig. 1a and Fig. S2a), the maximal spike rate modulation for both types of error neurons occurred before onset of feedback (Fig. 3b,c). An out-of-sample analysis of effect sizes (see Methods) confirmed this impression: spike rates of error neurons in the epoch between action and feedback onset carried significantly more information about the occurrence of an error than those in the post-feedback epoch (Fig. 3g; p < 10⁻¹⁰, t(199) = 98.3 in dACC, p < 10⁻¹⁰, t(199) = 288.2 in pre-SMA, paired t test). Thus, feedback onset did not reactivated error neurons or terminate their ongoing response on error trials (Fig. 3b,c). In summary, error neurons were action-triggered and encoded the detection of a mismatch between the intended action and the actual action performed.

Error-integrating neurons

We hypothesized that MFC neurons signal information about the history of self-monitored outcomes (Shima and Tanji, 1998, Kennerley et al., 2006). We identified a significant proportion of MFC neurons (see Fig. 3a; N = 46, 11.5% in the dACC; N = 58, 13.5% in pre-SMA, p < 0.001 for both areas, permutation test; also see Table S2) whose spike rates signaled whether the response in the preceding trial was an error or not (Fig. 2e-f, Fig. 3a, Fig. S2c-d). Response patterns of these ‘error-integrating’ neurons differed between dACC and pre-SMA: whereas dACC neurons (Fig. 3d) showed a peri-stimulus onset spike rate increase on trials that followed an error, responses in pre-SMA were characterized by an extended decrease starting in the pre-stimulus baseline period (Fig. 3e).

We next tested whether this response pattern was the result of error signals persisting from the preceding error trial, in which case the error-integrating neurons would also be classified as error neurons. While there was some overlap between the two categories (overlap: N= 12 and 20 for dACC and pre-SMA), many error-integrating neurons were not also error neurons (non-overlap: N= 34 and N=38 for dACC and pre-SMA, respectively). The time course of the population activity of all error-integrating neurons confirmed this: while these neurons did signal errors to some degree during the post-action epoch (definition see Fig. S2) on the preceding trial (Fig. 3h, orange; mean AUC for dACC 0.59±0.01, for pre-SMA 0.63±0.01; p < 0.05 versus chance for both areas, permutation tests), this error signal was attenuated after feedback (Fig. 3h, green; mean AUC for dACC 0.59±0.01, for pre-SMA 0.57±0.01), reinforced before stimulus onset, then continued on to after the stimulus onset on the next correct trial (Fig. 3h, blue; mean AUC for dACC 0.65±0.01, for pre-SMA 0.62±0.01; blue vs green, p < 0.001, z = 4.74 in dACC and p < 0.001, z = 4.72 in pre-SMA, rank sum test). In summary, we found error-integrating neurons carried a sustained error signal that was reinforced around stimulus onset on the subsequent trial, consistent with a putative role in post-error behavioral control.

Relationship between error and conflict neurons, and the signature of control

Conflict is thought to be the stimulus-evoked competition between a pre-potent but task-irrelevant response (reading the word) and a task-relevant response (the ink color) (Botvinick et al., 2001, Shenhav et al., 2013). In this framework, error signals are generated by conflict between the committed erroneous response and continuing development of the correct response. This implies that error neurons should not only signal errors, but also signal conflict as soon as it arises following stimulus onset. Here, we tested this hypothesis. We found that, as a group, the spike rates of error neurons within the post-stimulus epoch ([0 500ms] relative to stimulus onset; Fig. S2a) did not distinguish significantly between incongruent and congruent stimuli (Fig. S3c-d; see legend for statistics). For the second analysis, we first identified conflict neurons in both dACC (Fig. S3e; p = 0.03, N = 41, 6.7% of recorded neurons for Type I and p < 0.001, N = 43, 7% of recorded neurons for Type II; permutation tests) and pre-SMA (p < 0.001, N = 54, 10%, Type I only; permutation test), confirming earlier work (Sheth et al., 2012, Ebitz and Platt, 2015). These neurons changed their spike rates to signal conflict, with the signal culminating ~500ms after stimulus onset (Fig. S3f). The majority of error neurons were not conflict neurons (81% of error neurons in dACC and 87% of error neurons in pre-SMA were not conflict neurons) and vice-versa (Table S3). The number of neurons qualified as both error and conflict neurons was not significantly greater than what was expected if these two categories were independent (Fisher’s exact test for association, see Table S3). Also, error neurons are significantly more common in MFC relative to conflict neurons (28% vs 12%, p< 0.001, χ²(1) = 93.64, Chi-squared test). Thus, the substrates for error monitoring and conflict detection are largely separated at the neuronal level.

According to the model mentioned above, on an incongruent and correct trial, conflict arises accompanying stimulus onset and recruits cognitive control, which in turns resolves the conflict and results in a correct response. Neural activity reflecting conflict detection and the state of cognitive control are thus intermingled. To separate them, we compared spike rates within the post-stimulus epoch between error incongruent and correct incongruent trials for the previously identified groups of neurons. We found that, at the group level, only Type II error neurons in dACC (Fig. S3g) as well as conflict neurons in both dACC (Fig. S3j,k) and pre-SMA (Fig. S3l) carry a signature of control state according to this metric (See legend for statistics). We also confirmed these results by a multi-level Poisson regression model where the RT effect is controlled, with qualitatively similar results (data not shown). None of the other types of neurons changed their spike rates significantly to reflect the control state (p = 0.41, z = 0.82 for Type I error neuron in dACC; p = 0.87, z value = 0.16 for Type I error neuron and p = 0.26, z = −1.12 for Type II error neuron in pre-SMA; p = 0.17, z = −1.37 for error-integrating neurons in dACC, p = 0.24, z = −1.16 for error integrating neurons in pre-SMA; signed rank test). Notably, the Type I error neurons and error-integrating neurons in both dACC and pre-SMA did not carry this signature of control state, consistent a more specialized role in monitoring and control, respectively.

Waveforms of error neurons and error-integrating neurons

We quantified the duration of the extracellular waveforms of neurons (‘trough-to-peak time’) to differentiate between putative cell types (Bartho et al., 2004, Mitchell et al., 2007, Rutishauser et al., 2015). The distribution of spike duration is significantly bimodal in both dACC and pre-SMA (Fig. S5a,e; p < 0.001 for both areas, Hartigan’s dip test). 80% of neurons had broad waveforms (trough-to-peak time greater than 0.5ms), a feature indicative of putative pyramidal cells (Mitchell et al., 2007). Comparing the proportion of putative pyramidal and inhibitory neurons within each category with the overall population revealed that most error and error-integrating neurons are putatively excitatory (Fig. S5 legend for statistics).

Error neurons signal errors earlier in pre-SMA than in dACC

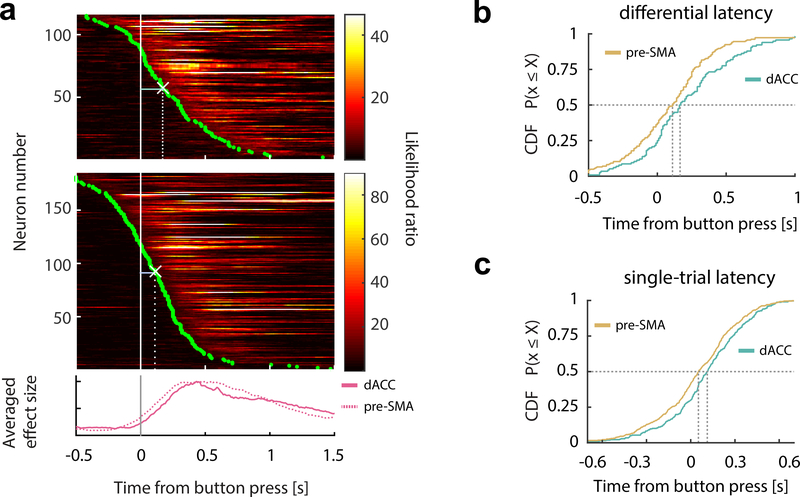
We next sought the point in time when error information first became available in each brain region. We first estimated the differential onset latency (the first point in time when the spike rates significantly differentiated between two conditions, see Methods), which showed that the error signal in pre-SMA occurred significantly earlier than in dACC by 55ms (Fig. 4a,b; median dACC latency, 165ms; median pre-SMA latency, 110ms; p = 0.002 and z = 3.05, rank sum test). A putative downstream readout (here a decoder), however, only has access to the response of an error neuron on a single trial. We used a Poisson-based method to detect, for each trial, the point of time the spike rate of a given error neuron departs significantly from the baseline (Type I only; see Methods for details). This analysis revealed that the error signal appeared first in pre-SMA 52ms after button press (Fig. 4c; p = 0.0025, z = 3.02, rank sum test), followed by the response in the dACC 60ms later (median difference). Repeating this analysis restricting to simultaneously recorded error neurons revealed quantitatively similar results (p = 0.002 and z = 2.89; one-tailed rank sum tests).

Figure 4. Error neurons in pre-SMA respond earlier than error neurons in dACC.

(a)Temporal profile of error information carried by the error neuronal population (Type I and II pooled), aligned at button press (gray bar) and sorted by the onset latencies of error information (green dots). Each row represents one error neuron in dACC (upper) or pre-SMA (middle). White crosses mark the medians of onset latencies. Bottom plot shows the average likelihood ratio normalized by the peak value (solid line, dACC; broken lines, pre-SMA).

(b)CDF of differential latencies (see Methods for details) are shown for error neurons.

(c)CDF of single-trial onset latencies for error neurons.

CDF=cumulative distribution function.

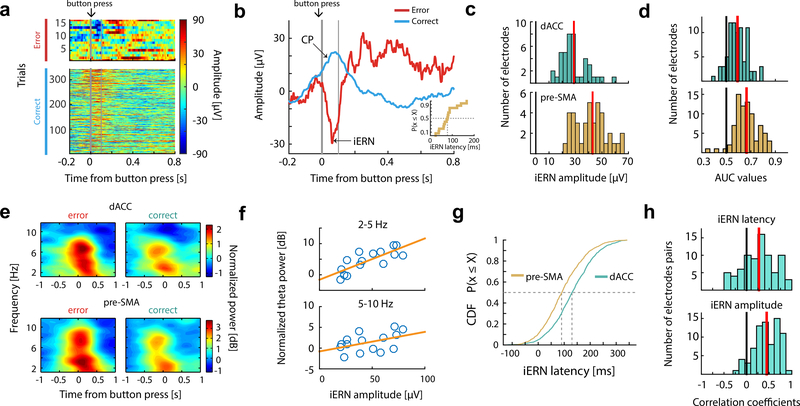
Error-related negativity (iERN)

Simultaneously with single neurons, we recorded the intracranial EEG (iEEG) using low-impedance macro contacts in both dACC and pre-SMA (see Table S1 and Fig. S1a). Following an erroneous button press, the iEEG revealed a prominent intracranial error-related negativity (iERN) visible on single trials in both dACC and pre-SMA (Fig. 5a-c, Fig. S6a-b). We also repeated the same task with scalp EEG in control subjects (see Methods) and found that the scalp ERN (Fig. S6c,d) had waveforms similar to the iERN, but with 5–10 times greater amplitude (Compare Fig. 5c and Fig. S6c). The extracted iERN amplitude values significantly distinguished error from correct trials (see Methods for details; Fig. 5d; median AUC for dACC electrodes is 0.59, p<10⁻¹⁰, z=7.72; median AUC for pre-SMA electrodes is 0.67, p<10⁻¹⁰, z=7.78; signed rank test).

Figure 5. Intracranial error-related negativity (iERN).

(a) Example single-trial event-related potentials recorded from dACC, sorted by RT (RT increases from top to bottom rows) and trial types. t=0 is button press. Thin vertical bar marks 100ms after button press.

(b)Average of data shown in (a) grouped by trial types (colors; red for error, green for correct), aligned at button press (t = 0, thick vertical gray bar). Inset, distribution of iERN latencies for the same data. Thin vertical bar marks 100ms after button press.

(c) Mean iERN amplitudes over all electrodes placed in dACC (green) and pre-SMA (brown). Red vertical bars show the median values.

(d)iERN amplitudes differ significantly between correct and error trials, evaluated using ROC analysis (see main text for details). Red vertical bars show the mean values.

(e)Spectral signature of the error signal. Power spectrum is aligned at button press (t = 0; averaged across n = 42 sessions). The region of power increase visibly splits into two frequency bands (2–5Hz and 5–10Hz). See Fig. S6e-f for statistics.

(f)Trial-by-trial correlation between iERN amplitude and slow-theta (2–5Hz; top) and (5–10Hz) power for the example session shown in (a,b).

(g)Comparison of iERN latency across all sessions. The iERN peak occurred significantly earlier in the pre-SMA compared to the dACC.

(h)Trial-by-trial correlation of iERN latency (upper) and iERN amplitude (lower) between pairs of iERNs recorded simultaneously in dACC and pre-SMA. For both, the correlation coefficients have a mean significantly greater than zero. Red vertical bars show the mean values.

Time-frequency analyses revealed that iEEG power increased following button press in two frequency bands: 2–5Hz (‘slow theta’) and 5–10Hz (‘theta’) on both error and correct trials (Fig. 5e), with a significantly stronger increase on error trials (Fig. S6e-f; see legend for statistics). Previous studies have demonstrated that volume conduction from the hippocampus can account for theta in neocortex (Sirota et al., 2008, Gerbrandt et al., 1978). For this reason, we next repeated the same analysis for simultaneously recorded hippocampal iEEG. This revealed that although there were significant differences between error and correct trials, these were of opposite sign (Fig. S6e-f; see legend for statistics), suggesting that the signals we reported in MFC are not volume conducted from the hippocampus.

Power increase in both bands (averaged within [−0.5s, +0.5s] around button press) was correlated with the iERN peak amplitude on the same trial (Fig. 5f shows this relationship for the data in Fig. 5a,b; Fig. S6g,h shows population summary; for theta-iERN correlation, mean correlation = 0.33, p < 10⁻¹⁰, t(78) = 12.15 in dACC and mean correlation = 0.41, p < 10⁻¹⁰, t(79) = 16.52 in pre-SMA; for slow theta-iERN correlation, mean correlation= 0.44, p < 10⁻¹⁰, t(78) = 19.2; mean correlation = 0.48, p < 10⁻¹⁰, t(79) = 19.4 in pre-SMA; mean-versus-zero comparisons, t-test). The ERN is thought to contain a combination of phase-locked theta-frequency band activity and non-phase-locked theta-frequency band power increases (Yeung et al., 2007, Trujillo and Allen, 2007, Wang et al., 2005, Luu et al., 2004). Induced theta power (Fig. S6i) alone in the same time-frequency region-of-interest was also significantly correlated with iERN amplitude (Fig. S6j-k; see legend for statistics).

Consistent with the spiking activity of error neurons reported above, the iERN amplitude, theta and slow theta power also did not differ significantly between congruent and incongruent errors (Fig. S4e,f; see legend for statistics). Although the iERN in dACC and pre-SMA had similar waveforms, their peak latency differed: the iERN occurred on average 40ms earlier in pre-SMA than in dACC (Fig. 5g; For a comparison with spike latency, see Fig. S6n; median dACC latency is 140ms, median pre-SMA latency is 100ms; p <10⁻¹⁰, z = 13.04, rank sum test; this effect held even after equalizing amplitudes across areas, p <10⁻¹⁰, z = 10.5, rank sum test). We also investigated the difference as well as correlation in latency and amplitude between pairs of simultaneously recorded iERNs. The distribution of these latency difference values between the iERN pairs have a significantly non-zero median (Fig. S6l; median = 18ms; p < 0.001, z =19.27, rank sum test), further confirming the leading role of pre-SMA. This latency difference also provides evidence against the hypothesis that the iERN is volume conducted because this would result in simultaneous onset (Logothetis et al., 2007). Similarly, the amplitude difference between iERN pairs was significantly positive (Fig. S6m; median = 11 μV; p < 0.001, z = 20.14, rank sum test). In addition, both the latency and amplitudes of pairs are significantly correlated (Fig. 5h; mean correlation coefficient for latency correlation is 0.27 and for amplitude correlation is 0.44; p < 0.001, t (77) = 6.81 for latency correlation and p < 0.001, t (77) = 0.29 for amplitude correlation, t test). Together, this data shows that the iERN is accompanied by theta and slow theta activity in MFC, and that the iERNs appeared earlier and with larger amplitude in pre-SMA.

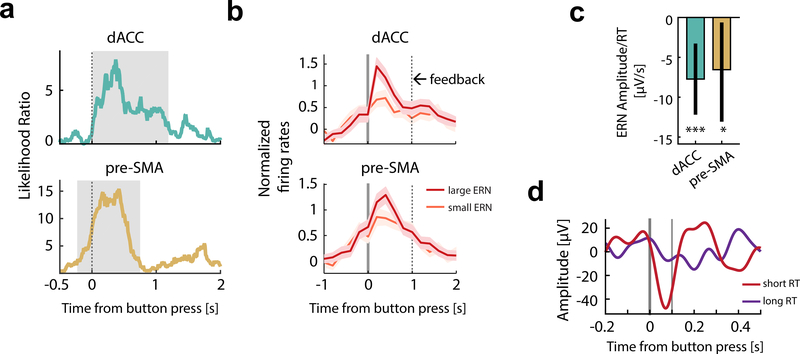
Linking spikes, iERN, and behavior

To gain insights into the processes that contribute to the iERN, we began by correlating its amplitude with the spike rates of error neurons. We used a multi-level linear model in which iERN amplitude was the dependent variable, and RT and spike rates were fixed effects. We then tested whether this model explained the data significantly better than a null model (see Methods). Here, the null model has the iERN amplitude as the dependent variable, and only RT as the fixed effect (and all the random effects remained the same as before). Note that only error trials were included in this analysis. The spike rates of Type I error neurons significantly co-varied with the iERN amplitude recorded in the same brain region in a trial-by-trial fashion (Fig. 6a, p = 0.01 for dACC error neurons, p < 0.001 for pre-SMA error neurons; cluster-based permutation test for the time course, details see Methods). This effect was evident at the single-cell level: each error neuron’s mean spike rate was greatest on trials with the largest iERN amplitude (Fig. 6b). This correlation began around action onset (button press), peaked ~400ms after erroneous actions with a maximal likelihood ratio of 7.9 for dACC and 15.4 for pre-SMA, and occurred earlier in pre-SMA compared to dACC (Fig. 6a). This is consistent with the shorter iERN latencies in pre-SMA reported above (Fig. 5g). This effect held when we used spike counts within the post-action epoch ([0 1s] after button press; Fig. S7a; p = 0.008, χ²(1) = 6.56 in dACC and p = 0.012, χ²(1) = 5.81 in pre-SMA). We found no significant correlation between iERN amplitude and spike rates of Type II error neurons (Fig. S7b; spike counts within [0 1s] after button press were used in the GLM; p = 0.19, χ²(1) = 1.64 in dACC, p = 0.07, χ²(1) = 3.36 in pre-SMA, likelihood ratio test) or non-error neurons (p > 0.1, cluster-based permutation test).

Figure 6. The iERN amplitude is correlated with error neuron spike rate and RT.

(a)iERN amplitude correlated significantly with the spike rates of error neurons (Type I). The likelihood ratio peaked around ~400ms after button press. t=0 is button press. Grey shading delineates the extent of the significant cluster as determined by a cluster-based permutation test. Note that the significant cluster started earlier in pre-SMA.

(b)Illustration of the relationship between iERN amplitude and spike rates of the error neurons (Type I). Color code: red for error trials with largest ERN (iERN larger than the 80^th percentile), orange for error trials with smallest ERN (iERN smaller than the 20^th percentile). t=0 marks button press. Solid bar marks button press; dotted bar marks feedback onset.

(c)iERN amplitude correlated significantly with RT. Bar plots represent values of regression coefficient for the fixed effect of RT in a mixed effect model. Error bars represent 95% confidence intervals (see Methods).

(d)Illustration of the relationship between RT and iERN amplitude (data from one session). iERN amplitudes were larger when the corresponding RTs were short (red; RTs shorter than the median) than when RTs were long (purple; RTs longer than the median). Thick vertical bar marks button press; thin vertical bar marks 100ms after button press. See panel c for statistics.

‘*’, ‘**’, and ‘***’ mark statistical comparisons with p value ≤ 0.05, ≤ 0.01, or ≤ 0.001, respectively.

Does the same relationship hold on correct trials? To answer this question, we first extracted the positive peaks on the correct trials as informed by the average ERP shape (Fig. 5b, see Methods). We then constructed a similar multi-level model but with evoked potentials on the correct trial (‘CP’) as the response variable, and spike rates of error neurons and RT on the same trial as fixed effects. We found no significant correlation between the evoked potential amplitude and spike rates of error neurons on correct trials (Fig. S7c; p = 0.34. χ²(1) = 0.92 for Type I error neurons and p = 0.74, χ²(1) = 0.11 for Type II error neurons in dACC; p = 0.88, χ²(1) = 0.023 for Type I error neurons and p = 74, χ²(1) = 0.11 for Type II error neurons in pre-SMA). The relationship between spiking activity and amplitude of evoked potential is thus specific to error neurons.

Each trial was characterized not only by whether an error occurred (indexed by error neurons) but also by its RT, which likely index the degree of cognitive control recruited as well as prediction of outcomes. Notably, RT and error neuron spike rates are internal variables indicative of different processes, as they were uncorrelated (Fig. S3a,b). We thus next investigated whether iERN amplitude might be correlated with RT using the same multi-level linear model approach (Fig. 6c). We found that larger iERN amplitudes were associated with shorter RTs in both dACC and pre-SMA (Fig. 6d shows this effect of RT on the iERN amplitude; Fig. 6c provides statistics; The significance of this RT effect was evaluated by a likelihood ratio test: For dACC, χ²(1) = 14.61, p = 0.0001; For pre-SMA, χ²(1) = 5.325, p = 0.021). This negative correlation was significant after controlling for stimulus congruence, which by itself would have resulted in RT differences (See Fig. S4g for RT comparisons for error trials; for dACC, χ²(1) = 9.54, p = 0.002; for pre-SMA, χ²(1) = 4.83, p = 0.028). Thus, the faster an error was made, the larger the iERN amplitude was on that trial. Together, these data revealed two distinct components of the iERN: one that is positively correlated with error neuron spike rate (action outcome information) and one that is negatively correlated with RT, putatively action-outcome prediction error (Alexander and Brown, 2011).

Neural signatures of PES in dACC

We next sought to determine which aspects of the performance monitoring circuitry interface with the control processes that result in PES. Note that previous efforts to correlate the magnitude of error monitoring signals measured using scalp EEG to PES have yielded contradictory results (Gehring and Fencsik, 2001, Debener et al., 2005, Nieuwenhuis et al., 2001, Hajcak et al., 2003). The evoked potential likely reflects synaptic inputs to a brain region. If so, this synaptic input would then subsequently cause the local responses we measure as spiking activity of neurons in the same region. Given this, we investigate the hypothesis that the ERN itself does not predict PES, but that the ensuing relationship between the ERN and the activity of error neurons does.

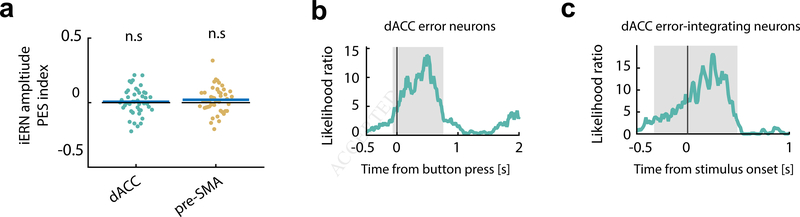
We first tested whether the amplitude of the iERN is indicative of PES. Error trials were separated into two groups (for each session): one that leads to PES larger than the median value, and the other that leads to PES smaller than the median value. We then assessed whether the iERN amplitude differed between these two groups (quantified by the ‘large/small PES’ index, zero equals no difference, see Methods). Consistent with some previous EEG studies (Gehring and Fencsik, 2001, Nieuwenhuis et al., 2001, Hajcak et al., 2003), we did not find a significant relationship between iERN amplitude and PES (Fig. 7a).

Figure 7. Error neuron-iERN synchrony during errors predicts engagement of control.

(a)iERN amplitude did not predict PES significantly. Mean values of the PES index (see Methods) for iERN amplitudes were not significantly different from zero. Blue bars denote mean values; black bars denote zero.

(b)The correlation between iERN amplitude and error neuron spike rates (as a function of time; quantified as the likelihood ratio in model comparison; see Methods) predicted the extent of post-error slowing (PES) in the dACC. t=0 is button press. Grey shading delineates the extent of the significant cluster as determined by a cluster-based permutation test (p < 0.05). The same analysis in the pre-SMA did not yield a statistically significant relationship.

(c)The spike rates of error-integrating neurons in dACC around the time of stimulus onset predicted PES.

‘*’, ‘**’, and ‘***’ mark statistical comparisons with p value ≤ 0.05, ≤ 0.01, or ≤ 0.001, respectively. Error bars represent ± s.e.m across cells.

We next investigated whether neural synchrony would predict PES. Here we assessed neural synchrony by the extent to which spike rates of an error neuron co-vary with the amplitude of the iERN (Nir et al., 2007). This correlation measure could also indicate the efficacy of iERN inputs in driving the local neuronal error signal that is important for control recruitment. We used a multilevel model (see Methods) to assess whether there was a significant interaction between spike rate of error neurons and the large/small PES categorical variable in predicting iERN amplitude trial-by-trial. This revealed that in dACC, the stronger the iERN- spike rate correlation around the time an error was committed, the larger was the subsequent PES (Fig. 7b; the maximal likelihood ratio is 13.9; p = 0.015 obtained by cluster-based permutation test. See Methods for details; the same analysis with Type II error neurons in dACC and both types of error neurons in pre-SMA did not yield a statistically significant relationship, see Fig. S7d,e). Note that while the strength of the correlation between the iERN and error neuron firing rate (in dACC) was thus predictive of PES, both underlying variables themselves were not (‘large/small PES’ index. p > 0.5, z = 0.46 for iERN and p > 0.5, z = −0.17 for spike rate within [0 1]s post button-press, signed rank test; See also Fig. 7a).

Error-integrating neurons in dACC signaled whether an error was committed in the previous trial by increasing their spike rates around stimulus onset. This pattern suggests that these neurons could be involved in implementing PES. To investigate this, we tested the relationship between spike rates of error-integrating neurons and PES (see Methods). Spike rates of dACC error-integrating neurons around the time of stimulus onset in post-error trials were significantly predictive of the size of PES (Fig. 7c; maximal likelihood ratio is 18.3; p < 0.001, cluster-based permutation test; as shown in Fig. 3d). This effect also holds if we used the spike counts within the peri-stimulus epoch ([−500ms 500ms] relative to the stimulus onset; Fig. S7f; p < 0.001, χ²(1) = 15.76, likelihood ratio test). We found no significant relationship between their spike rates and the levels of PES for pre-SMA error integrating neurons (Fig. S7f; p = 0.07, χ²(1) = 3.31, likelihood ratio test). We thus found two aspects of error monitoring that were predictive of the extent to which control was engaged (all in dACC only): iERN-error neuron spike rate coupling, and spike rates of error-integrating neurons. These two signals occurred at different points in time, suggesting that they are involved in bridging monitoring and corrective control.

Discussion

Here we provide direct recordings of single neurons in the human MFC that signal errors that are detected endogenously, before external feedback was presented and without the presence of an additional sensory signal to indicate task set (such as a stop signal). Error neurons were largely distinct from neurons signaling conflict shortly following stimulus onset, arguing that the representation of conflict detection and error monitoring in MFC are largely distinct. Conflict neurons were also modulated by the state of control: their activity differed between error incongruent and correct incongruent trials. This was not the case for Type I error neurons nor for error-integrating neurons, highlighting their putative roles in monitoring and actively mediating control, respectively. It remains an open question whether the error neurons that signal self-monitoring are functionally distinct from neurons that monitor external feedback, reward manipulations, or prediction errors that have been described in detail in macaques (Ito et al., 2003, Stuphorn et al., 2000, Scangos et al., 2013, Matsumoto et al., 2007, Matsumoto et al., 2003, Amiez et al., 2006, Ebitz and Platt, 2015, Hayden et al., 2011).

Despite evidence that the ERN (Gehring et al., 1993, Bonini et al., 2014, Brazdil et al., 2005, Godlove et al., 2011, Emeric et al., 2008, Falkenstein et al., 1991) originates from within dACC and/or pre-SMA (Dehaene et al., 1994, Debener et al., 2005), its relationship with neuronal spiking activity has not been clear. Our report shows that error neuron responses predict the amplitude of the iERN in both of these areas. Further, we showed that the iERNs recorded in pre-SMA 1) occurred earlier, 2) had larger amplitude, 3) were correlated in both amplitude and latency on a trial-by-trial basis with iERNs recorded simultaneously in dACC. These results are consistent with earlier studies (Bonini et al., 2014, Emeric et al., 2010). Our findings argue that both dACC and pre-SMA contribute to the ERN, but at different points in time.

This pattern of findings is consistent with two interpretations. One interpretation is that pre-SMA and dACC both receive inputs carrying error information in parallel, but pre-SMA receives the information earlier than dACC. This scenario is consistent with an influential computational account where synchronized disinhibition of dACC pyramidal cells by dopaminergic projections generates the iERN in dACC (Holroyd and Coles, 2002), and suggest that in pre-SMA similar disinhibition can also occur, but at earlier points of time. But a second possible interpretation is that pre-SMA provides error-related signals as an input to dACC, an interpretation which is consistent with a previous report where error-related evoked potentials in pre-SMA/SMA strictly precede those in the rostral cingulate zone (Bonini et al., 2014). Such a feedforward architecture could interpose additional relays as error signals are communicated indirectly from pre-SMA to dACC, for instance through the basal ganglia (Nachev et al., 2008, Jahanshahi et al., 2015). Future experiments utilizing causal manipulations will be necessary to probe the role of this putative feedforward connection in error processing.

Strong coupling between components of the LFP (here measured by the iERN) and spike rates is well documented in sensory cortices, where the coupling is often driven in part by common sensory inputs [but see (Kayser et al., 2004)]. However, in brain areas removed from direct sensory inputs, such as the hippocampus and inferior temporal cortex, these two measures of neural activity diverge and encode information independently (Kreiman et al., 2006, Ekstrom et al., 2007, Ekstrom, 2010). The strong and transient ERN-spike rate coupling in MFC reported we found is thus notable, because it shows that such phenomenon can occur in brain areas whose primary functions are not sensory information processing. Evoked potentials such as the ERN are thought to reflect spatial summation of large numbers of postsynaptic potentials that synchronize to a substantial degree. Previous work has demonstrated that variation in LFP – spike rate coupling strength is commensurate with the level of synchronization between two neurons within a local population (Nir et al., 2007) and that the LFP can serve as an index of local information content carried by neurons (Kreiman et al., 2006). The correlation between iERN amplitude and spike rates of error neurons we find here is likely a reflection of the neuronal synchronization that underlies the detection and representation of self-generated errors and/or more effective transmission of error information from other brain structures to the MFC. Notably, this relationship was specific to error neurons and to error trials: we found no significant correlation between similar deflections in the intracranial LFP during correct trials. It is thus likely the case that a separate group of neurons (which we did not describe here) receives the synaptic inputs that are synchronized during correct trials.

Post-error slowing is one of the most studied consequences of error detection. PES is thought to be jointly produced by two types of cognitive control processes. One type is concerned with sensory information processing, reflected in the up- and down-regulation of task-relevant and task-irrelevant sensory areas (Danielmeier et al., 2011, King et al., 2010), as well as adjustments to the parameters of parietal sensory integration processes (Purcell and Kiani, 2016). The second type is concerned with engagement of response inhibition by error monitoring, with MFC. BOLD activity within MFC is correlated with activity in task-related visual and motor areas, as well as the size of PES (Danielmeier et al., 2011, Kerns et al., 2004). Inactivation and lesioning of MFC abolishes PES (Narayanan et al., 2013, Kennerley et al., 2006), and individual differences in white matter integrity of inhibitory networks that include pre-SMA (Aron and Poldrack, 2006, Aron et al., 2007, Jahanshahi et al., 2015) are correlated with the size of PES (Danielmeier et al., 2011). Although these studies unequivocally demonstrate the involvement of MFC in PES, they do not provide insight into how MFC neurons communicate error signals to the control processes that mediate PES. Here, we show that neuronal synchronization may provide a basis for recruiting control by MFC. We find that the strength of the correlation between iERN amplitude and the spike rates of error neurons is predictive of PES in dACC (but not pre-SMA). This suggests that the more synchronized the dACC error neurons are with neighboring neuronal population during errors, the larger the ensuing PES is. Given that neuronal synchronization can potentially represent information with high fidelity (Rutishauser et al., 2010, Wong et al., 2016) and thus have stronger impact on downstream targets (Siegel et al., 2012), our finding suggests that neuronal synchronization may underlie dACC-mediated PES.

Our results suggest that coordinated neural activity can serve as a substrate for information routing that enables the performance-monitoring system to communicate the need for behavioral control to other brain regions, including those that maintain flexible goal information, such as the lateral prefrontal cortex and the frontal polar cortex (Koechlin and Hyafil, 2007, Tsujimoto et al., 2010, Mansouri et al., 2017, Voytek et al., 2015). The present study offers new insights into the mechanisms of ERN generation and provides potential neural targets for validating the use of the ERN as an endophenotype for psychiatric illness (Olvet and Hajcak, 2008).

STAR*Methods

Contact for Resource Sharing

Further information and requests for resources should be directed to the Lead Contact, Ueli Rutishauser (urut@caltech.edu).

Experimental Model and Subject Details

Depth electrode subjects.

29 patients (see Table S1 for age and gender) who were evaluated for possible surgical treatment of epilepsy using implantation of depth electrodes volunteered for the study and gave written informed consent. We only included patients with well-isolated single-neuron activity on at least one electrode in the areas of interest.

Scalp EEG subjects.

12 naïve non-surgical control subjects participated (seven females). All participants gave informed consent, and the protocol was approved by the Caltech Institutional Review Board. A BioSemi Active2 system collected EEG data and laptop event triggers at 1024 Hz. Electrode montages were in Biosemi’s standard 64 or 128 channel cap arrays, with additional electrodes for right eye vertical EOG.

Method Details

Task.

Subjects performed a speeded version of the classical color-word Stroop task. In each trial, the stimulus was chosen randomly to be one of the three words (red, green and blue) printed in either red, green, or blue color (see Fig. 1a). Subjects were instructed to indicate the color the word was printed in as quickly as possible (ignoring the meaning of the word) by pressing one of the three buttons on an external response box (RB-740, Cedrus Corp., San Pedro, CA). The stimulus was replaced with a blank screen immediately after the button press. One second after button press, subjects were given one of three types of feedback: correct, incorrect, or “too slow”. An adaptive staircase procedure was used to establish a reaction time threshold such that 10–15% of trials were rated as “too slow” regardless of the accuracy of the response. Correct trials with ‘too slow’ feedback were not considered as error trials. This dynamic threshold was implemented to encourage faster responses. The inter-trial interval varied randomly from 1–1.5s. The task was administered in blocks of 90 trials, 30–40% of which were incongruent (randomly intermixed). Patients performed 3 – 6 blocks in a session. Trials with RT larger than three standard deviations above the mean were excluded for all analyses. The task was implemented using the Psychophysics Toolbox (Brainard, 1997). Scalp EEG participants performed the same task as described above (350 trials total).

Electrophysiology.

We recorded from up to 4 electrodes in each subject (bilateral dACC and pre-SMA), each with eight high-impedance microwires at the medial end and eight low-impedance macro-contacts along the shaft (Fig. S1a; AdTech Medical Inc.). Here, we used only the most medial macro contact (which is located within the dACC or the pre-SMA) and all microwires. We recorded the broadband 0.1Hz-9kHz continuous extracellular signal with a sampling rate of 32–40kHz from each microwire and with a sampling rate of 2kHz from each macro-contact (ATLAS, Neuralynx Inc., Bozman, MT). One microwire on each electrode served as a local reference (bi-polar recording).

Electrode localization.

For each patient, two structural MRI scans were obtained: one before and one after implantation. Electrodes were localized based on these scans in each individual patient. Only electrodes that could be clearly localized to the dACC (cingulate gyrus or cingulate sulcus; for patients with a paracingulate sulcus, electrodes were assigned to the dACC if they were within the paracingulate sulcus or superior cingulate gyrus or the pre-SMA (superior frontal gyrus) were included. We also merged the subject-specific MRI onto an Atlas brain, which was used only for visualization purposes (all localization was based on individual MRIs without using an Atlas). We described the analysis pipeline for transforming the post-implantation MRI into the same space as a MNI152-based atlas previously

Spike detection and sorting.

We filtered the raw signal with a zero-phase lag filter in the 300–3000Hz band. Spikes were detected and sorted using a template-matching algorithm (Rutishauser et al., 2006). We carefully evaluated isolation quality of units and analyzed only well-isolated single units. We used the following criteria (see Fig. S1d-i): i) percentage of ISIs smaller than 3ms, ii) SNR of the waveform, calculated as the ratio of the peak amplitude of the mean waveform of each cluster and the standard deviation of the noise, iii) the pairwise projection distance as provided by the projection test (Pouzat et al., 2002) between all pairs of neurons isolated on the same wire, iv) the modified coefficient of variation of variability in the ISI (CV2), and v) the isolation distance (Schmitzer-Torbert et al., 2005, Harris et al., 2000), which we computed as previously defined (Rutishauser et al., 2006). Channels with inter-ictal epileptic events were excluded. All research protocols were approved by the institutional review boards of Cedars-Sinai Medical Center, Huntington Memorial Hospital and the California Institute of Technology.

Quantification and Statistical Analysis

Behavioral analyses.

We constructed a mixed-effect one-way ANOVA model with nested design to test for the Stroop effect. We entered reaction time (RT) as the response variable, the stimulus type (‘congruent’ or incongruent’) as the fixed effect and session numbers nested within subject ID as a random effect. To test for post-error slowing (PES) effects, we used two complementary approaches. First, we constructed a mixed-effect one-way ANOVA model with nested design, with RT as the response variable, the previous outcome and current trial stimulus type (‘congruent’ or ‘incongruent’) as the fixed effects and the session numbers nested within subject ID as the random effect. For this model, we also included an interaction term between the two fixed effects. Second, we identified quadruplets of trials that formed a ‘CCEC’ sequence (‘C’, correct trial. ‘E’, error trial) and the stimulus types (congruent or incongruent) were matched for the second and fourth trial within this sequence. This ensured that the PES measure was not confounded by the Stroop effect. For each quadruplet, we then defined the trial-by-trial PES as the difference in RT between the fourth and the second trial in this sequence. We then compared the mean of the trial-by-trial PES extracted this way with zero using a t-test to confirm the statistical significance of PES. This PES measure was used for subsequent iERN amplitude-error neuron spike rates correlation analyses and spike-field coherence analyses. This method restricted the post-correct trials to a subset that was directly preceded by the post-error trials to avoid confounding factors due to non-specific RT slowing, a caveat previously described (Dutilh et al., 2012).

Selection of neurons.

We only considered neurons that had a mean spike rate > 0.5 Hz. We sought neurons whose spike rate differed significantly between trial types of interest in two epochs that were defined with respect to stimulus onset or action onset (button press): (i) neurons signaling errors (‘error neurons’), (ii) neurons signaling preceding trial accuracy (‘error-integrating neurons’), (iii) neurons signaling conflicts We fit a generalized linear model (GLM) to each neuron (using matlab function “fitglm.m”) and then evaluated whether the model explained significant variance to determine whether a neuron was selective or not for a variable of interest. We entered the spike count in the epoch of interest as the response variable. We entered two predictor variables: i) a dummy variable coding for either trial outcome or previous trial outcome, and, ii) RT (to control for RT effect). A neuron was significantly selective for the outcome predictor variable if the p value for the first predictor was below 0.05 (p value as returned from the fitglm function). The epoch of interest for the error neurons was a 1 sec epoch starting immediately after button press (‘post-action epoch’ or ‘postBP epoch’, see Fig. S2a), comparing between error and correct trials. Only sessions with at least 7 error trials were considered for selecting error neurons, a minimum number of errors that has been demonstrated to be sufficient for stable error signals (Olvet and Hajcak, 2009). The epoch of interest for error-integrating neurons was −0.5 to 0.5s (1s length) centered on stimulus onset (‘peri-stimulus epoch’, see Fig. S2a), comparing between EC and CC trials. The epoch of interest for conflict neurons was 0 to 0.5s after stimulus onset (‘post-stimulus epoch’, see Fig. S2a), comparing between correct congruent and correct incongruent trials.

Each group of neurons was further divided into two sub-categories according to the sign of the spike rate difference (the sign of the regression coefficient of the outcome variable predictor; Type I and II, respectively; Fig. S2b). To estimate chance levels of this selection procedure, we repeated the selection procedure (two-tailed bootstrap) 1000 times after randomly permuting the labels to estimate a null distribution (see Fig. 3a; for conflict neurons, see Fig. S3e). We only analyzed groups of neurons larger than expected by chance (p < 0.05).

Single-neuron and group-averaged post-stimulus time histograms (PSTHs) were constructed using non-overlapping bins of 200ms width. PSTH plots were not smoothened and data points were plotted with respect to the center of the bin. Before averaging across neurons, spike rates for each neuron were standardized by subtracting the mean and dividing with the standard deviation of the baseline (−0.7 to −0.2s relative to the stimulus onset).

Single-neuron ROC analysis.

For each neuron, a receiver-operating characteristic (ROC) curve was constructed based on the spike rate in the time windows of interest. The ROC was parametrized by a threshold that varied from the lowest to the highest spike rates in 25 linearly-spaced steps. For each threshold, trials were classified as ‘label 1’ or ‘label 2’ according to whether the spike rate in a given trial was higher or lower than this threshold. True positive rates (‘TPR’) and false positive rates (‘FPR’) were then derived by comparing the assigned labels with the true labels for each threshold. The area under the curve (AUC) of the ROC was used as a summary metric. In order to aggregate AUCs from different neurons, we always assigned the trial type with higher spike rates in the ROI to ‘label 1’. We estimated the AUC values expected by chance by a permutation test.

For the error neurons (Both Type I and Type II, Fig. 3f), we computed AUC values using error- and correct-trial spike rates in the post-action epoch (0–1s relative to button press). For the error-integrating neurons, we computed AUC values for the spike rates estimated from the following three epochs: (i) 0–1s relative to feedback onset (error vs correct) in the preceding trials, (ii) −0.5–0.5s relative to stimulus onset (‘peri-stimulus epoch’) in the current trials (EC vs. CC) and (iii) 0–1s after button press in the current trials (‘postBP epoch’; error vs correct).

Temporal profile of neuronal response.

We used a sliding-window GLM to quantify the temporal profile of information conveyed by neuronal spike rates of a single neuron about trial outcome (error vs. correct; Fig. 4a). We first used a ±200ms bin moved across the spike train on each trial in successive 10ms steps. For each of these bins, we entered the spike count as the response variable and the trial outcome (error or correct) as one predictor variable, and RT as another predictor variable. This is because spike rates of the neurons in both dACC and pre-SMA can carry a component that covariates with reaction time (RT) and the effect of trial outcome on spike rates can be isolated after regressing out the RT effect in this principled way. For each bin-wise GLM model, the effect size of the trial outcome was quantified by a likelihood ratio, derived from a likelihood ratio test comparing the full model with null model (full model minus the trial outcome predictor). We used the time course of the likelihood ratio to estimate for each neuron the point of time at which it first differentiated between trial outcomes (error vs correct; Fig. 4b). These differential latencies were determined as the first point of time at which the effect size was significant by the likelihood ratio test (p < 0.05) for a consecutive 15 time steps (i.e 150 ms).

We used a cross-validated partial correlation analyses to determine the time window (post-action vs. post-feedback) in which a population of neurons conveyed the most information about error (Fig. 3g). Here, a Spearman’s partial correlation coefficient was computed by correlating the spike rates of error neurons in the postBP epoch, and the trial outcome dummy variable (error coded as 1, correct coded as 0), while controlling for RT on the same trial. Statistical comparisons between group averages of partial correlation coefficients in different time windows were made using Wilcoxon’s rank sum test. However, the group averages in the same time window used to previously select neurons is biased towards larger values. Here, we circumvented this problem by using cross validation to assure that the group averages were computed from out-of-sample data not used for selection. For this, we performed 200 runs of cross validation. In each run, we randomly subsampled 80% trials for selecting neurons and used the remaining 20% of trials to compute the partial correlation coefficients between spike rates and the relevant trial variable (levels of stimulus congruence or outcomes). The partial correlation coefficients used for the statistical comparisons were thus not biased by selection.

Single-trial spike train latency.

We estimated the onset latency in individual trials using Poisson spike-train analysis (Fig. 4c). This method detects points of time at which the observed interspike intervals (ISI) deviate significantly from that assumed by a constant-rate Poisson process. This is achieved by maximizing a Poisson surprise statistic (Hanes et al., 1995). We used the average spike rate of each neuron as the baseline rate of the underlying Poisson process. Since the error signal is related to action completion, we required that the detected bursts of spikes ended after the action was completed to exclude activation unrelated to button press. We included spikes in a window 300–2000ms after stimulus onset. The statistical threshold for detecting an onset was p < 0.01. Repeating the same procedure with a threshold of p < 0.001 did not affect our conclusions.

Single-trial iERN amplitude and latency extraction.

We determined the amplitude and latency of the iERN on individual trials using the following algorithm. First, for each electrode we determined the peak position of the average iERN waveform within a time window of [−50ms 200ms] relative to button press. We then defined a time window of 200ms centered on the peak of the average iERN as the region of interest for single-trial estimation. For each trial, we used ‘findpeak’ (MATLAB) to identify all local negative peaks within this time window and then picked the local peak closest to the peak position of the averaged iERN. The rationale for this approach is to determine the contribution of each single trial to the average iERN. Since the timing of the iERN is well understood and known (from the average), the negative peak closest in time has the highest likelihood of being the true single-trial iERN signal. The point of time (relative to button press) and absolute value of the potential of this negative-going peak was then used as the single-trial iERN latency and amplitude. In Fig. 7a, we assessed whether iERN amplitudes differed between PES levels using a PES modulation index computed from the iERN amplitudes. For this, we first separate the error trials into two groups: one that leads to PES values larger than the median value, and one that leads to PES values smaller than the median value (of this experimental session). We then compute the mean iERN amplitude across these two groups of error trials separately. The PES modulation index is equal to the difference of these two mean values divided by their sum.

Single-trial CP amplitude and latency extraction.

We determined the amplitude and latency of the CP on individual trials using the following algorithm. First, for each electrode we determined the peak position of the average iERN waveform within a time window of [−50ms 200ms] relative to button press. We then defined a time window of 200ms centered on this average CP peak position as the region of interest for single-trial estimation. For each trial, we used ‘findpeak’ (MATLAB) to identify all local negative peaks within this time window and then picked the local peak closest to the peak position of the averaged CP. The absolute value of the potential of this positive-going peak was then used as the CP amplitude.

ROC analysis of iERN.

For each electrode, a receiver-operating characteristic (ROC) curve was constructed based on the voltage values extracted by the iERN extraction algorithm (see above) on error and correct trials. The ROC was parametrized by a threshold that varied from the lowest to the highest voltage values in 25 linearly-spaced steps. For each threshold, trials were classified as ‘label 1’ or ‘label 2’ according to whether the voltage value on a given trial was higher or lower than this threshold. True positive rates (‘TPR’) and false positive rates (‘FPR’) were then derived by comparing the assigned labels with the true labels for each threshold. The area under the curve (AUC) of the ROC was used as a summary metric and characterizes how well the iERN amplitude on a given trial is indicative of whether the response was correct or incorrect.

Time-frequency analysis of iEEG signal.

We used the Hilbert transform to generate time-frequency representations of the iEEG signal. The continuous raw signal (for the entire task) was first down-sampled from 2kHz to 500Hz and then filtered with fourth-order Butterworth filters centered at 28 linearly-spaced frequencies between 1.2 to 11.7Hz. We used ‘filtfilt.m’ (MATLAB) to ensure zero-phase distortion and then Hilbert-transformed the filtered data to obtain the corresponding instantaneous amplitude and phase values. Next, we segmented this signal into trials with respect to time of stimulus onset or button-press separately. Trials with raw voltage amplitudes larger than 150uV were excluded (<1% of trials were excluded). Power estimates for each frequency bins were generated by squaring the corresponding instantaneous amplitude, averaged across trials and then combined to form a time-frequency representation. For this, we equalized the trial number and RT across conditions. For normalization, time-frequency spectrograms were divided by the corresponding baseline power for each frequency band and log-transformed into decibels (dB). Baseline power was estimated by averaging across all trials in the pre-stimulus epoch (−0.7s to −0.2s relative to stimulus onset). To test for a correlation between iERN amplitude and theta-band power, we computed the Spearman’s rank correlation coefficient for each session and tested the mean of correlation coefficients versus zero. To analyze induced power, we repeated above analyses after subtracting event-related potentials. For this, we first computed the event-related potentials and then subtracted these from each trial for each condition (error and correct trials) separately.

Multi-level models.

We constructed linear multi-level models (Aarts et al., 2014, Winter, 2013) to test for relationships between RT, iERN amplitude, and error neuron spike rates. For all of the following analyses, we used only data from error trials. For Fig. 6a, in the bin-wise model we entered iERN amplitude as the response variable, spike counts in each ±300ms bin (the center of the bin moved from −0.5s to 2s relative to button press in steps of 10ms) and RT as the fixed effects, session number as the random intercept and cell number nested within subject ID as the random slope for the effect of spike counts. For Fig. 6c, we entered iERN amplitude as the response variable, RT as the fixed effect, session number as the random intercept and session number nested within subject ID as the random slope for the effect of RT. For Fig. 7b, the model setup is the same as that in Fig. 6a except that we added a dummy variable (‘PES levels’) indicating whether an error trial corresponds to larger (assigned “1”) or smaller (assigned “0”) PES than the median PES (of the session) and estimated it as the main effect and its interaction with the spike counts. For Fig. 7c, the bin-wise model has the spike rates of error-integrating neurons within each ±300ms bin as the response variable, the PES level and RT as the fixed effects and session number nested within subject ID as the random slope for the effect of RT. For Fig. S7d, the spike counts of error neurons used in the models were all within the postBP epoch ([0 1s] after button press). The statistical significance of all the models described above was evaluated by a model comparison approach(Winter, 2013). Using the likelihood ratio test, we derived the likelihood ratio by comparing the full model and a null model obtained from the full model by removing the effect of interest, leaving all the other fixed or random effects unchanged. The log likelihood ratio distributes asymptotically as a chi-squared distribution and a theoretical p-value can be computed. For Fig. 6a and 7b-c, we performed cluster-based permutation test to control for multiple comparison (Maris and Oostenveld, 2007). To generate an empirical null distribution (1000 permutations) of likelihood ratio for each bin, we permuted the iERN amplitude data so that each iERN amplitude no longer matched with the spike rate data, while keeping the rest of the model unchanged. We then derived the likelihood ratio using the permuted data by the same model comparison approach. During each iteration, we thresholded the likelihood ratio at the value of 3.84 to identify connected clusters, and then computed the sum of likelihood ratio from each cluster and took the maximum of these sums as the test statistic. The true statistic for the cluster (computed using original un-permuted data) was finally compared with the empirical null distribution to derive a p-value.

Scalp EEG – Analysis.

Data were analyzed using Brainstorm 3 (Tadel et al., 2011). Data was re-referenced to average, and then band-pass filtered between 1–16 Hz. Eye-blinks were automatically marked and artifacts removed via peak detection in the VEOG and signal space projection algorithms. Button-press events were added to the EEG record based on the stimulus onset triggers and precise reaction times recorded by the response box (RB-740, Cedrus Inc.). Trial epochs were baseline corrected by the mean potential from −0.7s to −0.2s relative to button-press. To balance correct and error trials in number and reaction time, each subject’s correct trials were subsampled by selecting the trials with the RTs most closely matching each error trials’ RTs. ERPs were calculated for each subjects’ error trials (ERN) and correct trials (CRN). ERN statistics were calculated by taking each subjects’ ERP peak negativity between −50ms to 200ms relative to the button press. ERN and CRN peaks were compared across subjects by paired t-test. The control subjects demonstrated a robust Stroop effect (65.2 ± 0.9ms, mean ± s.e.m. across sessions, F(1,11) = 54.07, p <10⁻¹⁰, mixed-effect one-way ANOVA with random effect) and post-error slowing (69.0 ± 22.3ms, mean ± s.e.m. across sessions, F (1,32) = 7.3, p = 0.01) and made errors in 14.8 ± 1.3% of trials. During error, but not correct, trials the scalp EEG site Cz revealed an evoked potential analogous to the classical signature of error monitoring expected in this task: the error-related negativity (ERN) (Fig. S6c; mean peak amplitude −50−200 ms relative to button press, paired t-test t (11) = 4.53, p < 0.001). The theta power in error trials is significantly stronger than in correct trials (Fig. S6d; [0 500ms] relative to button press, 2–10 Hz in frequency, paired t-test t(11) = 6.47, p < 0.001).

Waveform analyses.

For each neuron, we extracted the trough-to-peak time d as the duration between the first negative peak of the mean waveform (‘trough’) and the first positive peak after the trough (Rutishauser et al., 2015). The mean waveform is obtained by averaging all the waveforms assigned to a particular cluster. We normalized the mean waveforms by its maximal amplitude and inverted the few waveforms that have the opposite polarity. We considered neurons with a trough-to-peak time < 0.5 as ‘narrow-spiking’ neurons and those >0.5s as ‘broad-spiking’ neurons.

Data and Software Availability

The spike detection and sorting toolbox OSort was used for data processing, which is available as open-source. Data and custom MATLAB analysis scripts are available upon reasonable request from Ueli Rutishauser (urut@caltech.edu).

Highlights.

• Single neurons in the human medial frontal cortex signal self-monitored errors

• Pre-supplementary motor area error signals precede those in anterior cingulate cortex

• Intracranial error-related negativity amplitude correlated with error neuron activity

• iERN amplitude-error neuron spike rate correlation predicts post-error slowing