GLANET: genomic loci annotation and enrichment tool

Abstract

Motivation

Genomic studies identify genomic loci representing genetic variations, transcription factor (TF) occupancy, or histone modification through next generation sequencing (NGS) technologies. Interpreting these loci requires evaluating them with known genomic and epigenomic annotations.

Results

We present GLANET as a comprehensive annotation and enrichment analysis tool which implements a sampling-based enrichment test that accounts for GC content and/or mappability biases, jointly or separately. GLANET annotates and performs enrichment analysis on these loci with a rich library. We introduce and perform novel data-driven computational experiments for assessing the power and Type-I error of its enrichment procedure which show that GLANET has attained high statistical power and well-controlled Type-I error rate. As a key feature, users can easily extend its library with new gene sets and genomic intervals. Other key features include assessment of impact of single nucleotide variants (SNPs) on TF binding sites and regulation based pathway enrichment analysis.

Availability and implementation

GLANET can be run using its GUI or on command line. GLANET’s source code is available at https://github.com/burcakotlu/GLANET. Tutorials are provided at https://glanet.readthedocs.org.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

High-throughput sequencing technologies are routinely used for cataloging genomic variants (McVean et al., 2012), profiling protein-DNA interactions, histone modifications (ChIP-seq), DNA methylation (e.g. BS-seq), and mapping of accessible chromatin (e.g. DNase-seq). Analyses of these experiments reveal sets of genomic intervals. Assessing the functional relevance of these genomic intervals requires integrating them with already known genomic and epigenomic annotations.

There are available tools for annotation and enrichment analysis of genomic regions. They are equipped with different functionalities with respect to the types of the inputs, annotation libraries, enrichment tests, and further, if any, downstream analysis they enable. We provide a comprehensive summary of these tools in Supplementary Table S1.

FunciSNP (Coetzee et al., 2012), HaploReg (Ward and Kellis, 2012), ALIGATOR (Holmans et al., 2009), Annotate-it (Sifrim et al., 2012), PANOGA (Bakir-Gungor et al., 2014) and FORGE (Dunham et al., 2015) only accept SNPs as input. ENCODE ChIP-Seq Significance Tool (Auerbach et al., 2013) is similarly limited by providing annotation and enrichment only for input gene lists. RegulomeDB (Boyle et al., 2012), SnpEff (Cingolani et al., 2012), Ensembl SNP Effect Predictor(VEP) (McLaren et al., 2010), ANNOVAR (Wang et al., 2010) and FunciSNP do not provide enrichment analysis.

There are a few tools available for annotation and enrichment analysis of longer genomic intervals (Heger et al., 2013; Lee et al., 2012; McLean et al., 2010). These are generally restricted by the annotation libraries they utilize. For example, INRICH tests for enrichment of only pre-defined gene sets (Lee et al., 2012). GREAT (McLean et al., 2010) takes a set of non-coding genomic regions and provides analysis with respect to the annotations of nearby genes. The enrichment analysis in GREAT does not take into account potential genomic biases involved in generation of the input genomic regions. GAT (Heger et al., 2013) takes as input genomic intervals and user-provided annotation libraries. Compared to INRICH and GREAT, GAT enables users to input a workspace to define a subset of the genome for estimating appropriate null distribution during enrichment analysis. However, GAT’s built-in capabilities are restricted, and it does not work with gene-sets. Furthermore, it relies on the user to define and provide input files to specify where the random samples will be generated from. This knowledge; however, is often not available to the user. On the other hand, GLANET adjusts for GC and mappability biases by matching each input interval with its default library. In summary, there are a number of notable shortcomings of the existing tools.

We developed GLANET both as an annotation and enrichment tool with several useful built-in analysis capabilities. GLANET annotation library includes a rich set of genomic intervals. Users can easily annotate their input intervals with the genomic elements defined in the annotation library. The genomic library includes (i) regions defined on and in the neighborhood of coding regions that encompass regulatory regions; (ii) ENCODE-derived potential regulatory regions that encompass binding sites for multiple transcription factors, DNaseI hypersensitive sites, modification regions for multiple histones across a wide variety of cell types; and (iii) gene sets derived from KEGG (Kanehisa et al., 2012) pathways and Gene Ontology (Ashburner et al., 2000) annotations. GLANET also allows the expansion of annotation library with user-defined gene sets and/or genomic intervals; with this feature users can design and conduct custom analysis of their inputs.

In order to evaluate whether the input intervals overlap significantly with the genomic elements in the GLANET annotation library, GLANET implements an enrichment procedure that accounts for mappability (Cheung et al., 2011; Chung et al., 2011; Rozowsky et al., 2009) and GC content (Benjamini and Speed, 2012; Chen et al., 2013; Dabney and Meyer, 2012) biases inherent to NGS. When the input intervals are derived from an NGS experiment, these biases constrain regions of the genome that can contribute to interval generation. Few of the existing tools account for these biases. For example, Forge (Dunham et al., 2015) randomly samples SNPs from regions that match the GC content of the input SNPs to estimate a null distribution for enrichment testing. GAT (Heger et al., 2013) divides the genome into isochore families that have similar GC content and performs sampling for each isochore separately and, as a result, provides a coarse level matching of GC content. As opposed to operating on the average properties of the input intervals, GLANET estimates a null model from randomly sampled intervals that match each interval of the input in terms of chromosome, length, mappability and GC content. Although this sampling strategy is computationally intensive, GLANET conducts these analyses rapidly by deploying efficient search strategies enabled by appropriately constructed representations of the genomic intervals. Accounting for GC and mappability is critical when the input’s GC and mappability distribution deviates from the whole genome’s GC and mappability distribution at a statistically significant level. This is true for inputs generated from NGS technologies (Benjamini and Speed, 2012; Chen et al., 2013; Cheung et al., 2011; Chung et al., 2011; Dabney and Meyer, 2012; Rozowsky et al., 2009) and can hold for other inputs due to natural biases. For example, promoter and gene-coding regions are known to be GC-rich, therefore, while performing sampling based enrichment test, it is critical to account for GC content in generating the null distribution for this type of input.

GLANET additionally provides several built-in analysis tools for specific input types. When the input is a SNP list, users can evaluate whether the SNPs reside in TF binding regions and, if so, whether they are located in the actual TF binding motifs obtainable via either the reference or the SNP allele and whether the variation potentially impacts the binding of TFs, either by enhancing or disrupting binding motifs. GLANET enables joint enrichment analysis for TF binding and KEGG pathways. With this option, users can evaluate whether the input set is enriched concurrently with binding sites of TFs and the genes within a KEGG pathway. This joint enrichment analysis provides a detailed functional interpretation of the input loci.

In order to assess the statistical power and Type-I error of GLANET across its available parameter settings, we designed data-driven computational experiments using large collections of ENCODE ChIP-seq and RNA-seq data. These computational experiments indicated that GLANET enrichment test has high statistical power with conservative Type-I error. We present comparisons of GLANET with GAT and GREAT, and finally illustrate applications of GLANET within different biological contexts.

2 Materials and methods

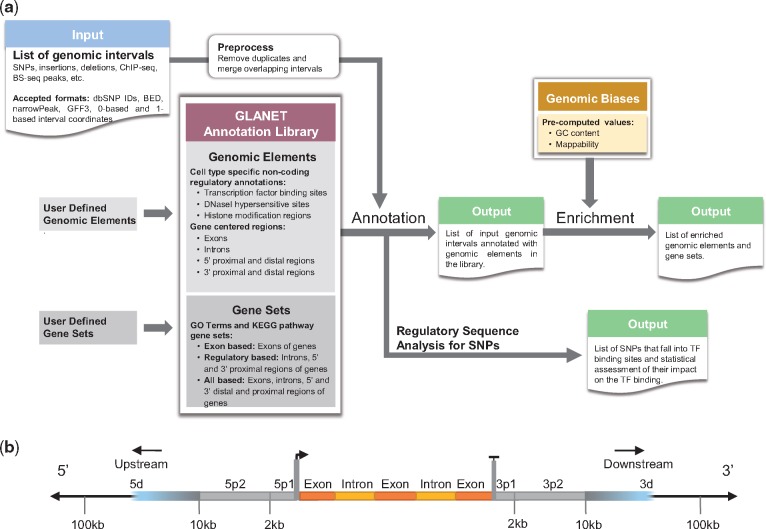
GLANET is an enrichment and analysis tool with a rich set of functionalities for the human genome. Figure 1a provides an overview and capabilities of GLANET. We describe below individual components in more detail.

Fig. 1.

(a) Overall functionality of GLANET. (b) Gene-centric genomic intervals are defined based on commonly used location analyses in ChIP-seq and related studies (Blahnik et al., 2010). GLANET uses these intervals to provide detailed annotation of user query with respect to known genes

2.1 User query

Users can query SNPs or varying length genomic intervals for annotation and/or enrichment analysis. GLANET supports commonly used input formats such as BED, GFF3, 0-based or 1-based coordinates, and reference identifiers for SNPs.

2.2 GLANET annotation library

GLANET annotation library contains lists of annotated genomic regions from the literature. We refer to these as GLANET elements, or genomic elements. Each of these elements is represented by a set of genomic intervals. Default GLANET annotation library consists of the following genomic elements:

• Non-coding regulatory elements: Regulatory elements encompass non-coding regions such as DNaseI hypersensitive sites (DHSs), TF binding and histone modification regions across multiple cell types from the ENCODE. Each element represents a set of genomic intervals that are identified as peaks by the ENCODE project in a biochemical high throughput assay. For example, STAT1_K562 represents genomic intervals bound by STAT1 in K562 cells.

• Gene-centric elements: Gene-centric elements are defined for each gene and are based on exons, introns and six different regulatory regions that are either proximal or distal to each gene. We adopt the nomenclature from commonly used location analysis (Blahnik et al., 2010) and define 5p1, 5p2 and 5d as the regions 0–2 kb, 2–10 kb and 10–100 kb upstream of first exon of the gene, respectively. Similarly, we define 3p1, 3p2 and 3d as the regions 0–2 kb, 2–10 kb and 10–100 kb downstream of last exon of the gene, respectively (Fig. 1b). These gene-centric elements enable users to annotate their input query with respect to known genes and more importantly non-coding regions around them. These regions are further incorporated into pathway and gene set enrichment analysis.

• Functional gene sets: The input set of genomic intervals can also be queried against pre-defined gene sets. GLANET includes gene sets derived from KEGG pathways and GO terms as its default functional gene sets. In the case of GO term gene sets, for each GO term, we curate a gene set that comprises genes that are annotated with that particular GO term based on at least one of the experimental evidence codes. GLANET further defines three classes of gene set elements as exon-based, regulation-based and all-based. Exon-based gene set elements include exons of the genes in each individual gene set. In contrast, regulation-based gene set elements consist of introns and the four different proximal non-coding regions, namely 5p1, 5p2, 3p1 and 3p2, of genes in each gene set. The third category, all-based gene set elements, consists of exons, introns and all six proximal and distal regions of genes in each gene set.

• User-defined annotations: Users can expand the GLANET annotation library with new genomic elements, i.e. genomic intervals or gene sets, and query against this extended library. This option broadens the applicability of GLANET to various settings. For example, it enables investigating the input set against an in-house generated ChIP-seq data analysis, or against gene sets derived from other analysis.

2.3 Library representation

A genomic interval is a continuous stretch of the genome with a chromosomal start and end coordinates denoted by $[t_1,t_2]$ with $t_1\le t_2$ where t₁ is the low endpoint and t₂ is the high endpoint of the interval. Each genomic element in the GLANET library is defined by a set of such genomic intervals. For example, a TF’s binding regions or histone modification sites are represented by a set of genomic intervals that corresponds to ChIP-Seq peaks. GLANET stores these genomic intervals in interval trees (Supplementary Fig. S1).

2.4 Annotation analysis

GLANET annotation overlaps each genomic interval in the input set with genomic elements in its annotation library and provides the following options for quantifying the overlap:

• Existence of overlap (EOO): This option simply evaluates whether a given input interval intersects at least 1 base pair (bp) with any of the intervals of a genomic element in the annotation library. GLANET also allows users to provide a higher threshold for overlap definition. Finally, the number of intervals overlapping each genomic element is reported as the query-level association statistics.

• Number of overlapping bases (NOOB):NOOB takes into account the actual number of overlapping bases. The total numbers of overlapping bases across all the input intervals for each element are reported as the query-level association statistics.

Annotation is performed by searching for each query interval in the interval tree. The runtime complexity of a query search in an interval tree is $\mathcal{O}(\min (n,k\hspace{0.17em}\text{log}\hspace{0.17em}n))$, where n is the number of all genomic intervals in the interval tree (number of nodes) and k is the number of genomic intervals overlapping the query interval. Typically, $k\hspace{0.17em}\text{log}\hspace{0.17em}n$ is smaller than n.

2.5 Regulatory sequence analysis for SNPs

GLANET provides a detailed regulatory sequence analysis for SNP input queries. GLANET first finds in which of the TFs’ binding regions, the SNP resides in. Then, the locations of the SNPs residing in a TF binding region are evaluated for overlap with a significant motif match using the position frequency matrices (PFMs) of the corresponding TFs. This evaluation is carried out with both the reference and the SNP alleles. Specifically, for evaluating a single SNP with respect to one PFM, GLANET retrieves DNA subsequence of the reference genome within a 41 bp window centered at the SNP locus. It then assesses whether this subsequence provides a significant match to the PFM with either the reference or the SNP allele with the RSAT tool (Thomas-Chollier et al., 2008). Both Jaspar Core (Mathelier et al., 2014) and ENCODE motifs (Kheradpour and Kellis, 2013) are utilized as part of GLANET’s PFM library.

Let P_ref and P_snp denote the P-values of motif matches with the reference and SNP alleles, respectively. Since we precondition our analysis on the fact that the SNP overlaps a TF binding region, we also evaluate whether the extended 401 bp region centered at SNP locus harbors a motif match to the PFM. Let P_extended denote the P-value of such a match. If P_snp is larger than P_ref and P_extended, the SNP has a potentially disrupting effect. If the converse holds, GLANET suggests that the SNP is creating a sequence motif that is more favorably recognized by the TF. Overview of regulatory sequence analysis can be found in Supplementary Figure S2.

2.6 Enrichment analysis

Enrichment analysis enables identifying one or more common functional themes in the input query set by assessing the statistical significance of the overlaps with the GLANET elements. To evaluate the statistical significance of the EOO and NOOB association statistics, GLANET estimates empirical null distributions by randomly sampling intervals that match the characteristics of the input query intervals.

We use a resampling based approach to obtain the empirical null distribution of the test statistic. We collect test statistics of B samplings, each with n randomly generated genomic intervals, where n is the number of input intervals in the query. bth sampling is represented by randomly generated genomic intervals, $S^b=\{s_1^b,s_2^b,\dots ,s_n^b\},\hspace{0.17em}\forall b\in \{1,\dots ,B\}$ that match the given genomic intervals properties. The collection of overlap statistics across multiple random samplings is then used to estimate an empirical null distribution for the overlap statistic and to calculate an empirical $P-value=\frac{1}{B}{\sum }_{b=1}^B{1}_{(k^b\ge k)}$. Here k denotes the observed test statistic and k^b is the overlap statistic of randomly generated genomic intervals S^b from b^th sampling. The indicator function returns 1 when the inequality holds and 0 otherwise. Multiple testing correction to account for large numbers of genomic elements is performed with two options: Bonferroni (1936) and Benjamini–Hochberg procedures (Benjamini and Hochberg, 1995).

The key part of estimating the empirical null distribution of enrichment test is the random interval sampling step. The random intervals are generated such that they match properties of the each member of the input interval set as opposed to the average properties of these intervals. User can account for GC content or mappability bias jointly or separately or choose not to match any of these properties. In matching the GC content, genomic intervals are matched with varying resolution depending on the length of given genomic intervals, i.e. the shorter the genomic interval, the more precise the GC content matching is. GLANET also offers an Isochore Family (wIF) option in matching GC. A detailed description of the GC, mappability and isochore family matching procedure is available in Supplementary Materials, Section 2.

If wGC option and/or wM is also selected, a random interval is repeatedly generated until a random interval close to input intervals GC content and/or mappability depending on the selected mode under a preset threshold is found. When wGC option is selected, wIF provides a good starting point for GC matching, when it is not selected, it provides a very coarse grain matching of GC. The different options for enrichment test is summarized in Table 1.

Table 1.

GLANET main parameters for enrichment test

Association statistic options
EOO	Existence of overlap: Overlap statistic is 1 or 0 based on whether the input interval overlaps with any of the genomic element intervals or not.
NOOB	Number of overlapping bases: Overlap test statistic is the exact number of overlapping bases between the input interval and the genomic element intervals.
Random interval generation matching options
wGC	with GC: For an input interval, randomly sample an interval with the same length from the same chromosome such that it matches the GC content of the query interval.
wM	with mappability: Randomly sample an interval with the same length from the same chromosome such that it matches the mappability of the query interval.
wGCM	with GC and mappability: Randomly sample an interval with the same length from the same chromosome such that it matches both mappability and GC content of the query interval.
woGCM	without GC and mappability: Randomly sample an interval with the same length from the same chromosome.
Random interval generation start options
wIF	with isochore family: Starts the random interval search within the same chromosome with a matching GC isochore family. When GC is on, it provides a good start for GC matching. When GC option is not selected, it provides coarse grain GC matching.
woIF	without isochore family: Starts the random interval search for an interval within the chromosome randomly.

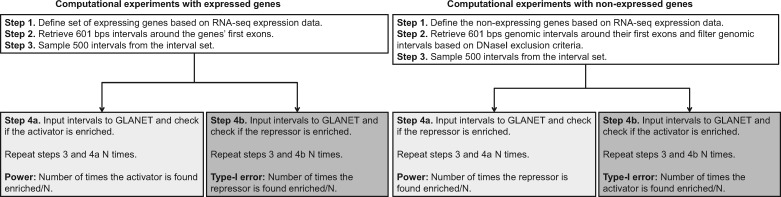
2.7 Data-driven computational experiments

In order to evaluate GLANET in terms of Type-I error and power, we designed novel data-driven computational experiments. The key idea of these experiments is that at the TSSs of expressed genes, we would expect to observe enrichment of DNA polymerase II (POL2) occupancy and modifications that are related to transcriptional activation. In contrast, for the TSSs of non-expressed genes, we would expect enrichment of histone modification elements that are associated with transcriptional repression.

We used data from K562 and GM12878 cells and defined expressed and non-expressed gene sets based on RNA-seq analysis of these cells. Genomic intervals that cover the 500 bp upstream and 100 bp downstream of the first exon of the genes in these sets were retrieved. For each simulation, we sampled non-overlapping intervals from the TSS regions of the relevant gene set (expressed or non-expressed genes) and evaluated enrichment of 12 histone modifications with roles on transcriptional repression or activation and POL2 occupancy separately. Based on these simulations, we calculated Type-I error and power as follows:

Type-I error experiments: These experiments evaluate whether GLANET enrichment procedure can control Type-I error considering settings where the null hypothesis is true. In the case of non-expressed genes, the null hypothesis is that intervals that are located around the TSSs of non-expressed genes’ are not enriched with activator elements. Similarly in experiments conducted with expressed genes, the null hypothesis is that the intervals around the TSSs of expressed genes are not enriched with repressor elements. Type-I error rate is the number of times we incorrectly reject the null hypothesis.

Power experiments: These experiments evaluate the power of GLANET enrichment procedure considering cases where the alternative hypothesis is true. In experiments conducted with non-expressed genes, our null hypothesis states that the intervals are not enriched with repressor elements. Similarly in the case of expressed genes, the null hypothesis is that the genomic intervals are not enriched with activator elements. Then, power is the number of times we correctly reject the null hypothesis.

Design for data-driven computational experiments is summarized in Figure 2. The list of genomic elements and further details on how we defined the sets of expressed and non-expressed gene sets, and the regions around the TSSs are detailed below.

Fig. 2.

Design for data-driven computational experiments. N is set to 1000. Activator elements are defined as H2AZ, H3K27ac, H3K4me2, H3K4me3, H3K79me2, H3K9ac, H3K9acb, H3K36me3, H3K4me1, H4K20me1, and POL2; whereas H3K27me3 and H3K9me3 are the repressor elements

Transcriptional activator and repressor elements: We considered histone modifications and POL2 occupancy in two groups as (i) activator elements including POL2 and modifications H2AZ, H3K27ac, H3K4me2, H3K4me3, H3K79me2, H3K9ac, H3K9acb, H3K36me3, H3K4me1, H4K20me1 associated with transcriptional activation at TSSs (Encode, 2012); (ii) repressor elements including modification H3K9me3 and H3K27me3 (Encode, 2012). However, some of these elements are either observed to exhibit both activator and repressor features and/or reported to be present in regions other than the TSSs such as gene bodies or 3′ end. We marked H3K36me3, H3K4me1, H4K20me1 and H3K9me3 modifications as ambigous elements as their roles in the TSSs site are ambigious (Barski et al., 2007; Cheng et al., 2014; Encode, 2012).

After processing the RNA-seq data of GM12878 and K562, we defined expressed and nonexpressed gene sets. Both GM12878 and K562 RNA-seq data included two biological replicates. For each gene, we utilized the lowest and highest transcripts per million (TPM) values across replicates for defining the expressed and non-expressed gene sets, respectively.

Genomic interval sets for expressed genes: We defined two sets of expressed genes with varying levels of stringency by considering the top 5th and top 20th percentiles of genes with respect to the their descending TPM values. In each case, genomic intervals that cover the 500 bp upstream and 100 bp downstream of the first exon of the genes in these sets are retrieved. We refer to these two genomic interval sets as Top5 and Top20.

Genomic interval sets for non-expressed genes: We labeled genes with zero TPM values as non-expressed genes and formed a tentative interval set by taking 500 bp upstream and 100 bp downstream of these genes’ first exons. (Shu et al., 2011) and others observed that DNaseI hypersensitivity and gene expression correlate positively; therefore, we further filtered these intervals with respect to their cell type specific DNaseI signal. We considered two modes of DNaseI overlap exclusion by (i) discarding the interval completely from the interval set (CompletelyDiscard) in case of any overlap with DNase-seq peak exists and (ii) keeping the interval by reducing it to the longest interval without DNase-seq peak overlap (TakeTheLongest). In experiments conducted with non-expressed genes, we operated with these two different interval sets: CompletelyDiscard and TakeTheLongest.

3 Results and discussion

In this section, we report results on these data-driven computational experiments and explore the effect of various GLANET enrichment parameters. Next, we compare GAT and GLANET through data-driven computational experiments. Finally, we illustrate biological applications where GLANET can be useful.

3.1 Validation with data-driven computational experiments

We performed the data-driven computational experiments summarized in Figure 2 under all possible enrichment analysis parameter settings of GLANET listed in Table 1. We varied the association measure modes, EOO or NOOB and considered cases where we accounted for GC, and/or mappability or ignored these two biases in random interval generation step. These settings are wGC, wM, wGCM and woGCM. Furthermore, we considered wIF and woIF options. These constituted 16 different parameter settings. As described in Materials and Methods, we varied the definitions of non-expressed and expressed genes too; for expressed gene setting we have Top5, which is the conservatively defined set of expressed genes and Top20 that is less conservatively defined. For the non-expressed interval set, CompletelyDiscard is a more stringent definition than the TakeTheLongest case. We repeated these experiments for K562 and GM12878 cell lines in order to get a complete picture of GLANET enrichment procedure performance.

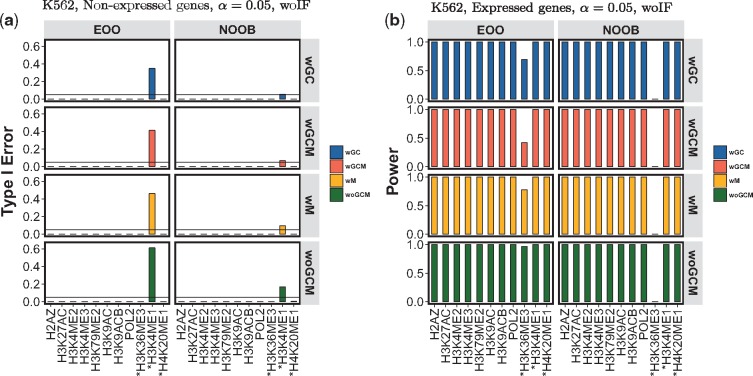
Figure 3 summarizes the results of experiments conducted with activator elements for expressed genes (Top5) and non-expressed genes (CompletelyDiscard) settings for K562. Overall, we observe that the Type-I error is well below the target significance level ($\alpha =0.05$) without sacrifice on power in all sixteen modes of the GLANET enrichment analysis. One exception to this is, H3K4me1, where Type-I error is significantly higher than the target level. This could potentially be attributed to its ambiguous role on the promoters as it acts also on the downstream of TSSs (Encode, 2012) and reported to exhibit repressor features (Cheng et al., 2014). Interestingly, enrichment assessment of this mark for non-expressed genes is most affected by the bias adjustment in the null distribution estimation. The Type-I error involving this mark improves significantly under the wGC, wM and wGCM regardless of the association statistics utilized for enrichment without a negative impact on power. Simililarly, using wIF option improves its Type-I error (Supplementary Fig. S3a). Another exception case is H3K36me3 mark with considerably low power. This is also one of the elements whose role on the promoters is ambigous; H3K36me3 is reported to have preference for the 3’ of active genes (Encode, 2012). When the same experiments are conducted in GM12878 cell line, we obtained similar results even with lower Type-I errors (Supplementary Fig. S7).

Fig. 3.

Assessment of GLANET Type-I error and power with data-driven computational experiments. Results for the two association statistics—existence of overlap (EOO) and the number of overlapping bases (NOOB)—together with GC (wGC), with Mappability (wM), with GC and Mappability (wGCM), and without GC and mappability (woGCM) null distribution generation modes are displayed. Histone marks with ambiguous activator roles are marked with *. (a, b) Type-I error and power estimated without Isochore Family (woIF) heuristic using K562, (Non-expressed Genes, CompletelyDiscard) and (Expressed Genes,Top5) results, for significance level of 0.05

When we use a less stringent definition of expressed genes (Top20) and a looser interval exclusion criteria in generating intervals of non-expressed genes (TakeTheLongest), the Type-I errors are higher (Supplementary Figs S4 and S8). This indicates that GLANET is not universally conservative across all settings. When we re-assessed Type-I errors and power at a more stringent level of significance such as 0.001, the Type-I errors are controlled in (CompletelyDiscard) and (Top5) experiments without loss of power (Supplementary Figs S5 and S9) with the exception of ambiguous elements H3K4me1, H3K36me3 and H4K20me1. When the less stringent settings are used at this significance level, there are few elements with Type-I error above the target significance level and power less than one (Supplementary Figs S6 and S10).

For repressor element, H3K27me3, experiments resulted in zero Type-I error except for a few cases in GM12878 (Supplementary Tables S3 and S4) and GLANET attained power of one across all settings as shown in Supplementary Tables S5 and S6. Experiments with the repressor element H3K9me3 resulted in Type-I error of zero for GM12878, and Type-I errors over the set significance level depending on the parameter selection in K562 cell (Supplementary Tables S3 and S4). The power in both cells for this histone mark is low (Supplementary Tables S5 and S6). H3K9me3 is also one of the ambiguous elements in terms of its repressive role on promoters.

Overall we observe that Type-I error control is significantly better with the NOOB association statistics. Accounting for GC and mappability biases and use of wIF option lower the Type-I error.

3.1.1 Comparison with GAT

We compared GLANET and GAT with the same data-driven computational experiments for all settings and compute element specific Type-I error and power of GAT at 0.001 and 0.05 significance levels. For more stringent experiment settings (CompletelyDiscard, Top5), GAT is also conservative in terms of Type-I error. Additionally, GLANET achieves better Type-I error rate for certain elements such as H3K4me1 and also better power for H3K36me3 and H4K20me1 elements compared to GAT as shown in Supplementary Figures S12 and S14. For less stringent experiment settings (TakeTheLongest, Top20), results show that GLANET Type-I error and power are comparable or better than GAT (Supplementary Figs S13 and S15). We extended this analysis with ROC curves by varying the significance level as detailed in Section 3.3.

3.2 Assessing GLANET enrichment parameters through Wilcoxon signed rank tests

To get a comprehensive view of how GLANET parameters would affect the enrichment test performance, we summarize our results across different experiments conducted with various activator and repressor elements and different parameter settings. We concentrate on Type-I error, as it is more variable than the power.

We carried out Wilcoxon signed rank tests to assess the statistical significance of the difference between the Type-I errors achieved by different GLANET parameter settings. The null states there is no difference in the mean of the ranks of the two distributions whereas alternative hypothesis is that the first distribution has lower mean of ranks than the second one. We carried out these tests for non-expressed and expressed simulations separately. Table 2 illustrates the P-values of the tests. As summarized in Table 3, we observed that for non-expressed genes, wGC achieved lower Type-I errors than the other options. For expressed genes, wGCM achieved lower Type-I errors than the others when woIF was on. However, when wIF was on, wM performed better in terms of Type-I error (Table 2). This is because wIF provides coarse grain GC matching. We also pooled the Type-I errors for (woIF,wIF) and observed that wIF achieves lower Type-I errors than woIF (Supplementary Table S8) in general and NOOB provides lower Type-I errors than EOO (Supplementary Table S9).

Table 2.

One-sided Wilcoxon signed rank test results for testing whether the Type-I error distribution of experiments generated under the parameter setting specified in the row has lower mean of ranks compared to the distribution of Type-I errors generated under the parameter setting specified in the column, where the null hypothesis states that there is no difference

	Wilcoxon signed rank test P-values
	wGC	wM	wGCM	woGCM	wGC	wM	wGCM	woGCM
	Non-expressed(EOO,woIF)				Non-expressed(NOOB,woIF)
wGC		2.2e-16	2.2e-16	2.2e-16		2.2e-16	2.2e-16	2.2e-16
wM				2.2e-16				2.2e-16
wGCM		2.2e-16		2.2e-16		2.2e-16		2.2e-16
woGCM
	Non-expressed(EOO,wIF)				Non-expressed(NOOB,wIF)
wGC		1.9e-04	2.2e-16	2.2e-16		1.004e-14	2.2e-16	6.524e-15
wM			2.2e-16	2.2e-16			2.2e-16
wGCM
woGCM						1.97e-04	2.39e-11
	Expressed(EOO,woIF)				Expressed(NOOB,woIF)
wGC				5.47e-12				1.2e-12
wM	1.18e-09			5.5e-12	1.75e-09			1.2e-12
wGCM	5.51e-10	1.17e-09		5.5e-12	3.75e-10	5.38e-10		1.2e-12
woGCM
	Expressed(EOO,wIF)				Expressed(NOOB,wIF)
wGC				1.43e-04				3.93e-03
wM	1.14e-09		2.78e-06	7.88e-10	2.57e-09		7.80e-06	1.75e-09
wGCM	1.15e-09			7.70e-10	2.56e-09			1.75e-09
woGCM

^*Note: A P-value presented in the cell indicates that setting in the corresponding row has a lower mean of ranks in Type-I error distribution than the setting in the corresponding column; if the cell is empty the opposite holds. The P-values are less than or equal to the actual test result. The best parameter setting in each experiment is shown in bold.

Table 3.

Table summarizes random interval generation option that achieves the lowest Type-I error for non-expressed and expressed gene intervals using association measures EOO and NOOB and the two isochore family options woIF and wIF

Gene-set(AssociationMeasure, IsochoreFamily)	Random interval generation mode
Non-expressed(EOO,woIF)	wGC
Non-expressed(EOO,wIF)	wGC
Non-expressed(NOOB,woIF)	wGC
Non-expressed(NOOB,wIF)	wGC
Expressed(EOO,woIF)	wGCM
Expressed(EOO,wIF)	wM
Expressed(NOOB,woIF)	wGCM
Expressed(NOOB,wIF)	wM

Finally, we notice an interesting difference in the experiment results conducted with expressed and non-expressed genes. As shown in Table 3, matching only GC in non-expressed genes results in the lowest Type-I errors. The experiments on expressed gene intervals show that matching mappability in addition to GC is required to achieve lower Type-I errors. We next asked whether the GC and mappability distributions of these interval sets can explain this result.

We considered the empirical GC and mappability distributions of the gene set intervals and compared them with the two distributions computed on the whole genome. We sampled 50 000 intervals of each 601 bp long from the human genome uniformly at random. Figure 4 and Supplementary Figure S11 display violin plots of GC and mappability of these random intervals, the intervals for the expressed and non-expressed genes in GM12878 and K562 cell lines, respectively. As shown in Figures 4a, GC distributions of non-expressed genes and expressed genes are similar to each other and they are both considerably different from the whole genome, especially in the lower tail (Kolmogorov-Smirnov test, P-value ≤ 2.2e-16). This provides support for the fact that matching for GC is important in both simulations conducted with the non-expressed and expressed genes sets. The same does not hold for the mappability distributions: mappability distribution of non-expressed genes promoter intervals is more similar to that of whole genome than the expressed genes’ intervals (Fig. 4b). Although both expressed and non-expressed gene intervals are significantly different than the genome based on two-sample Kolmogorov-Smirnov, test (P-value ≤ 2.2e-16); the test statistic, which quantifies the distance between the two compared distributions, is smallest between the mappability distributions of the human genome and the non-expressed gene set in both of the cell lines (Supplementary Table S7).

Fig. 4.

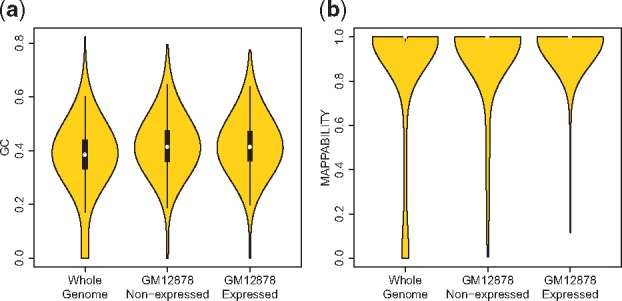
Violin plots for (a) GC of randomly sampled intervals from human genome, GC of intervals of GM12878 non-expressed genes and expressed genes. (b) Mappability of randomly sampled intervals from human genome, mappability of intervals from non-expressed and expressed gene-sets of GM12878

3.3 Assessing GLANET enrichment parameters through ROC curves and comparison with GAT

To compare quantitatively how GLANET parameters affect the enrichment performance, we also analyzed false positive rate versus true positive rate by varying the significance level and plotting ROC curves. To compare GLANET’s performance with GAT, we also include GAT results in the ROC curves. To plot a single ROC curve per an element in a certain cell line, simulation results that are conducted under the same parameter setting for expressed and non-expressed genes are combined. In calculating element-based ROC curves, we label each activator element as ‘enriched’ in expressed gene scenario and ‘not enriched’ in non-expressed genes scenarios. Similarly, the true label for each repressor element as ‘not-enriched’ and ‘enriched’ under expressed and non-expressed genes simulations, respectively.

To summarize the results obtained on all cell lines, elements and different experimental settings, we compared the difference in AUC of two ROC curves with each other using pROC R package(Robin et al., 2011). We utilized ‘delong’ method and count the number of wins, ties and losses. A win is registered whenever the first ROC curve is found to be higher than the second tested ROC curve at 0.05 significance level. A loss registers the reverse scenario; the first curve is found to be below the second one, and a tie indicates that there is no statistically significant difference between the two compared curves. We accumulated the number of wins, ties and losses across different histone modification elements and POL2 and cell line to summarize the results. The results for the simulations when association measure EOO and isochore family option woIF are used are shown in Table 4. Results for other settings are available in Supplementary Tables S11–S17. According to these results, matching mappability and/or GC improves upon the case where they are not matched. One exception to this is the case when NOOB and woIF option is used, where woGCM option achieves marginally better than the other options. In all cases number of wins favor GLANET’s settings in comparison to GAT.

Table 4.

ROC curves of simulation results conducted under different parameter settings where (EOO,woIF) setting is on are compared

(EOO,woIF)	GAT(woGCM)	GLANET(woGCM)	GLANET(wGC)	GLANET(wM)	GLANET(wGCM)	Number of
						Wins	Ties	Losses
GAT(woGCM)		1/44/5	3/37/10	3/38/9	3/37/10	10	156	34
GLANET(woGCM)	5/44/1		3/38/9	3/38/9	3/38/9	14	158	28
GLANET(wGC)	10/37/3	9/38/3		5/41/4	3/43/4	27	159	14
GLANET(wM)	9/38/3	9/38/3	4/41/5		3/42/5	25	159	16
GLANET(wGCM)	10/37/3	9/38/3	4/43/3	5/42/3		28	160	12

^*Note: A win indicates a case where the ROC curve obtained with settings specified in the row is statistically significantly above the ROC curve obtained with the settings specified in the column at significance level of 0.05. A loss indicates the opposite, while a tie indicates that there is no statistically significant difference between the two compared curves. The counts indicate the number of times win/tie/loss cases occur when the results for different elements, cell lines and other experimental conditions are compared. The best parameter setting is shown in bold.

3.4 GLANET GAT comparison with additional datasets

As an additional set of comparison experiments, we repeated the experiments provided in the GAT supplementary website (https://gat.readthedocs.org) with GLANET. These experiments evaluate the significance of the overlap of binding regions of TF Srf in Jurkat cells with three different sets of DHSs from Jurkat and HepG2 cells. These experiments also exemplify another use case of GLANET where the input intervals are TF binding regions.

The first experiment (Srf(Jurkat) versus DNaseI(Jurkat)) assesses whether Srf binding sites in Jurkat cells are enriched in DHSs from the same cells. Given that majority of the TF binding events resides in open chromatin regions, we expect to observe significant enrichment. The second experiment conducts the same analysis with the same input against DHSs from HepG2 cells. The third experiment checks whether DHSs from both cell types are significantly overlapping or not. Both GAT and GLANET report significant enrichment for these three experiments. The fourth experiment targets DHSs identified in HepG2 cells but not in the Jurkat cells (HepG2 Unique) as the genomic element. It evaluates whether Srf binding sites in Jurkat cells are enriched for these DHSs from HepG2 Unique. Both GAT and GLANET conclude that the observed overlap between Srf binding sites from Jurkat cells and DHSs specific to HepG2 cells are not statistically significant.

We observed no significant difference in P-values of GLANET and GAT enrichment tests for these four experiments (Supplementary Tables S18–S21). Along with a P-value quantifying enrichment, GAT reports fold change, which is defined as the ratio of the observed test statistic to the expected test statistic. In Figure 5, we observe that all enrichment modes of GLANET result in conclusions consistent with expectations and GAT results, while GLANET(wGCM,wIF) setting is the most conservative setting in terms of fold enrichment. Of the sixteen settings of GLANET, results with (NOOB,woGCM,woIF) parameter setting agree most closely with GAT results. This is expected because GAT uses NOOB as the association measure as well and does not account for GC and mappability in these experiments.

Fig. 5.

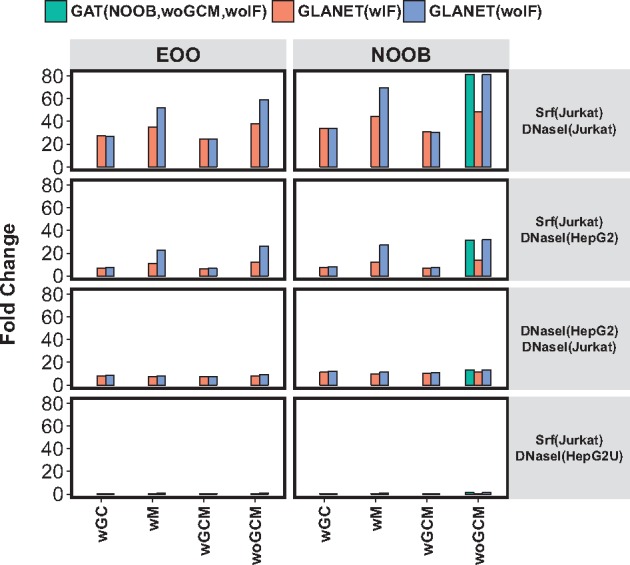
GLANET and GAT are run on four experiments ranging from high to low expected association between the compared genomic interval sets. Each row depicts an experiment where the first set is input query and the second set is a genomic element in the annotation library, e.g. experiment Srf(Jurkat) versus DNaseI(Jurkat) evaluates whether the binding regions of TF Srf in Jurkat cells are enriched for DNaseI accessible, i.e. open chromatin, regions in the same cells

3.5 Runtime comparison

We conducted a runtime comparison of GLANET with GAT and GREAT. GAT is compared on the basis of user defined library enrichment analysis as it does not provide gene set enrichment. GREAT is compared on the basis of GO term enrichment analysis as GREAT does not allow user defined library extension. To compare GAT and GLANET we conducted two experiments. In the first one, we the input genomic intervals that are randomly sampled from non-expressing genes promoter sites and each of them are 601 bp long. We conducted enrichment analysis against the ENCODE library by varying the number of input intervals and number of samplings. As it is shown in Table 5, in almost all cases GLANET is faster than GAT and the difference is more evident with the larger number of input intervals and larger number of samplings (More detailed version is provided in Supplementary Table S22). The second experimental set up is the same as the experiment described in Section 3.4. Except one case (DNaseI(HepG2)-DNaseI(Jurkat)) out of 4, GLANET outperforms GAT in terms of runtime (Supplementary Table S23). We provided GLANET’s runtimes in conducting GO Terms enrichment of GATA2 binding sites in K562 as described in Section 3.6.2 (Supplementary Table S24). We run GREAT through its web server and also supplied its runtime (Supplementary Materials, Section 11.2).

Table 5.

Elapsed CPU times (in seconds) for GLANET and GAT runs for given input query are provided

Number of input intervals	Number of samplings	Run times (in s)
		GLANET	GAT
500	1000	690	145
500	10 000	856	1463
500	100 000	2140	14 353
1000	1000	1283	147
1000	10 000	1165	1538
1000	100 000	3866	14 341
2000	1000	1179	155
2000	10 000	1270	1583
2000	100 000	6257	16 039

^*Note: Input intervals are randomly selected from promoter regions of non-expressing genes in GM12878 cell line from (Non-Expressing,CompletelyDiscard) pool, where each interval is 601 bp long. Used ENCODE subset library includes 12 histone modifications and POL2. Both GLANET and GAT are run under the parameter setting (NOOB,wIF,woGCM). Results for 1000 and 10 000 samplings are averaged over 10 runs. For 100 000 samplings, each run time in the table denotes the average run-time from 5 runs. Bold entries indicate the faster runtimes for each row.

3.6 Example use cases of GLANET

3.6.1 Enrichment analysis of OCD GWAS SNPs

We next illustrate how GLANET can be used to analyze 2340 SNPs identified as significant in either of case-control, trios, and/or combined case-control-trios analysis in genome-wide association study (GWAS) of obsessive compulsive disorder (OCD) (Stewart et al., 2013).

We first conduct KEGG pathway analysis using in three modes: exon-based, regulation-based and all-based. These modes vary the genic region definition as defined in Figure 1b. Interestingly, GLANET regulation-based enrichment analysis identifies glutamatergic synapse pathway (hsa04724) as enriched; this is one of the pathways that KEGG reports as associated with OCD. Both DLGAP1 and GRIK1 genes are part of this pathway and they overlap with OCD associated SNPs in their intronic regions: DLGAP1 overlap with rs1628281, rs767887, rs1791397, rs11081062, rs11663827, rs1116345, rs615916 and rs7230434 whereas GRIK1 overlaps with rs363524 and rs363514. The full list of genes where overlaps take place for glutamatergic synapse pathway are provided in Supplementary Table S27.

A key outcome of this application is that standard pathway analysis that only utilizes exonic regions of the pre-defined genes can fail to identify pathways that are biologically relevant through their regulatory roles. For example, long-term depression pathway (hsa04730) is significantly enriched only in the regulation-based analysis. The link between OCD and depression has long been established (Overbeek et al., 2002).

We also conducted enrichment analysis of OCD SNPs with default GLANET annotation libraries representing TF binding regions and histone modifications. The complete list of enrichment analysis is provided in Supplementary Table S28.

3.6.2 Regulatory sequence analysis of OCD SNPs

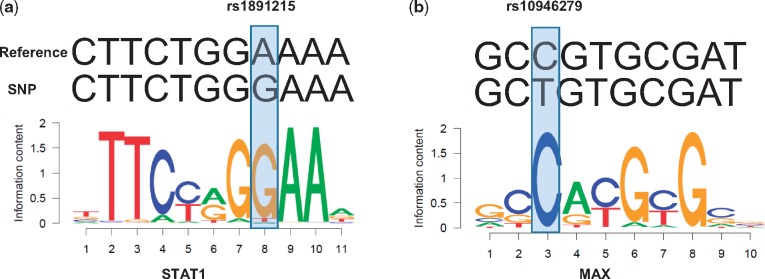
Following up OCD SNPs with GLANET regulatory sequence analysis revealed that some of these SNPs might be affecting TF binding. For example, SNP rs1891215 resides within a STAT1 binding region and has a match to STAT1 PFM with P_ref of 1.1e-3. As the SNP changes the allele from A to G, it generates a better STAT1 binding site with P_snp of 6.1e-5 (Fig. 6a). In contrast, the SNP rs10946279 resides within a MAX binding region. This location has a match to the MAX PFM with a P_ref of 6.1e-5; however, the SNP alters the match (P_snp = 1.5e-3), potentially disrupting the binding site (Fig. 6b). All regulatory sequence analysis results of OCD SNPs are available in Supplementary Table S29.

Fig. 6.

GLANET regulatory sequence analysis for the OCD SNPs annotated with TFs in the library. (a) SNP rs1891215 located at chr1:7,667,794 changes reference nucleotide A to G, and as a result, leads to a better match to the STAT1 PFM, i.e. the P-value of the match to the STAT1 PFM changes from 1.1e-3 to 6.1e-5. (b) SNP rs10946279 (chr6:170,553,248) changes reference nucleotide C to T, thereby decreasing the significance of the match to the MAX PFM, i.e. the P-value of the match increases from 6.1e-5 to 1.5e-3

3.6.3 GO enrichment analysis for GATA2 binding regions

For each GO term, we curate a gene set from genes that are annotated with that particular GO term based on experimental evidence codes. These gene sets are pre-defined in the GLANET annotation library. We used GATA2 binding regions (i.e. peaks from the relevant ChIP-seq experiment) from K562 cells as input to GLANET and assessed which of the GO term gene sets are enriched in these regions. GATA2 is a TF crucial in maintaining the proliferation and survival of early hematopoietic cells and preferential differentiation to erythroid or megakaryocytic lineages (Kitajima et al., 2006; Tsai and Orkin, 1997). As we expect a subset of GATA2 binding regions to be in close proximity of the genes that GATA2 regulates, such an analysis should identify the significantly enriched biological processes. We conduct this analysis with the three genic region definitions: exon-based, regulation-based and all-based. GLANET correctly identifies several enriched GO terms that are related to the specific biological role of GATA2 such as regulation of definitive erythrocyte differentiation (GO:0010724), platelet formation (GO:0030220) and eosinophil fate commitment (GO:0035854) (Supplementary Table S30).

To quantify similarity between the set of GO terms that GATA2 is annotated with and the set of GO terms GLANET found enriched, we calculate GO semantic similarity scores between these two sets using GOSemSim R package (Yu et al., 2010). Semantic similarity scores are computed using Wang measure with rcmax method. The resulting scores are provided in Table 6. The set of GO terms found enriched with GLANET are highly similar to the GO terms annotated with GATA2 gene and the similarity score increases once we incorporate non-coding regions of the genes in the gene set, where the GATA2 binding takes place. We repeated the same analysis with GREAT, which does not correct for GC and mappability biases. The semantic similarity score achieved by GREAT is 0.59, which is considerably lower than GLANET’s score, that is 0.99.

Table 6.

GO semantic similarity scores calculated between the set of biological process GO terms that GATA2 is annotated with and the set of GO terms where GATA2 binding regions are found enriched based on GLANET enrichment analysis in three different analysis modes (exon, regulatory based and all-based)

	Enrichment mode
	Exon	Regulatory	All
Similarity score	0.43	0.73	0.99

4 Conclusion

GLANET is an easy-to-run desktop and command line application that offers useful features for performing flexible annotation and enrichment analysis of a given set of fixed or varying length loci. GLANET utilizes a rich pre-defined annotation library that contains regions defined not only on exons of the genes but also on their intronic and regulatory regions, KEGG pathways, GO term based gene-sets and a large collection of regulatory genomic element libraries from the ENCODE project. One key feature of GLANET is that the user can expand its default library. This option makes GLANET especially suitable for research groups that generate genomic interval data or gene sets through a variety of high-throughput experiments and routinely perform enrichment analysis. Other unique features of GLANET include allowing gene-set enrichment analysis with non-coding neighborhood of the genes, regulatory sequence analysis for SNP queries, joint enrichment analysis of TF-pathway pairs and an enrichment procedure that allows accounting for mappability and GC content biases separately or jointly. To assess how accounting for these biases and other GLANET parameters affect the test’s Type-I error rate and power, we designed novel data-driven computational experiments. We observe that in input types where the mappability and/or GC distribution is not close to the distribution of the genome, not accounting for GC and/or mappability will result in large Type-I errors. Overall, our data-driven computational experiments illustrate that GLANET has high power for detecting enrichment with conservative Type-I error control. GLANET can be used in a variety of interesting biological applications, some of which we showcase in this work and earlier in (Yao et al., 2015).