FWER and FDR control when testing multiple mediators

Abstract

Motivation

The biological pathways linking exposures and disease risk are often poorly understood. To gain insight into these pathways, studies may try to identify biomarkers that mediate the exposure/disease relationship. Such studies often simultaneously test hundreds or thousands of biomarkers.

Results

We consider a set of m biomarkers and a corresponding set of null hypotheses, where the jth null hypothesis states that biomarker j does not mediate the exposure/disease relationship. We propose a Multiple Comparison Procedure (MCP) that rejects a set of null hypotheses or, equivalently, identifies a set of mediators, while asymptotically controlling the Family-Wise Error Rate (FWER) or False Discovery Rate (FDR). We use simulations to show that, compared to currently available methods, our proposed method has higher statistical power to detect true mediators. We then apply our method to a breast cancer study and identify nine metabolites that may mediate the known relationship between an increased BMI and an increased risk of breast cancer.

Availability and implementation

R package MultiMed on https://github.com/SiminaB/MultiMed.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Mediation analysis can be used to study how an exposure, E, affects a disease, Y (Baron and Kenny, 1986; MacKinnon, 2008; Ten Have and Joffe, 2012). In the simplest scenario, there is only a single putative mediator, M. In this scenario, mediation analysis tests whether M is a true mediator and, if so, decomposes the total effect of E on Y into a direct and indirect (i.e. via M) effect (Pearl, 2012; Robins and Greenland, 1992; VanderWeele and Vansteelandt, 2014). In other scenarios, there may be more than one possible mediator (Daniel et al., 2015; Nguyen et al., 2015; Taguri et al., 2015). We consider the scenario where a large number of biomarkers may potentially mediate an exposure/disease association (Boca et al., 2014; Chen et al., 2017; Huang and Pan, 2016) and we introduce procedures for selecting a subset of those biomarkers to be designated as probable mediators. The key is that the proposed procedures, developed for replicability analyses (Bogomolov and Heller, 2018), can asymptotically control the Family-Wise Error Rate (FWER) or the False Discovery Rate (FDR). Our motivation is a 836-person case/control study of ER+ breast cancer where the goal is to identify the subset of the 478 measured metabolites that are likely to be mediators of the well-known association between higher BMI and an increased risk of breast cancer (van den Brandt et al., 2000).

Although mediation analysis initially focused on scenarios with a single mediator, mediation analysis has recently been extended for scenarios with a small number of mediators. In this setting, the possible causal paths (e.g. E → M1 → M2 → Y) can be fully enumerated, the various indirect effects can be well defined using the language of causal inference, and the assumptions needed to obtain unbiased estimates can be formulated (Daniel et al., 2015; Taguri et al., 2015; VanderWeele and Vansteelandt, 2014). The next step is to extend mediation analysis to scenarios where there is a large number of mediators, such as when the potential mediator is a high-dimensional vector of voxels in an fMRI image (Chen et al., 2017; Zhao and Luo, 2016), serum metabolite levels (Boca et al., 2014), gene expression levels (Huang and Pan, 2016) or methylation levels (Zhang et al., 2016). Towards this aim, methods have been designed to test whether a set of biomarkers, considered together, mediate an exposure/outcome association (Huang and Pan, 2016), to identify the Direction of Mediation or the linear combination of biomarkers that best captures the mediating effect (Chen et al., 2017), and to model the relationship between exposure, biomarkers and outcome (Zhang et al., 2016). Here, our objective is to add to this growing body of literature by introducing a new multiple testing procedure that identifies probable mediators, while controlling for false positive findings.

Our paper proceeds as follows. In Section 2, we start by describing our newly proposed procedures for identifying probable mediators and competing procedures. We continue by describing the simulations used to compare the procedures and then finish by describing the motivating breast case cancer study. In Section 3, we assess the performance of these procedures on the simulated datasets and identify possible mediators in our motivating study. In Section 4, we summarize our findings, describe the novelty of our method in the context of the current literature, and explain why our method can only identify ‘probable’ mediators.

2 Materials and methods

2.1 Definitions

Let us consider n individuals. For individual i, let E_i be the exposure, Y_i be the outcome, and ${\vec{M}}_{i·}={\{M_{i1},\dots ,M_{im}\}}^T$ be a vector of m potential mediators. For this paper, our potential mediators will always be biomarkers and we will use the terms interchangeably. We will say that a biomarker j is a mediator if E_i is associated with M_ij and, conditional on E_i, Y_i is associated with M_ij. To formalize this statement, we define two null hypotheses

$$\left(A\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{H}_{01}^j:E_i\hspace{0.17em}\perp \perp \hspace{0.17em}{M}_{ij}$$ (1)

$$\left(B\right)\hspace{0.17em}\hspace{0.17em}{H}_{02}^j:Y_i\hspace{0.17em}\perp \perp \hspace{0.17em}{M}_{ij}|E_i$$ (2)

We therefore say that biomarker j is a mediator if and only if the two null hypotheses, $H_{01}^j$ and $H_{02}^j$, are false. We note that, in our primary discussion, we are not considering the stricter null hypothesis that outcome and biomarker j are independent conditional on the exposure and the set of all other biomarkers, as defined by

$$\left(B^{*}\right)\hspace{0.17em}\hspace{0.17em}{H}_{02}^{j*}:Y_i\hspace{0.17em}\perp \perp \hspace{0.17em}{M}_{ij}|E_i,{\vec{M}}_{i(-j)}$$ (3)

where ${\vec{M}}_{i(-j)}=\{M_{i1},\dots ,M_{i(j-1)},M_{i(j+1)},M_{im}\}$.

Let the combined data for individual i be denoted by ${\vec{D}}_i={[E_i,Y_i,M_{i1},\dots ,M_{im}]}^T$, and let the complete dataset be denoted by the $n\times (m+2)$ matrix $D={[{\vec{D}}_1,\dots ,{\vec{D}}_n]}^T$. The arrows (e.g. $\vec{D}$) indicate the corresponding variable is a vector. Furthermore, let ${\omega }^{*}=\{1,\dots ,m\}$ and let Ω be the $2^m$ possible subsets of ${\omega }^{*}$. Then we define a Multiple Comparison Procedure (MCP) to be a function, from ${\Re }^{n(m+2)}$ to Ω, that inputs the data and outputs the set of biomarkers that are likely to be mediators.

Let ω₁ be the set of m₁₁ biomarkers that are mediators and ω₀ be the set of $m_0=m-m_{11}$ biomarkers that are not mediators. For a set $\omega \in \Omega$, we let $C(\omega )$ be the number of elements in ω and we let $V(\omega )$ be the number of elements in $\omega \cap {\omega }_0$. We next define the Family-Wise Error Rate (FWER) of an MCP to be $E\left[1\right(V>0\left)\right]$ and the False-Discovery Rate (FDR) to be $E[V/max(C,1\left)\right]$, where the expectation is over D and we have used the abbreviations $C=C\left(MCP\right(D\left)\right)$ and $V=V\left(MCP\right(D\left)\right)$.

2.2 Models and assumptions

We will first assume that the biomarkers and outcome are continuous variables that can be expressed as

$$M_{ij}={\beta }_{0j}+{\beta }_j{E}_i+{\mathrm{ϵ}}_{Mij}$$ (4)

$$Y_i={\gamma }_0^{*}+{\gamma }_E^{*}{E}_i+\sum _j{\gamma }_j^{*}{M}_{ij}+{\mathrm{ϵ}}_{Yi}^{*}$$ (5)

where ϵ_Mij and ${\mathrm{ϵ}}_{Yi}^{*}$ are random error terms with ${\mathrm{ϵ}}_{Mij}\hspace{0.17em}\perp \perp \hspace{0.17em}{E}_i$$\forall$j and ${\mathrm{ϵ}}_{Yi}^{*}\hspace{0.17em}\perp \perp \hspace{0.17em}\{{\vec{M}}_{i·},E_i\}$. Equation 5 further implies

$$Y_i={\gamma }_0+{\gamma }_E{E}_i+{\gamma }_j{M}_{ij}+{\mathrm{ϵ}}_{Yij}$$ (6)

Assuming Equations 4 and 6 are true, the two null hypotheses can be restated as

$$\left(A\right)\hspace{0.17em}\hspace{0.17em}{H}_{01}^j:{\beta }_j=0$$ (7)

$$\left(B\right)\hspace{0.17em}\hspace{0.17em}{H}_{02}^j:{\gamma }_j=0$$ (8)

For each biomarker, we can test the two hypotheses by first fitting Equations 4 and 6 using linear regression to estimate ${\widehat{\beta }}_j$ and ${\widehat{\gamma }}_j$ and their standard errors ${\widehat{\sigma }}_{\beta j}$ and ${\widehat{\sigma }}_{\gamma j}$. We can next calculate their Wald test statistics, $Z_{1j}=\sqrt{n}{\widehat{\beta }}_j/{\widehat{\sigma }}_{\beta j}$ and $Z_{2j}=\sqrt{n}{\widehat{\gamma }}_j/{\widehat{\sigma }}_{\gamma j}$. We can then calculate the corresponding P-values assuming, if appropriate, that the test statistics follow a t-distribution with the appropriate degrees of freedom or, more generally, that the asymptotic normal approximation holds, $P_{1j}=2\Phi (-|Z_{1j}\left|\right)$ and $P_{2j}=2\Phi (-|Z_{2j}\left|\right)$ where $\Phi (·)$ is the cumulative normal distribution. We note that that the estimated parameters from linear regression are consistent estimates for β_j and γ_j even if M_ij and Y_ij are not normally distributed (Lumley et al., 2002). Furthermore, we note that stating the marginal relationship between a single biomarker and the outcome can be described by Equation 6 does not preclude a more complex relationship where multiple correlated biomarkers affect the outcome, as shown in our simulations.

We will also relax the assumptions and allow the outcome to be a binary variable. We will assume that a probit model holds, where $Y_i=1(Y_i^{†}>0)$ and

$$Y_i^{†}={\gamma }_0^{*}+{\gamma }_E^{*}{E}_i+\sum _j{\gamma }_j^{*}{M}_{ij}+{\mathrm{ϵ}}_{Yij}^{*}$$ (9)

which implies

$$Y_i^{†}={\gamma }_0+{\gamma }_E{E}_i+{\gamma }_j{M}_{ij}+{\mathrm{ϵ}}_{Yij}$$ (10)

We now let ${\widehat{\gamma }}_j$ be the estimate from fitting model 10. In this scenario, the two null hypotheses can, again, be restated by Equations 7 and 8. In fact, the requirement that the probit model holds is unnecessary, and we only require that the $E\left[{\widehat{\gamma }}_j\right]=0$ for biomarkers satisfying assumption $H_{02}^j$. Then, the only changes for a prospectively collected binary outcome is that we would obtain ${\widehat{\gamma }}_j$ and $P_{2j}$ by probit regression. For retrospective sampling (i.e. case/control studies), we must also perform weighted regressions to estimate β_Ej where a sample’s weight is inversely proportional to the probability of being sampled. In practice, epidemiologists will often choose to use logistic regression instead of probit regression for estimating the conditional association between biomarker and outcome. We have chosen to present our theoretical results using the probit link since the multi-variable model (i.e. Equation 9) and the marginal model (i.e. Equation 10) are consistent with each other in probit regression and ${\gamma }_j=0$ implies the null hypothesis of Equation 2. However, in practice, and as further discussed in the Supplementary Material, we have found that MCP’s still perform well when using the logit link.

With the above assumptions, by a combination of theoretical and empirical results, we are able to show that FWER and FDR for our proposed procedures are maintained in practical settings.

2.3 Multiple comparison procedures

We first describe two existing MCPs that are designed to achieve a specified FWER: MCP_B and MCP_P, where the subscripts ‘B’ and ‘P’ abbreviate ‘Bonferroni’ and ‘Permutation’, respectively. We then introduce three new MCPs, MCP_S, $MC{P}_S^{WY}$ and $MC{P}_S^{MV}$ that are designed to achieve, asymptotically, a specified FWER, where the subscript ‘S’ abbreviates ‘Subset’ and the superscripts ‘WY’ and ‘MV’ abbreviate ‘Westfall-Young’ and ‘Multivariate’, respectively. Finally, we introduce an MCP, MCP_D, that is designed to achieve, asympotically, a specified FDR in realistic scenarios, where the ‘D’ abbreviates ‘false Discovery rate’.

2.3.1 MCP—Bonferroni $\left(MC{P}_B\right)$

We claim biomarker j to be a mediator if $P_{1j}\le \alpha /m$ and $P_{2j}\le \alpha /m$, where α is the targeted FWER. $MC{P}_B\left(D\right|\alpha )=\{j:P_{1j}\le \alpha /m,P_{2j}\le \alpha /m\}$. We further define a Bonferroni-adjusted P-value $P_{Bj}=m\times max(P_{1j},P_{2j})$ and restate the definition as $MC{P}_B\left(D\right|\alpha )=\{j:P_{Bj}\le \alpha \}.$

2.3.2 MCP—permutation $\left(MC{P}_P\right)$

We claim biomarker j to be a mediator if $P_{Pj}\le \alpha$, where α is a constant and P_Pj is the P-value calculated by our prior permutation approach (Boca et al., 2014). $MC{P}_P\left(D\right|\alpha )=\{j:P_{Pj}\le \alpha \}$. Briefly, in this approach, we focus on the product $\left|\widehat{\rho }\right(E,M_j\left)\widehat{\rho }\right(M_j,Y\left|E\right)|$, where $\widehat{\rho }(E,M_j)$ is the Pearson correlation between E and M_j, and $\widehat{\rho }(M_j,Y|E)$ is the Pearson correlation between M_j and Y given E. We then use permutations to estimate the distribution of the $ma{x}_j\left(\right|\widehat{\rho }(E,M_j)\widehat{\rho }(M_j,Y|E\left)\right|)$ under the hypothesis that there is no mediator and define P_Pj to be the probability of observing a value larger than $\left|\widehat{\rho }\right(E,M_j\left)\widehat{\rho }\right(M_j,Y\left|E\right)|$ under this distribution.

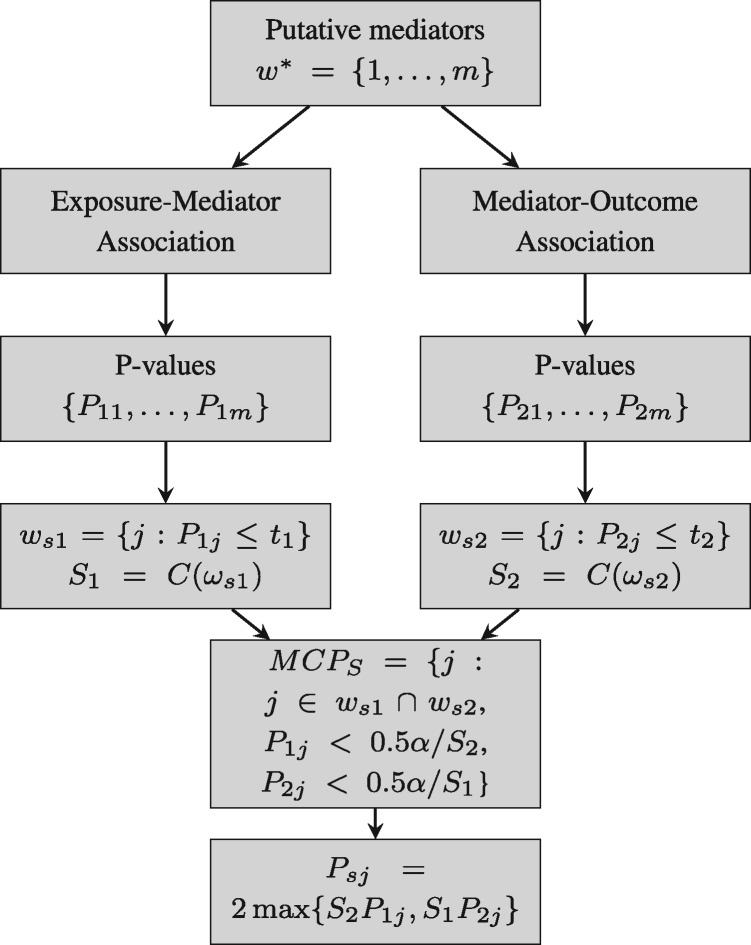
2.3.3 MCP—subset $\left(MC{P}_S\right)$

For the Bonferroni procedure, MCP_B, each P-value must meet the strict threshold of $\alpha /m$. Here, we suggest a different method, described in Figure 1, and based on work by Bogomolov and Heller (2018) restricts the testing of each hypothesis to a subset of biomarkers and therefore requires dividing α by a number smaller than m. We let t₁ be a threshold (i.e. scalar value) for a significant exposure/mediator relationship, and define ${\omega }_{S1}=\{j:P_{1j}\le t_1\}$ and $S_1=C\left({\omega }_{S1}\right)$ where $C(·)$ is the cardinality of a set. Similarly, let t₂ be a threshold for a significant mediator/outcome association, and define ${\omega }_{S2}=\{j:P_{2j}\le t_2\}$ and $S_2=C\left({\omega }_{S2}\right)$. We then claim biomarker j to be a mediator if $P_{1j}\le 0.5\alpha /S_2,\hspace{0.17em}{P}_{2j}\le 0.5\alpha /S_1$ and $j\in {\omega }_{S1}\cap {\omega }_{S2}$. $MC{P}_S\left(D\right|t_1,t_2,\alpha )=\{j:P_{1j}\le min(t_1,0.5\alpha /S_2),P_{2j}\le min(t_2,0.5\alpha /S_1)\}$. We further define a subset-adjusted P-value $P_{Sj}=2max(S_2{P}_{1j},S_1{P}_{2j})$ if $P_{1j}\le t_1$ and $P_{2j}\le t_2$, 1 otherwise. Note that $MC{P}_S\left(D\right|t_1,t_2,\alpha )=\{j:P_{Sj}\le \alpha \}.$ In practice, we set $t_1=t_2=\alpha /2$ because in order to be discovered by this procedure, $(P_{1j},P_{2j})\le (\alpha /2,\alpha /2)$. We stress that our use of a Bonferroni-type threshold on a set of prescreened metabolites is only valid because the P-values used for screening (e.g. P-values assessing exposure/metabolite association) are effectively independent of the P-values used in the second step (e.g. P-values assessing the metabolite/outcome association). Furthermore, we gain statistical power, compared to traditional Bonferroni approaches by eliminating tests that are irrelevant (e.g. testing for exposure/biomarker associations for biomarkers not associated with the outcome).

Fig. 1.

Diagram of the MCP_S approach showing that the procedure first selects two sets of biomarkers and then selects the shared subset that meet additional criteria

2.3.4 MCP—subset, Westfall-Young $\left(MC{P}_S^{WY}\right)$

In the previously defined version of MCP_S, the P-values must meet Bonferroni-type thresholds, $0.5\alpha /S_2$ and $0.5\alpha /S_1$, in the second step. However, we note that when the S₂ metabolites in ${\omega }_{S2}$ are highly correlated, the threshold $0.5\alpha /S_2$ would be conservative. A similar statement applies to ${\omega }_{S1}$ and $0.5\alpha /S_1$. To construct an alternative threshold, we borrow ideas from Westfall and Young (1993). We estimate the null distribution of $mi{n}_{j\in S_2}\left(P_{1j}\right)$ by a permutation procedure, and then replace S₂ by the approximate number of independent biomarkers $S_2^{WY}=0.5\alpha /q_{2,0.5\alpha }$ where $q_{2,0.5\alpha }$ is the ${(0.5\times \alpha )}^{th}$ quantile of this distribution. We similarly define a $S_1^{WY}$ and denote the resulting procedure by $MC{P}_S^{WY}\left(D\right|t_1,t_2,\alpha )=\{j:P_{1j}\le min(t_1,0.5\alpha /S_2^{WY}),P_{2j}\le min(t_2,0.5\alpha /S_1^{WY})\}$.

2.3.5 MCP—subset, multivariate $\left(MC{P}_S^{MV}\right)$

For MCP_S and $MC{P}_S^{WY}$, we aim to detect mediators as defined by $H_{01}^j$ and $H_{02}^j$. However, we might also consider replacing $H_{02}^j$ by $H_{02}^{j*}$. Unfortunately, we have no procedure that offers theoretical guarantees under the null $H_{01}^j$ and $H_{02}^{j*}$. Instead, we offer an ad-hoc procedure that performs well in practice. Instead of modeling each biomarker/outcome association marginally, we use stepwise regression. Specifically, we define $P_{2j}^{*}$ as the P-value for biomarker j when it is added to the multivariable biomarkers/outcome model (i.e. if biomarker j is the third biomarker added, then $P_{2j}^{*}$ is the P-value for biomarker j when there are three biomarkers in the model). We then define ${\omega }_{S2}^{\text{MV}}=\{j:P_{2j}^{*}\le t_2\},\hspace{0.17em}{S}_2^{\text{MV}}=C\left({\omega }_{S2}^{\text{MV}}\right)$ and $MC{P}_S^{MV}\left(D\right|t_1,t_2,\alpha )=\{j:P_{1j}\le min(t_1,0.5\alpha /S_2^{\text{MV}}),P_{2j}^{*}\le min(t_2,0.5\alpha /S_1)\}$.

2.3.6 MCP—subset, other modifications

Here, it is worth commenting on two other possible modifications to MCP_S, although neither will be further discussed in this paper. First, we could claim biomarker j to be a mediator if $P_{1j}\le c\alpha /S_2,\hspace{0.17em}{P}_{2j}\le (1-c)\alpha /S_1$ and $j\in {\omega }_{S1}\cap {\omega }_{S2}$, where c is any value in (0, 1). For example, letting c < 0.5 could be advantageous if exposure/mediator associations were far stronger and would be easily detectable at more stringent thresholds. Second, instead of prespecifying t₁ and t₂, we could choose thresholds so that the selected sets coincide with the rejected hypotheses in the second step.

2.3.7 MCP—FDR (MCP_D)

This procedure, based on work by Bogomolov and Heller (2018), builds on the adjusted P-values of MCP_S. For a given dataset, we calculate our subset-adjusted P-values $\{P_{S1},\dots ,P_{Sm}\}$ as in Section 2.3.3. We then claim biomarker $j\in {\omega }_{S1}\cap {\omega }_{S2}$ to be a mediator if

$$P_{Dj}=mi{n}_{j\prime :P_{Sj\prime }\ge P_{Sj}}\frac{P_{Sj\prime }}{rank\left(P_{Sj\prime }\right)}\le \alpha ,$$ (11)

where P_Dj is the FDR-adjusted P-value and $rank\left(P_{Sj}\right)$ is the rank of P_Sj for biomarker $j\in w_{S_1}\cap w_{S_2}$. Note that $MC{P}_D\left(D\right|t_1,t_2,\alpha )=\{j:p_{Dj}\le \alpha \}$.

2.4 Theoretical properties

We show that the asymptotic FWER for MCP_S is less than or equal to α (see Appendix for details):

Theorem 1: For $MC{P}_S(·|t_1,t_2,\alpha )$, if A1 holds and $\{M_{i1},\dots ,M_{im},Y_i\}$ follow Equations 4 and either 6 or 10, then $li{m}_{n\to \infty }FWER\le \alpha$. where Assumption A1 is defined by

Assumption A1: If $Y_i\hspace{0.17em}\perp \perp \hspace{0.17em}{M}_{i{j}^{†}}|E_i$ then $Y_i\hspace{0.17em}\perp \perp \hspace{0.17em}{M}_{i{j}^{†}}\left|\right\{E_i,M_{ij\prime }\}$$\forall$$\{j^{†},j\prime :{\gamma }_{j^{†}}=0,{\beta }_{j\prime }=0\}$.

We note that A1 is satisfied by many parametric models. Moreover, in the Appendix, we show that the asymptotic FDR of MCP_D is less than or equal to α:

Theorem 2: For $MC{P}_D(·|t_1,t_2,\alpha )$, if $M_{ij\prime }\hspace{0.17em}\perp \perp \hspace{0.17em}{M}_{i{j}^{†}}|E$$\forall$$j\prime ,j^{†}\in \{1,\dots ,m\}$ holds, $li{m}_{n\to \infty }FDR\le \alpha$.

We note, without proof, that a similar claim will also hold if blocks of putative mediators are conditionally independent and we let the number of blocks go to infinity.

In Section 3.1 of the Results and in the Supplementary Material, we show in simulations that the FWER and FDR are controlled at the nominal level for finite n and dependent mediators.

2.5 Simulations

We compare the performance of the MCPs in variations of the following simulated study. We consider a study with 500 individuals and m biomarkers, where $m\in \{110,1010\}$. In the first set of simulations, we let $E_i\sim N(0,1)$, M_ij follow Equation 4 with ${\mathrm{ϵ}}_{Mij}\sim N(0,{\sigma }_{Mj}^2)$, and

$$Y_i={\gamma }_0^{*}+{\gamma }_E^{*}{E}_i+\sum _j{\gamma }_j^{*}{M}_{ij}+{\mathrm{ϵ}}_{Yi}^{*}$$ (12)

with ${\mathrm{ϵ}}_{Yij}\sim N(0,{\sigma }_Y^2)$ where ${\sigma }_{Mj}^2$ and ${\sigma }_Y^2$ were chosen so $var\left(M_{ij}\right)=var\left(Y_i\right)=1$. We chose to fix the marginal variance at 1 because we believe that it reflects real datasets, where biomarkers and outcome are normalized. We let m₀₀ be the number of biomarkers with ${\beta }_j={\gamma }_j^{*}=0$, m₁₀ be the number with ${\beta }_j=0.18,{\gamma }_j^{*}=0$, m₀₁ be the number with ${\beta }_j=0,{\gamma }_j^{*}=0.18$ and m₁₁ be the number with ${\beta }_j={\gamma }_j^{*}=0.18$ (i.e. m₁₁ is the number of true mediators). We vary the chosen values $\{m_{00},m_{10},m_{01},m_{11}\}$, allowing m₁₀ to be large to reflect our motivating example where many biomarkers were likely associated with the exposure. For the primary analysis, all biomarkers are independent conditional on E. For the secondary analyses, with the exception of true mediators, blocks of biomarkers were correlated. We let ${\Sigma }_0$ be block diagonal, with blocks of size 5 (m = 110) or 20 (m = 1010), and let the off-diagonal elements be either 0, 0.5 or 0.9. If the correlation would result in var(Y) exceeding 1, we reduced ${\gamma }_j^{*}$. Biomarkers associated with E or Y were maximally spread across blocks with the rule that no block contained biomarkers associated with both E and Y. This restriction prevents the creation of ‘potential mediators’, where hypotheses 1 and 2 are both false, that would not qualify as ‘true mediators’ (see Section 4 for details). In a second set of simulations, we consider a binary outcome, $Y^{*}$, with $Y_i^{*}=1$ if $Y_i>0$, 0 otherwise. For each scenario, defined by outcome type, m and $\{m_{00},m_{10},m_{01},m_{11}\}$, we run 1000 simulations. In null simulations, we let $m_{11}=0$ and calculate the FWER as the proportion of simulations where our MCP selects at least one biomarker at $\alpha =0.05$. In non-null simulations, we calculate power as the average proportion of the 10 true mediators that are selected by our MCP set to $\alpha =0.05$ and we calculate the observed FDR when the FDR threshold is set to 0.2. Note, with 1000 simulations, the standard error of our estimated FWER should be no larger than $0.007=\sqrt{0.05\times (1-0.05)/1000}$.

2.6 Breast cancer study

This study, nested inside the Prostate, Lung, Colorectal and Ovarian Cancer Screening Study (PLCO), includes 418 estrogen-receptor positive (ER+) breast cancer cases and 418 controls matched on study entry age (±2 years), date of blood collection (±3 months) and hormone therapy use at baseline (Moore et al., 2017). Non-fasting serum samples were collected at the first follow-up visit, one-year post-baseline. Serum metabolites (<1 Kilodalton molecular weight) were measured by Metabolon Inc. using liquid chromatography-tandem mass-spectrometry. Of the 1057 serum metabolites measured, 478 were identified and present in at least 90% of the population. Metabolite peaks were normalized by dividing by batch median and then log transformed. All models were adjusted for age at serum collection, race, hormone use, age of menarche, parity, age of menopause, smoking and diabetes status. For purposes of sample weighting, the prevalence of ER+ breast cancer was 0.016.

3 Results

3.1 Simulations

The simulations demonstrate that the newly proposed MCPs have good operating characteristics. First, under the null scenarios with $m_{11}=0$, most MCPs achieved their targeted FWER of 0.05. These results are summarized in Table 1 for conditionally independent biomarkers and in Supplementary Tables for blocks of dependent biomarkers. The exception is that the FWER for the permutation approach could be as high as 0.07, an undesirable consequence of not having theoretical guarantees on the error rate. In general, the FWER was smallest for MCP_B, which relied on Bonferroni correction for determining significance. Second, under all scenarios, MCP_D achieved its targeted FDR (Supplementary Tables).

Table 1.

FWER from four multiple comparison procedures MCP_B, MCP_P, MCP_S and $MC{P}_S^{MV}$

				Continuous outcome				Binary outcome
m00	m10	m01	m11	MCPB	MCPP	MCPS	$MC{P}_S^{MV}$	MCPB	MCPP	MCPS	$MC{P}_S^{MV}$
110	0	0	0	0.00	0.03	0.01	0.01	0.00	0.01	0.00	0.00
95	15	0	0	0.00	0.04	0.01	0.01	0.00	0.03	0.01	0.01
70	40	0	0	0.01	0.07	0.03	0.03	0.02	0.06	0.02	0.02
95	0	15	0	0.00	0.04	0.02	0.03	0.00	0.07	0.01	0.02
80	15	15	0	0.01	0.05	0.04	0.04	0.01	0.08	0.05	0.08
55	40	15	0	0.02	0.04	0.05	0.04	0.01	0.02	0.03	0.02
1010	0	0	0	0.00	0.02	0.00	0.00	0.00	0.02	0.00	0.00
995	15	0	0	0.00	0.04	0.00	0.01	0.00	0.05	0.01	0.01
700	310	0	0	0.00	0.06	0.01	0.01	0.00	0.04	0.00	0.00
995	0	15	0	0.00	0.04	0.00	0.01	0.00	0.05	0.00	0.00
980	15	15	0	0.00	0.03	0.01	0.01	0.00	0.03	0.01	0.03
685	310	15	0	0.02	0.05	0.04	0.05	0.00	0.07	0.00	0.06

Note: The first four columns show the number (m₀₀) of biomarkers associated with neither exposure nor outcome, the number (m₁₀) associated with only the exposure, the number (m₀₁) associated with only the outcome and the number (m₁₁) associated with both exposure and outcome. The remaining columns show the FWER, defined to be the mean proportion of simulations with at least one biomarker identified as a mediator, when $\alpha =0.05$. Details of the simulation can be found in Section 2.

The newly proposed MCPs tended to have higher power for detecting true mediators. These results are summarized in Table 2 for conditionally independent biomarkers and in Supplementary Tables for blocks of dependent biomarkers. In the majority of scenarios, among all univariate approaches, MCP_S and $MC{P}_S^{WY}$ slightly outperformed MCP_P despite having lower FWER in the null simulations, but their relative performance depended on the exact scenario. The MCP_P test can select biomarkers with a single strong association (i.e. the m₁₀ and m₀₁ biomarkers with one true association) and biomarkers with two non-significant, but still modest, associations (i.e. the m₀₀ biomarkers with $P_{1j},P_{2j}\approx 0.1$). Note, we omit $MC{P}_S^{WY}$ from Tables 1 and 2, where biomarkers are independent, because it yields identical results to MCP_S. Furthermore, we found that the multivariate approach resulted in higher power, as compared to the univariate approaches, with $MC{P}_S^{MV}$ having the highest power in all scenarios. We emphasize that there is no equivalent to the multivariate approach, and no means for obtaining the corresponding increase in power, using a permutation based method. As expected, $MC{P}_S^{WY}$ only increased power, compared to MCP_S, when there was significant correlation (e.g. 0.9) among biomarkers and the total number of biomarkers was large (e.g. 1010) (Supplementary Material). Given its limited benefit and its failure to strictly control FWER in two simulations ($m=m_{00}=110$) with higher correlation (Supplementary Tables S3 and S7), we do not recommend using $MC{P}_S^{WY}$ in practice. In general, results were similar for the binary and continuous outcome.

Table 2.

Power from four multiple comparison procedures MCP_B, MCP_P, MCP_S and $MC{P}_S^{MV}$

				Continuous outcome				Binary outcome
m00	m10	m01	m11	MCPB	MCPP	MCPS	$MC{P}_S^{MV}$	MCPB	MCPP	MCPS	$MC{P}_S^{MV}$
100	0	0	10	0.54	0.68	0.72	0.81	0.30	0.49	0.49	0.58
85	15	0	10	0.54	0.61	0.68	0.80	0.28	0.37	0.40	0.49
60	40	0	10	0.55	0.54	0.64	0.79	0.28	0.30	0.34	0.43
85	0	15	10	0.54	0.58	0.68	0.77	0.28	0.42	0.44	0.65
70	15	15	10	0.54	0.54	0.64	0.77	0.25	0.33	0.36	0.66
45	40	15	10	0.55	0.50	0.60	0.76	0.29	0.30	0.33	0.66
1000	0	0	10	0.28	0.69	0.61	0.77	0.11	0.47	0.34	0.44
985	15	0	10	0.28	0.60	0.58	0.74	0.10	0.37	0.31	0.41
690	310	0	10	0.27	0.33	0.45	0.66	0.10	0.15	0.18	0.23
985	0	15	10	0.27	0.57	0.57	0.77	0.11	0.43	0.35	0.65
970	15	15	10	0.26	0.53	0.54	0.75	0.11	0.36	0.32	0.63
675	310	15	10	0.27	0.33	0.44	0.76	0.08	0.12	0.16	0.42

Note: The first four columns show the number (m₀₀) of biomarkers associated with neither exposure nor outcome, the number (m₁₀) associated with only the exposure, the number (m₀₁) associated with only the outcome and the number (m₁₁) associated with both exposure and outcome. The remaining columns show the power, defined to be the mean proportion of true mediators identified, when $\alpha =0.05$. Details of the simulation can be found in Section 2.

In an attempt to mimic our Breast Cancer study, we simulated data with a large number of exposure/metabolite associations. When m = 1010 and $m_{10}=310$, we found that the benefit of our newly proposed MCP_S approach, as compared to the Bonferroni approach, was less pronounced. Intuitively, this decline occurs because when S₁ is large, $P_{2j}$ will have to achieve near Bonferroni-level significance for the biomarker to qualify as a mediator.

3.2 Breast cancer study

The 478 metabolites were strongly associated with both BMI and breast cancer status, with 218 of the BMI/metabolite associations having a P-value below 0.05 and 103 of the breast cancer/metabolite associations having a P-value below 0.05. We found 24 metabolites, listed in Table 3, which were potential mediators connecting BMI and breast cancer risk (FDR < 0.2). Of those 24, only 2, 16-α-hydroxy-DHEA-3-sulfate and 3-methyl-glutaryl carnitine 1, were significant at FWER = 0.05. We note that the P-values from our new methods were lower than the P-values produced by alternative methods. However, as seen in the simulations with a large number number of exposure/biomarker associations, the P-values from these methods were not dramatically smaller.

Table 3.

We list metabolites with an FDR-adjusted P-value < 0.2 using MCP_D (p_D), along with their adjusted P-values based on MCP_B (p_B), MCP_P (p_p), MCP_S (p_S) and $MC{P}_S^{WY}$ ($p_S^{WY}$); 4A3B17B = 4-androsten-3beta, 17beta-diol

Name	pB	pp	pS	$p_S^{WY}$	pD
16a-Hydroxy DHEA 3-sulfate	0.021	0.055	0.014	0.008	0.0075
3-Methylglutarylcarnitine	0.046	0.29	0.015	0.018	0.0075
4A3B17B disulfate	0.31	0.67	0.06	0.094	0.02
Allo-isoleucine	0.12	0.2	0.083	0.056	0.021
4A3B17B monosulfate	0.59	0.61	0.11	0.14	0.023
Urate	0.24	0.084	0.16	0.086	0.027
3-Methyl-2-oxobutyrate	0.6	0.22	0.41	0.23	0.054
4A3B17B disulfate	1	0.99	0.43	0.38	0.054
Gamma-glutamylvaline	0.84	0.56	0.57	0.32	0.063
Alpha-hydroxyisovalerate	1	1	0.73	0.6	0.073
2-Methylbutyrylcarnitine	1	1	1	0.52	0.096
21-Hydroxypregnenolone disulfate	1	1	1	0.92	0.1
7-Methylguanine	1	0.98	1	0.66	0.1
Histidine	1	1	1	0.7	0.1
N-acetylalanine	1	0.86	1	0.68	0.1
Lactate	1	1	1	1	0.12
Succinylcarnitine	1	1	1	1	0.12
4A3B17B monosulfate	1	1	1	1	0.13
Alpha-tocopherol	1	0.79	1	1	0.15
Octanoylcarnitine	1	1	1	1	0.16
Dihomo-linolenate	1	1	1	1	0.17
Decanoylcarnitine	1	1	1	1	0.18
Euricoyl sphingomyelin	1	1	1	1	0.18
N1-methylguanosine	1	0.25	1	1	0.18

4 Discussion

We introduced a new method for testing multiple putative mediators. This computationally efficient method can maintain specified family-wise error rates (FWER) and false discovery rates (FDR), and should be very useful in modern studies evaluating high dimensional biomarkers. We then applied this new method to a study evaluating the mechanistic relationship between increased BMI and an increased risk of breast cancer.

We note that MCP_S and $MC{P}_S^{WY}$ test each biomarker individually. Therefore, we can only use these methods to claim that marginally, when considered in isolation, each selected biomarker has the defining characteristics of a mediator. We neither claim that exposure nor the outcome is correlated with the selected biomarker, conditional on all other biomarkers. We aim only to reject $H_{01}^j$ and $H_{02}^j$. Hence, the markers selected by these procedures may not all be true biological mediators. Consider the following example. Let $E⃗M_1⃗Y$ and $M_1⃗M_2$. Our MCP is designed to select M₂, but M₂ is not a true biological mediator. For this reason, we opted to call our selected biomarkers as ‘probable mediators’ and not ‘true mediators’. Given this limitation, when using either MCP_S or $MC{P}_S^{WY}$, we suggest a second step, following variable selection, that builds a graphical model containing the exposure, outcome and selected variables. A second option is to use $MC{P}_S^{MV}$, which identifies biomarkers marginally associated with the exposure and, to some extent, conditionally associated with the outcome. The caveat is that association is only conditional on those biomarkers that were included in the stepwise regression and this method does not carry theoretical guarantees.

The newly proposed MCP is an important contribution to the current literature on multivariate mediation analysis. First, the new methods improve upon our previous permutation approach in four ways. The new MCP is more powerful, provides theoretical guarantees on FWER, requires less computational time and can easily be extended to a multivariable analysis. Moreover, this new MCP provides a means for controlling FDR, in addition to FWER. Second, this MCP compliments those procedures that fit mediation models where the majority of putative mediators are presumed to be true mediators. Our MCP can be considered a preprocessing step to model fitting. Third, this paper brings the mathematical theory developed for the field of replicability to mediation analysis. The proofs guaranteeing asymptotic FWER and FDR control extend the theory to mediation analysis where the P-values, $\{P_{11},\dots ,P_{1m}\}$ and $\{P_{21},\dots ,P_{2m}\}$, are calculated from a common dataset.

The theory developed here builds upon the theory developed by Bogomolov and Heller (Bogomolov and Heller, 2018) for demonstrating replicability. In their work, the pair of P-values $(p_{1j},p_{2j})$ summarize the association between biomarker and outcome (e.g. SNP and disease) in two distinct study populations. Then, showing that their MCP selects biomarker j would be equivalent to stating that the biomarker/outcome association is replicable (i.e. the association is significant in both datasets). The common feature in their application and ours is that the two sets of P-values can be considered independent. This requirement limits further extensions, preventing, for example, its use in cases where the P-values are for two correlated traits in a common population.

In our breast cancer study, we identified 16a-hydroxy DHEA 3-sulfate and 3-methylglutarylcarnitine-1 as potential mediators of the BMI and ER+ breast cancer association. 16a-hydroxy DHEA 3-sulfate is the 16a-hydroxylated metabolite of DHEA and has been found in laboratory studies to be estrogenic and to be capable of binding and activating the ER$-\beta$ estrogen receptor. However, it has not been previously linked with breast cancer risk. 3-Methylglutarylcarnitine-1 is a marker indicative of incomplete degradation of leucine. Specifically, when the 3-hydroxy-3-methylglutaryl-coenzyme A lyase enzyme, which catalyzes the final step in leucine catabolism, is insufficiently active, 3-methylglutarylcarnitine-1 accumulates in the blood. For this reason, 3-methylglutarylcarnitine-1 is sometimes used in clinical settings to diagnose errors in leucine metabolism. No prior studies have examined this metabolite in relation to breast cancer risk. These findings point toward potentially new metabolic pathways that may link a high BMI with breast cancer risk.

Funding

Ruth Heller acknowledges support by Israel Science Foundation (grant no. 0603616831).

Conflict of Interest: none declared.