Abstract
Loading-induced interstitial fluid flow in the microporosities of bone is critical for osteocyte mechanotransduction and for the maintenance of tissue health, enhancing convective transport in the lacunar-canalicular system. In recent studies, our group has reported alterations of bone’s vascular porosity and lacunar-canalicular system microarchitecture in a rat model of postmenopausal osteoporosis. In this work, poroelastic finite element analysis was used to investigate whether these microstructural changes can affect interstitial fluid flow around osteocytes. Animal-specific finite element models were developed combining micro-CT reconstructions of bone microstructure and measures of the poroelastic material properties. These models were used to quantify and compare loading-induced fluid flow in the lacunar-canalicular system of ovariectomized and sham-operated rats. A parametric analysis was also used to quantify the influence of the lacunar-canalicular permeability and vascular porosity on the fluid velocity magnitude. Results show that mechanically-induced interstitial fluid velocity can be significantly reduced in the lacunar-canalicular system of ovariectomized rats. Interestingly, the vascular porosity is shown to have a major influence on interstitial fluid flow, while the lacunar-canalicular permeability influence is limited when larger than 10−20 m2. Altogether our results suggest that microstructural changes associated with the osteoporotic condition can negatively affect interstitial fluid flow around osteocytes in the lacunar-canalicular system of cortical bone. This fluid flow reduction could impair mechanosensation of the osteocytic network, possibly playing a role in the initiation and progression of age-related bone loss and postmenopausal osteoporosis.
Keywords: poroelasticity, bone fluid flow, lacunar-canalicular system, osteoporosis, osteocyte
1. Introduction
The movement of interstitial fluid within the bone microporosities is critical for bone physiology. Blood vessels and bone cells are embedded in the bone tissue inside interconnected porosities, where interstitial fluid permits the exchange of nutrients and signaling molecules. In cortical bone, blood vessels reside in the vascular porosity, and the osteocytes, the most abundant bone cells, reside in the lacunar-canalicular porosity. The two porosities are hierarchically interconnected and form a dual-porous structure where the extravascular fluid in the vascular porosity continually interchanges with the extracellular fluid in the lacunar-canalicular porosity (Cowin, 1999; Qin et al., 2002). Mechanically-induced deformation of bone tissue acts as a motive force for this fluid displacement, generating fluid pressure gradients that drive interstitial fluid into the lacunar-canalicular system towards the vascular porosity space and vice versa (Starkebaum et al., 1979; Zeng et al., 1994; Cowin et al., 1995). This loading-induced fluid flow has two important implications for bone physiology: (a) it enhances convective fluid transport in the lacunar-canalicular system, which is critical for osteocyte viability (Piekarski and Munro, 1977; Knothe-Tate et al., 2000; Wang et al., 2000); and (b) it generates forces on the osteocyte processes in the canalicular space, playing a critical role in bone mechanotransduction, coupling external mechanical loading with the osteocyte microenvironment (Weinbaum et al., 1994; You et al., 2001). Strong evidence suggests that osteocytes are able to translate these fluid-mediated physical stimuli to biochemical signals that regulate the processes of bone formation and bone resorption, maintaining the mechanical function of the bone structure (Klein-Nulend et al., 2013).
Alterations in the microstructure of cortical bone have been observed in several models of osteoporosis, including estrogen deficiency, aging, and disuse (Westerlind et al., 1997; Sharma et al., 2012; Tommasini et al., 2012; Britz et al., 2012). Both vascular porosity and lacunar-canalicular microarchitecture have been shown to change in response to a drop in estrogen level in a rat model of postmenopausal osteoporosis (Sharma et al., 2012, 2018). These microstructural changes possibly affect the fluid flow in the lacunar-canalicular system, impairing osteocyte mechanosensation or affecting fluid-mediated molecular transport in the lacunar-canalicular system. Alteration in the loading-induced convection of small molecules within the lacunar-canalicular system of ovariectomized rats was reported by our group, supporting the hypothesis that estrogen deficiency changes the interstitial fluid flow microenvironment (Ciani et al., 2014).
Theoretical and experimental studies have demonstrated that interstitial fluid velocity in the lacunar-canalicular system depends on characteristics of mechanical loading, such as strain rate and strain magnitude, as well as characteristics of the vascular and lacunar-canalicular porosities, such as vascular pore morphology and lacunar-canalicular system permeability (Zhang et al., 1998; Steck et al., 2003; Swan et al., 2003; Fornells et al., 2007; Remond et al., 2008; Kumar et al., 2012; Pereira and Shefelbine, 2014). In particular, using poroelasticity theory to estimate fluid flow, researchers have shown that both vascular and lacunar-canalicular porosities influence interstitial fluid flow at the microscale (i.e., single osteons) and macroscale (i.e., cortical bone section) (Wang et al., 1999; Fornells et al., 2007; Cowin et al., 2009). In cortical bone, interstitial fluid flow is particularly influenced by the vascular porosity, which acts as a low-pressure fluid reservoir, where the loading-induced fluid pressure in the lacunar-canalicular system mainly relaxes (Cowin, 1999; Wang et al., 1999; Goulet et al., 2008). Furthermore, bone interstitial fluid flow depends on the morphology of the lacunar-canalicular system and on the permeability of the pericellular space in which the fluid moves (Weinbaum et al., 1994; Smit et al., 2002; Goulet et al., 2009; Wang et al., 2014).
The objective of this study was to investigate how changes in cortical bone microporosities affect loading-induced fluid flow around osteocytes. High-resolution animal-specific poroelastic finite element models were used to quantify and compare interstitial fluid flow within the osteocytic network of ovariectomized rats and sham-operated control rats. In addition, a parametric study using idealized bone geometries was performed to estimate the specific influence of vascular porosity and lacunar-canalicular permeability on the fluid velocity in the lacunar-canalicular system. The results of this work can offer a better understanding of how fluid flow in the lacunar-canalicular system is altered during conditions of bone loss, possibly affecting osteocyte viability and bone mechanotransduction.
2. Material and Methods
2.1. Finite element analysis of interstitial fluid flow in the lacunar-canalicular system
To quantify fluid flow in cortical bone we used finite element analysis, assuming bone tissue to be an ideal fluid-saturated poroelastic material. The cortical bone tissue was modeled as a biphasic material with fully interconnected solid and fluid phases. Material parameters were assigned to model the bone matrix, where the solid phase represents the collagen-apatite mineralized structure, impermeable to fluids, and the porous space represents the fluid-saturated lacunar-canalicular system. The vascular porosity was included in all the models, but the fluid pressure and displacement in the vascular porosity were ignored because their influence on the fluid flow in the lacunar-canalicular system is negligible (Mak et al., 1997; Zhang et al., 1998). In addition, soft tissue within the vascular pores (i.e., blood vessels and nerves) and the lacunar-canalicular system (i.e., osteocyte body and processes) was not modeled because its influence on the poroelastic behavior of the tissue is negligible (Zeng et al., 1994; Weinbaum et al., 1994; Cowin, 1999).
Mechanically-induced deformation of bone tissue generates fluid pore pressure, which drives fluid displacement in the lacunar-canalicular porous space (Darcy’s law):
| (1) |
where is the fluid velocity within the lacunar-canalicular porosity and ∇p is the load-induced fluid pressure gradient. The intrinsic permeability, k, defines the resistance opposed by the lacunar-canalicular porosity to the fluid displacement, while ϕlc is the lacunar-canalicular porosity and μ is the dynamic viscosity of the interstitial fluid. The poroelastic problem was solved using the coupled pore fluid diffusion and stress analysis in Abaqus (v6.13, Dassault Systemes).
2.2. Micro-CT derived finite element models
Animal-specific finite element models were generated from micro-CT scans collected as part of a previous study that investigated changes in the cortical microporosities in a rat model of postmenopausal osteoporosis (Sharma et al., 2018). In that study, twelve 20-week-old female Sprague Dawley rats were divided in two groups: one underwent bilateral ovariectomy (OVX) while the other was sham-operated (SHAM). After 6 weeks animals were sacrificed and the right tibiae were scanned with a high-resolution micro-CT system (SkyScan 1172; Bruker) at a nominal isotropic voxel size of 1 μm (100 kV, 100 μA). Three-dimensional reconstructions were obtained with a back-projection algorithm (NRecon, v.1.6.5, SkyScan, Bruker), using beam hardening and ring-artifact correction algorithms, and a Gaussian low-pass filter to reduce noise. Density phantoms were scanned using the same parameters and were used to calibrate the grayscale images to obtain accurate measures of the mineral content. All procedures were conducted under Institutional Animal Care and Use Committee approval.
To create a finite element model for each animal, a volume of interest was selected from the anterior cortical region of the proximal tibial metaphysis, where we previously detected morphological changes in response to estrogen deficiency (Fig. 1) (Sharma et al., 2018). Three-dimensional datasets were segmented using the micro-CT analysis software (CTAn v1.14; Bruker). A global grayscale threshold value corresponding to a mineral content of 0.45 g/cm3 was applied to binarize images, separating bone tissue from soft tissue (Palacio-Mancheno et al., 2014). Image noise was removed using three-dimensional de-speckle filters and basic morphological operations, assuming that the vascular pores are interconnected and that their minimum volume is 1000 μm3 (Tommasini et al., 2012; Palacio-Mancheno et al., 2014). Similarly, the lacunar porosity was isolated from noise with three-dimensional filtering, assuming that a single lacuna volume falls in the range 100 μm3 to 600 μm3 (Tommasini et al., 2012). Vascular porosity morphology and lacunar density and porosity were quantified for each volume of interest (CTAn v1.14; Bruker). Vascular canal diameter and separation (Ca.Dm and Ca.Sp) were measured using the sphere-fitting algorithm, and vascular porosity (Ca.V/TV), lacunar density (N.Lc/TV), and lacunar porosity (ϕlac) were also calculated. In addition, the tissue mineral density (TMD) was estimated from the mean grayscale value of the voxels representing bone tissue, and converted to g/cm3 with a calibration curve derived from the known density values of the scanned phantoms.
Figure 1.

Micro-CT images of (a) a whole rat tibia and (b) a proximal metaphysis cross-section from a SHAM sample, demonstrating the volume of interest selected ~1 mm distal to the growth plate in the anterior region of the tibial cortex, including the periosteal and endosteal surfaces. (c) The corresponding micro-CT derived finite element model with the endosteal and vascular pore elements.
After segmentation and morphometric analysis, each volume of interest was converted to a three-dimensional voxel-based hexahedral/tetrahedral mesh with an adaptive meshing algorithm, obtaining approximately 2 million elements for each model (ScanIP v6.0; Simpleware) (Fig. 1c). A total of 12 models, 6 OVX and 6 SHAM, were created, each corresponding to a specific animal. These finite element models were exported to Abaqus software as orphan meshes of trilinear poroleastic elements (C3D8P), where sample-specific poroelastic properties were assigned, and loading and boundary conditions were defined, as described below.
2.3. Estimation of sample-specific poroelastic parameters
Animal-specific lacunar-canalicular poroelastic parameters were defined for each model based on morphological and structural measures. The porosity of the lacunar-canalicular system, ϕlc, was defined as the sum of the lacunar porosity, ϕlac, measured from the micro-CT scans, and the canalicular porosity, ϕcan, estimated using an adapted geometrical model as in Beno et al. (2006):
| (2) |
where the canalicular radius, rcan, was taken from our measurement in Sharma et al. (2012), and the total length of the canalicular space per lacuna, Lcan, was calculated as:
| (3) |
where rlac is the mean radius of a lacuna and Ncan is the mean number of primary canaliculi radiating from each lacuna. Factors t and b account for tortuosity and branching of canaliculi, respectively. These values were directly estimated from the three-dimensional representation of the canalicular network obtained using confocal microscopy in Sharma et al. (2012). The tortuosity (t) was defined as the mean ratio of the length of a canaliculus and the Euclidean distance between the two ends of the same canaliculus and was estimated to be 1.1 for all models. The branching factor (b) was defined as the average number of times the canaliculi radiating from a lacuna (primary canaliculi) branch to create secondary canaliculi and was estimated from Sharma et al. (2012) to be 3.25 for all models.
The lacunar-canalicular permeability, k, was calculated using the microstructural model formulated in Weinbaum et al. (1994):
| (4) |
where a is the radius of the osteocyte process and q is the ratio of the osteocyte process radius and canalicular radius (q = a/rcan). The ratio ncan/L2 represents the average density of canaliculi per unit area within the tissue, and was assumed to be equal to the number of secondary canaliculi per unit of area radiating from each lacuna measured in Sharma et al. (2012). The ratio of the canalicular radius over the thickness of the viscous layer near the canalicular wall, γ, was taken from Zhou et al. (2008), A1 and B1 are parameters depending on γ and q defined in Weinbaum et al. (1994), and I1 and K1 are modified Bessel functions of the first order.
The bone elastic constants were estimated from the micro-CT measurements of TMD. The bulk modulus and shear modulus of the solid phase (i.e., the collagen-apatite structure), Ks and Gs, respectively, were estimated as:
| (5) |
and
| (6) |
where the Poisson’s ratio of the solid phase, vs, was taken from Cowin et al. (2009) and the Young’s modulus of the collagen-apatite solid phase, Es, was estimated using the experimental relationship in Wagner et al. (2011):
| (7) |
where the hydroxyapatite density, ρHA, was assumed to be equal to the tissue mineral density (TMD). The drained porous elastic bulk modulus, Kd, and shear modulus, Gd, were estimated as in Christensen (1979):
| (8) |
and
| (9) |
The drained Young’s Modulus, Ed, and the drained Poisson’s ratio, vd, were then calculated as in Christensen (1979):
| (10) |
and
| (11) |
Finally, the bone interstitial fluid was considered equivalent to water and assigned a bulk modulus Kf = 2.3 GPa and a dynamic viscosity μ = 103Pa s (Cowin, 1999).
2.4. Idealized model of vascular porosity in cortical bone
To further quantify the influence of vascular porosity and lacunar-canalicular permeability on loading-induced fluid flow, three-dimensional idealized models of cortical bone were created. A small sample of cortical bone was modeled as a parallelepipedic volume (400 μm × 200 μm × 500 μm) with two of the six faces representing the periosteal and the endosteal surfaces and cylindrical lumens representing the vascular canals. Four different idealized models with vascular pore diameters of 15, 20, 25 or 30 μm were created to assess the effect of vascular canal diameter on fluid flow in the lacunar-canalicular system. Each model was converted to a mesh of hexahedral linear poroelastic elements (C3D8P) with Abaqus CAE (v6.13; Dassault Systemes) using an adaptive meshing algorithm, obtaining approximately 120,000 elements for each model. Poroelastic parameters for the bone tissue were derived from Smit et al. (2002) and Cowin (1999). A Young’s modulus (Ed) of 15.75 GPa and Poisson’s ratio (vd) of 0.33 were assigned to the porous elastic elements. The solid-phase of the tissue (i.e., collagen-apatite structure) was modeled as a compressible material with a 17.66 GPa bulk modulus (Ks), while a porosity of 5% was assigned to the lacunar-canalicular system (ϕlc). The bone interstitial fluid was considered equivalent to water and assigned a bulk modulus Kf = 2.3 GPa and a dynamic viscosity μ = 103 Pa s. To assess the influence of the lacunar-canalicular permeability (k), 5 different values were assigned to the models, varying from a minimum of 10−22 m2 to a maximum of 10−18 m2 (Zeng et al., 1994; Beno et al., 2006; Smit et al., 2002; Benalla et al., 2014; Gardinier et al., 2010).
2.5. Loading and boundary conditions
Loading conditions were defined with Abaqus CAE (v6.13; Dassault Systemes) to simulate physiological bone compression during walking. For both the micro-CT derived and idealized models, unconfined compression was obtained by applying Haversine time-varying displacement, with a maximum amplitude of 0.1% of the model heights (200 μm), to the nodes at the top surface of the models, at 1 Hz frequency. Nodes on the distal (bottom) surface were constrained in the top-down axial direction, allowing for radial displacement. A zero pore-pressure boundary condition was applied to the nodes of the vascular canals and endosteal surface to allow free fluid flow, assuming the vascular and the endosteal spaces act as low pressure fluid reservoirs (Zhang et al., 1998), while the periosteal surface and the top and bottom surfaces were modeled as completely impermeable to interstitial fluid (Li et al., 1987).
2.6. Fluid flow quantification and statistical analysis
Numerical solution for the coupled pore fluid diffusion and stress analysis was obtained with Abaqus Analysis (v6.13; Dassault Systemes) using a transient dynamic analysis with automatic time increments ranging from 0.01 to 0.05 s for a total of 1 s of simulation (i.e., one loading cycle). Fluid velocity within the lacunar-canalicular porosity (direction and magnitude) and fluid pore pressure were obtained for all nodes of the finite element models, and for each time increment of the dynamic solutions.
Mann-Whitney non-parametric tests were performed to assess differences in the mean interstitial fluid velocity between OVX and SHAM models, with a significance level of 0.05 (Prism 6; GraphPad). To compare results of the micro-CT derived models, we calculated the average fluid velocity magnitude within the regions around the vascular pores, at the time increment where fluid velocity reached the local maximum; numerical results for fluid velocity were extracted from nodes within approximately 10 μm of the vascular pore surfaces at time t = 0.3 s. Three-dimensional renderings of the fluid velocity and fluid pore pressure were created to assess regional variation. In addition, linear regression analyses were performed to investigate the correlation of fluid velocity magnitude with vascular porosity and vascular canal microarchitecture (Prism 6; GraphPad).
To analyze the idealized models, the instantaneous fluid velocity was quantified and plotted from one representative node at the surface of the vascular pore in the center of the models. Renderings of the fluid velocity output were created to visualize fluid flow direction and magnitude. Finally, the average fluid velocity of the nodes at the vascular pore surfaces was calculated and compared between the groups with different permeabilities and vascular pore diameters.
3. Results
3.1. Analysis of animal-specific poroelastic finite element models
The volumes of interest analyzed demonstrated significant differences in the cortical bone microstructure between the OVX and SHAM groups (Table 1). The vascular porosity and canal diameter were significantly larger in the OVX group, while no significant differences were observed in the vascular canal separation and tissue mineral density between the two groups. The lacunar density and lacunar porosity were significantly smaller in the OVX group compared to SHAM. However, no significant changes were observed in the estimated lacunar-canalicular permeability between SHAM (1.54 × 10−20 m2) and OVX (1.15 × 10−20 m2), as well as for the other estimated poroelastic properties (Table 2).
Table 1.
Results of micro-CT measurements of intracortical microarchitectural measures (mean ± SD) for volumes of interest analyzed in the rat proximal tibia (SHAM: n=6; OVX: n=6).
| SHAM | OVX | |
|---|---|---|
| Canal porosity, Ca.V/TV (%) | 5.0 ± 0.9 | 15.2 ± 6.43a |
| Canal diameter, Ca.Dm (μm) | 21.5 ± 2.3 | 30.7 ± 5.5a |
| Canal separation, Ca.Sp (μm) | 104.0 ± 20.09 | 86.9 ± 13.1 |
| Tissue mineral density, TMD (g/cm3) | 1.18 ± 0.04 | 1.23 ± 0.04 |
| Lacunar density, N.Lc/TV (#/mm3) | 6.18 ± 0.75 × 104 | 3.94 ± 0.78 × 104 a |
| Lacunar porosity, ϕlac (%) | 1.31 ± 0.18 | 0.83 ± 0.17a |
p < 0.05 compared to SHAM.
Table 2.
Poroelastic material parameters (mean ± SD) estimated from the micro-CT data and from confocal microscopy measurements of the lacunar-canalicular system in SHAM and OVX rats previously reported in Sharma et al. (2012).
| SHAM | OVX | |
|---|---|---|
| Canalicular radius, rcan (nm) | 140.8 | 145.8 |
| Number of canaliculi per lacuna, Ncan | 83.9 | 89.7 |
| Lacunar volume, Lc.V(μm3) | 352 | 393 |
| Canalicular porosity, ϕcan (%) | 1.90 ± 0.11 | 1.70 ± 0.19 |
| Lacunar-canalicular porosity, ϕlc (%) | 3.22 ± 0.30 | 2.53 ± 0.36 |
| Lacunar-canalicular permeability, k (m2) | 1.54 × 10−20 | 1.15 × 10−20 |
| Drained Young’s modulus, Ed (GPa) | 20.14 ± 0.76 | 21.42 ± 0.74 |
| Poisson’s ratio, vd | 0.319 ± 0.001 | 0.321 ± 0.001 |
| Bulk modulus of solid phase, Ks (GPa) | 20.50 ± 0.80 | 21.49 ± 0.73 |
The poroelastic finite element analysis showed that fluid pore pressure and the resulting fluid velocity in the lacunar-canalicular system are lower in the OVX models compared to SHAM (Figs. 2 and 3). In addition, linear regression analysis demonstrated that the average fluid velocity around vascular pores is negatively correlated with the diameter of the vascular canals and with the vascular porosity, r2 = 0.78 and r2 = 0.80, respectively, and positively correlated with the vascular canal separation (r2 = 0.49) (Fig. 3).
Figure 2.
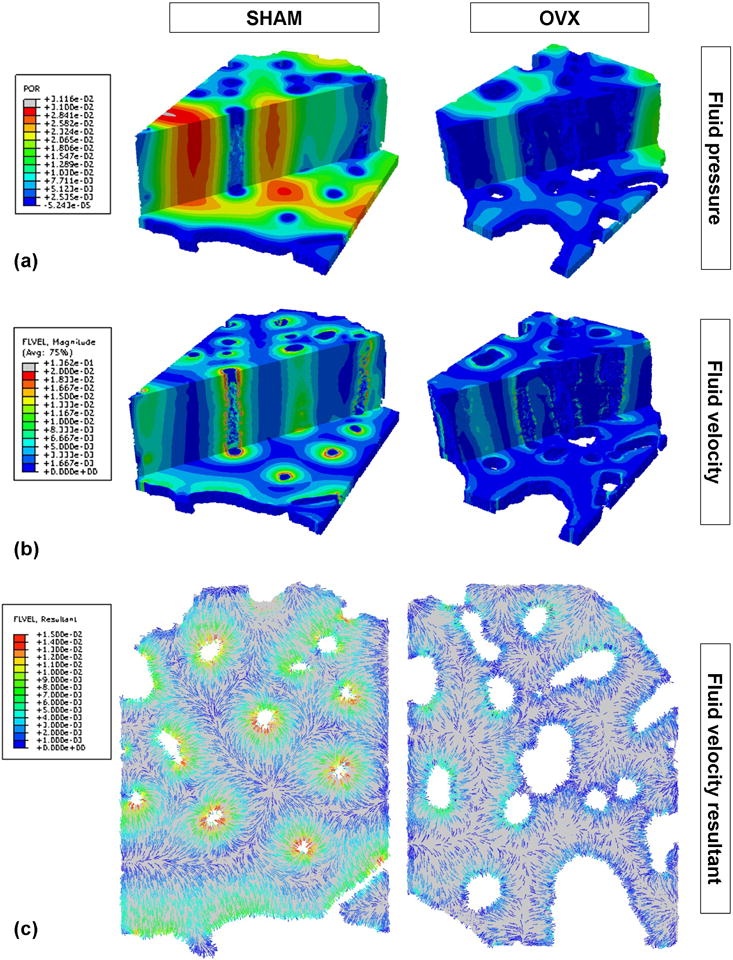
Representative SHAM and OVX three-dimensional renderings of (a) fluid pore pressure (MPa) and (b) fluid velocity magnitude (μm/s) within the lacunar-canalicular porosity at the time point when the fluid velocity is maximal. Axial and transverse sections are shown. (c) Cross-sectional renderings of fluid velocity vector direction and magnitude (μm/s) from a cross-section of the same SHAM and OVX models.
Figure 3.
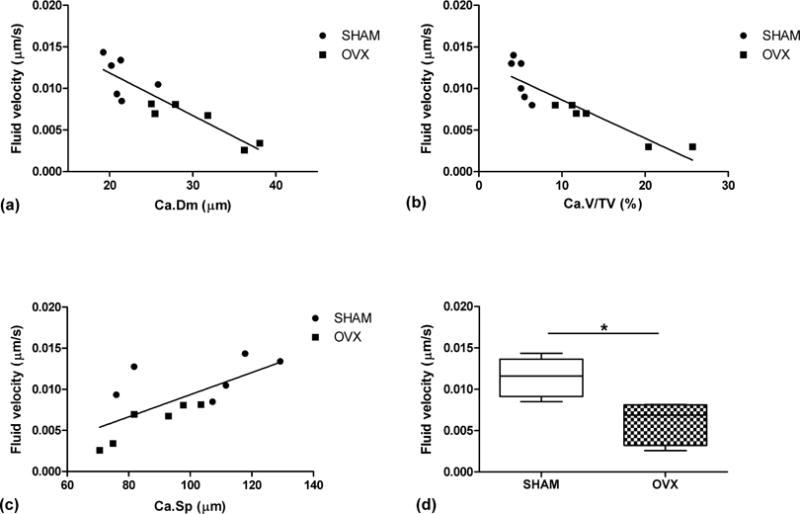
Linear correlation between average fluid velocity within the lacunar-canalicular porosity with (a) vascular canal diameter, Ca.Dm (r2 = 0.78), (b) vascular porosity, Ca.V/TV (r2 = 0.80), and (c) vascular canal separation, Ca.Sp (r2 = 0.49) for all models. (d) Box plots of average fluid velocity around vascular canals for SHAM and OVX (*p < 0.05).
3.2. Analysis of idealized bone finite element models
The parametric study performed with the idealized bone models confirm that loading-induced fluid displacement depends on the microstructure of both the vascular and lacunar-canalicular porosities (Fig. 4). Numerical solutions of the fluid velocity vector demonstrated that fluid within the lacunar-canalicular system moves towards the vascular canals when loading magnitude increases and in the opposite direction when loading magnitude decreases. The peak fluid velocity magnitude is reached in the first part of the loading curve at a time point more delayed in the models with lower permeability. Both the first positive peak of fluid velocity and the second negative peak of fluid velocity, corresponding to fluid flowing back into the lacunar-canalicular system from the vascular porosity, are strongly reduced with decreasing permeability (Fig. 4a). The mean fluid velocity magnitude at the vascular canal surface decreases as vascular canal diameter increases and lacunar-canalicular permeability decreases. However, for values larger than 10−20 m2, the lacunar-canalicular permeability has very little influence on the fluid velocity; only changes in the vascular canal diameter affect fluid velocity magnitude (Fig. 4b). Furthermore, spatial analysis shows that the influence of increased vascular porosity on fluid velocity is limited to regions around vascular pore surfaces, with smaller changes for regions more distant to the vascular surface (Fig. 5).
Figure 4.

(a) Instantaneous fluid velocity within the lacunar-canalicular porosity and strain over time for a node at the surface of a central vascular pore, from a model with vascular canal diameter of 15 μm and lacunar-canalicular permeabilites of 10−20,10−21 and 10−22 m2; the outputs for 10−19 and 10−18 m2 are not shown because they are almost identical to the 10−20 m2 output. Negative strain represents compression in the axial top-down direction. Positive fluid velocity represents fluid flowing towards the vascular pore surface. (b) Average fluid velocity magnitude within the lacunar-canalicular system from idealized models with different vascular pore diameters (15, 20, 25 and 30 μm) and lacunar-canalicular permeabilities (10−18 to 10−22 m2).
Figure 5.
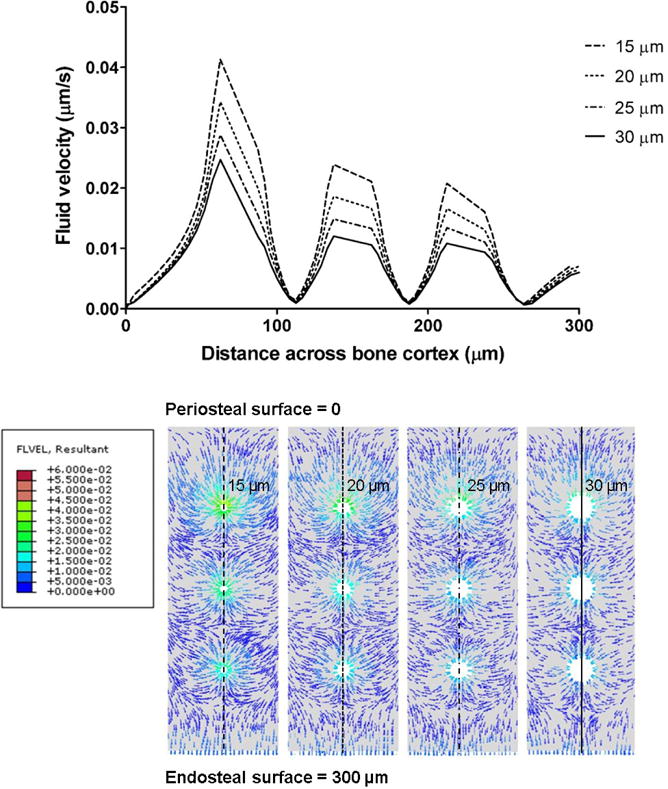
Spatial variation of the instantaneous fluid velocity within the lacunar-canalicular porosity at time point t = 0.3 s from the central region of the idealized models along the periosteal-endosteal direction, and cross-sectional renderings of the fluid velocity resultants (μm/s) at t = 0.3 s for k = 10−20m2 for the four vascular canal diameters (d = 15, 20, 25 and 30 μm).
4. Discussion
A poroelastic finite element analysis approach was used to investigate how microstructural changes associated with osteoporosis can affect interstitial fluid flow around osteocytes in cortical bone. The results indicate that the microarchitecture of both the vascular porosity and lacunar-canalicular system affects bone interstitial fluid flow. In particular, the increased vascular porosity associated with estrogen deficiency has a negative impact on interstitial fluid flow in the lacunar-canalicular system of cortical bone.
Decreased fluid velocity may alter how osteocytes embedded in the lacunar-canalicular system respond to bone mechanical loading. Osteocytes have the ability to sense mechanical loading via interstitial fluid flow, and can regulate bone resorption/formation balance accordingly (Bonewald and Johnson, 2008; Fritton and Weinbaum, 2009). A lower fluid velocity results in a smaller mechanical stimulus perceived by osteocytes and a potential up-regulation of bone resorption signals (Robling et al., 2008; Nakashima et al., 2011). Therefore, a fluid flow reduction in the early stages of estrogen loss could impact the mechanism by which osteocytes sense mechanical loading (i.e., bone’s mechanosensory system), leading to unbalanced bone resorption. This could trigger a potential positive feedback mechanism, where microstructural changes are both a cause and an effect of impaired fluid flow. Similarly to what is reported here, Goulet et al. (2008) showed that increased vascular canal porosity due to aging is associated with lower fluid velocity in the lacunar-canalicular system in human cortical bone. It is possible that the phenomenon observed here, in a rat model of postmenopausal osteoporosis, and by Goulet and colleagues, in relation to aging, leads to analogous consequences for bone pathophysiology, or underlies similar biophysical mechanisms. A number of morphological studies have shown that age and osteoporosis affect the lacunar-canalicular and vascular porosity in cortical bone (Cooper et al., 2007; Carter et al., 2013; Ashique et al., 2017; Kazakia et al., 2014). These changes can affect the fluid flow condition, potentially playing a role in the genesis and progression of osteoporosis.
Numerical results obtained from the idealized models of cortical bone help to explain the results of the animal-specific finite element models, demonstrating how changes in the lacunar-canalicular permeability and vascular canal diameter influence fluid motion around the osteocytic network of cortical bone. Fluid velocity is positively correlated with lacunar-canalicular permeability, as similarly observed in previous studies (Remond et al., 2008; Gardinier et al., 2010; Pereira and Shefelbine, 2014), but increased diameter of the vascular canals has a predominant influence on fluid velocity in the lacunar-canalicular system. In particular, fluid velocity was found to be negatively correlated with vascular canal porosity. This phenomenon is principally explained by the decreased distance between neighboring vascular canals and the increased free-flow surface where the fluid can move to relax the loading-induced pore pressure, consistent with what has been reported in other modelling studies (Zeng et al., 1994; Wang et al., 1999). Using micro-CT derived finite element modelling, Steck et al. (2003) were able to estimate fluid flow across the entire cross-section of a loaded tibia. In the present study, focusing on a smaller volume of interest, we incorporated higher resolution quantification of the intracortical porosity, which had a large influence on the fluid velocity results. In future studies, by combining macroscale and microscale models we should further improve the description of fluid-mediated mechanotransduction in bone tissue, coupling whole bone loading with osteocyte-scale phenomena.
Reduced fluid velocity in the lacunar-canalicular system may affect convective transport between the osteocytes and the blood vessels in the vascular porosity, potentially leading to apoptosis, which has been shown to play a critical role in the initiation of bone remodelling events (Cardoso et al., 2009; Kennedy et al., 2014). Previous work in estrogen deficient rats found changes in molecular transport around osteocytes in cancellous bone, but no changes in cortical bone (Ciani et al., 2014). Results of the finite element analyses in the present study show that the changes in fluid velocity are more pronounced in the proximity of the vascular pores. This suggests that solute transport in the estrogen-deficient state would be most affected for osteocytes that are proximal to the vascular pores. However, the experimental analysis in Ciani et al. (2014) did not assess the relationship between osteocyte proximity to vascular pores and solute transport due to mechanical loading; thus no conclusive comparison can be drawn here.
One important limitation of this work was the small region of interest analyzed. This was due to the high resolution of the micro-CT images, and the consequent limited volume of interest analyzed. In the analyzed volumes of interest, morphological analysis revealed that OVX animals have a larger vascular porosity and lower lacunar density than SHAM-operated controls. These microstructural changes negatively affect fluid flow in the bone cortex. However, in Sharma et al. (2018) analysis of the same micro-CT images from larger volumes of interest revealed similar but not exactly matching results. This reflects a high regional variability of lacunar-canalicular and vascular porosities. Because of this regional variability, the results of the micro-CT derived finite element analysis from the specific region that was analyzed in this study should not be generalized to the entire bone structure. In further studies, other regions and anatomical locations should be investigated to extend the conclusions drawn here. Not only the permeability of the pericellular porosity and the vascular porosity morphology, but also their spatial variation within the bone tissue are important to determine the fluid flow in the lacunar-canalicular system (Knothe-Tate et al., 2009). Therefore, fluid velocity can vary greatly among different anatomical locations and bone regions, being dependent on specific morphological and structural features, which in turn can vary among different animals and in response to treatment condition (e.g., ovariectomized vs. control).
Another limitation of our modeling approach was the simplification of uniaxial compression for the applied loading to mimic walking activity. In vivo, during walking the whole tibia is subjected primarily to bending, which leads to compressive and tensile deformations within the cortical bone of the metaphysis (Steck et al., 2003; Fan et al., 2016). However, within the relatively small volume of interest that we have considered in this study, the local variations of the resulting strain are relatively small, and therefore we assumed constant uniaxial compression for simplicity. In future studies, a multiscale finite element modelling approach could be used to refine the local boundary conditions for the smaller models.
In conclusion, the combination of micro-CT imaging and poroelastic finite element analysis proved to be a powerful tool to predict changes in bone fluid flow, which can be influenced by microstructural properties, treatment conditions, and altered mechanical environments. In future studies, other conditions, such as aging and disuse, as well as different anatomical regions should be investigated. Bone tissue is a complex system where mechanical loading is a fundamental driver in the physiological regulation of bone mass and continual regeneration of mineralized bone matrix. Mechanically-induced fluid flow couples external mechanical loading with the mechanosensing cellular network, which regulates bone metabolism. Impaired fluid displacement can cause alteration in such fine regulation, and may play a role in the initiation and progression of postmenopausal osteoporosis.
Acknowledgments
This study was supported with grants from the National Institutes of Health (NIH/NIAMS AR052866) and the National Science Foundation (CMMI-1400247).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of interest statement
The authors have nothing to disclose.
References
- Ashique AM, Hart LS, Thomas CDL, Clement JG, Pivonka P, Carter Y, Mousseau DD, Cooper DML. Lacunar-canalicular network in femoral cortical bone is reduced in aged women and is predominantly due to a loss of canalicular porosity. Bone Reports. 2017;7:9–16. doi: 10.1016/j.bonr.2017.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benalla M, Palacio-Mancheno PE, Fritton SP, Cardoso L, Cowin SC. Dynamic permeability of the lacunar-canalicular system in human cortical bone. Biomechanics and Modeling in Mechanobiology. 2014;13(4):801–812. doi: 10.1007/s10237-013-0535-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beno T, Yoon YJ, Cowin SC, Fritton SP. Estimation of bone permeability using accurate microstructural measurements. Journal of Biomechanics. 2006;39(13):2378–2387. doi: 10.1016/j.jbiomech.2005.08.005. [DOI] [PubMed] [Google Scholar]
- Bonewald LF, Johnson ML. Osteocytes, mechanosensing and Wnt signaling. Bone. 2008;42(4):606–615. doi: 10.1016/j.bone.2007.12.224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Britz HM, Jokihaara J, Leppanen OV, Jarvinen TL, Cooper DM. The effects of immobilization on vascular canal orientation in rat cortical bone. Journal of anatomy. 2012;220(1):67–76. doi: 10.1111/j.1469-7580.2011.01450.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cardoso L, Herman BC, Verborgt O, Laudier D, Majeska RJ, Schaffler MB. Osteocyte apoptosis controls activation of intracortical resorption in response to bone fatigue. Journal of Bone and Mineral Research. 2009;24(4):597–605. doi: 10.1359/JBMR.081210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter Y, Thomas CD, Clement JG, Cooper DM. Femoral osteocyte lacunar density, volume and morphology in women across the lifespan. Journal of Structural Biology. 2013;183(3):519–526. doi: 10.1016/j.jsb.2013.07.004. [DOI] [PubMed] [Google Scholar]
- Chennimalai Kumar N, Dantzig JA, Jasiuk IM. Modeling of cortical bone adaptation in a rat ulna: Effect of frequency. Bone. 2012;50(3):792–797. doi: 10.1016/j.bone.2011.12.008. [DOI] [PubMed] [Google Scholar]
- Christensen RM. Mechanics of Composite Materials. Wiley; 1979. pp. 41–47. [Google Scholar]
- Ciani C, Sharma D, Doty SB, Fritton SP. Ovariectomy enhances mechanical load-induced solute transport around osteocytes in rat cancellous bone. Bone. 2014;59:229–234. doi: 10.1016/j.bone.2013.11.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper DM, Thomas CD, Clement JG, Turinsky AL, Sensen CW, Hallgrimsson B. Age-dependent change in the 3D structure of cortical porosity at the human femoral midshaft. Bone. 2007;40(4):957–965. doi: 10.1016/j.bone.2006.11.011. [DOI] [PubMed] [Google Scholar]
- Cowin SC. Bone poroelasticity. Journal of Biomechanics. 1999 Mar;32(3):217–238. doi: 10.1016/s0021-9290(98)00161-4. [DOI] [PubMed] [Google Scholar]
- Cowin SC, Gailani G, Benalla M. Hierarchical poroelasticity: movement of interstitial fluid between porosity levels in bones. Philos Trans A Math Phys Eng Sci. 2009;367(1902):3401–3444. doi: 10.1098/rsta.2009.0099. [DOI] [PubMed] [Google Scholar]
- Cowin SC, Weinbaum S, Zeng Y. A case for bone canaliculi as the anatomical site of strain generated potentials. Journal of Biomechanics. 1995;28(11):1281–1297. doi: 10.1016/0021-9290(95)00058-p. [DOI] [PubMed] [Google Scholar]
- Fan L, Pei S, Lu XL, Wang L. A multiscale 3D finite element analysis of fluid/solute transport in mechanically loaded bone. Bone Research. 2016;4:16032. doi: 10.1038/boneres.2016.32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fornells P, Garcia-Aznar JM, Doblare M. A finite element dual porosity approach to model deformation-induced fluid flow in cortical bone. Annals of Biomedical Engineering. 2007;35(10):1687–1698. doi: 10.1007/s10439-007-9351-5. [DOI] [PubMed] [Google Scholar]
- Fritton SP, Weinbaum S. Fluid and Solute Transport in Bone: Flow-Induced Mechanotransduction. Annual Review of Fluid Mechanics. 2009;41:347–374. doi: 10.1146/annurev.fluid.010908.165136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardinier JD, Townend CW, Jen KP, Wu Q, Duncan RL, Wang L. In situ permeability measurement of the mammalian lacunar-canalicular system. Bone. 2010;46(4):1075–1081. doi: 10.1016/j.bone.2010.01.371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goulet GC, Coombe D, Martinuzzi RJ, Zernicke RF. Poroelastic evaluation of fluid movement through the lacunocanalicular system. Annals of Biomedical Engineering. 2009;37(7):1390–1402. doi: 10.1007/s10439-009-9706-1. [DOI] [PubMed] [Google Scholar]
- Goulet GC, Cooper DML, Coombe D, Zernicke RF. Influence of cortical canal architecture on lacunocanalicular pore pressure and fluid flow. Computer Methods in Biomechanics and Biomedical Engineering. 2008;11(4):379–387. doi: 10.1080/10255840701814105. [DOI] [PubMed] [Google Scholar]
- Kazakia GJ, Tjong W, Nirody JA, Burghardt AJ, Carballido-Gamio J, Patsch JM, Link T, Feeley BT, Ma CB. The influence of disuse on bone microstructure and mechanics assessed by HR-pQCT. Bone. 2014;63:132–140. doi: 10.1016/j.bone.2014.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy OD, Laudier DM, Majeska RJ, Sun HB, Schaffler MB. Osteocyte apoptosis is required for production of osteoclastogenic signals following bone fatigue in vivo. Bone. 2014;64:132–137. doi: 10.1016/j.bone.2014.03.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein-Nulend J, Bakker AD, Bacabac RG, Vatsa A, Weinbaum S. Mechanosensation and transduction in osteocytes. Bone. 2013;54(2):182–190. doi: 10.1016/j.bone.2012.10.013. [DOI] [PubMed] [Google Scholar]
- Knothe-Tate ML, Steck R, Anderson EJ. Bone as an inspiration for a novel class of mechanoactive materials. Biomaterials. 2009;30(2):133–140. doi: 10.1016/j.biomaterials.2008.09.028. [DOI] [PubMed] [Google Scholar]
- Knothe-Tate ML, Steck R, Forwood MR, Niederer P. In vivo demonstration of load-induced fluid flow in the rat tibia and its potential implications for processes associated with functional adaptation. The Journal of Experimental Biology. 2000;203(Pt 18):2737–2745. doi: 10.1242/jeb.203.18.2737. [DOI] [PubMed] [Google Scholar]
- Li GP, Bronk JT, An KN, Kelly PJ. Permeability of cortical bone of canine tibiae. Microvascular Research. 1987;34(3):302–310. doi: 10.1016/0026-2862(87)90063-x. [DOI] [PubMed] [Google Scholar]
- Mak AFT, Huang DT, Zhang JD, Tong P. Deformation-induced hierarchical flows and drag forces in bone canaliculi and matrix microporosity. Journal of Biomechanics. 1997;30(1):11–18. doi: 10.1016/s0021-9290(96)00121-2. [DOI] [PubMed] [Google Scholar]
- Nakashima T, Hayashi M, Fukunaga T, Kurata K, Oh-Hora M, Feng JQ, Bonewald LF, Kodama T, Wutz A, Wagner EF, Penninger JM, Takayanagi H. Evidence for osteocyte regulation of bone homeostasis through RANKL expression. Nature Medicine. 2011;17(10):1231–1234. doi: 10.1038/nm.2452. [DOI] [PubMed] [Google Scholar]
- Palacio-Mancheno PE, Larriera AI, Doty SB, Cardoso L, Fritton SP. 3D Assessment of cortical bone porosity and tissue mineral density using high-resolution microCT: effects of resolution and threshold method. Journal of Bone and Mineral Research. 2014;29(1):142–150. doi: 10.1002/jbmr.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pereira AF, Shefelbine SJ. The influence of load repetition in bone mechanotransduction using poroelastic finite-element models: the impact of permeability. Biomechanics and Modeling in Mechanobiology. 2014;13(1):215–225. doi: 10.1007/s10237-013-0498-8. [DOI] [PubMed] [Google Scholar]
- Piekarski K, Munro M. Transport mechanism operating between blood supply and osteocytes in long bones. Nature. 1977;269(5623):80–82. doi: 10.1038/269080a0. [DOI] [PubMed] [Google Scholar]
- Qin YX, Lin W, Rubin C. The pathway of bone fluid flow as defined by in vivo intramedullary pressure and streaming potential measurements. Annals of Biomedical Engineering. 2002;30(5):693–702. doi: 10.1114/1.1483863. [DOI] [PubMed] [Google Scholar]
- Remond A, Naili S, Lemaire T. Interstitial fluid flow in the osteon with spatial gradients of mechanical properties: a finite element study. Biomechanics and Modeling in Mechanobiology. 2008;7(6):487–495. doi: 10.1007/s10237-007-0111-0. [DOI] [PubMed] [Google Scholar]
- Robling AG, Niziolek PJ, Baldridge LA, Condon KW, Allen MR, Alam I, Mantila SM, Gluhak-Heinrich J, Bellido TM, Harris SE, Turner CH. Mechanical Stimulation of Bone in Vivo Reduces Osteocyte Expression of Sost/Sclerostin. Journal of Biological Chemistry. 2008;283(9):5866–5875. doi: 10.1074/jbc.M705092200. [DOI] [PubMed] [Google Scholar]
- Sharma D, Ciani C, Marin PA, Levy JD, Doty SB, Fritton SP. Alterations in the osteocyte lacunar-canalicular microenvironment due to estrogen deficiency. Bone. 2012;51(3):488–497. doi: 10.1016/j.bone.2012.05.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma D, Larriera AI, Palacio-Mancheno PE, Gatti V, Fritton JC, Bromage TG, Cardoso L, Doty SB, Fritton SP. The effects of estrogen deficiency on cortical bone microporosity and mineralization. Bone. 2018;110:1–10. doi: 10.1016/j.bone.2018.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smit TH, Huyghe JM, Cowin SC. Estimation of the poroelastic parameters of cortical bone. Journal of Biomechanics. 2002;35(6):829–835. doi: 10.1016/s0021-9290(02)00021-0. [DOI] [PubMed] [Google Scholar]
- Starkebaum W, Pollack SR, Korostoff E. Microelectrode studies of stress-generated potentials in four-point bending of bone. Journal of Biomedical Materials Research. 1979;13(5):729–751. doi: 10.1002/jbm.820130506. [DOI] [PubMed] [Google Scholar]
- Steck R, Niederer P, Knothe-Tate ML. A finite element analysis for the prediction of load-induced fluid flow and mechanochemical transduction in bone. Journal of Theoretical Biology. 2003;220(2):249–259. doi: 10.1006/jtbi.2003.3163. [DOI] [PubMed] [Google Scholar]
- Swan CC, Lakes RS, Brand RA, Stewart KJ. Micromechanically based poroelastic modeling of fluid flow in Haversian bone. Journal of Biomechanical Engineering. 2003;125(1):25–37. doi: 10.1115/1.1535191. [DOI] [PubMed] [Google Scholar]
- Tommasini SM, Trinward A, Acerbo AS, Carlo FD, Miller LM, Judex S. Changes in intracortical microporosities induced by pharmaceutical treatment of osteoporosis as detected by high resolution microCT. Bone. 2012;50(3):596–604. doi: 10.1016/j.bone.2011.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner DW, Lindsey DP, Beaupre GS. Deriving tissue density and elastic modulus from microCT bone scans. Bone. 2011;49(5):931–938. doi: 10.1016/j.bone.2011.07.021. [DOI] [PubMed] [Google Scholar]
- Wang B, Lai X, Price C, Thompson WR, Li W, Quabili TR, Tseng WJ, Liu XS, Zhang H, Pan J, Kirn-Safran CB, Farach-Carson MC, Wang L. Perlecan-Containing Pericellular Matrix Regulates Solute Transport and Mechanosensing Within the Osteocyte Lacunar-Canalicular System. Journal of Bone and Mineral Research. 2014;29(4):878–891. doi: 10.1002/jbmr.2105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Cowin SC, Weinbaum S, Fritton SP. Modeling tracer transport in an osteon under cyclic loading. Annals of Biomedical Engineering. 2000;28(10):1200–1209. doi: 10.1114/1.1317531. [DOI] [PubMed] [Google Scholar]
- Wang L, Fritton SP, Cowin SC, Weinbaum S. Fluid pressure relaxation depends upon osteonal microstructure: modeling an oscillatory bending experiment. Journal of Biomechanics. 1999;32(7):663–672. doi: 10.1016/s0021-9290(99)00059-7. [DOI] [PubMed] [Google Scholar]
- Weinbaum S, Cowin SC, Zeng Y. A model for the excitation of osteocytes by mechanical loading-induced bone fluid shear stresses. Journal of Biomechanics. 1994;27(3):339–360. doi: 10.1016/0021-9290(94)90010-8. [DOI] [PubMed] [Google Scholar]
- Westerlind KC, Wronski TJ, Ritman EL, Luo ZP, An KN, Bell NH, Turner RT. Estrogen regulates the rate of bone turnover but bone balance in ovariectomized rats is modulated by prevailing mechanical strain. Proc Natl Acad Sci U S A. 1997;94(8):4199–4204. doi: 10.1073/pnas.94.8.4199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- You L, Cowin SC, Schaffler MB, Weinbaum S. A model for strain amplification in the actin cytoskeleton of osteocytes due to fluid drag on pericellular matrix. Journal of Biomechanics. 2001;34(11):1375–1386. doi: 10.1016/s0021-9290(01)00107-5. [DOI] [PubMed] [Google Scholar]
- Zeng Y, Cowin SC, Weinbaum S. A fiber matrix model for fluid flow and streaming potentials in the canaliculi of an osteon. Annals of Biomedical Engineering. 1994;22(3):280–292. doi: 10.1007/BF02368235. [DOI] [PubMed] [Google Scholar]
- Zhang D, Weinbaum S, Cowin SC. Estimates of the peak pressures in bone pore water. Journal of Biomechanical Engineering. 1998;120(6):697–703. doi: 10.1115/1.2834881. [DOI] [PubMed] [Google Scholar]
- Zhou X, Novotny JE, Wang L. Modeling fluorescence recovery after photobleaching in loaded bone: potential applications in measuring fluid and solute transport in the osteocytic lacunar-canalicular system. Annals of Biomedical Engineering. 2008;36(12):1961–1977. doi: 10.1007/s10439-008-9566-0. [DOI] [PMC free article] [PubMed] [Google Scholar]


