Challenges and advances in atomistic simulations of potassium and sodium ion channel gating and permeation

Abstract

Ion channels are implicated in many essential physiological events such as electrical signal propagation and cellular communication. The advent of K⁺ and Na⁺ ion channel structure determination has facilitated numerous investigations of molecular determinants of their behaviour. At the same time, rapid development of computer hardware and molecular simulation methodologies has made computational studies of large biological molecules in all‐atom representation tractable. The concurrent evolution of experimental structural biology with biomolecular computer modelling has yielded mechanistic details of fundamental processes unavailable through experiments alone, such as ion conduction and ion channel gating. This review is a short survey of the atomistic computational investigations of K⁺ and Na⁺ ion channels, focusing on KcsA and several voltage‐gated channels from the K_V and Na_V families, which have garnered many successes and engendered several long‐standing controversies regarding the nature of their structure–function relationship. We review the latest advancements and challenges facing the field of molecular modelling and simulation regarding the structural and energetic determinants of ion channel function and their agreement with experimental observations.

Introduction

Ion channels are a diverse group of membrane transport proteins, with nearly 300 so far identified in the human genome (Southan et al. 2016). They are critical facilitators of the passive translocation of ions across cell membranes, since the hydrophobic nature of biomembranes surrounding cells and subcellular organelles makes them highly impermeable to charged species (Gennis, 1989). Ion channels are present in single‐cell organisms as well as in the majority of cell types of multicellular organisms (Hille et al. 1999), where they perform diverse functions such as biosensing, signalling and maintaining homeostasis. In electrically excitable cells such as neurons and cardiac myocytes, ion channels are responsible for the extremely rapid propagation of electrical signals driven by the generation of action potentials (Hille, 2001). Ion channels represent important drug targets (Overington et al. 2006), but there have been substantial challenges with therapeutic applications that are both sensitive and selective to specific ion channel subtypes. Moreover, some ion channels, such as K_V11.1, encoded by the human ether‐à‐go‐go‐related gene (hERG), are major drug anti‐targets since certain ion channel–drug interactions may cause deadly arrhythmias and other cardiac disorders (Vandenberg et al. 2012), often leading to the withdrawal of a prospective drug from the market (Colatsky et al. 2016). In addition, ion channel mutations may lead to various neurological, cardiac, muscular, systemic and other serious health disorders called channelopathies (Kass, 2005). Therefore, a molecular‐level understanding of ion channel physiology is of the utmost biomedical significance.

Publication of the first atomic‐resolution crystal structure of a bacterial K⁺ selective KcsA channel in 1998 (Doyle et al. 1998) brought about a breakthrough in understanding of ion channel molecular architecture, necessary for structural modelling studies. The structures of several voltage‐gated K⁺ (K_V) and Na⁺ (Na_V) channels followed (illustrated in Fig. 1 for K_V11.1), and revealed a common homotetrameric pore domain (PD), with each monomer comprising two transmembrane (TM) α‐helices (aqueous pore‐lining inner S6 and lipid‐facing outer S5) linked through extracellular loops and short pore helices, and the narrowest constriction of the pore forming a selectivity filter (SF) (Doyle et al. 1998; Jiang et al. 2003; Payandeh et al. 2011). For channels in the K_V and Na_V families, flexible linkers connect the PDs to voltage sensing domains (VSD), which typically consist of four TM helices (S1–S4) per monomer (see Fig. 1) and move in response to a change in TM electrical potential, thereby exerting a mechanical effect on the PD, leading to channel opening or closing (Jiang et al. 2003; Payandeh et al. 2011).

Figure 1. Topology of a K_V channel.

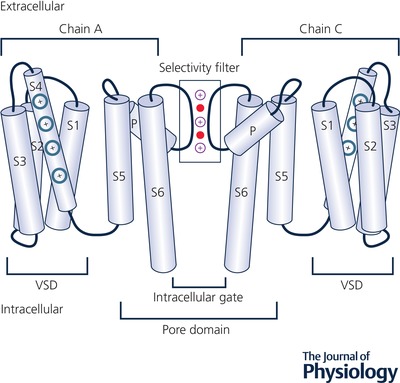
The voltage‐sensing domain (VSD), depicted in an activated conformation, is composed of transmembrane helices S1–S4 with charged residues on the S4 helix shown in blue. The pore domain is composed of transmembrane helices S5–S6, with an open intracellular gate near the bottom. α‐Helices are shown by light‐blue cylinders and loops by black curves. The selectivity filter (SF) region is shown by a rectangular box with three K⁺ and coordinating water molecules in purple and red, respectively. Illustration is adapted from the published structure of hERG (Wang & MacKinnon, 2017), with two opposite chains (A and C) of the homotetramer shown.

How molecular modelling and simulation methodology can complement experiment

Currently, there are several dozen structures of ion channels from different organisms and protein families in the Protein Data Bank (PDB). Most of them are bacterial and were obtained by high resolution by X‐ray crystallography, but in the past few years a resolution revolution in cryogenic electron microscopy (cryo‐EM) has led to the determination of many eukaryotic ion channel structures, but at lower resolution (e.g. 3–4 Å) than is possible with X‐ray structures (Shen et al. 2017; Wang & MacKinnon, 2017). In addition to resolution, one major concern with protein structures obtained from either X‐ray crystallography or cryo‐EM is whether they are representative of the structures at physiological conditions. There is the potential for ion channel protein structures to undergo substantial modifications from physiological conditions due to the incorporation of buffer solutions, detergents, crystal packing and heavy atom staining (in X‐ray), and vitreous ice and radiation damage (in cryo‐EM) (Ubarretxena‐Belandia & Stokes, 2010; Palamini et al. 2016; Rawson et al. 2016). Along with the extremely low temperatures used for structural determination, all of these factors have the potential to induce artificial protein conformations, although the close similarity between X‐ray detergent and cryo‐EM lipid nandodisc channel structures, such as that for K_V1.2/2.1 chimera (Matthies et al. 2018), is encouraging.

Molecular modelling can complement and overcome shortcomings of experimental techniques

Molecular modelling helps address some of the shortcomings of experimental structure determination by aiding in the refinement of low‐resolution structures, and by the generation of models of channel isoforms, for which structures do not yet exist. While functional studies are largely consistent with experimentally resolved structures (Jiang et al. 2003; Lenaeus et al. 2017; Wang & MacKinnon, 2017), computer simulation and atomistic modelling are often the only techniques that can provide the necessary temporal and spatial resolution for evaluating structural stability. Furthermore, as the structures of many ion channels and other membrane proteins remain unresolved at this time, molecular homology modelling can serve as a powerful predictive tool that circumvents the challenges of de novo protein modelling (Koehler Leman et al. 2015). Homology modelling approaches assume that protein structure is more conserved than sequence. Such is usually the case for ion channels, where relatively low sequence similarities of 30–40% are accompanied by strong structural resemblance, deviating only by a few angstroms (Forrest et al. 2006). Multiple programs are available for generating homology models of protein structures, such as MODELLER (Fiser & Sali, 2003), Schrodinger Prime (Jacobson et al. 2004), HHPred (Zimmermann et al. 2018) and ROSETTA (Song et al. 2013). They use different algorithms for protein structure and energy predictions (Koehler Leman et al. 2015), but each has been successfully used for ion channel structural modelling in the past (Khalili‐Araghi et al. 2010; Durdagi et al. 2012; Yarov‐Yarovoy et al. 2012), and as of yet, no strong consensus exists for choosing the best program for this task.

Studying the motion of ion channels with molecular dynamics simulations

Insight into potentially important molecular interactions within a particular state of a protein structure can be gained from homology modelling; however, it cannot provide accurate thermodynamic and kinetic quantities of a simulated system. Molecular dynamics (MD) simulations, on the other hand, can be used to predict such data and thus serve as an invaluable tool to fully understand molecular mechanisms such as ion conduction and channel gating discussed in more detail below. MD is based on the numerical integration of Newton's equations of motion for a collection of particles, representing a molecular system of interest (Allen & Tildesley, 1987). In an all‐atom representation of an ion channel, lipid membrane and solvent, a typical simulated system, illustrated in Fig. 2, totals around 10⁵ atoms. The fastest molecular motions in a simulated system are the vibrational motions of bonds and angles, which occur on the order of femtoseconds (fs), thereby making it an upper bound for the time step used in MD numerical integration. Constraining the fastest vibrational motions (i.e. fixing atomic bond lengths and/or angles), as done in SHAKE (Ryckaert et al. 1977), SETTLE (Miyamoto & Kollman, 1992) and LINCS (Hess et al. 1997) algorithms, allows for an increased MD time step, and thus improved performance in those simulations. Also, multiple time steps for different types of interactions in molecular systems can be used as implemented, for instance, in the RESPA method (Tuckerman et al. 1992).

Figure 2. A typical ion channel all‐atom MD simulation system consisting of hERG ion channel in hydrated lipid membrane.

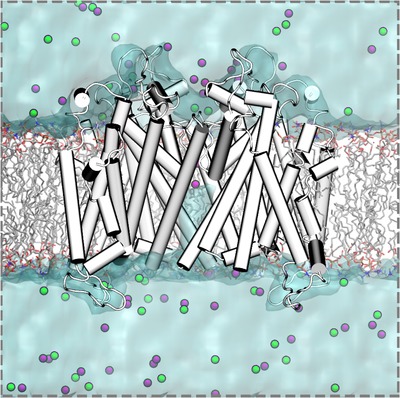
hERG ion channel with α‐helices and loops depicted as white/gray cylinders and white curves, respectively, POPC (1‐palmitoyl‐2‐oleoyl‐sn‐glycero‐3‐phosphocholine) lipid membrane in wireframe representation. C atoms, grey; O, red; N, blue; P, orange; H atoms are not shown; water is depicted as cyan molecular surface, and potassium and chloride ions are shown as purple and green balls, respectively.

Owing in part to the availability of faster and multiple‐core processors, computer clusters with a large number of nodes with fast interconnects, graphical processor unit (GPU) computing, as well as efficient and highly scalable MD codes such as NAMD (Phillips et al. 2005), GROMACS (Hess et al. 2008), CHARMM (Brooks et al. 2009), OpenMM (Eastman et al. 2017), Desmond (Bowers et al. 2006), Tinker (Ponder, 2004) and Amber (Case et al. 2005), simulations of up to a few microseconds in duration are currently possible; a vast improvement over the nanosecond time scales that were possible just a few years ago. While simulations as long as few microseconds are often enough to study ion conduction, the time scale of channel gating is still out of reach. Nevertheless, the advent of special purpose supercomputers, such as Anton 2 by DE Shaw Research (Shaw et al. 2014), has facilitated multi‐microsecond, and even millisecond, MD simulations, approaching the time scales of ion channel activation and deactivation. However, such long‐time‐scale MD simulations are still not feasible to run on most standard computer clusters. A timeline summarizing the physical and physiological time scales accessible with atomistic MD is shown in Fig. 3.

Figure 3. Time scales accessible with atomistic MD simulations and those related to ion channel function (gating and permeation, estimated based on IUPHAR/BPS data; Southan et al. 2016) as well as protein and solvent dynamics (adapted from Lindahl, 2008; Zwier & Chong, 2010; Harvey & De Fabritiis, 2012).

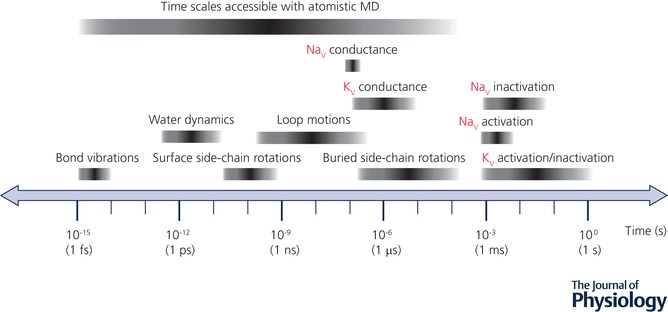
The fastest molecular motions in a simulated system are bond and angle vibrations (on the fs time scale) and serve as an upper limit of MD time step. A lower time limit of ion channel activation/inactivation transition at ∼1 ms practically coincides with an upper time limit of atomistic MD simulations.

Accessing long time scales with reduced system representations and enhanced sampling techniques

One alternative method to purpose‐built supercomputers for achieving longer time‐scale simulations is to reduce the number of atoms present in the system. For instance, the Grand Canonical Monte Carlo/Brownian Dynamics (GCMC/BD) is one such method, and has been used to study ion conduction (Im et al. 2000). In this reduced‐system representation, water and lipid molecules are represented implicitly as a dielectric field, stationary protein atoms have fixed partial charges, while the ions are included explicitly. An even more reduced representation is one in which ionic density is modelled implicitly using a Boltzmann distribution, where the resultant electrostatic potential is obtained via numerical solutions to the linearized Poisson–Boltzmann (PB) equation, and ion transport is approximated with the Poisson–Nernst–Planck model (Maffeo et al. 2012). Furthermore, coarse‐grained methodologies, in which a collection of atoms is represented as a single particle, have been used to study the large‐scale motions related to ion channel gating (Treptow et al. 2008) and obtain corresponding free energy profiles (Kim & Warshel, 2014).

Another alternative approach to bridge relatively short simulation to much longer experimental time scales is to use enhanced sampling techniques, which allow a modelled system to cross large energetic barriers and sample regions of conformational space otherwise not amenable to brute‐force application of unbiased MD methodology. This can be done in myriad ways, such as: (1) adding various restraints (umbrella sampling (Torrie & Valleau, 1977), adaptive biasing force (Darve et al. 2008) and metadynamics (Laio & Parrinello, 2002)), (2) application of additional forces or velocities to atoms moving in a set direction (steered (Isralewitz et al. 2001) or targeted MD (Schlitter et al. 1994)), (3) alchemical permutations of ions or amino acid residues (free energy perturbation; Kollman, 1993), or (4) so‐called replica‐exchange techniques that involve occasional system exchanges with a replica running at either increased temperature (Sugita & Okamoto, 1999) or with reduced interaction potentials (Fukunishi et al. 2002). All such techniques can be and have been applied to ion channel simulations (Roux et al. 2004; Maffeo et al. 2012), but the details extend beyond of scope of this review.

Atomistic force field accuracy and limitations

MD simulations are governed by empirical force field models, which describe atomic interactions in biomolecular systems using the laws of classical mechanics. Force fields are expressed as a potential energy function with empirically derived parameters for different chemical atom types (Mackerell, 2004), with the latter optimized to reproduce experimental and quantum‐mechanical (QM) reference data for relevant system components, typically emphasizing their properties in bulk aqueous solutions (Mackerell, 2004). For atomistic MD simulations of ion channels in explicitly hydrated lipid membranes (Fig. 2), empirical force fields for protein, lipids, water and ions are used. Examples of popular biomolecular force fields commonly used for such membrane protein simulations include CHARMM (Huang & MacKerell, 2013; Huang et al. 2017), Amber (Cornell et al. 1995), OPLS‐AA (Kaminski et al. 2001) and GROMOS (Schmid et al. 2011).

In most protein force fields, the building blocks are individual amino acid residue models, which can be used to simulate any protein molecule, thus satisfying an important force field requirement: parameter transferability (Lopes et al. 2015). Force field parameters for both protein backbone and side chains are of crucial importance, and recent improvements have focused on reproducing backbone dihedral angle (ϕ, ψ) Ramachandran maps and side chain dihedral angles (Lopes et al. 2015) derived from QM calculations or experimental data. Lipid force fields are designed in a similar way, with the same parameters for functional groups (for instance, saturated hydrocarbon lipid tail, glycerol, and phosphodiester moieties) combined to obtain lipid molecule models aimed at reproducing several experimental properties for hydrated lipid assemblies, such as membrane thicknesses, areas per lipid, and deuterium order parameter profiles (Lyubartsev & Rabinovich, 2016). Typically, simple three‐site (oxygen and two H atoms) rigid water models such as TIP3P (Jorgensen et al. 1983) and SPC/E (Berendsen et al. 1987), along with the aforementioned vibrational mode constraints (e.g. SHAKE or SETTLE), are used in combination for increased computational efficiency. However, more complex, and presumably more accurate, models such as TIP4P‐Ew (Horn et al. 2004) are being increasingly utilized in biomolecular simulations (Onufriev & Izadi, 2018). Ion parameters are intimately tied to water models (Joung & Cheatham III, 2008), and all the force fields representing system components should be compatible with one another in order to provide an accurate balance of protein–water–lipid–ion interactions that allows for a complete description of ion permeation and channel gating. This is achieved by a common force field optimization strategy existing for many biomolecular force fields (Zhu et al. 2012) as well as thorough testing of force field combinations (Cordomí et al. 2012).

One pertinent challenge with ion channel MD simulations has to do with the optimal combination of ion van der Waals (vdW) force field parameters with those for proteins, lipids and other ions. The problem arises from the fact that ion parameters are typically optimized to reproduce ion energetics in bulk water, but do not necessarily provide accurate estimates for their direct interactions with other components such as lipid head groups, counterions, or the protein backbone (critical for ion conduction in K⁺ channels). Thus, development of vdW parameters for specific interactions involving ions has been performed (see, e.g. Berneche & Roux, 2001; Luo & Roux, 2009; Venable et al. 2013; Kahlen et al. 2014; Li et al. 2015). However, direct experimental reference values, such as ion solvation energetics, are either not well defined (absolute ionic solvation free energy values are defined relative to unknown H⁺ solvation energetics), or not available. Therefore, surrogate markers, such as experimental salt solubilities (Yu et al. 2010), ion pair formation/dissociation constants (Kahlen et al. 2014), salt solution osmotic pressures (Luo & Roux, 2009) and charged membrane electrophoretic mobilities (Venable et al. 2013), typically combined with gas‐phase and/or condensed‐phase QM calculations are used instead.

The application of such special pairwise ion vdW parameter terms (force field patches) should, in principle, provide a more accurate description of different interactions in biomolecular systems and thus better agreement with experimentally determined values for ion permeation mechanisms and kinetics. However, no consistent picture has emerged so far. For instance, in one study the presence or absence of such a CHARMM force field patch had inconsistent results on ion permeation mechanisms for different channels (KcsA and K_V1.2/K_V2.1 chimera), and did not improve underestimated computed ion conductance values (Jensen et al. 2013). In another recent study, a choice of different ion parameters without special vdW terms, but optimized to be used with Amber and CHARMM biomolecular force fields, respectively, resulted in similar permeation mechanisms but substantially faster K⁺ conduction rates in KcsA for the former (Köpfer et al. 2014). In Na_V channel simulations, different choices of ion parameters with and without pairwise vdW parameter patches resulted in reasonable agreement between experimental and computed ion conductances (Ing & Pomes, 2016), likely due to substantially wider SF and thus weaker ion–protein interactions in those channels (see below). What many studies agree on is that the absence of explicit electronic reorganization in classical force field‐based MD simulations can lead to overestimated ion permeation barriers, and thus reduced computed conductances, especially for channels with narrow pores (Allen et al. 2006; Jensen et al. 2013). Unfortunately, at this time explicit representation of electronic degrees of freedom, as done in QM calculations, is impossible due to the large size of biomolecular systems and the associated exorbitant computational cost. Similarly, a hybrid approach that combines empirically derived molecular‐mechanical (MM) force fields with QM (known as QM/MM) can only reach picosecond time scales (Bucher & Rothlisberger, 2010) due to computational complexity.

An alternative to using QM or QM/MM is to use polarizable force fields in MD, where electronic degrees of freedom are approximated by auxiliary charged particles (known as Drudes), variable point multipoles, or restrained fluctuation of atomic charges in the field of other atoms (MacKerell, 2004; Lopes et al. 2015). Unlike classical fixed‐charge force fields, they allow for a substantial variation of a molecular electrostatic response in media of different polarities and thus potentially more accurate intermolecular interactions. For instance, in these models, the non‐polar environment of the membrane interior has a correct dielectric constant of around 2, allowing for accurate solvation of charged and polar species (Vorobyov et al. 2008). Despite the complications associated with parameterization of polarizable force fields, and higher computational overhead for MD runs, hybrid polarizable/additive and fully polarizable models have been used for prototypical gramicidin A ion channel simulations (Allen et al. 2004; Patel et al. 2009; Vorobyov et al. 2010; Peng et al. 2016), demonstrating reduced free energy barriers and thus providing more accurate channel conductance. And, fully polarizable MD simulations were reported recently for other ion channels as well (Dhakshnamoorthy et al. 2016; Kratochvil et al. 2016; Sun & Gong, 2017).

Here we will focus on the application of atomistic MD to the study of the processes of ion conduction and gating of K⁺ and Na⁺ ion channels, and we will discuss recent challenges and breakthroughs in the field as they relate to physiology.

Ion conduction

Ion movement across K⁺ channel selectivity filter

Selectivity filter structure is intimately tied to its function

The SFs of some K⁺ channels are responsible for the channels’ 10,000‐fold preference for K⁺ over Na⁺ (not explicitly discussed in this paper; see Roux, 2017 for a recent review) and can facilitate the flux of 10⁸ K⁺ ions per second (Hille, 2001) across a membrane. The SFs of such K⁺ channels as KcsA, K_VAP and K_V1.2 are narrow passageways that are lined with the backbone atoms of the highly conserved TVGYG amino acid sequence (Doyle et al. 1998; Lee et al. 2005; Long et al. 2005 a). Within the SF four cage‐like binding sites, Site₁–Site₄, have been identified via crystallography (Morais‐Cabral et al. 2001) and two more sites, Site₀ and Site_cav, located just above and just below the SF, respectively, have been elucidated via MD simulations (Aqvist & Luzhkov, 2000; Berneche & Roux, 2001). Despite putative agreement on the structure of the SF, the original crystallographic evidence leaves room for interpretation of the ion occupancy in the filter region. Distinct occupancy patterns that depend on the presence of water molecules between the adjacent ions give rise to several proposed mechanisms whereby ions traverse the narrow constriction of the SF (Köpfer et al. 2014; Kratochvil et al. 2016).

Proposed mechanisms of K⁺ conduction

The historically prevailing computational and experimental evidence has asserted that water molecules reside between adjacent ions in the SF. The KcsA X‐ray crystal structure confirmed the presence of at least two ions in the SF (Doyle et al. 1998), supporting a model of permeation known as the knock‐on mechanism, originally proposed by Hodgkin & Keynes (1955). This mechanism (Morais‐Cabral et al. 2001) is reinforced by MD simulations, and proposes that two ions are initially in positions [Site₃, Site₁], separated by water molecules (Fig. 4 A). As a third ion enters the Site_cav below the SF (not labelled in the figure), an intermediate configuration of ions in [Site₄, Site₃, Site₁] forms, at which point K⁺ in position Site₄ ‘knocks on’ the entire single‐file assembly of ions, causing it to undergo a concerted movement, such that the potassium ions end up in positions [Site₄, Site₂] (Aqvist & Luzhkov, 2000; Berneche & Roux, 2001; Bernèche & Roux, 2003).

Figure 4. Ion channel conduction mechanisms.

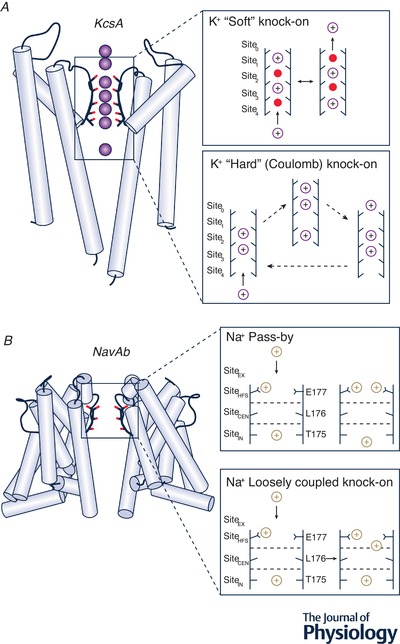
A, KcsA crystal structure (Zhou et al. 2001) (PDB ID: 1K4C, left) with crystallographic ion positions shown by purple spheres, α‐helices by light‐blue cylinders, loops by black curves and ion/water coordinating SF oxygen atoms by red sticks. The insets on the right demonstrate K⁺ conductance ‘soft’ knock‐on (Berneche & Roux, 2001) (top) and ‘hard’ or Coulomb knock‐on (Köpfer et al. 2014) (bottom) mechanisms. K⁺ ions shown in purple, water molecules shown in red; putative ion occupancy positions in each SF are labelled Site₀–Site₄. Site_cav is located below the SF and is not shown on the diagrams. B, Na_VAb crystal structure (Payandeh et al. 2011) (PDB ID: 3RVY, left) with α‐helices shown by light‐blue cylinders, loops by black curves and ion/water coordinating SF oxygen atoms by red sticks. The insets on the right demonstrate Na⁺ conductance by pass‐by (top) and loosely coupled knock‐on (bottom) mechanisms for prokaryotic Na_V channels (Boiteux et al. 2014). Na⁺ ions are shown in brown, water molecules are not shown for clarity, and putative ion occupancy positions in each SF are labeled Site_EX, Site_HFS, Site_CEN and Site_IN.

Uncertainty in the crystallographic interpretation of KcsA SF occupancy (Zhou & MacKinnon, 2003; Sheldrick, 2015) as well as suggestions from MD simulations that multiple ion pathways may exist (Berneche & Roux, 2001; Furini & Domene, 2009; Fowler et al. 2013) encouraged a second look at the mechanism of conduction. The difference between the conventionally accepted ‘soft’ knock‐on and Coulomb (direct or ‘hard’) knock‐on mechanisms is the absence of the intervening water molecules for the latter (Fig. 4 A). Initially K⁺ ions are found in Site₃ and Site₂. As the third ion fluctuates between Site_cav and Site₄ binding sites, it directly knocks on the ions above, pushing them into [Site₂, Site₁] as a result of direct electrostatic repulsion. According to 1D reduced‐representation model calculations, the conductance calculated on the basis of the Coulomb knock‐on mechanism is in much closer agreement with experiment (Köpfer et al. 2014). The plausibility of such a mechanism is still being debated, with a recent combined spectroscopic–MD study suggesting a better agreement for a traditional ‘soft’ knock‐on mechanism (Kratochvil et al. 2016), and an improved crystal structure refinement method pointing to the direct Coulomb knock‐on (Sheldrick, 2015). In a recent study, the authors performed multiple multi‐microsecond MD simulations on several K⁺ channels and argued that only the Coulomb knock‐on mechanism can account for a high conduction efficiency and K⁺/Na⁺ selectivity through direct interaction of completely dehydrated K⁺ ions in the SF (Kopec et al. 2018). What should be noted, however, is that the outcome of these simulations ultimately depends on the specific ion, water and protein force field parameters employed, discussed above and also mentioned in previous studies (Jensen et al. 2013; Köpfer et al. 2014). Moreover, a mechanism of ion permeation will likely depend on the specific channel as well as experimental conditions such as salt concentrations and applied voltages. In the majority of unbiased MD simulations to date, substantially higher voltages (hundreds of millivolts) and ion concentrations (e.g. 0.3–0.6 M) compared to physiological values (tens of millivolts and up to 0.15 M) have been used to observe ion conduction at the microsecond time scale (Jensen et al. 2013; Köpfer et al. 2014; Kopec et al. 2018). So, a direct correlation between MD and cell‐based electrophysiology measurements is not clear. Additional high‐resolution experimental data and MD simulations using accurate empirically derived models of water, ion and protein interactions will likely help resolve this controversy.

Ion movement across Na⁺ channel selectivity filter

Na⁺ binding sites from experimental structures and MD simulations

The last half a decade has seen a proliferation of voltage‐gated sodium channel crystal structures. A few examples are the Na_VAb channel from Arcobacter butzleri crystallized in putative open and closed states (Payandeh et al. 2011; Lenaeus et al. 2017), Na_VMs from Magnetococcus marinus, likely in the open state (Sula et al. 2017) and Na_VRh, from Rickettsiales sp. HIMB114, likely in an inactivated state (Zhang et al. 2012). A common element among the three channels is the structure of the SF region, which is composed of helix–loop–helix motif. The Pore 2 helix (P2) forms an electronegative funnel‐shaped opening to the extracellular region, attracting ions into the pore, whereas the ion selection itself takes place mostly in the loop region. Amino acid sequences of the loop differ among the various channels, but bacterial Na_V channels contain a highly conserved glutamic acid (Glu) residue in every subunit, forming a Glu ring (EEEE) around the dominant, high‐field‐strength Na⁺ binding site, Site_HFS, or Site₁ (Fig. 4 B) near the mouth of the SF (Clairfeuille et al. 2017). In multiple MD simulations of a closed Na_VAb ion channel, two dominant Na⁺ binding sites were identified (Ing & Pomes, 2016). In Site_HFS, Na⁺ was found in the octahedral coordination, bound directly by carboxylates of two Glu side chains, by water molecules H‐bonded to the two other Glu residues, as well as by two more water molecules from aqueous environment of the vestibule. The second dominant site, referred to as Site_IN or Site₃, is located deeper in the SF. Here Na⁺ sits in an almost square planar arrangement, coordinated by four water molecules H‐bonded to nearby threonine carbonyls and by a water from above. A less favourable, off‐axis Site_CEN or Site₂ site has been isolated as well (Carnevale et al. 2011). The substantially wider pore of Na_V channels creates a very different conduction environment from a single‐file ion/water arrangement in the SF of K⁺ channels.

Proposed mechanisms of Na⁺ conduction

An early MD simulation of Na_VAb ion translocation proposed a ‘loosely coupled knock‐on’ with a low permeation barrier for two‐ion occupancy of the SF (Corry & Thomas, 2012). Several subsequent studies confirmed initial findings and also proposed a three‐ion analogue (Fig. 4 B) (Ing & Pomes, 2016). A more standard, concerted, knock‐on mechanism, with two sodium ions in the SF of Na_VAb, has also been reported (Chakrabarti et al. 2013). In both cases, as the next ion approaches the external Site_EX or Site₀, it knocks on the filter‐dwelling ions pushing them farther down into the SF or to the central cavity. An observation of two sodium ions simultaneously occupying the same binding site, i.e. a ‘pass‐by’ configuration, has been also noted (Chakrabarti et al. 2013; Boiteux et al. 2014), made possible by the width of the selectivity filter and the number of available coordinating ligands (Fig. 4 B). Both rotameric and protonation states of the Glu side chains forming the Site_HFS have been shown to impact conduction. Conformational isomerization may distort this critical site, while protonating one or more Glu side chains was found to reduce or abolish conduction altogether (Ing & Pomes, 2016). Recently, a putative open‐state crystal structure of Na_VAb/1‐226 construct with nearly identical SF geometry was published (Lenaeus et al. 2017), reaffirming the findings from the previous closed‐state studies. In a microsecond‐long MD simulation of ion translocation through an open Na_VMs pore, five presumed Na⁺ binding SF sites, Site₀–Site₄, were identified as well (Ulmschneider et al. 2013) in good agreement with Na_VAb closed‐channel structure and simulations. Such consensus points to a possible common structural mechanism for bacterial Na_V channel conduction, but it requires further work for complete elucidation.

Eukaryotic Na_V channels have a different architecture with four homologous domains (DI–DIV) on a single polypeptide chain instead of four identical subunits in bacterial channels. Cryo‐EM structures of eukaryotic sodium channels, Na_VPaS from cockroach (Shen et al. 2017) as well as Na_V1.4 from electric eel (Yan et al. 2017) and human (Pan et al. 2018), have recently been determined. Their SFs display asymmetries with aspartic acid, glutamic acid, lysine and alanine (DEKA) from different channel domains forming Na⁺ binding site Site_HFS compared to the EEEE ring in prokaryotic channels. Several recent MD studies used eukaryotic Na_V homology models (Mahdavi & Kuyucak, 2015; Ahmed et al. 2017), hybrid models with a grafted SF eukaryotic Na_V channel SF onto bacterial structures (Li et al. 2017b; Flood et al. 2018) as well as new Na_VPaS structure (Zhang et al. 2018). These studies identified a unique asymmetric Na⁺ permeation pathway involving coordination with Asp and Glu residues in the DEKA ring as well as in the outer SF. A cationic Lys residue in the DEKA ring was also found to be crucial for the Na⁺ conduction mechanism and Na⁺/K⁺ selectivity in those studies, in particular participating in the knock‐on mechanism similarly to a permeating Na⁺ ion (Flood et al. 2018). No doubt future studies of the structural differences between prokaryotic and eukaryotic ion channels will bring about new understanding of ion permeation in sodium channels of different organisms, but extrapolating these findings to eukaryotic Na_V channel function due to their complexities remains a formidable task.

Connecting MD ion permeation with experiment

In MD simulations of ion channels, it is essential not only to elucidate the molecular mechanisms of ionic permeation across the SF but also to establish a connection with experimental observables such as the ionic current–voltage (I–V) relationship and the single channel conductance values derived from them (Hille, 2001). Physiologically, membrane voltage arises from different ion concentrations on both sides of the membrane. However, MD simulations of ion channels in hydrated lipid bilayers with periodic boundary conditions preclude any variation of ionic strength between the intra‐ and extracellular environments. One way to circumvent this difficulty is to design a dual bilayer system stacking the two membranes in the z direction and creating two separate aqueous compartments: one on the outside of both bilayers and the second one between them (Kutzner et al. 2011). An ion/water exchange between the compartments is carried out to maintain the desired ion gradient throughout the simulation. Application of this method to KcsA, MthK and K_V1.2 channels yielded good agreement with experiment (Kutzner et al. 2016). Another approach is to apply an extra force, proportional to the electric field, to every charged atom in the system. The resultant voltage can be computed as a product of the electric field and the size of the simulation box (Gumbart et al. 2012). This technique was applied to K_V1.2–2.1 chimera, but under physiologically relevant membrane voltage, the conductance was found to be almost 40‐fold below the experimental value (Jensen et al. 2013). This does not mean that this approach is inferior to a dual‐bilayer set‐up and, in principle, should provide comparable results. In fact, simulations of an open Na_VM_S channel pore using the constant electric field method provided a reasonable agreement with experiment (Ulmschneider et al. 2013). The sources of differences can be manifold (Fowler et al. 2013), ranging from different simulation protocols or convergences to the force field parameters, which can alter a fine balance of different intermolecular interactions and thus permeation mechanisms and kinetics. The latter factor is still important but arguably may be less sensitive for Na_V channels due to the relatively wider pores.

Notable disparity between theoretical and computational results may be rooted in the inherent differences in mechanical and chemical properties arising from system lipid composition. MD systems usually focus on an ion channel in a single‐lipid membrane patch, often omitting heterogeneity and asymmetry of membranes. The importance of lipid composition for proper ion channel function is well known experimentally and via MD simulations, e.g. for KcsA (Valiyaveetil et al. 2002; Deol et al. 2006; Marius et al. 2008; Rusinova et al. 2014) and K_V channels (Schmidt et al. 2006; Abderemane‐Ali et al. 2012; Rodriguez‐Menchaca et al. 2012; Kasimova et al. 2014; Yazdi et al. 2016), and can possibly contribute to observed differences in experimental and computed conductances as well as channel gating mechanisms, discussed below.

Mechanisms of ion channel gating

In the K_V and Na_V families of voltage‐gated cation channels (VGCCs), the voltage‐dependent variation of ionic current has been associated with a gating cycle of activation/deactivation, inactivation and recovery from inactivation (Hille, 2001). This cycle depends fundamentally on voltage sensing, whereby changes in the cell membrane potential engender widening or constriction of the channel's hydrophobic pore region through the movement of VSD. One structural hypothesis is that gating is a discrete process: one in which the global conformational transition between VSD‐activated and deactivated states causes the S6 helices of the PD to either open or close the ion passageway. The pore closing transition is often accompanied by dewetting of the hydrophobic region, and aqueous pore stability increases with its radius and polarities of pore‐lining residues, which has been observed in MD simulations (Jensen et al. 2010). Thus, the narrow hydrophobic pores of many K⁺ and Na⁺ channels often rely on stabilizing interactions with activated VSD for VGCCs, low pH for KcsA, or artificial restraints during MD simulations of pore‐only constructs.

An alternative structural hypothesis is that gating is a continuous process: one in which there are ensembles of conformations corresponding to open and closed states, as opposed to singular open or closed ion channel conformations. In their work on neuronal Na⁺‐activated K⁺ channels, Hite and MacKinnon found that there is an ensemble of structures representative of non‐conductive states that are in [Na⁺]‐dependent equilibrium with a structure exhibiting an open, conducting conformation (Hite & MacKinnon, 2017). Additionally, a recent MD study on the pore domain of K_VAP identified a distinct free energy minimum, corresponding to a possible stable intermediate state, along the gating pathway between open and closed states of the channel (Starek et al. 2017). A description of other recent MD simulation findings on the K⁺ and Na⁺ channel gating including both inactivation and deactivation phenomena is provided below.

N‐ and C‐type inactivation

Upon prolonged depolarization, VGCCs can undergo conformational changes that usher them into a non‐conducting, inactivated state, in which the channel is desensitized to membrane voltage perturbations, either through intracellular pore block (fast or N‐type inactivation) or through a SF distortion (slow or C‐type inactivation), as illustrated in Fig. 5. In K_V channels such as ones in the Shaker family, a ball‐and‐chain or hinged‐lid mechanism of N‐type inactivation has been proposed (Zagotta et al. 1990), where N‐terminal residues on the cytoplasmic side of the channel comprising ball and chain domains of one chain can occlude the channel pore. In eukaryotic Na_V channels N‐type inactivation has been mainly thought to occur via a pore occlusion by the cytoplasmic linker region between DIII and DIV, featuring an essential Ile‐Phe‐Met (IFM) sequence (DeMarco & Clancy, 2016), and is responsible for the rapid cessation of Na⁺ conduction during the upstroke of the action potential. So far, study of the molecular determinants of N‐type inactivation via molecular simulations has remained out of reach, largely due to a lack of structural data. However, the recently resolved structures of electric eel and human Na_V1.4 channels in presumably the inactivated state with intact IFM motif (Yan et al. 2017; Pan et al. 2018) will likely lead to more thorough and detailed MD studies of this phenomenon.

Figure 5. Ion channel gating cycle.

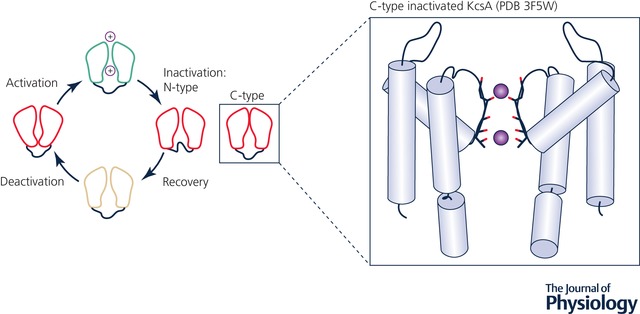
Activation/deactivation, C‐type and N‐type inactivation and recovery from inactivation (Rasmusson et al. 1998). A structure representing a putative C‐type inactivated state for the KcsA channel (Cuello et al. 2010 b) (PDB ID: 3F5W) is shown as an inset. Crystallographic ion positions are shown by purple spheres, α‐helices by light‐blue cylinders, loops by black curves and ion/water coordinating SF oxygen atoms by red sticks.

C‐type inactivation in K⁺ channels, illustrated in Fig. 5, has been investigated extensively in experimental structural and functional studies, as well as atomistic simulations, and several possible contributing factors have been analysed. Typically, SF distortions have been considered as a key feature of C‐type inactivation (Hoshi et al. 1991; Hoshi & Armstrong, 2013). This view has been challenged by a recent experimental KcsA study employing d‐Ala substitution of a critical Gly77 residue (G77dA mutation), which should have removed inactivation due to prevention of the SF backbone from buckling, but inactivation still took place for this mutant at low K⁺ concentration (Devaraneni et al. 2013). However, a 1.2 μs unbiased and 2D umbrella sampling MD simulation study of the same G77dA mutant demonstrated that the underlying premise of d‐Ala propping the SF open was not accurate (Li et al. 2017a), supporting the notion that SF distortion is indeed a hallmark of C‐type inactivation.

Structurally, one supposition is that polar interactions behind the SF stabilize the inactivated state. This idea is corroborated by computational and experimental studies of KcsA, in which Glu71(H⁺)–Asp80 carboxyl/carboxylate interaction was observed, leading to a ‘pinched’ SF conformation, eliminating K⁺ binding sites Site₂ and Site₃, and thus abolishing channel conductance (Cordero‐Morales et al. 2006; Cuello et al. 2010 b). This is similar to KcsA behavior in a low‐[K⁺] environment, which leads to SF pinching, making site Site₂ inaccessible and Site₁, Site₃, and Site₄ filled with water molecules according to MD simulations (Boiteux & Berneche, 2011). Earlier MD simulations of KcsA with an outwardly flipped SF Val76 backbone carbonyl also related it to inactivation (Berneche & Roux, 2005), although a recent combined spectroscopic/MD study suggests that such a flipped state for this channel can be an integral component of the ion permeation process with about 40% occurrence (Kratochvil et al. 2016). Interactions of SF with water molecules buried behind may induce a long‐lasting C‐type inactivated state as well, requiring their removal and rebinding of external K⁺ to promote the recovery process (Ostmeyer et al. 2013). The crucial role of these water molecules is reinforced by their presence in a recent crystal structure of a fast‐inactivating Y82A KcsA mutant with a SF collapse at Site2 and Site3 due to Gly77 and Val76 backbone movements (Cuello et al. 2017).

An alternative explanation of C‐type inactivation involves either SF dilatation at the K⁺ binding site Site₁ (Hoshi & Armstrong, 2013), or a constriction of the SF at Site₄ (Pau et al. 2017), leading to its partial dehydration and corresponding loss of an efficient knock‐on mechanism. A recent combined MD and experimental study of the Shaker K_V channel demonstrated that the SF widening associated with C‐type inactivation is a result of the pore domain being pulled outward towards the VSD (Conti et al. 2016). This study revealed a tight coupling between voltage‐induced activation, S4 helix movement and pore widening due to S6 rotation, leading to a concerted centrifugal motion of Glu416 at the top of S5 helix causing SF dilation and the loss of K⁺ binding (Conti et al. 2016). Such a mechanism is clearly impossible in KcsA since it completely lacks a voltage‐sensing domain, but a direct correlation between pore opening at the intracellular gate and SF K⁺ coordination was observed in a crystallographic study (Cuello et al. 2010 a) and explored further via MD simulations (Pan et al. 2011) and solid‐state NMR (Xu et al. 2017). Phe103 on the inner helix was shown to play a crucial role in allosteric coupling between proton binding at the intracellular pH sensor and K⁺ loss from the SF promoting inactivation (Xu et al. 2017).

A very recent multi‐microsecond MD study of KcsA has shown that there is a single free‐energy minimum corresponding to a partially open intracellular gate and a conductive SF (Li et al. 2018). In this work, the authors examined the conformational dynamics of the SF and corresponding interactions with associated ions and water in closed, intermediate and open states of the channel. They observed that the gating conformation of the pore is allosterically coupled to the spontaneous constriction in the SF at Gly77, induced by the rotation of the peptide bond between Gly77 and Val76 (Delemotte, 2018; Li et al. 2018), and that this constriction coincides with the infiltration and binding of three water molecules in the region behind the SF, which was observed in a previous MD study (Li et al. 2017a) and a recent crystal structure (Cuello et al. 2017). Furthermore, another recent combined MD simulation/experimental study of KcsA has suggested that the SF might actually act as the primary gate in certain K⁺ channels, and that some SF relaxation is necessary for ion conduction, with the interactions between outer transmembrane helix TM1 and P‐helix playing important role in this process (Heer et al. 2017).

MD simulations are also helping to identify possible mechanisms of C‐type inactivation in voltage‐gated sodium channels. A distortion of the SF coupled to S6 helix bending in Na_VAb was observed over the course of microsecond‐long MD simulations (Boiteux et al. 2014), and is supported by the existence of crystal structures of putative C‐type inactivated conformations of Na_VAb, which show a dimer‐of‐dimers configuration of the pore domain and SF as well (Payandeh et al. 2012). However, it is not clear if the SF distortions discussed above are directly related to inactivation. It is also possible that the thermodynamic instabilities observed in simulations are either due to inherent channel sub‐conducting states, or MD force field parameters. Substantially longer experimental time scales of channel inactivation compared to accessible atomistic MD simulation times (see Fig. 3) make a direct observation of a conformational transition from stably conducting to an inactivated state of K⁺ or Na⁺ channels not feasible unless an experimental structure, simulation conditions or force field parameters would predispose for it. And determining a major underlying cause of observed channel conducting and inactivated state stabilities and structural mechanisms of their transitions in between is far from trivial. Hopefully, comprehensive combined experimental/MD studies in the near future will be able to resolve these issues.

Activation and deactivation

The VSD movement during VGCC activation and deactivation has been thoroughly studied for several decades both experimentally and theoretically, recently culminating in a widely accepted consensus model (Vargas et al. 2012). Based on a number of functional studies that were later confirmed by X‐ray structures, such as that of K_V1.2 (Long et al. 2005 b), it is well established that the S1–S4 helices of VGCCs comprise the voltage sensing domains, as illustrated in Fig. 1, with several positively charged residues of S4 (typically, arginine or lysine followed by two hydrophobic residues) acting as gating charge carriers. Experimentally, a transient current across the capacitive membrane is measured, which, when integrated over time, reveals total macroscopic gating charge transported across the membrane (ΔQ) associated with the conformational change of the voltage sensor. Single channel conductance measurements and computer modelling studies estimated ΔQ to be ∼12–14e (Aggarwal & MacKinnon, 1996; Seoh et al. 1996; Bezanilla, 2000; Pathak et al. 2007) for the Shaker K⁺ channel. Many models of voltage sensing were developed, and MD simulations have been used to study their viability.

Helical screw and sliding 3₁₀‐helix models of voltage sensing

Over time, structural data led to the development of a model in which S4 was presumed to be a transmembrane α‐helix in both resting and activated states, with the positively charged S4 residues forming a series of ionic pairs with neighbouring residues in the surrounding S1–S3 helices that stabilize the VSD in different stages upon depolarization (Durell et al. 2004; Chen et al. 2010). The translocation of the S4 helix of the VSD was experimentally determined to involve the charged S4 residues passing, in steps, by a conserved phenylalanine residue that serves as a gating charge transfer centre (Tao et al. 2010). In a model known as the helical screw, the S4 α‐helix was proposed to translate ∼13.5 Å and rotate a total of 180° in three steps, in a screw‐like motion (Grizel et al. 2014) (Fig. 6 top). This model is illustrated by a recently resolved crystal structure of a voltage‐sensitive phosphatase from Ciona intestinalis (Ci‐VSP). Superimposition of its VSD with that of Na_VAb and K_V1.2 showed S4 movement being consistent with that of an α‐helical screw, and the gating charge transfer computed through MD simulation agreed with experiment (Li et al. 2014).

Figure 6. Models of voltage sensing.

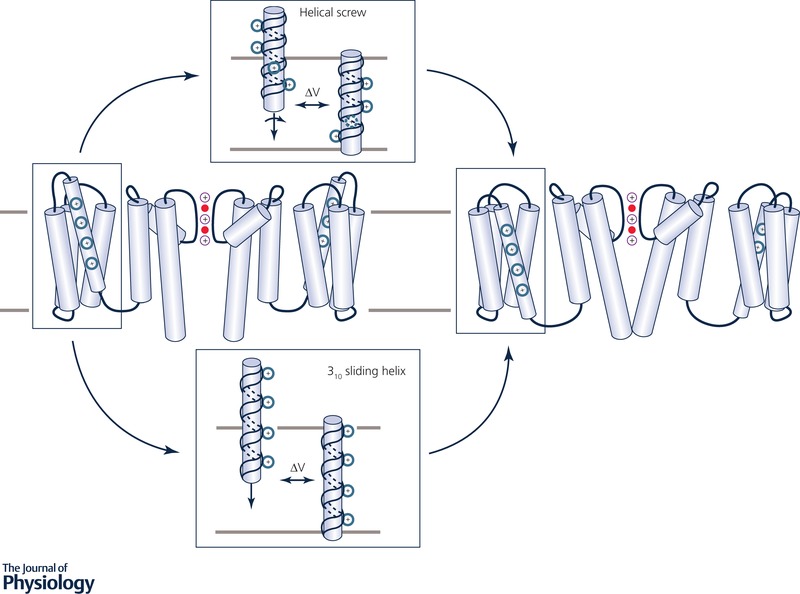
Voltage‐gated K⁺ channel model illustrated in an open pore state with activated VSD (left) and a closed pore state with resting VSD (right) based on hERG (Wang & MacKinnon, 2017) and EAG (Whicher & MacKinnon, 2016) cryo‐EM structures. Top and bottom insets show proposed S4 movement models during a channel deactivation process. Top: S4 helical screw model (Grizel et al. 2014), with S4 shown as an α‐helix, also depicting a 180° turn during activation, in a screw‐like motion. Bottom: S4 3₁₀‐helix consensus model (Vargas et al. 2012), depicting a more tightly wound 3₁₀‐helix undergoing a sliding motion. Charged residues on S4 are shown in blue. See Fig. 1 for more details.

Within the hydrophobic region of the VSD, S4 can also adopt a unique secondary structural element known as a 3₁₀‐helix, which has been observed in crystal structures (Long et al. 2007) and also predicted in several molecular modelling studies (Vargas et al. 2012; Yarov‐Yarovoy et al. 2012). A 3₁₀‐helical configuration changes the pattern of alternating charged residues on the S4 voltage sensor, allowing for a vertical translation of 2.0 Å per amino acid, as opposed to 1.5 Å for an α‐helix (Long et al. 2007), as illustrated in Fig. 6 bottom. For some time, the existence of a 3₁₀‐helix in transmembrane proteins was extremely controversial, because they were rarely seen in membrane protein crystal structures due to their inherent energetic instability (Tobias & Brooks, 1991; Karpen et al. 1992). MD simulations were not only able to reveal that the S4 can adopt a 3₁₀‐helical configuration spontaneously, but that such a structural arrangement allows for total ΔQ transfer of 10–14e (Khalili‐Araghi et al. 2010), within the range of what has been measured experimentally. A steered MD study of the K_V1.2 VSD showed that the energy barrier to S4 translocation past the gating‐charge transfer centre is reduced by a factor of 2 in the 3₁₀‐helical configuration as opposed to an α‐helical configuration, in which the S4 must turn (helical screw model) (Schwaiger et al. 2011). A consensus is now emerging that the 3₁₀‐helix is likely the voltage‐sensing element of activation in many VGCCs (Vargas et al. 2012). Its unique structural motif confirmed that the S4 basic residues were at 120° intervals on the S4 helix, consistent with early histidine scan experiments (Bezanilla, 2002). Nevertheless, the Ci‐VSP structure (Li et al. 2014) suggests that a helical screw model should not be discounted, and that structural mechanisms of voltage sensing can vary for different VSDs.

Simulations of voltage sensor motion

When the first K_V1.2 structure was resolved in an open, activated configuration, efforts were made almost immediately to induce a deactivated state of the channel in MD simulation. In one study, an applied electric field of 0.052 V nm⁻¹ (corresponding to a membrane potential drop of ∼500 mV) was used in an attempt to understand deactivation of K_V1.2; however, what was observed instead was 120° rotation of the S4 over the course of 1 μs of simulation, with little translation of the segment (Bjelkmar et al. 2009). Notably, however, the rotation of the S4 in such an applied electric field was coupled to the formation of a 3₁₀‐helical conformation, which is longer and more tightly wound and thinner compared to an α‐helix (see above), making S4 more disposed to downward motion with decreased perturbation of the rest of the VSD (Schwaiger et al. 2011). Since the translocation of S4 occurs on the order of microseconds, one study applied a very strong transmembrane potential drop of ∼800 mV in order to drive the voltage sensor down in an abbreviated simulation time frame (∼30 ns), and while they did not observe the formation of a 3₁₀‐helix, a ∼7 Å translocation and axial rotation as in the helical‐screw model was observed, with S4 going through two intermediate states corresponding to different arginine gating charge–glutamate counter charge interactions (Nishizawa & Nishizawa, 2008). Since there is a coupling between VSD movement and channel pore opening and closing, capturing a complete channel gating transition became the ultimate goal of K_V simulation studies.

In a landmark long‐time‐scale MD study on a special‐purpose Anton supercomputer, a K_V1.2/K_V2.1 channel structure with an open pore and activated VSD (Long et al. 2007; Tao & MacKinnon, 2008) was successfully driven into a resting VSD, closed pore state on a physiological time scale of ∼200 μs at a large negative membrane potential (Jensen et al. 2012). In this thorough study, the authors observed the S4 helix translating ∼15 Å in total across the membrane in sequential steps, while also rotating 120°, in keeping with what had been observed in previous simulation and modelling studies. Importantly, they also observed sequential movement of S4 charged residues past the gating charge centre F233 (on the S3 helix) identified earlier (Tao et al. 2010), and found that the activated voltage sensors delayed pore dewetting and closure, which were observed to occur after ∼20 μs of simulation and are required for complete deactivation. The downward movement of at least one gating charge on S4 past F233 was shown to precede pore closure, and the pore was always closed before all four VSDs fully deactivate. However, the pore opening required all four VSDs to move to an activated state first, with the S4–S5 linker packing against the S6 helix. (Jensen et al. 2012). It should be noted that the authors observed channel pore opening but were unable to capture a complete VSD activation upon applying a large depolarizing membrane potential to the putative resting channel structure. Moreover, in order to observe channel gating transitions, they used membrane potentials of ±750 mV, an order of magnitude larger than physiological values. However, the fact that their observed structural movement is in line with a number of experimental predictions, as well as other modelling and simulation studies (Vargas et al. 2012), makes it reasonable to extrapolate their findings to ion channel gating behaviour in their native environment.

Mechanisms of activation and deactivation can be channel‐dependent

Whether a similar structural mechanism of activation/deactivation applies to other VGCCs remains to be seen. Recently, cryo‐EM structures of EAG (Whicher & MacKinnon, 2016) and hERG (Wang & MacKinnon, 2017) channels were solved with activated VSDs and closed and open pores, respectively. They exhibit a very short non‐helical S4–S5 linker and lack a domain‐swapped architecture commonly seen in other VGCC structures, in which the S1–S4 VSD is adjacent to the neighbouring PD S5–S6, rather than its own subunit. Therefore, it is likely that those channels have a different gating mechanism, with interactions between VSD and adjacent intracellular helix–turn–helix extensions of S6, termed C‐linkers (Toombes & Swartz, 2016), or the juxtaposed intracellular N‐terminal tails (Vandenberg et al. 2017), suggested to play an important role. In a recent experimental/MD analysis study, a rack‐and‐pinion type of coupling between voltage sensors and pore gates involving interactions between S4 and S5 helices was suggested to be a dominant activation process of such channels and an alternative mechanism for K_V channels in the Shaker family (Fernández‐Mariño et al. 2018). Future MD simulations will likely be used to assess the validity of these assumptions.

In addition to structural activation/deactivation channel transitions, we need to know the underlying energetics that ultimately control the rates of those processes, and thus should provide a direct connection to electrophysiology experiments. Recently, free energy surface projections of K_V1.2 VSD activation have been computed from MD simulations, showing not only that the energetic barrier between resting and intermediate states of S4 activation is just ∼5 kcal mol⁻¹, but also that a voltage‐independent relaxation process can occur without a change in ΔQ (Delemotte et al. 2015; Delemotte et al. 2017). Interestingly, the same work demonstrated a nearly 0 kcal mol⁻¹ end‐point free energy difference when considering ΔQ as a reaction coordinate (Delemotte et al. 2015), indicating almost equal probabilities for resting and activated VSD states. In another recent study, a free energy profile for Na_VAb VSD transition between resting and pre‐activated states was computed using both additive and Drude polarizable MD simulations, demonstrating a similar –7 kcal mol⁻¹ free energy difference between end points, but a 2 kcal mol⁻¹ reduced barrier for the latter model due to a more faithful reproduction of charge–charge interactions. (Sun & Gong, 2017). Possible sources of discrepancies between the K_V1.2 and Na_VAb studies include altered intrinsic stabilities for different channel families or end‐states, as well as methodological differences; however, more information is needed to attribute such discrepancies more specifically.

Surprisingly, very similar outcomes were revealed for an isolated K_V PD energetics. A recent MD study computed almost equal stabilities of closed and open K_VAP pore states (Starek et al. 2017), in contrast to previous work suggesting a more stable K_V1.2 open PD state: by ∼7 kcal mol⁻¹ (Fowler & Sansom, 2013). This discrepancy was explained by excessive water trapping within the pore domain in earlier simulations that were relatively short (Starek et al. 2017). All of this indicates the crucial importance of force‐field selection and sufficiently long run times of simulations that aim to obtain accurate energetics and molecular mechanisms of ion channel gating. In addition, the free energy profiles for the gating transition of a complete VGCC structure still remain a formidable task. This has been recently done using coarse‐grained (Kim & Warshel, 2014) or continuum‐membrane (Silva et al. 2009) model calculations on several channel structures, also linking results to electrophysiological recordings, but atomistic MD studies of this process would be a long‐sought nexus between ion channel simulations and experiments provided that necessary accuracy and sampling are achieved.

Conclusions

Atomistic ion channel simulations are essential for providing the spatial and temporal resolution needed to understand their normal biological function as well as their pathophysiological behaviour associated with channel mutations, or unwanted drug interactions that can potentially lead to deadly human disorders. For many decades, only experimental functional characterization of ion channels was possible due to lack of high‐resolution channel structures, as well as limited computational resources and simulation methodology. The situation has changed markedly in the past 20 years with the dozens of X‐ray and cryo‐EM channel structures that have been made available, the advent of special‐purpose supercomputers capable of running microseconds of fully atomistic MD simulations in less than a day, as well the ongoing development of advanced simulation techniques. Therefore, as our review shows, modern simulations are more capable than ever of predicting intricate molecular mechanisms of complex physiological phenomena such as ion channel permeation and voltage sensing that can, in turn, be validated experimentally. However, there are still unresolved issues related to the accuracy of the empirical force field models used in such simulations, and the problem is often aggravated by a lack of experimental data necessary for model parameterization and/or hypothesis testing, which can lead to contradictory results. An accurate balance of protein–water–lipid–ion interactions is needed to predict correct channel permeation and gating behaviour, but at present most ion channel simulations utilize fixed‐charge force‐field models that do not account for the explicit electron polarization necessary to predict ionic solvation in environments of different polarities, such as water and lipid membrane. Polarizable models that do account for this are more computationally demanding and are still in the developmental stage, but their increased use in biomolecular simulations will likely lead to more accurate predictions of ion channel permeation and gating mechanisms along with associated kinetics. The latter is essential to make a connection with electrophysiological observables, such as I–V curves, single‐channel conductances and gating currents, where quantitative agreement has been achieved in some, but not all, cases, owing in large part to the accuracy limitations discussed above.

Moreover, the sampling enhancements now attainable with new computing hardware, and special simulation techniques will allow for longer simulation times, and inevitably provide a better connection to experiments as well, hence improving the predictive power of MD simulations in general. In particular, significant advancement is likely to be made in computing kinetic information for physiological processes that cannot easily be determined experimentally, such as ion channel gating, and state‐specific drug binding (entry) and unbinding (egress) rates. This type of simulation‐derived data can potentially be used to generate parameters for many of the function‐scale models used in predictive physiology, pathophysiology and pharmacology (Silva et al. 2009; Yarov‐Yarovoy et al. 2014; Clancy et al. 2016). We conclude that while many challenges and limitations in the field still exist, atomistic simulations of ion channels are entering a golden era of theoretical understanding and biomedical application, and although controversial findings and differing viewpoints will likely linger, such discourse is indispensable for moving the field forward.

Additional information

Competing interests

None declared.

Author contributions

K.R.D., S.B. and I.V. performed literature search, drafted and revised the manuscript and devised the figures. K.R.D. illustrated the figures. I.V. coordinated the project and prepared the manuscript. All authors have read and approved the final version of this manuscript and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

K.R.D. is supported by the American Heart Association Pre‐doctoral Fellowship (16PRE27260295), Western States Affiliate. K.R.D., S.B. and I.V. are supported by the National Institutes of Health NHLBI grants 5U01HL126273 and 5R01HL128537. K.R.D. and I.V. are also supported by the National Institutes of Health grant 1OT2OD026580.

Biographies

Kevin DeMarco obtained an MS in Physics from the University of Central Florida and PhD in Biophysics from the University of California, Davis, where he is currently a postdoctoral scholar. His academic interests range from quantum physics, to atomistic simulation of biomolecular systems, to applied multi‐scale computational approaches in predictive pharmacology.

Slava Bekker obtained a PhD in Chemistry in 2011 from the University of California, Davis, where she was a member of Toby Allen's lab. Her academic interests span computer simulations of proteins and cell membranes and chemistry education. She is currently a faculty member at American River College in Sacramento, CA and was a visiting scholar at the University of California, Davis in the summers of 2017 and 2018.

Igor Vorobyov obtained a PhD in Chemistry in 2003 from the University of Louisville and worked in the research laboratories of Alex MacKerell, Toby Allen and Arieh Warshel. He is currently an assistant professor at the University of California, Davis, School of Medicine. His research interests focus on molecular modelling and simulations of membrane proteins, protein–lipid and drug interactions as well as development of new accurate computational models for their description.