Noble‐Noble Strong Union: Gold at Its Best to Make a Bond with a Noble Gas Atom

Abstract

This Review presents the current status of the noble gas (Ng)‐noble metal chemistry, which began in 1977 with the detection of AuNe⁺ through mass spectroscopy and then grew from 2000 onwards; currently, the field is in a somewhat matured state. On one side, modern quantum chemistry is very effective in providing important insights into the structure, stability, and barrier for the decomposition of Ng compounds and, as a result, a plethora of viable Ng compounds have been predicted. On the other hand. experimental achievement also goes beyond microscopic detection and characterization through spectroscopic techniques and crystal structures at ambient temperature; for example, (AuXe₄)²⁺(Sb₂F₁₁ ⁻)₂ have also been obtained. The bonding between two noble elements of the periodic table can even reach the covalent limit. The relativistic effect makes gold a very special candidate to form a strong bond with Ng in comparison to copper and silver. Insertion compounds, which are metastable in nature, depending on their kinetic stability, display an even more fascinating bonding situation. The degree of covalency in Ng–M (M=noble metal) bonds of insertion compounds is far larger than that in non‐insertion compounds. In fact, in MNgCN (M=Cu, Ag, Au) molecules, the M−Ng and Ng−C bonds might be represented as classical 2c–2e σ bonds. Therefore, noble metals, particularly gold, provide the opportunity for experimental chemists to obtain sufficiently stable complexes with Ng at room temperature in order to characterize them by using experimental techniques and, with the intriguing bonding situation, to explore them with various computational tools from a theoretical perspective. This field is relatively young and, in the coming years, a lot of advancement is expected experimentally as well as theoretically.

1. Noble Gas Chemistry: The Beginning

The quote ‘the journey matters more than the destination’ applies perfectly to the noble gas (Ng) story. It takes 64 years after the discovery of krypton, neon, and xenon and 94 years after the first spectral evidence of He during solar eclipse, to set out their journey exhibiting chemical reactivity towards other elements.1 And then once it starts, it proceeds in a swift pace, crossing, if not thousands, at least hundreds of miles. With time, the perception of people towards the reactivity of Ng gets totally changed. In fact, now xenon has been treated as a quite useful ligand for reactive targets. But the beginning was not so smooth and it included many hurdles as all the initial efforts by the notable experimentalists to make Ng compounds went in vain. Some of the instances include the effort to carry out a reaction between argon and very reactive fluorine by Moissan in 1894, just after the discovery of argon, but nothing happened!2 After employing all the weapons in his arsenal, Paneth commented in 1924 that “the unreactivity of the noble gas elements belongs to the surest of all experimental results”, which clearly reflects the hopelessness of the scientists of that time about Ng reactivity.3 However, the failures make equal contributions like a success to develop a field. These failed attempts motivated scientists to properly understand the atomic structure which might explain such a unique unreactivity of Ng. Accordingly, while in 1913 Bohr's model4 was put forward, in 1916 the octet rule was proposed by Lewis,5 which implies that eight electrons in the outermost shell result in their most stable arrangement. Therefore, the scientists understood that the exceptional loneliness of Ng in the periodic table is because of their very stable ‘octet valence configuration’. Then, from the general perception and qualitative understanding, in 1924 von Antropoff6 and in 1932 Pauling7 argued that the chemical bonding might be possible in powerfully oxidizing conditions for the heavier Ng's since their outermost electronic shells are less strongly bound due to their relatively larger distance from the nuclei. However, it took another 30 years to come it to fruition in real life through the occurrence of the so‐called ‘Impossible Chemistry’ when the first Ng compound was reported in the form of xenon hexafluoroplatinate by British chemist Neil Bartlett in 1962.8 This great ‘myth‐breaking’ discovery has an interesting story behind, where the first step, which created the stage of this discovery, was purely an accident, whereas the second step came from a general understanding of the science involved.

2. The Fact Behind that Experiment and Thereafter

In 1960, Bartlett, a newly joined lecturer at the University of British Columbia, Canada in collaboration with Lohmann was trying to prepare PtF₂ by reduction of PtF₄ but the latter one was contaminated by Br₂ in the reaction, 3Pt+4BrF₃→3PtF₄+2Br₂. Then to remove Br₂, they heated the product in F₂ to oxidize Br₂ to BrF₅ with the expectation that BrF₅ would then be released from the product. For the fluorination process, they took a stream of diluted fluorine in a shallow Ni boat which was placed inside a Pyrex glass tube. Upon heating, PtF₄ started becoming darker, and finally, a deep red vapor liberated from the boat which was then condensed through cooling. The initial interpretation was that the fluorine perhaps attacked the glass tube producing O₂ and SiF₄, and O₂ formed a new oxide‐fluoride of platinum, PtOF₄.9 Then, after a thorough study via magnetic property, X‐ray diffraction, and hydrolysis analyses, they concluded at the end of 1961 (the paper came to the fore in 1962) that the actual formulation would be [O₂]⁺]PtF₆]⁻.10 This is an extraordinary achievement since PtF₆ proved to have a strong one‐electron oxidizing strength, which can even oxidize O₂ having very high ionization potential (IP=12.07 eV). This set the stage for the next invention, which eventually opened a new arena of science having astonishing prospects.

Early next year while Bartlett was preparing for a lecture, his eyes fell on the IP graph of the periodic table. He marked that Xe (12.13 eV) has almost the similar IP value as that of O₂. Therefore, he anticipated that if PtF₆ can oxidize the latter, it should be able to oxidize the former one as well. This was proven to be true when Bartlett mixed the red gaseous PtF₆ with colorless Xe and the glass vessel was instantly filled up with a yellow material – The Very First Noble Gas Compound. Though at that time he believed that the yellow product was Xe⁺[PtF₆]⁻, the correct characterization of this compound even at a later stage with much advanced experimental tools remained elusive. He later represented this compound as an XeF⁺ salt of Pt₂F₁₁ ⁻.11 Recently, Christe and co‐workers provided a plausible pathway for the preferential formation of [XeF]⁺[Pt₂F₁₁]⁻ from PtF₆.12 According to them, PtF₆ first forms non‐classical PtF₇ ⁻ and the latter one readily transfers F atom to Xe forming XeF radical and PtF₆ ⁻. The radical then reacts with another PtF₆ molecule producing [XeF]⁺[PtF₆]⁻. Subsequently, [PtF₆]⁻ gets decomposed into PtF₅ and F⁻ and finally PtF₅ combines with [XeF]⁺[PtF₆]⁻ forming [XeF]⁺[Pt₂F₁₁]⁻.

It hardly matters that whatever the structure, combination, and/or formation mechanism this yellow compound possesses, it served its purpose by breaking the existing dogmas and myths regarding absolute unreactivity of Ng. As a result, within less than one year a good number of Ng compounds including XeF₂, XeF₄, XeF₆, XeOF₄, XeO₃, and KrF₂ were bottled in the lab.13 Even, the fluorides of radioactive radon were also experimentally prepared.14 However, this is until 2000 when first Ar compound in the form of HArF was generated by the photolysis of HF in a solid argon matrix and was characterized by probing the vibrational spectral shift on isotopic substitution using infrared spectroscopy by Räsänen and co‐workers.15 This event was rightly marked in the commentary, ‘another noble gas conquered’ by Frenking on the occasion of this matrix isolation.16 The lightest two members in the Ng family, He and Ne were seemed to have too much rigid electron density to deform or to ionize them in order to make any meaningful compound. But weak complexes like NeAuF, NeBeS, NeBeCO₃, NeBeSO₂, (Ne)₂Be₂O₂, (NeAr)Be₂O₂ and (NeKr)Be₂O₂ were experimentally identified in a low‐temperature matrix.17 In another landmark work, very recently (in 2017) Dong et al.18 reported a solid compound of helium and sodium, Na₂He, having fluorite‐type structure under high pressure of greater than 113 GPa. The bonding situation in this compound is extraordinary as revealed by the solid‐state adaptive natural density partitioning analysis (SSAdNDP). In sodium sublattice without helium, each Na₈ cube possesses only one electron, and now when helium is incorporated in half of those cubes as in Na₂He, the helium pushes the electron density from the Na₈He cube into the adjacent empty Na₈ cube which helps to form an 8c–2e bond in the empty Na₈ cube. Such electron pushing gradually increases with pressure, and therefore, only after certain pressure, the formation of the 8c–2e bond becomes meaningful. This bond was marked as the crucial one for the stability of such a complex at high pressure. These results highlight the fascinating capability of helium to show reactivity in other planets of our solar system like in Jupiter or in Saturn where the pressure is very high. Therefore, presently, all the members in the Ng group are known to show reactivity, only as one moves to the top of the group, the required conditions might be different.

This is ironical that the first breakthrough for Ng compound comes with the help of a noble metal, Pt, although there is no direct Pt−Xe bond involved therein, rather it is the large oxidizing power of PtF₆ according to Bartlett and the high electron affinity of PtF₆ according to the mechanism proposed by Christe and co‐workers, which is responsible for the formation of the compound. The definition of noble metal is different in chemistry and in atomic physics and so is the list of the names. In former, noble metals are defined as the metals which exhibit resistant to corrosion and oxidation in moist air and the list is large that includes transition metals (TM) like Ru, Rh, Pd, Ag, Os, Ir, Pt, Au, Hg, Re, and Cu. On the other hand, in physics, the definition is more precise and it tells that the d bands of the electronic structure should be completely filled and d bands should lie lower to the Fermi level.19 In that consideration, only Cu, Ag, and Au are considered as noble metals. In general, noble metals are less reactive than their neighbors. So, this was quite unexpected that even a noble metal like Au could form a strong bond with Ng, and here came the twist and another giant leap in Ng chemistry took place in 2000.

3. Noble Metal Comes into Play: The Prelude

The first report on an interaction between a noble metal and Ng appeared in 1977 when Kapur and Müller detected AuNe⁺ species through mass spectroscopy (see Figure 1, and Table 1 for the names and structures of the Ng complexes involving a noble metal reported so far).20 Then, first high level computations using the self‐consistent‐field (SCF) based modified coupled‐pair functional (MCPF) approach,21 in conjunction with a basis set of quality slightly better than triple zeta plus two polarization functions on CuNg⁺ and NgCuNg⁺ (Ng=He, Ar, Kr), were carried out by Langhoff and co‐workers in 1990.22 CuNe⁺ was also considered in a theoretical study with the same functional but different basis sets from the previous one by the same group two years later.23 Their computations suggest that NgCuNg⁺ possesses a linear structure with ¹∑_g ⁺ ground electronic state. These systems also have very flat bending potential, which is because of the absence of any easily polarizable 4 s orbital in Cu, and, therefore, the Cu−Ng repulsion is not altered through bending of NgCuNg⁺. The zero‐point energy uncorrected dissociation energy (D _e) values for the CuNg⁺→Cu⁺+Ng pathway were reported as 2.2 (He), 2.6 (Ne), 10.7 (Ar), and 15.8 (Kr) kcal/mol, whereas the same for NgCuNg⁺→Cu⁺+2Ng were turned out as 4.8 (He), 23.1 (Ar) and 33.0 (Kr) kcal/mol. The corresponding D _e values show that the second Ng−Cu bond strength is somewhat stronger than that of the first Ng−Cu bond. Interestingly, at the same level, D _e value for Ne was noted to be slightly smaller than He, despite larger polarizability of former than that of the latter.23 Later on, this anomaly becomes quite well‐known to the community working on Ng chemistry as in many instances a similar trend was observed.24 The above‐mentioned study is one of those initial articles where such irregularity was reported. Although the actual reason behind such an anomalous behavior of Ne is still debatable and perhaps it needs a thorough in‐depth analysis, considering all the possible factors responsible for this, some opinions are available in the literature. Grandinetti, one of the today's leading theoreticians working on Ng compounds, argued in his article, ‘Neon behind the signs’, ‘Neon is bigger than helium, and possesses occupied p orbitals. This is thought to produce less effective electrostatic interactions and higher orbital repulsions, which typically make the neon compounds either unstable or only marginally stable, although the contributions of these factors are still to be further investigated.’25 In this context, he also supported the suggestion to shift helium to the top of group 2 of periodic table that can eventually remove this periodic irregularity. Very recently, Nunzi et al.26 found that in a polar environment like in HeBeO or HeAuF, the empty p orbital of He can accept electron density but Ne cannot. They argued that this additional stabilizing factor originated from the back‐donation stabilizes He complexes making the He bond strength either equal to or larger than that in Ne complexes. However, it does not seem to be the sole factor as in many cases even in polar systems the Ne bond strength is larger than the He bond strength following the periodic trend. Therefore, this topic is still open for further study!

Figure 1.

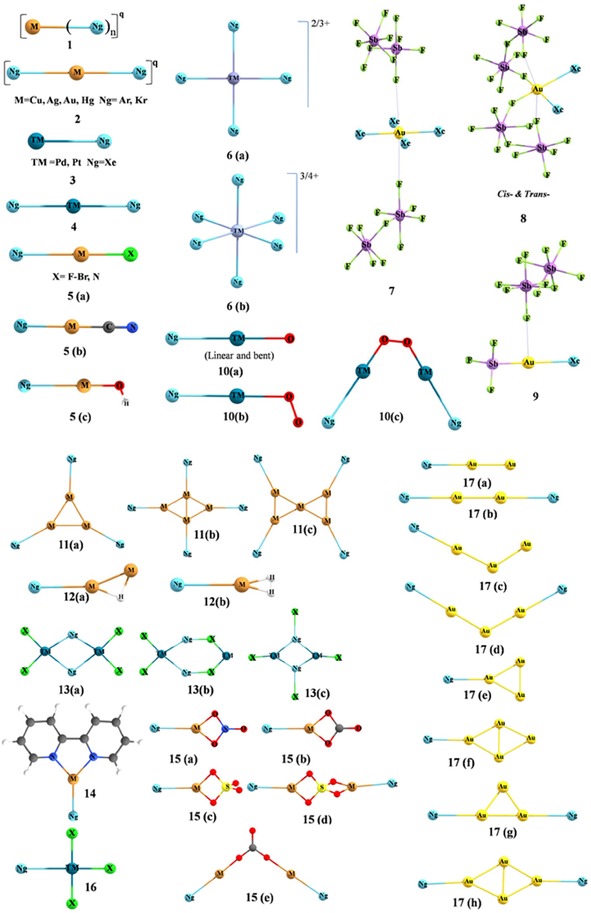
Structures of the non‐inserted Ng complexes involving a noble metal–noble gas bond.

Table 1.

Chronology of events in Ng compounds with M−Ng bonds (M=noble metal).

Year	Name	Structure[a]	Mode of characterization	Ref.
1977	AuNe+	1	mass spectroscopy	[20]
1990	CuNg+ and NgCuNg+ (Ng=He, Ar, Kr)	1, 2	theory	[22]
1992	CuNe+	1	theory	[23]
1995	NgAuNg+ and AuNg+ (Ng=He−Xe)	1, 2	theory	[29]
1998	XeAuXe+ and AuXe+	1, 2	theory+mass spectroscopy	[31]
1998	PdXe and PtXe,	3	theory	[32a]
2005–2006	Pt−Ng, Ng−Pd−Ng and Ng−Pt−Ng (Ng=Ar−Xe)	3, 4	theory	[32b, 32c]
2000	ArAgX (X=F, Cl, Br)	5 a	theory+rotational spectroscopy	[33]
2000	ArCuX (X=F, Cl, Br)	5 a	theory+rotational spectroscopy	[35]
2000	ArAuCl and KrAuCl	5 a	theory+rotational spectroscopy	[36]
2000	ArAuF and ArAuBr		theory+rotational spectroscopy	[37]
2000	AuXe4 2+(Sb2F11 −)2	7	single‐crystal structure determination+theory	[38]
2001	TM(Ng)4 2+ (TM=Ni, Zn, Pt, Au), Hg(Ng)2 2+, TM(Ng)6 3+ (TM=Cr, Co, Rh, Ir), Au(Ng)4 3+, Pt(Ng)6 4+, and TM(Ng)6 6+ (TM=Mo, W)	6 a, 6 b, 2	theory	[47]
2001	KrAgCl	5 a	theory+rotational spectroscopy	[49]
2001	[M(Ar)n]2+ (M=Cu, Ag, Au; n=1–6)	1	theory+mass spectroscopy	[51]
2002	KrAgF	5 a	theory+rotational spectroscopy	[52]
2002	Cu+(Ng)n (Ng=Ne, Ar)	1	theory+mass spectroscopy	[53]
2002	cis‐[AuXe2]2+([Sb2F11]−)2, trans‐[AuXe2]2+([Sb2F11]−)2, [Au2Xe2F]3+([SbF6])3, trans‐[AuXe2F]2+[SbF6]− [Sb2F11]−	8	single‐crystal structure determination	[54]
2003	[(F3As)AuXe]+[Sb2F11]− and [HgXe2]2+[SbF6]−[Sb2F11]−	9	single‐crystal structure determination+theory	[55]
2004	KrMF and XeMF (M=Cu, Ag, Au), KrAgBr, KrCuCl, XeAgCl, and XeCuCl	5 a	theory+rotational spectroscopy	[56]
2007	NgMIIO, NgMIIO2, where M=Hg, Pd, Pt, NgAuF3, NgAuN, NgAuO+, Xe−AuI−(O2 2−)−AuI−Xe	5 a, 10 a, 10 b, 10 c	theory	[58]
2008	NgAuOH (Ng=Kr, Xe)	5 c	theory	[60]
2008‐2014	M(Ng)n q (M=Cu, Ag, Au; n=1–6; q=‐−1, 0, +1, +2)	1	theory	[61]
2007‐2009	AuNg (Ng=Ar−Xe)	1	electronic spectroscopy+theory	[63]
2009	NgMF (Ng=He, Ne; M=Cu, Ag, Au)	5 a	theory	[65]
2010	CuXe+ complex in MFI‐type zeolite	1	synchrotron X‐ray absorption fine structure+theory	[67]
2012	Mn.Ng (M=Cu, Ag, Au; n=2, 3, 4; Ng=Kr, Xe, Rn)	17 a–17 h	theory	[68]
2013	Aun.Kr and Aun.Kr2 (n=2, 3, 4)	17 a–17 h	IR spectra+theory	[69]
2013	NeAuF	5 a)	low temperature matrix isolation+IR spectroscopy+theory	[70]
2015	Au2.Ngn and Au3.Ngn (Ng=Ar−Xe; n=1, 2)	17 a–17 e	far‐IR multiple photon dissociation experiments+experiment	[71]
2015	XeMF3 (M=Ru, Os, Rh, Ir, Pd, Pt, Ag, Au) and XeMF4 (M=Ru, Os, Ir)	16	theory	[72]
2015‐2016	NgMX (M=Cu, Ag, Au; X=CN, O)	5 b, 10 a	theory	[73]
2015	AunAgm +⋅Ark (n+m=3; k=1–3)	11 a	mass spectroscopy+IR spectroscopy+theory	[74a]
2015	AunAgm +⋅Ark (n+m=4, 5; k=1–4)	11 b, 11 c	mass spectroscopy+IR spectroscopy+theory	[74b]
2016	M3(Ng)3 + (M=Cu, Ag, Au; Ng=Ar−Rn)	11 a	theory	[74c]
2016	NgAu2H+ and NgAuH2 +	12 a, 12 b	theory	[76]
2016	[NgM(BiPy)]+ (M=Cu, Ag, Au; Ng=Ar−Rn)	14	theory	[77]
2016	NgCuNO3, NgAgNO3, NgCuSO4, NgAgSO4, Ng2Cu2SO4, Ng2Ag2SO4, Ng2Au2SO4, NgCuCO3, Ng2Ag2CO3, Ng2Au2CO3	15 a–15 e	theory	[78]
2018	Pt2Ng2F4 and [Au2Ng2F4]2+ (Ng=Kr−Rn).	13 a–13 c	theory	[79]

[a] See Figure 1 for corresponding structures.

The results for NgCuNg⁺ and the successful syntheses of XAuX⁻ (X=Cl‐I),27 SAuS³⁻, and EAuE⁵⁻ (E=P, As)28 motivated Pyykkö to investigate the stability and bonding of isoelectronic NgAuNg⁺ (Ng=Ar−Xe) species and their mono Ng (He−Xe) analogs via MP2 and CCSD(T) computations.29 The He and Ne were found to form weak complexes in AuNg⁺, having basis set superposition error (BSSE) corrected D _e values of 0.7 (He) and 1.4 (Ne) kcal/mol. However, for Ar−Xe, the corresponding D _e values are quite high, being 7.4 (Ar), 13.9 (Kr) and 24.8 (Xe) kcal/mol at the CCSD(T) level. In cases of two Ng bound congeners, the D _e values for NgAuNg⁺→Au⁺+2Ng are 24.8 (Ar), 38.9 (Kr) and 61.2 (Xe) kcal/mol at the MP2 level, and likewise for Cu congeners,22 the D _e value per Ng−Au bond is somewhat larger in NgAuNg⁺ than that in AuNg⁺. For a given Ng, the Ng−Au bond was noted to be slightly stronger than the Ng−Cu bond. The relativistic effects are responsible for the enhanced Ng binding ability of Au, which can be understood from the results of nonrelativistic calculations on AuXe⁺. While the Au−Xe bond was elongated by 0.34 Å, the D _e value got reduced by 14.5 kcal/mol, indicating that almost half of the bond strength is originated from the relativistic effects of Au.30 It is not unexpected since IP value of Au is 2.105 eV larger in relativistic calculation than that obtained in nonrelativistic computation. Therefore, it enhances the electronegativity of Au, which in turn induces larger Ng→Au electron transfer. A significant covalent character was predicted in Au−Ng (Ng=Ar−Xe) bonds. In fact, the Xe−Au bond distance in XeAuXe⁺ is very close to the sum of their covalent radii. Thereafter, it takes only three years when Schröder et al. in collaboration with Pyykkö detected AuXe⁺ and XeAuXe⁺ in mass spectroscopy.31 The Au−Xe bond strength in AuXe⁺ at CCSD(T) level with a larger basis set having g functions for Au was refined as 30.1 kcal/mol. This is fascinating that the Au−Xe bond is strong enough to make the transformation, Au(C₆F₆)⁺+Xe→C₆F₆+AuXe⁺ via ligand exchange reaction. In the same year, Pyykkö and co‐workers32a examined the Xe binding ability of other noble metals, Pd and Pt. The D _e values for the ¹∑⁺ state of PdXe and PtXe at the CCSD(T) level are 10.0 and 16.2 kcal/mol, respectively. Therefore, they have a significantly smaller affinity towards Ng than the isoelectronic Au⁺. Later on, Ng−Pt−Ng and Ng−Pd−Ng (Ng=Ar−Xe) species were also reported to be viable candidates for experimental realization.32b

4. 2000: The Year of the Noble Metal–Noble Gas Compounds

Then comes the year 2000, which might be called as the year of noble metal‐Ng compounds since a plethora of contributions emerged in that year enriching the list of noble metal‐Ng combinations. While in one side, for the first‐time neutral noble metal‐Ng compounds were detected, in another side the experiment goes beyond microscopic detection and a large‐scale synthesis was also succeeded. Gerry and co‐workers contributed remarkably through a series of studies in which they characterized Ng bound molecules via pure rotational spectroscopy and subsequently, they performed the ab initio computations to complement the experimental results. The first study in this series comes with the detection of ArAgX (X=F, Cl, Br) molecules which was originally accepted in October of 1999 but came online in early 2000.33 Their results showed that ArAgX possesses a linear structure with Ar−Ag stretching frequencies around 140 cm⁻¹. The equilibrium bond distances were also deduced from the corresponding rotational constants. The Ar−Ag bond lengths (ranging from 2.56 Å in ArAgF to 2.64 Å in ArAgBr) are significantly smaller than the van der Walls distances but also somewhat longer than the typical Ar−Ag covalent one (r _cov=2.24 Å).34 Therefore, some degree of covalent character is expected to be present there. The D _e value for the Ar−Ag bond of ArAgF at the MP2 level was turned out to be 5.6 kcal/mol. Then a few months later, the same group reported the spectral characterization of ArCuX (X=F, Cl, Br).35 The Ar−Cu stretching frequencies (∼200 cm⁻¹) were noted to be larger than that in Ag analogs. The Ar−Cu bond distances are smaller, being within 2.22 Å in ArCuF and 2.30 Å in ArCuBr, which are only slightly longer than the corresponding r _cov value of 2.08 Å. The Ar−Cu bond of ArCuF (D _e=11.3 kcal/mol) is significantly stronger than the Ar−Ag bond. Thereafter, in the same year, they extended their work to ArAuCl and KrAuCl.36 While the Ar−Au stretching frequency (198 cm⁻¹) was noted to be almost similar to that of Ar−Cu bond, the Kr−Au stretching frequency is 161 cm⁻¹. The Ng−Au bond distances are 2.47 (Ar) and 2.52 (Kr) Å which are pretty close to the corresponding r _cov values (2.20 and 2.41 Å for Ar−Au and Kr−Au bonds, respectively), indicating significant covalent character therein. The D _e values were computed as 11.2 kcal/mol for Ar−Au bond and 17.0 kcal/mol for Kr−Au bond in NgAuCl. Then, they reported the microwave spectra of ArAuF and ArAuBr where the Ar−Au stretching frequency and D _e value were estimated as ∼200 cm⁻¹ and 14.1 kcal/mol for ArAuF, respectively.37 A comparison of bond strength among these three noble metals gives the order as Au < Cu ≪ Ag. In fact, the Ar−AuF bond strength is larger than that of Ar−AuAr⁺ bond.

Then comes the big discovery in this field when the crystal structure was obtained for AuXe₄ ²⁺(Sb₂F₁₁ ⁻)₂ complex by Seidel and Seppelt in the middle of 2000.38 However, their original aim was not to make this complex, rather they were trying to prepare elusive gold(I) fluoride, AuF, through the reduction of AuF₃ by a weakly coordinating compound. They first reacted AuF₃ with AsF₃ in HF/SbF₅ solution which formed F₃As−Au⋅⋅⋅F⋅⋅⋅SbF₅ complex, a derivative of AuF. When they replaced AsF₃ with Xe, a very mild reducing and very weakly coordinating agent, the reaction resulted in the formation of a dark red crystal at −78 °C. The single‐crystal structure determination revealed the crystal as AuXe₄ ²⁺(Sb₂F₁₁ ⁻)₂ complex where AuXe₄ ²⁺ forms a regular square with Au−Xe bond lengths of 2.728‐2.750 Å, accompanied by three weak contacts between F centers of anion and Au. The bond lengths are only slightly longer than the Au−Xe covalent distance (2.55 Å). This compound is stable up to −40 °C, above which it gets liquified with the loss of gaseous Xe. The totally symmetric Au−Xe vibration in AuXe₄ ²⁺ was recorded as 129 cm⁻¹, which was corroborated well with the theoretical value of around 100 cm⁻¹ at different levels. The D _e value for AuXe₄ ²⁺→Au²⁺+4Xe was computed as 199 kcal/mol at the MP2 level. This is a major breakthrough in this field as it shows that Au−Ng compounds can also be bottled without any drastic lowering of temperature, and an appropriate binding center can even form some sort of covalent bonds with four Ng atoms which were unprecedented at that time. In that aspect, the remark of Hoffmann39 in his column entitled, ‘One Shocked Chemist’ is relevant which reads ‘Some new molecules are simply astounding. We have learned that xenon, a so‐called noble gas, is far from inert, forming bonds with halogens, oxygen and carbon. But I never imagined a bond between two relatively unreactive elements, gold (Au) and xenon (Xe), and, to boot, with a pretty naked xenon acting as a ligand…’ Interestingly, although the common oxidation states of Au are +1 and +3, in the first large‐scale synthesized Au−Xe compound, Au has its uncommon +2 oxidation state.

5. The Bonding in AuNg⁺: A Debate

Historically, AuNg⁺ is so important for the development of this field that several studies have been devoted to correctly understand the bonding in these species. In the two landmark papers, Pyykkö and co‐workers29,31 interpreted the Au⁺‐Ng bonding as the bonds having significant covalent character and the degree of covalency increases in moving from Ar to Xe. The atomic charges computation indicated that the bond in AuXe⁺ is essentially an Au⁺←Xe σ‐dative bond. In fact, Pyykkö40 underlined the nature of the bond as covalent in his commentary on the occasion of the discovery of AuXe₄ ²⁺(Sb₂F₁₁ ⁻)₂ complex. However, Read and Buckingham41 had different opinion, describing the Au⁺‐Ng interaction in terms of long‐range polarization and dispersion interactions, but not significant covalent interaction, with the dominant attractive term in the potential coming from the polarization of Ng by Au⁺. The charge‐induced dipole interaction is the largest contributor to the induction energy, although higher‐order effects are also considerable around the equilibrium bond distance. Bellert and Breckenridge42 further criticized the arguments of Read and Buckingham when they pointed out that the latter authors used an unphysical repulsive term in their model potential, and, therefore their model was not adequate to rationalize the higher‐level calculations of Pyykkö and co‐workers.31 In a further study, through their model potential analysis, the research group of Breckenridge and Wright43 found significant covalent interaction in Au⁺−Kr and Au⁺−Xe bonds, whereas Au⁺‐Ar bond is in the borderline between van der Waals and covalent interactions. Belpassi et al.44 noted an electron density accumulated region in between Au and Ng centers, delimited on both sides by a zone of electron depletion with larger extent at Ng, in their electron density deformation plots, reinforcing the formation of a polar covalent bond. Then, Zeng and Klobukowski45 also analyzed the bonding pattern in Au⁺−Xe to check with their the then newly developed relativistic model core potentials,46 in conjunction with coupled‐cluster method. Their results also indicated a significant covalent character in Au⁺−Xe bond. They concluded that the recognition of the contraction of the 6s orbital of Au and the diffuseness of the 5p orbital of Xe is crucial to get meaningful results of the bonding.

6. Aftermath of the Achievements in 2000

Very soon after this landmark discovery, in the early 2001 Hu and Huang47 reported the results of coupled‐cluster calculations on multiple Ng bound multicharged TM complexes, viz., TM(Ng)₄ ²⁺ (TM=Ni, Zn, Pt, Au), Hg(Ng)₂ ²⁺, TM(Ng)₆ ³⁺ (TM=Cr, Co, Rh, Ir), Au(Ng)₄ ³⁺, Pt(Ng)₆ ⁴⁺, and TM(Ng)₆ ⁶⁺ (TM=Mo, W) where Ng=Ar−Xe. All of these complexes possess very high binding energy. Fascinatingly, hexacoordinate complexes were predicted to possess octahedral geometries. They argued that higher‐level correlation effects are important to get accurate geometrical parameters, whereas density functional theory (DFT) like B3LYP method could give satisfactory binding energy values. Berski et al.48 performed an electron density analysis on Au(Ng)₄ ²⁺ (Ng=Ar, Kr, Xe) complexes to provide insights into the related nature of bonding. They found a positive Laplacian of electron density (∇² ρ(r_c)) at the bond critical point (BCP) of Au−Ng bond and the energy density (H(r_c)) with very small negative value. They concluded that the Au−Ng bonds are of closed‐shell nature with dominant electrostatic interaction. Gerry and co‐workers49 continued their research in the same line and in 2001, they reported the spectral signature of KrAgCl. While the Kr−Ag bond length was found to be 2.641 Å, the corresponding stretching frequency was recorded as 117 cm⁻¹. The D _e value was estimated to be fairly low as 6.7 kcal/mol. Prompted by the considerable number of reports on noble metal‐Ng complexes, the first review on transition metal‐Ng complexes was devoted in 2001 by Grills and George.50 Next year, KrAgF was also detected in Gerry's laboratory.51 The Kr−Ag bond stretches with 113 cm⁻¹ frequency and with a bond length of 2.594 Å. In moving from Cl to F, the D _e value gets improved by 1.0 kcal/mol. In a joint experiment and ab initio study, Walker et al.52 found spectral signatures of [M(Ar)_n]²⁺ (M=Cu, Ag, Au; n=1‐6) in mass spectroscopy and the corresponding geometrical structures were elucidated theoretically. They found larger stability for [MAr]²⁺ species than their larger analogs with D _e value of 26.6 (Cu), 25.4 (Ag) and 26.4 (Au) kcal/mol. The corresponding peaks for tetra‐ and hexacoordinate forms were also quite intense in the spectra which can be explained from their square‐planar and slightly distorted octahedral geometries, because of Jahn‐Teller effect, respectively. Then, Velegrakis and co‐workers53 characterized Cu⁺(Ng)_n (Ng=Ne, Ar) complexes via mass spectroscopy and their electronic structures were assessed by DFT based computations. The first coordination sphere was found to be n=12 for Ne (icosahedral structure) and n=6 for Ar (octahedral structure). Moreover, the tetracoordinate complexes possess planar form and not tetrahedral.

Thereafter, in two successive years, 2002 and 2003, Seppelt and co‐workers54,55 came with another set of masterpieces through the syntheses of a series of crystals, viz., cis‐[AuXe₂]²⁺([Sb₂F₁₁]⁻)₂, trans‐[AuXe₂]²⁺([Sb₂F₁₁]⁻)₂, [Au₂Xe₂F]³⁺([SbF₆]⁻)₃, trans‐[AuXe₂F]²⁺[SbF₆]⁻ [Sb₂F₁₁]⁻, [(F₃As)AuXe]⁺[Sb₂F₁₁]⁻ and [HgXe₂]²⁺[SbF₆]⁻[Sb₂F₁₁]⁻ complexes in super‐acidic conditions (anhydrous HF/SbF₅). While the Au−Xe bond distances lie in the range of 2.593–2.709 Å, the Hg−Xe bond distance was observed to be 2.769 Å (r _cov=2.64 Å). The cis isomer of [AuXe₂]²⁺ adopted an angular form, whereas in the corresponding trans form it has a linear structure. Crystal structures of [(F₃As)AuXe]⁺ and [HgXe₂]²⁺ are stable at room temperature; however, other Au−Xe complexes need a slightly lower temperature to remain stable. [Au₂Xe₂F]³⁺ was the first example of a molecule containing an Au−Xe bond with Au in +3 oxidation state and [HgXe₂]²⁺ is the first system having Hg(II)−Xe chemical bond.

In 2004, another series of studies were carried out by Gerry and co‐workers56 where they made spectral characterization of KrMF and XeMF (M=Cu, Ag, Au), KrAgBr, KrCuCl, XeAgCl, and XeCuCl, coupled with the MP2 level of computations, among which XeCuF and XeCuCl were reported two years later. The Ng binding energy is quite high, reflecting their stability with respect to dissociation, which is in general the largest for Au and the smallest for Ag. The improved ligand binding ability of Au is due to its relativistic effect, which contracts its radius and enhances its electronegativity. The effect of relativistic effect on the properties of Au was reviewed by Pyykkö.57 Similar to the other systems in this category, the Ng−M bonds in these NgMX molecules were found as rigid and apparently strongly anisotropic, in contrast to the usual situation for van der Waals bonds. From the short bond distances and electron density distribution, they noted ample evidence of chemical bonds formed between Ng and M centers. In 2007, Grochala58 wrote an excellent review summarizing the achievements in the field of Ng‐chemistry. Further, he anticipated several molecules/complexes to be stable from his general intuition and/or preliminary computations. He commented on the perspective of hard‐soft combinations, ‘it seems that in the rich world of chemical misalliances similarities continue to attract: hard Xe ²⁺ still prefers hard F⁻, soft Xe ⁰ adores softer Au²⁺, while noble sticks to noble…’ He expected that molecules similar to NgAuF, viz., NgM^IIO, NgM^IIO₂, where M=Hg, Pd, Pt, NgAuF₃, NgAuN, NgAuO⁺, Xe−Au^I−(O₂ ²⁻)−Au^I−Xe and more would very soon be realized in cold matrix. Possible formation of novel HgXe binary compound at pressures around 75 GPa was also predicted based on preliminary DFT computations. He further shed light on an important aspect of the possible utility of Xe as a mediator to achieve novel chemical compounds. Let us consider that AB forms from a direct reaction between A and B. Now, if AB is kinetically unstable, various side transformations would take place, making the direct synthesis unviable. For these cases, Xe might be used to get an intermediate phase, [AXe]B, upon compression of reagents. This would lead to the desired AB product upon decompression. In the next year, he with Kurzydłowski59 showed the role of formation of XeAuF to yield elusive AuF.

In 2008, in a couple of studies, Li and co‐workers60 analyzed the electronic structures and stability of NgMOH (M=Cu, Ag, Au; Ng=Ar, Kr, Xe) species. Their MP2 level of computations predicted quite large D _e values lying within the range of 3.3 (Ar−Ag) and 20.0 (Xe−Au) kcal/mol, with gradual increase along Ar to Xe and Ag−Cu−Au. In subsequent years, Xin‐Ying et al.61 carried out an exhaustive in silico investigation on evaluating the structures and dissociation energy on M(Ng)_n ^q (M=Cu, Ag, Au; n=1–6; q=−1, 0, +1, +2) species. Some other groups62 also considered some of these species in their theoretical studies. Electronic spectra of neutral AuNg (Ng=Ar−Xe) complexes were recorded and the corresponding spectral lines were assigned through high‐level computations by Breckenridge and co‐workers.63 In a further study, Fang and Zhang64 performed energy decomposition analysis (EDA) on XeMX (M=Cu, Ag, Au; X=F, Cl, Br) to shed light into the bonding. The electrostatic contribution was turned out to be larger than the orbital contribution in the Xe−M bond which indicated more ionic contribution than the covalent one. Quantum chemical calculations on HeAuF and NeAuF showed that while He is bonded with Au by 5.2 kcal/mol, Ne interacts very loosely by 1.7 kcal/mol at the CCSD(T) level.65a Boggs and co‐workers65b extended this study to the full family, NgMF (Ng=He, Ne; M=Cu, Ag, Au) and obtained only substantial binding energy for HeCuF and HeAuF. For a comprehensive review of the gas phase chemistry of coinage metals including their possibility to make complexes with Ng, the article by Roithová and Schröder66 is recommended.

In 2010, Torigoe et al.67 achieved an extraordinary result experimentally when they succeeded to get CuXe⁺ complex at room temperature in a copper ion‐exchanged MFI‐type zeolite. This is remarkable since for the first time the interaction between Cu⁺ encapsulated within MFI and an Xe atom, the nature of which is of covalent type, was probed experimentally through in situ synchrotron X‐ray absorption fine structure and heat of adsorption measurements. The Cu−Xe bond length was found as 2.45 Å and the corresponding binding energy was estimated as 14.4 kcal/mol. In 2012, via both DFT and ab initio methods, Jamshidi et al.68 assessed the Ng (Kr−Rn) binding ability of M_n clusters (M=Cu, Ag, Au; n=2–4). For a given Ng, the Ng binding ability varies as Au>Cu>Ag with D _e values lying in the range of 0.8–11.5 kcal/mol (at MP2 level). The electrostatic interaction was responsible for more than 60 % of the total attractive interaction, whereas the remaining part came from the orbital interaction. Most importantly, dispersion contribution was found to be very small, excluding any possibility of a prominent interplay of van der Waals interaction therein. In the next year, this prediction got confirmed by the experimental finding of alteration in IR spectra of gold clusters in presence of Ng (Kr). Ghiringhelli et al.69 reported that the gold clusters can interact with Kr strongly enough to induce changes in their vibrational spectra. In general, in the gas phase the clusters are generated in non‐reactive Ng matrix assuming that Ng does not interact with the cluster. However, if the name of the element is Au, this study showed that the situation would become different! It is also known that if we go from a single atom to the larger clusters, the reactivity diminishes. Here, the authors noted that for Au₂, Au₃ and Au₄, the predicted IR spectra of the Kr‐bound and pristine species differed (so still possess significant reactivity), whereas for Au₇, such change is only marginal. Such spectral alteration was explained in terms of a weak chemical bond formation between Kr and Au centers which made the Kr atom localized at a particular site. For bigger clusters, the interaction is mainly of van der Waals type and, therefore, the Kr adatom was delocalized surrounding the gold cluster. The first spectral detection of Ne−Au bond in NeAuF species in cryogenic situation was also made in the same year by Wang et al.70 At the CCSD(T)/aug‐cc‐pVQZ level, the Ne−Au bond strength was recorded as 2.1 kcal/mol. In a relevant work on Ng interaction with neutral cluster, Ghiringhelli and Levchenko71 observed an interesting phenomenon. Through their experimental and theoretical studies, they found that the absorption of Ng (Ar−Xe) reduces the electron‐electron repulsion in Au₂ and, hence, it strengthens this bond. On the other hand, for Au₃, the Ng adsorption helps populate the lowest unoccupied molecular orbital (LUMO) of Au₃ to some extent.

Chakraborty et al.72 considered noble metal trifluorides (MF₃; M=Ru, Os, Rh, Ir, Pd, Pt, Ag, Au) and tetrafluorides (MF₄; M=Ru, Os, Ir) and their Xe binding ability was investigated through DFT computations. For XeMF₃, the ZPE corrected dissociation energy, D ₀, is the largest for M=Au (17.0 kcal/mol) and the lowest for M=Ir (3.7 kcal/mol), whereas for XeMF₄ the D ₀ value is the largest for M=Ru (10.5 kcal/mol) and the smallest for M=Ir (0.2 kcal/mol). In another couple of studies, Pan et al.73 extended the NgMX (M=Cu, Ag, Au; X=F, Cl, Br) family to X=CN and O through the coupled‐cluster computations about their stability and bonding. Further, a comparison was made with those experimentally detected X=F, Cl, Br species. The study showed that CuCN and AgCN possess larger Ng binding ability than those of MCl and MBr (M=Cu, Ag), whereas AuCN has larger efficacy toward bond formation with Ng than that of AuBr.73a On the other hand, NgMO was found to have slightly smaller stability with respect to Ng dissociation than that of halides, but still the dissociation energy is large enough to be viable, particularly at cryogenic situation.73b For both the families, the M−Ng bond strength varies in the order, Au>Cu>Ag and the significant contributions from both orbital and electrostatic interactions were recorded.

In 2015, in two separate papers published almost at the same time, Shayeghi et al.74 reported the Ar tagged gold silver mixed clusters studied via both experimentally and theoretically. While in the first paper,74a they showed the drastic change in the binding behavior towards Ar in moving from Ag₃ ⁺→Ag₂Au⁺→Au₃ ⁺. In Ag₃ ⁺ cluster, the Ar atoms were only weakly tagged and the basic cluster was eventually unperturbed by the messenger Ar atoms. However, the Au‐rich compositions, the Ar tagged clusters started to behave like a molecule as a whole and they exhibited molecular‐like vibrational modes composed of six atoms. This is because although the Ag−Ar interaction is weak, the Au−Ar bond is quite strong and the orbital involvement is substantial to recognize it as a covalent bond. In the second contribution,74b the similar observation was noted in cases of larger mixed clusters, Au_nAg_m ⁺⋅Ar_k (n+m=4, 5; k=1–4). Prompted by these studies, Pan et al.74c performed an ab initio study to assess the stability and bonding in M₃(Ng)₃ ⁺ (M=Cu, Ag, Au; Ng=Ar−Rn) complexes. Both ZPE and BSSE corrected dissociation energy values were computed as 2.2 (Ar−Ag) to 19.0 (Rn−Au) kcal/mol with the trend as, Au>Cu>Ag for a given Ng, and Rn>Xe>Kr>Ar for a given M. The EDA‐NOCV75 results revealed that the M−Ng bonding interaction was originated from both orbital and electrostatic interactions, almost in equal contribution. The plots of most important deformation density for Au₃(Ng)₃ ⁺ are provided in Figure 2 where the electron density is moved from red to blue region. The plots show that the electron density from p orbital of Ng is transferred to the LUMO of M₃ ⁺. The associated orbital interaction for this deformation channel gradually increases from Ar to Rn. For a given Ng, it also varies similarly as that for bond dissociation energy. In a further work on such trinuclear system, Ghosh and Ghanty76 explored the effect of the replacement of Au in NgAu₃ ⁺ by isolobal H atom on the Ng−Au bond strength. They achieved a sharp enhancement in binding strength by this treatment. For example, in the case of Ar, the binding energy becomes 17.2 kcal in ArAuH₂ ⁺ from 7.7 kcal/mol in ArAu₃ ⁺. Such enhancement in the bonding strength is originated from the improved covalent character in the bond.

Figure 2.

The plots of deformation density in Au₃(Ng)₃ ⁺ complexes.

[M(BiPy)]⁺ (M=Cu, Ag, Au) is known to make complex with different ligands. Jana et al.77 studied whether Ng can also act as a weak ligand towards [M(BiPy)]⁺. The DFT calculation gave quite reasonable Ng−M dissociation energy (Ng=Ar−Rn) as 5.8–13.7 kcal/mol for Cu, 4.0–12.0 kcal/mol for Ag and 5.5–19.7 kcal/mol for Au. The partial covalent character in Ng−M bond was also understood by thorough bonding analyses. Moreover, such cationic species are also stable in presence of SbF₆ ⁻ counter‐ion. In another work, quite strong Ng (Ar−Rn) binding ability of metal nitrates (CuNO₃, AgNO₃), sulfates (CuSO₄, AgSO₄, Cu₂SO₄, Ag₂SO₄, Au₂SO₄) and carbonates (CuCO₃, Ag₂CO₃, Au₂CO₃) was reported.78 Most of them are turned out to be viable candidates for experimental realization. In the most recent study related to this topic, Moreno et al.79 presented the electronic structures of D _2h symmetric Pt₂Ng₂F₄ and isoelectronic [Au₂Ng₂F₄]²⁺ (Ng=Kr−Rn). Interestingly, in both the systems Ng acts as a bridging ligand. A thorough evaluation of thermodynamic stability (fragmentation routes), and kinetic stability (vibrational frequencies, energy barriers towards fragmentation) revealed these systems to be viable metastable species like that of [AuXe₄]²⁺. The bonding stabilization was originated from the electron transfer from positively charged Pt or Au via bridged Ng atom to negatively charged peripheral F centers.

7. Insertion Compounds Involving M−Ng Bonds

So far, the complexes we discussed are of regular (non‐insertion) NgXY type where Ng interacts with a binding center, X, while locating itself at a terminal position and then for a charged system, bulky counter ion may interact very loosely for the sake of charge neutralization. The stability of this category is decided by the thermochemistry. There is another category of Ng‐compounds of XNgY type which is called insertion compounds and they contribute significantly in this field. The stability of such compounds is driven by kinetics as they are thermochemically stable with respect to most of the dissociation channels but they always possess one or two channels which are exergonic at room temperature. So, their stability would depend on the activation barrier along those dissociation paths. Those competing paths, which are generally noted, are as follows [Eqs. (1) and (1)]:

$${\displaystyle \mathrm{XNgY}\to \mathrm{Ng}+\mathrm{XY}\left(2\text{-}\mathrm{B}\mathrm{dissociation}\right)}$$ (1)

$${\displaystyle \mathrm{XNgY}\to \mathrm{X}+\mathrm{Ng}+\mathrm{Y}\left(3\text{-}\mathrm{B}\mathrm{dissociation}\right)}$$ (2)

The two‐body (2‐B) dissociation is always highly exergonic, whereas the 3‐B dissociation is not always exergonic at room temperature or slightly spontaneous at room temperature. This dissociation is very crucial as it decides the overall stability. Very often, the related barrier is not substantial and only lower temperature is required to inhibit the dissociation. The computation of 3‐B dissociation barrier is also not easy as multi‐reference method is required to correctly describe the dissociation. On the other hand, the barrier for 2‐B dissociation is very often quite large to make it unviable process at moderate temperatures. It started with the pioneering experimental works complemented with the theoretical calculations of Räsänen and co‐workers.80 The usual procedure of synthesis of XNgY molecules is the production of X and Y fragments in solid Ng, prepared by the UV photolysis of suitable precursors. Therefore, in ideal cases, 3‐B path should be like that the corresponding association process does not have much higher barrier but the dissociation path should have enhanced barrier. From the computational perspective, the stability of such systems depends largely on the level of theory chosen. For NgXY type, the dissociation energy values would change in moving from DFT to ab initio method but not to such an extent that a stable species at one level may turn out completely unstable at another level. But for XNgY, this is a very common phenomenon. A system may turn out as a minimum energy structure at DFT and even at MP2 level; however, upon optimization at CCSD(T) level they would dissociate into X, Ng, and Y. Therefore, to get meaningful and reliable results CCSD(T) level of computations are mandatory, though it is not always computationally affordable. At present time, with the advent of more sophisticated computational resources, the most of the groups follow CCSD(T) level for single‐reference based problems, whereas CASSCF, CASPT2 or MRCI methods for multi‐reference based problems. But, in the earlier studies, MP2 was considered from ab initio methods to assess the stability, though later on MP2 method was found to considerably overestimate the dissociation energy.81

First work related to insertion compound involving Au−Ng bond was carried out by Ghanty in 2005.82 He studied the structure and stability of AuNgX (Ng=Kr, Xe; X=F, OH) at B3LYP and MP2 levels (see Figure 3 and Table 2 for the structure and name of the insertion compounds). As expected AuNgX is significantly less stable than Ng+AuX but the Au‐Ng−X bending mode involved a barrier of 17.9–38.4 kcal/mol. The same species was also found to be stable by 0.7, 27.0 and 4.5 kcal/mol for AuKrF, AuXeF, and AuXeOH, respectively, whereas AuKrOH is not stable with respect to this dissociation. These computations indicated that AuXeX (X=F, OH) are suitable candidates for experimental identification. In the next year, he reported MNgF (Ng=Ar, Kr, Xe; M=Cu, Ag) molecules.83 The MP2 level of results revealed that exergonic channel, MNgF→Ng+MF, possessed high barrier for Ng=Xe but rather low for Ng=Ar, Kr. Importantly, MNgF→M+Ng+F was also noted to be endergonic in nature. Bonding analyses showed that the proper representation of these systems should be (MNg)⁺F⁻ with M−Ng covalent bonds. More reliable data at the CCSD(T) level for the complete series of MNgX (M=Cu, Ag, Au; Ng=Ar, Kr, Xe; X=F, Cl. Br) were published in 2008.84 Minimum energy structures were found at the CCSD(T) level only for CuArX (X=F, Cl), CuNgX (X=F, Cl, Br; Ng=Kr, Xe), AgKrX (X=F, Cl), and MXeX (M=Cu, Ag, Au; X=F, Cl, Br), although at DFT and MP2 levels all MNgX molecules were turned out as minimum on the respective potential energy surfaces. It further confirmed the necessity of checking at a higher level so far the prediction of insertion compounds is concerned. At CCSD(T) level, the dissociation energy for MNgX→M+Ng+X are negative (ranging from −0.3 to −31.6 kcal/mol) in all cases, whereas for MNgX→Ng+MX although the process is highly exergonic, the barrier ranged from 2.0 (CuArF) to 31.7 (AuXeF) kcal/mol. At this level also, AuXeF has the best chance to get synthesized in the laboratory. Then in 2012 Liu et al.85 reported their MP2 and CCSD(T) results on XAuNgX⁻ and HAuNgX⁻ (X=F, Cl, Br; Ng=Ar, Kr, Xe) systems. However, the corresponding barrier for the release of Ng was turned out to be quite low (for example, for Ng=Xe, the barrier is 5–14 kcal/mol). Berski and co‐workers86 performed electron density analysis to understand the nature of the Au−Ng bond in AuNgX species (X=F, Cl, Br, I; Ng=Ar, Kr, Xe). Although the values of ρ(r_c) and ∇² ρ(r_c) at the BCP of Au−Ng bond indicated closed‐shell interaction, small negative H(r_c) values implied partial covalent interaction. The outcome of electron localization function (ELF) was found to depend on the level of theory. While DFT methods could not locate any bonding disynaptic basin V(Au,Ng) between the Au and Ng centers, the wavefunction based methods located such a V(Au,Ng) attractor at the valence region of the Ng atom, albeit with a very small basin population, representing partial covalent interaction. Later, detailed stability and bonding analyses for the heaviest Ng analogs, MRnX (M=Cu, Ag, Au; X=F−I and OH only for Au case) were discussed by Li.87

Figure 3.

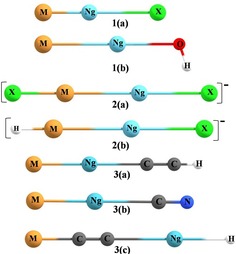
Structures of the Ng complexes involving a noble metal−noble gas reported insertion complexes.

Table 2.

Chronology of events in insertion compounds with M−Ng bonds.

Year	Name	Structure[a]	Mode of characterization	Ref.
2005	AuNgX (Ng=Kr, Xe; X=F, OH)	1 a, 1 b	theory	[82]
2006	MNgF (Ng=Ar, Kr, Xe; M=Cu, Ag)	1 a	theory	[83]
2008	MNgX (M=Cu, Ag, Au; Ng=Ar, Kr, Xe; X=F, Cl. Br)	1 a	theory	[84]
2012	XAuNgX− and HAuNgX− (X=F, Cl, Br; Ng=Ar, Kr, Xe)	2 a, 1 b	theory	[85]
2017	MRnX (M=Cu, Ag, Au; X=F−I and OH only for Au case)	1 a, 1 b	theory	[87]
2017	MNgCCH, MCCNgH and MNgCN (M=Cu, Ag, Au; Ng=Xe, Rn)	3 a, 3 b, 3 c	theory	[88]

[a] See Figure 3 for corresponding structures.

In a couple of recent studies, Chattaraj and co‐workers88 reported viable MNgCCH and MNgCN (M=Cu, Ag, Au; Ng=Xe, Rn) compounds. In fact, these two systems present first and second set of examples of having M−Ng‐C bonding motif. The free energy barrier for the exergonic isomerization channel, MNgCCH → NgMCCH, was found to be quite large (14.0‐34.8 kcal/mol) with a gradual increase from Xe to Rn for a given M, and from Au to Cu to Ag for a given Ng. MNgCCH → M+Ng+CCH was also noted to be endergonic in nature at room temperature, except for M=Ag. In this context, non‐insertion NgMCCH species were also turned out to be viable candidates. Bonding analysis revealed that while the Ng−C bonds are ionic in nature, the M−Ng bonds are of covalent‐type. In fact, they could be better represented as (MNg)⁺(CCH)⁻. On the other hand, MNgCN were found to be thermochemically stable with respect to all possible dissociation channels except for two 2‐B dissociation channels, MNgCN→Ng+MCN and MNgCN→Ng+MNC which are further connected to the internal isomerization processes, MNgCN→NgMCN and MNgCN→NgMNC, respectively. Although these processes are spontaneous, they are kinetically protected by substantial activation barriers (11.8–15.4 kcal/mol for Cu, 9.8‐13.6 kcal/mol for Ag, and 19.7–24.7 kcal/mol for Au). While the latter process is a single step process, the former one cannot occur in a single step but via an intermediate MNgNC. NgMNC can be transformed into the most stable NgMCN isomer but it needed to cross a certain barrier. The process involved two steps for Cu but single step for Ag and Au analogs, and most importantly corresponding barrier enhances in comparison to that in bare MNC → MCN process. Therefore, the presence of Ng increases the possibility of detection of elusive MNC species. This result corroborated with the finding of Grochala and co‐workers59 where they found the mediator role of Xe to yield elusive AuF species. The bonding situation in MNgCN systems is also unprecedented. While the natural charge distribution and Wiberg bond order implied covalent M−Ng and ionic Ng−C description, electron density, adaptive natural density partitioning (AdNDP), and energy decomposition analyses showed the presence of significant covalent contribution in both the bonds. In fact, the Ng−C bond of AuNgCN can also be described as an electron‐shared bond. AdNDP analysis recovered a polarized M−Ng 2c–2e σ‐bond and a 2c–2e Ng−C σ‐bond with appreciable occupation number, which shows that Ng is covalently bound with both the neighboring centers (see Figure 4). This observation is in contrast to the previous reports where XNgY was in general described as [XNg]⁺Y⁻. Hence, these results further indicate that the bonding behavior of Ng might be more puzzling than previously thought. In recent years, a lot of contribution in the field of Ng chemistry has been coming out which take this field to a new height.

Figure 4.

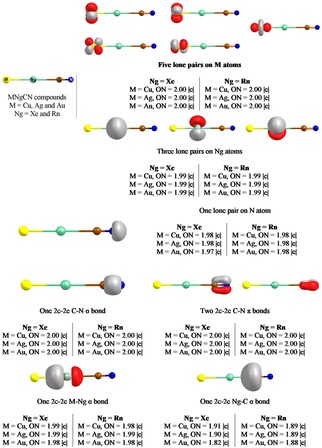
The bonding pattern recovered by the AdNDP analysis for MNgCN molecules (Ng=Xe, Rn). This figure has been reproduced from ref 88b.

8. Conclusions

In this review, we have provided a glimpse of initial difficulties in making noble gas compounds long after the discovery of noble gas and then eventually the start of noble gas chemistry in 1962 with the help of a noble metal, Pt, in form of experimental synthesis of the elusive molecule bearing the possible formula Xe⁺[PtF₆]⁻, albeit without the presence of any direct Pt−Xe bond. We have then summarized, in a chronological order, how the bonding between two nobles in the periodic table, viz., noble metal and noble gas, enriches the versatile aspect of this relatively young but very promising field, which started in 1977 with the detection of AuNe⁺ through mass spectroscopy. Theoretical prediction of NgAuNg⁺ and AuNg⁺ (Ng=He−Xe) by Pyykkö in 1995 and the detection of the fingerprints of their Xe analogs in mass spectra three years later also marked a significant achievement in this field. The year, 2000 is the renaissance time in this field when in one side a plethora of neutral NgMX (Ng=Ar−Xe; M=Cu, Ag, Au; X=F−Br) molecules was characterized by rotational spectroscopy, on the other side noble‐noble combination goes beyond microscopic detection and the crystals of AuXe₄ ²⁺(Sb₂F₁₁ ⁻)₂ was bottled in laboratory. Then a series of studies was made to synthesize or to predict stable compounds with noble metal‐noble gas bond. Experimental and computational chemists find synergy in their complementary roles in predicting, isolating, synthesizing, characterizing, and analyzing the noble gas compounds. Interestingly, two nobles make so strong bond with sufficient orbitalic involvement that some of them reach the covalent limit. Gold is really a golden candidate to form a chemical bond with a noble gas atom due to relativistic contraction in radius and subsequent enhancement in electronegativity. Gold has the highest capability to form strong bond with noble gas atoms followed by copper and silver. The bonding situation in noble gas insertion compounds is even more intriguing where in some cases the bonding between a noble gas and its two neighboring atoms might be represented as two classical 2c–2e σ‐bonds. Therefore, the present review provides a bird's eye‐view of the achievements in this field till date and particularly about to what extent noble gas is capable of forming a chemical bond, which may be even covalent in nature in some instances, when the other partner is a noble metal, particularly a gold atom. In coming years, we expect an inflation in such complexes with particularly strong Ng−Au bonds, not only on paper or microscopic amount in cryogenic situation, but also in large‐scale syntheses in laboratory which might be bottled at ambient temperature. The assessment of reactivity of such complexes certainly would also be an interesting topic in near future. We also expect a more important and widespread role of noble gas, from experimental point of view, to play as a mediator to achieve otherwise elusive species.

Conflict of interest

The authors declare no conflict of interest.

Biographical Information

Dr. Sudip Pan obtained his Ph.D. degree from the Indian Institute of Technology Kharagpur (India) in 2016 under the supervision of Prof. Pratim K. Chattaraj. In the same year, he moved to work as a Postdoctoral Fellow at Cinvestav Merida (Mexico) under Prof. Gabriel Merino. Towards the end of 2017, he moved to Nanjing Tech University (China) for another postdoctoral stay under Prof. Gernot Frenking and Dr. Lili Zhao, where he is currently working. His research interests include the theoretical predictions of viable noble gas compounds, effective hydrogen storage material, clusters with unusual bonding, nanomachinery, compounds with boron–boron triple bonds and reactivity, catalysis and reaction mechanism, planar hypercoordinate carbon and boron systems, and ligand stabilized species and reactivity.

Biographical Information

Gourhari Jana is a research scholar at the Indian Institute of Technology Kharagpur (India). He completed his B.Sc. degree in Chemistry (Hons.) from Midnapore College under Vidyasagar University (India) in 2013. He received his M.Sc. degree from the same university in 2015. He joined the research group of Professor P. K. Chattaraj for his Ph.D. degree in the Department of Chemistry, Indian Institute of Technology Kharagpur (India) as an Institute Fellow. His research activities include metastable behavior of noble gas insertion compounds and isomerization process, hydrogen storage, machine learning & deep learning, chemical reactivity, toxicity analysis and drug discovery, etc. in the domain of theoretical and computational chemistry.

Biographical Information

Professor Gabriel Merino obtained his Ph.D. in 2003 under the supervision of Professor Alberto Vela in Cinvestav (Mexico). In the same year, he started as a Postdoctoral fellow under the supervision of Professors Gotthard Seifert and Thomas Heine at TU Dresden (Germany). Returning to Mexico in 2005, he became a member of the Chemistry Faculty (currently Chemistry Department) of Universidad de Guanajuato. In April 2012, he joined the Applied Physics Department of the Centro de Investigación y de EstudiosAvanzadosdel IPN, Unidad Mérida (Mexico). His group is currently one of the most active in Theoretical and Computational Chemistry in Mexico and Latin America. He has focused his research on predicting new molecular systems that completely violate traditional chemistry by pushing to the limit basic concepts like structure, chemical bond, and aromaticity. His group also developed new tools to study electronic delocalization and aromaticity, including the analysis of the electronic response of a molecule under a magnetic field for a better understanding of the nature of these uncommon systems. In the same way, the Merino's group has designed new algorithms to find the most stable structures for small molecules, which has allowed finding a new series of clusters with exotic topologies.

Biographical Information

Pratim Kumar Chattaraj obtained his Ph.D. degree from the Indian Institute of Technology (IIT) Bombay (India) in 1988 under the supervision of Professor B. M. Deb. Currently he is an Institute Chair Professor in IIT Kharagpur (India). He is also a Distinguished Visiting Professor at IIT Bombay. He was a Research Associate at the University of North Carolina, Chapel Hill (USA) with Professor Robert G. Parr and also at the FAU, Erlangen‐Nürnberg (Germany) with Professor Paul v. R. Schleyer. He has been actively engaged in research in the areas of density functional theory, ab initio calculations, nonlinear dynamics, aromaticity in metal clusters, hydrogen storage, noble gas compounds, machine learning, chemical reactivity and quantum trajectories.

S. Pan, G. Jana, G. Merino, P. K. Chattaraj, ChemistryOpen 2019, 8, 173.