Abstract
Lingual orthodontics have become popular in modern society as they do not cause aesthetic impairment. From the translational medicine point of view, the use of biomechanical analysis to solve a clinical problem has rarely been reported. Here, we combined the clinical trial and 3-D finite element (FE) method to translate the clinical problem to the FE analysis and back to clinic. Twenty upper premolar extraction cases treated with customized lingual appliances were recruited in this study. Cephalometric films and cast records analysis showed that the “bowing effect”, which is a major side effect in lingual orthodontics, occurred during the first treatment stage with single lingual cable retraction. In order to translate the problem to biomechanical research, we introduced the 3-D finite element (FE) model of a customized lingual orthodontic system. The 3-D FE model including the maxilla, periodontal ligament (PDL), and dentition was constructed from human computed tomography data. The tendency of tooth movements in three dimensions and stress distribution in the PDL were analyzed by different mechanical loading methods. 3-D FE analysis confirmed the “bowing effects” and unexpected tooth movements with application of single lingual retraction force. Interestingly, we found that applying forces on both buccal and lingual sides, called “double cable” mechanics, could prevent the “bowing effect”. For the clinical trial, we applied the “double cable” force during space closure stage for 4 months, and confirmed “double cable” mechanics could correct and prevent the “bowing effect” clinically. Based on our results, both buccal and lingual forces should be used during space closure in lingual orthodontics to prevent and correct the “bowing effect”. Moreover, the magnitude of buccal force should not be lower than the force on the lingual side.
Keywords: Lingual orthodontics, orthodontic tooth movement, three dimensional finite element analysis, translational study
Introduction
The demand for aesthetic orthodontic appliances has rapidly increased in recent years. Current options for aesthetic orthodontic appliances include labial ceramic brackets, clear aligners, and lingual brackets. The lingual appliances are the most aesthetic choice among these options [1,2]. Lingual orthodontics (LiO) are becoming more popular in modern society due to their lack of aesthetic impairment, and patients prefer lingual appliances for their invisibility. Although clear aligners are widely used by clinicians, they have difficulties in resolving severe cases. However, lingual orthodontics as an invisible fixed appliance, can resolve most of these severe cases [3]. Moreover, previous clinical studies have demonstrated a reasonable acceptability in both the patients and doctors for lingual orthodontics [1,4]. However, it is believed that various clinical and biomechanical differences exist between the LiO and conventional labial orthodontics (LaO) techniques, which can be attributed to many factors such as, differences in the position of brackets, reduced arch perimeter, and variations in the lingual anatomy. However, the detailed underlying biomechanical mechanisms are not well understood. Also, some unexpected tooth movements might be encountered during the treatment with these appliances [5,6]. Particularly, during the space closure stage in lingual orthodontics, unwanted lingual inclination, extrusion of anterior teeth, inter-bicuspid width expansion and inter-molar width contraction, i.e. the “bowing effect”, may occur [7]. A few specific techniques have been used in clinical situations to prevent these unexpected tooth movements. It was previously claimed that when force applied at both the buccal and lingual sides, i.e. the “double cable” mechanics, the “bowing effect” could be avoided [7]. However, important questions like how to apply these forces and how the “double cable” mechanics work have not been investigated in either biomechanical or clinical research.
Finite element (FE) model methods have shown advantages in the biomechanical analysis of orthodontic tooth movement (OTM) [8,9], which have been used in several studies for biomechanical research related to orthodontic tooth movement, such as torque control [10,11], arch expansion [12,13], molar distalization [14], use of microscrews [15,16] and sliding mechanics in space closure for labial orthodontics [17]. Yet there are rare studies focusing on biomechanical research for lingual orthodontics.
FE methods can quantify the stress and displacement throughout the anatomy of a three-dimensional structure and are proven to be effective and accurate methods for the simulation and analysis of the application of biomechanical forces [3,18-20]. Though there are many application potentials for the FE methods in OTM, whether the findings can be translated into clinical situation still remains to be verified.
Thus, the purpose of this study is to evaluate the biomechanical effects of “double cable” mechanics during the stage of space closure using 3D finite element analysis. And we try to translate the FE analysis findings back to clinical research through conducting a preliminary trial by analyzing the width of cast model and using cephalometric measurements.
Materials and methods
Patients recruitment and study design
The study was designed as a pilot clinical trial using before and after self-control study. Patients were recruited between December 2011 to April 2012 at the department of orthodontics, Peking University Hospital of Stomatology (Figure 1).
Figure 1.
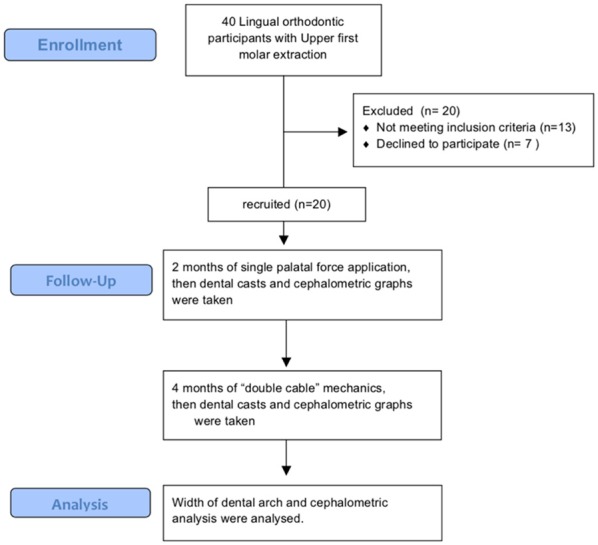
Flow chart showing enrollment, study inclusion, and data analysis.
Four inclusion criteria were included: 1. Permanent dentition without congenital missing tooth 2. Extraction of upper first premolars for the treatment need 3. Using customized lingual orthodontic appliance. 4. Adult patients.
Three exclusion criteria were included: 1. Moderate to severe periodontitis 2. Pregnant during the course of treatment 3. Patients with systemic diseases.
Twenty participants, none of which was a smoker, with upper premolar extraction were included in this study. The study protocol was approved by the Institutional Review Board of Peking University, Hospital of Stomatology (PKUSSIRB-2011019). All of the patients were fully informed and signed consent. This study was registered in Chinese Clinical Trial Registry Center (ChiCTR-ONB-17013261).
Intervention and primary outcome measurements
All participants were treated with customized lingual appliances (3M IncognitoTM) which were bonded on teeth with indirect bonding methods. The magnitude of forces applied in clinical settings was 1.5 N measured by dynamometer through Powerchain (OrmcoTM). The application of force was by the same doctor to assure uniformity. Dental casts and cephalometric films were obtained before space closure, after 2 months of single palatal force application and then at 4 months of “double cable” mechanics application (Figure 2A). Inter-canine width (ICW, the distance between cusp on each sides), inter-premolar width (IPW, the distance between buccal cusp on each sides), inter-first-molar width (IMW1, the distance between buccal cusp on each sides) and inter-second-molar width (IMW2) were measured on the dental casts (Figure 2B). The degree of upper incisor to SN plane (UI-SN), and the distance of upper first molar to palatal plane (UM-PP), upper incisor to pterrygomaxillary fissure (UIPTV) and upper molar to pterrygomaxillary fissure (UMPTV) were measured (Figure 2B).
Figure 2.
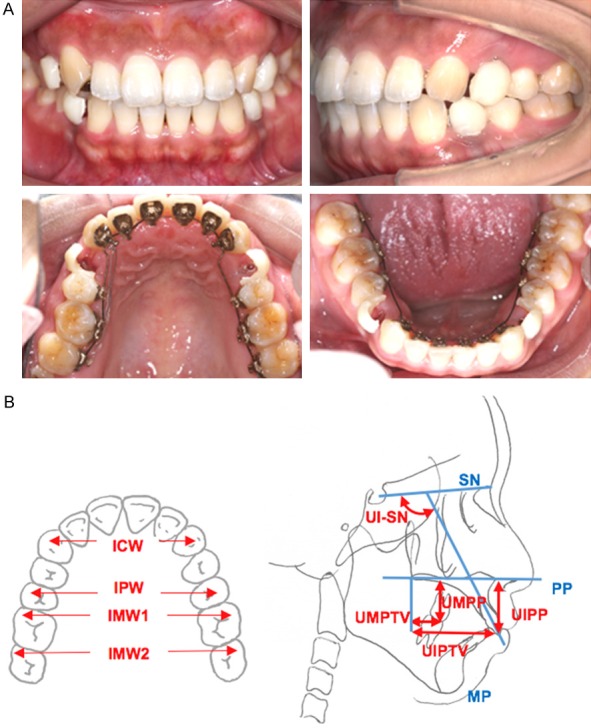
Clinical features of lingual orthodontics in space closure stage and the evaluation items in dental cast records and cepholometric analysis. A. Clinical orthodontic example of lingual orthodontics with 4 first premolars extraction to retract anterior teeth. B. Measurements Index, ICW, inter-canine-width, IPW, inter-premolar-width, IMW1, inter-first molar width, IMW2, inter-second molar width, UI, upper incisor, SN, sella nasion plane, pp, palatal plane.
Establishment of the model
Craniofacial spiral CT data (GE MEDICAL SYSTEMS/LightSpeedw VCT) of a volunteer with normal occlusion were collected (scan parameters 120 kV, 125 mA) as previously reported [21]. The data were imported into the MIMICS 11.0 software to generate the CAD model and the solid body information was saved in the IGES file format. Next, the IGES file format of the model was loaded into ANSYS software (version 11.0, ANSYS Inc., Canonsburg, Pennsylvania, USA). The model was meshed, consisting of 372,225 nodes and 256,739 units (Table 1). The tooth-PDL-lingual appliance model, tooth-PDL-maxilla-lingual appliance model and lingual appliance FE model were established.
Table 1.
Number of nodes and elements in the components of finite element model
| Nodes (n) | Elements (n) | |
|---|---|---|
| Bracket | 16,759 | 7,893 |
| Wire | 13,038 | 5872 |
| Teeth | 173,353 | 112,554 |
| Maxilla | 133,633 | 78,410 |
| PDL | 105,798 | 52,010 |
Biomechanical parameters of the material and mechanical loading
The boundary conditions we used is: The superior border of the maxilla was restricted with no displacement. The medium between tooth and PDL, archwire and bracket, bracket and tooth were bonded relationship, i.e. displacement of the shared point is the same with force application, however the stress on different sides can be varied.
According to previous studies, all materials were assumed to be homogeneous, isotropic, and linearly elastic. The material properties were established as follows according to previous study [22] (Table 2).
Table 2.
Properties assigned to the alveolar bone, tooth, PDL, bracket and wire
| Young’s modulus (MPa) | Poisson’s ratio | |
|---|---|---|
| Alveolar bone | 137,000 | 0.30 |
| Tooth | 203,000 | 0.30 |
| PDL | 50.0 | 0.49 |
| Bracket | 97,200 | 0.33 |
| Wire (stainless steel) | 206,000 | 0.30 |
Two loading patterns were applied: (1) single palatal force application (0.75 N, 1.0 N, 1.5 N) and, (2) palatal (P) plus buccal (B) force application (P 1.0 N + B 0.5 N, P 0.75 N + B 0.75 N, P 0.5 N + B 1.0 N).
Tooth movement trends were measured in the 3D coordinates, which were based on the occlusal plane: X-axis (transverse plane), y-axis (sagittal plane) and z-axis (vertical plane). The von-Mises stress distribution was measured for analyzing the concentrations of stress around the root with different force applications.
Statistical analysis
Numerical variables were given as mean ± standard deviation (SD) and compared using means. SPSS for Windows (version 21.0, IBM, Chicago, IL) was used for statistic analysis. Student t-test and one-way ANOVA were applied to evaluate the changes of measurements and a two-tailed p-value <0.05 was considered statistically significant.
Results
Single lingual retraction force caused both, vertical and horizontal “bowing effects” in the clinic
The data of twenty participated patients were pooled into analysis. After single lingual retraction for 2 months, both inter premolar width (IPW) and the inter-molar width (IMW1, IMW2) were reduced (Figure 3A). We used the ratio of inter premolar width to inter-molar width for evaluating the “bowing effect”. The ratio of inter premolar width to inter second molar width (IPW/IMW2) was increased (Figure 3B). These data showed that a transverse “bowing effect” occurred during single lingual retraction.
Figure 3.
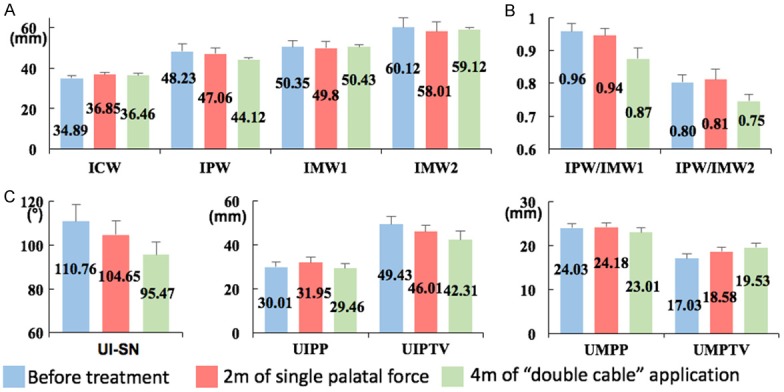
Clinical changes after two-month of single palatal force application and four months of “double cable” mechanics application. A. After two-month of single palatal force application, inter-premolar width (IPW) and the inter-molar width (IMW1, IMW2) decreased; inter-premolar width (IPW) decreased and the inter-molar width (IMW1, IMW2) increased with four months of “double cable” mechanics application. B. The inter-premolar width to the inter-second molars width ratio (IPW/IMW2) increased after two-month of single palatal force application. The inter-premolar width to the inter-second-molars width ratio (IPW/IMW2) decreased with four months of “double cable” mechanics application. C. The distances from the upper incisors to palatal plane (UIPP) and upper molars to the palatal plane (UMPP) increased after two-month of single palatal force application. The distances from the upper incisors to palatal plane (UIPP) was controlled with four months of “double cable” mechanics application.
The vertical dimension was evaluated using cephalometric analysis. The distances from the upper incisors to palatal plane (UIPP) and upper molars to the palatal plane (UMPP) increased after lingual retraction for 2 months (Figure 3C). The posterior and anterior teeth extrusion showed that a vertical “bowing effect” occurred during application of a single palatal force for retraction. Collectively, both transverse and vertical “bowing effects” were noticed clinically after single palatal force application for 2 months.
Both vertical and horizontal “bowing effects” were confirmed in the FE model by using single lingual retraction force
In order to mimic the clinical situation, we generated the FE model (Figure 4), in which the trends of each tooth movement could be observed in three dimensions after loading with retraction forces. In addition, the displacements in distance could be evaluated for each tooth.
Figure 4.
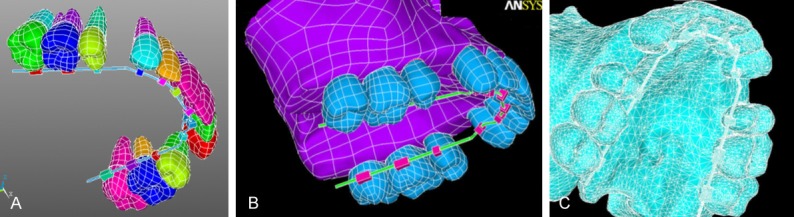
Establishment of the entity 3-D finite element model of lingual appliance. A. Tooth-PDL-Lingual appliance entity model. B. Tooth-PDL-Maxilla-Lingual Appliance entity model. C. Lingual appliance FE model.
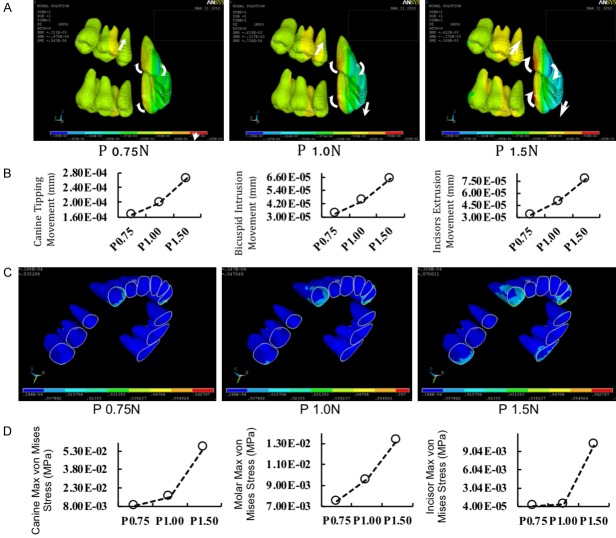
In the transverse dimension, the bicuspid expansion and molar restriction movements increased with augmentation of force, as shown in the x-axis view (Figure 5A and 5B). In the sagittal dimension, the incisors distal movement, canine distal movement and molar mesial movement increased with augmentation of force, as shown in y-axis view (Figure 5C and 5D). In the vertical dimension, the canine tipping movement, bicuspid intrusion movement, and incisors extrusion movement increased with the augmentation of force, as shown in the z-axis view (Figure 6A and 6B).
Figure 5.
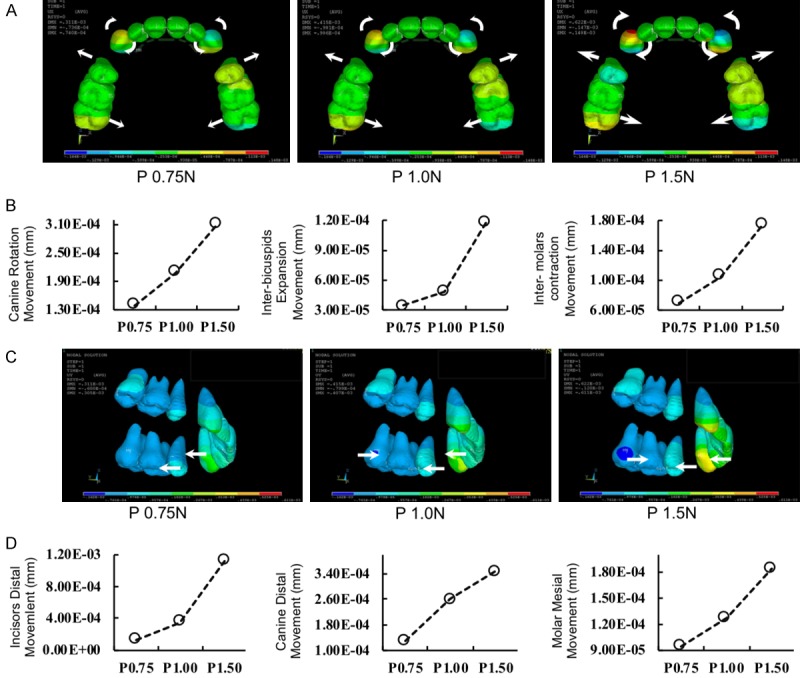
Transverse and sagittal tooth movement tendency and amount of changes in tooth displacement with different single palatal force application. A and B. Transverse tooth movement tendency and amount of changes (x-axis). The canine rotation, inter-bicuspids expansion and inter-molar contraction movement increased with the augmentation of single palatal force. C and D. Sagittal tooth movement tendency and amount of changes (y-axis). The incisor distal, canine distal and molar mesial movement increased with the augmentation of single palatal force.
Figure 6.
Vertical tooth movement and von-Mises stress distribution tendencies and amount of changes with different single palatal force application. A and B. Vertical movement tendency and amount of changes (z-axis). The canine tipping, bicuspids intrusion and incisors extrusion movement increased with the augmentation of single palatal force. C and D. von-Mises stress distribution. The canine, molar and incisor max von-mises stress increased with the augmentation of single palatal force.
The von-Mises stress distribution showed that the canine and molar max von-Mises stress increased with augmentation of the single palatal force application. While there was only a small change in max von-Mises stress on incisors when palatal force application increased from 0.75 N to 1.00 N, it increased rapidly when force application rose to 1.50 N (Figure 6C and 6D).
The “double cable” mechanics prevented the “bowing effect”
Since the single palatal retracting force resulted in a transverse and vertical “bowing effect”, we tried the “double cable” mechanics, which was also used for space closure in lingual orthodontics. The “double cable” mechanics was to apply elastomeric chains from canine to second molars on both, buccal and lingual sides in the clinic and we mimicked this process in the FE model (Figure 7A and 7B).
Figure 7.
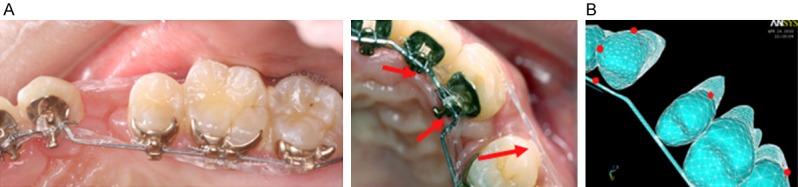
Clinical features of the “double cable” mechanic and its simulation in 3-D FE model. A. Clinical example of the “double cable” mechanics. B. The sites of the force application in clinical situation and its simulation in the 3-D FE model.
Compared to single palatal retraction, the trends in tooth movements changed markedly, as assessed by the 3D FE model. In the transverse dimension, the x-axis view showed that the canine rotation, inter premolar expansion, and inter-molar contraction movements decreased with the decline in palatal force and increase in buccal force application. When the buccal force exceeded the lingual force, the inter-premolars had a contraction trend. Meanwhile, expansion movements in the inter-lateral incisors increased with the decline in palatal force and increase in buccal force application (Figure 8A and 8B). In the sagittal dimension, the y-axis view showed that canine tipping, premolar tipping and incisor inclination movements decreased with a decline in palatal force and increase in buccal force application (Figure 8C and 8D). In the vertical dimension, the z-axis view showed that molar extrusion, canine intrusion and incisor intrusion movements decreased with a decline in palatal force and increase in buccal force application (Figure 9A and 9B).
Figure 8.
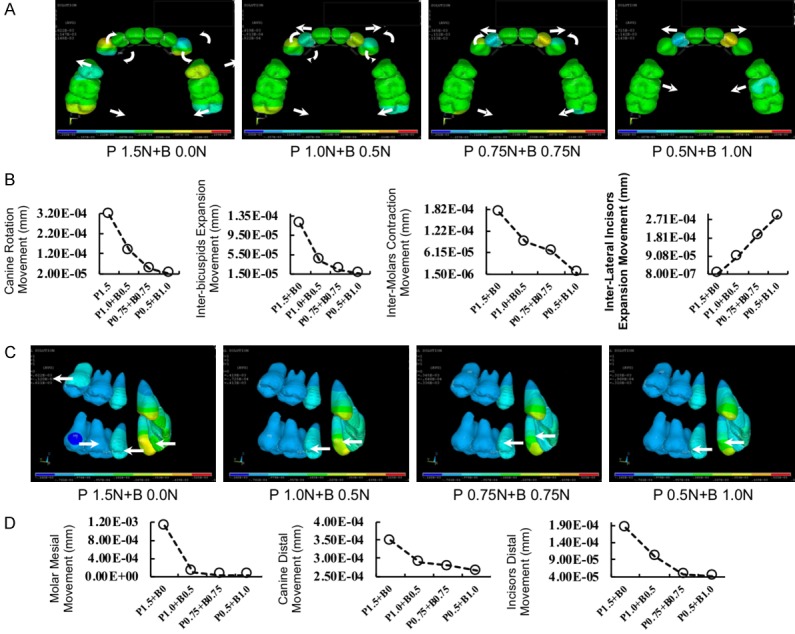
Transverse and sagittal tooth movement tendency and amount of changes in tooth displacement with different “double cable” mechanics application. A and B. Transverse tooth movement tendency and amount of changes (x-axis). The canine rotation, inter-bicuspids expansion and inter-molar contraction movement decreased with the augmentation of buccal force and reduction of palatal force. C and D. Sagittal tooth movement tendency and amount of changes (y-axis). The incisor distal, canine distal and molar mesial movement decreased with the augmentation of buccal force and reduction of palatal force.
Figure 9.
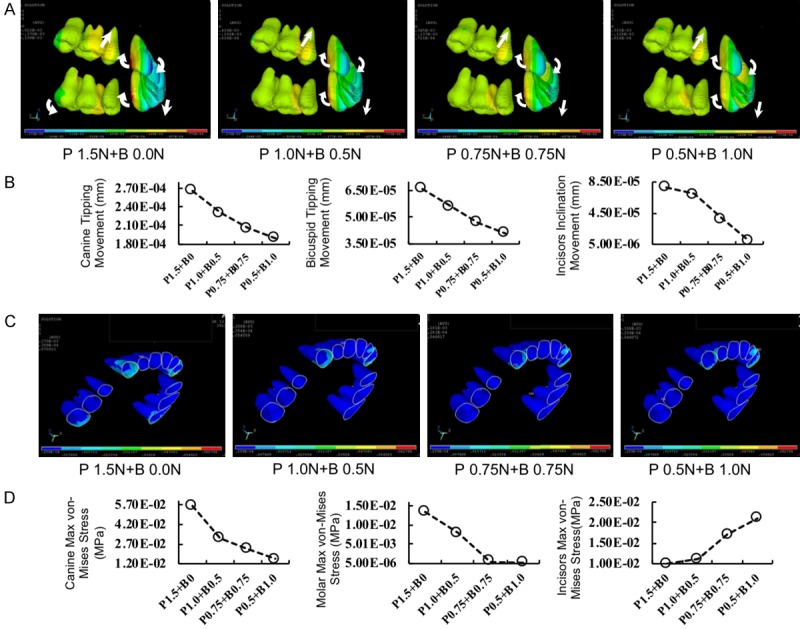
Vertical tooth movement and von-Mises stress distribution tendencies and amount of changes with different “double cable” mechanics application. A and B. Vertical movement tendency and amount of changes (z-axis). The canine tipping, bicuspids intrusion and incisors extrusion movement decreased with the augmentation of buccal force and reduction of palatal force. C and D. von-Mises stress distribution. The canine, molar and incisor max von-mises stress decreased with the augmentation of buccal force and reduction of palatal force.
The von-Mises stress distribution showed that single palatal force application would induce the concentrated stress distribution in the apical and cervical area of the canine. With the application of both palatal and labial force, the area of concentrated stress distribution decreased (Figure 9C). We also found that the canine and molar max von-Mises stress increased with the augmentation of single palatal force application. While there was a small change in max von-Mises stress distribution on the incisors when palatal force application increased from 0.75 N to 1.00 N, it increased rapidly when force application rose to 1.50 N (Figure 9D).
Application of “double cable” mechanics for 4 months corrected the “bowing effect” in the clinic
The FE model showed that “double cable” mechanics with a higher buccal retraction force would prevent the “bowing effect”. Hence, we applied double cable mechanics clinically. After 4 months of double cable retraction, the cephalometric film and dental cast were re-evaluated. The Inter premolar width (IPW), IPW/IMW1 and IPW/IMW2 decreased while the inter molar width (IMW1, IMW2) increased (Figure 3A and 3B). These data showed that the transverse “bowing effect” was corrected after 4-month of double cable retraction. Moreover, the distances from the upper incisor to the palatal plane (UIPP) was controlled (Figure 3C). These data showed that both the transverse and vertical “bowing effects” were prevented and corrected after application of the “double cable” mechanics.
Discussion
Advancements in computational techniques such as the finite element methods, which have created useful models in industry by predicting the initial response without the need of remodeling, have been widely used in the dental field [23-26]. However, whether these methods can be translated into clinical practice is unknown. Translational medical research has attracted more attention in recent years, aiming to fill the huge gap between research and clinical practice [27,28]. Here we showed that the application of “double cable” mechanics could prevent and correct the “bowing effect” in clinical situations as observed in 3-D finite element analysis.
In this study, we used realistic anatomy based CT data to construct a 3-D finite element model including the dentition, periodontal ligament, alveolar bone and the lingual orthodontic appliance. Merging these complex systems created a model that may provide answers to clinically relevant questions.
We focused on the space closure stage and analyzed the biomechanical properties of sliding mechanics in lingual orthodontics. We observed that the commonly occurred “bowing effect” was not a single tooth distortion, but a series of unwanted tooth movements in dentition during this stage, which can hamper the efficiency of lingual orthodontics [7]. Hence, in the current study, we evaluated whether application of the widely used “double cable” mechanics can avoid the “bowing effect” in lingual orthodontics.
In the 3-D FE model, and stress distribution in the PDL were analyzed using different loading conditions. When a single palatal force was applied, trends of unwanted tooth movements occurred, i.e. inclination of anterior teeth, expansion of premolars and intrusion of molars (the “bowing effect”). However, when “double cable” mechanics was applied, the “bowing effects” were prevented. Moreover, from a translational point of view, an imbalanced stress distribution may cause root resorption, which is a main side effect during orthodontic treatment in clinical situation. The von-Mises stress distribution analysis, which indicated the force received by the roots, showed that there was a more balanced stress distribution in PDL when the “double cable” mechanics was applied (Figure 9C and 9D).
The 3-D FE analysis is to predict the tendencies of tooth movements in three dimensions, yet orthodontic tooth movement is a complicated biological event. The predictions may vary in clinical situations, thus we then translated these findings into practice by testing the use of “double cable” mechanics in clinical situations.
For in clinical circumstances, if significant statistical findings were noted, it often implicated that serious clinical side effects have occurred, which would be difficult to be corrected or even caused the failure of treatment. Thus, seeking for significant difference in clinical situations was not the priority of our purpose. Instead, for the safety of the participants, we try to identify the trends rather than significant changes in the clinical trial. Our preliminary results indicated the trend of “bowing effect” after 2 months of single palatal force application. Specifically, during the course of orthodontic treatment with tooth extraction, the IPW will be reduced. When concerning to the “bowing effect”, the reduction of IPW would be slowed down. Thus, the more reduction of IPW after application of “double cable” mechanics for 4 months can be considered as an improvement. Moreover, the other indexes also indicated that there were tendencies of reduced “bowing effect” in this stage.
Based on the results of this translational research, both buccal and lingual forces should be applied during the space closure in LiO to prevent and correct the “bowing effect”. Moreover, the magnitude of buccal force should not be lower than the force on lingual side.
Acknowledgements
This trial has been registered in Chinese Clinical Trial Registry (ChiCTR-ONB-17013261). This work was supported by the Capital Health Research and Development of Special (No. 2016-1-4102, Y.Z.); the Young Scientists Fund of PKUSS (No. 20110203, No. 20170109) to D.L. and the New Clinical Technology Fund of PKUSS (No. PKUSSNCT-11A07) to D.L.; Peking University Medicine Seed Fund for Interdisciplinary Research (BMU2018MX007) to D.L. the National Natural Science Foundation of China (No. 81470717, Y.Z.), (No. 81600893, D.H.), (No. 81600865, R.Y.), (No. 81671015, X.W.), (No. 81571815, Y.L.) and (No. 81871492, Y.L.); the Beijing Natural Science Foundation (No. 7182182, R.Y.); the Beijing New-star Plan of Science and Technology (No. Z171100001117018, Y.L.); the Beijing Nova Programm Interdisciplinary Cooperation Project (No. Z181100006218135, Y.L.); the Young Elite Scientist Sponsorship Program by CAST (YESS, 2017QNRC001, R.Y.); the Beijing Municipal Science & Technology Commission (No. Z171100001017128, X.W.).
Disclosure of conflict of interest
None.
References
- 1.Fritz U, Diedrich P, Wiechmann D. Lingual technique--patients’ characteristics, motivation and acceptance. Interpretation of a retrospective survey. J Orofac Orthop. 2002;63:227–233. doi: 10.1007/s00056-002-0124-3. [DOI] [PubMed] [Google Scholar]
- 2.Russell JS. Aesthetic orthodontic brackets. J Orthod. 2005;32:146–163. doi: 10.1179/146531205225021024. [DOI] [PubMed] [Google Scholar]
- 3.Liang W, Rong Q, Lin J, Xu B. Torque control of the maxillary incisors in lingual and labial orthodontics: a 3-dimensional finite element analysis. Am J Orthod Dentofacial Orthop. 2009;135:316–322. doi: 10.1016/j.ajodo.2007.03.039. [DOI] [PubMed] [Google Scholar]
- 4.Hohoff A, Wiechmann D, Fillion D, Stamm T, Lippold C, Ehmer U. Evaluation of the parameters underlying the decision by adult patients to opt for lingual therapy: an international comparison. J Orofac Orthop. 2003;64:135–144. doi: 10.1007/s00056-003-0217-7. [DOI] [PubMed] [Google Scholar]
- 5.Mathew RN, Katyal A, Shetty A, Krishna Nayak US. Effect of increasing the vertical intrusive force to obtain torque control in lingual orthodontics: a three-dimensional finite element method study. Indian J Dent Res. 2016;27:163–167. doi: 10.4103/0970-9290.183120. [DOI] [PubMed] [Google Scholar]
- 6.Sung SJ, Baik HS, Moon YS, Yu HS, Cho YS. A comparative evaluation of different compensating curves in the lingual and labial techniques using 3D FEM. Am J Orthod Dentofacial Orthop. 2003;123:441–450. doi: 10.1067/mod.2003.9. [DOI] [PubMed] [Google Scholar]
- 7.Scuzzo G, Takemoto K. Lingual orthodontics: a new approach using stb light lingual system & lingual straight wire. Quintessence Pub Co; 2010. [Google Scholar]
- 8.Cattaneo PM, Dalstra M, Melsen B. The finite element method: a tool to study orthodontic tooth movement. J Dent Res. 2005;84:428–433. doi: 10.1177/154405910508400506. [DOI] [PubMed] [Google Scholar]
- 9.Field C, Ichim I, Swain MV, Chan E, Darendeliler MA, Li W, Li Q. Mechanical responses to orthodontic loading: a 3-dimensional finite element multi-tooth model. Am J Orthod Dentofacial Orthop. 2009;135:174–181. doi: 10.1016/j.ajodo.2007.03.032. [DOI] [PubMed] [Google Scholar]
- 10.Papageorgiou SN, Keilig L, Vandevska-Radunovic V, Eliades T, Bourauel C. Torque differences due to the material variation of the orthodontic appliance: a finite element study. Prog Orthod. 2017;18:6. doi: 10.1186/s40510-017-0161-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Papageorgiou SN, Sifakakis I, Keilig L, Patcas R, Affolter S, Eliades T, Bourauel C. Torque differences according to tooth morphology and bracket placement: a finite element study. Eur J Orthod. 2017;39:411–418. doi: 10.1093/ejo/cjw074. [DOI] [PubMed] [Google Scholar]
- 12.Mohlhenrich SC, Modabber A, Kniha K, Peters F, Steiner T, Holzle F, Fritz U, Raith S. Simulation of three surgical techniques combined with two different bone-borne forces for surgically assisted rapid palatal expansion of the maxillofacial complex: a finite element analysis. Int J Oral Maxillofac Surg. 2017;46:1306–1314. doi: 10.1016/j.ijom.2017.05.015. [DOI] [PubMed] [Google Scholar]
- 13.Park JH, Bayome M, Zahrowski JJ, Kook YA. Displacement and stress distribution by different bone-borne palatal expanders with facemask: a 3-dimensional finite element analysis. Am J Orthod Dentofacial Orthop. 2017;151:105–117. doi: 10.1016/j.ajodo.2016.06.026. [DOI] [PubMed] [Google Scholar]
- 14.Kang JM, Park JH, Bayome M, Oh M, Park CO, Kook YA, Mo SS. A three-dimensional finite element analysis of molar distalization with a palatal plate, pendulum, and headgear according to molar eruption stage. Korean J Orthod. 2016;46:290–300. doi: 10.4041/kjod.2016.46.5.290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Duaibis R, Kusnoto B, Natarajan R, Zhao L, Evans C. Factors affecting stresses in cortical bone around miniscrew implants: a three-dimensional finite element study. Angle Orthod. 2012;82:875–880. doi: 10.2319/111011-696.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lin CL, Yu JH, Liu HL, Lin CH, Lin YS. Evaluation of contributions of orthodontic mini-screw design factors based on FE analysis and the Taguchi method. J Biomech. 2010;43:2174–2181. doi: 10.1016/j.jbiomech.2010.03.043. [DOI] [PubMed] [Google Scholar]
- 17.Tominaga JY, Tanaka M, Koga Y, Gonzales C, Kobayashi M, Yoshida N. Optimal loading conditions for controlled movement of anterior teeth in sliding mechanics. Angle Orthod. 2009;79:1102–1107. doi: 10.2319/111608-587R.1. [DOI] [PubMed] [Google Scholar]
- 18.Gomez JP, Pena FM, Martinez V, Giraldo DC, Cardona CI. Initial force systems during bodily tooth movement with plastic aligners and composite attachments: a three-dimensional finite element analysis. Angle Orthod. 2015;85:454–460. doi: 10.2319/050714-330.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jones ML, Hickman J, Middleton J, Knox J, Volp C. A validated finite element method study of orthodontic tooth movement in the human subject. J Orthod. 2001;28:29–38. doi: 10.1093/ortho/28.1.29. [DOI] [PubMed] [Google Scholar]
- 20.Tominaga JY, Ozaki H, Chiang PC, Sumi M, Tanaka M, Koga Y, Bourauel C, Yoshida N. Effect of bracket slot and archwire dimensions on anterior tooth movement during space closure in sliding mechanics: a 3-dimensional finite element study. Am J Orthod Dentofacial Orthop. 2014;146:166–174. doi: 10.1016/j.ajodo.2014.04.016. [DOI] [PubMed] [Google Scholar]
- 21.Chen S, Lou H, Guo L, Rong Q, Liu Y, Xu TM. 3-D finite element modelling of facial soft tissue and preliminary application in orthodontics. Comput Methods Biomech Biomed Engin. 2012;15:255–261. doi: 10.1080/10255842.2010.522188. [DOI] [PubMed] [Google Scholar]
- 22.Yang B, Wang L, Yan B, Wei Z, Tang W, Yang F. Development of three-dimentional finite element model of maxillary dentition and edgewise appliance based on CT images. Stomatology. 2009;29:116–118. [Google Scholar]
- 23.Benazzi S, Nguyen HN, Kullmer O, Kupczik K. Dynamic modelling of tooth deformation using occlusal kinematics and finite element analysis. PLoS One. 2016;11:e0152663. doi: 10.1371/journal.pone.0152663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kang N, Wu YY, Gong P, Yue L, Ou GM. A study of force distribution of loading stresses on implant-bone interface on short implant length using 3-dimensional finite element analysis. Oral Surg Oral Med Oral Pathol Oral Radiol. 2014;118:519–523. doi: 10.1016/j.oooo.2014.05.021. [DOI] [PubMed] [Google Scholar]
- 25.Lu YJ, Chang SH, Ye JT, Ye YS, Yu YS. Finite element analysis of bone stress around micro-implants of different diameters and lengths with application of a single or composite torque force. PLoS One. 2015;10:e0144744. doi: 10.1371/journal.pone.0144744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sarrafpour B, Swain M, Li Q, Zoellner H. Tooth eruption results from bone remodelling driven by bite forces sensed by soft tissue dental follicles: a finite element analysis. PLoS One. 2013;8:e58803. doi: 10.1371/journal.pone.0058803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Steer CJ, Jackson PR, Hornbeak H, McKay CK, Sriramarao P, Murtaugh MP. Team science and the physician-scientist in the age of grand health challenges. Ann N Y Acad Sci. 2017;1404:3–16. doi: 10.1111/nyas.13498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Woolf SH. The meaning of translational research and why it matters. JAMA. 2008;299:211–213. doi: 10.1001/jama.2007.26. [DOI] [PubMed] [Google Scholar]