Detecting differential DNA methylation from sequencing of bisulfite converted DNA of diverse species

Abstract

DNA methylation is one of the most extensively studied epigenetic modifications of genomic DNA. In recent years, sequencing of bisulfite-converted DNA, particularly via next-generation sequencing technologies, has become a widely popular method to study DNA methylation. This method can be readily applied to a variety of species, dramatically expanding the scope of DNA methylation studies beyond the traditionally studied human and mouse systems. In parallel to the increasing wealth of genomic methylation profiles, many statistical tools have been developed to detect differentially methylated loci (DMLs) or differentially methylated regions (DMRs) between biological conditions. We discuss and summarize several key properties of currently available tools to detect DMLs and DMRs from sequencing of bisulfite-converted DNA. However, the majority of the statistical tools developed for DML/DMR analyses have been validated using only mammalian data sets, and less priority has been placed on the analyses of invertebrate or plant DNA methylation data. We demonstrate that genomic methylation profiles of non-mammalian species are often highly distinct from those of mammalian species using examples of honey bees and humans. We then discuss how such differences in data properties may affect statistical analyses. Based on these differences, we provide three specific recommendations to improve the power and accuracy of DML and DMR analyses of invertebrate data when using currently available statistical tools. These considerations should facilitate systematic and robust analyses of DNA methylation from diverse species, thus advancing our understanding of DNA methylation.

Introduction

DNA methylation, which refers to the addition of the methyl group to DNA, is the most extensively characterized epigenetic modification with important functional consequences. Typically, DNA methylation occurs at cytosine bases, although methylation of adenine nucleotides has also been reported in worms and microbes [1, 2]. In animal genomes, the majority of DNA methylation occurs at cytosines followed by guanine, or ‘CpG’ dinucleotides. In plants, in addition to CpG methylation, methylation of CHG and CHH nucleotides is also observed, where H stands for any of the A, T and C nucleotides [3–5].

The best understood DNA methylation systems are those of mammals, especially of humans and mice. Numerous DNA methylation studies in these systems, dating back several decades, have demonstrated that DNA methylation is critical in many regulatory processes such as silencing of gene expression, cellular differentiation, aging, genomic imprinting and X chromosome inactivation [6–11]. DNA methylation is also implicated in many diseases, in particular in cancers and neuropsychiatric diseases [10, 12, 13]. Consequently, much effort has been paid to characterize variation of DNA methylation across different biological samples, developmental stages and disease statuses.

In particular, advances in next-generation sequencing (NGS) technologies have enabled researchers to characterize genomic DNA methylation at unprecedented resolutions. Notably, the bisulfite-sequencing (also referred to as ‘BS-seq’ in this study) method has been rapidly adapted to the research community since the late 2000s. Briefly, BS-seq is a re-sequencing method after subjecting genomic DNA to sodium bisulfite conversion. Owing to the chemical properties of sodium bisulfite that converts unmethylated cytosines to uracils (which become thymines following PCR), methylated and unmethylated cytosines can be distinguished by sequencing as long as the sequence data before the conversion are available. BS-seq is highly scalable, from targeted DNA methylation analysis using smaller-scale PCR reactions [14] to moderate-scale analysis called reduced representation bisulfite sequencing (RRBS), which combines BS-seq with restriction digestion of the genomic sequences [15]. BS-seq can be used to re-sequence the whole genome (whole-genome bisulfite sequencing, ‘WGBS’), which provides the ultimate resolution by characterizing DNA methylation of nearly every nucleotide in the genome [4, 16–19].

Given the functional significance of DNA methylation, one of the foremost goals in DNA methylation studies is to detect differentially methylated loci (DMLs) and/or differentially methylated regions (DMRs) between different biological conditions. Consequently, in parallel to the advances in experimental methods, statistical tools to identify DMLs and DMRs from BS-seq data have also been eagerly developed [20–27]. However, many of these tools are tailored toward mammalian data sets, which, as we will demonstrate below, are fundamentally different from the increasingly popular invertebrate and plant systems used to study DNA methylation. As BS-seq data from non-mammalian species are rapidly accumulating, it is important to understand how the statistical tools developed and validated for mammalian data sets can be applied to data from other, diverse phylogenetic groups. Here, we first provide a succinct overview of currently available statistical tools for DML/DMR analyses of BS-seq data. We then discuss distinct properties of mammalian and non-mammalian data sets using humans and honey bees as examples, as well as unique statistical challenges stemming from the different data properties. Following this, we discuss three notable statistical points that are particularly relevant for the analyses of non-mammalian DNA methylation data. We further demonstrate these points and provide guidelines by analyzing the aforementioned example data.

Methods and materials

Overview of current statistical tools to detect DMLs and DMRs from BS-seq data

BS-seq analysis generates data in the form of cytosine and thymine reads for a specific cytosine. Initial preprocessing of these data involves a quality control step of the raw reads to ensure successful bisulfite conversion of DNA, testing for contamination and assessment of base sequence quality. Other aspects of the data, such as per base N content, read duplication levels, overrepresented sequences, are also evaluated in the first step of the analysis, typically by the tools provided by sequencer/reagent companies (e.g. the FASTQ Toolkit offered by the Illumina). After quality control, reads are trimmed and filtered to remove adapter sequences and low-quality reads [28]. The reads passing preprocessing and quality control steps can be aligned to a reference genome by a variety of short-read aligners that take into account the conversion of unmethylated Cs to Ts [29]. Following read alignment, BS-seq results can be summarized in a read-count table, which lists the number of C and T reads mapped to each cytosine. Most statistical tools described in this article take such a read-count file as the input file.

Basic parameters of DNA methylation can be easily estimated from the read-count file. For example, the ‘fractional methylation’ level of each cytosine is computed as the ratio of the number of cytosine reads to the numbers of total reads, and is commonly used to quantify methylation level of specific cytosines [4, 30]. In principle, given an extremely high sequencing coverage, we can have estimates of methylation levels of nearly every nucleotide in the genome. However, in reality, coverage for each base pair from the NGS data varies greatly [31, 32]. Given such limitation, representing DNA methylation level as a discrete variable solely based on the read coverage can cause biases. Thus, statistical methods that take into account the dynamic nature of read count distribution into the analysis are preferred. In addition, because of the very virtue of having information on nearly every cytosine in the genome, if the analyses were designed to test variation of DNA methylation on every available nucleotide, the number of hypotheses that can be tested becomes extremely high. For example, the total number of cytosines in the human genome when counting each strand separately is nearly 60 million. Statistically speaking, such a large number of CpG sites demands for a strict cutoff for the multiple hypothesis adjustment because both the Bonferroni and false discovery rate (FDR) cutoff can be considered too rigorous when there are only a small number of DMLs [33]. Consequently, it makes identification of DMLs/DMRs difficult when faced with an abundance of CpG sites. For this reason, identifying regions or specific loci that exhibit differential DNA methylation has become more realistic and important in analyses of large-scale BS-seq data. In Table 1, we list some of the currently available statistical tools for DML/DMR analyses of BS-seq data. These tools were selected for their popularity, recency and/or novelty. There are a number of excellent tools in this area of research that we could not include in the current work. We provide a simulation study to compare the performance of each tool. Several papers have previously provided complementary comparisons [34–37].

Table 1.

Basic properties of statistical methods used to find differential methylation

Properties		BSmooth [22]	RADMeth [21]	DSS-general [25]	HMM-Fisher [27]	MethylSig [24]	MethylKit [20]	BiSeq [23]	DMAP [26]
Compatible data		WGBS	WGBS	WGBS, RRBS	WGBS, RRBS	WGBS, RRBS	WGBS, RRBS	RRBS	WGBS, RRBS
Data type		Continuous	Discrete	Discrete	Categorical (0, 1/2, 1)	Discrete	Discrete	Continuous	Discrete
Smoothing		Polynomial logistic regression with tricube weight	✗	✗	Hidden Markov model with one degree	Local Beta-Binomial likelihood with tri-weight	✗	Local Binomial likelihood with triangular weight	✗
Covariates		✗	✓	✓	✗	✗	✓	✓	✗
Multiple groups		✗	✓	✓	✗	✗	✓	✗	✓
CpG modeling and testing		t-like test using locally estimated variance	Beta-binomial regression with logit link	Beta-binomial regression with arcsine link + GLSa	Fisher’s Exact test	Beta-binomial Likelihood ratio test	Logistic regression with SLIMb	Beta regression with probit link	Fisher’s Exact test, ANOVA, χ2 test
DMRs defining process		Merging DMLs by t-statistic	Merging DMLs by FDR q-value	Only DMLs	Merging DMLs by P-value	Merging DMLs by P or FDR q-value	Merging DMLs using adjusted P-value from SLIMb	Merging DMLs by hierarchical FDR q-value	Only DMRs
Validation data set		Human, Rhesus monkey	Mouse, Arabidopsis	Human	Human	Human	Human	Human	Human
Citations using mammalian samplesc	Human	22	3	0	0	4	19	3	2
	Mouse	3	1	1	0	2	18	1	0
	Other	2	0	0	0	0	9	0	0
Citations using invertebrate samplesc		0	1	0	0	0	2	0	0

Note. Each method was characterized according to the type of data they can accommodate and statistical steps used to detect DMLs and/or region. We also noted the types of data sets that were used in validation and in practice to emphasize the bias toward mammalian data.

^aGeneralized least square method.

^bSliding linear model to adjust P-values for multiple hypothesis testing.

^cData accessed on December 2, 2016.

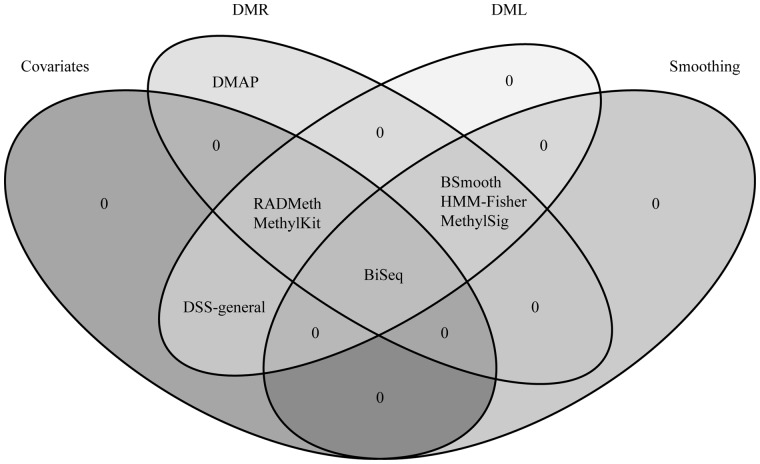
The tools in Table 1 can be divided into several groups according to the specific methods they use in some of the key steps in their analyses. Briefly, statistical tools first model methylation levels at individual sites according to an appropriate distribution before making comparisons. Methylation measurements at each site can be further adjusted via a smoothing strategy, using methylation measures from neighboring sites. The pertinent statistical test for each tool is then used to compare sites/regions and determine DMLs/DMRs. DMRs are typically derived from combining consecutive, differentially methylated CpGs within a predefined window. We summarize these methods in Table 1 and group them by their compatibility with different data sets, CpG modeling, presence of a smoothing step, ability to factor in covariates and/or multiple groups and statistical procedure for identifying DMLs and DMRs (Table 1, Figure 1).

Figure 1.

Shared characteristics of commonly used statistical tools to identify differential DNA methylation. A smoothing algorithm can be applied to incorporate the spatial correlation of neighboring CpGs, which is especially helpful for regions with a low number of mapped reads. Most of the methods are able to detect both DMRs and DMLs. Some methods allow for inclusion of covariates, granting researchers to account for confounding effects.

Data type and CpG modeling

This step determines the way methylation level is represented and used as input in DML/DMR methods. Methylation levels can be represented in one of three types, discrete, continuous or categorical. The way methylation levels are modeled somewhat narrows down subsequent statistical tests. The discrete way of representing the methylation level directly uses read count information (counts of C and T reads). Therefore, it can be connected to the binomial or beta-binomial distribution, which account for the highly dynamic nature of read coverage distributions of NGS data [32, 38, 39]. Some tools then use Fisher’s exact test or logistic regression to detect differential DNA methylation [20, 26]. However, these two tests are based on the hypergeometric and binomial distributions, respectively, which are insufficient to account for the variation of fractional methylation level between individual samples [37].

As a remedy, several methods use a beta-binomial regression to detect DMLs/DMRs [21, 24, 25]. Some other methods, instead of directly using read counts, use information from neighboring sites to consider methylation level as a continuous variable (i.e. the ‘smoothing’ approach, which is discussed in the following section). In such cases, ordinary linear regression or beta-regression can be applied to identify DMLs/DMRs. While these methods use estimates of fractional methylation levels directly, some other methods instead classify each CpG into two or more categories, for example, methylated, unmethylated and/or partially methylated. In these situations, contingency table tests such as Fisher’s exact test are used to identify DMLs/DMRs [27].

Smoothing

The methods in Table 1 can be also grouped by whether they incorporate a smoothing approach. To obtain smoothed fractional methylation levels, the general form of the likelihood is given as $L\left(\mathrm{y}||\mathrm{m},n,\mathrm{w}\right)={\prod }_{i=1}^k{L(m_i,n_i,y)}^{w_i}$, with $m_i$ representing the number of methylated reads, $n_i$representing the number of total reads and $w_i$ representing the weight at the i^th site in a window of a certain size with k number CpGs. The likelihood function L is usually based on the binomial distribution. BSmooth [22] additionally uses polynomial regression of the second degree [40]. Among the variables, $w_i$ is a function of distance from a target site. Specific weight functions used in each tool can be found in Table 1. To find the optimal estimate of smoothed methylation levels, i.e. y, the likelihood function is maximized.

Because methylation levels among adjacent CpG sites tend to be highly correlated [17, 31, 41, 42], using a smoothed methylation level among adjacent sites can improve statistical precision. However, if methylation levels fluctuate within a narrow region, smoothing within a large window size can be misleading [43, 44]. We will expand on this concept in more detail as it relates to the analyses of invertebrate methylation data in a later section. Most of the smoothing methods [22–24] can be interpreted as a weighted mean of fractional methylation level. An exception is the Hidden Markov model and Fisher’s exact test (HMM-Fisher) method [27] that instead determines the methylation state of a CpG using adjacent CpG states by a Hidden Markov model.

Statistics

Once the CpGs are modeled and a decision to use smoothed methylation measures is made, specific statistical methods can be used to identify DMRs and/or DMLs. These methods differ in the underlying distributions they assume, as well as by the link function they use to connect explanatory and the mean of response variables. Although the logit link function is the most commonly used type in many fields [45], other link functions are introduced to improve estimation. For example, the probit link in BiSeq [23] was introduced to fit the model in the presence of extreme fractional methylation levels. Dispersion shrinkage for sequencing (DSS)-general [25] uses the arcsine link to reduce the dependence of variance on mean. Note that the Fisher’s exact test is used differently in HMM-Fisher and differential methylation analysis package (DMAP) [26, 27]. HMM-Fisher uses it with categorically converted methylation status of each CpG, while the DMAP uses it with raw read counts to test group mean difference. Converting each CpG categorically removes the variance derived from using raw read counts. Therefore, HMM-Fisher is not affected by the type 1 error inflation problem that DMAP suffers from [34]. Moreover, MethylKit [20] uses logistic regression for DML/DMR detection which can induce type 1 error inflation, although it also provides advanced methods for multiple hypothesis adjustment.

Most methods provide both DML and DMR detection, with the exception of DSS-general, which only calculates DMLs, and DMAP which only calculates DMRs. Some methods first identify DMLs, and combine adjacent DMLs to define DMRs. To combine DMRs, some methods merge nearby DMLs as long as their P-values or t-statistics are smaller than a set threshold [22, 24, 27]. The authors’ suggested thresholds are typically 0.05 by default. Therefore, this approach can be considered more liberal than the approach that merges DMLs whose FDR q-values [21, 23, 24] or adjusted P-values from sliding linear model (SLIM) are smaller than a set threshold [20].

The option to include covariates or multiple groups into the model is another important aspect to consider. It is well known that many covariates such as age and sex are related to fractional methylation levels [7, 46, 47]. Therefore, meaningful covariates should be included in the model to avoid confounding effects with the variable of interest. In addition, the ability to compare multiple groups will become more important as the cost of sequencing goes down and new studies can include multiple groups in their experimental design.

As for the input data type, all methods accept either WGBS and/or RRBS data. However, this is not a strict division because the difference between WGBS and RRBS is only in whether they sequence whole genomes, or targeted regions, respectively. For example, BSmooth was originally developed to analyze WGBS data, but can also be used for RRBS if the RRBS data are long enough to sufficiently apply the smoothing procedure [22]. Thus, guidelines for compatible data sets are not set in stone.

Contrasting features of non-mammalian versus mammalian DNA methylation

The methods we discussed so far have been mostly developed and validated via BS-seq data from mammals, as shown in Table 1. However, DNA methylation is phylogenetically widespread [5, 48–51]. DNA methylation from invertebrate animals has been known for several decades [49, 52], yet remained somewhat enigmatic because typical ‘model invertebrate species’ (such as flies and worms) largely lack DNA methylation. In addition, no information on the molecular system of DNA methylation from invertebrates was available until a decade ago. In 2006, honey bee genome sequencing revealed a complete and functional DNA methylation system in this species [53]. Many subsequent studies showed that functional DNA methylation exists in a variety of invertebrate species. In particular, hymenopteran insects (bees, wasps and ants) are emerging as unique model systems to study DNA methylation [53–57]. For example, recent studies reveal that DNA methylation may be associated with caste differentiation [54], genome evolution [58], regulation of alternative splicing [14, 59], differential allelic expression [60] and response to pathogen infection [61]. DNA methylation in plants has also been known for several decades [62, 63]. Patterns of DNA methylation in plants are of great interest with respect to their roles in many aspects of their ecology and evolutionary processes [50, 64–66].

Interestingly, newly emerging genomic DNA methylation data from non-mammalian species represent a different pattern compared with those of humans and mice. For example, in contrast to mammals, methylation in insects is typically found in gene bodies of constitutively expressed genes and remains at low levels throughout the rest of the genome [54, 55, 67]. DNA methylation within insect gene bodies is biased toward the 5ʹ region and distinctly elevated in exons compared with introns in some hymenopteran insects [54, 55]. DNA methylation in plants is also largely concentrated in gene bodies, as well as in transposable elements. DNA methylation levels in plants are also moderate compared with mammals. Thus, it is imperative to consider how to apply DMR methods to non-mammalian data. In this work, we will mainly focus on data from invertebrates, with particular focus on hymenopteran insects. Nevertheless, the principles discussed here should be similarly applicable to other non-mammalian groups.

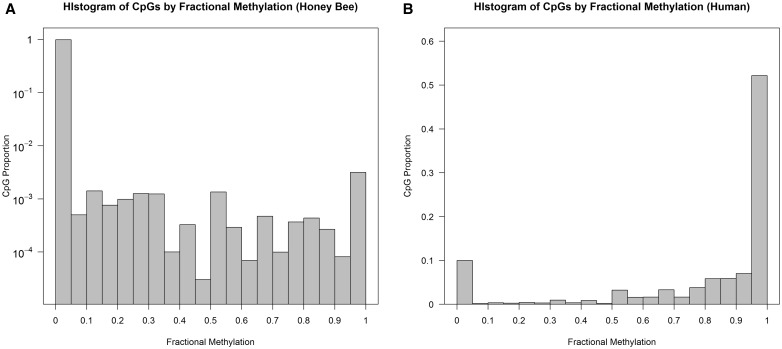
One of the most notable differences is that invertebrate genomes are typically lowly methylated overall. For example, previous studies have established that most CpGs in the human genome are heavily methylated [17, 19, 68]. In contrast, invertebrate genomes are mostly unmethylated. We demonstrate this contrast using WGBS data from honey bees and humans. The honey bee Apis mellifera is one of the first models for invertebrate methylome research. Here, we used published WGBS data from six nurse and six forager bees [69] through mapping raw read information to assembly 2.0 via BSMAP [70]. For the human example, we selected two previously published young and old human brain samples from frontal cortex, mapped using the bowtie program [16, 71]. We also analyzed these data after re-mapping using BSMAP (Supplementary Materials). Details of these data sets are shown in Table 2 and Figure 2. The primary difference between our two data sets is the mean fractional methylation levels (denoted as $\mathrm{\beta }$), which is ∼80% in the human data, and ∼1% in the honey bee data. Consequently, the proportion of highly methylated CpGs (defined as $\mathrm{\beta }\ge 0.7)$ is around 0.5% in honey bee samples, while it is >75% in the human data. Nearly 99% of CpGs are unmethylated (defined as $\mathrm{\beta }\le 0.1)\mathrm{ }$in honey bees, but this proportion is only around 10% in humans. In addition, as demonstrated in Figure 2, there is a substantial portion of partially or intermediately methylated CpGs in honey bees. In comparison, the human samples show a ‘bimodal’ pattern of methylation where methylated and unmethylated CpGs are relatively well separated. The proportion of partially methylated CpGs ($0.1\mathrm{ }<\beta <0.7$) occupies 65% of all methylated honey bee CpGs, while this proportion is 0.15 in the human data.

Table 2.

Summary statistics WGBS data sets used in the current study

Species	Subtype	Sample ID	Number of CpGsa	Mean coverage of CpGs (SD)	Mean of fractional methylation	Proportion of highly methylated CpGs (β ≥ 0.7)	Proportion of non- methylated CpGs (β ≤ 0.1)
Honey bee	Forager	SRR445767	16 219 569	3.52±2.74	0.0079	0.0044	0.987
		SRR445768	16 187 329	3.70±3.06	0.0082	0.0044	0.987
		SRR445769	16 067 650	3.53±2.74	0.0078	0.0044	0.988
		SRR445770	16 072 579	3.57±2.96	0.0081	0.0044	0.988
		SRR445771	16 651 919	4.03±3.17	0.0081	0.0045	0.987
		SRR445773	17 614 116	5.46±3.75	0.0074	0.0040	0.987
	Nurse	SRR445774	15 392 236	2.95±2.17	0.0074	0.0046	0.988
		SRR445775	16 583 546	3.98±3.16	0.0078	0.0043	0.987
		SRR445776	15 898 853	3.39±2.83	0.0077	0.0044	0.988
		SRR445777	16 610 077	4.03±3.25	0.0079	0.0043	0.987
		SRR445778	13 162 266	2.35±2.04	0.0083	0.0053	0.989
		SRR445799	16 061 822	3.63±2.93	0.0081	0.0044	0.987
Human (Brain)	Young	GSM1167005	50 681 659	9.74±5.60	0.8125	0.7770	0.089
		GSM1166274	50 584 845	9.40±5.53	0.8147	0.7767	0.089
	Old	GSM1173775	36 753 282	2.14±1.62	0.8019	0.7562	0.146
		GSM1173772	49 244 279	6.18±4.49	0.7859	0.7550	0.100

^aCounted each strand separately.

Figure 2.

Histogram of fractional methylation levels in (A) honey bee and (B) human. X-axis indicates fractional methylation, which is divided into 20 bins of 0.05 width. Y-axis is the proportion of CpGs in each bin. For the honey bee histogram, the Y-axis is log-transformed to clearly demonstrate distribution of DNA methylation. We used all CpGs in each species for the histogram. The number of total CpGs used are listed in Table 2.

Earlier approaches to detect DMLs/DMRs from BS-seq data in non-mammalian species have relied on traditional statistics such as Fisher’s exact test [72, 73], or generalized linear model [54, 59, 61, 74, 75]. However, these statistics may not be suitable for the comprehensive recent data sets of DNA methylation. For example, the Fisher’s exact test and logistic regression are based on the hypergeometric and binomial distributions, respectively, which may not be sufficient to account for dispersion in methylation levels among biological replicates of the same group [22, 25, 35]. In addition, as experimental designs incorporate multiple biological replicates, these methods may overestimate true differences between states and increase the number of false positives [35]. Other tests such as t-test analysis or analysis of variance (ANOVA) [74, 75] can also be problematic because these tests only use fractional methylation levels and do not account for the coverage information of each site. Considering such potential issues associated with traditional methods, using tools that are tailored for BS-seq data (as in Table 1) is preferred. However, currently, the number of invertebrate studies that have used such methods pales in comparison with the number of the mammalian studies (Table 1).

Results

Simulation study

We performed a simulation study to compare the performances of the tools listed in Table 1. Since DMRs are usually identified by clustering DMLs, we only focused on DML detection. Among the tools listed in Table 1, the DMAP [26] method uses Fisher’s exact test to identify DMLs and then DMRs. DMAP itself does not provide the list of DMLs directly. Therefore, we used the Fisher’s exact test directly to gauge the performance of DMAP.

We simulated WGBS data under various conditions. Specifically, we considered several factors that could affect the performance of tools, such as read coverage, fractional methylation level, sample size and the inter-individual variability of DNA methylation. Because the number of exhaustive combinations of all possible variation of factors is too large, we adopted a simple strategy where we examined the effect of a single factor while other factors are fixed. For each combination, we generated 1000 CpG sites in which the gap distances between adjacent CpGs are 100 bp. Following the structure of human data, we generated the read coverage of each CpG site from the negative binomial distribution with its variance three times larger than the mean coverage (Table 2). The number of methylated reads was determined from the binomial distribution with the fractional methylation level as a success probability. We compared two groups with equal sample sizes. For a given number of sample size for each group, we generated the methylated reads from the binomial distributions with the success probabilities π₀ = the fractional methylation level for the first group and π₁ = the fractional methylation level for the second group.

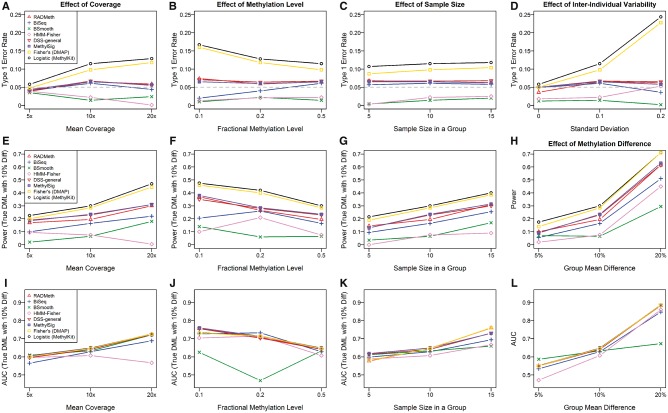
As evaluation measures, we considered the type 1 error rate, power and the area under the curve (AUC). For type I error comparison, we set the significance level to 5%. Figure 3 shows the simulation results. The first row summarizes the result of type I errors. With the exception of Fisher’s exact test and logistic regression, all methods tend to have low type I error rate despite variations in mean read coverage, mean fractional methylation level, the number of samples and the standard deviation of individual fractional methylation levels. Fisher’s exact test and logistic regression showed a large type I error except for cases when the mean coverage was small or the standard deviation of individual fractional methylation levels was small. As the mean read coverage and inter-individual variability of the level of fractional methylation increases, their type I errors increased rapidly to as much as 20%.

Figure 3.

Simulation results for performance comparisons of DMLs detection among listed tools. We used eight tools to compare performance in aspects of type 1 error (A–D), power (E–H) and AUC (I–L). The fixed parameters are: (A), (E), (I): Fractional methylation level is 0.5, sample size in a group is 10 and inter-individual variability is 0.1; (B), (F), (J): Mean coverage is 10x, sample size in a group is 10 and inter-individual variability is 0.1; (C), (G), (K): Mean coverage is 10x, fractional methylation level is 0.5 and inter-individual variability is 0.1; (D): Mean coverage is 10x, fractional methylation level is 0.5 and sample size in a group is 10; (H), (L): Mean coverage is 10x, fractional methylation level is 0.5, sample size in a group is 10 and inter-individual variability is 0.1.

For the power and AUC analysis, we defined the group effect Δ as the difference in fractional methylation levels between two groups and assumed Δ = 5%, 10%, 20%. For a given sample size, we generated the methylated reads from the binomial distributions with the success probabilities π₀ = the fractional methylation level for the first group and π₁ = π₀+Δ for the second group. The second row in Figure 3 shows the results of our power analysis. The first three plots are the results for Δ = 10%. As the coverage and sample size increase, the power increased as well. On the other hand, as the fractional methylation level increases, the power tends to decrease. While Fisher’s exact test and logistic regression resulted in the highest power, it is mainly owing to false positives. Among the listed tools, RADMeth, DSS-general and MethylSig performed similarly with higher power than the remaining tools. Note that these three tools commonly use the beta-binomial distribution for methylation information. BSmooth and HMM-Fisher provided the lowest power. The last plot in this row shows the results of the power analysis over different values of Δ. As Δ increases, the power increases. Also note that BSmooth showed the slowest rate of increase in power.

In the AUC analysis, we used the same settings as our power analysis. The last row of Figure 3 depicts the results of the AUC analysis. The first three plots are for Δ = 10%. With the exception of BSmooth and HMM-Fisher, all methods provided similar patterns. In general, as the coverage and sample size increase, the AUCs also tend to increase. On the other hand, as the fractional methylation level increases, the AUCs tend to decrease. BSmooth and HMM-Fisher showed different patterns from the rest and provided the lowest AUCs. The last plot in this row shows the results of the AUC analysis over different values of Δ. As Δ increases, the AUCs increased as well. Note that BSmooth also showed the slowest rate of increase rate in AUC.

In summary, the simulation study comparing eight different tools showed that Fisher’s exact test and logistic regression were inefficient to control for type I errors, yielding high false positives. The observation that tools using beta-binomial distribution to model CpGs reduce type I error is consistent with previous analyses [34, 76]. Among the six tools that control type I errors well, RADMeth, DSS-general and MethylSig performed similarly with higher powers and AUCs compared with other tools.

Three recommendations that can improve DML/DMR analyses of invertebrate BS-seq data

In the previous sections, we summarized key properties of DML/DMR methods and major differences in methylation patterns between mammals and invertebrates. Even though many of the newly devised BS-seq analyses methods should in principle be applicable to invertebrate data, there are some potential limitations that need to be additionally considered when working with invertebrate data sets. In the following sections, we provide suggestions that could improve the accuracy and power of DMR/DML analyses of DNA methylation data from invertebrates. We demonstrate each point by presenting analysis of the aforementioned WGBS data from honey bees and humans.

1. The effect of window sizes on the smoothing of invertebrate data

In this section, we discuss potential problems of a smoothing approach when applied to invertebrate data. As discussed above, a smoothing approach uses adjacent methylation information to improve the inference of fractional methylation of low coverage sites. This is based on the observation that methylation levels of adjacent CpGs are correlated in diverse species [31, 41, 42]. However, if there is a large fluctuation of true fractional methylation levels in a short region, a smoothing approach with large window size can result in unintended bias of estimation. Several studies have reported that some invertebrate species have sharp and fluctuating patterns in methylated regions because of methylated CpGs being clustered in short regions [54, 55, 67]. In addition, invertebrate species show distinct methylation patterns in coding and non-coding regions [55]. Consequently, smoothing over larger window sizes can distort the true methylation levels when regional correlation of methylation decreases rapidly, such as in invertebrates or plants [31]. In other words, too large a window size is likely to be disadvantageous for accurate estimation of CpG methylation in sparsely methylated genomes. In addition, a previous study of human tumors also reported that the efficiency of identifying correlated epi-alleles changed with window size [77].

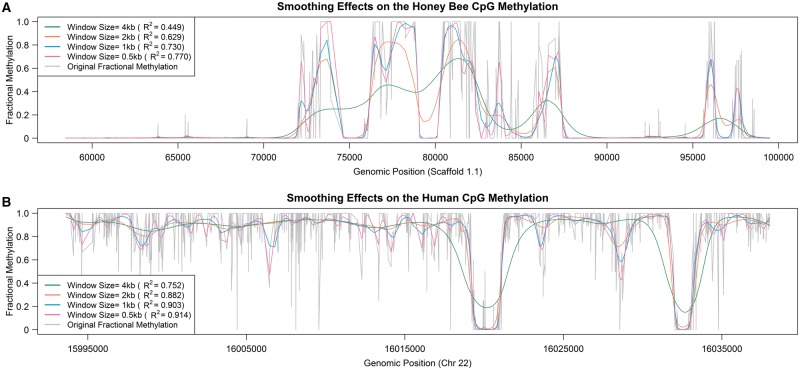
We demonstrate the effect of smoothing on invertebrate data from a comparative analysis of the honey bee and human data sets. We first used BSmooth [22] for smoothing, with window sizes of 4000, 2000, 1000 and 500 bp. The scaffold 1.1 and chromosome 22 for honey bee and human samples were used for this analysis, respectively. We show the R² values between the original and smoothed fractional methylation levels for each sample and window size (Figure 4). The coefficient of determination, or R² values, of honey bee data in the 4000 bp window are much lower. The mean R² value of 0.449 in honey bee data implies that the smoothing approach could not explain more than half of the total variation while it explained three quarters of the total variation in human data at the same window size. Indeed, smoothed fractional methylation levels in larger windows (>1 kb) are substantially different from the actual methylation levels for the honey bee data (Figure 4). Also, in the 4000 bp windows, methylation levels at the boundary are somewhat distorted even in the human data (Figure 4).

Figure 4.

Smoothing using large window sizes leads to poor estimation of local DNA methylation. Smoothed methylation levels in selected 2000 CpGs from the (A) honey bee and (B) human data.

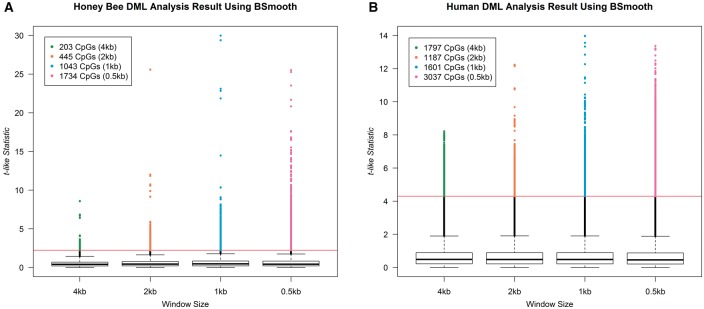
Using smoothed fractional methylation values and the modified t-test from BSmooth, we then obtained the t-like statistic at each CpG dinucleotide to identify significantly DMLs between forager and nurse bees, and between young and old human frontal cortices. Our findings for each window size are summarized as a boxplot (Figure 5). When we set the cutoff to 2.5% and 97.5% quantile of the actual t-distribution, the number of DMLs increases as the window size decreases in the honey bee data (Figure 5A). In contrast, no such trend is observed in the human data (Figure 5B). In addition, we also performed the AUC analysis [78]. AUC increased steadily with decreasing window size in the honey bee data (Supplementary Table S1). AUC also increases in the human data, but more slowly than in the honey bee data (Supplementary Table S1). Based on these results, when applying a smoothing technique to methylation data from invertebrate species, we recommend using smaller window sizes (e.g. under 1000 bp for BSmooth) than recommended for human data, and applying a looser cutoff threshold for DMLs/DMRs. This particular problem is not as evident for other tools that use smoothing because the default window sizes are small (80 bp for BiSeq [23], 2∼300 bp for MethylSig [24], one adjacent CpG for HMM-fisher [27]).

Figure 5.

The number of CpGs detected as significantly DMLs using BSmooth for several different window sizes. The Y-axis is a t-like statistic for differential DNA methylation provided by BSmooth. Red line is drawn at the cutoff of P = 0.05, when compared with a real t-distribution.

2. Handling of CpG sites that are unmethylated in all samples

As we have stated above, one of the most distinguishing features between mammalian and invertebrate methylation data is that only a small fraction of CpGs in the latter is methylated. When a CpG is unmethylated across all samples in a group, it does not need to be tested for methylation differences between groups, as these sites not only lack biologically meaningful information, but may hinder subsequent statistical tests. Having a large number of globally unmethylated CpG sites (defined as sites unmethylated in all biological samples) in a data set will be disadvantageous for multiple hypothesis testing procedures such as FDR [33], as the efficiency of such tests is affected by the proportion of true positives.

We thus suggest removing globally unmethylated CpGs before proceeding with statistical analyses. We applied this concept to the honey bee data set. In all 12 samples, 18 234 421 CpG sites have read information in at least one sample in each group (referred to as ‘unfiltered’ data set). We then used Bis-class [31] to identify and discard sites that were globally unmethylated in all 12 samples. We also removed CpG sites that did not have any mapped cytosine reads in any samples. Following these steps, we obtained a ‘filtered’ data set of 549 682 CpGs (approximately 3% of the unfiltered data set).

We first used regression analysis of differential methylation (RADMeth) for differential DNA methylation analyses of these data. RADMeth first generates P-values for individual CpGs, then derives the ‘combined P-values’ using a Z test, to combine the original P-values of the target site and its neighboring sites to increase the power to detect differential methylation [21]. The results are shown in Table 3. The numbers of significant DMLs (individual CpGs) and DMRs (clusters of adjacent differentially methylated CpGs) were much greater in the filtered data set compared with the results in the unfiltered data set. At the threshold of q $\le$0.20, only 14 CpGs were detected as differentially methylated between the nurse and forager bees from the unfiltered data set. In comparison, using the same threshold, 578 CpGs were detected as differentially methylated from the filtered data set. Sites detected as differentially methylated between the nurse and forager bees from the filtered data set exhibited substantial differences in fractional methylation (Figure 6). As there are only 14 DMLs in the unfiltered set, all of which are also found in the filtered set, we only visualized the data from the filtered analysis in Figure 6.

Table 3.

Differentially methylated CpGs (DMLs) between forager and nurse bees in the unfiltered and filtered data sets using RADMeth

Rank	Unfiltered data set					Filtered data set
	Location (scaffold:bp)	Log-ORa	Original-P	Combined-P	FDR q	Location (scaffold:bp)	Log-OR	Original-P	Combined-P	FDR q
1	Un.95:45 285	−1.56	0.025	4.22E-08	0.17	4.1:249 887	17.24	0.0015	1.12 $\times$ 10−9	0.00012
2	Un.95:45 286	−0.73	0.26	4.22E-08	0.17	4.1:249 888	16.20	0.0040	1.12 $\times$ 10−9	0.00012
3	Un.95:45 325	−1.66	0.047	9.52E-08	0.17	4.1:249 889	18.21	0.00068	1.12 $\times$ 10−9	0.00012
4	Un.95:45 326	−2.53	0.0093	9.52E-08	0.17	4.1:249 890	2.25	0.033	1.12 $\times$ 10−9	0.00012
5	Un.77:65 020	1.85	0.085	1.11E-07	0.17	4.1:249 905	−42.85	0.28	1.12 $\times$ 10−9	0.00012
6	Un.77:65 021	1.90	0.026	1.11E-07	0.17	4.1:249 940	0.84	0.48	4.47 $\times$ 10−9	0.00027
7	Un.77:65 063	1.04	0.13	1.11E-07	0.17	4.1:249 941	11.66	0.0023	4.47 $\times$ 10−9	0.00027
8	Un.77:65 064	2.63	0.0043	1.11E-07	0.17	4.1:249 956	0.91	0.45	4.47 $\times$ 10−9	0.00027
9	Un.77:65 081	10.95	0.011	1.11E-07	0.17	4.1:249 957	11.53	0.0014	4.47 $\times \mathrm{ }$10−9	0.00027
10	Un.77:65 082	12.90	0.0066	1.11E-07	0.17	Un.95:45 285	−1.56	0.026	4.22E-08	0.0021
11	Un.77:65 105	11.56	0.17	1.11E-07	0.17	Un.95:45 286	−0.73	0.26	4.22E-08	0.0021
12	Un.77:65 106	57.16	0.029	1.11E-07	0.17	Un.95:45 325	−1.66	0.047	9.52E-08	0.0029
13	12.16:628 752	−16.87	0.0080	1.44E-07	0.19	Un.95:45 326	−2.53	0.0093	9.52E-08	0.0029
14	12.16:628 753	−13.69	0.039	1.44E-07	0.19	Un.77:65 020	1.85	0.085	1.11E-07	0.0029
15	1.9:129 112	−0.84	0.12	3.08E-07	0.37	Un.77:65 021	1.90	0.026	1.11E-07	0.0029
16	12.16:628 812	−1.54	0.12	7.28E-07	0.76	Un.77:65 063	1.04	0.13	1.11E-07	0.0029
17	12.16:628 813	−0.85	0.49	7.28E-07	0.76	Un.77:65 064	2.63	0.0043	1.11E-07	0.0029
18	1.16:334 926	−0.66	0.30	7.89E-07	0.76	Un.77:65 081	10.95	0.011	1.11E-07	0.0029
19	1.16:334 927	0.62	0.39	7.89E-07	0.76	Un.77:65 082	12.90	0.0066	1.11E-07	0.0029
20	12.16:628 767	−14.58	0.0048	9.60E-07	0.76	Un.77:65 105	11.56	0.17	1.11E-07	0.0029
q $\le$ 0.05	0 (0)b					145 (22)
q $\le$ 0.10	0 (0)					299 (58)
q $\le$ 0.20	14 (3)					578 (113)

Note. Top 20 CpGs according to the q-values adjusted from combined P-values are shown. Note that the combined P-values are derived from the original P-values of the target site and its neighboring sites to increase the power to detect differential methylation [21]. The numbers of CpGs that are significantly differentially methylated for q-value thresholds of 0.05, 0.10 and 0.20 are shown. For only CpGs that failed in calculation of original-P, we used Fisher’s exact test result. In combining P-value step, we used a parameter of 1:100:100 for estimating correlations between adjacent CpGs.

^aOdds ratio of cytosine reads between forager and nurse groups.

^bNumbers in parenthesis indicate the number of significant DMRs.

Figure 6.

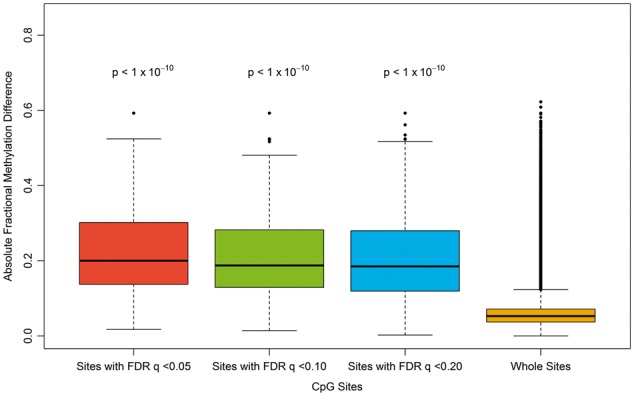
Boxplots of fractional methylation differences between forager and nurse honey bees. The first three are CpGs that were detected as differentially methylated between the two groups in the filtered data set (where globally unmethylated sites are removed). Compared with the rightmost one, which is drawn using whole sites in the filtered data set, they show highly significant differences (two-sample t-tests, P-values shown above each boxplot).

The difference in the results between the two data sets can be directly attributed to removing globally unmethylated sites. For example, the CpG at location 45 285 of scaffold Un.95 has the same P-value in both data sets, but different q-values (first row in Table 3). This is because of the fact that q-value is affected by the rank of combined P-values and the total number of hypotheses as well as the original P-values of adjacent CpGs. The total number of the CpGs, or the number of hypotheses to be tested, in ‘unfiltered’ data set is 33 times higher than that in the ‘filtered’ data set. Thus, even though the CpG at 129 112 of scaffold 1.9 (and other CpGs) have small combined P-values, their q-values are high. In addition, we detected new DMRs, for example between 249 887 and 249 957 of scaffold 4.1. In the ‘unfiltered’ data set, the combined P-values of this region were affected by globally unmethylated nearby CpGs with large P-values, thus leading to large q-values. In the filtered data set, the q-value of this region was 0.00012. These results demonstrate that removing globally unmethylated sites can significantly improve the efficiency of DML and DMR analyses.

We also performed a similar analysis using the human data set. In the human data set, the percent of globally unmethylated CpGs was only 7.4% (3 713 349 of 50 026 515). As expected, the numbers of DMLs and DMRs were also higher in the filtered data set compared with the unfiltered data set (Supplementary Table S2). However, the degree of improvement, as measured by the increase of DMLs, is small compared with that in the honey bee analysis, which experienced a 41-fold improvement in detected DMLs compared with just a 1.7-fold improvement in the human analysis.

Moreover, we also applied BiSeq to the filtered and unfiltered data sets to see if the removal process works well with predefined regions such as genes. We first identified honey bee CpGs located within mRNA coding regions only. This led to 90 364 CpGs in the filtered data set, and 3 096 291 CpGs in the unfiltered data set. After clustering adjacent CpGs, BiSeq calculates cluster-wise P-values, from which FDR-q-values are calculated (Table 4). As seen in Table 4, we found 13 CpG clusters in the filtered data set whose FDR q-values were <0.20. In contrast, no CpG clusters were detected in the unfiltered data set. The number of CpG clusters in the unfiltered data set was nine times greater than that in the filtered data set, which explained the difference in the power (Table 4). We also performed similar BiSeq analysis using the human data. We did not observe a difference in the number of significant DMRs between the filtered and unfiltered data sets (Supplementary Table S3).

Table 4.

Differentially methylated CpG clusters (DMRs) between forager and nurse bees in the unfiltered and filtered data sets using BiSeq

Rank	Unfiltered data set (Na =41 854)				Filtered data set (N=4606)
	Location (scaffold:start-end)	Methylation difference	Cluster-P	FDR q	Location (scaffold:start-end)	Methylation difference	Cluster-P	FDR q
1	11.8:11 370–11 393	0.121	2.45×10−6	0.41	11.8:11 370–11 393	0.142	3.22×10−5	0.079b
2	3.17:303 366–303 399	0.099	8.95×10−6	0.41	2.20:15 018–15 092	0.153	3.56×10−5	0.079b
3	2.20:14 953–15 092	0.035	1.06×10−5	0.41	6.11:242 720–242 765	0.077	7.70×10−5	0.12b
4	2.23:20 350–20 397	0.119	2.14×10−5	0.59	8.35:46 707–46 718	0.296	1.17×10−4	0.14b
5	6.37:24 719–24 792	0.066	2.44×10−5	0.59	5.23:24 001–24 062	0.181	1.40×10−4	0.14b
6	5.23:24 001–24 062	0.181	4.32×10−5	0.87	3.18:211 922–211 970	0.124	1.69×10−4	0.14b
7	1.38:14 704–14 832	0.006	8.98×10−5	1	Un.78:39 050–39 060	0.433	2.53×10−4	0.20b
8	3.18:211 922–211 970	0.062	9.61×10−5	1	8.1:286 401–286 446	0.114	3.27×10−4	0.20b
9	8.17:24 287–24 300	0.104	9.68×10−5	1	3.20:159 895–159 933	0.232	3.58×10−4	0.20b
10	Un.248:9781–9842	0.045	1.23×10−4	1	Un.167:44 251–44 275	0.253	4.09×10−4	0.20b
11	1.20:3859–3891	0.014	1.48×10−4	1	Un.248:9811–9842	0.138	4.22×10−4	0.20b
12	8.35:46 707–46 718	0.296	1.52×10−4	1	6.37:24 766–24 792	0.158	4.28×10−4	0.20b
13	8.16:405 220–405 229	0.100	2.15×10−4	1	10.40:104 750–104 800	0.275	4.45×10−4	0.20b
14	Un.78:39 050–39 060	0.433	2.29×10−4	1	3.20:160 474–160 525	0.148	6.10×10−4	0.23
15	8.16:402 067–402 101	0.065	3.06×10−4	1	11.5:35 894–35 925	0.082	6.12×10−4	0.23
16	7.27:36 394–36 461	0.098	3.36×10−4	1	8.17:24 287–24 300	0.104	6.45×10−4	0.23
17	Un.129:27 268–27 313	0.132	3.72×10−4	1	3.19:43 078–43 091	0.058	6.51×10−4	0.23
18	3.19:43 078–43 091	0.058	3.79×10−4	1	10.21:19 623–19 659	0.257	6.99×10−4	0.24
19	Un.167:44 251–44 275	0.253	5.06×10−4	1	8.16:405 220–405 229	0.100	7.23×10−4	0.24
20	4.13:106 236–106 257	0.027	5.22×10−4	1	7.27:36 394–35 461	0.098	8.10×10−4	0.25

Note. Top 20 CpGs clusters according to the q-values are shown. We used a minimum of 3 CpGs, a maximum gap of 50 bp for the clustering step and 80 bp window size for the smoothing step.

^aNumber of tested CpG clusters.

^bSignificant at FDR q $\le$ 0.20.

3. DML/DMR analyses using categorical classification of CpGs

Although most of the DML/DMR methods we consider here use discrete or continuous type of fractional methylation level, categorically converted methylation statuses have been also used in DML/DMR analyses [54, 69]. In general, using continuous or discrete type of fractional methylation level is more advantageous than using categorically converted fractional methylation levels because the former can represent methylation differences in more detail. However, categorical classification may be also appropriate in some cases, for example, when the overall methylation level is low and researchers are interested in the methylation status of a site rather than its methylation level.

Currently available tools in this regard typically classify each site as ‘methylated’ or ‘not methylated’. This binary classification of methylation status can best explain the original state of methylation level when it follows a bimodal pattern (Figure 2B). However, in some species, many sites are partially or intermediately methylated [53–55]. For example, many CpGs in the honey bee data are partially methylated (Figure 2A). Therefore, when we apply categorical approaches using a two-class classification (unmethylated and methylated) to the honey bee data, it will result in a loss of information. We thus propose that partially methylated CpGs need to be regarded as a separate group from the fully methylated CpGs to use more information from the data. Among the methods we discuss in Table 1, HMM-Fisher [27] can be used to classify sites into unmethylated, partially methylated or fully methylated categories. The idea of categorizing CpGs based on more than two classes has been previously proposed [79], although the criteria for classification was based on raw fractional methylation without consideration for adjacent CpG methylation. HMM-Fisher’s smoothing method [27] is able to incorporate neighboring CpG methylation information, allowing it to use low coverage sites that are discarded in the previous method.

Classifying to more than two methylation statuses reflects more realistic methylation states, and also improves the significance of DMR tests when applied to genomic regions whose composition of partially and fully methylated information is unequal between biological groups (Figure 7). In the region shown in Figure 7, the fractional methylation levels of many CpGs in forager bees are higher than those in nurse bees. Therefore, a two-class classification (unmethylated and methylated) classified all of them as methylated in forager samples and fails to detect any difference between the two groups, even though there was a true difference of means. The P-value from the two-class classification was 0.16 compared with 0.0051 from the three-class classification. Indeed, there was a greater relative proportion of CpGs classified as ‘partially methylated’ from the honey bee data than from the human data (Table 5).

Figure 7.

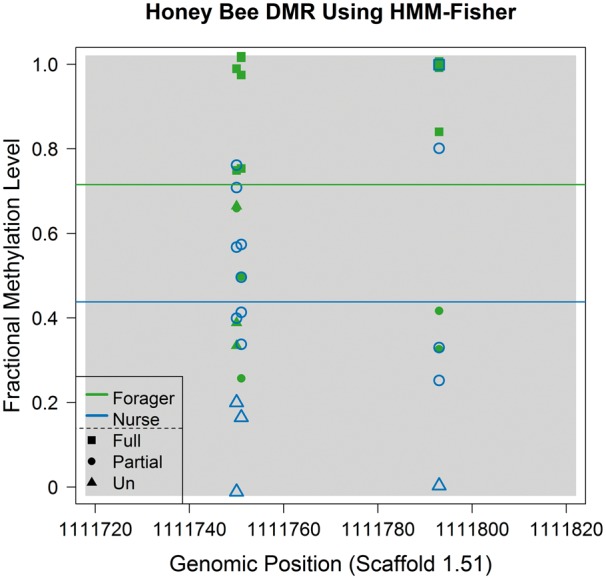
Plot of fractional methylation levels and their classification results within a DMR. Values from the forager and nurse bees are shown in green and blue. When we used a two-class classification (dividing methylated and unmethylated sites), P-values for differential DNA methylation (by Fisher’s exact test) was 0.16. In contrast, when a three-class classification (methylated, partially methylated and unmethylated: shown as squares, circles and triangles) was used, the P-value for the same region was 0.0051. Considering that the actual mean fractional methylation level difference between the two groups is 0.28, a three-class classification analysis appears more suitable.

Table 5.

Classification result of honey bee (group 1) and human (chr 22) data set by HMM-Fisher

		Proportion of methylation state			Classification results(number of DMLs)
Species	Condition	Un	Partial	Full	Two class	Three class
Honey bee	Forager	0.9955	0.0018	0.0027	209	371
	Nurse	0.9954	0.0018	0.0028
Human	Young	0.1171	0.1287	0.7542	2082	7049
	Old	0.1452	0.1131	0.7417

Note. The numbers of CpGs for each class of methylation state are shown. In addition, the numbers of DMLs from two- and three-class classification analyses are shown. DMLs were detected using P$\le$0.05.

Interestingly, the increase of DMLs detected between the two- and three-class classifications was also evident in the human data set (Table 5), suggesting that applying three-class classification is also useful for the analysis of human data sets. When we calculated AUCs between P-value of the HMM-Fisher method and binary status of methylation differences, AUC values also increased in both data sets (Supplementary Table S4). Furthermore, instead of a Fisher’s exact test, we can also apply a Cochran-Armitage [80] or Cochran-mantel-Haenztel test [81] by imposing ordinal weights such as 0, 1 and 2 to the unmethylated, partially methylated and fully methylated CpGs. Doing so may provide more significant results when the numbers of CpGs in each category linearly increases or decreases.

Aligner effect

As the honey bee data set was aligned with BSMAP and the human data set with bowtie in the literature, different aligners could have affected the observed methylation differences [82]. To determine whether our conclusions were robust when a different alignment program was used, we re-aligned our human data with BSMAP. We then conducted an empirical study to compare the newly aligned and the original human data to see the effects of using a different aligner. For the purpose of this comparison, we only focused on chromosome 22 of the human data, and repeated the same analyses. These results are summarized in supplementary figures and tables (Supplementary Figure S1–S3 and Supplementary Table S5–S7) according to each of our recommendations. In summary, our empirical study showed that the analysis of the newly aligned human data using BSMAP did not change our original conclusions for the three recommendations, although slight differences were observed.

Conclusions

In this study, we summarized current statistical tools to detect DMLs and DMRs from bisulfite sequencing data, and investigated crucial points that need to be considered when they are applied to data from invertebrates. Specifically, we focused on several distinct properties that are unique to invertebrate data when compared with mammalian data. These properties include narrow and fluctuating methylation patterns, extremely low proportion of methylated CpGs throughout the genome and the existence of many partially methylated CpGs. We developed our arguments based on these properties, and drew corresponding conclusions supported by data analysis. We recommend using small window sizes for smoothing, removing globally unmethylated CpG sites before DML/DMR analyses and applying a more specific categorical classification method. These considerations should be applicable to a variety of species that share similar methylation characteristics with invertebrate genomes.

Key Points

• Sequencing of bisulfite-converted genomic DNA is an important tool for the study of DNA methylation because it enables estimation of DNA methylation at single-nucleotide resolution. Hence, it is becoming popular.

• Sequencing of bisulfite-converted genomic DNA has been particularly useful for DNA methylation analyses of invertebrate animals, which are non-traditionally studied organisms for epigenetics.

• Many statistical tools have been developed to efficiently and accurately estimate DNA methylation from sequencing of bisulfite-converted genomic DNA.

• Key steps of currently available statistical tools for the analyses of sequencing of bisulfite-converted DNA are discussed.

• Practical guidelines for using currently available tools for DNA methylation analyses of invertebrates are provided with specific recommendations.

Iksoo Huh is a postdoctoral research scholar in the School of Biological Sciences at the Georgia Institute of Technology. He is a biostatistician currently focusing on epigenomic analysis.

Xin Wu is a graduate student in the School of Biological Sciences at the Georgia Institute of Technology. His current research is on epigenetic variation between different strains of insects.

Taesung Park is a professor in the Department of Statistics at Seoul National University. He is a biostatistician with over three decades of experience in tool development and data analyses.

Soojin V. Yi is a professor in the School of Biological Sciences at the Georgia Institute of Technology. Her research focuses on bioinformatics, genomics and epigenomics.