A comparative study of rank aggregation methods for partial and top ranked lists in genomic applications

Abstract

Rank aggregation (RA), the process of combining multiple ranked lists into a single ranking, has played an important role in integrating information from individual genomic studies that address the same biological question. In previous research, attention has been focused on aggregating full lists. However, partial and/or top ranked lists are prevalent because of the great heterogeneity of genomic studies and limited resources for follow-up investigation. To be able to handle such lists, some ad hoc adjustments have been suggested in the past, but how RA methods perform on them (after the adjustments) has never been fully evaluated. In this article, a systematic framework is proposed to define different situations that may occur based on the nature of individually ranked lists. A comprehensive simulation study is conducted to examine the performance characteristics of a collection of existing RA methods that are suitable for genomic applications under various settings simulated to mimic practical situations. A non-small cell lung cancer data example is provided for further comparison. Based on our numerical results, general guidelines about which methods perform the best/worst, and under what conditions, are provided. Also, we discuss key factors that substantially affect the performance of the different methods.

Introduction

The problem of rank aggregation (RA) is to combine multiple ranked lists, referred to as ‘base rankers’ [1], into one single ranked list, referred to as an ‘aggregated ranker’, which is intended to be more reliable than the base rankers. It has a rich history in the fields of information retrieval, marketing and advertisement research, applied psychology, social choice (political election), etc. In recent years, with the rapid development of technology, RA has been facing new challenges in areas like meta-search engine building for Web page ranking and the identification of ‘signal genes’ in high-throughput genomic studies, the latter of which is the main focus of this article.

For an important biological question, it is often the case that a large amount of genomic data from different laboratories or research groups has been collected over time. Such data are inherently noisy because of various sources of heterogeneity, which include, among others, different experimental designs, various platforms as well as (completely) different data preprocessing procedures, causing nonuniform inclusion of genes, different types of omics data, unequal sample sizes and possible inclusion of non-informative and noisy data. To integrate such data, researchers often take robust meta-analytic approaches based on ranked lists [1–6], without going all the way back to modeling the raw data, to arrive at more reliable conclusions as well as enhance the validity and reproducibility of individual studies [2]. For many such approaches, one main task is to conduct RA.

In the literature, various RA methods have been developed for particular applications; however, they are often ill-suited for other applications. In addition, most methods are not clear about which situations they can deal with. Several claim to work for partial or top ranked lists; however, the concepts of such lists are somewhat ambiguous. There exist several publications that summarize and compare existing aggregation methods [1, 3, 7–9]. Lin [3] provides an elaborate review of existing methods and serves as a good introduction to the RA topic; however, it compares different methods only through a data example, and so lacks a formal evaluation via simulation where the ground truth is known. Wald et al. [7] and Dittman et al. [8] compare several RA methods specifically for ensemble gene selection, the process of aggregating multiple feature selection runs into a final ranked list, and it is also based on data examples only. Boulesteix and Slawski [9] promote the use of RA to achieve stability of rankings when different ranking criteria are used on the same data set or when the input data set is slightly modified via perturbation (e.g. resampling and permutation), and they discuss the strengths and limitations of several RA methods under this context. Deng et al. [1] gives an informative overview on existing methods in addition to proposing a new Bayesian aggregation method. A relatively complete simulation study is also provided, but it omits situations where some of the items of interest are not included in some base rankers (resulting in partial lists). Also, the length of the lists considered (200) may not be adequate, especially for genomic settings, where it varies widely from list to list and can be up to a few thousands or even more than ten thousands.

In this article, we develop a systematic way of classifying RA methods, set up a clear framework for different situations that can occur frequently in genomic settings, discuss important practical considerations, compare the performance of up-to-date methods emphasizing those suitable for genomic applications via simulation and a data example and provide practical guidelines for users as well as point out directions of future research. For a list of important notation used in this article, see Section S1 in Supplementary Material.

Categorization of RA methods

Recent efforts to classify RA methods include Lin [3] and Deng et al. [1]. Lin [3] divides existing methods into three categories: distributional-based, heuristic and stochastic optimization algorithms, and provides a detailed overview of the methods falling in each category. Deng et al. [1] present a review based on a different categorization (i.e. methods based on summary statistics, based on optimization/Markov chains, based on weighted lists and via boosting). However, novel aggregation methods are constantly being proposed [1, 10, 11]. Below, we provide a systematic and updated classification, mainly based on differences in the methodologies used, of which a diagram is given in Figure 1.

Figure 1.

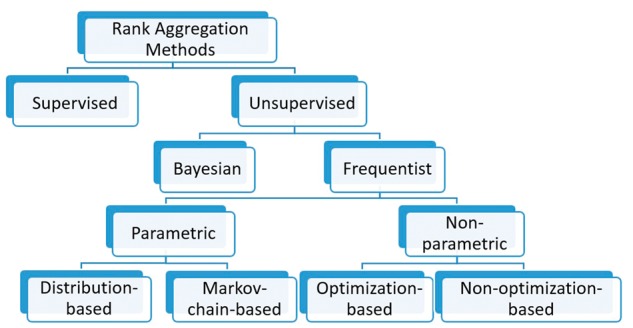
A classification diagram of RA methods.

In general, RA methods can be divided into two categories: supervised versus unsupervised methods. Supervised methods such as supervised rank aggregation (SRA) by Liu et al. [12] and RankBoost by Freund et al. [13] make use of training data sets containing true relative ranks of some items via supervised learning algorithms. Liu et al. [12] sets up a general framework to conduct SRA that corresponds to existing methods like Borda’s method [14] and Markov chain methods [15, 16] with a focus on the latter. RankBoost uses boosting, a machine learning method, to iteratively update a series of ‘weak rankers’ and finally use their weighted average as the aggregated ranker.

As no labeled data are available in most applications, unsupervised RA has been dominant in the literature. Below, we focus on unsupervised methods, which can be first grouped into Bayesian and frequentist methods. Performance evaluation will be done in ‘Performance evaluation’ and ‘Data example’ sections for unsupervised methods only.

Bayesian methods

In general, Bayesian methods rely on certain quantities involved in posterior inference (e.g. posterior probability, Bayes factor) to determine the aggregated ranking. Some Bayesian applications in RA are problem-specific. For example, [17] and [18] use Bayesian approaches to analyze rank data arising from primate intelligence experiments and to interpret review scores from peer assessments, respectively, and so they will not be considered in our performance evaluation. Other Bayesian methods, including Bayesian Aggregation of Rank Data (BARD) by Deng et al. [1] and Bayesian Iterative Robust Rank Aggregation (BIRRA) by Badgeley, Sealfon and Chikina [11], are applicable to general RA problems. BARD uses a Bayesian model selection formulation and associates a quality parameter to each base ranker to quantify the reliability of that ranker. It assigns entities into two groups: relevant and irrelevant, and ignores the actual rankings. For each base ranker, the relative ranks of all irrelevant items are assumed to be purely random, and that of a relevant item is assumed to follow a power law distribution. The posterior probability of each item being relevant is used to obtain the aggregated ranker. BIRRA starts with the mean ranks to obtain an initial aggregate ranking and assign top ranked items to be relevant and the rest to be irrelevant based on their prior probabilities. The data set is then discretized into multiple bins. The algorithm iteratively computes bin-wise Bayes factors for each base ranker and calculates the posterior probability of each item being relevant via the Bayes theorem to update the ranks until rankings are unchanged or a prespecified maximum number of iterations has been reached. Additionally, several heuristic techniques are used in BIRRA to make it more robust to noise. Yi, Li and Liu [19] propose a Bayesian model for Aggregating Rank data with Covariates (BARC) and its weighted version, BARCW, to incorporate covariates information and to distinguish high-quality rankers from spam rankers. Further detail of BARC is omitted as we focus on the more general case that has no covariates.

Frequentist methods

Although Bayesian methods have become increasingly popular, the majority of RA methods are frequentist, which can be classified into parametric and nonparametric methods. In this article, ‘nonparametric’ means no use of any underlying data model or other distributional information. Depending on whether a method aims to optimize a certain criterion, nonparametric methods can be grouped into non-optimization-based and optimization-based methods. In contrast, parametric methods are based on some underlying models or distributions, and can be further divided into distribution-based and Markov chain-based methods.

Non-optimization-based methods

Some of the earliest aggregation methods, including those in Borda’s collection [3, 14], simply use summary statistics such as the arithmetic mean, median, geometric mean and L2-norm of base rankers to aggregate rank data, denoted as MEAN, MED, GEO and L2, respectively. More recently proposed non-optimization methods include Stability Selection [20] and Round Robin methods [21]. The idea of Stability Selection is to rank an item higher if it is ranked high in many base rankers according to a chosen threshold. Round Robin assigns ranks through a simple and random manner: first randomly order base rankers and then assign the highest rank to the item that is ranked at the top from the first ranker, assign the second highest rank to the item that is ranked at the top from the second ranker and proceed in this way to the second top ranked items from every base ranker and so on until every item receives a rank. Although intuitive and easy to compute, these two ad hoc methods will not be considered for performance evaluation because they are much less known compared with Borda’s methods.

Optimization-based methods

Optimization-based methods have a long history dating back to 1950s [22–24]. They are designed to minimize some distance measure, so that the aggregated ranker is as close as possible to all base rankers. Two commonly used measures are Kendall’s tau and Spearman’s footrule distances, of which the first counts the number of pairwise disagreements between two rank lists, and the second sums up the absolute value of the element-wise differences in ranks between the two lists. The main distinction between the distance measures is that Kendall’s tau only accounts for discordant pairs, while Spearman’s footrule accounts for the magnitude of the rank differences. Lin and Ding [2] adopt the cross-entropy Monte Carlo (CEMC) approach to RA from the context of rare event simulation and combinatorial optimization [25] by proposing the Order Explicit Algorithm. The optimization criteria they use with CEMC are based on the generalized Kemeny guideline [1, 3], which uses either the weighed Kendall’s tau or Spearman’s footrule distance. The corresponding CEMC methods for RA, denoted by CEMC.k and CEMC.s, use importance sampling to iteratively search for the list that minimizes the overall distance.

When initially proposed, optimization-based methods were computationally formidable even with moderate-size data. With the availability of modern computational power, they have become more feasible. However, they typically need a much longer time to run than other methods, especially for relatively long lists that occur in genomic settings.

Distribution-based methods

A method is categorized as distribution-based if it assumes a probabilistic latent model or uses distributional information of any statistic calculated from the rank data. Thurstone’s model/Thurstone’s scaling is one of the earliest distribution-based RA methods and was proposed in a series of papers by Thurstone dating back to the 1920s [26–29]. It was originally proposed for applications in psychology and sociology, but many efforts were made to extend it to other applications. Thurstone’s model often requires many base rankers to estimate parameters. This is generally not the case for genomic studies; therefore, it will not be included in our performance evaluation.

Stuart [30] proposes an RA method to identify pairs of genes that are co-expressed from experiments in multiple organisms. Pairs of genes whose expression is significantly correlated in multiple organisms are identified and then ranked according to Pearson correlation. P-values are calculated based on distributions of order statistics. An improved version of Stuart’s method is later given by Aerts et al. [31].

Robust rank aggregation (RRA) by Kolde et al. [10] is another example of distribution-based methods. The position of an item in each ranked list is compared with a null model, where all the lists are non-informative, i.e. random shuffles of the items. A numerical score is assigned to each item based on the reference distributions of order statistics, i.e. beta distributions. P-values are computed based on the Bonferroni correction of the numerical scores to avoid intensive computation required to obtain exact P-values. The final aggregated rank is obtained by sorting P-values.

Markov chain-based methods

These methods are developed under a Markov chain modeling framework, where the union of items from all base rankers forms the state space. A transition matrix is then constructed in a way such that its stationary distribution will have larger probabilities for states that are ranked higher. Therefore, the aggregate ranker is determined by the stationary probability of each state. A few ways of constructing the transition matrix have been proposed [15, 16]. MC1–MC3, as denoted in Lin [3], are three examples, which will be included in our performance evaluation.

MC1: The next state is generated uniformly from the set of all states that are ranked at least as high as the current state by at least one base ranker.

MC2: The next state is generated uniformly from the set of all states that are ranked at least as high as the current state by at least half of base rankers.

MC3: The probability of moving to a certain state is proportional to the number of base rankers that rank this state higher than the current state.

Practical considerations

We cover several key issues about RA, including various types of ranked lists that practitioners may encounter frequently (especially in genomic studies), their connections with the knowledge status of the space of a base ranker, preferred data structures of different methods, software availability, data input formats and measures used for evaluating the performance of RA methods.

Characterization of various types of lists

Suppose, there are J ranked lists (or base rankers) to be aggregated. For each list j, let ${\mathcal{T}}_j$ denote the set of the top k_j items, where the rank of each item is reported, and let ${\mathcal{B}}_j$ denote the set of items that are known to be ranked lower than any item in ${\mathcal{T}}_j$, but the specific rank of each item is unknown, and these items can be thought of as those ranked at the bottom as ties. Further, let ${\mathcal{I}}_j$ denote the set of items input by list j, satisfying ${\mathcal{I}}_j={\mathcal{T}}_j\cup {\mathcal{B}}_j$. It would be reasonable to assume that ${\mathcal{I}}_j$ is the set of all items known to be investigated by (base) ranker j, so that list j contains the maximum amount of information that is available from ranker j. Here, saying an item is investigated means that it is considered in the ranking process of a base ranker.

Now, let $\mathcal{I}=\underset{j=1}{\overset{\mathrm{\hspace{0.17em}J}}{\cup }}{\mathcal{I}}_j$ be the complete set of items of interest in the RA problem, that is any item that does not have any available ranking information from all the J input lists is automatically not considered. Every item $i\in \mathcal{I}$ can be categorized into four disjoint groups with respect to ranker j: the first two are ${\mathcal{T}}_j$ (top ranked items) and ${\mathcal{B}}_j$ (bottom ties); the third is ${\mathcal{N}}_j$, the set of items known to be not investigated by ranker j because of reasons like missing laboratory measurements or removals in steps of preprocessing raw data, and their ranking information is represented by ‘NA’, and the last is ${\mathcal{Q}}_j$, the set of items that have either state: (i) not investigated in ranker j; or (ii) ranked at the bottom as ties, but which of the two states the items belong to is unknown; therefore, their ranking information is represented by ‘?’. We further define ${\mathcal{S}}_j$ to be the set of items in $\mathcal{I}$ that are originally investigated by ranker j. We refer to ${\mathcal{S}}_j$ as the space of ranker j relevant to $\mathcal{I}$, the space of the RA problem. A visualization of these sets is provided in Figure 2.

Figure 2.

Four different states that an item can belong to in list j.

Note that ${\mathcal{I}}_j$ is always known from the ranked list j, but ${\mathcal{S}}_j$ can be unknown. Clearly, $\mathcal{I}={\mathcal{T}}_j\cup {\mathcal{B}}_j\cup {\mathcal{N}}_j\cup {\mathcal{Q}}_j$, ${\mathcal{I}}_j\subseteq {\mathcal{S}}_j$ and ${\mathcal{N}}_j\cap {\mathcal{S}}_j=\varnothing$ for all $j=1,\dots ,J$.

Below, we define various types of lists that often occur in practice:

• A locally full list (say j) satisfies ${\mathcal{T}}_j={\mathcal{I}}_j={\mathcal{S}}_j$, that is every item investigated by ranker j is explicitly ranked (exact ranking is known) in list j, so that ${\mathcal{B}}_j={\mathcal{Q}}_j=\varnothing$.

• A globally full list j satisfies ${\mathcal{T}}_j=\mathcal{I}$, meaning that every item in $\mathcal{I}$ is explicitly ranked by ranker j, so that ${\mathcal{B}}_j={\mathcal{N}}_j={\mathcal{Q}}_j=\varnothing$. Clearly, a globally full list is a special case of a locally full list. For RA problems, ideally, all of the base rankers give globally full lists. However, that is often not the case in genomic studies.

• A top-k list j is the opposite of a locally full list, satisfying ${\mathcal{B}}_j\cup {\mathcal{Q}}_j\ne \varnothing$, meaning that some items in this list are bottom ties or have unknown states. Obviously, $k_j<\left|{\mathcal{S}}_j\right|$.

• A special case of a top-k list is a top-k only list, which has only the top k_j items ranked explicitly and the ranking information about any other item in $\mathcal{I}$ is ‘?’. Here, ${\mathcal{B}}_j=\varnothing$ and ${\mathcal{Q}}_j=\mathcal{I}-{\mathcal{T}}_j\ne \varnothing$.

• A partial/incomplete list j satisfies ${\mathcal{I}}_j\subset \mathcal{I}$, that is ${\mathcal{N}}_j\cup {\mathcal{Q}}_j\ne \varnothing$, meaning that some items in the list of all items of interest are either ‘NA’ or ‘?’.

Depending on whether the underlying space ${\mathcal{S}}_j$ is known, there exist two scenarios, A and B, for a base ranker. In Scenario A, ${\mathcal{S}}_j$ is known, so that ${\mathcal{S}}_j={\mathcal{I}}_j$ and ${\mathcal{Q}}_j=\varnothing$, and in Scenario B, ${\mathcal{S}}_j$ is unknown, so that ${\mathcal{Q}}_j\ne \varnothing$. Obviously, a locally full list belongs to Scenario A, and a top-k only list belongs to Scenario B. Also, any list under Scenario B must be a partial and top-k list. Further, under Scenario A, we have the following results: (i) for a partial/incomplete list, ${\mathcal{N}}_j\ne \varnothing$; (ii) for a top-k list, ${\mathcal{B}}_j\ne \varnothing$; (iii) for a top-k and partial list, ${\mathcal{N}}_j\ne \varnothing$ and ${\mathcal{B}}_j\ne \varnothing$; and (iv) for a locally full but partial list, i.e. not globally full, ${\mathcal{N}}_j\ne \varnothing$ and ${\mathcal{B}}_j=\varnothing$. In genomic applications, an example of a top-k list that falls into Scenario A is when the top-k genes associated with a certain disease are published in a paper but the data analyzed can be found in some public database; therefore, ${\mathcal{S}}_j$ can be recovered and there are bottom ties $({\mathcal{B}}_j\ne \varnothing$); an example of a top-k list that falls into Scenario B is when a paper reports a top-k only list as well as a subset of the items originally studied without their individual rankings, such as the set of deferentially expressed genes; therefore, there are items known to be in the space of this base ranker and not ranked in the top k (${\mathcal{B}}_j\ne \varnothing$) as well as items that appeared in other ranked lists whose status with respect to ranker j is unknown (${\mathcal{Q}}_j\ne \varnothing$).

Most of the existing methods are not clear about which of the above situations they can handle. To the authors’ knowledge, methods in [2, 10, 15, 16, 30, 32] are the only ones that explicitly state that they are able to deal with lists that are not globally full. The most common way that these methods deal with such lists is to simply replace all of the missing ranks with the maximum rank in each list plus one (k_j + 1) without distinguishing the status of the corresponding items as elements of either ${\mathcal{B}}_j,\hspace{0.17em}{\mathcal{N}}_j$, or ${\mathcal{Q}}_j$. This modification can also be applied to other RA methods that are designed for globally full lists, so that they can handle non-globally full lists as well. However, this modification may not be the best strategy in some situations, as it ignores the exact status of these items as mentioned above. For Scenario A, a better modification could be to use k_j + 1 as the rank for items in ${\mathcal{B}}_j$, and NA for items in ${\mathcal{N}}_j$, so that the method can handle the two types of items differently. For Scenario B, k_j + 1 could still be used as the rank for items in ${\mathcal{B}}_j$, but either k_j + 1 or NA could be preferred for ${\mathcal{Q}}_j$ depending on the situation.

Preferred data structures

As mentioned in the introduction, RA has been applied widely in various fields. Fields such as genomic studies and meta-search tend to generate ‘a few long ranked lists’, while fields such as marketing and sociology tend to generate ‘many short ranked lists’. Such inherent characteristics of the data available from specific fields make certain methods become more appropriate than others. Methods such as Markov chain methods, CEMC methods, RRA, Stuart, BARD and BIRRA are developed specifically under the settings of genomic experiments or meta-search engine building; therefore, they are expected to perform better for ‘a few long lists’. Methods like Thurstone’s models, paired comparison models and multistage models require ‘many short lists’ to work well [3, 16]. Also, methods like Borda’s have been shown to work reasonably well for both data structures.

Implementation

Software availability

Whether there is any software package or program readily available for implementing a RA method is an important consideration for practitioners. R packages ‘TopKLists’ and ‘RobustRankAggreg’, cover many methods mentioned in ‘Categorization of RA methods’ section, as summarized in Table 1. These two packages will be used in our performance evaluation. Note that they implement Borda’s methods in different ways, as will be discussed in ‘Performance evaluation’ section. In addition, BARD and BIRRA have accessible programs for implementation in C ++ and R, respectively, and more information about the source code can be found in [1] and [11].

Table 1.

RA methods implemented in R packages

R package	RA methods implemented
TopKLists	MEAN, MED, GEO, L2, MC1-MC3, CEMC.k, CEMC.s
RobustRankAggreg	MEAN, MED, GEO, RRA, Stuart

Input data format

There are two ways of arranging rank data. The first is item-based, where each row represents an item (say i), each column represents a study (say j) and the (i, j)th cell displays the rank of item i in study j. The second is rank-based, where each row is a particular rank (say i), each column represents a study (say j) and the (i, j)th cell displays the item that receives rank i in study j. An example is given to illustrate each format in Table 2.

Table 2.

Two data formats; capital letters denote items and numbers denote their ranks

	Study 1	Study 2	Study 3	Study 4
Item-based format
A	1	2	4	2
B	3	3	2	3
C	2	1	1	4
D	4	4	3	1
Rank-based format
1	A	C	C	D
2	C	A	B	A
3	B	B	D	B
4	D	D	A	C

The item-based format can better accommodate different real situations presented in ‘Characterization of various types of lists’ section than the rank-based format. For example, suppose that in Study 1, B and D are tied with the lowest rank. With the item-based format, an equal rank (3 or 3.5) can be assigned to both; however, with the rank-based format, one has to randomly break the tie to enforce the exact ranks. Also, unlike the item-based format, the ranked-based format cannot handle items that have the ‘?’ status.

Some RA implementations (e.g. algorithms in ‘RobustRankAggreg’ and BARD’s C ++ program) work with both types of input format, while other implementations (e.g. algorithms in ‘TopKLists’) only work with one format or the other. In fact, if rank-based format input is supplied to algorithms in ‘RobustRankAggreg’, the data are converted into the item-based format before applying the RA methods.

Performance evaluation measures

One main task in many genomic studies is to identify genes that are associated with some complex human disease. With that in mind, a good measure to evaluate the performance of RA methods should assess each method’s ability to rank relevant genes accurately. Suppose only a limited amount of resources are available to further investigate the genes originally studied, then the ordering of genes ranked at the top of the list is crucial, whereas the ordering of genes that are ranked close to the bottom is almost irrelevant. In other words, rather than considering measures that can only evaluate the entire aggregated list like AUC (area under the receiver operating characteristic curve), we are more interested in measures that are feasible in evaluating the top-ranked portion of the aggregated list. Such measures include Spearman’s correlation (Pearson correlation applied to the rankings instead of the actual values of two lists), Kendall’s correlation (the ratio of number of concordant pairs minus discordant pairs to total number of pairs), Spearman’s footrule distance, Kendall’s tau distance and coverage rate (percentage of relevant genes covered by the subset of top-ranked genes in the aggregated list). One advantage of the correlation measures and coverage rate over the distance measures is that they fall into fixed ranges: Spearman’s and Kendall’s correlations both take on values in $[-1,1]$, and the coverage rate takes on values in $[0,1]$. Note that Spearman’s footrule and Kendall’s tau distances, as defined in ‘Frequentist methods’ section, are designed for full lists. In Lin [33], these distance measures are modified to be applicable to top-k lists.

The correlation and modified distance measures may be misleading in some situations. To illustrate this, we present a hypothetical example. Suppose 1000 genes are considered by three studies and three genes labeled as Gene 1 to Gene 3 represent the ‘signal’. In other words, it is only of interest to correctly identify these three genes by having them ranked highly in an aggregated rank list. The true rank and three aggregated ranks (A1–A3) of Gene 1 to Gene 3 are listed in Table 3. If either Spearman or Kendall correlation is used to compare the aggregated ranks, one would conclude A2 performs better than A3 which performs better than A1, which is clearly not the case. If Spearman’s footrule distance is used, then one would conclude that A1 performs better than A2, which is correct; however, A2 would be deemed better than A3, which is not necessarily desirable. Similarly, if Kendall’s tau distance is used, one would arrive at the wrong conclusion that A2 performs better than A3, which performs better than A1. However, if one uses coverage rates with two specific cutoffs (3 and 10), the conclusions are more reasonable. Clearly, A1 has the best performance, and the coverage rates using either cutoff correctly identify this. Comparing A2 and A3 is more difficult as the better performing one varies with the choice of the cutoff, which usually depends on the resources available. Therefore, in our performance evaluation, coverage rates with different cutoffs will be used.

Table 3.

Examples where correlation and distance measures are misleading

	True rank	A1	A2	A3
Gene 1	1	3	8	2
Gene 2	2	2	9	21
Gene 3	3	1	10	1
Spearman correlation	–	−1	1	−0.5
Kendall correlation	–	−1	1	−0.33
Spearman distance	–	4	21	22
Kendall distance	–	999	0	666
Coverage rate with top 3	–	1	0	0.67
Coverage rate with top10	–	1	1	0.67

We note that there exist applications where the complete ranking of items is of interest, e.g. combining people’s rankings on general knowledge such as ranking the 44 US presidents in a chronological order [34] and people’s preference on 10 types of sushi [35]. In such situations, global measures such as correlations and distances are useful.

Performance evaluation

We conduct several sets of simulation studies to evaluate the performance of RA methods commonly used in genomic applications. Each method is tested under various settings. Methods compared include: four non-optimization-based methods, MEAN, MED, GEO and L2, all from Borda’s collection; two optimization-based methods, CEMC.s and CEMC.k; two distribution-based methods, RRA and Stuart; three Markov chain-based methods, MC1–MC3; and two Bayesian methods, BARD and BIRRA. As mentioned in ‘Implementation’ section, R packages ‘TopKLists’ and ‘RobustRankAggreg’ have different implementations for MEAN, MED and GEO, and so we add a lower case letter in front of these methods to indicate which package is used for implementation: ‘r’ for ‘RobustRankAggreg’ and ‘t’ for ‘TopKLists’. Specifically, ‘RobustRankAggreg’ uses the normalized rank for all the methods implemented. For MEAN, it assigns P-values for each mean rank whose distribution is asymptotically normal. ‘TopKLists’ preprocesses the input data set, primarily incorporating information about the space of a base ranker (if available) and replacing missing ranks with the maximum rank plus one.

For each of these methods, the default setting is used in our evaluation. For example, for MC and CEMC methods, we use the default stopping criteria, and for BARD, we use the default number of Gibbs steps, etc. Two models based on different data-generating mechanisms are used to evaluate the methods. Model I is based on a popular setup used in previous papers [10, 11], where the underlying truth of a gene is dichotomous, i.e. either relevant or not. Model II is based on a latent variable setup that allows for varying quality of base rankers, where the latent variables are continuous, measuring the global importance of genes involved. For each mechanism, different types of ranked lists under Scenarios A and B, as outlined in ‘Characterization of various types of lists’ section, are examined. All simulation results are based on 1000 replications.

Besides having high coverage rates, a desirable RA method should be able to work with long input lists (a few thousands or more) within a reasonable amount of time. Therefore, another simulation is conducted to evaluate the computing time of different methods, as we increase the length of input lists.

Simulation under model I

Let $\mathcal{I}=\{1,\dots I\}$ (I = 1000) denote the set of genes of interest, and $J=J_1+J_2$ ($J_1=5,J_2=0,5$) denote the number of base rankers to be aggregated, where J₁ represents the number of reliable rankers, which contain signals, and J₂ represents the number of unreliable rankers, which do not contain any signal, i.e. pure noise. Signal rates γ (i.e. the proportion of signal genes in $\mathcal{I}$) of 0.01 and 0.05 are examined. For signal genes, we draw values from either N(1, 1) or Exponential(1) for reliable studies, and from N(0, 1) for unreliable studies. For non-signal genes, we draw values from N(0, 1). Observed gene ranking in each study is determined by sorting these generated values. Note that under Model I, a true ranking is not available because the underlying status of each gene is either signal or non-signal. As mentioned in ‘Characterization of various types of lists’ section, it is common for studies to provide only exact ranks for the top-ranked genes, and the parameter p_T ($p_T=0.01,0.05,0.1,0.2,1$) is used to control the proportion of top ranked genes. When $p_T=1,$ the base ranker gives a locally full list, otherwise a top-k list. Finally, an inclusion rate λ ($\lambda =0.6,0.8,1$) is used to control the chance that each gene is investigated by each base ranker. When $\lambda \ne 1,$ the base ranker gives a partial list. When $p_T=\lambda =1,$ the base ranker gives a globally full list. Note in practice p_T and λ could be different across base rankers.

When p_T≠1, base rankers are generated under Scenarios A and B, respectively. For Scenario A, top-k lists are generated, where bottom ranked genes are set as ties; for Scenario B, top-k only lists are generated by omitting bottom-ranked genes. To better separate the effect of these parameters, the same values of (λ, p_T) are used across all base rankers first, referred to as the fixed settings. Additionally, to assess the effect of each design parameter individually, all other parameters are held constant. The setting where p_T = 0.2, $\lambda =0.8,\hspace{0.17em}{J}_2=0,\hspace{0.17em}\gamma =0.05$ and signal genes are generated from N(1, 1) is selected as the controlled setting, denoted as C^A∕B for Scenarios A/B. When assessing the effect of the proportion of top ranked genes p_T, p_T varies, while other parameters are fixed as in the controlled setting, and these settings are denoted using the notation of the form $P_{p_T}^{A/B},$ for example $P_{0.1}^A$ represents the setting where p_T = 0.1 under Scenario A. Similarly, when assessing the effect of the inclusion rate λ, all other parameters are fixed as in the controlled setting, and the notation of the form $L_{\lambda }^{A/B}$ is used for these settings. Here, $C^{A/B},\hspace{0.17em}{L}_{0.8}^{A/B}$ and $P_{0.2}^{A/B}$ all represent the controlled setting, and we consistently use $C^{A/B}$ for this setting. There are four additional settings included to assess the performance when J₂ = 5, when γ = 0.01, when signals are generated from Exponential(1) and when globally full lists are used, denoted as $J_2^{A/B},\hspace{0.17em}{G}^{A/B},\hspace{0.17em}{E}^{A/B}$ and F, respectively. Finally, a mixed setting, denoted by $M^{A/B}$, is examined as well, where for each base ranker, we randomly select p_T from $\{0.01,0.05,0.1,0.2,1\}$, λ from $\{0.6,0.8,1\}$ and the others remain the same as in C^A∕B. Three coverage rates are recorded based on top 10, 50 and 100 genes of each aggregated list for all settings except for cases where there are <50 or 100 genes in the aggregated lists.

The CEMC methods are much more computationally expensive than the other methods, as will be discussed in ‘Computation time’ section. Therefore, they are excluded for most of the parameter configurations except for low p_T values (0.01 and 0.05) that produce much smaller input data sets. It turns out that neither CEMC.k nor CEMC.s is among the best-performing methods, and so their performance is not reported hereafter.

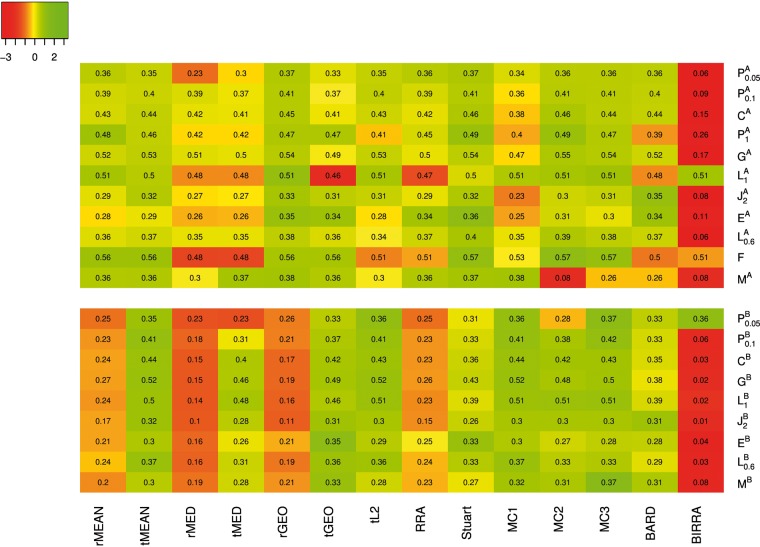
Figure 3 presents a heat map for standardized coverage rates based on top 50 genes in each aggregated list. Under a given setting, the standardized coverage rate of each method is calculated by subtracting the mean coverage rate over all methods in this setting and then being divided by the corresponding SD. Results for coverage rates based on top 10 and 100 genes are provided in Supplementary Figures S1–S2. Overall, the patterns of relative performance of the methods are similar, while the differences between methods are smaller as the cutoff for the top genes moves up. Under Scenario A, Stuart seems to be the best method, followed closely by rGEO and MC3. The performance of MC2 is similar to Stuart in most settings, but it performs poorly under the mixed setting M^A. Among all, BIRRA is clearly the worst except for the settings $L_1^A$ and F, where all the methods perform similarly. All the other methods fall somewhere between the top four (i.e. Stuart, rGEO, MC3, MC2) and BIRRA, and their performance is typically closer to the top group than to BIRRA. Under Scenario B, the top group includes five methods, tMean, tGEO, tL2, MC1 and MC3; the bottom group includes rMEAN, rMED, rGEO, RRA and BIRRA, among which BIRRA is much worse than the other four in most settings, and the other methods including Stuart and BARD form the middle group. In addition, we find that BARD is the best when there are unreliable base rankers included (i.e. $J_2^{A/B}$). This is not surprising as BARD takes into account the varying quality of base rankers, as mentioned in ‘Bayesian methods’ section. For MEAN, MED and GEO, the performance of the two implementations is not particularly different under Scenario A, but ‘TopKLists’ does uniformly better than ‘RobustRankAggreg’ under Scenario B. As mentioned previously, these implementations mostly differ in whether missing ranks are replaced with the maximum ranks plus one under Scenario B. There seems to be evidence in favor of the replacement.

Figure 3.

Heat map of standardized coverage rates based on the top 50 genes in the aggregated list using data generated from Model I. The actual coverage rates of different methods in various settings are superimposed to the colored map.

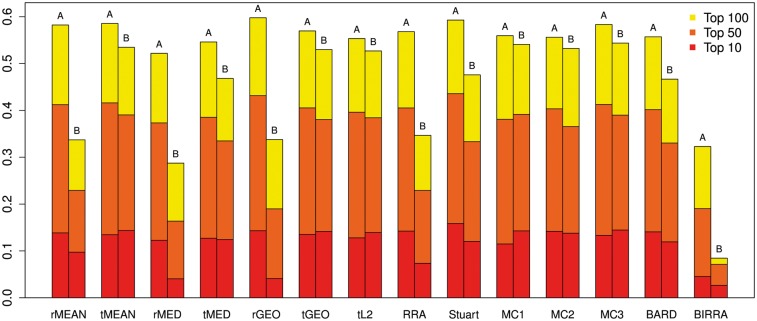
To understand the overall performance of each method under the different scenarios, we further plot the mean coverage rates (based on top 10, 50 and 100 genes) over all the settings under each scenario in Figure 4. As we expect, every method has better overall performance as the percentage of genes used to capture the signal increases, regardless of the scenario. The mean performance of most methods drops in Scenario B compared with that in Scenario A in most cases as less information is known in Scenario B. Also, the relative performance of the methods can change depending on the cutoff used to calculate the coverage rate. For example, MC2 has better coverage than MC3 with cutoff 10, but MC3 has better coverage than MC2 with cutoff 50 and 100.

Figure 4.

Average coverage rates of different methods (based on top 10, 50 and 100 genes) across all settings of each scenario using data generated from Model I. For each method, the left bar is for Scenario A and the right bar for Scenario B.

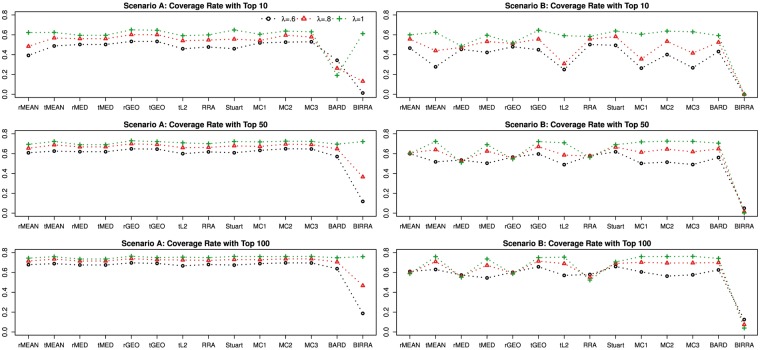
Figure 5 shows how the performance changes as the gene inclusion rate λ changes, while other parameters are held constant. Under Scenario A, the coverage rate of each method decreases as λ decreases from 1. This can be easily seen from the three left panels, in each of which the line for λ = 1 is completely above that for λ = 0.8, which is completely above that for λ = 0.6. Note that BIRRA performs comparably with the other methods when λ = 1, but its performance deteriorates substantially as λ moves away from 1. Under Scenario B, some of the methods, including rMEAN, rMED, rGEO, RRA and BIRRA, seem to be robust to the decrease of λ, while the others have a similar pattern as in Scenario A.

Figure 5.

Coverage rates of different methods using data generated from Model I with varying gene inclusion rate λ, while other parameters are held constant.

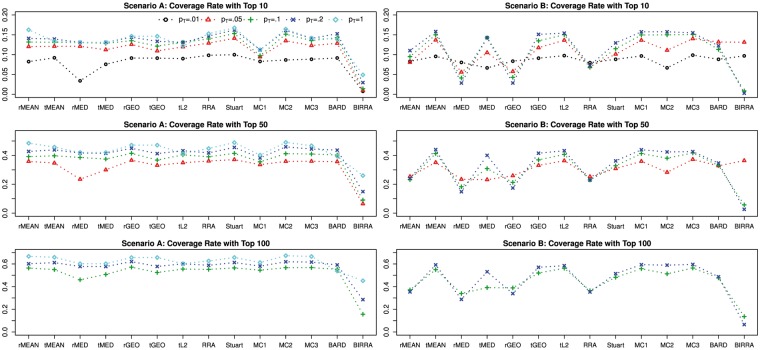
Figure 6 displays how the performance changes as the proportion of top ranked genes p_T changes, while other parameters are held constant. With an increasing p_T, more and more ranking information becomes available, and there is a generally nondecreasing trend for all the methods except for BARD under Scenario A. However, under Scenario B, there are methods that (sometimes) show the opposite pattern, such as rMED, rGEO, RRA and BIRRA. Under either scenario, when the number of top ranked items (p_T × I) becomes much greater than the cutoff for the coverage rate, the gain in performance, if any, tends to be smaller and smaller, which is reflected by the observation that the lines tend to be closer as p_T goes up.

Figure 6.

Coverage rates of different methods using data generated from Model I with varying proportion of top ranked genes p_T, while other parameters are held constant. For the cutoff 50, coverage rates are not reported for p_T = 0.01. This is because all five base rankers only provide rankings for their own top 10 items, and their union is likely to contain <50 items because items from different base rankers tend to overlap. The same reasoning applies to the cutoff 100 for $p_T=0.01,0.05$, and so the coverage rates in these settings are not reported.

Supplementary Figure S3 displays results under settings $J_2^{A/B}$, $G^{A/B},\hspace{0.17em}{E}^{A/B},\hspace{0.17em}{M}^{A/B}$ and F, with the controlled setting C^A∕B as a reference. For a detailed discussion about comparison between the different settings and C^A∕B, see Section S2.1 in Supplementary Material.

Simulation under Model II

Many genomic studies involve large-scale multiple testing, and gene rankings are then produced based on statistics from Z, T or nonparametric tests. This motivates us to consider Model II, a latent-variable model, for generating rank data: $z_{ij}={\theta }_i+{\mathrm{ϵ}}_{ij}$, where the observed rank of gene i in study j (say y_ij), is determined by z_ij, that is if $z_{ij}>z_{i\prime j}$, then $y_{ij}<y_{i\prime j}$ (larger values are ranked higher). The z_ij can be thought of as some function of the test statistic used, whose value is typically not available when performing RA. Further, the true rank of gene i is determined by θ_i, which measures the global importance of gene i. We assume that all θ_is are independent and identically distributed, and they are mutually independent from the error terms ϵ_ijs. We further assume ${\mathrm{ϵ}}_{ij}\stackrel{iid}{\sim }N(0,{\tau }_j)$, where τ_j is the study-specific precision. Note that ${\tau }_j=1/({\rho }_j^{-2}-1)$, where ρ_j is the Pearson correlation between z_ijs and θ_is for all genes in study j, measuring the quality of study j. Our simulation setup under Model II is presented in Section S3.1 of the Supplementary Material.

Figure 7 presents a heat map for standardized coverage rates based on top 50 genes under Model II. Results for coverage rates based on top 10 and 100 genes are provided in Supplementary Figures S4 and S5. Under Scenario A, we find that rGEO and MC2 are the best two, which perform consistently well in all settings. Other methods including tMEAN, tGEO and MC3 perform well and can offer performance comparable or close with the best in most settings. On the other hand, BIRRA and BARD are the worst two. But BARD improves substantially as the cutoff for the top genes moves up. Under Scenario B, the performance of the different methods shows greater heterogeneity, compared with Scenario A. Overall, tGEO, MC2 and BARD are the best three in Scenario B, where tGEO tends to be a bit better than the other two. Stuart appears to perform well, but with a bit less consistency. BIRRA is still the worst among all. In addition, rMEAN, rMED, rGEO and RRA tend to perform poorly, especially for the cutoffs 50 and 100, which is consistent with what we observe in Scenario B under Model I.

Figure 7.

Heat map of standardized coverage rates based on the top 50 genes in the aggregated list using data generated from Model II. The actual coverage rates of different methods in various settings are superimposed to the colored map.

As to how design parameters (e.g. ρ, λ, p_T) affect the performance of the methods; see results presented in Section S3.2 in Supplementary Material.

Computation time

To assess computational efficiency of different methods, (J = 5) full lists are generated with varying number of genes (I = 10, 50, 100, 200, 1000, 5000, 10 000). All the methods except for CEMC, BARD and MC1–3 are computationally efficient, all with running time of a few seconds even when I = 10 000, using Scientific Linux 6 (64 bit) operating system with Intel® Xeon® CPU X5560 @ 2.80 GHz. The results are summarized in Table 4. We can see that CEMC methods are substantially more computationally intensive than the others and are essentially unrealistic to be used when there are more than a few hundred genes. MC methods are computationally efficient for I < 1000, but they ramp up the running time considerably as I further increases. BARD, on the other hand, ramps up more slowly.

Table 4.

Computation time for BARD, MC and CEMC methods

I	10	50	100	200	1000	5000	10 000
BARD	~10 s	~1 min	2–3 min	~5 min	~10 min	~3 h	~10 h
Average of MC1–3	<1 s	<1 s	~1 sec	<10 s	A few minutes	~5 h	~2 days
CEMC	<1 min	~1 min	A few hours	A few days	>30 days	–	–

Data example

We compare RA methods using rank data from four non-small cell lung cancer (NSCLC) studies listed in Table 5. In our simulation, we evaluated different methods where either the spaces of all base rankers are known (Scenario A) or unknown (Scenario B), mainly to separate effects of the two scenarios. However, in some applications, the spaces of base rankers can be a mixture of the two, and we use this example to illustrate this situation. As seen in Table 5, there are three lists from Scenario B and one from Scenario A. After carefully examining how the original studies generated ranked lists (based on formal analyses), we believe all the four lists fit in Simulation Model II better than Model I, as they all relied on statistics that reflect statistical significance of individual genes to rank genes. Also, as the inclusion rates and proportions of top ranked genes vary among studies, the mixed setting from the simulation is the one most comparable with this example. The union of genes from all the four studies consists of ∼14 000 distinct genes. However, researchers rarely consider more than a few hundred genes ranked at the top in the aggregated list, so we consider coverage rates based on the top 10, 50, 100, 200, 300, 400 and 500 genes. Also, the computing times of Markov chain methods and BARD are sensitive to the lengths of input lists as mentioned in ‘Computation time’ section. Based on these considerations, genes that are not ranked in the top 1000 in any of the four lists are omitted to save computing time, as they would almost certainly not get in the top 500 anyways. After omitting these genes, there are over 2000 genes left.

Table 5.

Sources of ranked lists in the NSCLC example

Study (data set name)	Platform	Type of list	Scenario	k
[37]	Affymetrix Microarray	Top-k only	B	100
[38] (Moff)	Affymetrix Microarray	Top-k and partial	A	200
[39]	Affymetrix Microarray	Top-k only	B	3502
[40]	Illumina RNAseq	Top-k only	B	2273

The challenge to evaluate RA methods with real data applications is that the underlying ‘truth’ about the genes is unknown. Here, we use a list of genes that are believed to be highly related to NSCLC in the lung cancer literature as the surrogate of the ‘truth’. This list was obtained by merging the cancer gene lists for NSCLC from four sources: the Catalogue Of Somatic Mutations In Cancer (COSMIC), MalaCards and The Cancer Genome Atlas (TCGA) (these gene names are provided in Section S4 of the Supplementary Material), plus a similar list used in Chen et al. [36].

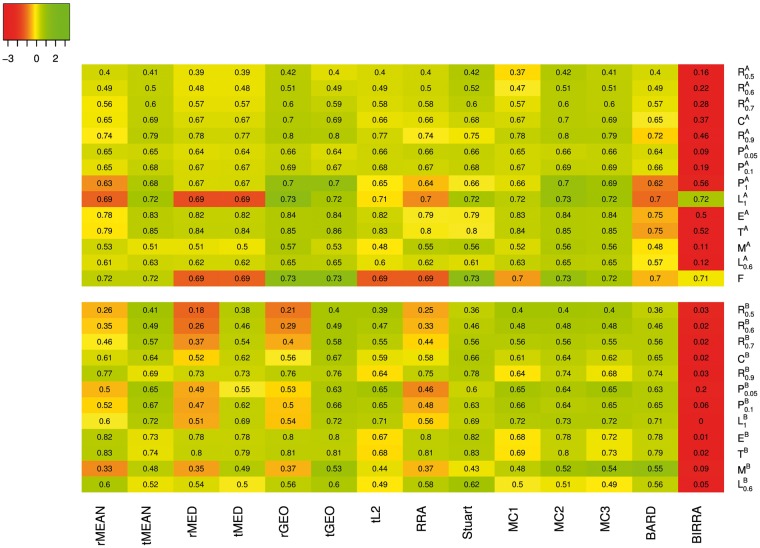
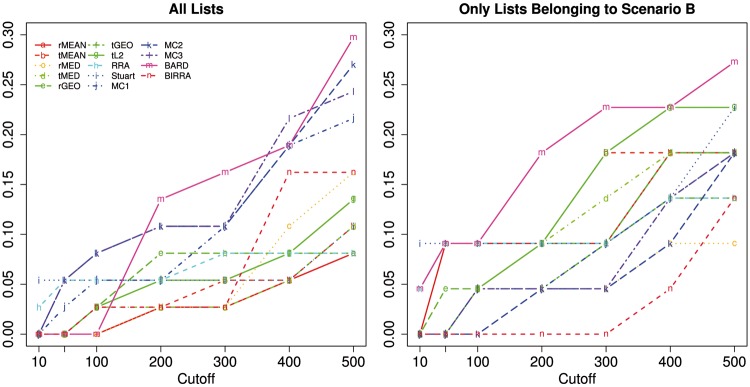
The left panel of Figure 8 shows coverage rates from aggregating all the four lists based on different numbers of top genes (used as the cutoff) for each of the methods. In this example, BARD, MC2 and MC3 appear to work better than the other methods, and Borda’s methods tend to perform poorly, regardless of the implementation. When the cutoff is low (≤ 100), BARD performs poorly and the coverage rate is zero, but it tends to outperform the others for larger cutoff values. BIRRA seems to perform better on real data than on simulated data, especially for larger cutoffs, although it is still among the bottom group. Further, it is not surprising to observe that MC2 is among the top group—recall in ‘Simulation under Model II’ section, MC2 is the only method reported to perform well for both scenarios under Model II.

Figure 8.

Coverage rates of different methods for the NSCLC example.

To understand the behaviors of the methods better, we also report results from aggregating the three lists from Scenario B in the right panel of Figure 8. Obviously, BARD is the best and BIRRA is the worst, which is consistent with simulation results for the mixed setting M^B (where p_T, λ and ρ all vary across base rankers) under Model II. Thus, it is not hard to understand why BARD is one of the best when combining all the four lists, of which only one is from Scenario A. By comparing the two panels of Figure 8, we find that adding an extra list (from the different scenario) would not necessarily increase the coverage rate.

Discussion

In this article, a systematic way of classifying RA methods is provided, along with an updated review. Then important practical issues that have been largely overlooked in regard to the RA problem are discussed in-depth. A formal framework is developed to characterize different situations of a base ranker depending on the availability of ranks of items investigated and whether the underlying space is known. Specifically, the concepts of globally/locally full lists, top-k/top-k only lists and partial lists are rigorously defined. Previous work on RA methods often focuses on full lists, which may be restrictive in genomic applications. Kolde et al. [10] discusses adhoc solutions to accommodate top-k lists and partial lists. However, these situations are not included in their simulation study. Deng et al. [1] provides a formal way of handling these situations with their proposed method BARD and includes the case of top-k only lists in their simulation study but not the case of partial lists. In contrast, a comprehensive simulation study is carried out in this article with four unique features: (i) we distinguish top-k lists from top-k only lists; (ii) we introduce a parameter for the gene inclusion rate to allow for partial lists; (iii) in addition to the popular data-generating mechanism used in Model I, we consider the latent variable model, which seems to be more natural in generating ranked data in genomic applications, as suggested by our data example; and (iv) the evaluation measure used (coverage rate) is carefully selected and evaluated for multiple cutoffs.

Based on our simulation, the performance of a RA method may depend largely on the amount of information available about each base ranker (whether the space is known, the proportion of top ranked items available, whether every item of interest is originally investigated, the quality of ranking, etc.) as well as the amount of resources available that determines the cutoff that can be afforded. As to the relative performance of the different methods evaluated, we summarize our simulation results from ‘Performance evaluation’ section in Table 6, to provide general guidelines in practical situations for the selection of an appropriate method (or avoidance of any method with poor performance). Several conclusions can be drawn from the table: (i) BIRRA appears to perform poorly, regardless of the model and scenario; (ii) rGEO, MC2 and MC3 (in boldface in the table) often perform well under Scenario A, and tGEO (underlined) performs well under Scenario B, regardless of the underlying model; (iii) RRA and the ‘RobustRankAggreg’ implementation of Borda’s methods MEAN, MED and GEO tend to perform poorly under Scenario B, regardless of the underlying model.

Table 6.

The best and worst RA methods by model and scenario based on the overall performance from simulation

Model	Scenario	Best	Worst
I	A	Stuart, rGEO, MC3	BIRRA
		MC2
	B	tMEAN, tGEO, tL2	BIRRA, rMEAN,
		MC1, MC3	rMED, rGEO,RRA
II	A	rGEO, MC2	BIRRA, BARD
		tMEAN, tGEO, MC3
	B	tGEO, MC2, BARD	BIRRA, rMEAN,
		Stuart	rMED, rGEO,RRA

Note: Methods that perform well for both models under Scenario A and Scenario B are bolded and underlined, respectively.

We find that when comparing results from Scenario A with those from Scenario B, RA methods tend to improve their performance, as the information about those bottom ties becomes available, and the mean differences seem to be not negligible and even sizable sometimes. This suggests that such information is helpful to improve the performance and if available, it should be used. Two different implementations of several Borda’s methods (MEAN, MED, GEO) are also evaluated in our simulation, where the differences lie in variations in how ranked data are processed to allow for non-full lists before applying the methods. The simulation results suggest that different data preprocessing procedures could greatly affect the performance. According to our findings, the adjustment of replacing missing ranks with the maximum rank plus one seems to improve the performance of Borda’s methods in most cases with top-k only lists that belong to Scenario B, whereas other adjustments such as normalizing ranks can have either a positive or negative effect on a case-to-case basis. This seems to further suggest that how to use the information available for different types of items in the entire space $\mathcal{I}$ (based on the formal characterization of ranked lists and items in ‘Characterization of various types of lists’ section) would be critical to further enhance the RA performance. Thus, for partial and top ranked lists that often occur in genomic applications, a (Bayesian) approach that can rigorously distinguish items from ${\mathcal{T}}_j$, ${\mathcal{B}}_j$ and ${\mathcal{N}}_j$ for each base ranker, in addition to distinguishing base rankers of different quality (which BARD offers), would be of great interest for future research.

Finally, we mention that in our data example, genes that were never put in the top 1000 list by any base ranker are omitted when defining the entire space of items $\mathcal{I}$, to purposefully filter out non-useful information. Such an idea would greatly facilitate computing for those computationally intensive methods, with little impact on their performance.

Key Points

• An updated review and a systematic way of classifying RA methods are provided.

• A framework for different types of ranked lists that occur frequently in genomic settings is formalized.

• Important practical issues that have been largely overlooked in the past are discussed.

• RA performance may depend largely on amounts of information available about base rankers and resources available for follow-up investigation.

• Information about bottom ties, if available, should be used, and how to use such information can make a significant difference.

Funding

This work was supported by the NIH grants R15GM113157 (PI: Xinlei Wang) and R01CA172211 (PI: Guanghua Xiao).

Biographies

Xue (Lily) Li is a recent PhD graduate in Department of Statistical Science at Southern Methodist University, Dallas, TX 75275.

Xinlei (Sherry) Wang is Professor in Department of Statistical Science at Southern Methodist University, Dallas, TX 75275. She received her PhD degree from University of Texas at Austin in 2002.

Guanghua (Andy) Xiao is Associate Professor, Department of Clinical Sciences, University of Texas Southwestern Medical Center, Dallas, TX 75390. He received his PhD from University of Minnesota in 2006.