Universal scaling across biochemical networks on Earth

Studying biochemical networks at a planetary scale reveals a deeper level of organization than what has been understood so far.

Abstract

The application of network science to biology has advanced our understanding of the metabolism of individual organisms and the organization of ecosystems but has scarcely been applied to life at a planetary scale. To characterize planetary-scale biochemistry, we constructed biochemical networks using a global database of 28,146 annotated genomes and metagenomes and 8658 cataloged biochemical reactions. We uncover scaling laws governing biochemical diversity and network structure shared across levels of organization from individuals to ecosystems, to the biosphere as a whole. Comparing real biochemical reaction networks to random reaction networks reveals that the observed biological scaling is not a product of chemistry alone but instead emerges due to the particular structure of selected reactions commonly participating in living processes. We show that the topology of biochemical networks for the three domains of life is quantitatively distinguishable, with >80% accuracy in predicting evolutionary domain based on biochemical network size and average topology. Together, our results point to a deeper level of organization in biochemical networks than what has been understood so far.

INTRODUCTION

There is increasing interest in whether biology is governed by general principles, not tied to its specific chemical instantiation or contingent upon its evolutionary history (1–3). Such principles would be strong candidates for being universal to all life (4, 5). Universal biology—if it exists—would have important implications for our search for life beyond Earth (6–9), for engineering synthetic life in the laboratory (10, 11), and for solving the origin of life (12, 13). Systems biology provides promising quantitative tools for uncovering such general principles (14–16). So far, systems approaches have primarily focused on specific levels of organization within biological hierarchies, such as individual organisms (17, 18) or ecological communities (19, 20), and have rarely been applied to the biosphere as a whole. However, biology exhibits some of its most notable regularities moving up in levels of organization from individuals to ecosystems, and these regularities may only truly manifest at the level of ecosystems and, ultimately, the biosphere (21, 22). For example, while individual organismal lineages fluctuate through time and space, the functional and metabolic composition of ecological communities is stable (23, 24). To understand the general principles governing biology, we must understand how living systems organize across levels, not just within a given level (25–27).

To explore regularities within and between levels of organization, we adopt a network view of biochemistry (17, 28–30) by constructing biochemical reaction networks from genomic and metagenomic data. We show that biochemical networks share universal organizational properties across levels, characterized by scaling laws determining how topology and biochemical diversity change with network size. These scaling relations exist independent of evolutionary domain or level of organization, applying across the nested hierarchy of individuals, ecosystems, and the biosphere. The biochemical diversity and network properties driving this scaling behavior are predictive of evolutionary domain, indicating that the biochemical network structure for each domain is distinct even though all three conform to the same scaling behavior. Our results provide a first quantitative demonstration that the application of network theory at a planetary scale can uncover properties existing across different levels of organization within the biosphere and can be predictive of major divisions within a given level (such as evolutionary domains). On the whole, our results provide new paths forward for identifying universal properties of life.

Our analysis begins with a global database of genomes and metagenomes, sampled from across life on Earth. We leverage available existing annotated genomic data representing the three domains of life, including genomes of 21,637 bacterial taxa and 845 archaeal taxa from the Pathosystems Resource Integration Center (PATRIC) (31), and 77 eukaryotic taxa from the Joint Genome Institute (JGI) (32). Our metagenomic data include 5587 metagenomes from JGI, cataloging ecosystem-level biochemical diversity across the planet (see Fig. 1).

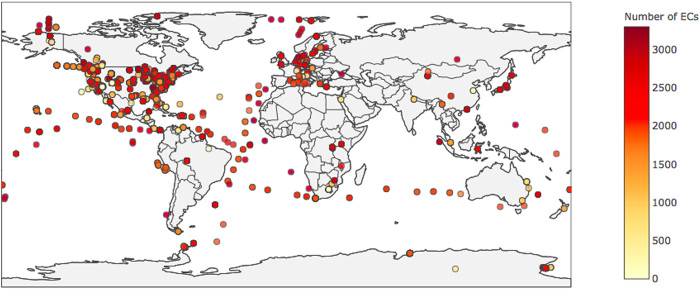
Fig. 1. Enzyme diversity of ecosystems across Earth.

Shown is the geographical distribution of the 5587 ecosystems in our study, colored by the number of different enzyme functional classes [enzyme commission (EC) numbers] encoded in sampled metagenomes (data from JGI). Despite large variances in the enzyme diversity and what enzymes are present in each ecosystem, all ecosystems sampled are found to conform to the same scaling behavior for biochemical diversity and topology as a function of biochemical network size (see Fig. 3).

From these data, we constructed biochemical networks for each individual organism (genome) and ecosystem (metagenome) using reaction data cataloged in the Kyoto Encyclopedia of Genes and Genomes (KEGG) (33). Building on prior work studying biosphere-level models of metabolism (34–36), we use the database of all 8658 enzymatically catalyzed reactions cataloged in KEGG (at the time of data retrieval) as a proxy for the biochemistry of the biosphere as a whole, modeled as a “soup of enzymes” by disregarding the boundaries of individual species (19). Network representations of ecosystem-level and biosphere-level biochemistry are “compartment free” in that no knowledge of individual species is included. Previous topological analyses of biochemical networks have primarily focused on the subset of biochemical reactions associated with metabolism (29, 30). Since we are interested in properties universal across life, and not just subsets of living processes, we instead construct networks inclusive of every known catalyzed reaction (regardless of pathway) coded by the respective genome or metagenome, provided the reaction is cataloged in KEGG.

Adopting a network representation allows systematic quantification of topological properties using graph theory and statistical mechanics (16, 17, 37–42). Using two different graph projections, we compare biochemical networks across levels to test whether they are similar or different and compare to biologically motivated, randomly sampled networks (see Materials and Methods for details on network construction). Our use of the term “random” herein refers to the random sampling procedures we implement to generate ensembles sharing some—but not all—properties with the ensemble of real biochemical networks (described below and in the Materials and Methods). These are specifically used to isolate those properties of the real biochemical networks driving the reported scaling behavior and should be distinguished from more generic random networks, such as Erdös-Rényi random graphs typically contrasted to chemical or biochemical networks (see, e.g., (28, 43, 44)). A widely implemented framework for assessing commonality across different systems is to look at their scaling behavior (45–50). If scale-invariant properties are found, then it can be suggestive of deeper, underlying organizing principles (3, 51, 52), such as when distinctive scaling laws emerge in critical systems (53). We therefore sought to determine whether biochemical networks display scaling laws governing their topology and chemical diversity, which are similar across levels, indicative of the existence of self-organizing principles universal across biological levels.

There are three alternative scenarios to be tested relating network structure across individuals, ecosystems, and the entire biosphere; each is shown in Fig. 2. In the first, biochemistry does not have shared network structure across levels, and different scaling behaviors emerge at different levels. In the second scenario, biochemistry has shared network structure across levels, but this shared structure can be fully explained by the structure of random chemical networks (generated from random collections of biochemical reactions used by biology). In this case, real biochemical reaction networks would be statistically indistinguishable from random reaction networks, implying that the self-organizing principles are solely chemical and not biological in origin. In a third scenario, biochemistry has shared structure across levels, which is different from that of random reaction networks. We find the third scenario to be consistent with our analysis, suggesting the presence of universal organizing principles unique to biology that recur across biological levels of organization. We show that these can be explained as an emergent property of the topological structure of the most common reactions participating in living processes.

Fig. 2. Three alternative scenarios for how biochemical network structure might be similar or dissimilar across levels of organization.

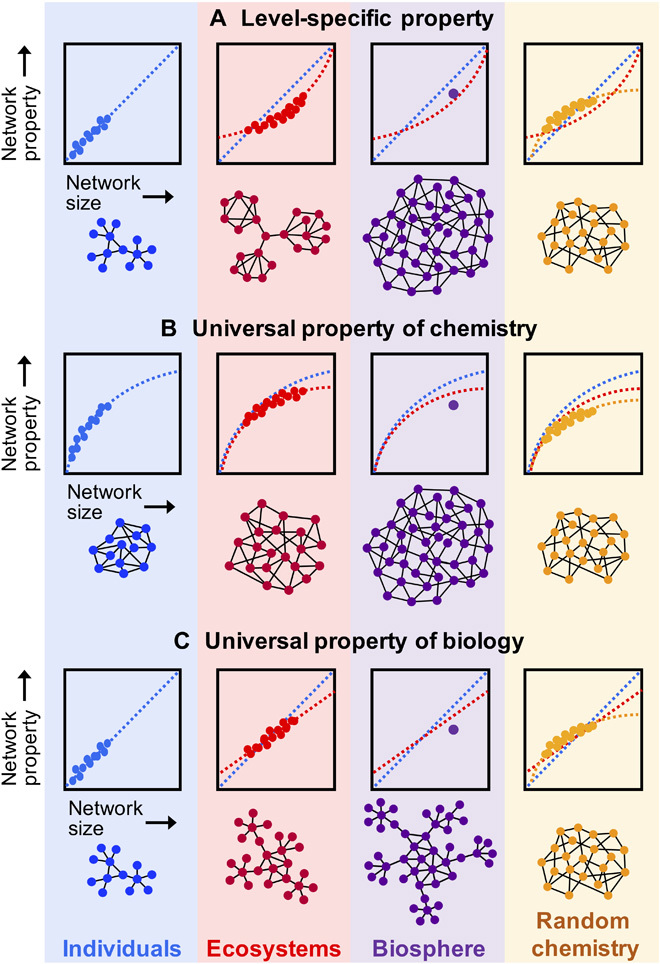
For each scenario, illustrative plots show examples of scaling behavior of some network property as function of network size, where each data point corresponds to the measure for a single instance of a network. In the first (A), biochemistry does not exhibit common network structure across levels, and different properties emerge at different levels. In the second (B), biochemistry has a common network structure across all levels, but this structure is also shared by random chemical networks. In the final scenario (C), biochemistry has shared structure across all levels, which is different from that of random chemical networks. Our results are consistent with this third scenario, indicative of universal organizing principles recurring across biological levels, which are unique to biology (not shared by random chemistry), which we show arises due to the network structure of common reactions shared across life on Earth.

Before proceeding to the details of our results, it is worth noting the well-known challenges associated with the introduction of statistical artifacts when coarse graining real-world systems to generate graphical representations (54, 55). For example, bipartite network representations of biochemistry (treating reactions and substrates as two disjoint sets of nodes) have information that cannot be recovered from unipartite representations (which treat only substrates as nodes). The challenge of choosing a projection arises because biochemical networks are themselves a multilayer system consisting of enzymes and their catalyzed reactions; enzymes (often abstracted away in network representations) control the biological organization we aim to characterize. To ensure that the regularities we report are reflective of the true underlying organization of biochemistry and are not statistical artifacts introduced by a specific choice of coarse graining, we therefore consider both a unipartite and bipartite projection in our analysis (54). We also compare catalytic diversity—quantified in terms of the number of enzymes and reactions—across levels, which is independent of network representation. As we will show, common scaling laws describing biochemical networks across levels of organization are consistently observed in each of these different views of biochemistry, confirming our results are independent of the type of network representation.

One remaining consideration once a network representation is adopted is how to analyze it. So far, the majority of network analyses applied to biochemistry have focused on the “scale-free” structure of metabolic networks (28, 56, 57). For example, in a seminal paper by Jeong et al. (28), it was shown (using a unipartite representation) that metabolic networks from all three domains of life exhibit the characteristic power-law degree distribution of a scale-free network, with similar scaling exponents for bacteria, archaea, and eukaryotes. This and other previous work have focused primarily on properties within single instances of a network (e.g., an individual organism’s metabolism), with similar structure to biology (such as the scale-free property) reported in chemical networks more generally (43, 44, 58, 59). However, as we stated earlier, our interest is in looking at properties across networks (e.g., describing ensemble properties of biochemical networks at the individual and ecosystem levels). We therefore focus on topological measures such as average shortest path length, average clustering coefficient, and assortativity (degree correlation coefficient), which are directly comparable across different networks, allowing us to make statements about regularities existing across biochemistry sampled from different levels of organization in a manner that has not been possible in previous work focusing only on a given level.

RESULTS

Scaling laws describe biochemical networks and catalytic diversity across levels

Organisms can vary widely in their number of genetically encoded reactions, and ecosystems generally include more encoded reactions than individuals do. We therefore compared topological properties relative to the size of biochemical networks as a relevant scaling parameter for our analysis. We defined network size as the number of molecules connected through catalyzed reactions within the largest connected component (LCC) for a given biochemical network. We focused analyses on the LCC since some measures are not defined on disconnected networks. The LCC included >90% of compounds for all but the smallest networks in our study, and >97% of compounds for the largest (see section S2, fig. S1, and table S1). The fact that the LCC is not 100% of the network could be attributable to missing data in the annotation of genomes and metagenomes. We therefore verified that our results are not sensitive to a similar magnitude of missing data by confirming the scaling trends reported here are not affected when 10% of nodes are randomly removed (see fig. S2). Furthermore, our results reported below suggest larger proportions of missing data (as often occurs for genomes or metagenomes missing many annotated genes) would not significantly affect our results, as we find the reported scaling behavior is primarily driven by the topological structure of the most common reactions found across all of biology. We also verified that our results hold when analyzing a more balanced subset of our data, avoiding disproportionately large contributions by genetically similar taxa (see figs. S8 and S9).

We calculated several frequently implemented topological measures for the LCC for each network (see section S2). We classified properties (e.g., topological or diversity measures) as universal when they scale in the same way across levels. We identified these cases by properties that scale according to the same fit across levels (e.g., network average clustering coefficient scales linearly with network size for both individuals and ecosystems, and we thus identified this scaling as universal across levels). Shared fit functions across levels suggest mechanisms driving the structure of biochemical networks may be independent of level of organization; in such a case, individuals and ecosystems could both be subject to the same general principles acting to architect them. That is, we did not require the scaling coefficients to be exactly the same (indicating the tuning of mechanisms generating structure in individuals and ecosystems), but we did require the same fit to be shared across our data (indicating the possibility of shared generative mechanisms) to qualify as universal.

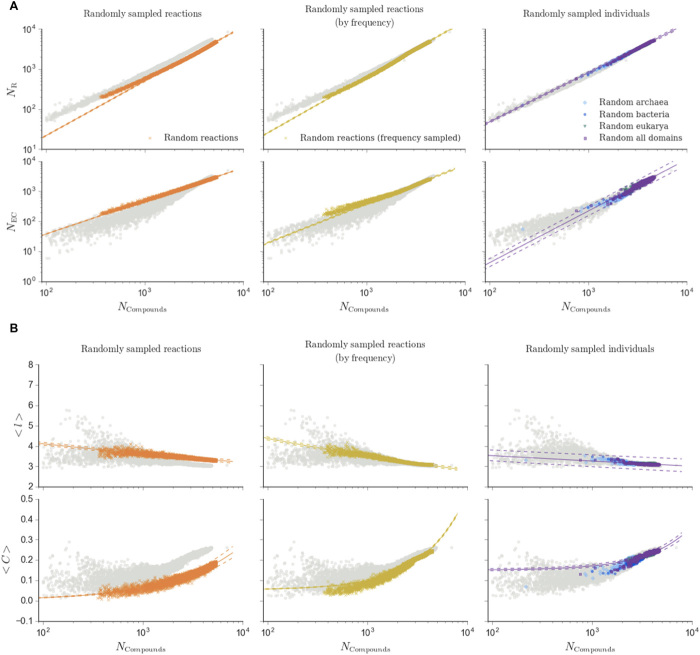
To test whether biology exhibits universal scaling behavior across levels, we first determined how topological properties and biochemical diversity vary with size for all individuals and ecosystems in our dataset. Measured values for the unipartite representation and catalytic diversity (enzymes and reactions) are shown in Fig. 3 as a function of network size (see fig. S4 for data on bipartite representation, which exhibits similar consistency across levels). We found individuals and ecosystems scale according to the same functional form for each network and diversity measure, with similar scaling coefficients (for fits and confidence intervals, see data file S1). Scaling for individuals and ecosystems is therefore universal. For some measures (assortativity and betweenness), the biosphere fell within the 95% confidence interval observed for fits of ecosystem level scaling. An exception is clustering coefficient, where the biosphere significantly departed from the observed ecosystem scaling: This could be attributable to missing data on global enzymatic diversity (which falls slightly below what our scaling laws would predict). Topological measures that scaled following power-law fits (y = y₀ x^β, where β = β_ind for individuals and β = β_eco for ecosystems) included the following: average betweenness (β_ind = −1.1581, β_eco = 1.136), average shortest path length (β_ind = −0.117, β_eco = −0.084), and number of edges (β_ind = 1.219, β_eco = 1.243). Both biochemical diversity measures also scaled according to power-law fits: number of enzyme classes (a proxy for enzymatic diversity) (β_ind = 1.294, β_eco = 1.838) and number of reactions (β_ind = 1.229, β_eco = 1.319). Average clustering coefficient scaled with a linear fit (y = mx + y₀, m = m_ind for individuals and m = m_eco for ecosystems) for individuals and ecosystems (m_ind = 3.77 × 10⁻⁵, m_eco = 3.32 × 10⁻⁵). These results rule out the possibility that scaling laws are level specific (Fig. 2A). The observed scaling laws confirm biochemical networks exhibit shared structure across levels of organization, where network properties and biochemical diversity are largely determined by size as the relevant scaling parameter.

Fig. 3. Common scaling laws describe biochemical networks across levels of organization.

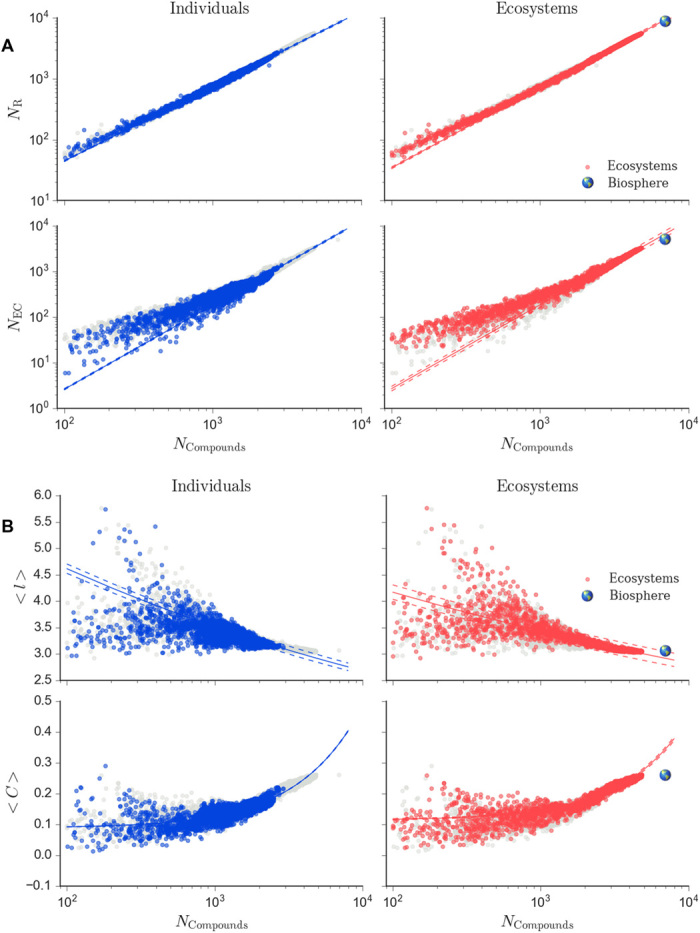
Scaling of biochemical measures for individuals (left column) and ecosystems (right column) shared the same functional form for biochemical diversity (enzyme and reaction diversity) and for topological measures. Shown from top to bottom are the following: (A) number of reactions (N_R) and number of enzyme classes (N_EC). (B) Average shortest path (<l>) and average clustering coefficient (<C>). All measures are as a function of the size of the LCC (N_Compounds). Ecosystems include metagenomes (red) and the biosphere-level network (Earth icon). Fits for each dataset (solid lines) are shown with 95% confidence intervals (dashed lines). For reference, shown in light gray are data for all biochemical networks (individuals, ecosystems, and biosphere). Additional measures are shown in fig. S3, and scaling for bipartite networks is shown in fig. S4.

Real networks exhibit different scaling behavior than random chemical networks

The observed universal scaling across individuals and ecosystems could be unique to biology, or it could arise due to self-organizing principles of chemistry. If the latter is true, then we should expect randomly sampled chemical networks to exhibit the same fit functions across networks as real biochemical networks do. Testing this possibility requires comparison to randomly sampled chemical networks, which must be generated with an appropriate biologically relevant control to be informative (60). Since we are interested in the global organization of biochemistry, we constructed control random chemical reaction networks (henceforth called random reaction networks) by merging randomly sampled reactions from the KEGG database following a flat distribution, where all reactions are equally likely to be sampled (see Materials and Methods for details on network construction). This random sampling produces ensembles of random reaction networks that globally (over the ensemble) share the same chemical reactions as our biosphere.

We performed the same analyses on the ensemble of random reaction networks as real biochemical networks. We observed that random reaction networks do not scale according to the same functional form as biochemical networks for some network topology measures (Fig. 4, first column). The fits for average clustering coefficient of random reaction networks favored a power-law function (y = y₀ x^β, with β_ran = 0.6401), compared with the linear function favored by the biochemical networks. Fits for assortativity favored a linear function for random reaction networks (y = mx + y₀, m_ran = −4.5255), whereas for biochemical networks, it was found to not scale with size (data file S1). That is, there are certain aspects of the topology of random reaction networks that scale with network size in a manner that is entirely distinct from that of real biochemistry. The qualitative differences in scaling behavior indicate the real and random biochemical networks represent different universality classes. In addition to these qualitative differences in scaling behavior, we also observed statistically significant quantitative differences in the random chemical networks: Scaling relationships for randomly sampled biochemical networks did not overlap with real biological individuals in many cases. Topological measures in random reaction networks that scaled according to power-law fits (y = y₀ x^β, β = β_ran for random reaction networks) included the following: average betweenness (β_ran = −1.0595), average shortest path length (β_ran = −0.0543), and number of edges (β_ran = 1.2459). Both biochemical diversity measures also scaled according to power-law fits: number of enzyme classes (β_ran = 1.10156) and number of reactions (β_ran = 1.3590). We conclude that the organizational properties of random chemical networks cannot alone explain the scaling laws observed for real biochemical networks.

Fig. 4. Scaling laws distinguish biochemical networks from random networks across levels of organization.

Shown are random reaction networks created by sampling biochemical reactions from a flat distribution (left column), frequency-sampled random reaction networks created by sampling reactions based on the frequency distribution observed across all organisms (center column), and random genome networks (right column). Merged networks composed of individuals include bacteria only (light blue), archaea only (dark blue), eukarya only (blue-green), and all domains combined (purple). (A) Scaling of biochemical diversity. Diversity measures and fit are as described in Fig. 3. For reference, all real biochemical network data from Fig. 3 are shown in light gray. Additional measures are shown in fig. S5. (B) Scaling of network structure. Measure and fit descriptions match those described in Fig. 3. For reference, all real biological networks from Fig. 3 are shown in light gray. Additional measures are shown in fig. S5, and scaling for bipartite networks is shown in fig. S6. We found that random reaction networks do not recover the same fit functions as real biological networks for assortativity and clustering, whereas frequency-sampled random reaction networks and random genome networks only differed for assortativity, but nonetheless were statistically distinguishable from real biochemical networks for some measures.

Scaling laws represent shared constraints reemerging across levels

Our results establish that Earth’s biochemistry exhibits universal scaling behavior across levels of organization not explainable by the organizational patterns of randomly sampled chemistry alone. A natural next question is whether ecosystems inherit their properties from individuals, or whether they instead exhibit similar structure due to similar constraints reemerging at different levels. Addressing this requires determining whether scaling behavior for individuals is statistically distinguishable from ecosystems. We assumed as a null hypothesis that scaling relationships are consistent across levels of organization, and we performed a permutation test (61) using the scaling coefficient as the test statistic (see “Fitting network measure scaling and permutation tests” section in Materials and Methods). We found that scaling relationships are not distinguishable for individuals and ecosystems when analyzing average node betweenness and average shortest path length (table S2). However, scaling coefficients were distinguishable for a number of reactions, number of edges, number of enzyme classes, and mean clustering coefficient, with P < 10⁻⁵ in most cases. Confidence intervals on scaling coefficients for ecosystem topology were narrower than for individuals, indicating that ecosystem scaling is more tightly constrained. Although biochemical networks for individuals and ecosystems shared a similar scaling behavior, they were not drawn from the same distributions, allowing the possibility that shared constraints operate at each level separately.

We next sought to identify sufficient constraints for recovering the observed scaling across levels. To do so, we constructed a different ensemble of random reaction networks by merging randomly sampled reactions from the KEGG database, but this time weighting the sampling frequency of biochemical reactions by the number of individual genomes where the reactions are found (henceforth called frequency-sampled random reaction networks; see Materials and Methods for details of their construction). This random sampling produced ensembles of random chemical networks that, as before, globally (over the ensemble) share the same reactions as our biosphere, but also had the additional property of sharing the same frequency distribution of reactions over “individuals” as our biological dataset. This random ensemble therefore more closely reproduced properties of real biological networks than those introduced in the previous section. Since most highly connected nodes (participating in many reactions) are common to all three domains, e.g., adenosine 5′-triphosphate (ATP) and H₂O (28, 62), this sampling procedure yielded random control networks that tended to include the most common compounds used by life. We found the scaling behavior of this ensemble of random networks much more closely matched the observed scaling trends in real biology (Fig. 4, second column). Whereas we observed qualitative differences for scaling of clustering in the previous case, here the fit function was the same as for the clustering coefficient for both the real biochemical networks and the frequency-sampled random reaction networks. All fit functions were the same as those for real biochemical networks, with the exception of assortativity. In addition, for measures sharing the same fit functions, fewer measures distinguished biological networks from frequency-sampled random reaction networks than from random reaction networks without this constraint. We can therefore conclude that the network structure of the most frequently occurring reactions across life on Earth is an important driver of the observed scaling behavior for the real networks.

To further confirm that scaling emerges due to these shared properties across all life, we next generated simulated ecosystem-level networks by merging randomly sampled genome networks from each domain individually and from all three domains together (see Supplementary Materials and Methods for details on network construction). This allows us to determine how scaling behavior could be the same or different for an archaeasphere (archaea alone), bacteriasphere (bacteria alone), eukaryasphere (eukarya alone), or artificial ecosystems (all three domains) (Fig. 4, third column). We found that the functional forms of scaling relationships were the same for real ecosystems and these randomly merged organismal networks (hereafter called random genome networks). This result was somewhat unexpected given it is not in general true that randomly selected subnetworks of a network have the same structure as the original network (e.g., individuals as subnetworks of ecosystems do not necessarily have to share the same structure) (63). However, we also checked whether scaling exponents and coefficients are statistically distinguishable for real ecosystems and random genome networks, using the same permutation tests as before, and found that they were for most measures (see table S2). Random genome networks and real ecosystems exhibited exponents distinguishing their scaling coefficients for most topological measures and for a number of enzymes, with P < 10⁻⁵. Scaling of betweenness was indistinguishable between the two datasets. These results indicate that random genome networks differ from real ecosystems in many of the same ways individuals do. However, just as scaling of assortativity qualitatively distinguished individual biochemical networks from the frequency-sampled random reaction networks, scaling of assortativity also distinguished random genome networks from real ecosystems, whereas it did not distinguish real individuals from real ecosystems (Fig. 5). Taken as a whole, these results suggest that scaling behavior for real ecosystems arises due to organizing principles operative at the level of ecosystems and is not solely an emergent property due to merging individual-level networks.

Fig. 5. Scaling laws for individuals and ecosystems are statistically distinguishable for some network and catalytic diversity measures.

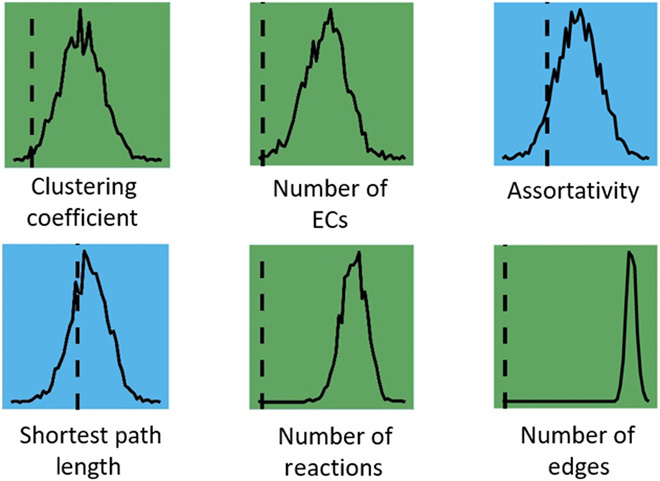
Shown are the results of a permutation test to determine whether properties of biochemical networks constructed from individual genomes scale differently than those constructed from metagenomes (ecosystems). For each network measure, the test statistic is shown as a vertical dashed line, while the null distribution is shown as a solid line (see “Fitting network measure scaling and permutation tests” section in Materials and Methods on for more details). Blue squares indicate that the scaling behavior is indistinguishable between levels of organization, while green squares show measures that can distinguish scaling of individuals from that of ecosystems.

Combining these results for frequency-sampled random reaction networks with that of random genome networks indicates that the existence of individuals sharing a common set of biochemical reactions is a sufficient condition for networks of all sizes (from small individuals to large ecosystems) to exhibit the scaling behavior observed in real living systems. Together with the results of the previous section, we can conclude that the particular form of the scaling relations observed across life on Earth emerges due to the structure of interactions among compounds common across all life, which is not in general characteristic of nonbiological chemical reaction networks.

Network structure predicts evolutionary domain

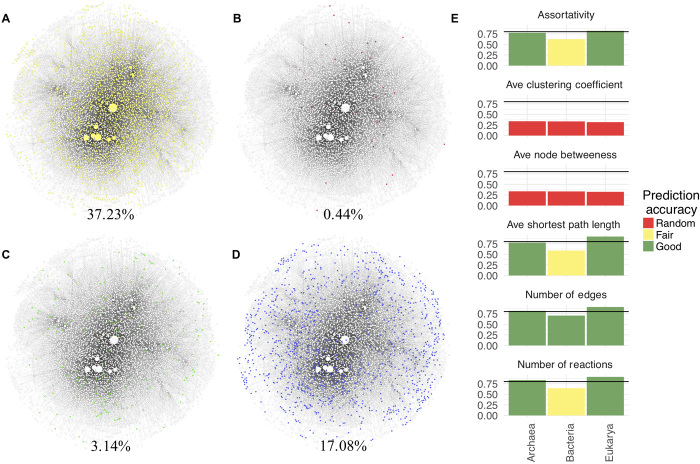
Any general organizing principles in biology must be consistent with the variation responsible for the diversity of life we are already familiar with. Since the three domains of life represent the most significant evolutionary division in the history of life (64), we therefore also tested whether network structure can distinguish individuals sampled from the three domains (see “Predicting evolutionary domain from topology” section in Materials Methods). To approach this question, we first investigated compounds shared across all domains to determine which compounds are distinct to each domain and which are universal to all three. We identified the contributions of each domain to the biosphere as a whole by comparing compounds at the biosphere level to those across the networks of individuals, identified by evolutionary domain. We did so by identifying which compounds were unique to each domain and which were shared across all three domains, determined from annotated data in the 22,559 genomes in our dataset. At the biosphere level, 0.44% of compounds were unique to archaea, 3.14% were unique to bacteria, and 17.08% were unique to eukarya, reaffirming that each domain represents significantly different metabolic strategies and genetic architectures, as is well established by earlier work (64). However, it is also well established that all life on Earth shares a common set of core biochemistry (65): A higher percentage of compounds, constituting 37.23% of the biosphere-level network, were shared across all three domains in our dataset (Fig. 6, A to D), including hubs such as ATP and H₂O, as mentioned previously. Since many more chemical compounds were shared across all three domains than are unique to each, one might a priori expect the organization of these compounds into biochemical networks to not be predictive of domain.

Fig. 6. The biosphere-level chemical reaction network.

The biosphere-level network was constructed from the union of all 22,559 genomic networks in our study. Each panel shows the same biosphere-level network, with nodes (representing compounds) in white and edges (representing their connections) in gray. Node size indicates degree within the network. Colors indicate biochemical compounds used in (A) all three domains of life (yellow), (B) in archaea only (pink), (C) in eukarya only (green), and (D) in bacteria only (blue). Although many more chemical compounds are shared across all three domains than are unique to each, the organization of these compounds into biochemical networks was distinct for each domain based on statistical testing, which shows (E) that catalytic diversity and biochemical network topology can predict evolutionary domain. Shown is the estimated prediction accuracy (y axes) for each measure and each domain. The colors of each bar indicate prediction accuracy of a given measure for a particular domain: Red is comparable to random guessing (y ≤ 33% accuracy); yellow is better than random but not completely predictive (33% < y ≤ 67%); green is predictive of domain (67% < y). The horizontal line indicates 80% prediction accuracy.

We found the opposite to be true: Despite a large fraction of shared biochemical compounds, the organization of those compounds into networks was distinct for each domain. We found in most cases, that average topology normalized to size could reliably predict evolutionary domain (Fig. 6E). In many cases, the prediction accuracy was >80%, when only a single topological measure was used. By contrast, topology or size alone provided significantly less accurate predictions. This demonstrates that biochemical network structure can be predictive of the taxonomic diversity of individuals. Combined with our other results, this suggests the same biochemical network properties (topology and catalytic diversity) driving regularity across levels of organization can also be predictive of major evolutionary divisions within a given level, providing evidence the regularities identified herein are consistent with a signature of global organizing principles for biochemistry.

DISCUSSION

Our analyses reveal that biochemical networks display common scaling laws governing their topology and biochemical diversity that are independent of the level of organization they are sampled from. These scaling laws cannot be fully explained by the structure of random reaction networks that do not account for the structure of the subset of reactions shared across life on Earth. We were also able to confirm that the same topological regularities occurring across levels of organization within the biosphere can be predictive of evolutionarily divisions within a level, using the three domains as an exemplar. Collectively, our results indicate a deeper level of organization in biochemical networks than what is understood so far, providing a new framework for understanding the planetary-scale organization of biochemistry and how nested hierarchical levels are structured within it.

A key implication of our analysis is the importance of individuals sharing a common set of biochemical reactions in shaping the universal scaling laws observed across hierarchical levels. Scaling laws often emerge in systems, where universal mechanisms operate across different scales, yielding the same effective behavior independent of the specific details of the system. It is in this sense that scaling laws can uncover universal properties, motivating their widespread use in physics and increasing application to biology (45, 49, 51, 66–69). Here, we have shown the relevant scaling parameter for biochemical organization is the number of biochemical compounds (in a network representation this is the size of the network). Individuals, ecosystems, and the biosphere obey much the same scaling behavior for biochemical network structure, indicating that the same universal mechanisms could operate across all three levels of organization. In physics, this kind of universality usually implies there is no preferred scale or basic unit. However, in the biological example uncovered here, the presence of specific scaling relations observed in real biochemical networks can be explained by biological individuals (lower-level networks) sharing a common set of reactions as basic “units.”

Future work should explore the connections between the scaling relationships reported here and other work characterizing scaling behavior across living processes. For example, our results indicate that ecosystems are more tightly constrained than individuals, better displaying the regularities of biochemical network architecture. However, projecting ecosystem-level scaling to the biosphere as a whole does not recover the observed network properties for the biosphere-level network. Recently, scaling laws describing microbial diversity were used to predict Earth’s global microbial diversity and in particular to highlight how much diversity remains undiscovered (47). It could be an analogous case here, where the uncovered scaling relations could be used to predict missing enzymatic diversity in the biosphere. Furthermore, one area of intensive investigation is allometric scaling relations (47, 66, 69), including how shifts in metabolic scaling could be indicative of major transitions in evolutionary hierarchies (45). Allometric scaling laws are derived by viewing living systems as localized physical objects with energy and power constraints. Here, scaling emerges due to an orthogonal view of living systems as distributed processes transforming matter within the space of chemical reactions. The connections between these different aspects of scaling in a living organization remain to be elucidated.

A final implication of our work is the consequences for our understanding of the origin of life, before the emergence of species. The existence of common network structure across all scales and levels of biochemical organization suggests a logic to the planetary-scale organization of biochemistry (70), which—if truly universal—would have been operative at the origin of life. While our analysis has uncovered universal scaling behavior for extant life, arising due to the structure of connectivity and diversity among the most common biochemical compounds and reactions, it remains to be determined whether the particular scaling reported is a by-product of shared biochemistry across all life or whether fundamental constraints on biochemical network structure, operative across scales from individuals to planets, drives lower-level individuals to necessarily share common reactions. If the latter is true, then it would have important implications for understanding the processes operative at the time of the last universal common ancestor. If the same global network structure, characterized by the same scaling laws, described Earth’s biosphere throughout its evolutionary history, then the emergence of individuals (as selectable units) with a shared biochemistry would have played an important role in mediating a transition in the organization of Earth’s chemical reaction networks. Even if we could assume the same planetary-scale chemistry for a lifeless world, we should expect to see dramatically different scaling for a hierarchically organized biosphere of nested evolutionary units, where units are defined by a shared subset of biochemical architecture across all life (71, 72). An important question for future work is identifying the planetary drivers of Earth’s biosphere-level biochemical network structure and how this has structured living systems across nested levels over geological time scales. This will require characterizing the organization of planetary-scale biochemistry, as developed here, within the broader context of studying a planet’s geologic and atmospheric evolution. It remains an open question as to what will ultimately explain the universal structure of Earth’s biochemical networks, or whether we should expect all life to exhibit a similar scaling behavior, even on other worlds.

MATERIALS AND METHODS

Obtaining genomic and metagenomic information

Genomes (PATRIC)

Archaea and bacteria genomic datasets were obtained from PATRIC (31). EC numbers were obtained from the “ec_number” column in the pathway data of each taxon. Eukarya genomic datasets were obtained from the JGI integrated microbial genomes and microbiomes comparative analysis system (IMG/M) (32). All eukarya data used in this study were sequenced at JGI. All EC numbers used to construct eukarya biochemical networks were obtained from the list of total enzymes associated with each eukaryote. EC numbers were used in conjunction with KEGG enzyme and reaction data to build biochemical networks for each taxon.

Metagenomes (JGI)

Metagenomic data were obtained from JGI IMG/M (32). All metagenomic data used in this study were sequenced at JGI. All EC numbers used to construct metagenomic biochemical networks were obtained from the list of total enzymes associated with each metagenome. These EC numbers were used in conjunction with KEGG enzyme and reaction data to build biochemical networks for each metagenome.

Our metagenomic data came from a wide variety of ecosystems associated with the natural environment, host organisms, and human-made environments from across the globe (see Fig. 1). The metagenomes were sampled from a variety of locations, inclusive of 51 different bodies of water, countries, or Antarctica. The largest categories of sampled ecosystems include aquatic, terrestrial, plant, wastewater, fungi, insect, mammal, and air, among many others. They come from, for example, soil, marine and freshwater environments, thermal springs, digestive systems, sediments, sludges, and the deep subsurface. Metagenomes were collected over a variety of altitudes, from sea level to a few thousand meters above sea level. Terrestrial and aquatic metagenomes include surface samples as well as those from depths of centimeters to thousands of meters below the surface. Samples also range in pH from nearly 0 to over 9, and in temperature from just above 0° to 90°C. At present, it is impossible to say how representative the diversity of life sampled so far is of the total biodiversity of life on Earth (which is presently unknown and not well constrained), and it is likely that our metagenomic dataset is not inclusive of all of that biodiversity, particularly given current limitations arising to incomplete characterization of metagenomic samples. Nonetheless, the breadth of environments in our sample suggests that our dataset includes a reasonable representation of known biodiversity. Additional environmental and omic information is publicly available on JGI’s IMG website (https://img.jgi.doe.gov/cgi-bin/m/main.cgi).

Biosphere

To create the biosphere network, we included all (at the time our data were retrieved) 8658 enzymatically catalyzed reactions in KEGG.

Network construction

In this study, all biochemical reaction networks consisted of chemical compounds that were involved in biochemical reactions: Two chemical compounds were connected to each other when one was a reactant and the other was a product of the same biochemical reaction (see section S1 for more details). The different types of biochemical reaction networks came from how we select a set of reactions to be included in each network, which is described below. Note that all edges in the networks in this paper were represented as undirected and unweighted since our interests lied on the presence or absence of particular reactions in given networks, and, in principle, all biochemical reactions could happen in both directions depending on the environment.

Biological networks

For each biological network, we included all catalyzed biochemical reactions annotated in each genome or metagenome. More specifically, we considered three different levels of organization: individual organisms, ecosystems, and the biosphere. For the construction of individual networks, we used the genome data of 21,637 bacterial taxa and 845 archaeal taxa from the PATRIC (31) and 77 eukaryotic taxa from the JGI (32). From these data, we obtained the set of classes of enzymes for each genome. All reactions catalyzed by this set of enzymes and present in the KEGG (33) database were included in the network representation of the corresponding genome. Similarly, for the network representation of each of the 5587 ecosystems from JGI, we included all reactions catalyzed by the ecosystem’s coded enzymes, provided they were cataloged in the KEGG dataset. Lastly, for the biosphere network, we included all 8658 enzymatically catalyzed reactions in KEGG.

Parsed biological networks

We also analyzed a parsed subset of biological data to reduce the relative size differences between each of our domain datasets. This allowed us to test whether our results are consistent with a more balanced representation of biodiversity from each domain. Starting with all bacteria genomes, we selected one representative genome containing the largest number of annotated ECs from each genus. Unique genera (genera only represented by a single genome) were also included in our parsed data. Uncultured/candidate organisms without genera level nomenclature are also included in the parsed dataset. The parsed archaea dataset was created in the same way. Because we have much less extensive data from eukarya, the parsed results included all eukarya (there is no “parsed” eukarya).

Random genome networks

To construct a random genome network, we sampled individual networks uniformly at random from the set of all individual organisms in our dataset and merged them into one random genome network. When a set of multiple individual networks were merged, every node and edge present in any individual network are added to the resulting network with equal weight regardless of how many individual networks included them. We built four types of random genome networks with individual networks sampled from only archaea, only bacteria, only eukarya, and from integration of all the three domains. The number of individual networks merged to form each random genome networks was defined as the sample size. The sample size ranges from 1 to 200 for 845 archaea genomes, from 1 to 200 for 21,637 bacteria genomes, from 1 to 77 for 77 eukarya genomes, and from 1 to 477 for all genomes in the three domains. We selected 10 sets of individual networks for every sample size and merged them to generate 2000 random genome networks from individual archaea networks, 2000 from individual bacteria networks, 770 from individual eukarya networks, and 4770 from all individual networks across the three domains.

Random reaction networks

In this paper, random reaction networks were generated by merging randomly sampled reactions from all biochemical reactions from the KEGG data regardless of whether a known enzyme was cataloged for the reaction. We note 31.46% of chemical compounds in the biosphere network were not included in the genomic data in our study, therefore for our construction uniformly sampling the entire KEGG database; the random reaction networks could include enzymatically catalyzed reactions not included in our genomic data. Nonetheless, our sampling procedure was biased to generate networks with similar biochemistry to that of the genomic networks [since compounds common to all three domains tended to be highly connected (participate in many reactions), this uniform sampling procedure yielded random networks biased to include the most common compounds used by life]. Most biological networks for real individual organisms and ecosystems contained 200 to 5000 reactions. To build the random reaction networks with size similar to real individual organisms and ecosystems, we selected a random number between 200 and 5000, sampled that number of reactions from KEGG data uniformly at random, and merged these into a random reaction network. Repeating this, we constructed 5000 random reaction networks in total.

Frequency-sampled random reaction networks

With the goal of creating an ensemble of random networks more similar to real biological networks, we also generated random reaction networks by sampling reactions with probability proportional to their frequency across the set of all individual biological networks. We computed the frequency of every reaction as the number of genomes that includes enzymes catalyzing that reaction to generate a frequency distribution for the occurrence of reactions across our genome-level networks. We then selected a random number between 200 and 5000 and sampled that same number of reactions according to this frequency distribution. By repeating this procedure, we generated 5000 frequency-sampled random networks. As a check to confirm that our results are independent of the relative sizes of our domain datasets, we also generated 5000 random reaction networks with the same size as members of the ensemble of frequency-sampled random reaction networks, but instead sampled reactions according to the sum of domain frequencies, computed within each domain and normalized by size of the domain (see fig. S9).

Fitting network measure scaling and permutation tests

For each network measure, a scaling relationship was fit as a function of the size of the LCC of the network. For each measure, three different models were tested: a power law of the form y = y₀ x^β, a linear relationship of the form y = βx + y₀, and a quadratic function of the form y = β₁x + β₂x² + y₀. For both the assortativity measures, the preferred fit was also compared with a constant y = β. The preferred model was chosen as the one that minimized cross-validation errors, according to 10-fold cross validation, across the entire dataset.

Once a model was chosen, a simulated permutation test was performed to determine whether the scaling relationship for a given attribute was the same for ecosystems and individuals or whether it was distinct (61). We took as the null hypothesis that the scaling relationship across different levels of organization is constant and used the fitted scaling parameters (for individuals and ecosystems) as the test statistic. We used fitted 1,000,000 resamples of the complete dataset to estimate the likelihood of the fit for individuals (or ecosystems) to have been drawn randomly from the complete dataset. We performed this test for both the ecosystem and individuals; if there was a difference in the estimated likelihoods, we took the greater of the two. These likelihoods are the (two-sided) P values reported in table S2. The same procedure was followed to determine the distinguishability of ecosystem networks with the randomized controls (random genome networks and random reaction networks). Random reaction networks were distinguishable from ecosystems networks for all measures, with P = 10⁻⁶.

To estimate the true scaling parameters and 95% confidence intervals, a bootstrap sample of 100,000 was used for each network attribute (61). If the permutation test allowed us to reject the hypothesis of a constant scaling relationship across individuals and ecosystems to a confidence greater than 0.01, then the scaling parameters were estimated separately for the individuals and ecosystems, otherwise the complete dataset was fit. The scaling parameters (and confidence intervals) for distinct domains were also estimated using a bootstrap of 100,000 samples. For scaling fits and confidence intervals, see data file S1.

Predicting evolutionary domain from topology

To demonstrate that topological features of genomes from different domains are distinct, multinomial regression was used. Specifically, we implemented models where the domain of the network was the response class, and a single topological feature, normalized by the size of the LCC of the network, was the dependent variable. We found topological features of networks alone were often not predictive of the domain, but the ratio of the topological properties to the size of the network provided a more accurate prediction. Prior to the regression, these normalized topological measures were scaled and centered (61). The regression was implemented in base R using the glm(..), function. To control for overfitting, the training data were composed of an equal number of samples from each domain. In particular, only 35 networks of each domain were sampled, and the model was tested on the remaining data. This process was repeated 100 times, and the average model error is reported in the text (Fig. 6E).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/1/eaau0149/DC1

Section S1. Network representations of catalyzed biochemical reaction

Section S2. Topological measures

Fig. S1. Percentage of nodes in the LCC of a network versus the size of its LCC.

Fig. S2. Reaction knockout for unipartite networks.

Fig. S3. Additional network measures for individuals and ecosystems show universal scaling across levels.

Fig. S4. Scaling of bipartite network structure for individuals and ecosystems.

Fig. S5. Additional network measures for randomly sampled individuals and randomly sampled reactions.

Fig. S6. Scaling of bipartite network structure for randomly sampled individuals and randomly sampled reactions.

Fig. S7. Distributions of network sizes for each domain and across levels of organization.

Fig. S8. Biochemical diversity and network topology measures for parsed datasets.

Fig. S9. Biochemical diversity and network topology measures for domain-weighted frequency-sampled random reaction networks.

Table S1. Percentage of networks in each dataset with x% of nodes in the LCC.

Table S2. Distinguishability of individuals and ecosystems, and ecosystems and random genome networks.

Data file S1. Scaling parameters for topological measures with 95% confidence intervals.

Data file S2A. Summary of measured network properties, by domain.

Data file S2B. Summary of measured network properties, by levels (parsed data only).

Data file S2C. Summary of measured network properties, by levels (parsed data excluded).

References (73–75)