High pressure-temperature experiments suggest late delivery of life-essential elements to Earth by a large differentiated body.
Abstract
Earth’s status as the only life-sustaining planet is a result of the timing and delivery mechanism of carbon (C), nitrogen (N), sulfur (S), and hydrogen (H). On the basis of their isotopic signatures, terrestrial volatiles are thought to have derived from carbonaceous chondrites, while the isotopic compositions of nonvolatile major and trace elements suggest that enstatite chondrite–like materials are the primary building blocks of Earth. However, the C/N ratio of the bulk silicate Earth (BSE) is superchondritic, which rules out volatile delivery by a chondritic late veneer. In addition, if delivered during the main phase of Earth’s accretion, then, owing to the greater siderophile (metal loving) nature of C relative to N, core formation should have left behind a subchondritic C/N ratio in the BSE. Here, we present high pressure-temperature experiments to constrain the fate of mixed C-N-S volatiles during core-mantle segregation in the planetary embryo magma oceans and show that C becomes much less siderophile in N-bearing and S-rich alloys, while the siderophile character of N remains largely unaffected in the presence of S. Using the new data and inverse Monte Carlo simulations, we show that the impact of a Mars-sized planet, having minimal contributions from carbonaceous chondrite-like material and coinciding with the Moon-forming event, can be the source of major volatiles in the BSE.
INTRODUCTION
The initial budget and distribution of volatile elements among early-forming reservoirs [chiefly, core versus mantle/magma ocean (MO)] remain largely unknown for all terrestrial bodies (1, 2). Because the budget of major volatile elements in MOs also has a key influence on the composition of the early atmosphere (1, 3, 4), understanding the role of early planetary differentiation is essential in setting the boundary conditions for the subsequent evolution of carbon (C)–nitrogen (N)–sulfur (S) volatile cycles. Hafnium (Hf)–Tungsten (W) chronometry of iron meteorites suggests that metal-silicate separation in protoplanetary bodies occurred as early as ~1 million years after the formation of the Solar System (5). Accordingly, core formation would have set the initial elemental distribution among planetary reservoirs (1–4, 6). Therefore, to understand the origin of volatiles on Earth, delivery by putative building blocks needs to be considered in tandem with early differentiation. Comparisons between the nonradiogenic isotopes of geochemical and cosmochemical reservoirs for a wide suite of nonvolatile elements reveal that planetary embryos in the inner Solar System were originally volatile-depleted because of the accretion of material that was isotopically similar to enstatite (E-type) chondrites (6, 7). However, isotopic similarity of 15N/14N and D/H ratios among the silicate reservoirs of all measured bodies in the inner Solar System with carbonaceous chondritic material, especially CI chondrites (8, 9), suggests that volatile-rich, CI chondrite-like material was the primary source of major volatiles, i.e., C, N, S, and water, in the bulk silicate Earth (BSE = atmosphere + hydrosphere + crust + mantle). The suggestion for the mixing of compositionally and isotopically distinct cosmochemical reservoirs is supported by dynamic simulations, which suggest that the early two-stage, inward-and-outward movement of giant planets scattered carbonaceous chondrite-like material into the inner Solar System, thereby presenting a heterogeneous mixture of volatile-depleted and volatile-rich planetary embryos in the source zone of Earth’s accretion (10). Yet, the timing of volatile delivery to Earth, as well as the mechanism for delivery, remains debated, with suggestions for delivery both during and after the main phase of Earth’s accretion.
Recent findings on the similarity of Ru isotopic compositions of the BSE and E-type chondrites mean that Earth’s late veneer had an E-chondrite–like isotopic signature (6, 11), thereby making post–core formation delivery an unlikely primary source for major volatiles on Earth. In addition, although the C/S ratio of the BSE is nearly chondritic, the superchondritic C/N ratio challenges the proposition that C and N delivery solely occurred via undifferentiated CI chondrite–like material after core formation was complete (1, 2, 12). Although the literature estimates of the C/N ratio of the BSE vary, with one study (9) proposing a mean value of ~313 and other studies (7, 13) providing values in the range of ~40 to 50, a growing consensus (1, 2) on the C/N ratio of the BSE has converged on the lower estimate (40 ± 8, all reported errors are 1−σ, unless stated otherwise). This estimated BSE C/N ratio is distinctly greater than the C/N ratio of CI chondrites (20.66 ± 3.88), as well as other carbonaceous chondrites (mean value in the range of ~16 to 24), with no overlap within the 1−σ range and a statistically insignificant overlap (~0.05 probability density area) within the 2−σ range (fig. S1 and table S1). Therefore, if major volatiles in the BSE, such as C and N, had a CI-chondritic origin, then an early differentiation process is required to elevate the C/N ratio of the BSE relative to CI chondrites.
Alloy-silicate partitioning experiments with C-N (S-free)– and C-S. (N-free)–bearing alloy-silicate systems in a limited range of pressure (P)–temperature (T) conditions reveal that > and > ( = alloy-silicate partition coefficient of element i = concentration of element i in alloy/concentration of element i in silicate). Therefore, volatile delivery during core formation should have left subchondritic C/N and C/S ratios in the BSE (1–4, 12, 14). Consequently, the superchondritic C/N ratio in the BSE has been explained either via the accretion of C-rich, ureilite-like bodies or via the loss of an early, N-rich atmosphere (1, 2, 12, 15). However, the similarity of the 15N/14N and D/H ratios in the BSE with CI chondrites (8, 9) suggests that CI chondrites, rather than ureilite-like bodies, were the primary source of volatiles in the BSE. On the other hand, a higher solubility of N relative to C in MOs (an indicator that early atmospheres were C rich) (1) and a lack of fractionation of volatile metals (16) make impact-induced early atmospheric loss(es) and isotopic fractionation during thermal escape, respectively, as unlikely explanations for the superchondritic C/N ratio in the BSE.
Hf-W Chronometry reveals that, unlike Mars-sized planetary embryos that formed in the first few million years (17), a larger planet, like Earth, had a protracted growth period proceeded by the collision and accretion of differentiated planetary embryos over tens of millions of years (18). The addition of differentiated bodies with S-rich cores during the active phase of Earth’s growth period has been suggested to explain the chondritic C/S ratio of the BSE (4, 14); however, the C/S ratio provides a nonunique constraint because the near-chondritic C/S ratio of the BSE can also be satisfied by the accretion of an undifferentiated chondritic late veneer (19). It remains unclear whether the superchondritic C/N ratio in the BSE, which necessitates the role of early differentiation, can be explained by the merger of a volatile-bearing, differentiated planetary embryo without violating the isotopic constraints of other nonvolatile elements. The chief mechanism by which strong C depletion in a post–core formation MO could be avoided is via a decreased solubility of C in the alloy caused by strong, nonideal interactions between S and C in the Fe-alloy melt (4, 14). However, if similar nonideal interactions were operative between S and N in the alloy melt, then the siderophile behavior of C and N could diminish similarly in the presence of S. If this is true, then establishing a superchondritic C/N ratio in the bulk silicate reservoirs of planetary embryos with S-rich cores may not be possible. Hence, to test whether the accretion of differentiated planetary embryos can be a plausible delivery mechanism for all life-essential volatiles to Earth, alloy-silicate fractionation needs to be investigated in mixed C-N-S-bearing systems.
Experimental and analytical procedure
To constrain the effect of alloy-silicate equilibration on early C-N-S fractionation applicable for an assortment of planetary embryos that accreted in a range of S-poor to S-rich conditions, we performed high P-T experiments using piston cylinder (PC) and multi-anvil (MA) devices. We used Fe-Ni-N-C±S alloys and mafic silicate mixtures (table S2) in graphite capsules at 1 to 7 GPa and 1600° to 1800°C in a limited oxygen fugacity range (fO2) of IW −1.31 to −0.83 (except for one experiment, which was more reduced at IW −1.71; IW refers to fO2 relative to the iron-wüstite buffer, defined by the coexistence of Fe and FeO) (table S3). The limited and relatively low P range of our experiments is justified as we explored the effect of alloy-silicate equilibration on C-N-S budgets in bulk silicate reservoirs of planetary embryos that are much smaller than Earth, while a relatively oxidized fO2 range was explored to simulate accretion of relatively oxidized planetary embryo(s) that had a late-stage merger with a more reduced proto-Earth (20, 21). The concentrations of major elements, N, and C in the experimental alloy phases (table S4) and of major elements and N in the quenched silicate melts (table S5) were determined using an electron microprobe. The C and H contents of the silicate glasses were determined using an ion microprobe. Raman spectroscopy was used to evaluate the C-O-N-H speciation in the silicate glasses (see Materials and Methods for details).
RESULTS
Texture of experimental products
All of the experiments produced quenched metal blobs in silicate glass pools (fig. S2), except for the experiments at 6 and 7 GPa, which had a uniform distribution of microcrystals in their silicate melts, thereby making their silicate phase unsuitable for C measurement. In agreement with previous studies that used N-free systems (22, 23), S-bearing alloys at P > 1 GPa showed quenched textures of S-rich and S-poor microphases, while at 1 GPa, they formed two immiscible alloy phases (S-rich and S-poor alloy melts). Because of their immiscibility, the alloy products at 1 GPa were not considered for any further discussion in this study.
N and C in the alloy and silicate melts
At any given P-T condition, the N content in the alloy melt is indistinguishable between experiments with alloys that are S free and intermediate S bearing [~12 to 15 weight % (wt %) S] and lies in a narrow range of ~1.7 to 3.4 wt %. However, at high-S contents (~21 to 28 wt % S), the N content in the alloy melt drops by ~50% and lies in a range of ~0.75 to 1.5 wt % (Fig. 1A). In contrast, the C solubility in the alloy melt drops monotonically from ~3.1 to 4.5 wt % in the S-free alloy melt to ~1.5 to 2.5 wt % in the intermediate S-bearing alloys, and further to ~0.3 to 0.6 wt % with high S contents in the alloy (Fig. 1B). This means that the presence of S has a strong negative effect on the abundance of C but a minor effect on the presence of N in the alloy melt structure. The C solubility in the silicate melt increases from ~200 to 650 parts per million (ppm), with an increase of the N content in the silicate melt from ~200 to 1900 ppm (fig. S3). In all our experiments, the C solubility in the alloy melt is lower than previous studies conducted under similar conditions in N-free systems, while the C solubility in the silicate melt is higher (3, 4, 14, 24, 25). Raman spectra confirm that, in addition to the peaks indicating the presence of N2 and N-H and C-H complexes, there is another peak at ~2110 cm−1, which can correspond to C-N–bearing cyanide complexes (26, 27), thereby explaining the higher C saturation in N-bearing glasses (fig. S4, see Materials and Methods for details).
Fig. 1. Experimentally determined N contents and C solubilities as a function of S contents in Fe-Ni alloy melts.
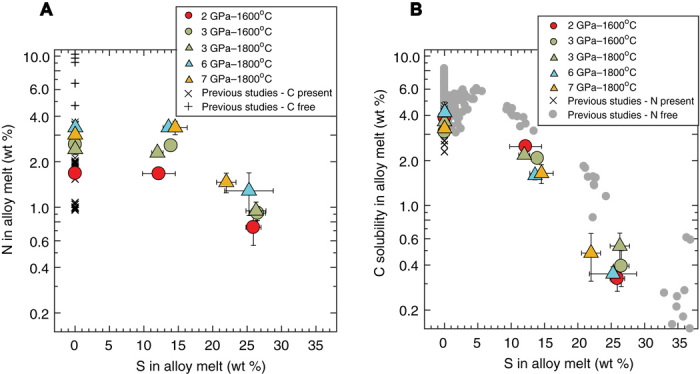
(A) The N content in the alloy melt is not significantly affected by the presence of S. The N content does not show a significant change between experiments with S-free and low S-bearing (~12 to 15 wt %) alloy melts for a given P-T condition, while it drops by 50% for high S-bearing (~21 to 28 wt %) alloys. The N content in a C-free system (29) is higher than that in a C-present system in this study and previous studies (12, 63). (B) The C solubility in the alloy melt decreases steadily with an increasing S content in the alloy melt with an order of magnitude difference between S-free and high S-containing alloys. The C solubility in a N-free system (3, 4, 14, 24, 25, 56) is higher than that in a N-present system in this study and previous studies (12, 63). Error bars in both cases are 1−σ and, if absent, are smaller than the symbol size.
DISCUSSION
Partitioning of N and C between the alloy and silicate melts
The lies in a very narrow range (~10 to 31) across the entire range of starting compositions, from S-free to S-rich systems, with the S-free to intermediate S-bearing alloy systems having slightly higher values relative to the high S-bearing alloy systems (Fig. 2A). However, in the presence of N, high S in the alloy leads to a drop in the to an order of magnitude lower values in comparison to the intermediate S-bearing or S-free alloy systems (Fig. 2B). Because of a simultaneous expulsion of C from the alloy melt and an increase in its solubility in the silicate melt caused by N, the is distinctly lower in comparison to those in N-free systems (Fig. 2B) (3, 4, 14, 24, 25). Because the is largely unaffected by the presence of S in the alloy, while the drops considerably, mainly because of an increase in the S content of the alloy and also partly because of C-N complexation in the silicate melt, our / and / values reveal that C is less siderophile than both N and S for MO systems with >25 wt % S in the alloy, while C is more siderophile than N but less siderophile than S for those with ~12 to 25 wt % S in the alloy (Fig. 3, A and B).
Fig. 2. Partition coefficients of N and C between the Fe-Ni alloy melt and the silicate melt as a function of S content in the alloy melt.
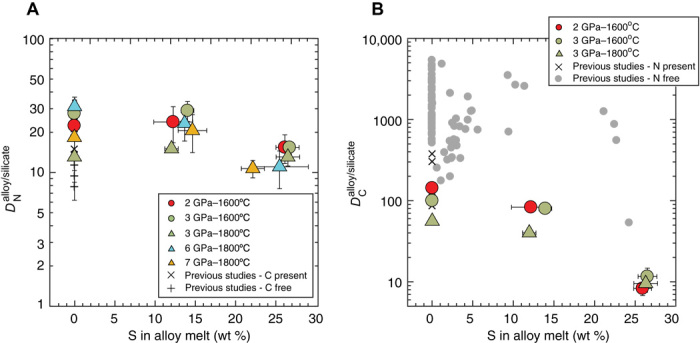
(A) For a given P-T condition, the does not vary notably with an increase in S in the alloy melt. (B) In the presence of N in the alloy melt, the drops by an order of magnitude from S-free to high S-bearing alloys with values as low as ~10 for N-bearing, S-rich alloys. The in a N-free system (3, 4, 14, 24, 25, 56) is higher than that in a N-present system in this study and a previous study (12). Error bars in both cases are 1−σ and, if absent, are smaller than the symbol size.
Fig. 3. Ratios of the measured partition coefficients of C and N and C and S between the alloy melt and the silicate melt as a function of S content in the alloy melt.
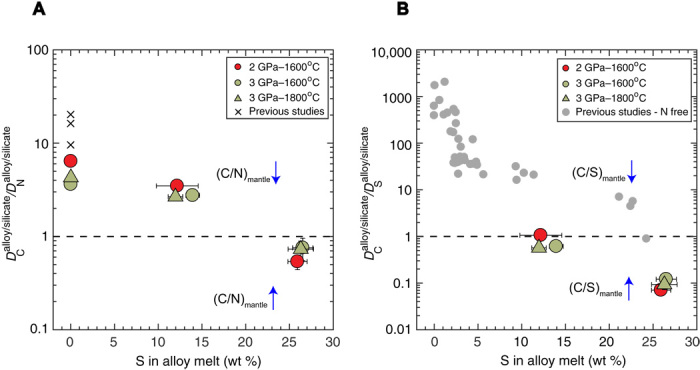
(A) The / ratios show that with S-free and intermediate S contents in the alloy melt, C is more siderophile than N, while for high S contents in the alloy, C is less siderophile than N. (B) The / ratios show that under S-poor conditions, C is more siderophile than S (for N-free systems), while at intermediate S (for N-bearing systems) and high S contents (for both N-free and N-bearing systems) in the alloy melt, C is less siderophile than S. Dashed horizontal lines in both panels delineate data fields where the (C/N)mantle and (C/S)mantle increase (↑) or decrease (↓) from the initial values due to equilibrium alloy-silicate fractionation. Error bars in both cases are 1−σ and, if absent, are smaller than the symbol size.
Mode of accretion and core-mantle differentiation
Previous studies have suggested that the C, N, and S budgets of the BSE cannot be satisfied via traditional single- or multi-stage core formation models (1–3, 12, 24). Earth’s core can contain up to 2 wt % S (28); however, the effect of S in the core-forming alloy on the was hitherto unknown. Combining the negligible effects of low S in the alloy from this study and high P-T constraints on the from this study and from a previous study (29) and the parameterization of the (fig. S5 and Eq. 4) and (30) relevant for an average single-stage core formation in Earth [e.g., P = 50 GPa and T = 4000 K (31)], this study reaffirms that the availability of C-N-S via ~1.5 wt % of present-day Earth’s mass of CI-chondritic material (32) during a single-stage core formation on Earth cannot explain the C-N-S abundances in the present-day BSE (fig. S6A). Varying the degree of alloy-silicate equilibration and the loss of an early atmosphere do not change this conclusion (fig. S6, A and B; see Materials and Methods for details).
On the other hand, for a planetary embryo with a core-forming alloy that can have much higher S contents than the postulated S content of Earth’s core of ~2 wt %, the superchondritic C/N ratio in its silicate reservoir can be attained either via a C-undersaturated core, if < , or via a C-saturated core, if > . If the C solubility in the alloy melt (Csolubility) is less than the C concentration in the alloy based on the (Ccalculated), then the Csolubility along with the , sets the C content in the alloy (Calloy), and the excess C contributes to the silicate MO of the planetary embryo. For example, for a bulk C content of 1 wt %, = 100, and alloy/silicate ratio = 0.5, mass balance calculations would yield a C content of the alloy core (Ccalculated) of ~2.9 wt %. However, if the Csolubility is 1 wt % under those conditions, then the Calloy would be fixed at 1 wt % and the excess C would be added into the silicate reservoir of the planetary embryo. However, this is an example calculation and only shows that a planetary embryo with a S-rich core. could potentially achieve a superchondritic C/N ratio in its silicate fraction during core-MO equilibration. Once such a superchondritic C/N ratio is achieved via the formation of a S-rich core, it can be elevated further in the embryo’s MO via the loss of an early overlying atmosphere, because at the fO2 conditions considered for differentiation here, N is less soluble than C in the silicate MO [e.g., (1)], but the effects of such an atmospheric loss scenario for the embryo is not quantified further in our study. The question is, however, whether a planetary body with a S-rich core could be responsible for delivering the volatiles to Earth in the right proportions and what the composition, size, and structure of such a body are.
Identity of the planetary embryo delivering volatiles to Earth
To test whether a differentiated planetary body of any reasonable composition can deliver the major volatiles to the proto-Earth and to determine its possible size and architecture, we performed multiple sets of ~109 inverse Monte Carlo simulations, exploring the composition and mass range of the impactor, which, on merger with a volatile-depleted proto-Earth, satisfies the present-day BSE C (108 ± 20 ppm), N (2.7 ± 0.7 ppm), and S (225 ± 25 ppm) abundances [Fig. 4A; data from (1, 2)]. The bulk C and S contents in the impactor were varied from 0.05 to 6 wt % and from 0.05 to 8 wt %, respectively, to test the complete spectrum of chondritic values, while the bulk N was fixed at an average CI chondrite C/N ratio of ~21. The alloy/silicate mass ratio of the impactor (alloy/silicateimp) was varied from 0.05 to 0.5 (within the range for all rocky bodies in the inner Solar System, except Mercury), while the mass of the impactor relative to the present-day Earth’s mass (Mimpactor/MEarth) was varied from 0.01 to 0.5. In accordance with recent studies based on the geochemical abundances of C (4), Ni, Co, and W (21) and fluid dynamic simulations (33), we have assumed a core-merging scenario in which a large differentiated planetary embryo’s core merges with that of the proto-Earth without significant equilibration with the proto-Earth’s mantle (Fig. 4A).
Fig. 4. C-N-S delivery via a giant planetary impact with proto-Earth and the results of inverse Monte Carlo simulations used to obtain the composition and the mass of the impactor.
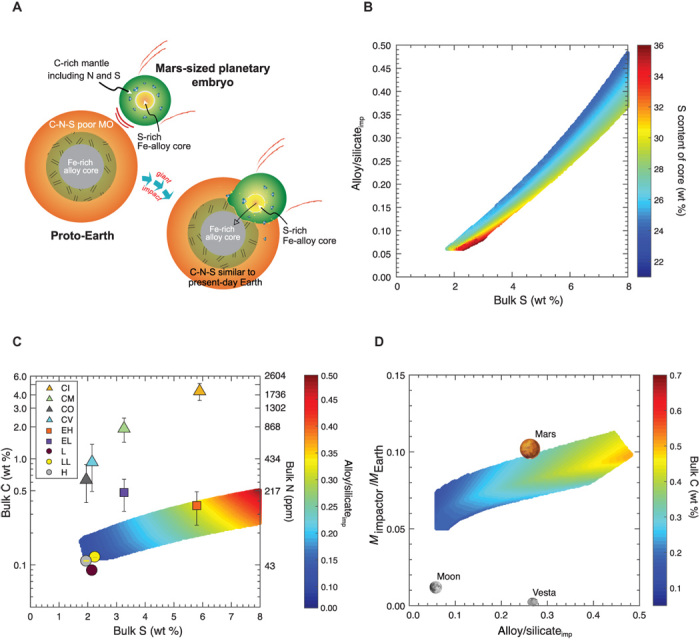
(A) Illustration showing the merger scenario of a volatile-bearing planetary embryo with a C-saturated, S-rich core to volatile-depleted proto-Earth. (B) The alloy/silicate ratio and the bulk S content are mutually dependent on the S content in the alloy of the impactor (the controlling variable from our experiments and calculations). (C) The bulk C content of the impactor as a function of the bulk S content as well as the alloy/silicate ratio of the impactor that yields possible volatile delivery solutions. Various chondritic meteorites are also plotted for comparison. (D) The mass of the impactor is constrained in a narrow range similar to that of Mars.
Through our simulations, we independently constrained the impactor’s mass, its bulk C content, and the S content of its core (Salloy,imp). The bulk S content of the impactor and the alloy/silicateimp ratio were dependent variables set by the Salloy,imp. An example forward model calculation (which represents one of the successful solutions from the Monte Carlo simulations) in fig. S7A shows that the target alloy/silicateimp is successfully constrained if the required C/N and C/S ratios of the impactor’s mantle match those of the present-day BSE, while the target mass of the impactor is constrained by the present-day C-N-S abundances in the BSE (fig. S7B). The Salloy,imp was directly proportional to the bulk S content of the impactor and inversely proportional to the alloy/silicateimp (Fig. 4B). The required bulk C content of the impactor, with maximum number of solutions at ~3000 ppm C, increases with increasing bulk S and alloy/silicateimp (Fig. 4C). Because the Csolubility varies inversely with the Salloy,imp (Fig. 1B), the bulk C content was affected by a combination of the bulk S content and the alloy/silicateimp, causing C enrichment in the mantle of the impactor via the expulsion of C from a C-saturated alloy. All model solutions favor a C-saturated core because the alloy/silicate partitioning alone yields a subchondritic C/N and C/S in the impactor’s mantle. The mass of the impactor was constrained to be MEarth, which is close to the mass of Mars (Fig. 4D).
The above inverse Monte Carlo simulations assume a proto-Earth whose bulk silicate fraction was volatile free. Given that C and N are expected to be strongly volatile/siderophile during the accretion of planetesimals, even if the proto-Earth accreted some volatiles before the giant impact, its silicate fraction would be essentially devoid of C and N due to impact-related losses/MO processing (24, 25), thereby validating our assumption of a volatile-depleted proto-Earth. However, our model results do not change substantially with the presence of volatiles in the proto-Earth, i.e., with a silicate fraction of proto-Earth containing either a small amount of C-N-S in a chondritic relative abundance or a C-N-S inventory affected by terrestrial core formation and atmospheric loss(es) (Fig. 5). In addition, using a fixed C/N ratio to determine the bulk N content of the impactor is not critical as our results are also mostly unaltered by varying the bulk C/N ratio of the planetary embryo within a 1−σ range (10–30) of the mean C/N ratio of all classes of carbonaceous chondrites (fig. S8).
Fig. 5. Effect of a nonzero volatile content in the bulk silicate portion of proto-Earth on the composition and the mass of the impactor, which establishes the C-N-S budget of the present-day BSE.
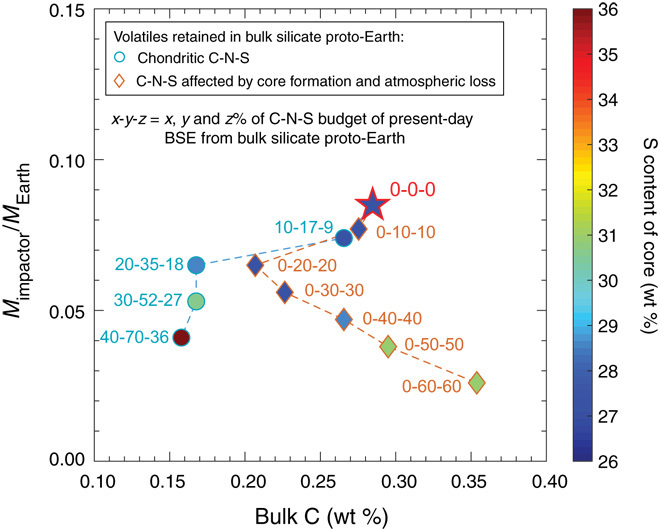
Increasing the C-N-S abundance in chondritic proportions in the silicate portion of proto-Earth (represented by circles) results in a decreasing bulk C content and mass of the impactor and an increasing S content in the impactor’s core. A decrease in the mass of the impactor is due to the delivery of a smaller fraction of the C-N-S budget of the present-day BSE by the impactor, while a superchondritic C/N ratio greater than that of the present-day BSE in the impactor necessitates a higher C enrichment in the impactor’s mantle via C exsolution from the core, which results in a higher S content of the core and lower bulk C content of the impactor. However, if the C-N-S inventory in the silicate portion of proto-Earth was affected by terrestrial core formation and atmospheric loss(es) (represented by diamonds), then, owing to the highly siderophile character of C, the bulk silicate portion of proto-Earth would be essentially C free but could retain N and S. Increasing the N-S abundance in the silicate portion of proto-Earth by up to 20% of the N-S budget of the present-day BSE results in a decreasing mass and bulk C content of the impactor, while the S content of the core almost remains constant. However, with greater than 20% of the N-S budget of the present-day BSE in silicate proto-Earth, the S content of the impactor’s core increases, delivering C/N and C/S ratios that are much greater than the C/N and C/S ratios of the BSE, and the bulk C of the impactor also increases, delivering the present-day C budget of the BSE via a proportionally smaller impactor. The star represents a C-N-S–free bulk silicate proto-Earth.
Our models predict a much lower bulk C in the impactor (~0.1 to 0.5 wt %) relative to CI chondrites (Fig. 4C). Therefore, the impactor can be mostly composed of volatile-depleted material that is isotopically similar to E-type chondrites. A minimal contribution from CI chondrite–like materials to the embryo can satisfy the C-N-S budget of the BSE as well as the isotopic similarity between major volatiles of the BSE and CI chondrites. However, the exact contribution from CI chondrites for such a body depends on the volatility-induced C-N loss during accretion of the impactor. If the impactor incurred minimal C-N loss during accretion, the contribution of CI chondrites to the overall makeup can be as low as 0.1 to 2 wt %. However, higher degrees of C-N loss would favor a greater contribution from CI chondrites to the impactor (greater than ~2 wt %). A higher contribution from CI chondrites to the impactor could also supply the water budget to the present-day BSE, whereas an E-chondritic impactor would be essentially dry (34).
Effect of equilibration of the impactor’s core with proto-Earth’s mantle
Unlike the above calculations where the impactor’s core directly merges with the proto-Earth’s core, if the impactor’s core undergoes small degrees of equilibration with the post-merger MO of the proto-Earth, then some of the C-N-S budget of Earth’s BSE can also be supplied by the impactor’s core along with its bulk silicate reservoir. The most probable bulk C content of the impactor increases, while the mass of the impactor decreases with increasing degree of equilibration of the impactor’s core (Fig. 6; see Materials and Methods for details). With an increasing degree of equilibration of the impactor’s core, the C-N-S abundances in the BSE are supplied not only by the impactor’s mantle but also by the equilibrating impactor’s core, which is rich in C-N-S. Therefore, an increase in the degree of equilibration of the impactor’s core with post-merger MO of the proto-Earth favors a decrease in the mass of the impactor. If a significant alloy-silicate equilibration occurs during the late-stage impacts of differentiated bodies, then the predicted small size of the impactor (Fig. 6B) required for the C-N-S delivery can match the recent dynamic constraints on the delivery of a late veneer via a small differentiated body (35).
Fig. 6. Results of inverse Monte Carlo simulations showing the effect of the degree of equilibration of the impactor’s core with the post-merger MO on the estimated bulk C content and the mass of the impactor.
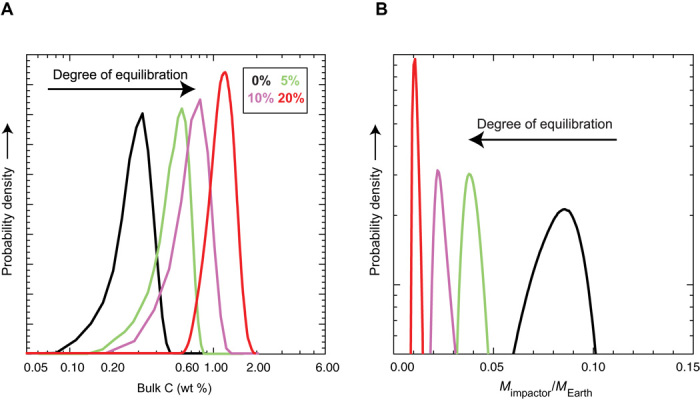
(A) The most probable bulk C content (wt %) of the impactor as shown by the peak increases with an increasing degree of equilibration of the impactor’s core with the post-merger MO. (B) The most probable mass of the impactor with respect to the present-day Earth’s mass decreases with an increasing degree of equilibration of the impactor’s core with the post-merger MO (see Materials and Methods for details). These calculations assume the bulk silicate portion of the proto-Earth to be C-N-S free (star in Fig. 5).
Relative timing of volatile delivery
The similarity between N and H isotopic compositions of lunar glasses and the BSE (36, 37) suggests a common origin for the major volatiles in the BSE and the Moon, which makes volatile delivery after the Moon-forming event, as a late veneer, unlikely. Therefore, in our simulations, a scenario in which the impactor’s core undergoes almost no equilibration after impact with the proto-Earth’s mantle is more plausible. However, in contrast to volatile delivery before the Moon-forming impact (7), a Mars-sized impactor, predicted by our simulations, points toward volatile delivery during the Moon-forming event (38). Because Earth and the Moon have C, N, and H isotopic compositions that are indistinguishable from CI chondrites (8), whereas O, Ca, Ti, and Cr isotopic compositions are akin to E-type chondrites (6), we suggest that the impactor that brought C, N, and S to the BSE could be the Moon-forming impactor, if it were made with a small contribution from CI chondrites. Our study also explains the similarity between the terrestrial isotopic ratios of C, N, and H with eucrite meteorites (8), which suggests an early accretion of CI-chondritic material in the inner Solar System. This, along with the early formation of differentiated planetary embryos (5), may indicate that the timing of the accretion of the impactor’s volatiles, similar to the accretion of the volatiles in Vesta (8), was within ~5 to 20 million years of the Solar System’s formation. However, the delivery of the volatiles to Earth via the merger of a larger planetary embryo was at a later stage. Because the postimpact silicate Earth achieves the present-day C-N-S abundances in our model, any late-stage sulfide segregation event in the proto-Earth (39) should predate the accretion of the planetary embryo.
Last, the positive correlation of C and N abundances in the silicate melts, along with the spectroscopic confirmation of possible C-N species, suggests that the codelivery of C, N, and S to the BSE via a giant impactor may also explain the generation of essential reduced precursors for prebiotic organic molecules, such as HCN, NH3, and CH4, through the incorporation of the impactor’s atmosphere (40, 41).
MATERIALS AND METHODS
Starting materials
The experiments were performed with homogeneous mixtures of ~60 to 70 wt % silicate and ~30 to 40 wt % alloy mixes in graphite capsules. A synthetic tholeiite basalt (ThB1), similar to the composition of a natural tholeiite basalt (ThB) used in several previous high-pressure, metal-silicate partitioning experiments (3, 4, 24, 25), was used as the silicate mix. To avoid the interference of a N Kα line and a fluorescence line produced by Ti Lα in microprobe analyses (42), we constructed a TiO2-free silicate mix. ThB1 was prepared by mixing reagent-grade oxides (SiO2, Fe2O3, Al2O3, Cr2O3, MnO, and MgO) and carbonates (CaCO3, Na2CO3, and K2CO3). The reagent oxides and carbonates were mixed under ethanol in an agate mortar and pestle for 2 to 3 hours. To devolatilize the mixture and convert Fe2O3 into FeO, the mixture was fired at 1000°C and logfO2 ~FMQ −2 [FMQ (Fayalite-Magnetite-Quartz buffer)] using a CO-CO2 Deltech gas mixing furnace for 24 hours. The alloy compositions were made using reagent-grade Fe and Ni metals, with fine powders of either Fe4N or Fe7N3 as the source of N and either reagent-grade FeS or natural FeS2 as the source of S. Metal mixes were prepared under ethanol using an agate mortar and pestle, and when dry, they were stored in a desiccator for >72 hours.
High pressure (P)–temperature (T) experiments
The experiments at 1 to 3 GPa and 1600° to 1800°C were performed using an end-loaded PC device, and experiments at >3 GPa were performed using a 1100–metric ton Walker-style MA device at Rice University. The PC experiments used a 12.7 mm BaCO3/MgO assembly, following the P-T calibrations and procedural details similar to several previous studies (24, 25, 43). MA experiments were performed using WC anvils with 8-mm truncations and an octahedral assembly with a 14-mm edge length following calibrations detailed in a previous study (14). Both PC and MA experiments used type C thermocouples placed within 1 mm of the capsule to control and monitor the experimental temperature set using Eurotherm controllers.
Three sets of experiments with different alloy mixes (S-free, intermediate S-bearing, and high S-bearing) were repeated at a given pressure (1 to 7 GPa) and in a narrow temperature interval (1600° to 1800°C) to study the effect of S content in the alloy on and . Graphite capsules were used to hold the alloy-silicate mixes to study C solubility in the alloy and the silicate melt, as well as to achieve a T approaching planetary MO conditions. MA experiments were conducted using three-chambered graphite capsules with starting compositions loaded in separate sample chambers, while PC experiments were conducted by loading a single composition into graphite capsules. All the experiments were pressurized to the target pressure at room temperature, followed by heating at a rate of 100°C/min. To reduce the porosity in the graphite capsules and prevent leakage of the alloy melt, the experiments were held at 850° to 900°C overnight and then raised to the target temperature. The experiments were quenched by cutting off power to the heater, and after depressurization, the recovered samples were cut into half using a tungsten-wire saw. Three-chambered capsules were cut transversely into two halves using a tungsten-wire saw to observe all three sample chambers simultaneously, while single-chambered capsules were cut longitudinally. Both halves were mounted in Crystalbond, ground using 1200-grit sandpaper, and polished using a 0.3-μm alumina slurry on a velvet cloth. Polished samples were soaked in acetone overnight to remove the Crystalbond. The polished surfaces were analyzed using an electron microprobe, an ion microprobe [secondary ion mass spectrometry (SIMS)], and Raman spectroscopy.
Analytical procedure
Electron probe microanalysis
Electron probe microanalysis data acquisition was performed at Rice University on a JEOL JXA 8530F Hyperprobe using five wavelength-dispersive spectrometers (WDSs). Silicate melt analysis was performed on C-coated samples. Natural glass standards provided by the Smithsonian Institute and mineral standards from SPI Supplies were used for measuring the characteristic Kα x-ray lines of the measured elements as follows: Na (Glass 5 Reference A NMNH-117218-4), Si (Glass 6 Reference B NMNH-117218-1), Ca (Glass 3 Basalt_NMNH-113716-1), K (Glass 8 Reference D NMNH-117218-3), S (Glass 6 Reference B NMNH-117218-1), Fe (Glass_3_Basalt_NMNH-113716-1), Cr (chromite), Mn (rhodonite), Ni (pentlandite), Al (Glass 10 IR-W NMNH 117084), and Mg (Glass 3 Basalt NMNH-113716-1).
Analytical sessions with various accelerating voltages (10, 15, 20, and 25 kV), beam currents (10, 20, 50, and 100 nA), and counting times (10 s/5 s, 80 s/60 s, and 100 s/80 s per peak on each of the lower [bk−] and upper [bk+] backgrounds, respectively) were performed to determine the optimum peak/background ratio when analyzing N Kα with the N standard [boron nitride (BN)] for silicate melt. An accelerating voltage of 15 kV, a beam current of 50 nA, and counting times of 80 s/60 s were found to be the optimum conditions to analyze N in silicate melts. To incorporate a more robust matrix correction, in contrast to N analyzed separately by a previous study (12), N was measured during the same analytical routine as all the other major and minor elements with a spot size of 20 μm. The use of a defocused electron beam also allowed the integration of quenched FeS microinclusions in the silicate melt, which are interpreted to be a portion of the dissolved S in the melt under experimental conditions (44). Some of the silicate melts were also analyzed for major elements using an accelerating voltage of 15 kV and a beam current of 10 nA, and it was verified that concentrations of nonvolatile and volatile elements, such as Na and K, were similar to the measurements taken when using a higher beam current of 50 nA. After several peak searches for N in the glass samples, narrow background offsets were set manually ([bk−], 2.2 mm; [bk+], 2.5 mm) to (i) avoid errors in measuring the high lower background (bk−) of N, (ii) lower the effect of the background curvature of N, and (iii) avoid or minimize the interferences of the background measurements with x-ray lines or fluorescence peaks of other elements (45). The average detection limit of N in the glass analysis lies between ~100 to 200 ppm, with an average instrumental SD (1σ) of ~12%. The N Kα line was measured using an LDE2 diffracting crystal. An LDE2 diffracting crystal was preferred over an LDE1 because of its significantly higher counts per second for a similar accelerating voltage and beam current. In addition, several WDS scans in the L-value region of the N peak on BN and Ti metal standards show that both LDE1 and LDE2 crystals give similar critical interferences between N Kα and Ti secondary peaks, especially when the two elements are similar in concentration or Ti > N. A low curvature of the background between the narrow offsets ([bk−], 2.2 mm; [bk+], 2.5 mm) under the N peak meant that a straight background method approximated well the correct background values and net N intensity. The alloy phase was analyzed in separate sessions using freshly aluminum-coated samples and standards in the same coating session. Natural- and laboratory-synthesized standards used for the alloy phase analyses were Si (Si metal), C [laboratory-synthesized stoichiometric Fe3C (46, 47)], Fe (Fe metal), and S (natural troilite). Fe3N was the standard material used for N calibration in the alloy. The Fe3N standard was synthesized in a PC apparatus using a similar BaCO3/MgO assembly to the one mentioned earlier. Fe3N powder was loaded in a crushable MgO assembly and held at 1.5 GPa and 750°C for 120 hours. To determine whether the targeted stoichiometry of Fe3N was achieved, x-ray diffraction (XRD) spectra of the run product were obtained using a Rigaku D/MAX West Micro XRD system at Rice University. The obtained XRD pattern was in good agreement with the previously published spectra of Fe3N (48). Larger background offsets were manually selected for N analysis in alloys ([bk−], 5 mm; [bk+], 10 mm) as the concentration of N in metals is much higher and the peak is relatively wide.
To minimize hydrocarbon contamination (relevant for C analyses) on the alloy surface during analysis, an accelerating voltage of 12 kV and an emission current of 80 nA was used to produce a stable and high peak/background ratio for C Kα, following the findings of a previous study (46). A spot size of 20 μm was used, and the counting times were 10 s for peak and 5 s on each of the lower and upper backgrounds, respectively, except for N where 80 s for peak and 60 s for background were used. A ZAF matrix correction method was used for the quantification of both glasses and alloys.
Secondary ion mass spectrometry
The total amount of C and H dissolved in the experimental glasses was determined using a Cameca IMS 1280 ion microprobe at the Woods Hole Oceanographic Institution. Repolished samples were placed in an indium mount, cleaned, and then dried in a vacuum oven at 100°C. The mounts were coated with gold and placed under vacuum before analysis. A spot size of 10 μm in diameter was focused on by a beam of 133Cs+ ions with a 1- to 1.5-nA current and 12-kV energy and rastered over a 30 μm by 30 μm area. Negatively charged ions were accelerated at 10 kV into a double-focusing mass spectrometer. The central 15 μm by 15 μm portion of the beam-rastered area was analyzed by placing a mechanical aperture in the focal plane of the secondary ion optics. Spots were presputtered for 240 s and then measured over at least 10 cycles of ion intensities. 12C, 1H16O, and 30Si were recorded, and intensity ratios of 12C/30Si and 1H16O/30Si were converted to C and H2O contents during each cycle using the calibration curves developed in the same analytical session as was done in previous studies (3, 4, 24).
Raman spectroscopy
The nature of dissolved C-O-N-H in glassy samples was determined using a Renishaw inVia Raman microscope at Rice University following the methodologies detailed in previous studies (3, 4, 24). A 514-nm laser was used to measure the spectra in the frequency range of 200 to 5000 cm−1 using a 50× objective lens and an output power of 23 mW. Each spectrum was accumulated five times at an exposure time of 30 s to increase the signal/noise ratio.
Estimation of oxygen fugacity
Oxygen fugacity (fO2) in the experiments was estimated on the basis of the coexistence of the Fe-alloy and the silicate melt via the equilibrium reaction
| (1) |
from which the fO2 relative to the fO2 of the iron-wüstite buffer (ΔIW) at a given P-T is defined by
| (2) |
where and represent the activity of the FeO component in the silicate melt and the activity of the Fe component in the alloy melt, respectively; and represent the mole fraction and activity coefficient of the FeO component in the silicate melt, respectively; and and represent the mole fraction and activity coefficient of the Fe component in the alloy melt, respectively. The fO2 calculations were performed using the nonideal solution model, assuming a fixed of 1.5 (49). The in the alloy liquids was calculated using the ε approach in Wagner equations, taking into account nonideal interactions between the components in the alloy melt (50). The activity of Fe in the alloy melt was calculated using the “Online Metal Activity Calculator” (http://norris.org.au/expet/metalact/). The fO2 calculations show that the calculated nonideal fO2 values are between IW −1.71 and −0.83, while the calculated ideal fO2 values are between IW −1.76 and −1.03.
Speciation of C-O-H-N volatiles in glasses
Typical Raman spectra are shown in fig. S4. The narrow band at ~2335 cm−1, which appears across the entire experimental range, belongs to the main vibron of the N2 molecule (51, 52). The peak near 3290 cm−1 has been assigned to N-H stretching in N+H–bearing complexes, such as (51, 52). As all our experiments were performed in a limited fO2 range, we did not see an interchange of N speciation from relatively oxidized N2 molecules to reduced N-H–bearing species as experimental conditions become more reduced (51, 53). The broad peak at ~3570 cm−1 has been attributed to the total water content, either as OH species bonded as Si-OH or as molecular H2O (3, 4, 52, 54, 55). A weak band at ~1600 cm−1 has also been assigned to vibrations of the OH group (52, 55). A small peak at ~2900 cm−1 has been associated with dissolved CH4 in silicate glasses (3, 4, 54).
In previous studies with C-bearing and N-free systems, the peak at ~2110 cm−1 has been assigned to either vibrations of isolated CO groups (56) or CO vibrations in Fe-carbonyl complexes (54, 57). Graphite-saturated C solubility in N-bearing experiments is systematically higher than previous studies under similar conditions for N-free systems. Figure S3 shows that the C solubility in the silicate glasses increases with an increase in the N content, which would point toward the possible formation of C-N species. As CN− and CO are isoelectronic species, as well as strong-field, π-bonding ligands, vibrational similarity is expected between them (26). The vibrational spectra of CN− in various inorganic molecules were placed at a Raman peak of ~2090 to 2130 cm−1 (26, 27, 58, 59). Taking into account our elevated C solubility data and the vibrational similarity of CN− and CO, we assigned the peak at ~2110 cm−1 to CN−. The observation of a similar peak in N-free studies might have been due to contamination related to atmospheric N during preparation and packing of the experimental capsules. However, the presence of both CN− and CO peaks in a similar vibrational frequency range cannot be ruled out.
Volatile delivery to Earth during single-stage core formation
To test whether C, N, and S abundances and ratios in the present-day BSE can be satisfied by volatile delivery during a single-stage core formation, with or without an early atmospheric loss, we assumed the P-T conditions of alloy-silicate equilibration in a deep MO based on Ni and Co abundances in the BSE (31). To incorporate the effect of S on the alloy, the equilibrating alloy was assumed to contain 2 wt % S based on the estimates of the composition of Earth’s core (28). As Earth’s core was predicted to have undergone incomplete equilibration with the mantle (60), the percentage of alloy-silicate equilibration was varied between 0 and 100%, where 0% alloy-silicate equilibration would simulate volatile delivery of CI-chondritic material after core formation as a late veneer, while 100% alloy-silicate equilibration would simulate complete equilibration of Earth’s core with the mantle (fig. S6). For a deep MO, the was not experimentally constrained, whereas the [for S-free alloys (29)] and (30) are known for deep MO conditions. Using the parameterized relationship defined in Eq. 4, a ~5500 was assumed, while a ~10 was predicted using the parametric equation from (30). Relatively low P-T experiments in this study predict that the remains unchanged between S-free and S-poor alloys. Therefore, using relatively higher P-T data for S-free alloys (29), a ~20 was used in our models.
To account for the effect of early atmospheric loss in addition to the effect of core formation (fig. S6B), an atmosphere overlying an MO that equilibrates with a core-forming alloy was assumed. The composition of the MO was calculated on the basis of the vapor pressure–induced solubilities of C, N, and S in the overlying atmosphere that equilibrates with the MO (1, 12). On the basis of their solubilities under relevant fO2 conditions during single-stage core formation, the solubility constants (parts per million/megapascal) for C, N, and S were assumed to be 0.55, 5, and 5000, respectively, based on the results of several previous studies (1, 53, 56, 61). The C, N, and S concentrations of the BSE after early atmospheric loss were calculated by subtracting their abundances in the atmosphere from the pre-atmospheric loss BSE reservoir (mantle + atmosphere).
Setup of Monte Carlo simulations
As the C solubility in the alloy (C content in the alloy at graphite/diamond saturation) and the are strongly dependent on the S content in the alloy (Figs. 1B and 2B), using the current set of alloy-silicate partitioning experiments with a C-N-S system and data from similar previous studies with C (24, 62), C-S (3, 4), and C-N (12, 63) systems, we formulated empirical thermodynamic parameterizations for the and C solubility in an Fe alloy on the basis of the P, T, S content in the alloy, and N content in the alloy
| (3) |
| (4) |
where represents the C solubility in the alloy (wt %), represents the S content in the alloy (wt %), represents the N content in the alloy (wt %), T represents the temperature (K), and P represents the pressure (GPa).
For Earth, late-stage accretion of oxidized impactors has been postulated as a possible reason for the associated increase in fO2 (64, 65). Therefore, we chose to focus on a relatively oxidizing range of metal-silicate equilibration because a differentiated impactor made up of some contribution from volatile-rich, oxidized CI chondrites would have been accreted under oxidized conditions. As the experimental data from this study and selected data from previous studies lie in a narrow fO2 range (~IW −1.7 to −0.3), the fO2 term was not included in the parametric relationships. Although our parametric relationships for the C solubility in the alloy and the do not include an fO2 term, we can still well reproduce the experimental values within a factor of 2 through linear least-squares analyses (fig. S5, A and B). This new parameterization also reveals that the silicate melt composition has a less significant effect in modifying the because extrapolation based on NBO/T formulation [where NBO/T is a measure of degree of silicate melt polymerization and is expressed as total nonbridging oxygens per tetrahedral cations; NBO/T = (2 × total O)/T − 4, where T = Si + Ti + Al + Cr + P] tends to overestimate the effects of a changing melt composition, from mafic to ultramafic, on enhancing the C solubility in a silicate melt, and hence, lowering the (66).
The concentrations of C, N, and S in the silicate portion and the core of the present-day Earth were calculated, assuming a disequilibrium merger of an impactor containing C, N, and S with a volatile-free proto-Earth
| (5) |
| (6) |
where denotes the concentration of C, N, or S in the BSE (parts per million), denotes the concentration of C, N, or S in the core of Earth (wt %), alloy/silicateimp represents the alloy/silicate ratio of the impactor, and Mimpactor/MEarth represents the ratio of the mass of the impactor with respect to the present-day Earth’s mass.
Sensitivity analysis
Because the varies in a narrow range of 10 to 31 for the relevant P-T-fO2 conditions and the S content in the alloy, we used a fixed mean value of 19. At 3 GPa, the decreases by a factor of 2 with an increase in T from 1600° to 1800°C at low S and intermediate S contents in the alloy; however, at high S contents, the at 1600° and 1800°C (15 and 13, respectively) are almost identical (Fig. 2A). As our model calculations for a volatile-rich impactor are based on an equilibrating alloy containing >15% S, it is reasonable to use a fixed mean value for the based on the relevant experimental data. For core formation in a small planetary embryo, the range of the for the relevant fO2 conditions and S content in the alloy (>10 wt %) lies between 73 and 165, with a mean value of 119 (fig. S9). Assuming a shallow MO during alloy-silicate equilibration of the volatile-bearing impactor, we used a peridotite liquidus temperature of T = 2200 K at P = 5 GPa (67).
The , in conjunction with the alloy/silicate ratio, would determine the S content in the core of the impactor, which, in turn, would determine the C solubility and the . In addition, we also performed a sensitivity analysis for the entire range of applicable and values. The variation of the between 5 and 35 (Fig. 2A) does not show any significant effect on the model results. For the lower end, with a = 73, the most probable S content in the core of the impactor lies in a lower range (21 to 26 wt %) (fig. S10A), which, in turn, would mean that a higher bulk C (0.17 to 0.73 wt %) is required to attain the C enrichment in the impactor’s mantle (fig. S10B) via C expulsion from the core, resulting in a relatively smaller size ( MEarth) of the pertinent impactor (fig. S10C). For the higher end, with a = 165, the most probable S content in the core of the impactor lies in a higher range (26 to 31 wt %) (fig. S10D), indicating that a lower bulk C (0.09 to 0.37 wt %) is needed to attain the C enrichment in the impactor’s mantle (fig. S10F) via C expulsion from the core, resulting in a relatively larger size ( MEarth) of the corresponding impactor (fig. S10F). Variation of the over the entire applicable range shows that an increase in the from 73 to 165 decreases the most probable bulk C content of the impactor from 0.5 to 0.2 wt % and increases the most probable mass of the impactor from 0.06 to 0.11 MEarth (fig. S11). For the mean value of = 119, the most probable bulk C content of the impactor was calculated to be 0.3 wt %, and the most probable mass ratio of the impactor was calculated to be 0.085 MEarth, i.e., similar to a Mars-sized body (fig. S11).
Effect of equilibration of the impactor’s core with the terrestrial MO on the bulk composition and size of the impactor
The results presented in Fig. 4 (B to D) do not take into account the effect of equilibration of the impactor’s core with the post-merger mantle (proto-Earth’s mantle + impactor’s mantle). Accretion models based on Hf/W and U/Pb chronometry predict that only 36% of Earth’s core must have formed in equilibrium with Earth’s mantle (60). Model calculations using high P-T alloy-silicate partition coefficients of Ni, Co, and W to match their BSE abundances predict that the initial 60 to 70% of the accretion of Earth’s mass was from smaller planetesimals and planetary embryos, the cores of which would efficiently equilibrate with the growing Earth’s mantle, while the last 30 to 40% of Earth’s accreted mass was provided by larger impactors, the cores of which did not equilibrate with proto-Earth’s MO (21). Therefore, the late-stage merger of a large impactor would imply that its core would undergo a small degree of equilibration, if any, with the mantle of the growing Earth before it coalesced with the proto-Earth’s core (Fig. 4A). As a result, we varied the degree of equilibration with the impactor’s core over a range of 0 to 20%.
The effect of equilibration of the impactor’s core with the proto-Earth’s silicate fraction was calculated by assuming an MO depth at P = 50 GPa and T = 4000 K (31). As metal segregation happens at much faster rates than accretion (60), before the merger of the impactor, proto-Earth’s mantle would be metal free. This would mean that the only metal that would be equilibrating with the post-merger MO would be from the impactor’s core, i.e., the S-rich metal from the impactor’s core. Experimental constraints on the and under the relevant conditions for S-rich alloys are lacking, although there was a recent study that constrained the (30) under these conditions. We varied the between 100 and 500, from 10 to 25, and from 10 to 150 for a postimpact MO equilibration with the impactor’s core in accordance with our calculations at lower P-T conditions, taking into account the possible roles of P-T and S in the alloy on the parameterized (Eq. 4). Our calculations show that variation of the , , and do not show any significant effect on the calculations as the degree of equilibration of the impactor’s core is the controlling variable under these conditions (Fig. 6, A and B).
Supplementary Material
Acknowledgments
We acknowledge B. Monteleone for help with the ion probe analyses and L. Carter for providing informal comments to improve the clarity of our communication. We thank G. Gaetani for handling the manuscript and three anonymous reviewers for constructive comments. Funding: This work received support from NASA grants NNX13AM51G, 80NSSC18K0828, and 80NSSC18K1314; the Deep Carbon Observatory; and a Packard Fellowship for Science and Engineering to R.D. Author contributions: D.S.G. and R.D. conceived the project and designed the experiments. D.S.G. performed and analyzed the experiments. K.T. and G.C. oversaw the experiments and electron microprobe analyses, respectively. D.S.G. and C.S. performed the Monte Carlo simulations. D.S.G. and R.D. interpreted the data, developed the ideas, and cowrote the paper. All authors commented on the manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/1/eaau3669/DC1
Fig. S1. Comparison between the estimated C/N ratios of the BSE and measured C/N ratios of CI and other carbonaceous chondrites.
Fig. S2. Backscattered electron images of typical experimental products.
Fig. S3. Experimentally determined C solubility of the silicate melt at graphite saturation as a function of N content of the silicate melt.
Fig. S4. Raman spectra of the experimental silicate glasses from this study showing peaks associated with C-O-N-H volatile species.
Fig. S5. Comparison between experimentally measured C solubility in the alloy melt and the and the predicted C solubility in the alloy melt and the based on the parameterizations developed in this study.
Fig. S6. Application of the experimental and parameterized alloy/silicate partition coefficients to examine whether a single-stage core formation along with an early atmospheric loss can explain the present-day abundances and ratios of C, N, and S in the BSE.
Fig. S7. An example forward calculation to showcase the methodology used to determine the alloy/silicate ratio and the mass of the impactor for a successful inverse Monte Carlo simulation.
Fig. S8. Effect of varying bulk C/N ratios on the composition and the mass of the impactor, which could establish the C-N-S budget of the present-day BSE.
Fig. S9. Measured partition coefficients of S between the alloy and silicate melt as a function of S in the alloy melt.
Fig. S10. Results of inverse Monte Carlo simulations to obtain the composition and mass of the impactor with end-member values.
Fig. S11. Results of inverse Monte Carlo simulations showing the effect of a variable on the estimated bulk C content and the mass of the impactor.
Table S1. Comparison between the estimated C/N ratios of CI and other carbonaceous chondrites with that estimated for the BSE.
Table S2. Chemical compositions of the starting materials (in wt %).
Table S3. Summary of the experimental conditions, quench products, oxygen fugacity, and alloy-silicate partitioning coefficients of C, N, and S.
Table S4. Major element compositions (in wt %) of the alloy melts at 1 to 7 GPa.
Table S5. Major element compositions (in wt %) of the silicate melts at 1 to 7 GPa.
REFERENCES AND NOTES
- 1.Hirschmann M. M., Constraints on the early delivery and fractionation of Earth’s major volatiles from C/H, C/N, and C/S ratios. Am. Mineral. 101, 540–553 (2016). [Google Scholar]
- 2.Bergin E. A., Blake G. A., Ciesla F., Hirschmann M. M., Li J., Tracing the ingredients for a habitable earth from interstellar space through planet formation. Proc. Natl. Acad. Sci. U.S.A. 112, 8965–8970 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Li Y., Dasgupta R., Tsuno K., The effects of sulfur, silicon, water, and oxygen fugacity on carbon solubility and partitioning in Fe-rich alloy and silicate melt systems at 3 GPa and 1600°C: Implications for core–mantle differentiation and degassing of magma oceans and reduced planet. Earth Planet. Sci. Lett. 415, 54–66 (2015). [Google Scholar]
- 4.Li Y., Dasgupta R., Tsuno K., Monteleone B., Shimizu N., Carbon and sulfur budget of the silicate Earth explained by accretion of differentiated planetary embryos. Nat. Geosci. 9, 781–785 (2016). [Google Scholar]
- 5.Kruijer T. S., Touboul M., Fischer-Gödde M., Bermingham K. R., Walker R. J., Kleine T., Protracted core formation and rapid accretion of protoplanets. Science 344, 1150–1154 (2014). [DOI] [PubMed] [Google Scholar]
- 6.Dauphas N., The isotopic nature of the Earth’s accreting material through time. Nature. 541, 521–524 (2017). [DOI] [PubMed] [Google Scholar]
- 7.N. Dauphas, A. Morbidelli, Treatise on Geochemistry (Elsevier, ed. 2, 2014), vol. 6, pp. 1–35. [Google Scholar]
- 8.Sarafian A. R., Nielsen S. G., Marschall H. R., McCubbin F. M., Monteleone B. D., Early accretion of water in the inner solar system from a carbonaceous chondrite-like source. Science 346, 623–626 (2014). [DOI] [PubMed] [Google Scholar]
- 9.Marty B., The origins and concentrations of water, carbon, nitrogen and noble gases on Earth. Earth Planet. Sci. Lett. 313–314, 56–66 (2012). [Google Scholar]
- 10.Walsh K. J., Morbidelli A., Raymond S. N., O’Brien D. P., Mandell A. M., A low mass for Mars from Jupiter’s early gas-driven migration. Nature. 475, 206–209 (2011). [DOI] [PubMed] [Google Scholar]
- 11.Fischer-Gödde M., Kleine T., Ruthenium isotopic evidence for an inner Solar System origin of the late veneer. Nature. 541, 525–527 (2017). [DOI] [PubMed] [Google Scholar]
- 12.Dalou C., Hirschmann M. M., von der Handt A., Mosenfelder J., Armstrong L. S., Nitrogen and carbon fractionation during core–mantle differentiation at shallow depth. Earth Planet. Sci. Lett. 458, 141–151 (2017). [Google Scholar]
- 13.Halliday A. N., The origins of volatiles in the terrestrial planets. Geochim. Cosmochim. Acta. 105, 146–171 (2013). [Google Scholar]
- 14.Tsuno K., Grewal D. S., Dasgupta R., Core-mantle fractionation of carbon in Earth and Mars: The effects of sulfur. Geochim. Cosmochim. Acta. 238, 477–495 (2018). [Google Scholar]
- 15.Tucker J. M., Mukhopadhyay S., Evidence for multiple magma ocean outgassing and atmospheric loss episodes from mantle noble gases. Earth Planet. Sci. Lett. 393, 254–265 (2014). [Google Scholar]
- 16.Humayun M., Clayton R. N., Potassium isotope cosmochemistry: Genetic implications of volatile element depletion. Geochim. Cosmochim. Acta. 59, 2131–2148 (1995). [Google Scholar]
- 17.Dauphas N., Pourmand A., Hf–W–Th evidence for rapid growth of Mars and its status as a planetary embryo. Nature. 473, 489–492 (2011). [DOI] [PubMed] [Google Scholar]
- 18.Chambers J. E., Wetherill G. W., Making the terrestrial planets: N-Body integrations of planetary embryos in three dimensions. Icarus. 136, 304–327 (1998). [Google Scholar]
- 19.Wang Z., Becker H., Ratios of S, Se and Te in the silicate Earth require a volatile-rich late veneer. Nature. 499, 328–331 (2013). [DOI] [PubMed] [Google Scholar]
- 20.Wade J., Wood B. J., Core formation and the oxidation state of the Earth. Earth Planet. Sci. Lett. 236, 78–95 (2005). [Google Scholar]
- 21.Rubie D. C., Frost D. J., Mann U., Asahara Y., Nimmo F., Tsuno K., Kelger P., Holzheid A., Palme H., Heterogeneous accretion, composition and core–mantle differentiation of the Earth. Earth Planet. Sci. Lett. 301, 31–42 (2011). [Google Scholar]
- 22.Corgne A., Wood B. J., Fei Y., C- and S-rich molten alloy immiscibility and core formation of planetesimals. Geochim. Cosmochim. Acta. 72, 2409–2416 (2008). [Google Scholar]
- 23.Dasgupta R., Buono A., Whelan G., Walker D., High-pressure melting relations in Fe–C–S systems: Implications for formation, evolution, and structure of metallic cores in planetary bodies. Geochim. Cosmochim. Acta. 73, 6678–6691 (2009). [Google Scholar]
- 24.Chi H., Dasgupta R., Duncan M. S., Shimizu N., Partitioning of carbon between Fe-rich alloy melt and silicate melt in a magma ocean—Implications for the abundance and origin of volatiles in Earth, Mars, and the Moon. Geochim. Cosmochim. Acta. 139, 447–471 (2014). [Google Scholar]
- 25.Dasgupta R., Chi H., Shimizu N., Buono A. S., Walker D., Carbon solution and partitioning between metallic and silicate melts in a shallow magma ocean: Implications for the origin and distribution of terrestrial carbon. Geochim. Cosmochim. Acta. 102, 191–212 (2013). [Google Scholar]
- 26.Kettle S. F. A., Diana E., Marchese E. M. C., Boccaleri E., Croce G., Sheng T., Stanghellini P. L., The vibrational spectra of the cyanide ligand revisited: Double bridging cyanides. Eur. J. Inorg. Chem. 2010, 3920–3929 (2010). [Google Scholar]
- 27.Barsan M. M., Butler I. S., Fitzpatrick J., Gilson D. F. R., High-pressure studies of the micro-Raman spectra of iron cyanide complexes: Prussian blue (Fe4[Fe(CN)6]3), potassium ferricyanide (K6[Fe(CN)3]), and sodium nitroprusside (Na2[Fe(CN)5(NO)].2H2O). J. Raman Spectrosc. 42, 1820–1824 (2011). [Google Scholar]
- 28.Dreibus G., Palme H., Cosmochemical constraints on the sulfur content in the Earth’s core. Geochim. Cosmochim. Acta. 60, 1125–1130 (1996). [Google Scholar]
- 29.Roskosz M., Bouhifd M. A., Jephcoat A. P., Marty B., Mysen B. O., Nitrogen solubility in molten metal and silicate at high pressure and temperature. Geochim. Cosmochim. Acta. 121, 15–28 (2013). [Google Scholar]
- 30.Suer T.-A., Siebert J., Remusat L., Menguy N., Fiquet G., A sulfur-poor terrestrial core inferred from metal–silicate partitioning experiments. Earth Planet. Sci. Lett. 469, 84–97 (2017). [Google Scholar]
- 31.Siebert J., Badro J., Antonangeli D., Ryerson F. J., Metal-silicate partitioning of Ni and Co in a deep magma ocean. Earth Planet. Sci. Lett. 321–322, 189–197 (2012). [Google Scholar]
- 32.Drake M. J., Righter K., Determining the composition of the Earth. Nature. 416, 39–44 (2002). [DOI] [PubMed] [Google Scholar]
- 33.Dahl T. W., Stevenson D. J., Turbulent mixing of metal and silicate during planet accretion—And interpretation of the Hf–W chronometer. Earth Planet. Sci. Lett. 295, 177–186 (2010). [Google Scholar]
- 34.Morbidelli A., Lunine J. I., O’Brien D. P., Raymond S. N., Walsh K. J., Building terrestrial planets. Annu. Rev. Earth Planet. Sci. 40, 251–275 (2012). [Google Scholar]
- 35.Marchi S., Canup R. M., Walker R. J., Heterogeneous delivery of silicate and metal to the Earth by large planetesimals. Nat. Geosci. 11, 77–81 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Saal A. E., Hauri E. H., Van Orman J. A., Rutherford M. J., Hydrogen isotopes in lunar volcanic glasses and melt inclusions reveal a carbonaceous chondrite heritage. Science 340, 1317–1320 (2013). [DOI] [PubMed] [Google Scholar]
- 37.Marty B., Hashizume K., Chaussidon M., Wieler R., Nitrogen isotopes on the Moon: Archives of the solar and planetary contributions to the inner solar system. Space Sci. Rev. 106, 175–196 (2003). [Google Scholar]
- 38.Canup R. M., Asphaug E., Origin of the Moon in a giant impact near the end of the Earth’s formation. Nature. 412, 708–712 (2001). [DOI] [PubMed] [Google Scholar]
- 39.Rubie D. C., Laurenz V., Jacobson S. A., Morbidelli A., Palme H., Vogel A. K., Frost D. J., Highly siderophile elements were stripped from Earth’s mantle by iron sulfide segregation. Science 353, 1141–1144 (2016). [DOI] [PubMed] [Google Scholar]
- 40.Sagan C., Mullen G., Earth and Mars: Evolution of atmospheres and surface temperatures. Science 177, 52–56 (1972). [DOI] [PubMed] [Google Scholar]
- 41.Zahnle K., Schaefer L., Fegley B., Earth’s earliest atmospheres. Cold Spring Harb. Perspect. Biol. 2, a004895 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lengauer W., Bauer J., Guillou A., Ansel D., Bars J.-P., Bohn M., Etchessahar E., Debuigne J., Ettmayer P., WDS-EPMA nitrogen profile determination in TiN/Ti diffusion couples using homotypic standard materials. Mikrochim. Acta. 107, 303–310 (1992). [Google Scholar]
- 43.Tsuno K., Dasgupta R., Melting phase relation of nominally anhydrous, carbonated pelitic-eclogite at 2.5–3.0 GPa and deep cycling of sedimentary carbon. Contrib. Mineral. Petrol. 161, 743–763 (2011). [Google Scholar]
- 44.Boujibar A., Andrault D., Bouhifd M. A., Bolfan-Casanova N., Devidal J.L., Trcera N., Metal-silicate partitioning of sulphur, new experimental and thermodynamic constraints on planetary accretion. Earth Planet. Sci. Lett. 391, 42–54 (2014). [Google Scholar]
- 45.Bastin G. F., Heijligers H. J. M., Quantitative electron probe microanalysis of carbon in binary carbides. X-ray Spectrometry 15, 135–141 (1986). [Google Scholar]
- 46.Dasgupta R., Walker D., Carbon solubility in core melts in a shallow magma ocean environment and distribution of carbon between the Earth’s core and the mantle. Geochim. Cosmochim. Acta. 72, 4627–4641 (2008). [Google Scholar]
- 47.Walker D., Dasgupta R., Li J., Buono A., Nonstoichiometry and growth of some Fe carbides. Contrib. Mineral. Petrol. 166, 935–957 (2013). [Google Scholar]
- 48.Jack K. H., The iron–nitrogen system: The crystal structures of ε-phase iron nitrides. Acta Crystallogr. 5, 404–411 (1952). [Google Scholar]
- 49.Holzheid A., Palme H., Chakraborty S., The activities of NiO, CoO and FeO in silicate melts. Chem. Geol. 139, 21–38 (1997). [Google Scholar]
- 50.Ma Z., Thermodynamic description for concentrated metallic solutions using interaction parameters. Metall. Mater. Trans. B. 32, 87–103 (2001). [Google Scholar]
- 51.Mysen B. O., Fogel M. L., Nitrogen and hydrogen isotope compositions and solubility in silicate melts in equilibrium with reduced (N+H)-bearing fluids at high pressure and temperature: Effects of melt structure. Am. Mineral. 95, 987–999 (2010). [Google Scholar]
- 52.Kadik A. A., Litvin Y. A., Koltashev V. V., Kryukova E. B., Plotnichenko V. G., Tsekhonya T. I., Kononkova N. N., Solution behavior of reduced N–H–O volatiles in FeO–Na2O–SiO2–Al2O3 melt equilibrated with molten Fe alloy at high pressure and temperature. Phys. Earth Planet. Inter. 214, 14–24 (2013). [Google Scholar]
- 53.Libourel G., Marty B., Humbert F., Nitrogen solubility in basaltic melt. Part I. Effect of oxygen fugacity. Geochim. Cosmochim. Acta. 67, 4123–4135 (2003). [Google Scholar]
- 54.Wetzel D. T., Rutherford M. J., Jacobsen S. D., Hauri E. H., Saal A. E., Degassing of reduced carbon from planetary basalts. Proc. Natl. Acad. Sci. U.S.A. 110, 8010–8013 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Mysen B. O., Yamashita S., Chertkova N., Amorphous materials: Properties, structure, and durability: Solubility and solution mechanisms of NOH volatiles in silicate melts at high pressure and temperature-amine groups and hydrogen fugacity. Am. Mineral. 93, 1760–1770 (2008). [Google Scholar]
- 56.Armstrong L. S., Hirschmann M. M., Stanley B. D., Falksen E. G., Jacobsen S. D., Speciation and solubility of reduced C–O–H–N volatiles in mafic melt: Implications for volcanism, atmospheric evolution, and deep volatile cycles in the terrestrial planets. Geochim. Cosmochim. Acta. 171, 283–302 (2015). [Google Scholar]
- 57.Stanley B. D., Hirschmann M. M., Withers A. C., Solubility of C–O–H volatiles in graphite-saturated martian basalts. Geochim. Cosmochim. Acta. 129, 54–76 (2014). [Google Scholar]
- 58.Ferrari A. C., Rodil S. E., Robertson J., Resonant Raman spectra of amorphous carbon nitrides: The G peak dispersion. Diam. Relat. Mater. 12, 905–910 (2003). [Google Scholar]
- 59.Han J., Blackburn N. J., Loehr T. M., Identification of the cyanide stretching frequency in the cyano derivative of copper/zinc-superoxide dismutase by IR and Raman spectroscopy. Inorg. Chem. 31, 3223–3229 (1992). [Google Scholar]
- 60.Rudge J. F., Kleine T., Bourdon B., Broad bounds on Earth’s accretion and core formation constrained by geochemical models. Nat. Geosci. 3, 439–443 (2010). [Google Scholar]
- 61.O’Neill H. S. C., Mavrogenes J. A., The sulfide capacity and the sulfur content at sulfide saturation of silicate melts at 1400°C and 1 bar. J. Petrol. 43, 1049–1087 (2002). [Google Scholar]
- 62.Dasgupta R., Ingassing, storage, and outgassing of terrestrial carbon through geologic time. Rev. Mineral. Geochem. 75, 183–229 (2013). [Google Scholar]
- 63.Kadik A. A., Koltashev V. V., Kryukova E. B., Plotnichenko V. G., Tsekhonya T. I., Kononkova N. N., Solubility of nitrogen, carbon, and hydrogen in FeO–Na2O–Al2O3–SiO2 melt and liquid iron alloy: Influence of oxygen fugacity. Geochem. Int. 53, 849–868 (2015). [Google Scholar]
- 64.O’Neill H. S. C., The origin of the moon and the early history of the earth—A chemical model. Part 2: The moon. Geochim. Cosmochim. Acta. 55, 1159–1172 (1991). [Google Scholar]
- 65.Wanke H., Dreibus G., Chemical composition and accretion history of terrestrial planets. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 325, 545–557 (1988). [Google Scholar]
- 66.Duncan M. S., Dasgupta R., Tsuno K., Experimental determination of CO2 content at graphite saturation along a natural basalt-peridotite melt join: Implications for the fate of carbon in terrestrial magma oceans. Earth Planet. Sci. Lett. 466, 115–128 (2017). [Google Scholar]
- 67.Herzberg C., Zhang J., Melting experiments on anhydrous peridotite KLB-1: Compositions of magmas in the upper mantle and transition zone. J. Geophys. Res. 101, 8271–8295 (1996). [Google Scholar]
- 68.Alexander C. M. O., Bowden R., Fogel M. L., Howard K. T., Herd C. D., Nittler L. R., The provenances of asteroids, and their contributions to the volatile inventories of the terrestrial planets. Science 337, 721–723 (2012). [DOI] [PubMed] [Google Scholar]
- 69.Pearson V. K., Sephton M. A., Franchi I. A., Gibson J. M., Gilmour I., Carbon and nitrogen in carbonaceous chondrites: Elemental abundances and stable isotopic compisitions. Meteorit. Planet. Sci. 41, 1899–1918 (2006). [Google Scholar]
- 70.Hirschmann M. M., Comparative deep Earth volatile cycles: The case for C recycling from exosphere/mantle fractionation of major (H2O, C, N) volatiles and from H2O/Ce, CO2/Ba, and CO2/Nb exosphere ratios. Earth Planet. Sci. Lett. 502, 262–273 (2018). [Google Scholar]
- 71.O’Brien D. P., Walsh K. J., Morbidelli A., Raymond S. N., Mandell A. M., Water delivery and giant impacts in the “Grand Tack” scenario. Icarus 239, 74–84 (2014). [Google Scholar]
- 72.Laurenz V., Rubie D. C., Frost D. J., Vogel A. K., The importance of sulfur for the behaviour of highly-siderophile elements during Earth’s differentiation. Geochim. Cosmochim. Acta. 194, 123–138 (2016). [Google Scholar]
- 73.Rose-Weston L., Brenan J. M., Fei Y., Secco R. A., Frost D. J., Effect of pressure, temperature, and oxygen fugacity on the metal-silicate partitioning of Te, Se, and S: Implications for earth differentiation. Geochim. Cosmochim. Acta. 73, 4598–4615 (2009). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/1/eaau3669/DC1
Fig. S1. Comparison between the estimated C/N ratios of the BSE and measured C/N ratios of CI and other carbonaceous chondrites.
Fig. S2. Backscattered electron images of typical experimental products.
Fig. S3. Experimentally determined C solubility of the silicate melt at graphite saturation as a function of N content of the silicate melt.
Fig. S4. Raman spectra of the experimental silicate glasses from this study showing peaks associated with C-O-N-H volatile species.
Fig. S5. Comparison between experimentally measured C solubility in the alloy melt and the and the predicted C solubility in the alloy melt and the based on the parameterizations developed in this study.
Fig. S6. Application of the experimental and parameterized alloy/silicate partition coefficients to examine whether a single-stage core formation along with an early atmospheric loss can explain the present-day abundances and ratios of C, N, and S in the BSE.
Fig. S7. An example forward calculation to showcase the methodology used to determine the alloy/silicate ratio and the mass of the impactor for a successful inverse Monte Carlo simulation.
Fig. S8. Effect of varying bulk C/N ratios on the composition and the mass of the impactor, which could establish the C-N-S budget of the present-day BSE.
Fig. S9. Measured partition coefficients of S between the alloy and silicate melt as a function of S in the alloy melt.
Fig. S10. Results of inverse Monte Carlo simulations to obtain the composition and mass of the impactor with end-member values.
Fig. S11. Results of inverse Monte Carlo simulations showing the effect of a variable on the estimated bulk C content and the mass of the impactor.
Table S1. Comparison between the estimated C/N ratios of CI and other carbonaceous chondrites with that estimated for the BSE.
Table S2. Chemical compositions of the starting materials (in wt %).
Table S3. Summary of the experimental conditions, quench products, oxygen fugacity, and alloy-silicate partitioning coefficients of C, N, and S.
Table S4. Major element compositions (in wt %) of the alloy melts at 1 to 7 GPa.
Table S5. Major element compositions (in wt %) of the silicate melts at 1 to 7 GPa.


