Reliable and practical computational description of molecular crystal polymorphs

Quantum-mechanical calculations enable reliable computation of structures and stabilities for molecular crystal polymorphs.

Abstract

Reliable prediction of the polymorphic energy landscape of a molecular crystal would yield profound insight into drug development in terms of the existence and likelihood of late-appearing polymorphs. However, the computational prediction of molecular crystal polymorphs is highly challenging due to the high dimensionality of conformational and crystallographic space accompanied by the need for relative free energies to within 1 kJ/mol per molecule. In this study, we combine the most successful crystal structure sampling strategy with the most successful first-principles energy ranking strategy of the latest blind test of organic crystal structure prediction methods. Specifically, we present a hierarchical energy ranking approach intended for the refinement of relative stabilities in the final stage of a crystal structure prediction procedure. Such a combined approach provides excellent stability rankings for all studied systems and can be applied to molecular crystals of pharmaceutical importance.

INTRODUCTION

The ability to reliably predict the structures and stabilities of a molecular crystal and its (often numerous) polymorphs without any previous experimental information would be an invaluable tool for a number of fields, with specific and immediate applications in the design and formulation of pharmaceuticals (1). Accurate and reliable crystal structure prediction (CSP) methods would be able to furnish detailed knowledge of the energetic landscape corresponding to a given molecular crystal and its thermodynamically relevant polymorphs. With access to the structures and relative thermodynamic stabilities of these varied crystal-packing motifs, one can gain crucial insight into whether the existing structure of a pharmaceutical drug candidate is the most thermodynamically stable solid form at ambient conditions. This insight, in turn, enables an informed and critical assessment of the potential risk associated with the assumed stable form disappearing at some point during the manufacturing process or consumable shelf life (2). In this case, a polymorph with similar stability but different (and often unwanted) properties could emerge as the dominant solid form—an event that can trigger a cascade of deleterious health-related, social, and financial repercussions. Hence, the utilization of accurate and reliable computational CSP methods in conjunction with experimental polymorph screening efforts offers a comprehensive and sustainable solution to this grand challenge (3). However, the computational prediction of the structures and stabilities of molecular crystal polymorphs is particularly challenging due to the high dimensionality of conformational and crystallographic space accompanied by the need for relative (free) energies to within ≈1 kJ/mol per molecule.

In general, the accuracy and reliability of a given CSP methodology depend on two distinct but equally important theoretical elements: (i) sufficiently complete sampling of the conformational and crystallographic space spanned by a given molecular crystal and (ii) sufficiently accurate ranking of the numerous low-energy polymorphs according to their relative thermodynamic stabilities (3, 4). In this regard, major advances have been made along both of these lines over the past few years, resulting in substantial progress in the field of molecular CSP (5–12). By and large, the most important benchmarks for assessing the utility of a given molecular CSP approach are the regular blind tests organized by the Cambridge Crystallographic Data Centre (CCDC) (4, 13, 14), wherein participants predict the structure of a given molecular crystal based solely on the two-dimensional (2D) chemical formula for the individual molecule(s) involved. Over the past few decades, the chemical diversity and complexity of the CCDC blind test have gradually increased and now include small and rigid molecules as well as elaborate polymorphic systems involving large and flexible molecules, salts, and cocrystals. A general overview of the protocol used in a typical molecular CSP methodology is illustrated in Fig. 1. Starting with the 2D chemical formula for each molecule, 3D molecular structures are first computed using standard geometry optimization techniques that are supplemented with additional sampling of all energetically relevant conformational isomers for flexible molecules. Next, a vast number of possible crystal-packing arrangements are generated by comprehensively sampling different intermolecular orientations, space groups, unit cell sizes, and molecular conformations. Last, the generated crystal structures are ranked according to their relative (free) energies.

Fig. 1. General overview of a CSP protocol.

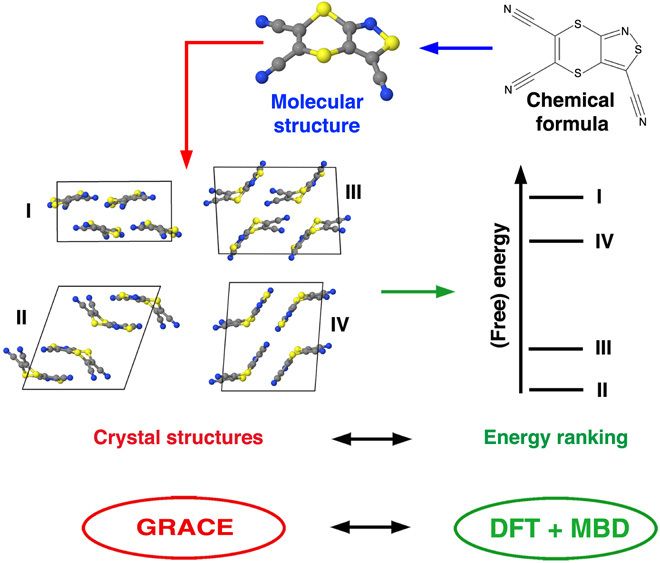
Starting with the 2D chemical formula for each molecule, this procedure generates molecular crystal structures and (free) energy rankings for all thermodynamically relevant polymorphs. In this work, we combine the crystal structure sampling strategy provided by the GRACE software package with the highly accurate (free) energy ranking strategy provided by the first principles–based DFT + MBD framework.

In this study, we demonstrate that an accurate, reliable, and computationally feasible protocol for the prediction of molecular crystal polymorphs can be obtained by combining the most successful crystal structure sampling strategy (Neumann and co-workers) with the most successful first-principles energy ranking strategy (Tkatchenko and co-workers) from the latest sixth CCDC blind test (4, 15). In this regard, the approach for generating crystal structures by Neumann and co-workers was able to correctly predict all experimentally observed structures (except for one) within the top 100 most stable structures, building on top of their major successes in previous blind tests (13, 14, 16). The fact that, among all participating sampling methods in the latest blind test (4), several experimental structures could be found only by this approach again highlights the complexity associated with sufficiently sampling wide swaths of crystallographic space. In this approach, initial molecular crystal structures are created with a Monte Carlo parallel tempering algorithm that uses a tailor-made force field (17) within the GRACE (Generation Ranking and Characterization Engine) software package developed by Neumann and colleagues (16, 17). Following this initial screening, a set of candidate crystal structures are then reoptimized in a hierarchical and statistically controlled process using dispersion-inclusive density functional theory (DFT) (4, 16, 18). Beyond the robust sampling of the essential regions of crystallographic space, these initial energy rankings can be substantially improved upon by using state-of-the-art first-principles methodologies as detailed below. Here, we introduce and discuss a hierarchical first-principles energy ranking approach for the refinement of stability rankings in the final stage of a CSP procedure.

RESULTS

Energy ranking approach

As the foundation for the presented stability ranking approach, we use the top 100 molecular crystal structures (for every system of the latest blind test) from the abovementioned sampling approach of Neumann and co-workers using GRACE [see the supplementary materials of (4)]. Form E of system XXIII is the only experimental structure that was not present in this set of initial structures and is included for completeness. We note in passing that this form was generated by Neumann and co-workers but was located just outside the energetic window considered for the Z′ = 2 structures. In total, this set includes 501 structures (with unit cell sizes ranging from 15 to 992 atoms) and therefore provides a large-scale benchmark structural database under realistic CSP conditions.

On the basis of these initial molecular crystal structures, we have developed a robust hierarchical first-principles approach for energetically ranking all relevant polymorphs. This approach is directly applicable to pharmaceutically relevant systems and includes three important theoretical aspects that are commonly neglected in typical CSP protocols: (i) a sophisticated treatment of Pauli exchange repulsion and electron correlation effects with hybrid functionals, (ii) inclusion of many-body dispersion (MBD) interactions and dielectric screening effects, and (iii) an account of harmonic (and sometimes anharmonic) vibrational contributions to the free energy. In this regard, the hybrid PBE0 functional (19) in conjunction with the MBD model (20–24) is able to predict absolute experimental lattice energies to within 1 kcal/mol (25, 26) and relative stabilities of several polymorphic systems to within 1 kJ/mol (12, 25, 27, 28). Hence, the PBE0 + MBD approach is used for all calculations of static lattice energies. Geometry and lattice optimizations, as well as vibrational free energies, are computed with the Perdew-Burke-Ernzerhof (PBE) functional (29) in conjunction with the effective-pairwise Tkatchenko-Scheffler (TS) dispersion correction (denoted as PBE + TS) (30). A detailed description of the computational approaches used in this work is available in Materials and Methods and in tables S1 to S3.

Polymorphic energy landscapes

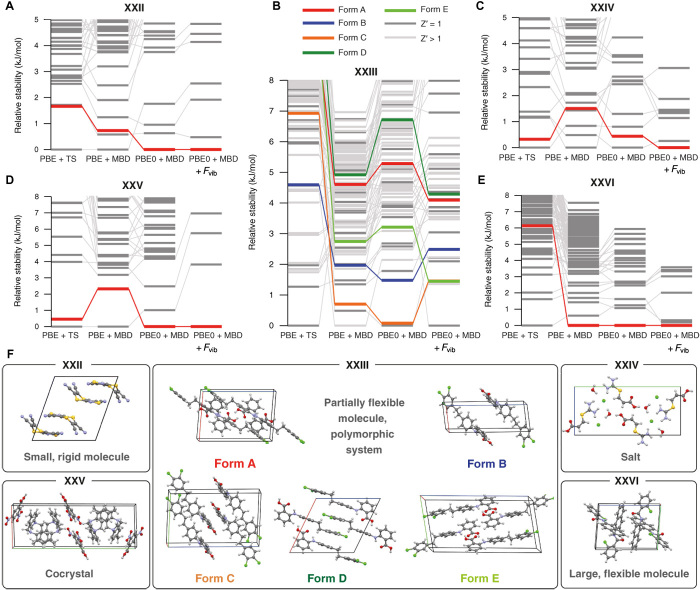
The stability rankings obtained for the five blind test systems are shown in Fig. 2 (all relative energies are available in tables S4 to S8, and all structures are included in data S1). Our proposed energy ranking, which includes all of the aforementioned theoretical contributions, is shown for every system in the last column and marked with PBE0 + MBD + F_vib. To illustrate the importance of each contribution to the stability ranking, Fig. 2 shows not only the final stability rankings but also several intermediary steps, in which one or more of the three aforementioned theoretical contributions are not accounted for in the rankings. The first ranking considers only static lattice energies computed at the PBE + TS level, while the second ranking accounts for beyond-pairwise MBD interactions (PBE + MBD). In the third ranking, we include a more sophisticated treatment of Pauli exchange repulsion via PBE0 + MBD. In doing so, the deleterious effects of self-interaction error (a DFT artifact in which an electron interacts with itself) are notably ameliorated, which leads to a substantial improvement in the description of electrostatic and charge-transfer effects. In the final ranking, we supplement the PBE0 + MBD energies with harmonic vibrational free energy contributions (+F_vib) at the PBE + TS level. This leads to our proposed PBE0 + MBD + F_vib final stability ranking based on Helmholtz free energies, which accounts for thermal entropic effects.

Fig. 2. Obtained polymorphic energy landscapes.

Relative stabilities for all steps in the present CSP stability ranking procedure for systems: (A) XXII, (B) XXIII, (C) XXIV, (D) XXV, and (E) XXVI. For each ranking, the energy of the most stable crystal structure defines the zero of the energy. Experimentally observed structures are highlighted in color, while all other structures are in gray. The final ranking for each system corresponds to the Helmholtz free energies at the PBE0 + MBD + F_vib level, computed at the corresponding experimental temperatures: 150 K for XXII, 240 K for XXIV, and 300 K for XXIII, XXV, and XXVI. All relative energies are reported per chemical unit, i.e., for XXII, XXIII, and XXVI, the energies are normalized per molecule, and for XXIV and XXV, the energies are given per trimer and dimer, respectively. (F) Unit cells for all highlighted structures.

We first consider systems XXII, XXIV, XXV, and XXVI. For all of these systems, our final stability ranking at the PBE0 + MBD + F_vib level predicts the experimental structure as the most stable form—the ideal outcome of any CSP protocol. As seen from the intermediate stability rankings, all of the three previously mentioned theoretical effects are required to obtain this result. For example, Pauli exchange repulsion (through the PBE0 functional) plays a crucial role for system XXII (31), while MBD effects are the most important factor for system XXVI. In addition, all structures with free energies that are within 1 kJ/mol of the experimental structure are essentially minor variations of the latter (see Supplementary Text), which demonstrates the robustness of our CSP approach in dealing with pharmaceutically relevant systems such as salts, cocrystals, and molecular crystals involving large and flexible molecules.

Next, we address the most challenging system in the blind test (XXIII). This system involves a conformationally flexible molecule and has five experimentally confirmed polymorphs (4). The fact that this compound is also a former drug candidate (32) makes it an ideal testing ground for CSP of pharmaceutically relevant molecules. Because of the flexibility of the involved molecule, various conformations are possible within the crystal, leading to a fairly complex polymorphic landscape with numerous crystal structures located within a very small energy window. As shown in Fig. 2, the PBE + TS method is again insufficient for quantitative energy rankings and places all experimentally observed structures within the top 11 kJ/mol—an energy window containing 84 structures. Each refinement of the energetic rankings changes their relative stabilities, with all experimental structures observed within the top 4.3 kJ/mol (≈1 kcal/mol) in the final ranking with PBE0 + MBD + F_vib. At this level, all experimental structures were found within an energy interval of 3 kJ/mol, which is within the expected energy range associated with coexisting polymorphs (1). We note here that our procedure finds one structure (Str. N70) that is ≈1.5 kJ/mol more stable than all experimentally observed structures, a remarkable finding that is discussed in more detail below.

The computational cost of the procedure presented here depends heavily on the system size (and other system attributes) and is discussed below based on central processing unit (CPU) timings obtained on 2.4-GHz Intel Xeon E5-2680 v4 cores. For the static lattice energies obtained with PBE0 + MBD, a single-point energy evaluation (using the settings described in Materials and Methods) needs 3.5 CPU hours for the smallest unit cell (XXII-N44, 15 atoms) and approximately 750 CPU hours for the largest unit cell (XXV-N39, 896 atoms). For an average-sized system with 172 atoms in the unit cell (e.g., form A of XXIII), a single PBE0 + MBD energy evaluation is very reasonable and requires only 60 CPU hours. The computational cost associated with PBE + TS lattice and geometry optimizations depends on the number of optimization steps but typically amounts to about two to three times that of the corresponding PBE0 + MBD single-point energy evaluation. The cost of the harmonic PBE + TS vibrational free energies depends on the size, shape, and symmetry of the unit cell, as these properties determine the required supercell size and the number of finite-difference displacements. For example, the time required for the PBE + TS vibrational free energy calculations ranges from 180 CPU hours (XXII-N2) to 45,000 CPU hours (XXIII-N3). In the case of structure XXII-N2, only 90 finite-difference displacements were required and the used supercell consisted of 120 atoms, while the calculation involving structure XXIII-N3 required 516 finite displacements and a supercell containing nearly 1400 atoms. The vibrational free energy calculation for the average-sized form A of system XXIII requires 258 finite displacements and a supercell equivalent to the unit cell, which results in a computation time of 750 CPU hours. Overall, we note that these computational resources are within reach of academic institutions and industrial laboratories.

Stability ranking results

For all systems with only one known polymorph, the systematic and hierarchical energy ranking protocol presented here (PBE0 + MBD + F_vib) correctly produced the experimental structure as the most stable forms (rank 1). This protocol represents a substantial improvement over the ranks 2 (XXII), 2 (XXIV), 6 (XXV), and 1 (XXVI) obtained by the unrefined results of Neumann and co-workers, which again stresses the critical importance of an energy ranking protocol based on state-of-the-art first principles–based methodologies. For system XXIII, all experimental structures were found within the top 18 structures, with the two Z′ = 2 structures assigned ranks 3 (form E) and 4 (form C). When only considering the Z′ = 1 structures, we find all three experimental structures among the top 10 structures, as compared to the top 26 in the initial ranking by Neumann and co-workers. Moreover, all of our predicted structures agree to within 0.5 Å of the experimental structures, as quantified by the root mean square deviation (RMSD) measure of a cluster consisting of 20 molecules. These so-called RMSD₂₀ values also agree to within 0.05 Å with the RMSD₂₀ values of the initial structures obtained by Neumann and co-workers. Overlays of the predicted and experimental structures are provided in Fig. 3, and additional information about the accuracy of the structures is provided in table S9.

Fig. 3. Accuracy of structures.

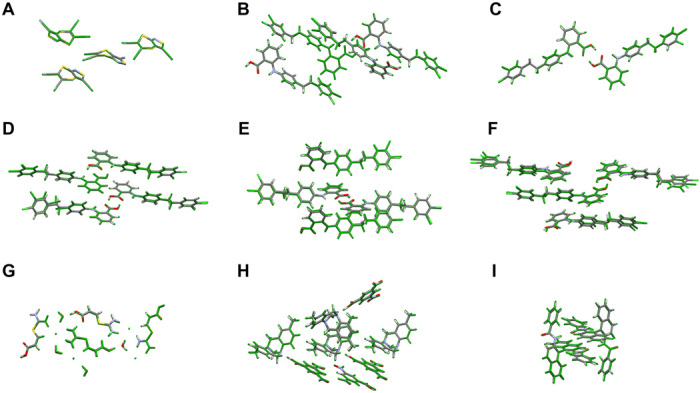
Overlay between the experimentally determined structures (element-specific colors) and the corresponding PBE + TS–optimized structures (green) for systems: (A) XXII, (B) XXIII-A, (C) XXIII-B, (D) XXIII-C, (E) XXIII-D, (F) XXIII-E, (G) XXIV, (H) XXV, and (I) XXVI. These overlays are shown for the molecules constituting the respective unit cell.

Beyond the harmonic approximation for free energies

While our presented approach yields very good stability rankings, vibrational free energies were only calculated within the harmonic approximation on top of fully relaxed structures. Therefore, the geometry and lattice optimizations did not include temperature (thermal expansion) effects, and the calculated vibrational free energies lack anharmonic effects. The missing thermal expansion can be seen in our obtained unit cell volumes. Comparing the obtained PBE + TS unit cell volumes with the experimental volumes measured at 300 K (all experimental structures except XXII and XXIV) shows that we underestimate these unit cell volumes by 3.6% on average. With five known polymorphs, system XXIII is the most experimentally studied system, and it exhibits the most complicated polymorphic energy landscape among the systems investigated in this work. Hence, we specifically address how thermal expansion and anharmonicity affect a small set of XXIII structures, from which we estimate their effect on relative stabilities in general. This set includes all experimentally observed structures of system XXIII (forms A, B, C, D, and E) as well as the first four Z′ = 1 structures (Str. N70, N31, N18, and N42), which have yet to be experimentally observed.

The effects of thermal expansion can be calculated in the so-called quasi-harmonic approximation (QHA) (33), in which vibrational free energies are calculated within the harmonic approximation for several unit cell volumes. The unit cell volume corresponding to a certain temperature is then determined by the minimum of the Helmholtz free energy at that temperature, which is evaluated by fitting the energy-volume curves to the Murnaghan (34) equation of state. It has been shown for several molecular crystals that the QHA is capable of capturing a majority of the thermal expansion (35–38). Here, we calculated the unit cell volumes corresponding to a temperature of 300 K using PBE + TS (see Materials and Methods for more details). With this approach, we are now able to predict room temperature unit cell volumes to within 1.0% on average. Hence, the QHA provides a simple but effective way of including thermal effects in molecular crystal structures using first principles–based methodologies. A detailed comparison of these thermally expanded structures with experiment is available in table S10. Stability rankings calculated with PBE0 + MBD + F_vib on top of these thermally expanded structures are shown in Fig. 4. We note in passing that these relative Helmholtz free energies can also be interpreted as relative Gibbs free energies because the additional pV term has only a negligible effect at ambient pressure. The largest observed change in relative stabilities stemming from the use of thermally expanded structures (as compared to fully optimized 0 K structures) amounts to 1.4 kJ/mol at the PBE0 + MBD + F_vib level but is only 0.4 kJ/mol on average. Therefore, we observe some reordering of stability rankings, but the general picture and the energy interval remain essentially the same.

Fig. 4. Stability rankings for thermally expanded structures.

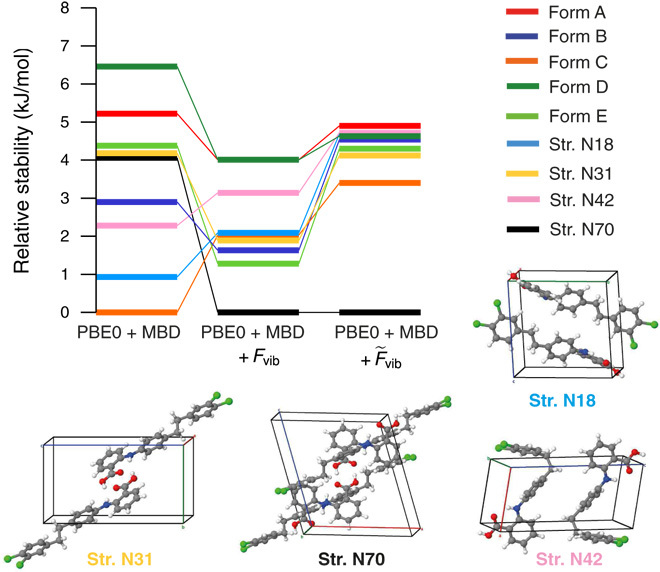
Energetic rankings for all experimentally observed (forms A, B, C, D, and E) and theoretically predicted (N18, N31, N42, and N70) structures for system XXIII. All energies were evaluated using thermally expanded PBE + TS structures optimized at 300 K with the QHA. The last two rankings include harmonic (F_vib) and Morse anharmonic (${\tilde{\mathit{F}}}_{\text{vib}}$) vibrational free energy contributions.

In addition to thermal expansion, the vibrational contributions to the free energy also contain anharmonic effects. Here, we estimate these anharmonic effects by replacing the harmonic oscillators obtained via the harmonic approximation with Morse oscillators (39, 40). The Morse oscillator models a particle in an anharmonic potential, for which dissociation is possible. It is the next logical step after the harmonic oscillator because it is also one of the few quantum-mechanical model systems, for which an analytic solution of the Schrödinger equation is known (41). The Morse oscillator provides a more realistic picture than the harmonic oscillator because it has a finite number of nonequispaced energy levels. This model has been used to describe the spectra of diatomic molecules and to improve upon harmonic vibrational frequencies for the hydroxyl groups in methanol, phenol, thymol, and the water dimer (41–43). Here, we create four displaced structures per vibrational mode and use the corresponding PBE + TS energies to fit the parameters of the Morse potential and determine the Morse vibrational free energies (see Materials and Methods for more details). In this work, the Morse oscillators are independent of each other, i.e., we do not account for coupling between vibrational modes. The corresponding free energy stability rankings with such an anharmonic treatment of the vibrational free energy are denoted by PBE0 + MBD + ${\tilde{\mathit{F}}}_{\text{vib}}$ and shown in Fig. 4. At this level, all experimental structures are found within an energy window of only 1.5 kJ/mol, which is well within the expected energy range for coexisting polymorphs. We note in passing that Brandenburg and Grimme (10) have also studied the experimental structures of system XXIII using a semiempirical tight-binding approach within the QHA; however, their values lie within a much larger energy window of ≈8 kJ/mol.

The unobserved polymorph of XXIII (Str. N70) is substantially more stable than any of the experimentally determined crystal structures, even after accounting for thermal expansion in the underlying crystal structures as well as anharmonic vibrational free energy contributions. In this regard, this polymorph is actually further stabilized by vibrational entropy and shares many structural features with form A. The most notable difference is the stacking pattern of the molecular sheets (see fig. S1). Hence, we hypothesize that form A might be kinetically favored over Str. N70, and this hitherto unobserved polymorph could potentially be crystallized by slowly melting form A or introducing surfactants during the crystallization procedure (see Supplementary Text). In addition, from a thermodynamic standpoint, Str. N18, N31, and N42 might also be observed experimentally, although Str. N42 involves a twisted molecular conformation that might not be easily accessible in solution. Experimental evidence (4) suggests that form A should be the most stable structure at low temperatures and form D should be the most stable structure at room temperature. We observe that form D is stabilized by thermal effects and predicted to be more stable than form A at the PBE0 + MBD + ${\tilde{\mathit{F}}}_{\text{vib}}$ level. In addition, inclusion of anharmonic vibrational free energies brings all of the experimentally determined structures closer together, i.e., all of the Z′ = 1 structures are now within 0.4 kJ/mol.

In terms of the computational cost, the QHA adds 4700 CPU hours to the 950 CPU hours required for the initial PBE0 + MBD + F_vib calculation in the average-sized form A of system XXIII. For comparison, the corresponding Morse free energy calculation needs an additional 4300 CPU hours when all Γ-point modes are taken into account. Therefore, the QHA and subsequent Morse free energy calculation increase the computation time by approximately a factor of 10.

Last, accounting for thermal expansion and anharmonic effects by using Morse oscillators changes the relative stabilities of structures for system XXIII on average by only 1.1 kJ/mol with a maximum observed change of 2.9 kJ/mol compared with the harmonic approximation on top of fully optimized 0 K structures. Because the harmonic vibrational free energies have (by far) the largest impact on the stability rankings of systems XXIII and XXV, we expect that the effects associated with the QHA and anharmonicity will be substantially less pronounced for the other systems. In the case of system XXV, in particular, the structures in the final ranking are already very well separated; accounting for QHA and anharmonicity will not change the ranking assigned to the experimentally observed structure.

DISCUSSION

The recommended and most reliable level of theory in our hierarchical computational approach (PBE0 + MBD + F_vib) yields excellent stability rankings for the highly diverse set of molecular crystals considered here. Even for the most challenging polymorphic system XXIII, all five polymorphs known to date are located within the top 4.3 kJ/mol. However, further benchmarks on other complex and realistic molecular crystals would be helpful for demonstrating the general applicability of the presented computational procedure. Because of the computational cost of the involved quantum-mechanical calculations, this computational procedure is intended for the final stability ranking of a molecular CSP using a limited structure set. Therefore, this approach has to rely on the accuracy of the preceding crystallographic space sampling and initial stability ranking, which, in this case, is provided by GRACE (4, 16–18). Furthermore, we have also shown how thermal expansion and anharmonicity can be accounted for in several structures of the highly flexible system XXIII. The resulting PBE0 + MBD + ${\tilde{\mathit{F}}}_{\text{vib}}$ free energies based on thermally expanded structures could also be calculated for several additional structures to obtain further insight into challenging polymorphic energy landscapes.

In the broad context of molecular crystal polymorphism, our findings suggest that late-appearing crystal forms (2) are ubiquitous among molecules of pharmaceutical interest, further reinforcing recent experimental and computational predictions for coumarin (12), dalcetrapib (44), rotigotine (2, 45), and ritonavir (46). In the case of system XXIII, the stability of a new potential form N70 is substantially higher (by 3 kJ/mol) than that of all experimentally found forms. Systematic tests carried out in this work ensure the reliability of our CSP procedure to about 1 to 2 kJ/mol, suggesting that the so far unobserved Str. N70 should be the thermodynamically stable form at ambient conditions. Experimental confirmation of this fact would be desirable, and our suggestions for crystallization experiments should be useful in this endeavor.

In general, an increasing number of studied molecular crystals exhibit complex polymorphic energy landscapes with numerous structures located within an energy window of a few kilojoules per mole. For these molecules, thermodynamics alone is insufficient for understanding polymorph crystallization under typical conditions (47). Hence, novel developments are required to model kinetic effects during the nucleation and crystal growth and must also take into account the specific solvent used in the crystallization experiment. Furthermore, a proper treatment of disorder in molecular crystals proves challenging due to the required increase in the supercell size and crystallographic space complexity (9, 12, 48, 49).

We also stress that further improvements of the presented CSP procedure are desirable and possible. For instance, the geometry optimizations and harmonic vibrational free energies could be calculated with PBE + MBD instead of PBE + TS. This would increase the cost of the force calculations for an average-sized system by about 50%, and the impact on geometry and relative stabilities is discussed elsewhere (50). Furthermore, one could improve the accuracy of free energy calculations with more advanced dynamical approaches using either path integral molecular dynamics (51) or the vibrational self-consistent field approach (52–54).

By far, the most expensive part of these calculations is the evaluation of the vibrational free energies. To make such an approach broadly applicable, more efficient methods with roughly the same accuracy have to be developed. Hence, PBE0 + MBD energies could serve as reference data to develop more accurate tailor-made force fields or efficient machine learning energy models. Furthermore, one could also envision a machine learning model of lattice energies based on PBE + MBD Hessians computed for a few polymorphs. These developments would enable us to markedly reduce the calculation time for vibrational free energies. Furthermore, efficient machine learning models could be used in path integral molecular dynamics, especially when coupled with sophisticated enhanced sampling techniques (9, 48).

In summary, we have introduced a robust and computationally feasible procedure that yields accurate and reliable descriptions of the structures and stabilities for the thermodynamically relevant polymorphs of molecular crystals. The diverse set of systems studied in this work includes complex molecular crystals such as a salt, a cocrystal, and crystals consisting of flexible large molecules of pharmaceutical interest. Our approach explicitly accounts for all relevant enthalpic and entropic effects, including sophisticated treatments of Pauli exchange repulsion, MBD interactions, and vibrational free energies at finite temperatures, all of which are directly obtained from quantum-mechanical calculations. The approach presented here takes us one step closer to obtaining an enhanced fundamental understanding of polymorphic energy landscapes and to routinely using computational molecular CSP in conjunction with experimental polymorph screening. Such a joint theoretical-experimental procedure offers a comprehensive and sustainable solution to the grand challenges associated with molecular crystal polymorphs, whose very existence offers us the promise of novel and hitherto unexplored pharmaceutical agents on one hand, and quite devastating public health and economic repercussions on the other.

MATERIALS AND METHODS

For each system in the latest blind test, we used the top 100 crystal structures from the submission of Neumann and co-workers [which are available in the supplementary materials of (4)] as initial structures for this study. For systems with two submitted lists, we used the list that also included Z′ = 2 structures, i.e., structures that have two molecules in the asymmetric unit. Form E of system XXIII was the only experimental structure not present in this set and was therefore added for completeness. All calculations were performed using the all-electron FHI-aims (Fritz Haber Institute ab initio molecular simulations) code (55–61). Throughout this work, we used two different accuracy levels in FHI-aims, which are denoted as “light” and “tight.” For the light level, we used the light species default setting in FHI-aims for all numerical atom-centered basis functions and integration grids. The number of k-points (n) in each direction was determined by the smallest integer satisfying n × a ≥ 25 Å, with a being the unit cell length in a given direction. For the tight level, we used the tight species default settings in FHI-aims, and the number of k-points was determined by the criterion that n × a ≥ 30 Å. MBD interactions were evaluated at the MBD@rsSCS level with a reciprocal-space implementation that used the same k-point mesh as the DFT calculations (20, 22). Convergence criteria of 10⁻⁶ eV, 10⁻⁵ electrons/ų, 10⁻⁴ eV/Å, and 10⁻³ eV were used for the total energy, charge density, forces, and sum of eigenvalues, respectively.

First, we performed full lattice and geometry relaxations (without any symmetry constraints) using the PBE functional (29) in conjunction with the effective-pairwise TS dispersion correction (30), ensuring that the smallest force component is less than 0.005 eV/Å. Duplicate structures were identified using Mercury (62). Structures were considered similar if 20 of 20 molecules within the crystals matched within 25% in terms of distances and within 25° in terms of angles, which are the same criteria used in (4) to identify matches. Two similar structures were considered to be identical if their PBE + TS energy (light) agreed to within 1 kJ/mol and their RMSD₂₀ is smaller than 0.5 Å. This ensures that we are removing real duplicate structures but still consider similar structures with sufficiently different stabilities due to, for instance, slightly different torsion angles. Only the most stable structure among identical structures was retained throughout the protocol. These optimized structures were symmetrized using PLATON (63) and are provided in data S1. All structures were named according to their rank in the initial ranking by Neumann and co-workers. To determine whether an experimental structure was found, we used the same settings for the crystal similarity search as described above.

Next, relative energetic stabilities were computed on the basis of these PBE + TS optimized structures using PBE + TS and PBE + MBD (20, 22) with tight settings. To ensure the convergence of the relative energies, we have created a benchmark set consisting of eight small structures of system XXII and four small structures of system XXIV. For these structures, PBE + MBD energies were computed using really tight settings for the integration grids and tier 3 basis functions (see table S1). When considering all possible relative energies between structures from the same system, the mean absolute deviation (MAD) for the tight settings amounts to only 0.1 kJ/mol with a maximum deviation of 0.3 kJ/mol (see table S2). This illustrates the fact that tight settings provide converged relative energies.

Because PBE0 (19) calculations with tight settings are not possible for all of the studied systems due to the massive computational cost and memory requirements, we approximated the PBE0 + MBD energies by adding the difference between PBE0 + MBD and PBE + MBD evaluated at the light level to the PBE + MBD energies calculated at the tight level. For the aforementioned benchmark set, this approximation has a MAD of only 0.4 kJ/mol with a maximum deviation of 0.8 kJ/mol, when compared to PBE0 + MBD energies evaluated with tight settings (see table S3). In contrast, PBE0 + MBD energies at the light level yield a MAD of 0.8 kJ/mol with a maximum deviation of 2.6 kJ/mol. Therefore, our approximation provides relative energies that are in very good agreement with tight PBE0 + MBD energies. PBE0 + MBD energies were computed for all structures of systems XXII, XXIII, and XXIV. For the remaining systems, PBE0 + MBD calculations are available for (at least) the structures located within the top 4.5 kJ/mol of the PBE + MBD rankings.

Vibrational free energies (F_vib) were computed at the PBE + TS level with light settings using the Phonopy code (64) and the finite-difference method within the harmonic approximation. Therein, the vibrational free energy F_vib can be calculated according to

$${\mathit{F}}_{\text{vib}}(\mathit{T})={\displaystyle \int }\mathrm{d}\mathrm{\omega } \mathit{g}(\mathrm{\omega })\frac{\mathrm{\hslash }\mathrm{\omega }}{2}+{\displaystyle \int }\mathrm{d}\mathrm{\omega } \mathit{g}(\mathrm{\omega }){\mathit{k}}_{\mathrm{B}}\mathit{T} \text{ln}[1- \text{exp}(-\frac{\mathrm{\hslash }\mathrm{\omega }}{{\mathit{k}}_{\mathrm{B}}\mathit{T}}\left)\right]$$ (1)

where g(ω) is the phonon density of states and T, ω, and k_B describe the temperature, frequency, and Boltzmann constant, respectively. The final stability rankings in Fig. 2 were always based on PBE0 + MBD + F_vib energies evaluated at temperatures corresponding to the experimental crystal structure measurements. For the finite-difference calculations, we used displacements of 0.005 Å and (when necessary) supercells that ensure cell lengths greater than 10 Å in every direction. Furthermore, the vibrational free energy was evaluated in reciprocal space, where the number of q-points (n) in each direction was determined by the smallest integer satisfying n × a ≥ 50 Å. All structures had no imaginary frequencies at the Γ-point, and the magnitude of the three acoustic modes was smaller than 0.1 cm⁻¹ in most cases and always smaller than 0.5 cm⁻¹. Vibrational free energies were calculated for (at least) all structures that are located within the top 3 kJ/mol according to the PBE0 + MBD ranking. For system XXIII, vibrational free energies were calculated for all Z′ = 1 structures and for all Z′ = 2 structures containing up to eight molecules per unit cell within the top 4.8 kJ/mol of the PBE0 + MBD ranking.

For the QHA, we performed PBE + TS lattice and geometry optimizations of several structures from system XXIII using light settings with external hydrostatic pressures of 0.4, 0.2, −0.2, −0.4, and −0.6 GPa to obtain optimized structures with different unit cell volumes. A negative hydrostatic pressure constitutes a so-called thermal pressure (26). Temperature effects in molecular crystals can substantially affect the unit cell volume. These thermal effects can approximately be accounted for by lattice optimizations under an appropriate thermal pressure, which leads to the volumetric expansion of the cell (26, 35). A minimization of the Gibbs free energy at a certain temperature with regard to the cell volume enables the calculation of the corresponding thermal pressure, which is defined as the derivative of the vibrational free energy with regard to the volume. Then, harmonic vibrational free energies were computed for all of the obtained structures. On the basis of the light PBE + TS energies and harmonic vibrational free energies, the unit cell volume corresponding to 300 K was determined via the Murnaghan equation of state (34). On the basis of these thermally expanded structures, the stability rankings were calculated as described above.

For all thermally expanded structures of system XXIII, we computed the anharmonic vibrational contributions to the free energies by replacing the harmonic oscillators by Morse oscillators. This is performed for all phonon modes at the Γ-point of cells containing four molecules, i.e., for forms A, C, D, and E and Str. N70, this corresponds to the unit cell, while for form B and Str. N18, N31, and N42, this corresponds to a 2 × 1 × 1 supercell. The structures were displaced along all normal modes in both directions, corresponding to energy changes of 0.5k_BT and k_BT according to the harmonic approximation, where k_B is the Boltzmann constant and T = 300 K. The energies of all displaced structures were calculated with PBE + TS using light settings. To have a consistent sampling of the thermally accessible energy window, we demanded that the largest observed energy change with respect to the optimized thermally expanded structure always lies between k_BT and 1.5k_BT. Therefore, the displacement amplitudes of a few low-frequency modes had to be reduced to sample the desired energy window. Next, we fitted a Morse potential (39, 40), given by

$$\mathit{V}(\mathit{x})=\mathit{D}{(1-{\mathit{e}}^{-\mathit{a}(\mathit{x}-{\mathit{x}}_0)})}^2$$ (2)

to the obtained data points for each mode. In this expression, x is the displacement amplitude, and the parameters D, a, and x₀ describe the well depth, the width of the potential, and the minimum of the potential, respectively. The energy of a vibrational mode in state ν can be calculated by

$$\mathit{E}(\mathrm{\nu })=\mathrm{\hslash }{\mathrm{\omega }}_0(\mathrm{\nu }+\frac{1}{2})-\frac{{\mathrm{\hslash }}^2{\mathrm{\omega }}_0^2}{4\mathit{D}}{(\mathrm{\nu }+\frac{1}{2})}^2$$ (3)

with

$${\mathrm{\omega }}_0=\sqrt{\frac{2{\mathit{a}}^2\mathit{D}}{\mathrm{\mu }}}$$ (4)

where μ is the reduced mass. The anharmonic vibrational free energy (${\tilde{\mathit{F}}}_{\text{vib}}$) at the Γ-point was computed according to

$${\tilde{\mathit{F}}}_{\text{vib},\mathrm{\Gamma }}=-{\mathit{k}}_{\mathrm{B}}\mathit{T} \text{ln}{\mathit{Q}}_{\text{vib}}$$ (5)

with

$${\mathit{Q}}_{\text{vib}}={\displaystyle \prod _{\mathit{i}}}{\displaystyle \sum _{\mathrm{\nu }}}\text{exp}\left(\frac{-{\mathit{E}}_{\mathit{i},\mathrm{\nu }}}{{\mathit{k}}_{\mathrm{B}}\mathit{T}}\right)$$ (6)

where i runs over phonon modes. This approach yields anharmonic vibrational free energies at the Γ-point for cells including four molecules. To also account for other q-points, we relied on the harmonic approximation and calculated the total vibrational free energies according to

$${\tilde{\mathit{F}}}_{\text{vib}}={\mathit{F}}_{\text{vib},\text{full}}+{\tilde{\mathit{F}}}_{\text{vib},\mathrm{\Gamma }}-{\mathit{F}}_{\text{vib},\mathrm{\Gamma }}$$ (7)

where F_vib,full is the fully converged harmonic vibrational free energy and F_vib,Γ is the harmonic vibrational free energy evaluated at the Γ-point only for the cells described above.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/1/eaau3338/DC1

Supplementary Text

Fig. S1. Rank 1 (XXIII-N70) and form A (XXIII-N85) share a sheet structure (red boxes), in which the molecules are arranged according to the same pattern, but the sheets are stacked differently.

Table S1. Relative energies of a benchmark set of structures with small unit cells calculated with different methods.

Table S2. Convergence of relative stabilities with basis set and grid settings.

Table S3. This table shows the MAD and the maximum absolute deviation (MAX) for all possible relative energies (within a system) from table S1 with regard to PBE0 + MBD calculations with tight settings for basis set and grids.

Table S4. Stability ranking for system XXII in kilojoules per mole per molecule.

Table S5. Stability ranking for system XXIII in kilojoules per mole per molecule.

Table S6. Stability ranking for system XXIV in kilojoules per mole per trimer.

Table S7. Stability ranking for system XXV in kilojoules per mole per dimer.

Table S8. Stability ranking for system XXVI in kilojoules per mole per molecule.

Table S9. Errors of PBE + TS–optimized structures with regard to experimental structures.

Table S10. Errors of the thermally expanded structures (corresponding to 300 K within the QHA) with regard to experimental structures.

Data S1. All PBE + TS–optimized structures (light settings) and the thermally expanded structures for system XXIII.