Abstract
Internal fixation of bone fractures using plates and screws involves many choices—implant type, material, sizes, and geometric configuration—made by the surgeon. These decisions can be important for providing adequate stability to promote healing and prevent implant mechanical failure. The purpose of this study was to develop mathematical models of the relationships between fracture fixation construct parameters and resulting 3D biomechanics, based on parametric computer simulations. Finite element models of hundreds of different locked plate fixation constructs for midshaft diaphyseal fractures were systematically assembled using custom algorithms, and axial, torsional, and bending loadings were simulated. Multivariate regression was used to fit response surface polynomial equations relating fixation design parameters to outputs including maximum implant stresses, axial and shear strain at the fracture site, and construct stiffness. Surrogate models with as little as three regressors showed good fitting (R2=0.62–0.97). Inner working length was the strongest predictor of maximum plate and screw stresses, and a variety of quadratic and interaction terms influenced resulting biomechanics. The framework presented in this study can be applied to additional types of bone fractures to provide clinicians and implant designers with clinical insight, surgical optimization, and a comprehensive mathematical description of biomechanics.
Keywords: Finite element, Fracture fixation, Locking plate and screw, Response surface
Introduction
Bone fracture fixation with internal plating is a common orthopaedic procedure. Locked connections between plates and screws have become increasingly popular over the last ten years and are now ubiquitous in many types of fracture fixation.3,29 The locking plate has the benefits of improving angular stability, fixation strength, and blood supply at the periosteal bone surface.23 Despite these advantages of locking plates, complications such as nonunions, malaligned unions, delayed fracture healing, or hardware failure occur in up to 10% of patients,15,28 and the implants are more expensive than conventional plates and screws.10
In locked plate fracture fixation there are many available options in geometric configurations, sizings, and materials. These options include plate length, number and type of screws, screw configurations, and in some cases residual fracture gap size. These variables affect stresses in the implants, stability of the fracture healing site, and strains in healing tissue that can substantially affect fracture healing.5,7,11,23 To optimize fracture fixation procedures and improve outcomes for patients, it is important to understand these biomechanical relationships.25,28 However the three-dimensional biomechanics associated with locked plated fixation can be complex and involve interactions among the variables of the fixation construct. Previous studies have described general principles of locking plates,7,23,28,30 and experimental and numerical studies have investigated effects of individual parameters on fracture fixation.18,19,21,22,29 However these studies have focused on particular aspects of fracture fixation, not with the goal of providing a comprehensive mathematical description of the interrelated factors involved.
In so-called computer experiments, parametric variation of the inputs of a computer model are used to generate large numbers of “designs”, outputs are determined for each design by computer simulation, and statistical methods can then be used to fit surrogate models, i.e. mathematical equations that relate outputs to inputs.27 These resulting surrogate models have important potential uses: (1) insight into which inputs have a large effect on the output and which do not; (2) prediction of output for a new combination of inputs; and (3) optimization.
The objective of this study was to develop surrogate mathematical models, specifically quadratic polynomial regression equations, of locked fracture fixation biomechanics based on finite element analysis simulations. It was hypothesized that the working length of the fracture fixation construct would be strongly predictive of interfragmentary strains and implant maximum stresses. In addition relationships between other input variables (and their quadratic and interaction terms) and output variables were quantified.
Materials and Methods
Finite element model cases and DOE
Diaphyseal midshaft fracture fixation was modeled such as would occur in the treatment of midshaft femur or tibia fractures. Long bone was modeled with a hollow cylinder for cortical bone (30 mm outer diameter and 4.3 mm cortical thickness) and 400 mm total length including the fracture gap. Fractures were simulated with simple transverse cuts, and seven cases for fracture gap sizes were considered (dgap = 0.2, 0.5, 1, 1.5, 2.0, 2.5, and 3 cm). Five lengths of plate (4.5 mm Narrow Locking Compression Plate, 4 mm thickness, Depuy Synthes, West Chester, PA) were modeled: Lplate (# of holes) = 15.2 cm (8), 18.8 cm (10), 22.4 cm (12), 26 cm (14) and 29.6 cm (16). Locking screws were modeled without considering screw threads (5 mm diameter, biocortical, Depuy Synthes, West Chester, PA) (Table 1). The gap between plate and bone was 1 mm.5
Table 1.
Listing of combinations of plate length, fracture gap, number of screws, and associated screw positions used to create all fracture fixation models used for FEA simulations. (The forward slash (/) shows the different cases in fracture gaps and screw configurations.)
| Plate length (Lplate cm) | Fracture gap (dgap, cm) | Number of screws (Nscrews | Screw position (symmetry) e.g. 1,3 = screws in both 1 & 3 positions |
|---|---|---|---|
| 15.2 | |||
| 0.2 | 1 | 1 / 3 | |
| 2 | 1,3 | ||
| 0.5 / 1 / 1.5 / 2 / 2.5 / 3 | 1 | 1 / 2 / 3 | |
| 2 | 1,2 / 1,3 / 2,3 | ||
| 3 | 1,2,3 | ||
| 18.8 | |||
| 0.2 | 1 | 1 / 3 | |
| 2 | 1,3 | ||
| 0.5 / 1 / 1.5 / 2 / 2.5 / 3 | 1 | 1 / 3 / 4 | |
| 2 | 1,3 / 1,4 / 3,4 | ||
| 3 | 1,3,4 | ||
| 4 | 1,2,3,4 | ||
| 22.4 | |||
| 0.2 | 1 | 1 / 4 | |
| 2 | 1,4 | ||
| 0.5 / 1 / 1.5 / 2 / 2.5 / 3 | 1 | 1 / 3 / 5 | |
| 2 | 1,3 / 1,5 / 3,5 | ||
| 3 | 1,3,5 | ||
| 5 | 1,2,3,4,5 | ||
| 26 | |||
| 0.2 | 1 | 1 / 3 / 5 | |
| 2 | 1,3 / 1,5/ 3,5 | ||
| 3 | 1,3,5 | ||
| 0.5 / 1 / 1.5 / 2 / 2.5 / 3 | 1 | 1 / 3 / 5 / 6 | |
| 2 | 1,3 / 1,5 / 1,6 / 3,5 / 3,6 / 5,6 | ||
| 3 | 1,3,5 / 1,3,6 / 1,5,6 / 3,5,6 | ||
| 4 | 1,3,5,6 | ||
| 6 | 1,2,3,4,5,6 | ||
| 29.6 | |||
| 0.2 | 1 | 1 / 2 / 4 / 6 | |
| 2 | 1,2 / 1,4/ 1,6 | ||
| 3 | 1,2,4 / 1,2,6 / 1,4,6 | ||
| 4 | 1,2,4,6 | ||
| 0.5 / 1 / 1.5 / 2 / 2.5 / 3 | 1 | 1 / 2 / 4 / 6 / 7 | |
| 2 | 1,2 / 1,4 / 1,6 / 1,7 | ||
| 3 | 1,2,4 / 1,2,6 / 1,2,7 / 1,4,6 / 1,4,7 / 1,6,7 | ||
| 4 | 1,2,4,6 / 1,2,4,7 / 1,2,6,7 / 1,4,6,7 | ||
| 5 | 1,2,4,6,7 | ||
| 7 | 1,2,3,4,5,6,7 | ||
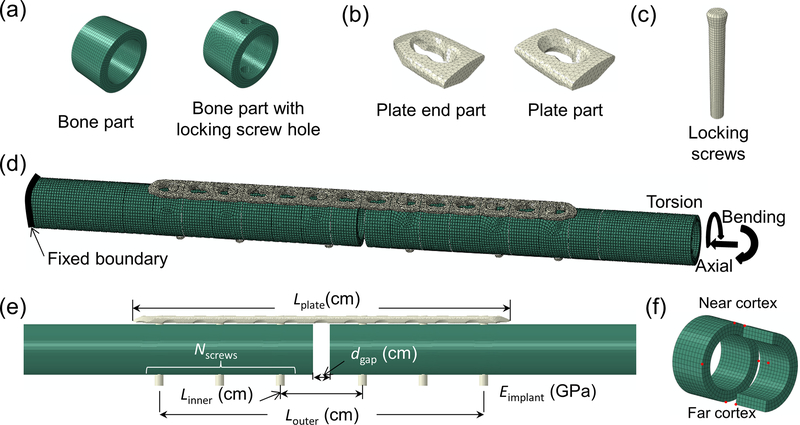
Number and configuration of screws were varied according to Table 1. Additional design variables included implant material elastic modulus (stainless steel and titanium alloy), making a total of 774 fracture fixation models. Three different loading types (axial, torsion, and bending) were simulated on each model. For automatic creation of all fixation designs, modularized finite element models for bone, plate and screw were created using Abaqus (ver6.13–2, Dassault, Providence, RI) and assembled using custom-written code in Matlab (ver14, Mathworks, Natick, MA) (Fig. 1). Node-matched surfaces of each module were combined with tie constraints. Matlab code was calling each module based on screw configurations and writing Abaqus input files. Models built using this novel modular build approach were verified using traditionally constructed models.
FIGURE 1.
Modularized finite element modeling used to generate large numbers of fracture fixation design configurations. (a) bone with or without screw hole; (b) locking plate parts; (c) locking screw; (d) an example of fracture fixation design achieved by automated assembly of bone, plate, and screw parts, in this case with 5 mm fracture gap, 14 hole plate, and screws positioned at holes 1, 3, and 6; (e) design variables of fracture fixation designs which served as regressors in the response surface statistical models; (f) Eight points (red dots) at the fracture gap used to compute strains in this region.
Additionally Design of Experiments (DOE) was used to identify a much smaller subset of simulations that were run and used to develop surrogate models, independent of the above ‘large’ dataset. The Custom Design module in JMP (SAS Institute Inc., Cary, NC) was used for DOE, and appropriate constraints for relationships between working length, plate length, and number of screws were defined. DOE resulted in 28 recommended fracture fixation models for which axial loading was simulated.
Finite elements
Quadratic tetrahedral elements (Abaqus type C3D10) were utilized for the plate model which was meshed from manufacturer-supplied CAD files, and hexahedral elements (C3D8R) were used to model the bone and screws. Mesh convergence testing was performed in seven different fixation designs using a range from 80,000 to 1,400,000 total elements. Using approximately 100,000 elements, results (gap displacement, construct stiffness, and maximum stress) converged with a 2–8% difference compared to the model with the largest number of elements.
Materials, interactions, and constraints
A transversely isotropic linear elastic material model was used for the non-osteoporotic cortical bone (Ex=17 GPa, Ey=Ez=11.5 GPa, νxy=νxz=0.31, νyz=0.58, Gxy=Gxz=3.3 GPa, Gyz=3.6 GPa).8 Fracture fixation implants were modeled as linear isotropic materials (stainless steel: E= 200 GPa, ν=0.3 and titanium: E=110 GPa, ν=0.3), and nonlinear contact with Coulomb friction (μ=0.3) was applied for the surface interaction between plate and bone (for cases which bone fragments around fracture gap contacted the plate bottom).19 The surfaces between the thread of locking screw head and plate, and between bicortical locking screw thread and bone hole, were tied together. Loading and boundary conditions were based on previous studies.5,29 Axial compression loading of 400 N was applied to simulate postoperative toe-touching weight bearing.5 This loading was applied to a center point of the proximal end of the bone. For torsional loading, 2 Nm was applied to the center of the proximal end of bone around the diaphyseal shaft axis.17 For bending, a pure moment of 10 Nm was applied to the proximal end (Fig. 1). In axial and torsional loading cases, proximal end translations were constrained to zero in directions perpendicular to the long axis of bone, and the distal end of the bone was rigidly fixed, as reported previously.5,29 For bending this proximal end constraint was not applied and the distal end was rigidly fixed.
Sensitivity analyses
Although the present study focused largely on surgical variables and not patient variables, sensitivity to bone geometry was tested as follows. Three alternate combinations of outer diameter and bone thickness (25 mm outer diameter and 4.3 mm cortical thickness, 30 mm outer diameter and 3.6 mm cortical thickness, and 30 mm outer diameter and 5.1 mm thickness) were modeled. Sensitivity to bone material properties was also tested. Two alternate material property sets were applied by scaling all properties by 75% and 50%. For each of these bone geometries and material property cases, ten different fracture fixation constructs were modeled and simulated in axial loading. Sensitivity to plate geometry was tested. 28 simulations of different fracture fixation constructs were carried out using a generic rectangular plate and cylindrical screw geometries.
Finite element model outputs
Maximum von Mises stresses of the plate (σplate_max) and screws (σscrew_max) were determined using the stresses from all elements. Stresses at the interfaces between the screw heads and the plate holes were ignored because of difficulty in accurately modeling these threaded interfaces, and because these interfaces were not considered the weakest part of system if screws were well aligned with plate hole and tightened with proper torque.23,28 Stiffness of the fracture fixation construct (kaxial, ktorsion, and kbending) was computed as the ratio of applied load (axial, torsional, or bending) to proximal bone displacement (axial or rotational). Interfragmentary axial strain at the fracture gap was determined by dividing relative axial displacement between the two fragments by gap size.16 Interfragmentary shear strain was determined similarly but using the relative interfragmentary displacement magnitude in the plane perpendicular to the bone axis.12 Interfragmentary displacements were determined at the center of the fracture gap consistent with previous literature.16
Full quadratic regression models
Polynomial regression-based surrogate models, or response surfaces, were developed for each model output separately with the statistical software SAS (Release9.3, SAS Institute Inc., Cary, NC). The regressor variables were defined based on the modeling inputs and included Lplate, dgap, number of screws (Nscrews), screw working lengths (between inner screws (Linner), and between outer screws (Louter)) (Fig. 1e), and hardware material elastic modulus (Eimplant). Different units (cm, N mm-1, MPa, and GPa) were used to prevent very large or very small fit model coefficients and facilitate ease of interpretation. Linear, quadratic, and interaction forms of the regressors (a total of 26) were included: six linear, five quadratic, and 15 interaction regressor variables.
Simplified regression models
Because the above full quadratic models are complex and can be challenging to interpret, three different approaches for simplified regression models with a smaller number of the more influential regressors were tested, in which new models were fit (treating each response variable separately):
R2-based selection (5%): the best R2 value was calculated for each possible subset model from minimum 3 regressors model to full quadratic model, and then selected a model with the least number of regressors which produced an R2 value less than 5% different than that of the full quadratic model
Stepwise selection: a stepwise addition and elimination approach, in which regressors were added one by one to the model with the significance threshold of 15%. After each variable addition, any variable that was not significant (5%) among all the current model variables was removed, with the above steps repeating until no regressors outside the model meet the entry significance threshold and no regressors inside the model meet the removal threshold (Stepwise method in SAS),26 and
Linear regressors: a simple linear model that only included the six linear regressors.
Pairwise correlation analysis
In addition to the above polynomial regression analysis, pairwise correlations between model outputs and inputs were determined by Pearson correlation coefficients, and null hypotheses of r=0 were tested (SAS). Statistical significance was set at p < 0.05.
Experimental validation
Polyvinyl chloride (PVC) tubing (33.4 mm outer diameter and 4.5 mm wall thickness) with 400 mm length (including fracture gap), two lengths of plates, and locking screws were used for experimental validation. PVC was used due to cost considerations.13 Simple transverse cuts were made to simulate the fracture, and three fracture gaps (0.2, 1, and 2 cm) were tested. Two lengths of plates (18.8 cm and 26 cm length, 4.5 mm Narrow LCP plate, Depuy Synthes, West Chester, PA) and locking screws (5 mm diameter, bicortical self-tapping, Depuy Synthes, West Chester, PA) were used for fixation, and nine screw configurations for each plate were tested (Fig. S-1). All screws were tightened to 4 Nm torque and 1 mm gap was applied to elevate the plate from PVC tube.4 Similar constraints and loadings were applied to the experimental setup as described above for the finite element model. Axial or torsion loading was applied with a dual actuator servo-hydraulic test machine (Interlaken 3300 with Flextest 40 controller, MTS, Eden Prairie MN). Actuator force or torque was measured by in-line load cells (axial force: 2224 N capacity, Interface, Scottsdale, AZ; and torque: 45 Nm capacity, Omegadyne, Sunbury, OH). The recorded actuator displacement or rotation, and force or torque, were used to calculate structural stiffnesses, and for axial loading the interfragmentary displacement was measured at the cortex opposite the plate with a digital caliper with a 0.01 mm resolution. Axial gap strain was calculated with dividing the infragmentary displacement by gap sizes. Finite element models of the above experiments were generated (with same geometry and PVC material properties), and outputs were compared to each other for validation.
Results
Finite element model outputs
The averages of σplate_max were 156 MPa (94–314), 114 MPa (97–184), and 884 MPa (212–943) across the axial, torsion, and bending loading simulations, respectively. In axial loading, these σplate_max generally occurred at the plate’s bone-side surface, near an open screw hole within the inner working length. The location of σplate_max during torsion loading was generally at the top surface of plate holes between two screws closest to the fracture gap. The averages of σscrew_max were 85 MPa (40–263) for axial loading, 104 MPa (72–185) for torsion loading, and 357 MPa (270–637) for bending loading. These maximums generally occurred at the screw shaft closest to the interface between bone and screw, in the screw closest to the fracture. Averages of kaxial, ktorsion, and kbending were 2397 N mm-1 (421–4095), 1405 N mm °−1 (316–2255), and 421 Nmm mm-1 (181–738) respectively. Averages of εaxial were 2.2% (0.3–33.2), 0.001% (0–0.02), and 20.5% (4.3–55.0) for axial, torsion, bending loading respectively. Averages of εshear were 10.2% (0.2–248.1), 2.9% (0.3–20.4), and 1.4% (0.2–5.0) for axial, torsion, bending loading respectively. Visualizations of select fracture fixation constructs under axial loading are shown in Fig. 2.
FIGURE 2.
Examples of FEA results for fracture fixation with 26 cm plate and axial loading. Left and right columns show 0.5 and 1.5 cm fracture gap, respectively, and each row shows a different screw configuration. Von Mises stresses are displayed for the plate. White circles indicate screw locations.
According to sensitivity analyses, results were fairly insensitive to tested changes in bone geometry, material properties, and plate geometry. Tested changes in bone geometry resulted in very small shifts in σplate_max, σscrew_max, εaxial, and εshear (Fig. S-2a). Changes in bone geometry resulted in slightly larger shifts in kaxial. Reduction of 75% in bone material properties resulted in very small shifts in most result variables, but a 50% reduction in material properties resulted in larger shifts (Fig. S-2b). Good correlations were found between the commercial and corresponding generic locking plate results (R2=0.90–0.99, Fig. S-3b).
Full quadratic regression models
The full quadratic models showed good fitting between surrogate model predictions and FEA results with R2 ranging from 0.80 to 0.99, 0.68 to 0.99, and 0.65 to 0.95 for axial, torsion, and bending loading, respectively (Table 2). The number of regressors that was statistically significant (p<0.05) ranged from 6 to 19 across all loading conditions and output variables (Table S-1). Maximum leverage, defining level of influence of a single FEA result in the fit surrogate model (SAS), was 0.14.
Table 2.
Number of regressors and resulting R2 fit for the full quadratic surrogate model, and the various simplified surrogate models tested. The simplified surrogate model using the R2-based selection (5%) method (shaded column) is focused on further in Table 3 and Figs. 3 and 4.
| Model selection method | |||||
|---|---|---|---|---|---|
| Axial loading | Full quadratic | R2-based selection (5%) | Stepwise | Linear | |
| σplate_max | # of Regressors | 26 | 4 | 9 | 6 |
| R2 | 0.90 | 0.88 | 0.90 | 0.82 | |
| σscrew_max | # of Regressors | 26 | 3 | 12 | 6 |
| R2 | 0.95 | 0.91 | 0.95 | 0.79 | |
| kaxial | # of Regressors | 26 | 3 | 12 | 6 |
| R2 | 0.99 | 0.97 | 0.99 | 0.95 | |
| εaxial | # of Regressors | 26 | 4 | 8 | 6 |
| R2 | 0.81 | 0.78 | 0.72 | 0.53 | |
| εshear | # of Regressors | 26 | 4 | 7 | 6 |
| R2 | 0.80 | 0.77 | 0.80 | 0.51 | |
| Torsion loading | Full quadratic | R2-based selection (5%) | Stepwise | Linear | |
| σplate_max | # of Regressors | 26 | 7 | 12 | 6 |
| R2 | 0.88 | 0.87 | 0.88 | 0.41 | |
| σscrew_max | # of Regressors | 26 | 4 | 15 | 6 |
| R2 | 0.94 | 0.90 | 0.94 | 0.69 | |
| ktorsion | # of Regressors | 26 | 3 | 11 | 6 |
| R2 | 0.99 | 0.96 | 0.99 | 0.92 | |
| εaxial | # of Regressors | 26 | 8 | 9 | 6 |
| R2 | 0.68 | 0.66 | 0.66 | 0.40 | |
| εshear | # of Regressors | 26 | 5 | 8 | 6 |
| R2 | 0.78 | 0.75 | 0.78 | 0.50 | |
| Bending loading | Full quadratic | R2-based selection (5%) | Stepwise | Linear | |
| σplate_max | # of Regressors | 26 | 5 | 7 | 6 |
| R2 | 0.65 | 0.62 | 0.64 | 0.34 | |
| σscrew_max | # of Regressors | 26 | 11 | 19 | 6 |
| R2 | 0.77 | 0.74 | 0.77 | 0.45 | |
| Kbending | # of Regressors | 26 | 7 | 12 | 6 |
| R2 | 0.76 | 0.74 | 0.76 | 0.55 | |
| εaxial | # of Regressors | 26 | 3 | 11 | 6 |
| R2 | 0.95 | 0.91 | 0.95 | 0.80 | |
| εshear | # of Regressors | 26 | 5 | 9 | 6 |
| R2 | 0.80 | 0.77 | 0.79 | 0.74 | |
Simplified regression models
Using the R2-based selection (5%) method, the number of regressors was further reduced with some concomitant loss in model fitting: a range of 3 to 4 (R2=0.77–0.97), 3 to 8 (R2=0.66–0.96), and 3 to 11 (R2=0.62–0.91) for axial, torsion, and bending loading respectively (Table 2, Fig. 3). Using the Stepwise selection method, the number of regressors ranged from 7 to 12 (R2=0.72–0.99), 8 to 15 (R2=0.66–0.99), 7 to 19 (R2=0.64–0.95) for axial, torsion, and bending loading respectively. Using the linear regressors method, σplate_max and kaxial in axial loading, ktorsion in torsion loading, and εaxial in bending loading were fit well, although with resulting R2 values less than that when using the R2-based selection (5%) method. All estimated regressor coefficients and R2 values are provided in supporting information (Table S-2 to S-4).
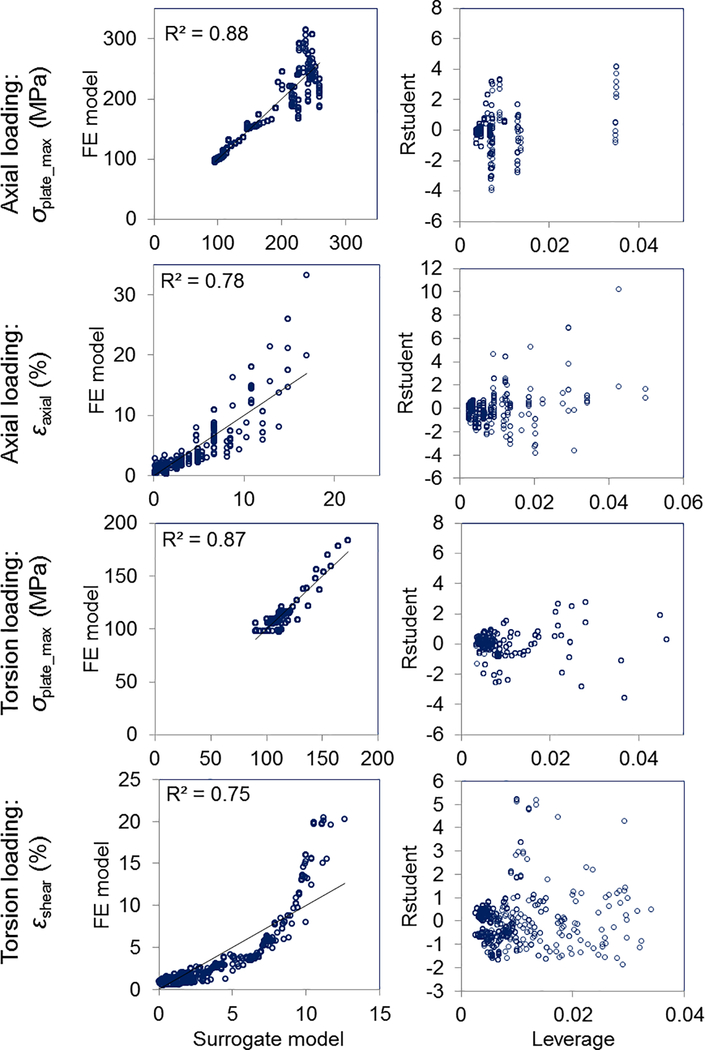
FIGURE 3.
Scatter plots of surrogate models. (Left column) Scatter plots show example fits between R2-based selection (5%) surrogate statistical model- predicted values and FE model ‘observed’ values that were used to fit the surrogate model (45° line indicates perfect fitting). (Right column) Plots of leverage vs. R-Student for the same models.
Simplified regression models: focus on R2-based selection (5%) method
The R2-based selection (5%) method was focused on further because it provided models with as little as 3–11 regressors with good R2 values. The resulting regressor coefficients were all statistically significant (Table 3) (p<0.0001). Surrogate model equations for each output can be expressed with the regressor coefficients listed in Table 3. Some examples for axial loading (Eq. (1)–(2)), torsion loading (Eq.(3)-(4)), and bending loading (Eq.(5)-(6)) are as follows:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
Considering a numerical example, if Louter is 23 cm, Eimplant is 200 GPa, and dgap is 1 cm, when Linner is increased from 5 cm to 20 cm, the predicted increase in σplate_max under axial loading will be from 110 to 250 MPa.
Table 3.
Regression coefficients for the surrogate model using the R2-based selection (5%). These coefficients combine to form linear equations for predicting each respective output variable as shown Eqs. (1) to (6). Coefficients for εaxial in torsional loading are not provided because only very small εaxial (<0.1%) were predicted for all constructs under this loading mode.
| Regression coefficient (p<0.0001) |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Plate stress | Screw stress | Axial strain | Shear strain | |||||||||
| Regressor variables | σplate_max (MPa) | σscrew_max (MPa) | εaxial (%) | εshear (%) | ||||||||
| Axial | Torsion | Bending | Axial | Torsion | Bending | Axial | Bending | Axial | Torsion | Bending | ||
| R2 | 0.88 | 0.87 | 0.62 | 0.91 | 0.9 | 0.74 | 0.78 | 0.91 | 0.77 | 0.75 | 0.77 | |
| Intercept (β0) | −5.7 | 81.3 | 822.1 | 30.0 | 65.3 | 710.0 | 2.9 | 70.5 | −24.2 | 11.9 | 4.7 | |
| Linear variables | Lplate (β1, cm) | - | - | - | - | - | 16.7 | - | - | - | - | - |
| dgap (β2, cm) | - | - | 308.8 | - | - | - | −5.3 | −42.2 | - | −10.4 | −1.9 | |
| Nscrews (β3) | - | 5.8 | - | - | - | −160.9 | - | - | - | - | - | |
| Linner (β4, cm) | 19.8 | 6.6 | −34.3 | 12.9 | 10.8 | −46.1 | 0.6 | - | 7.0 | - | 0.1 | |
| Louter (β5, cm) | - | - | - | - | - | −16.2 | - | - | - | - | - | |
| Eimplant (β6, GPa) | 0.4 | - | - | - | - | - | - | −0.07 | - | - | −0.02 | |
| Quadratic variable | Lplate2 (β7) | - | - | - | - | - | - | - | - | - | - | - |
| dgap2 (β8) | - | - | −90.4 | - | - | - | 1.7 | 8.6 | 3.7 | 2.4 | 0.2 | |
| Nscrews2 (β9) | - | - | - | 2.2 | - | 10.6 | - | - | - | - | - | |
| Linner2 (β10) | −0.4 | 0.2 | 0.6 | - | - | 1.2 | - | - | - | −0.007 | - | |
| Louter2 (β11) | - | - | - | - | - | - | - | - | - | - | - | |
| Lplate × | dgap (β12) | - | - | - | - | - | - | - | - | - | - | - |
| Nscrews (β13) | - | - | - | - | - | −10.0 | - | - | - | - | - | |
| Linner (β14) | - | −0.2 | - | - | - | - | - | - | - | - | - | |
| Louter (β15) | - | - | - | - | - | - | - | - | - | - | - | |
| Eimplant (β16) | - | 0.008 | - | - | - | - | - | - | - | - | - | |
| dgap × | Nscrews (β17) | - | - | - | - | - | - | - | - | - | - | - |
| Linner (β18) | - | - | 7.8 | - | - | - | −0.2 | - | −2.2 | - | - | |
| Louter (β19) | - | - | - | - | - | −0.9 | - | - | - | - | - | |
| Eimplant (β20) | - | - | - | - | - | 0.2 | - | - | - | - | 0.003 | |
| Nscrews × | Linner (β21) | - | −1.1 | - | −4.3 | −3.1 | 7.4 | - | - | - | 0.1 | - |
| Louter (β22) | - | - | - | - | 0.5 | 11.7 | - | - | - | - | - | |
| Eimplant (β23) | - | - | - | - | - | - | - | - | - | −0.004 | - | |
| Linner × | Louter (β24) | - | - | - | - | −0.2 | - | - | - | - | - | - |
| Eimplant (β25) | - | −0.02 | - | - | - | - | - | - | −0.01 | - | - | |
| Louter × Eimplant (β26) | −0.01 | - | - | - | - | - | - | - | - | - | - | |
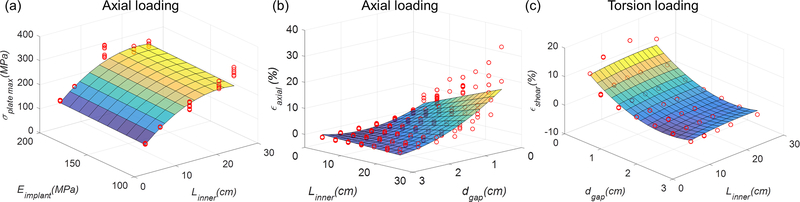
The fit of the response surfaces of several of these surrogate models are visualized in Fig. 4. Residuals increased with an increase of σplate_max and εaxial for axial loading, and with an increase in εshear for torsion loading (Figs. 3 and 4). Moreover, some influential and outlying FEA results were observed in the plot of studentized residual (R-Student) by leverage values (SAS) (Fig. 3). Higher leverages and residuals generally occurred in fixation designs having longer Lplate and Linner, with Nscrews = 1.
FIGURE 4.
Response surfaces based on R2-based selection (5%) surrogate models reported in Table 3. Red dots are the FEA results used to fit the surrogate models. (a): in axial loading σplate_max response surface as a function of Linner and Eimplant. (b): in axial loading εaxial response surface as a function of dgap and Linner. (c): in torsion loading εshear response surface as a function of dgap and Linner. In (a), Louter was constant (26.5 cm), and Eimplant and was Nscrews constant (200 GPa and 2 respectively) in (d).
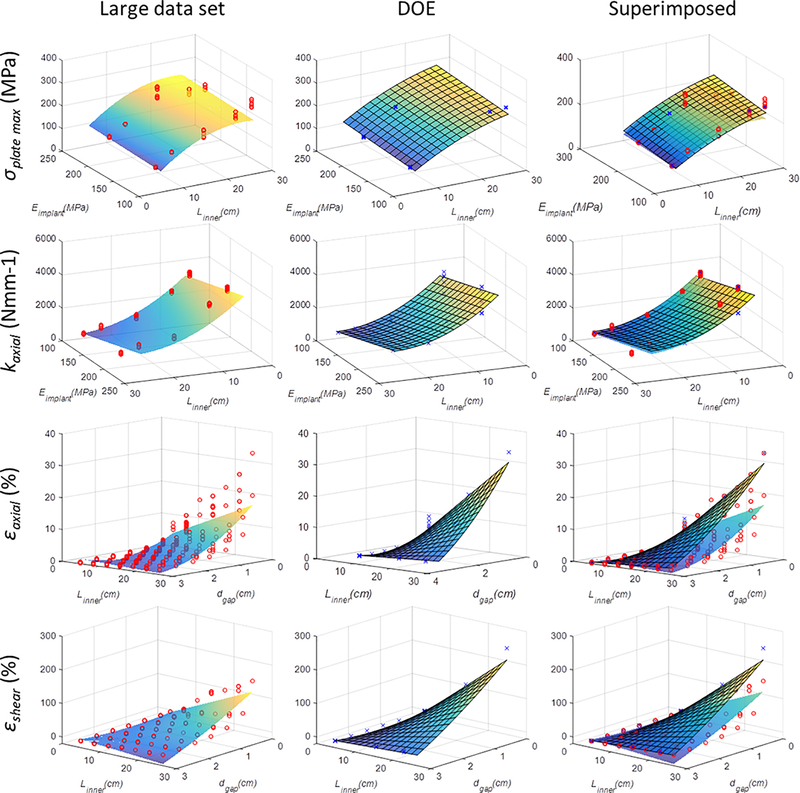
DOE-based surrogate models
Comparisons between DOE-based surrogate models and the above surrogate models are provided in Table S-5 and Figure 5. Results show similarity between the models (R2-based selection (5%) surrogate models) and associated response surfaces. Largest differences in response surfaces appear for axial and shear strain results (Fig. 5).
FIGURE 5.
Comparison of response surfaces between statistical models based on large data set and DOE-based data set (also see Table S-5). Response surface plots similar to those presented in Fig. 4 are presented, with individual data points resulting from FE analyses also visible. In the right-sided column of images, response surfaces derived from both the large and DOE-based data set are superimposed on one another for comparison. In order to enable 3D plotting of the surrogate models that included more than two independent variables, additional variables were set constant: In response surface of σplate_max, Louter was constant (26.5 cm), and Eimplant was constant (200 GPa) in response surface of εshear.
Pairwise correlation analysis
In constructs subject to axial loading, the parameter that had the strongest pairwise correlation to model outputs was Linner (p<0.05, Table S-6). In torsion loading, strong correlation was observed between ktorsion and Linner, and between Linner and σscrew_max (p<0.05, Table S-6). In bending loading, there was a strong correlation between dgap and εaxial.
Experimental validation
For axial loading differences between experimental results and FEA results averaged 16% (±7%) (R2=0.83) for kaxial and 5% (±3%) (R2=1.0) for axial gap strain. For torsional loading, the differences between experimentally determined and corresponding FEA for ktorsion averaged 18% (±8%) (R2=0.91) (Fig. S-1).
Discussion
This study is the first, to the best of our knowledge, to develop surrogate mathematical models of bone fracture fixation biomechanics based on large numbers of finite element simulations. These surrogate models provide new comprehensive insight and quantitative predictions in how the design of a fracture fixation construct affects implant stresses and mechanical stability at the healing fracture site. Large numbers of finite element models for ‘computer experiments’ were automatically generated using a novel modularized block method. The methods described in this paper could be used for other types of fractures. Surrogate models showed generally good fitting with the FEA results with R2 ranging from 0.62 to 0.97 (Table 3). Regression results indicate that Linner was the most influential variable for predicting σplate_max, σscrew_max, kaxial and ktorsion. Larger σplate_max and strains were associated with large Linner interacting with large Eimplant and small dgap, respectively. Strain at the fracture gap was strongly influenced by Linner, dgap, and Eimplant. Interaction variables Louter × Eimplant, Nscrews × Linner, Louter × Eimplant, and dgap × Linner, Linner× Eimplant affected outcomes σplate_max, σscrew_max, kaxial, εaxial,and εshear, respectively, in axial loading. In torsion and bending loading more interactions between parameters were influential (Table 3). DOE-based surrogate modeling of axial loading required a much smaller number of simulation runs and produced results with similarity to those produced from the large dataset, suggesting that DOE may provide a highly efficient tool for future similar surrogate modeling efforts. Results for the separate generic plate models support that the study’s findings are also generally applicable to other locking plates.
There are several potentially important uses of surrogate models of biomechanics in orthopaedic surgeries. First is basic insight into which surgical variables have the largest effect, and which have little effect, on resulting biomechanics. Second is quantitative prediction of biomechanics following a fracture fixation procedure (e.g. Eqns. 1–6, Table 3). Third is in design optimization for predicting the fixation construct which minimizes or maximizes particular biomechanical variables.
Relationships between particular fracture fixation design variables and resulting biomechanics in the present study are generally consistent with previous literature which looked at these variables more in isolation and generally did not consider interactions between variables. Working length between screws was previously reported as an important parameter for affecting axial and torsional stiffness19,21,29 and interfragmentary movement at the fracture gap.18 Results are also consistent with a previous study which showed minimal effect of the fracture gap on construct stiffness in axial loading.21 Increased working length resulted in decreasing the stiffness of fracture fixation and increasing interfragmentary movement, and this is consistent with previous studies.9,18,19,29 The effect of working length on plate stress in axial loading is in agreement with the study of Stoffel et al.29 showing that plate stress was increased with increasing working length. The unsymmetrical pattern of stress at the plate in axial loading (Fig. 2) differs from some other studies21,22 which show symmetrical stress distribution, and this difference can be explained by differences in boundary conditions. The deformed shape of plate observed in this study is similar to the classical unsymmetrical buckle shape of a column pinned at one end and fixed at the other end. The effect of working length on plate stress in bending loading is in agreement with previous studies25,28 showing that smaller inner working lengths resulted in higher plate stress.
Strain is believed to play a major role in controlling fracture healing. A moderate level of axial interfragmentary motion has been shown to be beneficial to fracture healing, whereas the role of shear motion is more controversial.12,16 Studies in animals have reported that shear strains are predictive of tissue differentiation during healing, specifically that higher shear strains lead to increased cartilage and decreased woven bone formation.1,20,24 Most previous studies of human fracture fixation constructs have reported interfragmentary displacements5,19,21 or a strain based on a single displacement.23
Regarding sensitivity of results to bone geometry, results from axial loading with two different construct designs were compared with corresponding models built from a computed tomography scan of a patient’s femur. As described in Supplementary Data (Fig. S-4), differences in stress distributions and interfragmentary strains were small, with qualitatively similar plate stress distributions and less than 2% differences in σplate_max. Differences in axial stiffness were larger; this is likely partly associated with larger thickness of the cortex (9 mm) in the patient CT-derived model. Although the present study was focused on the surrogate modeling approach and fracture fixation surgical construct design variables, future studies should further consider the influence of bone and fracture geometry.
Surrogate models for σplate_max and σscrew_max fit to the bending results were less well fit than the surrogate models for other loading modes (R2 in Table 3). Upon further investigation it was determined that in constructs with small 2 mm fracture gap size, the gap closed during loading and substantially offloaded the plate and screws. This dichotomy of stress results based on gap size may have led to poorer surrogate model fitting.
The development of surrogate models using computational experiments has been utilized in other fields such as simulation-based design of aircraft and automobile components14,27 In orthopaedic biomechanics, Bah et al.2 investigated the stability of a cementless hip stem according to variation in femur morphology. A Kriging-based surrogate model was fit to FEA-determined implant micromotions using Bayesian processes. Casha et al.6 developed a quadratic mathematical model of the relationship between rib height and FEA-determined intercostal muscle force.
In the development of surrogate mathematical models there are a series of modeling choices to be made, including alternatives for the mathematical form of the model such as Kriging. In the present study polynomial models were used because they can be readily interpreted and have been used for many years in the response surface literature. Models were limited in complexity to full quadratic models. These models appear to provide fitting comparable to more complex models which included 3-, 4-, 5-, and 6-way interactions and model reduction by stepwise selection (analysis provided in Supplementary Data Table S-7), although a more thorough analysis of more complex polynomial models is left for future work.
In experimental validation there was generally good agreement between experiments and computer model predictions (Fig. S-1). The deviation between FEA results and experimental results might be due to difficulty in getting perfect alignment of fracture implants with synthetic bone, and alignment of the specimen with the loading axis. In addition, the tie condition between screw and bone in FE models is idealized compared to reality.
Boundary conditions were simplified compared to real physiologic loading. Considering the variability in physiologic loading across patients and activities, in this study three fundamental simplified loads were applied instead. In axial loading simulations, displacement perpendicular to the bone longitudinal axis at the proximal end was fully constrained, whereas physiologically there is partial constraint. Without this constraint, axial loading can result in large translations perpendicular to the long axis, and substantial bending of the construct.
Limitations of the study include modeling of simplified generic bone and fracture scenarios, and the study’s focus was on the surgical, not patient, variables. Bone geometric and material parameters could be surrogate model variables in future study. Fracture geometry from actual patients and compression plating with no fracture gap were not considered. The immediate post-operation period was modeled, thus the effects of tissue formation within the fracture gap were not considered. Von Mises stresses in the implants were used to characterize risk of implant failure;19,21,22,29 these implants often fail by a fatigue mechanism, and thus the tensile or compressive nature of these stresses should be further characterized. Only symmetrical screw configurations with non-cannulated locking screws were considered. Methods of surrogate model selection such as use of the Akaike information criterion would be useful to explore in future work.26
Supplementary Material
Acknowledgement
This project is funded, in part, under a grant with the Pennsylvania Department of Health using Tobacco CURE Funds. Additional support was received from the National Center for Advancing Translational Sciences, Grant KL2 TR000126. Fracture fixation plates and screws were donated by Depuy Synthes. Disclosure: H.W. and V.M.C. have no conflicts of interest to disclose. G.S.L. has received implants and CAD files for research as PI from Depuy-Synthes. J.S.R. is a speaker for product related instructional courses for Smith and Nephew, andis a consultant for Depuy-Synthes.
Symbols
- Lplate
Length of plate
- dgap
Fracture gap size
- Nscrews
Number of screws
- Linner
Working length between inner screws
- Louter
Working length between outer screws
- Eimplant
Implant material elastic modulus
- σplate_max
Max von Mises stress of plate
- σscrew_max
Max von Mises stress of screw
- kaxial
Axial stiffness of the fracture fixation construct
- ktorsion
Torsional stiffness of the fracture fixation construct
- kbending
Bending stiffness of the fracture fixation construct
- εaxial
Interfragmentary axial strain
- εshear
Interfragmentary shear strain
References
- 1.Augat P, Burger J, Schorlemmer S, Henke T, Peraus M, and Claes L. Shear movement at the fracture site delays healing in a diaphyseal fracture model. J. Orthop. Res. 21:1011–1017, 2003. [DOI] [PubMed] [Google Scholar]
- 2.Bah MT, Shi J, Heller MO, Suchier Y, Lefebvre F, Young P, King L, Dunlop DG, Boettcher M, Draper E, and Browne M. Inter-subject variability effects on the primary stability of a short cementless femoral stem. J. Biomech. 48:1032–1042, 2015. [DOI] [PubMed] [Google Scholar]
- 3.Bonyun M, Nauth A, Egol KA, Gardner MJ, Kregor PJ, McKee MD, Wolinsky PR, and Schemitsch EH. Hot Topics in Biomechanically Directed Fracture Fixation. J. Orthop. Trauma 28:S32–S35, 2014. [DOI] [PubMed] [Google Scholar]
- 4.Bottlang M, Doornink J, Fitzpatrick DC, and Madey SM. Far cortical locking can reduce stiffness of locked plating constructs while retaining construct strength. J. Bone Jt. Surg. 91:1985–1994, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bottlang M, Doornink J, Lujan TJ, Fitzpatrick DC, Marsh JL, Augat P, von Rechenberg B, Lesser M, and Madey SM. Effects of Construct Stiffness on Healing of Fractures Stabilized with Locking Plates. J. Bone Jt. Surg. 92:12–22, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Casha AR, Camilleri L, Manché A, Gatt R, Attard D, Gauci M, Camilleri-Podesta M-T, and Grima JN. External rib structure can be predicted using mathematical models: An anatomical study with application to understanding fractures and intercostal muscle function. Clin. Anat. 28:512–519, 2015. [DOI] [PubMed] [Google Scholar]
- 7.Claes L Biomechanical Principles and Mechanobiologic Aspects of Flexible and Locked Plating. J. Orthop. Trauma 25:S4–S7, 2011. [DOI] [PubMed] [Google Scholar]
- 8.Cowin SC, and Doty SB. Tissue mechanics. New York, NY: Springer, 2007, 357 pp. [Google Scholar]
- 9.Duda GN, Mandruzzato F, Heller M, Kassi J-P, Khodadadyan C, and Haas NP. Mechanical conditions in the internal stabilization of proximal tibial defects. Clin. Biomech. 17:64–72, 2002. [DOI] [PubMed] [Google Scholar]
- 10.Egol KA, Capriccioso CE, Konda SR, Tejwani NC, Liporace FA, Zuckerman JD, and Davidovitch RI. Cost-Effective Trauma Implant Selection. J. Bone Jt. Surg. 96:e189, 2014. [DOI] [PubMed] [Google Scholar]
- 11.Egol KA, Kubiak EN, Fulkerson E, Kummer FJ, and Koval KJ. Biomechanics of Locked Plates and Screws. J. Orthop. Trauma Sept. 2004. 18:488–493, 2004. [DOI] [PubMed] [Google Scholar]
- 12.Elkins J, Marsh JL, Lujan T, Peindl R, Kellam J, Anderson DD, and Lack W. Motion Predicts Clinical Callus Formation: Construct-Specific Finite Element Analysis of Supracondylar Femoral Fractures. J. Bone Joint Surg. Am 98:276–284, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ellis T, Bourgeault CA, and Kyle RF. Screw Position Affects Dynamic Compression Plate Strain in an In Vitro Fracture Model. J. Orthop. Trauma June 15:333–337, 2001. [DOI] [PubMed] [Google Scholar]
- 14.Fang K-T, Li R, and Sudjianto A. Design and modeling for computer experiments. New York, NY: Chapman & Hall/CRC Press, 2006, 20–24 pp. [Google Scholar]
- 15.Gardner MJ, Evans JM, and Dunbar RP. Failure of Fracture Plate Fixation. J. Am. Acad. Orthop. Surg. 17:647–657, 2009. [DOI] [PubMed] [Google Scholar]
- 16.Klein P, Schell H, Streitparth F, Heller M, Kassi J-P, Kandziora F, Bragulla H, Haas NP, and Duda GN. The initial phase of fracture healing is specifically sensitive to mechanical conditions. J. Orthop. Res. Off. Publ. Orthop. Res. Soc 21:662–669, 2003. [DOI] [PubMed] [Google Scholar]
- 17.MacLeod AR, Simpson AHRW, and Pankaj P. Age-related optimisation of screw placement for reduced loosening risk in locked plating. J. Orthop. Res. Off. Publ. Orthop. Res. Soc, 2016.doi: 10.1002/jor.23193 [DOI] [PubMed] [Google Scholar]
- 18.Märdian S, Schaser K-D, Duda GN, and Heyland M. Working length of locking plates determines interfragmentary movement in distal femur fractures under physiological loading. Clin. Biomech. 30:391–396, 2015. [DOI] [PubMed] [Google Scholar]
- 19.Moazen M, Jones AC, Leonidou A, Jin Z, Wilcox RK, and Tsiridis E. Rigid versus flexible plate fixation for periprosthetic femoral fracture—Computer modelling of a clinical case. Med. Eng. Phys. 34:1041–1048, 2012. [DOI] [PubMed] [Google Scholar]
- 20.Morgan EF, Salisbury Palomares KT, Gleason RE, Bellin DL, Chien KB, Unnikrishnan GU, and Leong PL. Correlations between local strains and tissue phenotypes in an experimental model of skeletal healing. J. Biomech. 43:2418–2424, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nassiri M, MacDonald B, and O’Byrne JM. Computational modelling of long bone fractures fixed with locking plates – How can the risk of implant failure be reduced? J. Orthop. 10:29–37, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Oh J-K, Sahu D, Ahn Y-H, Lee S-J, Tsutsumi S, Hwang J-H, Jung D-Y, Perren SM, and Oh C-W. Effect of fracture gap on stability of compression plate fixation: A finite element study. J. Orthop. Res. 28:462–467, 2010. [DOI] [PubMed] [Google Scholar]
- 23.Perren SM Evolution of the internal fixation of long bone fractures. The scientific basis of biological internal fixation: choosing a new balance between stability and biology. J. Bone Joint Surg. Br. 84:1093–1110, 2002. [DOI] [PubMed] [Google Scholar]
- 24.Prendergast PJ, Huiskes R, and Søballe K. Biophysical stimuli on cells during tissue differentiation at implant interfaces. J. Biomech. 30:539–548, 1997. [DOI] [PubMed] [Google Scholar]
- 25.Ruedi TP, Murphy WM, and others. AO principles of fracture management. New York, NY: Thieme Medical Publishers, 2007, 292–294 pp. [Google Scholar]
- 26.SAS Institute. SAS/IML 9.3 User’s Guide. SAS Institute, 2011, 6340–6475 pp.at <https://support.sas.com/documentation/cdl/en/imlug/64248/PDF/default/imlug.pdf>
- 27.Simpson TW, Booker AJ, Ghosh D, Giunta AA, Koch PN, and Yang R-J. Approximation methods in multidisciplinary analysis and optimization: a panel discussion. Struct. Multidiscip. Optim. 27:302–313, 2004. [Google Scholar]
- 28.Smith WR, Ziran BH, Anglen JO, and Stahel PF. Locking Plates: Tips and Tricks. J. Bone Jt. Surg. 89:2298–2307, 2007. [DOI] [PubMed] [Google Scholar]
- 29.Stoffel K, Dieter U, Stachowiak G, Gächter A, and Kuster MS. Biomechanical testing of the LCP – how can stability in locked internal fixators be controlled? Injury 34, Supplement 2:11–19, 2003. [DOI] [PubMed] [Google Scholar]
- 30.Wagner M General principles for the clinical use of the LCP. Injury 34, Supplement 2:31–42, 2003. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.