Robust gene-environment interaction analysis using penalized trimmed regression

Abstract

In biomedical and epidemiological studies, gene-environment (G-E) interactions have been shown to importantly contribute to the etiology and progression of many complex diseases. Most existing approaches for identifying G-E interactions are limited by the lack of robustness against outliers/contaminations in response and predictor spaces. In this study, we develop a novel robust G-E identification approach using the trimmed regression technique under joint modeling. A robust data-driven criterion and stability selection are adopted to determine the trimmed subset which is free from both vertical outliers and leverage points. An effective penalization approach is developed to identify important G-E interactions, respecting the “main effects, interactions” hierarchical structure. Extensive simulations demonstrate the better performance of the proposed approach compared to multiple alternatives. Interesting findings with superior prediction accuracy and stability are observed in the analysis of TCGA data on cutaneous melanoma and breast invasive carcinoma.

1. Introduction

Despite significant main effects of genetic (G) and environmental (E) risk factors, recent studies have shown that gene-environment interactions also demonstrate important implications in medical genetics and epidemiology. There are a large number of successful approaches developed for detecting important G-E interactions associated with the etiology, diagnosis and prognosis of many complex diseases. Among them, one of the most popular strategy is to describe interactions using the products of two factors and then conduct a marginal [1,2] or joint [3,4] regression analysis. Recently, joint analysis has attracted increasing interest as it can accommodate all G factors and their interactions in a single model, given that the biological processes are usually dominated by the joint effects of multiple genetic changes. To facilitate the estimation and interpretation, the “main effects, interactions” hierarchical constraint is often imposed [5,6], where an interaction can be identified only if its corresponding main effects are also identified. Compared to marginal analysis, there are more challenges in joint analysis due to the high dimensionality of genomic measurements and hierarchical constraint. We refer to [7], [8] and [9] for comprehensive discussions.

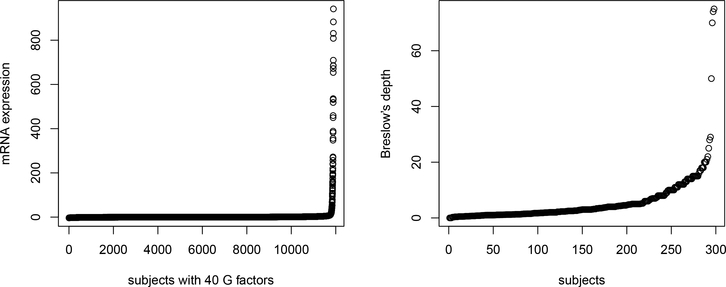
Despite many advantages, most of the existing interaction analysis approaches have the limitation of nonrobustness. They usually assume that data have no outliers/contaminations. However, in practice, outliers/data contaminations are not uncommon in both predictor and response spaces [10], which are known as leverage points and vertical outliers. More specifically, for some types of G factors, such as gene expression, outliers/contaminations may occur because of technical problems in profiling, human errors and genetic abnormalities [11]. For the disease-related clinical response (for example, Breslow’s depth for skin cutaneous melanoma), outliers/contaminations can be caused by errors in data collection and recording and inadvertently uncorrect sampling. In addition, sometimes there are extremely long or short survivals in prognosis studies due to the mistakes in death records as well as misclassification in the cause of death. In Figure 1, we show the distributions of some G factors and Breslow’s depth for the SKCM (skin cutaneous melanoma) data collected by TCGA (The Cancer Genome Atlas), where both leverage points and vertical outliers are clearly observed. More information on this data is available in the data analysis section of this article. For nonrobust approaches, it has been shown that these outliers can lead to biased estimation and false marker identification. Recently, a few approaches have been developed for robust G-E interaction analysis, including those based on quantile regression [12] or correlation [13], least absolute deviation (LAD) loss [6], rank-based loss function [3], and others. However, these approaches are only robust to outliers in response but cannot accommodate leverage points in predictor space. The interaction studies on both vertical outliers and leverage points are still much limited [14].

Figure 1.

Analysis of SKCM data: the distributions of some G factors and the Breslow’s depth.

In this study, we develop a joint model respecting the “main effects, interactions” hierarchical structure for G-E interaction analysis. The unique characteristic of this study is accommodating outliers/contaminations in both predictor and response spaces. The proposed approach is built on the robust trimmed regression technique, which can accommodate many types of data, such as continuous biomarkers and censored survival times. It significantly differs from least absolute deviation regression and other robust approaches which only have robustness property towards vertical outliers. Our study extends the traditional trimmed regression to interaction analysis and develops the “coefficient decompostion+penalization” framework for hierarchical selection, which may have independent methodological value. Advanced from the existing trimmed regression approaches which are usually built with the predefined size of trimmed set, we propose a more flexible data-driven process to determine the number of outliers, leading to satisfactory efficiency and robustness. In addition, a stability selection strategy is adopted to more accurately select the trimmed subject set. Overall, this study provides a practically useful new venue for G-E interaction analysis.

2. Methods

For a subject, let y be the response of interest, which can be a continuous marker, categorical disease status, or survival time. Let z = (z₁,…, z_q) be the q environmental/clinical variables and x = (x₁,…, x_p) be the p genetic variables. We consider the joint regression model with all G and E effects and their interactions,

$$\mathbb{E}(y;\mathit{z},\mathit{x})=\varphi \left({\alpha }_0+\mathit{z}\mathit{\alpha }+\mathit{x}\mathit{\beta }+\sum _{k=1}^q{\mathit{w}}^{(k)}{\mathit{\eta }}_k\right),$$ (1)

where ϕ is the known link function, $\mathbb{E}(·)$ denotes expectation, α₀ is the intercept, α = (α₁,…, α_q)′, β = (β₁,…, β_p)′ and η_k = (η_k1,…, η_kp)′ k = 1,…, q are the regression coefficients for main E factors, main G factors and their interactions, respectively, and w^(k) = (z_kx₁,…, z_kx_p).

We assume n independent subjects and use the subscript “i” to denote the ith subject. Denote the design matrices of E and G variables as Z_n×q and X_n×p, and the response vector as y_n×1. Under model (1), the unknown parameters $\mathit{\theta }={\left({\alpha }_0,{\mathit{\alpha }}^{\prime },{\mathit{\beta }}^{\prime },{\mathit{\eta }}_1^{\prime },\cdots ,{\mathit{\eta }}_q^{\prime }\right)}^{\prime }$ can be estimated by minimizing the negative log-likelihood function,

$$L(\mathit{\theta };\mathit{Z},\mathit{X},\mathit{y})=\frac{1}{n}\sum _{i=1}^n{l}_i(\mathit{\theta }),$$

with the deviance l_i (θ), which are usually not robust to vertical outliers or leverage points.

2.1. Robust trimmed estimation and selection

Instead of using the negative log-likelihood function directly, we propose the following robust objective function based on trimming technique,

$$L(\mathit{\theta };\mathit{Z},\mathit{X},\mathit{y},\mathcal{S})=\frac{1}{\left|\mathcal{S}\right|}\sum _{i\in \mathcal{S}}{l}_i(\mathit{\theta }),$$ (2)

where $\mathcal{S}$ is an outlier-free subset of {1,2,…, n} and $\left|\mathcal{S}\right|$ denotes the cardinality of set $\mathcal{S}$. We first consider the most popular linear regression model,

$$y_i={\alpha }_0+{\mathit{z}}_i\mathit{\alpha }+{\mathit{x}}_i\mathit{\beta }+\sum _{k=1}^q{\mathit{w}}_i^{(k)}{\mathit{\eta }}_k+{\epsilon }_i,$$ (3)

with

$$l_i(\mathit{\theta })={\left(y_i-{\alpha }_0-{\mathit{z}}_i\mathit{\alpha }-{\mathit{x}}_i\mathit{\beta }-\sum _{k=1}^q{\mathit{w}}_i^{(k)}{\mathit{\eta }}_k\right)}^2\triangleq r_i^2,$$

where ε_i is the random error.

Let r = (r₁,…, r_n)′, then $\mathcal{S}$ is defined as

$$\mathcal{S}=\left\{1\le i\le n:\left|r_i-\mathrm{median}(\mathit{r})\right|<\mu \mathrm{MAD}(\mathit{r})\right\},$$ (4)

where median(r) and MAD(r) are the median and median absolute deviation of vector r adjusted by a factor 1.4826, and μ > 0 is a tuning parameter.

The penalization is adopted for regularized estimation and variable selection, which has been a popular choice in several recent studies. For respecting “main effects, interactions” hierarchy, the coefficient for the interaction term η_k is decomposed as η_k = β ⊙ γ_k, where ⊙ represents the component-wise multiplication. Then, the following robust penalized objective function is proposed,

$$\begin{gathered} L_p(\mathit{\theta };\mathit{Z},\mathit{X},\mathit{y},\mathcal{S})=\frac{1}{\left|\mathcal{S}\right|}\sum _{i\in \mathcal{S}}{\left(y_i-{\alpha }_0-{\mathit{z}}_i\mathit{\alpha }-{\mathit{x}}_i\mathit{\beta }-\sum _{k=1}^q{\mathit{w}}_i^{(k)}\left(\mathit{\beta }\odot {\gamma }_k\right)\right)}^2 \\ +\sum _{j=1}^p\rho \left(\left|{\beta }_j\right|;{\lambda }_1,\xi \right)+\sum _{k=1}^q\sum _{j=1}^p\rho \left(\left|{\gamma }_{kj}\right|;{\lambda }_2,\xi \right), \end{gathered}$$ (5)

Where $\rho \left(\left|\nu \right|;{\lambda }_1,\xi \right)={\lambda }_1{\int }_0^{\left|\nu \right|}{\left(1-\frac{x}{{\lambda }_1\xi }\right)}_{+}dx$ is the minimax concave penalty (MCP) [15], λ₁ and λ₂ are data-dependent tuning parameters, and ξ is the regularization parameter. The proposed estimate $\widehat{\mathit{\theta }}$ is defined as the minimizer of (5) with the optimal subset $\widehat{\mathcal{S}}$. The nonzero components of $\widehat{\mathit{\beta }}$ and $\widehat{\mathit{\beta }}\odot {\widehat{\mathit{\gamma }}}_k(k=1,\cdots q)$ are regarded as the important main G effects and interactions that are associated with the response.

The proposed approach is motivated by the following considerations. As opposed to the nonrobust squared loss, the robust trimmed squared loss is adopted in (5) based on a subset $\mathcal{S}$ of subjects. The definition of $\mathcal{S}$ in (4) can exclude those subjects with extreme absolute residuals due to the deviated values in the spaces of predictors and/or response. It significantly advances from the existing robust G-E interaction analyses [3, 6,12] which can only accommodate outliers in response but not in predictors. Besides, the robust measures of central location (median) and scale (MAD) are adopted in $\mathcal{S}$, leading to more accurate detection of the number of outliers. Different from the existing studies on the least trimmed squares estimator [16,17] where the size of $\mathcal{S}$ is predefined, the proposed approach determines the value of $\left|\mathcal{S}\right|$ based on the residuals themselves and data-driven parameter μ. The identification of $\mathcal{S}$ becomes more flexible to achieve sufficiently high efficiency for the dataset without outliers and satisfactory robustness against data contamination. When μ is large enough, the proposed approach is reduced to the squared loss. In addition, motivated by the pairwise interaction analysis with strong hierarchial constraint developed in [18], we adopt the decomposition η_k = β⊙γ_k so that if an interaction term is selected (β_jγ_kj ≠ 0), the corresponding main genetic effect must also be selected (β_j ≠ 0). The MCP penalty is then imposed on β_j and γ_kj for variable selection given its satisfactory statistical and numerical properties. Here, E factors are not subject to penalized selection and always included in the model as they are usually pre-selected by clinical evidences and with low dimensionality. This decomposition framework for respecting hierarchical G-E interaction structure has the advantage of lucid interpretation and a less complex computational algorithm.

We also modify l_i (θ) to accommodate other types of response variables. For example, for the right-censored survival response with observed logarithm survival time y and censoring indicator δ, we consider the weighted squared loss under the accelerated failure time (AFT) model,

$$l_i(\mathit{\theta })=w_i{\left(y_i-{\alpha }_0-{\mathit{z}}_i\mathit{\alpha }-{\mathit{x}}_i\mathit{\beta }-\sum _{k=1}^q{\mathit{w}}_i^{(k)}{\mathit{\eta }}_k\right)}^2\triangleq {\left(r_i^{(w)}\right)}^2,$$

where the data {(x_i, z_i, y_i, δ_i),i = 1,…,n} have been sorted by y_i in ascending order, and the weight w_i is the Kaplan-Meier (KM) estimator defined as $w_1=\frac{{\delta }_1}{n},w_i=\frac{{\delta }_{\text{t}}}{n-i+1}\prod _{j=1}^{i-1}{\left(\frac{n-j}{n-j+1}\right)}^{{\delta }_j},i=2,\cdots ,n$. This weighted approach has been adopted in many published studies due to its considerably low computational cost and good statistical properties [19]. Using the subjects with nonzero weights and their corresponding $r_i^{(w)}$, the proposed approach can then proceed in the same manner. For categorical and count data under generalized linear model, a similar weighted squared loss can be conducted based on the Taylor series expansion. In numerical study, we examine both continuous data under the linear regression model and survival data under the AFT model.

2.2. Algorithm

A modified C-steps algorithm is developed to obtain the optimal subset $\widehat{\mathcal{S}}$ and corresponding estimation $\widehat{\mathit{\theta }}$, which is motivated by the stability selection [20]. We present the proposed algorithm in Algorithm 1. In this algorithm, the most challenging step is the optimization of the objective function (5) given the outlier-free subset $\mathcal{S}$. In Algorithm 2, we adopt an iterative coordinate descent (CD) algorithm, which optimizes L_p (θ; Z, X, y, $\mathcal{S}$) with respect to one parameter at a time and iteratively cycles through all parameters until convergence. Denote ${\mathit{y}}_{\mathcal{S}}$ as the components of y indexed by $\mathcal{S}$ and ${\mathit{X}}_{\mathcal{S}}$ as the rows of X indexed by $\mathcal{S}$.

Algorithm 1: Robust trimmed estimation and selection

Step 1: For t = 1,…, T,

Step 1.1 Set m = 0. Draw q + 10 observations from the dataset at random as the elemental subset ${\mathcal{S}}^{(t,0)}$. Compute

$${\mathit{\theta }}^{(t,0)}={\mathrm{argmin}}_{\mathit{\theta }}{L}_p\left(\mathit{\theta };\mathit{Z},\mathit{X},\mathit{y},{\mathcal{S}}^{(t,0)}\right)$$

Step 1.2 Set m = m + 1. Compute

$$\begin{gathered} {\mathit{r}}^{(t,m)}=\mathit{y}-{\alpha }_0^{(t,m-1)}-\mathit{Z}{\mathit{\alpha }}^{(t,m-1)}-\mathit{X}{\mathit{\beta }}^{(t,m-1)}-\sum _{k=1}^q{\mathit{W}}^{(k)}\left({\mathit{\beta }}^{(t,m-1)}\odot {\mathit{\gamma }}_k^{(t,m-1)}\right), \\ {\mathcal{S}}^{(t,m)}=\left\{1\le i\le n:\left|r_i^{(t,m)}-\text{median}\left({\mathit{r}}^{(t,m)}\right)\right|<\mu \mathrm{MAD}\left({\mathit{r}}^{(t,m)}\right)\right\}, \end{gathered}$$

and

$${\mathit{\theta }}^{(t,m)}={\mathrm{argmin}}_{\mathit{\theta }}{L}_p\left(\mathit{\theta };\mathit{Z},\mathit{X},\mathit{y},{\mathcal{S}}^{(t,m)}\right)$$

Step 1.3 Repeat Step 1.2 until convergence, where the convergence criterion is taken as

$$\frac{\left|L_p\left({\mathit{\theta }}^{(t,m)};\mathit{Z},\mathit{X},\mathit{y},{\mathcal{S}}^{(t,m)}\right)-L_p\left({\mathit{\theta }}^{(t,m-1)};\mathit{Z},\mathit{X},\mathit{y},{\mathcal{S}}^{(t,m-1)}\right)\right|}{\left|L_p\left({\mathit{\theta }}^{(t,m-1)};\mathit{Z},\mathit{X},\mathit{y},{\mathcal{S}}^{(t,m-1)}\right)\right|}<{10}^{-4}.$$

Step 1.4 Return the subset ${\mathcal{S}}^{\left(t,m_{\text{stop}}\right)}$ of the subjects selected at the stopping iteration m_stop.

Step 2: Compute the final set $\widehat{\mathcal{S}}$ of the selected subjects,

$$\widehat{\mathcal{S}}=\left\{i:\frac{1}{T}\sum _{t=1}^{T}I\left(i\in {\mathcal{S}}^{\left(t,m_{\text{stop}}\right)}\right)>\tau \right\},$$

where I(·) is the indicator function and τ ∈ (0, 1) is a tuning parameter.

Step 3: Compute the final estimation $\widehat{\mathit{\theta }}$ of the unknown parameters,

$$\widehat{\mathit{\theta }}={\mathrm{argmin}}_{\mathit{\theta }}{L}_p(\mathit{\theta };\mathit{Z},\mathit{X},\mathit{y},\widehat{\mathcal{S}}).$$

Algorithm 2: Iterative coordinate descent (CD) algorithm

Step 1 Initialize $b=0,{\left({\alpha }_0^{(b)},{\left({\mathit{\alpha }}^{(b)}\right)}^{\prime }\right)}^{\prime }={({\tilde{\mathit{Z}}}_{\mathcal{S}}^{\prime }{\tilde{\mathit{Z}}}_{\mathcal{S}})}^{-1}{\tilde{\mathit{Z}}}_{\mathcal{S}}^{\prime }{\mathit{y}}_{\mathcal{S}}$ with $\tilde{\mathit{Z}}=\left({\mathbf{1}}_{n\times 1},\mathit{Z}\right)$, β^(b) = 0, and ${\mathit{\gamma }}_k^{(b)}=\mathbf{0}$, where we denote b as the index of iteration.

Step 2 Set b = b + 1. With α₀, α and γ_k fixed at ${\alpha }_0^{(b-1)},{\alpha }^{(b-1)}$ and ${\gamma }_k^{(b-1)}$, optimize (5) with respect to β. Let ${\tilde{\mathit{y}}}^{(b)}=\mathit{y}-\mathit{Z}{\mathit{\alpha }}^{(b-1)}-{\alpha }_0^{(b-1)}$ and ${\tilde{\mathit{X}}}^{(b)}=\mathit{X}+{\sum }_{k=1}^q{\mathit{W}}^{(k)}\odot {\left({\mathbf{1}}_{n\times 1}{\gamma }_k^{(t-1)}\right)}^{\prime }$, then

$${\mathit{\beta }}^{(b)}=\mathrm{argmin}\frac{1}{\left|\mathcal{S}\right|}{\Vert {\tilde{\mathit{y}}}_{\mathcal{S}}^{(b)}-{\tilde{\mathit{X}}}_{\mathcal{S}}^{(b)}\mathit{\beta }\Vert }_2^2+\sum _{j=1}^p\rho \left(\left|{\beta }_j\right|;{\lambda }_1,\xi \right).$$ (6)

For j = 1,…, p, conduct the following steps sequentially,

Step 2.1 Compute

$${\mathit{r}}_{(-j)}^{(b)}={\tilde{\mathit{y}}}_{\mathcal{S}}^{(b)}-\sum _{l<j}{\tilde{\mathit{x}}}_{\mathcal{S},l}^{(b)}{\beta }_l^{(b)}-\sum _{l>j}{\tilde{\mathit{x}}}_{\mathcal{S},l}^{(b)}{\beta }_l^{(b-1)},{\chi }_j^{(b)}=\frac{1}{n}{\left({\tilde{\mathit{x}}}_{\mathcal{S},j}^{(b)}\right)}^{\prime }{\tilde{\mathit{x}}}_{\mathcal{S},j}^{(b)},{\phi }_j^{(b)}=\frac{1}{n}{({\tilde{\mathit{x}}}_{\mathcal{S},j}^{(b)})}^{\prime }{\mathit{r}}_{(-j)}^{(b)},$$

Step 2.2 Update the estimate of β_j as

$${\beta }_j^{(b)}=\{\begin{array}{ll}\text{ST}\left({\phi }_j^{(b)},{\lambda }_1\right)/\left({\chi }_j^{(b)}-\frac{1}{\xi }\right)\hfill & \left|{\phi }_j^{(b)}/{\chi }_j^{(b)}\right|\le {\lambda }_1\xi ,\hfill \\ {\phi }_j^{(b)}/{\chi }_j^{(b)}\hfill & \text{else,}\hfill \end{array}$$

where ST(ν,λ₁) = sgn(ν)(|ν| − λ₁)₊ is the soft-thresholding operator.

Step 3 With α₀, α and β fixed at ${\alpha }_0^{(b-1)},{\alpha }^{(b-1)}$ and β^(b), optimize (5) with respect to γ_k,k = 1,…, q. Let ${\breve{\mathit{y}}}^{(b)}=\mathit{y}-\mathit{Z}{\mathit{\alpha }}^{(b-1)}-\mathit{X}{\mathit{\beta }}^{(b)}-{\alpha }_0^{(b-1)}$ and ${\left({\tilde{\mathit{W}}}^{(k)}\right)}^{(b)}={\mathit{W}}^{(k)}\odot {\left({\mathbf{1}}_{n\times 1}{\beta }^{(b)}\right)}^{\prime }$, then

$${\left({\left({\mathit{\gamma }}_1^{(b)}\right)}^{\prime },\cdots ,{\left({\mathit{\gamma }}_q^{(b)}\right)}^{\prime }\right)}^{\prime }=\mathrm{argmin}\frac{1}{\left|\mathcal{S}\right|}{\Vert {\breve{\mathit{y}}}_{\mathcal{S}}^{(b)}-\sum _{k=1}^q{\left({\tilde{\mathit{W}}}_{\mathcal{S}}^{(k)}\right)}^{(b)}{\mathit{\gamma }}_k\Vert }_2^2+\sum _{k=1}^q\sum _{j=1}^p\rho \left(\left|{\gamma }_{kj}\right|;{\lambda }_2,\xi \right),$$ (7)

For k = 1, …, q and $j\in \left\{j:{\beta }_j^{(b)}\ne 0\right\}$, conduct the two steps similar to Step 2.1 and Step 2.2 sequentially.

Step 4 Compute

$${\left({\alpha }_0^{(b)},{\left({\mathit{\alpha }}^{(b)}\right)}^{\prime }\right)}^{\prime }={\left({\tilde{\mathit{Z}}}_{\mathcal{S}}^{\prime }{\tilde{\mathit{Z}}}_{\mathcal{S}}\right)}^{-1}{\tilde{\mathit{Z}}}_{\mathcal{S}}^{\prime }\left({\mathit{y}}_{\mathcal{S}}-{\mathit{X}}_{\mathcal{S}}{\mathit{\beta }}^{(b)}-\sum _{k=1}^q{\mathit{W}}_{\mathcal{S}}^{(k)}\left({\mathit{\beta }}^{(b)}\odot {\mathit{\gamma }}_k^{(b)}\right)\right).$$

Step 5 Repeat Steps 2–4 until convergence, where the convergence criterion is taken as

$$\frac{\left|L_p\left({\mathit{\theta }}^{(b)};\mathit{Z},\mathit{X},\mathit{y},\mathcal{S}\right)-L_p\left({\mathit{\theta }}^{(b-1)};\mathit{Z},\mathit{X},\mathit{y},\mathcal{S}\right)\right|}{\left|L_p\left({\mathit{\theta }}^{(b-1)};\mathit{Z},\mathit{X},\mathit{y},\mathcal{S}\right)\right|}<{10}^{-4}.$$

Different from the original C-steps algorithm which conducts a sufficiently large number of initial subsampling (500 adopted in [16,17]) and returns the results with the smallest objective function, the proposed algorithm identifies the optimal outlierfree subset based on the stability selection. With stability selection, we do not simply select one model which may not be optimal with insufficient initializations. The subset selection depends on the whole process where the outliers have smaller probability to be included, leading to more accurate detection and the lower requirement for a large number of initializations. In our numerical study, we set T = 50, which generates satisfactory result. Another advantage of the proposed algorithm is in Step 3 of Algorithm 2. Due to the decomposition η_kj = β_jγ_kj, we only need to update γ_kj when β_j ≠ 0, dramatically reducing the searching space and computational cost. Both algorithms are guaranteed to converge as the value of the objective function (5) decreases at each step. It is observed that convergence is achieved in a small to moderate number of iterations in both simulation and case study. For a simulated dataset with q = 5, p = 1000 and n = 250, the analysis with T = 50 takes about five minutes using a laptop with standard configurations.

Tuning parameters

We set μ = 2.5 in our numerical studies based on the 99.5% quantile of the standard normal distribution, motivated by that 1% of the observations are expected to be outliers for the normal distribution. For simulation scenarios with continuous G factors and AR structure under linear model (see the next section for details), we further examine the outlier detection results (as a function of μ) to better comprehend the effects of μ. In Table A1, two specific measures are considered, including true positive (TP) and false positive outliers (FP). For the five different error distributions, a larger μ detects fewer false positives but also fewer true positives. On the other hand, a smaller μ produces more true positives as well as more false positives. When μ = 2.5, it is observed to be able to effectively control the false positives and have satisfactory performance on the detection of true positives. As suggested by [20], the stability selection results are not sensitive to the threshold value τ in a range of (0.6,0.9). In our numerical studies, we set τ = 0.6. For the regularization parameter ξ in the MCP penalties, we follow the published studies [21] and set ξ = 6. A grid search is conducted to choose the values of (λ₁,λ₂) of the MCP penalties using BIC criterion with model size as the degrees of freedom.

3. Simulation

We assess the performance of the proposed analysis with extensive simulations. A total of forty simulation scenarios are considered. Under all scenarios, we set q = 5 and p = 1,000. There are thus a total of 1,005 main effects and 5,000 interactions. (a) Two types of G factors are considered, mimicking continuous gene expression and categorical SNP data, respectively. The continuous G variables are generated from a multivariate normal distribution with marginal means 0 and marginal variances 1. We consider two correlation structures. The first is an AR (auto-regressive) structure where the correlation between the jth and kth G variables is 0.3^|j−k|. The second is a Band (banded) structure where the correlation between jth and kth G variables is 0.33 if |j−k| = 1 and 0 otherwise. For the discrete G variables, we further dichotomize the above continuous variables at the 1st and 3rd quartiles and generate 3-level measurements (0,1,2). (b) There are three continuous and two binary E factors, where the three continuous ones are simulated from a multivariate normal distribution with marginal means 0 and the AR structure as mentioned above, and the two binary ones are simulated from a binomial distribution with a success probability of 0.6. (c) All E factors, eight main G factors and fourteen G-E interactions are assumed to have nonzero coefficients randomly generated from Uniform(0.6, 1), where the strong hierarchy is satisfied. The rest coefficients are zero. (d) We consider two types of response variables and models. The first is a continuous response under the linear model (3). The second is the censored survival data under the AFT model, where the observed logarithm survival times are generated based on model (3), and the censoring times generated from an exponential distribution with the parameter adjusted so that the censoring rate is around 20%. (e) Five types of data contaminations are considered. The first three ones have no outliers in predictors. The first one (D1) has error distribution N(0,1) which is also without outliers in response. The second (D2) and third (D3) ones have error distribution 90%N(0,1)+10%Cauchy(0,5) and 90%N(0,1)+10%N(20,1), where outliers exist in response. The fourth (D4) and fifth (D5) ones are assumed to contain leverage points. Specifically, for dataset with continuous G factors, 2% and 8% of the subjects have G factor measurements added by 20 and N(0,2), respectively. For dataset with categorical G factors, 10% of the subjects are re-generated from a multinomial distribution with probability (0.5,0.3,0.2) for (0,1,2). The error distributions for D4 and D5 are N(0,1) and 90%N(0,1) + 10%Cauchy(0,5). Thus, D4 only has outliers in predictors, while D5 has outliers in both predictor and response spaces. (f) We set the sample size n = 250 and n = 300 for the continuous and survival responses, respectively.

Besides the proposed approach (referred to as “LTS-MCP-Hier”), the following alternatives for joint analysis are also considered. The first four approaches conduct variable selection on all G factors and G-E interactions directly, without considering the hierarchical structure. LS-MCP is based on the nonrobust squared loss function and MCP penalty, implemented by the R package ncvreg. LAD-LASSO consists of the robust least absolute deviations and LASSO penalty which has robustness property towards vertical outliers. It is realized using the R package quantreg. RLARS is the robust least angle regression with robust correlation measure for variable selection [22] and is realized using the R package robustHD. It has been demonstrated to be robust to both vertical outliers and leverage points. LTS-MCP is similar to the proposed, except that the hierarchical structure is not reinforced and the original C-steps algorithm is used instead of stability selection. The last one is LS-MCP-Hier, which has the same modeling framework as the proposed, except that the nonrobust squared loss function is adopted. The above alternative approaches cover different types of G-E interaction analyses and can comprehensively evaluate the merits of the proposed approach. They are chosen due to their popularity and competitive performance among the existing approaches.

For each approach, we evaluate the identification performance for main effects (M) and interactions (I) separately, by the number of true positives M:TP and I:TP and the number of false positives M:FP and I:FP. In addition, the root of the sum squared error ${\Vert \widehat{\mathit{\theta }}-{\mathit{\theta }}^0\Vert }_2$ (RSSE) is used to assess the estimation accuracy, where $\widehat{\mathit{\theta }}$ and θ⁰ are the estimated and true values of θ. We also examine the prediction performance using an independent testing set with 100 subjects under the same simulation scenarios. We adopt the prediction mean squared error (PMSE) for continuous outcome and C-statistic (Cstat) for survival outcome. The C-statistic quantifies the overall adequacy of risk prediction for censored survival data based on the time-integrated AUC (area under curve), where a larger value indicates better prediction [23].

For each scenario, 200 replicates are simulated, and summary statistics (mean and standard deviation) are computed. Summary results for the scenarios with continuous G factors and AR structure under linear and AFT models are shown in Tables 1 and 2, respectively. The rest of the results are provided in Appendix. The proposed LTS-MCP-Hier is observed to have competitive performance under all simulation scenarios. For the dataset without contamination (D1), the proposed approach can achieve satisfactory efficiency that is comparable to the nonrobust LS-MCP-Hier, and outperforms the robust alternatives and even nonrobust LS-MCP. The majority of true positives are identified by the proposed approach while with a small number of false positives. The advantage of the proposed approach over the alternatives becomes prominent for the datasets with different types of contaminations. For example, for the scenario with outliers in predictors (D4) under linear model (Table 1), the proposed approach has (M:TP, M:FP, I:TP, I:FP)=(7.4, 3.8, 11.1, 2.7), compared to (1.4, 22.6, 3.1, 68.0), (4.1, 4.0, 4.2, 13.4), (7.2, 0.7, 6.9, 11.6), (6.2, 7.9, 10.0, 30.1), and (5.4, 54.5, 3.9, 5.4) for LS-MCP, LAD-LASSO, RLARS, LTS-MCP and LS-MCP-Hier, respectively. The superior identification performance of the proposed approach over LAD-LASSO and RLARS provides a strong support to the proposed trimming strategy for accommodating outliers. In addition, it performs better than LTS-MCP, which suggests that the “coefficient decomposition” and stability selection framework can improve the identification of both main effects and interactions. The proposed approach also behaves better in terms of estimation and prediction. For example, for the scenario with contamination type D2 under AFT model (Table 2), the proposed approach has (ESSE, Cstat)=(2.71, 0.89), compared to (46.11, 0.55), (4.11, 0.74), (4.83,0.73), (3.71,0.82), and (59.00,0.58) for LS-MCP, LAD-LASSO, RLARS, LTS-MCP and LS-MCP-Hier, respectively. For the datasets with categorical G variables, the similar pattern is observed that the proposed approach demonstrates superior or comparable performance compared to five alternatives in identification, estimation and prediction accuracy.

Table 1.

Summary results under simulation scenarios with continuous G factors and AR structure under linear model. In each cell, mean (sd) based on 200 replicates.

	M:TP	M:FP	I:TP	I:FP	RSSE	PMSE
			D1: N(0,1)
LTS-MCP-Hier	7.8(0.4)	0.6(1.6)	12.7(1.9)	0.7(0.8)	2.15(0.49)	0.99(0.43)
LS-MCP	5.7(0.9)	3.0(3.5)	10.8(0.9)	10.7(10.7)	2.80(0.41)	1.29(0.56)
LAD-Lasso	8.0(0.0)	10.6(5.6)	13.3(1.2)	28.0(11.4)	1.68(0.33)	1.35(0.45)
RLARS	7.5(0.6)	0.5(0.8)	7.3(1.9)	12.5(8.2)	3.27(0.42)	2.51(0.91)
LTS-MCP	6.4(0.9)	6.9(2.8)	11.0(1.1)	26.4(7.4)	2.39(0.53)	1.23(0.28)
LS-MCP-Hier	8.0(0.0)	0.3(1.2)	13.0(1.0)	0.4(0.6)	1.70(0.30)	0.80(0.18)
			D2: 0.9N(0,1) + 0.1Cauchy(0,5)
LTS-MCP-Hier	7.9(0.3)	0.6(1.8)	12.0(1.5)	0.9(0.9)	2.12(0.38)	1.12(0.34)
LS-MCP	2.2(1.8)	18.0(8.0)	2.7(2.6)	71.0(10.6)	30.42(40.46)	555.38(1853.39)
LAD-Lasso	7.8(0.5)	2.2(1.5)	7.6(2.3)	7.0(3.3)	3.01(0.36)	3.85(1.23)
RLARS	7.2(0.7)	0.7(1.0)	5.7(1.8)	11.0(5.7)	3.68(0.41)	3.55(1.24)
LTS-MCP	6.2(1.1)	7.8(3.3)	10.6(1.3)	30.9(9.7)	2.55(0.55)	1.18(0.32)
LS-MCP-Hier	5.8(1.5)	151.3(125.9)	2.6(3.4)	25.6(59.8)	28.80(42.28)	1351.47(5973.38)
			D3: 0.9N(0,1) + 0.1N(20,1)
LTS-MCP-Hier	7.9(0.3)	0.6(1.8)	12.0(1.6)	0.9(0.8)	2.01(0.41)	1.03(0.40)
LS-MCP	2.9(1.2)	24.3(4.7)	3.1(1.4)	66.2(5.5)	9.82(0.68)	32.66(6.95)
LAD-Lasso	7.5(0.7)	2.6(1.7)	6.1(2.3)	8.2(3.2)	3.29(0.33)	4.68(1.46)
RLARS	6.3(1.0)	1.4(1.5)	3.8(1.7)	11.7(5.8)	4.25(0.48)	5.23(1.79)
LTS-MCP	6.4(1.0)	7.6(3.0)	10.9(1.1)	28.3(6.2)	2.44(0.53)	1.09(0.27)
LS-MCP-Hier	6.5(0.9)	94.1(5.9)	2.4(1.5)	5.8(5.6)	8.81(0.64)	33.23(7.21)
			D4: N(0,1) and with leverage points
LTS-MCP-Hier	7.4(1.0)	3.8(8.0)	11.1(3.1)	2.7(2.1)	2.12(0.79)	1.08(2.02)
LS-MCP	1.4(0.9)	22.6(5.1)	3.1(2.0)	68.0(6.4)	7.38(1.03)	19.15(6.64)
LAD-Lasso	4.1(1.3)	4.0(2.4)	4.2(2.2)	13.4(3.6)	3.99(0.35)	9.27(2.47)
RLARS	7.2(0.8)	0.7(1.2)	6.9(2.0)	11.6(7.1)	3.42(0.34)	2.92(0.91)
LTS-MCP	6.2(1.2)	7.9(3.6)	10.0(1.3)	30.1(9.2)	2.47(0.60)	2.43(0.40)
LS-MCP-Hier	5.4(1.5)	54.5(37.3)	3.9(3.2)	5.4(3.1)	5.52(1.39)	14.61(9.16)
			D5: 0.9N(0,1) + 0.1Cauchy(0,5) and with leverage points
LTS-MCP-Hier	7.7(0.7)	3.4(8.4)	10.6(2.6)	2.3(2.3)	2.20(0.75)	1.02(1.77)
LS-MCP	0.7(0.7)	18.0(8.9)	1.5(1.4)	69.3(17.5)	25.80(32.38)	271.98(796.53)
LAD-Lasso	3.8(1.4)	4.0(1.9)	4.0(2.0)	12.5(3.5)	4.02(0.36)	9.20(2.59)
RLARS	6.8(0.9)	0.9(1.2)	5.6(2.0)	11.4(6.8)	3.79(0.42)	3.77(1.04)
LTS-MCP	6.3(1.1)	8.6(3.9)	10.8(1.2)	31.9(10.1)	2.47(0.57)	2.05(0.32)
LS-MCP-Hier	4.5(1.5)	152.6(99.4)	1.0(1.6)	24.6(62.0)	27.97(39.71)	1088.91(4898.79)

Table 2.

Summary results under simulation scenarios with continuous G factors and AR structure under AFT model. In each cell, mean (sd) based on 200 replicates.

	M:TP	M:FP	I:TP	I:FP	RSSE	Cstat
			D1: N(0,1)
LTS-MCP-Hier	7.8(0.5)	5.6(9.6)	11.0(2.7)	0.9(1.1)	2.48(0.52)	0.90(0.03)
LS-MCP	6.3(1.1)	12.3(4.8)	11.3(1.2)	38.3(9.6)	2.39(0.66)	0.92(0.02)
LAD-Lasso	7.5(0.8)	15.5(8.1)	8.4(3.9)	36.5(15.7)	3.06(0.59)	0.85(0.05)
RLARS	7.3(0.7)	10.3(3.8)	3.2(1.6)	21.8(4.3)	4.22(0.35)	0.78(0.04)
LTS-MCP	6.0(1.0)	14.8(4.9)	6.4(1.8)	57.4(10.4)	3.37(0.34)	0.85(0.04)
LS-MCP-Hier	8.0(0.2)	1.0(1.9)	12.1(1.5)	0.6(0.8)	1.94(0.34)	0.92(0.02)
			D2: 0.9N(0,1) + 0.1Cauchy(0,5)
LTS-MCP-Hier	7.7(0.5)	5.5(4.1)	9.1(2.8)	1.3(1.1)	2.71(0.58)	0.89(0.03)
LS-MCP	1.2(1.4)	13.9(8.6)	1.1(1.4)	59.6(10.7)	46.11(87.78)	0.55(0.07)
LAD-Lasso	5.8(1.7)	4.6(2.1)	1.7(1.3)	12.0(3.4)	4.11(0.40)	0.74(0.07)
RLARS	6.3(1.6)	7.6(4.9)	1.6(1.3)	22.9(6.3)	4.83(0.68)	0.73(0.06)
LTS-MCP	6.0(1.0)	15.4(4.0)	5.5(1.8)	59.7(5.5)	3.71(0.33)	0.82(0.03)
LS-MCP-Hier	5.4(1.5)	196.6(162.2)	2.0(2.4)	70.9(223.4)	59.00(119.77)	0.58(0.07)
			D3: 0.9N(0,1) + 0.1N(20,1)
LTS-MCP-Hier	8.0(0.2)	2.2(4.8)	11.9(1.6)	0.9(0.9)	2.01(0.38)	0.92(0.01)
LS-MCP	2.5(1.1)	24.6(4.9)	2.4(1.4)	72.2(6.1)	10.72(0.71)	0.64(0.04)
LAD-Lasso	6.6(1.2)	3.9(2.2)	2.7(1.6)	11.1(3.3)	3.79(0.28)	0.78(0.04)
RLARS	6.4(1.0)	4.2(3.2)	1.4(1.1)	12.4(6.3)	4.41(0.42)	0.78(0.04)
LTS-MCP	6.1(1.0)	11.4(4.1)	9.0(1.7)	48.9(10.3)	2.95(0.49)	0.89(0.02)
LS-MCP-Hier	5.8(1.1)	100.5(7.8)	2.5(1.5)	8.3(7.2)	9.75(0.56)	0.66(0.03)
			D4: N(0,1) and with leverage points
LTS-MCP-Hier	7.1(1.0)	10.9(14.7)	9.0(4.0)	1.2(1.2)	3.18(0.83)	0.84(0.07)
LS-MCP	3.4(1.1)	14.7(4.5)	4.9(2.1)	52.7(6.5)	4.89(0.60)	0.75(0.05)
LAD-Lasso	6.1(1.2)	7.2(5.0)	3.4(2.0)	17.8(11.8)	3.88(0.31)	0.77(0.04)
RLARS	7.0(0.8)	11.9(3.6)	2.6(1.4)	21.5(4.5)	4.37(0.36)	0.77(0.04)
LTS-MCP	5.5(1.3)	17.0(4.0)	5.2(1.8)	61.4(6.0)	3.77(0.42)	0.81(0.04)
LS-MCP-Hier	6.4(1.0)	42.4(24.3)	4.6(2.5)	2.9(2.1)	4.08(0.66)	0.78(0.05)
			D5: 0.9N(0,1) + 0.1Cauchy(0,5) and with leverage points
LTS-MCP-Hier	7.1(1.1)	12.9(14.1)	9.3(3.9)	1.5(1.4)	3.08(0.81)	0.85(0.07)
LS-MCP	1.1(1.1)	12.6(7.8)	1.3(1.3)	56.3(9.8)	35.96(69.84)	0.56(0.06)
LAD-Lasso	5.7(1.5)	4.3(2.3)	2.0(1.5)	12.2(3.4)	4.12(0.36)	0.74(0.06)
RLARS	6.5(1.4)	8.8(4.6)	2.2(1.5)	21.6(6.4)	4.79(1.30)	0.74(0.06)
LTS-MCP	5.7(1.1)	16.1(4.2)	5.1(2.0)	60.4(4.6)	3.77(0.37)	0.81(0.04)
LS-MCP-Hier	5.1(1.6)	174.4(158.2)	2.4(2.6)	67.4(229.7)	54.36(131.61)	0.57(0.07)

In practical genetic interaction analyses, the important interactions may have different magnitude of signals, including those with weak but nonzero effects [24]. To be thorough, we also examine the scenarios with both moderately large and weak effects. Specifically, we consider data with continuously distributed G factors and AR correlation structure, and with a continuous outcome under the linear regression model. The simulation settings for coefficients are similar to those in (c) as mentioned above. One different is that seven of the fourteen important interactions are with weaker signals equal to 0.2. Results with five types of data contaminations are shown in Table A8. It can be seen that the performance of all approaches decay compared to those in Table 1. However, the proposed approach is again observed to have favorable performance. For example, under the scenario with D4, the values of (I:TP, I:FP) for interactions are (7.7, 1.4) (proposed), (2.3, 69.4) (LS-MCP), (3.2, 14.2) (LAD-LASSO), (5.0, 10.1) (RLARS), (7.2, 27.0) (LTS-MCP), and (3.7, 5.1) (LS-MCP-Hier).

In the interaction analysis literature, it has been suggested that there may exist important interactions in the absence of the corresponding main effects [7]. For comprehensive consideration, we conduct another analysis on scenarios where the “main effects, interactions” hierarchy is violated for some interactions. Specifically, data with continuous G factors, AR correlation structure, and a continuous response are generated. Besides the fourteen nonzero G-E interactions as described above, six additional nonzero interactions are considered without the corresponding main G effects. As shown in Table A9, the proposed approach performs slightly worse than LTS-MCP which is similar to the proposed but does not reinforce the hierarchy. However, it still outperforms other alternatives, including two nonrobust approaches LS-MCP and LS-MCP-Hier, and two robust ones LAD-Lasso and RLARS which do not respect the hierarchy and may be favored here.

4. Data Analysis

The Cancer Genome Altas (TCGA) provides comprehensive profiling data in various cancer types. With high quality and public availability, the TCGA data have contributed to thousands of genetic studies and serve us as an ideal testbed. In this study, we analyze TCGA data on skin cutaneous melanoma (SKCM) and breast invasive carcinoma (BRCA). The processed level 3 data are considered which can be downloaded from TCGA Provisional using the R package cgdsr.

4.1. Skin Cutaneous Melanoma (SKCM) Data

Cutaneous melanoma, the most dangerous type of skin cancer, has been demonstrated to account for approximately 75% of all deaths from skin cancer. The response of interest is the continuous (log2-transformed) Breslow’s depth, which is analyzed using a linear model. It describes the thickness of the tumor, which is considered as one of the most significant factors in predicting progression of melanoma [25]. For E variables, we include age, American Joint Committee on Cancer (AJCC) tumor pathologic stage, gender, and Clark level. For G variables, we consider mRNA gene expressions, which are collected using the IlluminaHiseq RNAseq V2 platform and have been lowess-normalized, log-transformed, and median centered. There are 298 subjects available with 18,355 measurements of gene expressions. We conduct a simple prescreening as the number of cancer-related genes is not expected to be large, which selects the top 2,000 genes with the largest variances across all the samples for downstream analyses.

The estimated coefficients with the proposed approach are listed in Table 3. Compared to age and gender, stage and Clark level are more relevant to the Breslow’s depth, which is consistent with the literature. The proposed approach identifies a total of 43 important genes and 26 G-E interactions associated with Breslow’s depth. Existing literature shows potentially useful implications of our findings. For instance, gene FGFR3 has been shown to deactivate the malignant transformation as a tumor suppressor in melanoma cancer cells. An increased expression of antigen from gene FMR1NB has been found in melanoma stem cells, which may be a cause of treatment failure. Gene LAMP1 has been observed to express on the surface of metastatic melanoma cells, and its downregulation could reduce lung metastasis. Gene SPRR1A has been found to express dramatically higher levels in thin melanomas. In addition, gene SPRR2G has been characterized as keratinocyte-associated and has been found to have decreased expression in the primary melanoma. Gene S100A7, known as psoriasin, has been observed to significantly over-express in human epithelial skin tumors, as well as in breast and bladder cancer.

Table 3.

Analysis of SKCM data using the proposed approach: coefficients of identified main effects and interactions

	Main:G	Age	Stage	Gender	Clark level
Main:E		−0.0100	1.2197	−0.0587	0.3307
AADACL3	0.0004
AMBN	0.0005
ATP1A2	−0.0011
BCAR4	0.0004
BPIFA2	0.0001
C7ORF69	0.0038		0.0046
C8ORF34	0.0056		0.0101
CALCA	0.0029	0.0010	0.0008
CLNS1A	0.0066		0.0118	0.0020
CNBD2	0.0011
CYP1A2	0.0008
CYP7A1	0.0031		0.0025
DEFA5	0.0056		0.0100
DEFB4A	0.0023		0.0016
DGKB	−0.0029	0.0027
DGKK	0.0029		0.0018
DPRX	0.0018		0.0004
FAM131B	−0.0025		−0.0014
FAM9B	0.0028	0.0020
FGF4	0.0006
FGFR3	0.0026		0.0015
FMR1NB	0.0038		0.0042
GLYATL3	−0.0006
IFNA14	−0.0004
IL17A	0.0012
KRT16	0.0065		0.0124
LAMP1	0.0010
LCE3C	0.0002
LPO	0.0001
MEP1A	0.0029		0.0019
NPS	−0.0006
OR2V2	−0.0002
OR5M8	0.0011
PHOX2B	−0.0026		−0.0018
RETNLB	−0.0028	−0.0004
RIIAD1	0.0079	0.0103	0.0111
S100A7	−0.0006
S100A7A	−0.0003
SEMG2	0.0002
SPINK9	−0.0049		−0.0046
SPRR1A	−0.0026			−0.0003
SPRR2G	0.0011				0.0003
TRIM55	−0.0019			−0.0010

We also analyze the data using the alternatives, and the comparison results are summarized in Table A10. The numbers of overlapping identifications of main effects and interactions are presented, respectively, along with the corresponding RV-coefficients [26]. The RV-coefficient evaluates the similarity of two data matrices with a larger value indicating a higher degree of similarity. It is observed that significantly different sets of main effects and interactions are found by different approaches with moderate RV-coefficients. LS-MCP, LAD-LASSO, RLARS and LTS-MCP, which do not reinforce the hierarchical structure, identify much smaller number of main effects compared to that of interactions. Both LTS-MCP-Hier and LS-MCP-Hier identify a moderate number of main effects and interactions.

To provide an indirect support to the identification analysis, we evaluate the prediction accuracy using PMSE based on 200 times resampling (9/10 training subjects and 1/10 testing subjects), which has also been adopted in the literature. The proposed approach is observed to have the best prediction performance with PMSE=0.26, compared to 1.01 (LS-MCP), 0.32 (LAD-LASSO), 0.49 (RLARS), 0.87 (LTS-MCP) and 0.58 (LS-MCP-Hier). We also examine the selection stability by calculating the observed occurrence index (OOI) [19]. Using the same resampling strategy, the OOI measures the identified probability for each main effect or interaction, where a larger value indicates better stability in identification among random samples. The mean OOI of the identified main effect and interactions using the proposed approach is 0.85, compared to 0.32 (LS-MCP), 0.81 (LAD-LASSO), 0.50 (RLARS), 0.10 (LTS-MCP) and 0.81 (LS-MCP-Hier), suggesting satisfactory stability of the proposed approach.

4.2. Breast Invasive Carcinoma (BRCA) Data

Breast cancer is the second cause of cancer death among female, which can be influenced by a number of environmental and genetic factors [27]. The response of interest is the censored survival time, which is analyzed based on AFT model. In this study, we focus on the female Whites with primary tumor. Data are available on 353 subjects, with 60 deaths during the follow-up period. For E variables, we include age, AJCC tumor pathologic stage, ER status (positive/negative) and weight. For G variables, there are 16,277 measurements of mRNA expressions and the top 2,000 genes are selected for the downstream analyses using the same prescreening as described in the previous section.

The coefficients estimated from the proposed approach are provided in Table 4. The three E variables age, stage and weight have negative coefficients, indicating that higher levels are associated with shorter survival, and the positive coefficient of ER status suggests that the subjects with negative ER status tend to have better prognosis. In addition, there are 32 important main effects along with 43 interactions. These findings are validated by the literature search. For example, gene ASH2L has been shown to be over-expressed in human breast cancer among other candidate oncogenes. Gene ATAD1 has been found to be down-regulated in different subtypes of breast tumors in gene expression profiling, whose interactions with age, tumor stage and ER status are identified using the proposed approach. Abnormal expression of gene FGF4 has been found in human breast cancer cells, and the up-regulation of endogenous FGF4 expression indicates its biological significance in tumorigenesis. Gene KAT6A has been suggested to be a novel oncogene in breast cancer as a chromatin modifier. Gene MED1 has been demonstrated a key role in tamoxifen resistance of human breast cancer cells, suggesting its potential as a therapeutic target in cancer treatment. Over-expression of gene MTBP has been observed to be strongly correlated with reduced breast cancer patient survival. Gene NSD3 has been showed to be amplification in primary breast carcinomas, suggesting a possible involvement in human tumorigenesis. Gene PHB2 has been demonstrated to play a crucial role in modulation of ER status in breast cancer cells.

Table 4.

Analysis of BRCA data using the proposed approach: coefficients of identified main effects and interactions

	Main:G	Age	Stage	ER status	Weight
Main:E		−0.1594	−0.1089	0.2705	−0.1219
AASDHPPT	0.0885	0.0347		−0.0069
ASH2L	0.0006
ATAD1	0.1274	0.0058	0.0016	−0.0078
AXDND1	−0.1061				−0.0094
BRD1	0.0293
CCT6A	−0.0701	−0.0076
CD5L	−0.0776
FGF4	0.0292
ITLN2	−0.1221	−0.0113			0.0069
KAT6A	0.0123
MAEA	0.0453
MED1	−0.0649	−0.0226	−0.0254	−0.0013	−0.0058
MRPL45	0.0512				−0.0013
MTBP	0.0127
NARS2	0.0197
NSD3	0.0112
NUFIP2	−0.0297
PHB	0.0984	0.0015		0.0008	0.0005
PHB2	0.0832			−0.0032	0.0025
PMVK	0.1227	0.0064	−0.0016	−0.0216	−0.0564
RAD21	−0.0555	−0.0311
SEZ6	−0.1450	−0.0320	−0.0017
SMIM19	0.0950	0.0379	0.0127	0.0022	−0.0136
SUPT4H1	−0.1278		0.0127		0.0027
SUPT5H	−0.0240
TBC1D21	−0.0571
TBC1D23	−0.0526
TRIM11	−0.1352	−0.0314			0.0071
UBE2Z	0.0895	−0.0003	−0.0031		0.0002
UBE4A	−0.0055
ZNF572	0.0053
ZNF597	0.0932	0.0065	0.0205

Data are also analyzed using the alternatives. The summary results of comparison are shown in Table A11. Small numbers of overlapping main effects and interactions are found across different approaches, whereas moderate common information is contained among different identifications given the values of RV-coefficients. We also compute C-statistics to evaluate the prediction accuracy of survival response using the same resampling process. The proposed approach demonstrates improved prediction ability with a C-statistic value of 0.55, compared to 0.49 (LS-MCP), 0.49 (LAD-LASSO), 0.47 (RLARS), 0.51 (LTS-MCP) and 0.47 (LS-MCP-Hier). In addition, the proposed approach has better stability with the average OOI as 0.49, compared to 0.09 (LS-MCP), 0.43 (LAD-LASSO), 0.27 (RLARS), 0.08 (LTS-MCP) and 0.4 (LS-MCP-Hier). The improved prediction and stability confirm the validity of the proposed analysis.

5. Discussion

Identifying important G-E interactions associated with complex multifactorial human diseases is an important goal of high-dimensional cancer studies. In this study, we propose a novel effective interaction analysis approach based on the least trimmed regression. The proposed approach can accommodate the vertical outliers as well as the leverage points, which are not uncommon in practice but have not been well studied. It differs significantly from the existing robust interaction analyses that usually focus on model mis-specification or outliers/contaminations in response. A robust criterion based on the (weighted) residuals is developed for choosing the optimal number of outliers, which can accommodate multiple types of responses, such as continuous biomarkers and censored survival time. The coefficient of each interaction is decomposed as the product of the corresponding main effect and interaction-specific coefficient, which has an intuitive formulation to automatically respect the strong hierarchial structure. The modified stability selection-based C-steps algorithm and iterative coordinate descent algorithm are adopted to optimize the objective function, which leads to the estimation of main effects and interactions as well as the optimal outlier-free subject set. Extensive simulations are conducted, including various scenarios without data contamination, with vertical outliers, and with leverage points. The results demonstrate the competitive performance of the proposed analysis in terms of identification, estimation and prediction. In the data analysis of cutaneous melanoma and breast invasive carcinoma with gene expression measurements, the proposed approach identifies biologically sensible markers with better prediction performance and stability.

In this study, we have considered a continuous response under the linear model and a censored survival time under the AFT model. For the categorical and count data under generalized linear models, the iterated weighted squared loss can be adopted as an approximation to the negative log-likelihood. Thus, with minor modifications, the proposed approach can be extended to accommodate other types of responses. The proposed approach is built on the trimmed regression which has been demonstrated to have solid statistical properties for the analysis of low-dimensional data and high-dimensional main effects. Thus it may be reasonable to conjecture that the proposed approach also has good theoretical properties. The detailed study is postponed to future research. In simulation, we focus on the leverage points in G factors, more extensive numerical studies with outliers in E factors are deferred to future investigation. In data analysis, more biological and functional analyses are needed to provide more evidence of the identified interactions.

Appendix A. The additional numerical results

Table A1.

Outlier detection results under simulation scenarios with continuous G factors and AR structure under linear model. TP: true positive outliers. FP: false positive outliers. In each cell, mean (sd) based on 200 replicates.

μ	D1: N(0,1)		D2: 0.9N(0,1)+0.1Cauchy(0,5)		D3: 0.9N(0,1)+0.1N 20,1		D4: N(0,1) and with leverage points		D5: 0.9N(0 1)+0.1Cauchy(0,5) and with leverage points
	TP	FP	TP	FP	TP	FP	TP	FP	TP	FP
1.0	0.0(0.0)	98.6(4.5)	17.9(2.1)	80.2(4.9)	25.0(0.1)	71.5(3.9)	12.9(2.1)	87.4(4.1)	19.2(2.0)	80.3(5.2)
1.1	0.0(0.0)	85.0(4.5)	17.5(2.2)	68.8(4.6)	25.0(0.1)	61.6(4.3)	11.9(2.1)	76.4(4.7)	18.9(2.2)	68.3(5.0)
1.2	0.0(0.0)	75.0(4.2)	17.0(2.4)	59.6(4.8)	25.0(0.0)	53.1(4.5)	11.0(2.0)	65.8(4.1)	18.3(2.0)	58.6(4.6)
1.3	0.0(0.0)	65.2(5.8)	16.7(2.5)	50.9(5.1)	25.0(0.0)	45.4(4.7)	10.2(2.0)	56.8(4.3)	18.0(2.2)	49.4(4.8)
1.4	0.0(0.0)	55.9(6.4)	16.5(2.4)	42.9(5.8)	25.0(0.0)	37.5(5.2)	9.7(1.8)	47.6(4.5)	17.8(2.2)	41.7(5.1)
1.5	0.0(0.0)	47.4(6.4)	16.1(2.6)	36.1(5.5)	25.0(0.0)	30.9(5.6)	9.0(1.8)	40.0(3.7)	17.5(2.3)	34.1(5.1)
1.6	0.0(0.0)	40.3(7.1)	15.9(2.6)	30.1(5.4)	25.0(0.0)	25.2(5.5)	8.2(1.6)	33.4(4.7)	17.2(2.2)	27.6(4.7)
1.7	0.0(0.0)	33.7(6.8)	15.7(2.8)	24.7(5.4)	25.0(0.0)	20.1(5.1)	7.9(1.5)	27.2(4.4)	16.9(2.3)	22.5(4.3)
1.8	0.0(0.0)	28.3(6.8)	15.3(2.8)	19.5(4.8)	25.0(0.0)	15.9(4.7)	7.5(1.4)	23.1(4.8)	16.7(2.4)	17.6(4.3)
1.9	0.0(0.0)	23.4(6.4)	15.1(2.8)	15.7(4.5)	25.0(0.0)	12.7(4.4)	7.3(1.3)	18.2(4.4)	16.4(2.4)	14.3(4.0)
2.0	0.0(0.0)	19.1(5.7)	14.8(2.7)	12.6(3.9)	25.0(0.0)	10.0(4.2)	7.0(1.3)	14.6(3.9)	16.1(2.5)	11.0(3.6)
2.1	0.0(0.0)	15.7(5.4)	14.4(2.7)	10.0(4.0)	25.0(0.0)	7.9(3.9)	6.6(1.2)	11.4(3.9)	15.7(2.5)	8.7(3.2)
2.2	0.0(0.0)	12.8(5.4)	14.2(2.7)	7.8(3.6)	25.0(0.0)	5.8(2.9)	6.3(1.1)	9.0(3.5)	15.4(2.5)	6.9(3.3)
2.3	0.0(0.0)	10.4(4.7)	13.9(2.7)	5.8(3.2)	25.0(0.0)	4.4(2.3)	6.3(1.0)	6.9(2.9)	15.1(2.6)	5.2(2.9)
2.4	0.0(0.0)	8.5(4.0)	13.6(2.8)	4.5(2.7)	25.0(0.0)	3.4(2.2)	6.1(0.9)	5.3(2.7)	14.8(2.7)	3.6(2.4)
2.5	0.0(0.0)	6.9(3.5)	13.2(2.9)	3.4(2.3)	25.0(0.0)	2.5(1.9)	5.8(0.9)	4.1(2.1)	14.4(2.6)	2.5(1.8)
2.6	0.0(0.0)	5.4(3.2)	12.9(2.9)	2.5(2.0)	25.0(0.0)	1.9(1.6)	5.7(0.8)	3.3(2.0)	14.0(2.7)	2.0(1.7)
2.7	0.0(0.0)	4.2(2.9)	12.7(2.8)	2.0(1.9)	25.0(0.0)	1.5(1.5)	5.5(0.8)	2.4(1.8)	13.7(2.8)	1.5(1.7)
2.8	0.0(0.0)	3.2(2.5)	12.4(2.9)	1.5(1.7)	25.0(0.0)	1.0(1.3)	5.2(0.9)	1.9(1.6)	13.2(2.8)	1.2(1.2)
2.9	0.0(0.0)	2.4(2.0)	12.1(2.9)	1.2(1.4)	25.0(0.0)	0.7(1.1)	5.2(0.9)	1.4(1.4)	13.0(2.6)	1.0(1.1)
3.0	0.0(0.0)	1.8(1.7)	11.9(2.8)	0.9(1.2)	25.0(0.0)	0.4(0.7)	5.0(0.9)	1.0(1.2)	12.3(2.6)	0.7(1.0)
3.1	0.0(0.0)	1.4(1.4)	11.6(2.9)	0.8(1.1)	25.0(0.0)	0.3(0.6)	5.0(0.6)	0.8(1.1)	12.1(2.6)	0.6(1.0)
3.2	0.0(0.0)	1.1(1.3)	11.4(2.8)	0.6(1.0)	24.6(2.6)	0.2(0.5)	5.0(0.7)	0.6(0.9)	11.9(2.6)	0.4(0.7)
3.3	0.0(0.0)	0.9(1.1)	11.1(2.9)	0.4(0.8)	24.1(3.6)	0.2(0.5)	4.9(0.7)	0.6(1.0)	11.4(2.5)	0.4(0.7)
3.4	0.0(0.0)	0.7(1.0)	10.8(3.0)	0.3(0.7)	23.1(5.6)	0.2(0.4)	4.9(0.6)	0.4(0.7)	11.0(2.7)	0.2(0.5)
3.5	0.0(0.0)	0.6(0.9)	10.6(3.0)	0.3(0.6)	21.0(8.1)	0.1(0.4)	4.8(0.6)	0.3(0.6)	10.9(2.7)	0.1(0.4)
3.6	0.0(0.0)	0.4(0.7)	10.4(2.9)	0.2(0.5)	15.5(10.0)	0.1(0.4)	4.7(0.7)	0.2(0.6)	10.6(2.6)	0.1(0.4)
3.7	0.0(0.0)	0.4(0.7)	10.0(2.9)	0.1(0.4)	12.1(10.4)	0.0(0.2)	4.6(0.8)	0.2(0.7)	10.4(2.5)	0.1(0.4)
3.8	0.0(0.0)	0.2(0.5)	9.9(2.8)	0.1(0.3)	8.3(9.2)	0.0(0.1)	4.6(0.8)	0.1(0.5)	9.9(2.5)	0.0(0.2)
3.9	0.0(0.0)	0.2(0.5)	9.7(2.7)	0.1(0.3)	5.1(7.4)	0.0(0.1)	4.6(0.8)	0.1(0.3)	9.4(2.3)	0.0(0.2)
4.0	0.0(0.0)	0.1(0.3)	9.5(2.7)	0.1(0.3)	2.8(4.4)	0.0(0.1)	4.6(0.9)	0.1(0.2)	9.4(2.4)	0.0(0.2)

Table A2.

Summary results under simulation scenarios with continuous G factors and Band structure under linear model. In each cell, mean (sd) based on 200 replicates.

	M:TP	M:FP	I:TP	I:FP	RSSE	PMSE
D1: N(0,1)
LTS-MCP-Hier	7.8(0.4)	0.8(1.9)	12.0(2.0)	1.0(1.1)	2.34(0.53)	0.99(0.53)
LS-MCP	5.5(0.9)	3.9(4.4)	10.9(0.9)	12.9(11.1)	2.92(0.45)	1.31(0.62)
LAD-Lasso	8.0(0.1)	11.4(5.6)	13.1(1.5)	30.4(11.6)	1.78(0.39)	1.47(0.56)
RLARS	7.4(0.7)	0.7(1.1)	7.5(1.8)	11.4(7.2)	3.25(0.44)	2.29(0.80)
LTS-MCP	6.0(1.0)	6.5(3.3)	10.7(1.0)	25.8(8.9)	2.63(0.49)	1.34(0.25)
LS-MCP-Hier	8.0(0.1)	0.5(1.7)	12.7(1.1)	0.5(0.7)	1.79(0.35)	0.81(0.19)
D2: 0.9N(0, 1) + 0.1Cauchy(0,5)
LTS-MCP-Hier	7.8(0.4)	0.9(2.9)	11.4(2.0)	1.1(1.0)	2.28(0.50)	1.14(0.60)
LS-MCP	2.1(1.8)	18.2(8.0)	2.3(2.4)	71.9(11.6)	30.32(40.12)	547.58(2145.90)
LAD-Lasso	7.5(0.6)	2.8(2.2)	7.0(2.4)	7.5(3.4)	3.13(0.35)	4.11(1.22)
RLARS	7.1(0.8)	0.8(1.1)	6.0(1.8)	11.4(6.8)	3.67(0.50)	3.33(1.23)
LTS-MCP	5.8(0.9)	8.4(3.9)	10.4(1.1)	29.5(10.3)	2.80(0.43)	1.37(0.36)
LS-MCP-Hier	5.8(1.4)	150.7(118.1)	2.4(3.2)	27.2(74.9)	28.76(42.09)	1181.23(5245.02)
D3: 0.9N(0,1) + 0.1N(20,1)
LTS-MCP-Hier	7.8(0.4)	0.9(2.3)	11.7(1.8)	1.0(1.1)	2.15(0.47)	1.05(0.50)
LS-MCP	2.7(1.0)	24.1(5.2)	2.7(1.4)	67.9(5.2)	9.96(0.68)	33.43(7.57)
LAD-Lasso	7.3(0.8)	3.0(1.8)	5.4(2.1)	8.0(2.7)	3.39(0.34)	5.09(1.51)
RLARS	5.8(1.2)	1.4(1.4)	3.7(1.8)	11.4(4.9)	4.31(0.48)	5.55(2.15)
LTS-MCP	6.0(0.9)	7.3(3.7)	10.7(1.0)	26.4(8.9)	2.67(0.49)	1.20(0.28)
LS-MCP-Hier	6.1(0.9)	94.6(7.1)	2.4(1.5)	5.3(5.2)	8.79(0.62)	33.32(6.65)
D4: N(0,1) and with leverage points
LTS-MCP-Hier	7.0(1.3)	6.8(13.7)	9.9(3.5)	2.8(2.2)	2.91(0.90)	1.26(2.64)
LS-MCP	1.3(0.9)	22.2(5.2)	3.1(1.9)	69.0(6.5)	7.21(0.86)	18.85(6.15)
LAD-Lasso	3.9(1.2)	4.1(2.3)	4.0(1.6)	12.8(3.5)	4.05(0.33)	9.23(2.16)
RLARS	7.1(0.8)	0.8(1.1)	6.9(1.9)	12.1(7.9)	3.42(0.43)	2.88(0.96)
LTS-MCP	5.8(1.2)	8.9(4.4)	10.4(1.3)	31.7(11.1)	2.78(0.58)	3.12(0.68)
LS-MCP-Hier	5.2(1.2)	56.4(35.5)	3.4(2.7)	5.0(3.3)	5.44(1.27)	14.17(8.50)
D5: 0.9N(0,1) + 0.1Cauchy(0,5) and with leverage points
LTS-MCP-Hier	7.2(1.2)	5.6(12.7)	9.8(2.9)	2.7(2.2)	2.75(0.87)	1.09(2.28)
LS-MCP	0.5(0.7)	18.0(9.6)	1.5(1.5)	69.0(16.7)	25.10(32.12)	258.07(680.53)
LAD-Lasso	3.6(1.4)	4.4(2.1)	4.0(2.1)	12.4(3.4)	4.06(0.36)	9.17(2.26)
RLARS	6.7(0.9)	1.1(1.3)	5.9(1.6)	13.3(7.4)	3.77(0.43)	3.65(1.24)
LTS-MCP	6.0(1.0)	9.3(4.0)	10.7(1.2)	32.7(8.5)	2.67(0.52)	2.55(0.35)
LS-MCP-Hier	4.3(1.6)	154.0(110.7)	1.0(1.8)	26.0(61.5)	27.86(39.79)	1019.76(4540.05)

Table A3.

Summary results under simulation scenarios with continuous G factors and Band structure under AFT model. In each cell, mean (sd) based on 200 replicates.

	M:TP	M:FP	I:TP	I:FP	RSSE	Cstat
D1: N(0,1)
LTS-MCP-Hier	7.8(0.5)	8.0(9.5)	10.1(2.7)	0.8(1.0)	2.67(0.50)	0.90(0.03)
LS-MCP	6.2(1.0)	13.0(5.4)	11.0(0.9)	38.9(10.2)	2.59(0.54)	0.92(0.02)
LAD-Lasso	7.4(0.9)	13.8(7.9)	6.6(4.0)	31.1(16.6)	3.32(0.61)	0.83(0.06)
RLARS	7.2(0.8)	10.5(2.8)	3.1(1.4)	22.2(4.4)	4.22(0.35)	0.78(0.05)
LTS-MCP	5.8(1.0)	14.8(4.6)	6.6(1.7)	57.8(7.4)	3.36(0.31)	0.85(0.03)
LS-MCP-Hier	8.0(0.2)	2.6(4.4)	11.7(1.3)	0.8(1.1)	2.04(0.35)	0.92(0.02)
D2: 0.9N(0,1) + 0.1Cauchy(0,5)
LTS-MCP-Hier	7.7(0.6)	7.5(7.6)	9.2(2.7)	1.2(1.1)	2.88(0.58)	0.88(0.03)
LS-MCP	1.1(1.2)	12.9(7.8)	1.2(1.5)	61.1(8.9)	46.82(93.14)	0.56(0.07)
LAD-Lasso	5.8(1.5)	4.9(2.4)	1.8(1.5)	12.4(3.4)	4.08(0.35)	0.74(0.06)
RLARS	6.1(1.6)	7.3(3.9)	1.5(1.1)	24.1(5.9)	5.42(5.41)	0.72(0.06)
LTS-MCP	5.7(1.2)	16.0(4.1)	5.7(1.7)	58.5(6.1)	3.66(0.35)	0.83(0.03)
LS-MCP-Hier	5.5(1.4)	193.2(160.4)	2.1(2.4)	73.5(236.8)	57.08(118.64)	0.58(0.07)
D3: 0.9N(0,1) + 0.1N(20,1)
LTS-MCP-Hier	8.0(0.1)	3.8(6.7)	11.4(1.7)	0.9(1.0)	2.12(0.42)	0.92(0.01)
LS-MCP	2.5(1.0)	26.6(5.4)	2.6(1.3)	70.5(6.3)	10.76(0.69)	0.63(0.04)
LAD-Lasso	6.6(1.1)	4.3(2.2)	2.9(1.9)	11.0(3.0)	3.77(0.33)	0.78(0.05)
RLARS	6.3(1.1)	4.2(2.9)	1.4(1.2)	12.0(5.7)	4.40(0.39)	0.77(0.04)
LTS-MCP	6.0(1.1)	11.2(4.0)	9.2(1.8)	47.4(9.4)	2.93(0.50)	0.89(0.02)
LS-MCP-Hier	5.9(1.1)	101.8(7.3)	2.5(1.6)	7.0(6.3)	9.68(0.59)	0.66(0.04)
D4: N(0,1) and with leverage points
LTS-MCP-Hier	6.8(1.2)	10.3(9.7)	9.1(3.4)	1.7(1.5)	3.46(0.71)	0.84(0.07)
LS-MCP	3.1(1.1)	15.2(4.5)	4.9(2.1)	53.2(6.0)	4.98(0.62)	0.74(0.05)
LAD-Lasso	6.0(1.3)	7.2(5.8)	3.4(2.5)	18.8(10.2)	3.92(0.38)	0.76(0.05)
RLARS	6.8(1.0)	12.1(4.0)	2.8(1.6)	21.8(4.7)	4.41(0.39)	0.76(0.04)
LTS-MCP	5.4(1.3)	15.8(3.9)	5.5(1.9)	61.7(5.9)	3.73(0.41)	0.81(0.04)
LS-MCP-Hier	5.8(1.1)	42.5(23.6)	4.5(2.4)	2.9(2.1)	4.18(0.64)	0.77(0.05)
D5: 0.9N(0,1) + 0.1Cauchy(0,5) and with leverage points
LTS-MCP-Hier	7.1(1.1)	10.1(12.0)	9.5(3.2)	1.8(1.3)	3.30(0.75)	0.84(0.06)
LS-MCP	0.9(1.0)	13.1(7.1)	1.1(1.3)	57.1(10.2)	36.77(71.77)	0.56(0.06)
LAD-Lasso	5.2(1.7)	4.6(2.3)	1.8(1.5)	12.9(3.7)	4.16(0.33)	0.73(0.06)
RLARS	6.2(1.3)	8.5(4.6)	2.5(1.5)	22.6(6.7)	6.82(16.01)	0.73(0.06)
LTS-MCP	5.8(1.1)	15.9(4.3)	5.1(1.6)	61.1(5.2)	3.74(0.42)	0.81(0.04)
LS-MCP-Hier	5.0(1.7)	173.4(152.1)	2.0(2.3)	66.5(240.4)	52.85(129.70)	0.57(0.06)

Table A4.

Summary results under simulation scenarios with categorical G factors and AR structure under linear model. In each cell, mean (sd) based on 200 replicates.

	M:TP	M:FP	I:TP	I:FP	RSSE	PMSE
D1: N(0,1)
LTS-MCP-Hier	7.9(0.3)	0.3(1.0)	12.3(1.5)	0.6(0.9)	2.03(0.42)	0.95(0.44)
LS-MCP	6.2(1.1)	4.5(4.2)	11.3(1.3)	14.3(11.5)	2.48(0.54)	1.13(0.37)
LAD-Lasso	8.0(0.0)	10.7(5.7)	13.4(1.0)	27.9(10.1)	1.68(0.31)	1.37(0.41)
RLARS	4.1(1.2)	13.2(5.8)	2.3(1.6)	8.4(5.0)	4.73(0.44)	8.87(3.01)
LTS-MCP	6.7(0.9)	7.0(3.3)	11.3(1.1)	27.6(8.1)	2.19(0.49)	1.19(0.25)
LS-MCP-Hier	8.0(0.0)	0.3(0.8)	13.1(0.9)	0.5(0.7)	1.66(0.27)	0.80(0.17)
D2: 0.9N(0,1) + 0.1Cauchy(0,5)
LTS-MCP-Hier	8.0(0.2)	1.0(2.8)	11.8(2.0)	0.9(1.1)	2.13(0.47)	1.07(0.45)
LS-MCP	1.9(1.8)	21.1(8.4)	2.2(2.4)	74.7(11.4)	35.47(49.17)	712.17(2635.35)
LAD-Lasso	7.8(0.4)	2.4(1.7)	7.8(2.3)	7.2(3.5)	3.02(0.34)	4.05(1.16)
RLARS	4.0(1.1)	11.4(5.3)	1.9(1.4)	7.8(4.4)	4.85(0.41)	9.86(3.38)
LTS-MCP	6.5(1.0)	8.5(3.5)	11.1(1.2)	32.1(7.9)	2.35(0.52)	1.24(0.28)
LS-MCP-Hier	6.0(1.5)	153.5(116.8)	2.4(3.2)	24.5(72.4)	28.86(41.92)	1214.97(5318.06)
D3: 0.9N(0,1) + 0.1N(20,1)
LTS-MCP-Hier	8.0(0.2)	0.5(1.4)	12.3(1.6)	0.8(0.9)	1.94(0.41)	0.93(0.41)
LS-MCP	2.8(1.1)	25.0(5.4)	2.7(1.4)	67.2(6.0)	9.90(0.71)	34.37(7.31)
LAD-Lasso	7.5(0.6)	2.8(1.9)	5.6(2.2)	8.4(2.6)	3.33(0.33)	5.04(1.54)
RLARS	3.8(1.1)	10.1(3.8)	0.9(0.9)	6.3(3.2)	5.14(0.50)	11.87(3.95)
LTS-MCP	6.7(1.1)	7.6(3.5)	11.4(1.1)	28.0(7.5)	2.21(0.52)	1.03(0.22)
LS-MCP-Hier	6.4(1.0)	94.4(7.5)	2.2(1.5)	5.1(5.6)	8.64(0.53)	31.64(6.01)
D4: N(0,1) and with leverage points
LTS-MCP-Hier	7.7(0.6)	7.7(12.3)	10.1(3.0)	1.3(1.1)	2.50(0.61)	1.71(1.08)
LS-MCP	4.4(1.3)	21.5(5.7)	6.8(1.9)	55.4(7.3)	4.95(0.79)	6.95(2.98)
LAD-Lasso	7.0(0.9)	7.6(4.0)	4.7(2.4)	9.0(4.1)	3.51(0.37)	6.35(1.97)
RLARS	5.7(1.1)	13.7(6.6)	2.7(1.7)	8.7(4.8)	4.46(0.42)	7.11(2.26)
LTS-MCP	6.2(1.1)	11.9(5.1)	10.5(1.6)	34.4(7.0)	2.67(0.59)	2.17(0.56)
LS-MCP-Hier	7.7(0.6)	52.4(20.8)	6.5(2.2)	2.4(2.4)	3.61(0.67)	4.38(1.90)
D5: 0.9N(0,1) + 0.1Cauchy(0,5) and with leverage points
LTS-MCP-Hier	7.9(0.4)	1.7(4.7)	11.2(2.3)	1.0(1.1)	2.27(0.53)	1.56(0.78)
LS-MCP	1.4(1.4)	22.2(7.7)	1.6(2.0)	76.1(10.6)	39.92(54.72)	771.74(2428.31)
LAD-Lasso	7.2(0.9)	4.5(2.6)	4.6(2.2)	8.0(2.9)	3.51(0.31)	6.12(1.65)
RLARS	5.6(1.1)	11.0(5.6)	2.7(1.8)	9.3(5.8)	4.50(0.40)	7.18(2.21)
LTS-MCP	6.4(0.9)	10.1(4.2)	11.1(1.4)	32.8(7.5)	2.43(0.55)	1.86(0.38)
LS-MCP-Hier	5.4(1.5)	164.5(117.5)	1.7(2.4)	29.5(75.9)	31.75(42.57)	1196.18(4354.42)

Table A5.

Summary results under simulation scenarios with categorical G factors and AR structure under AFT model. In each cell, mean (sd) based on 200 replicates.

	M:TP	M:FP	I:TP	I:FP	RSSE	Cstat
D1: N(0,1)
LTS-MCP-Hier	7.8(0.4)	6.4(10.0)	10.1(2.7)	0.8(1.0)	2.43(0.53)	0.90(0.03)
LS-MCP	7.0(1.0)	12.3(4.6)	12.1(1.2)	38.1(8.7)	1.92(0.67)	0.92(0.01)
LAD-Lasso	7.5(0.7)	14.6(8.2)	8.0(4.1)	33.2(16.6)	3.16(0.60)	0.85(0.05)
RLARS	2.6(1.3)	3.5(2.8)	0.7(0.9)	34.4(6.8)	5.65(0.54)	0.61(0.07)
LTS-MCP	6.1(1.0)	15.2(4.3)	6.7(1.7)	57.4(8.5)	3.27(0.32)	0.85(0.03)
LS-MCP-Hier	7.9(0.3)	1.3(3.0)	12.3(1.2)	0.5(0.8)	1.89(0.36)	0.92(0.02)
D2: 0.9N(0,1) + 0.1Cauchy(0,5)
LTS-MCP-Hier	7.8(0.4)	6.2(5.4)	9.3(3.3)	1.1(1.1)	2.64(0.59)	0.88(0.04)
LS-MCP	1.1(1.4)	16.5(8.8)	1.2(1.5)	63.9(9.9)	58.01(114.22)	0.55(0.07)
LAD-Lasso	5.8(1.6)	4.7(2.4)	1.9(1.3)	12.1(3.4)	4.09(0.33)	0.74(0.06)
RLARS	1.0(1.1)	2.8(2.3)	0.5(0.8)	32.4(8.8)	232.54(898.65)	0.55(0.05)
LTS-MCP	6.2(0.9)	15.5(4.3)	5.6(1.7)	59.7(4.9)	3.57(0.33)	0.83(0.03)
LS-MCP-Hier	5.4(1.5)	198.8(160.5)	2.0(2.7)	70.5(239.0)	59.85(123.92)	0.58(0.08)
D3: 0.9N(0,1) + 0.1N(20,1)
LTS-MCP-Hier	8.0(0.2)	1.2(3.0)	12.4(1.3)	0.6(0.8)	1.90(0.34)	0.92(0.01)
LS-MCP	2.5(1.1)	26.5(5.0)	2.5(1.5)	71.4(5.6)	10.67(0.75)	0.63(0.04)
LAD-Lasso	6.5(1.1)	4.3(2.5)	2.8(1.7)	10.8(3.5)	3.79(0.29)	0.78(0.04)
RLARS	1.2(1.0)	1.6(1.7)	0.5(0.7)	25.7(9.8)	5.75(0.75)	0.60(0.06)
LTS-MCP	6.3(0.8)	12.2(4.0)	9.4(1.7)	48.6(9.6)	2.77(0.52)	0.90(0.02)
LS-MCP-Hier	5.9(1.2)	101.6(7.2)	2.2(1.7)	7.6(6.1)	9.60(0.61)	0.66(0.04)
D4: N(0,1) and with leverage points
LTS-MCP-Hier	7.2(0.8)	15.4(10.4)	8.7(2.4)	1.2(1.1)	3.67(0.44)	0.85(0.05)
LS-MCP	3.3(1.3)	18.8(4.1)	3.0(1.7)	53.8(5.1)	6.07(0.70)	0.67(0.05)
LAD-Lasso	2.3(1.6)	11.5(4.9)	0.3(0.7)	14.5(6.7)	4.48(0.29)	0.63(0.05)
RLARS	3.9(1.2)	21.4(6.0)	0.3(0.5)	17.4(6.3)	5.38(0.40)	0.64(0.04)
LTS-MCP	5.6(1.1)	19.2(5.3)	4.2(1.6)	59.4(5.9)	4.00(0.35)	0.78(0.04)
LS-MCP-Hier	5.9(1.1)	66.0(8.2)	1.7(1.3)	2.9(2.7)	5.03(0.67)	0.71(0.05)
D5: 0.9N(0,1) + 0.1Cauchy(0,5) and with leverage points
LTS-MCP-Hier	7.5(0.7)	13.6(19.0)	9.1(3.4)	1.0(1.1)	3.28(0.62)	0.84(0.05)
LS-MCP	0.5(0.8)	16.2(7.7)	0.4(0.7)	64.4(9.4)	63.10(119.35)	0.52(0.03)
LAD-Lasso	1.6(1.6)	12.9(5.6)	0.2(0.5)	10.1(5.0)	4.60(0.27)	0.60(0.05)
RLARS	3.4(1.6)	15.4(8.1)	0.4(0.7)	18.8(6.2)	63.57(153.77)	0.61(0.06)
LTS-MCP	6.0(1.0)	16.8(4.2)	5.0(2.0)	59.0(5.1)	3.82(0.37)	0.81(0.03)
LS-MCP-Hier	4.6(2.2)	201.0(155.2)	1.6(2.8)	87.9(263.4)	63.33(132.06)	0.51(0.05)

Table A6.

Summary results under simulation scenarios with categorical G factors and Band structure under linear model. In each cell, mean (sd) based on 200 replicates.

	M:TP	M:FP	I:TP	I:FP	RSSE	PMSE
D1: N(0,1)
LTS-MCP-Hier	7.9(0.3)	0.4(1.1)	11.6(1.9)	0.8(1.0)	2.18(0.49)	0.98(0.45)
LS-MCP	5.9(1.2)	4.8(5.0)	11.1(1.0)	15.4(13.4)	2.64(0.59)	1.19(0.52)
LAD-Lasso	8.0(0.1)	12.7(5.5)	13.2(1.3)	31.8(11.8)	1.72(0.34)	1.42(0.48)
RLARS	4.1(1.4)	13.4(6.1)	2.3(1.4)	9.0(4.8)	4.72(0.46)	9.01(3.04)
LTS-MCP	6.2(1.1)	6.5(3.9)	11.0(1.1)	25.7(8.3)	2.40(0.59)	1.26(0.26)
LS-MCP-Hier	8.0(0.0)	0.4(1.1)	13.1(1.0)	0.5(0.7)	1.67(0.33)	0.79(0.18)
D2: 0.9N(0,1) + 0.1Cauchy(0,5)
LTS-MCP-Hier	7.9(0.3)	0.6(1.8)	11.8(1.5)	0.9(1.0)	2.14(0.40)	1.10(0.43)
LS-MCP	1.8(1.8)	21.8(8.9)	2.2(2.4)	74.2(10.9)	35.32(48.40)	673.99(2547.57)
LAD-Lasso	7.6(0.6)	2.7(2.0)	7.2(2.3)	7.3(3.2)	3.12(0.40)	4.32(1.44)
RLARS	4.0(1.4)	11.5(5.4)	1.8(1.4)	8.2(4.0)	4.81(0.41)	9.70(3.17)
LTS-MCP	6.3(1.0)	8.4(3.7)	10.8(1.3)	31.8(8.1)	2.52(0.51)	1.28(0.29)
LS-MCP-Hier	5.9(1.6)	152.2(118.4)	2.4(3.3)	25.3(74.6)	28.95(42.00)	1126.17(4531.24)
D3: 0.9N(0,1) + 0.1N(20,1)
LTS-MCP-Hier	7.9(0.2)	0.6(1.5)	12.0(1.4)	0.7(0.8)	2.07(0.41)	0.99(0.43)
LS-MCP	2.6(1.1)	25.3(5.3)	2.6(1.5)	68.3(5.4)	9.98(0.74)	33.57(6.78)
LAD-Lasso	7.2(0.8)	2.9(1.8)	5.6(2.2)	8.3(2.9)	3.41(0.33)	5.31(1.51)
RLARS	3.7(1.3)	9.6(3.9)	0.9(1.0)	6.4(3.0)	5.06(0.52)	11.42(4.16)
LTS-MCP	6.4(1.1)	7.8(3.3)	11.0(1.1)	27.5(7.3)	2.41(0.58)	1.16(0.23)
LS-MCP-Hier	6.1(1.1)	93.7(6.3)	2.4(1.4)	5.7(5.4)	8.57(0.49)	30.92(5.83)
D4: N(0,1) and with leverage points
LTS-MCP-Hier	7.5(0.6)	7.5(8.7)	9.3(2.8)	1.2(1.2)	2.72(0.56)	1.82(1.11)
LS-MCP	4.1(1.2)	21.6(4.9)	6.7(1.7)	55.9(5.9)	5.00(0.69)	7.12(2.55)
LAD-Lasso	6.6(0.9)	7.0(3.9)	4.5(2.2)	9.1(3.5)	3.61(0.36)	6.63(1.89)
RLARS	5.3(1.3)	13.1(7.1)	2.7(1.6)	8.7(5.4)	4.52(0.37)	7.49(1.89)
LTS-MCP	6.0(1.1)	13.3(6.4)	10.0(2.0)	34.8(8.3)	2.85(0.55)	2.54(0.79)
LS-MCP-Hier	7.3(0.6)	49.5(21.6)	6.2(2.1	2.1(2.2)	3.66(0.67)	4.63(1.97)
D5: 0.9N(0,1) + 0.1Cauchy(0,5) and with leverage points
LTS-MCP-Hier	7.7(0.6)	2.3(6.9)	10.9(2.6)	0.9(1.0)	2.33(0.57)	1.55(0.81)
LS-MCP	1.4(1.5)	22.0(7.8)	1.6(1.8)	77.6(10.0)	39.63(52.58)	743.55(2252.92)
LAD-Lasso	6.8(0.9)	4.4(2.9)	4.5(1.9)	8.9(3.3)	3.60(0.31)	6.35(1.59)
RLARS	5.3(1.3)	10.0(5.2)	2.6(1.6)	9.3(5.7)	4.50(0.37)	7.29(2.12)
LTS-MCP	6.2(1.1)	9.6(3.8)	10.8(1.0)	32.7(7.3)	2.64(0.49)	1.93(0.37)
LS-MCP-Hier	5.3(1.6)	160.8(108.0)	1.6(1.6)	32.8(78.2)	31.77(42.35)	1097.13(4234.09)

Table A7.

Summary results under simulation scenarios with categorical G factors and Band structure under AFT model. In each cell, mean (sd) based on 200 replicates.

	M:TP	M:FP	I:TP	I:FP	RSSE	Cstat
D1: N(0,1)
LTS-MCP-Hier	7.9(0.4)	7.0(11.8)	11.8(2.8)	0.9(1.2)	2.52(0.56)	0.89(0.03)
LS-MCP	6.8(1.1)	14.4(5.1)	11.7(1.2)	41.4(7.5)	2.15(0.66)	0.92(0.02)
LAD-Lasso	7.3(1.0)	14.1(7.8)	6.8(4.2)	32.0(15.9)	3.36(0.58)	0.82(0.06)
RLARS	2.3(1.3)	2.9(1.9)	0.7(0.8)	34.7(7.6)	5.51(0.55)	0.61(0.06)
LTS-MCP	6.2(1.0)	14.8(4.0)	7.0(2.0)	56.1(7.2)	3.24(0.36)	0.85(0.04)
LS-MCP-Hier	7.9(0.2)	1.5(3.6)	12.2(1.3)	0.6(0.8)	1.92(0.36)	0.92(0.02)
D2: 0.9N(0,1) + 0.1Cauchy(0,5)
LTS-MCP-Hier	7.7(0.5)	8.9(7.4)	9.6(3.1)	1.1(1.1)	2.75(0.58)	0.88(0.04)
LS-MCP	1.0(1.3)	16.5(8.9)	0.8(1.1)	64.9(10.7)	56.73(108.19)	0.54(0.06)
LAD-Lasso	5.8(1.3)	4.9(2.4)	1.7(1.3)	12.9(3.5)	4.11(0.32)	0.74(0.05)
RLARS	0.9(0.9)	2.7(2.4)	0.4(0.6)	32.2(8.6)	198.16(1027.54)	0.54(0.05)
LTS-MCP	6.1(1.1)	15.9(3.9)	5.9(1.9)	59.1(5.8)	3.58(0.39)	0.82(0.03)
LS-MCP-Hier	5.5(1.6)	196.3(157.2)	1.9(2.4)	66.8(224.0)	57.70(118.80)	0.58(0.08)
D3: 0.9N(0,1) + 0.1N(20,1)
LTS-MCP-Hier	8.0(0.1)	1.8(3.4)	12.2(1.2)	0.6(0.7)	1.96(0.36)	0.92(0.01)
LS-MCP	2.5(1.0)	26.4(5.9)	2.2(1.2)	72.3(5.5)	10.74(0.70)	0.62(0.04)
LAD-Lasso	6.5(1.0)	4.6(1.8)	2.7(1.8)	11.1(3.0)	3.78(0.31)	0.77(0.04)
RLARS	1.2(0.9)	1.4(1.2)	0.4(0.6)	25.3(9.1)	81.94(762.49)	0.59(0.06)
LTS-MCP	6.2(1.1)	11.4(4.0)	9.5(1.6)	47.3(8.5)	2.81(0.41)	0.90(0.02)
LS-MCP-Hier	5.9(1.1)	101.8(8.3)	2.3(1.5)	7.4(6.8)	9.60(0.58)	0.66(0.04)
D4: N(0,1) and with leverage points
LTS-MCP-Hier	7.0(1.0)	18.7(9.7)	8.5(2.3)	0.9(1.0)	3.85(0.42)	0.85(0.05)
LS-MCP	3.0(1.3)	18.7(4.0)	2.6(1.5)	54.4(4.6)	6.12(0.59)	0.65(0.04)
LAD-Lasso	2.2(1.4)	11.9(4.9)	0.3(0.5)	15.4(7.8)	4.52(0.25)	0.62(0.04)
RLARS	3.6(1.2)	21.3(4.4)	0.4(0.6)	18.0(5.5)	5.34(0.43)	0.63(0.05)
LTS-MCP	5.4(1.1)	20.1(4.8)	4.3(1.7)	58.0(4.9)	4.04(0.39)	0.78(0.04)
LS-MCP-Hier	5.5(1.2)	67.6(9.0)	1.7(1.4)	2.5(2.1)	5.06(0.60)	0.70(0.06)
D5: 0.9N(0,1) + 0.1Cauchy(0,5) and with leverage points
LTS-MCP-Hier	7.4(0.7)	12.1(10.4)	9.0(3.0)	1.2(1.1)	3.35(0.59)	0.84(0.05)
LS-MCP	0.5(0.9)	15.3(7.7)	0.5(0.7)	65.6(9.7)	64.24(125.79)	0.52(0.03)
LAD-Lasso	1.6(1.7)	12.9(5.4)	0.3(0.5)	9.7(4.9)	4.62(0.30)	0.60(0.05)
RLARS	3.0(1.6)	15.2(8.2)	0.4(0.7)	19.5(6.6)	104.31(331.36)	0.60(0.06)
LTS-MCP	5.8(1.1)	18.0(4.9)	5.3(1.9)	57.6(5.9)	3.76(0.39)	0.81(0.04)
LS-MCP-Hier	4.3(2.2)	204.0(159.3)	1.4(2.6)	81.3(250.6)	60.77(122.85)	0.51(0.05)

Table A8.

Summary results under simulation scenarios with some weak signals. In each cell, mean (sd) based on 200 replicates.

	M:TP	M:FP	I:TP	I:FP	RSSE	PMSE
D1: N(0,1)
LTS-MCP-Hier	8.0(0.2)	0.4(1.2)	8.0(1.4)	0.6(0.7)	1.54(0.32)	0.92(0.25)
LS-MCP	6.7(0.9)	2.3(3.0)	7.7(1.3)	9.5(10.2)	2.14(0.45)	1.07(0.39)
LAD-Lasso	8.0(0.0)	5.7(3.2)	8.6(1.3)	16.5(8.3)	1.44(0.26)	1.21(0.32)
RLARS	7.8(0.4)	0.2(0.6)	5.0(1.5)	8.2(5.6)	2.43(0.41)	1.45(0.41)
LTS-MCP	6.8(0.8)	6.9(3.7)	7.2(1.4)	25.3(9.1)	2.03(0.46)	0.97(0.22)
LS-MCP-Hier	8.0(0.0)	0.5(1.0)	9.0(1.2)	0.7(0.7)	1.38(0.21)	0.76(0.14)
D2: 0.9N(0,1) + 0.1Cauchy(0,5)
LTS-MCP-Hier	8.0(0.1)	0.6(1.4)	8.3(1.4)	0.8(0.9)	1.56(0.26)	0.89(0.20)
LS-MCP	1.8(1.7)	18.9(8.0)	1.5(1.5)	73.9(10.1)	38.28(56.15)	761.65(2767.61)
LAD-Lasso	8.0(0.2)	2.3(1.5)	5.8(1.6)	7.3(2.4)	2.03(0.30)	1.96(0.58)
RLARS	7.6(0.6)	0.8(1.1)	4.3(1.4)	10.3(6.8)	2.71(0.39)	1.82(0.58)
LTS-MCP	6.7(0.9)	8.2(3.8)	7.1(1.4)	31.1(10.3)	2.12(0.49)	1.00(0.27)
LS-MCP-Hier	5.5(1.5)	166.6(124.1)	1.3(1.6)	31.3(79.7)	32.79(45.78)	1446.11(5735.58)
D3: 0.9N(0,1) + 0.1N(20,1)
LTS-MCP-Hier	8.0(0.1)	0.4(1.2)	8.6(1.4)	0.7(0.9)	1.48(0.24)	0.82(0.18)
LS-MCP	2.9(1.1)	25.2(5.4)	2.0(1.0)	67.4(5.0)	9.44(0.63)	31.63(6.25)
LAD-Lasso	7.9(0.3)	2.6(1.7)	5.1(1.7)	7.8(2.4)	2.18(0.36)	2.29(0.77)
RLARS	6.5(1.1)	1.4(1.4)	3.0(1.4)	11.6(5.7)	3.31(0.40)	3.04(1.08)
LTS-MCP	6.8(0.9)	6.5(3.2)	7.4(1.2)	28.2(9.1)	2.01(0.48)	0.93(0.20)
LS-MCP-Hier	5.9(1.0)	93.1(6.0)	1.7(1.4)	5.4(4.6)	8.07(0.52)	28.15(5.19)
D4: N(0,1) and with leverage points
LTS-MCP-Hier	7.8(0.6)	1.4(2.7)	7.7(2.0)	1.4(1.8)	1.75(0.54)	1.01(0.93)
LS-MCP	1.5(0.9)	22.1(4.8)	2.3(1.4)	69.4(6.4)	6.41(0.85)	14.50(4.92)
LAD-Lasso	4.5(1.2)	4.0(2.2)	3.2(1.8)	14.2(3.5)	3.27(0.32)	6.70(1.77)
RLARS	7.6(0.6)	0.5(0.7)	5.0(1.4)	10.1(6.3)	2.53(0.38)	1.65(0.59)
LTS-MCP	6.5(1.2)	6.7(4.3)	7.2(1.4)	27.0(12.7)	2.12(0.58)	1.30(0.35)
LS-MCP-Hier	5.5(1.3)	27.1(29.1)	3.7(2.4)	5.1(2.7)	3.99(0.85)	7.47(4.51)
D5: 0.9N(0,1) + 0.1Cauchy(0,5) and with leverage points
LTS-MCP-Hier	7.7(0.9)	1.5(2.8)	8.0(2.1)	1.3(1.3)	1.76(0.53)	1.04(1.04)
LS-MCP	0.5(0.8)	17.1(8.9)	1.1(1.1)	69.2(18.5)	32.48(44.17)	600.83(2389.98)
LAD-Lasso	4.5(1.4)	4.0(2.1)	3.5(1.8)	12.6(3.4)	3.28(0.32)	6.54(1.70)
RLARS	7.3(0.7)	1.0(1.1)	4.3(1.7)	11.3(6.7)	2.81(0.39)	1.98(0.63)
LTS-MCP	6.7(0.9)	8.4(3.9)	7.0(1.4)	32.0(10.5)	2.17(0.51)	1.31(0.29)
LS-MCP-Hier	4.4(1.5)	168.7(117.3)	1.0(1.5)	27.6(71.1)	31.14(43.24)	1186.95(4305.08)

Table A9.

Summary results under simulation scenarios where the hierarchy is violated for some interactions. In each cell, mean (sd) based on 200 replicates.

	M:TP	M:FP	I:TP	I:FP	RSSE	PMSE
D1: N(0,1)
LTS-MCP-Hier	7.8(0.4)	4.0(4.4)	10.5(2.0)	2.5(1.7)	3.46(0.35)	3.90(0.95)
LS-MCP	5.5(1.0)	5.0(4.4)	16.8(1.0)	17.8(9.8)	2.95(0.44)	1.51(0.60)
LAD-Lasso	7.9(0.4)	15.0(7.4)	17.9(2.9)	36.0(12.1)	2.23(0.59)	2.25(1.17)
RLARS	7.3(0.7)	1.0(1.5)	8.9(2.2)	14.4(7.9)	4.02(0.38)	4.29(1.08)
LTS-MCP	6.2(1.1)	7.0(3.0)	16.8(1.3)	26.8(6.9)	2.48(0.57)	1.11(0.35)
LS-MCP-Hier	7.8(0.4)	6.0(5.9)	11.3(1.9)	2.9(1.6)	3.40(0.45)	3.78(1.28)
D2: 0.9N(0,1) + 0.1Cauchy(0,5)
LTS-MCP-Hier	7.7(0.5)	6.0(5.9)	10.1(2.0)	2.9(1.6)	3.58(0.34)	4.19(1.02)
LS-MCP	2.2(1.8)	17.0(7.4)	3.5(3.2)	71.4(10.6)	38.37(84.37)	2057.01(11618.56)
LAD-Lasso	7.2(0.7)	2.0(1.5)	8.2(2.7)	7.7(3.1)	3.88(0.36)	6.93(1.99)
RLARS	7.0(0.9)	1.0(1.5)	7.1(2.3)	12.4(7.2)	4.44(0.43)	5.43(1.59)
LTS-MCP	6.1(1.0)	8.0(3.0)	16.2(1.6)	33.2(6.8)	2.78(0.53)	1.39(0.48)
LS-MCP-Hier	5.8(1.4)	110.0(32.6)	2.4(2.6)	34.2(95.9)	29.73(50.07)	1510.65(6857.39)
D3: 0.9N(0,1) + 0.1N(20,1)
LTS-MCP-Hier	7.6(0.6)	5.0(4.4)	10.2(2.2)	2.8(1.6)	3.60(0.47)	4.32(1.49)
LS-MCP	2.6(1.1)	22.0(5.2)	4.0(1.6)	66.9(5.3)	10.47(0.68)	38.04(6.53)
LAD-Lasso	6.9(0.9)	2.5(2.2)	6.4(2.2)	8.7(3.1)	4.13(0.34)	8.07(2.19)
RLARS	5.8(1.1)	1.0(1.5)	4.4(1.9)	11.9(5.8)	5.12(0.49)	8.10(2.43)
LTS-MCP	6.2(1.0)	8.0(3.0)	16.6(1.4)	29.2(6.1)	2.61(0.54)	1.18(0.37)
LS-MCP-Hier	6.2(1.0)	96.5(8.2)	2.7(1.6))	7.3(5.7)	9.76(0.64)	42.01(9.31)
D4: N(0,1) and with leverage points
LTS-MCP-Hier	7.3(1.1)	7.5(8.2)	9.4(3.2)	2.8(1.8)	3.78(0.76)	5.35(3.54)
LS-MCP	1.1(0.9)	21.0(4.4)	4.9(2.5)	67.0(6.2)	7.90(0.91)	22.21(7.30)
LAD-Lasso	3.8(1.2)	4.0(3.0)	6.0(2.4)	13.0(4.3)	4.56(0.35)	11.86(2.85)
RLARS	6.8(1.0)	0.0(0.0)	8.1(1.9)	12.8(6.6)	4.27(0.42)	4.78(1.44)
LTS-MCP	6.2(1.1)	9.0(3.0)	16.5(1.5)	32.4(6.6)	2.64(0.57)	1.24(0.43)
LS-MCP-Hier	4.8(1.3)	91.0(7.4)	2.2(2.1)	5.0(4.1)	7.55(1.16)	28.00(10.44)
D5: 0.9N(0,1) + 0.1Cauchy(0,5) and with leverage points
LTS-MCP-Hier	7.5(0.9)	8.0(4.4)	9.5(2.5)	3.0(2.0)	3.77(0.71)	5.32(3.72)
LS-MCP	0.6(0.7)	19.0(5.9)	2.0(1.8)	68.5(17.0)	32.80(78.33)	1370.28(8180.45)
LAD-Lasso	3.9(1.3)	4.0(1.5)	5.5(2.1)	12.2(3.5)	4.57(0.33)	12.16(3.24)
RLARS	6.6(1.0)	1.0(1.5)	6.8(2.2)	12.2(6.5)	4.57(0.40)	5.88(1.67)
LTS-MCP	6.2(1.1)	10.0(3.0)	16.4(1.5)	34.4(7.1)	2.68(0.57)	1.28(0.44)
LS-MCP-Hier	4.4(1.6)	113.0(25.2)	1.4(2.1)	31.8(88.0)	28.25(46.51)	1477.08(7265.55)

Table A10.

Analysis of SKCM data: numbers of overlapping interactions (RV-coefficients) identified by different approaches.

Main: G	LTS-MCP-Hier	LS-MCP	LAD-Lasso	RLARS	LTS-MCP	LS-MCP-Hier
LTS-MCP-Hier	43	0(0.58)	1(0.00)	0(0.00)	12(0.33)	22(0.48)
LS-MCP		13	0(0.00)	0(0.00)	0(0.03)	0(0.03)
LAD-Lasso			1	0(0.00)	0(0.00)	1(0.00)
RLARS				0	0(0.00)	0(0.00)
LTS-MCP					50	15(0.98)
LS-MCP-Hier						47
Interaction	LTS-MCP-Hier	LS-MCP	LAD-Lasso	RLARS	LTS-MCP	LS-MCP-Hier
LTS-MCP-Hier	26	0(0.02)	0(0.73)	0(0.28)	3(0.00)	4(0.58)
LS-MCP		72	0(0.02)	1(0.03)	6(0.00)	1(0.02)
LAD-Lasso			25	0(0.48)	2(0.01)	3(0.41)
RLARS				31	1(0.00)	0(0.20)
LTS-MCP					110	4(0.03)
LS-MCP-Hier						24

Table A11.

Analysis of BRCA data: numbers of overlapping interactions (RV-coefficients) identified by different approaches.

Main: G	LTS-MCP-Hier	LS-MCP	LAD-Lasso	RLARS	LTS-MCP	LS-MCP-Hier
LTS-MCP-Hier	32	1(0.27)	5(0.41)	0(0.22)	2(0.37)	14(0.73)
LS-MCP		6	1(0.27)	0(0.16)	0(0.11)	1(0.23)
LAD-Lasso			27	0(0.21)	0(0.33)	3(0.43)
RLARS				12	1(0.22)	0(0.27)
LTS-MCP					17	2(0.47)
LS-MCP-Hier						51
Interaction	LTS-MCP-Hier	LS-MCP	LAD-Lasso	RLARS	LTS-MCP	LS-MCP-Hier
LTS-MCP-Hier	39	1(0.09)	0(0.20)	0(0.15)	0(0.20)	6(0.33)
LS-MCP		17	2(0.19)	0(0.17)	0(0.12)	1(0.15)
LAD-Lasso			36	3(0.26)	0(0.21)	1(0.32)
RLARS				35	0(0.24)	0(0.09)
LTS-MCP					60	0(0.15)
LS-MCP-Hier						21