Genomic prediction for crossbred performance using metafounders

Abstract

Future genomic evaluation models to be used routinely in breeding programs for pigs and poultry need to be able to optimally use information of crossbred (CB) animals to predict breeding values for CB performance of purebred (PB) selection candidates. Important challenges in the commonly used single-step genomic best linear unbiased prediction (ssGBLUP) model are the definition of relationships between the different line compositions and the definition of the base generation per line. The use of metafounders (MFs) in ssGBLUP has been proposed to overcome these issues. When relationships between lines are known to be different from 0, the use of MFs generalizes the concept of genetic groups relying on the genotype data. Our objective was to investigate the effect of using MFs in genomic prediction for CB performance on estimated variance components, and accuracy and bias of GEBV. This was studied using stochastic simulation to generate data representing a three-way crossbreeding scheme in pigs, with the parental lines being either closely related or unrelated. Results show that using MFs, the variance components should be scaled appropriately, especially when basing them on estimates obtained with, for example a pedigree-based model. The accuracies of GEBV that were obtained using MFs were similar to accuracies without using MFs, regardless whether the lines involved in the CB were closely related or unrelated. The use of MFs resulted in a model that had similar or somewhat better convergence properties compared to other models. We recommend the use of MFs in ssGBLUP for genomic evaluations in crossbreeding schemes.

INTRODUCTION

In pig and poultry breeding, crossbreeding programs are generally used. The breeding objective is therefore to improve crossbred (CB) performance. Traits expressed in purebred (PB) and CB individuals are genetically not the same (Wei and Van der Werf, 1995; Wientjes and Calus, 2017). Therefore, it seems reasonable to use performance and genotypic data on CB individuals for genomic prediction of CB performance. However, collecting CB information might be difficult and expensive.

In breeding programs using genomic selection, single-step genomic best linear unbiased prediction (ssGBLUP) is the model of choice, as it enables to use phenotypes of both animals with and without genotypes (Aguilar et al., 2010; Christensen and Lund, 2010). In the implementation of ssGBLUP, ensuring compatibility between the pedigree-based relationship matrix and the genomic relationship matrix is one of the main issues (Christensen, 2012; Legarra et al., 2014, 2015). In crossbreeding, genomic prediction enables to accurately link CB phenotypes to PB animals, and considers multiple breed compositions simultaneously. Important challenges are the definition of relationships between different line compositions and to appropriately define the different base generations. A proposed solution to both make the pedigree based and the genomic relationship matrix compatible and to appropriately deal with multiple base generations is the use of metafounders (MFs), which are pseudo-individuals that are included in the pedigree as founders without known parents (Legarra et al., 2015). These MFs are arbitrarily grouped based on, for example line, sex, and age, similar to genetic groups. Genetic groups are considered unrelated, while MFs are considered to be related, and their relationships are computed by genotypes of their descendants. Xiang et al. (2017) showed that single-step genomic evaluation with MFs performs at least as good as the breed-of-origin-based ssGBLUP in genomic prediction for crossbreeding breeding programs. Our objective was to investigate the effect of using MFs in genomic prediction for CB performance, depending on the relatedness of lines involved in the cross, on the accuracy and bias of GEBVs. In addition, the impact of the use of MFs on estimated variances was evaluated. To address these questions, we used simulated data for a three-way cross reflecting a pig breeding scheme.

MATERIAL AND METHODS

Data Simulation

To investigate the effect of using MFs in genomic prediction on the accuracy and bias of GEBV, data for the historical, PB, and CB lines were simulated using the software QMSim (Sargolzaei and Schenkel, 2009). Phenotypes and genotypes of the individuals were simulated using a crossbreeding scheme. We simulated five correlated traits; one trait for each line composition, respectively, the three PB lines 1, 2, and 3, and the CB animals 23 and 123. Phenotypes and true breeding values (TBVs) for the line composition to which they belonged were simulated under additive gene action using a custom Fortran program.

The traits were correlated, by assuming the same correlations among QTL effects as the genetic correlations between traits. Genetic correlations between traits were randomly sampled in the range of 0.2 to 0.8 from a uniform distribution (Table 1), and heritabilities were randomly sampled in the range of 0.2 to 0.4 from a uniform distribution. Within a line composition, 4,500 QTLs that explained 95% of the total additive genetic variance, and a residual polygenic effect that explained 5% of the total additive genetic variance, were underlying the associated simulated trait. TBVs were computed as the sum of the products of the simulated allele substitution effects with the genotypes of the 4,500 QTLs coded as 0, 1, and 2, and a polygenic effect. Allele substitution effects of QTLs were sampled from a multinormal distribution with means of 0 and variances of 1. Within each line composition to which a trait belongs, the variance explained by all QTLs was computed as the sum of the variances across all QTLs, assuming no correlation between the QTLs. The variance of each jth QTL was calculated as ${\sigma }_j^2=2p_j\left(1-p_j\right){\alpha }_j^2$, where $p_j$ is the allele frequency and ${\alpha }_j$ is the allele substitution effect of jth QTL. Within each line composition, the allele substitution effects of the associated trait were rescaled to obtain a variance explained by all the QTLs equal to 1. Finally, the phenotypes for each animal for the trait associated with its line composition were generated by summing the TBVs and a residual error sampled from a normal distribution with a mean 0 and a variance computed such that the heritability within a line composition was equal to the simulated heritability. Marker and QTL mutation rates of 2.5 × 10^–5 were assumed. In total, 52,908 markers were available with a minor allele frequency (MAF) > 0.05, spread across 18 chromosomes representing the pig genome.

Table 1.

Genetic correlations used for simulated true breeding values for related and unrelated lines

Line	PB-1	PB-2	PB-3	CB-23
PB-2	0.46
PB-3	0.27	0.80
CB-23	0.33	0.58	0.30
CB-1(23)	0.55	0.31	0.26	0.69

The simulation process was started with the simulation of a historical population with 100 generations. The size of the historical generations was set to 18,840, with equal numbers of males and females, for the first 70 generations. In the next 10 generations, the population gradually decreased to 390 individuals to mimic a bottleneck. During the last 20 generations (81 to 100) the population size increased up to 18,840 again. The number of males in the last generation was 90.

After formation of the historical generations, breeding of lines 1, 2, and 3 started. Each line used 30 founder males and 1,000 founder females. A litter size of 2 was assumed with one male and one female progeny, such that each generation consisted of 2,000 individuals. All animals were replaced each generation. Matings were done at random between 30 males (randomly selected) and the 1,000 females. This scheme of line breeding was continued for 10 generations to represent a scenario with closely related lines and 100 generations to represent a scenario with unrelated lines, before starting the three-way crossbreeding program. Hereafter, these will be referred to as the related and unrelated scenarios, respectively.

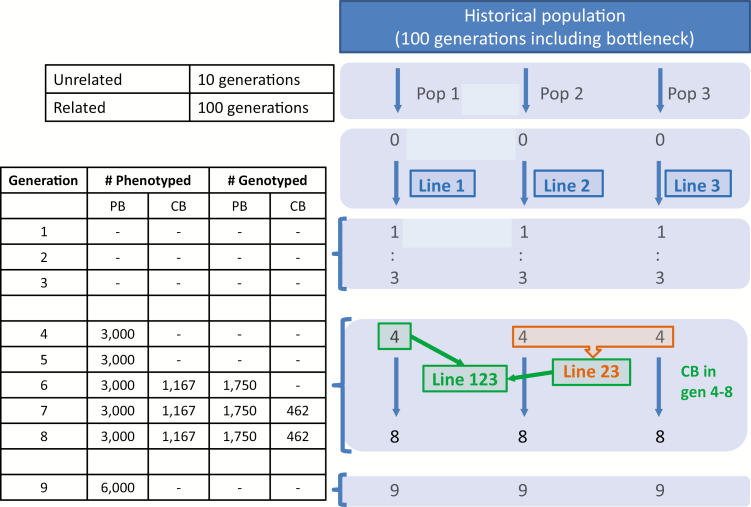
Starting from the last of those 10 or 100 generations, a three-way crossbreeding program with nine generations of random selection was simulated (see Figure 1 for a schematic overview). Random selection was used for simplicity, as selection would especially complicate the interpretation of estimated variances. In generations 1 to 3 of line breeding only pedigree was recorded, no genotypes or phenotypes. From generation 6 onwards crossbreeding started by crossing lines 2 and 3, after which this two-way cross was crossed with line 1, creating a three-way cross representing a pig breeding scheme. This crossbreeding was performed in generations 6 to 8. To mimic a practical situation where not all animals are phenotyped, and to limit the total number of phenotypes to enable computations within reasonable time, about 15,000 PB phenotypes were randomly recorded for generations 4 to 8, and about 3,500 CB phenotypes were randomly recorded for generations 6 to 8. About 5,250 PB genotypes were randomly recorded for generations 6 to 8, and about 925 CB genotypes were randomly recorded for generations 7 and 8. Random mating was applied in generations 1 to 8.

Figure 1.

Schematic overview of the simulation for the unrelated scenario, indicating which animals were genotyped or phenotyped, and the average numbers across replicates.

In total, about 2,125 individuals had both a phenotype and a genotype. Finally, the 9th generation consisted of selection candidates for which only genotypes were available. The 9th generation contained 6,000 individuals, i.e., 2,000 for each of the PB lines 1, 2, and 3.

Additionally, the same simulations were run with 500 individuals genotyped for each line composition within each genotyped generation, with the aim to test the influence of the number of genotypes on the estimation of MF relationships, variance components, and GEBV. Results were, however, very similar and therefore only the results for the initial scenarios are presented in this paper. The complete simulation was replicated 10 times.

Statistical Analysis

A five-trait ssGBLUP model (Aguilar et al., 2010; Christensen and Lund, 2010; Legarra et al., 2014) was used where the five traits modeled the PB performance of lines 1, 2, and 3 and the CB performance of crosses 23 and 1(23). The ssGBLUP model uses the inverse of a matrix with combined pedigree and genomic relationships. Inverses of the different combined pedigree genomic relationship matrices$$were computed using calc_grm (Calus and Vandenplas, 2016), considering MFs or not. The different inverses are described below. The variance components were estimated using Gibbs2f90 (Misztal et al., 2002) for which 50,000 samples were used, a burn-in of 3,500 and each 10th sample being stored. To limit the computational burden for the variance components estimation, all the genotyped animals of generation 9 were discarded from the datasets. The GEBV were computed using MiXBLUP (ten Napel et al., 2017). When the MFs were not considered, a genomic relationship matrix G required for the computation of the inverse of the combined pedigree-genomic relationship matrix ${\mathit{H}}^{-1}$ was computed without line-specific adjustments. The matrix G was equal to:

$$\mathit{G}=0.95{\mathit{G}}_a+0.05{\mathit{A}}_{22}$$

where ${\mathit{A}}_{22}$ stores the pedigree relationships among genotyped animals, and the adjusted genomic relationship matrix ${\mathit{G}}_a$ is computed as follows:

$${\mathit{G}}_a=\left(1-\stackrel{-}{f_{\text{p}}}\right){\mathit{G}}^{\text{*}}+2\stackrel{-}{f_{\text{p}}}\mathit{J}$$

where ${\mathit{G}}^{\text{*}}$ is a raw genomic relationship matrix computed following the first method of VanRaden (2018) using current allele frequencies computed from all genotyped animals, J is a matrix of ones, and $\stackrel{-}{f_{\text{p}}}$ is the average pedigree inbreeding coefficient across genotyped animals, according to the F_ST method (Powell et al., 2010; Vitezica et al., 2011).

When the MFs were considered in the ssGBLUP model (ssGBLUP_MF), one MF was assigned to each PB line, making a total of three MFs. Self-relationships and relationships between MFs were estimated based on genotypes of their descendants, and pedigree information, following the generalized least squares (GLS) method for multiple populations as shown by Garcia-Baccino et al. (2017), and implemented in the software createHmf (Legarra, 2016b). Briefly, the MF (self-)relationships are computed as twice the (co)variances of the estimated allele frequencies for the base generation of the pedigree. These base population allele frequencies were computed using the GLS method and all PB and CB genotypes (Garcia-Baccino et al., 2017). The computation of the inverse of the combined pedigree-genomic relationship matrix including MFs, ${\mathit{H}}^{\left(\gamma \right)-1}$, was performed using the software calc_grm (Calus and Vandenplas, 2016), following Legarra et al. (2015) and assuming a residual polygenic effect of 5%, by giving a weight of 0.05 to ${\mathit{A}}_{22}$ as explained above, while in this case ${\mathit{G}}_a={\text{MM}}^{\mathit{\text{'}}}/(1/2)n$, where n is the number of SNPs and M stores the genotypes coded as $\left\{-1,0,1\right\}$. Note that this ${\mathit{G}}_a$ can be obtained using the first method of VanRaden (2018) assuming that all allele frequencies are equal to 0.5. Finally, for reasons of comparison, the same model was also applied using the ordinary inverse of the pedigree based relationship matrix ${\mathit{A}}^{-1}$. This model is hereafter referred to as PBLUP.

Evaluation of Model Performance

Several aspects of the results were evaluated, between analyses with and without MFs. Estimated genetic variances were compared against true variances. True variances were empirically calculated as the variances of TBV of all the PB 2,000 animals in generation 1, and of all the 2,000 CB animals in generation 4. Similarly, true residual variances were empirically calculated as the variances of errors of all the 2,000 PB animals in generation 1, and of all the 2,000 CB animals in generation 4. Genetic variances estimated with the ssGBLUP_MF model were rescaled to get them on the same scale as the estimates of the other models where the genetic parameters relate to a base generation of supposedly unrelated animals (Legarra et al., 2015; Xiang et al., 2017). This scaling involved multiplying the genetic variances for the PB traits with $\left(1-({\gamma }_{\text{PB}}/2)\right)$, where ${\gamma }_{\text{PB}}$ is the self-relationship in the corresponding PB line. For the CB traits, this transformation should be done for each breed-of-origin-specific genetic variance component, and then summing across breed of origins. We did not consider breed of origin in the model, however, computed a weighted average of the scaling factor $\left(1-({\gamma }_{\text{PB}}/2)\right)$ across the PB lines involved in the CB animals, where weights were based on the breed composition of the cross. This approach is valid under the assumption that the genetic variance for CB performance is the same for each PB line. Finally, estimated genetic correlations were compared to simulated values. For ssGBLUP_MF, the estimates were computed from the unscaled estimated (co-)variances following Xiang et al. (2017).

The accuracy of GEBV for both PB and CB performance was computed as the correlation between the TBV and the GEBV for the PB selection candidates in generation 9. The bias of the level of the GEBV and the bias of the scale of the GEBV were evaluated, respectively, as the intercept and slope of the regression of the TBV on the GEBV. Accuracies and bias were computed for each PB line separately. Finally, the convergence of ssGBLUP was compared in both situations with and without MFs.

RESULTS

Genetic Differentiation Between Lines

For the two scenarios, i.e. related and unrelated scenarios, the level of genetic differentiation between the three PB lines was measured using the global Wright’s F_ST statistic, as implemented in the software Genepop (4.2) (Raymond and Rousset, 1995; Rousset, 2008). Using the genotypes of all PB animals in generation 6, the estimated global Wright’s F_ST statistics were on average equal to 0.06 for the related scenario, and to 0.36 for the unrelated scenario, across the five replicates.

Relationships Among MFs and Estimated Variance Components

The estimated self-relationships of the MFs were around 0.17 for the related and around 0.74 for the unrelated scenario (Table 2). The relationships among MFs showed to be very similar in the scenarios with related or unrelated lines, ranging from 0.045 to 0.049.

Table 2.

Relationships among metafounders for related and unrelated scenarios (average of 10 replicates; SE within brackets)

	Related scenario			Unrelated scenario
	Line 1	Line 2	Line 3	Line 1	Line 2	Line 3
Line 1	0.171 (0.005)	0.049 (0.002)	0.047 (0.002)	0.746 (0.020)	0.046 (0.005)	0.045 (0.006)
Line 2	0.049 (0.002)	0.171 (0.007)	0.046 (0.002)	0.046 (0.005)	0.741 (0.016)	0.046 (0.005)
Line 3	0.047 (0.002)	0.046 (0.002)	0.171 (0.006)	0.045 (0.006)	0.046 (0.005)	0.743 (0.020)

The average variance component estimates (and SD) for the related and unrelated scenarios are presented for PBLUP, ssGBLUP and ssGBLUP_MF (Tables 3 and 4). For comparison, presented genetic variances estimated with the ssGBLUP_MF model were rescaled as described in a previous section. The estimated variances were compared against the empirically calculated true values outlined in Table 5. For both the related and unrelated scenarios, estimated residual variances were close to the empirically calculated true values for all three models, with deviations from the simulated values ranging from −5.3% to 2.6%. Estimated genetic variances differed for the related and unrelated scenarios. In the related scenario, the genetic variances were in all cases overestimated, with deviations from the simulated values ranging from 1.7% to 32.4%. Genetic variances were on average overestimated by 12.9, 14.9, and 11.5%, respectively, with the models PBLUP, ssGBLUP, and ssGBLUP_MF. In the unrelated scenario, the most extreme estimates across the models underestimated the genetic variance by 4.1% or overestimated it by 27.3%. The genetic variance was on average underestimated by 3.8% and 0.3% by PBLUP and ssGBLUP_MF, respectively, while it was overestimated by 16.8% for ssGBLUP. For both scenarios, not performing the scaling of the estimates for ssGBLUP_MF yielded genetic variances that were overestimated by 22.0% and 58.7% for the related and unrelated scenarios, respectively (Supplementary Table 3).

Table 3.

Estimated variance components for the related scenario for three different models: PBLUP, ssGBLUP, and ssGBLUP using metafounders. Residual and genetic variances estimates are presented for purebred traits 1, 2, and 3 and crossbred traits 23 and 1(23)

			Genetic variances and correlations1
Model	Trait	Residual	1	2	3	23	1(23)
PBLUP	1	2.672	1.141	0.614	0.236	0.534	0.505
	2	1.659	0.614	1.063	0.291	0.466	0.212
	3	3.699	0.236	0.291	1.182	0.308	0.195
	23	1.907	0.534	0.466	0.308	1.092	0.512
	1(23)	3.456	0.505	0.212	0.195	0.512	1.286
ssGBLUP	1	2.656	1.173	0.653	0.096	0.576	0.506
	2	1.651	0.653	1.079	0.186	0.528	0.249
	3	3.690	0.096	0.186	1.202	0.288	0.183
	23	1.862	0.576	0.528	0.288	1.155	0.517
	1(23)	3.497	0.506	0.249	0.183	0.517	1.256
ssGBLUP-MF2	1	2.689	1.110	0.754	0.035	0.550	0.474
	2	1.652	0.754	1.071	0.095	0.521	0.376
	3	3.687	0.035	0.095	1.196	0.253	0.215
	23	1.846	0.550	0.521	0.253	1.159	0.530
	1(23)	3.539	0.474	0.376	0.215	0.530	1.160

¹Variances are on the diagonal, correlations are on the off-diagonal. Standard errors of the variances ranged 0.031 to 0.062, and from 0.023 to 0.130 for the genetic correlations. Standard errors for each estimate are presented in Supplementary Table 1.

²Genetic variances after scaling are presented.

Table 4.

Estimated variance components for the unrelated scenario for three different models: PBLUP, ssGBLUP, and ssGBLUP using metafounders in the model

			Genetic variances and correlations1
Model	Trait	Residual	1	2	3	23	1(23)
PBLUP	1	2.673	1.112	0.604	0.115	0.352	0.410
	2	1.670	0.604	1.039	0.187	0.516	0.300
	3	3.720	0.115	0.187	1.099	0.269	0.106
	23	1.856	0.352	0.516	0.269	0.904	0.510
	1(23)	3.581	0.410	0.300	0.106	0.510	0.900
ssGBLUP	1	2.615	1.244	0.597	0.069	0.341	0.517
	2	1.640	0.597	1.126	0.151	0.490	0.332
	3	3.651	0.069	0.151	1.245	0.245	0.158
	23	1.827	0.341	0.490	0.245	1.041	0.533
	1(23)	3.544	0.517	0.332	0.158	0.533	1.018
ssGBLUP-MF2	1	2.688	1.080	0.729	0.183	0.468	0.506
	2	1.680	0.729	1.026	0.292	0.475	0.469
	3	3.714	0.183	0.292	1.100	0.297	0.094
	23	1.903	0.468	0.475	0.297	0.826	0.554
	1(23)	3.518	0.506	0.469	0.094	0.554	0.835

Residual and genetic variance estimates are presented for purebred traits 1, 2, and 3 and crossbred traits 23 and 123.

¹Variances are on the diagonal, correlations are on the off-diagonal. Standard errors of the variances ranged from 0.035 to 0.074, and from 0.040 to 0.130 for the genetic correlations. Standard errors for each estimate are presented in Supplementary Table 2.

²Genetic variances after scaling are presented.

Table 5.

Empirically calculated true variance components for the related and unrelated scenarios

Trait	Related scenario			Unrelated scenario
	Residual variancea	Additive genetic variancea	Heritabilityb	Residual variancea	Additive genetic variancea	Heritabilityb
1	2.720	1.040	0.28	2.670	1.060	0.28
2	1.635	1.045	0.39	1.645	1.061	0.39
3	3.697	1.074	0.22	3.857	1.070	0.22
23	1.859	0.985	0.35	1.873	0.817	0.30
1(23)	3.580	0.971	0.21	3.554	0.871	0.20

^aAll standard errors were <0.045.

^bAll standard errors were <0.01.

Estimates of the genetic correlations among PB lines showed large deviations from the simulated values, and were on average underestimated, both for the unrelated and related scenarios. Estimated genetic correlations between the PB lines 1, 2, and 3 and the CB 23 and 1(23) animals were generally close to the simulated values. Across models, estimated genetic correlations were similar, both within the related and the unrelated scenario. The largest differences were observed for the related scenario, where the estimated genetic correlations of the PBLUP and ssGBLUP model were on average 0.06 to 0.07 lower than those of ssGBLUP_MF, whose estimates were closer to the simulated values.

Accuracy and Bias

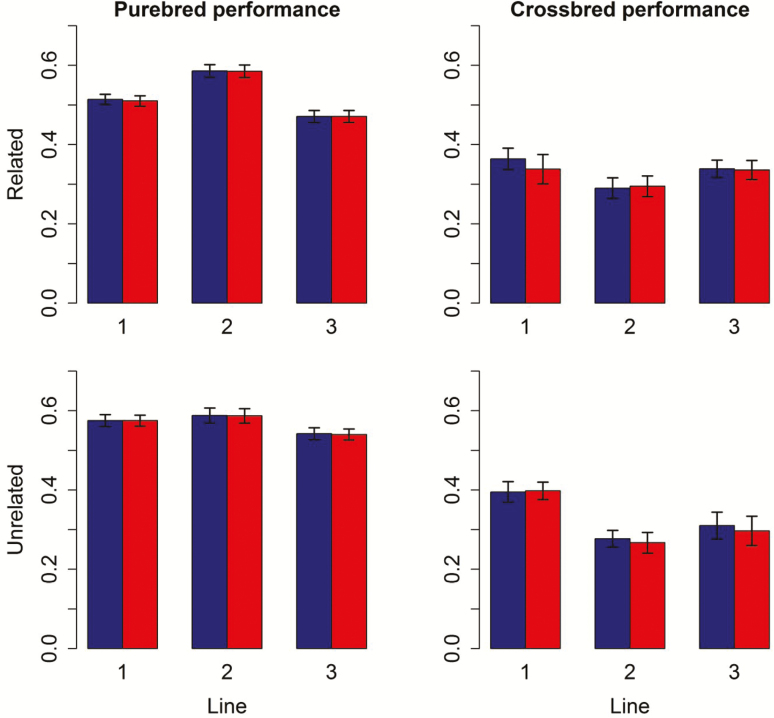
A total of 2,000 genotyped selection candidates per line were used for computing accuracy and bias. Across the related and unrelated scenarios, for PB performance the accuracies ranged from 0.37 to 0.47 with PBLUP (Supplementary Table 4), and from 0.47 to 0.59 for ssGBLUP (Figure 2; Supplementary Table 4). For CB performance the accuracies ranged from 0.13 to 0.27 with PBLUP, and from 0.27 to 0.40 with ssGBLUP. Accuracies of ssGBLUP and ssGBLUP_MF within the same scenario were very similar, with any differences being smaller than the standard errors (Figure 2; Supplementary Table 4). Accuracies of PBLUP were very similar between the related and unrelated scenario, because effectively no information was used across lines due to lack of pedigree links between the lines, leading to very similar amounts of information being available in both scenarios. Accuracies of ssGBLUP were comparable across the related and unrelated scenarios, except for PB performance of lines 1 and 3, where the accuracies were higher for the related scenario (Figure 2; Supplementary Table 4).

Figure 2.

Accuracies of GEBV for purebred selection candidates in generation 9, either for purebred or crossbred performance, using ssGBLUP models with or without metafounders, for lines with related and unrelated pedigrees in purebred and crossbred performances. Red (blue) bars represent models with (without) metafounders.

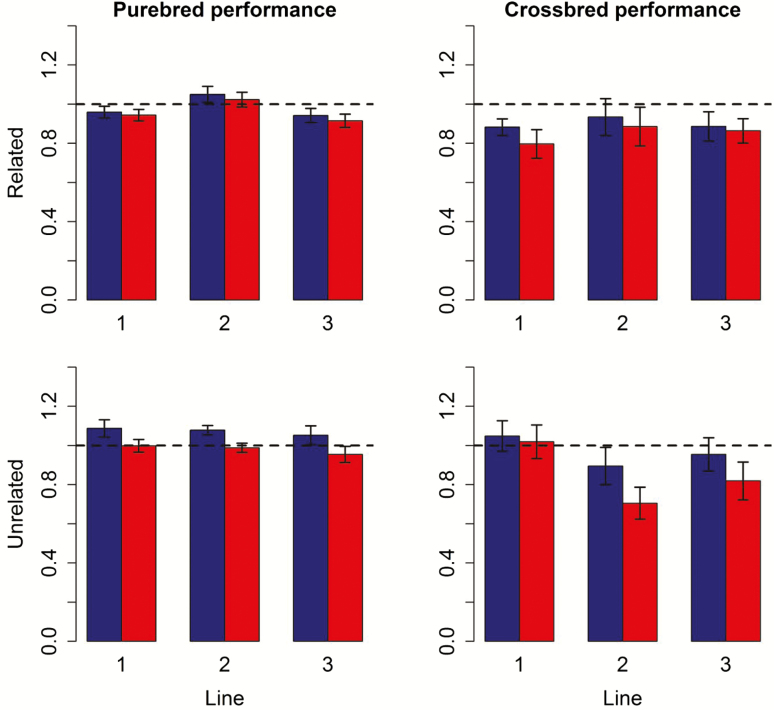
The mean values of all sets of (G)EBV were unbiased, as the intercepts of the regression of TBV on EBV were in most cases not significantly different from 0 (Supplementary Table 5). The coefficients of the regression of TBV on EBV were in all cases close to 1 for PB performance (Figure 3; Supplementary Table 6). The regression coefficients for CB performance were in most cases smaller than 1, indicating that the variance of the GEBV tended to be somewhat inflated. Intercepts and regression coefficients for ssGBLUP and ssGBLUP_MF were very similar within the same scenario.

Figure 3.

Bias, defined as the regression slope of the true on the GEBV for purebred selection candidates in generation 9, either for purebred or crossbred performance, using obtained for ssGBLUP models with and without using metafounders for lines with related and unrelated scenarios in purebred and crossbred performances. Red (blue) bars represent models with (without) metafounders.

Convergence of ssGBLUP

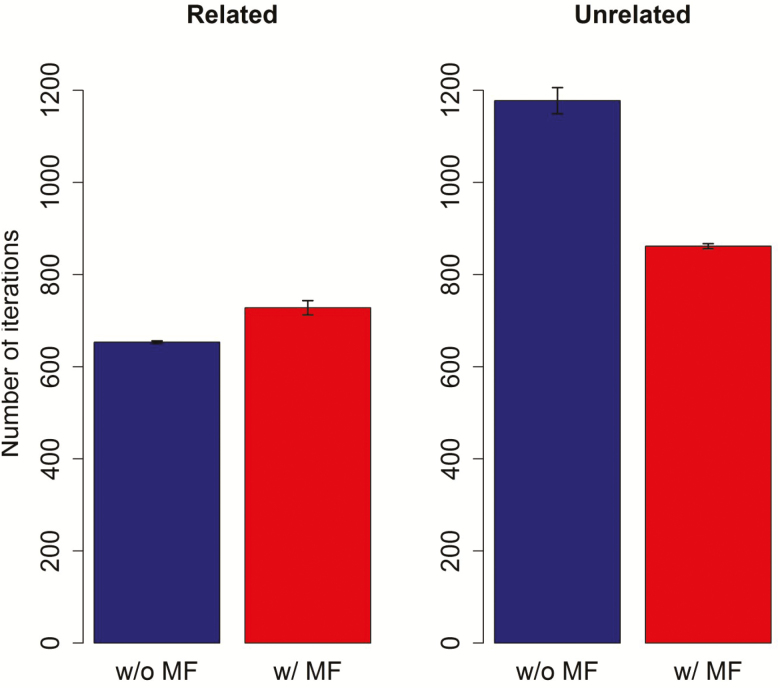
In the closely related scenario, ssGBLUP and ssGBLUP_MF required a similar number of iterations to reach convergence. In the unrelated scenario ssGBLUP needed substantially more iterations compared to ssGBLUP_MF, resulting in ~30% additional computation time (Figure 4).

Figure 4.

Convergences of ssGBLUP models with and without using metafounders (MFs) for related and unrelated scenarios. Red bars represent models with MF.

DISCUSSION

The models ssGBLUP and ssGBLUP_MF have been compared in terms of estimated variance components, accuracy, bias, and computational efficiency in order to evaluate the possible benefit of MFs in genomic evaluations for a crossbreeding program. Our results showed that using MF in genomic prediction for CB performance does not affect the prediction accuracies, while it may speed up convergence in specific cases. At the same time, estimated variances for ssGBLUP_MF, after appropriate scaling, were in closer agreement with the empirical true values than ssGBLUP.

Relationships Among MFs

Models used in breeding value estimation commonly assume that parents with unknown ancestors are sampled from an infinite base population with common genetic variance, and that these base animals are unrelated. In practice, due to pedigree incompleteness, in addition to animals from the oldest generation in the pedigree, in later generations there usually are also animals with unknown ancestors. In this case, animals from the same generation may in fact be more closely related to each other. This is commonly solved by allocating genetic groups to animals with unknown parents that can be grouped based on line, generation, birth date, sex or a combination of these or other factors (Westell et al., 1988). All base animals within the same genetic group are assumed to come from ancestors with similar breeding values, while the animals between genetic groups all have a considered relationship of zero. By using MFs instead of genetic groups, relationships between the pseudo individuals representing genetic groups are computed based on the genotypes of the descendants (Legarra et al., 2015), and used in the model. Because MFs are considered to represent a finite-size pool of gametes, the MFs also have a self-relationship (Legarra et al., 2015).

We obtained a self-relationship of the MFs of ~0.17 for the related and ~0.74 for the unrelated scenario. This suggests that the base generation of the related scenario is much more diverse than the base generation of the unrelated scenario. In fact, the base generation of the unrelated scenario had its base generation after 90 generations more of line breeding than the related scenario, and was therefore subject to considerably more accumulated inbreeding. This was reflected in the higher self-relationship of the MF for the unrelated compared to the related scenario. The self-relationship of the MFs in the unrelated scenario is very similar to the values found for pigs (Xiang et al., 2017), and close to the expected value of 2/3 when assuming that base generation allele frequencies are uniformly distributed (see Supplementary Appendix 1). Other reported values in literature varied from values of 0.55 for Holstein and 0.77 for Jersey cattle (Legarra et al., 2015), and 0.30 to 0.47 for dairy goat and sheep (Legarra et al., 2015; Colleau et al., 2017). The latter values are closer to the level of the self-relationship of the MFs in our related scenario, suggesting higher diversity in the base generations of those populations. It should be noted that in all those cases, including our study, a 50k type of chip was used, where the SNPs were selected based on MAF, which is expected to have some impact on the estimated MF relationships. If the relationships among MF would be computed using whole-genome sequence instead, considering that this would have a U-shaped rather than a uniform distribution of allele frequencies, it is expected that higher values would have been obtained in all those cases.

Estimated Variance Components

The estimated residual variances were similar across the different models and not significantly different from the empirical true values. However, this was not the case for all the estimated genetic variances of the three models. Estimates of the models PBLUP and ssGBLUP should be expressed in an unrelated base population. While the estimated genetic variances for the PBLUP models were similar to the empirical true values, genetic variance estimates for the ssGBLUP model overestimated the empirical true variances. This could be explained by the fact that across-breed allele frequencies and across-breed adjustments of the genomic relationship matrix were used to make it compatible with the pedigree relationship matrix. While such across-breed adjustments may not affect the accuracy (Makgahlela et al., 2014; Lourenco et al., 2016), they may affect the compatibility between the two types of relationships and the estimates of genetic (co)variances (Legarra, 2016a; Wientjes et al., 2017). For the ssGBLUP_MF model, estimated genetic variances were similar to the empirical true genetic variances, after rescaling. Rescaling for the ssGBLUP_MF model was needed because the estimated genetic variance components from the ssGBLUP_MF model are expressed in a hypothetical related base population with allele frequency of 0.5 for all SNPs (Legarra et al., 2015; Garcia-Baccino et al., 2017).

Estimated genetic correlations were similar across the three models, even if some deviations were observed from the simulated values. For example, the estimated genetic correlation among the PB lines 2 and 3 especially deviated from the simulated value, most likely because of the weak link between the lines, and because of the limited amount of information available for this particular genetic correlation. On the other hand, estimated genetic correlations between PB and CB performances, for which more information was available, were generally close to the simulated values. For the unrelated scenario, overall ssGBLUP_MF in fact yielded estimated genetic correlations that were closest to the simulated values. This superiority for the unrelated scenario compared to PBLUP may be due to the higher importance of having genomic information to provide stronger links between the different categories of animals, while ssGBLUP_MF additionally profits from making pedigree and genomic relationships better compatible, and therefore may have more correct estimated variance components compared to ssGBLUP. This could be explained by the fact that across-breed allele frequencies and across-breed adjustments of the genomic relationship matrix were used to make it compatible with the pedigree relationship matrix.

Based on these results, further studies are required to develop and validate an approach to estimate easily (co)variance components for ssGBLUP_MF in the context of crossbreeding and multivariate evaluations, when switching from PBLUP (or ssGBLUP) routine evaluations to ssGBLUP_MF evaluations. A straightforward approach would be to re-estimate variance components, however, such an approach may be time-consuming. Legarra et al. (2015) proposed an approach to compute variance components for ssGBLUP_MF by scaling the ones from PBLUP (or ssGBLUP) with the following factor: $k=1+\overline{\stackrel{}{\text{diag}\left(\Gamma \right)}}/2-\stackrel{-}{\Gamma }$, where the matrix $\Gamma$ describes the relationships among MFs. According to Legarra et al. (2015), the scaling factor $k$ should be <1, meaning that the genetic variances assuming related founders are larger in comparison to the ones assuming unrelated founders. This is also what we observed for our estimated genetic variances, especially for the unrelated scenario. However, scaling the estimated genetic variances for PBLUP or ssGBLUP as proposed by Legarra et al. (2015) for the related and unrelated scenarios did not result in estimated genetic variances of ssGBLUP_MF that were in agreement with the empirical true values. The scaling factor for the related scenarios was close to 1 (i.e., 0.996), and the one for the unrelated scenario was larger than 1 (i.e., 1.09), meaning that the estimates for the unrelated scenario only deviated more from the empirical true values (results not shown). Based on our results, a third approach could be to compute variance components expressed in a related base population from variance components obtained with PBLUP (or ssGBLUP) and MFs’ relationships. Covariance components could be computed from genetic correlations estimated with PBLUP (or ssGBLUP) and variance components expressed on a related base population.

Effect of MFs on Performance of Genomic Evaluations

Adding the MF in ssGBLUP did not affect the prediction accuracy. It did reduce the number of iterations until convergence by ~27% for the unrelated scenario. For the unrelated lines, the G and A matrix may be less compatible, because the considered base generation falls after 100th generations of line breeding, compared to only 10 for the related lines. Poor compatibility of G and A may have affected the convergence of ssGBLUP. The use of MFs likely results in a more consistent relationship matrix in ssGBLUP_MF, as it adjusts the base of the pedigree relationships to have the same base as the genomic relationships (Garcia-Baccino et al., 2017). This is the likely explanation for the observation that the use of MFs for the unrelated scenario resulted in improved convergence and estimated genetic variances and genetic correlations that were closer to the simulated values compared with ssGBLUP.

Results from Xiang et al., (2017) show that in terms of model-based reliabilities and predictive abilities, ssGBLUP_MF performs at least as well as ssGBLUP using the breed of origin of alleles in the CB animals which requires a step of phasing genotypes and of assigning breed of origin of alleles in CB animals. These additional steps are computationally time-consuming. Use of MFs only requires to compute the relationships among MFs, which can be done using the general least squares estimator of base generation allele frequencies (McPeek et al., 2004; Garcia-Baccino et al., 2017), whose computing time using sparse matrices (Strandén et al., 2017) is trivial relative to all computations needed for ssGBLUP (Aldridge et al., 2018). The ssGBLUP_MF model is therefore more convenient while achieving similar accuracies and biases. Also, while this issue was not considered in this study, fitting genetic groups in ssGBLUP is not as straightforward as for PBLUP, and requires additional computations for the contributions of genotyped animals to genetic groups (Misztal et al., 2013). Using MFs instead only influences the computation of the inverse of pedigree-based relationship matrix. Finally, in genomic evaluations with multiple lines or breeds it is not easy to scale G and A properly (Legarra et al., 2015), unless relationships are dissected by breed of origin (Christensen et al., 2014, 2015), but this is straightforward with the use of MF. Therefore, there are several advantages and no clear obstructions to use MFs in genomic evaluations, and especially in crossbreeding schemes.

CONCLUSIONS

Based on the results in our study, the ssGBLUP model using MFs is the preferred model for implementation of genomic prediction for CB performance in practical breeding programs. The MFs can easily accommodate for differences in base populations for different lines involved, as the genomic and pedigree relationships are compatible by construction. In comparison to ssGBLUP, this leads, potentially, to improved convergence behavior of the iterative solver, without affecting the prediction accuracies. Our results also suggest that rescaled variance components estimated with ssGBLUP_MF may be more accurate than those of ssGBLUP. Further studies are needed for developing and validating approaches to easily compute or approximate variance component estimates for ssGBLUP_MF.