Imaging of local structures affecting electrical transport properties of large graphene sheets by lock-in thermography

A novel technique for fast and precise quality evaluations of graphene devices.

Abstract

The distribution of defects and dislocations in graphene layers has become a very important concern with regard to the electrical and electronic transport properties of device applications. Although several experiments have shown the influence of defects on the electrical properties of graphene, these studies were limited to measuring microscopic areas because of their long measurement times. Here, we successfully imaged various local defects in a large area of chemical vapor deposition graphene within a reasonable amount of time by using lock-in thermography (LIT). The differences in electrical resistance caused by the micrometer-scale defects, such as cracks and wrinkles, and atomic-scale domain boundaries were apparent as nonuniform Joule heating on polycrystalline and epitaxially grown graphene. The present results indicate that LIT can serve as a fast and effective method of evaluating the quality and uniformity of large graphene films for device applications.

INTRODUCTION

Owing to its exceptional physical properties such as extremely high carrier mobility (1) and mechanical flexibility (2), graphene has opened the way for realizing various novel devices in electronics and optoelectronics (3, 4). For these device applications, bottom-up methods such as chemical vapor deposition (CVD) (5–10) are needed for making wafer-sized single crystals. A relatively high-quality atomic layer can be obtained by using a top-down method such as mechanical peel-off (11), but the result is a mixture of various layers ranging from a single layer to several dozen layers, and the flake size is limited to a few tens of micrometers. On the other hand, single-domain single-layer graphene on the millimeter scale has been fabricated by using CVD, in which the nucleation density is dramatically reduced through control of growth conditions such as the surface oxidation of the copper substrate (10). Nevertheless, graphene samples prepared by CVD are considered to have lower quality than those produced by the mechanical peel-off method. Many defects such as cracks (12, 13), wrinkles (14–18), and those at domain boundaries (DBs) (17–24) are unavoidably formed in CVD graphene sheets during growth and/or transfer processes, which drastically impairs their electrical transport properties (12, 14–24). Undesirable fluctuations in device performance have been reported in transistors on the basis of large sheets of CVD graphene (5, 8, 9). Hence, techniques enabling the measurement of the local defect distributions that affect electrical property over a wide area are required.

The electrical characterization of defects in CVD graphene sheets has been studied mainly through a combination of four-terminal measurements with a Hall bar device (12, 14, 19, 20, 22, 24) and microscopic techniques such as scanning tunneling microscopy (STM) (21, 23), Kelvin probe force microscopy (15, 16), and conductive atomic force microscopy (AFM) (17). Although these techniques show the electrical properties of local structures at nanoscale spatial resolution, it is very difficult to use them to evaluate the sample’s qualities in a large area within a reasonable time frame. To achieve high-resolution measurements, time-consuming processes are required for preparing and measuring the devices. Meanwhile, there are several methods for characterizing the electrical properties of graphene sheets covering a large area. Terahertz spectroscopy mapping can assess the electrical mobility of graphene quantitatively without complicated patterning of devices, and it directly images these physical parameters by scanning the whole sheet area (25, 26). However, its low spatial resolution (under a hundred micrometers to under a millimeter) makes it difficult to detect local structures on a graphene sheet. In addition, because the measurement is performed under the current-off condition, the obtained results do not reflect the electrical properties of operating active devices. Infrared (IR) thermography (27–30) enables characterization of large areas by imaging heat radiated from a biased sample. Although the spatially inhomogeneous charge carrier distribution (27–29) and the location of electrical failures in samples covered with a dielectric layer (30) can be imaged, this method cannot provide a clear image of local structures at micrometer resolution because of significant broadening of the thermal radiation spot by the heat stored in the substrate supporting the graphene (28, 29).

Lock-in thermography (LIT) (31–35) is a nondestructive and fast electrical characterization method of large-area samples, and it has micrometer-scale spatial resolution (32, 33, 35). Detection of Joule heating in a biased device enables local structures to be imaged without the influence of heat broadening in a short acquisition time. Furthermore, because of its wide field of view, typically from submillimeter to subcentimeter (32–34), one LIT image can characterize local structures in large samples. For instance, this method has been used to check for local structural failures in large-scale semiconductor devices such as integrated circuits (32, 33) and solar cells (34). Recently, we experimentally demonstrated LIT imaging of carbon nanotube (CNT) network paths in a centimeter-scaled CNT composite at micrometer resolution (35). These results strongly suggest that LIT would be a powerful tool for quickly visualizing local structures in conductive materials that have large areas. Here, we present the electrical characterization of a large CVD graphene sheet by using the LIT technique. It is shown that LIT successfully visualizes the difference in electrical resistance caused by local defects as inhomogeneous thermal radiation. Furthermore, LIT exposes the presence of various defects, not only micrometer-scale structures such as cracks and wrinkles but also atomic defects such as DBs in large sheets. We discuss the observation of thermal radiation and current flow patterns on a graphene sheet in combination with local resistance measurements and morphological and spectroscopic characteristics.

RESULTS

LIT of polycrystalline CVD graphene

Figure 1A shows a schematic diagram of the present experimental setup. LIT is carried out by applying a bias voltage to the samples with two electrodes. The bias is modulated at 25 Hz, with a 50% duty cycle. Figure 1B shows a schematic illustration of the LIT operation principle with respect to thermal radiation detection. The thermal emission from a sample is two-dimensionally imaged by using an InSb charge-coupled device (CCD) camera, which runs with multiple shutter timings synchronized with a 25-Hz pulsed bias. Consequently, the LIT provides two pieces of information about thermal radiation: amplitude and phase. The amplitude images are constructed by subtracting the background photons, such as those due to heat radiated from the substrate and the dark counts of the CCD, and thus, the Joule heat component from the biased sample can be separately detected. The phase images are related to the timing of the heat generation. For example, a fast phase angle indicates that heat is generated only after applying the voltage. The heat dissipation behavior in the sample can be observed as the phase angle is increased.

Fig. 1. LIT characterization of large-area graphene sheets.

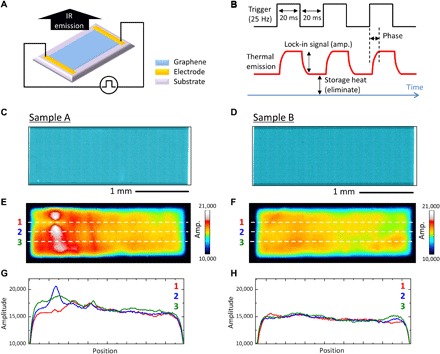
(A) Schematic representation of measurement setup. (B) Operation principle of LIT. (C and D) Optical microscopy images of two polycrystalline graphene sheets. (E and F) Amplitude images of samples A and B, respectively. The measurement time was 10 min for both samples. Cross-sectional profiles of thermal amplitude along lines 1 to 3 in (E) and (F) are also shown in (G) and (H), respectively.

LIT of polycrystalline graphene grown on Cu foil was conducted first. Figure 1 (C and D) shows optical microscopy images of two polycrystalline graphene sheets on quartz substrates. The quartz is a good material for thermal microscopy measurements because of its low thermal conductivity. Both samples were etched to the same size of 3 mm × 1 mm, and the electrical resistances measured with the two probes were 450 ohms for sample A and 420 ohms for sample B. (Note that throughout this article, resistances are normalized by the length and width of the graphene sheet.) Although the resistance of sample A was slightly higher than that of sample B, no difference can be seen in the optical images (Fig. 1, C and D). Note that both samples were constructed with a single-layer graphene. The Raman spectrum exhibited low D band intensities compared with the G band (I_D/I_G < 0.2; fig. S1B), and the domain size was estimated to be 4 to 5 μm on average from the scanning electron microscopy (SEM) observations (fig. S1, C to F).

Figure 1 (E and F) shows amplitude images of LIT of samples A and B that are exactly the same areas as in the optical images of Fig. 1 (C and D). The images were measured under applied biases of 12.0 and 11.5 V for samples A and B, respectively, which corresponded to a power consumption of 35 mW/mm². The LIT image for sample A shows inhomogeneous thermal distributions (Fig. 1E). Several peaks appear in the cross-sectional profiles of the thermal amplitude (Fig. 1G). The images for sample B (Fig. 1, F and H), on the other hand, reveal a relatively flat thermal distribution without a prominent peak. To investigate the origins of the inhomogeneous heat distribution observed in sample A, we remeasured the LIT of the left side of the sheet at a high magnification. Figure 2 (A and B) displays amplitude and phase images, respectively. The images show two characteristics. The first is a lack of heat generation, as indicated by the dotted arrows; the second is the straight lines indicated by the dashed arrows. Figure 2C is a high-magnification optical microscopy image at the center of the “cold” area. A critical crack can be seen on the graphene sheet, resulting in a lack of heat. Figure 2D shows the phase angle dependence of the amplitude images around the crack. For a fast phase angle of 38°, intense peaks appear at the upper and lower parts of the crack, while the crack area itself shows a very low signal intensity. As the phase angle increases from 98° to 143°, the amplitude in the crack area becomes higher through thermal diffusion from the hot spots. The heat propagation can be more easily understood from the point intensity analysis, as shown in Fig. 2E. The results indicate that the current flows through the upper and lower parts around the crack avoid the damaged area. A simple simulation of Joule heating around the crack under current flow reproduced the present observations (see fig. S5C).

Fig. 2. High-magnification LIT image and detailed analysis of thermal properties.

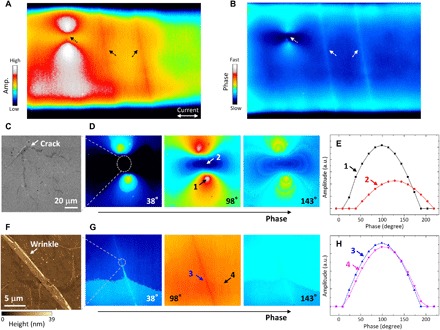
(A) Amplitude and (B) phase images focused on a part of sample A. Characterization of thermal emission around (C to E) a crack and (F to H) wrinkle. The (C) crack and (F) wrinkle are optical microscopy and AFM images, respectively. Phase angle dependence of (D and G) amplitude images and (E and H) point intensities. a.u., arbitrary units.

On the other hand, Fig. 2F shows an AFM image of the position at which the line-shaped heat pattern was observed (Fig. 2A). It shows a wrinkle about 2 μm wide and 2 to 25 nm in height across the graphene sheet. The wrinkle consists of multiple graphene layers and probably was formed during the wet transfer process rather than the growth process (36). Because an additional D band was not observed in the spectral Raman mapping along the wrinkle (see fig. S2), there was no significant structural damage such as cracks or tears. Figure 2G shows the phase-dependent LIT amplitude images. In contrast to the case of the crack discussed above, the phase dependences were similar between the wrinkle (position 3) and the single-layer area (position 4; Fig. 2H). This suggests that the wrinkle acted as a heat source.

Correlation between LIT pattern and local resistances of polycrystalline graphene

We investigated the relationship between the observed LIT pattern and the local resistance distribution on the graphene sheet. Four-probe electrical measurements were performed in steps of 300 μm in the horizontal direction (along the two lines indicated by the schematic illustration in the inset of Fig. 3A). The crack (Fig. 2C) is on the upper line, and both lines pass through the wrinkles (Fig. 2F). The obtained local sheet resistances were plotted as a function of the sample position along the lines (Fig. 3A). The highest resistance (~740 ohms/sq) occurs around the crack location. The wrinkles induce slightly higher resistances (~670 ohms/sq) than in the neighboring area (~640 ohms/sq). Figure 3B shows the amplitude intensity profile of the LIT along the corresponding area (the white box in the inset). The highest peak position corresponds to the location just below the crack in which the current concentrated. The two relatively high peaks are at the positions of the wrinkle structures. These results show that the LIT pattern visualized the local defects of graphene associated with electrical transport through Joule heating (∝ I²R) (35).

Fig. 3. Correlation between thermal emission and electrical properties.

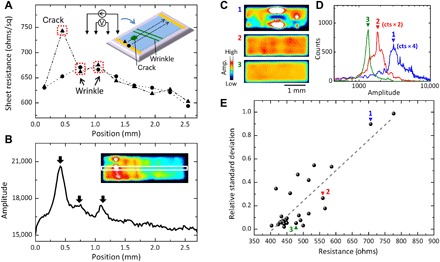
(A) Mapping result of local electrical resistance in sample A as measured by four-terminal probe method. The measurement setup and scanning area are schematically shown in the inset. The cross-sectional profile of the thermal amplitude is indicated in (B) for comparison. (C to E) Systematically investigated changes in thermal distribution properties versus resistance. The measurements were carried out under a constant current of 6 mA for all devices. All the LIT measurements were taken with a 10-min accumulation time. The dashed line in Fig. 3E is a guide to the eye.

To clarify the relationship between the inhomogeneity of the heat distribution in LIT and the electric resistance of the sample, we investigated 28 graphene devices. Figure 3C shows LIT images of three examples with different resistances. Resistances of 706, 560, and 478 ohms were obtained for devices 1, 2, and 3, respectively. Apparently, the heat distribution becomes more homogeneous as the resistance decreases. The histograms of signal amplitudes show that the peak position shifts toward larger amplitudes and the intensity increases as the electric resistance increases (Fig. 3D). Figure 3E exhibits the relative SDs (RSDs) of the amplitude distribution as a function of macroscopic sheet resistance. A positive correlation between the RSD and the resistance is visible, which strongly suggests that LIT directly observes the origin of the high resistance (defects) as a uniformity in the generated heat.

The above demonstrations show the advantages of the “lock-in” technique that efficiently detects the Joule heating while eliminating heat broadening. Thus, LIT can visualize local structures with a sufficient spatial resolution (2 to 3 μm; see fig. S8). It is a more precise form of imaging than any of the other tools available for characterizing the electrical properties of graphene over a large area, such as terahertz spectroscopy (25, 26) and conventional thermography (27–30).

LIT of epitaxially grown CVD graphene

Next, we focused on the effects of the DB on the LIT. The epitaxially grown CVD graphene was suited for that purpose because large domains can be synthesized by aligning the orientations of the individual domains (20, 24, 37). The domain size in our sample was estimated to be 50 to ~100 μm (fig. S3), i.e., much larger than the spatial resolution of LIT. The thermal radiation was examined by applying a bias at both ends of the continuous domains of graphene (Fig. 4A). Individual graphene domains and the boundary locations can be identified with an optical microscope (Fig. 4B). Figure 4C is a LIT image of graphene on the same spatial scale as the optical image. It reveals an inhomogeneous thermal distribution. Positions 1 and 2 show high amplitudes, while position 3 has a relatively low amplitude. Enlargements showing positions 1 and 2 reveal a line-shaped thermal pattern (arrows in Fig. 4D). By making a comparison with the optical image (Fig. 4B), it can be understood that this thermal pattern appears exactly along the boundary between adjacent domains. In contrast, position 3 shows a featureless thermal pattern, although this location also corresponds to a boundary. The cross-sectional analysis across the boundaries reveals the differences in thermal properties (Fig. 4E). Similar results were obtained for another continuous domain pattern, as shown in Fig. 4 (F to I). In this case as well, the highest thermal peak associated with a line-shaped structure at position 4 (Fig. 4H) was located at the DB.

Fig. 4. Thermal visualization of DB defects.

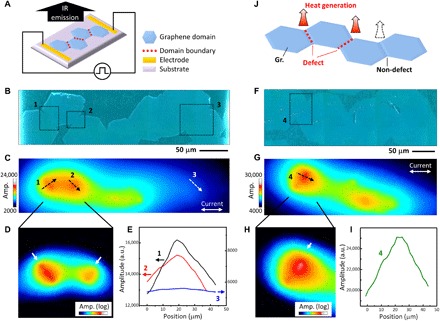
(A) Schematic diagram of measurement setup with multiple coalesced graphene domains and (B to E) experimental results. (B) Optical microscopy and (C) LIT images. (D) Expanded view on a logarithmic scale and (E) cross-sectional profile along the dashed arrows in Fig. 4C. (F to I) Results for another sample. All LIT images were obtained in 10 min. (J) Heat generation mechanism of DB.

To investigate the different heat generation behaviors at the DBs, we conducted micro-Raman mapping and SEM measurements (Fig. 5). At position 1 (Fig. 5A), intense D bands are visible along the boundary in the I_D/I_G image (middle panel). The right panel in Fig. 5A is an SEM image of the white dashed area in the Raman images. Several areas along the boundary (indicated by the arrows) show the same contrast as that of the quartz substrate, indicating an intermittently disconnected boundary (schematically illustrated in Fig. 6C). A clear D band line is also observed at position 2 (Fig. 5B). In the SEM image, on the other hand, there is a line showing dark contrast along the boundary. These are characteristic features of overlapping graphene between two domains (Fig. 6D) (22). Certainly, the AFM measurement indicated that the height of the line was less than 1 nm (fig. S6), which is consistent with the previous report on overlapping graphene (24).

Fig. 5. Spectroscopic and morphological characterization of graphene DBs.

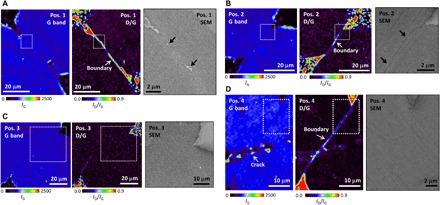
(A to D) Micro-Raman mapping and SEM images at positions 1 to 4 (Fig. 4, B and F). The locations in the SEM images correspond to the white dashed areas in the Raman images.

Fig. 6. LIT intensities at DB defects.

(A) Normalized peak intensity as a function of I_D/I_G ratio. Error bars correspond to 1σ, and the dotted line is a guide to the eye. The DB types are listed in (B) to (E).

Meanwhile, no D band feature can be seen in the micro-Raman mapping image at position 3 (Fig. 5C). This result suggests that the graphene domains were seamlessly stitched together (Fig. 6B), and this is confirmed by inspecting the SEM image (Fig. 5C, right). In contrast, at position 4, a significant D band line appears in the micro-Raman mapping image, while the SEM image does not show any information. This is a characteristic signature of an atomic-scale topological defect (20) (with a different lattice orientation; Fig. 6E), which may include pentagon and heptagon ring pairs (19) or vacancies (38).

Relationship between LIT intensity and DB defect of epitaxially grown CVD graphene

The observed structural features are quite consistent with the LIT pattern. Because heat is inevitably generated at electrical bottleneck sites, LIT can characterize even atomic-scale DB defects. Figure 6A shows the LIT amplitude at the DB defects as a function of the I_D/I_G ratio, where the LIT amplitudes were normalized by that at a clean graphene surface (P_DB/P_Gr). Because the current flowed almost orthogonally to the boundary in the present experiment, it is unlikely that the current value changed across the boundary. Consequently, we can say that P_DB/P_Gr reflects the ratio of the electrical resistance at the DB to that of a clean graphene surface (=R_DB/R_Gr) because the LIT amplitude can be explained by Joule heating (P ∝ I²R) (35).

Apparently, the height of the LIT peaks was positively correlated with the I_D/I_G ratio (dotted line in Fig. 6A). The areas showing less thermal radiation indicate seamless stitching of domains without the D band. On the other hand, disconnection (Fig. 6C), overlaps (Fig. 6D), and atomic disorder (Fig. 6E) increase the electric resistance and induce a corresponding amount of heat (Fig. 4J). In particular, a relatively large electric resistance was generated when there was a disconnection region.

Although electrical characterizations of DB defects have been carried out using STM (21, 23) and scanning Joule expansion microscopy (18), the long measurement time they require [typically several days (16)] limits their use in practice to areas on submicrometer scales. In contrast, LIT can image the electrical properties of DB defects over a large area (over a millimeter in size) within a reasonable time frame.

CONCLUSIONS

We successfully imaged local defects affecting the electrical transport properties of large graphene sheets by LIT. The observed heat resulted from increases in electrical resistance and current caused by local defects such as cracks, wrinkles, and DBs. The millimeter-sized graphene samples could be characterized by accumulating data for a few minutes. The present results indicate that the LIT is quite useful for fast and precise quality evaluations of large graphene devices in terms of their electrical uniformity and local defect detection. Furthermore, this method should be applicable to transition metal dichalcogenides such as MoS₂ (39) and WS₂ (40). LIT observations promise new findings in two-dimensional material devices.

MATERIALS AND METHODS

Sample fabrication

Polycrystalline CVD graphene

Commercially available thermal CVD graphene on copper foil was used. Because of the small domain size (4 to 5 μm), the DB defects cannot be spatially resolved using LIT (see section S1). After coating the as-grown graphene surface with poly(methyl methacrylate) (PMMA) (2% in anisole) layers, the copper foil was etched away with an ammonium persulfate aqueous solution. The resulting PMMA/graphene film was rinsed in deionized water and transferred onto a quartz substrate in deionized water. The PMMA layer was removed by immersing the sample in acetone after it had dried in ambient air at room temperature over 12 hours. To eliminate PMMA residue from the graphene surface, the sample was annealed at 300°C for 3 hours in an Ar/H₂ atmosphere (100 Pa).

The patterned graphene devices attached to electrodes were fabricated using a conventional semiconductor device fabrication process (i.e., photolithography, dry etching, and metal deposition). The graphene films were patterned with O₂ plasma, and electrodes (Ni/Au = 50/200 nm) were formed on them.

Epitaxially grown CVD graphene

The graphene was synthesized on a heteroepitaxial Cu film deposited on the α-Al₂O₃(0001) substrate. The CVD process was conducted at a high temperature (1075°C) and at a low CH₄ concentration (10 parts per million) under ambient pressure. The as-grown graphene was transferred onto a quartz substrate using PMMA, thermal tape, and an aqueous solution of FeCl₃ and HCl. After this transfer process, thermal annealing and device-related processing were performed in the same manner as that of the polycrystalline graphene sample.

LIT measurement

A thermal emission microscope (THEMOS-1000, Hamamatsu Photonics) was used. The instrument has two manual probes to apply a voltage to the sample. The current-voltage properties were measured with a semiconductor parameter analyzer (B1500, Keysight). During the LIT measurement, there was no change in the current-voltage curve, which meant that LIT provided the intrinsic properties of graphene without any damage due to the applied voltage. The pulsed bias was formed by a 25-Hz external trigger. Note that the trigger had a finite time delay to shutter timing of IR camera, and this caused the LIT phase image to have the wrong phase angle. To calibrate the time delay, we used a Cu wire sample with high electrical conductivity for reference. The phase angles after calibration were used in Fig. 2 (D, E, G, and H). In the LIT measurement, objective lenses with magnifications of ×0.8, ×4.0, and ×8.0 were selectively focused onto the sample surface, and the signal from the sample was detected by an InSb CCD detector with 640 × 512 pixels. The field of view corresponded to 12 mm × 9.6 mm, 2.4 mm × 1.9 mm, and 1.2 mm × 0.96 mm for magnifications of ×0.8, ×4.0, and ×8.0, respectively. The objective lenses used for Figs. 1, 2, 3, and 4 had magnifications of ×0.8, ×4.0, ×0.8, and ×8.0, respectively. The spatial resolution was estimated to be 2 to 3 μm regarding the detected IR wavelength (3 to 5 μm) and the numerical aperture (NA) of 0.75 (in the case of ×8.0 magnification). In the case of the ×0.8 and ×4.0 magnifications, the image resolution was not determined by the spatial resolution but by the pixel resolution. All LIT images in this study were taken over the course of 10 min in ambient air. Throughout this study, the LIT measurements were performed on samples on a low thermal conductivity quartz substrate (~1.5 W/m K). The LIT images taken from a sample on a Si substrate (without an oxide layer), which is usually used in graphene research, were unclear. This problem is mainly due to the relatively high thermal conductivity of silicon (140 to 160 W/m K). The effect of the substrate on the LIT measurements will be discussed elsewhere.

Micro-Raman mapping measurement

The micro-Raman mapping was carried out using a confocal microscope (inVia, Renishaw) equipped with a 532-nm laser excitation source. The laser, attenuated to about 0.5 mW, was focused on the sample surface with a ×50 objective lens with an NA of 0.75. The Raman signals from the sample were introduced to an electron-multiplying CCD detector (Andor) through a grating with 1800 grooves per millimeter. The step size of the measurements in Fig. 5 (A to C) was 0.7 μm and 0.6 μm in Fig. 5D. The CCD integration time was 0.5 s for all measurements. The Raman spectra were fitted using a Voigt function, and the Raman images were obtained by plotting the peak intensities of the fitting results.

AFM/SEM measurements

The AFM device (Nano Search, Shimadzu) was used, which combined optical and laser microscopes. All SEM measurements (using a Hitachi SU8220 microscope) were performed at an acceleration voltage of 2.0 kV and emission current of 10 μA. Magnifications of ×3000, ×6000, and ×7000 were used to acquire Fig. 5C, Fig. 5D, and Fig. 5 (A and B), respectively.

Four-terminal probe measurement

Four-terminal probe measurements were conducted with a probe pitch of 300 μm (NTT Advanced Technology). A constant current of 100 μA was applied at the ends of the probes. To change the measured voltage V into a sheet resistance R_sh, we used a standard calibration equation, ${\mathit{R}}_{\text{sh}}=\frac{\mathrm{\pi }}{\text{ln}2}\cdot \frac{\mathit{V}}{\mathit{I}}$. The scanning step of the x axis (y axis) corresponded to 300 μm (100 μm).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/2/eaau3407/DC1

Section S1. Characterization of polycrystalline graphene sheets

Section S2. Wrinkle in polycrystalline graphene

Section S3. Characterization of epitaxially grown graphene sheets

Section S4. Numerical simulation of Joule heat image of graphene sheets

Section S5. Structural characterization of DB

Section S6. Speed of LIT imaging

Section S7. Heat broadening of LIT measurement in graphene films

Section S8. Direction of defects in LIT measurement

Fig. S1. Optical microscopy image, Raman spectrum, and SEM image of polycrystalline graphene.

Fig. S2. Structural and optical characterization of wrinkle in polycrystalline graphene.

Fig. S3. Optical microscopy image of epitaxially grown graphene domains.

Fig. S4. Micro-Raman spectroscopy with epitaxially grown graphene.

Fig. S5. Simulation of Joule heat imaging.

Fig. S6. Structural analysis of overlapped boundary defect.

Fig. S7. LIT image dependence on data accumulation time.

Fig. S8. Cross-sectional analysis of thermal pattern of LIT.

Fig. S9. Effect of the direction of defects in LIT measurements.

Table S1. Fitting results of Raman spectrum with polycrystalline graphene.