Learning the space-time phase diagram of bacterial swarm expansion

Significance

Most living systems, from individual cells to tissues and swarms, display collective self-organization on length scales that are much larger than those of the individual units that drive this organization. A fundamental challenge is to understand how properties of microscopic components determine macroscopic, multicellular biological function. Our study connects intracellular physiology to macroscale collective behaviors during multicellular development, spanning five orders of magnitude in length and six orders of magnitude in time, using bacterial swarming as a model system. This work is enabled by a high-throughput adaptive microscopy technique, which we combined with genetics, machine learning, and mathematical modeling to reveal the phase diagram of bacterial swarming and that cell–cell interactions within each swarming phase are dominated by mechanical interactions.

Abstract

Coordinated dynamics of individual components in active matter are an essential aspect of life on all scales. Establishing a comprehensive, causal connection between intracellular, intercellular, and macroscopic behaviors has remained a major challenge due to limitations in data acquisition and analysis techniques suitable for multiscale dynamics. Here, we combine a high-throughput adaptive microscopy approach with machine learning, to identify key biological and physical mechanisms that determine distinct microscopic and macroscopic collective behavior phases which develop as Bacillus subtilis swarms expand over five orders of magnitude in space. Our experiments, continuum modeling, and particle-based simulations reveal that macroscopic swarm expansion is primarily driven by cellular growth kinetics, whereas the microscopic swarming motility phases are dominated by physical cell–cell interactions. These results provide a unified understanding of bacterial multiscale behavioral complexity in swarms.

Collective migration of flagellated cells across surfaces, termed swarming, is a fundamental bacterial behavior that facilitates range expansions and the exploration of nutrient patches, with profound implications for disease transmission, gene flow, and evolution (1–9). Due to its biomedical and ecological importance, bacterial swarming has been widely investigated in microbiology and biophysics as a model system for multicellular self-organization, development, motility, and active matter (10–27). Previous studies have revealed important physiological and biophysical factors that control particular aspects of the local swarming behavior, such as the differentiation into distinct cell types (28–35) and the role of osmolarity gradients and surfactant production in maintaining thin liquid films above the surface, through which the cells swim during swarming (36–43). However, the causal connection between the microscopic processes at the single-cell level and the macroscale swarm dynamics has yet to be established. Due to technical limitations, fast simultaneous data acquisition at microscopic and macroscopic scales has not been possible. Therefore, a complete characterization of the spatiotemporal swarming dynamics across multiple length and time scales has remained an unsolved challenge, fundamentally limiting the understanding of the links between molecular, physiological, and physical mechanisms that underlie collective bacterial migration. Here, we bridge the gap between gene expression, microscale, and macroscale dynamics by combining an adaptive high-speed microscopy technique with unsupervised machine learning and computational modeling to quantitatively identify the nonequilibrium dynamical phases of bacterial swarming and their spatiotemporal evolution. We then use this phase identification together with particle-based simulations to infer that physical cell–cell interactions are sufficient for describing the dynamics in all phases.

Results and Discussion

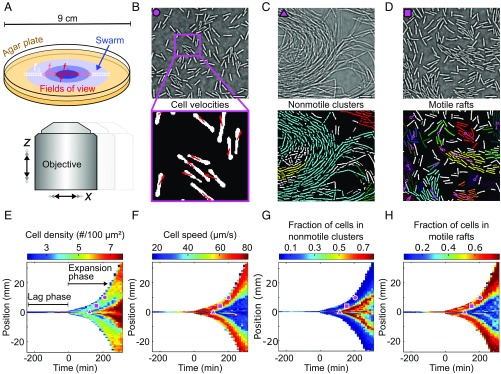
To track the swarming behavior of B. subtilis over five orders of magnitude in space at the single-cell level, we developed an adaptive microscope that acquires high-speed movies at times and locations determined by a live feedback between image feature recognition and an automated movement of the scanning area (Fig. 1A). This technique allows us to image a radially expanding swarm at single-cell resolution in space and time (Fig. 1), acquiring movies at a frame rate of 200 Hz over the 10-h duration of a single experiment. Movies were recorded along one line through the swarm (Fig. 1A), with the length of the line determined adaptively based on the swarm diameter (Materials and Methods). From each movie, we extracted the time-dependent positions, orientations, and velocities of all individual cells (Fig. 1B and SI Appendix, Fig. S1). To compress, analyze, and visualize this large amount of microscopic time-resolved data, we represent each movie by a list of statistical observables, which include single-cell parameters such as aspect ratio and motility, as well as emergent parameters that characterize the formation of nonmotile clusters and moving rafts (Fig. 1 C and D). The full list of 23 observables extracted at each space-time coordinate is described in Materials and Methods and SI Appendix, Table S4. The spatiotemporal evolution of these observables during swarming is visualized in heatmaps (Fig. 1 E–H and SI Appendix, Figs. S2–S6), where the color of each pixel is assigned according to an averaged statistical observable of a movie. In our online interactive data explorer (http://drescherlab.org/data/swarm/), the space-time heatmap coordinates are linked to the associated microscopic movies within the swarm, to allow for a direct inspection of the connection between microscopic and macroscopic dynamics.

Fig. 1.

Adaptive microscopy reveals complete multiscale dynamics of bacterial swarm expansion. (A) Movies at single-cell resolution are acquired at different locations in the swarm, starting from 1 cell to 100 cells, and follow swarm expansion until the agar plate is completely colonized. The number of movies and locations where movies are acquired (indicated by colored squares) are determined adaptively, depending on the detected swarm size. B–D, Top show qualitatively different bacterial behavioral dynamics observed at distinct space-time points, which are marked in E–H by corresponding magenta symbols. B–D, Bottom demonstrate automated extraction of single-cell positions, orientations, and cell velocities (B) as well as collective behaviors, such as formation of nonmotile clusters (C) and motile rafts (D), corresponding to groups of aligned cells that move in the same direction. Cells assigned to the same nonmotile cluster or motile raft by the classification algorithms share the same color; cells labeled in white have not been identified as belonging to any motile raft or nonmotile cluster. Magenta arrows in D indicate the average velocity of a raft. (Scale bars, 10 $\mathrm{\mu m}$.) (E) Heatmap of the cell density, obtained by averaging single-cell data as in B–D for each movie at each space-time coordinate. The lag phase, a period following inoculation during which the swarm does not expand, as well as the expansion phase, is indicated. (F–H) Additional heatmaps for the cell speed, fraction of cells that are in nonmotile clusters in a given field of view, and fraction of cells that are in motile rafts. A total of 23 statistical observables analogous to E–H were determined at each space-time position (Materials and Methods and SI Appendix, Table S4).

Transition from Initial Lag Phase to Swarm Expansion.

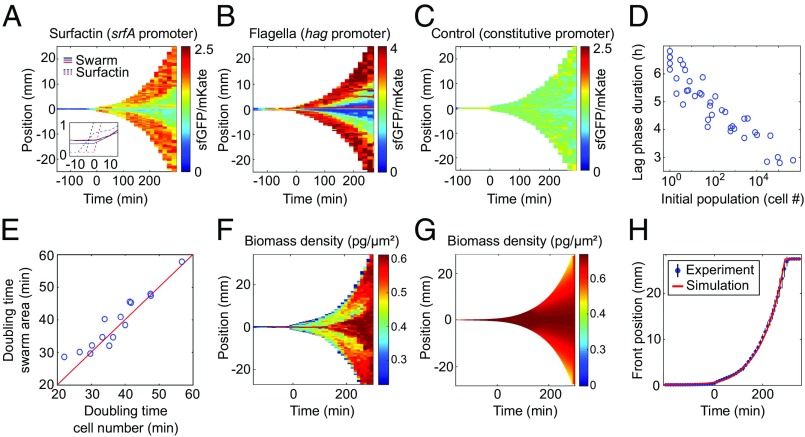
The swarming dynamics display striking macroscopic spatiotemporal patterns (Fig. 1 E–H): A long initial lag phase in which the swarm does not migrate outward for several hours (2) is followed by an abrupt transition to an exponential expansion phase, eventually resulting in the complete coverage of the 9-cm agar plate within 5 h (Fig. 1E). Previous investigations have shown that the production of a peptide-based surfactant, termed surfactin, is necessary, but not sufficient, for rapid swarm expansion of B. subtilis (29, 44, 45). To test whether srfA (surfactin synthase) expression coincides with the transition to the expansion phase, we constructed a sfGFP-based srfA transcriptional reporter, calibrated by a constitutively expressed mKate2 signal (SI Appendix, Fig. S7). By coupling our adaptive microscope control algorithms to a confocal microscope, we were able to measure spatiotemporal dynamics of fluorescent reporters during swarm expansion. Since the simultaneous acquisition of high-speed movies was technically not possible, the mechanical observables were recorded in a separate set of experiments that exhibited the same highly reproducible expansion dynamics. Using the adaptive confocal approach, we tracked gene transcriptional activity in space and time during all phases of swarm development (Fig. 2 A–C) and found a strong increase in surfactin production just before the expansion phase (Fig. 2A). Noting the 14-min maturation time of sfGFP (46), srfA expression likely starts earlier, yet a visible surfactin front appeared only directly before the expansion phase (Fig. 2A, Inset). Interestingly, flagellin transcription also strongly increased before the transition to the expansion phase, as indicated by the hag reporter (Fig. 2B), hinting that there might be an increase in flagellar density. This interpretation was supported by direct visualization of the flagella on cells, using electron microscopy (SI Appendix, Fig. S10), which revealed that the number of flagella per cell increases during the lag phase, consistent with findings of hyperflagellation as an essential phenotype for swarming (32, 47). Surfactin production is regulated by quorum sensing in B. subtilis (48), which is in agreement with our observations of a strong increase in cell density at the end of the lag phase (Fig. 1E) and that the duration of the lag phase is a logarithmic function of the seeding density (Fig. 2D) for the range of initial cell densities investigated in our study. However, it is important to note that the lag-phase duration is determined not only by the cell density, because a differentiation of the cells accompanied by the synthesis of additional flagella is necessary, which poses a lower limit to the minimal lag time (49, 50). Together with existing evidence (2, 28, 29, 32) our findings indicate that cell-density–dependent physiological changes, including surfactin and flagella production, drive the transition to the expansion phase.

Fig. 2.

Spatiotemporal gene-expression and macroscopic swarm expansion dynamics. (A) Heatmap of the srfA promoter fused to a green fluorescent protein (sfGFP), reporting transcriptional activity of surfactin production, normalized by constitutively expressed mKate2 fluorescence, in units of sfGFP levels per mKate2 levels. (A, Inset) A surfactin front becomes visible in phase-contrast microscopy just before the swarm expansion begins. (B) Fluorescence signal for the hag-promoter reporter, indicating that flagella production also increases (SI Appendix, Fig. S10) before expansion. (C) Control experiment in which sfGFP and mKate2 levels are driven by the same constitutively expressed promoter, showing no space-time variation in signal. (D) Lag-phase duration depends logarithmically on the initial seeding population size. (E) The average cellular doubling time per experiment correlates with the swarm area doubling time; the red line corresponds to exact equality of both time scales. (F–H) The experimentally determined biomass density (F) agrees with the predictions of the continuum model (G and H), indicating that growth pressure drives the exponential front expansion. The experiments in A–C and F displayed lag times of 5–5.5 h, yet the reporter results are shown only for times larger than −120 min, because at earlier times the fluorescent signals were too low to determine a reliable ratio of GFP/mKate levels.

Macroscopic Swarm Expansion Driven by Population Growth.

Although the swarm expansion phase dominates the macroscopic dynamics of swarming, there is no theory or mechanistic explanation for the expansion rate. By performing swarming experiments at different cellular growth rates, we found that despite the high cell speeds and collective movement in the form of cellular rafts inside parts of the swarm (Fig. 1 F and H), the swarm area doubling time is approximately equal to the cellular doubling time (Fig. 2E and SI Appendix, Fig. S8), consistent with the early observation of a correlation between growth and swarm rates (45). Our results show that while individual cell motility is necessary for swarming, the average cell speed in a swarm is not strongly correlated with the expansion rate (SI Appendix, Fig. S9), and the speeds of individual cells (20–80 μm/s) are more than an order of magnitude larger than the observed swarm front speed (0.6–5.6 μm/s). Although surfactin production and flagellar motility are necessary for swarming, our findings support the hypothesis that the cell growth rate is a factor that quantitatively determines the macroscopic swarm front expansion.

To test this hypothesis in more detail, we developed a 2D mathematical continuum model for the bacterial biomass density $\rho$. The model accounts for local population growth, cell motility, and global growth pressure through the spatiotemporal equation

$${\partial }_t\rho =\alpha \rho +\left(D_0+D_g{N}_e\left(t\right)\right){\nabla }^2\rho ,$$ [1]

where $\alpha$ represents the cellular biomass growth rate and the local diffusivity $D_0$ is due to the effect of swimming motility, which are both parameters that can be estimated directly from our data. The nonlocal $D_g$ term describes an additional cell transport caused by growth pressure, which is motivated as follows: The presence of surfactant above a critical cell density facilitates predominantly planar spreading on the agar surface, with cells pushing each other apart when dividing, rather than forming a vertical biofilm structure (4, 51–55). In the absence of surfactant, the fluid enclosing the swarm would prefer to minimize its surface area to reduce its surface energy at the liquid–air interface, favoring a curved droplet shape realizing approximately a spherical cap with a height significantly larger than the cell diameter. By contrast, consistent with earlier studies (1, 29, 56), our data show that the bacterial swarming dynamics take place in a thin fluid layer with the cells spreading across the agar surface forming a radially expanding 2D monolayer. This expansion arises from the combination of locomotion and biomass increase due to cell divisions and growth. In hydrodynamic models that include a velocity field in addition to the density field, the effect of population-growth pressure has been modeled by postulating an equation of state in which pressure increases exponentially with local density. In our reduced model, we describe this effect through the effective mean-field growth flux $-D_g{N}_e\left(t\right)\nabla \rho$, where $N_e$ denotes the excess population size above a critical local density when this additional cell movement occurs (SI Appendix). Analogous to an exponential equation state in hydrodynamic models, the growth flux prevents the local cell density from increasing beyond the physically permitted value of a single cell per cell area. The model is complemented by an effective slip condition for the front of the liquid-covered swarm (SI Appendix). Using fitted values for $D_g$ and the slip parameter, Eq. 1 yields good qualitative agreement with our data (Fig. 2 F–H). In particular, the model reproduces the experimentally observed lag phase and the exponential swarm front expansion quantitatively (Fig. 2H). The effective growth pressure term is essential for obtaining an exponential front expansion. Reduced models lacking the $D_g$ term or the $D_0$ term do not fit the experimental data, highlighting the importance of both growth kinetics and bacterial motility, with the latter serving to homogenize biomass density during swarm expansion.

Microscopic Swarming Dynamics and Space-Time Phase Diagram.

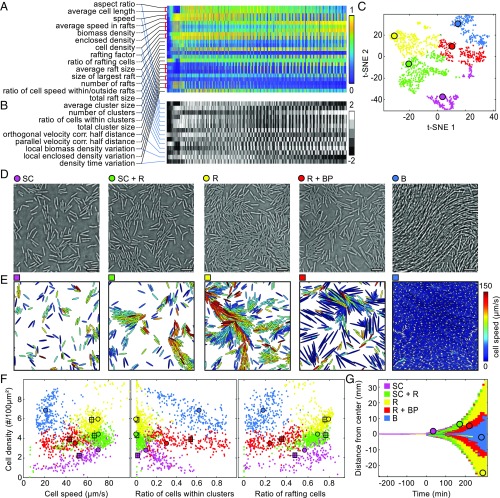
During the lag and expansion phase, the swarm shows remarkable behavioral complexity at the microscopic level at different points in space and time (Fig. 1 B–D). To identify and characterize the microscopic motility behaviors during swarming, and to understand the origins of the wide range of different behaviors that occur at different space-time points, we summarized the dynamics of statistical observables in heatmaps (Fig. 1 E–H). The strong spatiotemporal variation of each observable indicates the presence of different regimes of bacterial dynamical behaviors. However, some features of the motility behaviors remain hidden when only one or few observables are taken into account, and high-dimensional datasets with many observables that vary in space and time are intrinsically difficult to visualize (57). We therefore applied unsupervised machine learning to identify the dynamical phases from the full set of statistical observables in space and time. To avoid a bias resulting from double counting strongly correlated observables, we first determined their pairwise normalized mutual information. Discounting redundant observables reduced the total number of observables from 23 to 14 (Fig. 3A and SI Appendix, Fig. S11 and SI Text). To denoise and normalize the data, each of the remaining 14 observables was binned into five categories of equal size (Fig. 3B and SI Appendix, Fig. S12). After this preprocessing, we used t-stochastic neighborhood embedding (t-SNE) (58) to obtain 2D and 3D representations, followed by the application of k-means clustering to the t-SNE data (Fig. 3C and SI Appendix, Movie S1). We found that the resulting division into five clusters is robust under variations of target dimensionality and distance metrics used for t-SNE (SI Appendix, Figs. S13–S16 and SI Text). Across independent replicas of the swarming experiment (SI Appendix, Figs. S13–S16), we consistently observe three pure and two coexistence phases: a single-cell phase (SC) characterized by low cell densities and little collective behavior, a rafting phase (R) exhibiting high fractions of comoving cells, and a biofilm phase (B) where cells are organized in nonmotile structures reminiscent of liquid crystals (52); the coexistence phases are the mixture of single-cell and rafting behavior (SC + R), as well as the mixture of rafts and biofilm precursors (R + BP), which differ qualitatively (Fig. 3D) and quantitatively (Fig. 3 E and F) from the pure phases (SI Appendix, Movie S1). The phase classification also correlates with the spatiotemporal dynamics of the hag and srfA reporters, which were measured in independent experiments and did not contribute to the phase identification (SI Appendix, Fig. S17). The biofilm phase and the rafting phase are consistent with observations of chaining cells in the center of the swarm and rafting cells near its edge (29). Identifying factors that determine transitions between phases and the fate of individual cells, rafts, and nonmotile clusters during the swarming dynamics pose an important future challenge.

Fig. 3.

Machine learning the swarming phases from microscopic dynamics. (A) Raw data of one swarm expansion experiment, consisting of $\sim$1,500 space-time points (columns) in a 23-dimensional observation space (rows). Additional replicates are shown in SI Appendix, Fig. S11. Color bar indicates relative magnitudes scaled to [0,1]. In the case of strongly correlated observables with high normalized mutual information (marked by red brackets), only one of them is included in the machine-learning analysis. (B) The values of the 14 remaining observables (rows) were binned into five categories as indicated by the color bar, providing the input data for machine learning. (C) The 2D representation of the data in B, obtained with t-SNE; k-means clustering robustly identifies five main dynamical phases during swarm expansion across independent experiments (n = 3; SI Appendix, Figs. S13–S16 and SI Text). Phases are labeled with different colors. t-SNE coordinates highlighted as large circles for each phase correspond to experimental snapshots shown in D. (D) Typical images for the phases (SI Appendix, Movie S1) identified in C: low-density single-cell phase (SC); high-density rafting phase (R) with a high percentage of comoving cells; biofilm phase (B) characterized by long, unseparated cells; and coexistence phases that contain single cells and rafts (SC + R) or rafts and biofilm precursors (R + BP). (E) For each phase, simulations were run with the cell shape, motility, and density extracted from the particular phase as input parameters (SI Appendix, Movie S2 and SI Text). (Scale bars, 10 μm.) (F) Detailed quantitative comparisons between experiments (small circles), the particular experimental states shown in D (large circles), and simulations (squares; error bars are SDs, n = 20) yield good quantitative agreement, except for the B phase, confirming that physical effects determine the four motility-based swarming phases. (G) The emergence of the different phases in time and space during swarm expansion. Colored circles correspond to space-time coordinates of images from D.

Physical Cell–Cell Interactions Dominate During Swarming Phases.

The identification of the five phases of collective behavior in swarms simplifies our high-dimensional single-cell dataset to the point where we can now address the question of which cell–cell interaction mechanisms govern the dynamics within each phase and whether these phases can be explained in terms of common physical principles. To test whether physical forces can account for the dynamics within each behavioral phase and for the differences between phases, we performed individual-based active matter simulations, in which cells are modeled as elliptical particles moving in a 2D space with periodic boundaries. In these simulations, cells interact through physical contact, which is implemented by a repulsive interaction potential between cells, and through hydrodynamic interactions (SI Appendix) (22, 53, 59–63). The variable parameters for each simulation are the number of cells, their shape, and their motility, which are all directly extracted from the experimental data for each phase. The simulated dynamics are in good quantitative agreement with the experimentally determined phases (Fig. 3F and SI Appendix, Movie S2). Anticipated differences exist for the biofilm phase, as the ellipsoid model does not account for highly elongated and flexible cells, yet an extended model captures the qualitative dynamics (SI Appendix). Our numerical investigations showed that hydrodynamic interactions (SI Appendix, Figs. S18–S19) are not a dominant effect, but that steric interactions and motility suffice to explain the collective behavior among bacterial cells in our data and account for differences in distinct dynamical regimes (Fig. 3 D–F and SI Appendix, Fig. S20). A representation of the t-SNE phase diagram in terms of basic observables (Fig. 3F) confirms that the machine-learning approach successfully identifies the distinct dynamical phases. Finally, mapping the distinct phases back onto the space-time heatmap of swarm expansion reveals the complete dynamical phase evolution of bacterial swarming (Fig. 3G).

Conclusions

Building on an adaptive microscopy approach, the above results connect gene-expression and microscopic single-cell motility dynamics to macroscopic swarming dynamics, spanning five orders of magnitude in space and six orders of magnitude in time. Because cell proliferation and swarming are both far-from-equilibrium biophysical processes, the absence of fundamental conservation laws makes it difficult to identify and characterize qualitatively distinct dynamical phases with conventional equilibrium–thermodynamic approaches. To overcome this conceptual challenge, we combined experiments and particle-based active matter modeling with machine learning to identify and characterize the spatiotemporal evolution of three pure and two coexistence phases during swarm development. This integrated approach revealed that steric interactions and motility are sufficient for explaining the observed dynamics within each phase, which enables a unified conceptual understanding of the emergent multiscale behavioral complexity in swarms in terms of basic biophysical parameters. We expect that the combination of similar adaptive microscopy techniques and data-learning methods is a universal approach for bridging the gap in length and time scales between intracellular biochemical processes, single-cell dynamics, and tissue-scale morphogenesis and regeneration.

Materials and Methods

Data Availability.

Data are available at the online interactive data explorer tool created for this publication (drescherlab.org/data/swarm/).

Bacterial Strains and Media.

Escherichia coli and B. subtilis strains for normal propagation were grown in Luria–Bertani (LB) liquid medium or on 1.5% LB agar plates. When appropriate, media were supplemented with the following antibiotics: ampicillin (100 μg/mL), erythromycin (1 μg/mL and 150 μg/mL for B. subtilis and E. coli, respectively), and spectinomycin (100 μg/mL). For standard B. subtilis transformation, competent cells were prepared as described earlier (64). B. subtilis strains used in this study were derived from B. subtilis strain NCIB3610 and are listed in SI Appendix, Table S1. For genetic modifications in B. subtilis, we used a $\mathrm{\Delta }$comI derivative of strain NCIB3610 (65).

Additional details of experiments and data analysis methods are described in SI Appendix, SI Text.