Biohybrid valveless pump-bot powered by engineered skeletal muscle

Significance

Engineered living systems is a rapidly emerging field where functional biohybrid machines are built by integration of cells or tissues with engineered scaffolds for countless technological applications. Here, we present a biohybrid pumping machine or “pump-bot,” capable of generating unidirectional flow powered by engineered skeletal muscle tissue. It utilizes a bioinspired mechanism for valveless pumping and can achieve flow rates that are at least three orders of magnitude higher than previously reported biohybrid pumps. The proposed design offers several merits, including flexibility of material choices, ease of fabrication, robustness, and ability to operate without the need for valves, blades, or other moving parts. This biological pumping system can have broad utility and impact in tissue engineering, microfluidics, and biomedical devices.

Abstract

Pumps are critical life-sustaining components for all animals. At the earliest stages of life, the tubular embryonic heart works as a valveless pump capable of generating unidirectional blood flow. Inspired by this elementary pump, we developed an example of a biohybrid valveless pump-bot powered by engineered skeletal muscle. Our pump-bot consists of a soft hydrogel tube connected at both ends to a stiffer polydimethylsiloxane (PDMS) scaffold, creating an impedance mismatch. A contractile muscle ring wraps around the hydrogel tube at an off-center location, squeezing the tube with or without buckling it locally. Cyclic muscle contractions, spontaneous or electrically stimulated, further squeeze the tube, resulting in elastic waves that propagate along the soft tube and get reflected back at the soft/stiff tube boundaries. Asymmetric placement of muscle ring results in a time delay between the wave arrivals, thus establishing a net unidirectional fluid flow irrespective of whether the tube is buckled or not. Flow rates of up to 22.5 μL/min are achieved by the present pump-bot, which are at least three orders of magnitude higher than those from cardiomyocyte-powered valve pumps of similar size. Owning to its simple geometry, robustness, ease of fabrication, and high pumping performance, our pump-bot is particularly well-suited for a wide range of biomedical applications in microfluidics, drug delivery, biomedical devices, cardiovascular pumping system, and more.

The heart is the first functional organ to emerge in vertebrate embryos. At its earliest stage of development, the tubular embryonic heart begins pumping blood through a simple vascular network before the formation of valves or chambers (1). The pumping mechanism results from an impedance mismatch that establishes unidirectional blood flow by means of wave propagation and reflection in the heart tube (2). Inspired by this phenomenon, a variety of abiotic valveless impedance pumps (3–6) have recently been developed and studied due to their potential value for biomedical applications and their beneficial characteristics, such as simple geometry, ease of fabrication, and lack of moving parts. However, these artificial pumps driven by solid-state actuators have clear limitations, such as poor miniaturization ability (7), cumbersome actuation systems (8), or high driving voltage (9). Furthermore, they are not biocompatible and not able to sense and adapt to environmental cues and applied stimuli, which greatly limit their suitability for biomedical applications (10).

Recently, biohybrid living machines consisting of living cells integrated with flexible engineered scaffolds have shown promising outcomes for achieving a multitude of complex functions, such as sensing, processing, and responding to environmental cues in real time (11–18). In addition, these biohybrid machines can be stimulated noninvasively by electrical, optical, or chemical signals, without the need for large-scale external driving systems, which makes them favorable for biomedical applications (10). Some of the promising examples are biohybrid pumps (19–21) that generate unidirectional flow in a microfluidic system as a result of cyclical muscle contraction. Tanaka et al. (19) developed a diaphragm pump using a 2D cardiomyocyte sheet as the actuator to pump fluid through a microsystem, consisting of a microchannel equipped with a check valve layer and a push-bar structure. Park et al. (20) fabricated a biohybrid nozzle/diffuser pump, using a thin cell-polymer membrane as a diaphragm to drive unidirectional flow in a microfluidic channel. Although these examples demonstrate feasibility, such systems are often plagued by complicated fabrication procedures (with valves or diffusers) and low pumping performance (flow rates in the nL/min range). Their reliance on spontaneous contractility of cardiac muscle further limits the potential of these pumps due to the difficulty to control them. In contrast, skeletal muscle allows for more precise control via external stimulation and can also interface with multiple other cell types such as neurons and endothelial cells, making it an ideal platform for developing more complex biological machines (13).

In this paper, we present a simple design of a biohybrid valveless pump-bot powered by “living” engineered skeletal muscle with either spontaneous contraction or electrical stimulation. This pump-bot is comprised of a soft hydrogel tube connected to stiffer polydimethylsiloxane (PDMS) channels at both ends, with an engineered muscle ring wrapping around the hydrogel tube at an off-center position. The pump-bot platform and hydrogel tubes are fabricated using simple casting scaffolds. Muscle rings are formed by differentiating a mouse myoblast cell line (C2C12). Cyclic muscle contraction develops a series of elastic waves which propagate along the hydrogel tube and reflect from the PDMS/hydrogel junction due to the impedance discontinuity. This dynamic wave interaction results in a time-averaged pressure gradient driving a net unidirectional flow. This biohybrid valveless pump is capable of generating unidirectional flow as high as 22.5 μL/min. Due to its simple design, ease of fabrication, and high pumping performance, our pump-bot is suitable for many biological applications.

Results

Impedance Pumping Mechanism.

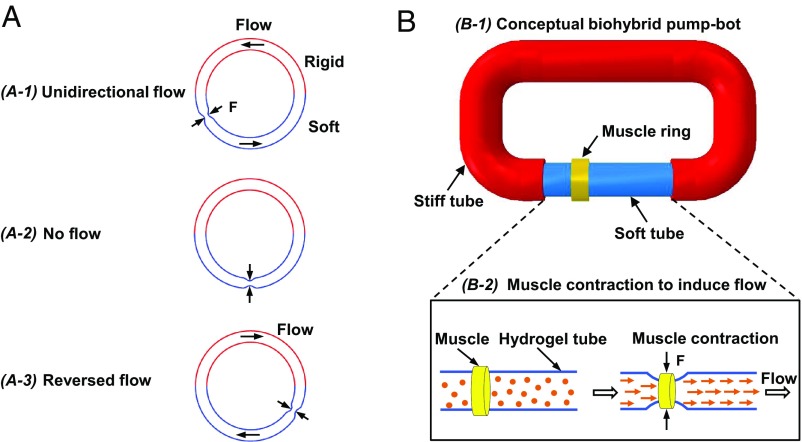
A valveless impedance pump is realized by using a fluid-filled flexible tube, connected at its ends to an inelastic tubing with higher impedance. Here, impedance is the resistance to transmission of a wave propagating along the tube and is dependent on the frequency components or spectral composition of the wave being transmitted (22). By complete or partial pinching of the flexible tube periodically at an off-center position, a complex series of propagating waves is developed. These waves travel along the tube and get reflected back at the junctions between two tubes with different impedances. As a result of these wave dynamics, a time-averaged pressure gradient is established between the two ends of the flexible tube, generating a net flow (3–6). A schematic of the impedance pump is shown in Fig. 1A, in which the soft tube is connected to a rigid tube to form a closed flow loop. Rhythmic compression of the soft tube at an asymmetric location generates net flow from the shorter toward the longer passive portion of the flexible tube (Fig. 1, A-1 and A-3). Note that rhythmic compression at the mid-length (point of symmetry) does not generate unidirectional flow (Fig. 1, A-2).

Fig. 1.

Concept design of a biohybrid valveless pump-bot. (A) Closed-loop tube filled with liquid, consisting of a soft tube (blue) connected to a rigid tube (red). Periodic compression (black arrows) at an asymmetric site of the soft tube section generates unidirectional flow (A-1), while at the symmetric site, no flow is generated (A-2). The flow direction reverses when the compression site nears the other end (A-3). (B) Proposed biohybrid pump-bot, consisting of a flexible soft tube connected to a rigid tube and a skeletal muscle ring wrapping around the soft tube at an off-center position (B-1). Muscle contraction along the circumferential direction compresses the hydrogel tube in the radial direction which drives a unidirectional flow (B-2).

Inspired by this unique pumping mechanism, we propose a conceptual design of a biohybrid valveless pump-bot capable of generating unidirectional flow powered by engineered skeletal muscle (Fig. 1, B-1). In addition to the muscle driving excitation, the two requirements for the proposed biohybrid valveless pumping system are the presence of impedance mismatch and the location for asymmetric excitation. Coupling a soft tube to a stiffer tube creates an impedance mismatch and therefore a site for wave reflection. An engineered muscle ring is placed on top of the soft tube at an off-center position (Fig. 1, B-2, Left). The muscle contraction along the circumferential direction induces radial compression of the soft tube, which results in a net unidirectional flow (Fig. 1, B-2, Right).

Design and Fabrication of Pump-Bot.

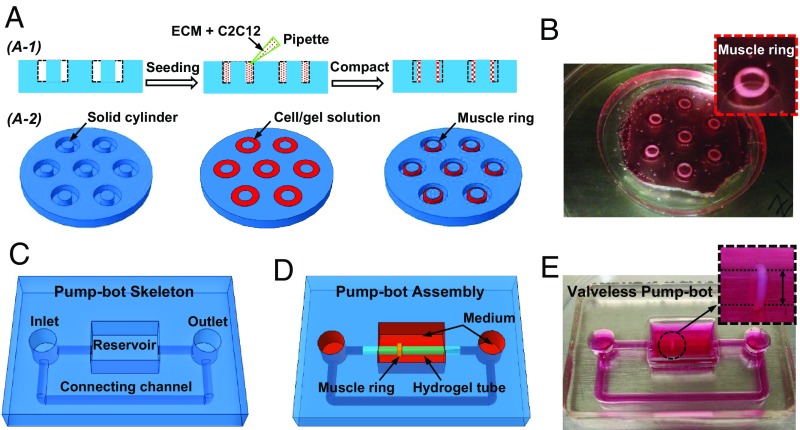
Muscle rings are formed by seeding cells and ECM mixture onto circular PDMS molds with 12-mm outer diameter, 5- or 6-mm inner diameter, and 3-mm depth (SI Appendix, Fig. S1 A and B). C2C12 mouse skeletal myoblasts are suspended at a density of 2.5 × 10⁶ cells/mL in a reconstituted ECM mixture of type I collagen and Matrigel at 2 mg/mL each and seeded into the PDMS mold (Fig. 2A). The suspended cells compact the fibrous matrix (23) around the solid cylinder into a 3D muscle ring over time (Fig. 2B). Thin PDMS caps with 12-mm diameter and 0.5-mm thickness are partly glued atop the mold to prevent the muscle rings from escaping from the mold (Fig. 2B and SI Appendix, Fig. S1 C and D). After polymerization of the ECM solution, the entire system is filled with culture medium.

Fig. 2.

Design and fabrication of a biohybrid valveless pump-bot. (A) Schematic illustration of the fabrication process for muscle ring from 2D cross-sectional view (A-1) and 3D titled top view (A-2). (B) Optical image of prepared muscle rings in the cell culture media. The Inset highlights one muscle ring in the PDMS mold with a thin cap covered partly on the top (magnification: 3×). (C) Schematic illustration of pump-bot skeleton including reservoirs for keeping cell culture media and round channels connected to the hydrogel tube. (D) Schematic of the assembly process of the pump-bot by inserting the hydrogel tube into the round PDMS channels with a muscle ring wrapping around the tube at an off-center location. (E) Optical image of the pump-bot after in muscle differentiation media (magnification: Inset, 4×).

To construct the pump-bot, we first machine an aluminum mold to serve as the template for casting PDMS base (SI Appendix, Fig. S2). PDMS precursor and cross-linker are mixed at 10:1 ratio by weight, poured onto the aluminum mold, and then cured at 60 °C for 12 h. After separating from the aluminum mold (SI Appendix, Fig. S2A), the PDMS base structure consists of a reservoir for keeping cell culture medium, inlet and outlet, and one connecting channel to form a closed flow loop (Fig. 2C and SI Appendix, Fig. S2B). Separately, soft hydrogel tubes are fabricated by adding precursor solution of acrylamide and N,N′-methylenebisacrylamide into the glass tube mold (SI Appendix, Fig. S3). The elastic modulus of resulting hydrogel tube is around 10 KPa (SI Appendix, Fig. S4). After 2 d of incubation, the muscle ring is transferred onto the hydrogel tube. Next, the hydrogel tube-muscle ring is inserted into the PDMS round channels to complete the pump-bot (Fig. 2 D and E). After assembly, pump-bots are incubated in muscle differentiation medium to induce formation of contractile myotubes within the muscle ring.

The muscle ring with myotubes applies a contractile force, T, on the elastic hydrogel tube as a taut rubber band on a tube segment (SI Appendix, Fig. S5). T may be large enough to buckle the tube. Buckling might be facilitated by nonuniformity of the muscle force and geometry and/or the nonuniformity of the tube thickness along the circumferential direction. A buckled hydrogel tube (SI Appendix, Fig. S6B) shows folding or crease when viewed transversely (see Fig. 5 A–C). Also, the apparent diameter of the tube decreases significantly after buckling (see Fig. 5B). An unbuckled tube maintains circular geometry (SI Appendix, Fig. S6A), but the diameter decreases elastically due to muscle contraction. The tube offers elastic restoring force against muscle contraction, which is expected to be significantly lower for the buckled tube compared with that due to the unbuckled one. For the former, the restoring force originates from bending of the thin tube wall (compared with radius), whereas for the latter, from the circumferential contraction. The force scales as (t/R)³ for bending and as (t/R) for circumferential contraction, where t is the thickness of the tube wall and R is the radius. Since t/R is ∼0.1, buckled tubes offer negligible resistance to muscle contraction compared with the unbuckled tubes.

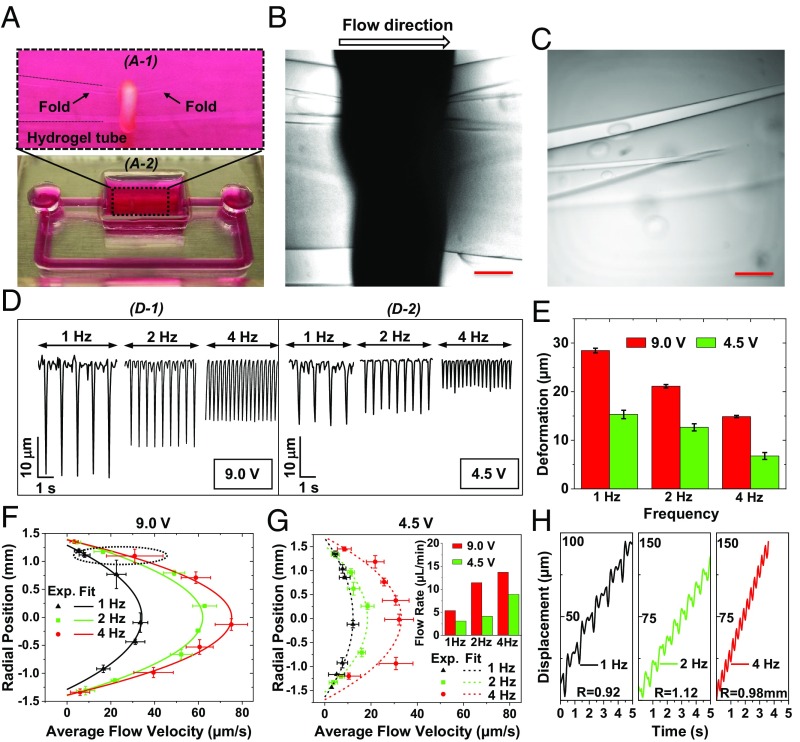
Fig. 5.

Pump-bot performance when the hydrogel is buckled. (A) Optical image of the pump-bot (magnification: Top, 4.5×). (B) Phase-contrast image of the muscle ring wrapping around the folded hydrogel tube. (C) Optical image of the fold or crease in the hydrogel tube. (D) Time-varying deformation of hydrogel tube induced by muscle rings at electrical stimulation frequencies with the voltage of 9 V (D-1) and 4.5 V (D-2), respectively. (E) The tube deformation measured close to the muscle ring at the electrical stimulations. (F) Flow patterns along cross-section of hydrogel tube in the middle at electrical stimulation voltage of 9 V. (G) Flow patterns at electrical stimulation voltage of 4.5 V. (H) Flow velocities at 0.92, 1.10, and 0.98 mm away from tube center (dotted region in F) at 1, 2, and 4 Hz with the voltage of 9 V. (Scale bar, 500 μm.)

Muscle rings typically twitch spontaneously after about 7 d in myogenic differentiation media. This results in a cyclic squeezing of the hydrogel tube, with or without buckling. After several (∼14) days, twitching subsides and muscle reaches a steady contractile state. The ring can then be stimulated to contract more by applying cyclic electric field. Since the elastic restoring force of the buckled tube is low, the muscle can contract as a free ring. Hence, the muscle contraction due to cyclic electrical field is expected to be larger and frequency dependent for the buckled tube compared with that due to unbuckled tube. In the following, we present three cases of pumping. They are due to a self-twitching muscle and electrically stimulated muscles with unbuckled and buckled tubes.

Net Flow Generated by Spontaneous Muscle Twitching.

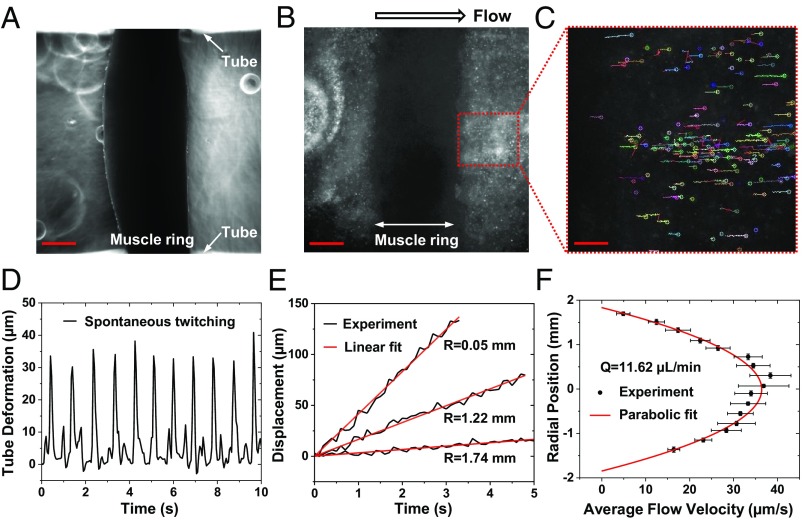
Fig. 3A shows a twitching muscle ring wrapping around the hydrogel tube (Movie S1), where the arrows show the inner surface of the tube. The images are acquired by focusing at the mid-plane of the tube. The pump-bot skeleton and the hydrogel tube are filled with muscle differentiation medium. To visualize the fluid flow, fluorescent beads of 1 μm in diameter are added to the closed flow loop (Fig. 3B). As the muscle twitches, unidirectional net flow is observed indicated by the motion of the fluorescent beads (Movie S2). Fluid flow rates are measured by tracking the trajectories of fluorescent beads, which indicate the net unidirectional flow direction (Fig. 3C and Movie S3). After 14 d, spontaneous muscle twitching diminishes, and no unidirectional flow is observed (Movie S4).

Fig. 3.

Unidirectional flow generated by spontaneous muscle twitching. (A) Phase-contrast image of a muscle ring wrapping around the hydrogel tube, with the white arrows indicating the inner surface of hydrogel tube. (B) Fluorescent images of beads inside the hydrogel tube, tracking unidirectional flow. (C) Trajectories of all detected particles (dotted region in B) in the flow. (D) The dynamic deformation of hydrogel tube induced by muscle spontaneous twitching. (E) Resultant flow velocity at three radial positions of 0.05, 1.22, and 1.74 mm from the center, i.e., the middle, in between and close to the edge of the cross section. (F) Flow pattern along the cross-section of hydrogel tube with a net flow rate of 11.62 µL/min based on the parabolic profile. (Scale bars: A and B, 500 μm; and C, 150 μm.)

Tube deformation caused by muscle twitching is measured by image processing. Spontaneous muscle twitching with ∼1.33-Hz frequency induced an average tube wall displacement of around 35 µm at the diametric plane of the tube (Fig. 3D). Trajectories of beads from three different radial positions are demonstrated in Fig. 3E. Linear fitting gives the average velocity as a function of radial position with the maximum average velocity of 39.9 µm/s at the tube axis. The time-mean flow profile over the cross section is parabolic (Fig. 3F), which gives a net flow rate $Q=\pi r^2\overline{V}=11.62$ $\text{μl/min}$, where $\overline{V}$ is the average flow velocity along the tube cross-section. For this pump-bot, the Reynolds number is $\mathrm{Re}=\rho \overline{V}d/\mu =0.08$, where ρ is the fluid density, μ the dynamic viscosity of culture medium, and $d$ the inner diameter of hydrogel tube (see SI Appendix, Supplementary Information Text and Table S1 for detailed parameters). The low Reynolds number implies a laminar, viscous-dominated flow with negligible influence of inertial forces, consistent with the parabolic (average) velocity distribution across the cross section.

However, the flow fluctuates periodically with muscle contraction cycles (Fig. 3E and Movie S3). This results in high instantaneous velocity during the power stroke of the muscle contraction. Velocity reverses sign as muscle returns to rest. Such unsteadiness may lead to inertial effects, causing the average flow to deviate from the parabolic distribution. A measure of the importance of these effects can be estimated from the ratio of inertial to viscous forces given by the Womersley number, $\alpha =\frac{d}{2}\sqrt{\rho \omega /\mu }=5.87$, where $\omega =2\pi f$ is the cycle frequency in radians per second. Flow deviates from a parabolic velocity distribution as the Womersley number $\alpha$ approaches to 10 (24, 25). The low value of $\alpha =5.87$ in our experiment is consistent with the observed parabolic velocity distribution. (see parameter list in SI Appendix, Table S1).

Net Flow Generated by Electrical Stimulations.

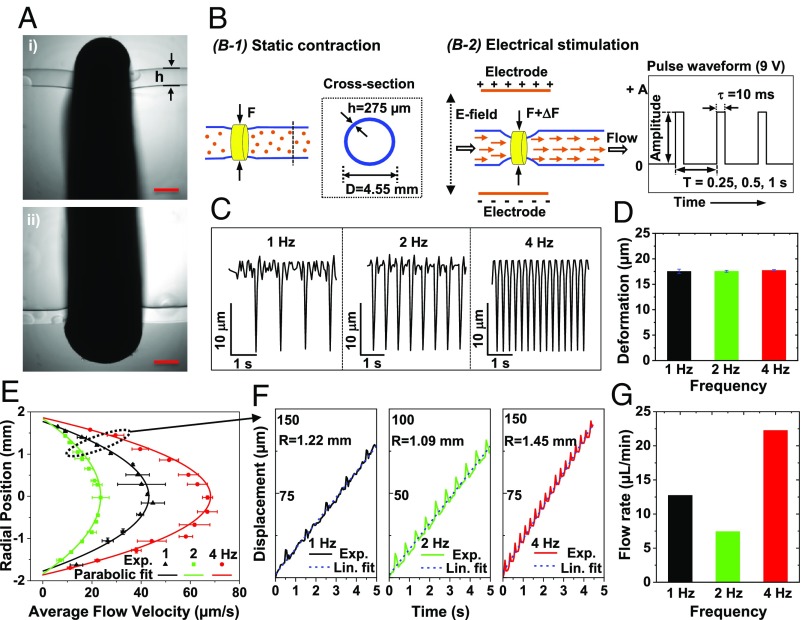
To externally control muscle contraction, we use a custom designed setup (SI Appendix, Fig. S7) that stimulates contraction of excitable cells within the muscle ring at frequencies of 1, 2, and 4 Hz. Electric field is applied by delivering 9-V pulses with 10-ms pulse width, across two wire electrodes positioned 20 mm apart (Fig. 4B). Here, the stimulation results in a coordinated contraction of multiple myotubes within the muscle ring, which collectively generate sufficient force to deform the hydrogel tube and drive fluid flow.

Fig. 4.

Unidirectional flow generated by electrical stimulations. (A) Phase-contrast image of a muscle ring wrapping around the hydrogel tube. (Scale bar, 500 μm.) (B) Schematic illustration of tube deformation under static muscle contraction (B-1) and electrical stimulations (B-2). (C) Time-varying deformation of hydrogel tube compressed by muscle rings at electrical stimulation frequencies of 1, 2, and 4 Hz. (D) Maximum tube deformation (reduction in diameter) at electrical stimulation frequencies of 1, 2, and 4 Hz. (E) Flow patterns along the diameter of the tube at midsection due to electrical stimulation frequencies of 1, 2, and 4 Hz. (F) Position–time curves of florescent beads at 1.22, 1.10, and 1.45 mm away from tube center (dotted region in E) at 1, 2, and 4 Hz. (G) Net flow rates computed from velocity profiles at 1, 2, and 4 Hz.

We choose a pump-bot that does not show any folding or crease in the tube when viewed transversely (Fig. 4A). The outer diameter and wall thickness of the tube are 4.55 and 0.275 mm, respectively. The dimeter reduces by about 60 µm due to static contraction of the muscle ring with the width of about 1.5 mm (Fig. 4A and Fig. 4, B-1). Muscle contractions induced by electrical stimulation produced a decrease in tube diameter by ∼17.5 µm for all stimulation frequencies of 1, 2, and 4 Hz (Fig. 4 C and D). We expect that the tube does not buckle. To verify, we choose a different tube with similar geometry and with a muscle ring that also does not show any folding or crease. We sever the tube about 5 mm away from the muscle ring on both sides. We then mount the tube vertically using a glass rod, 1 mm in diameter, to take a cross sectional image of the muscle and the tube (SI Appendix, Fig. S6A). The tube is not buckled even with the electrical stimulation (Movie S5).

Electrical stimulation of the muscle ring results in a parabolic flow velocity across the cross-section for all applied frequencies (Fig. 4E). The trajectories of fluorescent beads have linear position-time curves on the average, indicating the constant cycle-averaged axial velocity (Fig. 4F). Furthermore, average flow velocities as well as flow rate are nonlinearly related with frequency (Fig. 4G), a typical characteristic of impedance pumping systems (2–6, 22). For example, the stimulation at 1 Hz causes a larger bulk flow than that at 2 Hz. However, the higher flow at 1 Hz stimulation might be induced by self-twitching of the muscle ring between electrical stimulations (SI Appendix, Fig. S8 and Movie S6). The flow rates obtained by this pump-bot are 12.60, 8.28, and 22.68 µL/min for 1, 2, and 4 Hz stimulations, respectively. Reynolds and Womersley numbers for this pump-bot can be found in SI Appendix, Table S1.

Folded Hydrogel Tube as a Pump.

We then choose a pump-bot where the tube shows significant reduction in diameter and crease when imaged transversely (Fig. 5 A–C). Here the soft tube is 4 mm in outer diameter. It reduces to about 2.3 mm due to muscle contraction. The muscle ring is formed using a mold with inner diameter of 5 mm (as opposed to 6 mm for the previous pump-bot) (SI Appendix, Fig. S1B). The tube is thus expected to be buckled. To verify, we again choose a different tube with a muscle ring that shows the two signatures of buckling, i.e., significant reduction of diameter and crease. We sever the tube to about 1 cm in length with muscle ring at the middle. We mount the tube vertically using a 1-mm glass rod. The cross-sectional image clearly shows buckling of the tube (SI Appendix, Fig. S6B and Movie S7), similar to the buckling of the rubber tube by the taut rubber band (SI Appendix, Fig. S5C).

With the application of electrical stimulation on the pump-bot, the buckled tube area decreases in a pulsatile fashion which generates a flow. We again measure the wall deformation of the tube due to muscle contractions. However, this change cannot be considered as the change in diameter as the tube cross section is not circular. We again add florescent beads into the hydrogel tube (Movie S8) and apply electrical stimulations of 1, 2, or 4 Hz with amplitudes of 9 and 4.5 V. We find that the deformation of hydrogel tube decreases with increasing stimulation frequency (Fig. 5, D-1). Tube deformation decreases by 50% when voltage decreases from 9 to 4.5 V for all applied frequencies (Fig. 5, D-2 and Fig. 5E). The flow pattern is parabolic at all frequencies, showing the viscous-dominated flow (Fig. 5F). With 9-V stimulation, the maximum flow velocity at frequencies of 1, 2, and 4 Hz are 34.4, 59.5, and 71.6 μm/s, respectively. Decreasing the voltage amplitude to 4.5 V reduced the maximum flow velocity to 13.84, 20.27, and 31.89 μm/s at frequencies of 1, 2, and 4 Hz (Fig. 5G). As in case of the unbuckled tube, flow velocity at any point fluctuates with time, in synchrony with the applied cyclic stimulations (Movie S9). We determine the time-averaged velocities to estimate the flow (Fig. 5H). The net flow rates for all cases are given in SI Appendix, Table S1.

Discussion

We present three examples of pump-bots, one with spontaneously twitching muscle ring and the other two electrically stimulated. The self-twitching ring and one of the stimulated rings are formed by 6-mm-diameter mold. The third ring has 5-mm mold. In all cases, the tubes are first folded or collapsed to slide the muscle ring to the prescribed location. The tubes are then filled with cell culture media, when they unfold elastically against muscle force, reaching an equilibrium state. In case of the self-twitching ring, the muscle relaxes periodically from the contractile state (Fig. 3D and Movie S1). During these bursts of partial relaxation, the tube diameter increases periodically. This results in a periodic area change of the tube and a corresponding net flow of fluid. In case of the stimulated ring from 6-mm mold, we did not observe any signs of buckling of the tube, i.e., no crease or significant reduction of diameter. With electrical stimulation, the muscle ring contracts periodically without buckling the tube. We verified by imaging the cross-section of a similar tube and applying similar electric field stimulation (SI Appendix, Fig. S6A and Movie S5).

We then studied a pump-bot where the muscle contraction buckles the hydrogel tube. Buckling is verified by imaging the cross section of a similar tube with a muscle ring (SI Appendix, Fig. S6B and Movie S7). At the buckled state, the restoring force of the tube against muscle contraction is expected to be low compared with the unbuckled tube with circular section. Hence, the muscle ring can contract much more upon electrical stimulation compared with that of the unbuckled tube. However, due to viscoelasticity of the muscle, it needs time to relax after electrical stimulation is turned off. Hence, if the stimulation frequency is high and an electrical pulse arrives during relaxation, the cyclic contraction amplitude decreases giving rise to frequency dependence of contraction amplitude. The higher the frequency, the lower is the amplitude of cyclic contraction (Fig. 5 D and E). For the unbuckled case, restoring force of the elastic tube is high compared with the buckled tube, and cyclic contraction amplitude is less sensitive to frequency. Thus, for the unbuckled tube, the contraction at all three frequencies is the similar, about 17 µm (Fig. 4 C and D). Irrespective of whether the soft tube is buckled or not, muscle-actuated impedance pump generates a net flow, and the flow rates are comparable for similar sized tube diameter. This robustness is a unique attribute of the pump-bot.

To summarize, we present a biohybrid valveless pump-bot with the ability to transport flow through a synthetic conduit, powered by skeletal muscle in a spontaneous or electric-responsive manner. Such pump-bot utilizes bioinspired pumping mechanism based on wave propagation and reflection along the hydrogel tube. This wave-based pumping mechanism offers several unique advantages, including a wide variety of materials’ choice, simplicity of design, and ease of fabrication and robustness. In addition, there are no moving parts required, which enables our biohybrid pump-bots more suitable for implantable devices. Furthermore, skeletal muscle can be actuated by electrical stimulation, or light, and can also interface with multiple other mammalian cell types, such as neurons and endothelial cells (26, 27). The study thus provides a foundation for developing a class of smart biological pumping machines by hybridizing soft materials and engineered living tissue.

Materials and Methods

Fabrication of Muscle Ring Mold.

PDMS is prepared by thoroughly mixing silicone elastomer and curing agent (Sylgard 184; Dow Corning) with a weight ratio of 10:1. The mixture is then degassed in a vacuum desiccator for a period of 30 min to remove any trapped air bubbles. After degassing, the mixture is then cured in an oven at 60 °C for 12 h (12). A circular punch of 12-mm diameter is used to make holes on a PDMS sheet of 3-mm thickness; 5- or 6-mm-diameter punches are used to make solid cylinders from the same 3-mm-thick PDMS sheet. These parts are then glued on top of another flat PDMS substrate using uncured liquid PDMS, with the solid cylinders positioned at the center of the 12-mm diameter holes. Upon complete curing, the PDMS mold is cleaned by first sonicating in ethanol for 20 min and then autoclaving at 121 °C for 45 min while immersed in deionized water. The mold is then blow dried and sterilized by autoclaving at 121 °C for another 45 min with 30-min drying time.

Cell Culture.

C2C12 mouse skeletal myoblasts are maintained until 60–80% confluency in growth medium consisting of DMEM (Corning), supplemented with 10% FBS (Gibco), and 1× penicillin-streptomycin (Corning) (13). To facilitate myotube formation by C2C12 myoblasts, they are cultured in muscle differentiation medium consisting of high-glucose DMEM supplemented with 10% vol/vol horse serum and 2 mM l-glutamine (all from Gibco) (14). C2C12 cells are used at passage number 5.

Formation of Muscle Ring.

For all tissue seeding procedures, ECM solution is prepared on ice by first neutralizing type I collagen from rat tail (Corning) with 1 M sodium hydroxide (Sigma), 10× PBS (Lonza), and molecular biology grade water (Corning) and then mixing neutralized collagen thoroughly with growth factor reduced Matrigel (Corning) (28). Collagen and Matrigel are used at final concentrations of 2 mg/mL each. To form muscle rings, C2C12 cells are suspended in ECM solution at a density of 2.5 × 10⁶ cells/mL. Cell–ECM mixtures are seeded into sterile PDMS molds by pipetting and are polymerized at room temperature for 30 min. Samples are then inundated in growth medium and incubated for 2 d while they compacted the ECM gel and form muscle rings.

Hydrogel Tube Preparation.

Stretchable tough polyacrylamide hydrogel tube is synthesized by mixing 1 mL of 28% wt/vol of acrylamide and 4 µL of 2% wt/vol of N,N′-methylenebisacrylamide with controlled concentrations in aqueous solution. In a mixture aqueous solution, ammonium persulfate, at 0.1% vol/vol (the volume of total volume), and N,N,N′,N′-tetramethylethylenediamine, at 0.2% vol/vol (the volume of total volume), as a radical-initiator and a crosslinking accelerator, respectively. The gel precursor mixture is added into the glass tube mold and cured for 1 h at room temperature. To remove the remained monomers, the resulting hydrogel tube is incubated in distilled water for 12 h. Mechanical properties and tests can be found in SI Appendix, Figs. S3 and S4.

Pump-Bot Fabrication and Assembly.

PDMS pump-bot skeleton is replicated from machined aluminum mold (SI Appendix, Fig. S4). PDMS base and cross-linker are mixed at a 10:1 ratio by weight, poured onto the aluminum molds, and degassed using a vacuum desiccator. Samples are cured at 60 °C for 12 h and peeled off the aluminum mold. To assemble the pump-bot, firstly, the hydrogel tube is inserted into the muscle ring. Hydrogel tube-muscle ring assembly is then transferred into the PDMS skeleton by inserting the tube into the round PDMS channels. Samples are then inundated in muscle differentiation medium and incubated for 7 d.

Image Acquisition and Electrical Stimulation.

All imaging is performed on an Olympus IX81 inverted microscope (Olympus America) with a digital complementary metal–oxide semiconductor camera (Hamamatsu), mounted on a vibration isolation table (Newport). The microscope is equipped with an environmental chamber to maintain samples at 37 °C and 5% CO₂ during imaging. For flow-rate assays, green fluorescent polystyrene beads (Molecular Probes) are dispersed in cell culture media, and fluorescent images are taken at 20 frames per second (fps) using a GFP filter coupled to an X-Cite 120PC Q wide-field fluorescent light source (Excelitas Technologies). For tube-deformation assays, phase-contrast images are taken at 20 fps using a 4× air objective. For electrical stimulation, wire electrodes are sterilized in 70% ethanol, rinsed with PBS, and positioned on either side of the hydrogel tube-muscle ring assembly; 9- or 4.5-V pulses of 10-ms duration are applied at 1, 2, or 4 Hz, controlled by an Arduino board.

Measurement of Tube Deformation and Flow Rate.

The diameter change of hydrogel tube induced by muscle contractions are measured from video recordings using the image analysis software Tracker (physlets.org/tracker). The trajectories of fluorescent beads inside the hydrogel tube are measured by particle tracker, a point-tracking tool for detection and tracking of particle trajectories (https://imagej.net/Particle_Tracker).