Abstract
There has arisen a considerable body of research addressing the estimation of association between paired failure times in the presence of competing risks. In a 2002 paper, Bandeen-Roche and Liang proposed the conditional cause-specific hazard ratio (CCSHR) as a measure of this association and a parametric method by which to estimate it. The method features an interpretable decomposition of the CCSHR into factors describing the association between a pair’s times to first failure among multiple failure causes and the association in pair members’ propensities to fail due to a common cause. There were indications of sensitivity to model assumptions, however, in the 2002 work. Here we report a detailed study of the method’s sensitivity to its parametric assumptions. We conclude that the method’s performance is most sensitive to mis-specification of temporality in the association between pair members’ first-failure times and of correlation between propensity to fail early or late and the propensity to fail of a specific cause. Implications for methods development are highlighted.
Keywords: multivariate, survival, dependence, frailty, conditional hazard ratio, conditional cause-specific hazard ratio
1. Introduction
Until recent decades, research on survival analysis mostly concerned univariate data, with observations assumed to be independent. In many modern studies, however, data of interest contain observations that are clustered and so may be associated. Characterizing failure time associations may sometimes then be of direct interest. Addressing this, multivariate survival function estimators have been developed by Dabrowska (1988) [11], Pruitt (1991) [16], Prentice and Cai (1992) [15], van der Laan (1996) [13], and Prentice (2014) [14]. Their implementation and the functions’ interpretation, however, may be complex. Employing a simple summary measure of dependence structure can ameliorate this problem. Along these lines, Clayton (1978) [10] suggested representing the dependence structure as a ‘cross’ (or conditional) hazard ratio. When generalized to vary with time, this quantity is defined as follows:
| (1) |
It can be interpreted as the ratio comparing an individual’s hazard of failure at t2 given failiure of his pair partner at t1 to the hazard given that the partner has not yet failed by t1.
Multivariate survival analysis may have particular benefits to offer in re-search involving competing risks. Most such research has focused on the uni-variate setting in which only one type of failure may be observed per sampling unit. Multivariate survival analysis with competing risks informs the study of relationships among failure types in ways univariate analysis cannot, because multiple failure types may be observed in a cluster. Among many available measures of association in the competing risks setting (e.g. Cheng, Fine & Korosok, 2007, 2009 [8] [9]; Scheike et al., 2010 [18]), this paper focuses on the modified conditional hazard ratio, and a parametric model and estimator for this, proposed by Bandeen-Roche and Liang (2002) [3]. Bandeen-Roche and Ning (2008) [4] developed a nonparametric estimator of the modified conditional hazard ratio and proved its distributional properties; Cheng, Fine and Bandeen-Roche (2010) [7] extended it to exchangeable data in which the cluster size may be greater than two. Gorfine and Hsu (2011) [12] suggested a frailty-based conditional regression model in which the frailty processes have general distributional structure, and which subsumes the Bandeen-Roche and Liang parametric model as a special case.
The parametric model of Bandeen-Roche and Liang (2002) has an appeal-ing feature that is not shared by the nonparametric approaches to estimation of the modified conditional hazard ratio, nor is retained in the Gorfine and Hsu (2011) formulation: a conceptually intuitive decomposition of failure time associations into ‘size’ and ‘shape’ components. To explicate the idea, consider two failure causes: onset of a given disease, or death. The ‘size’ component governs clustering between times to earliest failure from any cause - either disease onset or death. It does this through cluster-specific frailties that multiply the overall, population failure hazard. The ‘shape’ component governs clustering in the tendency to fail preferentially from certain causes as opposed to others. It does this through cluster-specific compositional frailty processes (time-varying vectors of proportions) that generate cause-specific hazards by multiplying the overall cluster hazard. Such a decomposition opens prospects for distinguishing shared genetic or environmental in uences that predispose faster overall health declines from those that speed or delay some diseases as opposed to others. The methodology was never pursued beyond the 2002 paper, however, because it performed badly in simulation scenarios in which its underlying assumptions were replaced by alternative reasonable assumptions. Our goal herein is to better understand the source of this sensitivity, with an eye to correcting it.
The remainder of this paper proceeds as follows. Section 2 introduces notation and relevant background. Section 3 investigates sensitivity to one of the methodology’s major assumptions: Dirichlet distribution of the shape frailty. We study the behavior of the estimator when the data are generated from a logit-normal distribution and also investigate the potential influence of mis-specified size frailty. Section 4 investigates the second major assumption: that size and shape frailty variables are statistically independent. Both investigations employed simulation studies. Section 5 concludes.
2. Background and Motivation
2.1. Notation
We consider a simple setting in which the data are independently and identically distributed across clusters, there are two types of competing risks, and there are two units per cluster (pairs). For members j = 1, 2 of a given pair (subscript i tracking pairs suppressed for the time being), let Tj1 denote the failure time of interest and Tj2 the failure time for the competing risk, with respective hazard functions λ1(t) and λ2(t). Then the time of the first failure is Xj = Tj1 ∧ Tj2; if events truly are competing, only Xj is observable, whereas for semicompeting risks Tj1 and Tj2 both may be observed in certain instances. The data also includes a failure type indicator Kj which is 1 when Xj = Tj1 and 2 when Xj = Tj2. For now we treat the data as fully observed; later we introduce the possibility of censoring independent of the occurrence of both types of risks.
2.2. The conditional cause-specific hazard ratio (CCSHR)
The CCSHR compares two instances of the cause-specific hazard - a fundamental quantity estimable from observed data in the competing risks setting. In the univariate setting, the cause-specific hazard is defined as λk(x) = limh↓0 Pr (x ≤ X < x + h, K = k|X ≥ x)/h, and λi,k(x) denotes the i-th individual’s cause-specific hazard. Its generalization to the bivariate setting is given by λ(k1,k2)(x1, x2) = lim(h1,h2)↓0 Pr (x1 ≤ X1 < x1 + h1, K1 = k1, x2 ≤ X2 < x2 + h2, K2 = k2|X1 ≥ x1, X2 ≥ x2)/(h1h2); Bandeen-Roche and Liang (2002) considered a corresponding joint density for the failure times and causes, given by f(x1, x2, k1, k2) = lim(h1,h2)↓0 Pr(x1 ≤ X1 ≤ x1 + h1, x2 ≤ X2 ≤ x2 + h2, K1 = k1, K2 = k2)/(h1h2). Then, the conditional cause-specific hazard ratio (CCSHR) may be defined as
| (2) |
where S(x1, x2) denotes the joint survival function. Roughly it is the factor by which an individual’s risk of failure at x1 due to cause k1 is changed if his pair partner fails at x2 due to cause k2 versus has not yet failed at all by x2. It generalizes the conditional hazard ratio which has similar definition as in (2), only omitting all references to causes k.
2.3. A parametric model for the CCSHR
The model we seek to study is grounded in the frailty modeling (Vaupel et al., 1979 [21]). A frailty variable, A, is an unobserved random effect that multiplicatively modifies the hazard function of an individual, or of related individuals. Taking G as the frailty distribution and a as a generic realization, the bivariate survival function can be expressed as follows:
where are survival functions and are corresponding hazard functions conditional on A = 1 (henceforth, ‘reference’ survival or hazard functions). The conditional hazard ratio defined in Equation (1) then can be represented in terms of A and as
| (3) |
.
Importantly for what follows, the survival function for each j-th pair member conditional on A = a is , and the corresponding hazard function is
| (4) |
.
To represent the CCSHR, Bandeen-Roche and Liang observed that because the overall failure hazard is the sum of cause-specific hazards , the cause-specific hazard can be written as a proportion of the overall hazard, with , k = 1, 2. To characterize a hazard specific to both pair and cause k, then, they proposed to modify the right-hand side of (4) by multiplying the frailty for overall failure, A, by a proportional shape frailty vector B(x) = {B1(x), B2(x)} having mean function {R1(x), R2(x)}. This yields
| (5) |
where . Conceptually, A amplifies or diminishes a pair’s tendency to fail early, regardless of cause, and B(x) tailors the pair’s allocation of the overall hazard to the respective causes.
To develop an estimator for the CCSHR, Bandeen-Roche and Liang imposed two assumptions upon (5): Dirichlet distribution of the shape frailty B(x), and independence between the size frailty A and the shape frailty B(x). With the independence assumption, the CCSHR for causes k1 and k2 becomes
| (6) |
If B(x) has Dirichlet distribution with parameter δ(x) and mean function R(x) and we set δ(x) = ΔR(x), the first multiplicand becomes
| (7) |
Here, can be estimated by a nonparametric method reported in a separate paper by the authors, or by a method explained in Appendix I of Bandeen-Roche and Liang (2002) when the term is assumed to be time-invariant. The parameter Δ can be estimated by solving the score equation (15) in Bandeen-Roche and Liang paper. The second multiplicand is the conditional hazard ratio for the frailty model without competing risks. The first and second multiplicands have interpretations as association in failure causes and in times to first failure, respectively. The distributional assumptions yield convenient estimators.
Notwithstanding these advantages, prior studies have suggested that estimators employing (6) and (7) may be sensitive to assumptions made. In the next two sections we study this issue seeking means to ameliorate the sensitivity.
3. Sensitivity to assumption 1: Dirichlet distribution of shape frailty
To evaluate the sensitivity of the Bandeen-Roche and Liang (2002) parametric estimator just described (henceforth, BRL estimator) to the Dirichlet distribution assumption, a natural comparator is one incorporating a logit-normal distribution instead. In this section, we propose an estimator based on logitnormal-distributed shape frailty and then compare the performance of the two estimators for simulated data sets in which the shape frailty has Dirichlet versus logit-normal distribution. Additionally, we repeated simulation scenarios in which the underlying assumptions of the BRL framework were replaced by alternative reasonable assumptions, but revisited estimation not only of the shape frailty component of our model but also the size frailty component – a source of sensitivity not considered in the 2002 paper.
3.1. Introduction of distributions to be studied
The Dirichlet distribution is frequently used to model vectors of multivariate proportions, W, which sum to one (i.e. ‘compositional’ data). Thus it is suited to allocate proportions of hazards of the various failure types to the overall hazard. It has density where , and . [1] It arises intuitively by dividing a collection of ‘amounts’ by their sum when the amounts are mutually independent, and the proportions resulting from dividing the amounts by their sum are independent of the sum, or when the amounts are independent gamma random variables with common scale, or in certain cases when amounts are positively correlated. [5] In the failure time context, if disease A and disease B arise independently within families, and the type of failure that occurs first is independent of the total propensity to fail, then the assumptions of the Dirichlet distribution are satis ed. If diseases A and B have a common cause, these assumptions are likely to be violated because the propensities to fail from two diseases are correlated. Moreover, the Dirichlet distribution constrains the covariance between any pair of proportions to be negative. If there are only two types of failures (i.e. a single proportion and its difference from one to be modeled), the Dirichlet distribution reduces to the beta distribution.
The logit-normal distribution is a primary alternative to the Dirichlet for modeling compositional data. [2] Suppose that a (K – 1)-dimensional random vector Y follows a multivariate normal distribution over . Then W with and define the logit-normal distribution of dimension K. The associated density function is given by where . The logit-normal distribution has parameters compared with only K parameters for the Dirichlet distribution; in fact, a suitably chosen logit-normal can closely approximate any Dirichlet. It relaxes some of the assumptions underlying the Dirichlet class, for example independence of the bases, making it a worthwhile choice for further study.
Following on the 2002 paper by Bandeen-Roche and Liang, we proceed to study the case of two competing causes.
3.2. Methods
We began by implementing a maximum likelihood estimator for the parameters of a logit-normal shape distribution in the BRL framework, assuming that Bj(x) = Bj for all x. The likelihood function for hazard and frailty quantities based on a sample of pairs i = 1, …, n is given by
| (8) |
(Bandeen-Roche and Liang, 2002). Additionally assuming size and shape independence factorizes this into quantities involvinng only the shape frailty distribution versus only the reference hazard and size frailty distribution. Inference for the pair-specific hazards and size frailty can be accomplished by existing methods such as Shih and Louis (1995). [19] Inference for the shape frailty involves only the first multiplicand of Equation (8), taking the likelihood function for the logit-normal parameters proprotional to
| (9) |
where Y is a normal, and B, a logit-normal, random variable, and I1, I2, and I3 refer respectively to sets of pairs whose members both fail of cause 1, both fail of cause 2, and fail of different causes. Then the log-likelihood is
| (10) |
where μ and σ are the mean and standard deviation of the logit, n1 is the number of pairs whose members both fail due to cause 1, n2 is the number of pairs whose members both fail due to cause 2, and n3 is the pairs whose members fail of different causes. For improved numerical stability, we replaced the standard deviation σ with exp(log(σ)) and then estimated log(σ). The values of μ and log(σ) that maximize the log-likelihood function were obtained using the ‘optim’ function with L-BFGS-B method in the R Statistical Software package.
When we have censored observations, we can still use the same likelihood function to estimate μ and σ. First, we count the number of pairs whose members both fail due to cause 1, both fail due to cause 2, and fail of different causes among pairs in which both members are observed to fail. Using the proportional frequencies of these three groups of pairs, we can get imputed frequencies of three groups for singly and doubly censored pairs. Then adding the observed and imputed frequencies of pairs gives us n1, n2, and n3. This method is described in more detail in Step 1~3 in the Appendix 1 of Bandeen-Roche and Liang (2002).
A simulation study was conducted to assess the performance of the estimator with logit-normal shape frailty assumption and the sensitivity of both it and the previously proposed Dirichlet-based estimator to violations of their respective distributional assumptions. The simulation settings and procedures mimicked those of Bandeen-Roche and Liang (2002). A first set of studies assessed the accuracy of the logit-normal parameter estimation. It assumed that the pair members’ earliest failure times regardless of cause followed a Clayton copula distribution. To create such failure times, we first generated 1,000 replicates of n = 100 or n = 500 size frailties. ‘A’ drawn independently from a gamma distribution with mean = 1 and variance = 1. Per replicate and pair i, we generated two failure times drawn independently from an exponential distribution with rate parameter Ai. Next, we allocated ‘causes’ of failure. Per replicate and pair, we drew shape frailties ‘Bi’ independently from a logit-normal distribution with mean of the logit equal to μ and standard deviation of the logit equal to σ. Parameters μ = 0, 0.75, and 1.5 and σ = 1 and 3 were varied as true values of the logit-normal parameters. The resulting distribution is symmetric when μ = 0 and increasingly left skewed as is larger; σ = 1 results in unimodal distributions and σ = 3 results in a bi-modal (U-shaped) distribution. In each case, to decide the failure type for each failure time in a pair, we generated independent uniformly distributed random numbers and compared these to the shape frailties Bi; if an individual’s uniform realization was less than or equal to Bi, we assigned cause 1, and otherwise, cause 2. Finally, we estimated μ and σ as the values maximizing the log-likelihood equation (10) and then the CCSHR according to (6). In the first multiplicand of CCSHR1,1 (between cause 1 and cause 1), E(B2) and E(B) were calculated using numerical integration, plugging in the estimated logit-normal parameters. The numerical integration was implemented using the ‘integrate’ function in R with default settings. [17] The first multiplicand of CCSHR1,2 and CCSHR2,2 can be obtained by numerical integration of and respectively. The second CCSHR multiplicand is the conditional hazard ratio without competing risks: it was obtained using two-stage semiparametric estimation of Shih and Louis (1995) assuming Clayton’s copula. [19]
A next set of studies assessed sensitivity of estimators to mis-specified shape distribution, within the BRL framework. To assess sensitivity of the original, Dirichlet-based estimator to violation of its assumption of distribution for the shape frailty, we applied an estimator assuming beta shape distribution (detailed in Section 4.1, Bandeen-Roche and Liang, 2002) to the same data as described above. Here, we used maximum likelihood method to estimate Dirichlet parameters instead of closed-form formula in their paper. Conversely, to assess performance of the logit-normal estimator under a Dirichlet shape assumption, we t both estimators to data generated as described earlier in this paragraph except replacing logit-normal shape frailties with beta frailties, varying the beta parameters as (α, β) = (0.2, 0.8), (1, 4), (0.5, 0.5), and (2, 2).
A third set of studies employed a generating mechanism outside of the BRL framework. This mechanism imagines a ‘latent’ failure time for each cause of which only the first is observed. For each of 1,000 replicates, we first generated n = 500 pairs of ‘cause 1’ (say, ‘disease’) failure times as exponential conditional on gamma frailties, Ai1, exactly as in the first step of the first set of studies. Then, we independently generated n = 500 pairs of ‘cause 2’ (say, ‘death’) failure times, also exponential conditional on gamma frailties, Ai2; for each individual, we considered the pairwise minimum of the ‘disease’ and ‘death’ failure times as the failure time (with associated cause). For both causes the gamma scale parameter was set equal to 1. The gamma shape parameter was set equal to 1/(t1 − 1) for ‘disease’ (yielding ‘marginal’ CHR of t1) and to 1/(t2 − 1) for ‘death’, varying of t1 and t2 as in Table 1. For ‘disease’ the exponential rate parameters were set to l1 × Ai1 and l2 × Ai1 for the respective members of the pair; for ‘death’, they were set equal to l3 × Ai2 and l4 × Ai2. Values of l1, l2, l3, and l4 also were varied as in Table 1, for a total of six scenarios. CCSHRs were estimated through the same estimation procedures as in the second simulation study (falsely assuming data generated according to the Bandeen-Roche and Liang framework).
Table 1.
Exponential rate (l) and association (gamma shape-defining; t) parameters for the 3rd and 4th sets of simulation studies
| Cause 1 |
Cause 2 |
|||||
|---|---|---|---|---|---|---|
| Scenario | l1 | l2 | t1 | l3 | l4 | t2 |
| 1 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2 | 2 | 2 | 2 | 2 | 2 | 4 |
| 3 | 2 | 2 | 2 | 2 | 3 | 2 |
| 4 | 2 | 2 | 2 | 2 | 3 | 4 |
| 5 | 2 | 2 | 2 | 3 | 3 | 2 |
| 6 | 2 | 2 | 2 | 3 | 3 | 4 |
A fnal set of simulation studies was similar to the third one in all ways with one exception: rather than generating cause-specific failure times as expo-nential conditional on the pairwise frailty, we generated them to be marginally exponential. Details are provided in the Appendix. The gamma, exponential, normal, beta, and uniform random numbers needed for the studies just de-scribed were generated using standard R functions.
3.3. Results
The first and second sets of simulation studies addressed the estimation of the logit-normal parameters μ and σ (Table 2) and resulting CCSHR (Table 3). The estimator of μ exhibited bias at most 5.3% for completely observed data and at most 7.6% for 30% censored data. The estimator of σ exhibited bias which increased in absolute value with σ, but bias as a percentage of the estimand decreased. For both estimators based on beta and logit-normal shape distributions, biases decreased considerably comparing n = 500 to n = 100 and increased for 30% censored data compared to complete data. Precision of estimation improved substantially for n = 500 compared to n = 100, with standard errors in estimation generally smaller by 50% to 60% for both μ and σ. Standard errors for the censored data were greater than those for complete data by 35~60% for both μ and σ.
Table 2.
Simulation study findings: Performance of ML estimation of logit-normal distribution parameters (Equation (10)). Data were generated according to the Bandeen-Roche and Liang parametric model with gamma size frailty and logit-normal shape frailty.
| Estimates of μ | ||||||||
|---|---|---|---|---|---|---|---|---|
| True values | No censoring | 30% censoring | ||||||
| µ | σ | Mean | SD | Bias | Mean | SD | Bias | |
| 0 | 1 | −0.002 | 0.188 | −0.002 | −0.001 | 0.278 | −0.001 | |
| 0 | 3 | −0.003 | 0.400 | −0.003 | 0.017 | 0.548 | 0.017 | |
| n=100 | 0.75 | 1 | 0.770 | 0.221 | 0.020 | 0.789 | 0.342 | 0.039 |
| 0.75 | 3 | 0.778 | 0.437 | 0.028 | 0.801 | 0.629 | 0.051 | |
| 1.5 | 1 | 1.537 | 0.294 | 0.037 | 1.585 | 0.472 | 0.085 | |
| 1.5 | 3 | 1.579 | 0.537 | 0.079 | 1.614 | 0.775 | 0.114 | |
| µ | σ | Mean | SD | Bias | Mean | SD | Bias | |
| 0 | 1 | 0.002 | 0.082 | 0.002 | 0.005 | 0.120 | 0.005 | |
| 0 | 3 | 0.003 | 0.170 | 0.003 | 0.004 | 0.245 | 0.004 | |
| n=500 | 0.75 | 1 | 0.756 | 0.096 | 0.006 | 0.762 | 0.142 | 0.012 |
| 0.75 | 3 | 0.751 | 0.179 | 0.001 | 0.748 | 0.261 | −0.002 | |
| 1.5 | 1 | 1.511 | 0.127 | 0.011 | 1.519 | 0.186 | 0.019 | |
| 1.5 | 3 | 1.506 | 0.218 | 0.006 | 1.512 | 0.306 | 0.012 | |
| Estimates of σ |
||||||||
| True values |
No censoring |
30% censoring |
||||||
|
µ |
σ |
Mean |
SD |
Bias |
Mean |
SD |
Bias |
|
| 0 | 1 | 0.998 | 0.406 | −0.002 | 1.029 | 0.567 | 0.029 | |
| 0 | 3 | 3.025 | 0.657 | 0.025 | 3.010 | 0.903 | 0.010 | |
| n=100 | 0.75 | 1 | 0.997 | 0.457 | −0.003 | 1.010 | 0.685 | 0.010 |
| 0.75 | 3 | 3.083 | 0.686 | 0.083 | 3.126 | 0.993 | 0.126 | |
| 1.5 | 1 | 0.951 | 0.515 | −0.049 | 0.963 | 0.737 | −0.037 | |
| 1.5 | 3 | 3.120 | 0.757 | 0.120 | 3.146 | 1.078 | 0.146 | |
| µ | σ | Mean | SD | Bias | Mean | SD | Bias | |
| 0 | 1 | 0.990 | 0.177 | −0.010 | 0.985 | 0.260 | −0.015 | |
| 0 | 3 | 2.987 | 0.300 | −0.013 | 2.994 | 0.430 | −0.006 | |
| n=500 | 0.75 | 1 | 0.990 | 0.191 | −0.010 | 0.972 | 0.292 | −0.028 |
| 0.75 | 3 | 2.991 | 0.315 | −0.009 | 2.991 | 0.451 | −0.009 | |
| 1.5 | 1 | 0.999 | 0.214 | −0.001 | 0.980 | 0.334 | −0.020 | |
| 1.5 | 3 | 2.993 | 0.327 | −0.007 | 2.998 | 0.477 | −0.002 | |
Table 3.
Comparison of CCSHR estimators based on beta and logit-normal distributions when the true failure types respectively are generated from logit-normal and beta distributions. Estimators are those detailed in Section 3.1.
| No censoring | 30% censoring | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Beta | Logit-normal | Beta | Logit-normal | |||||||
| µ | σ | TRUE | Mean | SD | Mean | SD | Mean | SD | Mean | SD |
| 0 | 1 | 2.347 | 2.336 | 0.163 | 2.336 | 0.163 | 2.304 | 0.220 | 2.305 | 0.220 |
| 0 | 3 | 3.081 | 3.075 | 0.208 | 3.068 | 0.207 | 3.038 | 0.291 | 3.029 | 0.288 |
| 0.75 | 1 | 2.177 | 2.169 | 0.135 | 2.169 | 0.135 | 2.138 | 0.182 | 2.138 | 0.182 |
| 0.75 | 3 | 2.762 | 2.755 | 0.178 | 2.751 | 0.177 | 2.721 | 0.244 | 2.717 | 0.243 |
| 1.5 | 1 | 2.080 | 2.075 | 0.123 | 2.076 | 0.122 | 2.048 | 0.165 | 2.049 | 0.165 |
| 1.5 | 3 | 2.529 | 2.521 | 0.158 | 2.519 | 0.157 | 2.489 | 0.216 | 2.487 | 0.216 |
| α | β | TRUE | Mean | SD | Mean | SD | Mean | SD | Mean | SD |
| 0.2 | 0.8 | 6.000 | 6.000 | 0.614 | 5.830 | 0.527 | 5.959 | 0.843 | 5.757 | 0.709 |
| 1 | 4 | 3.333 | 3.299 | 0.466 | 3.293 | 0.470 | 3.218 | 0.607 | 3.223 | 0.602 |
| 0.5 | 0.5 | 3.000 | 2.990 | 0.198 | 2.987 | 0.198 | 2.950 | 0.275 | 2.946 | 0.273 |
| 2 | 2 | 2.400 | 2.388 | 0.163 | 2.388 | 0.163 | 2.352 | 0.216 | 2.352 | 0.216 |
Table 3 compares performance in estimating CCSHR1,1 between procedures based on a logit-normal shape distribution and on a beta distribution when the true failure types are generated by various parameters of these two distributions. Each column displays mean and standard deviation of the CCSHR estimates using estimators based on logit-normal and beta distribution respectively. The upper and lower parts of the table show the results when the true failure type distribution was beta and logit-normal, respectively. Two estimators exhibited bias no greater than 1.2% for complete data and 2.0% for censored data in all scenarios except for (α, β) = (0.2, 0.8) scenario where logit-normal based estimator had biases of 2.8% and 4.0%, respectively. The coefficient of variation (CV) for CCSHR1,1 was no greater than 14.3% for complete data and no greater than 18.9% for censored data, and there were little differences between beta-based and logit-normal-based estimators for most scenarios. For the most highly skewed scenario, (α, β) = (0.2, 0.8), logit-normal-based estimator was less accurate than beta-based one, but also less variable. For all the other scenarios, both estimators were highly accurate.
The third set of simulation studies addressed the estimation of CCSHR for failure times arising as the pairwise minimum of cause-specific failure times (Table 4). When failure rates due to cause 1 equaled those for cause 2 for both pair members (l1 = l3 and l2 = l4; Scenarios 1 and 2), the bias of CCSHR estimator was very small (<1%). When the cause-specific failure rates differed across causes for only one member of the pair (l1 = l3 and l2 ≠ l4; Scenarios 3 and 4), the estimator was moderately biased (up to 2.7%). When the cause-specific hazard rates differed for both pair members (l1 ≠ l3 and l2 ≠ l4; Scenarios 5 and 6), the biases inflated further (up to 8.9%). In most of the scenarios, biases in estimating CCSHR1,2 were smaller than those of CCSHR1,1. The coefficients of variation of CCSHR1,2 estimates, however, were greater than those of CCSHR1,1. Beta-based and logit-normal-based estimators performed similarly in all scenarios.
Table 4.
Comparison of the CCSHR estimators based on beta and logit-normal distributions (3rd simulation study); Data generated from distributions with CCSHR1,1 = 2 and CCSHR1,2 = 1
| CCSHR1,1 |
CCSHR1,2 |
|||
|---|---|---|---|---|
| Scenario | Beta | Logit-normal | Beta | Logit-normal |
| Mean (SD) | Mean (SD) | Mean (SD) | Mean (SD) | |
| 1 | 2.006 (0.138) | 2.001 (0.151) | 1.000 (0.084) | 1.006 (0.103) |
| 2 | 2.001 (0.117) | 1.993 (0.115) | 0.997 (0.099) | 1.023 (0.085) |
| 3 | 2.054 (0.131) | 2.054 (0.131) | 1.018 (0.092) | 1.018 (0.092) |
| 4 | 2.036 (0.108) | 2.029 (0.106) | 0.996 (0.099) | 1.015 (0.086) |
| 5 | 2.177 (0.150) | 2.177 (0.150) | 1.021 (0.086) | 1.021 (0.085) |
| 6 | 2.085 (0.121) | 2.077 (0.119) | 0.958 (0.094) | 0.980 (0.080) |
The fourth set of simulation studies differed from the third set only in the distributions of T1 and T2 (exponential marginally versus conditionally on the pair frailty; Table 5). We observed a pattern of findings quite similar to the third set of studies, however with biases that were much more severe. For scenarios in which the strength of association was equal across causes (Scenarios 1, 3, and 5), the bias increased with increasing differentiation in the cause-specific marginal distributions. (0~10%) For scenarios in which the strength of association differed across causes (Scenarios 2, 4, and 6), the estimators were severely biased regardless of the marginal distributions. (30~60%) For each estimand, beta- and logit-normal-based estimators performed similarly. For the beta estimator, this finding replicates that in the Bandeen-Roche and Liang (2002) paper.
Table 5.
Comparison of the CCSHR estimators based on beta and logit-normal distribu-tions (4th simulation study); Data generated from distributions with CCSHR1,1 = 2 and CCSHR1,2 = 1
| CCSHR1,1 |
CCSHR1,2 |
|||
|---|---|---|---|---|
| Scenario | Beta | Logit-normal | Beta | Logit-normal |
| 1 | 2.006 (0.139) | 1.999 (0.155) | 1.002 (0.080) | 1.010 (0.105) |
| 2 | 2.689 (0.200) | 2.682 (0.206) | 1.009 (0.097) | 1.017 (0.111) |
| 3 | 2.061 (0.131) | 2.061 (0.131) | 1.038 (0.084) | 1.038 (0.084) |
| 4 | 2.808 (0.218) | 2.806 (0.216) | 1.082 (0.099) | 1.083 (0.097) |
| 5 | 2.273 (0.168) | 2.273 (0.168) | 1.029 (0.085) | 1.029 (0.085) |
| 6 | 3.200 (0.257) | 3.194 (0.253) | 1.107 (0.099) | 1.111 (0.095) |
3.4. Data Analysis: Cache County Study
The estimators considered in the previous subsections were applied to data from the Cache County Study on Memory Health and Aging. (Breitner, 1999) This study was conducted to investigate the prevalance of dementia in terms of age, education, sex, and APOE genotype. To this end, the study collected information on dementia onset from the permanent residents of Cache County, Utah, U.S.A., aged 65 and over (the ‘proband’) on themselves and all their family members. This data set has been used to illustrate methods related to multivariate failure time data. (Bandeen-Roche and Liang, 2002, Bandeen-Roche and Ning, 2008, Cheng and Fine, 2008, and Cheng, Fine, and Bandeen-Roche, 2010)
To simplify the analysis, we included data only from the participants’ mother and the eldest sibling inclusive of self. This subset has 4,522 pairs of observations, (Xi1, Xi2, Ki1, Ki2), where Xi1 is the age of event occurence of the eldest sibling, Xi2 is the event time of the mother, and Kij is the event type corresponding to Xij, j = 1, 2. The event type is 0 if the subject was censored or not demented at the end of the study, 1 if demented, and 2 if died without dementia. We included 3,635 pairs of observations for which some data were observed and who had not yet failed due to either cause by age Among these, 1,431 pairs had no censored component, that is, both pair members either were demented or died. The proportion of data censored was 60.4% among the eldest siblings and 4.0% among mothers. Among those expe-riencing events, 13~14 % of participants experienced dementia before death. Both members of a pair became demented in 40 pairs, both members died without dementia in 1,132 pairs, and the members failed of different causes in pairs.
We aimed to estimate the CCSHR of dementia onset between the child and mother using the two methods introduced in the previous sections: the estimators based on the Dirichlet distribution and logit-normal distribution. To characterize the variability of the estimates, we obtained 95% bootstrap condence intervals: 500 bootstrap samples were generated by random selection at the pair level with replacement taking records as vectors of failure times and failure cause indicators of both child and mother. For the Dirichlet estimator, the CCSHR was 6.81 (different from displayed in the Bandeen-Roche and Liang 2002 paper because we used MLE for parameter estimation instead of MME of theirs) with 95% confidence interval (6.03, 7.56). For the logit-normal estimator, we obtained CCSHR of 6.89 with 95% confidence interval (5.99, 7.62). The size component’s estimate was 1.16 with 95% bootstrap CI (1.09, 1.20). The shape component’s estimate by Dirichlet estimator was 5.88 with 95% bootstrap CI (5.49, 6.44) and that by logit-normal estimator was 5.92 with 95% bootstrap CI (5.44, 6.48). This suggests that association between the causes of failure contributes most to the excess hazard for a dementia failure given a family member having experienced a dementia failure as opposed to remaining alive and dementia free, rather than association between times to a first adverse outcome. Commensurate with our simulation studies, the two estimators were quite similar.
3.5. Application of Diagnostic to Assess Model Fit
In seeking to understand biases in estimating the CCSHR observed in the 3rd and particularly the 4th set of simulations, estimation of the size (second) multiplicand (Equation (6)) and not only the shape (fie) multiplicand of the CCSHR must be considered. Specifically, even though the dependence between bivariate failure times for each cause follows a gamma frailty model where the strength of association does not change over time, the dependence in observed failure times (generated as the minimum of cause-specific failure times) may not. This was a possibility not considered by Bandeen-Roche and Liang in their 2002 paper. We used the diagnostic method of Chen and Bandeen-Roche (2005) [6] to assess whether the pairwise minimum retained gamma frailty dependence structure. If so, the ‘size’-associated conditional hazard ratio, θ* (S(t1, t2)), should be constant considered as a function of the survival function. The results of this diagnostic are displayed in Table 6. The numbers in the table are the mean and standard deviation of the CHR (for time to first failure) over 200 replicates of simulation studies when the joint survival function is 0, 1/6, 2/6, 3/6, 4/6, 5/6, and 1, respectively. For Scenarios 2, 4, and 6 of the 4th simulation study in which the bias in estimating the CCSHR was most severe (bottom of Table 6), the ratios were strikingly non-constant. This implies that the association between the first failure times of a pair regardless of cause may not follow gamma frailty dependence structure even though the association for the cause-specific failure time does. Thus, both herein and in the 2002 paper by Bandeen-Roche and Liang, the bias in CCSHR estimation may reflect mis-specification in estimating its size multiplicand rather than undue sensitivity to the shape distributional assumption.
Table 6.
CHR as a function of joint survival function S(t). Non-constant trends with S(t) (marked with *) indicate departure from gamma frailty dependence structure in paired times to first failure (Chen and Bandeen-Roche, 2005)
| Simulation 3: | S(t)=0 | S(t)=1 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario 1 | Mean | 1.491 | 1.561 | 1.519 | 1.506 | 1.469 | 1.505 | 1.456 | |
| SD | 0.230 | 0.238 | 0.252 | 0.257 | 0.323 | 0.412 | 0.639 | ||
| Scenario 2 | Mean | 1.805 | 1.760 | 1.801 | 1.788 | 1.780 | 1.812 | 1.834 | |
| SD | 0.267 | 0.238 | 0.269 | 0.293 | 0.319 | 0.439 | 0.771 | ||
| Scenario 3 | Mean | 1.494 | 1.508 | 1.493 | 1.524 | 1.481 | 1.548 | 1.531 | |
| SD | 0.213 | 0.214 | 0.244 | 0.265 | 0.330 | 0.413 | 0.718 | ||
| Scenario 4 | Mean | 1.805 | 1.736 | 1.773 | 1.742 | 1.817 | 1.706 | 1.824 | |
| SD | 0.317 | 0.243 | 0.267 | 0.296 | 0.350 | 0.454 | 0.721 | ||
| Scenario 5 | Mean | 1.491 | 1.496 | 1.504 | 1.480 | 1.552 | 1.531 | 1.416 | |
| SD | 0.219 | 0.212 | 0.220 | 0.252 | 0.327 | 0.414 | 0.692 | ||
| Scenario 6 | Mean | 1.812 | 1.805 | 1.765 | 1.724 | 1.751 | 1.689 | 1.823 | |
| SD | 0.259 | 0.242 | 0.251 | 0.295 | 0.306 | 0.419 | 0.875 | ||
| Simulation 4: | S(t)=0 | S(t)=1 | |||||||
| Scenario 1 | Mean | 1.547 | 1.517 | 1.498 | 1.524 | 1.512 | 1.498 | 1.526 | |
| SD | 0.245 | 0.232 | 0.206 | 0.242 | 0.320 | 0.389 | 0.646 | ||
| Scenario 2 | Mean | 1.752 | 1.857 | 1.848 | 1.914 | 1.928 | 1.995 | 2.034 | * |
| SD | 0.267 | 0.241 | 0.282 | 0.353 | 0.322 | 0.434 | 0.821 | ||
| Scenario 3 | Mean | 1.524 | 1.507 | 1.512 | 1.520 | 1.487 | 1.464 | 1.517 | |
| SD | 0.208 | 0.232 | 0.226 | 0.232 | 0.333 | 0.369 | 0.672 | ||
| Scenario 4 | Mean | 1.800 | 1.876 | 1.890 | 2.003 | 1.935 | 1.974 | 2.162 | * |
| SD | 0.294 | 0.252 | 0.276 | 0.366 | 0.371 | 0.475 | 0.829 | ||
| Scenario 5 | Mean | 1.519 | 1.484 | 1.545 | 1.522 | 1.537 | 1.526 | 1.452 | |
| SD | 0.250 | 0.197 | 0.227 | 0.246 | 0.294 | 0.406 | 0.661 | ||
| Scenario 6 | Mean | 1.967 | 1.920 | 1.961 | 2.036 | 2.091 | 2.146 | 2.233 | * |
| SD | 0.310 | 0.306 | 0.290 | 0.344 | 0.410 | 0.548 | 0.880 | ||
We applied the diagnostic we have just introduced to the Cache County data described in Section 3.4: The CHR as a function of joint survival function S(t) ranged from 1.01 to 1.34. This calls into question the assumption of a gamma frailty model for the failure times, and supports the non-parametric analyses conducted in the papers by Bandeen-Roche & Liang (2002) and Bandeen-Roche and Ning (2008).
4. Sensitivity to assumption 2: Independence of size and shape frailty
The simplicity of the Bandeen-Roche and Liang method becomes possible by assuming that the size frailty A and the shape frailty B(x) are statistically independent. This means that the overall tendency to fail early or late should not relate to the propensity to fail of a specific cause at any time. This assumption allows the CCSHR (Equation (6)) to be decomposed into multiplicands which respectively characterize the propensity to fail from a particular cause and dependence in the timing of one’s earliest failure regardless of cause.
In this section we evaluate the e ect which the dependence structure between the size and the shape frailty has on estimation of the CCSHR when the size frailty A is gamma distributed and the shape frailty B(x) is beta distributed. Assuming only the ‘size-shape frailty’ framework and not the independence of A and B(x),
| (11) |
where . This is Equation (9) in Bandeen-Roche and Liang (2002). Equation (10) in this paper,
| (12) |
on the other hand, decomposes based on the assumption that A and B(x) are independent. Thus the effect of the assumption of in-dependence between A and B(x) can be assessed by directly comparing the CCSHR calculated by Equation (11) and parametrically estimated using Equation (12).
In this section, we will approximate true values of the CCSHR for various degrees of dependence between size and shape frailty. Then we compare them with parametric and nonparametric estimates of CCSHR.
4.1. Methods
First, we studied the difference between the CCSHR surfaces as functions of t1 and t2 when A and B(x) are independent versus dependent. To approximate these surfaces, we generated a random sample of 2000 realizations of size frailty A and shape frailty B, with scenario-specific details to follow shortly. CCSHR1,1, CCSHR1,2, and CCSHR2,2 were obtained using Equation (11), replacing expectations by sample means and using . These CCSHRs were evaluated on a grid consisting of Cartesian products of 1st to 99th percentiles of failure time points generated from an exponential distribution as in the first set of simulation studies in Section 3.
For an independent case, we generated gamma-distributed size frailty A with mean 1 and variance 1 and time-invariant, beta-distributed shape frailty B with parameters 0.2 and 0.8 sampled independently from A. To construct a dependent sample (A*, B*) from A and B, we generated a bivariate standard normal-distributed sample with a pre-specified correlation value. We obtained ranks within the first components of the bivariate sample and ranks within the second components; then we re-ordered A and B yielding A* with the same ranks as the first components of the bivariate sample and B* with the second components.
After studying the effect of varying the joint distribution of A and B on the true CCSHR values, we evaluated the performance of the Bandeen-Roche and Liang’s parametric and nonparametric estimator when A and B are not independent. The parametric estimator of CCSHR was obtained by plugging in maximum likelihood estimates of R1 and Δ from the beta distribution model into Equation (7). We implemented the time-invariant nonparametric estimator of CCSHR described by Bandeen-Roche and Liang (2002) for the CCSHR between cause 1 and cause 1. This estimator compares concordances and discordances for parings of pairs, where a concordance occurs if both failure times of cause 1 for one pair in the pairing are greater than both failure times of cause 1 in the other pair in the pairing, and a discordance occurs otherwise. If all four members of a pairing were observed to fail of cause 1, then a concordance or discordance can be confirmed. If the smaller observation among the first components of the two pairs and the smaller one among the second components were observed to fail of cause 1, then we can confirm concordance/discordance status since the concordance/discordance among observed or latent cause 1 failure times coincides with that among observed (minimum) failure times. On the other hand, either in the first components or the second components, if the smaller observation failed of cause 2, then we cannot decide whether it is concordant or discordant.
4.2. Results
When A and B are statistically independent, θCS(x1, x2; 1, 1) = 6 for all (x1, x2), and indeed our approximation of this function using the method described in the first paragraph of the previous section was virtually constant near 6. As the correlation of the bivariate normal distribution used to generate dependence between A and B increased, we observed the CCSHR to increase throughout the (x1, x2) space (Figure 1), particularly rapidly in the upper-right region. Conversely, the CCSHR decreased throughout the (x1, x2) space as the correlation decreased below 0. Table 7 displays CCSHR values at three diagonal (x, x) points. Our work further indicates that the CCSHR increases with x1 and x2 when A and B are positively correlated and decreases with x1 and x2 when A and B are negatively correlated(Figure 1). As electronic supplementary material we present CCSHR contour plots for various degrees of dependence between A and B.
Fig. 1.
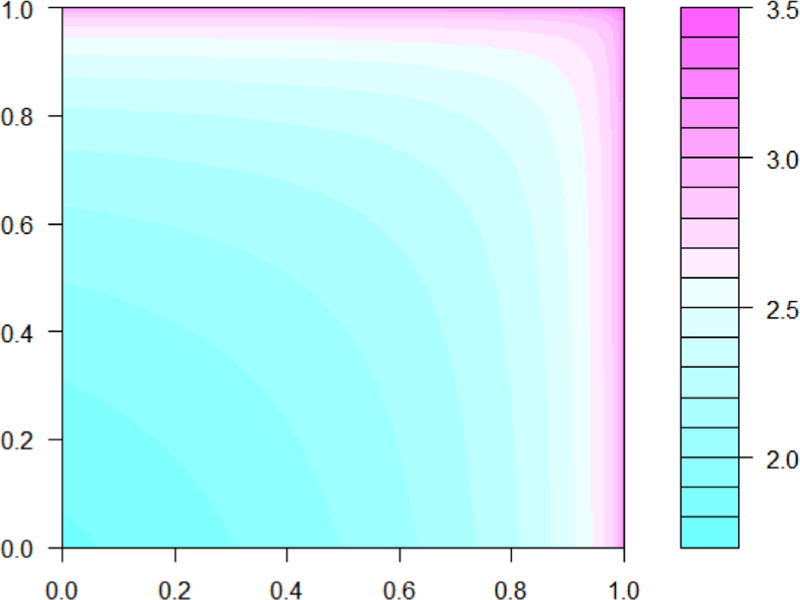
Contour plot of log(CCSHR1,1) when the correlation of the bivariate normal distribution inducing dependence between A and B (Section 4.1) is 0.4. The horizontal and vertical axes are failure time percentiles.
Table 7.
CCSHR1,1 values resulting for three values of (x, x) and various degrees of correlation between A and B
| Correlation | CCSHR1,1(0.2, 0.2) | CCSHR1,1(0.5, 0.5) | CCSHR1,1(0.8, 0.8) |
|---|---|---|---|
| 1 | 7.909 | 20.857 | 115.207 |
| 0.7 | 7.275 | 11.992 | 26.169 |
| 0.4 | 6.640 | 8.234 | 12.061 |
| 0 | 5.977 | 6.074 | 6.421 |
| −0.5 | 4.514 | 3.882 | 3.213 |
| −1 | 1.614 | 1.295 | 1.315 |
Global (time-invariant) estimates of CCSHR1,1 are presented for comparison: the 2nd column of Table 8 presents parametric estimates of CCSHR as in Bandeen-Roche and Liang (2002), and the 3rd column presents nonparametric estimates of CCSHR1,1. Since the parametric estimation does not take the dependence between A and B into consideration, the estimates for all correlation values were close to 6, the true value under independence. In contrast, the nonparametric estimates of the CCSHR increase as the correlation increases, resembling the pattern of underlying values of the CCSHR.
Table 8.
Comparison of parametric and nonparametric estimates of CCSHR1,1 for various degrees of dependence between A and B
| Correlation | Parametric |
Nonparametric |
|---|---|---|
| Mean (SD) | Mean (SD) | |
| 1 | 5.992 (0.296) | 8.150 (0.566) |
| 0.7 | 6.001 (0.290) | 7.871 (0.552) |
| 0.4 | 6.005 (0.283) | 7.266 (0.559) |
| 0 | 6.000 (0.296) | 6.040 (0.505) |
| −0.5 | 6.008 (0.299) | 3.892 (0.355) |
| −1 | 5.994 (0.301) | 1.344 (0.14) |
5. Discussion
This paper addressed association among paired failure times subject to a competing risk, as defined by conditional cause-specific hazard ratios (CCSHRs), and estimated in the parametric framework proposed by Bandeen-Roche and Liang (2002). This framework partitions the CCSHR into two factors—one reflecting association between times to earliest failure regardless of cause (overall hazard ‘size’) and a second reflecting association between the causes of failure (cause allocation ‘shape’). We implemented a new estimator in this framework based on a logit-normal shape frailty distribution and compared its performance with an existing one based on a beta shape frailty distribution, in data scenarios generated from each distribution within the framework as well as scenarios outside the framework. We also studied the effect of dependence between overall failure propensity and the allocation of this among causes on the CCSHR magnitude and temporal variation, and we evaluated the robustness of the Bandeen-Roche and Liang estimator of the CCHSR to such dependence. We found little difference in estimator performance between the two shape-generating distributions but large implications of dependence between size and shape frailty for the magnitude and temporal variation of failure time associations hence for estimator performance.
When size and shape were generated independently, both beta- and logit-normal-based estimators estimated the CCSHR accurately when data were generated according to the Bandeen-Roche and Liang framework, regardless of the underlying shape distribution. When data were generated according to models outside the Bandeen-Roche and Liang framework, both estimators exhibited biases comparable to those observed in the 2002 paper; however, based on our application of diagnostics for model fit, we suspect that this owes primarily to mis-modeling of the association in first failure times (‘size’ association) rather than sensitivity to the ‘shape’ distributional assumption. We conclude that parametric estimation of shape component of CCSHR will adequately estimate the CCSHR in many circumstances, provided that association in first failure times is characterized carefully as a function of time. The estimator employing a beta distribution assumption was comparably accurate and precise as the logit-normal-based estimator, hence we recommend both for paired failure-time data.
Independence between the size and shape frailty is a key feature enabling the simplified likelihood formulation in the Bandeen-Roche and Liang framework. Dependence in size and shape induces a mathematically complex likelihood form as well as a complicated time dependence of the resulting CCSHR. It remains to be seen whether a simply estimable, and interpretable, methods can be developed to accommodate this scenario. We conjecture that this model is only weakly identi able from one in which independence of size and shape frailty is maintained but the overall (‘size’-dependent) association is allowed to vary arbitrarily with time. If so, one might retain a parametric estimation of shape component of CCSHR together with nonparametric estimation of size component, a flexibly time-varying conditional hazard ratio with CC-SHR estimator as a multiplication of shape and size components. In such an approach, methods which accommodate estimation of a time varying ratio of cause-specific to overall hazard, R(t), within the shape component of CCSHR (Equation (7)) may well be needed.
A limitation of our work is that we have only evaluated scenarios with two competing causes and two candidate shape distributions. The similarity we observed in estimator performance comparing beta and logit-normal models, as well as for generalized beta distributions (data not shown), is not surprising because logit-normal and Dirichlet distributions closely approximate each other when there are only two categories to be modeled. More substantive differences likely would emerge for 3 or more competing causes, because the logit-normal distribution admits more exible correlation structures in this case.
We believe there is merit in distinguishing contributions to associations among clustered failures of multiple types into shared overall failure risk and shared failure cause propensities. Multimorbidity–an important and common setting in which clustered failures of multiple types arises–may reflect, both, individuals’ overall vulnerability to physiological declines and disease-specific mechanisms (Varadhan et al., 2014 [20]). By partitioning disease heritability into these two components, methodology as discussed in this paper could inform the etiology of psychiatric disorders, metabolic syndrome, frailty in aging, and other medical syndromes. Whether the partitioning proposed here well addresses this goal, or alternative means and measures for achieving the goal are needed, frames another area of needed work.
A Generation of correlated failure times with marginally exponential distribution
To generate ‘disease’ failure time of the first component of a pair, we generated gamma distributed random numbers as in the third set of simulation studies (see methods). Then we used the fact that is exponentially distributed where U is uniformly distributed, l1 is the exponential parameter, and A is gamma distributed with a shape parameter 1/(t − 1) and a scale parameter 1. The ‘disease’ failure time for the second component and the ‘death’ failure times for two components were generate similarly.
To see that this method yields the distributions as claimed, let us consider a univariate frailty model with a random effect denoted by α, with distribution G and Laplace transformation , where the marginal survival function for individual j in the cluster is . Then, , that is, where q is the inverse function of p (See Equation (1) of Bandeen-Roche and Liang (1996)).
For exponential distribution, and for Claytoncopula, . Thus,
| (13) |
For gamma frailty, conditionally on frailty, is uniformly distributed, thus . Then,
| (14) |
Supplementary Material
References
- 1.Aitchison J: The statistical-analysis of compositional data. Journal of the Royal Statistical Society Series B-Methodological 44(2), 139–177 (1982) [Google Scholar]
- 2.Aitchison J, Shen SM: Logistic-normal distributions - some properties and uses. Biometrika 67(2), 261–272 (1980) [Google Scholar]
- 3.Bandeen-Roche K, Liang KY: Modelling multivariate failure time associations in the presence of a competing risk. Biometrika 89(2), 299–314 (2002) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bandeen-Roche K, Ning J: Nonparametric estimation of bivariate failure time associations in the presence of a competing risk. Biometrika 95(1), 221–232 (2008) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bandeen-Roche K, Ruppert D: Source apportionment with one source unknown. Chemometrics and Intelligent Laboratory Systems 10(1–2), 169–184 (1991) [Google Scholar]
- 6.Chen MC, Bandeen-Roche K: A diagnostic for association in bivariate survival models. Lifetime Data Analysis 11(2), 245–264 (2005) [DOI] [PubMed] [Google Scholar]
- 7.Cheng Y, Fine JP, Bandeen-Roche K: Association analyses of clustered competing risks data via cross hazard ratio. Biostatistics 11(1), 82–92 (2010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cheng Y, Fine JP, Kosorok MR: Nonparametric association analysis of bivariate competing-risks data. Journal of the American Statistical Association 102(480), 1407– 1415 (2007) [Google Scholar]
- 9.Cheng Y, Fine JP, Kosorok MR: Nonparametric association analysis of exchangeable clustered competing risks data. Biometrics 65(2), 385–393 (2009) [DOI] [PubMed] [Google Scholar]
- 10.Clayton DG: Model for association in bivariate life tables and its application in epidemiological-studies of familial tendency in chronic disease incidence. Biometrika 65(1), 141–151 (1978) [Google Scholar]
- 11.Dabrowska DM: Kaplan-meier estimate on the plane. Annals of Statistics 16(4), 1475–1489 (1988) [Google Scholar]
- 12.Gorne M, Hsu L: Frailty-based competing risks model for multivariate survival data. Biometrics 67(2), 415–426 (2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.van der Laan MJ: Nonparametric estimation of the bivariate survival function with truncated data. Journal of Multivariate Analysis 58(1), 107–131 (1996) [Google Scholar]
- 14.Prentice RL: Self-consistent nonparametric maximum likelihood estimator of the bivariate survivor function. Biometrika 101(3), 505–518 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Prentice RL, Cai J: Covariance and survivor function estimation using censored multivariate failure time data. Biometrika 79(3), 495–512 (1992) [Google Scholar]
- 16.Pruitt RC: On negative mass assigned by the bivariate kaplan-meier estimator. Annals of Statistics 19(1), 443–453 (1991) [Google Scholar]
- 17.R Core Team: R: A language and environment for statistical computing (2013) [Google Scholar]
- 18.Scheike TH, Sun YQ, Zhang MJ, Jensen TK: A semiparametric random e ects model for multivariate competing risks data. Biometrika 97(1), 133–145 (2010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shih JH, Louis TA: Inferences on the association parameter in copula models for bivariate survival data. Biometrics 51(4), 1384–1399 (1995) [PubMed] [Google Scholar]
- 20.Varadhan R, Xue QL, Bandeen-Roche K: Semicompeting risks in aging research: methods, issues and needs. Lifetime Data Analysis 20(4), 538–562 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Vaupel JW, Manton KG, Stallard E: The impact of heterogeneity in individual frailty on the dynamics of mortality. Demography 16(3), 439–54 (1979) [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


