Anthropogenic Aerosol Indirect Effects in Cirrus Clouds

Abstract

We have implemented a parameterization for forming ice in large‐scale cirrus clouds that accounts for the changes in updrafts associated with a spectrum of waves acting within each time step in the model. This allows us to account for the frequency of homogeneous and heterogeneous freezing events that occur within each time step of the model and helps to determine more realistic ice number concentrations as well as changes to ice number concentrations. The model is able to fit observations of ice number at the lowest temperatures in the tropical tropopause but is still somewhat high in tropical latitudes with temperatures between 195°K and 215°K. The climate forcings associated with different representations of heterogeneous ice nuclei (IN or INPs) are primarily negative unless large additions of IN are made, such as when we assumed that all aircraft soot acts as an IN. However, they can be close to zero if it is assumed that all background dust can act as an INP irrespective of how much sulfate is deposited on these particles. Our best estimate for the forcing of anthropogenic aircraft soot in this model is −0.2 ± 0.06 W/m², while that from anthropogenic fossil/biofuel soot is −0.093 ± 0.033 W/m². Natural and anthropogenic open biomass burning leads to a net forcing of −0.057 ± 0.05 W/m².

Key Points

• A new version of the CAM/IMPACT atmospheric model that includes gravity waves and the effect of aerosols on cirrus clouds is presented

• The best representation of the particles that act as ice nuclei results in a climate forcing of −0.2 W/m² for aircraft soot

• The use of all dust particles as ice nuclei lowers this forcing to near zero

1. Introduction

Ice in cirrus clouds can form through either homogeneous freezing of supercooled aqueous solutions (Koop et al., 2000) or through different mechanisms of heterogeneous nucleation (deposition, contact, immersion, and condensation) triggered by insoluble aerosol particles, termed heterogeneous ice nuclei (IN; Pruppacher & Klett, 1997) or ice nuclei particles (INPs). The aerosol indirect effect in cirrus clouds is complicated because of these two very different and competing ice nucleation processes. Homogeneous freezing of supercooled aqueous solutions, such as mixed sulfate haze particles, requires high relative humidity with respect to ice (RHi): greater than 145% if temperatures are less than 235 K (Koop et al., 1998). As sulfate haze particles are ubiquitous and abundant in the upper troposphere (several hundred cm⁻³ in the Aitken mode outside of the tropics (e.g., Minikin et al., 2003) and as large as several 1,000 cm⁻³ in the tropics, Clarke & Kapustin, 2002), the nucleated ice number can be easily more than 1 cm⁻³ or even more than 10 cm⁻³ if homogeneous freezing occurs. On the other hand, heterogeneous nucleation triggered by insoluble INPs, like dust particles and soot (i.e., black carbon, BC, and its associated organic carbon, OC), requires much lower ice supersaturations. Though our understanding of the ability of aerosol particles serving as heterogeneous INPs is still limited (Hoose & Möhler, 2012), the number of INPs is generally thought to be small relative to the number of sulfate haze particles. According to the estimate of Hendricks et al. (2005), which was based on in situ observational results by Rogers et al. (1998), INP concentrations larger than 0.5 cm⁻³ in the upper troposphere and lower stratosphere are comparatively rare (~60% of the measured INP concentrations are smaller than 0.01 cm⁻³, and ~95% are smaller than 0.1 cm⁻³). Since heterogeneous nucleation requires lower ice supersaturations, it can occur prior to homogeneous nucleation in a rising air parcel, and the newly formed ice crystals can consume the available water vapor above ice saturation thereby inhibiting homogeneous freezing, if there are enough INPs and the cooling rate is moderate. Thus, the addition of aerosol INPs to a rising air parcel can lead to reduced ice numbers. This effect is termed the negative Twomey effect (Kärcher & Lohmann, 2003). The magnitude of this effect depends on the updraft velocity, temperature, and the number and freezing properties of the ice nuclei (Jensen & Toon, 1994). If heterogeneous INPs are added to a parcel already dominated by heterogeneous IN particles, they lead to increases in ice crystal numbers similar to the Twomey effect from adding more soluble aerosols in liquid clouds.

These competing effects can cause both net positive and net negative forcing, depending on whether homogeneous or heterogeneous nucleation dominates prior to the addition of heterogeneous IN. Shortwave and longwave cirrus cloud radiative effects are sensitive to the cirrus cloud optical depth, which depends on the ice crystal diameter (or equivalently, the number concentration, if the ice water path, IWP, is constant). The absolute value of the negative shortwave radiative effect is generally smaller than the absolute value of the positive longwave radiative effect (Penner et al., 1999), thereby explaining the general warming effect of cirrus clouds. If the optical depth increases in a cirrus cloud, both the longwave and shortwave radiative effects increase, causing a positive forcing. However, because heterogeneous IN can both increase and decrease ice number concentrations, the addition of heterogeneous IN to an air parcel can both increase and decrease the optical depth. If the optical depth increases (as when heterogeneous IN are added to a parcel in which heterogeneous IN dominate), this will lead to increases in the net positive radiative effect of a cirrus cloud leading to a net positive radiative forcing. A decrease in optical depth, as in the negative Twomey effect, will lead to a decrease in the net positive radiative effect of a cirrus cloud causing a net negative forcing. We also note that since the negative Twomey effect increases the size of the ice crystals, the optical depth can further decrease through sedimentation (Gasparini & Lohmann, 2016). Zhou and Penner (2014) demonstrated how different formulations and predictions of the number of heterogeneous and homogeneous ice‐nucleating particles in models used to predict aircraft soot forcing can lead to climate forcings that differ in sign as well as magnitude.

Differences in the number concentrations of heterogeneous and homogeneous ice forming particles in models are partly a result of model choices, as well as different aerosol modeling techniques. For example, the IMPACT aerosol model predicts separate nucleation, Aitken, and accumulation modes for pure sulfate particles and follows the coagulation of these particles with other aerosol types, while the standard CAM5 model only treats internally mixed sulfate aerosols in the Aitken, accumulation, and coarse modes (Liu et al., 2012, 2016). Thus, the former model has a direct prediction of the haze particles that might nucleate homogeneously, while the latter requires one to assume the fraction of sulfate that would not be mixed with solid phase particles in order to calculate the number concentrations of haze particles. As a result of these different model treatments, the IMPACT model predicts much higher Aitken‐mode particle number concentrations than does the standard CAM5 treatment (see Figure S1 in Penner et al., 2015). In addition, in the past, the IMPACT/CAM has always included all dust size modes as possible heterogeneous ice nuclei, whereas the standard CAM5 only included the coarse mode.

Other differences include that some models only treat heterogeneous ice nucleation on dust particles (Kuebbeler et al., 2014), while others have also considered fossil fuel and biofuel soot as well as particles produced from open biomass burning (Gettelman et al., 2012; Wang & Penner, 2010). Other model treatments have also considered secondary organic aerosols (SOAs; Penner et al., 2015; Zhou et al., 2016) or crystalline ammonium sulfate particles (Abbatt et al., 2006).

Another source of differences in the prediction of ice crystals in cirrus clouds has to do with assumptions regarding the subgrid scale updraft velocity used in the nucleation scheme (or equivalently the cooling rate). For example, Penner et al. (2009) used a probability distribution of updraft velocities based on in situ observations, while Wang and Penner (2010) used a single updraft velocity based on the standard deviation of mesoscale temperature fluctuations associated with gravity waves as reported by Gary (2006, 2008). On the other hand, the standard procedure used in CAM is to set the updraft velocity to the square root of two thirds of the predicted turbulent kinetic energy, but to limit the updraft to less than 0.2 m/s to prevent the formation of ice number concentrations that are too high (Liu et al., 2012). The standard ECHAM model uses a subgrid scale updraft calculated from

$$w=w_{\mathrm{LS}}+0.7\sqrt{\mathit{TKE}}$$

where w _LS is the large‐scale updraft and TKE is the turbulent kinetic energy. Kuebeller et al. (2014) on the other hand, reformulated the updraft in ECHAM to explicitly model orographically produced gravity waves, according to

$$w=w_{\mathrm{LS}}+k·U·min\left(\mathit{\delta h},\delta h_{\mathrm{sat}}\right)$$

where k is the wave number (related to the width of the mountain), U is the horizontal wind speed, δh the amplitude of a gravity wave (determined by the height of the mountain), and δh _sat the saturation amplitude of a gravity wave (see Joos et al., 2008). The updraft using this formulation is considerably larger than that based on the TKE (Joos et al., 2008). Figure S1 in the supporting information shows the subgrid scale updrafts determined in the standard CAM formulation and that used by Wang and Penner (2010) and Wang et al. (2014), which are based on Gary (2006, 2008). Because homogeneous nucleation will be preferred at high subgrid scale velocities, differences in the treatment of subgrid scale updraft velocities will lead to differences in predicted ice number concentrations (see also Zhou et al., 2016).

Finally, differences in model results arise because of differences in the treatment of preexisting ice during the nucleation step. Kuebbeler et al. (2014) was the first model to treat the presence of preexisting ice during the nucleation process. They found that this addition lowered the predicted supersaturations within ice clouds and, for a representation that included heterogeneous nucleation on dust and coated dust, competing with homogeneous nucleation found good agreement of their predicted RHi with observations within ice clouds. However, due to their treatment of cloud fraction, all new ice particles were formed within clouds. Shi et al. (2015) added preexisting ice during nucleation in CAM5, and this allowed them to remove the tuning procedure that limited updraft velocities to less than 0.2 m/s in the standard CAM5. Zhou et al. (2016) examined the ability of different updraft and preexisting ice treatments to fit observed ice number concentrations using three different treatments for the mean updraft velocity, different treatments of preexisting ice, the inclusion of 0.1% of SOA particles as ice nuclei as well as two different accommodation coefficients (0.1 and 1.0) for water vapor deposition on ice.

To estimate the effect of anthropogenic aerosols on cirrus clouds in a model, one needs to correctly take account of the competition between heterogeneous IN and homogeneous haze particles during ice formation. Parameterizations for ice formation in cirrus clouds for use in general circulation models (GCMs) have been developed using empirical fitting or analytical formulas from air parcel models that determine the formation of ice in a rising air parcel (Barahona & Nenes, 2009; Kärcher et al., 2006, hereafter KL; Liu & Penner, 2005). In these parameterizations, the soluble haze droplet number, the updraft velocity (or cooling rate) associated with the rising parcel, and the number concentration of heterogeneous IN are the three most important parameters. As large haze particles generally freeze first via homogeneous freezing, the total haze droplet number and size is an important parameter. The updraft velocity determines the adiabatic cooling rate of a parcel, and together with deposition of water vapor onto growing particles, determines how fast the ice supersaturation grows in the rising parcel. The heterogeneous INP number determines how many ice crystals can form prior to the ice supersaturation required by homogeneous freezing and thus determines whether homogeneous freezing can be inhibited. In most ice nucleation parameterizations, it is assumed that the relevant time scale for ice nucleation (i.e., a few minutes) is sufficiently short such that the vertical velocity and associated adiabatic cooling rate can be assumed to be constant over the climate model time step, usually of order 30 min (e.g., Barahona & Nenes, 2008; Kärcher et al., 2006; Liu & Penner, 2005).

While ice formation is thought to be controlled by the vertical velocities associated with gravity waves, none of the aforementioned GCM studies follow the formation of ice throughout the time variations in the updrafts and downdrafts associated with gravity waves. Rather, they assume a single updraft (or a probability density distribution of updrafts) and predict the ice number concentration assuming this updraft holds until a steady state ice number concentration is reached. This is not actually what one anticipates when gravity waves are superposed with large‐scale updrafts such as those associated with Kelvin or Rossby waves (Spichtinger & Krämer, 2013). Here we add an improved ice nucleation scheme based on nucleation predicted using the KL simplified parcel model in the CAM5 model. We use a parameterization of the spectrum of observed gravity waves presented by Podglajen et al. (2016). Thus, instead of assuming a constant updraft velocity, we used the fitted wave spectrum from the superpressure balloon observations by Podglajen et al. (2016), which accounts for the fluctuations of vertical velocities as well as the vertical stratification of atmospheric stability. This is the first ice nucleation parameterization implemented in a GCM that we are aware of which uses a wave spectrum instead of constant updraft velocities.

In this application, we did not include the deposition of water vapor onto pre‐existing ice during nucleation. Primarily, this choice is dictated by the fact that within the CAM model, the cloud fraction is first updated at the new time step (the cloud fraction is determined by the grid box averaged RH). When this takes place, one does not know if the cloud that forms is newly formed, had already existed at the previous time step, or is partially newly formed. If the ice cloud fraction or some of the cloud fraction was present during the previous time step, not including the rate of vapor deposition onto existing ice will overestimate ice number, since without deposition onto existing ice, the supersaturation predicted within the KL model can be too large. Alternatively, one can assume that all new ice formation takes place within clouds but use the grid average ice number concentration to determine the rate of deposition of water onto pre‐existing ice, as do Shi et al. (2015) and Kuebbeler et al. (2014). This procedure is also incorrect, although, since the grid average ice number is smaller than the in‐cloud ice number, the use of this smaller ice number may somewhat account for the fact that some ice nucleation is expected within ice‐free portions of the grid. Ideally, one must determine the newly formed cloud fraction within the ice‐free portion of the grid and average this new ice with the ice number carried and/or newly formed in the existing cloud fraction from the previous time step, as did Wang and Penner (2010), to correctly predict the new grid average ice number to carry forward. Here, however, we use the expedient choice of using the grid box average RH to determine if ice forms under cloud‐free conditions. If it does and this ice number is larger than the ice number in existing clouds, we replace it. This method will overestimate ice number if there is preexisting ice and the cloud fraction does not increase, but underestimates ice number if cloud fraction increases, and the RH is in between that from the previous time step and the current step. We examine our predicted ice number concentration in comparison with observations as a method for calibrating any over‐prediction.

In section 2, we describe the aerosol model and treatment of INPs, section 2 further describes the implementation of the gravity wave parameterization of Podglajen et al. (2016), section 3 compares our model results with observations, and section 4 presents results for the forcing by anthropogenic INPs forming ice in cirrus clouds. Section 5 presents a summary and our conclusions.

2. Methods

2.1. Treatment of Homogeneous and Heterogeneous Ice Forming Aerosol Particles

For this study, we used a modified version of the NCAR CAM5.3 model coupled to the IMPACT aerosol model (Zhou & Penner, 2014). We used the specified dynamics version of CAM, where the winds were nudged toward ECMWF wind fields using a nudging time of 6 hr for the years 2006–2011 (Zhang et al., 2014). We use the three‐size mode representation of the number and mass of pure sulfate aerosols and their interactions with other aerosol types (Herzog et al., 2004; Liu et al., 2005; Weisenstein et al., 2007) in the University of Michigan global aerosol model (IMPACT). The IMPACT model includes a sulfate‐initiated boundary layer nucleation scheme (Wang & Penner, 2009), together with the version that treats three fossil fuel soot (i.e., primary particulate organic matter, POM, and its associated BC) aerosol types: hydrophobic (less than one monolayer of sulfate); hydrophilic (one to three monolayers sulfate), and hygroscopic (greater than three monolayers sulfate; Yun et al., 2013). This allows us to account for observations that show that only hydrophobic and hydrophilic soot aerosols may act to heterogeneously nucleate ice crystals at supersaturations below that of homogeneous nucleation (Koehler et al., 2009). In total, this version of the IMPACT aerosol model distinguishes 17 different non‐SOA aerosol modes or types: three pure sulfate modes, three fossil fuel soot modes, two aircraft soot modes (preconditioned by inclusion in contrails to form ice at lower supersaturations and not preconditioned; see Zhou & Penner, 2014), one biomass soot mode, four size‐differentiated dust modes, and four size‐differentiated sea salt modes. We also have the capability to read in the total concentration of SOA, with the natural and anthropogenic sources of the latter predicted by a separate version of the IMPACT model (Lin et al., 2012, 2014). Each nonsulfate aerosol type also carries information about how much sulfate has been deposited on it or coagulated with it. We added this level of detail in order to properly estimate the number of particles present in the troposphere for both warm‐cloud studies of indirect effects as well as to differentiate the ice nucleation capabilities of different aerosols (Wang & Penner, 2009; Yun et al., 2013; Zhou & Penner, 2014).

Table 1 summarizes the INP aerosol size distributions and other properties that affect their abilities to act as heterogeneous ice nuclei. We also explore the potential for dust with varying amounts of sulfate to act as IN. Cziczo et al. (2009) studied Arizona test dust particles at temperatures from −20 to −45 °C and showed that particles coated with sulfate required higher supersaturations, often similar to that of pure aqueous solutions, and thus were not effective heterogeneous ice nuclei. Therefore, most of our simulations do not use dust as a heterogeneous IN unless there are fewer than three monolayers of sulfate as a coating. This treatment is consistent with the results of field studies by DeMott et al. (2003), Cziczo et al. (2004), and Richardson et al. (2007). Cziczo et al. (2004) report that dust particles in ice crystal residuals measured during the CRYSTAL‐FACE campaign over Florida had very little sulfate or other soluble material associated with them even though the dust had traveled from Africa over a period of more than 5 days (DeMott et al., 2003). In addition, Richardson et al. (2007) studied dust present in spring at the Storm Peak Laboratory and showed that the particles that were counted as IN in the Colorado State University Continuous Flow Diffusion Chamber (CFDC) instrument only had small amounts of soluble sulfates or organics. Despite this field evidence, we test one case where all dust can act as heterogeneous ice nuclei. This mimics to some extent previous model treatments by Kuebbeler et al. (2014), who allow the dust particles with deposited sulfates to act as immersion freezing ice nuclei, consistent with some laboratory studies of dust (Hoose & Möhler, 2012).

Table 1.

Parameters for Aerosols Used in Ice Nucleation Scheme

			Size distribution
Aerosol component	Relative humidity for activation	Fraction that may activate	Mass fraction in size	r i (μm)	σi	Reference for size	Density (g/cm3)
Fossil/bio‐fuel OM/BC	135%	0.05% and 0.1%a	1.0	0.07	1.5	Pueschel et al. (1992)	1.5
Biomass OM/BC	135%	0.1%b	1.0	0.07	1.5	Pueschel et al. (1992)	1.0
Aircraft OM/BC	135%	0.6%c	1.0	0.038	1.6	Barrett et al. (2010)	1.0
Dust	120%	1%d	0.152	0.01	2.3	de Reus et al. (2000)	2.6
			0.727	0.045	1.6
			0.121	0.275	2.5
SOA	135%	20%–30%e	1.0	0.07	1.5	Pueschel et al. (1992)	1.0
Crystalline sulfate	120%	20%f		r > 0.05	1.5	Calculated, Herzog et al. ( 2004)	1.7

Note. OM = organic matter; BC = black carbon; SOA = secondary organic aerosol; INP = ice nuclei particle; RHi = relative humidity with respect to ice.

^aNote that 0.05% is applied for particles with less than one monolayer of sulfate and 0.1% is applied for particles with one to three monolayers of sulfate based on Koehler et al. (2009).

^bPratt et al. (2011).

^cFractions that have previously frozen in contrails and have less than three monolayers of sulfate. Note that we assume or emissions are nonvolatile based on Petzold and Schröder (1998) and Petzold et al. (2003).

^dFraction with less than three monolayers of sulfate at about 200 hPa (see Figure S2).

^eEquations (3) and (4) in Wang et al. (2012) were applied to determine the fraction of 30% of the total SOA that could act as an INP, resulting in 20–30% able to act as INP for T < −40 °C (see Figure S3).

^fThe fraction of accumulation mode sulfate (r > 0.05 μm) particles that have undergone freezing (i.e., experienced <34% RHi). Three modes of nucleated sulfate particles are followed: r < 0.005 μm, 0.005 to 0.05 μm, and r > 0.05 μm, with assumed geometric mode radius of 1.5 (Herzog et al., 2004; Penner et al., 2009; see Figure S4).

We also assume that 0.1% of biomass particles are good IN based on field observations of soot from biomass fires (at −34 °C; e.g., Pratt et al., 2011), although Prenni et al. (2012) report smaller fractions at −30 °C. We use 0.05% and 0.1% of our predicted fossil/biofuel soot as an effective IN if they have less than one monolayer of sulfate and one to three monolayers of sulfate, respectively. These choices are based on the study by Koehler et al. (2009) who report that between 0.01% and 0.1% of their less hygroscopic soots from the fossil fuels they tested act as good IN (at supersaturations near 140% RHi) at low temperatures (−51 °C). Hygroscopic fossil/biofuel soot (i.e., containing greater than three monolayers of sulfate) does not act as a heterogeneous ice nuclei (Koehler et al., 2009). In addition, aircraft soot that has previously frozen as a result of being included as an INP in a contrail and has less than three monolayers of sulfate is considered a heterogeneous IN based on experimental data summarized in Zhou and Penner (2014). As a result, the fraction of total soot aerosol from aircraft that may act as heterogeneous IN is 0.6%.

Finally, we mention the role of SOA in ice nucleation. While a significant number of papers have noted the ability of SOA to form glassy particles, and subsequently to act as IN, most have primarily treated specific molecules, rather than the complex mixtures expected within atmospheric aerosols. Schill et al. (2014) summarize data showing the effective RHi for complex mixtures as well as simple sugars and acids. While most simple sugars and acids may form ice at lower RHi, complex organic glasses require RHi only slightly below homogeneous freezing thresholds. They further show that mixtures of ammonium sulfate with SOA formed in aqueous reactions of methylglyoxal and methylamine typically have an organic coating, but nucleate ice at RHi from 120% to 140% on ammonium sulfate crystalline islands at temperatures ranging from 230 to 215 °K. Since we find that most of our predicted SOA is mixed with sulfate aerosols (Zhu et al., 2017), this mechanism for ice formation is possibly of high importance. Thus, for our model simulations, we would expect that (NH₄)₂SO₄ could crystallize within an organic shell and this would dictate both the onset of ice nucleation and the fraction of particles that nucleate. The nucleation of ammonium sulfate and SOA measured by Schill et al. (2014) took place between an RHi of 120% and 140% depending on temperature. However, it is not clear what fraction of the mixed (NH₄)₂SO₄/organic particles might nucleate at these RHi. Here we approximate the nucleation of SOA assuming 30% of the organic/sulfate particles might nucleate ice at about 135% RHi. This is roughly consistent with the fractional composition of INPs that are organics/sulfates compared to the fractional composition of organics/sulfates in particles with D > 0.6 μm measured by Richardson et al. (2007). Ladino et al. (2014) also examined the nucleation efficiency of (NH₄)₂SO₄ mixed with the water soluble portion of alpha‐pinene SOA and found that the RHi needed for nucleation was about 1.4, while fresh alpha‐pinene SOA (or the water soluble portion) did not nucleate prior to homogeneous freezing conditions, unless it was preconditioned by cooling to 233 °K.

Note that Ladino et al. (2014) as well as Wagner et al. (2017) did not find that pure alpha‐pinene SOA was a good heterogeneous IN, in keeping with the behavior of complex organic mixtures of SOA summarized by Schill et al. (2014). However, Ignatius et al. (2016) recently measured the ice nucleation activation of alpha‐pinene‐produced particles. Unlike Ladino et al. (2014), their particles were able to nucleate at RHi of 130–140% at temperatures near −37 °C. Ignatius et al. (2016) produced their SOA at temperatures from −38 to −10 °C, ensuring that they would be in a semisolid or glassy state. In contrast both Ladino et al. and Wagner et al. produced their SOA particles at room temperature, although Wagner et al. concluded based on freeze‐drying experiments that they would be highly viscous (i.e., glassy) at the initial conditions present in their cloud chamber.

Based on the pure alpha‐pinene results reported in their paper, Wagner et al. (2017) speculated that organics in the Tropical Tropopause Layer (TTL) would not be effective heterogeneous ice nuclei despite their abundance (Froyd et al., 2009). Nevertheless, they discuss the liquefaction of initially glassy alpha‐pinene SOA that may occur as a result of the humidification that takes place within their cloud chamber. We note that this process would allow mixed ammonium sulfate‐SOA particles to act as immersion ice nuclei via the crystallization of (NH₄)₂SO₄ as outlined in Schill et al. (2014). Since, as noted above, we expect that most SOA is mixed with sulfate or (NH₄)₂SO₄ aerosols, this is the mechanism that may be of primary importance in the TTL. We test the possible impact of this mechanism in a simulation with SOA acting as a heterogeneous IN. We note that our use of an assumed externally mixed SOA number concentration as defining the number concentration for this heterogeneous IN experiment rather than crystalline (NH₄)₂SO₄ or mixed SOA‐(NH₄)₂SO₄ is a simplification. But since our number concentration of sulfate aerosols in the accumulation mode is not greatly changed in the internally mixed SOA simulation reported in Zhu et al. (2017), we think this simplification is acceptable. We used equations (3) and (4) in Wang et al. (2012) to determine the glass transition temperature and relative humidity for SOA that allows it to act as an INP but only applied these equations to 30% of our total SOA concentration.

We also test a simulation where crystalline (NH₄)₂SO₄ is able to act as a heterogeneous IN. To track the formation of these solid ammonium sulfate particles, we first predicted the ratio of ammonium to sulfate (ASR) to account for the spatial/temporal distributions of ammonium sulfate concentrations using the CAM5/MAM7 model (Liu et al., 2012). The ASR determines the neutralization level of sulfate aerosols. When this ratio is larger than 1.5, sulfate‐containing aerosols are in the form of ammonium sulfate. Otherwise the sulfate aerosols take other forms (e.g., ammonium bisulfate). We used the monthly average value of ASR from CAM5/MAM7 and assumed this same ASR would be applicable in the IMPACT model. We then tracked the efflorescence and deliquescence of ammonium sulfate, which is controlled by the history of the relative humidity with respect to water (RHw) that they experience. When RHw is below ~34%, ammonium sulfate becomes solid, and when RHw is above ~79%, it dissolves (Cziczo et al., 1997). Our results show that about 20% of the total simulated pure sulfate aerosol mass is in the solid state and is mainly distributed in the Northern Hemisphere from ~50 to ~200 hPa (Figure S4). We set the RHi at which these particles are able to form ice at 120% (Abbatt et al., 2006).

2.2. Parameterization for Ice Particle Nucleation

Our parameterization for ice particle nucleation is built upon the parameterized parcel model described in Kärcher et al. (2006). The Kärcher et al. (2006) parameterization is based on the solution of the equations of a cloud parcel model simulation (with some simplifications) using a chosen updraft velocity to determine the maximum RHi and the number of ice crystals that nucleate. We ran the parcel model using a time step of 1 s starting with the grid box average RHi as the initial condition. We tracked the rising or falling parcel following a discrete reconstructed updraft velocity series. The reconstructed updraft velocity is updated every 2.2 min as recommended by Podglajen et al. (2016) while all other atmospheric conditions (T, RHi, etc.) and ice particles properties (number and size) are updated every second. The integration stops after 30 min and the last computed ice number concentration is passed back as the grid box mean ice number concentration. The use of a constant updraft velocity for each 2.2‐min interval was based on fitting observed gravity wave behavior (see below). The parameterization accounts for the continuous competition between homogeneous and heterogeneous nucleation at any temperature and allows homogeneous nucleation to occur in the rising parcel even if some heterogeneous nucleation has already taken place as long as the supersaturation is able to continue to grow (see Kärcher et al., 2006). The fraction of soot (i.e., aircraft, fossil/biofuel, and biomass burning) and dust acting as heterogeneous IN were set to activate at an RHi of 135% and 120%, respectively, in this parameterization. The accommodation coefficient for water vapor deposition was set to 0.1.

We generated the series of updraft velocities (W) at each grid point using a combination of the methodology outlined in Podglajen et al. (2016) and Gary (2006, 2008). Formulas are given in the supporting information. Podglajen et al. (2016) measured wave‐induced Lagrangian fluctuations of temperature and vertical velocity using measurements from superpressure balloons flying near 19 km in the tropics and near 17 km poleward of 60°S. They propose a parameterization to fit their tropical measurements, which specifies a random time series of vertical velocities determined by a Laplace distribution with a standard deviation of 0.17 m/s. They specify a time interval of 2.2 min, so that the Nyquist frequency of a synthetic time series roughly coincides with a measure of the Brunt‐Väisälä frequency (N) in the stratosphere.

The wave series generated from Podglajen et al. (2016) lacks any global or seasonal variations. We extended these measurements to other latitudes and seasons by using the parameterization proposed by Gary (2006, 2008) who fit their aircraft measurements of temperature variations with a standard deviation which varies with latitude, season, and topography. This parameterization has been used in our previous studies (Wang & Penner, 2010; Zhou et al., 2016). Here the normalized global and seasonal variations are applied to the wave series generated from Podglajen et al. (2016) so that the annual mean standard deviation of the wave series is still 0.17 m/s at 19 km at the equator as measured by Podglajen et al. (2016).

Changes of this spectrum with altitude followed a combination of density scaling and scaling with the Brunt‐Väisälä frequency (N) following Podglajen et al. (2016). Thus, a factor of sqrt(0.02/N), where 0.02 s⁻¹ is close to the Brunt‐Väisälä frequency at the equator at 19 km, was used to reflect changes in vertical stratification, while a factor of (ρ/ρ ₀)^−0.5, where ρ ₀ is the density at 19 km in the tropics, was used to reflect changes in the wave amplitudes with altitude. We also tested one case where the time interval used for the vertical velocities in the Podglajen et al. (2016) spectrum varied with the Brunt‐Vaisala frequency at different altitudes. Thus, instead of a constant interval, dt, of 2.2 min, we used dt = 2.2 × (0.02/N). This may better reflect changes in the frequency of gravity waves expected throughout the atmosphere (J. Alexander, private communication, September 3, 2017).

Figure 1 shows our reconstructed probability density function of updraft velocities at 19 km in the tropics together with an example of a reconstructed wave series. As shown there, the updrafts and downdrafts reverse the phase of the waves with a time scale of minutes, which is close to the time scale of ice nucleation events. This suggests that the wave phase reversal of high‐frequency waves can inhibit ice nucleation events as suggested by Spichtinger and Krämer (2013).

Figure 1.

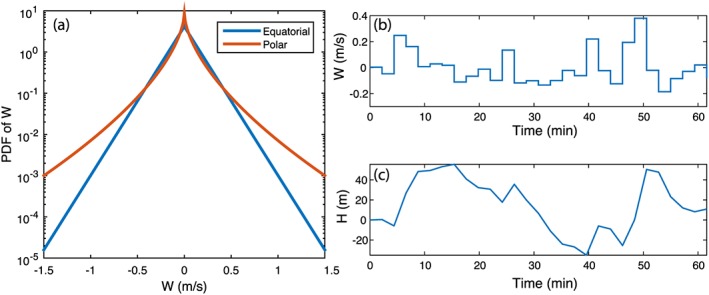
(a) The probability distribution of updraft velocities recommended by Podglajen et al. (2016). The polar pdf was developed from data that did not sample a full year. (b) A 1‐hr sample of updraft velocities from the Podglajen et al. (2016) parameterization. (c) As in (b) but for the vertical height of a parcel following the updrafts in (b). pdf = probability distribution frequency.

Figure 2 shows a histogram of the predicted ice number concentration (N _i) generated for 20,000 simulations of the parcel model using the probability distribution frequency (pdf) of updraft velocities for two different conditions, a cold cirrus using a standard deviation for the updraft velocities of 0.2 m/s and warmer conditions with a standard deviation of the updraft velocities set to 0.5 m/s. The sulfate number concentration was set to 200 cm⁻³, while dust concentrations were 10/L and 20/L, respectively. The parcel model generates two populations of ice number concentrations, with the higher number concentration representing primarily homogeneous nucleation on the sulfate aerosols, while the lower population represents primarily heterogeneous nucleation on dust particles. Also shown are the median and mean values of ice number concentrations as well as the value that would be predicted using a single updraft velocity set equal to the standard deviation of the gravity wave spectrum. The median value of N _i predicted using the pdf is significantly smaller than the value predicted using the standard deviation of the updraft pdf. These examples demonstrate that the predicted ice number concentration can decrease significantly when using a gravity wave spectrum within a global model. The mean ice number concentration can also become larger than the ice number concentration for a constant updraft, if the standard deviation of W is large (compare Figure 2b with Figure 2a).

Figure 2.

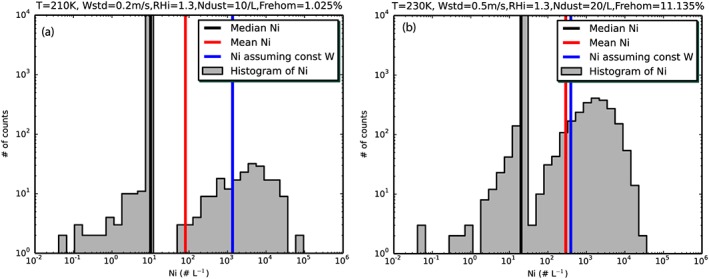
(a) Histogram of predicted ice number concentration for 20,000 parcel model simulations using a pdf of updraft velocities based on the Podglajen et al. (2016) parameterization with a standard deviation of 0.2 m/s at a temperature of 210 K and with heterogeneous IN concentration of dust equal to 10 L⁻¹. (b) As in (a) but for a standard deviation of 0.5 m/s at a temperature of 230 K with heterogeneous IN concentration of dust equal to 20 L⁻¹. IN = ice nuclei.

3. Model Experiments and Comparison to Observations

We set up a series of experiments using differing assumptions for the number of background heterogeneous IN. We also ran one simulation varying the time interval for changing the updraft velocities in the time series (dbfc_dt) and one simulation using a single constant updraft velocity based on the local standard deviation of the updraft pdf (dbfc_w). In addition, one simulation including crystalline ammonium sulfate as an INP was included (but without contrail soot as an IN). Table 2 provides a summary of these experiments.

Table 2.

Description of Simulations

Simulation name	Description of INP treatment in model
dbfc	Dust <3 monolayers sulfate; 0.1% of biomass aerosols; standard fossil/biofuel aerosols; aircraft soot incorporated in contrails (with <3 monolayers of sulfate)
d100bfc	As in dbfc but with 100% of dust as INP
dbfa	As in dbfc but with 100% of aircraft soot as INP
dbfcs30	As in dbfc but adding 30% of SOA particles as INP
dbfc_hom	No heterogeneous nucleation in model
dbfc_dt	As in dbfc but varying the time interval for the updraft velocity
dbfc_w	As in dbfc but using a constant updraft velocity based on the local standard deviation from the parameterization
dbfc_mg10	As in dbfc but using a cutoff for moving cloud ice to snow of 400 μm instead of 250 μm
dbfSO4_mg10	As in dbfc without aircraft soot and including crystalline ammonium sulfate and using a cutoff for moving cloud ice to snow of 400 μm

Note. The default version of the cloud microphysical scheme is Morrison and Gettelman (2008; version 1.5 or mg15) if not specified in the simulation name; mg10 is version 1.0 of the scheme. SOA = secondary organic aerosol; INP = ice nuclei particle.

Table 3 compares several global average parameters from the current simulations with those from CAM5.1 and from observations. The high cloud fraction with the current model is increased significantly compared to that from CAM5.1 and is much closer to observations from the DARDAR analysis of the CALIPSO‐CloudSat data (Hong & Liu, 2015). However, previous estimates of high cloud amount based on ISCCP data for the years 1983–2001 and HIRS for the years 1979–2001 are much smaller.

Table 3.

Comparison of Global Average Parameters From Selected Simulations to Observations

Parametera	Obs.	dbfc	dbfc_mg10	d100bfc	dbfa	dbfcs30	hom	dbfc_dt	dbfc_w	dbfSO4_mg10	CAM5.1 (Wang et al., 2014)
FSNT (W/m2)		222.96	229.53	223.13	224.37	223.79	222.42	221.10	224.68	228.73
FLNT (W/m2)		−223.25	−225.49	−222.38	−224.10	−223.49	−222.37	−220.12	−223.22	−223.92
FLNTC (W/m2)		−256.64	−257.56	−256.94	−256.94	−256.76	−256.58	−256.79	−257.18	−257.44
CLDTOT (%)	65–75b	71.3%	69.3%	71.2%	70.6%	71.3%	71.4%	72.2%	71.1%	69.8%	65.64
CLDLOW (%)	#	43.7%	42.2%	43.7%	43.5%	43.6%	43.7%	43.8%	43.4%	42.4%	45.28
CLDHGH (%)	21–33, 53c	47.8%	46.3%	47.1%	46.5%	47.9%	47.5%	48.9%	47.9%	46.9%	38.91
SWCF (W/m2)	−46 to ‐53d	−64.40	−58.50	−64.23	−62.97	−63.55	−64.94	−66.31	−62.68	−59.32	−54.78
LWCF (W/m2)	29–31d	33.39	32.07	34.56	32.84	33.27	34.21	36.68	33.96	33.52	25.40
LWP (g/m2)	50–87e	57.15	45.66	56.91	56.64	56.93	57.37	57.73	56.77	45.77	53.23
IWP (g/m2)	21‐28f, 29.2g	13.87	20.33	14.50	13.83	13.43	14.19	15.05	13.46	20.35	18.82
TIWP (g/m2)	10–65h, 75±30i, 109j, 122g, (all sky mean)	69.81	69.80	70.73	70.43	69.65	70.08	70.95	69.99	69.32	66.93
Nd (1010 m−2)	#	1.757	1.391	1.740	1.733	1.751	1.771	1.774	1.734	1.407	1.75
Ni (1010 m−2)	#	0.1231	0.106	0.1068	0.0968	0.0944	0.1282	0.1334	0.1007	0.1001	0.010
PRECT (mm/day)	2.67k	2.786	2.788	2.769	2.801	2.788	2.769	2.727	2.785	2.760	2.973
WMV (kg/m2)	24.6l	27.25	27.18	27.27	27.06	27.16	27.34	27.65	27.09	27.35	25.75

^aAll‐sky outgoing shortwave flux (FSNT), longwave flux (FLNT) and long wave clear sky flux (FLNTC), total cloud fraction (CLDTOT), low cloud fraction (CLDLOW), high cloud fraction (CLDHGH), shortwave cloud forcing (SWCF), longwave cloud forcing (LWCF), column‐integrated grid‐mean hydrometeor water path (LWP, liquid water path; IWP, ice water path); TIWP, total ice water path (TIWP), column‐integrated grid‐mean hydrometeor number concentrations (Nd, cloud droplets; Ni, ice crystals), precipitation rate (PRECT), and column‐integrated water vapor (WMV).

^bTotal cloud fraction observations are obtained from ISCCP for the years 1983–2001 (Rossow & Schiffer, 1999), MODIS data for the years 2001–2004 (Platnick et al., 2003), and HIRS data for the years 1979–2001 (Wylie et al., 2005).

^cHigh cloud fraction observations are obtained from ISCCP data for the years 1983–2001, HIRS for the years 1979–2001. The CloudSat and CALIPSO ice cloud frequency for the years 2007–2010 is also shown (Hong & Liu, 2015).

^dSWCF, LWCF are from ERBE for the years 1985–1989 (Kiehl & Trenberth, 1997) and CERES for the years 2000–2005 (Loeb et al., 2009).

^eLiquid water path is derived from SSM/I (for the years 1987–1994, Ferraro et al., 1996; for August 1993 and January 1994, Weng & Grody, 1994; and for August 1987 and February 1988, Greenwald et al., 1993) and ISCCP for the year 1987 (Han et al., 1994). SSM/I data are restricted to oceans.

^fApproximate range of observed ice water path from different CloudSat/CALIPSO analyses (Figure 2 in Li et al., 2012).

^gIWP and TWIP from 2C‐ICE CloudSat/CALIPSO data (J.‐L. F. Li, private communication, 2017) for the years 2007 to 2010.

^hTotal ice water path from NOAA NESDIS, ISCCP, MODIS (Figure 18 in Waliser et al., 2009).

ⁱTotal ice water path from CloudSat (Austin et al., 2009).

^jTotal ice water path from DARDAR CloudSat/CALIPSO mean for the years 2007–2010 (Hong & Liu, 2015).

^kPrecipitation rate is taken from the Global Precipitation Climatology Project (GPCP) for the years 1979–2010 (Adler et al., 2003; https://climatedataguide.ucar.edu/climate‐data/gpcp‐monthly‐global‐precipitation‐climatology‐project).

^lPrecipitable water is from the NASA water vapor project (NVAP) for the years 1988–1999 (Randel et al., 1996; https://eosweb.larc.nasa.gov/GUIDE/dataset_documents/base_nvap_dataset.html#a6).

As shown in Table 3, the integrated ice number concentrations in our simulations range from 9 × 10⁷ m⁻² to 13 × 10⁸ m⁻², while those in CAM5.1 were 1 × 10⁷ m⁻². This is caused in part by the representation of aerosols in IMPACT, which has significantly larger aerosol sulfate numbers than those in CAM5.1 (Penner et al., 2015; Zhou & Penner, 2014). Also, in CAM5.1 the sulfate numbers that were able to freeze were limited to those having radii greater than 0.1 μm. However, when using the same representation of aerosols, the primary factor determining ice number concentrations is the updraft velocity. Table S1 summarizes previous simulations from Zhou et al. (2016) based on the use of a constant updraft velocity of increasing magnitude as well as the constant updraft and wave formulations calculated here. These simulation comparisons show the large variation in ice number concentration when the updrafts as well as sulfate number concentrations are varied. The standard deviation of updraft at 19 km used in our current simulations is 0.17 m/s, which can be compared to that in previous simulations based on Gary (2006, 2008) of approximately 0.1 m/s (Wang & Penner, 2010; Zhou et al., 2016). The predicted ice number with constant updraft based on this higher standard deviation is 10.1 × 10⁸ m⁻², while that for the wave formulation (case dbfc) is slightly higher, 12.3 × 10⁸ m⁻². The higher mean number for the wave formulation differs from the slightly lower numbers shown in Figure 2b, but this is caused by the fact that the use of a spectrum of updraft velocities can, at times, lead to predicted ice number concentrations that are significantly larger than that computed using the value of the standard deviation and this is more prevalent if the standard deviation becomes large. This can be seen by comparing the mean number concentrations for the constant updraft case and for the wave spectrum case in Figures 2a and 2b, where the latter figure has a significantly larger standard deviation for the updrafts, leading to much closer mean values. This latter point is of particular importance when comparing differences between the current simulations and all previous simulations which only used a fixed (local) updraft for each 30‐min time step in CAM.

The second major difference between the current simulations and those of the CAM5.1 simulation is the smaller IWP and larger liquid water path (LWP). For case dbfc, the IWP is 13.87 g/m², while the LWP is 57.15 g/m². This can be compared to observations, which range from 21–28 g/m² and 50–87 g/m², respectively. The CAM5.1 values were 18.82 g/m² and 53.23 g/m². The lower IWP is probably caused by our use of a cutoff diameter of 250 μm to move cloud ice to snow rather than the CAM5.1 default value of 400 μm (the mg10 case). We adopted this value based on the analysis of Zhang et al. (2013), who found that the predicted effective diameter of ice particles agreed better with that from the SPARTICUS campaign when a lower value of the cutoff diameter was used. The use of the 400‐μm cutoff diameter (case dbfc_mg10) increases the IWP in the dbfc simulation to 20.33 g/m² although the total IWP (TIWP) is similar to that in case dbfc. The higher IWP in the dbfc_mg10 case is accompanied by a lower LWP of 45.66 g/m². Higher LWPs in case dbfc might be caused by the lower temperatures in the lower and middle troposphere which accompanies the decreased IWP and allows more convection leading to more liquid water clouds.

As shown in Table 3, the comparison of the current simulations with observations of shortwave and longwave cloud forcing (SWCF and LWCF) indicates that the SWCF is in the range from −63 to −65 W/m², significantly larger (more negative) than the observed values which range from −46 to −53 W/m². In addition, the LWCF for the current simulations is of order 33–35 W/m², which is larger than the observed values (29–31 W/m²) shown in Table 3. In comparison, the simulation with the higher cutoff for removal of cloud ice to snow (dbfc_mg10) has both a better prediction of cloud ice water path (20 g/m² compared to the observed values of 29 g/m² from the 2C‐ICE product from CALIPSO/CloudSat) and somewhat better values for SWCF and LWCF (i.e., −58.5 and 32.07 W/m², respectively), although the CERES‐based observations of SWCF are significantly smaller, −46 W/m². We note that adding crystalline (NH₄)SO₄ as an IN (and not using contrail processed soot as IN; case dbfSO4_mg10) as well as using a cutoff of 400 μm for the conversion of cloud ice to snow provides the best estimate of SWCF and LWCF in comparison to observations, although the SWCF is still quite large compared to CERES. Figure S5 compares the dbfc, d100bfc, dbfa, dbfc‐mg10, and dbfSO4_mg10 simulations with the CERES‐based observations (which are the lowest of the observed estimates shown in Table 3). The figure shows both the dbfc simulation with the 250 μm cutoff (dbfc_mg15) as well as the CAM default value of 400 μm (dbfc_mg10). Both are significantly larger than the CERES‐based observations (as are all of the simulations shown in Figure S5). The overprediction of shortwave and longwave cloud forcing is especially large in the tropics. Because the TIWP is smaller than the CALIPSO/CloudSat observations, improving the IWP to fit these observations without a compensating decrease in the LWP would make the overprediction of SWCF worse. Moreover, the LWP in dbfc_mg10 is smaller by >10 mg/m² than that in dbfc_mg15 and yet the SWCF is still much larger in magnitude than the observations. Hence, adjustments of the LWP are unlikely to fix this problem unless they exceed 10 mg/m². Therefore, overprediction of the SWCF might mainly be associated with an overprediction of the cloud fractions, which are similar in the two versions (i.e., 71.3% vs. 69.3% for CLDTOT). We note that the use of the significantly smaller updraft velocities associated with the old implementation of the Gary (2006, 2008) parameterization provides a significantly better fit to these observations, but these smaller updrafts are not supported using the new parameterization.

Comparisons of predicted ice number concentrations with observed ice number concentrations are shown in Figure 3. The observational data plotted in Figure 3 have been expanded to include more flights than the data originally reported by Krämer et al. (2009), (M. Krämer, private communication, March 15, 2018). Flights from the tropics dominate the observations shown between temperatures from 185 to 205 °K, while the observations above that temperature include data from both the tropics and midlatitudes. Figure 3a shows several of the simulations from Table 2. Data from the model have been selected to have ice water mixing ratios >10⁻⁸ to match values seen in the in situ observations (Krämer et al., 2016). All model simulations do a reasonable job of representing the lowest temperature ice number concentrations but are somewhat higher than the observations between 195 and 215 °K. Above 215 °K, the dbfa and d100bfc simulations are almost outside of the range of observations.

Figure 3.

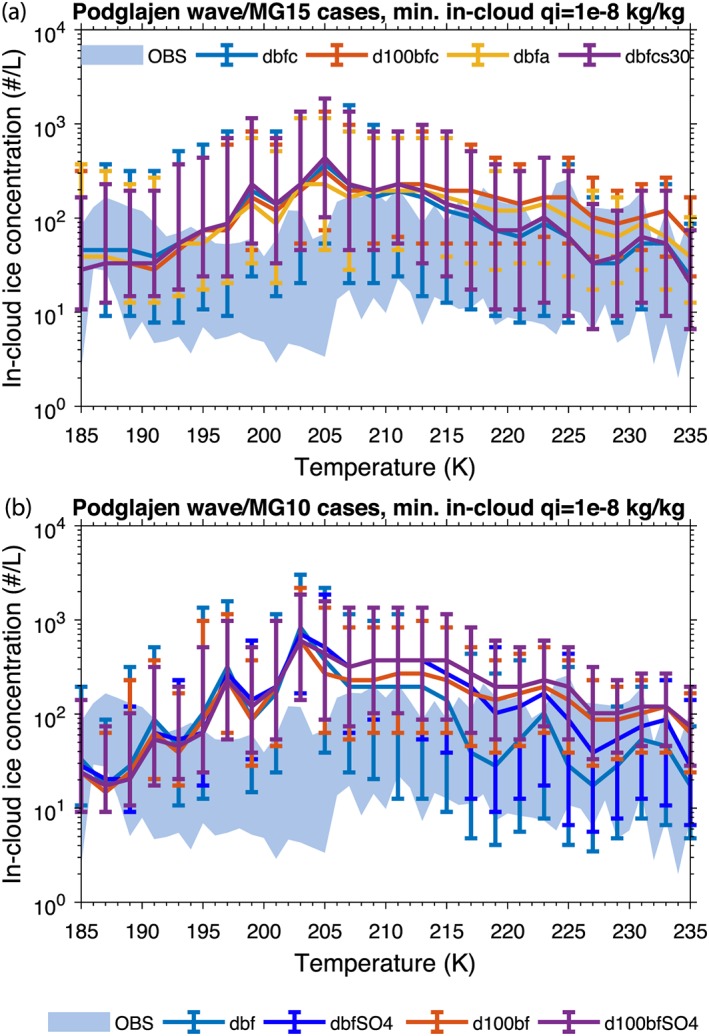
(a) In‐cloud ice crystal number concentration L⁻¹ versus temperature from several of the cases outlined in Table 2. Solid lines show the 50th percentile values for each 1 K bin. Error bars show the 25th–75th percentiles. Background shaded region shows the 25th–75th percentiles from an extended set of observations originally compiled by Krämer et al. (2009). (b) As in (a) but including two cases with crystalline ammonium sulfate acting as an INP (dbfSO4 and d100bfSO4). None of the cases plotted in (b) included contrail processed soot as an INP. They were run assuming a cutoff diameter of 400 μm to move cloud ice to snow. INP = ice nuclei particle.

Figure 3b shows a similar comparison for a set of simulations using the standard cutoff of 400 μm. The dbf simulation and d100bf simulations follow the specifications for dbfc and d100bfc but do not include contrail‐processed soot as an INP. When solid ammonium sulfate is included as an INP, ice number concentrations increase, especially above 205 °K. This makes the simulated ice number concentrations even higher than the cases in Figure 3a between about 205 and 215 °K.

We further compare ice number concentrations with observations taken during the SPARTICUS campaign in Figure S6. The SPARTICUS field campaign took place from January 2010 to June 2010 over the Southern Great Plain (SGP) site of the DOE Atmospheric Radiation Measurement (ARM) Program. The comparison shows that all versions of the model have somewhat lower ice number concentrations than observations in the temperature range between 205 and 215 °K. The dbfc and d‐only simulations have somewhat lower concentrations than the observations in the temperature range from 215 to 225 °K, while both d100fbc and dfba are reasonable agreement with observations. In the range from 225 to 230 °K both d100fbc and dbfa simulations overpredict observations, but dbfc and d‐only are quite good. These comparisons are quite similar to the comparisons shown in Wang et al. (2014) using both the CAM5.1 model as well as the version with the Gary (2006, 2008) subgrid updraft velocities.

Finally, Figure 4 shows a comparison of modeled ice number concentrations in the Northern Hemisphere with CALIPSO satellite observations, while Figure S7 shows a similar set of plots for the Southern Hemisphere. The observational data summarized in Figures 4 and S7 used the N(D)1 = 0 assumption based on fitting the SPARTICUS data as described in Mitchell et al. (2018) and thus approximately gives the upper bound for ice number concentrations from among four separate retrievals. The model results are those for the dbfc simulation and included values with ice water mixing ratios >10⁻⁶ and optical depths between 0.3 and 3. The simulations are somewhat high for tropical latitudes with T > 195 °K, similar to the comparisons with in situ data (Figure 3). They are somewhat low in both hemispheres in midlatitudes, but would be in better agreement if we had used one of the other retrievals presented in Mitchell et al. (2018). The winter season for both polar regions compares well with observations, but ice concentrations in the summer season are low in some cases by a factor of up to 100. The simulations with large numbers of heterogeneous IN from dust or aircraft (d100bfc and dbfa) do a somewhat better job of reproducing the observations in the North Polar summer as well as at Northern Hemisphere midlatitudes for T > 210 °K (see Figures 5 and S8). However, another possibility that might explain the summer season discrepancies is that we used the Gary (2006, 2008) formulas to convert the Podglajen et al. (2016) tropical formula for the standard deviation of the updraft velocity to other latitudes and seasons. In contrast, the observations of Podglajen et al. (2016) for the South Pole indicate updrafts that are considerably higher than those measured in the tropics, even over ocean regions which are not as subject to mountain‐induced waves, while the Gary (2006, 2008) formulas only increase toward the South Pole in the winter season. Since the Podglajen et al. (2016) data near the South Pole were obtained during local summer (between September and January) they would indicate higher updraft velocities than those recommended using the extrapolation to polar regions recommended by Gary (2006, 2008). This might be a primary cause of predicted number concentrations at polar latitudes in the summer hemisphere that are smaller than the observed ice number concentrations.

Figure 4.

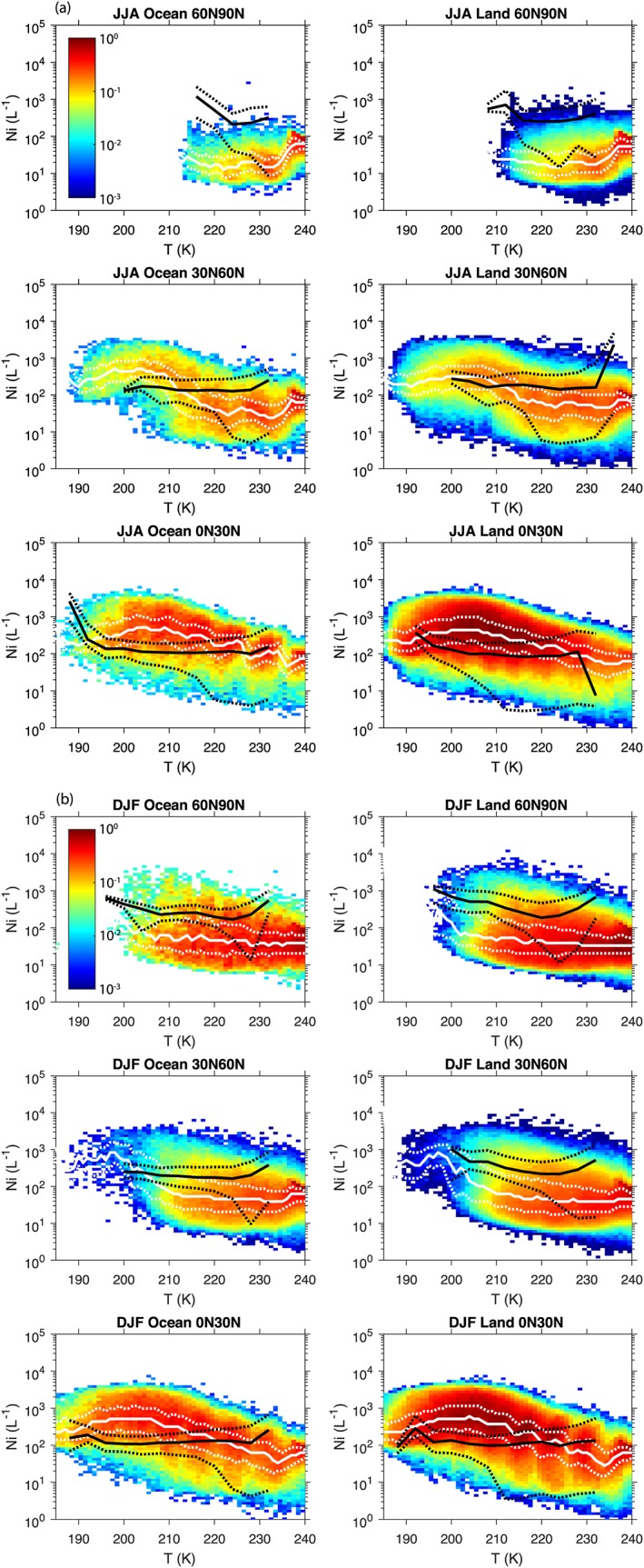
(a) In‐cloud ice number concentrations for JJA in the Northern Hemisphere from the N(D)₁ = 0 assumption for CALIPSO observations summarized by Mitchell et al. (2018) together with the dfbc simulation. The modeled cloud optical depth is restricted to the range from 0.3 to 3.0. (b) As in (a) for DJF in the Northern Hemisphere. The black full and dotted lines show the median, 25th and 75th percentile values of the observations, while the white lines as well as the color contours show the simulations. CALIPSO = Cloud‐Aerosol Lidar and Infrared Pathfinder Satellite Observation; JJA = June‐July‐August; DJF = December‐January‐February.

Figure 5.

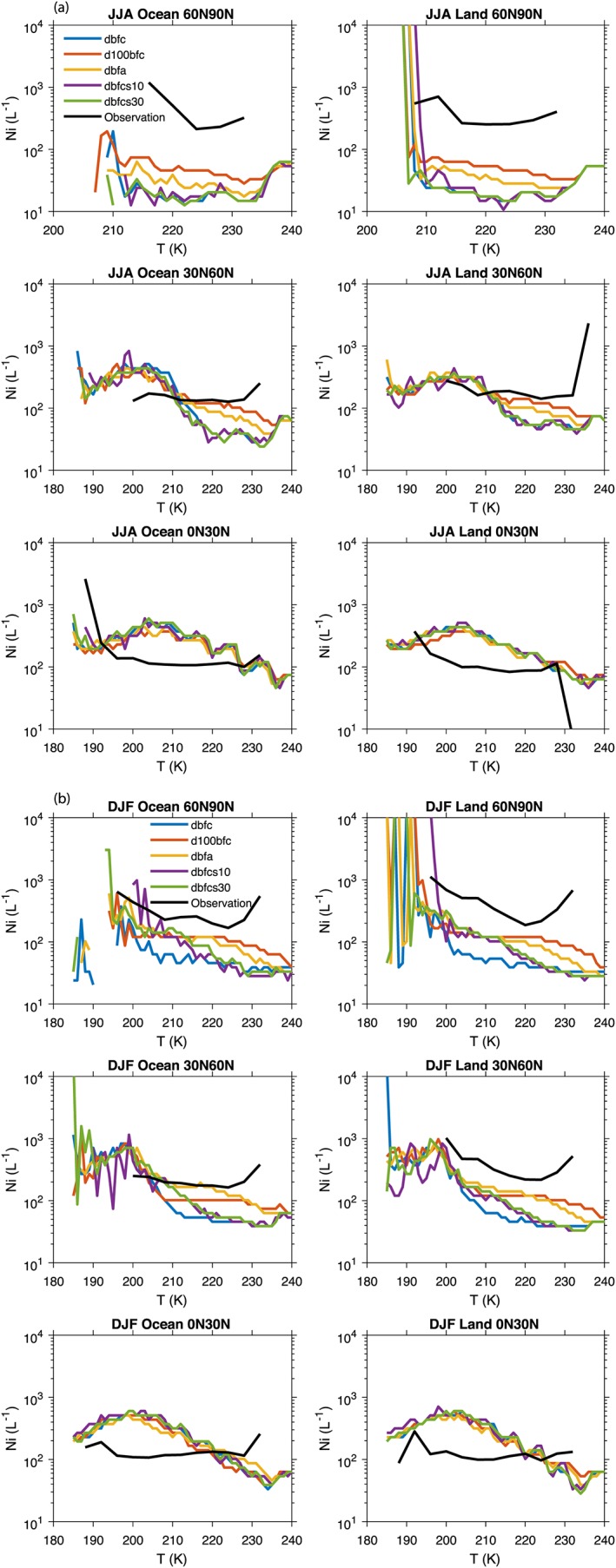
(a) Median in‐cloud ice number concentration from the N(D)₁ = 0 assumption for CALIPSO observations summarized by Mitchell et al. (2018) together with the median predicted ice number concentrations from a set of simulations given in Table 2 for JJA in the Northern Hemisphere. The modeled cloud optical depth is restricted to the range from 0.3 to 3.0. (b) As in (a) for DJF in the Northern Hemisphere. CALIPSO = Cloud‐Aerosol Lidar and Infrared Pathfinder Satellite Observation; JJA = June‐July‐August; DJF = December‐January‐February.

We note that the overprediction of SWCF and LWCF especially in the tropics is consistent with the general overprediction of Ni from CALIPSO at these latitudes. The situation is somewhat improved with the smaller ice number concentrations predicted in d100bfc and dbfca, but not enough to fit the SWCF and LWCF observations. Originally, we thought that further reduction of Ni might be possible if crystalline ammonium sulfate were able to act as an additional heterogeneous ice nuclei (Zhou et al., 2016; Zhou & Penner, 2017). However, our initial simulations with crystalline ammonium sulfate (dbfSO4_mg10) did not reduce ice crystal numbers. In fact, at temperatures above 200 °K, the addition of this species as an INP increases ice number concentrations and SWCF and LWCF are hardly impacted (see Figure S5).

Finally, Figure 6 compares the probability distribution frequency of RHi with data from the Measurements of Ozone, Water Vapor, Carbon Monoxide, and Nitrogen Oxides by Airbus In‐Service Aircraft (MOZAIC) project (Gierens et al., 1999) and the Atmospheric Infra‐Red Sounder (AIRS) satellite (Gettelman et al., 2006). The frequency predicted in the simulations is underestimated at the higher observed relative humidities. This underestimation may primarily result from an underestimation at lower altitudes (200–300 hPa; see Wang & Penner, 2010). Similar to the findings in Wang and Penner (2010), the case with all dust acting as INP (d100bfc) underestimates the frequency of ice supersaturation more than the other cases, as does the dbfa case. We note that when Liu et al. (2012) removed all homogeneous ice nucleation, they found an increase in the occurrence frequency of higher relative humidities. They argued that these higher occurrence frequencies occur because of the inability to remove RHi sufficiently when there are low ice crystal numbers formed (Liu et al., 2012). However, we have not found an increase in RHi when heterogeneous IN were increased.

Figure 6.

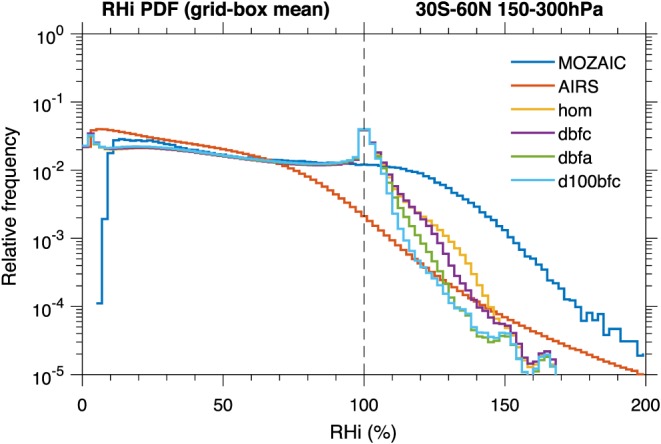
Probability distribution frequency (PDF) of relative humidity in 150–300 hPa from 30°S to 60°N from different simulations, in comparison with humidity observations in the upper troposphere from the measurements of ozone, water vapor, carbon monoxide, and nitrogen oxides by Airbus in‐service aircraft (MOZAIC) and from the atmospheric infrared sounder (AIRS) satellite. RHi = relative humidity with respect to ice.

Figure S9 shows the occurrence frequency of RHi greater than 100%. This may be compared to a similar graph based on the Microwave Limb Sounder (MLS) data shown in Figure 7 in Wang and Penner (2010). Notably the pattern of the frequency of occurrence is quite similar to the observations for the dbfc simulation and is improved over that first shown in Wang and Penner (2010). Adding more heterogeneous IN, as in the d100bfc and dbfa simulations does not improve the comparison very much. Clearly, the model produces a reasonable representation at 143 hPa. However, the values of supersaturation at 198 hPa occur more frequently than shown by the observations in both the tropics and regions near the South Pole. This is in opposition to the comparison with MOZAIC data at lower altitudes in the tropics, which are underestimated (not shown). Further progress in understanding supersaturation in tropical regions may require further observations as well as model results to clarify this issue.

Figure 7.

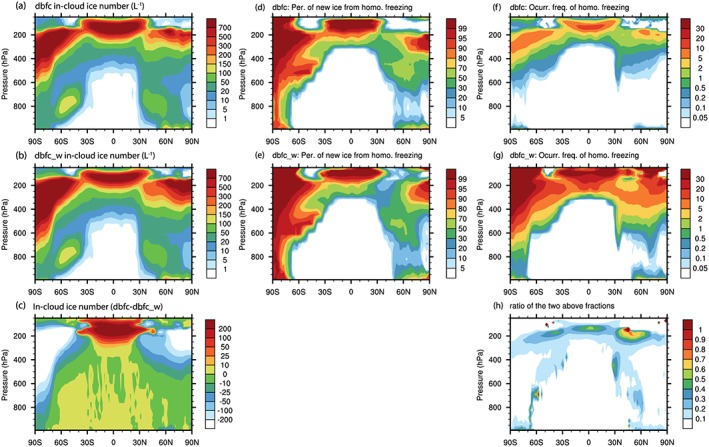
In‐cloud ice number concentration as a function of latitude and pressure for the dbfc (a) and dbfc_w (b) simulations and their difference (c). Percentage of new ice formed from homogeneous freezing for the dbfc (d) and dbfc_w (e) simulations. Cloud‐weighted occurrence frequency of homogeneous freezing in the dbfc (f) and dbfc_w (g) simulations, and the ratio of the occurrence frequency (h).

3.1. Frequency of Homogeneous and Heterogeneous Freezing

Jensen et al. (2013) discuss observations that indicate infrequent, but high concentrations of cirrus ice particles (of order 1,000 L⁻¹) interspersed with low‐concentration layers (less than 100 L⁻¹) in the tropical TTL. The high concentrations of cirrus ice particles are an indication that these clouds formed as a result of homogeneous ice particle nucleation. Jensen et al. (2013), however, were unable to discern whether the low‐frequency high‐cirrus particle concentrations resulted from high‐frequency gravity waves or the specific aerosol conditions under which these clouds formed. For the data shown, a rough estimate of the occurrence frequency (time intervals with high concentrations compared to all times with cloud) of these high‐concentration layers is of order 15%. Figures 7f and 7g show the occurrence frequency of homogeneous freezing for dbfc and dbfc_w as a function of latitude and height. For dbfc, the occurrence frequency varies from 5% to 20% in the upper tropical regions, well within the magnitude expected based on Jensen et al. (2013). In contrast the dbfc_w simulation shows frequencies ranging from 20% to 40%. Thus, the occurrence frequency of our simulations is consistent with the frequency of high concentration layers forming as a result of gravity waves periodically leading to high updrafts and cooling rates that allow high supersaturations and promote homogeneous freezing events. However, our predicted ice number concentrations can increase well above the maximum of 10,000 L⁻¹ seen by Jensen et al. (2013). Figure 8 shows the absolute counts of different ice number concentrations for 30°S to 30°N for homogeneous freezing events in different temperature ranges for both dbfc and dbfc_w. For gravity waves, there is a much broader distribution than when a constant updraft is used. Both simulations indicate a large number of cases with Ni > 10,000 L⁻¹ at the lowest temperatures (i.e., the highest altitudes). This is caused by the distribution of high as well as low updrafts. Therefore, averaging over all counts with both homogeneous and heterogeneous freezing events could lead to average concentrations of Ni above those seen in observations, as shown in Figures 3 and 4. We note that the occurrence of freshly produced Ni above 10,000 L⁻¹ may not be consistent with the observations of Jensen et al. (2013), who saw maximum ice concentrations of 10,000 L⁻¹ but were not necessarily counting freshly nucleated ice particles. Decreases in these counts would require excluding some of the higher updraft velocities within the pdf we are using or perhaps increasing the number of heterogeneous IN. Interestingly, the dbfc_w simulation is biased toward the higher ice number concentrations for the lowest temperature ranges.

Figure 8.

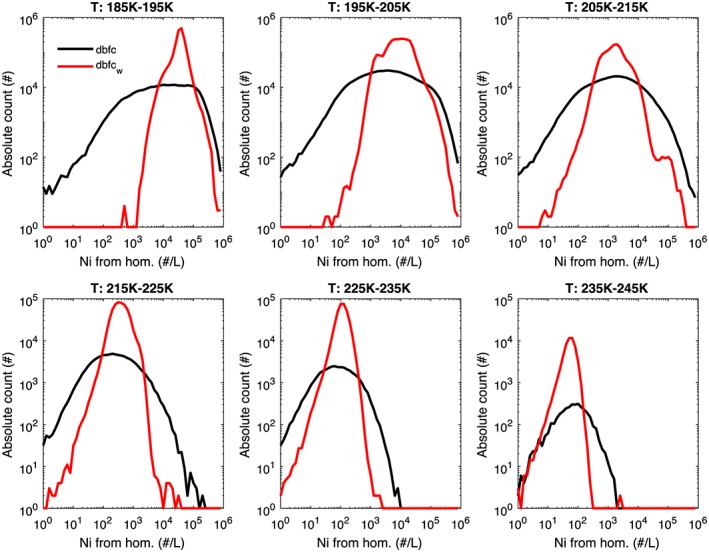
Absolute counts of ice number concentrations produced during homogeneous nucleation events for different temperature ranges in the dbfc and dbfc_w simulations in the tropics (30°S to 30°N).

4. Simulations of Climate Forcing

Here we examine the use of different sources of heterogeneous IN to determine their effects on the change in the incoming top of the atmosphere shortwave, longwave, and total net radiative fluxes in cloudy skies (i.e., total all‐sky change minus clear sky change; SWCF, LWCF, and CF) and the total all‐sky shortwave, longwave, and total net fluxes (FSNT, FLNT, and FNT). We also examine the use of a constant updraft velocity in comparison to the use of the wave formulation. We note that the forcing is estimated as the difference between a simulation with the emission category included and not included. These differences represent the total anthropogenic forcing for fossil/biofuel BC/OC and aircraft BC/OC. However, since many estimates of climate forcing use 1750 as a reference, and fossil/biofuel emissions were nonzero in 1750, our estimates do not capture the same thing as an estimate using the difference from emissions in 1750. However, it is close, since anthropogenic emissions are thought to be small in 1750 (Hoesly et al., 2018; Ito & Penner, 2005; Lamarque et al., 2010). In addition, the emissions that we use for open biomass burning are not just those from anthropogenic activities, since they are primarily based on satellite data that captures both anthropogenic and natural sources of open fires (Lamarque et al., 2010). The total emissions for each category in the model are listed in Table S2.

We have not tested the effect of altering the emissions of sulfur compounds in determining the number concentrations of fossil/biofuel soot or aircraft soot on forcing. Larger concentrations of sulfate would be expected to remove a larger fraction of particles from the pool that act as INPs, since they might acquire greater than three monolayers of sulfate sooner than if preindustrial or only natural emissions of sulfur were used. We used the total PD emissions of soot and removed them in their entirety to define the indirect climate forcing in cirrus clouds to avoid this complication. One test using preindustrial emissions of sulfur changed the fossil/biofuel INP concentrations from 1–2 L⁻¹ in the present day to 2–3 L⁻¹ at 200 hPa for preindustrial emissions, a 50% overall increase (see Figure S10). Thus, including changes in sulfur emissions over time is expected to decrease our forcing estimates.

Table 4 summarizes the differences for all simulations performed here. The summary also includes changes to the integrated ice number concentration, the cloud ice water path, liquid water path, and total precipitable water. First, notice that in all simulations, the ice water path decreases when one of the heterogeneous IN agents is added. This is the result of smaller ice number concentrations in the simulations with additional heterogeneous IN. Smaller ice number concentrations lead to larger cloud ice sizes and more snow formation (not shown). In addition the LWP decreases in most of the cases (except dbfc‐dbc). The slight decrease of IWP in the tropical region leads to cooling the upper troposphere. This increases the lapse rate of temperature and enhances the convection which causes a shorter cloud lifetime and thus smaller LWP. This was first found and explained in Wang and Penner (2010) possibly due to the decreased SW radiation at the surface, leading to less convection and formation of low‐level clouds. In addition, except for dbfc‐dbc, the LWCF is always smaller than the all‐sky longwave forcing, FLNT. This is due to the decrease in precipitable water (WMV), which causes an increase in the clear sky outgoing radiation thereby increasing the LWCF (LWCF is calculated from the difference of all‐sky forcing and clear sky forcing; Wang & Penner, 2010). Most models rely on the cloud forcing to report the effects of different aerosol indirect effects, but here we include this feedback as it is significant for the total impact of aerosols on climate forcing.

Table 4.

Forcing and Cloud Changes Associated With Changes in Aircraft Soot, Biomass Burning Soot, and Fossil/Biofuel Soot

Casea	IWP (g/m2)	LWP (g/m2)	WMV (kg/m2)	Ni (1.e7 m−2)	SWCF (W/m2)	LWCF (W/m2)	CF (W/m2)	FSNT (W/m2)	FLNT (W/m2)	FNT (W/m2)
dbfc‐dbf	−0.190 ± 0.026	−0.172 ± 0.041	−0.080 ± 0.007	−2.781 ± 1.197	0.366 ± 0.061	−0.515 ± 0.047	−0.149 ± 0.050	0.358 ± 0.065	−0.558 ± 0.063	−0.200 ± 0.062
dbfc_w‐ dbf_w	−0.168 ± 0.034	−0.296 ± 0.075	−0.129 ± 0.013	−1.267 ± 1.443	0.519 ± 0.069	−0.766 ± 0.064	−0.247 ± 0.072	0.512 ± 0.069	−0.819 ± 0.073	−0.307 ± 0.074
d100bfc‐d100bf	−0.003 ± 0.030	−0.006 ± 0.035	−0.005 ± 0.006	−0.218 ± 1.598	0.056 ± 0.051	−0.060 ± 0.036	−0.005 ± 0.059	0.058 ± 0.051	−0.084 ± 0.041	−0.027 ± 0.055
dbfa‐dbf	−0.234 ± 0.055	−0.675 ± 0.064	−0.265 ± 0.016	−29.090 ± 2.679	1.798 ± 0.136	−1.062 ± 0.112	0.736 ± 0.066	1.773 ± 0.132	−1.410 ± 0.114	0.363 ± 0.066
dbfc‐dbc	−0.026 ± 0.011	0.002 ± 0.058	−0.002 ± 0.012	−0.613 ± 0.924	0.008 ± 0.061	−0.045 ± 0.024	−0.037 ± 0.051	0.011 ± 0.063	−0.068 ± 0.027	−0.057 ± 0.051
dbc‐dc	−0.103 ± 0.026	−0.032 ± 0.037	−0.012 ± 0.008	−0.731 ± 1.149	0.083 ± 0.073	−0.178 ± 0.059	−0.095 ± 0.043	0.079 ± 0.072	−0.172 ± 0.072	−0.093 ± 0.033
dbfc‐dc	−0.129 ± 0.030	−0.030 ± 0.033	−0.014 ± 0.005	−1.343 ± 1.188	0.091 ± 0.066	−0.223 ± 0.047	−0.132 ± 0.020	0.090 ± 0.065	−0.240 ± 0.056	−0.150 ± 0.022
dbfc‐d	−0.329 ± 0.033	−0.211 ± 0.032	−0.097 ± 0.008	−3.736 ± 1.119	0.543 ± 0.036	−0.816 ± 0.026	−0.274 ± 0.032	0.535 ± 0.039	−0.858 ± 0.035	−0.323 ± 0.040
dbfcs30‐dbfs30	−0.166 ± 0.025	−0.157 ± 0.052	−0.069 ± 0.008	−2.600 ± 0.549	0.368 ± 0.042	−0.433 ± 0.026	−0.065 ± 0.046	0.362 ± 0.040	−0.466 ± 0.040	−0.104 ± 0.060
dbfc_dt‐dbf_dt	−0.149 ± 0.018	−0.146 ± 0.046	−0.061 ± 0.010	−1.923 ± 0.827	0.267 ± 0.048	−0.423 ± 0.032	−0.156 ± 0.041	0.259 ± 0.051	−0.437 ± 0.042	−0.177 ± 0.041
dbfc_mg10‐dbf_mg10b	−0.135 ± 0.017	−0.131 ± 0.040	−0.077 ± 0.007	−1.038 ± 0.367	0.391 ± 0.028	−0.499 ± 0.026	−0.108 ± 0.020	0.378 ± 0.030	−0.516 ± 0.031	−0.138 ± 0.019
dbfc‐dbfc_hom	−0.321 ± 0.056	−0.222 ± 0.035	−0.095 ± 0.012	−5.15 ± 1.552	0.546 ± 0.070	−0.819 ± 0.043	−0.273 ± 0.074	0.539 ± 0.070	−0.879 ± 0.052	−0.340 ± 0.070

^aThe subtracted cases remove individual INPs, for example, dbf includes dust (d, with three monolayers of sulfate), biomass aerosols (b), and fossil and biofuel soot (f), but does not include contrail processed soot (c).

^bThis simulation used the CAM5.1 standard cutoff for moving ice cloud water to snow (i.e., 400 μm rather than the 250 μm value used for most of the other simulations).

Second, notice that the simulations that report the sum of different aerosol effects are very similar to the sum of the individual aerosol effects. Thus, the total net forcing of biomass aerosols and fossil/biofuel aerosols (dbfc – dc) is −0.15 W/m² whereas the sum of the individual forcing by fossil/biofuel aerosols (dbfc – dbc; −0.057 W/m²) and that from biomass aerosols (dbfc – dfc; −0.093 W/m²) is also −0.15 W/m². Similarly, the forcing from the sum of contrail‐processed aircraft soot together with biomass and fossil/biofuel aerosols is −0.323 W/m², while the sum of the individual forcings is −0.35 W/m². Clearly in this range of aerosol impacts, changes are close to linear.

Also, note that the total forcing by all heterogeneous IN (dbfc – dbfc_hom) is nearly identical to the total forcing by just biomass, fossil/biofuel, and contrail processed aircraft soot (−0.34 vs. −0.323 W/m²). This suggests that only treating dust with less than three monolayers of sulfate as IN does not change the number concentration of ice particles very much compared to treating only homogeneous nucleation. Rather, heterogeneous freezing in the dbfc simulation is primarily determined by biomass, fossil/biofuel and contrail heterogenous IN.

Among the simulations reported here, the forcing by contrail‐processed aerosols is the largest single forcing. Therefore, we evaluated this forcing using the other representations outlined in Table 2. First, consider the forcing calculated using a constant updraft velocity based on the standard deviation of the updraft at each grid point in the model (dbfc_w ‐ dbf_w). In section 4 we discussed the occurrence frequency of homogeneous ice nucleation in the dbfc_w simulation compared to dbfc (Figure 7). The much higher homogeneous freezing occurrence frequency in dbfc_w compared to the wave treatment in dbfc leads to a smaller decrease in the ice number concentration as a result of the addition of contrail soot (−1.27e7 m⁻² compared to −2.78e7 m⁻²) and this is accompanied by a somewhat smaller change in the IWP (−0.17 g/m² compared to −0.19 g/m²) but a larger decrease in the LWP (−0.30 g/m² compared to −0.17 g/m²). The decreases in both total cloud fraction and high cloud fraction are both significantly larger than those in the dbfc case, and this would contribute to larger forcing. If we examine the horizontal changes in IWP (Figure S11), however, the magnitude of the IWP change is larger in the major regions of cooling in the Northern Hemisphere (i.e., over North America, the North Atlantic Ocean, Central America, and the Indian Ocean region) in the dbfc_w case. This is because with the wave spectrum the largest updraft velocity is larger than that when using a constant updraft so that it is more difficult for aircraft soot to suppress the homogeneous freezing in the wave case when the updraft velocity (W) is large. This seems contradictory to the findings from the parcel model simulations (e.g., Figure 2) in which we showed that when using varying updrafts associated with waves, it easier for homogeneous freezing to be suppressed when W is modest. Yet the wave amplitudes in these major cooling areas are still larger and do not fall into the modest regime (not shown here). The globally averaged reduction of IWP in the two cases are nearly the same. However, as noted above, a closer look reveals that the decreases in IWP for the constant updraft case are slightly larger in regions like the North America and the North Atlantic Ocean. Unlike the tropical regions, the longwave cloud forcing is not canceled by the shortwave cloud forcing in the middle latitudes and dominates the net cloud forcing. The larger decrease of IWP in the constant updraft case over these regions causes a larger decrease in the high cloud fraction, leading to the significant decrease in cloud fraction in dbfc_w‐dbf_w compared to dbfc‐dbf, and this is reflected in the larger negative forcing for the constant updraft case. This also leads to a larger cooling in the upper troposphere and an overall larger global temperature lapse rate, increased convection and thus decreased LWP, leading to a larger net forcing of −0.31 W/m² compared to −0.20 W/m² in the base case (dbfc).

If all dust is allowed to act as a heterogeneous IN (d100bfc‐d100bf), the addition of contrail‐processed aircraft soot acts over a much smaller region to decrease the ice number concentration. Figure 9 compares the change in integrated ice number concentration with latitude and longitude between dbfc‐dbf and d100bfc‐d100bf. With higher concentrations of dust acting as IN, regions with large dust sources such as Eastern Asia as well as the Sahara show increases in ice number concentrations when contrail‐processed aircraft soot is added. Since a net positive longwave forcing is associated with increases in number concentration (compare the spatial distribution of positive and negative change in ice number with the FLNT forcing in Figure 9), the net forcing decreases substantially from −0.20 W/m² for dbfc‐dbf to −0.03 W/m² for d100bfc‐d100bf.

Figure 9.

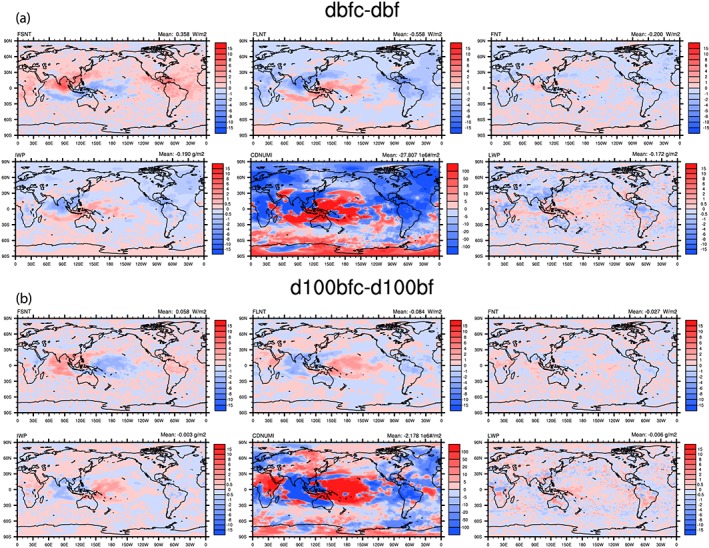
Annual mean plots of shortwave forcing (FSNT), longwave forcing (FLNT), and net forcing (FNT) as well as the change in the vertically integrated ice water path (IWP), grid box‐averaged ice number concentration (CDNUMI), and liquid water path (LWP) for the difference between dbfc and dbf simulations (a) and the d100bfc and d100bf simulations (b).

If all aircraft soot is able to act as a heterogeneous IN (dbfa‐dbf), the net forcing is positive, 0.363 W/m². In this case the global average integrated ice number concentration decreases by roughly a factor of 10 more than the case with only contrail‐processed soot. However, most of this decrease occurs in the tropics, where the negative longwave forcing is largely canceled by the positive shortwave forcing. In the northern midlatitudes, where ice number concentrations increase, the longwave forcing is positive and dominates the shortwave forcing, leading to a net positive forcing which is larger than the net forcing in the tropics. (see Figure S12). We note that the all‐sky shortwave forcing (FSNT) is positive and dominates the longwave forcing. This is because of the large forcing in the tropics, where FSNT is nearly canceled by FLNT. The global average negative values of FLNT are smaller than the global average FSNT due to the addition of positive FLNT in the midlatitudes (Figure S12).

If 30% of our predicted SOA is a heterogeneous IN, then the background number concentration of IN is again increased, primarily in the tropics where our SOA mass concentrations are largest. However, the change in the mean integrated ice number concentration when contrail soot is added only changes from −2.78 × 10⁷ m⁻² with dbfc to −2.60 × 10⁷ m⁻² in dbfcs30. The shortwave forcing (FSNT) is nearly the same in the two simulations (0.358 W/m² and 0.362 W/m²), but the longwave forcing is smaller in dbfcs30 (−0.558 W/m² vs. −0.466 W/m²). As a result the net forcing is decreased from −0.20 W/m² to −0.10 W/m².

Finally, we examine the simulation that uses the standard CAM5.1 cutoff diameter of 400 μm to move cloud ice to snow (i.e., dbfc_mg10) rather than the value of 250 μm used in dbfc. Recall that this simulation produced 20 g/m² ice water path, closer to the observations, although the SWCF was still too small. The integrated ice number concentration is somewhat smaller in these simulations compared to dbfc (i.e., 1.06e9 m⁻² vs. 1.23e9 m⁻², Table 3) and the change in integrated ice number concentration is also smaller (−1.04°E + 07 m⁻² vs. −2.78°E + 07 m⁻², Table 4). This leads to only slight differences, however, in the changes to FSNT (0.38 W/m² vs. 0.36 W/m²), FLNT (−0.52 W/m² vs. −0.56 W/m²) and thus FNT (−0.14 W/m² vs. −0.2 W/m²). In addition, if we examine the simulations where the time interval for changing the updraft velocity is scaled by one over the Brunt‐Vaisala frequency (dbfc_dt‐dbf_dt), the integrated ice number concentration is somewhat higher than the dbfc case (1.33e9 m⁻² vs. 1.23e9 m⁻²), but there is a smaller decrease between the case with and without contrail soot as IN (−1.92e7 m⁻² vs. −2.78e7 m⁻²). Both the shortwave and longwave forcings decrease in magnitude compared to dbfc, leading to a net forcing that is nearly the same, −0.18 W/m².

5. Conclusions

We have implemented a parameterization for forming ice in large‐scale cirrus clouds that accounts for the changes in updrafts associated with a spectrum of waves acting within each time step in the model. This allows us to account for the frequency of homogeneous and heterogenous freezing events that occur within each time step of the model and helps to determine more realistic ice number concentrations as well as changes to ice number concentrations. The model is able to fit observations of ice number at the lowest temperatures in the tropical tropopause but is still somewhat high in tropical latitudes with temperatures between 195 °K and 215 °K. Adding more heterogeneous IN to the model does not correct this deficiency. Rather, some combination of adding ice nucleation within existing clouds or, perhaps, a lower standard deviation of updraft velocities might fit the observations in this range.

The use of the Podglajen et al. (2016) tropical parameterization of updraft velocities (in combination with the Gary (2006, 2007) parameterization to extend these results to other latitudes and seasons, supports the updraft velocities explored here. Thus, the addition of a parameterization that separates regions with cloud from clear regions during ice nucleation (as implemented in Wang and Penner (2010)) may be the best step forward for correcting the treatment of ice formation.

The use of the higher updrafts in this parameterization also leads to shortwave and longwave cloud forcings that are significantly larger than the CERES observations (but closer to the ERBE observations). These large cloud forcings would be exacerbated if we were able to change the model to better fit the CALIPSO/CloudSat observations of ice water path. A better fit to the CERES observations may be possible by tuning the cloud fraction produced in the model.

We also examined the climate forcing associated with different anthropogenic heterogeneous ice nuclei. These climate forcings are primarily negative unless large additions of IN are made, such as when we assume that all aircraft soot acts as an IN. However, they can be close to zero if it is assumed that all the background dust acts as an INP irrespective of how much sulfate is deposited on these particles. Our best estimate for the forcing of aircraft soot in this model is −0.2 ± 0.06 W/m²; however, this can be decreased considerably if more heterogeneous IN are present in the background atmosphere. In particular, since both SOA and crystalline ammonium sulfate are expected to act as heterogeneous IN, the actual forcing is expected to be smaller than −0.2 W/m². Nevertheless, the small positive forcings for aircraft soot found in some models (Gettelman & Chen, 2013; Pitari et al., 2015) are not supported by our calculations. This is probably due to variations in the relative amounts of sulfate haze aerosols versus heterogeneous IN (Zhou & Penner, 2014), from different treatments of updraft velocities (Zhou et al., 2016), or perhaps variations in the fraction of aviation soot particles included as INPs (Gettelman et al., 2012; Gettelman & Chen, 2013). Our ice active fraction of aviation soot is based on observations that show that organic particles that have previously acted as an INP will form ice at lower RHi or higher temperatures during a second freezing event (Adler et al., 2013; Edwards et al., 1970; Evans, 1967; Wagner et al., 2012; see discussion in Zhou & Penner, 2014). We further do not allow aviation soot with greater than three monolayers of sulfate to act as an INP, consistent with observations of dust and other heterogeneous IN (Cziczo et al., 2009). If this latter requirement were relaxed, we might find a larger (negative) forcing for aviation soot as long as the fraction of aviation soot acting as an INP is not too large (as in the dbfa case). The forcing from both fossil/biofuel soot and open biomass burning is smaller than that from aviation, namely, −0.093 ± 0.033 W/m² and −0.057 ± 0.05 W/m², respectively.

Finally, we note that since this model overestimates both the SWCF and LWCF in comparison with CERES observations, especially in the tropics (Figure S5), this may bias our estimates of forcing. If the cause of these overestimates lie in the representation of cirrus cloud fraction, for example, then we would expect our results to be overestimates. However, if the cause is related to the representation of warm clouds, then our cirrus cloud forcing would not substantially change.

Supporting information

Supporting Information S1

Penner, J. E. , Zhou, C. , Garnier, A. , & Mitchell, D. L. (2018). Anthropogenic aerosol indirect effects in cirrus clouds. Journal of Geophysical Research: Atmospheres, 123, 11,652–11,677. 10.1029/2018JD029204