Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2018 Oct 30;45(20):11399–11405. doi: 10.1029/2018GL079474

Quantifying the Importance of Rapid Adjustments for Global Precipitation Changes

G Myhre 1,✉, R J Kramer 2, C J Smith 3, Ø Hodnebrog 1, P Forster 3, B J Soden 2, B H Samset 1, C W Stjern 1, T Andrews 4, O Boucher 5, G Faluvegi 6,7, D Fläschner 8, M Kasoar 9,10, A Kirkevåg 11, J‐F Lamarque 12, D Olivié 11, T Richardson 3, D Shindell 13, P Stier 14, T Takemura 15, A Voulgarakis 9, D Watson‐Parris 14
PMCID: PMC6360531  PMID: 30774164

Abstract

Different climate drivers influence precipitation in different ways. Here we use radiative kernels to understand the influence of rapid adjustment processes on precipitation in climate models. Rapid adjustments are generally triggered by the initial heating or cooling of the atmosphere from an external climate driver. For precipitation changes, rapid adjustments due to changes in temperature, water vapor, and clouds are most important. In this study we have investigated five climate drivers (CO2, CH4, solar irradiance, black carbon, and sulfate aerosols). The fast precipitation responses to a doubling of CO2 and a 10‐fold increase in black carbon are found to be similar, despite very different instantaneous changes in the radiative cooling, individual rapid adjustments, and sensible heating. The model diversity in rapid adjustments is smaller for the experiment involving an increase in the solar irradiance compared to the other climate driver perturbations, and this is also seen in the precipitation changes.

Keywords: precipitation changes, climate drivers, radiative kernels, PDRMIP

Key Points

  • Separation of instantaneous and rapid adjustment contributions to precipitation changes

  • Contributions of rapid adjustments to precipitation changes differ substantially between climate drivers

  • Radiative kernels are applied to understand individual rapid adjustment terms

1. Introduction

Global and regional projections of precipitation changes are uncertain (Flato et al., 2013; Knutti & Sedlacek, 2013). Although some of the regional and seasonal precipitation changes are robust between global climate models (GCMs) and resemble observed patterns (IPCC, 2013), many areas lie in the transition zone between drier and wetter regions and have highly uncertain GCM projections. The precipitation changes from a single climate driver, such as CO2, are not well constrained (Richardson, Forster et al., 2016). This is exacerbated for historical and future predictions when several climate drivers contribute to precipitation changes. Internal variability of the climate system further complicates the picture when comparing observed and simulated changes.

On a global scale, the precipitation change is tightly coupled to the energy budget (Allen & Ingram, 2002; Fläschner et al., 2016; Myhre et al., 2017; O'Gorman et al., 2012; Pendergrass & Hartmann, 2014). Since various climate drivers influence the total radiative cooling differently (Andrews et al., 2010; Ming et al., 2010), understanding these differences better can also help to understand projections of regional precipitation changes. In this respect it is valuable if the intermodel variability is smaller or larger for any of the climate drivers. Precipitation changes can be divided into a fast response and a slow response (Andrews et al., 2010), where the latter is purely driven by climate feedback processes through changes in the surface temperature. Richardson et al. (2018) show that the slow precipitation change is very similar for different climate drivers, but for the fast response, there are large differences. Andrews et al. (2010) showed that the fast precipitation change scales with atmospheric absorption, while the slow changes scale with top of the atmosphere (TOA) forcing. This has been supported in a multimodel study (Samset et al., 2016). The fast precipitation change can further be divided into two effects: those caused by the climate drivers' instantaneous change in radiative cooling (Myhre et al., 2017) and those caused by rapid adjustments (RAs) in water vapor, temperature, and clouds, which occur as a response to the fast tropospheric radiative cooling (Boucher et al., 2013; Sherwood et al., 2015). Additionally, sensible heat influences precipitation changes on fast and slow time scales (Myhre et al., 2018).

In this study, we separate the instantaneous and RA contribution to fast precipitation changes to further contribute to the understanding how different climate drivers influence the global precipitation changes.

2. Methods

2.1. Climate Model Simulations

We use GCM simulations from 11 modeling groups within the Precipitation Driver Response Model Intercomparison Project (PDRMIP) initiative (Myhre et al., 2017). In addition to the 10 models described in Myhre et al. (2017), simulations from the ECHAM‐HAM model are included for one of the PDRMIP perturbations (see Figure S1 in the supporting information for details). The ECHAM‐HAM model has many similarities with the MPI‐ESM model, described by Myhre et al. (2017, Table 3), except that ECHAM‐HAM includes the microphysical aerosol model HAM (Zhang et al., 2012) and a different two‐moment cloud microphysics scheme (Lohmann et al., 2007). In PDRMIP, simulations of at least 15 years using fixed sea‐surface temperatures (fsst) and 100 years using a fully coupled ocean are included. Following Forster et al. (2016) and Richardson, Samset et al. (2016), fast changes in precipitation and radiative cooling are diagnosed using the average of years 6–15 of the fsst experiments. The fsst experiments include a small land surface warming. Slow changes are diagnosed by subtracting the fast change from the total change calculated from the last 50 years of the fully coupled simulations. Results from the five core PDRMIP perturbation simulations are used in this study; a doubling of CO2 concentrations (denoted CO2x2), a tripling of CH4 concentrations (CH4x3), a 2% increase in solar insolation (Solar), a 10‐fold increase in black carbon (BC) concentrations or emissions (BCx10), and a fivefold increase in SO4 concentrations or emissions (Sulx5).

2.2. Calculating Rapid Adjustments Using Radiative Kernels

The radiative kernel technique (Soden et al., 2008) is applied to the atmospheric energy budget (Fläschner et al., 2016; Previdi, 2010) to quantify individual RAs and their collective contribution to atmospheric radiative cooling. In this approach, an RA in surface temperature, air temperature, surface albedo, or water vapor is the product of the direct radiative response to an incremental change in the respective variable and the total climate response of that variable. The former term is the radiative kernel, derived from a single offline radiative transfer model, while the latter is estimated from the response of a given PDRMIP model. For a robust evaluation of each RA, we use five sets of radiative kernels generated from HadGEM2 (Smith et al., 2018), GFDL (Soden et al., 2008), NCAR‐CESM (Pendergrass et al., 2018), ECHAM6 (Block & Mauritsen, 2013), and new radiative kernels (Text S1 in the supporting information) from the Oslo radiative transfer model (Myhre et al., 2011). Cloud adjustments are estimated from the change in cloud radiative forcing corrected for the cloud masking of noncloud adjustments and instantaneous radiative perturbation (Soden et al., 2004, 2008), herein referred to as the kernel cloud‐masking method. Using the Oslo radiative transfer model, cloud and water vapor adjustments are estimated from an alternative method akin to the partial radiative perturbation approach (Colman & McAvaney, 1997), described in Text S1.

Radiative cooling (dQ) is defined as the difference between top of the atmosphere and surface flux changes, where the global radiative cooling constrains precipitation changes (dP) and changes in sensible heat (dSH) through the following equation: LdP = dQ − dSH, where L is the latent heat of vaporization. All results are given for global and annual mean conditions. From the fsst PDRMIP model output, dP, dQ, and dSH are calculated as 10‐year means (6–15 years). Here we separate the initial (instantaneous) and RA contributions to dQ, calculating RA using radiative kernels and the initial perturbation as the residual between dQ and RA.

3. Results

3.1. Individual Rapid Adjustment Contributions

Figure 1 shows various RA terms and the total RA for each of the PDRMIP models for five PDRMIP perturbations, where positive values indicate radiative cooling (causing a positive change in precipitation). The main diversity in RA among the PDRMIP models is from temperature, water vapor, and clouds. As there are substantial differences in stratospheric temperature changes between the PDRMIP perturbations (Stjern et al., 2017), we look separately at tropospheric and stratospheric temperature changes in Figure 1. The tropopause is defined as 100 hPa at the equator, increasing linearly with latitude to 300 hPa at the poles. In the cases where results from several radiative kernels are available, a mean is provided. Figure S1 shows all the results from individual PDRMIP models and individual radiative kernels.

Figure 1.

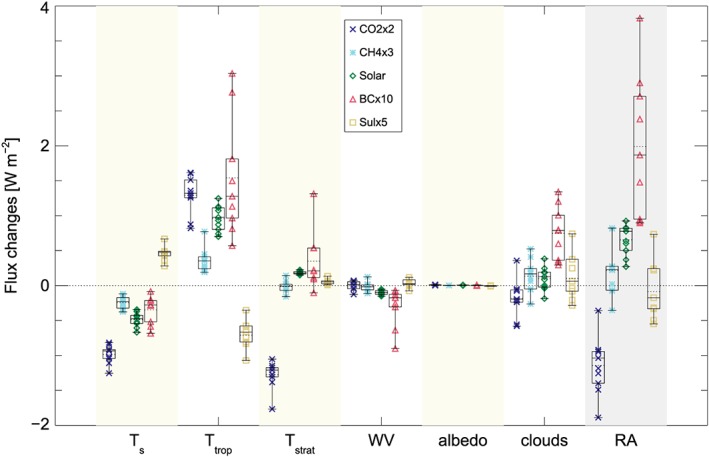
Figure 1

Open in a new tab

Rapid adjustment terms (surface temperature, tropospheric temperature, stratospheric temperature, water vapor, albedo, and clouds) and the total rapid adjustment for the various Precipitation Driver Response Model Intercomparison Project (PDRMIP) models given for five core PDRMIP perturbations. Positive flux changes show radiative cooling (causing an increase in precipitation). The bars show the 25–75% ranges and whiskers showing maximum to minimum ranges of the PDRMIP models. The medians are shown with solid lines and the means with dotted lines.

The total RA reduces the radiative cooling for CO2x2 and increases it for Solar and BCx10. For CH4x3 and Sulx5 the signals are weaker. The difference in total RA between CO2x2 and BCx10 originates from very different responses in clouds and stratospheric temperature.

An increase in surface temperature leads to more longwave (LW) absorption in the atmosphere and thus reduced radiative cooling. On the other hand, an increase in temperature in the atmosphere causes more radiation to be emitted to space and toward the surface, therefore increasing radiative cooling. Shortwave (SW) absorption due to water vapor enhances the atmospheric absorption (causing reduced radiative cooling), whereas the LW may either increase or decrease the radiative cooling depending on the altitude of the water vapor changes (Previdi, 2010). Surface albedo changes have little impact on the radiative cooling. In CO2x2, a reduction in low level clouds and an increase in high clouds reduce radiative cooling. This is in contrast to BCx10, where an increase in low level clouds and a reduction in middle and high level clouds enhance radiative cooling. See Stjern et al. (2017) for changes in the vertical profiles of clouds in the PDRMIP simulations.

For CO2x2 the tropospheric and stratospheric temperature rapid adjustments are opposite in sign. LW radiative cooling is driven by a warming troposphere and offset by a cooling stratosphere, a well‐known fingerprint of CO2 forcing. For Sulx5 the stratosphere warms slightly, in contrast to the cooling troposphere, whereas for CH4x3, the sign of the stratospheric adjustment depends on whether or not SW absorption of methane is included in the model's radiation scheme (Smith et al., 2018).

The model diversity is large in the BCx10 perturbation, at least partly due to different burdens, vertical profiles, and optical properties of BC (Stjern et al., 2017). Despite this large spread in the total RA for BCx10, the individual RA terms are mostly consistent among the PDRMIP models in terms of sign. Interestingly, the spread in RA caused by clouds is smaller in magnitude than the spread in RA from temperature changes for BCx10. For this experiment the maximum to minimum range for the PDRMIP models is a factor 2 smaller for clouds compared to tropospheric temperatures. Model diversity in total RA is also significant for CO2x2, but this spread is not dominated by any of the individual RA terms specifically. Notably, the model diversity for the Solar perturbation is much smaller than for any of the other PDRMIP perturbations—both for the total RA and the individual RA terms.

3.2. Rapid Adjustment Contributions to Fast Precipitation Changes

Figure 2 shows the PDRMIP model‐mean contribution of the instantaneous radiative perturbation, RA, and sensible heat to fast precipitation changes. The fast precipitation changes are caused by very different factors in the PDRMIP simulations, as exemplified by CO2x2 and BCx10, which have almost the same fast precipitation change but for very different reasons. The changes in precipitation amounts to a model‐mean flux change of about −2.5 and −2.0 W m−2 or around −25 mm/yr. To a large degree RA and reduction in sensible heat (Myhre et al., 2018) offset the strong instantaneous atmospheric absorption for BCx10, whereas for CO2x2 the fast precipitation change is caused by almost equal contributions from instantaneous atmospheric absorption and RA. The RA offsets the instantaneous atmospheric absorption changes for CH4x3 and Solar, causing weak fast precipitation changes. All terms are weak for Sulx5 causing a very small fast precipitation change.

Figure 2.

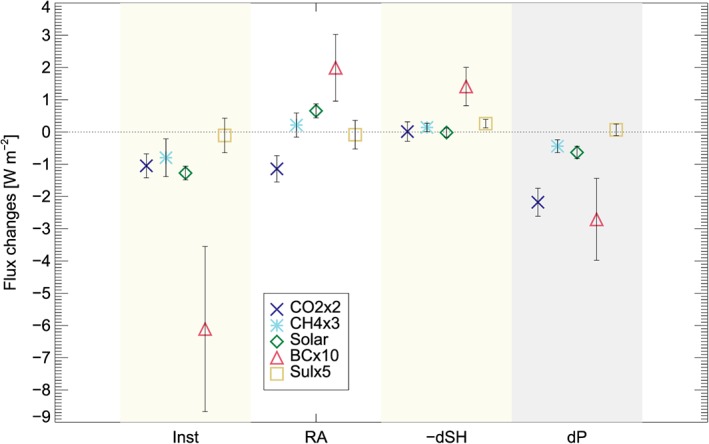
Figure 2

Open in a new tab

Contribution to fast precipitation change (dP) from instantaneous perturbation (Inst), rapid adjustment (RA), and sensible heat (‐dSH). Model mean for the PDRMIP models is shown. Inst is taken as the residual between model simulations of dQ and RA. The whiskers show one standard deviation among the PDRMIP models.

In Figure 2, the instantaneous contribution was calculated as a residual between the dQ calculated from model output of radiative fluxes and the total RA, estimated from radiative kernels. To investigate the uncertainty in this assumption we have used simulations where the instantaneous radiative cooling is known. Figure 3 shows the LW radiative cooling from the fsst simulations where the LW instantaneous radiative cooling is zero (or extremely small). For all Solar cases the LW instantaneous radiative cooling is zero, for BCx10 it is zero or very small, and for some of the Sulx5 cases it is zero (for those models neglecting aerosol‐cloud interactions). In these cases, the residual between dQ and RA should be very small or zero.

Figure 3.

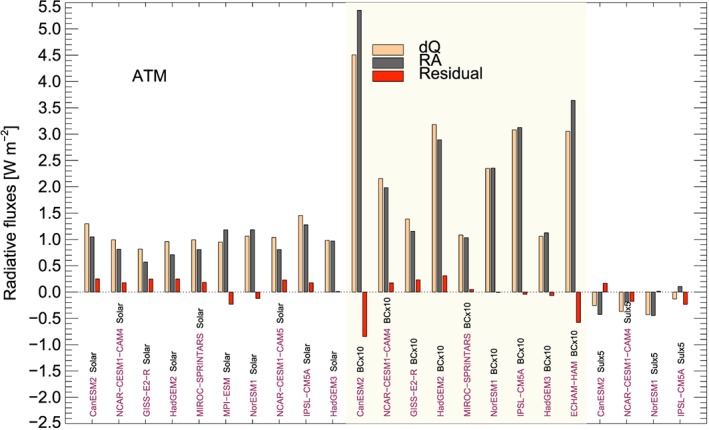
Figure 3

Open in a new tab

The longwave (LW) fast radiative cooling (dQ), where the LW instantaneous radiative cooling is zero (or extremely small). For all solar cases the LW instantaneous radiative cooling is zero, for BCx10 the LW instantaneous radiative cooling is zero or very small, and for some of the Sulx5 cases the LW instantaneous radiative cooling is zero (for those models neglecting aerosol‐cloud interactions). The LW dQ is the output from the PDRMIP models, and the LW rapid adjustment (RA) is calculated by the radiative kernel methods. The residuals are the difference between LW dQ and the LW RA.

For all of the Solar and BCx10 cases the calculated RA from the kernel methods has the same sign as the model simulations of dQ. The residuals are, with a few exceptions, small. In general the residuals are less than 20% of LW dQ or less than 0.2 Wm−2. The largest residual is for the CanESM model for the BCx10 case. This is a model with a small BC absorption included in the LW spectrum, but we assume this absorption to be sufficiently weak (Bäumer et al., 2007) to justify inclusion in the figure. A PDRMIP model‐mean of the residual is 11%, 4%, and 19% of the dQ for Solar, BCx10, and SO4x5, respectively. Using the same approach, SW dQ, RA, and the residual are shown for CH4x3 in Figure S2 for those models with no SW absorption by CH4. The SW dQ is weak for CH4x3 and much smaller in magnitude than the LW dQ for Solar and BCx10. Calculated residuals for CH4x3 for the SW are also small in magnitude and are dominated by meteorological variability, with the exception of HadGEM2, which shows slight nonlinear behavior (Smith et al., 2018).

3.3. Rapid Adjustment Contributions to Total Precipitation Changes

In a decomposition of total precipitation change into fast and slow changes, Andrews et al. (2010) showed that TOA effective radiative forcing (ERF) is a strong predictor of the slow precipitation response (their Figure 2b). This holds because surface temperature change is both a response to TOA ERF and a driver of slow precipitation changes. Since RA is an important component of ERF at the TOA (Smith et al., 2018), it follows that RA also influences slow precipitation changes. Here we investigate the radiative constraints on total precipitation change by evaluating the relative contributions of instantaneous perturbations and RA to fast and slow precipitation changes. The split between the instantaneous and RA is performed using kernels, whereas the split between fast and slow precipitation changes is calculated directly from the PDRMIP simulations (see section 2).

Figure 4 shows the model‐mean total precipitation change and its decomposition into fast and slow precipitation change. Furthermore, the instantaneous radiative perturbation and RA that dictate the fast and slow precipitation change are shown. Corresponding to the fast precipitation response, the split between instantaneous and RA contributions to radiative cooling are taken from Figure 2 (herein IF and RAF). The contributions of instantaneous perturbations and RA to the slow precipitation response (herein Is and RAs) are calculated by linearly scaling the slow radiative cooling change by the instantaneous radiative forcing and RA at the TOA. The TOA flux changes are taken from Smith et al. (2018) and listed in Table S1 in the supporting information. Their scaled contributions to radiative cooling (through change in surface temperature) are given in Table S2. The radiative cooling (dQ) per change in TOA ERF has a PDRMIP multimodel mean of about 1.3 for the climate drivers, except for BCx10 where it is close to 1.0. This radiative cooling can be derived from adding IS and RAS in Table S2, whereas ERF is given in Table S1. Fast and slow changes in sensible heat are also included; thus, all contributions to precipitation changes are accounted for.

Figure 4.

Figure 4

Open in a new tab

Net precipitation changes for the five Precipitation Driver Response Model Intercomparison Project climate drivers split into fast and slow changes (thin bars). The thick bars show the fast and slow precipitation changes split into instantaneous, rapid adjustment (hatched), and changes in sensible heat.

The relative contribution of fast versus slow precipitation change to total precipitation change differs across PDRMIP drivers, as do the contributions of instantaneous perturbations and RA. The RA for CO2x2 enhances the instantaneous perturbation changes both for the slow and the fast change (TOA radiative forcing and atmospheric radiative cooling, respectively). This is opposite to the BCx10 case where the RA offsets the instantaneous changes. The combined effect of RA on fast and slow precipitation changes is a small positive contribution to total precipitation change for all PDRMIP drivers, except for a very weak negative change for the Solar case and Sulx5 (see Table S2). For some of the RA terms the influence on TOA forcing and atmospheric radiative cooling is opposite, such as for tropospheric temperature changes, whereas for surface temperature changes the influence has the same sign (compare Figure 1 with Figure 3 from Smith et al., 2018). Robust relationships between RAS and RAF for the respective water vapor and cloud adjustments are less obvious than for temperature adjustments since these are strongly dependent on vertical profiles, and both LW and SW contributions are important. In Sulx5 all terms other than the instantaneous TOA forcing are small.

4. Summary and Conclusions

Rapid adjustment is crucial in the understanding of the global precipitation changes and differences among climate drivers. The RAs have a strong influence on fast and slow precipitation changes, in particular for changes in the atmospheric abundance of CO2 and BC. However, the RA influence on total precipitation changes is small for the climate drivers investigated in this study since the contribution of RA to TOA ERF and radiative cooling partly cancel each other.

We have used radiative kernels to quantify RA and show that for cases where RA can also be approximated by dQ from PDRMIP model output (since the instantaneous perturbations are small), the residuals are less than 20% or 0.2 Wm−2. There are some differences among the five radiative kernels used in this study, but this difference is generally smaller than the spread among the PDRMIP models in the various RA terms. It is noteworthy that there is much smaller PDRMIP model diversity in our calculated RA for the Solar case compared to CO2x2. This can also be seen from the direct model output of precipitation and sensible heat changes.

Supporting information

Supporting Information S1

Click here for additional data file. (619.8KB, pdf)

Acknowledgments

GM, ØH, BHS, and CWS were funded by the Research Council of Norway, through the grant NAPEX (229778). RJK was supported by NASA grant 17‐EARTH17R‐015. CJS and PF acknowledge support from the Regional and Global Climate Modeling Program of the U.S. Department of Energy Office of Environmental and Biological Sciences under grant DESC0012549 and UK Natural Environment Research Council grant NE/N006038/1. DWP acknowledges funding from Natural Environment Research Council projects NE/L01355X/1 (CLARIFY) and NE/J022624/1 (GASSP). DO and AK were supported by the Norwegian Research Council through the projects EVA (229771), EarthClim (207711/E10), NOTUR (nn2345k), and NorStore (ns2345k). OB acknowledges HPC resources from TGCC under the gencmip6 allocation provided by GENCI (Grand Equipement National de Calcul Intensif). PS acknowledges funding from the European Research Council project RECAP under the European Union's Horizon 2020 research and innovation program with grant agreement 724602 and support from the Alexander von Humboldt Foundation. TA was supported by the Met Office Hadley Centre Climate Programme funded by BEIS and Defra. MK and AV were supported by the Natural Environment Research Council under grant NE/K500872/1. TT was supported by the supercomputer system of the National Institute for Environmental Studies, Japan, the Environment Research and Technology Development Fund (S‐12‐3) of the Environmental Restoration and Conservation Agency of Japan, and JSPS KAKENHI grant JP15H01728. Simulations with HadGEM3‐GA4 were performed using the MONSooN system, a collaborative facility supplied under the Joint Weather and Climate Research Programme, which is a strategic partnership between the Met Office and the Natural Environment Research Council. Climate modeling at GISS (DS and GF) is supported by the NASA Modeling, Analysis, and Prediction program, and GISS simulations used resources provided by the NASA High‐End Computing Program through the NASA Center for Climate Simulation at Goddard Space Flight Center. The ECHAM6‐HAM2 simulations were performed using the ARCHER UK National Supercomputing Service. The PDRMIP data are publicly available https://www.cicero.oslo.no/en/PDRMIP/PDRMIP‐data‐access.

Myhre, G. , Kramer, R. J. , Smith, C. J. , Hodnebrog, Ø. , Forster, P. , Soden, B. J. , et al. (2018). Quantifying the importance of rapid adjustments for global precipitation changes. Geophysical Research Letters, 45, 11,399–11,405. 10.1029/2018GL079474

References

  1. Allen, M. R. , & Ingram, W. J. (2002). Constraints on future changes in climate and the hydrologic cycle. Nature, 419(6903), 224–232. 10.1038/nature01092 [DOI] [PubMed] [Google Scholar]
  2. Andrews, T. , Forster, P. , Boucher, O. , Bellouin, N. , & Jones, A. (2010). Precipitation, radiative forcing and global temperature change. Geophysical Research Letters, 37, L14701 10.1029/2010GL043991 [DOI] [Google Scholar]
  3. Bäumer, D. , Lohmann, U. , Lesins, G. , Li, J. , & Croft, B. (2007). Parameterizing the optical properties of carbonaceous aerosols in the Canadian Centre for Climate Modeling and Analysis Atmospheric General Circulation Model with impacts on global radiation and energy fluxes. Journal of Geophysical Research, 112, D10207 10.1029/2006JD007319 [DOI] [Google Scholar]
  4. Block, K. , & Mauritsen, T. (2013). Forcing and feedback in the MPI‐ESM‐LR coupled model under abruptly quadrupled CO2. Journal of Advances in Modeling Earth Systems, 5, 676–691. 10.1002/jame.20041 [DOI] [Google Scholar]
  5. Boucher, O. , Randall, D. , Artaxo, P. , Bretherton, C. , Feingold, G. , Forster, P. , et al. (2013). Clouds and aerosols In Stocker T. F., Qin D., Plattner G.‐K., Tignor M., Allen S. K., Doschung J., et al. (Eds.), Climate change 2013: The physical science basis. Contribution of working group I to the fifth assessment report of the Intergovernmental Panel on Climate Change (pp. 571–657). Cambridge, UK and New York: Cambridge University Press; 10.1017/CBO9781107415324.016 [DOI] [Google Scholar]
  6. Colman, R. A. , & McAvaney, B. J. (1997). A study of general circulation model climate feedbacks determined from perturbed sea surface temperature experiments. Journal of Geophysical, 102(D16), 19,383–19,402. 10.1029/97JD00206 [DOI] [Google Scholar]
  7. Fläschner, D. , Mauritsen, T. , & Stevens, B. (2016). Understanding the inter‐model spread in global‐mean hydrological sensitivity. Journal of Climate, 29(2), 801–817. 10.1175/JCLI-D-15-0351.1 [DOI] [Google Scholar]
  8. Flato, G. , Marotzke, J. , Abiodun, B. , Braconnot, P. , Chou, S. C. , Collins, W. , et al. (2013). Evaluation of climate models In Stocker T. F., Qin D., Plattner G.‐K., Tignor M., Allen S. K., Doschung J., et al. (Eds.), Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (pp. 741–882). Cambridge, UK and New York: Cambridge University Press; 10.1017/CBO9781107415324.020 [DOI] [Google Scholar]
  9. Forster, P. M. , Richardson, T. , Maycock, A. C. , Smith, C. J. , Samset, B. H. , Myhre, G. , Andrews, T. , Pincus, R. , & Schulz, M. (2016). Recommendations for diagnosing effective radiative forcing from climate models for CMIP6. Journal of Geophysical Research: Atmospheres, 121, 12,460–12,475. 10.1002/2016JD025320 [DOI] [Google Scholar]
  10. IPCC (2013). Summary for policymakers In Stocker T. F, Qin D, Plattner G.‐K, Tignor M, Allen S. K, Boschung J, et al. (Eds.), Climate change 2013: The physical science basis. Contribution of working group I to the fifth assessment report of the Intergovernmental Panel on Climate Change (pp. 1–30). Cambridge, UK and New York: Cambridge University Press. [Google Scholar]
  11. Knutti, R. , & Sedlacek, J. (2013). Robustness and uncertainties in the new CMIP5 climate model projections. Nature Climate Change, 3(4), 369–373. 10.1038/nclimate1716 [DOI] [Google Scholar]
  12. Lohmann, U. , Stier, P. , Hoose, C. , Ferrachat, S. , Kloster, S. , Roeckner, E. , & Zhang, J. (2007). Cloud microphysics and aerosol indirect effects in the global climate model ECHAM5‐HAM. Atmospheric Chemistry and Physics, 7(13), 3425–3446. 10.5194/acp-7-3425-2007 [DOI] [Google Scholar]
  13. Ming, Y. , Ramaswamy, V. , & Persad, G. (2010). Two opposing effects of absorbing aerosols on global‐mean precipitation. Geophysical Research Letters, 37, L13701 10.1029/2010GL042895 [DOI] [Google Scholar]
  14. Myhre, G. , Forster, P. M. , Samset, B. H. , Hodnebrog, Ø. , Sillmann, J. , Aalbergsjø, S. G. , Andrews, T. , Boucher, O. , Faluvegi, G. , Fläschner, D. , Iversen, T. , Kasoar, M. , Kharin, V. , Kirkevåg, A. , Lamarque, J. F. , Olivié, D. , Richardson, T. B. , Shindell, D. , Shine, K. P. , Stjern, C. W. , Takemura, T. , Voulgarakis, A. , & Zwiers, F. (2017). PDRMIP: A precipitation driver and response model intercomparison project—Protocol and preliminary results. Bulletin of the American Meteorological Society, 98(6), 1185–1198. 10.1175/bams-d-16-0019.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Myhre, G. , Samset, B. H. , Hodnebrog, Ø. , Andrews, T. , Boucher, O. , Faluvegi, G. , Fläschner, D. , Forster, P. M. , Kasoar, M. , Kharin, V. , Kirkevåg, A. , Lamarque, J. F. , Olivié, D. , Richardson, T. B. , Shawki, D. , Shindell, D. , Shine, K. P. , Stjern, C. W. , Takemura, T. , & Voulgarakis, A. (2018). Sensible heat has significantly affected the global hydrological cycle over the historical period. Nature Communications, 9(1), 1922 10.1038/s41467-018-04307-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Myhre, G. , Shine, K. P. , Rädel, G. , Gauss, M. , Isaksen, I. S. A. , Tang, Q. , Prather, M. J. , Williams, J. E. , van Velthoven, P. , Dessens, O. , Koffi, B. , Szopa, S. , Hoor, P. , Grewe, V. , Borken‐Kleefeld, J. , Berntsen, T. K. , & Fuglestvedt, J. S. (2011). Radiative forcing due to changes in ozone and methane caused by the transport sector. Atmospheric Environment, 45(2), 387–394. 10.1016/j.atmosenv.2010.10.001 [DOI] [Google Scholar]
  17. O'Gorman, P. A. , Allan, R. P. , Byrne, M. P. , & Previdi, M. (2012). Energetic constraints on precipitation under climate change. Surveys in Geophysics, 33(3–4), 585–608. 10.1007/s10712-011-9159-6 [DOI] [Google Scholar]
  18. Pendergrass, A. G. , Conley, A. , & Vitt, F. M. (2018). Surface and top‐of‐atmosphere radiative feedback kernels for CESM‐CAM5. Earth System Science Data, 10(1), 317–324. 10.5194/essd-10-317-2018 [DOI] [Google Scholar]
  19. Pendergrass, A. G. , & Hartmann, D. L. (2014). The atmospheric energy constraint on global‐mean precipitation change. Journal of Climate, 27(2), 757–768. 10.1175/jcli-d-13-00163.1 [DOI] [Google Scholar]
  20. Previdi, M. (2010). Radiative feedbacks on global precipitation. Environmental Research Letters, 5(2), 025211 10.1088/1748-9326/5/2/025211 [DOI] [Google Scholar]
  21. Richardson, T. B. , Forster, P. M. , Andrews, T. , & Parker, D. J. (2016). Understanding the rapid precipitation response to CO2 and aerosol forcing on a regional scale. Journal of Climate, 29(2), 583–594. 10.1175/JCLI-D-15-0174.1 [DOI] [Google Scholar]
  22. Richardson, T. B. , Samset, B. H. , Andrews, T. , Myhre, G. , & Forster, P. M. (2016). An assessment of precipitation adjustment and feedback computation methods. Journal of Geophysical Research: Atmospheres, 121, 11,608–11,619. 10.1002/2016JD025625 [DOI] [Google Scholar]
  23. Richardson, T. B. , Forster, P. M. , Andrews, T. , Boucher, O. , Faluvegi, G. , Fläschner, D. , et al. (2018). Drivers of precipitation change: An energetic understanding. Journal of Climate. 10.1175/JCLI-D-17-0240.1 [DOI] [Google Scholar]
  24. Samset, B. H. , Myhre, G. , Forster, P. M. , Hodnebrog, Ø. , Andrews, T. , Faluvegi, G. , Fläschner, D. , Kasoar, M. , Kharin, V. , Kirkevåg, A. , Lamarque, J. F. , Olivié, D. , Richardson, T. , Shindell, D. , Shine, K. P. , Takemura, T. , & Voulgarakis, A. (2016). Fast and slow precipitation responses to individual climate forcers: A PDRMIP multimodel study. Geophysical Research Letters, 43, 2782–2791. 10.1002/2016GL068064 [DOI] [Google Scholar]
  25. Sherwood, S. C. , Bony, S. , Boucher, O. , Bretherton, C. , Forster, P. M. , Gregory, J. M. , & Stevens, B. (2015). Adjustments in the forcing‐feedback framework for understanding climate change. Bulletin of the American Meteorological Society, 96(2), 217–228. 10.1175/BAMS-D-13-00167.1 [DOI] [Google Scholar]
  26. Smith, C. J. , Kramer, R. J. , Myhre, G. , Forster, P. M. , Soden, B. , Andrews, T. , et al. (2018). Understanding rapid adjustments to diverse forcing agents. Geophysical Research Letters, 45 10.1029/2018GL079826 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Soden, B. J. , Broccoli, A. J. , & Hemler, R. S. (2004). On the use of cloud forcing to estimate cloud feedback. Journal of Climate, 17(19), 3661–3665. [DOI] [Google Scholar]
  28. Soden, B. J. , Held, I. M. , Colman, R. , Shell, K. M. , Kiehl, J. T. , & Shields, C. A. (2008). Quantifying climate feedbacks using radiative kernels. Journal of Climate, 21(14), 3504–3520. 10.1175/2007jcli2110.1 [DOI] [Google Scholar]
  29. Stjern, C. W. , Samset, B. H. , Myhre, G. , Forster, P. M. , Hodnebrog, Ø. , Andrews, T. , Boucher, O. , Faluvegi, G. , Iversen, T. , Kasoar, M. , Kharin, V. , Kirkevåg, A. , Lamarque, J. F. , Olivié, D. , Richardson, T. , Shawki, D. , Shindell, D. , Smith, C. J. , Takemura, T. , & Voulgarakis, A. (2017). Rapid adjustments cause weak surface temperature response to increased black carbon concentrations. Journal of Geophysical Research: Atmospheres, 122, 11,462–11,481. 10.1002/2017JD027326 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Zhang, K. , O'Donnell, D. , Kazil, J. , Stier, P. , Kinne, S. , Lohmann, U. , Ferrachat, S. , Croft, B. , Quaas, J. , Wan, H. , Rast, S. , & Feichter, J. (2012). The global aerosol‐climate model ECHAM‐HAM, version 2: Sensitivity to improvements in process representations. Atmospheric Chemistry and Physics, 12(19), 8911–8949. 10.5194/acp-12-8911-2012 [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information S1

Click here for additional data file. (619.8KB, pdf)

Articles from Geophysical Research Letters are provided here courtesy of Wiley

RESOURCES