Anchor: trans-cell type prediction of transcription factor binding sites

Abstract

The ENCyclopedia of DNA Elements (ENCODE) consortium has generated transcription factor (TF) binding ChIP-seq data covering hundreds of TF proteins and cell types; however, due to limits on time and resources, only a small fraction of all possible TF-cell type pairs have been profiled. One solution is to build machine learning models trained on currently available epigenomic data sets that can be applied to the remaining missing pairs. A major challenge is that TF binding sites are cell-type–specific, which can be attributed to cellular contexts such as chromatin accessibility. Meanwhile, indirect TF-DNA binding and interactions between TFs complicate this regulatory process. Technical issues such as sequencing biases and batch effects render the prediction task even more challenging. Many pioneering efforts have been made to predict TF binding profiles based on DNA sequence and DNase-seq footprints, but to what extent a model can be generalized to completely untested cell conditions remains unknown. In this study, we describe our first place solution to the 2017 ENCODE-DREAM in vivo TF binding site prediction challenge. By carefully addressing multisource biases and information imbalance across cell types, we created a pipeline that significantly outperforms the current state-of-the-art methods. The proposed method is sufficiently complex enough to model nonlinear interactions between TF binding motifs and chromatin accessibility information up to 1500 bp from the genomic region of interest.

Transcription factors (TFs) regulate gene expression by binding to specific DNA sequence patterns (Pabo and Sauer 1992; Badis et al. 2009). The TF binding landscapes vary in different cell types and genetic contexts (Kasowski et al. 2010). Understanding TF binding behaviors is critical to decoding the regulatory mechanisms underlying transcription processes and diseases (Shilatifard et al. 2003; Thomas and Chiang 2006; Hawkins et al. 2011; Kornblihtt 2012; Yin et al. 2017). Chromatin immunoprecipitation followed by DNA sequencing (ChIP-seq) is a widely used method for detecting genome-wide in vivo TF binding profiles (Johnson et al. 2007; Kulakovskiy et al. 2010). The ENCyclopedia of DNA Elements (ENCODE) consortium has generated thousands of ChIP-seq profiles; however, these data only cover a small fraction of all possible TF and cell-type pairs. Performing enough ChIP-seq experiments to complete binding profiles for each cell type is unrealistic due to constraints in time and resources. Therefore, accurate computational approaches for predicting TF binding sites are needed to impute the missing data, not only acting as a complement to ChIP-seq results but also for providing insights on regulatory genomics (Bulyk 2003; Blanchette et al. 2006).

Many advances have been made in the computational prediction of TF binding profiles (GuhaThakurta 2006). The position weight matrix (PWM), as derived from experimental observations of TF-DNA interactions, is a classic method of representing TF binding patterns, also known as motifs (Staden 1984; Berg and von Hippel 1988; Stormo 2000). These probabilistic matrices assume that each nucleotide is independent, ignoring the interdependency between nucleotide positions (Stormo 2000). Early neural network approaches considering the nonindependence between positions have shown improved performance, but data set sizes limited the feasibility of these highly complex models (Horton and Kanehisa 1992). Recent development of deep learning algorithms takes advantage of large omics-scale data sets and predicts genome-wide regulatory function de novo from sequences (Alipanahi et al. 2015; Zhou and Troyanskaya 2015; Kelley et al. 2016; Quang and Xie 2016). Unfortunately, these computational methods make predictions based on sequence alone, which does not contain enough information to discriminate cell-type–specific binding sites. In addition to sequence, TF binding is highly associated with cellular contexts such as chromatin accessibility (Gross and Garrard 1988; Stormo and Fields 1998; Gaszner and Felsenfeld 2006). For example, a specific genome position may be open and bound to a TF in one cell type, but the same genome position may be closed and unbound in another cell type (Neph et al. 2012). The DNase-seq assay has been developed to measure chromatin accessibility genome-wide (Sabo et al. 2004; Crawford et al. 2006; John et al. 2013). “Footprinting” algorithms attempt to recover cell-specific TF binding sites (TFBSs) from DNase cleavage signals (Zhang et al. 2008; Hesselberth et al. 2009; Boyle et al. 2011; Pique-Regi et al. 2011; Cuellar-Partida et al. 2012; Piper et al. 2013; Gusmao et al. 2014, 2016; Sherwood et al. 2014; Sung et al. 2014; Yardımcı et al. 2014; Kähärä and Lähdesmäki 2015; Chen et al. 2017; Schmidt et al. 2017; Quach and Furey 2017).

The ENCODE and NIH Roadmap Epigenomics Mapping Consortium (The ENCODE Project Consortium 2012; Roadmap Epigenomics Consortium et al. 2015) projects provide a large data set of TF ChIP-seq and DNase-seq results in diverse cell types and conditions, which is an invaluable source of information for understanding the regulatory process. In 2017, the Dialogue on Reverse Engineering Assessment and Method (DREAM) (Stolovitzky et al. 2007) organized the ENCODE-DREAM in vivo TF binding site prediction challenge (https://www.synapse.org/#!Synapse:syn6131484/wiki/; accessed February 9, 2018). This challenge provides a systematic benchmark to evaluate computational methods for predicting cell-type–specific TF binding profiles. Here, we describe our algorithm, Anchor, which shared a co-first place with J-Team (Keilwagen et al. 2017) in this challenge. Our approach considers both the interdependencies between neighboring nucleotide positions and nonlinear interactions between TF motifs. It advances the computational predictions of in vivo TF binding sites, and key features used in our model are informative for future method development and regulatory mechanism exploration.

Results

Overview of the experimental design for cross-cell type TF binding predictions

In this paper, we use data sets provided by the ENCODE-DREAM challenge, which consists of 84 ChIP-seq experiment results covering 32 TFs and 13 cell types (https://www.synapse.org/#!Synapse:syn6131484/wiki/402033; accessed February 9, 2018). DNase-seq data are available for all 13 cell types. A subset of the 13 ChIP-seq data sets were held out as the evaluation testing set on which final rankings are based, 28 were held out for the “leaderboard” where competitors can compare results to each other in real time, and the remaining ChIP-seq data sets were used for training. For each 200-base pair (bp) interval at 50-bp sliding window steps, a gold standard binary label “Bound” or “Unbound,” according to the ChIP-seq signals, is assigned. “Ambiguous” labels may also be assigned to a bin, but such bins are ignored in training and evaluation. Binding data for Chromosome (Chr) 1, Chr 8, and Chr 21 were excluded from all ChIP-seq data sets, including the training ChIP-seq data sets; final evaluation on the leaderboard and testing set were based on the quality of predictions exclusively on these three held-out chromosomes. Chr Y was ignored in training and evaluation, and ChIP-seq binding data for the remaining 20 chromosomes were available for training in select TF–cell type pairs. GRCh37 was used as the reference genome. The test set consists of ChIP-seq binding profiles of 13 TF-cell type pairs covering 12 unique TFs (CTCF, E2F1, EGR1, FOXA1, FOXA2, GABPA, HNF4A, JUND, MAX, NANOG, REST, and TAF1) and four unique cell types (liver, iPSC, PC-3, and K562). All test data were unpublished prior to the conclusion of the challenge and completely blind to all participants. The liver cell type comprised nine of the 13 testing pairs and was a particularly difficult cell type for making predictions because it did not have any available reference training binding data for any TF. In addition, whereas 12 of the cell types represented pure cell lines, liver was primary tissue from two different donors, which further complicated predictions. More information about the data and evaluation metrics can be found on the ENCODE-DREAM website (https://www.synapse.org/#!Synapse:syn6131484/wiki/402032; accessed February 9, 2018).

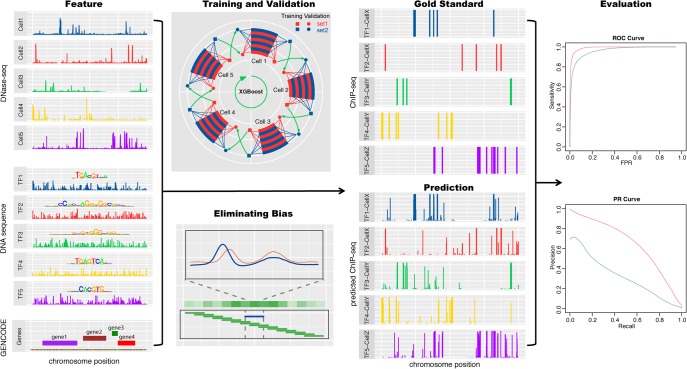
Our method, which we have named Anchor, consists of four major components in order to extract informative features and reduce errors. First, we use a “crisscross” validation-based early stopping strategy such that training is performed on one half of the 20 training chromosomes for one cell type. Model training proceeds iteratively until the error on a validation set, which is comprised of binding data on the remaining training chromosomes for another cell type, fails to decrease. The error on the validation set is used as a proxy for the generalization error in determining when overfitting has begun, which helps the model generalize across cell types and chromosomes. Without this step, a model trained on a single ChIP-seq experiment may memorize artifacts, hindering the model. These artifacts may result from biological contexts unique to a single cell type or batch effects. Second, features are extracted from a 1500-bp window surrounding each bin in TF binding in order to capture longer range contexts that influence binding. Information of the neighboring sequence and chromatin accessibility is integrated to delineate the TF binding landscape. Third, TF-TF interaction is a known crucial regulatory component. The Anchor model incorporates motifs of a variety of TFs in the feature generation step to capture events such as indirect binding and anticorrelated binding, which are not detectable by using a single TF motif. For example, a model that predicts REST binding may incorporate CTCF PWM scans as features because true REST binding sites are less likely to overlap true CTCF binding sites. Finally, the Anchor pipeline includes a preprocessing step to counteract errors induced by heterogeneity in the DNase-seq signals. Cell-type- and chromosome-specific DNase cleavage biases greatly affect the predictive performance. This is because current sequencing techniques to detect chromatin accessibility, including DNase-seq, depend on enzymatic treatments. These enzymes have inherent sequence cleavage biases related to the DNA shape and chemical modification status (Koohy et al. 2013; Lazarovici et al. 2013; Yardımcı et al. 2014; Martins et al. 2018). These biases need to be carefully rectified to build a model generalizable in multiple cell types. Furthermore, DNase-seq experiments can vary greatly in terms of read depth and signal-to-noise, and these differences must be corrected. To discriminate true chromatin accessibility signals from artifacts, we leveraged information from multiple cell types by quantile normalization of the DNase-seq data and extracting the differences between a query cell type and the average level across all training cell types. By integrating these components, the Anchor pipeline provides a robust and accurate method for predicting TF binding profiles across cell types (Fig. 1).

Figure 1.

Overview of the TF binding profile prediction. The DNase-seq signals, TF binding motifs, and distances to the nearest genes are the input features. After eliminating sequencing and cell-type–specific DNase-seq biases, XGBoost models are trained and validated in a cross-cell type and cross-chromosome fashion to exploit the limited data and avoid overfitting. In the training and validation panel, two randomly partitioned chromosome sets are shown in red and blue. The square sets are used to train XGBoost models, and the validation circle sets are used to select hyperparameters. The evaluation is based on the AUROC and AUPRC between the genome-wide predictions and the gold standard ChIP-seq profiles.

Crisscross training and validation to reduce cell type and chromosome biases

To create a useful model of predicting ChIP-seq results at the genome scale, it is crucial to make the model generalizable to different cell types. However, overfitting is an especially difficult issue for this application because the testing set (e.g., the untested cell types and chromosomes) is not entirely reflective of the training set. In addition to the endogenous biological differences between training cell types and held-out testing cell types, batch effects, which occur because measurements are affected by laboratory conditions, reagent lots, and personnel differences, can also greatly impact evaluation results. While a model may perform well on the training cell types, the same model is not necessarily guaranteed to perform well on a held-out testing cell type. To exploit information contained in the training data and avoid overfitting, we implemented a crisscross validation-based early stopping procedure as follows (Supplemental Fig. S1; see details in Supplemental Material−Extended Methods):

Step 1: Randomly divide the training chromosomes into two fixed sets, A and B, as the training and validation sets (Supplemental Fig. S1A; Supplemental Table S1). This partition allows us to train models on one chromosome set and validate models on the other. If we train and validate models on the same chromosome set, models will overfit to the training chromosomes. The cross-chromosome design reduces the overfitting and makes our models generalizable across chromosomes.

Step 2: Given a query TF, we collect all available training cell types of this TF, cell 1, cell 2, … , cell N. We train models on one cell type with the training chromosomes and validate models against another cell type with the validation chromosomes (Supplemental Fig. S1B). If we train and validate models on the same cell type, models will overfit to the training cell type. Similar to the cross-chromosome design, the cross-cell type design further reduces the overfitting and makes our models generalizable across cell types.

Step 3: Train the first XGBoost (Chen and Guestrin 2016) model on chromosome set A in cell type 1 with 1000 iterations and validate on set B in cell type 2 (setA-cell1-setB-cell2) (Supplemental Fig. S1C). This validation step is necessary to select the best performing hyperparameters among the 1000 iterations, without which the XGBoost model will overfit to the training data. Then, we train and validate on setA-cell2-setB-cell3. In this way, repeatedly train N models (Supplemental Table S2) in the crisscross fashion to avoid overfitting to a specific chromosome or cell type.

Step 4: Similar to step 3 but switch the train and validation chromosome sets (Supplemental Fig. S1D): train on chromosome set B in cell 1 and validate on chromosome set A in cell 2 (setB-cell1-setA-cell2). Repeat and obtain another N model to fully utilize the available ChIP-seq data.

Step 5: Average the predictions of the total 2N models in steps 3 and 4 as our final predictions to incorporate information from multiple cell types (Supplemental Fig. S1E).

In this crisscross experiment design, our models are trained on one cell type and validated against another cell type in a cross-chromosome fashion, diminishing potential bias toward a specific cell type or chromosome set. Meanwhile, every part (chromosome and cell type) of the training data is used to train once and validate once, effectively considering all available information. Of note, the validation in Step 3 is crucial to control overfitting in iterative base learners such as XGBoost. For comparison, we trained an overfitted model with 1000 iterations without validation, which has lower performance across TF-cell type pairs (Supplemental Fig. S2).

Predictive performance varies widely across cell types and evaluation schemes

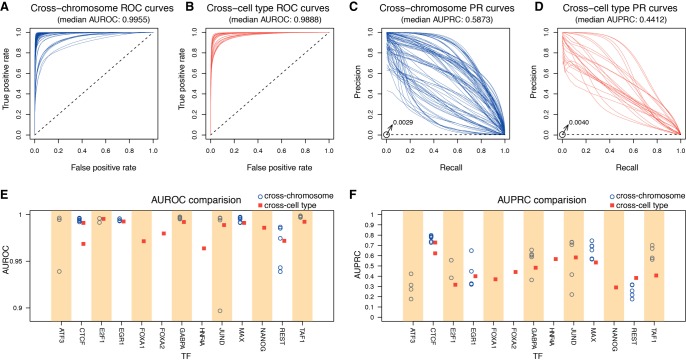
We calculated the area under receiver operating characteristic curves (AUROCs) (see Methods; Supplemental Table S3). The AUROCs, as evaluated in a “within-cell” cross-chromosome fashion, have a median value of 0.9955 (Fig. 2A). When evaluated in a “cross-cell” fashion, the median AUROC decreases to 0.9888 but remains high (Fig. 2B). Given the extreme class imbalance (<0.5% of all genomic intervals are bound), we also calculated the area under precision-recall curves (AUPRCs), which can provide a less inflated measure (see Methods). Whereas the random baseline model in the ROC curve corresponds to a diagonal line with an area of 0.5, the random baseline model in the PR curve corresponds to a horizontal line with an area equal to the proportion of positive samples. The median cross-chromosome and cross-cell AUPRCs are 0.5873 and 0.4412, respectively (Fig. 2C,D). In comparison, the median AUPRC of the random baseline model is 0.0029 for cross-chromosome and 0.0040 for cross-cell; hence, our Anchor model demonstrates a more than hundredfold improvement over random guessing. Nevertheless, the AUPRC of a perfect model is 1, indicating that there is space for improvement in the current field of computational prediction of TF binding sites. We provided the prediction performances of our model and multiple evaluation metrics (e.g., the number of true positives; false negatives, or missed binding sites; false positives or misassigned binding sites) using different cutoffs in Supplemental Figure S3 and Supplemental Table S4. It should be noted that the discrepancy between cross-chromosome and cross-cell type performance is consistent with the observed differences between the within-cell round and the final cross-cell round during the ENCODE-DREAM challenge (Supplemental Fig. S4; Supplemental Table S5)—it is easier to make correct predictions within the same cell type (Quach and Furey 2017). This reflects a critical issue in current evaluation schemes that have been published intensively in the field (Boyle et al. 2011; Pique-Regi et al. 2011; Piper et al. 2013; Sherwood et al. 2014; Sung et al. 2014). Our Anchor scheme improves the predictions of TF binding across cell types, which are comparable to the within-cell performances across chromosomes (red squares in Fig. 2E,F). Of note, the cross-cell type results were evaluated on the held-out testing data set in the ENCODE-DREAM challenge (ATF3 was not evaluated and CTCF was evaluated in two cell lines), whereas the cross-chromosome results were evaluated on the training data set. Since FOXA1, FOXA2, HNF4A, and NANOG each have only one training cell line to build models, we did not plot the cross-chromosome results for them (which would be overestimated due to overfitting). The complete table of the training and testing cell types for the 13 TFs is shown in Supplemental Table S2, and the corresponding prediction performances are shown in Supplemental Table S3. To further comprehensively evaluate the robustness of our method, we made predictions for 55 publicly available ENCODE ChIP-seq results outside the ENCODE-DREAM challenge, covering eight TFs (ATF3, CTCF, EGR1, FOXA1, GABPA, JUND, REST, TAF1). The prediction performances on data within and outside the challenge are comparable (Supplemental Figs. S5–S7; Supplemental Table S6). In addition, we also evaluated our method using DNase-seq data outside of the ENCODE-DREAM challenge and made predictions on a total of nine TF-cell type combinations, covering eight different TFs. The prediction performances are also very similar using DNase-seq data inside and outside ENCODE (Supplemental Figs. S8, S9; Supplemental Table S7). The difference in performance for the 20 training chromosomes versus the three testing chromosomes is almost negligible (Supplemental Fig. S10). These results demonstrate that our models have great generalizability, especially in untested cell types.

Figure 2.

The cross-chromosome and cross-cell type performances of different TFs. The cross-chromosome and cross-cell type performances are shown in blue and red, respectively. (A,B) The ROC curves of all TF-cell type pairs. The baselines of random predictions are shown as dashed lines with area of 0.5. (C,D) The PR curves of all TF-cell type pairs. The baselines of random predictions are shown as dashed lines with the areas of 0.0029 and 0.0040. (E) The AUROC comparison of 13 TFs. (F) The AUPRC comparison of 13 TFs.

The predictability of the 13 TFs varies across cell types, which is clearly shown in the AUPRC space. The AUPRCs range between 0.1769 (REST in H1-hESC) and 0.7988 (CTCF in IMR-90) (Fig. 2F; see the complete AUPRC values in Supplemental Table S3). Among all 12 TFs, CTCF is consistently the easiest to predict, with the highest average AUPRC of 0.7724 and standard deviation of 0.0274 in seven cell types. In contrast, REST is harder to predict, with the lowest average AUPRC of only 0.2565. The main reason is that CTCF ChIP-seq data contain more binding events than other TFs, resulting in a higher AUPRC baseline of random prediction. The baseline equals the ratio of binding intervals over all intervals in the genome under consideration. We observed significant correlations between AUPRC/AUROC and the corresponding baseline (Supplemental Fig. S11). The prediction for HNF4A in liver has relatively high AUPRC but the lowest AUROC, which is also related to the AUPRC baseline (Supplemental Fig. S12). In addition, JUND displays the largest variation in performance, ranging between 0.7322 and 0.2209 among five cell types.

Preprocessing DNase-seq features affects prediction accuracy

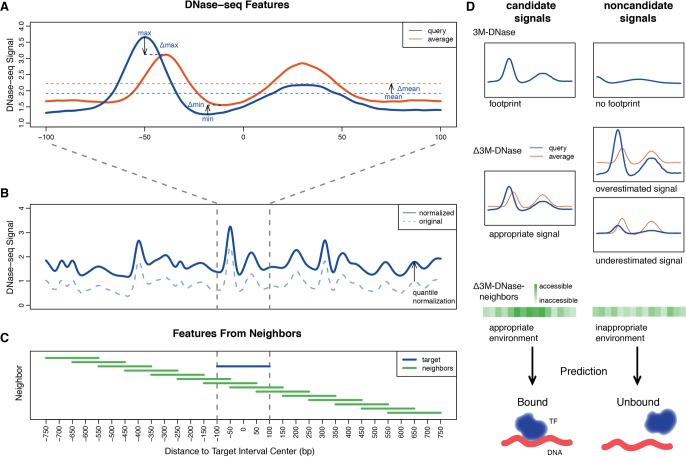
To correct for heterogeneity of DNase-seq signals, we first calculated the maximum, minimum, and mean DNase-seq signal values (hereafter referred to as the 3M-DNase features) as the simplest features (Fig. 3A). Specifically, we used both the filtered read alignment file and the fold-enrichment signal coverage tracks provided by the ENCODE-DREAM challenge. The fold-enrichment signals represent the fold-enrichment of smoothed (150-bp smoothing window) DNase cut-sites (5′ end of reads) counts relative to the expected number of reads from a local Poisson simulated background distribution of reads at each nucleotide in the genome using the signal processing engine of the MACS2 peak caller (Zhang et al. 2008). These three basic features are able to represent the chromatin accessibility, but the strength of the signal may be overestimated or underestimated due to the local biases introduced by different chromosomes and cell types. Different local chromatin contexts (e.g., related to different DNA shapes and chemical modification statuses) lead to the inherent sequence cleavage biases of enzymes in the DNase-seq experiments. To rectify these local biases, we calculate Δmaximum, Δminimum, and Δmean DNase-seq values (hereafter referred to as the Δ3M-DNase features), which are the differences between the query cell type and the average level of all 13 cell types. These Δ3M-DNase features are able to correct the predictions even if the signals are skewed. For example, if the 3M-DNase features are overall higher at some genomic regions in a query cell type, a model without Δ features rectification may predict a false positive binding event at these regions. In contrast, the Δ features are large in these regions and enable the model to learn and distinguish the false positive and true positive binding events. We also normalized the DNase-seq signals by genome-wide quantile-normalizing all DNase-seq signals against the DNase-seq signal of the liver testing cell type, since liver represented the majority of the evaluation scheme (Fig. 3B). This process is similar to normalizing the entire DNase cleavage profile based on the control experiment, yet we quantile-normalize the distribution to the test cell type, further eliminating the systematic biases (Supplemental Fig. S13). In addition, the TF binding events are not only dependent on the accessibility of the 200-bp interval of interest but highly associated with the neighboring chromatin architecture. Therefore, we add the 3M-DNase and Δ3M-DNase features of upstream and downstream neighboring intervals as extra features, to capture the local chromatin environment (Fig. 3C). Including these 14 neighbors expands the covered chromosome positions from 200 bp to a much larger space of 1500 bp (hereafter referred to as the Δ3M-DNase-neighbors features) (Fig. 3D). The details of generating these features are provided in the Supplemental Material−Extended Methods. To demonstrate the patterns of these DNase-seq features, we plot the original read alignment coverage signals and the corresponding features of two example “Bound” and “Unbound” genomic intervals (Supplemental Fig. S14). The read alignment coverage (Supplemental Fig. S14A) profile and the 3M-DNase-neighbors features (Supplemental Fig. S14B) are similar for these two intervals. However, the Δ3M-DNase-neighbors features (Supplemental Fig. S14C) show distinct patterns: The “Bound” interval has values around 0 and the “Unbound” one has many values above 0, indicating an overestimation of the DNase-seq signals. By integrating these Δ3M-DNase-neighbors features, our Anchor framework is able to distinguish the true binding events from the unbound cases even if biases exist. The prediction values are distinct for the “Bound” (0.9989) and “Unbound” (0.1847) intervals. The corresponding motif-based and distance-to-gene features are also shown in Supplemental Figure S15. In sum, we preprocessed the DNase-seq data to extract discriminative features, reducing various global and local biases introduced by different cell types and batches. We will describe the improvement of performance by adding these features in the next section.

Figure 3.

Processing DNase-seq signals to limit cell-type–specific biases. (A) For each 200-bp genomic interval, the maximum, minimum, and mean and the Δmaximum, Δminimum, and Δmean DNase-seq values are extracted as features to correct for the heterogeneity of DNase-seq signals and eliminate local sequencing biases. (B) The dashed original DNase-seq profile is quantile normalized to the test cell type profile to eliminate the cell-type–specific biases. (C) The features from 15 intervals ranging between upstream and downstream 750 bp are considered to capture the neighboring chromatin accessibility. (D) Example scenarios of candidate and noncandidate signals captured by 3M-DNase, Δ3M-DNase, and Δ3M-DNase-neighbors features.

Nonredundancy of feature engineering in the Anchor framework

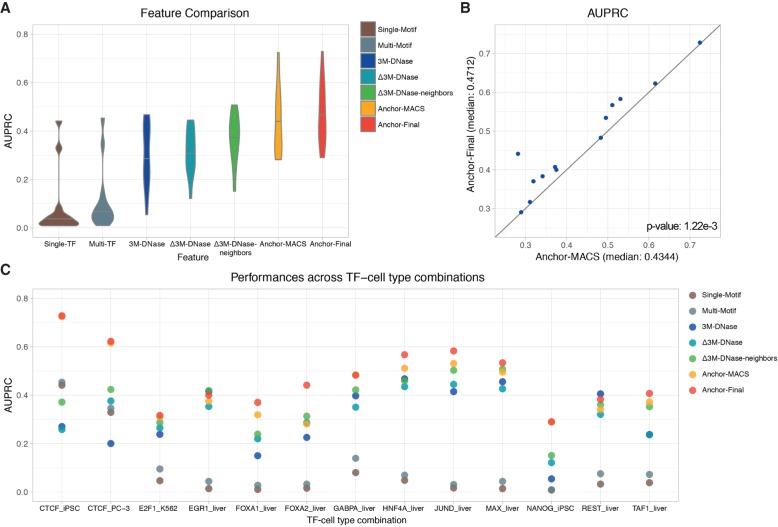
Nonredundant feature engineering strategies are implemented in our Anchor framework, integrating both DNase-based and sequence-based information after bias reduction. To compare the performance of using different types of features and data processing, we calculate the AUROCs and AUPRCs for 12 TFs in the held-out cell types (Fig. 4; Supplemental Fig. S16; Supplemental Table S8). We first test two models, “Single-Motif” and “Multi-Motif,” using sequence-based features only: “Single-Motif” consists of the scanning signal of target TF motif only, whereas “Multi-Motif” comprises signals of all 12 TF motifs (brown and blue-gray models in Fig. 4; Supplemental Fig. S16). The “Multi-Motif” model has higher AUROC and AUPRC than the “Single-Motif” model in all test cases, indicating the indispensable roles of multiple TF interactions in TF binding. However, the AUPRCs of most TFs, except for CTCF, are very low, barely above the baseline random predictions, even after considering the interactions between TFs. This indicates that the cell-context-specific information, such as DNase-seq results, are extremely useful for accurate prediction. To demonstrate the unique information provided by chromatin accessibility, we further compare three models using DNase-based features (blue, teal, and green models in Fig. 4; Supplemental Fig. S16). The “3M-DNase” model only considers signals within the target 200-bp interval. It achieves better performances than sequence-based models in most cases except for CTCF. When we add the Δ3M-DNase features to correct the local biases, the performance is improved in terms of both AUROC and AUPRC. Furthermore, the signature of the 1500-bp chromatin architecture in the “Δ3M-DNase-neighbors” model provides essential information and greatly increases the median AUPRC from 0.3208 to 0.3712. To integrate both sequence-based and DNase-based features, we combine the features mentioned above into the “Anchor-MACS” model, leading to a further improvement (yellow model in Fig. 4; Supplemental Fig. S16). The feature comparison demonstrates that these sequence-based and DNase-based various types of features are nonreductant, and incorporating them into our model is essential to achieve high performance. The high performance across chromosome and cell types indicates that our model is useful for future studies of a broader range of TFs in diverse cell types.

Figure 4.

The performance comparison of models using different features in 13 testing TF-cell type pairs. The prediction performances of two sequence-based models (Single-Motif and Multi-Motif), three DNase-based models (3M-DNase, Δ3M-DNase, and Δ3M-DNase-neighbors), and two ensemble models (Anchor-MACS and Anchor-Final). (A) The median AUPRCs of models using different types of features across 13 TF-cell type pairs. (B) The AUPRCs of the Anchor-MACS (x-axis) and Anchor-Final (y-axis) models in 13 TF-cell type pairs are shown as blue dots. If a dot is above the diagonal line, it means the AUPRC of the Anchor-Final model is higher. The paired Wilcoxon signed-rank test was performed between the predictions of these two models and the P-value= 1.22 × 10⁻³. (C) The AUPRCs of 13 TF-cell type pairs using different types of features. Some yellow dots are covered by the red dots, due to similar performances. The complete listing of the AUPRCs can be found in Supplemental Table S8.

To further improve performance, we developed a new, simpler DNase-seq signal processing pipeline, to replace the MACS pipeline. Although MACS is a popular “go-to” peak calling preprocessing algorithm commonly used in DNase-seq and ChIP-seq signal processing, its signal processing engine does not necessarily provide the optimal representation needed for TF binding prediction. When predicting TF-binding sites across cell types, however, we find that quantile-normalizing the original read-depth DNase-seq signal profile of each training cell type to the testing cell type (see Methods; Supplemental Fig. S13) achieves better performance than using the fold-coverage signal tracks provided by the challenge using the signal processing engine of the MACS2 peak caller. In Figure 4, the only difference between the “Anchor-MACS” model and the “Anchor-Final” model is the DNase-seq signal processing—by MACS or Anchor, respectively (yellow and red models in Fig. 4; Supplemental Fig. S16). In the “Anchor-Final” version, we simply counted the DNase-seq read pile-up at each nucleotide and performed quantile-normalization across all the training cell types. In the 13 TF-cell pairs, our “Anchor-Final” model achieves significantly higher AUROCs (P-value = 0.000488) (Supplemental Fig. S16) and AUPRCs (P-value = 0.00122) (Fig. 4B) using the paired Wilcoxon signed-rank test (see Methods). This result indicates that when trans-cell type predicting TF binding profiles, our Anchor strategy can be a better and simpler alternative to preprocessing signals from multiple cell types. In addition, we compared the performances of our Anchor model and three other methods (Gusmao et al. 2016; Keilwagen et al. 2017; Quang and Xie 2017) across the 13 testing TF-cell type pairs (Supplemental Fig. S17). Of note, these methods use both DNase-seq data and DNA sequence as inputs, whereas other previous methods such as DeepSEA (Zhou and Troyanskaya 2015) and DeepBind (Alipanahi et al. 2015) are only sequence-based approaches. We observe clearly much lower prediction performances without the DNase-seq features (“Single-TF”/“Multi-TF” versus others in Fig. 4A; Supplemental Fig. S16A), which has been reported by the J-team (Keilwagen et al. 2017) and Kipoi (Avsec et al. 2018) as well.

Distant chromatin architecture and TF-TF interactions determine site-specific TF binding

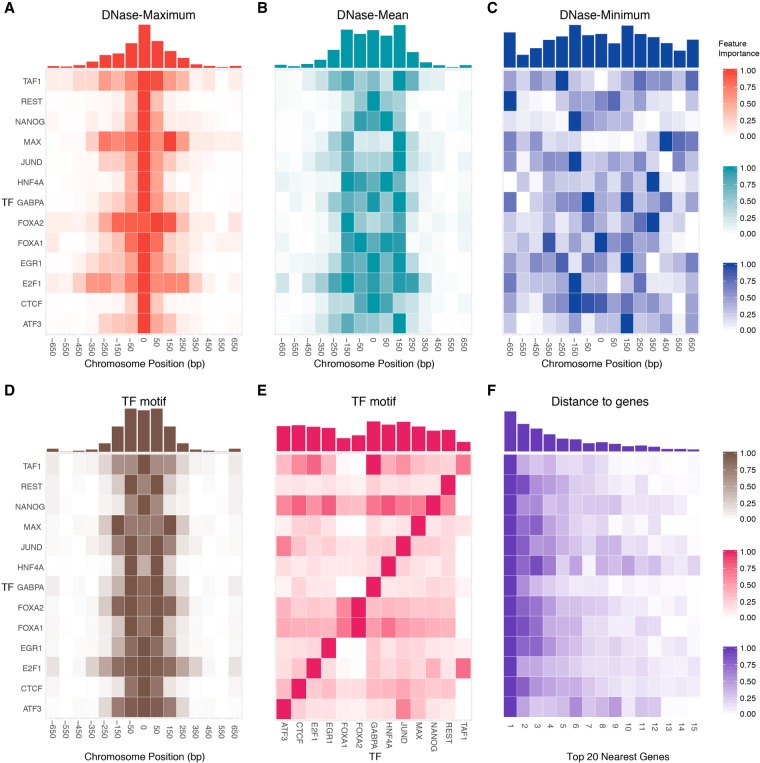
TF binding is not only controlled by the immediate local chromatin architecture but also by a much wider neighboring region. We evaluate the importance of neighboring locations and observe a TF-specific spatial distribution of “high intensity bins” in the vicinity of the binding sites (Fig. 5). Each bin represents a 200-bp genomic interval, and the contributions to prediction of the 14 upstream and downstream neighboring intervals were investigated. For each feature, we first calculated the relative feature importance by normalizing the original values to the range [0,1]; more important bins are shown in a darker color. The complete feature importance values can be found in Supplemental Table S9. When we consider the feature “Maximum” of DNase-seq signals, the highest intensity bin resides in the target center (Fig. 5A). Many TFs have a distribution with a narrow peak, except for TAF1, MAX, FOXA2, and E2F1, which have a widespread distribution range between ±250-bp regions around the center of interest. The pattern may be caused by the related large protein complexes—the TAF family is involved in the RNA polymerase II preinitiation complex (Louder et al. 2016), and E2F and MAX families are involved in the E2F-p130 complex (Ogawa et al. 2002). In contrast, for the “Mean” DNase-seq feature, we observe nearly uniformly distributed feature importance ±150 bp around the center. For MAX, JUND, FOXA2, and ATF3, the most important feature resides in the ±150-bp region, instead of the center. We find that MAX, JUND, and ATF3 belong to the same TF superclass “basic domains,” classified based on the characteristics of DNA-binding domains (Wingender et al. 2018). Their unique patterns of the “Mean” feature importance may be related to the TF classification, since the TF-DNA binding is determined by both the protein structure and the local chromatin accessibility. The superclass of the 13 TFs in this study is provided in Supplemental Table S10. The “Minimum” feature does not display a clear pattern, which is likely covered by the local biases. When we consider the “ΔMinimum” feature, the pattern emerges as a single-peaked distribution around the center (Supplemental Fig. S18). These results indicate that the long-range DNase cleavage signatures play an essential role in determining TF binding. It has been reported that TF binding mainly occurs in a dense cluster, spreading less than 1–2 kilobases in both Drosophila and mammalian cells (Moorman et al. 2006; Garber et al. 2012; Gerstein et al. 2012; Yan et al. 2013). Within the dense cluster, the nearest TF binding peaks form a geometric distribution with a mean value of 362 bp in human cells (Yan et al. 2013). The distribution of feature importance (“Maximum,” “Minimum,” and “ΔMinimum”) observed in our model mainly ranges ±350 bp around the binding sites, which may be related to the previously reported neighboring TF binding peaks. Furthermore, the prevalent symmetric feature importance patterns can be associated with the symmetric homodimeric or heterodimeric TF-TF-DNA complex structures, including HNF (Chi et al. 2002; Yan et al. 2013), E2F (Morgunova et al. 2015), and MAX (Nair and Burley 2006) TF families.

Figure 5.

The spatial distributions of DNase-based, sequence-based, and distance-to-gene feature importance. The relative feature importance heat maps of DNase-based (A) “maximum,” (B) “mean,” and (C) “minimum” features display common and TF-specific distributions in the vicinity of the TF binding site. For each feature, the original feature importance values were normalized to the range [0,1], and more important bins are shown in a darker color. The x-axis represents the relative distance to the center of a binding site in bp units, and each bin represents a 200-bp genomic interval. The corresponding accumulated feature importance is shown in histograms above the heat maps. Of note, the symmetric binding pattern is not clearly shown in C, the “DNase-minimum” feature, due to the relatively low values of the minimum signal. However, when we use the “ΔDNase-Minimum” feature (Supplemental Fig. S13C) to capture the difference across cell types, the pattern emerges. (D) Similarly, the relative feature importance of sequence-based features calculated using the motif of query TF itself. (E) The feature importance heat map when we consider the interdependency between different TFs (e.g., using the motif of one TF to predict another TF). (F) The importance heat map of the top 15 closest distances to genes.

In addition, DNA sequence-based features also display a spatial pattern (Fig. 5D,E). Similar to DNase features, the high intensity bins locate in the vicinity of TF-binding center, ranging from −150 to +150 bp. This similarity indicates the “synchronization” of TF motif and chromatin accessibility. Furthermore, TFs are regulated by the interaction between TFs and DNA, including TF-TF complexes, co-occurrence of TFs, low-affinity binding, and indirect binding (Siggers and Gordân 2014; Crocker et al. 2016; Inukai et al. 2017; Morgunova and Taipale 2017). In Figure 5E, we calculate the contribution of each TF motif to the binding of other TFs. As we expected, most TFs mainly rely on themselves (the strong diagonal signals in Fig. 5E). NANOG relies on almost all other TF motifs. This may be related to the unique role of NANOG in embryonic stem cells (ChIP-seq of NANOG - H1-hESC in this work). It has been reported that NANOG contains variant elements related to its nonspecific DNA binding at the protein structure level (Jauch et al. 2008), and a protein interaction network of NANOG-associated proteins has been proposed to function as a module of maintaining cell pluripotency (Wang et al. 2006). In addition, we observe a high dependency between ATF3 and JUND (Fig. 5E), which may be associated with the known interaction between these two TFs (Chu et al. 1994). Although the TF-specific patterns cannot be perfectly explained, this feature importance analysis provides new insights into TF-DNA binding and TF-TF interactions from the computational perspective. Finally, we evaluate the importance of the shortest 15 distances to the nearest genes (Fig. 5F). If a target interval is closer to a gene, it's more likely that it binds to a TF. The importance diminishes for distant genes.

Discussion

In this study, we create a feature-enriched method, Anchor, to exploit ChIP-seq and DNase-seq data in a crisscross fashion; training on one cell type–chromosome pair and validating against another. This strategy avoids overfitting to the training data, and our model retains high performance even in a completely untested cell type. To reduce the effects of the global and local sequencing and cleavage biases, we map the entire DNase-seq profile to a reference cell type and extract the differential features between cell types. In addition to the normalization, we integrate the information of the flanking 1500-bp-wide chromatin architecture and the nonlinear interactions between TFs. These features prove to be essential in determining the TF-binding events for various TFs. Moreover, we find TF-specific heat map patterns in the vicinity of the binding sites.

In previous pioneering computational footprinting methods (Pique-Regi et al. 2011; Gusmao et al. 2014; Sherwood et al. 2014; Sung et al. 2014; Yardımcı et al. 2014), the DNase-seq artifacts due to sequencing biases have been addressed. It has been reported that cross-cell type predictions are worse than within-cell type predictions (Quach and Furey 2017). However, it remains unclear how to correctly leverage information from multiple cell types where cell-specific biases and batch effects exist. In contrast to previous signal processing and peak calling methods (Zhang et al. 2008, 2014), our Anchor approach directly normalizes the entire training DNase-seq profile to the testing profile, effectively avoiding multisource artifacts across cell types. In addition, our signal normalization step is independent of the chromatin accessibility assay type and machine learning method; it can potentially be adapted to other experimental techniques such as ATAC-seq (Buenrostro et al. 2015), or other classification and regression models such as neural networks.

The success of our method is not incidental; in fact, there are many commonalities between our Anchor algorithm and the shared first place method developed by the J-team (Keilwagen et al. 2017) in the ENCODE-DREAM challenge. They find that TF binding motifs and chromatin accessibility are the most informative features, which are sufficient to build computational models and yield high performance. Our Anchor framework is also built on these two types of features, without other genomic inputs such as RNA-seq data. When processing the DNase-seq data, instead of using base pair-level features, they calculated bin-level aggregate features (minimum, maximum, median, and other statistics) due to the constraint in hard drive size, computer memory, and runtime. Similar strategies were used in our method (the “3M-DNase” features) for capturing the major bin-level signals and building models within acceptable computational resources. In addition, the interactions between TFs are considered in our method by using motif features of multiple TFs (the “Multi-Motif” features). Similarly, the J-team considered a set of “peer” motifs instead of a single motif, to integrate the TF-TF interactions such as competitive binding of “peer” TFs for the same site. The J-team also calculated the distance to the closest transcription start sites on either DNA strand orientation from GENCODE annotations, whereas we used the top 20 closest distances to a gene as features. The similar ideas embedded in these two methods provide new perspectives for us to understand transcription factor binding events in regulatory genomics.

Our algorithm is also related to the recent emerging neural network approaches, including DeepSEA, DeepBind, Basset, and DanQ (Alipanahi et al. 2015; Zhou and Troyanskaya 2015; Kelley et al. 2016; Quang and Xie 2016). In those methods, the distant sequence-based information is learned by the neural network in an implicit way. In our model, both sequence-based and DNase-based distant information is considered. We also evaluated the importance of features extracted from −650 to +650 bp, and plotted the distribution of high-intensity bins in a TF-specific fashion. Neural network approaches that integrate both sequence and DNase information have been also proposed for this problem (Quang and Xie 2017), and such approaches can implicitly model information across long sequences. Furthermore, our crisscross multicell strategy helps reduce overfitting when generalizing from training cell type to testing cell type. Given that overfitting is a common issue in deep learning, it would be interesting to see how our normalization and crisscross strategies would benefit a deep learning approach.

Methods

AUROC and AUPRC

Since the ChIP-seq results are highly unbalanced with only a small portion of positive TF binding signals (<0.5% genome-wide), the differences are not apparent in the ROC space. This is because the number of negative cases largely exceeds the number of positive cases and a large increase in false positives (FPs) only results in a small change in FP rate, which equals FPs divided by the total number of negative cases. However, precision is able to capture the differences of FPs by calculating the true positives (TPs) over all positive predictions. Therefore, a precision-recall (PR) curve and AUPRC are commonly used to evaluate predictive performance for unbalanced data, in addition to AUROC. The AUROCs and AUPRCs were calculated using the R package PRROC (Grau et al. 2015). The R version is 3.4.3 (2017-11-30) (R Core Team 2017).

Partition of training and validation chromosomes and cells

The 20 training chromosomes are randomly partitioned into two sets, A and B, for the training and validation process (Supplemental Table S1). For a TF that has N training cells in Supplemental Table S2, the first XGBoost model is trained on chromosome set A in cell 1 and validated (i.e., select hyperparameters) on set B in cell 2 (setA-cell1-setB-cell2). Then, the next (N − 1) models are trained and validated on setA-cell2-setB-cell3, setA-cell3-setB-cell4, … , setA-cellN-setB-cell1. Similarly, other N models are trained and validated on the reverse chromosome sets: setB-cell1-setA-cell2, setB-cell2-setA-cell3, … , setB-cellN-setA-cell1. For TFs that have only one training cell line, only two models are trained using setA-cell1-setB-cell1 and setB-cell1-setA-cell1. The final predictions are the average predictions of the total 2N models.

XGBoost model

XGBoost is a fast and effective tree boosting method for classification and regression (Chen and Guestrin 2016). Similar to tree-based methods such as random forest, XGBoost can learn the nonlinear interactions between multiple features (Breiman 2001; Li et al. 2018a,b,c). In an XGBoost model, boosted trees are added into the model by optimizing the loss function from previous trees. For each TF-cell pair, we train a total of 1000 boosted trees and select the best performing one based on the validation set in the cross-chromosome and cross-cell fashion. As a result of averaging many trees, overfitting is avoided and the effects of outliers and noises are reduced. A total of 556 features are extracted and used in our Anchor scheme (416 sequence-based features + 120 DNase-based features + 20 distance features; see below).

Genome-wide quantile normalization of cell-type–specific DNase-seq profiles

The original genome-wide DNase-seq data of multiple technical and biological replicates from the same cell types are summed and ranked in decreasing order (Supplemental Fig. S8). The training DNase-seq profile is quantile-normalized to the test liver cell profile to reduce the cell-specific cleavage and sequencing biases. After quantile-normalization, the signals are natural log-transformed and reordered back to the original profile.

Extraction of DNase-based features

For each 200-bp interval of interest, the maximum, minimum, and mean DNase-seq signal values are calculated as the 3M-DNase features (Fig. 3A). To correct local bias, we further calculate Δmaximum, Δminimum, and Δmean DNase-seq values of each interval as the Δ3M-DNase features. In addition, the 3M-DNase and Δ3M-DNase features of another 14 neighboring intervals are added, resulting in the Δ3M-DNAse-neighbors features (Fig. 3C). Therefore, a total of 90 = (3 + 3) × 15 DNase-based features are used. Moreover, the number (the “frequency” features) and Δnumber of signal occurrence in the corresponding 15 intervals are counted as another 30 features.

Extraction of sequence-based features

The 13 TF binding PWMs are downloaded from the HOCOMOCO website: http://hocomoco10.autosome.ru/ (Kulakovskiy et al. 2018). TF motifs obtained from different assays and methods were compared (Supplemental Fig. S19), and the PWMs of these TFs from different sources are very similar. The human reference genome (GRCh37) is scanned against each PWM to obtain a score of each nucleotide position. For each 200-bp interval of interest and its seven neighboring intervals, the top four highest scores are used as the 32 = 4 × 8 sequence-based “Single-TF” features. We further consider the motifs of all 13 TFs as the “Multi-TF” features, resulting in a total of 416 = 32 × 13 features.

Extraction of distance features to closest genes

For the center of each 200-bp interval, the distances to the 20 nearest protein-coding loci are calculated based on GENCODE annotations (Harrow et al. 2012). These distance features are used to describe the closeness to possible protein-coding genes.

Evaluation of feature importance by XGBoost

For each feature, the importance is evaluated by counting the number of its occurrences in all boosted trees. If a feature occurs a lot in the nodes of multiple trees, it is more important. For each type of feature in Supplemental Figure S13, the relative importance is calculated by scaling the importance to the range [0,1].

Statistical analysis

The paired Wilcoxon signed-rank test was performed between predictions of the “Anchor-MACS” and “Anchor-Final” models across 13 TF-cell type pairs (Fig. 4B; Supplemental S11B; Supplemental Table S8) using R version 3.4.3 (2017-11-30) (R Core Team 2017).

The reference genome

GRCh37/hg19 was used as the reference genome in this study. If all the reads were realigned to GRCh38, we surmise the conclusions in this manuscript would not be significantly affected. GRCh38 has improvements over GRCh37 in regard to genome assembly, such as the reduction in the number of gaps, but these differences should not greatly impact the patterns of transcription factor binding. Anchor relies on sequence contexts up to about 1.5 kb away; in comparison, one of the major differences between the references is that GRCh38 fills in many of the gap regions (e.g., centromeres). In our experience, ∼99.9% of all TF binding sites are located more than 2 kb away from these gap regions. Therefore, if evaluation is confined entirely outside of the gap regions, we expect the choice in reference genome would have a relatively small impact on accuracy. Other sources of biases, such as differences in batches and read depth across experiments, should have a more profound effect on performance in comparison.

Public data used for model training and testing

The ChIP-seq data were downloaded from ENCODE project website: https://www.encodeproject.org/. The accession numbers are provided in Supplemental Table S6.

The DNase-seq data from the ENCODE project were downloaded from:

• http://hgdownload.soe.ucsc.edu/goldenPath/hg19/ encodeDCC/wgEncodeUwDnase/

• https://www.synapse.org/#!Synapse:syn6112317 (the ENCODE-DREAM challenge data)

The DNase-seq data from the Roadmap project were downloaded from:

• https://www.encodeproject.org/experiments/ENCSR794OFW/

• https://www.encodeproject.org/experiments/ENCSR477RTP/

Software availability

Anchor software source code is available in the Supplemental Material and at GitHub (https://github.com/GuanLab/Anchor).

Competing interest statement

Y.G. serves as President of Yuanfang Guan and Company, as a consultant at Eli Lilly and Company, and as a consultant at Merck Group.