Cochlear Frequency Tuning and Otoacoustic Emissions

Abstract

Otoacoustic emissions (OAEs) evoked from the inner ear are the barely audible, signature byproduct of the delicate hydromechanical amplifier that evolved within its bony walls. Compared to the sounds evoked from the ears of common laboratory animals, OAEs from human ears have exceptionally long delays, typically exceeding those of cats, guinea pigs, and chinchillas by a factor of two to three. This review asks “Why are human OAE delays so long?” and recounts efforts to locate answers in the characteristics of mechanical frequency selectivity in the inner ear. The road to understanding species differences in OAE delay leads to the identification of new invariances and to the emergence of new questions.

INTRODUCTION

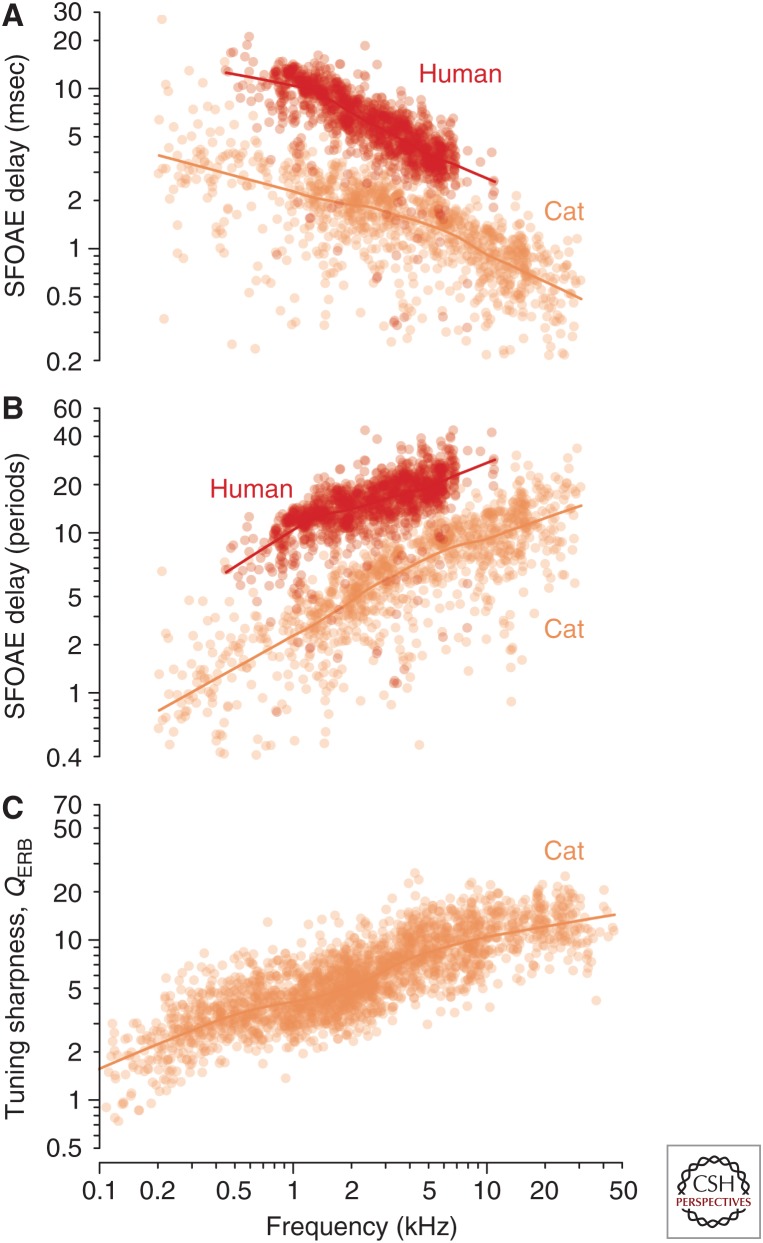
It is a truth universally acknowledged that a human ear in possession of good hearing must not be in want of delay. Indeed, human ears have the longest otoacoustic emission (OAE) delays of any species whose emissions have yet been assessed. For example, Figure 1A compares stimulus-frequency OAE delays measured in humans with those in domestic cats. Although their frequency dependence is similar—in both species, the delays are longest at low frequencies and decrease with increasing frequency—the human delays are everywhere a factor of two or three longer than their feline counterparts, and delays in cats are similar to those of other common laboratory animals, such as guinea pigs and chinchillas.

Figure 1.

Otoacoustic delays and neural tuning. Stimulus-frequency otoacoustic emission (OAE) group delay versus frequency in humans and cats. (A) The delays (in msec) are shown as scatterplots (dots) with their corresponding loess trend lines. (From Shera and Guinan 2003; adapted, with permission, from the authors.) (B) The group-delay data and trends from panel A replotted in natural units (periods of the stimulus frequency). (C) Sharpness of tuning in cat. The values of Q_ERB and their trends were computed from auditory-nerve-fiber (ANF) tuning curves in cat using standard algorithms (e.g., Evans and Wilson, 1973). (From the laboratories of P.X. Joris, M.C. Liberman, and B. Delgutte via Joris et al. 2011; adapted and reprinted, with permission, from the authors.)

There and Back Again

Why, then, are human otoacoustic delays so long? Stimulus-frequency OAEs evoked at stimulus levels near the threshold of hearing are thought to arise predominantly, although perhaps not exclusively, from the peak region of the traveling wave (e.g., Brass and Kemp 1993; Zweig and Shera 1995; Lichtenhan 2012; Charaziak and Siegel 2014). Because the measured delays are longest at low frequencies, which map tonotopically to the apical end of the cochlea, and shortest at high frequencies, which map closer to the base, it is natural to suppose that OAE delays reflect distances traveled along the basilar membrane (BM). Perhaps round-trip travel times are longer in humans for purely anatomical reasons—because our BMs are themselves unusually long. If so, the waves giving rise to OAEs in humans would travel farther than they do in cats, both as the stimulus journeys inward to reach its tonotopic place and then as it reverses course to travel back outward to the ear canal as an OAE. In fact, humans do have longer BMs than cats, but the difference is only about 30%–40%, not the factor of two or three suggested by the OAE delays. So explanations for the longer human delays cannot rely solely on the greater distances traversed.

Converting to Natural Units

An important clue to a more compelling account of the long OAE delays emerges by replotting the data in “natural” units. In other words, rather than measure cochlear delays in seconds—a conventional but arbitrary timescale originally defined by the period of the earth’s rotation—we measure them in units appropriate to the system being studied. Because the emitting cochlea presumably cares little about the rotation of the earth, a more meaningful timescale might be the period of the stimulus (or emission) frequency itself. This timescale, of course, is not fixed but varies with the stimulus; expressing the delay in periods is equivalent to forming the dimensionless product of the delay (in seconds) and the stimulus frequency (in Hertz). Replotting the data in these natural, dimensionless units yields the representation shown in Figure 1B, which differs markedly from the conventional depiction of OAE delay (cf. Fig. 1A). When measured in stimulus periods, otoacoustic delays (N_SFOAE) no longer decrease with frequency but increase. Unlike delays expressed in milliseconds, delays in periods are shortest at low frequencies and longest at high frequencies.

The important clue here to the physical meaning of OAE delay is that its power-law dependence on frequency—a nearly linear increase on log–log axes—strongly resembles plots of the quality factors (such as the Q_ERB) that characterize the tuning bandwidths of auditory nerve fibers (ANFs). (The equivalent rectangular bandwidth [ERB] is a parameter-free measure of tuning equal to the bandwidth of the rectangular filter with the same peak amplitude that passes the same total power in response to white noise.) Just like the delay functions shown in Figure 1B, neural Q_ERB values are generally small at low characteristic frequencies (CFs) near the apex, where ANFs are broadly tuned, and increase at high CFs near the base, where tuning is sharper (Fig. 1C). Although imperfect, the resemblance seems to hint at something deeper than mere coincidence. For one thing, quality factors, like OAE delays measured in periods, are also expressed in natural units. The Q_ERB is simply the reciprocal of the ERB when the bandwidth is measured not in Hertz but in units appropriate to the tuning curve, namely, the CF of the fiber. Furthermore, not only are the units of the Q_ERB natural, they are also the same units used to express the OAE delay in periods. When the emission arises from the peak region of the traveling wave, the stimulus frequency and the mean CF in the region of OAE generation are the same.

So perhaps the resemblance is no accident? Perhaps OAE delays somehow reflect the sharpness of cochlear frequency tuning and its variation, both from base to apex and from one species to another. In other words, perhaps the most important determinant of the delay is not how far waves travel along the cochlear spiral to reach their characteristic places, but the quality of frequency tuning they find when they get there. In this review, we develop these ideas while describing connections between OAEs and frequency tuning in the mammalian cochlea. We close with speculations about the possible origins of species differences in tuning and by briefly discussing unresolved questions and complications encountered along the way.

COHERENT REFLECTION AND FILTER THEORY

Scattering from Micromechanical Irregularities

When a sound consisting of a single pure tone is presented in the ear canal and subsequently transduced by the middle ear, the motion of the stapes launches a transverse, hydromechanical wave that travels along the cochlea to its tonotopic place, beyond which it is strongly attenuated. When the mechanics of the cochlear partition are made to vary smoothly with position—an unphysical condition attainable only within the idealized world of a mathematical model—the action ends there. But when small, densely distributed mechanical irregularities of a sort unavoidable in biological structures are introduced into the model organ of Corti, something remarkable happens—the cochlea, once silent and uncommunicative, begins to echo what it hears, making sound while listening to sound.

In a nutshell, the process by which the ear responds to queries by emitting sound is this: As the stimulus wave propagates along the cochlea, the micromechanical irregularities (impedance perturbations) act as tiny reflectors and induce wave backscattering, predominantly near the wave peak, where vibrations are largest. A subset of the many scattered wavelets combine coherently, giving rise to a reverse traveling wave that propagates back toward the stapes. After passing through the middle ear into the ear canal, the reverse wave appears as an OAE at the stimulus frequency (i.e., as a stimulus-frequency OAE [SFOAE]). Analysis of the scattering mechanism using perturbation theory indicates that the emission delay depends on the wavelength of the traveling wave—or, almost equivalently, on the group delay of the BM frequency response—in the region of emission generation (Zweig and Shera 1995; Talmadge et al. 1998; Shera et al. 2005).

Frequency Tuning and Delay

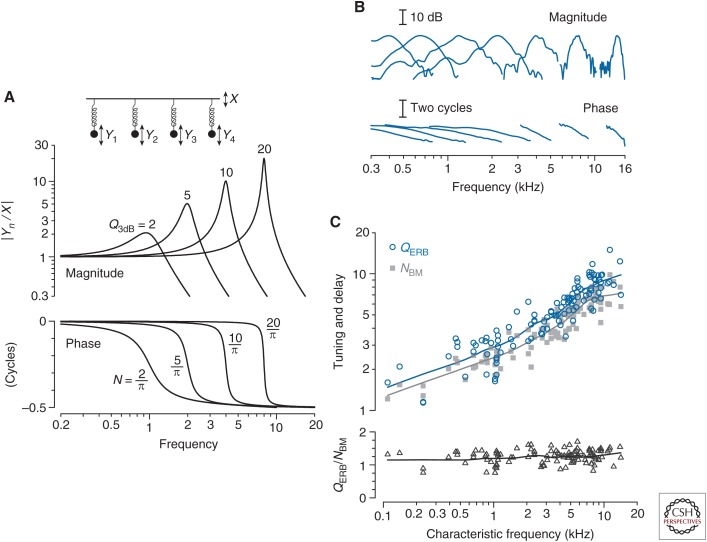
What controls the group delay of the BM frequency response? Consider the simple example in Figure 2A, which shows a collection of harmonic oscillators—masses hanging on springs and moving in a viscous medium—with different resonant frequencies and quality factors (Q). Each oscillator has a frequency response (or filter function) whose peak height and bandwidth depend on the Q value; the larger the Q (e.g., the smaller the damping), the higher the peak. Each filter also has a phase, whose lag increases by one half cycle near the resonant frequency. Computing the group delay—the negative slope of the phase-versus-frequency function—at the response peak and expressing the result in natural units yields the delay (N) in periods of the resonant frequency. Note that N is always just 1/π times the corresponding Q. In other words, the delay in periods is proportional to the sharpness of tuning; the two vary together, with sharper tuning implying longer delay. Illustrated here for filters consisting of a mass on a spring, an approximate proportionality between N and Q is a general property of filters of fixed order. Although cochlear filters are doubtless more complicated than harmonic oscillators, one cannot help but wonder whether they manifest a similar proportionality between tuning and delay.

Figure 2.

Covariation of mechanical tuning and delay in the damped harmonic oscillator. (A) The four oscillators shown have different resonant frequencies and quality factors. The figure shows the magnitudes (top) and phases (bottom) of the displacement ratios Y_n/X versus driving frequency. Values of the quality factor (Q_3dB) and near-peak, phase-gradient delay in periods (N) are shown adjacent to each curve. (B) Example neural measurements of cochlear tuning in chinchilla. The figure shows the magnitude and phase of seven representative second-order Wiener kernels derived from responses to near-threshold noise in auditory-nerve fibers with characteristic frequencies (CFs) spanning the range of chinchilla hearing (Recio-Spinoso et al. 2005; Temchin et al. 2005). Response magnitudes are normalized to the same peak value. (From Shera et al. 2010; adapted, with permission, from the authors.) (C) Covariation of cochlear tuning and delay in the chinchilla. The top panel shows values of Q_ERB (circles) and N_BM (gray squares) computed from 113 Wiener-kernel measurements of the amplitude and phase of cochlear tuning obtained from auditory-nerve responses to near-threshold noise (Recio-Spinoso et al. 2005). The bottom panel shows the ratio Q_ERB/N_BM computed from individual Wiener kernels. Values of Q_ERB were obtained from the Wiener-kernel magnitude using standard algorithms (e.g., Evans and Wilson 1973); values of N_BM were computed from the gradient of the Wiener-kernel phase near CF. Loess trend lines (Cleveland 1993) have been drawn to guide the eye. (From Figs. 2–4 in Shera et al. 2010; adapted, with permission, from the authors.)

Remarkably, naïve expectations from filter theory are borne out by the data. Figure 2B shows a handful of filter functions obtained from ANF responses to white noise at CFs spanning the entire length of the chinchilla cochlea (Recio-Spinoso et al. 2005; Temchin et al. 2005). From these and similar measurements one can compute both the quality factor of tuning (in this case, the Q_ERB) and the group delay in periods of the CF, here denoted N_BM on the presumption that neural tuning near the tip of the tuning curve reflects the mechanical tuning of the BM. Figure 2C shows that Q_ERB and N_BM vary together in almost constant proportion along the length of the cochlea. Evidently, the group delays of BM frequency responses are controlled by—or at least mirror—the sharpness of cochlear tuning.

To review the results that brought us here, we have found that:

1. Cochlear modeling predicts that SFOAE delay depends on the mechanical group delay in the region of emission generation near the peak of the traveling wave; and

2. Neural and BM measurements corroborate suggestions from filter theory that the near-CF mechanical group delay, expressed in natural units, is proportional to the sharpness of frequency tuning at the same location.

Together, these two statements make it clear that the resemblance between N_SFOAE and Q_ERB apparent in Figure 1 is no mere coincidence: OAE delays are telling us about cochlear tuning.

TUNING RATIOS AND THEIR APPLICATION

Species Invariance of the Tuning Ratio

We have illustrated the arguments so far with data drawn rather indiscriminately from both cats and chinchillas. But is the relationship between tuning and delay actually similar across species? To answer this question, we need to quantify the relationship between neural tuning and SFOAE delay. Because Q_ERB and N_SFOAE vary together across frequency, it proves useful to take their ratio, dividing out the common frequency dependence (Shera et al. 2002). We therefore introduce the “tuning ratio,” defined as

$$r(\mathrm{CF})={\overline{Q}}_{\mathrm{ERB}}(\mathrm{CF})/{\overline{N}}_{\mathrm{SFOAE}}{(f)|}_{f=\mathrm{CF}},$$ (1)

where the diacritical bars indicate that the function r(CF) is defined as a ratio of trend lines—such as those shown for cat in Figure 1B and C—rather than of individual data points. Ideally, the tuning ratio would be computed using values of Q_ERB and N_SFOAE from the same animals, but because such measurements are not available, we pool data across different animals (and different laboratories), contenting ourselves with capturing species trends rather than individual differences.

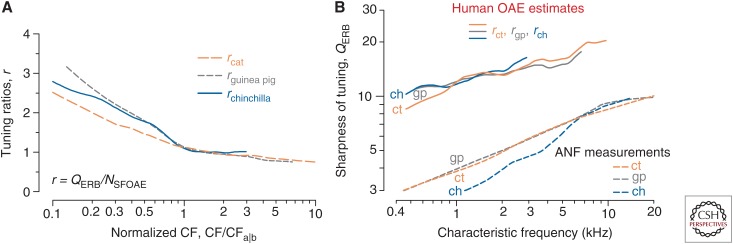
Are tuning ratios similar across species? Figure 3A shows that the answer is “yes,” when the data are plotted in the right way. The figure plots tuning ratios for cat, guinea pig, and chinchilla against a special, normalized frequency coordinate (Shera et al. 2010). Plotted in this way, the tuning ratios in all three species have a common form—a basal, high-frequency region where the tuning ratios are almost constant, and an apical, low-frequency region where the tuning ratios vary more with frequency (and somewhat more across species). The CF at which the tuning ratio changes form effectively divides the cochlea into two regions, apical and basal. We therefore call this frequency the “apical–basal transition CF” and denote it CF_a|b. Although CF_a|b varies from species to species, plotting the tuning ratios versus CF/CF_a|b normalizes out these differences and aligns the curves on the transition. The observation that the tuning ratios then fall nearly on top of one another suggests that r(CF/CF_a|b) can be well approximated by a common, “universal” curve.

Figure 3.

Tuning ratios in cat, guinea pig, and chinchilla. (A) The tuning ratios $r={\overline{Q}}_{\mathrm{ERB}}/{\overline{N}}_{\mathrm{SFOAE}}$ were computed from loess trend lines and are plotted versus the characteristic frequency (CF) normalized by the location of apical–basal transition (CF/CF_a|b). Values of CF_a|b for the three species are {3, 3, 4} kHz, respectively. (B) Otoacoustic estimates of human cochlear tuning. The solid lines give values of human ${\overline{Q}}_{\mathrm{ERB}}$ computed from Equation 2 using measured values of ${\overline{N}}_{\mathrm{SFOAE}}$ (Fig. 1) and the tuning ratios for cat, guinea pig, and chinchilla shown in panel A. For comparison, the dashed lines give ${\overline{Q}}_{\mathrm{ERB}}$ values for cat (ct), guinea pig (gp), and chinchilla (ch) obtained from auditory nerve fiber (ANF) measurements. OAE, Otoacousic emission. (From Figs. 9 and 12 in Shera et al. 2010; adapted, with permission, from the authors.)

Noninvasive Estimation of Cochlear Tuning

If we run awhile with this suggestion and assume that tuning ratios in other mammals are indeed similar to those in cats, guinea pigs, and chinchillas, then we can use OAE measurements to provide noninvasive estimates of the sharpness of tuning. Taking the human species (H) as the exemplar, the procedure is simply to rewrite the definition of the tuning ratio as an equation for ${\overline{Q}}_{\mathrm{ERB}}$:

$${\overline{Q}}_{\mathrm{ERB}}^{\mathrm{H}}(\mathrm{CF})\approx r({\mathrm{CF}/\mathrm{CF}}_{\mathrm{a}|\mathrm{b}}^{\mathrm{H}}){\overline{N}}_{\mathrm{SFOAE}}^{\mathrm{H}}{(f)|}_{f=\mathrm{CF}}.$$ (2)

Because the tuning ratio is assumed invariant, evaluating this equation requires only two additional pieces of information: the trend line ${\overline{N}}_{\mathrm{SFOAE}}^{\mathrm{H}}(f)$, which can be obtained from pooled OAE measurements in humans, and the approximate location of the apical–basal transition, CF_a|b^H, whose value can be estimated using the inflection point in the function ${\overline{N}}_{\mathrm{SFOAE}}^{\mathrm{H}}(f)$ (Shera et al. 2010). In humans, OAE data suggest that the transition occurs near the midpoint of the cochlea (CF_a|b^H ∼ 1.2 kHz).

Figure 3B shows otoacoustic estimates of the sharpness of human cochlear tuning ${\overline{Q}}_{\mathrm{ERB}}^{\mathrm{H}}(f)$ obtained in this way. The three, nearly identical curves show results computed using tuning ratios derived from neural and OAE measurements in cat, guinea pig, and chinchilla. How do these estimates of human tuning compare with actual neural measurements? Unfortunately, the necessary measurements in humans are not available, but we can compare with neural measurements in other animals, such as cats. As the figure makes clear, the otoacoustic method predicts that cochlear tuning in humans is significantly sharper—by a factor of 2 to 3—than the tuning in these common laboratory animals. Although these findings run contrary to the conventional wisdom, which asserts that frequency tuning in all mammals is essentially the same, it does suggest an answer to our original question: Human OAE delays are so much longer because human cochlear tuning is so much sharper.

TESTING OTOACOUSTIC PREDICTIONS IN MACAQUE

The route taken to answering our puzzle may strike you as somewhat circular. As outlined above, our estimates of human cochlear tuning were obtained by exploiting the assumed species-invariance of the tuning ratio. But if the ratio of tuning sharpness to OAE delay is assumed similar across species, longer delays are guaranteed to imply sharper tuning! Has our roundabout argument, and its ostensible challenge to conventional wisdom, produced a credible explanation for the long human delays, or has unsubstantiated extrapolation from a handful of common laboratory species led us astray?

Breaking the circle requires an independent check on the assumption that tuning ratios are similar across species, preferably in a mammal whose tuning and delay are markedly different from what they are known to be in cats, guinea pigs, and chinchillas. On this cue, enters the macaque. As Old World monkeys, macaques are phylogenetically closer to human primates than the small laboratory animals often taken as models of human hearing. Thus, there is reason to suspect that tuning and delay in macaques may more closely resemble those in their human relatives and hence provide a compelling test of the interpretive framework (Joris et al. 2011).

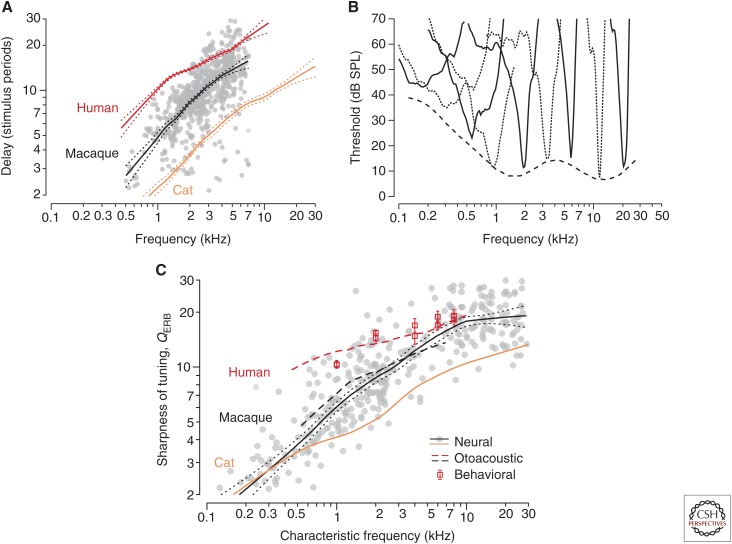
Figure 4A compares SFOAE delays in macaques with delays in cats and humans; the dotted lines represent 95% confidence intervals for the trend. As anticipated, macaque delays are intermediate between those of cats and humans; closer to feline values at low frequencies, the delays appear closer to human values at high frequencies. If the macaque tuning ratio approximates those of other laboratory species, as the framework suggests that it should, then the delay measurements immediately imply that the sharpness of macaque cochlear tuning must also be intermediate between cat and human. One can make this qualitative prediction more precise by using Equation 2 for macaque (M) to estimate the function ${\overline{Q}}_{\mathrm{ERB}}^{\mathrm{M}}(\mathrm{CF})$, as shown in Figure 4B. For the invariant tuning ratio, we used the average of the tuning ratios in cat, guinea pig, and chinchilla, and for the macaque transition CF we adopted the value CF_a|b^M ∼ 1.7 kHz estimated from the OAE data. As expected, the values of ${\overline{Q}}_{\mathrm{ERB}}^{\mathrm{M}}(\mathrm{CF})$ predicted by Equation 2 are similar to those in cats at low CFs and approach the estimated human values above 4–5 kHz.

Figure 4.

Stimulus-frequency otoacoustic emission (SFOAE) delays in macaques compared with trends from other species. (A) The gray dots and trend (black line with 95% confidence intervals) show macaque group delays in natural units (N_SFOAE). The blue and red lines show species trends in cats and humans (Fig. 1). (B) Example of auditory-nerve tuning curves in macaques. For clarity, tuning curves are shown using alternating solid and dashed lines. The dashed line shows the smoothed lower envelope of the neural threshold data. (C) Sharpness of tuning in macaques and other species. The gray dots and trend (black line with flanking dots delimiting 95% confidence intervals for the trend) show macaque Q_ERB values derived from auditory-nerve-fiber tuning curves. The blue line shows the neural trend ${\overline{Q}}_{\mathrm{ERB}}$ in cats. The red dashed line gives the human trend derived from SFOAE delay; the red squares and standard errors show behavioral values (Oxenham and Shera 2003). The black dashed line gives the macaque ${\overline{Q}}_{\mathrm{ERB}}$ trend obtained from Equation 2 using the values of ${\overline{N}}_{\mathrm{SFOAE}}$ in panel A. (From Figs. 2–4 in Joris et al. 2011; adapted, with permission, from the authors.)

Direct measurements of cochlear frequency tuning in the macaque auditory nerve provide a definitive test of the otoacoustic predictions. The gray dots and their trend superposed on Figure 4B show values of Q_ERB obtained from neural tuning curves. By themselves, the neural data and their deviation from those in cat provide a counterexample to the conventional wisdom that cochlear frequency selectivity varies little among mammals. More striking, however, is the close agreement with the otoacoustic predictions. Equation 2 for ${\overline{Q}}_{\mathrm{ERB}}^{\mathrm{M}}(\mathrm{CF})$ captures both the overall sharpness and the frequency dependence of cochlear tuning in macaque, providing reliable values of Q_ERB over the full frequency range for which predicted values can be compared with the neural recordings. The match verifies that even though the frequency dependence of macaque tuning and delay differs from that in other animals, the ratio of the two variables (i.e., the tuning ratio $r={\overline{Q}}_{\mathrm{ERB}}/{\overline{N}}_{\mathrm{SFOAE}}$) remains almost invariant across species.

A remarkable consilience with human psychophysics provides additional, independent support for the framework (Shera et al. 2002; Oxenham and Shera 2003). When designed specifically to mimic the measurement of neural tuning curves, behavioral methods that estimate cochlear frequency selectivity using notched-noise masking yield tuning bandwidths that match the otoacoustic values (see Fig. 4B). Although discussion of the many issues involved requires its own dedicated review, key elements of the behavioral paradigm include presenting the signal at a fixed sound level near threshold in quiet (e.g., 10 dB SL [sensation level]) and using forward rather than simultaneous masking to avoid suppressive interactions between the masker and signal (Oxenham and Shera 2003). Taken as a whole, the evidence is compelling that humans have significantly sharper tuning than common laboratory animals.

SPECULATIONS: WHY IS HUMAN COCHLEAR TUNING SO SHARP?

Returning to our initial question, it appears that humans (and macaques at high frequencies) have such long OAE delays for the very reason suggested by the resemblance achieved following the introduction of natural units in Figure 1B and C. Humans have longer OAE delays because humans have sharper tuning, and sharper tuning brings longer mechanical delays, and longer mechanical delays are reflected in OAE latencies. Needless to say, this answer explains the long delay by invoking an even deeper mystery: Why is human cochlear tuning so sharp?

One obvious avenue for evolutionary speculation highlights the survival benefits of robust communication in complex acoustic environments. For example, narrower filters can improve signal-to-noise ratios, and finer frequency resolution both enhances the auditory coding of spectrotemporally complex sounds, such as speech in noise, and may facilitate the segregation and localization of competing sounds. The attendant just-so story might invoke the intense selective pressures faced by our simian ancestors at raucous prehistoric cocktail parties held under African skies.

A less direct but perhaps more intriguing kind of explanation is that sharper filters may be evolutionary spandrels (Gould and Lewontin 1979), arising through no direct adaptive value of their own, but as byproducts of the evolution of other features. For example, the development of sharper tuning in humans, whatever its subsequent exaptive utility for signal processing, may have been driven by changes in the cochlear tonotopic map and spatial constraints imposed by hair-cell-based mechanisms of traveling wave amplification. This suggestion stems from the observation that the spatial spread of excitation produced by a low-level tone is more similar across species than the bandwidth of frequency tuning (Shera et al. 2010). What does this mean and what is the evidence for it? Because the cochlea maps sound frequency to place, frequency intervals such as bandwidths (Δf) correspond to spatial distances (Δx) along the BM. The spatial distance corresponding to the ERB is known as the equivalent rectangular spread (ERS). Just as the value of ERB(CF) measures the frequency selectivity of the cochlear filter at the specified location, the value of ERS(f) measures the spatial width of the traveling-wave envelope at the specified frequency. When the cochlear map is exponential, the ERS for a tone of frequency f = CF is related to the ERB at the CF location through the formula,

$$\mathrm{ERS}=l\cdot \mathrm{ERB}/\mathrm{CF}=l/Q_{\mathrm{ERB}},$$ (3)

where l is the “space constant” of the cochlear map (i.e., the distance over which the CF changes by a factor of e).

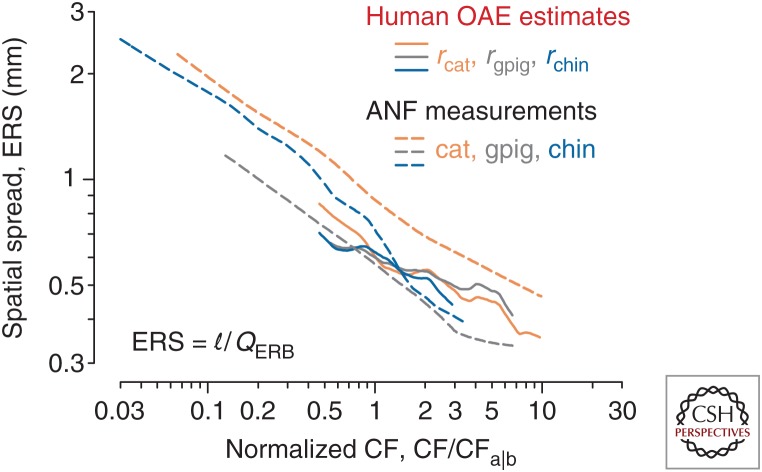
Figure 5 shows the functions ERS(f) computed from Equation 3 using the trends ${\overline{Q}}_{\mathrm{ERB}}\left(\mathrm{CF}\right)$ and parameters of the cochlear map for four different species, including humans. As suggested above, the data confirm that the spatial spread of excitation is more similar across species than the sharpness of tuning. Similarity of spatial spread appears especially salient if, as here, one normalizes out the location of the apical–basal transition, so that the apical and basal regions of each species are properly aligned and compared. These results support the seemingly paradoxical conclusion that species differences reflect species invariances—that the sharpness of tuning varies among species because the spatial spread of excitation at corresponding cochlear locations remains nearly the same. The apparent species invariance of spatial spread occurs despite significant differences in both the space constant of the cochlear map and the overall length of the cochlea.

Figure 5.

Estimates of the spatial spread of excitation (the equivalent rectangular spread [ERS]) in four species. The curves show values of $\mathrm{ERS}=l/{\overline{Q}}_{\mathrm{ERB}}$ for cat, guinea pig, chinchilla, and human space constants of the cochlear map. OAE, Otoacoustic emission; ANF, auditory nerve fiber; gpig, guinea pig; chin, chinchilla; CF, characteristic frequency; ERB, equivalent rectangular bandwidth. (From Fig. 16 in Shera et al. 2010; adapted, with permission, from the authors.)

Why might the width of the spatial excitation pattern be more invariant across species than the bandwidth of frequency tuning? Fundamentally, the answer may be that the laws of physics operate over space and time, not directly in the frequency domain. In essence, the mammalian cochlea consists of a regular array of discrete, oscillatory sensors and effectors—the hair cells—arranged with an almost invariant longitudinal spacing between rows (d ∼ 10 µm). Approximate species invariance of both the spatial spread of excitation and the spacing between rows implies that the corresponding number of hair cells spanned by the peak of the traveling wave envelope (n_row ∼ ERS/d) also varies little across species. Coupling between the hair cells—via the motion and electrical conductivity of the surrounding fluids (e.g., Karavitaki and Mountain 2007), by a labyrinthine scaffold of supporting cells (e.g., Steele et al. 1993; Geisler and Sang 1995; Yoon et al. 2011; Soons et al. 2015), and through ancillary structures such as the tectorial membrane (e.g., Ghaffari et al. 2007)—facilitates the mechanical interactions and coherent amplification that give rise to and shape the cochlea’s response to sound. If the cochlea evolved to exploit the physical interactions of invariant units, spatial intervals such as the widths of excitation patterns or the wavelengths of traveling waves are presumably more tightly constrained than derived quantities, such as tuning bandwidths. Recent work provides direct support for this view: Mutations that disrupt the longitudinal coupling provided by the tectorial membrane, thereby modifying the effective spatial spread of excitation, have pronounced effects on the sharpness of tuning (Ghaffari et al. 2010). Furthermore, the spatial decay constants of human tectorial-membrane waves match those measured in mice, despite significant differences in frequency tuning (Farrahi et al. 2016).

CONUNDRUMS AND CONCLUSIONS

Following advice from the King of Hearts (Carroll 1865)—begin at the beginning, go on until you come to the end, then stop—we find we have returned full circle. When taken together with approximate species invariance of spatial spread, our analysis of Equation 3 implies that species differences in the sharpness of tuning at any given CF (Q_ERF = l/ERS)—and therefore species differences in OAE delay at the corresponding frequency (N_SFOAE = Q_ERB/r)—arise in large part because of species differences in the space constant of the cochlear map (l) and the location of the apical–basal transition (CF_a|b). Upon revisiting our earlier there-and-back-again discussion of travel times along the BM, we discover that the length of the BM matters after all! The underlying reason, however, is rather different than previously supposed. The length of the BM matters not because it sets how far waves have to travel, but because it affects the sharpness of mechanical tuning by determining the space constant of the cochlear map.

Although we have returned to our original question with the rough outlines of an answer, several important unresolved issues arose along the way. Of these, two broad topics seem to merit emphasis here:

1. What factors control changes in the spatial spread of excitation and concomitant changes in the sharpness of mechanical tuning along the cochlea? Although much of our discussion has focused on variations—or the lack thereof—across species, changes in the bandwidths of tuning along the cochlea are clear and uncontroversial. How do these changes arise? Do they reflect changes in BM width? In the mechanoelectrical properties of the organ of Corti? Or of the tectorial membrane?

2. What mechanisms give rise to the apical–basal transition? Why does the transition appear to be so abrupt? Why does its location vary across species? Interestingly, the value of CF_a|b estimated from the OAE measurements corresponds to a similar transition evident in other aspects of cochlear physiology, such as the shapes of neural tuning curves and the characteristics of the traveling wave. What is the functional significance of the transition for the encoding of sound? Whatever the origin(s) of this apparent “seam” between the apical and basal regions of the cochlea, the transition clearly reflects a CF dependence in cochlear mechanics whose significance remains poorly understood.

May the curious reader find in these unanswered questions a promising avenue for their own future investigations.