Predicting the cardiac toxicity of drugs using a novel multiscale exposure-response simulator

Abstract

A common but serious side effect of many drugs is torsades de pointes, a rhythm disorder that can have fatal consequences. Torsadogenic risk has traditionally been associated with blockage of a specific potassium channel and an increased recovery period in the electrocardiogram. However, the mechanisms that trigger torsades de pointes remain incompletely understood. Here we establish a computational model to explore how drug-induced effects propagate from the single channel, via the single cell, to the whole heart level. Our mechanistic exposure-response simulator translates block-concentration characteristics for arbitrary drugs into three-dimensional excitation profiles and electrocardiogram recordings to rapidly assess torsadogenic risk. For the drug of dofetilide, we show that this risk is highly dose-dependent: at a concentration of 1x, QT prolongation is 55% but the heart maintains its regular sinus rhythm; at 5.7x, QT prolongation is 102% and the heart spontaneously transitions into torsades de points; at 30x, QT prolongation is 132% and the heart adapts a quasi-depolarized state with numerous rapidly flickering local excitations. Our simulations suggest that neither potassium channel blockage nor QT interval prolongation alone trigger torsades de pointes. The underlying mechanism predicted by our model is early afterdepolarization, which translates into pronounced U waves in the electrocardiogram, a signature that is correctly predicted by our model. Beyond the risk assessment of existing drugs, our exposure-response simulator can become a powerful tool to optimize the co-administration of existing drugs and, ultimately, guide the design of new drugs towards reducing life threatening drug-induced rhythm disorders in the heart.

1. Introduction

In October 1999, a new class III antiarrhythmic drug, dofetilide, was approved for treatment of atrial fibrillation in the United States (Pfizer, 2011). Atrial fibrillation, the most common sustained cardiac arrhythmia, affects more than 6 million people in the United States (American Heart Association, 2015) and 33 million worldwide (Chugh, Havmoeller, Narayanan, Singh, Rienstra, Benjamin, Gillum, Kim, McAnulty, Zheng, Forouzanfar, Naghavi, Mensah, Ezzati, and Murray, 2014). Dofetilide cardioverts persistent atrial fibrillation to sinus rhythm by selectively blocking the rapid delayed rectifier potassium current, which slows the efflux of potassium ions, reduces the repolarization rate of the cell, and widens the plateau of the action potential (Mirams, Cui, Sher, Fink, Cooper, Heath, McMahon, Gavaghan, and Noble, 2011). However, on the whole heart level, this controlled widening of the action potential induces a pronounced prolongation of the QT interval, a signature that has been associated with a high risk of torsades de pointes (Bohnen, Peng, Robey, Terrenoire, Iyer, Sampson, and Kass, 2017). Torsades de pointes is a special form of ventricular tachycardia characterized by a rapid twisting of QRS complexes around the electrocardiogram baseline that can lead to sudden cardiac death (Dessertenne, 1966). The reporting rate of torsades de pointes increased exponentially in the early 1990s when numerous drugs–not just cardiac drugs–were recognized to trigger QT interval prolongation and increase proarrhythmic potential (Stockbridge, Morganroth, Shah, and Garnett, 2013). In response, 14 drugs were removed from the market, amongst them dofetilide, the first oral antiarrhythmic agent approved for treatment of atrial arrhythmias in almost a decade (Allen LaPointe, Kramer, Weinfurt, and Califf, 2002) and the only drug that was approved after the implementation of new the regulatory guidelines (Stockbridge et al., 2013).

Dofetilide, or by its chemical formula C19H27N3O5S2, remains a controversial drug. It continues to be unavailable in Europe and Australia (Stockbridge et al., 2013). In the United States, it marketed under the trade name Tikosyn by Pfizer, available in three dosage strengths, 0.125mg in orage/white, 0.250mg in peach, and 0.500mg in peach/white. It is well known that the QT interval and torsades de pointes risk increase linearly with the dose and concentration of dofetilide (Pfizer, 2011). To no surprise, the use of dofetilide is tightly regulated by a mandated risk-management program that restricts distribution of the drug, requires prescriber education on the drug, and recommends at least three days of hospitalization to monitor correct dosing of the drug (Allen LaPointe, Chen, Hammill, DeLong, Kramer, and Califf, 2003). In a study of n = 1,346 arrhythmia patients, the incidence of torsades de pointes was 0.8% overall, but increased with increasing dose, with no incidence for doses below 0.250mg, 0.3% for 0.250mg, 0.9% between 0.250 and 0.500mg, and 10.5% for doses above 0.500mg (Pfizer, 2011). The risk of dofetilide mismanagement is high and the mechanisms that contribute to dofetilide-induced arrhythmias remain incompletely understood (Briceno and Supple, 2017).

Several initiatives are underway to develop and validate new paradigms for cardiac safety evaluation using a more accurate and comprehensive mechanistic-based assessment of proarrhythmetic potential (Colatsky, Fermini, Gintant, Pierson, Sager, Sekino, Strauss, and Stockbridge, 2016; Sager, Gintant, Turner, Pettit, and Stock-bridge, 2014; Vicente, Stockbridge, and Strauss, 2016). Motivated by these objectives, this study presents the first mechanistic-based computational model to predict how drug-induced fractional current block on the ion channel level translates into action potential profiles on the single cell level and into electrocardiograms on the whole heart level (Sahli Costabal, Yao, and Kuhl, 2018). Our model is broadly applicable to any drug for which the blockage-concentration relation is known from single cell experiments (Crumb, Vicente, Johannesen, and Strauss, 2016). Here we focus exclusively on the drug dofetilide because of its high clinical relevance, its management controversies, and its high specificity towards a single channel (Johannesen, Vicente, Mason, Sanabria, Waite-Labott, Hong, Lin, Guo, Mutlib, Wang, Crumb, Blinova, Chan, Stohlman, Florian, Ugander, Stockbridge, and Strauss, 2016).

We hypothesize that low concentrations of dofetilide will moderately prolong of the QT interval without affecting the overall sinus rhythm, whereas high concentrations of dofetilide will significantly prolong the QT interval and trigger the spontaneous development of ventricular arrhythmias. We test this hypothesis at dofetilide concentrations of 0x, 1x, 5.7x and 30x of the effective free therapeutic plasma concentration. We illustrate how dofetilide-induced alterations in potassium channel dynamics propagate across the spatial and temporal scales to modify the action potential duration on the cellular level, the QT interval on the whole organ level, and the excitation pattern across the heart. This will allows us to visualize and explore how different cell types in the heart, endcardial, midwall, epicardial, and Purkinje cells, respond and interact under the action of dofetilide. We anticipate that our multiscale computational model will become a useful tool to better understand the mechanisms of drug-induced arrhythmias with a view towards a more mechanistic drug dosing and risk management.

2. Methods

2.1. Modeling cardiac electrophysiology

Our model represents the electrical excitation of the myocardium through the classical monodomain model parameterized in terms of the transmembrane potential ϕ. The spatio-temporal evolution of the transmembrane potential follows a reaction-diffusion equation,

$$\stackrel{.}{\varphi }=\text{div}(\mathit{D}\cdot \nabla \varphi )+f^{\varphi }.$$ (1)

For the flux term, div(D · ∇ϕ), we assume an anisotropic conductivity D with a fast contribution D^∥ parallel to the myocardial fiber direction f and a slow contribution D^⊥ perpendicular to it (Sahli Costabal, Concha, Hurtado, and Kuhl, 2017),

$$\mathit{D}=D^{\Vert }\mathit{f}\otimes \mathit{f}+D^{\perp }[\mathit{I}-\mathit{f}\otimes \mathit{f}].$$ (2)

For the source term, we use different ionic models for different cell types and introduce the source, f^ϕ = —I_ion/C_m, as the ionic current I_ion scaled by the membrane capacitance C_m (Nordsletten, Niederer, Nash, Hunter, and Smith, 2011). The ionic current is a function of the transmembrane potential ϕ and a set of states variables q(ϕ) (Göktepe, Wong, and Kuhl, 2010; Lee, Sundnes, Genet, Wenk, and Wall, 2016),

$$I_{\text{ion}}=I_{\text{ion}}(\varphi ,\mathit{q}(\varphi );t).$$ (3)

The state variables obey ordinary differential equations as functions of the transmembrane potential ϕ and their current values q,

$$\stackrel{.}{\mathit{q}}=\mathit{g}(\varphi ,\mathit{q}(\varphi );t).$$ (4)

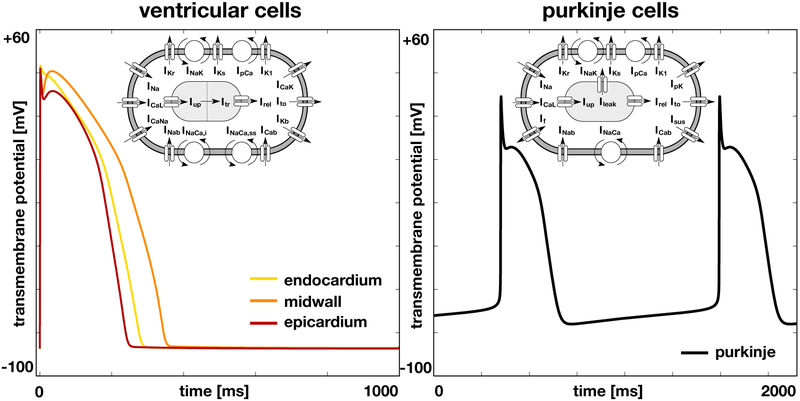
The number of ionic currents I_ion and state variables q determines the complexity of the model and varies for different cell types (Wong, Abilez, and Kuhl, 2012; Wong, Göktepe, and Kuhl, 2013). Here we select different cell models for ventricular cells and Purkinje cells. To model the cells in the ventricular wall, we follow the guidelines proposed by the CiPA initiative (Dutta, Chang, Beattie, Sheng, Tran, Wu, Wu, Strauss, Colatsky, and Li, 2017) and adopt the O’Hara-Rudy model for human ventricular cardiomyocytes (O’Hara et al., 2011). Figure 1, left, illustrates the 15 ionic currents of the the O’Hara-Rudy model,

$$\begin{gathered} I_{\text{ion}}=I_{\text{CaL}}+I_{\text{Na}}+I_{\text{CaNa}}+I_{\text{CaK}}+I_{\text{Cab}}+I_{\text{Nab}}+I_{\text{Kb}} \\ +I_{\text{Kr}}+I_{\text{Ks}}+I_{\text{K1}}+I_{\text{to}}+I_{\text{NaK}}+I_{\text{pCa}}+I_{\text{NaCa,i}}+I_{\text{NaCa,ss}}, \end{gathered}$$ (5)

the L-type calcium current I_CaL, the fast and late sodium currents I_Na, the calcium sodium and calcium potassium currents I_CaNa and I_CaK, the background calcium, sodium, and potassium currents I_Cab, I_Nab, and I_Kb, the rapid and slow delayed rectifier potassium currents I_Kr and I_Ks, the inward rectifier potassium current I_K1, the transient outward potassium current I_to, the sodium potassium pump current I_NaK, the sarcolemmal calcium pump current I_pCa, and the sodium calcium exchange currents I_NaCa,i and I_NaCa,ss. To appropriately model signal propagation in real heart scale simulations (Priest, Gawad, Kahlig, Yu, OHara, Boyle, Rajamani, Clark, Garcia, Ceresnak, Harris, Boyle, Dewey, Malloy-Walton, Dunn, Grove, Perez, Neff, Chen, Maeda, Dubin, Belardinelli, West, Antolik, Macaya, Quertermous, Trayanova, Quake, and Ashley, 2016), we replaced the fast sodium current I_Na of the original O’Hara-Rudy model with a modified fast sodium current of the ten Tusscher model (ten Tusscher, Noble, Noble, and Panfilov, 2004) . The 15 currents are defined through a total of 39 state variables. To account for regional specificity, the O’Hara-Rudy model has been parameterized for three different cell types, endocardial, midwall, and epicardial cells. Figure 1, left, illustrates the single cell action potential of the O’Hara-Rudy model for endocardial, mid, and epicardial human ventricular cardiomyocytes. Figure 2 shows the distribution of these three cell types across the ventricular wall. To model cells of the Purkinje fiber network, we choose the Stewart model for human Purkinje fiber cells (Stewart et al., 2009). An distinguishing feature of this model is its automaticity, which enables the cells to self-excite without an external stimulus. Figure 1, right, illustrates the 14 ionic currents of the Stewart model,

$$\begin{gathered} I_{\text{ion}}=I_{\text{CaL}}+I_{\text{Na}}+I_{\text{Cab}}+I_{\text{Nab}}+I_{\text{Kr}}+I_{\text{Ks}}+I_{\text{K1}}+I_{\text{to}} \\ +I_{\mathrm{f}}+I_{\text{sus}}+I_{\text{NaK}}+I_{\text{pCa}}+I_{\text{pK}}+I_{\text{NaCa}}, \end{gathered}$$ (6)

the L-type calcium current I_CaL, the fast and late sodium currents I_Na, the background calcium and sodium currents I_Cab and I_Nab, the rapid and slow delayed rectifier potassium currents I_Kr and I_Ks, the inward rectifier potassium current I_K1, the transient outward potassium current I_to, the hyperpolarization-activated current I_f, the sustained potassium current I_sus, the sodium potassium pump current I_NaK, the calcium and potassium pump currents I_pCa and I_pK, and the sodium calcium exchange current I_NaCa. The 14 currents are defined through 20 state variables. Figure 1, right, illustrates the single cell action potential for human Purkinje cells. Figure 2 shows the distribution of the Purkinje fiber network across the endocardial wall.

Figure 1.

Single cell action potential for human ventricular cardiomyocytes, left, and Purkinje fiber cells, right. The ventricular cell model distinguishes between endocardial, midwall, and epicardial cells and is based on the modified O’Hara Rudy model with 15 ionic currents and 39 state variables (O’Hara et al., 2011). The Purkinje cell model displays inherent automaticity and is based on the Stewart model with 14 ionic currents and 20 state variables (Stewart et al., 2009).

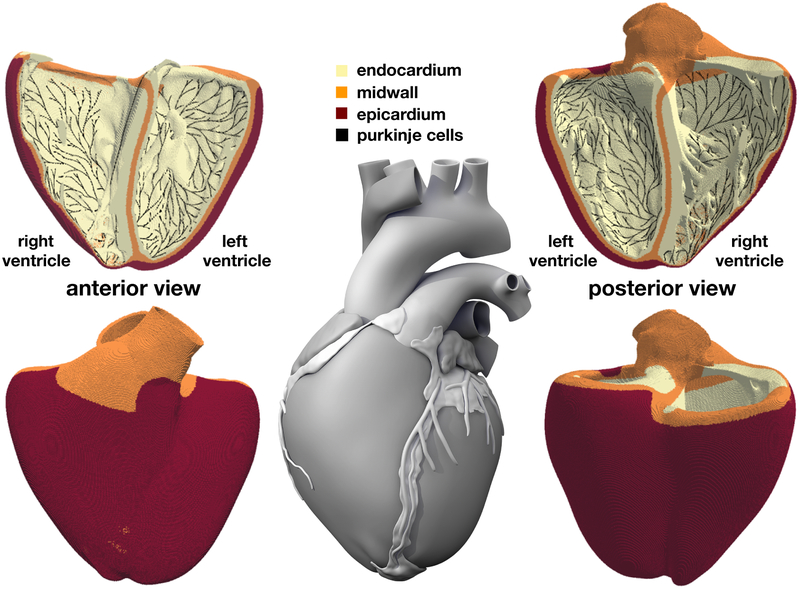
Figure 2.

Human heart model created from high resolution magnetic resonance images of a healthy male adult (Zygote Media Group, 2014). The ventricular wall is discretized with 6,878,459 regular linear hexagonal finite elements with an edge length of 0.3 mm, a total number of 7,519,918 nodes, and 268,259,901 internal variables. The Purkinje fiber network is discretized with 39,772 linear cable elements, a total number of 39,842 nodes, and 795,440 internal variables. It is connected to the ventricles at its terminals through 3,545 resistor elements. Endocardial, midwall, and epicardial cells are marked in yellow, orange, and red; Purkinje cells are shown in black.

2.2. Modeling the human heart

We discretize the set of continuum equations (1) to (6) in space using finite elements and in time using finite differences (Sahli Costabal et al., 2018). To solve the resulting system of equations, we adopt the finite element software package Abaqus (Dassault Systèmes, SIMULIA, 2017). Since the governing equations of cardiac electrophysiology are structurally similar to the classical heat transfer problem, we adopt finite elements designed for heat transfer with a non-linear heat source. We discretize the transmembrane potential as nodal degree of freedom and the ionic currents and gating variables as internal variables (Göktepe and Kuhl, 2009). Motivated by the small time step size to resolve the fast dynamics during the upstroke of the action potential, we adopt an explicit time integration scheme.

Figure 2 illustrates our finite element model of the left and right ventricles with endocardial, midwall, and epicardial cells are marked in yellow, orange, and red. The Living Heart model, an anatomically accurate four-chamber model of the healthy human heart, forms the basis of our heart geometry (Baillargeon, Rebelo, Fox, Taylor, and Kuhl, 2014). The Living Heart model was initially created as a tetrahedral mesh from magnetic resonance images of a healthy, 21-year-old, 50th percentile U.S. male (Zygote Media Group, 2014). Motivated by the relationship between element size and critical time step size in explicit methods, we convert this initial geometry (Rausch, Zöllner, Genet, Baillargeon, Bothe, and Kuhl, 2017) into a regular discretization of cube elements with a constant edge length of 0.3 mm across the entire heart (Sahli Costabal et al., 2018). This results in a discretization with a total of 6,878,459 regular linear hexagonal finite elements, 7,519,918 nodes, and 268,259,901 internal variables. For the flux term, we assume a faster conduction along the fiber direction f (Baillargeon et al., 2014) with the conductivities parallel and perpendicular to the fiber direction as D^∥ = 0.090 mm²/ms and D^⊥ = 0.012 mm²/ms (Niederer, Kerfoot, Benson, Bernabeu, Bernus, Bradley, Cherry, Clayton, Fenton, Garny, Heidenreich, Land, Maleckar, Path-manathan, Plank, Rodríguez, Roy, Sachse, Seemann, Skavhaug, and Smith, 2011). For the source term, we employ a body flux subroutine to incorporate the ionic currents I_ion in the finite element formulation (Dassault Systèmes, SIMULIA, 2017). To account for regional variations in cell type, we simulate a series of Laplace problems using our finite element mesh with different essential boundary conditions (Perotti, Krishnamoorthi, Borgstrom, Ennis, and Klug, 2015). Figure 2 shows the resulting cell type distribution across the ventricular wall with 20% endocardial cells, 30% midwall cells, and 50% epicardial cells. This arrangement ensures positive T-waves (Hurtado and Kuhl, 2014) to simulate the healthy baseline electrocardiogram (Okada, Washio, Maehara, Momomura, Sugiura, and Hisada, 2011).

Figure 2 illustrates our finite element model of the Purkinje fibers as a dense black network covering the endocarial wall. Including the Purkinje network is critical to accurately model cardiac excitation and drive a regular baseline beat. We generate the Purkinje network as fractal tree that grows on the endocardial surface of the heart (Sahli Costabal, Hurtado, and Kuhl, 2016). We initialize tree growth at four anatomical locations, the right bundle branch, the left bundle branch, and the anterior and posterior fascicles of the left ventricle. To tightly cover the endocardial surface, every newly created branch repels existing branches and follows the gradient of the distance of all existing branches. This results in a discretization with 39,772 linear cable elements, 39,842 nodes, and 795,440 internal variables. For these Purkinje elements, we implement a user element with a discrete one-dimensional version of equations (1) to (6). At the terminals of the fractal tree, we connect the Purkinje network to the neighboring myocardium (Ponnaluri, Perotti, Ennis, and Klug, 2016). At these connections, we use 3,545 resistor elements with a resistance of 1.78 Ωm (Niederer et al., 2011) between each endpoint of the network and the closest node of the ventricular mesh (Bordas, Gillow, Lou, Efimov, Gavaghan, Kohl, Grau, and Rodriguez, 2011). The resistor elements allow us to adopt distinct cellular models with different resting potentials for ventricular and Purkinje cells and ensure a bi-directional conduction between the Purkinje network and the surrounding tissue. For the flux term, we choose a conductivity of D^∥ = 3.0 mm²/ms. Figure 2 illustrates how densely our discrete Purkinje fiber network covers the endocardium of the left and right ventricles.

2.3. Modeling the effect of drugs

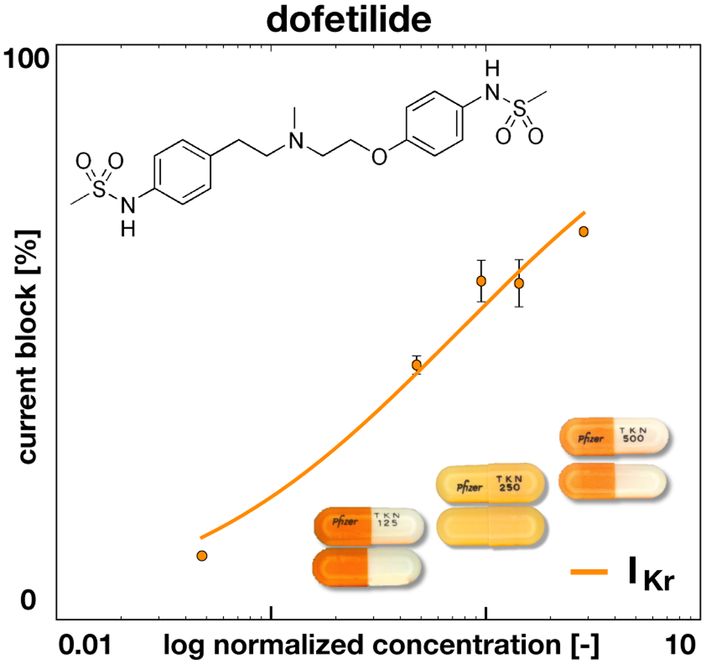
We model the effect of drugs on the single cell action potential by selectively blocking the relevant ionic currents. The fractional blockage of individual ion channels at varying drug concentrations can be measured using patch clamp electrophysiology (Crumb et al., 2016). To estimate the fractional block β at arbitrary concentrations C, we can fit a Hill-type equation to the discrete data points,

$$\beta =\frac{C^h}{I{C}_{50}^h+C^h}.$$ (7)

The Hill-type equation has two parameters, the exponent h and the concentration IC₅₀ required to achieve a 50% current block. Figure 3 illustrates the effect of dofetilide, which selectively blocks the rapid delayed rectifier potassium current I_Kr. The graph highlights the fractional block of I_Kr for varying concentrations C, log-normalized with respect to the free plasma concentration of dofetilide, C_max = 2.1 nM. The dots and error bars summarize the experimentally measured fractional blockage (Crumb et al., 2016) and the solid line represents the fitted Hill model with h = 0.6 and IC₅₀ = 1.0 nM. To apply the drug, we select a desired concentration C, calculate the fractional blockage β, and scale the rapid delayed rectifier potassium current I_Kr by the fractional blockage [1 − β],

$$I_{\text{Kr}}^{\text{drug}}=[1-\beta ]I_{\text{Kr}}.$$ (8)

Figure 3.

Effect of dofetilide on ionic current. Dofetilide selectively blocks the rapid delayed rectifier potassium current I_Kr. The concentration is normalized with respect to the free plasma concentration of Dofetilde, C_max = 2.1 nM. The solid line represents the fitted Hill model, $\beta =C^h∕[I{C}_{50}^h+C^h]$, with h = 0.6 and IC₅₀ = 1.0 nM; the error bars represent the standard error mean (Crumb et al., 2016).

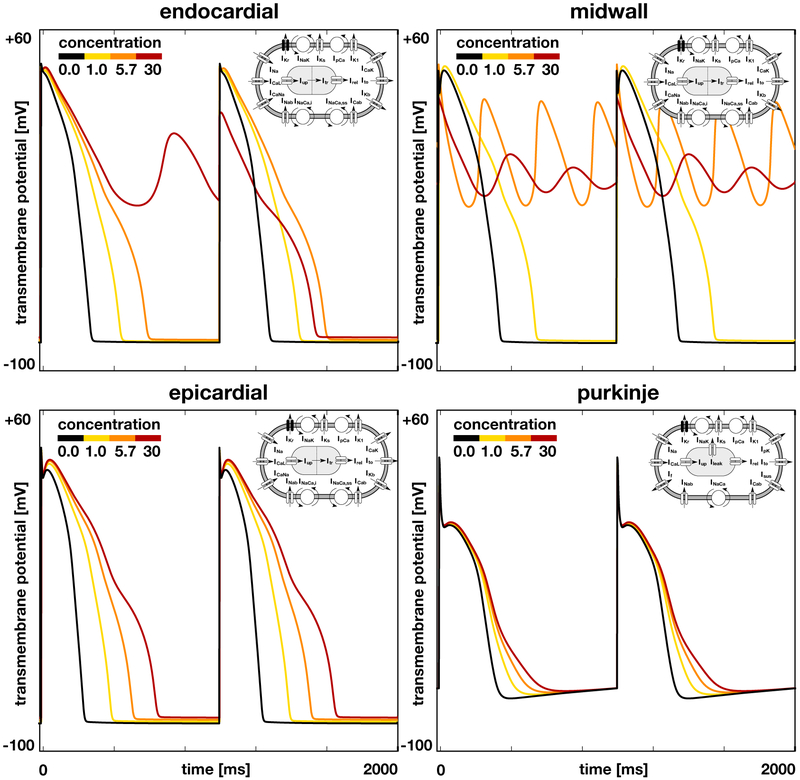
Figure 4 illustrates the effects of dofetilide on the single cell action potential of endocardial, midwall, epicardial, and Purkinje cells. The black lines highlight the baseline action potential without drugs and the yellow to red lines represent the modified action potential for drug concentrations of 1x, 5.7x, and 30x, where a dose of 1x corresponds to an equivalent plasma concentration of 2.65 ng/mL. In all four cell types, dofetilide prolongs the plateau of the action potential and increases the overall action potential duration. This effect increases with increasing concentration. In endocardial cells, dofetilide concentrations of 30x trigger early afterdepolarizations in every second beat, red lines. In midwall cells, early afterdepolarizations are present at every beat and already occur at dofetilide concentrations of 5.7x, orange lines; at concentrations of 30x, the action potential oscillates even more tightly around the neutral state with a transmembrane potential of zero, red lines. Epicardial cells experience a marked increase of the action potential plateau, but show no signs of early afterdepolarizations in response to dofetilide. Purkinje cells remain almost unaffected by dofetilide, even at concentrations of 30x.

Figure 4.

Effect of dofetilide on the single cell action potential of different cell types. Black lines represent the baseline action potential of endocardial, midwall, epicardial, and Purkinje cells without drugs, yellow to red lines represent the modified action potential at drug concentrations of 1x, 5.7x, and 30x. By blocking the rapid delayed rectifier potassium current I_Kr, dofetilide prolongs the plateau of the action potential and increases the overall action potential duration. This effect increases with increasing concentration, from yellow to red. Beyond a critical concentration, endocardial and midwall cells experience early afterdepolarizations and become self-oscillatory, orange and red lines. Epicardial and Purkinje cells display no signs of early afterdepolarizations within the simulated concentration range.

To explore how drug-induced alterations in the single-cell action potential affect the excitation profile of the entire heart, we excite the heart through the automaticity of the Purkinje network and post-process the resulting transmembrane profile to calculate pseudo electrocardiograms (Kotikanyadanam, Göktepe, and Kuhl, 2010). At every point of the heart, we project the gradient of the transmembrane potential, ∇ϕ, onto the direction vector, ∇(1/∥r∥), and integrate this projection across the entire cardiac domain, ${\varphi }_{\mathrm{e}}({\mathit{x}}_{\mathrm{e}})=-{\int }_{\mathcal{B}}\nabla \varphi \cdot \nabla (1∕\Vert \mathit{r}\Vert )\text{dV}$. The vector r = ∥x_e − x∥ points from current point x to the position of the virtual electrode x_e (Sahli Costabal et al., 2018). To model a pre-cordial lead in the clinical electrocardiogram, we place the electrode 2 cm away from the left ventricular wall. This pre-cordial lead is commonly used to study T waves and QT intervals (Hii, Wyse, Gillis, Duff, Solylo, and Mitchell, 1992), which are critical signatures to quantify the risk of drug toxicity (Sadrieh, Domanski, Pitt-Francis, Mann, Hodkinson, Ng, Perry, Taylor, Gavaghan, Subbiah, Vandenberg, and Hill, 2014).

3. Results

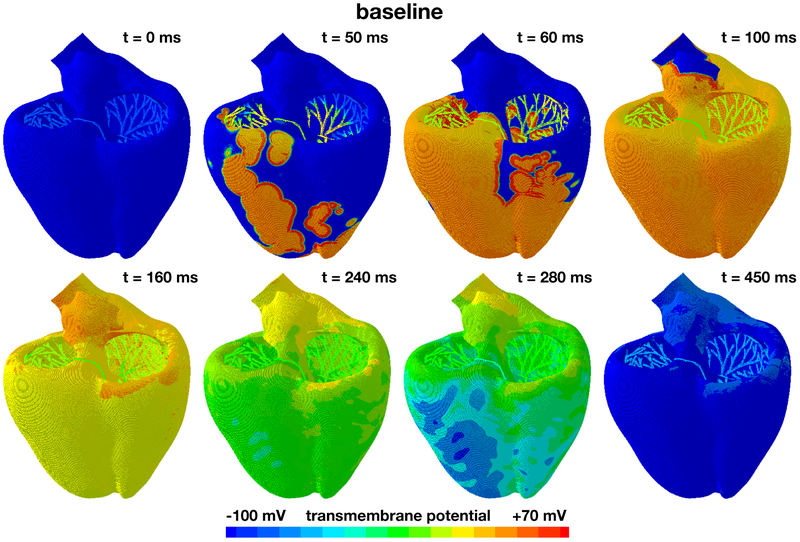
Figure 5 shows the baseline excitation profile for the simulation without drugs. The eight snapshots illustrate the state of the left and right ventricles between the beginning of the QRS complex at 50 ms and the end of the T wave at 450 ms. During depolarization, from 0 ms to 100 ms, the Purkinje network drives the excitation from apex to base with a sharp depolarization front propagating rapidly across the heart. At 100 ms, both ventricles are fully excited. During repolarization, from 100 ms to 450 ms, the heart gradually returns to its resting state. At 450 ms, both ventricles are fully repolarized. The self-exciting Purkinje cells determine the heart rate to 60.15 beats per minute. This implies that the displayed excitation pattern repeats itself identically every 1,000 ms, five times within the simulated time window of 5,000 ms.

Figure 5.

Evolution of the transmembrane potential at baseline without drugs. Snapshots are taken between the beginning of the QRS complex at 50 ms and the end of the T wave at 450 ms. During depolarization, from 0 ms to 100 ms, the Purkinje network drives the excitation from apex to base with a sharp depolarization front propagating across the heart. During repolarization, from 100 ms to 450 ms, both ventricles gradually return to their resting state. The Purkinje network determines the heart rate to 60.15 beats per minute. The displayed excitation pattern repeats itself identically every 1,000 ms, five times within the simulated time window of 5,000 ms.

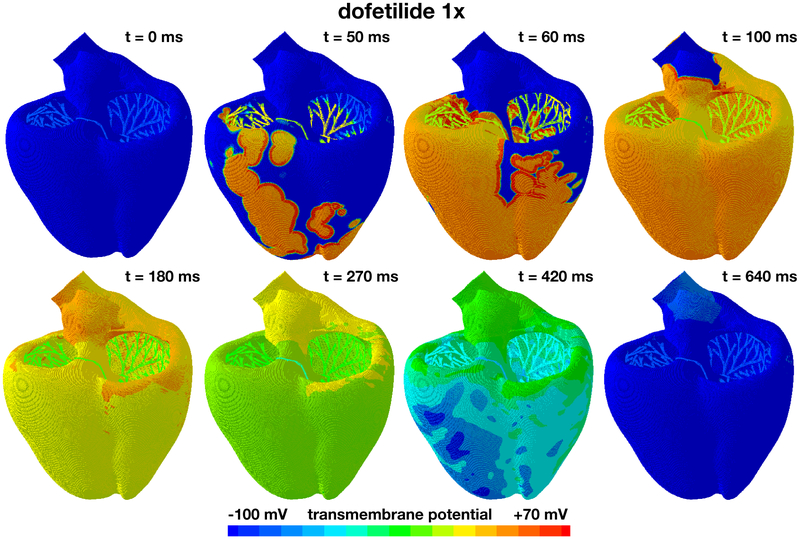
Figure 6 shows the excitation profile for the simulation with dofetilide at a concentration of 1x. The eight snapshots illustrate the state of the left and right ventricles between the beginning of the QRS complex at 50 ms and the end of the T wave at 640 ms. During depolarization, from 0 ms to 100 ms, the Purkinje network drives the excitation from apex to base with a sharp depolarization front propagating rapidly across the heart. Since dofetilide primarily affects the rapid delayed rectifier potassium current I_Kr, which is not involved in the upstroke of the action potential, the depolarization pattern looks virtually identical to the baseline case without drugs in Figure 5. At 100 ms, both ventricles are fully excited. During repolarization, from 100 ms to 640 ms, the heart gradually returns to its resting state. Since dofetilide prolongs the action potential plateau as illustrated in Figure 4, repolarization is delayed compared to the baseline case without drugs. At 640 ms, 190 ms later than for the baseline case, both ventricles are fully repolarized. The Purkinje cells are only marginally affected by dofetilide as illustrated in Figure 4. Accordingly, their self-exciting automaticity determines the heart rate to 60.15 beats per minute, similar to the baseline case. The displayed excitation pattern repeats itself identically every 1,000 ms, five times within the simulated time window of 5,000 ms. This suggests that dofetilide is safe at concentrations of 1x: The heart maintains its regular rhythm and displays no signs of fibrillation.

Figure 6.

Evolution of the transmembrane potential with dofetilide at a concentration of 1x. Snapshots are taken between the beginning of the QRS complex at 50 ms and the end of the T wave at 640 ms. During depolarization, from 0 ms to 100 ms, the Purkinje network drives the excitation from apex to base with a sharp depolarization front propagating across the heart, almost identical to the baseline case without drugs. During repolarization, from 100 ms to 640 ms, both ventricles gradually return to their resting state, however, with a delayed repolarization compared to the baseline case. The Purkinje network determines the heart rate to 60.15 beats per minute. The displayed excitation pattern repeats itself identically every 1,000 ms, five times within the simulated time window of 5,000 ms.

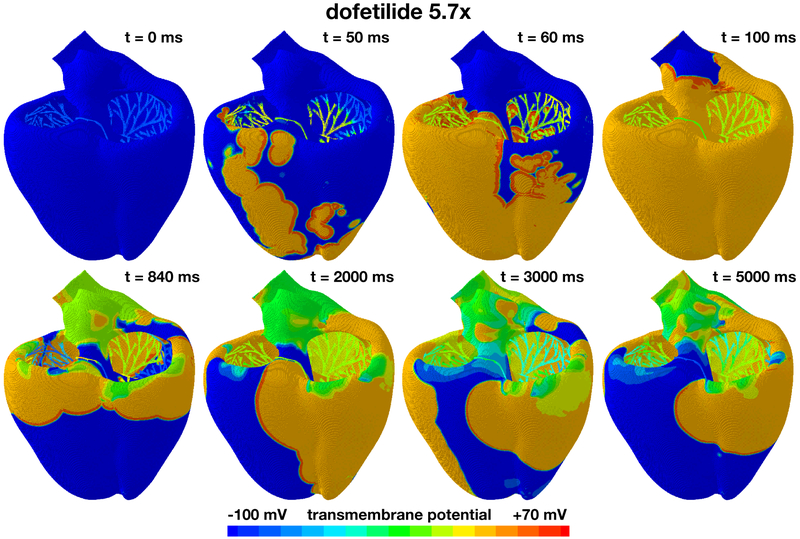
Figure 7 shows the excitation profile for the simulation with dofetilide at a concentration of 5.7x. The eight snapshots are taken at the beginning of the QRS complex at 50 ms, at the end of depolarization at 100 ms, and at selected points within the simulation window of 5,000 ms. During the initial depolarization, from 0 ms to 100 ms, the Purkinje network drives the excitation from apex to base, virtually unaffected by dofetilide. At 100 ms, similar to the baseline case and the dofetilide concentration of 1x in Figures 5 and 6, both ventricles are fully excited. After a significantly prolonged ST segment, the heart spontaneously transitions into ventricular fibrillation. Figure 4 suggests that at a dofetilide concentration of 5.7x, cells in the midwall experience early afterdepolarizations. They become self-oscillatory and their transmembrane potential alternates rapidly around the neutral state with a zero transmembrane potential. Figure 2 shows that the base of our heart model consists primarily of orange midwall cells. These regions of the model spontaneously transition from the initially negatively charged state into the neutral state with a zero transmembrane potential highlighted in green. The base of the heart rapidly oscillates around this neutral state throughout the entire simulation window of 5000 ms. Excitation of the remaining myocardium is no longer driven by the Purkinje network, but by large re-entrant waves that excite the heart in chaotic patterns, from base to apex, from base to apex, from right to left, from front to back, and from right to left. These rotating spiral waves are characteristic features of torsades de pointes. This suggests that dofetilide is associated with a high torsadogenic risk at a concentration of 5.7x: The heart spontaneously transitions from regular excitation into ventricular fibrillation with classical hallmarks of torsades de pointes including large spiral waves that originate from different locations across the heart.

Figure 7.

Evolution of the transmembrane potential with dofetilide at a concentration of 5.7x. Snapshots are taken at the beginning of the QRS complex at 50 ms, at the end of depolarization at 100 ms, and at selected points within the simulation window of 5,000 ms. During the first 100 ms, the Purkinje network drives the excitation from apex to base with a sharp depolarization front propagating across the heart, almost identical to the baseline case without drugs. After a prolonged QT interval, the propagation of the excitation wave becomes irregular and asynchronous. Excitation is no longer driven by the Purkinje network, but by large re-entrant waves that excite the heart in chaotic patterns, from base to apex, from right to left, from front to back, and from right to left. These are characteristic hallmarks of torsades de pointes.

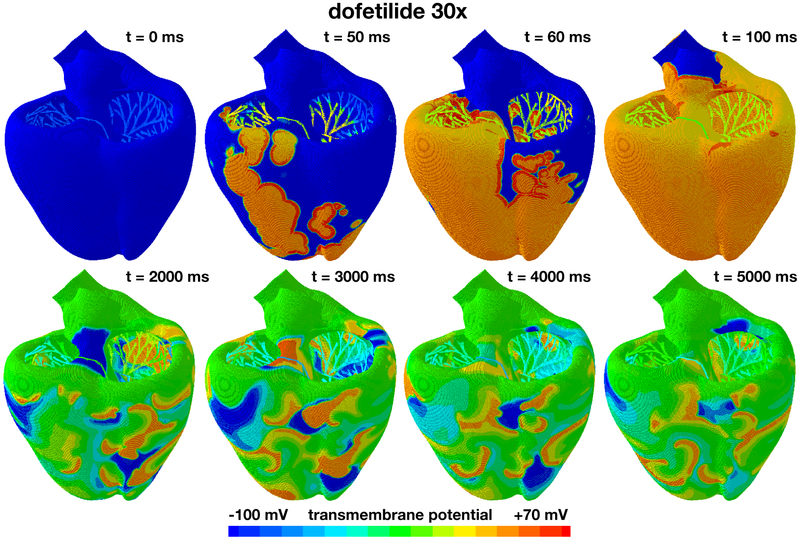
Figure 8 shows the excitation profile for the simulation with dofetilide at a concentration of 30x. The eight snapshots are taken at the beginning of the QRS complex at 50 ms, at the end of depolarization at 100 ms, and at selected points within the simulation window of 5,000 ms. During the initial depolarization, from 0 ms to 100 ms, the Purkinje network drives the excitation from apex to base, virtually unaffected by dofetilide. At 100 ms, similar to all previous cases in Figures 5 to 7, both ventricles are fully excited. After a significantly prolonged ST segment, the heart spontaneously transitions into ventricular fibrillation. Figure 4 suggests that at a dofetilide concentration of 30x, both endocardical cells and midwall cells experience early afterdepolarizations. While endocardial cells only display early afterdepolarizations in every other heart beat, midwall cells become self-oscillatory and their transmembrane potential alternates rapidly around the neutral state with a zero transmembrane potential. Figure 2 shows that at a dofetilide concentration of 30x, 50% of cells lose their natural rhythm, 20% in the endocardium, shown in yellow, and 30% in the midwall, shown in orange. This implies that half of the ventricular myocardium spontaneously transitions from the initially negatively charged state into the neutral state with a zero transmembrane potential highlighted in green. Excitation of the entire myocardium is no longer driven by global excitation waves, neither from the Purkinje network as in Figures 5 and 6, nor from the neutral midwall cells at the base as in Figure 7. Rather, early afterdepolarizations of the endocardial and midwall cells overwrite the natural rhythm. The ventricles excite locally by numerous small re-entrant waves that flicker around the heart and excite it in uncoordinated chaotic patterns. The heart is largely frozen at the neutral state at a zero transmembrane potential with several local self-oscillatory regions. This suggests that dofetilide is associated with an extremely high arrhythmogenic risk at a concentration of 30x: The heart spontaneously transitions from regular excitation into ventricular fibrillation with a complete loss of a global excitation and numerous local small spiral waves that flicker around the heart and oscillate tightly around the neutral state.

Figure 8.

Evolution of the transmembrane potential with dofetilide at a concentration of 30x. Snapshots are taken at the beginning of the QRS complex at 50 ms, at the end of depolarization at 100 ms, and at selected points within the simulation window of 5,000 ms. During the first 100 ms, the Purkinje network drives the excitation from apex to base with a sharp depolarization front propagating across the heart, almost identical to the baseline case without drugs. After a markedly prolonged QT interval, the global excitation disappears. Excitation is no longer driven by the Purkinje network, but by numerous small re-entrant waves that flicker around the heart and excite it in chaotic patterns. The heart is largely frozen at the neutral state at a transmembrane potential of zero with several local self-oscillatory regions.

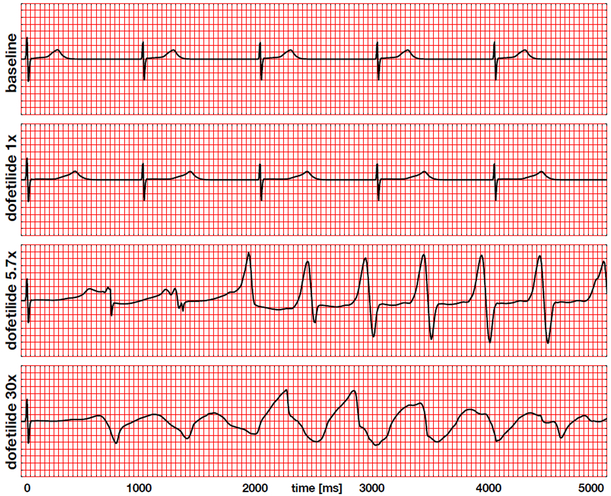
Figure 9 summarizes the electrocardiogram recordings for the baseline case at 0x in Figure 5 and drug treatment with dofetilide at concentrations of 1x, 5.7x, and 30x in Figures 6 through 8. The baseline electrocardiogram displays a regular periodic activation pattern with characteristic QRS complexes and T waves, which repeat themselves identically every 1,000 ms at a heart rate of 60.15 beats per minute. The dofetilide 1x electrocardiogram displays a regular periodic activation pattern similar to the baseline case. A dofetilide concentration of 1x moderately prolongs the plateau of the single cell action potential in Figure 4, which translates into a prolongation of the QT interval of 55% compared to baseline. This agrees well with the delayed repolarization patterns in Figure 6. Although this is a quite significant prolongation, the heart maintains its normal sinus rhythm, which repeats itself identically every 1,000 ms at a similar heart rate as the baseline case. The dofetilide 5.7x electrocardiogram displays a regular depolarization during the first 50 ms. With increasing drug concentration, the plateau of the single cell action potential in Figure 4 increases, which translates into an increase of the QT interval in the electrocardiogram. A concentration of 5.7x prolongs the initial QT interval by 102% compared to baseline. This significantly prolonged QT interval makes the heart vulnerable to the spontaneous formation of ventricular fibrillation. During the first and second cycle, the T wave is followed by a marked U wave, a classical indicator for early afterdepolarizations or prolonged repolarization of myocardial midwall cells. After the first two cycles, at about 1,500 ms, the dofetilide 5.7x electrocardiogram spontaneously transitions into a sequence of rapid, widened irregular QRS complexes, a characteristic hallmark of torsades de pointes, which agrees well with the observed excitation patterns in Figures 7. The dofetilide 30x electrocardiogram displays a regular depolarization during the first 50 ms. A concentration of 30x prolongs the initial QT interval by 132% compared to baseline. After the first T-wave, the electrocardiogram shows a complete loss of coordinated excitation with irregular uncoordinated patterns that bear no resemblance with the regular sinus rhythm of the baseline case. This agrees well with the uncoordinated small local excitation patterns in Figures 8.

Figure 9.

Electrocardiogram recordings for the baseline case and drug treatment with dofetilide at concentrations of 1x, 5.7x, and 30x. The baseline and dofetilide 1x electrocardiograms display regular periodic activation patterns at a heart rate of 60.15 beats per minute determined by the Purkinje fiber network. Dofetilide 1x prolongs the QT interval by 55% compared to baseline. The dofetilide 5.7x and 30x electrocardiograms display a regular depolarization during the first 50 ms, followed by a significant prolongation of the QT interval by 102% and 132%. Dofetilide 5.7x triggers the formation of U waves during the first two cycles, followed by a spontaneous transition into a sequence of rapid, widened irregular QRS complexes, a characteristic feature of torsades de pointes. Dofetilide 30x causes a complete loss of coordinated excitation.

4. Discussion

Many drugs–not just cardiac drugs–can have serious undesired side effects. Prominent side effects that play a central role in several regulatory guidelines are lethal cardiac arrhythmias in the form of tosardes de pointes (Stockbridge et al., 2013). Historically, drug-induced tosardes de pointes has been explained by a fractional blockage of the rapid delayed rectifying potassium channel I_Kr, which increases the action potential duration in individual cells and prolongs the QT interval in the electrocardiogram (Mirams et al., 2011). Existing guidelines therefore focus on monitoring two torsadogenic risk factors: potassium channel block and QT interval prologation (Vicente et al., 2016). This strategy has been successful in the sense of torsade risk management; yet, its broad definition comes at the cost of low specificity (Colatsky et al., 2016): Many drugs that affect potassium channel block and QT interval length are not torsadogenic in practice, but never make it to the market under the current conservative regulatory paradigm (Vicente et al., 2016). The major challenge is to understand how and to which extent potassium channel block and QT interval length increase the proarrhythmic risk of the heart.

Here we propose to correlate potassium channel block and QT interval length to electrocardiogram recordings via mechanistic multiscale modeling. We establish a computational model that uses drug-induced current block signatures from single cell electrophysiology as input and generates action potential profiles, cardiac excitation patterns, and electrocardiograms as output. By design, out model allows us to characterize the interaction of different channel blocks (Sahli Costabal et al., 2018), the interaction of different drugs (Johannesen et al., 2016), and the interaction of different cell types across the heart. Here we focus on the spatio-temporal interaction of different cell types in response to a single channel blocker at different concentrations. Because of its known dose-sensitive risk of torsades de pointes, we choose the drug dofetilide, a pure strong rapid delayed rectifying potassium channel blocker (Vicente, Johannesen, Manson, Crumb, Pueyo, Stockbridge, and Strauss, 2015), and quantify its effects at concentrations of 1x, 5.7x, and 30x, in comparison to the baseline case without drugs.

Our drug-modulated action potential profiles in Figure 4 agree well with the common understanding that–by design–through blocking the rapid delayed rectifying potassium current I_Kr, dofetilide prolongs the plateau of the action potential and increases action potential duration (Pfizer, 2011). Beyond a critical concentration, midwall cells begin to display early afterdepolarizations (Antzelevitch and Sicouri, 1994). While their action potential profiles in Figure 4 nicely capture the underlying characteristic oscillatory potential, the ionic basis for the development of early afterdepolarizations remains unclear (Pugsley, Curtis, and Hayes, 2015).

As a class III antiarrhythmic agent, dofetilide increases the refractory period of atrial, ventricular, and Purkije cells, but, in contrast to class I agents, it maintains the overall conduction velocity (Ibrahim and Bhimji, 2017) and heart rate (Pfizer, 2011). Because of its high specificity and a low side-effect profile, dofetilide has advanced as one of the most effective antiarrhythmic agents (Briceno and Supple, 2017). Figure 4 supports the general notion that its effects are strongly dose dependent: Action potential durations increase with increasing dose up to a critical dose beyond which dofetilide triggers early afterdepolarizations. The dose-response effects of dofetilide are highly cell-specific with midwall cells being most sensitive to the drug followed by endocardial, epicardial, and Purkinje cells (Antzelevitch and Sicouri, 1994).

Our baseline excitation profile of the left and right ventricles in Figure 5 agrees well with the excitation sequence in healthy human hearts. Critical to this sequence is the Purkinje fiber network that quickly and reliably transmits the signal from the atrioventricular node down to the apex of the heart to excite the heart from the bottom up (Sahli Costabal et al., 2016). There is a general agreement that, within the healthy activation sequence, the posterior basal region of the right ventricle is the last region to activate (Durrer, van Dam, Freud, Janse, Meijler, and Arzbaecher, 1970), which agrees well with our predicted excitation profile at 60ms. The timing of repolarization and depolarization also agree well with those of healthy human hearts, where complete the activation takes between 62ms and 80ms (Durrer et al., 1970), compared to 72ms in our model.

Our simulated effects of dofetilide on cardiac excitation in Figures 6 through 8 agree well with the label of Tikosyn (Pfizer, 2011) and with the results of clinical studies in patients (Abraham, Saliba, Vekstein, Lawrence, Bhargava, Bassiouny, Janiszewski, Lindsay, Militello, Nissen, Poe, Tanaka-Esposito, K., and Wilkoff, 2015). Our simulations support the common notion that, at low doses, dofetilide is a safe drug and effective drug with low pro-arrhythmic risk (Pfizer, 2011). For a dofetilide concentration of 1x in Figure 6, it takes our simulation 640ms to return to the resting state, compared to 450ms for the baseline case with no drugs in Figure 5. Similar to a recent clinical study, which reported a QT prolongation of 78ms (Johannesen, Vicente, Mason, Sanabria, Waite-Labott, Hong, Guo, Lin, Sørensen, Galeotti, Florian, Ugander, Stockbridge, and Strauss, 2014), our simulation predicts a substantial but safe prolongation of the effective refractory period. This agrees well with the general notion that dofetilide can have dramatic consequences if not dosed correctly (Briceno and Supple, 2017): In a retrospective cohort study of 1,404 patients loaded on dofetilide for a five-year period, dofetilide was stopped in 105 patients because of QT prologation. A total of 17 patients developed torsades de pointes; of those, ten had an episode of cardiac arrest and one resulted in death. In agreement with our simulations, the study found a dose-related increase in torsades de pointes, with a higher incidence when taking the 0.500mg dose twice per day (Abraham et al., 2015). According to the label, the maximum single dose for dofetilide is 0.500mg (Vicente et al., 2015).

For a dofetilide concentration of 5.7x in Figure 7, our simulation predicts a spontaneous transitions from a sharp but smoothly propagating excitation pattern into rapid, irregular, asynchronous activation patterns of torsades de pointes type. Our model inherently captures the regional specificity of the ventricular myocardium and probes the dynamic interplay of its endocardial, midwall, epicardial, and Purkinje cells. A closer look at our activation sequences can help us identify the onset of torsadogenesis both in space and time: Our activation profiles in Figure 7 suggest that the mechanisms that triggers torsades de pointes are early afterdepolarizations(Antzelevitch and Sicouri, 1994) and not prolonged action potential duration. It is well known that a variety of drugs that block sodium and potassium channels can induce early afterdepolarizations, which may ultimately result in torsades de pointes; yet, the genesis and maintainance of early afterdepolarization-induced arrhythmias remain unclear (Pugsley et al., 2015). At a dofetilide concentration of 5.7x, according to the input to our model in Figure 4, only midwall cells experience early afterdepolarizations (Antzelevitch and Sicouri, 1994), while endocardial, epicardial and Purkinje cells display a regular, yet prolonged, action potential profile. In the thin layer of midwall cells in the ventricular wall, endocardial and epicardial cells can overwrite this early afterdepolarization, as evidenced by the global excitation pattern of large re-entrant waves, highlighted by the orange and blue colors. In the region near the great vessels, which we have represented by midwall cells, early afterdepolarizations freezes the transmembrane potential close to the neutral state, highlighted by the green color. This region overwrites the activation of the Purkije fiber network and excites the heart in chaotic twisting patterns, a classical hallmark of torsades de pointes (Dessertenne, 1966).

For a dofetilide concentration of 30x in Figure 8, our simulation predicts a spontaneous transitions from a sharp but smoothly propagating excitation pattern into numerous small re-entrant waves that flicker around the heart and excite it in chaotic patterns. This agrees well with clinical observations in response to overdosing: A patient who received two doses of 0.500mg of dofetilide one hour apart developed ventricular fibrillation and cardiac arrest (Ibrahim and Bhimji, 2017). At a dofetilide concentration of 30x, according to the input to our model in Figure 4, both midwall and endocardial cells display early afterdepolarizations. A majority of the ventricular wall has now lost its regular action potential profile. Unlike in Figure 7, the irregular region is now large enough to entirely overwrite any form of globally coordinated excitation (Antzelevitch and Sicouri, 1994). With the exception of small flickering wave fonts, the heart is frozen at the neurtal state with a transmembrane potential of zero.

Our simulated electrocardiograms in Figure 9 provide a simple zero-dimensional summary of the complex three-dimensional activation profiles in Figures 5 through 8. While electrocardiograms help us to quickly categorize rhythm disorders (Dubin, 1996), the mechanistic origin of these disturbances can only be uniquely assessed in combination with three-dimensional activation profiles. Our simulations accurately reproduce the common notion that dofetilide causes a dose- and concentration-dependent increase in the QT interval (Vicente et al., 2016), with predicted QT interval prolongations of 55%, 102%, and 132% compared to baseline. Our predicted QT interval prolongation is in excellent agreement with clinical observations: For the 1x case, we apply an equivalent plasma concentration of 2.65 ng/mL and record a QT prolongation of 55%. This value compares closely to the projected value of 56% reported by a recent prospective clinical trial (Johannesen et al., 2016). Our QT alterations are slightly larger than the reported increase of 15-25ms/ng/mL after the first dose and 10-15ms/ng/mL after day 23 (Pfizer, 2011), which might be caused by fact that our simulated QT interval prolongations are highly sensitive to the block-concentration characteristics (Crumb et al., 2016) summarized in Figure 3.

Recent studies have challenged the focus on the QT interval alone and suggest that more information may be present in electrocardiogram including T wave morphology, flatness, asymmetry, and notching (Vicente et al., 2015). The T wave of our dofetilide 1x electrocardiogram clearly differs in flatness and asymmetry from the T wave of the baseline electrocardiogram in Figure 9. Another characteristic feature that has been largely overlooked in the risk assessment of torsades de pointes is the U wave. Our simulated electrocardiograms only display two pronounced U waves, both during the first two cycles of the dofetilide 5.7x electrocardiogram. The appearance of pronounced U waves in the electrocariogram is known to be a potential indicator of early afterdepolarizations, particularly in midwall cells (Antzelevitch and Sicouri, 1994). This common notion agrees well with the U waves in our dofetilide 5.7x electrocardiogram in Figure 9, which coincide with the early afterdepolarizations of our midwall cells in Figure 4. Pronounced U waves are a common side effect of antiarrythmic drugs (Antzelevitch and Sicouri, 1994) and closely associated with the formation of torsades de pointes (Pugsley et al., 2015). This agrees well with our simulation, which, after the first two cycles, at about 1,500 ms, spontaneously transitions into a sequence of rapid, widened irregular QRS complexes, a distinguishing feature of torsades de pointes (Dessertenne, 1966).

Although our study provides valuable insight into the mechanistic origin of ventricular tachycardia and torsades de pointes, it has several important limitations that we need to keep in mind when interpreting its results: First, the major unknowns in arrhythmogenic risk assessment are pharmacodynamic variability caused by variability in drug action at the cellular, tissue, whole-organ, and whole organism levels and pharmacokinetic variability caused by variability in concentration at the target site of action (Roden, 2016). Both are essentially inputs to our model (Crumb et al., 2016), summarized in Figure 3, and can be easily generalized to include more variability once this information becomes available. For example, by personalizing the block-concentration response, we could use our model for personalized drug screening. Second, ideally, we would also personalize the cellular heterogeneity across the ventricular wall. Here for simplicity, we have assumed a generic distribution of endocardial, midwall, and epicardial cells. Our simulations suggest torsadogenic risk assessment is particularly sensitive to the regional distribution of midwall cells, which display the highest dose-response sensitivity of all cell types, and are most closely associated with early afterdepolarizations and torsadogenesis (Antzelevitch and Sicouri, 1994). However, even without personalized pharmacodynamics, pharmacokinetics, and personalized heart models (Chabiniok, Wang, Hadjicharalambous, Asner, Lee, Sermesant, Kuhl, Young, Moireau, Nash, Chapelle, and Nordsletten, 2016), we can already use our current model to perform uncertainty quantification and predict an arrhythmogenic risk regime rather than a single quantifier (Chang, Dutta, Mirams, Beattie, Sheng, Tran, Wu, Wu, Cotlasky, Strauss, and Li, 2017). Third, while our current study is limited to a single drug that selectively blocks a single channel, our model can be equally used to study the effect of drugs that block several interacting channels (Sahli Costabal et al., 2018) or the effect of co-administration of several compensatory drugs (Johannesen et al., 2016).

Conclusion

Various drugs display undesired side effects in the form of torsades de pointes, an abnormal heart rhythm that can lead to sudden cardiac death. The initiation of torsades de pointes has traditionally been associated with potassium channel blockage and QT interval prolongation; yet, the underlying mechanisms of torsades de pointes remain poorly understood. Here we present a multiscale computational model to explore the effects of drugs on the single channel, single cell, and whole heart levels. Our mechanistic exposure-response simulator translates block-concentration characteristics of arbitrary drugs into three-dimensional excitation profiles and electrocardiogram recordings to provide a rapid assessment of torsadogenic risk. A typical input to our model could come from the block-concentration profiles generated and recommended by the CiPA initiative. Here, we illustrate the features of our exposure-response simulator for the drug dofetilide, a controversial drug with high specificity to block a single channel, the rapid delayed rectifier potassium current I_Kr. We show that the proarrhythmic risk of dofetilide is highly dose-dependent with a low torsadogenic risk at and below concentrations of 1x and a high torsadogenic risk at and above concentrations of 5.7x. Our exposure-response simulator can identify the mechanistic origin of torsadogenesis, both in space and time, and provide a more accurate and comprehensive mechanistic assessment of proarrhythmeic potential. For the example of dofetilide, our simulations suggest that neither potassium channel blockage nor QT interval prolongation alone trigger torsades de pointes. Rather, the underlying mechanism predicted by our model are early afterdepolarizations, which translate into pronounced U waves in the electrocardiogram, a signature that is correctly predicted by our simulation. Beyond the risk assessment of existing drugs, our exposure-response simulator can serve as a powerful tool for cardiologists, drug design companies, and regulatory agencies to optimize the co-administration of existing drugs and, ultimately, guide the design of new drugs with potentially compensatory effects.