Automatic Multichannel Intramuscular Electromyogram Decomposition: Progressive FastICA Peel-off and Performance Validation

Abstract

The progressive FastICA peel-off (PFP) is a recently developed blind source separation approach for high-density surface EMG decomposition. This study explores a novel application of PFP for automatic decomposition of multi-channel intramuscular electromyogram signals. The automatic PFP (APFP) was used to decompose an open access multichannel intramuscular EMG dataset, simultaneously collected from the brachioradialis muscle using 6 to 8 fine wire or needle electrodes. Given usually limited number of intramuscular electrodes compared with high-density surface EMG recording, a modification was made to the original APFP framework to dramatically increase the decomposition yield. A total of 131 motor units were automatically decomposed by the APFP framework from 10 multichannel intramuscular EMG signals, among which 128 motor units were also manually identified from the expert interactive EMGLAB decomposition. The average matching rate of discharge instants for all the common motor units was (98.71±1.73) %. The outcomes of this study indicate that the APFP framework can also be used to automatically decompose multichannel intramuscular EMG with high accuracies, even though the number of recording channels is relatively small compared with high-density surface EMG.

I. Introduction

Electromyography (EMG) decomposition is the process of breaking down the multi-unit EMG signal into the contributions of the underlying motor unit action potential (MUAP) trains. It provides a unique approach to observing the behavior of spinal motor neurons in human subjects and the MUAP waveform information, thus playing a fundamental role for investigation of motor control and examination of neuromuscular diseases. EMG decomposition is usually performed using intramuscular (needle or fine wire) EMG signals. Various intramuscular EMG decomposition methods have been developed, among which template matching is most frequently used to sort out different motor units based on MUAP morphological features. Due to the invasive character of needle or fine wire electrode, most intramuscular EMG studies use single channel recording[1–4]

The strategy of template matching, however, is very difficult to apply to conventional surface EMG because of much higher levels of MUAP superposition and MUAP similarity (from different motor units), as well as lower SNRs, compared with intramuscular EMG. In recent decades, advances in amplification technology and manufacture of high-density surface electrode arrays make it feasible to simultaneously record dozens or even hundreds channels of surface EMG signals from a single muscle[5, 6]. The spatial information of an electrode array can supplement temporal information for EMG decomposition through 2-dimensional MUAP template matching [7], which allows extraction of a small number of motor units at low muscle contraction levels. More importantly, advanced blind source separation (BSS) techniques can be applied to perform high-density surface EMG decomposition. For example, two BSS approaches, the Convolution Kernel Compensation (CKC)[8, 9] and the Progressive FastICA Peel-off (PFP)[10, 11], have been proposed to decompose high-density surface EMG, which allow extraction of a relatively large number of motor units at higher muscle contraction levels.

Although BSS techniques have achieved great success in high-density surface EMG decomposition, they are not necessarily limited to surface EMG processing. In principle, BSS techniques can also be extended to multichannel intramuscular EMG decomposition [12]. In this study, we set to explore application of the PFP framework for automatic decomposition of multichannel intramuscular EMG signals. The PFP framework was proposed for high-density surface EMG decomposition, which combines FastICA[13] with a peel-off strategy for progressive identification of motor unit firing spike trains [10]. To facilitate its convenient and wide application, the automatic version of the PFP, i.e. the automatic PFP (APFP), has also been developed to automatically decompose high-density surface EMG[11]. The performance of the APFP has been validated with different approaches, including mathematical modeling of high-density surface EMG signals [10, 11], comparison of its decomposition yield with the CKC decomposition[14], two-source validation using simultaneous high-density surface EMG and intramuscular EMG recordings[15]. In addition, taking advantage of surface EMG characteristics of amyotrophic lateral sclerosis, we have developed a novel two-source approach for validating the performance of APFP[16].

In this study, we present an application of the APFP framework for automatic decomposition of a set of multichannel intramuscular EMG signals. These signals were previously decomposed by EMGLAB, an interactive EMG decomposition program designed for intramuscular EMG[2]. In this novel APFP application, we have made a modification to the original framework to make it more suitable for decomposition of multichannel intramuscular EMG with relatively a small number of recording channels. To evaluate the decomposition performance, the automatic decomposition results of the APFP were compared with those from expert interactive decomposition using EMGLAB [2]. The findings indicate that the APFP framework can be applied to automatically decompose multichannel intramuscular EMG signals with high accuracy.

II. METHODS

A. Data description

The multichannel intramuscular EMG dataset used in this study is an open access dataset, which can be freely downloaded for research purposes at http://www.emglab.net, a forum for sharing software, data, and information related to EMG decomposition, developed by McGill et al. [2]. The dataset was previously used to test an automatic multichannel intramuscular EMG decomposition method proposed by Florestal et.al [17]. (The data are available as dataset R008 at http://www.emglab.net). In this study, the same dataset was processed by the APFP framework to automatically extract motor unit activities from the multichannel intramuscular EMG.

The downloaded or processed multichannel intramuscular EMG signals were collected from the brachioradialis muscles of three male healthy subjects (age: 36, 27, 27). The signals were recorded simultaneously from three or four pairs of fine wire electrodes (custom, Jari Electrode Supply, Gilroy, CA) and a 27 gauge disposable monopolar needle electrode (EMG Wholesale Supply, Milford, OH) inserted at different locations (by distances ranging from 10 to 100 mm to different wire pairs) along the proximodistal axis of the muscle during 20 second low-level or moderate-level isometric contractions. The signals were recorded in a monopolar fashion, resulting in a total of 6 to 8 signals per contraction. Several contractions were recorded per subject, with the fine wire electrodes remaining in place and the needle electrode being moved between contractions. The signals were amplified and filtered (5 Hz to 5 kHz) (Viking, Nicolet Biomedical, Madison, WI), and digitized at a sampling rate of 10 kHz per channel. A total of 10 multichannel intramuscular EMG signals were recorded from the three subjects and digitally high-pass filtered using a 500 Hz first-order filter. We were able to access all the 10 signals (data files) from the aforementioned website. For each of the 10 data files, the relevant information (channel location, type of electrode) is indicated in the corresponding hea file.

Favorably, each multichannel intramuscular EMG data was also decomposed by EMGLAB, an interactive EMG decomposition program [2]. The decomposition results from this expert interactive or manual processing can also be found in the corresponding eaf file. For each decomposed motor unit, the most confident channel (for extracting this motor unit) is indicated in the eaf files, with a label from c1 to c8, representing channel 1 to channel 8, respectively. If an uncertain motor unit occurs which cannot be clearly identified from any of the channels, the motor unit is labeled as c0. Those motor units with a label of c0 were, therefore, excluded from the analysis in this study. If a motor unit is an anomalous one that only fired a couple of times during the contraction, it was also excluded from further analysis.

B. APFP

The APFP framework can be viewed as a process of progressively expanding the set of motor unit spike trains [10, 11]. In the framework, the initial set of motor unit spike trains can be estimated by FastICA. Then, a peel-off procedure is employed to subtract the estimated MUAPs of the identified motor units from the original signal. Such a procedure mitigates the effect of the already identified motor units on the FastICA convergence, so more motor units can emerge when processing the residual signal again with FastICA. In order to ensure the reliability of the extracted motor unit spike trains, a series of automatic screening and revision steps can be performed before the peel-off procedure. For each output of FastICA, a valley-seeking clustering method is used to extract and cluster the spikes. Then, a constrained FastICA is applied to assess each clustered spike train and correct possible erroneous or missed spikes. Multiple constrain parameters are proposed for final screening of the spike trains according to motor unit firing behavior. The framework is iterative by repeatedly running the peel-off procedures until no additional new motor units can emerge. For more details about APFP framework, please refer to [11].

C. Modification to APFP

When applying the APFP framework to the downloaded multichannel intramuscular EMG signals, we found that the decomposition yield was not as high as what we could usually achieve from high-density surface EMG signals. After careful analyses, we found that this performance degradation was attributed to the constrained FastICA procedure, which is the most important or featured step in the APFP framework. In the previous PFP/APFP framework used for high-density surface EMG decomposition, we recommended that constrained FastICA should be applied to the original surface EMG signals to avoid possible cumulative errors in the residual signals induced by the peel-off processing, thus facilitating identification and correction of any possible erroneous or missed spikes. However, although this approved to be effective for high-density surface EMG decomposition, we found it was difficult to achieve a similar effect when applying this strategy to the multichannel intramuscular EMG signals with only 6 to 8 recording channels. Based on the characteristics of multichannel intramuscular EMG signals, we modified to apply constrained FastICA to the residual signals instead of the original signals. The justification and benefits of this modification can be found in the discussion section. Note that when updating the residual signal, we used all the identified firing spike trains to estimate MUAP waveforms from the original signal, rather than using the new identified spike trains to perform estimation from the previous residual signal. The APFP decomposition program was terminated when no new motor units could be extracted from the iterative peel-off procedures.

D. Performance evaluation

In order to evaluate the automatic decomposition performance of the multichannel intramuscular EMG using the APFP framework, we compared its decomposition results with those from the expert interactive decomposition using EMGLAB [2]. The two decompositions of the same signals were performed independently using two methods of different nature. It is expected that common motor units from the two decompositions can be found. Cross-checking of the agreement on the timing of the common motor units discharge can give an estimation of the decomposition accuracy. If the two independent decompositions of the same signals agree on the timing of a particular motor unit discharge, we judge they are both correct. Otherwise, they would both have to involve an error of exactly the same amount. The probability of this situation arising is very small. In this study, we calculated the matching rate (MR)[14], false negative rate (FNR)[18] and false discovery rate (FDR)[19] of common motor units as follows [14–16]:

$$MR=\frac{2\cdot N_{COM}}{N_A+N_M}\cdot 100\%$$

$$FNR=\frac{N_M-N_{COM}}{N_M}\cdot 100\%$$

$$FDR=\frac{N_A-N_{COM}}{N_A}\cdot 100\%$$

where N_A and N_M are the total number of the spikes identified by APFP and manual decomposition using EMGLAB, respectively. N_COM stands for the number of the common spikes.

Considering the slight time shift of the estimated spike train by APFP, the cross-correlation function [10] was used to facilitate alignment of the two spike trains before calculating the parameters mentioned above. In this study, we accepted two spikes from different spike trains as corresponding spikes when they were located within ±0.1 ms (after alignment). Note that the matching rate measures the matching degree of two spike trains, and it can be used as an indicator to determine whether two spike trains are corresponding or common spike trains (from the same motor unit). We accepted that the two spike trains were corresponding spike trains when their matching rate was greater than 80% [15]. In addition to matching rate, the false negative rate and the false discovery rate of common motor units were used to measure the proportion of mismatches of the interactive EMGLAB decomposition and the APFP decomposition, respectively.

For a more comprehensive view of the consistency of two decompositions, we also calculated the mean discharge rate (MDR) and the coefficient of variation (COV) of the inter-spike intervals of each identified motor unit for both decompositions. For each of the two indexes, the difference between EMGLAB and APFP decompositions was measured by unpaired sample t-test. In addition, the signal-to-interference ratio (SIR), as defined in [20], was calculated for each of the decompositions:

$$SIR(i)=\left(1-\frac{E\left[{\left(x_i(n)-\sum _j{z}_{ij}(n)\right)}^2\right]}{E\left[x_i^2(n)\right]}\right)\cdot 100\%$$

where x_i (n) denotes the ith EMG channel and z_ij (n) is the MUAP train of the jth motor unit reconstructed form the ith channel. For motor units decomposed from EMGLAB, their MUAPs were also estimated by the peel-off method used in the APFP framework. Then, we compared SIR of the two decompositions by paired sample t-test to examine if there was a significant difference in the energy of residual signals.

Finally, in order to quantify the difficulty of the decomposition, we calculated the decomposability index (DI) for each common motor unit [17]:

$$D{I}_{ki}=\frac{\text{min}\left\{\Vert m_{ki}\Vert ,\Vert m_{ki}-m_{k*i}\Vert \right\}}{V_i^{RMS}}$$

where m_ki is the MUAP of the kth motor unit in the ith channel, m_k*i is the MUAP most similar to m_ki among the other MUAPs in the ith channel. $V_i^{RMS}$ is the root mean square amplitude (RMS) of the ith channel, and ǁ ǁ stands for the Euclidean norm. The DI measures the separation between m_ki and the template nearest to it (or the baseline), normalized by the RMS of the EMG channel (interference plus baseline noise). The overall decomposability of the kth motor unit was measured by the composite DI (CDI), defined as the norm of the individual DIs [17].

III. RESULTS

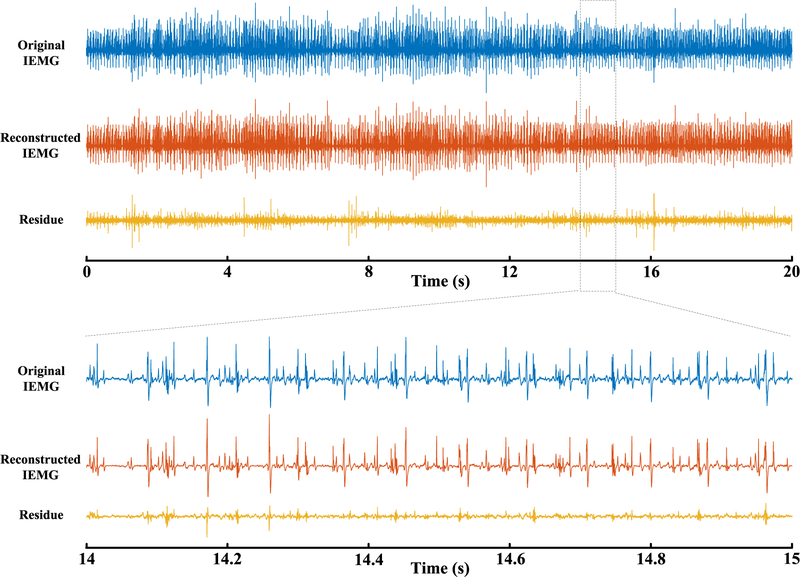
A total of 10 sets of multichannel intramuscular EMG signals were automatically decomposed using the APFP framework. Figure 1 shows an example of the raw intramuscular EMG signal of one channel (Dataset R0081310), the reconstructed signal using the decomposed motor units from the APFP, and the residual signal, respectively. For this multichannel intramuscular EMG signal, 16 motor units were automatically extracted using the APFP framework. By contrast, 25 motor units were manually extracted from this multichannel intramuscular EMG signal by the expert interaction decomposition using EMGLAB, including all the 16 motor units from the APFP decomposition.

Fig. 1.

An example of the original signal (one channel, after high-pass filtering), the reconstructed signal from the 16 motor units automatically extracted by APFP, and the residual signal (Dataset R0081310).

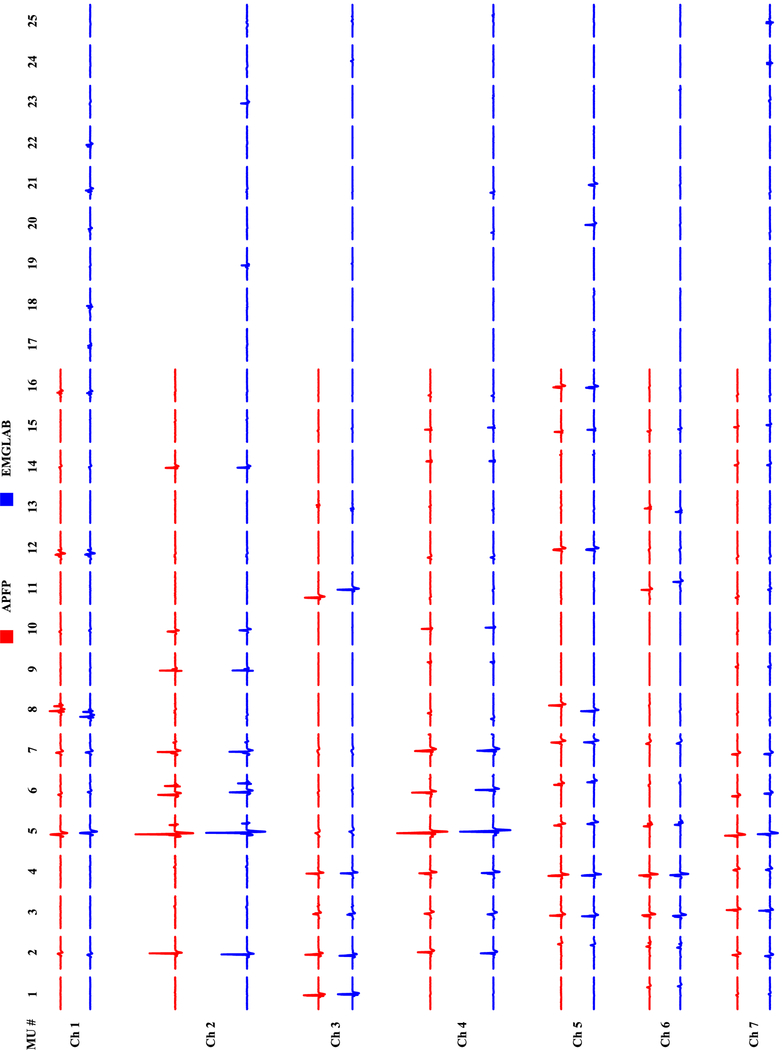
Figure 2 shows the MUAP templates obtained from the two decompositions on 7 different channels (Dataset R0081310). The MUAP templates estimated from APFP are marked in red, and those from EMGLAB are marked in blue. We can observe that the MUAP templates of the 16 common motor units are very consistent, and the 9 additional motor units identified by EMGLAB but not by APFP have relatively small amplitude. Note that we did not align the spike trains before MUAP estimation (thus drifts between the corresponding MUAP waveforms of the two groups can be observed in the figure). For each of the 16 common motor units, a comparison of the discharge instants is shown in Figure 3. The motor unit discharge instants are represented by red bars for the automatic decomposition with APFP and blue bars for the expert interactive decomposition with EMGLAB. The black dots in the figure indicate all the inconsistent discharge instants from the two decomposition methods (by visual observation). An interesting observation is that although the two motor unit spike trains (MU 8 and MU 12) appear identical in all the discharge instants, the calculation of their matching rate does not reach 100%. This implies that the calculated matching rate might be slightly lower than the actual matching rate. A discussion is provided (in the Discussion section) to better understand the origins of this phenomenon (slight underestimation of the matching rate).

Fig. 2.

The estimated MUAP templates at 7 different channels from the two decompositions. The red MUAPs are estimated from APFP, and the blue ones are estimated from EMGLAB (Dataset R0081310).

Fig. 3.

A comparison of discharge instants of common motor units determined from APFP (red bars) and EMGLAB (blue bars) respectively. The black dots indicate (visually) inconsistent discharge instants. The calculated matching rate of each common motor unit is indicated on the right. (Dataset R0081310)

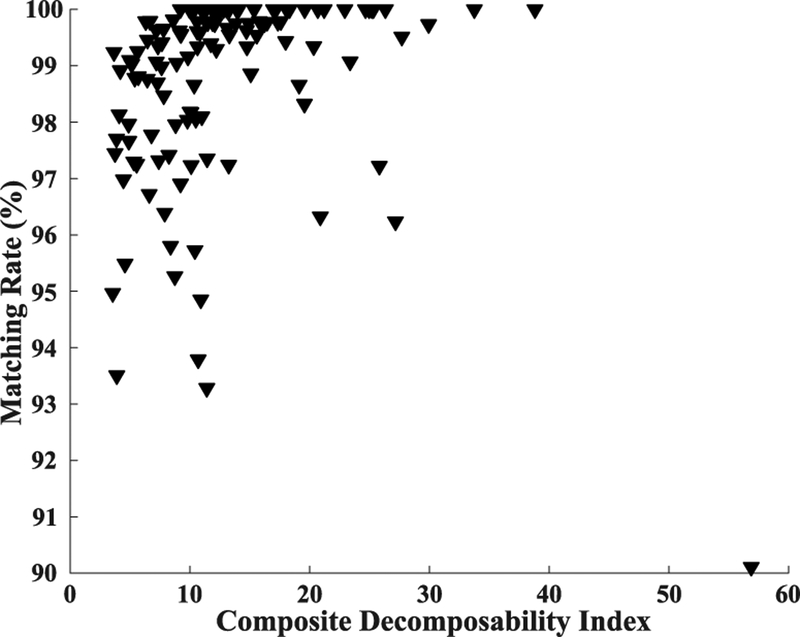
Figure 4 plots the relationship between matching rate and composite decomposability index (CDI), which shows how the matching rates vary with SNR of the motor units. Note that there is an outlier in the bottom right corner. This motor unit has the highest CDI but the lowest matching rate. This is also an example showing the phenomenon of matching rate underestimation, which is discussed in the Discussion section.

Fig. 4.

The relationship between matching rate and composite decomposability index.

Table I presents the decomposition results of all the 10 multichannel intramuscular EMG signals. For each signal, the number of identified motor units using the two different decomposition methods and the number of common motor units are illustrated. The signal-to-interference ratio, mean discharge rate and coefficient of variance of inter-spike intervals are also presented in the table. For these three parameters, ‘*’ indicates that the two groups have a significant difference with p<0.05. For the common motor units of each signal, the calculated matching rates (including minimum, maximum, and average values) of the discharge instants can also be found in the table, together with the average false negative rate, and the average false discovery rate.

TABLE I.

Summary of The Decomposition Results From APFP and EMGLAB

Signal (#Channels)	#MUs APFP/EMGLAB [Common]	MR (%)	FNR (%)	FDR (%)	SIR (%) APFP/EMGLAB	MDR (Hz) APFP/EMGLAB	COV (%) APFP/EMGLAB
R0080101 (8)	11 / 12 [10]	99.50±0.72 [97.70, 100]	0.31±0.63	0.68±0.87	86.05±17.05 85.88±17.19	10.1±1.4 9.9±1.5	11.1±2.3 10.6±2.9
R0080112 (8)	13 / 20 [12]	98.80±1.71 [95.49, 100]	1.23±2.18	1.15±1.65	90.22±8.11 93.52±1.86	11.0±1.8 11.2±1.6	14.0±4.4 11.8±4.0
R0080121 (8)	14 / 22 [14]	99.45±0.66 [98.10, 100]	0.38±0.69	0.71±0.81	92.07±3.66 93.77±4.20	10.9±2.2 10.9±1.9	12.0±5.3 9.6±4.1
R0080124 (8)	16 / 24 [16]	98.57±1.88 [93.51, 100]	0.94±1.18	1.89±2.63	91.93±3.79 93.12±3.99	11.0±2.1 11.2±1.8	14.0±5.7 9.9±4.1*
R0081006 (7)	14 / 15 [14]	98.84±1.33 [94.97, 100]	0.74±0.84	1.52±2.05	90.02±4.86 89.48±4.70	10.7±1.0 10.6±1.0	16.7±4.3 14.0±2.7*
R0081009 (6)	11 / 24 [11]	97.79±3.01 [90.11, 100]	1.96±3.27	2.44±3.23	68.05±19.69 89.69±5.60*	12.8±1.2 13.1±0.9	18.4±5.9 15.5±5.5
R0081012 (7)	13 / 12 [12]	99.62±0.63 [97.96, 100]	0.42±0.60	0.34±0.80	87.12±5.99 87.17±6.04	10.5±2.0 10.4±2.0	20.1±6.9 19.2±7.2
R0081306 (7)	9 / 12 [9]	98.44±2.29 [93.79, 100]	1.35±2.32	1.77±2.40	87.36±10.50 89.42±5.74	11.1±1.6 11.6±1.7	18.9±5.3 16.7±4.4
R0081307 (7)	14 / 20 [14]	98.19±1.82 [93.28, 99.79]	1.40±1.45	2.19±2.36	84.27±16.48 91.03±5.25	12.4±1.1 14.0±6.1	20.5±5.9 17.0±5.8
R0081310 (7)	16 / 26 [16]	98.41±1.38 [95.26, 100]	1.63±1.80	1.54±1.42	88.52±7.01 94.70±2.22*	12.5±1.2 12.5±1.2	20.8±5.9 18.8±7.2

To summarize, from the 10 processed multichannel intramuscular EMG signals, a total of 131 motor units were automatically decomposed by the APFP framework, while a total of 187 motor units were manually identified from the expert interactive EMGLAB decomposition. There are a total of 128 common motor units identified from the two different decomposition methods (which indicates that almost all the identified motor units by the APFP can also be found from the EMGLAB decomposition). Calculated from all the common motor units, the average matching rate of discharge instants was (98.71±1.73)%, the average false negative rate was (1.05±1.67)%, and the average false discovery rate was(1.49±2.08) %.

IV. Discussion

A. Modification to original APFP

This study investigates automatic decomposition of multichannel intramuscular EMG using the APFP framework, which has previously been tested and validated in high-density surface EMG decomposition. In the APFP framework, the peel-off processing is crucial to decompose superimposed motor units. To overcome the cumulative errors induced by the peel-off processing, the constrained FastICA was designed to apply to the original high-density surface signal to assess the reliability of the identified firing spike train from FastICA output, and fix possible erroneous or missing spikes. This strategy approved to be effective for high-density surface EMG decomposition. However, for the multichannel intramuscular EMG signals processed in this study, we found that although applying the constrained FastICA to the original signal could extract large amplitude motor units, this processing sometimes had a difficulty in automatically extracting small amplitude motor units. More specifically, during the peel-off procedures, even we can visually identify a clear spike train from the FastICA output of a residual signal (indicating a new motor unit), it is likely that the output of applying constrained FastICA to the original signal may still be a mix of several spike trains. This is mainly due to insufficient number of intramuscular EMG channels. For the to-be-assessed small amplitude motor units (by constrained FastICA), applying the constrained FastICA to the original signal can maximize the amplitude at their corresponding discharge instants. However, with the information provided by only 6 to 8 intramuscular EMG channels (or actually even less number of channels for a specific motor unit given the selectivity of the electrode), the constrained FastICA output of the discharge instants of the relatively large amplitude motor units in the original signal cannot be sufficiently suppressed. As a result, the small amplitude motor units will be discarded by the automatic judgement criteria of APFP, thus affecting the decomposition yield (but not the accuracy of the identified motor units).

Given the above, we adjusted to apply constrained FastICA directly to the residual signals rather than the original signal in this multichannel intramuscular EMG decomposition task. The rationale for this is that compared with surface EMG signal, intramuscular EMG signal usually has considerably higher SNRs and less MUAP superposition levels, thus the estimation of motor unit spike trains and MUAP waveforms tends to be more reliable than surface EMG. As a result, the residual signal can be considered as an alternative to the original signal to apply the constrained FastICA. For the small amplitude motor units, we found this modification can smoothly pass the constrained FastICA validation, thus significantly increasing the decomposition yield. In this study, we were able to automatically identify an average of 7 motor units from each multichannel intramuscular EMG by applying the constrained FastICA to the original signal. In contrast, an average of 13 motor units can be automatically extracted if applying the constrained FastICA to the residual signals. It should be noted that this modification is a compromised solution to overcome insufficient number of intramuscular EMG channels. If there are sufficient channels, we still recommend to apply constrained FastICA to the original signal.

B. Firing instants drift

During APFP, only those spike trains extracted from clear output of FastICA or constrained FastICA can be accepted as reliable motor unit firing spike trains. One interesting observation in this study is that even two firing spike trains look exactly the same, the calculated matching rate does not reach 100% (Figure 2). This is due to the phenomenon of firing instants drift. A similar phenomenon can be suggested by the outlier motor unit (in the bottom right corner) of Figure 4, which has the highest CDI but the lowest matching rate. After carefully examining the two spike trains of this motor unit, we found that in fact they are very consistent. This motor unit discharged sparsely and lasted approximately 10 seconds. However, a small amount of spike drift beyond the preset time tolerance (0.1 ms) resulted in a lower match rate. When extracting the firing spike train from the output of FastICA or constrained FastICA, we set the positions with maximal amplitude as spike firing instants. However, due to noise, superposition and the MUAP waveform instability, there might be a small amount of firing instants with imposed drift that exceeds the preset time tolerance, thus being excluded from common firing instants. In addition, different pre-processing filters may also influence identification of the MUAP peak positions. Given these, one should note that the firing instants estimated by EMGLAB or APFP (both having the firing instants drift phenomenon) are not necessarily the gold standard representing the true firing instants, and as a result, the spike drifts between the two decomposition methods are not necessarily the true drifts from the real firing instants. Therefore, the time tolerance requirement can be appropriately relaxed to avoid underestimation of the matching rate. For example, the matching rate of the outlier motor unit in Figure 4 will increase to 98.9% if the tolerance is increased to0.5 ms. Note that due to the sparsity of firing spike train, an appropriate tolerance increase will hardly introduce fake-matched firing instants.

Although the slight firing instant drifts do not necessarily affect the correct estimation of the firing analysis of motor unit spike train, they are among various factors that affect the accuracy of the MUAP waveform estimation during the peel-off procedures. The extraction of motor unit firing spike train and waveform estimation actually have a mutual effect, and therefore, affect each other. Once the motor unit firing spike trains are determined, the APFP provides an optimal solution of estimating MUAP waveforms in the sense of least-squares error. This is sufficient to fulfill the primary motivation of applying the peel-off strategy, i.e. mitigating the effect of the already identified motor units on the convergence of FastICA, thus facilitating extraction of more motor units.

C. APFP vs. EMGLAB

The performance of EMGLAB and APFP was compared in decomposing the same multichannel intramuscular EMG signals. It was found that for the dataset used in this study, the decomposition yield of the interactive EMGLAB program is usually higher than that from the automatic decomposition with the APFP framework. This is primarily due to the different signal processing strategies used by the two approaches. The APFP is essentially a BSS technique with automated serial peel-off procedures. It remains a challenge to extract those motor units in the residual signal that have small amplitude, comparable to background noise or accumulative errors induced by previous multiple peel-off procedures. In contrast, EMGLAB decomposition is a manually supervised method primarily based on template matching. It is possible to decompose the small amplitude motor units if their MUAP templates can be determined, although the decomposition accuracy of these small amplitude motor units is anticipated inferior to those large amplitude ones.

In addition, due to high selectivity of intramuscular EMG recording (especially given the large distance between the fine wire electrodes in this study), it is very likely that a specific motor unit may not be captured by all the intramuscular electrodes (Fig. 2). This can be viewed as an advantage for EMGLAB decomposition but will affect the performance of FastICA. Note that with random initial values we set to FastICA, the small amplitude motor units are difficult to emerge. To facilitate extraction of these motor units, one approach is to first search their samples at the firing instants and then accordingly set the FastICA’s initial values, which may help drive FastICA to converge to these small amplitude motor units. This remains further investigation for improving the decomposition yield of the APFP framework.

In a previous study, Negro et.al. proposed a BSS method by essentially combining the CKC and PFP designs to decompose multichannel intramuscular EMG signals (recorded by a novel thin-film 16 to 32-channel electrode array) and high-density surface EMG signals (recorded by a 64-channel surface grid)[12]. The BSS decomposition results of intramuscular EMG were also compared with its expert interactive decomposition using EMGLAB. With a dramatically higher number of intramuscular EMG channels (than the current study), up to 8 to 24 motor units were decomposed using the BSS. However, the number is still lower than that extracted using EMGLAB. In addition, we note that the reported rate of agreement (ROA) [12, 20], which is an indicator measuring the matching degree of two decompositions, varied from 45% to 100%. By definition, ROA used in [12] and matching rate used in this study should be very close when the number of mismatches is much smaller than the number of matches. Therefore, a motor unit with ROA as low as 45% between BSS and EMGLAB (processing the same intramuscular EMG signal), or as low as 70% between intramuscular and surface EMG signals (processed by the same BSS method), may indicate the decomposition performance of this motor unit is not reliable or stable. The occurrence of this phenomenon may be due to the low ROA threshold (30%) in judging whether two spike trains can be accepted as a common motor unit[12]. Similar to matching rate, ROA of random spike train pairs from two different decompositions should demonstrate a bimodal distribution [15]. Therefore, it is more reasonable to set the threshold relatively high, since a too low threshold is likely to overestimate the number of decomposed motor units and compromise the decomposition accuracy.

V. Conclusion

This study explored automatic decomposition of multichannel intramuscular EMG signals using the APFP framework, which was previously developed for high-density surface EMG decomposition [10, 11]. To facilitate the best performance of APFP for the limited number of intramuscular EMG channels, a modification was made to the original APFP framework. The automatic decomposition results of APFP were compared with those manually achieved from the interactive EMGLAB[2] decomposition. The outcomes indicate that APFP can be extended as a reliable approach for decomposition of multi-channel intramuscular EMG signals, even when the number of recording channels is relatively small compared with high-density surface EMG.