Uniform magnetic force impact on water based nanofluid thermal behavior in a porous enclosure with ellipse shaped obstacle

Abstract

In the present research, aluminum oxide- water (Al₂O₃-H₂O) nanofluid free convection due to magnetic forces through a permeable cubic domain with ellipse shaped obstacle has been reported. Lattice Boltzmann approach is involved to depict the impacts of magnetic, buoyancy forces and permeability on nanoparticles migration. To predict properties of Al₂O₃- water nanofluid, Brownian motion impact has been involved. Outcomes revels that considering higher magnetic forces results in greater conduction mechanism. Permeability can enhance the temperature gradient.

Introduction

By suggesting nanoparticles from nanoscience as useful working fluid, thermal performance enhances. Nano sized metallic particles are dispersed into common fluid to generate such fluid. Nanofluids must be utilized to augment the conduction and can be more stable with better mixing^1,2. Nano science can suggest appropriate working fluid to reach thermal efficiency enhancement^3–6. The furthermost current publications on nanofluids with new applications can be demonstrated in^7–12. Kumar et al.¹³ involved the Brownian motion impact on characteristics of nanoparticles in bioconvective flow. Irfan et al.¹⁴ displayed the roles of chemical terms on transient energy equation. Ahmed et al.¹⁵ illustrated the carbon nanotubes flow between Riga sheets in existence of viscous dissipation. Kumar et al.¹⁶ employed the non-Fourier heat flux model for investigation of magnetic force effect on Carreau fluid convective transient flow. Ali et al.¹⁷ demonstrated hidden events during magnetohydrodynamic (MHD) migration in a permeable media. Soomro et al.¹⁸ employed Finite difference method (FDM) for dual solution of nanoparticle migration over a cylinder. They used water as pure fluid. Reddy et al.¹⁹ depicted the impact of magnetic terms on fluid flow along a sheet considering heat sink. Raizah et al.²⁰ illustrated the power law nanofluid natural convection inside a titled permeable duct. The furthermost recent articles about Nano sized particles transportation by involving various methods were reported by Shah et al.^9,21,22. Choosing active working fluid becomes popular subject in recent decade^23–51.

The main aim of current research is to simulate and examine nanoparticles migration within a cubic porous cavity under the influence of constant magnetic force. Hydrothermal behaviors for various permeability, Lorentz and buoyancy forces are mainly focused and shown through graph.

Geometry Explanation

Figure 1 displays the permeable cubic cavity which is full of alumina. Cold, adiabatic and hot surfaces are depicted in this graph. One direction magnetic force has been involved. (θ_z = 0.5 π = θ_x).

Figure 1.

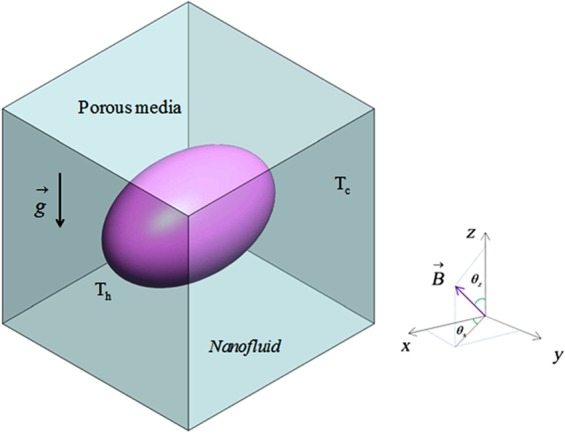
Current porous cubic cavity.

Simulation by Mesoscopic Method

Mesoscopic method

To find the temperature and velocity, distribution functions were used namely (g and f). Boltzmann equations help to find functions g and f. According to assumptions exist in³⁸, we have:

$$\mathrm{\Delta }t{\tau }_C^{-1}[-g_i(x,t)+g_i^{eq}(x,t)]=g_i(x+\mathrm{\Delta }t{c}_i,t+\mathrm{\Delta }t)-g_i(x,t)$$ 1

$$\mathrm{\Delta }t{\tau }_v^{-1}[-f_i(x,t)+f_i^{eq}(x,t)]+f_i(x,t)+\mathrm{\Delta }t{c}_i{F}_k=f_i(x+\mathrm{\Delta }t{c}_i,t+\mathrm{\Delta }t)$$ 2

Here τ_c, Δt, τ_v and c_i are, relaxation time for T, time step, relaxation time for u and lattice velocity.

D₃Q₁₉ model is good method for such problem (as shown in Fig. 2):

$$c_i=\left(\begin{array}{llllllllllllllllll}0\hfill & 0\hfill & 0\hfill & 0\hfill & -1\hfill & -1\hfill & -1\hfill & -1\hfill & 1\hfill & 1\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & -1\hfill & 1\hfill & 0\hfill \\ -1\hfill & -1\hfill & 1\hfill & 1\hfill & 0\hfill & -1\hfill & -1\hfill & 1\hfill & 0\hfill & -1\hfill & 1\hfill & 0\hfill & 0\hfill & -1\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill \\ -1\hfill & 1\hfill & -1\hfill & 1\hfill & -1\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & -1\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right)$$ 3

Figure 2.

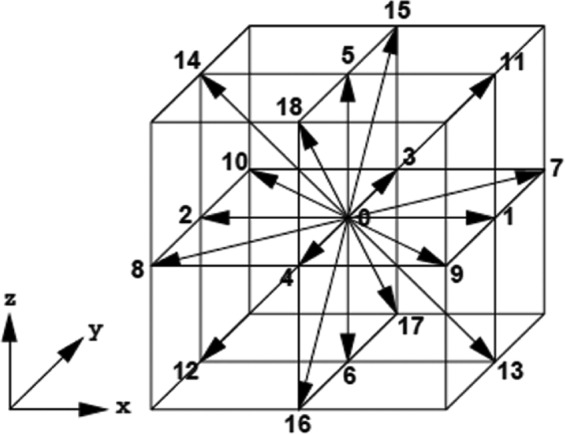
Diagram of D₃Q₁₉ model.

$g_i^{eq}$ & $f_i^{eq}$ are:

$$g_i^{eq}=w_{i}T\left[1+\frac{c_i.u}{c_s^2}\right]$$ 4

$$f_i^{eq}=\left[\frac{1}{2}\frac{{(c_i.u)}^2}{c_s^4}-\frac{1}{2}\frac{u^2}{c_s^2}+1+\frac{c_i.u}{c_s^2}\right]w_i\rho$$ 5

$$w_i=\left\{i=7:181/36;i=01/3;i=1:61/18\right\}$$ 6

Body forces can calculate as:

$$\begin{array}{lll}\hfill F& \hfill =\hfill & F_y+F_z+F_x\hfill \\ \hfill F_y& \hfill =\hfill & \begin{array}{l}3A{w}_i\rho [-(-\sin \left(2{\theta }_z\right)\sin \left({\theta }_x\right)\left(0.5\right)w+v{\cos }^2\left({\theta }_z\right))\\ +(-v{\cos }^2\left({\theta }_x\right){\sin }^2\left({\theta }_z\right)+0.5u\sin \left(2{\theta }_x\right){\sin }^2\left({\theta }_z\right))]-3BB{w}_i\rho v,\end{array}\hfill \\ \hfill F_x& \hfill =\hfill & 3w_{i}A\rho [-\sin \left({\theta }_x\right)(-v{\sin }^2\left({\theta }_z\right)\cos \left({\theta }_x\right)+\sin \left({\theta }_x\right)u{\sin }^2\left({\theta }_z\right))\hfill \\ \hfill & \hfill & -\left(u{\cos }^2\left({\theta }_z\right)+w\cos \left({\theta }_x\right)\left(\frac{1}{2}\right)\sin \left(2{\theta }_z\right)\right)]-BB\left(3\right)\rho w_{i}u,\hfill \\ \hfill F_z& \hfill =\hfill & 3w_i\rho [A\cos \left({\theta }_x\right)\left(-\cos \left({\theta }_x\right){\sin }^2\left({\theta }_z\right)w+\left(\frac{u}{2}\right)\cos \left(2{\theta }_z\right)\right)\hfill \\ \hfill & \hfill & +\sin \left({\theta }_x\right)A\left(-\sin \left({\theta }_x\right){\sin }^2\left({\theta }_z\right)w+\sin \left(2{\theta }_z\right)\frac{v}{2}\right)+\beta \left(T-T_m\right)g_z]-BB\left(3w_i\right)w\rho ,\hfill \\ \hfill Ha& \hfill =\hfill & L{B}_0\sqrt{\frac{\sigma }{\mu }},A=H{a}^2\mu L^{-2},\hfill \\ \hfill Da& \hfill =\hfill & \frac{K}{L^2},BB=\frac{\upsilon }{Da{L}^2}\hfill \end{array}$$ 7

To calculate scholars we have:

$$\begin{array}{l}\mathrm{Flow}\mathrm{density}:\rho =\sum _i{f}_i,\\ \mathrm{Momentum}:\rho \mathrm{u}=\sum _i{\mathrm{c}}_i{f}_i,\\ \mathrm{Temperature}:T=\sum _i{g}_i.\end{array}$$ 8

Working fluid

Density, (ρβ)_nf, (ρC_p)_nf, σ_nf, μ_nf and k_nf are (³⁹):

$$\frac{{\rho }_{nf}}{{\rho }_f}=-\phi +\frac{{\rho }_s}{{\rho }_f}\phi +1,$$ 9

$${\left(\rho \beta \right)}_{nf}=\phi {\left(\rho \beta \right)}_s+(1-\phi ){\left(\rho \beta \right)}_f$$ 10

$${\left(\rho C_p\right)}_{nf}/{\left(\rho C_p\right)}_f=-\phi +1+{\left(\rho C_p\right)}_s/{\left(\rho C_p\right)}_f\phi$$ 11

$$\frac{{\sigma }_{nf}}{{\sigma }_f}=1+{\left(\frac{\left(\mathrm{\Delta }+2\right)-\phi \left(\mathrm{\Delta }-1\right)}{3\phi \left(-1+\mathrm{\Delta }\right)}\right)}^{-1},\mathrm{\Delta }={\sigma }_s/{\sigma }_f$$ 12

$${\mu }_{nf}=\frac{{\mu }_f}{{\left(1-\phi \right)}^{2.5}}+\frac{{\mu }_f}{\mathrm{Pr}}\frac{k_{Brownian}}{k_f}$$ 13

$$\begin{array}{l}\frac{k_{nf}}{k_f}=1+5\times {10}^{4}g\prime (\phi ,T,d_p)\phi {\rho }_f{c}_{p,f}\sqrt{\frac{{\kappa }_{b}T}{d_p{\rho }_p}}+\frac{3\left(-1+\frac{k_p}{k_f}\right)\phi }{\left(\frac{k_p}{k_f}+2\right)-\left(\frac{k_p}{k_f}-1\right)\phi },\\ R_f=4\times {10}^{-8}k{m}^2/W,R_f=-d_p(1/k_p-1/k_{p,eff}),\\ g\prime \left(\phi ,d_p,T\right)=Ln\left(T\right)\left(a_1+a_{3}Ln\left(\phi \right)+Ln{\left(d_p\right)}^2{a}_5+a_{2}Ln\left(d_p\right)+a_{4}Ln\left(d_p\right)Ln\left(\phi \right)\right)\\ +\left(a_{8}Ln\left(\phi \right)+Ln\left(d_p\right)a_7+a_6+a_{10}Ln{\left(d_p\right)}^2+Ln\left(d_p\right)a_{9}Ln\left(\phi \right)\right)\end{array}$$ 14

Tables 1 and 2³⁹ can be used to find needed parameters. Nu_ave and Nu_loc over the hot surface are:

$$N{u}_{loc}=-\frac{k_{nf}}{k_f}{\frac{\partial T}{\partial X}|}_{X=0}\mathrm{and}N{u}_{ave}={\int }_0^1{\int }_0^{1}NudYdZ$$ 15

Table 1.

Properties of Water, Al₂O₃.

	σ(Ω · m)−1	k(W/m.k)	Cp(j/kgk)	ρ(kg/m3)
Pure water	0.05	0.613	4179	997.1
Al2O3	10−12	25	765	3970

Table 2.

Related coefficient for alumina.

Coefficient values	Al2O3−Water
a6	−298.19819084
a7	−34.532716906
a8	−3.9225289283
a9	−0.2354329626
a10	−0.999063481
a1	52.813488759
a2	6.115637295
a3	0.6955745084
a4	4.174555527E-02

The fluid kinetic energy is:

$$E_c=0.5\left[{\left(w\right)}^2+{\left(v\right)}^2+{\left(u\right)}^2\right]$$ 16

Mesh Independency and Validation

No alter should be seen in outputs by changing mesh sizes. So, various sizes must be employed. As an example, we presented Table 3. Figure 3 illustrates the agreement of Lattice Boltzmann Method (LBM)^40,41. Also, previous paper⁴² indicates that this code is verified for MHD flow.

Table 3.

Nu_ave over the hot surface with various grid sixes when Da = 100, ϕ = 0.04, Ra = 10⁵, and Ha = 60.

Mesh size	51 × 51 × 51	61 × 61 × 61	71 × 71 × 71	81 × 81 × 81	91 × 91 × 91
Nuave	0.13622	0.14805	0.15061	0.15073	0.15097

Figure 3.

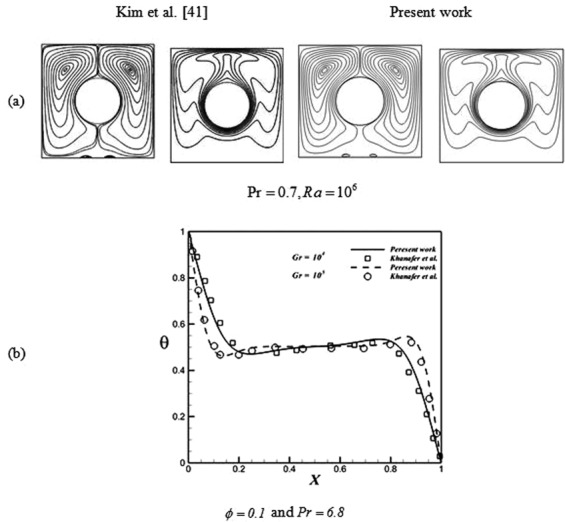
Verification of current LBM code for (a) free convention⁴⁰; (b) nanofluid flow⁴¹.

Results and Discussion

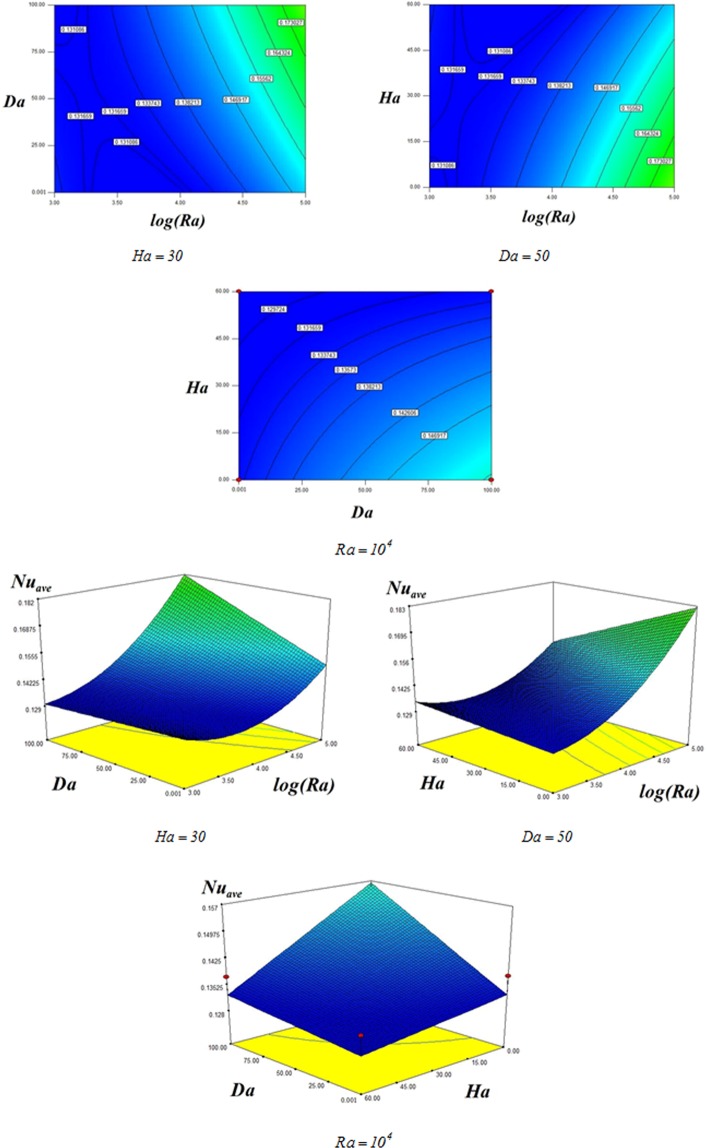
Water-Aluminum oxide mixture hydrothermal behavior in a permeable three dimensional domain was modeled with mesoscopic method. Numerical outputs are depicted the variations of magnetic force (Ha = 0 to 60), buoyancy term ($Ra={10}^3,{10}^4$ and 10⁵) and Darcy number (Da = 0.001 to 100).

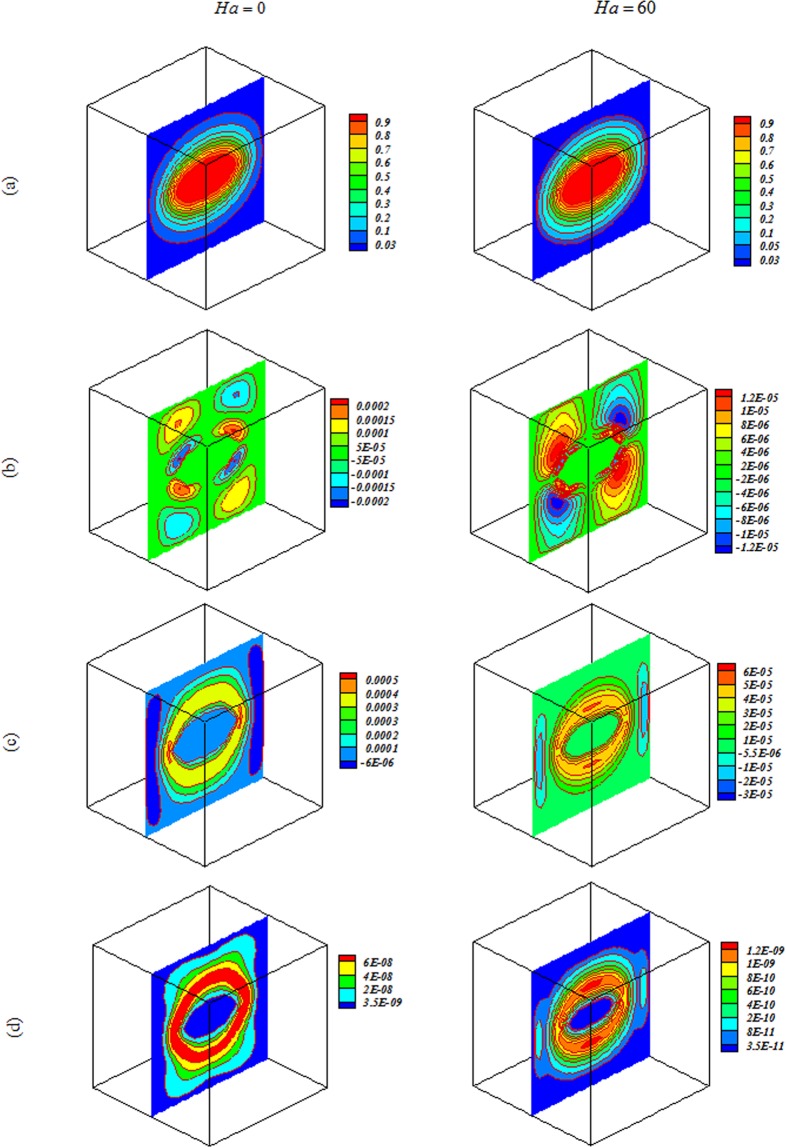
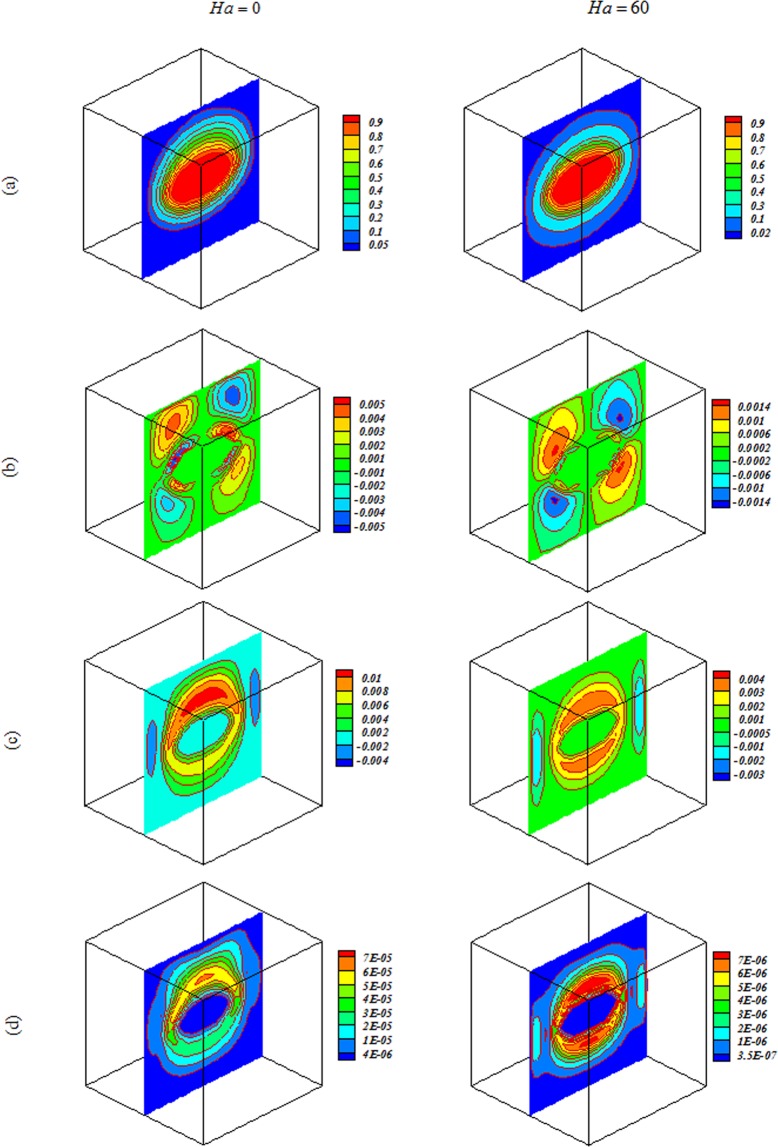
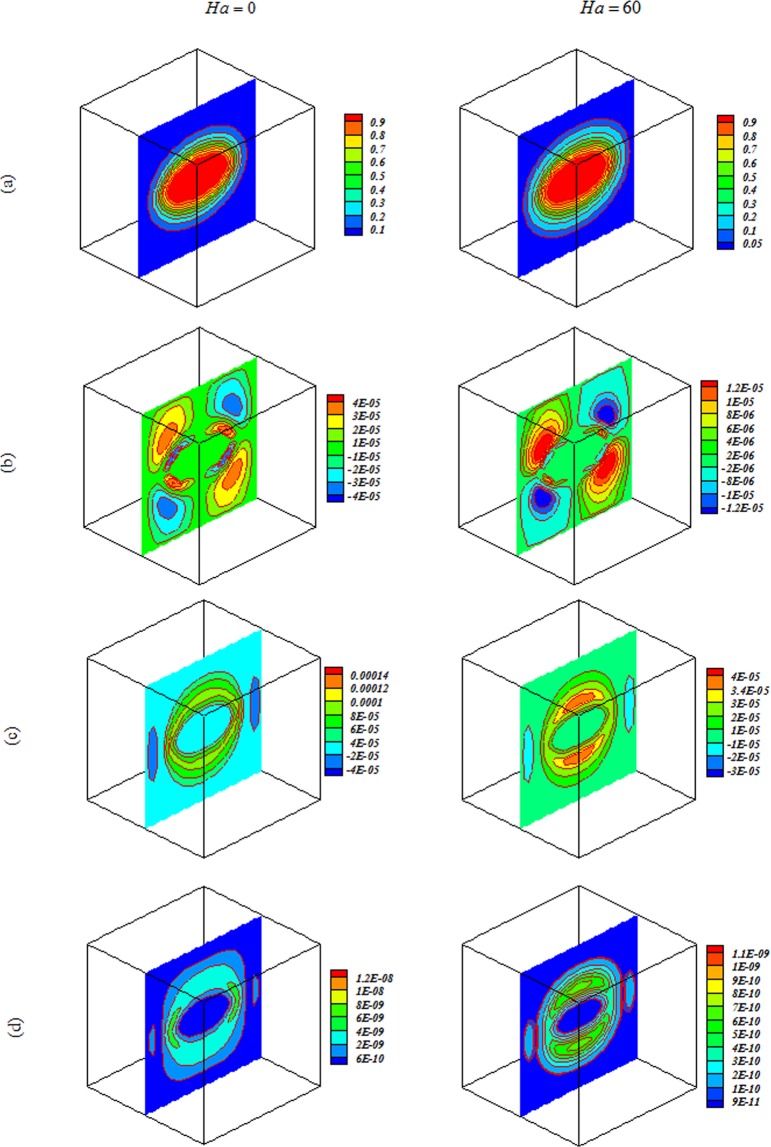
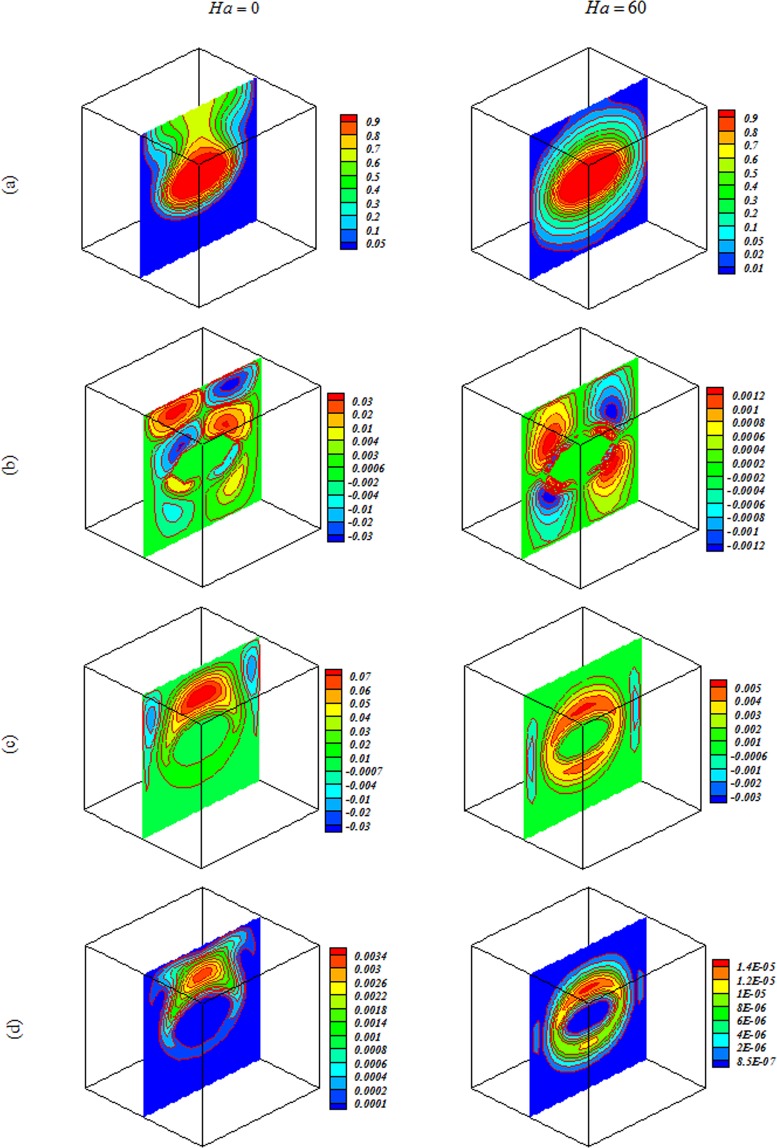
Nanofluid behavior with change of $Ra,Ha$ and Da are displayed in Figs 4–7. In cases with low $Ra$ and Da, convection mode is not strong enough to change flow style and isotherms has shape of geometry. Convection enhancements with increase of permeability and isotherms convert to complex shape. Thermal plume appears as a result of strong convection mode. Employing magnetic forces makes conduction to be more sensible and thermal plumes vanish. Due to reduction effect of Ha on velocity, E_c detracts with rise of Ha. By augment of buoyancy force, main vortex stretch in z direction and convection mode rises.

Figure 5.

Impacts of magnetic forces on (a) isotherm, (b) x velocity, (c) z velocity, (d) isokinetic energy at Y = y/L = 0.5 when Ra = 10³, Da = 100, ϕ = 0.04.

Figure 6.

Impacts of magnetic forces on (a) isotherm, (b) x velocity, (c) z velocity, (d) isokinetic energy at Y = y/L = 0.5 when Ra = 10⁵, Da = 0.001, ϕ = 0.04.

Figure 4.

Impacts of magnetic forces on (a) isotherm, (b) x velocity, (c) z velocity, (d) isokinetic energy at Y = y/L = 0.5 when ϕ = 0.04, Da = 0.001, Ra = 10³.

Figure 7.

Impacts of magnetic forces on (a) isotherm, (b) x velocity, (c) z velocity, (d) isokinetic energy at Y = y/L = 0.5 when Ra = 10⁵, Da = 100, ϕ = 0.04.

Changes in Nu_ave due to altering variables are illustrated in Fig. 8. Equation (17) is extracted for Nu_ave:

$$N{u}_{ave}=0.14+0.017\log \left(Ra\right)+6.8\times {10}^{-3}Da-7.2\times {10}^{-3}Ha+9\times {10}^{-3}\left(\log \left(Ra\right)\right)\left(Da\right)-9\times {10}^{-3}\left(\log \left(Ra\right)\right)\left(Ha\right)-4.7\times {10}^{-3}\left(Da\right)\left(Ha\right)+0.012{\left(\log \left(Ra\right)\right)}^2.$$ 17

Figure 8.

Various values of Nu_ave for different Ra, Da, Ha.

Due to augment in temperature gradient with rise of permeability and buoyancy terms, Nu_ave is enhancing function of $Da,Ra$. Furthermore, conduction mode boosts with augment of Hartmann number. Thus, Nu_ave detracts with rise of magnetic force.

Conclusions

In the current article, uniform magnetic force impacts on momentum equations were considered in a 3D porous enclosure. Mesoscopic approach was applied to analyze alumina nanofluid in these conditions. Brownian motion impact can changes the properties of working fluid. LBM was involved to report the impacts of Ha, Ra, Da on nanofluid behavior. Outcomes display that interaction of nanoparticles augments with augment of Da,Ra. Isotherms become less complex with applying magnetic force.

Author Contributions

M.I. and Z.S. modeled and solved the problem and wrote the manuscript. I.K. and A. Sh. thoroughly checked the mathematical modeling and English corrections. Z.S. contributed in the results and discussions. All the corresponding authors finalized the manuscript after its internal evaluation.

Competing Interests

The authors declare no competing interests.