Advances in Computational Human Phantoms and Their Applications in Biomedical Engineering – A Topical Review

Abstract

Over the past decades, significant improvements have been made in the field of computational human phantoms (CHPs) and their applications in biomedical engineering. Their sophistication has dramatically increased. The very first CHPs were composed of simple geometric volumes, e.g., cylinders and spheres, while current CHPs have a high resolution, cover a substantial range of the patient population, have high anatomical accuracy, are poseable, morphable, and are augmented with various details to perform functionalized computations. Advances in imaging techniques and semi-automated segmentation tools allow fast and personalized development of CHPs. These advances open the door to quickly develop personalized CHPs, inherently including the disease of the patient. Because many of these CHPs are increasingly providing data for regulatory submissions of various medical devices, the validity, anatomical accuracy, and availability to cover the entire patient population is of utmost importance. The article is organized into two main sections: the first section reviews the different modeling techniques used to create CHPs, whereas the second section discusses various applications of CHPs in biomedical engineering. Each topic gives an overview, a brief history, recent developments, and an outlook into the future.

I. Modeling techniques for realistic computational human phantoms (CHPs) as applied in biomedical engineering

Over the last 50 years, many computational human phantoms (CHPs) have been developed across different research communities for a variety of applications. The following section discusses various methods to create CHPs, the verification, validation, and quality assurance techniques involved with these phantoms, the modeling of tissue properties, and a survey of libraries of models currently available.

A. Advanced Phantom Geometries

The construction of a CHP must consider multiple factors such as anatomy, tissue properties, computational efficiency, and geometrical compatibility with simulation codes, e.g., Monte Carlo (MC) or analytical. As a first step, a phantom must be generated by explicitly defining the surfaces and tissue properties of the necessary tissues in which interactions occur. For defining the tissue surfaces two general modeling methods from the computer graphics community have been widely used: i) constructive solid geometry (CSG) and ii) boundary representation (BREP) [1] [2] [3]. The following sections review these two established methods and three additional evolving methods.

1). Constructive solid geometry (mathematical and voxelized) phantoms:

CSG allows the modeler to create a solid geometric object utilizing simple shapes, called primitives. Examples of these primitives include cuboids, cylinders, prisms, pyramids, spheres, cones and ellipsoids—surfaces that are easily described by quadratic equations. Overlap, cut planes, and intersections of the geometric objects can be used to construct organs.

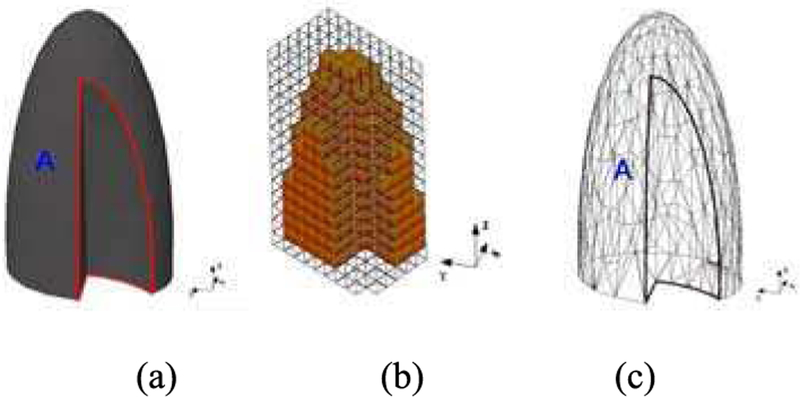
As an example, the left lung can be represented in the CSG method by “half an ellipsoid with a section removed” [4]. The cut-out section can be defined by a Boolean operation subtracting one ellipsoid from the other, see Figure 1 (a) [5] [6]. These surface equations used in the CSG method are computationally efficient and compatible by nearly all MC radiation transport simulation codes. Even with complicated and carefully designed Boolean operations, phantoms based on quadratic equations have limited anatomical accuracy.

Fig. 1.

A model of the left lung defined by different modeling methods; (a) The CSG-type modeling after the Boolean operation (subtraction) is performed involving two ellipsoids; (b) A voxel representation of the lung; (c) A BREP-type of modeling of the same lung using a polygon mesh [5] [6].

Voxels have also been used as a CSG modeling technique. Figure 1 (b) shows an example where the left lung is defined as an assembly of 3D cuboids or voxels. Medical image data, e.g., Computed Tomography (CT) images, can be converted to a voxel-based geometry that provides a direct way of realistically describing the human anatomy [5] [6]. This can be done by segmenting imaging data and then assigning standard tissue properties to the segmented objects, see Section I.B.3. Automatic methods have also been investigated to directly convert image values (CT numbers for example) into tissue properties for a voxel-based phantom [7]. The geometry of a voxel is very easy for existing simulation codes to handle. However, the boundary of a voxel object is defined by a stair-stepped surface instead of a smooth surface, as shown in Figure 1 (b). Thus, the anatomical fidelity depends on the voxel size, which can be an issue especially for thin and small tissues, e.g., the micrometer-thick radiosensitive target layers of the alimentary and respiratory tract organs. In addition, an adjustment to the organ shape will likely involve all underlying voxels, which is computationally inefficient.

2). Boundary representation BREP (NURBS or mesh) phantoms:

The human anatomy can also be defined by advanced BREP modeling techniques involving non-uniform rational b-spline (NURBS) or polygon mesh surfaces. The most common technique to create a BREP-based phantom involves the surface contour extraction of each organ from a tomographic image dataset. NURBS are lofted through the contours defined for each structure creating smooth, continuous surfaces. The individual surfaces for the tissues are then integrated into a whole-body assembly. In essence, the contours convert the voxels into NURBS that are smooth and anatomically realistic. These phantoms are commonly referred to as “NURBS,” “mesh”, or “BREP” phantoms. Figure 1 (c) shows the triangular mesh of a left lung, derived from high-resolution tomographic images [5] [6].

In BREP-based design, the exterior of an object can be defined as NURBS, which offer very smooth surfaces. These surfaces can alternatively be represented as polygons whose vertices are defined by a set of coordinate values x, y, and z. In principle, NURBS and polygon meshes are interchangeable BREP data structures. Unlike the CSG representation, BREP is much more flexible because a richer set of operation tools are available, e.g., extrusion, chamfering, blending, drafting, shelling, and tweaking. These features allow BREP-based models to include very complex anatomical features. Furthermore, the BREP technique is ideally suited for surface deformation. NURBS and polygon meshes can be altered easily by applying transformations (rigid or non-rigid) to the surface or vertex points. Such flexibility is necessary for the adjustment of organ size, for organ motion simulations, and for changing the posture of phantoms.

3). Morphing and posing techniques:

A range of applications require CHPs with different characteristics, such as posture, height, weight, body-mass-index (BMI), or organ volume and shape. Unfortunately, significant effort is required to create new whole-body models, e.g., 7 years for the Visible Korean male phantom [8]. For this purpose, morphing techniques have been developed, which permit modification of the volume and shape of tissues of existing reference phantoms. Three types of morphing and posing approaches are found in the literature: i) geometrical approaches, ii) physics-based methods, and iii) image registration mapping techniques.

Geometrical methods vary in complexity and anatomical realism, ranging from simple heuristics for scaling and repositioning of individual organs, to computer graphics deformation approaches. Na et al. [9] created 100 adult phantoms based on the Rensselaer Polytechnic Institute (RPI) male and female reference models. Body dimensions and individual organ volumes were deformed to match statistical volumes from the NHANES study [10] using iterative scaling along the tissue surface normal, including collision detection to avoid overlapping tissues. Similar techniques were used to create a library of pediatric models based on reference models from the Virtual Population [11] [12]. Interactive tools to change the posture of anatomical models permit positioning of bones around articulated joints in real-time and interpolate the tissue deformation using techniques such as dual quaternion skinning [13] [14] [15].

A second category includes methods which constrain the morphing by a biomechanical tissue deformation model. In this approach the tissue is modeled as a hyper-elastic material, with soft tissues and stiff bones. Combined with articulated joints, this formulation permits posture changes with realistic deformations. By incorporating a model of tissue growth, analogous to thermal expansion, this approach was used to change the BMI of the Virtual Population [16].

The third group of approaches deforms a template or reference model into a target anatomy using image, or surface, registration. For example, the XCAT models are based on reference anatomies (originally the Visible Human male and female [17]) by performing image registration of the references to CT images of patients [18] [19]. Only few others have worked on personalization of full body models [20] [21]. Several approaches have been presented using mouse image data [22] [23].

4). Organ motion techniques:

In medical imaging, reconstruction algorithms typically assume that everything is static during image acquisition. Patient movements result in image artifacts that can mimic, or mask, disease indicators. Patient motion must also be accounted for in radiation therapy. Motion of the tumor and background tissues need to be assessed in order to best target the tumor while sparing the healthy tissues. With the ability to simulate any number of motion variations, time-changing 4D computational phantoms provide a vital research tool to investigate and understand the effects of motion, and to compensate for them.

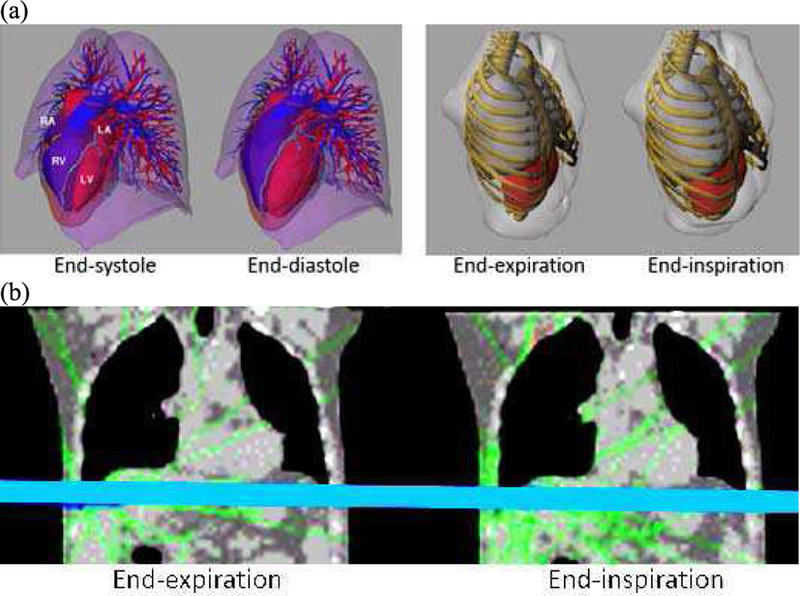
Motion can be simulated by applying transformations (rigid and non-rigid) to the phantom’s anatomical structures. For surface-based phantoms such as the XCAT [17] and the VIP-Man [24], the transformations can be simply applied to the surface or vertex points defining the objects, see Figure 2 (a). For voxelized phantoms, e.g., Han et al. [25], transformations are applied to each individual image voxel and interpolation is used to generate deformed images, see Figure 2 (b).

Fig. 2.

(a) Cardiac and respiratory motion models of the surface-based XCAT (left) and VIP-Man (right) phantoms. Transformations are applied to the surfaces to deform them. (b) 4D voxelized respiratory phantom of Han et al. [25]. Transforms are applied to the individual voxels to deform the image. Full animation of the respiratory motion and deformation can be found elsewhere (http://hurel.hanyang.ac.kr/Phantom/4DVoxel.gif)

Gated patient imaging data, such as CT or Magnetic Resonance Imaging (MRI) has been typically used to define the time-changing transformations for the organs and structures allowing a model to realistically simulate motion. However, only one realization of the motion is captured, specifically that derived from the imaging data. To simulate variations in a given motion, parameters can be setup to alter the deformations of the surfaces, but these alterations lack a physiological basis [17].

Finite element (FE) techniques, e.g., Eom et al. [26] and Segars et al. [27], are currently being investigated to create more robust and flexible models for patient motions. FE methods simulate the physiological and physical interactions of the tissues on multiple scales from the cell to the organ. Many different parameters can be altered in a realistic, physiologically based manner, to realistically simulate normal and abnormal variations in motion.

5). Direct use of mesh phantoms in Monte Carlo simulation:

Although providing significant advantages over the stylized and voxel phantoms, BREP-based phantoms suffer from a technical issue: the compatibility with MC particle transport codes. NURBS phantoms cannot be directly used in MC codes because implementing ray-tracing functions for particle transport in NURBS geometry is technically very challenging, requiring highly complex and time-consuming algebraic calculations. Therefore, the NURBS phantoms need to be converted to voxel phantoms, via a so-called “voxelization” process. The resulting voxel phantoms cannot preserve thin or small tissues, such as the skin target layer (~50 μm), the detailed eye structure, and the micrometer-thick radiosensitive target layers of the alimentary and respiratory tract organs.

The issue has been addressed at least for polygon mesh phantoms. A polygon mesh phantom, called the PSRK-Man, has been successfully implemented, without voxelization, in the Geant4 code using the G4Tessellated Solid class, which was originally designed for importing computer-aided design (CAD) models [28]. The implementation was possible because the phantom is composed of perfect meshes of organs and tissues, i.e., without abnormal facets. It was then found that the polygon mesh phantom was significantly slower (e.g., 70–150 times slower for photons) in transporting particles than its counterpart voxel phantom, i.e., the HDRK-Man.

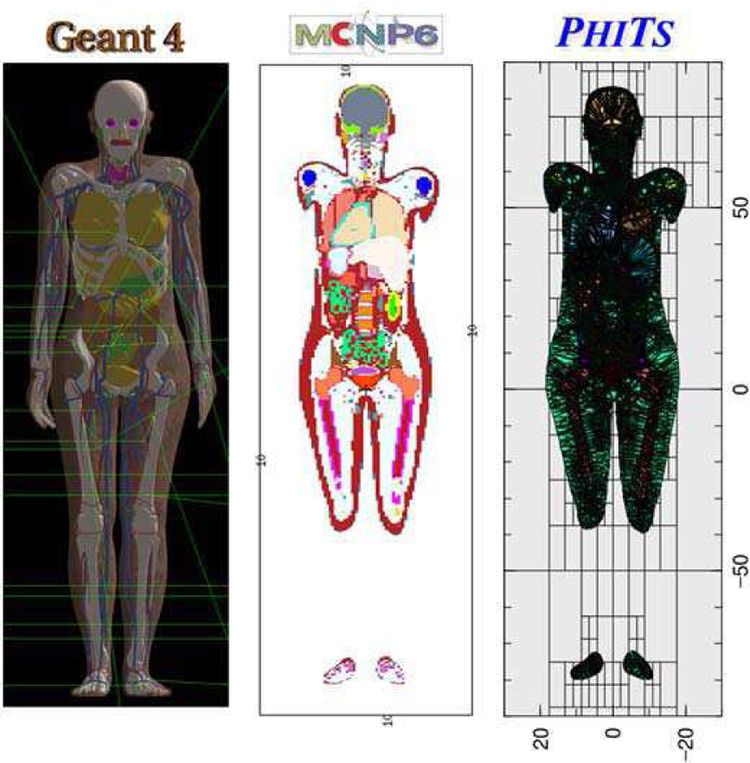
The issue of the slow computational speed was then overcome by converting the geometry format into a tetrahedral mesh (TM), and implementing the TM phantom in the Geant4 code using the G4Tet class, resulting in a 2 to 3 order of magnitude increase in computational speed depending on particles and energies [29]. This improvement in computational speed is mainly due to the large number of facets to be checked by the computionally expensive ray-tracing functions in the polygon mesh, reducing the TM geometry to just four facets. Acknowledging both the limitations of the voxel geometry and the advantages of the TM geometry, the International Commission on Radiological Protection (ICRP) recently decided to convert the voxel-type reference CHPs [30] into the TM format. The adult male and female phantoms, called MRCPs (Mesh-type Reference Computational Phantoms), have been completed and tested with the Geant4, MCNP6, and PHITS codes [31] for initialization time, computation speed, and memory requirements as shown in Figure 3.

Fig. 3.

The adult female mesh-type reference CHP implemented in Geant4 (left), MCNP6 (middle) and PHITS (right).

Note that the MCNP6 code, i.e., merger of MCNP5 and MCNPX, provides a new features: i) the EMBED card, for importing an unstructured mesh geometry (e.g., TM geometry) and ii) the PHITS code providing a new option in the LATTICE card for importing the TM geometry.

The result of computational speed shows that the male TM phantom on the PHITS code was 2–3 times faster than the male voxel-type reference CHP on the PHITS code for all particles (photons, electrons, and helium ions) and energies considered. This result implies that, if ICRP keeps using the PHITS code for most dose coefficient calculations, the use of the new TM phantoms will even improve the computational speed of dose coefficients. The TM phantom on the Geant4 code was even faster than the voxel phantom on the PHITS code for photons and electrons, by up to 20 times. However, the TM phantom on the MCNP6 code was slower than the voxel phantom on the PHITS code by up to 20 times.

The spatial variation of tissue composition and mass density in a tissue cannot be modeled in a BREP-based phantom, because BREP meshes define only the boundary of a tissue. The tissues in a BREP-based phantom are therefore all internally uniform. On the other hand, the composition and density variation in a tissue can be defined in a TM phantom using the volumetric 3D structure of the tetrahedral mesh [32]. The organs and tissues of the TM phantom can also be continuously moved or deformed during a MC simulation, leading to more realistic 4D MC simulations.

B. Numerical aspects, verification, and validation (V&V)

1). Verification, validation, and quality assurance:

Credibility assessment of simulations include verification and validation (V&V), among other aspects such as applicability analysis [33] and quality assurance (QA). Verification, simply put, asks the question, “did you implement the computational model correctly/as intended?”; whereas validation asks, “did you implement the correct computational model?” The objective of verification, as defined by the ASME V&V40 subcommittee [34], is to ensure that the computational model is implemented correctly and then accurately solved. The objective of validation is to assess the accuracy of the prediction as compared to real world experimental data. Important factors to consider include the assessment of the model form, model inputs, along with assessing the experimental comparator, which includes test conditions and test samples. The assessment of the model prediction accuracy lies in the nature of the comparison between the output from the model and the output from the experimental comparator, and the identification and quantification of the uncertainties related to both. Lastly, the relevance and “goodness” of the validation outcome is judged based on the context-of-use of the computational model, i.e., the scope and role of the computational model for decision making or answering a question of interest, and is tied to the relevant real-world behavior of quantities-of-interest. Hence, while a computational model can be considered universally verified, CHPs can typically only be considered sufficiently validated with regard to certain given context-of-uses.

V&V of CHPs may be performed as a standalone activity when not used in simulations. However, the definitive V&V of CHPs will occur alongside the simulation and in the context of an application, mainly as part of the assessment of model form and model inputs, e.g., anatomical geometries, tissue properties, and solution verification, e.g., discretization errors. This section will discuss the concepts of V&V in the context of CHPs. Simulation V&V is outside the scope of this paper.

a). Verification:

Verification in the context of CHPs covers the process of model generation, the involved tools, and the obtained models. An example of the first is the assessment of the image segmentation quality and processes by anatomical experts, as documented, e.g., in the quality assurance report [35]. Examples of model generation tool verification include: i) assessing the fidelity of extracted surfaces to the original segmentation or the distance between initially extracted surfaces and simplified surfaces [12], ii) ascertaining the fidelity and accuracy of the process of morphing an existing CHP to match specific medical image data [36] [37], e.g., in the process of building model populations or personalized models, and iii) investigating the reproducibility of performing a certain segmentation task across tools and operators, e.g., in a round-robin [38] [39]. Verification of the generated CHP can again include a realism assessment by experts, comparison of organ volumes, weights, and morphological descriptors with corresponding (statistical) information, e.g., from literature [18], and ascertaining of formal and numerical model correctness (respecting formats, watertight surfaces, etc.; see I.B.2) “Numerical/implementation considerations” and the study of Gosslin et al. [12]. Some of the latter aspects can be automatized and/or integrated as part of the QA process. The verification of the involved steps and tools should be based on identified relevant features that need to be reproduced with sufficient fidelity, as dictated by the context-of-use for the CHP.

b). Validation:

The assessment of the validation outcome is necessarily application specific and cannot be performed once in a general manner for all possible applications of the CHP. In fact, the suitability of CHPs is also application related. For example, a CHP suitable for traditional ionizing or non-ionizing electromagnetic (EM) radiation dosimetry does not necessarily make them suitable for, e.g., biomechanics applications, where information about tissue interfaces (sliding vs. connected) and detailed tendon and ligament representations are required, or for ultrasound modeling, where bone heterogeneity representation is crucial. Even for EM dosimetry applications at 5G frequencies, where skin layers become important and need to be correctly represented, typical dosimetric CHPs with simple skin representations might not be suitable. In some cases, the applicability range of CHP can be extended by complementing them with additional information, such as image-based tissue heterogeneity maps, e.g., the Diffusion Tensor Imaging (DTI)-based anisotropic conductivity maps co-registered to the MIDA model [40], or high resolution sub-region models.

Validation by comparison of measurements obtained using an experimental setup representing the use-case measurements with simulation predictions is a compromise between being as close as possible to the real application and context-of-use (to reduce the necessary leap-of-faith and safety margin), and offering optimal experimental control, validation sensitivity, and data richness, at an affordable effort/cost. Validation should be – according to some experts: must be – complemented by an uncertainty assessment, to ascertain the strength of the validation and to judge the agreement between measurement and predictions. For a strong validation, the agreement-success of the chosen experiment must depend on, and hence tests, the model correctness in a highly sensitive manner. The ASME V&V 40 Committee [34] recommends that the rigor of the validation should be commensurate to the risk associated with the context-of-use of the simulation. The risk is a combination of the severity of the consequences from, for example, making an incorrect decision, and the influence the simulation results have on the decision. Another approach to judge the necessary validation rigor is to assess the safety margin between the model-predicted exposure, the danger thresholds, and to demand that the validation be sufficiently robust to keep the confidence interval associated with the model well below that safety margin [41]. Uncertainty assessment should consider relevant factors such as numerical modeling uncertainty, population/inter-person variability, tissue property variability and uncertainty. For many applications involving the human body, the uncertainty about the underlying model equations is also essential, e.g., how well does the commonly applied Pennes Bioheat Equation (PBE) [42] represent the thermal impact of tissue perfusion and blood flow, even if the parameters were perfectly known. To judge the validation success, the measurement uncertainty typically also needs to be included.

As the purpose of CHPs is to represent the anatomy, validation of the CHP generally necessitates experiments including humans. For example, while experiments on a physical phantom may provide validation evidence for a computational model of dosimetric applications – including simulations that involve a CHP –, they cannot be considered a validation of the CHP for dosimetric modeling. The need to involve human anatomies in CHP validation experiments limits the (ethical) ability to perform such experiments and/or restricts measurement access. An example of experimental validation of CHPs in the context of MRI radiofrequency (RF)-exposure related tissue heating assessment for safety purposes can be found in [43], which also includes a systematic modeling- and validation-uncertainty assessment. In this case, non-invasive means, e.g., surface temperature and MRI-based in vivo magnetic field measurements, have been used. Therapeutic applications, such as hyperthermic oncology, which modeling-wise, is similar to the MRI exposure safety case, can justify more comprehensive, invasive validation measurements [44]. Alternatively, cadaver or animal experiments can be used to validate CHPs, or at least the approach of CHP generation. Recent advances in imaging, e.g., MRI thermometry, increasingly permit extensive and non-invasive data in vivo collection, and, hence, richer and more reliable CHP validation.

When creating an entire population of CHPs, validation should also ascertain proper coverage, and statistical representation, of the targeted population. This can involve statistics about the variability of features and comparison with corresponding statistics of the model population, [18] [45] [46], potentially considering correlations.

Validation should not be limited to the CHP, but also encompass associated tools. For example, for a tool to parameterize the BMI or fitness of a CHP by growing or shrinking fat or muscle tissues must be validated.

The issue of validation is also related to the question of CHP detailedness. In various applications, stylized models are in use [47]. However, it typically comes at the cost of increased CHP uncertainty intervals, and hence can result in the necessity for larger safety margins. Once these safety margins have been determined, typically using more detailed and realistic CHPs, they can be factored into safety guidelines and standards, and stylized models can then be used for compliance testing or similar purposes.

c). Quality assurance (QA):

Complementing the CHP generation process with QA procedures, further increases the trustworthiness of the models. Standardized, and ideally automatized, QA procedures can include: (i) following standardized segmentation protocols, (ii) directives about the tissues to be distinguished and how to deal with ambiguities, (iii) examination by an independent expert, (iv) assessment of realistic organ/tissue weights and morphologies, (v) checking for unwanted intersections (overlaps) between tissue surfaces, self-intersecting surfaces, holes, or inverted elements (wrong vertex ordering), etc. [12] [35].

2). Numerical/implementation considerations:

In addition to V&V and QA, numerical aspects play an important role in CHP usability and applicability. To increase CHP usability and applicability for simulations, open data formats and compatibility with major software packages are beneficial. For example [28] and [48] make phantoms available in the simple and open surface mesh file format stl(from Stereolithography).

Different considerations apply, depending on whether the region definitions in the model are explicit, e.g., a triangle mesh, or implicit, e.g., based on constructive geometry. To avoid placing a heavy pre-processing burden on users, the following should be considered: all surfaces should be self-intersection free. For models that are to be voxelized, i.e., discretization using a rectilinear, sometimes homogeneous, grid, it is frequently enough to ascertain, “water-tight” surfaces. When unstructured, e.g., tetrahedral, meshing is required, the demands on the model increase considerably: It is very helpful, if the model features compatible (shared) interfaces, if there are no small gaps of thin filling material layers, and if surface elements are of high quality, i.e., no degenerated, or sliver-like triangles. As the complexity of detailed anatomical models frequently challenges unstructured meshers, it can also be helpful to have multiple versions of the models with varying complexity scales available, such as the V2 models of the Virtual Population [48].

A fundamental aspect relating to modeling the human anatomy using a CHP is to be conscious of common CHP approaches simplifing the anatomy by representing it as homogeneous, neatly delimited regions, when in reality tissue can be heterogeneous, and interfaces can be continuous. To a certain degree, this can be amended by using tissue property maps rather than tissue-specific values during simulations. Furthermore, any CHP involving a segmentation that implies one (or multiple) scale(s) and resolution(s) – typically on an organ/tissue level, while the human body involves a large range of scales, such as the cellular scale.

Part of careful computational modeling is the assessment of solution convergence and mesh independence by performing mesh refinement studies. However, unrealistic tissue/organ surfaces, e.g., stair-cased, or non-smooth, or too smooth, can converge to a mesh independent solution that is still unrealistic. This occurs particularly when surface effects, e.g., convective surface cooling, or small geometric features are important. The effect is partly related to the model-inherent scale choice and partly a result of the selected model generation procedure. Offering multiple model versions with varying detailedness, as well as employing surface descriptions that permit flexible discretization at varying resolution, can help control the impact of surface discretization.

3). Tissue properties:

Predictive simulations of physical (and physiological) interactions with the human body can be achieved only with accurate knowledge of the underlying tissue properties. This section gives an overview of organ and tissue material parameters used in different applications of CHPs, grouped by physics.

The applications driving the development of CHPs include non-ionizing EM [49]and acoustic radiation [50], both of which lead to tissue heating [43], as well as ionizing radiation studies [51]. Mechanical tissue properties have been studied extensively, and have been used in conjunction with car crash simulations [52] and other application areas, such as bone fracture risk analysis, and cerebrospinal fluid modeling.

As described in Section I.A, CHPs are 3D representations (voxels or closed surfaces/solids) of the anatomical structures that separate organs and tissues into individual regions, sometimes referred to as “standard tissues” [53] [54]. These tissue regions are implicitly assumed to be similar in structure and composition, with uniform tissue properties. While this assumption is reasonable in many cases, some tissues clearly have inhomogeneous, or even anisotropic properties, as observed for the anisotropic electrical conductivity of muscle tissues and white matter [55] [56].

Unlike engineered materials, biological tissue is a living material with complex responses that, in many cases, obey laws yet unknown. Living tissues undergo constant change, including relatively fast thermoregulation in response to tissue heating, gradual decrease of water content with aging, and disease-related responses. There is natural variability among individuals, which in some cases must be accounted for, e.g., in realistic breast imaging studies, where knowledge of the non-uniform breast density and composition are crucial [57].

All tissue properties have a variety of uncertainties associated with the measurement technique, tissue handling, and the environment conditions (e.g., the temperature). In many cases, tissue property measurements in humans, i.e., in vivo, are not possible, and values are instead estimated from animal experiments or ex vivo. But even when reference measurements for human tissue are available, a certain level of uncertainty remains in regard to the inter-subject variability.

Below we examine the physical tissue properties needed for simulation of physical phenomena in, and around, the human body. Several useful and important resources and databases that provide collections of tissue properties and references are described.

4). Databases of tissue properties:

Tissue properties are usually documented in one of three forms: i) as a list of measured values, ii) as a functional relationship obtained by fitting the measured values, or iii) as relationships to, e.g., the constituents of the tissue, derived on the basis of an underlying theory. One of the broadest attempts to collect tissue properties for different applications was made by Francis Duck [58] ¹, who described tissue properties for mechanics, acoustics, non-ionizing and ionizing radiation, and MRI. The CRC Handbook of Mechanical Engineering [59] lists tissue properties and references for several standard tissues, including density, mechanical, acoustic, and thermal properties. For properties related to ionizing radiation, the ICRP has published authoritative references listing tissue composition (constituent elements) and tissue densities for all major organs and tissues [54].

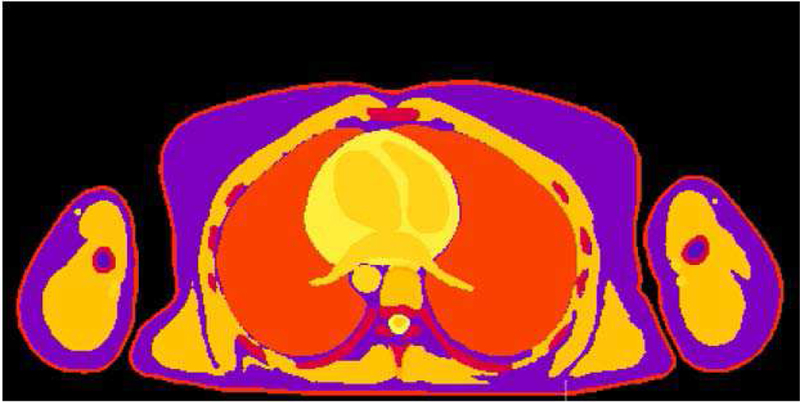
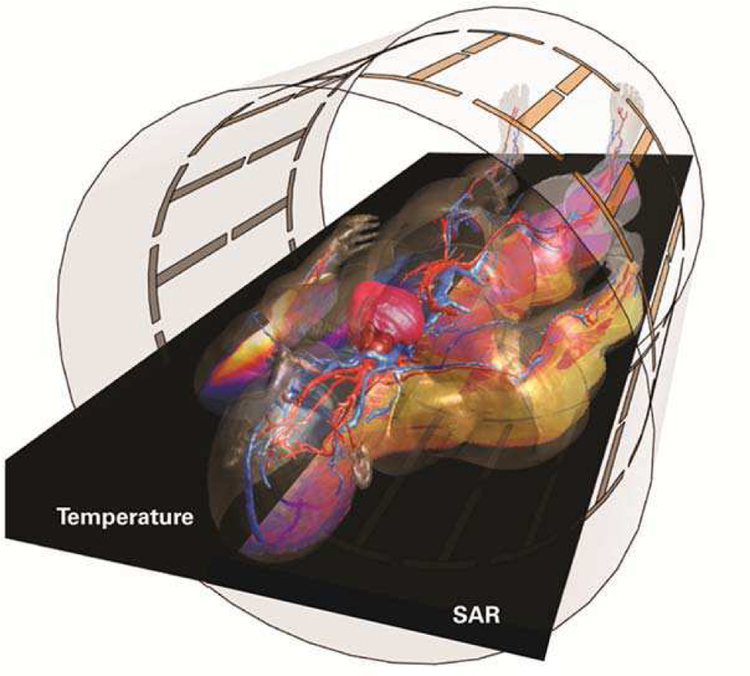
To date, the Foundation for Research on Information Technologies in Society (IT’IS) Tissue Database [60] [61] represents the only continuously updated and curated comprehensive resource. It includes dielectric properties and values of density, heat capacity, thermal conductivity, heat generation rate, transfer (perfusion) rate, low-frequency electrical conductivity (including information about anisotropy in fibrous tissues), viscosity, acoustic propagation, absorption, and magnetic properties (T₁/T₂ relaxation times) for more than 100 biological tissues. Figure 4 shows an example of thermal conductivity values within the body.

Fig. 4.

Thermal conductivity values taken from the IT’IS Tissue Database [61] depicted in a cross-section of a female CHP.

The IT’IS database can be viewed online and downloaded free-of-charge in several human- and machine-readable formats [60]It provides averaged estimates and statistical information about the spread and standard deviation for various thermal, density, perfusion, magnetic properties, acoustic propagation and low-frequency dielectric parameters. For some tissue properties, e.g., perfusion, the variation can be more than an order of magnitude. The number of data points from which the average for a given property and tissue is calculated varies from 1 to 88 and is provided for each tissue property. Where no values for a standard tissue are available, a proxy tissue is proposed based on consideration of the histological, physiological, and biological composition of the tissue.

While the scientific community has already made an effort to quantify tissue properties accurately, various physical properties exhibit substantial gaps. For example, dielectric tissue properties at low and very high frequencies still have large measurement uncertainties.

5). Tissue properties in different physics:

a). Mass density:

The mass density ρ, which is needed for acoustic, mechanical, thermal, EM, and ionizing radiation simulations, is expressed in kg/m³. The density of a tissue can be measured by comparing the mass of a sample in air with the apparent volume displaced in water [58] [62]. A comprehensive and curated collection of tissue mass density values and references can be accessed in the IT’IS Tissue Properties Database[60].

b). Non-ionizing electromagnetic tissue properties:

The dielectric tissue properties from direct current (DC) to 100 GHz are best described by the electrical conductivity σ and the relative permittivity ${\epsilon }_r^{\prime }$ ². The most comprehensive report of measurements of properties for many tissues was performed by Gabriel in 1996 [56] [63]. This data was used to fit a frequency-dependent Cole-Cole model, which remains the de facto standard for frequencies 1 MHz – 1 GHz [64]. Coefficients for the Cole-Cole model [65] and references for evaluating σ and ${\epsilon }_r^{\prime }$ of certain tissues are available as an online resource: i) IFAC-CNR [66] and ii) the IT’IS Tissue Database [61].

For frequencies <1 MHz, the measurement technique used by Gabriel is known to be less accurate. While other measurements have been performed, low-frequency values are sparse and less reliable with larger uncertainties. Tissue anisotropy at low frequencies further complicates accurate measurement and assignment of tissue conductivity. Realistic anisotropic conductivity distributions can be inferred from DTI and should be included in the CHP, as for, e.g., the MIDA head phantom [40].

At high frequencies, the EM field penetrates only to a narrow region below the body surface. Accordingly, at these frequencies, the skin composition plays a more important role [67] [68].

c). Thermal tissue properties:

Heat transfer in biological tissues is usually modeled with the PBE [42], which describes diffusive heat conduction within a tissue and the magnitude of heat transfer between tissue and blood:

$$\rho C_t\frac{\partial T}{\partial t}=k{\nabla }^{2}T+Q+W{C}_b\left(T-T_a\right)+M$$ (1)

The thermal conductivity k quantifies the ability of a material to conduct heat. The specific heat capacity C is the amount of heat required to raise the temperature of a tissue by one Kelvin. Other important properties include the blood-perfusion heat-transfer rate and metabolic heat generation rate M. Non-metabolic heat generation sources Q used in various applications of CHPs include absorbed power from EM radiation to, e.g., investigate tissue heating for mobile phone users and MRI implant safety. Tables with reference values for various thermal tissues properties are available in, e.g., the CRC Handbook of Mech. Eng. 2^nd Ed. [59] or the IT’IS Tissue Database [60].

While the PBE is clearly most widely applied, it suffers from a range of known limitations, such as insufficient consideration of larger vessels; absence of whole-body thermoregulation and local thermoregulation; absence of tissue anisotropy and inhomogeneity; body-core heating; spatial variability of arterial blood temperature; and tissue damage-related property changes, to name a few. A range of extended or alternative models have been proposed [69] [70] to increase realism or extend the application range. Many of these models, however, require a large number of additional parameters that are rarely available or highly variable.

d). Acoustic tissue properties:

Acoustic modeling of wave propagation in biological tissues is described by the density and speed of sound c in the medium and the attenuation of acoustic energy. The absorption coefficient is frequency-dependent and can be modeled with the non-linear relationship:

$$\alpha ={\alpha }_0{f}^b$$ (2)

where a₀ is a medium constant and b is a non-linearity parameter. Data on non-linearity is sparse and has been reported for only a subset of standard tissues. Kyriakou suggests that, apart from bone characteristics, acoustic tissue properties of human tissues are poorly quantified in the literature [71]. Imaging techniques are more promising and allow acoustic properties to be mapped at high resolution with, e.g., empirical relationships between CT intensity values measured in Hounsfield units and the speed of sound, the density, and the non-linearity parameter [72] [73].

e). Other tissue properties:

In contrast to thermal and EM field modeling, ionizing radiation tissue properties are commonly expressed in terms of the elemental composition of the tissues [74]. For a mixture, such as biological tissue, the behavior of photons in the higher EM spectrum (x-ray and gamma radiation) traversing through the medium is described by the mass attenuation coefficient μ, which can be approximated closely with the density and mass attenuation coefficients of the constituent elements:

$$\frac{\mu }{\rho }=\sum _i{\omega }_i\frac{{\mu }_i}{{\rho }_i}$$ (3)

where w_i is the proportion of the element by weight. Therefore, the mass attenuation of a specific tissue can be computed as a function of the weight proportion of its constituents.

Computed mass attenuation coefficients for various tissues can be found in [58]. Tables listing the composition and relevant parameters for different standard tissues are published in reports and guidance documents by the ICRP [54].

Tissues exhibit a complex range of mechanical behaviors, including non-linear, anisotropic, viscoelastic, and, in some cases, also viscoplastic behavior. A detailed discussion of mechanical properties is beyond the scope of this article, and we refer to other references [59] [75]. Imaging techniques for measuring elastic tissue properties are reviewed in [76].

C. Libraries of computational human phantoms

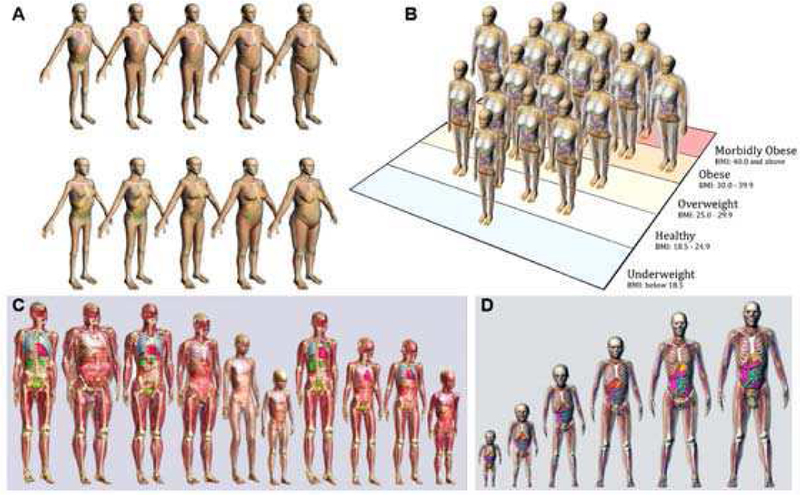
Utilizing the techniques described above, many CHPs have been developed and validated for use in the research community. While initially, researchers used simplified or stylized geometries to represent the human body, the growing availability of 3D medical imaging techniques and high-performance computing infrastructure and software made it possible to create detailed realistic CHPs as seen in Section A. In recent years, the development has shifted towards deformation techniques, making it possible to modify existing anatomical models to match certain anthropometric characteristics, such as height, weight, BMI, or organ mass. Deformation techniques allow anatomical shapes to be easily and effectively changed, reducing the time and effort needed to create large cohorts of models [16] [77] [78].

Although the ionizing radiation, non-ionizing EM, and automotive communities have been developing similar models with similar tools, there are some important differences and limitations. For example, the ionizing radiation community, guided by the ICRP [54], has placed particular emphasis on creating models with specific organ masses based on the concept of a “Reference Man” for adults and children of different ages ³. As a result, most models are not based fully on medical image data of a single subject, but instead have organ masses that are adjusted/scaled to match the ICRP reference model.

The models developed for use by the non-ionizing community have been created directly from human image data without modification of organ sizes, e.g., to comply with ICRP. On the contrary, modification of organ sizes without careful modeling of the muscle, fat, and connective tissues surrounding the organs can lead to unrealistic distributions of electrical currents caused by the relatively large differences in electrical conductivities of the various tissue types. Finally, virtual car-crash dummies developed by the automotive industry must allow for realistic mechanical simulations of bone strength and contact response for which, accordingly, the focus has been on accurate representations of cortical bone and ligament function.

The detailed review from 2014 by Xu [6] documents the rapid growth of CHPs (excluding the automotive industry) over the past 50 years. This section provides an update of the developments since 2014, and includes a brief summary of the phantom libraries currently in use and the key license conditions for many of the well-known phantoms. It also contains some of the model developments that have been underway in parallel in the automotive industry. Due to limited space, several phantom libraries could not be discussed in detail, e.g., [79] [80] [81]. A more comprehensive list can be found in the review papers by Zaidi and Xu [82], Zaidi and Tsui [83] and Xu [6].

1). Phantom libraries:

a). The IT’IS Virtual Family and Virtual Population:

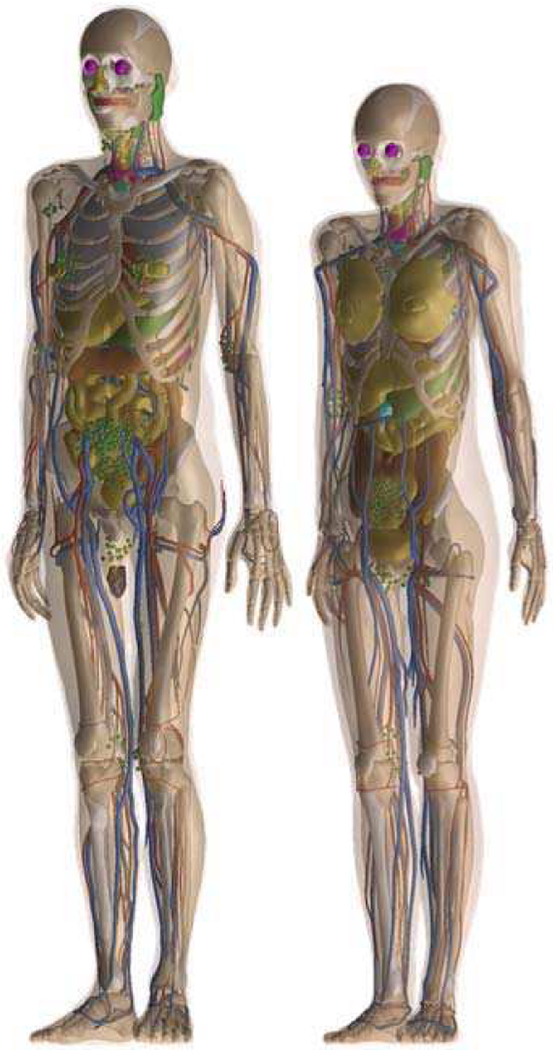
The Virtual Population (ViP) library of models, developed in a collaboration between the IT’IS Foundation, the US Food and Drug Administration (FDA), and several other groups, consists of more than 10 different anatomical models developed from MRI data of healthy volunteers, including male and female adults and children of various ages, an obese male, an elderly male, a pregnant woman and newborn [11]. A subset of the ViP models are available in version V2.0 as surface mesh models optimized for finite element simulations. The latest version of the ViP, V3.0 released in 2014, is based on higher resolution segmentations (0.5 × 0.5 × 0.5 mm³) of organs and tissues developed according to strict quality guidelines [12]. To expand the population coverage, and to be able to parametrize certain characteristics (e.g., the body fat content), all phantoms have been made posable and morphable. The morphing and posing approach is based on a realistic biomechanics model to simulate articulation and tissue deformation, expansion, and shrinkage [16].

The ViP models shown in Figure 5 along with other phantom libraries are widely applied in research and industry. Moreover, they are frequently used in applications to obtain approval from regulatory bodies, e.g., related to implant and MRI safety. As part of more recent developments, in particular in the medical sector, the models are increasingly used to study interactions of electric fields with neurophysiology [84].

Fig. 5.

Example libraries of computational phantoms. Models are shown from (a) RPI, (b) UF/NCI, (c) IT’IS, and (d) the XCAT series. Only selected phantoms are shown from each population.

b). The XCAT models:

The XCAT Models, developed at Johns Hopkins and Duke University, are NURBS-based CHPs able to model cardiac and respiratory motions based on 4D tagged MRI and 4D respiratory gated CT data, respectively [51]. From the initial standard male and female models based on the Visible Human images [17] the XCAT models have been expanded to include a population of anatomically variable phantoms that cover a wide range of height and weight percentiles [18] [19]. The technique is based on an image registration allowing template XCAT anatomy to be mapped to target patient CT data. More recently, volumetric textures that simulate tissue heterogeneity within organs and structures have been added [85] [86] [87], thereby making it possible to simulate more realistic medical imaging data. Moreover, blood flow models have been embedded to simulate contrast-enhanced imaging [88] and finite element models have been investigated to explore variations in cardiac motion [27]. The XCAT phantoms are widely applied to perform virtual clinical trials in medical imaging research, to simulate radiation doses from radiography and radiotherapy, and to improve imaging devices and techniques [89].

c). The GSF voxel phantoms:

The models generated at the German Research Center for Environmental Health (GSF, now the Helmholtz Institute) consist of a collection of 12 voxel phantoms based on CT data of living patients. One exception is the 8-week-old baby model generated from image data of a dead infant [90]. The group includes adult male, female, pediatric, and pregnant-woman phantoms.

The GSF voxel phantoms were originally developed to be used for radiation transport calculations in clinical dosimetry, environmental and occupational exposures, from external and internal sources. Therefore, the GSF voxel phantoms contain a large number of organs and tissues, including most of the ICRP critical organs.

d). The RPI library of models:

Various models were developed at the Rensselaer Polytechnic Institute (RPI), including VIP-Man [91], which was the first CHP created from the Visible Human image data [92] and the RPI Male and RPI Female models, which have both been carefully adjusted to match ICRP Pub. 89 reference organ masses [77]. These two reference models were later scaled to create different percentiles of weight-specific phantoms. The RPI models are commonly used in studies related to ionizing radiation. The RPI collection of models also include a pregnant female model at different gestational phases.

e). The University of Florida Family of Models:

The University of Florida (UF) “Family of Models”, developed at the UF and the National Cancer Institute of the National Institutes of Health (NIH/NCI), is a series of hybrid CHPs that includes models of an adult male, adult female, pregnant female, and pediatric models of various ages (newborn to 15-year-old) and both genders [93] [94] [95]. Assembled from CT image data obtained from both cadavers and living patients, the library covers variations in body size and shape among the US population of adults and children.

The UF hybrid phantom series are available as NURBS and polygon mesh surfaces (hybrid-NURBS/PM phantoms) that allow users to apply morphing techniques to develop non-reference phantoms.

f). HDRK-Man, HDRK-Woman:

The High-Definition Reference Korean-Man (HDRK-Man) and Korean-Woman (HDRK-Woman) are models that have been developed by researchers at Hanyang University in Korea [96] [97]. These models have been generated from the segmented Visible Korean Human cryosection image data [8]. The quality and resolution of the data (0.2 × 0.2 × 1.0 mm³) allow accurate segmentation of organs and tissues. These models, originally developed for radiation protection purposes, have been adjusted to match the reference Korean data, including height, weight, and organ masses.

g). Open source models:

AustinMan and AustinWoman, based on the Visible Human data [92], are open-source voxel models developed at the University of Texas at Austin [98] with a focus on EM simulations. The models are available under the Creative Commons license with a non-commercial, no redistribution clause [99]. A female and child models, which are being actively developed by the European projects PIPER [100] and ViVa [101] for car-crash safety applications, are available under open source licenses (with a noncommercial clause).

h). Models developed for the automotive industry:

There are several efforts in the automotive industry to develop CHPs for car-crash safety simulations. The Global Human Body Models Consortium (GHBMC) is an international consortium of seven different partners, most of whom are automobile manufacturers [102]. The consortium is working on the development of both male and female CHPs of different heights ⁴ in both standing and sitting positions [103] [104] [105]. The Total Human Model for Safety (THUMS) is a family of models developed by Toyota that include a 5^th percentile adult female, 50^th and 95^th percentile adult males, and 3, 6, and 10 year-old children [106] [107].

2). Availability of CHPs:

Many of the well-known CHPs are owned by their creators, usually a research institute [12] [18] [95]. In some cases, a consortium has joined forces to share the effort and costs of developing new models [102]. There are also several open source projects [78] [98] [100], which try to establish wider community access and involvement. While access to the models is typically granted to collaborators, license conditions for academic and commercial use are not always clear. Table I provides an overview of the license conditions for commonly used CHPs. Most CHPs can be obtained free of charge for academic use. For commercial use, many CHPs are available for a fee, while for some CHPs commercial applications are prohibited. The original image data used to create the phantoms is in most cases not available, with the exception of the phantoms derived from the widely used Visible Human [92] and Visible Korean data [8].

TABLE I.

Source and availability of CHPs

Name, owner	Format	Academic use	Commercial use	Image data	Reference
ViP V1.x, IT’IS Foundation, Switzerland	voxels proprietary (Sim4Life1)	free	license fees may apply	MRI	[11]
ViP V3.x, IT’IS Foundation, Switzerland	proprietary (Sim4Life1)	free	license fees may apply	MRI	[12]
XCAT, Duke University, USA	NURBS surface mesh voxels	license fees may apply	license fees may apply	NLM Visible Human chest CT used for personalization modified to ICRP-89 reference	[18]
GSF Voxel Phantoms, Helmholtz Institute, Germany	voxels	free	prohibited	CT modified to ICRP-89 reference	[90]
RPI Phantoms, Rensselaer Polytechnic Institute, USA	surface mesh voxels	free (collaborators)	n/a	NLM Visible Human CT modified to ICRP-89 reference	[77]
UF Library, University Florida/ NIH NCI, USA	NURBS surface mesh voxels	free	license fees may apply	CT modified to ICRP-89 reference	[93]
HDRK, Hanyang University, South-Korea	voxels surface mesh tetrahedral mesh	free	unknown	Visible Korean modified to reference Korean	[96]
Japanese Voxel Phantoms, Japan Atomic Energy Agency	voxels	unknown	unknown	CT modified to ICRP-89 reference	[80] [211]
Chinese Voxel Phantoms Institute for Radiation Protection, China	voxels	unknown	unknown	Visible Chinese	[79] [210]
Pediatric Phantom Library Geneva University Hospital	voxels	unknown	unknown	modified from Virtual Population pediatric models	[81]
GHBMC, GHBMC/ Elemance, USA	voxels surface mesh proprietary (LS-DYNA, PAM-CRASH, …)	license fees may apply	license fees may apply	CT and population statistics (e.g., cortical thickness)	[102] [212]
THUMS, Toyota, LSTC, USA	proprietary (LS-DYNA)	unknown	unknown	CT	[106]
AustinMan/Woman, University of Texas at Austin, USA	voxels	free CCBY-NC-ND 3.0 [99]	prohibited CCBY-NC-ND3.0 [99]	NLM Visible Human	[98]
PIPER project, Open Source	proprietary (LS-DYNA)	free GPLv3	free GPLv3	unknown	[100]

¹Sim4Life is a commercial physics simulation platform for computational life-science, www.zurichmedtech.com.

II. Applications of Realistic Computational Human Phantoms in Biomedical Engineering

The libraries of CHPs discussed above, and countless others, have been utilized for many applications, including ionizing radiation dosimetry and imaging, non-ionizing EM radiation leading to tissue heating and neurostimulation, and passive car safety. The following section highlights the many uses of CHPs within various fields of research.

A. Applications to external and internal dosimetry for ionizing radiation

The assessment of radiation absorbed dose to the internal organs and tissues of patients in the field of biomedicine has relied heavily upon the development and application of CHPs. With only few exceptions (OSLD, MOSFET, radiochromic film measurements on the patient’s body surface, for example), direct measurement of radiation dose to exposed tissues during medical imaging or radiotherapy is not feasible, and thus tissue dosimetry is assessed computationally through various dose algorithms. Increasingly, however, MC transport techniques are used with CHPs of the patient to assess organ dose. These CHPs can range in both format type – stylized, voxel, or hybrid – and morphometric category – reference (small library of average height/weight individuals), patient dependent (expanded library of variable height/weight models), patient sculpted (model morphed to match the patient’s outer body contour), or patient specific (model developed from the patient’s own CT or MRI images) [108]. The ultimate goal of patient dosimetry in medical imaging would be the use of a patient-specific CHP. However, this is not clinically feasible given current limitations in organ segmentation algorithms, and one must instead select, and then potentially sculpt, an existing CHP that best morphometrically matches the given patient.

Another use of CHPs for medical dosimetry is to explore changes in radiation dose with variations in imaging or therapy technique factors (x-ray entrance fluence, x-ray beam quality, or level of injected activity, as examples) across different populations of patient morphometry (height, weight, BMI) and possibly organ morphometry (organ size, shape, and depth in the body). In the vast majority of cases, it would be impracticable and potentially unethical to perform these dose sensitivity studies in a clinical trial using real patients. However, with the scalability and morphing capabilities of CHPs, digitally based studies of dose sensitivity are feasible.

The following section summarizes selected articles covering a broad range of medical dosimetry applications which highlight the utility and applications of difference CHP libraries.

In 2012, Ding et al. [109] reported on the development of an extended CHP library based upon the RPI-adult male and female, and their use in quantifying CT imaging dose with changes in body size. Ten phantoms were developed with BMIs ranging from 23.5 kg/m² (normal weight) to 46.4 kg/m² (morbidly obese). CT imaging doses were assessed for their computational source model of a GE LightSpeed 16-slice scanner operated at 120 and 140 kVp. With a constant mAs, radiation doses to abdominal organs such as the colon were found to be up to ~60% smaller for the obese compared to the normal weight phantoms. Increasing the tube potential from 120 to 140 kVp for the same obese individual resulted in increased organ doses by as much as 56% for organs within the scan field, such as the stomach, and 62% for those out of the scan field, such as the thyroid. These phantoms have been since integrated within the commercial software package VirtualDose™ [110].

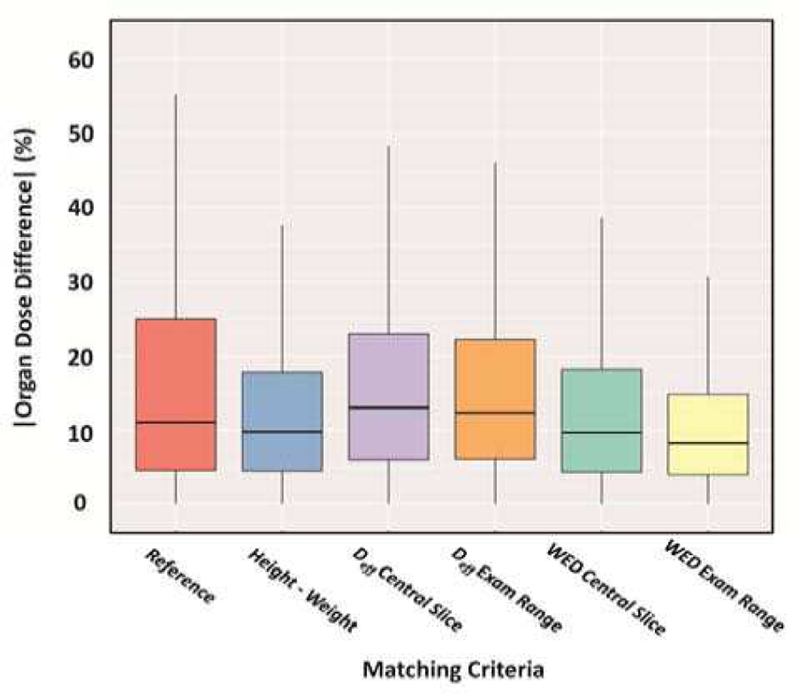
In 2017, Stepusin et al. [111] assessed six different patient-to-phantom matching criteria for CT dosimetry. These criteria included i) age-matching to reference phantoms, ii) height/weight matching to members of the UF/NCI hybrid phantom library, [112] iii) effective diameter matching as assessed in the central slice of the scan range, iv) effective diameter matching as averaged across the entire scan range, v) water equivalent diameter matching as assessed in the central slice of the scan range, and vi) water equivalent diameter matching as averaged across the entire scan range, see Figure 6. The study was conducted using two phantom libraries – a series of 52 patient-specific voxel phantoms (representing “real” patients) and the 351-member UF/NCI library of hybrid phantoms. The study concluded that while water equivalent diameter matching is superior in terms of dose accuracy, height-and-weight matching is an acceptable and reliable method for matching patient to a member of a CHP library for CT dosimetry.

Fig. 6.

Boxplots comparing all organ dose percent differences for each of the six matching parameters. The vertical lines extend at most 1.5 times the interquartile range.

In 2017, Fu et al. [113] reported a study in which 21 members of the XCAT CHP library [18] were used to compare organ doses delivered by the GE Revolution CT scanner under either tube current modulation (TCM) or organ-dose modulation (ODM). In the XCAT phantom series, two breast glandularities (ratio of glandular to adipose tissue mass) were modeled at 50/50 and 20/80. ODM was found to significantly reduce organ doses.

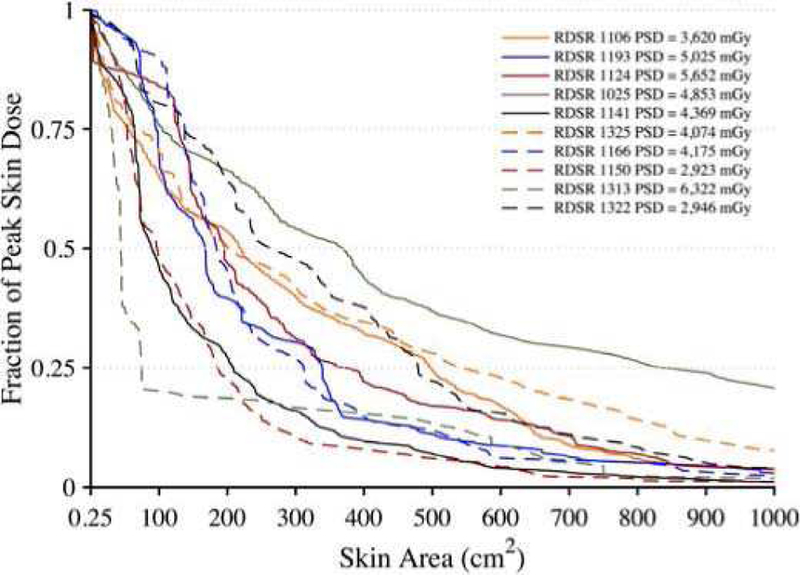
In 2017, Borrego et al. [114] used the UF/NCI CHP library to explore patient skin and organ dose in fluoroscopically guided interventions. Ten high cumulative reference air kerma radiation dose structured reports (RDSRs) were selected for dosimetric analysis as applied to height-weight matched members of the CHP library. The RIPSA algorithm was applied, demonstrating the ability to report dose-area histograms of skin dose for each individual patient [115], see Figure 7. Detailed dosimetric analyses of two patients undergoing a bilateral uterine artery embolization and an abdominal angiography were performed, demonstrating that individual irradiative events⁵ provide contributions to cumulative organ dose that vary by up to three orders of magnitude. These results provide for the possibility of truncating the number of MC simulations required with minimal impact on dose accuracy.

Fig. 7.

Dose-area histograms (DAHs) for 10 select high-dose cases normalized to peak skin dose. Ordinate indicates what fraction of peak skin dose is delivered to an area of exposed patient skin given on the abscissa.

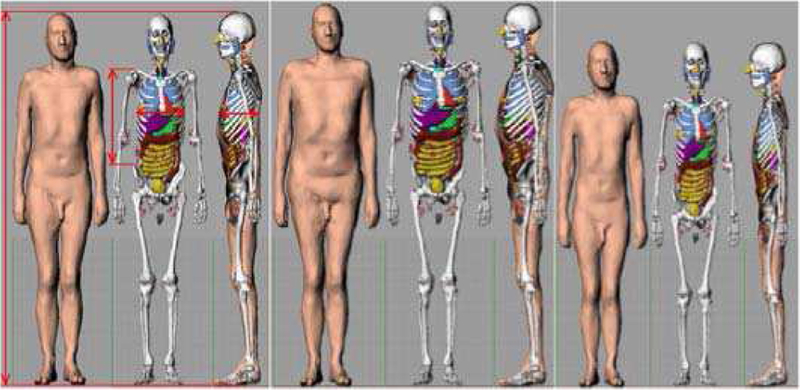
In 2017, Zvereva et al. [116] reported on a feasibility study to reduce differences in diagnostic nuclear medicine doses that are traditionally based upon MC simulations of photon and electron transport in an age-matched reference phantom. The study focused on the Positron Emission Tomography (PET)-based tumor imaging agent (S)-4-(3–18F-fluoropropyl)-L-glutamic acid, and used the MIRD schema for dose assessment [90]. The study employed two hypothetical patients selected from the HMGU (Helmholtz Zentrum Munchen voxel phantom library): the 103.2 kg male Visible Human phantom (patient #1) and the 51.5 kg Irene female phantom (patient #2) [90], see Figure 8. Organ doses were further assessed in the ICRP Publication 110 reference computational phantoms in both their voxelized [30] and polygon-mesh formats [117]. Finally, the polygon-mesh phantoms were sculpted to match either patient #1 or #2 through a multi-step process to include separate and proportional scaling of the legs, torso, and arms. Importantly, no further adjustments were made to individual organ size, shape, and depth to “match” the targeted hypothetical patients. The study concluded that it is feasible to estimate patient-specific nuclear medicine organ doses within a relative uncertainty of 25% or less using phantom sculpting to the outer body dimensions and shape of the nuclear medicine patient.

Fig. 8.

Polygon mesh version of the ICRP 110 reference phantom with selected dimensions and the result of its adjustment to patient #1 and patient #2.

In 2017, Petroccia et al. [118] explored the use of the UF/NCI computational phantom library [112] to represent patients historically treated with cobalt-60 gamma-rays for the treatment of Hodgkin’s lymphoma. This patient population is ideal for radiation epidemiology studies of late clinical effects for both secondary cancer and cardiac disease. To perform dose-response studies, however, organ doses – both in and outside the treatment field – must be obtained. In this study, the authors looked at patients treated in the early 1960s to early 1970s in which only patient gender, age, height, and weight were available, along with treatment planning information. In this study, the authors developed a detailed workflow resulting in a complete radiation treatment model of the historical radiotherapy using height/weight-matched CHPs from the UF/NCI series. Organ doses could be reported for the first time for these patients by individual treatment field, as well as cumulative over the full course of radiotherapy.

Papadimitroulas et al. [119] published in 2018 a new methodology to estimate the absorbed dose in organs. The method is based on specified clinically derived radiopharmaceutical biodistributions and personalized anatomical characteristics. The authors use realistic MC simulations and pediatric CHPs to calculate a parameter called the “specific absorbed dose rate” (SADR), i.e., a unique quantitative metric which is specific to a particular organ. The SADR is defined as the absorbed dose rate in an organ when the biodistribution of radioactivity over the whole body is considered. SADR enhances the personalization of dosimetry in pediatric nuclear medicine and provides time-dependent organ dose rate curves.

As a final example, we look at a 2012 study by Senthamizhchelvan et al. who explored tumor dosimetry and response for ¹⁵³Sm-EDTMP (Quadramet™) therapy in patients with high-risk osteosarcoma [120]. In this study, radiation absorbed dose in 19 tumors within 6 osteosarcoma patients were treated with ¹⁵³Sm-EDTM. The dose was assessed within the 3D-RD software package in which the CT portion of the SPECT/CT patient image is used as the patient-specific voxel phantom and the SPECT portion is used to define, at the voxel level, the time-integrated activities of the radiopharmaceutical. Patients were treated first, with a low-dose protocol (37–52 MBq/kg), then following bone marrow recover, by a high-dose protocol (222 MBq/kg). Tumor doses determined by MC radiation transport within 3D-RD were determined and compared to doses reported by the spherical tissue models of the OLINDA nuclear medicine code [121]. Mean tumor doses were reported to range from 1.5 to 15 Gy for the low-dose therapy, and from 3 to 60 Gy for the high-dose therapy. Mean tumor absorbed dose reported by the OLINDA code were within 5% of the mean values reported by 3D-RD.

B. Applications to External and Internal Dosimetry of Non-Ionizing Radiation

Research on human exposure to EM fields and the development of safety guidelines and compliance standards began in the second half of the 20^th century [122]. At the beginning, due to lack of computational resources, only very generic representations of the body, such as prolate spheroids [123] or one-dimensional stratified representations of the tissue structures [124], could be used. Nevertheless, these simple models provided fundamental insight for the assessment of the whole-body absorption and local absorption in the far-field [123], and in the near-field [125].

In the development of safety guidelines [126] [127], defined in terms of basic restrictions (induced fields) and reference levels (incident fields), CHPs are applied with the objectives to i) identify the key anatomical parameters for quantification of the fields absorbed in the body and ii) correlate the external fields and the absorbed fields in terms of an exposure mechanism.

For compliance testing [128] [129] [130], anatomical models are applied for i) the development and validation of CHPs for testing against the basic restrictions and ii) statistical evaluation of the basic restrictions by means of numerical simulations of a representative set of CHPs.

In cell phone compliance testing, the correct rendering of the proportions of the human head is a key parameter, because the exposure of tissue in the close environment of an EM field source strongly depends on the distance of the exposed tissue from the source [125] [131] [132] [133]. Simulation results of detailed CHPs of adults and children [131] [134] [135] served as basis for the design of the dosimetric head phantom that is now used in cell phone compliance testing standards [128] [129]. It has been continually validated versus the latest available anatomical head models of adults and children [136] [137] [138], see Figure 9.

Fig. 9.

Tissue losses, i.e., absorption in a cross section of DUKE (member of ViP), and the E-field lines generated by the transmitter in the vicinity of the phone.

A similar approach was chosen for the compliance testing of base station antennas [139], where a large number of whole body CHPs [11] in different exposure situations were used to develop a heavily simplified body phantom that takes height, BMI, and tissue layering of the exposed population group into consideration [140].

For low-frequency applications, such as resonant wireless charging or induction cooking [141] [142], there are no available standardized experimental phantoms. As the reference levels may be exceeded in the close near field of these applications [126] [127], compliance with basic restrictions is tested with CHPs.

Although there are practically no alternatives to the numerical assessment of the fields induced in the body in the low frequency range, standardization efforts for numerical and combined numerical and experimental methods have so far focused on the RF range. The IEC/IEEE 62704 series of standards gives guidance on the numerical assessment of the peak-spatial Specific Absorption Rate (psSAR) based on both body phantoms and anatomical models [143] [144].

The safety standards for MRI scanners IEC 60601–2–33 [145] are currently also revised based on advanced modeling techniques combined with thermal modeling using perfusion tissue models [146] [147]. ISO/TS 10974 standard [148], defines a method based on CHP to demonstrate MRI safety of active implants [149], see Figure 10. The shortcomings of the experimental approach described in [150] have been largely overcome with ISO/TS 10974 [148], which allows for significantly more realistic modeling of the tissue heating due to induced currents on the implant and for the statistical risk evaluation for particular patient groups and implant types.

Fig. 10.

Induced absorption of the B1-field in DUKE (ViP) during MRI scans (right side) and the associated local tissue temperatures (left side).

With the latest wireless devices technologies, frequencies above 10 GHz are applied, whereby the penetration depth of EM fields in the body drops to a few millimeters or less. In the upcoming revisions of the ICNIRP guidelines [126] and IEEE C95.1 [127], basic restrictions will be introduced in terms of the transmitted power density. The low penetration depth poses additional demands on anatomical modeling as the skin can no longer be regarded as bulk tissue, i.e., the distinct dielectric properties of its layers need be considered [151] [152].

C. Radiation protection

The system of radiation protection is built upon several principles: its main aim is to limit the potential health detriment due to exposure to radiation below certain acceptable limits. The central assumption of a linear dose-response relationship for the induction of cancer and heritable effects directly connects the limitation of the potential health detriment with a limitation of the dose to the human body from radiation. Since radiation doses in the human body cannot be measured directly, a complex system involving various types of quantities has been established. So-called “operational” quantities, such as the personal dose equivalent Hp(d) and the ambient dose equivalent, H*(d) [153] can be measured by personal or environmental dosimeters. In contrast to the “protection quantities” in the human body: the organ equivalent dose H_T and the effective dose E [154], where the latter is a weighted average of organ equivalent doses reflecting the different radiation sensitivity of individual organs and tissues of the body. Since the system of radiation protection is also of a prospective nature, the dose quantities are not determined on an individual basis, but consider rather whole populations.

Due to these principles, CHPs play a central role in radiation protection dosimetry. The first CHPs used for this purpose were based upon mathematical expressions representing planes, cylindrical, conical, elliptical, and spherical surfaces describing the shape and position of idealized body organs [4] [47] [155] [156]. For this first generation of CHPs, the organ masses and volumes were in accordance with the ICRP data of former Reference Man [53].

With the advent of more powerful computers in the 1980s, various groups have developed voxel phantoms based on three-dimensional images as an extension and improvement to these earlier models [82] [90] [91] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167]. Various authors have shown that the organ shapes of the earlier mathematical phantoms present an over-simplification that has an influence on the energy distribution, which may deviate for some cases systematically from that calculated for voxel phantoms. For external radiation, the parameters influencing the organ doses are: i) the depth of the organ below the body surface, ii) the exterior shape of the trunk, and iii) the trunk diameter relative to the incoming radiation beam [168] [169] [170] [171] [172]. For internal dosimetry, the influencing parameters are: i) the relative position of source, ii) the target organs (for organ cross-fire), and iii) the organ mass (for organ self-absorption) [173] [174] [175] [176].

However, most of these CHPs do not represent the average Caucasian man or woman, due to being derived from a specific individual. Hence, the ICRP decided to construct voxel CHPs being representative of the adult Reference Male and Reference Female [54] with respect to their external dimensions, their organ topology, and their organ masses [30], with the organ dose conversion coefficients following the recent ICRP Recommendations [154].

Two male and female voxel CHPs were selected with external dimensions close to the reference data [167] [177]. These two CHPs were then adjusted to the reference values of ICRP Publication 89 [54] in several steps: i) adjustment of the body height and the skeleton mass by voxel scaling; ii) adjustment of the individual organ and tissue masses to the reference values by adding or subtracting the required number of voxels; iii) additional organ and body region modifications. The bones were subdivided into a cortical shell and a spongiosa region accommodating the bone trabeculae together with the marrow cavities – structures that are both much smaller than the voxel resolution of the phantoms. The method of constructing the adult male and female reference computational phantoms is described in detail in ICRP Publication 110 [30].

The adult reference CHPs of ICRP Pub. 110 are the official CHPs representing the Reference Male and Reference Female [54] [154], see Figure 11. Each of these reference CHPs has 140 different organs and tissues. The male phantom consists of approximately 1.9 million voxels with a resolution of 2.137 ×2.137 ×8.0 mm³, and the female phantom consists of approximately 3.9 million voxels at a slightly finer resolution of 1.775×1.775×4.84 mm³. The ICRP has recently published (Pub. 116 [178] and Pub. 133 [179]) recommended values for dose coefficients for both external and internal exposures using these two phantoms.

Fig. 11.

Adult male and female mesh-type ICRP reference computational phantoms [180].

Although these phantoms have reference organ masses, they still have individual organ topology reflecting the tomographic data used for their construction. Obviously, both models cannot represent real individuals, and thus they should not be used to assess doses for specific individuals.

Further limitations of the reference CHPs are due to their voxel resolution of the order of millimeters, specifically concerning the slice thickness of several millimeters, which results in stepped organ surfaces and non-closed contours for skin and hollow organs, coarse and unrealistic representation of the eye lenses, and the inability to represent very fine structures, such as some specific source and target regions in the alimentary and respiratory tracts having micrometer dimensions. This resulted in the necessity to use several stylized CHPs in addition to the voxel CHPs for the calculation of reference dose coefficients for high-resolution source and target regions and radiations of low penetration.

These limitations are being addressed by a research project for creating BREP versions of the reference CHPs. The resulting mesh-type reference CHPs closely resemble the ICRP Pub. 110 [30] phantoms in their main anatomical features and thus meet the requirement of being “exact replicas”. However, they include micrometer-fine source and target regions that could not be represented in the Pub. 110 phantoms. The methods applied to create these mesh-type reference CHPs [180] are similar to those described in Section 1.A Advanced Phantom Geometries.

D. Biomedical imaging

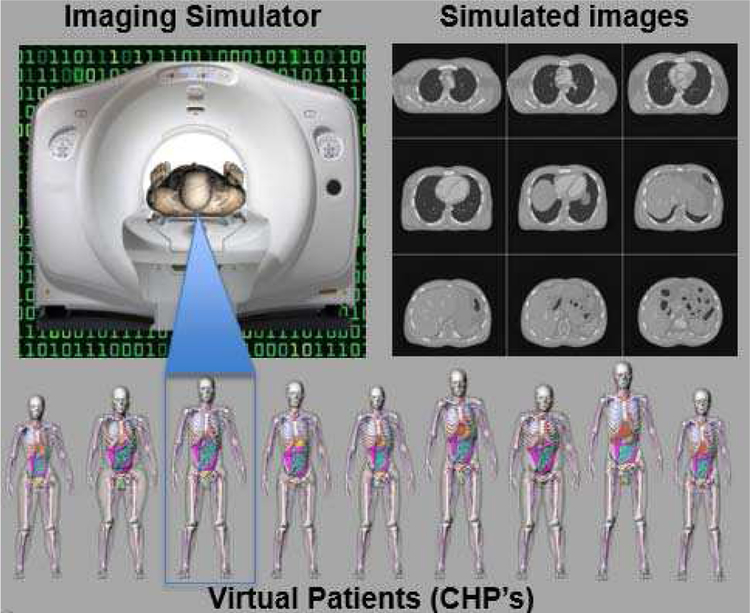
CHPs serve as virtual patients within biomedical imaging simulation studies. They are imaged by means of accurate simulation methods, e.g., MC or analytical, with models that emulate the characteristics of the particular imaging modality, instrumentation, and system configuration, as well as the physics of the imaging process including all artifacts. The simulation codes generate imaging data that can be reconstructed and analyzed on clinical workstations [86]. Through the combination of CHPs with medical imaging simulation methods, realistic biomedical images that closely mimic those acquired from live subjects can be generated entirely on the computer, as shown in Figure 12.

Fig. 12.

CT simulation using an CHP. Imaging data is acquired from the CHP using the scanner model; the data is then reconstructed into the simulated CT images.

Simulated images from the CHP include the image degradation effects by the imaging system and the imaging process. They can be compared to the original phantoms, which represent the known “truth”, and the difference can provide quantitative evaluation of the imaging instrumentation, the image processing, and reconstruction methods. The ultimate goal is to improve image quality for more accurate detection of abnormalities and diagnosis of diseases.

With this ability, CHPs are able to assess the effects of anatomical, physiological, physical, and instrumentational factors on the imaging process, and to study image acquisition strategies, processing and reconstruction methods, and visualization techniques. In this section, we present examples to illustrate the applicability of CHPs for biomedical imaging.

1). Effect of noise or artifacts of the imaging process:

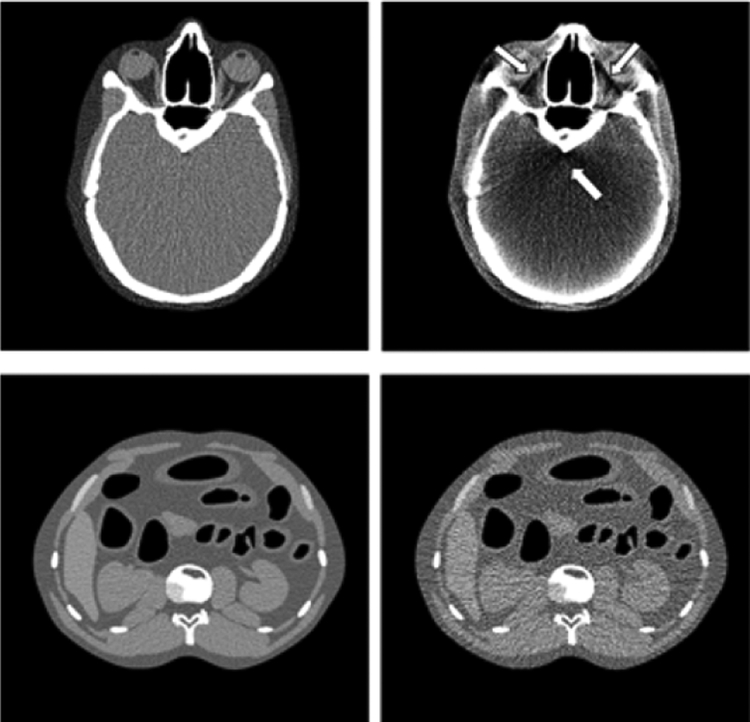
Within medical imaging simulation, one can easily alter system design parameters and acquisition techniques and witness these effects on the resulting images as compared to the known phantom. Different effects can be singled out and studied independently of other potential sources of artifacts. Figure 13 shows examples of cross-sectional CT images using the XCAT series of CHPs showing the effects of noise and beam-hardening.

Fig. 13.

(Top) Sample transaxial-slice CT images of the head at 80 kVp (Left) and 120 kVp (Right) showing a beam-hardening artifact (arrow). (Bottom) Sample noisy transaxial-slice abdominal CT images at 1 mAs/view (Left) and 0.1 mAs/view (Right).

2). Optimization and comparison of modalities:

CHPs can be imaged repeatedly to find the system values or techniques that give the highest image quality. In addition, the radiation dose to the organs and structures can be calculated to assess the radiation exposure from different imaging systems and techniques. CHP’s therefore provide the basis to optimize and compare imaging applications in terms of image quality and dose.

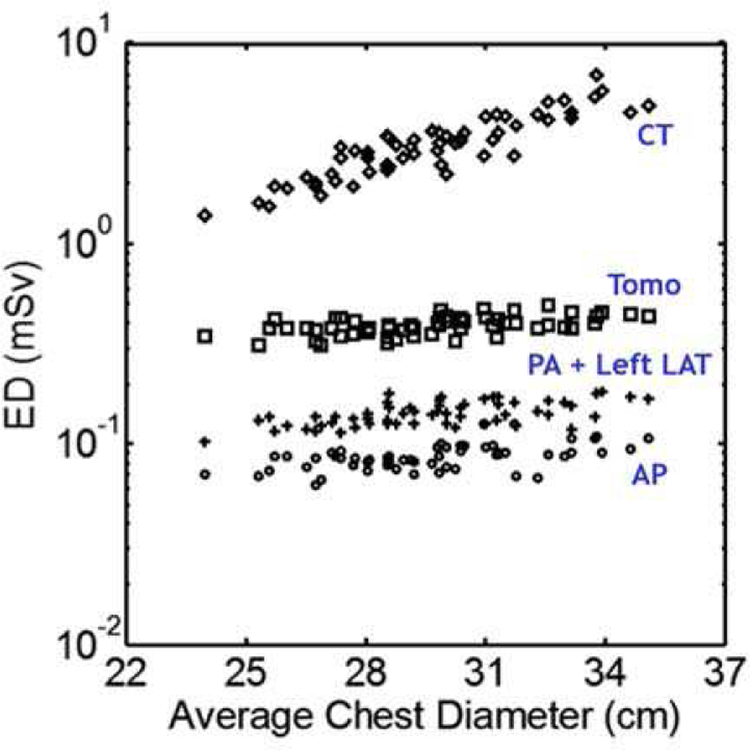
Figure 14 shows a comparison of chest CT, tomosynthesis, and radiography in terms of the effective dose (ED) in patients of various sizes. Fifty-nine anatomically variable CHPs were imaged with each modality and the organ doses and effective doses were estimated using MC simulations [181]. It can be seen in the figure that CT, as expected, has the highest dose, followed by tomosynthesis and radiography. Patient body size can also be seen to have more of an impact on the CT dose, meaning that patients of larger size may benefit from choosing tomosynthesis over CT.

Fig. 14.

Effective dose (ED) plotted as a function of patient size for CT, Tomosynthesis (Tomo), posteroanterior + left lateral radiography (PA + Left LAT), and anteroposterior radiography (AP).

Studies such as this, which involve imaging patients with different modalities or imaging multiple times with varying parameters, would be ethically and practically impossible to perform using live subjects.

3). Development of image processing and reconstruction methods:

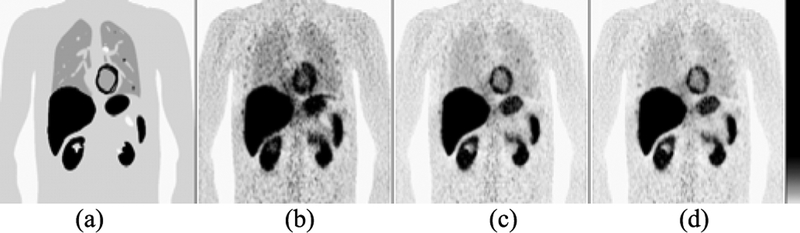
Realistic CHPs have played an important role in the development of image reconstruction methods compensating for artifacts. Figure 15 shows an example of the evaluation of a SPECT image reconstruction method that provides significant improvement in both image quality and quantitative accuracy, as seen in a comparison to the “true” radioactivity distribution modeled in the particular phantom.

Fig. 15.

Simulated myocardial SPECT images reconstructed using an iterative order-subset expectation-maximization (OS-EM) method with accurate models, i.e., the XCAT phantom, of the system response and imaging physics for significant improvement in both image quality and quantitative accuracy. From top to bottom row, OS-EM images obtained without any modeling (1^st row), with the collimator-detector response (CDR) (2^nd row), with CDR and attenuation (3^rd row), and with CDR, attenuation and scatter modeling (4^th row). From the left to right column: OS-EM with 1, 2, 3, 4, 5, 10 and 20 iterations.

4). Effect of cardiac and respiratory motions:

Motions such as the cardiac, respiratory, and patient voluntary motions can cause artifacts in medical images which can lead to misdiagnosis. CHPs can be used to simulate different types, and extents, of motions artifacts, e.g., Figure 16 shows the effect of cardiac motion on CT imaging of the coronary arteries. Streak artifacts can be seen on the arteries that move the most while the heart beats.

Fig. 16.

Sample noise-free transaxial-slice cardiac CT images at mid-diastolic phase with fast full scan (Left) and at 333ms/rotation short scan (Right) showing the effect of motion of the coronary artery (arrows). Images were sharpened to show the artifacts more clearly.

Figure 17 shows the use of simulation methodologies demonstrating cardiac SPECT imaging artifacts due to respiratory heart motion. The heart moves up and down with the diaphragm, causing artifacts mimicing defects, or areas of cardiac tissue receiving less blood perfusion.

Fig. 17.

Simulated myocardial SPECT images demonstrating the effect of respiratory motion. (Left column). Same sample short-axis slice through the center of the heart. (Right column). From the 4D XCAT phantom (Top row) without respiratory motion, and with (Middle row) 2 cm and (Bottom row) 4 cm respiratory motion amplitude showing the increasing motion artifacts on the superior and inferior wall of the myocardium.

5). Motion compensation:

Methods for motion artifacts include various acquisition strategies such as gating, patient instructed breathing, and 4D reconstruction algorithms. CHPs and simulation techniques provide a nice toolset to quantitatively evaluate and optimize these methods.

In Figure 18, we demonstrate the application of the 4D XCAT phantom in the development and evaluation of a 4D respiratory motion estimation technique and a 4D PET image reconstruction method with accurate motion compensation. The simulated images show the effect of respiratory motion, blurring, and thereby decreasing, the lung lesion detectability. It also demonstrates the ability of the 4D image reconstruction method, with accurate motion modeling and compensation, to provide improved lesion detection.

Fig. 18.

Evaluation of a 4D PET image reconstruction method with respiratory motion (RM) compensation using the 4D XCAT phantom with respiratory motion capabilities. (a) A sample coronal slice from the 3D XCAT phantom with three lung lesions and no RM. The PET images of the same coronal slice obtained from (b) a 3D Maximum Likelihood-Expectation Maximization (ML-EM) image reconstruction algorithm with no RM compensation, (c) a 4D ML-EM image reconstruction with RM compensation using known RM modeling, and (d) a 4D ML-EM image reconstruction with RM compensation using an estimated 4D RM model.

E. Regulatory applications

CHPs currently play an increasingly significant role in the regulatory approval process for medical devices by helping characterize the safety of MRI systems and devices entering the MRI environment. CHPs have the potential to significantly impact future regulatory approvals, particularly in the context of virtual clinical trials (VCTs), in which simulated human clinical trials (HCTs) are performed in-silico. VCTs are part of a broader in-silicoclinical trial framework [182] where computer simulation data, i.e., digital evidence, are used for regulatory decision-making along with traditional sources such as bench testing, animal testing, HCTs, and adverse event reporting. Currently HCTs serve as the gold standard, providing reasonable assurance of safety and effectiveness for high-risk medical devices. This is mainly because HCTs allow for evaluation of complex biological, chemical, and physical interactions between the human body and a medical device. As computational modeling techniques improve, and trust in the predictive capability of computational models grow, the reliance on HCTs may be reduced as they are augmented by digital evidence from in-silico VCTs.

During the life cycle of a medical device, from ideation, to development, regulatory approval, and ultimately real-world clinical use, evidence regarding device performance in the intended patient population is essential for ensuring public health. Each of the sources of data, i.e., bench, animal, HCT, etc., has advantages and limitations [183]. Therefore, the appropriate combination of data from each source, particularly in the context of regulatory approval depends on the risks in the intended use for the device. Evaluation of a low-risk device may primarily rely upon bench testing and adverse event reporting, while for a high-risk device, evaluation may require HCT data. A major advantage of HCTs is the assessment in actual patients, which provides assurance that the data will be indicative of clinical use. However, significant barriers broadly impede the use of HCTs in device evaluation. Cost and patient safety are frequent concerns; recruitment of patients is required, and significant demands may be made upon physicians’ time and a hospitals’ resources (e.g., Institutional Review Boards). HCTs are usually costly and lengthy, potentially taking years to complete. They may also expose patients to novel or unproven technologies that pose a risk of harm.

In-silico clinical trials have become widely adopted for regulatory use in the evaluation of RF-induced heating during MRI. The RF fields created by MRI systems deposit energy into the patient, generating heat, particularly if electrically conductive implants are present, that can potentially cause tissue damage [184]. This is an important safety concern that should be addressed, both for MRI systems [185] and MRI compatible medical devices [186]. Implantable medical devices are concerning because they could potentially act as antennas, focusing energy deposition, resulting in thermal tissue damage. The amount of energy deposited and how it is distributed within the patient is related to the patient’s anatomy, weight, MRI landmark positioning, and the location and orientation of the implant(s). Testing in simplified physical phantoms cannot adequately capture this variability, whereas evaluation of potential RF heating in patients is not ethical, or even feasible. Thus, there is a strong regulatory need for in-silico clinical trials that can provide alternative data. That need is currently being met by CHPs such as the Virtual Family [11] and the Virtual Population [12]. Finite Difference Time Domain (FDTD) simulations allow for localized estimates of energy deposition and temperature rise [187], which can be used to determine the worst-case scenario in the patient population and help ensure MRI systems, and implants, will not exceed safe temperature limits in real patients.

A potentially important future role of VCTs is performance evaluation of imaging systems. Such a virtual evaluation typically involves CHPs, a model of the device physics, the image reconstruction process, and a model for image interpretation for a specified clinical task. As outlined below, this is an active research area, particularly for breast imaging devices such as mammography and digital breast tomosynthesis (DBT), a limited-angle tomographic imaging system. These devices use ionizing radiation to screen millions of women per year, thus safety and efficacy are significant public health concerns. Currently DBT devices are considered high risk devices (Class 3) in the United States, indicating the need for HCTs. Conducting an HCT for DBT devices can however be burdensome due to the use of ionizing radiation and periodic design changes. Bench testing with physical phantoms is routinely performed, however the complex and variable texture of breast images can make it difficult to infer clinical performance from simple phantom-based measurements alone, particularly when there are nonlinearities in the imaging system. The desire to limit patient radiation exposure and noted inadequacies of bench testing has motivated the development of VCTs and associated breast CHPs, targeted at both technology development and regulatory approval.

Virtual imaging clinical trials for cancer screening devices typically assess the detectability of cancerous lesions and require modeling of the imaging process from the patient to image interpretation. A CHP population consisting of cancer positive and negative patients is required. The population must be imaged virtually using physics-based simulation of the image acquisition process for each device in the study. Images are then reconstructed and interpreted by a human, or algorithm, to determine some measure of cancer detectability, thus simulating a breast cancer screening HCT. Anthropomorphic breast CHPs are a vital component of these VCTs due to the influence of surrounding anatomical structures on lesion detectability. Breast phantoms generally follow one of two design philosophies, segmentation of 3D breast CT data [188] [189] or procedural generation of random breast tissue structures [190] [191] [192] [193]. Segmentation of CT images allows for accurate representation of large scale breast anatomy, but CT image resolution does not currently allow for segmentation of fine structures such as ligaments that are visible in higher resolution mammographic and DBT systems. The size of the virtual population is also limited to the number of CT data sets available, though some efforts have been made to solve this problem with eigenfunction analysis [194]. Procedural generation on the other hand allows for a virtual patient population of arbitrary size at an arbitrary voxel resolution, but current phantoms generated in this manner have limitations in terms of realism. A combination of segmentation and procedurally generated fine structures has been proposed to provide some of the advantages of each technique [195]. Models for cancerous breast lesions have also been developed [196] [197]. Several research groups have made significant progress in creating breast VCT platforms and have used them for performance evaluation studies [198] [199]. An open source software framework for managing VCT data has also been made available [200] [201]. VCTs are not currently used for regulatory evaluation of imaging systems, but the FDA has commenced the research project Virtual Imaging Clinical Trials for Regulatory Evaluation (VICTRE) [202] to study the issues with the hope to adopt VCT for regulatory use in the future.

In a VCT, virtual patients are enrolled, and analogous to an HCT, where the interaction between the device and the virtual patient is studied. This process typically involves multiple inputs (CHPs and device parameters) and computational models. Increased use of VCT data for regulatory decision making will certainly be contingent upon proper V&V of the CHP and the different VCT models. As previously described, V&V of a computational model is “the process of determining the degree to which a model is an accurate representation of the real world” [203]. This definition implies that an important part of a VCT validation is careful consideration of the regulatory question to be answered. Validation of VCT models for imaging device efficacy have traditionally involved “fool the reader” type studies intended to characterize how difficult it is for an expert to subjectively distinguish a real image from a simulated one [204]. On the other hand, it has been suggested that validity and applicability of VCTs for regulatory use should hinge upon whether regulatory decisions based on the VCT are as good as, and more efficient than, decisions based upon data from currently used experimental methods [205]. Validation would thus involve input from the regulatory agency regarding how VCT data is used in the decision-making process. Alternatively, considering the effort involved in validation and potential applicability to multiple devices, VCT tools that incorporate a CHP could be evaluated as part of the Medical Device Development Tools (MDDT) program independent of a regulatory submission for a particular device [206]. This process could qualify a VCT platform for a specific context-of-use, potentially encompassing a range of regulatory questions or device types.

There are many regulatory questions that could be addressed more efficiently with CHPs, e.g., post-market quality control of clinical protocols could be a useful application of simulated images generated in a VCT due to the knowledge of ground truth [207]. Collecting and assessing validation evidence for CHPs, and simulations performed with them, is critical for their adoption in the regulatory process.

III. Discussion and Conclusions

If care is taken to proceed with the necessary rigor and caution, CHPs are an invaluable door opener for a wide range of computational life science applications that will benefit safety and efficacy assessments, including the development of novel therapies and medical devices, VCTs, and personalized medicine.

CHPs are becoming more detailed and realistic, more available and in greater number, and benefit from the rapid progress in simulation technology allowing increasingly complex simulations. This has opened new avenues in their use, beyond classic dosimetric applications, such as in medical device design and VCTs. For that purpose, it is important to achieve sufficient patient population coverage; a demand that is likely to be met through the development of morphing techniques, rather than continued de novo segmentation. Morphing techniques capable of adapting existing CHPs to information about an individual person (e.g., through medical image-registration) could broaden the use of detailed CHPs to patient-specific applications, such as personalized treatment planning and optimization, personalized dosimetry, and safety management for medical imaging. Hence, in parallel to the development of simpler model creation approaches, e.g., using artificial intelligence techniques in medical image processing, it is expected that research efforts will shift from brute force segmentation to the facilitation of model parameterization and personalization through morphing techniques.

For biomedical imaging applications, CHPs allow experimentation which are too risky or impossible with real patients. CHPs allow complete control over the patient’s anatomy, the imaging device and any number of different imaging scenarios can be quickly and cost effectively investigated. CHPs provide a known truth that does not exist in real patients, providing a means with which to quantitatively evaluate, optimize, and compare different imaging system designs and configurations, data acquisition techniques, and image reconstruction and processing methods. As such, they are providing a valuable precursor or ultimately an alternative to HCTs.

Another important step will be the transition from developing CHPs as static geometrical representations of anatomy to incorporating information about dynamic behavior [16]. This includes, e.g., functionalization with nerve trajectories that have been enhanced with dynamic electrophysiological behavior [84], with breathing/heart-beat motion models, with vascular blood flow, or with thermoregulation models. Incorporating dynamics and physiology models in CHPs will broaden their application and facilitate sharing, compatibility, and interoperability of such physiology models, as well as their use in multiphysics modeling [208]. Recent developments use CHPs in multi-scale simulations to estimate the radiobiological effect of clinical ionizing radiotherapy. This novel simulation technique combines multi-scale MC simulations from organ to cell levels. At the cellular level, accumulated damages are computed using a spectrum-based accumulation algorithm and a predefined cellular damage database. Multi-scale modeling is then performed under conventional fractionated irradiation [209]. Anatomical geometry and physiological dynamics can frequently not be treated as independent, therefore, integrated, functionalized CHPs are required.

However, the increasingly simple applicability of CHPs carries the risk of users incorporating such models in their simulations without awareness of the assumptions and limitations involved in creating such models. Even if the tissue delineation were perfect and the resolution infinitely detailed, as already the process of segmenting the complex and inhomogeneous tissue distribution into clearly distinct, locally homogeneous regions, is an approximation (unless the model is supplemented with tissue inhomogeneity maps). Approximations that are suitable for some applications are not acceptable for others, e.g., biomechanical applications require superior modeling of tendons and ligaments, as well as sliding tissue interfaces, which might not be necessary for most dosimetry applications [210]. Hence, the use of CHPs in applications that have not been previously validated, should typically be accompanied by careful consideration and discussion of the limitations, V&V, and uncertainty assessment. It is expected, that increasing model detailedness and fidelity, as well as improved statistics through an increasing number of independently created CHPs, will reduce the uncertainty and provide information into the magnitude of certainty, e.g., randomly distributed modeling errors. However, such considerations will not provide insights into systematic errors that can only be analyzed through conscious investigation of the involved approximations and through experimental validation in a setup sufficiently relevant to the model context-of-use.

Finally, although the requirements for applications used by the different research communities (ionizing dosimetry, non-ionizing EM radiation, passive car safety, etc.) in terms of segmented tissues and target heights, weights, and organ masses can be extremely variable, there is considerable overlap regarding techniques and tools under development for processing and modifying existing phantoms. While CHPs for ionizing and non-ionizing radiation often have similar file formats, the models developed for car-crash safety contain the actual computational meshes and vendor-specific annotations. Nevertheless, sharing and re-use of segmentations created to cover specific target populations is likely to benefit all fields and could significantly reduce the effort needed to create new CHPs from image data.

IV. Disclaimer

The opinions and/or conclusions expressed herein are solely those of the author and in no way imply a policy or position of the Food and Drug Administration. The mention of commercial products, their sources, or their use in connection with material reported herein is not to be construed as either an actual or implied endorsement of such products by the Department of Health and Human Services.