Automatic Segmentation and Supervised Learning-Based Selection of Nuclei in Cancer Tissue Images

Abstract

Analysis of preferential localization of certain genes within the cell nuclei is emerging as a new technique for the diagnosis of breast cancer. Quantitation requires accurate segmentation of 100–200 cell nuclei in each tissue section to draw a statistically significant result. Thus, for large-scale analysis, manual processing is too time consuming and subjective. Fortuitously, acquired images generally contain many more nuclei than are needed for analysis. Therefore, we developed an integrated workflow that selects, following automatic segmentation, a subpopulation of accurately delineated nuclei for positioning of fluorescence in situ hybridization-labeled genes of interest. Segmentation was performed by a multistage watershed-based algorithm and screening by an artificial neural network-based pattern recognition engine. The performance of the workflow was quantified in terms of the fraction of automatically selected nuclei that were visually confirmed as well segmented and by the boundary accuracy of the well-segmented nuclei relative to a 2D dynamic programming-based reference segmentation method. Application of the method was demonstrated for discriminating normal and cancerous breast tissue sections based on the differential positioning of the HES5 gene. Automatic results agreed with manual analysis in 11 out of 14 cancers, all four normal cases, and all five noncancerous breast disease cases, thus showing the accuracy and robustness of the proposed approach.

Introduction

Breast cancer is the second most common cancer in woman. It is estimated that approximately one in eight women in the US will be diagnosed with breast cancer and it is the primary reason behind the death of approximately 40,000 women, annually (1). Nevertheless, there have been major improvements in the past decade that have caused these numbers to decline, largely, due to: (i) increased awareness,(ii) early detection/screening, and (iii) treatment advances. Early detection has been the focus of extensive research and there is accumulating evidence that if breast cancer is diagnosed early, the average survival rate can be extended to 98%, from only 23% if the cancer has already metastasized before being diagnosed (1).

Recently, it has been shown that genetic alterations to normal cells play a significant role in causing cancer (2). Concurrently, due to improvements in optical microscopy and fluorescent labeling, it has been shown that the cell nucleus is compartmentalized into well-defined subregions and that the spatial position of genes in the nucleus correlates with their expression and cellular activities (3–5). Furthermore, the positioning of certain genes, such as HES5 and FRA2, has been shown to differ between normal and cancer cells in a cell culture model of cancer (6) and in patient tissue sections (7). This novel discovery could emerge as a diagnostic and/or prognostic tool for breast cancer.

Determining gene positioning begins with multichannel optical microscopic imaging of nuclei with fluorescence in situ hybridization (FISH)-labeled genes of interest in DNA-counterstained nuclei, where the FISH signals appear as punctate spots. Since discerning preferential gene positioning is virtually impossible by visual examination, quantitative analysis of the images is required. This involves: (i) accurate nuclear segmentation, (ii) detection of FISH signals, and (iii) spatial localization of the FISH signals with respect to the nuclear center and boundary. Using manual image analysis of 100–200 nuclei per sample, Meaburn et al. showed that this method reliably detected breast cancer across a panel of 11 normal and 14 cancer samples (7), using the nonparametric Kolmogorov–Smirnov (KS) test to distinguish spatial gene localization between samples. Scaling up this approach for high-throughput clinical studies involves analysis of several thousands of nuclei across hundreds of normal and cancerous tissue samples. Analysis of this nature would be too time consuming, subjective, and tedious if done manually, thus warranting automation. Hence, the goal of this study was to automate the procedure of Meaburn et al. The first step to automate was nuclear segmentation in tissue samples, which in itself is a challenging task.

Cell and nuclear segmentation in histopathology and fluorescence microscopy is an active area of research, resulting in the development of several automatic (8,9) and semiautomatic (10,11) strategies. The majority of these methods, in general, use preprocessing for noise reduction and intensity/gradient-based thresholding for foreground identification. This is followed by independent or combined application of segmentation algorithms (e.g., gradient-based methods (12,13), active contours, watershed, and dynamic programming (DP) (10,14)) for delineation of individual objects within the foreground. Watershed-based algorithms (15,16), which split thresholded objects into fragments, are often referred to as “universal segmenters,” but over-segmentation is a common problem requiring subsequent merging strategies (17). Active contours are generally considered state-of-the-art due to high accuracy, adaptability to image topology, and ability to incorporate regularity features (18,19). However, computational load, correct initialization, and numerical instability are major concerns.

Most of the aforementioned segmentation techniques yield desirable results for specific cell culture images, but their extension to complex tissue sections has been less promising, especially for cancer tissue where there is considerable variation in the morphological and textural properties of nuclei along with severe nuclear clustering. However, the nuclear segmentation requirements for our application are different because thousands of nuclei are available for imaging in each tissue section, of which less than 10% (100–200 per sample) are needed for detecting cancer based on gene positioning. Thus, our requirement is highly accurate segmentation of only a subset of nuclei rather than attempting to segment as many nuclei as possible. Therefore, we built a computational framework that uses a supervised pattern recognition engine (PRE) to perform the task of selecting accurately delineated nuclei from a robust, multistage segmentation algorithm.

Pattern recognition and machine-learning principles have been proven useful in several quantitative imaging applications related to cell biology (20,21), and more specifically in breast cancer (e.g., Wisconsin Breast Cancer Database (22,23)). Some of the relevant biological applications of PREs at the cellular and subcellular levels include classification of cells and nuclei based on their morphological, textural, and appearance features (24,25), and interpreting and analyzing localization of proteins, antibodies, and subcellular structures within the cell (26–29). For instance, Hill et al. (30) assessed the impact of imperfect segmentation on the quality of high-content screening data using a support vector machine (SVM)-based PRE to identify accurately delineated nuclei. In a similar line, to make the segmentation algorithm itself intelligent and data driven, Gudla et al. (31) used classifiers interleaved with the segmentation algorithm to identify optimal parameters for segmenting and selecting accurately delineated nuclei in cell culture images.

In this work, we mimicked, as closely as possible, the manual analysis procedure (7) in the form of an integrated workflow to automatically segment nuclei in tissue-section images using a multistage watershed-based method, followed by an artificial neural network (ANN)-based supervised PRE to screen out well-segmented nuclei, with a high degree of confidence. Because of large morphological and textural variations, standard segmentation algorithms (e.g., graph cuts and watershed on gradient-magnitude) failed to accurately segment a significant number of nuclei in each dataset. The nuclear segmentation algorithm reported here could handle the significant nuclear variations among datasets in a robust way, resulting in a satisfactory yield of well-segmented nuclei for analyzing the spatial positioning of the genes.

The rest of the article is organized as follows. The next section provides a description of the samples and images, followed by an explanation of the analytical methods: (1) segmentation of nuclei, (2) the PRE for selecting accurately delineated nuclei, and (3) boundary accuracy assessment of selected nuclei. The following section reports the performance results of the PRE and the boundary accuracy assessment in comparison to a 2D DP-based segmentation algorithm (14) which serves as a reference. Subsequently, the proposed method is applied to tissue section images for detecting breast cancer based on gene localization in the nuclei. The final section provides discussion, draws conclusions, and comments on the future directions for the work.

Materials and Methods

Samples and Images

Sample preparation and labeling were described in Ref. 7. Four to five micrometer thick formalin-fixed, paraffin-embedded human breast tissue sections were imaged using an Olympus IX70 microscope controlled by a Deltavision System (Applied Precision, Issaquah, WA) with SoftWORX 3.5.1 (Applied Precision), and fitted with a charge-coupled device camera (CoolSnap; Photometrics, Tucson, AZ), using a 60×, 1.4 oil objective lens, and an auxiliary magnification of 1.5. Nonconfocal 3D Z-stacks were acquired with a step size of 0.2 or 0.5 μm. The image size was 1,024 × 1,024, with a pixel size of 0.074 μm in both X and Y directions. For this study, the fields of view to be acquired were manually selected and focused. Large regions of interconnective tissue were not imaged, to increase the number of epithelial nuclei acquired. Beyond this, the fields of view were randomly selected over the tissue to reduce bias based on FISH signals or tissue morphology/heterogeneity. For experiments, 23 datasets (500 images) were used, of which four contained normal (N1–N4), 14 contained cancer (C1–C14), and the rest contained noncancerous breast disease (NCBD) (fibroadenoma and hyperplasia) tissue section images (B1–B5).

The red and green FISH channels were deconvolved using SoftWORX 3.5.1 to reduce background noise. The deconvolved version of the 4′,6-diamidino-2-phenylindole, dihydrochloride (DAPI) channel, although available, was not used due to increased texture that deteriorated segmentation. All three channels were reduced from 3D to 2D using maximum intensity projection (MIP). By manual analysis and manual inspection of the resulting MIPs, the increased step size of 0.5 μm gave identical results to 0.2 μm. Although 3D analysis would provide more accurate gene position measurements, the image acquisition method adopted here had been shown to produce accurate results from manual analysis (7).

Overview of Image Analysis

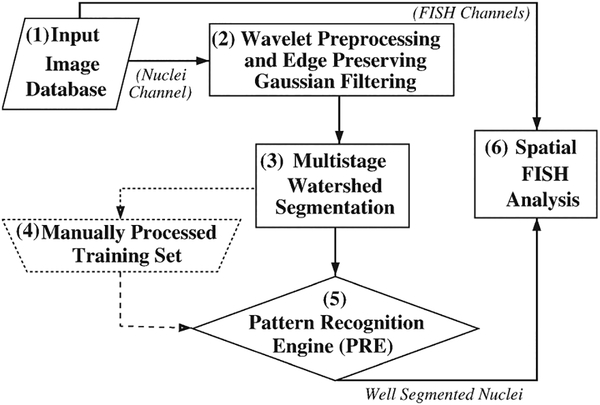
Figure 1 illustrates in block diagram form the computational framework for nuclear segmentation and the associated PRE for the identification of “well-segmented” nuclei used in spatial FISH analysis. The nuclei channel of the original images (Fig. 1-1) were first wavelet preprocessed (Fig. 1-2) and segmented (Fig. 1-3). A small portion of the dataset was manually processed and used as the training set (Fig. 1-4) for the PRE (Fig. 1-5). The set of accurately segmented nuclei were then used for spatial analysis of the gene (Fig. 1-6).

Figure 1.

Flow diagram showing the computational framework.

Preprocessing

To improve nuclear segmentation accuracy, boundaries of foreground objects (e.g., cell nuclei) were enhanced using a modified version of Mallat-Zhong’s extrema algorithm (31,32). This wavelet preprocessing step involved: (i) using a bicubic spline wavelet to decompose and identify the extremas in the DAPI-channel up to 5 scales; (ii) multiplying the chain-coded extremas (edges) in scales 2–4 by a factor of 3; (iii) and using the enhanced extremas in the wavelet reconstruction step. As this processing was isotropic, noise and structures orthogonal to nuclear boundaries were also enhanced. This undesirable effect was ameliorated by smoothing with an edge-preserving adaptive Gaussian filter (33), of standard deviation of 2 pixels and 0 pixels, along the direction of edges and in the perpendicular direction to the edges, respectively. Figure 2(a) shows an original nuclei channel image and Figure 2(b) shows the same after preprocessing.

Figure 2.

Representative image and the corresponding outputs at different segmentation steps. (a) Original DAPI channel nuclei image. (b) Preprocessed nuclei channel. (c) Seeded intensity watershed output on image foreground. (d) GDT output. (e) Merged output of intensity and GDT watershed. (f) Final segmentation output after the cluster-breaking watershed and tree-based merging.

Segmentation of Nuclei

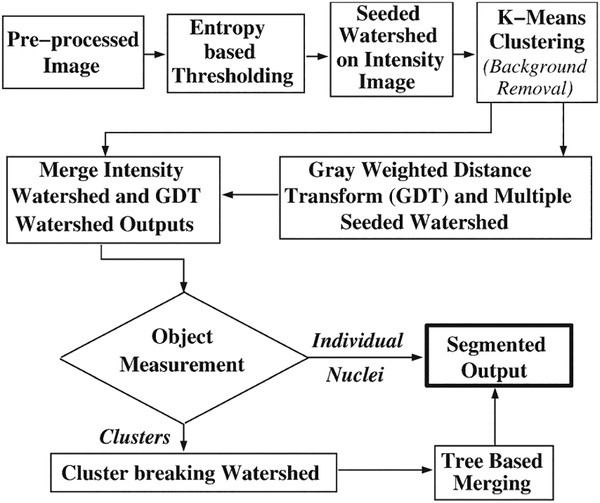
The multistage watershed nuclear segmentation algorithm is outlined in Figure 3. It first identifies nuclear foreground regions to be used for watershed in subsequent steps, by performing an entropy-based texture filtering followed by iterative isodata thresholding (34).

Figure 3.

Multistage watershed segmentation algorithm.

A seeded watershed algorithm (35) was used on the thresholded preprocessed intensity image to split the nuclear foreground regions into individual objects. Although the intensity-based watershed found object boundaries accurately, it over-segmented most of the objects. The seeds were identified from the same image using an extended-maxima transform, which was the regional maxima of the morphological reconstruction-based H-maxima transform (36). Intensity variations within nuclei made it very difficult to identify unique local maxima for each individual nuclei, resulting in over- or under-segmentation. Hence, for more reliable segmentation, we performed maxima identification using multiple values of H followed by seeded watershed. Watershed boundaries that appeared at all H values were retained as the prospective edges (Fig. 2(c)). To remove spurious fragments in the background, a k-means intensity-based clustering (37) with five cluster centers was performed on the watershed output, and the cluster having the lowest intensity average per pixel was rejected.

To merge nuclei fragments from the first watershed, we took advantage of the known morphology of nuclei through the use of the gray-weighted distance transform (GDT) (38). After applying the GDT (Fig. 2(d)), the aforementioned seeded watershed was repeated to identify high-intensity GDT-transformed nuclei regions. However, in this case, edges that appeared for more than 40% of the H values were retained as prominent edges. Although this method identified the general location and extent of the high-intensity objects, boundary accuracy of the segmented objects was low since the method was not performed directly on the preprocessed image. Hence, the output of the GDT and intensity watershed was combined as follows. Each intensity-based watershed fragment was associated with the GDT-based watershed fragment to which it had highest overlap. Then intensity-based watershed fragments associated with the same GDT-based fragments were merged into a single object. The resulting segmentation (Fig. 2(e)) was more accurate compared to the segmentation results from either the intensity or GDT watershed, which was visually verified for a large subset of the data.

The previous steps often failed to segment nuclei in large clusters. Thus, the next step identified such clusters using size and shape factor (normalized perimeter squared-to-area ratio (P2A) that is 1.0 for a perfect circle) values. It was observed that the average size of a nucleus across datasets was around 10,000 pixels, with considerable variation among datasets, and the average P2A value was 1.2 for well-segmented nuclei and ranged between 1 and 1.4. A large and irregular cluster was hence defined as one having a size ≥10,000 pixels and P2A > 1.4. Clusters were split by application of the nonseeded watershed to the cluster region of interest (ROI) of the preprocessed image.

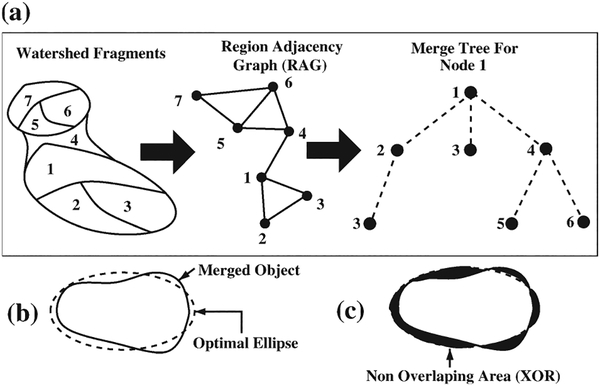
Because of nuclear size variations across datasets, the watershed algorithms, which partially depend on size criteria, over-segmented potentially good nuclei. Therefore, a tree-based hierarchical merging strategy (refer to Fig. 1 Supporting Information) coupled with nuclear shape modeling (39) was used to merge over-segmented fragments. Briefly, the procedure built a region adjacency graph of neighboring fragments from which a merging tree was created, for a given node (Fig. 4a). From the merge tree, each combination of fragments was merged and an optimal ellipse fitting was performed (Fig. 4b). If the overlap of the object and the optimal ellipse (1-[Nonoverlapping area (Exclusive OR [XOR])(Fig. 4c)/area of merged object (Fig. 4b)]) was more than 80%, the objects were merged. The final output of the segmentation module after merging is shown in Figure 2(f).

Figure 4.

(a) Process of building up the merge tree for a node. (b) Merged fragment and optimal ellipse fit. (c) Nonoverlapping (XOR) area.

PRE: Feature Measurement and Selection

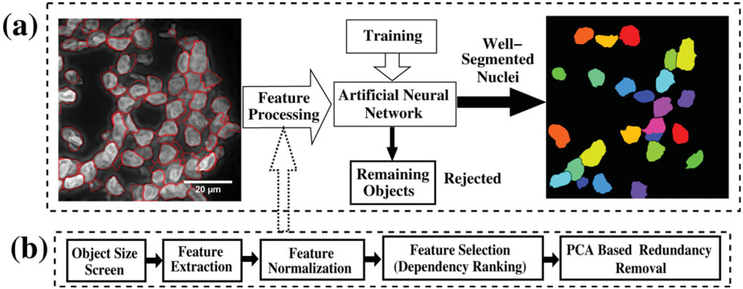
Well-segmented nuclei were selected from the segmented objects using an ANN-based supervised PRE. The problem was posed as a two-Class classification problem, with Class-1 and Class-2 representing accurately segmented nuclei and remaining segmented objects, respectively. The workflow for the PRE is shown in Figure 5.

Figure 5.

(a) PRE for identifying accurately segmented nuclei. (b) Details of the feature processing.

In order for the PRE to perform well, the feature set must capture pertinent characteristics of accurately segmented nuclei, which was done using a 64-dimensional feature set (refer to Feature Set in Supporting Information). The features are composed of 3 groups: shape-based (e.g., Feret diameters, P2A, PodczeckShapes (40), size, and ratio of object area to convex hull area), intensity-based (e.g., gray inertia, mean intensity, intensity standard deviation), and texture-based (e.g., Haralick texture features) (41).

As ANNs require feature normalization to ensure numerical stability and to overcome problems such as neural network saturation while training with the backpropagation algorithm (37,42), features were processed in the following three steps (Fig. 5b). In step one, five normalization techniques (43) were tested, namely (i) linear scaling to unit range, (ii) Z-Score scaling, (iii) linear scaling to unit variance, (iv) transformation to uniform distribution, and (v) rank normalization (refer to Table 1 in Supporting Information). In step two, dependency ranking (44) was used to select features that to some extent correlated with the output classification. Dependency ranking was calculated using:

$$D\left(i\right)=\iint p\left(x_i,y\right)\left|\text{log}\frac{p\left(x_i,y\right)}{p\left(x_i\right)p\left(y\right)}\right|d{x}_i{d}_y,$$

where D(i) is the dependency ranking score, x_i is the value of the ith feature, and y is the vector of output labels. The ranking provided a correlation score (dependency values) for each feature relative to the output classes, which are based on the mutual information between the feature vectors and the output label vector (refer to Fig. 2 Supporting Information). The third step reduced the number of features selected from dependency ranking using principal component analysis (PCA). This step removed redundancies caused by strong correlation between features.

Object Classification Using an ANN

We had observed in 3D space considerable overlap of the three most significant features from PCA between correctly and incorrectly segmented nuclei (refer to Fig. 3 Supporting Information), which in turn meant that a nonlinear discriminant function was required to discriminate between the two object classes. Hence, we used an ANN that comprised three layers: an input layer, a single hidden layer containing neurons with tansigmoidal transfer-function, and an output layer with a linear transfer-function. ANN training used 45 images (10% of the entire data), where correctly segmented nuclei had been manually identified. Training was performed by the Levenberg-Marquardt back propagation training algorithm (45), the conjugate gradient backpropagation with Powell-Beale restarts(46), or Resilient backpropagation (47) from the Neural Network Toolbox in MATLAB 2008a (48).

Performance Assessment

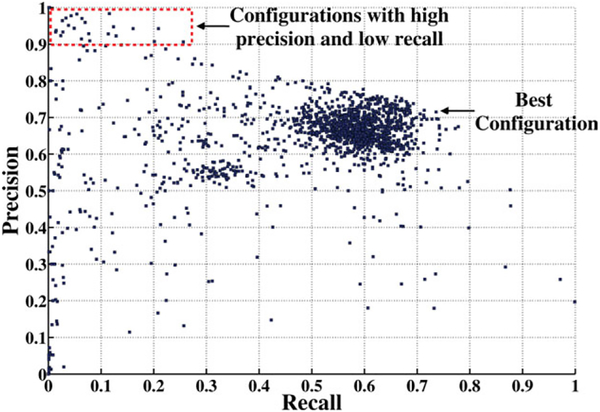
Performance of the processing pipeline was assessed in two ways. The first measured the accuracy of identifying well-segmented nuclei in a validation set of images using precision recall plots for all 1,620 configurations of the PRE by varying the number of neurons in the hidden layer of the ANN (nine settings), the normalization method (five normalizations and no-normalization), the number of PCA dimensions (five settings), and the number of features selected using dependency ranking (six settings). Precision and recall were defined as TP/TP + FP), and TP/(TP + FN), respectively, where TP = true positive, FP = false positive, and FN = false negative. As ideally both precision and recall should equal 1, the PRE configuration closest (in terms of Euclidean distance) to the point (1,1) was selected as the best possible configuration. This implicitly decided the cut off for the features used from the feature selection procedure.

The second way measured the boundary delineation accuracy of automatically segmented nuclei by comparison to control segmentations generated by human interaction. However, given the notorious tedium in precisely delineating nuclei by hand, an efficient 2D DP-based semiautomatic algorithm (SAA) (14) was used to generate control segmentations. Thus, the initial task was to validate the accuracy of SAA using synthetic control images of nuclei. Images of 20 synthetic nuclei were created by starting with 20 manually segmented nuclei from tissue sections, to capture the typical morphology of actual nuclei. Then known distortions of the image acquisition process, such as blurring and noise, were estimated from the actual tissue images and were used to distort the idealized nuclei images. Background and nuclear intensities were set to 16 and 90, respectively. Next, these bilevel images were Gaussian blurred by the lateral resolution of the microscope given by 0.51 λ/NA, where λ is the emission wavelength of the DAPI channel (450 nm) and NA (1.4) is the numerical aperture of the objective lens. Taking into consideration a pixel resolution of 74 nm, the standard deviation of the Gaussian was 0.9407 pixels. The noise level in tissue images was estimated by subtracting a Gaussian blurred version of the images from original images and calculating the variance, resulting in a standard deviation of 3.3, which was added to the synthetic images as Poisson noise.

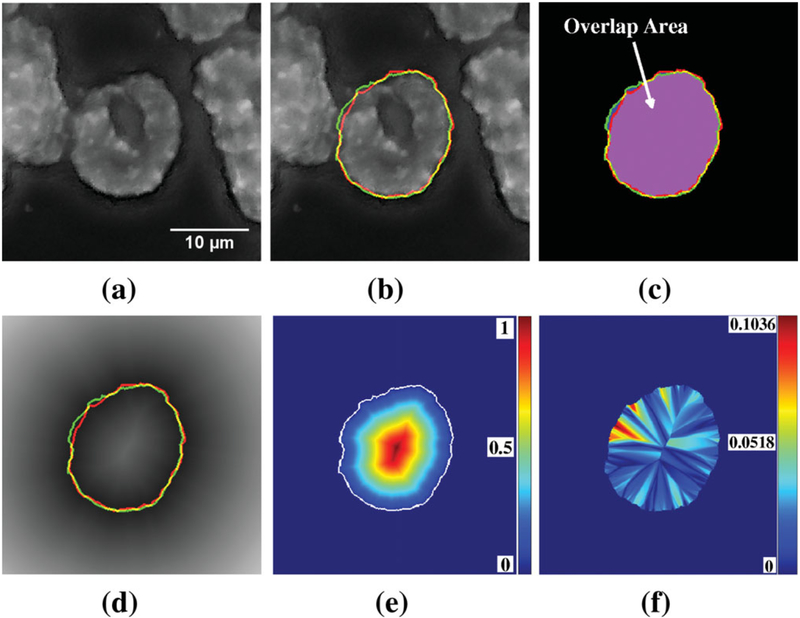
Three parameters were used to measure boundary delineation accuracy. The first measured the overlap between test and control segmentations using area similarity (AS) (49–52) defined as (2 × A[T ∩ C])/(A[T] + A[C]), where A[·] is the area of an object, ∩ is the intersection of two objects, T is the test segmentation mask, and C is the control segmentation mask. Thus, AS ranged from 1 for perfect agreement between test and control segmentations, down to 0 for no overlap between test and control and for cases where either the test or control segmentation did not exist. This metric provided a combined accuracy from all the automatically selected nuclei including the false positives. Consequently, it was the true accuracy measure for the automatic analysis procedure. Figure 6a shows a sample nucleus and Figure 6b shows the two boundaries (control and test) overlaid on it. Figure 6c shows the overlap area used to calculate AS. The second parameter was a Euclidean distance transform (EDT)-based boundary metric explicitly designed to measure error at the nuclear boundary. For each nucleus, the EDT was performed on the control segmentation, with progressively higher values assigned to pixels farther from the control boundary. Pixel values in the EDT image at the position of the test segmentation boundary were averaged to calculate boundary error. Figure 6d shows boundaries superimposed on the EDT image calculated with respect to the control segmentation boundary. The third parameter measured the normalized mean spatial deviation of all pixels in the overlapping area of the control and test segmentations of a nucleus. It was used to assess the effects of nuclear segmentation inaccuracies on the gene localization measurement. The EDT assigned a value of 0 to the boundary locations of the nucleus and increasing values to points farther within the nucleus (Fig. 6e). The parameter was the mean of the absolute differences between the EDT images of the control and test segmentations where the two segmentations overlapped. Figure 6f shows a heat map of the differences. Correlation analysis was performed between the three parameters to determine whether the parameters measured independent features of segmentation errors or alternatively whether one parameter would suffice.

Figure 6.

(a) Example nucleus for boundary accuracy assessment. (b) Example nucleus with control. (C) (Green) and test (T) (Red) segmentation. (c) Overlap area (purple) used to measure AS. (d) Distance transform-based boundary accuracy calculation. Distance transform was calculated with respect to control segmentation. (e) Normalized EDT calculation on control segmentation mask used to measure difference in relative distance measure. Control segmentation boundary is shown in white. (f) Difference in normalized EDT-based relative distance measure.

Results

The proposed image analysis steps were implemented in MATLAB (Release 2008a, Mathworks, Natick, MA), except for wavelet-based edge enhancement, which was implemented in LastWave (32). All the necessary code is available online (http://ncifrederick.cancer.gov/atp/omal/flo/Ann.aspx) through a license agreement with the National Cancer Institute. Raw datasets (2D MIP, R-G-B images only) and the output from the proposed workflow are also available through a material transfer agreement with the National Cancer Institute (contact corresponding author).

Classification Performance

We assessed the accuracy of identifying well-segmented nuclei from precision-recall plots (Fig. 7) for 1,620 different configurations of the PRE using a manually annotated verification set of 133 images that were acquired from the same patient samples as the training set. The three ANN training algorithms mentioned earlier provided similar results in terms of performance and training time. The backpropagation algorithm was used for the ANN training. Prior to selection by the PRE, segmentation output had a precision of only 17% of segmented objects accurately representing individual nuclei based on visual inspection. The best PRE configuration used the 15 top features from dependency ranking, all 15 dimensions from PCA, rank normalization, and 15 neurons in the hidden layer, resulting in a precision = 71.5% and recall = 73.6%. Some false positive errors (debris, nuclear clusters, etc.) closely resembled well-segmented nuclei in shape, size, and other morphological features. Figure 4 in the Supporting Information shows samples of objects screened by the PRE as well segmented and rejected.

Figure 7.

PRE precision-recall plot for 1,620 configurations and the best configuration (closest to (1,1)). Configurations with high precision and low recall are shown in the red box.

Segmentation Accuracy of Selected Nuclei

The first step in assessing the segmentation accuracy of automatically selected nuclei was to ensure that the SAA was at least as accurate as hand delineation of nuclei using synthetic control images. Measurements over 20 nuclei showed this was the case for all three segmentation accuracy parameters (Table 1 and Fig. 5, Supporting Information). Therefore, the SAA was used as the control for subsequent assessments of automatic segmentation accuracy.

Table 1.

Mean and standard deviation of accuracy parameters

MEAN/STANDARD DEVIATION	AREA SIMILARITY PER NUCLEI	MEAN EDT-BASED BOUNDARY ERROR (IN PIXELS)	EDT-BASED RELATIVE DISTANCE ERROR PER PIXEL
(I) By hand versus control boundary	0.9804/0.0036	1.2050/0.2407	0.0171/0.0031
(II) SAA versus control boundary	0.9843/0.0034	1.042/0.0580	0.0137/0.0033
(III) Automatic versus SAA	0.913/0.12	3.639/2.084	0.073/0.081

For assessing segmentation accuracy of the proposed workflow, AS was measured for all automatically selected nuclei, setting the value 0 for false positive nuclei. The mean value was 76%, which, as expected, was lower than other reported accuracies that were measured over only true positive objects. When we evaluated AS for true positive objects only, to be consistent with other reported results, we obtained91.3% (Table 1), which is equivalent to the accuracy we have achieved for nuclei in cell culture (31) and is significantly improved over reported accuracy in cancer tissue of 80% (53).

We calculated the mean error at the boundary and the mean normalized internal error for only true positive objects (Table 1) because these metrics are indeterminate for false positive objects. Both the mean boundary and internal errors of 3.6 pixels and 7.3%, respectively, are approximately equivalent to the optical resolution limit.

Comparing the segmentation accuracy metrics showed correlations of 96% between AS and the internal pixel difference, 33% between AS and the boundary parameter, and 33% between the internal pixel difference and boundary parameter. This shows that only one of the parameters AS or internal pixel difference is needed, while the boundary parameter does provide extra information not provided by either AS or internal pixel difference. However, depending on the application, either AS or the internal pixel difference may be more useful than the other.

Application to Gene Localization for Breast Cancer Detection

The set of nuclei identified as well segmented by the PRE were used for discriminating normal and cancer tissue sections using spatial analysis of the FISH signals. In this study, we only analyzed HES5, a gene in the NOTCH pathway (54) that occupies different nuclear positions in normal and cancer tissues (7).

Spatial Analysis of FISH Signals

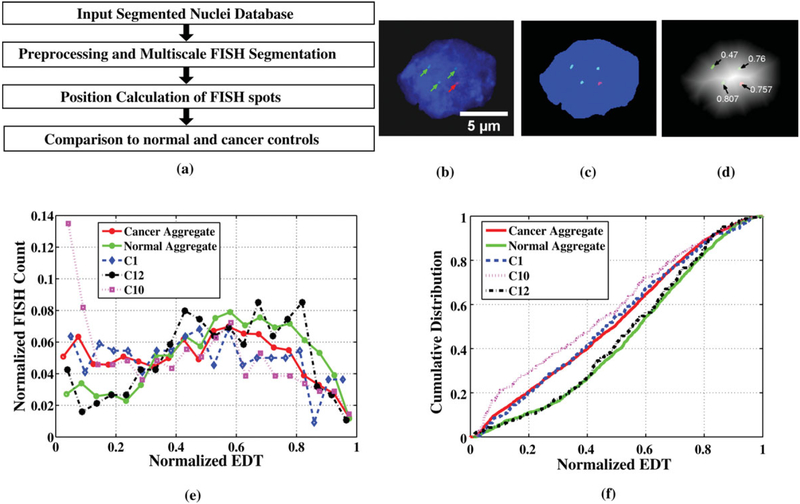
Figure 8a shows the procedure for spatial analysis of FISH signals in segmented nuclei. The spot-like FISH signals (Fig. 8b) were segmented (Fig. 8c) using a derivative scale-space method (55). The position of the spots with respect to the nuclear center and periphery was calculated using a shape-independent EDT-based metric and was normalized relative to the highest EDT value in the nucleus (Fig. 8d). The KS test was used to compare the distributions of gene positions in the nuclei of normal versus cancer specimens. Two samples were considered significantly different if the probability of them being from the same distribution obtained via the KS test was less than or equal to 1%.

Figure 8.

(a) Flow diagram showing steps for spatial gene localization analysis. (b) Original image of segmented nucleus showing red and green FISH spots marked by arrows. (c) Nucleus ROI showing segmented FISH spots. (d) EDT nucleus ROI showing normalized distance transform metric for each FISH spot. (e) Histogram of FISH signal positions binned by normalized EDT values for aggregate cancers, aggregate normals, and cancer samples C1, C10, and C12. (f) Cumulative distribution of FISH spots against normalized EDT values for aggregate cancers, aggregate normals, and cancer samples C1, C10, and C12.

Manual Analysis

For manual analysis, individual cell nuclei were manually delineated using the lasso tool in Photoshop 7.0 (Adobe Systems Incorporated, San Jose, CA) and were saved as separate image files. The red and green channels (FISH channels) of each nucleus were adjusted to reduce the background. After 130 nuclei were segmented, no further tissue images were processed for a dataset. Spatial FISH analysis was performed using the same procedure that was used for the automated analysis. Data from the manual analysis of these tissues have previously been reported (7).

Results for Gene Localization

Twenty-three tissues were analyzed, consisting of four normal (N1–N4), five NCBD (B1–B5), and 14 cancer samples (C1–C14). The set of nuclei selected by human experts and the PRE did not have a 100% correspondence. Table 2 shows the number of well-segmented nuclei selected both manually and automatically.

Table 2.

Manual and well-segmented automatic nuclei count

DATASET	NUMBER OF IMAGES	MANUAL NUCLEI COUNT	AUTOMATIC NUCLEI COUNT
N1–N4	114	536	676
C1–C14	257	1,965	2,588
B1–B5	129	699	736
Total	500	3,200	4,000

As expected, the copy number distribution of detected FISH signals per nucleus showed that the cancer samples had significantly more than two copies per nucleus (refer to Table 2 in Supporting Information). However, as it was rare for nuclei to have more than 10 FISH spots, such nuclei were rejected as potentially having spuriously detected spots.

Performance of the proposed processing pipeline was assessed by its ability to discriminate between normal, NCBD, and cancer, and its agreement to manual analysis. Figure 8e shows the automatically calculated distribution of gene positions aggregated for all cancers, for all normal, and for three individual cancers (C1, C10, and C12), and Figure 8f shows the equivalent cumulative distributions. From Figure 8e, we observe that cancer samples have significantly more nuclei where the HES5 gene is closer to the periphery (normalized EDT 0.2) than in normal samples. This is consistent with findings of the manual analysis of these tissues (7).

Comparison of normals with each other and with NCBD showed no significant differences when analyzed automatically. Manual analysis reported similar results except that one pair of normal samples (N2 vs. N3) was significantly different and one normal sample (N3) was significantly different from two (B1 and B5) out of five NCBDs (green cells in Table 3). The red cells in Table 3 denote the cases where cancer samples were not significantly different from the normal samples. Among 56 cancer versus normal comparisons, the results of the manual and the proposed method are in accord for more than 80% of cases. When the majority vote of normal specimens versus a cancer specimen was used, manual and automatic analyses concur for 11 out of 14 cancers. In the remaining three cases (C2, C10, and C14), either manual or automatic analysis gave an uncertain result and there were no outright contradictions.

Table 3.

Probability of similarity of FISH signal distribution between normal, cancer and NCBD tissue sections using manual and automatic processing^a,b,c

	N1	N2	N3	N4	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13	C14	B1	B2	B3	B4	B5
											Manual Analysis
N1	1	0.46	0.1	0.66	0	0	0.7	0	0	0	0	0	0	0.01	0	0.01	0	0.4	0.29	0.2	0.05	0.44	0.13
N2	*	1	0	0.51	0	0	0.12	0	0	0	0	0	0	0	0	0	0	0.13	0.4	0.51	0.01	0.87	0.56
N3	*	*	1	0.18	0	0	0.47	0	0	0	0	0	0	0.15	0	0.39	0.05	0.15	0	0.02	0.78	0.01	0
N4	*	*	*	1	0	0	0.83	0	0	0	0	0	0	0	0	0.01	0	0.5	0.17	0.24	0.06	0.26	0.18
											Automatic Analysis
N1	1	0.41	0.67	0.12	0.00	0.00	0.81	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.96	0.00	0.02	0.17	0.43	0.64	0.49	0.30
N2	*	1	0.12	0.20	0.00	0.01	0.41	0.01	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.40	0.00	0.03	0.25	0.80	0.12	0.55	0.96
N3	*	*	1	0.06	0.00	0.00	0.92	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.78	0.00	0.00	0.02	0.13	0.22	0.12	0.11
N4	*	*	*	1	0.04	0.10	0.29	0.10	0.00	0.00	0.00	0.01	0.00	0.00	0.08	0.34	0.01	0.00	0.01	0.21	0.19	0.04	0.16

^aTwo samples were considered significantly different if the probability from the KS test was less than or equal to 1%.

^bGreen cells denote cases where normal or NCBD samples were not similar to normal samples.

^cRed cells denote cases where cancer samples were similar to normal samples.

^*Means that the comparison value for example N2 vs N1 is the same as that for N1 vs N2.

Discussion and Conclusion

We have demonstrated an integrated workflow featuring an automatic nuclei segmentation and a supervised ANN-based PRE for nuclei screening, which, along with statistical analysis of the spatial localization of the HES5 gene in cell nuclei, has the potential to detect breast cancer from tissue sections. As manual analysis of tissue sections is subjective and time consuming, our supervised method is essential and opens up the possibility of a future procedure for diagnosis and/or prognosis of breast cancer through reliable and robust automation.

Aspects of the analysis strategy adopted in this study warrant further discussion. Although the use of 2D MIPs from the original 3D DAPI channel showed that the segmentation algorithm could potentially be used for segmenting nonconfocal 2D images acquired on conventional fluorescence microscopes, a future, separate study will answer which is the best acquisition mode. Confocal, nonconfocal 3D followed by deconvolution (done in this case), and nonconfocal 2D are all technically feasible. We would want to first determine which is the most accurate and then determine how much performance degrades using conventional fluorescence microscopy. Given the fact that the method works successfully in a 2D setting, as shown by the reported experiments, a full 3D analysis, which is more accurate, will be considered next.

We compared methods to assess the boundary accuracy of nuclei screened by the PRE in terms of the unique requirements for gene localization analysis. The assessment was aided by a DP-based semiautomatic segmentation to rapidly and accurately generate validation data. Several methods have been devised previously to assess the boundary accuracy of segmented objects, of which manual identification of over-, under-, and correctly segmented nuclei (10,11) is the most common. However, as reported earlier, utilization of simulated objects (10) enables quantitative identification of the performance limits of a segmentation algorithm. For our work, we used three accuracy parameters: area intersection between control and test segmentation, mean EDT-based boundary deviation of the test segmentation from the control segmentation (31), and a novel EDT-based relative distance error per pixel to assess the impact of boundary inaccuracies on FISH localization measurements. As evident from Table 1, the average error of 0.073 per pixel corresponds to AS of 91.3% and a mean boundary error of 3.639 pixels. A close examination of Figure 8e reveals that cancer detection results are not adversely affected by an error of 0.073 per pixel. This is further justified by the fact that a left-shifted normal cumulative plot or a right-shifted cancer cumulative plot (Fig. 8f), by normalized EDT value of0.073, does not affect the statistically significant difference between the normals and the cancers obtained by the KS test.

Sensitivity analysis was qualitative at this stage. Many iterations of the nuclear segmentation algorithm were tested during development and, in particular, the method described herein out-performed an earlier published method based on a hybrid levelset-watershed-based algorithm (56). In general, it was observed that the current segmentation algorithm satisfactorily handled significant intensity variations in the DAPI channel, including cases of interimage intensity variation across datasets and also internucleus intensity variation within a single image. Although we considered that all our samples were of the same quality because they had been labeled and imaged under the same protocol, the quality of segmentation did depend on certain sample characteristics. As an example, the segmentation results for normal datasets were not as good as cancer datasets because normals showed significantly more nuclear clustering compared to cancer samples. Although the robustness of the multistage watershed algorithm to morphological, textural, and size variations of the nuclei was further verified by the consistent results in a much larger tissue micro-array dataset containing approximately 1,700 images (results not shown), we envision additional opportunities for improvements by merging results from multiple segmentation algorithms. Often, different algorithms successfully segment different subsets of nuclei, thus merging the output from different algorithms should increase the yield of well-segmented nuclei. As mentioned above, the ease of segmentation did correlate to some extent to the disease progression. However, we have no evidence that the automated analysis is biasing the data using only easily segmentable nuclei. Future studies with the system will address such issues further.

In the case of the PRE, the future improvement would involve the use of online learning systems (57) to enable the system to learn from its mistakes. Similarly, visual inspection of automatically selected nuclei to admit only true positives would further improve performance. A small subset of new data can be provided to a user and the manual decisions made on that subset can be used to further improve the discriminating power of the PRE. Although the supervised PRE was trained on breast cancer tissue images that had a range of nuclear morphologies, we expect it would successfully screen other tissue images as long as the dominant features identifying well-segmented nuclei remain the same. Conversely, cancers from different organ sites likely have a different set of distinctive features, and therefore the PRE would need to be retrained. In this study, ANN was used to identify the well-segmented set of nuclei. However, other pattern classification methods (e.g., SVM and random forests) could provide improved precision-recall performance. Furthermore, to enhance the accuracy and effectiveness of this cancer diagnostic system, spatial analysis of multiple genes could be combined (7).

One of the strengths of the workflow is that it is modular. That is, each step (e.g., nuclear segmentation and pattern analysis) can be substituted by an improved algorithm providing scope for continuous improvement of the processing pipeline. The same workflow can be applied to a broader spectrum of cell biology applications [e.g., cancer malignancy classification and grading from histopathology sections (58) and DNA ploidy analysis (59)], where the quality of nuclei segmentation is paramount and where a larger pool of nuclei is acquired than is required for drawing a statistically significant conclusion. In this context, we point out that the segmentation algorithm required no manual intervention for segmenting nuclei in the reported tissue section datasets. The robustness of the algorithm was achieved by the use of multiple stages of watershed-based segmentation and pattern classification that can be viewed as the merger of a bottom-up (intensity watershed followed by GDT-based and tree-based merging) and a top-down (cluster identification and further nuclear segmentation within the clusters) method. For users having minimal experience in image analysis and pattern recognition, a user-friendly software tool is being developed, which can be used to perform all the analysis steps illustrated in the framework with minimal manual intervention. We have made the software for the reported work available at: (http://ncifrederick.cancer.gov/atp/omal/flo/Ann.aspx), which will enable image analysis experts to further advance the method. However, the value of the work does not lie solely in the utility of the software. A key value is the discovery that automatically selecting cell nuclei is not only feasible but can lead to valuable biomedical results. Also, another goal of this study was to show that a successful manual method can be automated. Further characterization, such as quality of nuclei selected/rejected, quality of FISH signal selected/rejected, and sensitivity analysis, is for a future study.

The results from our workflow, both in terms of cancer detection and nuclei screening, are very encouraging. Comparing the spatial distribution of FISH spots for the HES5 gene obtained by manual and automatic procedures show very good correspondence, justifying the effectiveness of the automation. We have also shown that the system selects almost 70% of the well-segmented nuclei and the screened nuclei have high boundary accuracy when compared to validated semiautomatic nuclear segmentation. In summary, these very promising results show for the first time the potential of a supervised learning-based high-throughput and objective test for breast cancer using localization statistics of certain genes within the cell nucleus. With further validation across large numbers of samples, it could have a subsidiary role in diagnosis, prognosis, or further understanding of the mechanisms of cancer development.