Bivariate Left-Censored Bayesian Model for Predicting Exposure: Preliminary Analysis of Worker Exposure during the Deepwater Horizon Oil Spill

Abstract

In April 2010, the Deepwater Horizon oil rig caught fire and exploded, releasing almost 5 million barrels of oil into the Gulf of Mexico over the ensuing 3 months. Thousands of oil spill workers participated in the spill response and clean-up efforts. The GuLF STUDY being conducted by the National Institute of Environmental Health Sciences is an epidemiological study to investigate potential adverse health effects among these oil spill clean-up workers. Many volatile chemicals were released from the oil into the air, including total hydrocarbons (THC), which is a composite of the volatile components of oil including benzene, toluene, ethylbenzene, xylene, and hexane (BTEXH). Our goal is to estimate exposure levels to these toxic chemicals for groups of oil spill workers in the study (hereafter called exposure groups, EGs) with likely comparable exposure distributions. A large number of air measurements were collected, but many EGs are characterized by datasets with a large percentage of censored measurements (below the analytic methods’ limits of detection) and/or a limited number of measurements. We use THC for which there was less censoring to develop predictive linear models for specific BTEXH air exposures with higher degrees of censoring. We present a novel Bayesian hierarchical linear model that allows us to predict, for different EGs simultaneously, exposure levels of a second chemical while accounting for censoring in both THC and the chemical of interest. We illustrate the methodology by estimating exposure levels for several EGs on the Development Driller III, a rig vessel charged with drilling one of the relief wells. The model provided credible estimates in this example for geometric means, arithmetic means, variances, correlations, and regression coefficients for each group. This approach should be considered when estimating exposures in situations when multiple chemicals are correlated and have varying degrees of censoring.

Introduction

On April 20, 2010, the Deepwater Horizon (DWH) oil rig exploded and sank two days later, resulting in the release of almost 5 million barrels of oil into the Gulf of Mexico over the ensuing 3 months. Thousands of workers were involved in the response and clean-up effort (hereafter oil spill workers).

Oil can release many harmful chemicals into the air, which are typically reported as total hydrocarbons (THC). THC is a composite of the volatile components of oil. Some of the more volatile, toxic components include benzene, toluene, ethylbenzene, xylene, and hexane (BTEXH). A review of the literature by Aguilera et al. (2010) found that increased exposure to oil-related chemicals in prior spills was associated with a variety of detrimental health effects. The National Institute for Environmental Health Sciences (NIEHS) is conducting the GuLF STUDY (Kwok et al. 2015) to investigate potential adverse health effects from exposure to these spill-related chemicals. Once estimates of exposure levels have been developed, epidemiologists will use these estimates to assess the relationships between various health outcomes and these exposures.

Exposures were measured using passive dosimeters worn by workers. Over 26,500 personal air samples (each sample was analyzed for 5–10 different chemicals resulting in about 150,000 measurements) that met the study criteria included a number of results at or below the analytic methods’ limits of detection (LODs). The proportion of measurements below the LOD is, in part, a function of the analytic method’s sensitivity and the duration of the sampling. Low levels of exposure are of interest for several reasons. In epidemiological studies, health effects at low level exposures have not always been studied. Possible additive or synergistic adverse health effects may occur in the presence of other exposures experienced at the time (e.g. other oil components, dispersants, particulates, heat, and long working hours). The actual exposure threshold where adverse outcomes occur may not be known. Finally, a low exposed group is often used in epidemiological studies as the reference population to which higher exposed groups are compared. Therefore, although measurement values may be below the LOD, the low or censored measurement values are not zero and could be informative.

We, therefore, sought a statistical model that allows us to predict exposure levels to oil-related chemicals using the corresponding THC measurements because censoring is much more prevalent among the BTEXH measurements. Equally important, we seek to quantify the uncertainty in both our estimate of each censored observation and in our estimate of the relationship between BTEXH and THC. This provides us insight beyond current approaches for handling censored observations. Therefore, we constructed a hierarchical Bayesian regression model that accounts for censored observations in both THC and the chemical of interest (including pairs when both the chemical and THC are censored). In this paper, we model THC concentration as the predictor (X) and consider the response (Y) to be the concentration of one of the BTEXH chemicals. After establishing a relationship between THC and the chemical, we can use this relationship to generate relatively unbiased exposure estimates for that chemical for groups of workers expected to have similar exposure distributions [hereafter exposure groups (EGs)].

In the next section, we briefly describe the measurement of the chemicals and underlying chemical relationships. Then we describe the method and provide an example of xylene exposure estimates for a subset of EGs on a rig ship called the Development Driller III (DDIII), although this method should generalize to the other BTEH chemicals.

Exposures During the DWH Oil Spill

Airborne exposure measurements were collected by industrial hygiene personnel working for a BP (the responsible party) contractor using 3M 3500, 3M 3520 or Assay Technology 521 passive organic vapor dosimeters. Sampling lasted from <1 to >24 hours, but we use measurements with durations of 4–18 hours to reflect the worker’s full-shift of 8–12 hours. Each measurement used in the model was analyzed for a number of chemicals, including THC, BTEX, and for a subset, hexane. THC was determined using a modified NIOSH method Naphthas 1550, whereas, BTEXH was determined using OSHA Organic Vapors Method 7 (NIOSH, 1994; OSHA, 2000). The gas chromatographs used in the analyses were equipped with dual detectors: one to determine the THC concentration and the other, the individual BTEXH chemicals concentrations. THC was determined as the composite of the volatile chemicals collected with the dosimeter: the area under all the peaks eluded from the sample (including the BTEXH chemicals) was integrated to determine the THC area-count. The THC detector was calibrated using known standards of n-hexane and reported in ppm. With the second detector, the area under each BTEXH chemical peak was integrated to determine an area-count (except for xylene that eludes as two peaks (m- and p-xylene as one peak and o-xylene as the other). The areas under both peaks were added to obtain a total xylene). Each BTEXH chemical was calibrated using a series of standards of the specific chemical. The LODs were established at the point where the detector response was significantly different from the corresponding response in the sampler blanks (generally about 3 times the response of the sampler blanks). All samples were analyzed by laboratories accredited by the American Industrial Hygiene Association Laboratory Accreditation Programs, LLC.

Approximately 10% by weight of the crude oil released in the DWH spill was THC and about 2% was BTEXH (see Supplementary Materials, available at Annals of Work Exposures and Health). This means for a particular exposure measurement, the concentration of the specific BTEXH chemical is a small fraction of the THC concentration. The analytical method is more sensitive for BTEXH than for THC (about 3 ppb for the former vs. 100 ppb for THC). Despite the higher sensitivity for BTEXH, the fact that the BTEXH components comprised <20% of the THC resulted in greater censoring of BTEXH measurements than THC measurements.

In the Gulf STUDY, THC is correlated with each of these chemicals since the primary source of exposure was likely the crude oil, and the composition of the oil was approximately constant within each of the study’s time periods. These time periods were established based on events such as oil flowing from the well, activities being performed, and degree of oil weathering.

The bases for the relationships of the oil components or other mixtures are the Ideal Gas Law and Raoult’s Law (Stenzel and Arnold, 2015). The vapor concentration (VC) of a pure chemical in the air above a chemical’s liquid surface at a specific liquid temperature is the ratio of the chemical’s vapor pressure (VP) divided by the atmospheric pressure. With mixtures such as crude oil, the VP of each component in the mixture is lower than that of the pure chemical. The degree of VP lowering is related to the chemical’s percent composition in the mixture and its molecular weight. This lower VP is called the chemical’s adjusted vapor pressure (AVP). Once the AVP is determined, it can be divided by atmospheric pressure to estimate the VC of the chemical in the air above the mixture surface. If the composition of the mixture (in mass percent) generating the vapor is constant, then the VC of each component will be constant, resulting in the relative VCs of the components of the mixture being constant (Stenzel and Arnold, 2015). This relative relationship of two components in the air can be estimated from the correlation of the components in a group of two corresponding sets of air measurements. The correlation (or linear regression) approach is often used in assessing exposure when data from one chemical in a mixture are used to estimate exposures to another chemical in the mixture (Stenzel and Arnold, 2015). In this paper, we develop a regression equation for predicting the mean of Y for a group of interest of the form β₀ + β₁X_i containing an intercept (β₀) and slope (β₁) with predictor X_i.

The concentration of these chemicals cannot be zero because each of these chemicals is found at ambient levels due to consumer and industrial sources of release. Therefore, by using a naturally logged response and predictor, we prevent the predicted exposure for the chemical of interest from being exactly zero.

Occupational exposures are affected by a variety of determinants such as job title, activity, and location. Since EGs were identified for a unique set of determinants, within an EG, exposure distributions were assumed to be similar. Exposure can vary among EGs because of variations in tasks performed and the duration of these tasks, but the correlations between the specific chemicals and THC concentrations should be constant because the dominant source of the exposure is likely the crude oil. Since the ultimate goal in exposure assessment is to provide exposure estimates for each of these EGs, we simultaneously modeled multiple EGs, each having its own regression equation (intercept and slope coefficient) to distinguish different exposure levels among the EGs. To better inform estimates with limited information, we allowed the slope and intercept estimates to be influenced by other EGs in the model when censoring was high or sample size was low. This makes the model estimates for particular EGs more stable because the model formulates a global intercept and global slope estimate to use when information is limited.

Left censoring statistical methods

Several methods have been proposed to account for left-censored responses (May et al., 2011; Chen et al., 2013; Ganser and Hewitt, 2010; Chu et al., 2005). After reviewing the most promising frequentist methods, Huynh et al. (2014) compared maximum likelihood estimation, β-substitution, and reverse Kaplan–Meier methods. Huynh et al. (2014) concluded that the β-substitution method was less biased and provided lower root mean squared error estimates than the other two methods under conditions of high censoring (>50$\%$ ) and small (n = 5–10) sample sizes. Huynh et al. (2016) then compared Bayesian models to the β-substitution method. At various censoring levels, Bayesian models performed similarly (for bias and root mean squared error) to the β-substitution method for generating exposure estimates. The Bayesian models, however, also provided variance estimates, i.e. credible intervals, whereas the β-substitution method did not provide equations for calculating confidence intervals (comparable to credible intervals) for many statistics of interest (i.e. geometric means (GMs), geometric standard deviations (GSDs), and 95^th percentiles). Therefore, Huynh et al. (2016) suggest that Bayesian models have advantages over frequentist methods such as β-substitution for censored analyses in occupational health studies. Our contribution here is to expand upon the earlier work of Huynh et al. (2014, 2016) and propose a method for regression settings where either the dependent variable or the independent variable, or both, may be censored in one or more EG(s).

Statistical Methods

Bayesian methods account for uncertainty by identifying the posterior distribution of parameters of interest, including censored observations (see, e.g. Gilks et al., 1996; Marin and Robert, 2007; Carlin and Louis, 2008; Gelman et al. 2013; Brooks et al., 2011).

First, consider a typical hierarchical linear regression framework assuming all measurements on Y (natural log of xylene) and X (natural log of THC) are above their respective LODs. Instead of focusing solely upon the conditional distribution of Y|X (Y given X), which proves restrictive when extending to censored or partially observed measurement pairs (X and Y), we prefer to work with a joint distribution for Y and X. We build this joint distribution by first modeling $X\sim N(\mu ,{\sigma }_X^2)$ where µ is the mean and ${\sigma }_X^2$ is the variance. Then, we use the following regression parameterization of the mean of Y [E(Y)].

$$E(Y)={\beta }_0+{\beta }_{1}X$$ (1)

where β₀ is the intercept, and β₁ is the slope. This parameterization can be written more formally as $Y|X\sim N({\beta }_0+{\beta }_{1}X,{\sigma }_{Y|X}^2)$ . A Bayesian hierarchical model is formulated by assigning prior distributions on these parameters. We use a customary univariate normal prior for µ, the mean of X, with mean θ_µ and variance ${\sigma }_{\mu }^2$ , a bivariate normal prior for β = (β₀,β₁) with mean vector µ_β and variance–covariance matrix V_β, and inverse-gamma priors for the variances ${\sigma }_X^2$ and ${\sigma }_{Y|X}^2$ . This yields the joint distribution of all model parameters

$$\begin{array}{l}IG({\sigma }_{Y|X}^2|a,b)\times IG({\sigma }_X^2|c,d)\times N(\mu |{\theta }_{\mu },{\sigma }_{\mu }^2)\times N(\beta |{\mu }_{\beta },V_{\beta })\\ \times {\displaystyle \prod }_{j=1}^{m}N(X_j|\mu ,{\sigma }_X^2)\times {\displaystyle \prod }_{j=1}^{m}N(Y_j|{\beta }_0+{\beta }_1{X}_j,{\sigma }_{Y|X}^2),\end{array}$$ (2)

where we use the standard parametrization for the normal $N(\cdot ,\cdot )$ and inverse-gamma $IG(\cdot ,\cdot )$ distributions, as given in, e.g. the text by Gelman et al. (2013). The shape parameters ($a$ and $c$ ) and scale parameters ($b$ and $d$ ) in the IG densities stipulate the extent of prior information on the variance components. The a priori means for ${\sigma }_{Y|X}^2$ and ${\sigma }_X^2$ are $\frac{b}{a-1}$ and $\frac{d}{c-1}$ (for a > 1 and c > 1), respectively, while the variances are $\frac{b^2}{{(a-1)}^2(a-2)}$ and $\frac{d^2}{{(c-1)}^2(c-2)}$ (for a > 2 and c > 2), respectively.

Now consider the situation we face: some measurements on X and Y are below the LOD and, hence, not known exactly. Let LOD_j (X) and LOD_j (Y) be the LODs on a natural log scale for the j-th observation on X and Y, respectively. Let C_X = {j:X_j ≤ LOD_j(X)} and C_Y = {j:Y_j ≤ LOD_j(Y)} be the sets of indices for which Xs and Ys are censored, and let O_X and O_Y denote the observed values of X and Y, respectively. The Bayesian hierarchical model is the joint distribution (of all model parameters and censored values)

$$\begin{array}{l}IG({\sigma }_{Y|X}^2|a,b)\times IG({\sigma }_X^2|c,d)\times N(\mu |{\theta }_{\mu },{\sigma }_{\mu }^2)\times N(\beta |{\mu }_{\beta },V_{\beta })\\ \times {\displaystyle \prod }_{j\in O_X}N(X_j|\mu ,{\sigma }_X)\times {\displaystyle \prod }_{j\in C_X}\Phi \left(\frac{LO{D}_j(X)-\mu }{{\sigma }_X}\right)\\ \times {\displaystyle \prod }_{j\in O_Y}N(Y_j|{\beta }_0+{\beta }_1{X}_j,{\sigma }_{Y|X}^2)\times {\displaystyle \prod }_{j\in C_Y}\Phi \left(\frac{LO{D}_j(Y)-({\beta }_0+{\beta }_1{X}_j)}{{\sigma }_{Y|X}}\right),\end{array}$$ (3)

where Ф(u) denotes a standard normal cumulative density function (CDF) at u. To obtain standard normal distributions of X and Y, respectively, we standardize all values (using its mean and standard deviation). Therefore, if Z is a standard normal random variable, then Ф(u) = P(Z ≤ u) is the value of integral of a standard normal density below the value u.

The above assumes that the relationship between Y and X remains the same across EGs. We now extend (equation 3) to multiple EGs by allowing the slope and intercept to vary across EGs (here called the hierarchical Bayesian EG model). Let Y_ij and X_ij be the j-th measurement on Y and X, respectively, in EG i, where i = 1, 2, …, N_EG, and j = 1, 2, …, m_j. With analogous definitions of O_X, O_Y, C_X, and C_Y, the joint distribution of all model parameters and censored values is

$$\begin{array}{l}IW(V_{\beta }|S,\omega )\times N({\mu }_{\beta }|{\theta }_{\mu },V_{\mu })\times {\displaystyle \prod }_{i=1}^{N_{EG}}N({\mu }_i|\nu ,{\gamma }^2)\times N({\beta }_i|{\mu }_{\beta },V_{\beta })\\ \times {\displaystyle \prod }_{i=1}^{N_{EG}}IG({\sigma }_{Y|X_i}^2|a_i,b_i)\times IG({\sigma }_{X_i}^2|c_i,d_i)\times {\displaystyle \prod }_{(i,j)\in O_X}N(X_{ij}|{\mu }_i,{\sigma }_{X_i}^2)\\ \times {\displaystyle \prod }_{(i,j)\in C_X}\Phi \left(\frac{LO{D}_{ij}(X)-{\mu }_i}{{\sigma }_{X_i}}\right)\times {\displaystyle \prod }_{(i,j)\in O_Y}N(Y_{ij}|{\beta }_{0i}+{\beta }_{1i}{X}_{ij},{\sigma }_{Y|X_i}^2)\\ \times {\displaystyle \prod }_{(i,j)\in C_Y}\Phi \left(\frac{LO{D}_{ij}(Y)-({\beta }_{0i}+{\beta }_{1i}{X}_{ij})}{{\sigma }_{Y|X_i}}\right),\end{array}$$ (4)

where β_0i and β_1i are the intercept and slope parameters for EG i, µ_i is the mean of X’s for each EG i, ${\sigma }_{Y|X_i}^2$ is the conditional variance of $Y|X_i$ for EG i and ${\sigma }_{X_i}^2$ is the variance of X_i for EG i. These two variances are assumed to be distributed independently across the EGs as inverse-gamma distributions. While the shape and scale of these inverse-gamma distributions are allowed to vary across the EGs in (equation 4), in practice it is difficult to have strong prior information regarding these distributions, so we will assume that a_i= a, b_i= b, c_i= c, and d_i= d and specify values for a, b, c, and d. The µ_i’s are also modeled a priori as normal distributions, independent across EGs. For prior distributions on the regression coefficients, we define β_i = (β_0i,β_1i) as the $2\times 1$ vector containing the intercept and the slope for EG i, which is distributed as a bivariate normal distribution with mean µ_β and a $2\times 2$ variance–covariance matrix V_β. Again, these coefficients are assumed to be independent across EGs, but they borrow strength by shrinking the EG means to µ_β. Finally, µ_β is assigned a Gaussian prior and V_β is modeled a priori with an inverse-Wishart (IW) distribution with parameters S⁻¹ and ω (see, e.g. Gelman et al., 2013).

The posterior distribution for the model parameters is proportional to the corresponding joint distribution in the respective models in equations (2), (3), and (4). The posterior distribution is evaluated using numerical methods, arguably the most popular being Markov chain Monte Carlo (MCMC) algorithms such as the Gibbs sampler (as described in Gelfand et al., 1992 for censored data) and Metropolis-Hastings algorithms (see, e.g. Gilks et al., 1996; Marin and Robert, 2007; Carlin and Louis, 2008; Gelman et al., 2013; Brooks et al., 2011). MCMC algorithms produce samples from the marginal posterior distribution of each unknown parameter in equation (2). All subsequent inference proceeds from these samples. Models in equations (2), (3), and (4) are easily implemented in both OpenBUGS (http://www.openbugs.net/w/FrontPage; last accessed 11 November 2016) and RJAGS (https://cran.r-project.org/web/packages/rjags/rjags.pdf; http://mcmc-jags.sourceforge.net/; last accessed 11 November 2016) and easily evaluated. Censored observations using the above standard normal CDF notation were introduced in OpenBUGS using the $I(,)$ notation. In JAGS, censored observations were implemented using the dinterval() function (for programs see Supplementary Materials, available at Annals of Work Exposures and Health). Descriptions of GM, arithmetic mean (AM), and GSD calculations can be found in the Supplementary Materials, available at Annals of Work Exposures and Health.

Posterior predictive model comparisons

Once the posterior distribution has been evaluated, e.g. using MCMC, Bayesian model assessment often proceeds from simulating replicates of the observed data (e.g. Gelman et al., 2013). To be specific, for equation (2), the joint posterior predictive distribution of the replicates for the i-th observation, Y_rep,i and X_rep,i, is given by

$$\begin{array}{l}p(Y_{rep,i},X_{rep,i}|y_{obs},x_{obs})={{\displaystyle \int }}^{\text{}}N(Y_{rep,i}|{\beta }_0+{\beta }_1{X}_{rep,i},{\sigma }_{Y|X}^2)\times \\ N(X_{rep,i}|\mu ,{\sigma }_X^2)\times p(\theta |y_{obs},x_{obs})d\theta ,\end{array}$$ (5)

where y_obs and x_obs are the observed Y’s and X’s, respectively, and $\theta =\{{\beta }_0,{\beta }_1,\mu ,{\sigma }_X^2,{\sigma }_{Y|X}^2\}$ . We draw samples from equation (5) by first sampling ${\theta }^{(l)}$ from the posterior distribution $p(\theta |y_{obs},x_{obs})$ , then sampling $X_{rep,i}^{(l)}\sim N({\mu }^{(l)},{\sigma }_X^{2(l)})$ , and finally sampling $Y_{rep,i}^{(l)}\sim N({\beta }_0^{(l)}+{\beta }_1^{(l)}{X}_{rep,i}^{(l)},{\sigma }_{Y|X}^{2(l)})$ . This is repeated for i = 1, 2, …, n.

For the censored model in equation (3), how the replicates will be generated depends upon how X and Y have been measured. If both X and Y are above their respective LODs for the i-th observation, the posterior predictive distribution is the same as in equation (5), and we generate the replicates Y_rep,i and X_rep,i as described above. When X is above the LOD for the i-th observation, we draw the replicates $X_{rep,i}^{(l)}\sim N({\mu }^{(l)},{\sigma }_X^{2(l)})$ for each posterior sample ${\theta }^{(l)}.$ This is done irrespective of whether Y is above its LOD for that observation.

Now suppose that for the i-th observation, Y is above its LOD, but X is below its LOD. Bayesian inference treats unquantified variables as unknown parameters, and any imputation of unquantified variables must be carried out by sampling from the posterior distribution of the unmeasured variable. To be specific, let X_c,i be the random variable denoting the unquantified, or censored, X for the i-th observation. Note that replicates are defined only for observed data, so X_c,i is not a replicate and will not be used in model assessment. However, it will be sampled in order to correctly sample the replicate Y_rep,i. Using the posterior samples ${\mu }_X^{(l)}$ and ${\sigma }_X^{2(l)}$ , we will draw $X_{c,i}^{(l)}\sim N({\mu }_X^{(l)},{\sigma }_X^{2(l)})I(X_{(c,i)}<LO{D}_j(X_{(c,i)}))$ , where these values can be described as samples from a normal distribution (with mean ${\mu }_X^{(l)}$ and variance ${\sigma }_X^{2(l)}$ ) below the LOD_j (X_c,i) (Gelfand et al., 1992). Then, for each $X_{c,i}^{(l)}$ , we draw $Y_{rep,i}^{(l)}\sim N({\beta }_0^{(l)}+{\beta }_1^{(l)}{X}_{c,i}^{(l)},{\sigma }_{Y|X}^{2(l)})$ .

Finally, consider the model in equation (4). This extends equation (3) by allowing the parameters to vary by EG. Sampling the replicates will be the same as for equation (3) with θ now being the collection of all model parameters in equation (4).

For model comparisons, we use the replicated data to construct Gelfand and Ghosh’s “D-statistic” for Bayesian predictive model assessment. The “D-statistic” can be computed for each model and used to compare different models fitted to the same dataset. Specifically, we compare the replicated data to the observed data by computing a goodness-of-fit measure G and a predictive variance P that penalizes more complex models. For equation (4), we compute

$$G={\displaystyle \sum }_{(i,j)\in O_Y}{\left(y_{ij}-{\mu }_{Y_{rep},ij}\right)}^2+{\displaystyle \sum }_{(i,j)\in O_X}{\left(x_{ij}-{\mu }_{X_{rep},ij}\right)}^2\text{\hspace{0.17em}and\hspace{0.17em}}$$

$$P={\displaystyle \sum }_{(i,j)\in O_Y}{\sigma }_{Y_{rep,ij}}^2+{\displaystyle \sum }_{(i,j)\in O_X}{\sigma }_{X_{rep,ij}}^2,$$ (6)

where y_ij and x_ij are the observed measurements on Y and X, respectively, ${\mu }_{Y_{rep},ij}$ and ${\mu }_{X_{rep},ij}$ are the means, and ${\sigma }_{Y_{rep,ij}}^2$ and ${\sigma }_{X_{rep,ij}}^2$ are variances of $Y_{rep,ij}$ and $X_{rep,ij}$ , respectively. The means and variances of Y_rep,ij and X_rep,ij used in equation (6) are computed from their samples. We then calculate D = G + P as a metric for comparing models. Lower D-statistics are preferred (Gelfand and Ghosh, 1998).

Our model was first assessed through simulation studies at low, moderate, and moderate-to-high censoring levels in Y while censoring remained low in X. Results indicated that under a scenario where groups of workers were set to have different slopes and intercepts, our hierarchical Bayesian EG model would be preferred based on the D-statistic compared to simpler models, regardless of the percentage censoring. Likewise, credible intervals contained the true parameters in all scenarios (see Supplementary Materials, available at Annals of Work Exposures and Health).

Results: Illustrative Example of Estimation of Xylene Exposure During the DWH Oil Spill

In this preliminary analysis, we focused on seven EGs between May 15 and July 15, 2010 on the DDIII, a rig ship charged with drilling a relief well. During this time, other vessels were trying to stop or contain the oil release. In addition, dispersants were being injected near the Gulf floor and on the surface of the water to break up the oil and reduce atmospheric concentrations of oil-derived substances. Our goal is to estimate summary statistics for exposure to xylene, one of the volatile oil components from the THC measurements. Censoring in these measurements ranged from 0 to 25% and in the xylene measurements from 0 to 32.3% (Table 1). Censoring was higher for xylene than for THC in most of groups. Sample sizes ranged from 6 to 96 measurements.

Table 1.

Description of EGs (number of EGs = 7) on the DDIII between May 15 and July 15, 2010, assessed in this preliminary analysis as part of the GuLF STUDY.

Exposure Group	N	% Censored THC	% Censored xylene
Derrick hand	6	0.0	0.0
Floorhand/roughneck	10	10.0	10.0
Crane operator	16	12.5	31.3
Roustabout	96	19.8	32.3
Operations technician or operator	10	20.0	20.0
ROV technician	12	25.0	25.0
IH-safety	19	10.5	5.3

These exposure groups included Derrick hands, floorhands/roughnecks, crane operators, roustabouts, operation technicians and operators, remotely operated vehicle (ROV) technicians, and IH-safety workers.

Details on the prior specifications can be found in the Supplementary Materials, available at Annals of Work Exposures and Health. In this paper, we present results using weakly informative inverse-gamma priors on the variance components. We compared these results to a setting where we had informative uniform priors on the standard deviation of the natural log of THC and standard deviation of the natural log of xylene $|$ THC (restricting the GSDs 1.01–12 based on known characteristics of our data). Figures of the intercepts, slopes, correlation coefficients, GMs, GSDs, and AMs using the uniform priors are provided in the Supplementary Materials, available at Annals of Work Exposures and Health.

Convergence diagnostics, as assessed by Gelman Rubin statistics and trace plots, indicated that convergence was almost immediate. The Gelman Rubin diagnostics were less than 1.2 for all parameters of interest for the first 5000 iterations of the model. Therefore, to ensure all parameters had converged adequately, we used 25,000 iterations after 5000 iterations of burn-in.

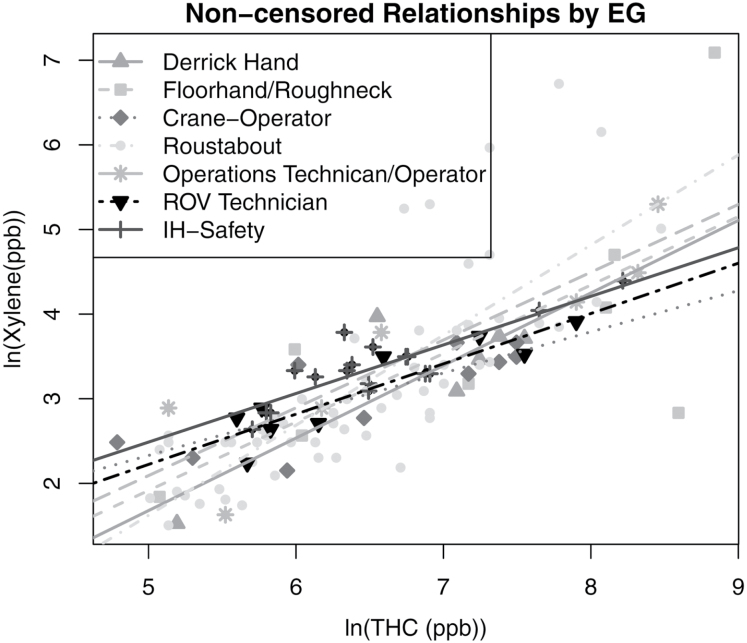
A plot of the non-censored datapoints and separate linear regression lines for each EG shows that particular EGs had slightly different linear relationships (Figure 1). In general, most points tended to follow a linear trend that could be summarized by a single regression line. However, the censored information needs to be included to know how the relationships differed among EGs. The plot also indicates that a few of the observations may be outliers. Since every point is considered real in our dataset, outliers were not excluded.

Figure 1.

Non-censored relationships by EG on the DDIII from May 15 to July 15, 2010. The plot displays all the non-censored datapoints for each EG and the corresponding linear relationship for each of those non-censored EG datasets.

We compared our Hierarchical Bayesian EG model to other simpler models. For model comparisons, we replicated the observed Xs and observed Ys from the respective models. In the first model, only an intercept was included for prediction of X and Y; X was not used in the estimation of Y, and each EG was modeled separately. This assumed different variances for each EG where we simply modeled means, not accounting for additional information. The second model had a common intercept and common slope, where EGs were not modeled separately but as one EG. The third model used varying intercepts for EGs but assumed that all EGs had the same slope estimate. In all of the above models, we account for censoring in X and Y. D-statistics were used to compare models.

The common intercept and slope model accounting for censoring in X and Y had the lowest D-statistic of the models tested (Table 2). This is likely due to the relatively low degree of censoring in this example and the highly linear trend among most of the non-censored data points (Figure 1). In addition, the P-statistic was elevated in the hierarchical Bayesian EG model because many additional parameters were estimated compared to other models. However, we still argue that our hierarchical model provides additional inference that may be useful. The common slope and common intercept model uses all the data as one EG, and does not allow us to differentiate differences among EGs. Meanwhile, the Hierarchical Bayesian EG model allows us to model each EG separately and compare the relationships among the different EGs. Although these findings suggest that the common intercept and common slope and intercept model performed the best, the Hierarchical Bayesian EG model was the best choice for our analytic needs, which include the ability to distinguish between the EGs.

Table 2.

Model comparisons metrics for the different models discussed in the text relating worker exposure to xylene on the DDIII.

Model	D-statistic	P	G
Intercept only model	772.0	479.1	292.8
Common intercept and common slope	732.4	406.0	326.4
Common slope and varying intercepts	750.3	440.6	309.8
Hierarchical Bayesian EG model	790.2	471.0	319.2

Limited work has been done to incorporate a linear relationship in estimation while accounting for censoring in X and Y in previous studies. From this model comparison, we can see that a common slope with a common intercept model and a common slope with a varying intercept model were superior to the intercept only model. Therefore, accounting for the additional information from the linear relationship was useful.

The global parameter estimate from the Hierarchical Bayesian EG model shows that the overall intercept posterior median estimate was −1.49 in natural log units and non-significant (Table 3). The lack of significance suggests that when ln(THC) = 0 (or THC = 1 ppb), ln(xylene) = 0 (or xylene = 1 ppb). The global slope estimate was significantly positive with a median posterior estimate of 0.70. This indicates that for every unit increase in ln(THC), there is a corresponding 0.70 ln unit increase in ln(xylene). The large amount of variance in the intercepts (33.31) is likely due to the low accuracy and precision of the analytical method near the chemical’s LOD. However, the relatively low variability in the slope estimates (0.06) suggests that there is likely to be only one major source generating these exposures.

Table 3.

Posterior inference for the hyperparameter (global parameter) estimates in equation (4) on the DDIII between May 15 and July 15, 2010.

Model Parameter	Median	95% Credible interval
${\mu }_{{\beta }_0}$	−1.49	(−6.47, 3.46)
${\mu }_{{\beta }_1}$	0.70	(0.45, 0.97)
V11	33.31	(13.06, 123.21)
V22	0.06	(0.02, 0.27)
ρ(β0,β1)	−0.16	(−0.75, 0.58)

The parameters V₁₁ and V₂₂ are the diagonal elements of V_β. The correlation between the intercepts and slopes is reported as ρ(β₀,β₁). It was not significant and does not feature in the substantive inference.

We reported the median and 95% credible intervals for the intercept, slope, correlation, GSD of xylene, GSD of THC, GSD of xylene$|$ THC, AM of THC, and AM of xylene (Table 4). The corresponding figures, including figures for the GMs, are included in the Supplementary Materials, available at Annals of Work Exposures and Health.

Table 4.

Preliminary results: DDIII May 15–July 15, 2010 Hierarchical Bayesian EG model parameter estimates.

	Derrick hand		Floorhand/roughneck		Crane operator		Roustabout		Operations technician or operator		ROV technician		IH-safety
Parameter	Median	95% CI	Median	95% CI	Median	95% CI	Median	95% CI	Median	95% CI	Median	95% CI	Median	95% CI
Intercept	−1.98	(−4.76, 0.86)	−1.65	(−4.67, 1.24)	−1.34	(−3.51, 0.61)	−2.84	(−4.29, −1.51)	−0.96	(−3.86, 1.65)	−1.03	(−2.49, 0.21)	−0.49	(−1.73, 0.58)
Slope	0.76	(0.36, 1.17)	0.72	(0.33, 1.13)	0.62	(0.32, 0.95)	0.91	(0.69, 1.14)	0.68	(0.28, 1.09)	0.64	(0.44, 0.86)	0.59	(0.43, 0.78)
Correlation	0.78	(0.32, 0.97)	0.64	(0.27, 0.89)	0.69	(0.35, 0.88)	0.70	(0.57, 0.80)	0.67	(0.27, 0.91)	0.94	(0.77, 0.99)	0.89	(0.70, 0.96)
GSD of THC	2.55	(1.73, 8.50)	4.63	(2.72, 16.11)	2.90	(2.12, 5.21)	3.09	(2.63, 3.83)	5.45	(2.88, 25.05)	3.24	(2.08, 9.05)	2.68	(2.00, 4.57)
GSD of xylene$|$ THC	1.76	(1.38, 3.70)	3.76	(2.32,11.79)	2.00	(1.57, 3.39)	2.82	(2.40, 3.50)	3.48	(2.12, 12.38)	1.31	(1.19, 1.66)	1.36	(1.24, 1.61)
GSD of xylene	2.64	(1.80, 7.55)	6.04	(3.31, 20.47)	2.68	(1.95, 4.86)	4.32	(3.46, 5.80)	5.87	(3.02, 25.49)	2.24	(1.65, 4.55)	1.95	(1.63, 2.67)
AM of THC (ppb)	1472	(701, 12 168)	3454	(1170, 60 690)	871	(503, 2321)	675	(517, 944)	2050	(601, 98 761)	852	(420, 5030)	889	(554, 2016)
AM of xylene (ppb)	42	(20, 277)	144	(39, 3487)	20	(12, 50)	35	(24, 59)	121	(33, 4747)	23	(15, 57)	32	(24, 50)

The EGs of floorhand/roughneck and the operations technician/operator had the highest median GSDs and AMs for both THC and xylene, as well as the highest credible intervals for these statistics. These EGs were characterized by having some very high and some very low measurements for each of the two chemicals (e.g. for the floorhand/roughneck, the measurements ranged for THC >5000 ppb to <LOD of 100 ppb). These groups were directly involved in the drilling, tasks that had the highest exposures, but the day-to-day work was quite variable, resulting in the high GSDs.

The correlation estimates between ln(THC) and ln(xylene) were all quite strong; all were significantly positive with median posterior estimates above 0.6. The correlations were strongest for the Remotely Operated Vehicle (ROV) technician (median correlation posterior estimate: 0.94) and IH-safety (0.89). The floorhand/roughneck and operations technician/operator had the lowest median correlation posterior estimates but the credible intervals were once again very wide. Given the various activities performed, these jobs may have more than one source of THC or xylene exposure.

Discussion

Importance of censored data

Censoring levels are moderate to high in our study datasets overall (19–88 $\%$ for THC and BTEXH). We evaluated the influence of censored data on the relationship between oil-related chemicals. To do so, we analyzed data from various EGs on one of the drilling rigs charged with stopping the oil release, the Discoverer Enterprise. While our primary analysis focuses on xylene exposure on the DDIII, the Discoverer Enterprise provides a particularly vivid example of the importance of censored data. An overall regression was performed of all outside measurements of workers who spent most of the time outside of the rig’s living areas accounting for censoring and not accounting for censoring. Associated 95% credible intervals were obtained for the slope and intercept. We found that there was a difference in the intercepts and slopes between the two sets of measurements. For example, for benzene and THC, approximately 86% and 11%, respectively, of the measurements in this subset of the data were censored. We found a significantly positive 95% credible interval for the slope when including censored data [median = 0.81, confidence interval (CI) = (0.62, 1.10)], while the credible interval for the slope included 0 when censored data were excluded [median = 0.03, CI = (−0.10,0.18)].

Although we recognize that bias cannot be formally assessed using the comparison of these two datasets due to not knowing the true concentration, we believe that these findings demonstrate that additional censored data provide important information that could result in biasing the results if not used. If the slope was truly 0, we would expect the benzene exposure levels to be constant for all levels of THC. This is contrary to expectations arising from the oil composition. After accounting for censored information, we clearly saw that lower THC levels were associated with lower benzene exposure levels, as expected from physical and chemical laws. Similar discrepancies in slope and intercept estimates were found for TEXH when comparing non-censored models to models including censored data (not shown). Thus, including the censored observations allows us to utilize more information over a wider range of values and yields more statistical power (because of larger sample sizes) to detect significant relationships between the chemicals.

Results from the DWH oil spill

The exposures to THC and BTEXH as experienced by workers who participated in the DWH oil spill response, could have come from a number of sources. These include the spilled crude oil; various solvents used in cleaning agents or in paints; chemicals associated with specific activities such as using drilling mud when drilling of the relief wells or operating equipment and vessels; fuels; or engine exhaust. The composition of the chemicals of interest varies substantially in these substances and their use/presence varied across the EGs. Therefore, exposure to BTEXH likely varies substantially among EGs, resulting in a differing and less consistent picture than shown in Figure 1. If the predominant source of the THC was crude oil, and the composition of the oil did not change over the period of these measurements, a strong correlation should be observed between the measurements for each of the chemicals and THC across the various EGs, as shown in Figure 1 (effect of oil weathering see Supplementary Materials, available at Annals of Work Exposures and Health). In contrast, if the predominant source of exposure was the solvents and other chemicals in the workplace, weaker correlations would be expected because the composition of the solvents and other chemicals likely varied across the products used at the worksites and thus across the EGs. If the primary source was fuel or fuel exhausts, the composition of the fuel or exhaust would be relatively constant but neither would be consistent with the composition of crude oil, so that a different correlation would be observed for those EGs whose primary exposure was fuel/exhaust.

Our application of the methodology to the GuLF STUDY data for xylene indicated patterns consistent with the measurement data and tasks being performed. Expected high exposure jobs that involved a variety of tasks had higher exposure levels, higher variability, and wider credible intervals than jobs that were expected to have lower exposures. Higher censoring and smaller sample sizes increased the width of the credible intervals.

These results for xylene suggest that the correlation between THC and its volatile components may be a powerful tool to use for generating exposure estimates, particularly when censoring is lower in one chemical than in another chemical. The correlations (ρ) between ln(xylene) and ln(THC) were surprisingly strong (median posterior estimates from 0.64 to 0.94) in all EGs. Due to the strength of these linear relationships, these linear associations can be used as reasonable Bayesian priors (along with other pertinent information) when assessing exposure.

General discussion

This method also properly accounts for censored data by allowing there to be a distribution for the censored observations. Instead of simply ignoring censored data or substituting a single value, we are able to estimate the distribution of each chemical and account for uncertainty in each censored observation. Our simulation study showed that the model performed well under low, moderate, and moderate-to-high levels of censoring in Y while having censoring levels low in X. D-statistics indicated that our model was consistently the best model in each scenario of the simulation study. Estimation was relatively robust for small sized EGs or with EGs with higher levels of censoring (see Supplementary Materials, available at Annals of Work Exposures and Health). We were able to use the known information that the chemical was censored to generate estimates. This helped us avoid having potentially biased estimates.

Our results are dependent on the level of censoring. Although we evaluated a range of censoring for X and Y in the simulation study, for some EGs in our study, we see even higher censoring or smaller sample sizes. These occurrences are likely to result in increased uncertainty, and therefore, it is recommended that our model be used with caution at higher levels (>80%) and smaller sample sizes (<5) than evaluated in the simulation study.

These results depended on the relationship between THC and its volatile components being linear in nature, even below the LOD. If the relationships were not linear, this methodology would not work sufficiently. We also assumed that each volatile component on a natural log scale was normally distributed. Other distributions were not investigated.

Future work could also incorporate repeated measurements within a worker. Kim et al. (2011), Xing et al. (2013), and Tielemans et al. (1998) have shown that accounting for within worker variability in epidemiological studies is important for inference and leads to narrower standard error estimates on the effect of exposure on the heath outcomes of interest. Burstyn et al. (2000) and Rappaport et al. (2009) provide excellent examples of how repeated measures should be treated in epidemiological studies.

Additionally, here only one chemical was used for predicting each BTEXH chemical. Future work should explore expanding this work to a scenario with multiple X censored variables. It is possible that by including multiple chemicals as predictors, we can obtain even stronger estimates of exposure.

Supplementary Data

Supplementary data are available at Annals of Work Exposures and Health online.