De novo prediction of cross-effect efficiency for magic angle spinning dynamic nuclear polarization

Abstract

Magic angle spinning dynamic nuclear polarization (MAS-DNP) has become a key approach to boost the intrinsic low sensitivity of NMR in solids. This method relies on the use of both stable radicals as polarizing agents (PAs) and suitable high frequency microwave irradiation to hyperpolarize nuclei of interest. Relating PA chemical structure to DNP efficiency has been, and is still, a long-standing problem. The complexity of the polarization transfer mechanism has so far limited the impact of analytical derivation. However, recent numerical approaches have profoundly improved the basic understanding of the phenomenon and have now evolved to a point where they can be used to help design new PAs. In this work, the potential of advanced MAS-DNP simulations combined with DFT calculations and high-field EPR to qualitatively and quantitatively predict hyperpolarization efficiency of particular PAs is analyzed. This approach is demonstrated on AMUPol and TEKPol, two widely-used bis-nitroxide PAs. The results notably highlight how the PA structure and EPR characteristics affect the detailed shape of the DNP field profile. We also show that refined simulations of this profile using the orientation dependency of the electron spin-lattice relaxation times can be used to estimate the microwave B₁ field experienced by the sample. Finally, we show how modelling the nuclear spin-lattice relaxation times of close and bulk nuclei while accounting for PA concentration allows for a prediction of DNP enhancement factors and hyperpolarization build-up times.

Graphical Abstract

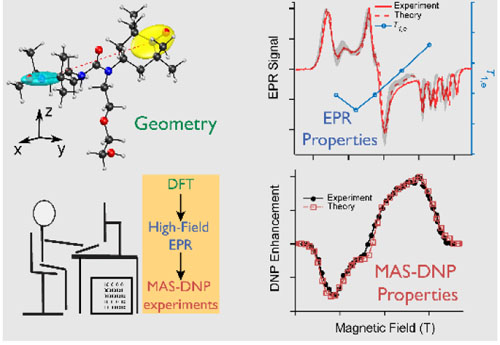
From the polarizing agent geometry and EPR properties to the prediction of magic angle spinning dynamic nuclear polarization efficiency

1. Introduction

Dynamic nuclear polarization (DNP) attracts large interest because it can provide impressive sensitivity gains to solid-state Nuclear Magnetic Resonance (ssNMR) spectroscopy. In DNP, the large intrinsic polarization of electron spins is transferred to nuclei. While this method was established under static conditions, its extension to spinning samples^1–3 and high magnetic field (> 5 T) combined with high-power, high-frequency microwaves^4,5 has provided large nuclear hyperpolarization along with high spectral resolution for ssNMR. This has enabled NMR experiments that would have been otherwise impracticable^6–14.

It was with the introduction of nitroxide biradicals¹⁵ that the highest Magic Angle Spinning (MAS) NMR sensitivities have been obtained using DNP. Based on the cross-effect (CE) mechanism under MAS, which requires two coupled electron spins and a mutually-coupled nuclear spin,^16–18 these bis-nitroxides can provide a fast build-up of relatively high nuclear polarization levels. Nowadays, two main categories of bis-nitroxides are being developed, based on different chemical linkers that tether the two nitroxide moieties: the bTbK family (based on a bis-Ketal linker),¹⁹ and the bTurea family (based on a urea linker).^20,21 The chemical structures for these families were designed based on empirical approaches that have shown that both the relative orientation of the g-tensors of the two electron spins and their inter-spin distance affects the DNP efficiency.^19,20,22,23 Each family now has several substructures and colossal synthesis and experimental work has been performed to optimize the structures further.^23–27 These studies notably highlighted that electron relaxation times are key parameters for efficient DNP,²² which can be tuned by changing the molecular weight of the radical.²⁸ Nowadays, derivatives of the bTbK^25,29 and bTurea^26,27,30 families, in particular TEKPol²⁴ and AMUPol,²³ are commonly used and considered as highly-efficient and versatile polarizing agents (PAs) for CE-DNP.

In parallel to this experimental work, theoretical/numerical analyses have supplied some substantial elements to the understanding of the CE under MAS.^16–18,31 First, it differs strikingly from the static case as the MAS induces energy level anti-crossings, called rotor events.^18,32–35 When considering the smallest spin system (2 electrons, one nucleus), there are 4 rotor-event types: microwave (μw), dipolar/J, cross-effect and solid-effect (SE). These occur (predominantly) sequentially at different rotor positions. Each rotor event occurs with a given efficiency that depends on the 3D structure of the PA, the crystal orientation, and the magnitude of the effective coupling at stake during the level anti-crossing as well as the duration of the crossing (that can thus be related to the MAS frequency and the static magnetic field). The size of the nuclear polarization enhancement results from the combination of these events and the relaxation mechanisms.

So far, the complexity of the MAS-DNP mechanism has severely limited the ability to predict reliably the performance of a given PA. For instance, even if a biradical is modeled by a simple three-spin system (2 electron spins and one ¹H spin), it already requires determining at least 21 parameters (see SI for details). In addition, the complexity of the modulation induced by the sample spinning has prevented the derivation of an analytical solution. For this reason, the development of numerical simulations^{16–18,31,33} appears as a good strategy to provide insight into the structure-efficiency relationship.^18,33,36 In addition, since numerical simulations tend to require substantial computation time, there have been recent efforts towards developing a fast and accurate simulation tool, that can be used to scan through the multiple parameters involved in the mechanism.³³

In this article we demonstrate that this fast simulation tool can be used to predict the performance of a bis-nitroxide. To that purpose, we combined density functional theory (DFT), high-field electron paramagnetic resonance (EPR) and MAS-DNP simulations to predict the behavior of well-known biradicals. The approach is applied to the bTbK and bTurea families, for which we compare simulations and experimental data obtained on the TEKPol and AMUPol biradicals.

2. Material and methods

DNP-sample preparation

The biradical families used in this study are shown in Figure 1. The TEKPol sample was prepared by dissolution in CHCl₃/1,1,1,2-tetrabromoethane(TBE)/D₄-MeOH (65/30/5 v%) to form a 15 mM solution. This solvent mixture was chosen as it forms a relatively good and reproducible glass. The AMUPol sample was prepared by dissolution in a 2 M ¹³C–urea D₈-glycerol/D₂O/H₂O (60/30/10 v%) mixture to form a 10 mM solution. For each sample, the experiments have been carried out in 3.2 mm outer-diameter sapphire MAS rotors.

Fig. 1.

Chemical structure of nitroxide biradicals used in this study. (a) bTbK family, (b) bTurea family.

DFT calculations

The initial geometrical structures have been obtained using Ghemical v3.0.2³⁷ and the Tripos 5.2 force field.³⁸ Using the random conformation search on a reduced (i.e. protonated) nitroxide, the most energetically-favorable radical conformation was used as the input structure for DFT calculations.

The ORCA program package (v. 3.0.2)³⁹ was employed for all electronic structure calculations. All geometry optimizations were performed in two steps: a quick optimization using the LDA functional and Def2-SVP basis set⁴⁰ with the RI approximation, and the resulting structure was then further optimized using the GGA BP86 functional and Def2-TZVP basis set.^41,42 This final structure was then used for the calculations of the g-tensors using the B3LYP^43–45 functional with Def2-TZVP basis.^41,42 The electron-electron dipolar coupling was obtained in the same way, calculating only the spin-spin contribution with B3LYP and EPR-II basis.⁴⁶ Note that our aim is to obtain the geometry of the biradical and therefore not much effort has been put to compute accurately the g-values or the ¹⁴N hyperfine coupling as they depend on the solvent.^47,48 In addition, the J exchange interaction in these biradicals is too small to be accurately computed via DFT.

Experimental setup

The MAS-DNP properties were measured on a Bruker 9.4 T / 264 GHz DNP-NMR Avance III spectrometer, installed in Grenoble (France), and on a Bruker 14.1 T / 395 GHz DNP system installed in Tallahassee (FL, USA)⁴⁹ operating at proton Larmor frequencies of 400 MHz and 600 MHz, respectively. Both systems are equipped with low-temperature 3.2 mm wide-bore MAS probes able to spin samples up to ~15 kHz at ~100 K.⁵⁰ Sample temperature was set to ~110 K for all experiments, adjusting the sample-cooling gas flow accordingly to account for temperature variations due to different MAS rates and μw irradiation.⁵¹ The μw power was optimized to give the maximum signal intensity at a MAS frequency of 8 kHz. All experiments for a given sample were performed without ejecting the sample to ensure a consistent glass quality. For signal-averaging, a recycle delay of 7×^1HT_B was used to ensure a complete return to equilibrium of ¹H spins between transients, where T_B is the time constant for polarization build up after saturation. ¹H spectra were obtained using a π/2 excitation pulse of 100 kHz RF field strength. ¹³C spectra were measured using {¹H-}¹³C-CP^52–54 (cross-polarization) with SPINAL-64⁵⁵ heteronuclear decoupling at 83 kHz field strength. The DNP field profile of TEKPol and AMUPol were recorded using the optimal μw power for each biradical solution.

The 285 GHz continuous-wave (CW) EPR spectra were recorded at the Laboratoire National des Champs Magnétiques Intenses (LNCMI, Grenoble, France) on a custom-built CW EPR spectrometer.^56,57 The EPR spectrum was recorded at 100 K, using a microwave irradiation frequency of 285 GHz, a field modulation of ~ 0.4 mT and a sweep rate of 0.30 mT/s.

The 240 GHz CW and pulsed EPR data have been recorded on the 112/240/336 GHz quasi-optical spectrometer installed in Tallahassee.^58,59 The sequences used were either a 2-pulse Hahn echo or for the T₁ measurements an echo-detected saturation recovery experiment, using pulses of 700 ns – τ – 900 ns for the echo detection and a 1 ms saturation pulse, respectively. A CW spectrum was also recorded using a modulation of 0.3 mT and 40 μW irradiation power with a sweep rate of 0.2 mT/s at a temperature of 100 K.

Data analysis

The DNP enhancement ∊_on/off, the ratio of the intensities of the NMR signal obtained in presence and absence of μw irradiation can be measured on the ¹³C signal of urea or chloroform. It was verified that this ratio also corresponds to the enhancement measured directly on the ¹H spectrum. The Boltzmann polarization gain ∊_B and the depolarization, ∊_Depo, have been quantified using a previously-described method by following the absolute intensity of the integrated ¹H signal in presence and absence of μw irradiation.³² ∊_on/off, ∊_B, and ∊_Depo are connected by the following relation ∊_on/off = ∊_B × ∊_Depo.^32,33

EPR and MAS-DNP simulations

The high-field EPR spectra of TEKPol and AMUPol were fitted using the Easyspin toolbox v.5.1.⁶⁰ The initial electron-electron dipolar tensor and the g-tensors relative orientation were obtained from the DFT calculations, whereas the initial principal axis frame values for g-tensor and ¹⁴N hyperfine tensor were extracted from the literature.^47,48,61,62 The line broadening used, corresponding to a g-strain equal to [1.3×(g_x-2), g_y-2_, g_z-2]×6%, led to a satisfying result. Note that the EPR spectra were computed with the “matrix” method, which relies on the diagonalization of the Hamiltonian.

The MAS-DNP simulations were carried out following the approach described previously^16,18,32 and using the latest computational implementation.³³ The spin systems considered in the rest of the manuscript are composed either of a box containing multiple copies of two electrons and one proton {¹H₁-e_a-e_b} (referred to as the box model) or two electrons linked to N protons (referred to as the multi-nuclei model), as previously described.³³

The simulations include dipolar and J exchange interactions between the two electrons within a biradical, intermolecular electron-electron dipolar couplings for the box model, as well as the presence of g-strain.

The code has been improved for the computation of the μw rotor events: the electron resonant frequencies now include the frequency shift induced by the intramolecular dipolar/J exchange interaction (see SI for details), in addition to the frequency shift induced by the hyperfine coupling to the ¹⁴N spin present in the nitroxide moieties.

The multi-nuclei model³³ is composed of 4 strongly hyperfine coupled protons (about 3 MHz of hyperfine coupling each) and 5 layers of protons (corresponding to 220 nuclei with a hyperfine coupling smaller than 3 MHz). Note that the 3 MHz hyperfine coupling for the closest protons was chosen (except specified otherwise) as an average value and corresponds to protons from the nitroxide moiety and/or from surrounding molecules.⁶³ The numerical details can be found in the SI.

Powder averaging is performed using two angles 987 ZCW crystal file.^64–66 For the box-model,³³ the powder averaging is performed by generating 32 boxes each containing 30 randomly oriented biradicals. Their orientations were chosen from the crystal file such that each crystal orientation can only be selected once. When using the multi-nuclei model, N = 437 and N = 476 ¹H nuclei were considered for TEKPol and AMUPol respectively, and the powder averaging was performed using the 610 ZCW crystal file, which is sufficient for evaluating the final polarization and its corresponding build-up time. Note that two or three angles powder averaging led to identical results.

These simulations where performed assuming a temperature of 100 K in order to define the Boltzmann equilibrium density matrix and where carried out for two different μw irradiation frequencies: 263.73 GHz and 395.175 GHz. The μw frequency is kept fixed when the magnetic field is varied for the simulation of the DNP field profile. In addition, unless otherwise specified, the μw Rabi frequency was ω₁/2π = 0.35 MHz.

3. Determining biradical configuration and EPR parameters in the frozen state using DFT and high-field EPR

The first step before computing CE MAS-DNP efficiency is to determine relevant input parameters that include the polarizing agent geometry and EPR characteristics. To this end, DFT calculations were conducted on simplified structures mimicking AMUPol and TEKPol. In the computed structures, corresponding to bTbK and a modified bTurea^21,25,30 with a short PEG chain, rings in alpha of the nitroxide function (which are present in TEKPol and AMUPol) were excluded for simplicity but the calculations still provide good approximations of TEKPol and AMUPol structures. The results of the optimized structures are shown in Figure 2. The g-tensor orientations are schematically represented with an ovoid using the convention that axis length is proportional to the (g_i-2), while the dipolar coupling is represented by a dashed line. Table 1 details the DFT-calculated g-values, dipolar couplings, and their relative orientations in the molecular frame.

Fig. 2.

Structure of bTbK (a) and modified bTurea with a PEG chain(b), obtained via DFT. The g-tensors and dipolar coupling are represented schematically, (the axis length is proportional to the principal axis frame tensor value). In blue and yellow, the g-tensor of electron spin a and b, respectively. The colour coding for the atoms is: black corresponds to carbon (C), red to oxygen (O), blue to nitrogen (N), and grey to hydrogen (H)). The structures have been generated with a home-written Matlab code.

Table 1:

List of the calculated (DFT) and experimental geometric parameters (after fitting) for the TEKPol and AMUPol biradicals. Euler angles are given in degrees with respect to the first g-tensor, using the Easyspin’s v 5.1 rotation convention (active rotation).⁶⁷ The g-strains for the simulations are proportional to ([1.3×(g_x-2), g_y-2_, g_z-2]×6%) and are [0.8,0.35,0.13]×10⁻³ for TEKPol and [0.8,0.3,0.12]×10⁻³ for AMUPol. ^an.c. = not calculated.

Biradical	g-tensor [gx, gy, gz]	g-tensor relative orientation (α, β, γ)	14N hyperfine coupling (MHz)	Dipolar coupling – J-exchange interaction (MHz)	Dipolar orientation (ϕ, θ)
TEKPol DFT	[2.0094, 2.0070, 2.0024]	[−70.4, 79.7, −63.7]	n.c.a	30.5 – n.c.	[10, 66.3]
TEKPol Exp.	[2.0095, 2.0060, 2.0021] ±2.10−4	[−75.4, 79.6, −58.6] ±2.5	[18, 16, 98] ±2	30.5 ± 1 – 1 ±1	[10, 66.3] ±3
AMUPol DFT	[2.0091, 2.0067, 2.0024]	[125.1, 129.7, −46.6]	n.c.a	34.75 – n.c.	[−174.6, 74]
AMUPol Exp.	[2.0092, 2.0061, 2.0020] ±2.10−4	[123.1, 129.8, −46] ±[2.5, 5, 2.5]	[18, 17, 100] ±2	35 ± 2 – 16 ± 2	[−174, 76] ±5

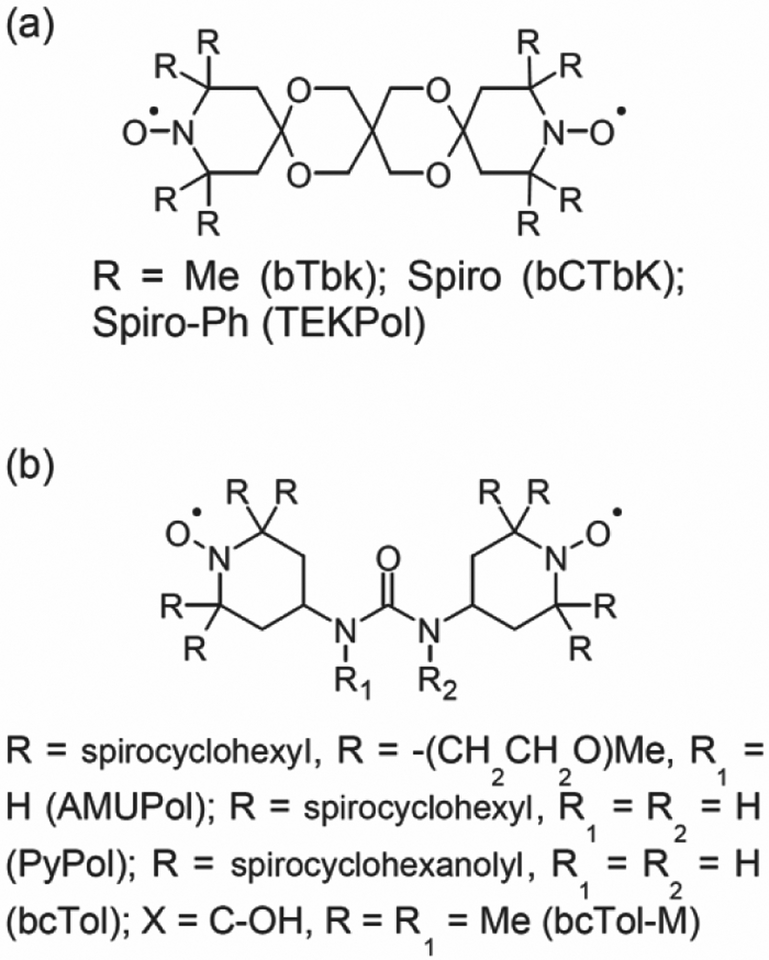
These parameters (obtained by DFT) can be combined with ¹⁴N hyperfine couplings reported in the literature^48,61,62 to compute an EPR spectrum that can be compared to experimental data. This comparison needs to be conducted at high magnetic field (8.5 and 10.1 T in this work) in order to improve the resolution and to allow further refining these parameters by fitting the EPR data. The result of this procedure is presented in Figure 3 for TEKPol and AMUPol.

Fig. 3.

High-field EPR spectra of 15 mM TEKPol in CHCl₃/TBE/MeOH-D₄ (65/35/5 v%) (black) and 10 mM AMUPol in D₈-glycerol/D₂O/H₂O (60/30/10 v%) + 2M ¹³C-urea (red), both recorded at 100 K with a microwave frequency of 285 GHz. Best fits obtained from the DFT-calculated parameters are shown with black and red dashed lines for TEKPol and AMUPol, respectively. The grey overlays represent the errors reported in Table 1.

The agreement between simulation and theory is good for both AMUPol and TEKPol. These two biradicals have very different spectral features in the g_x and g_z regions, reflecting their different geometrical properties.

Table 1 summarizes and compares the EPR parameters obtained by DFT alone and fits to experiments, refined from the DFT-calculated parameters. The grey overlays in Figure 3 and Figure 4 represent the corresponding errors reported. Our analysis notably provides an electron-electron dipolar coupling of ~30 MHz for TEKPol. which is consistent with the previous work conducted on bTbK.^19,61 This confirms that biradicals within the bTbK family have almost identical geometrical properties. For AMUPol, the analysis reveals the presence of a dipolar coupling of ~ 35 MHz and an exchange interaction of magnitude ~ 15 MHz, in line with previous predictions of the dipolar coupling²³ and the liquid-state analysis performed in reference [30]. These values as well as the relative orientations for AMUPol obtained here are in very good agreement with a recent multi-frequency EPR analysis.⁶⁸ The experimental data were fitted using a step-by-step simplex approach, fitting first the g-values, then the exchange interaction and finally the relative orientations.

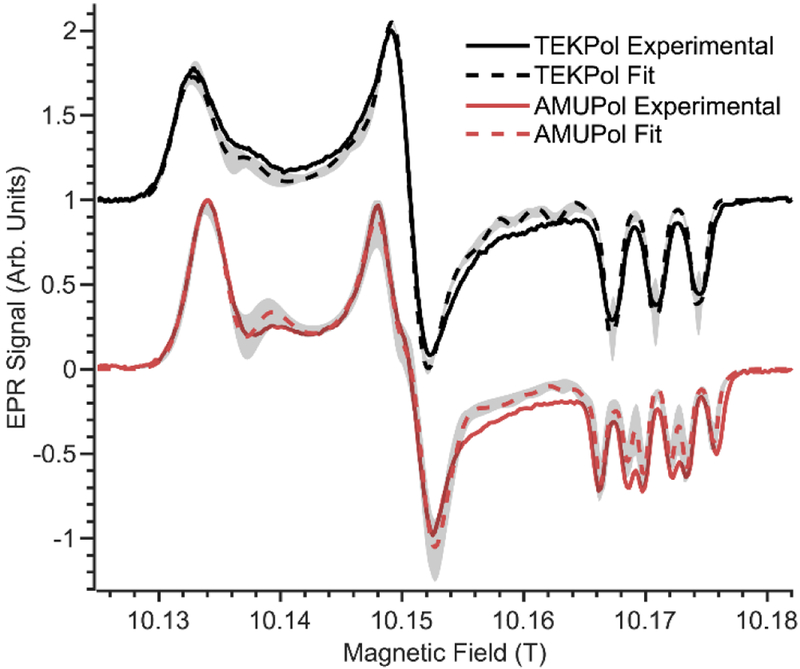
Fig. 4.

High-field EPR spectrum of 10 mM of AMUPol in D₈-glycerol/D₂O/H₂O (60/30/10 v%) + 2M ¹³C-urea, recorded at 100 K, for a microwave frequency of 240 GHz. The red curve represents the experimental spectrum and the red dashed line represents the theoretical EPR spectrum obtained with fitted parameters reported table 1. The blue dots correspond to the measured electron spin-lattice relaxation times, T_1e (right axis).

It is important to stress that the parameters obtained using DFT were key for the success of the refinement procedure reported here since it provides a good starting point for both biradicals. This allows finding a satisfying solution using only one EPR frequency, whereas multi-frequency EPR fitting is usually required.^68–70 We also check the robustness of the fit by varying each parameter around its optimum value. This was used to estimate the associated errors for each of the values shown in Table 1. As a side note, it is interesting that in the AMUPol case, the α and γ angles have a strong effect on the EPR lineshape in the low-field region. Finally, we verify the accuracy of the parameters by fitting EPR spectra recorded at lower magnetic field, as shown in Figure 4.

The CW EPR lineshape analysis was complemented by conducting high-frequency pulsed EPR measurements to estimate the electron spin relaxation times as a function of the field position. The results obtained for AMUPol are shown in Figure 4 and are consistent with previous work.^27,47,62,71 The electron spin-lattice relaxation time varies throughout the EPR line, with shorter T_1e values between the g_x and g_y component and longer T_1e values around the g_z component. Contrastingly, the phase memory time was constant throughout the EPR lineshape at T_m = 2.5±0.5 μs. The phase memory time for TEKPol was too short to be measured within the capabilities of the EPR setup. Such a short T_m for TEKPol compared to AMUPol could be due to the solvent mixture employed.^28,47 The T_1,e dependency was then plotted a function of the g-value and fitted via a 2^nd order polynomial. The obtained function was later used in the MAS-DNP simulations, to compute the relaxation time for each radical orientation and it was assumed that TEKPol and AMUPol have similar electron spin relaxation times.^27,47,62,71

4. On the prediction of MAS-DNP field profiles

DNP field sweep profiles provide an additional spectral fingerprint for biradicals

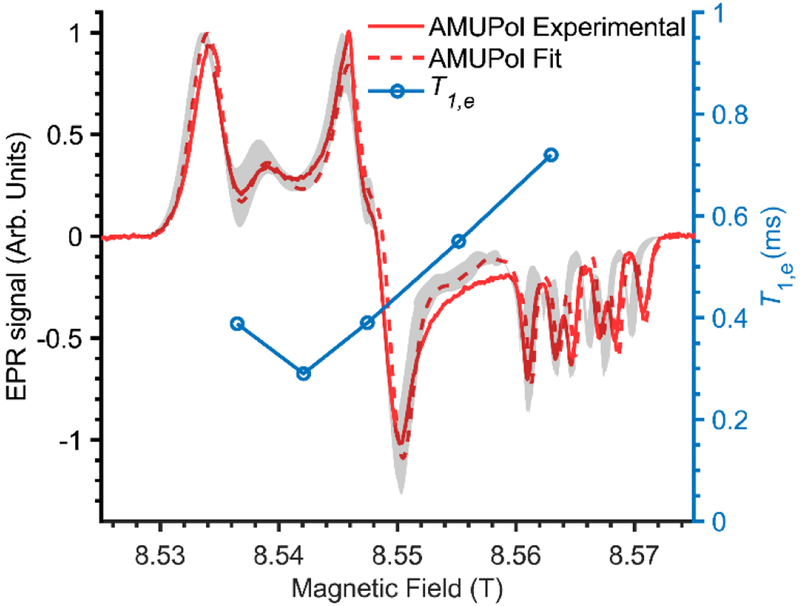
Since AMUPol and TEKPol display different EPR spectra, one should expect that this is also the case for the DNP field profiles, which were measured at 9.4 and 14.1 T for TEKPol and AMUPol, respectively, and are reported in Figure 5. As expected, not only do their shapes differ significantly, but the ratio between the positive and negative maximum as well: ~0.45 for TEKPol and ~0.75 for AMUPol. This highlights the potential of these field profiles to be used as spectral fingerprints for PAs, provided that the effect of the microwave B₁ field strength is accounted for.

Fig. 5.

Experimental (black circles) and simulated (red squares) MAS-DNP field profiles, i.e. the enhancement ∊_on/off as a function of the magnetic field while keeping the μw irradiation frequency constant, for TEKPol (a) and AMUPol (b) at 9.4 T and 14.1 T, respectively.

Obtaining the microwave B₁ field at the sample from accurate simulations of the MAS-DNP field profile

As shown in detail in previous work,^18,33 MAS-DNP simulations are sensitive to many intrinsic parameters that define a PA. This includes the g-tensors, their relative orientations, the electron spin relaxation times (and their dependency with field, temperature, solvent etc.), the strength of the electron-electron dipolar coupling, as well as the exchange interaction (if present). All these intrinsic variables were determined in the previous section and are used in the following simulations.

MAS-DNP simulations also depend on many external parameters such as the magnetic field, the temperature, the MAS frequency, and the microwave B₁ field strength at the sample. All of these parameters, except the last one, can be experimentally determined easily. Therefore, the last undetermined variable, the microwave B₁ field strength, was varied to best fit the simulated MAS-DNP field profile to experimental data, as shown in Figure 5. We obtained a very good fit for both AMUPol and TEKPol, using a microwave Rabi frequency ω₁/2π = 0.35 MHz. Figure 5 clearly demonstrates that the simulations are able to reproduce the overall shape of the DNP field profile, some specific details (shoulders, bumps, etc.) and also the relative ratio between the positive and negative maxima. Note that the microwave field strength has a direct effect on the shape of the DNP field profile (see Figure S1), but not on the relative ratio between the positive and negative maxima.

Notably, this value of the microwave Rabi frequency for a 3.2 mm probe is consistent with recent reports.^72,73 For completion, the simulated MAS-DNP field profiles for AMUPol and TEKPol at 9.4 and 14.1 T, respectively, are reported in Figure S2. Here we used ω₁/2π = 0.35 MHz as an optimal value but 0.3 MHz and 0.4 MHz would have led to satisfying fits as well. Introducing a distribution of microwave Rabi frequencies (throughout the sample)^72,73 may improve the overall quality of the fit but this was not attempted in this work.

Effect of the orientation dependence of the electronic T_1,e

The MAS-DNP field profile changes when accounting for the orientation dependency of the electronic relaxation time T_1,e. Interestingly, the overall lineshape is not heavily affected, as opposed to the relative ratio between the two maxima (more details in Figure S3).

It is also important to stress that, within reasonable limits, the nuclear relaxation times (from 0.1 to 10’s of s) and the electron-proton hyperfine couplings (<10 MHz) have no effect on the DNP field profiles, both for the shape and the relative ratio between positive and negative maxima. Nonetheless, these parameters do have a strong effect on the absolute values that can be reached for the enhancement factor (ε_on/off or ε_B). A change in these parameters acts as an overall scaling factor for the entire DNP field profile.

Effect of the MAS-induced spectral diffusion on the DNP field profile

When using the “box” model,³³ the DNP field profile has identical shape whether inter-molecular electron-electron dipolar couplings were considered or not. In other words, for realistic PA concentrations (< 20 mM), inter-PA electron spin interactions are not large enough to directly perturb the MAS-DNP field profile, although they can have other effects (such as reduced electron spin relaxation times,⁷⁴ which can modify the field profile (vide supra) and increase nuclear depolarization).³³

Predicting DNP field profiles with simulations

We have shown in the previous paragraphs that the DNP field profile acts as a spectral fingerprint that encodes the PA’s properties (EPR parameters including the hyperfine coupling to the ¹⁴N spin but excluding the hyperfine coupling to the ¹H spins) and the microwave B₁ field strength. We note that for the PAs considered in this work, it was not necessary to consider the presence of a conformational distribution in the frozen solvent matrix. Although this could possibly improve further the quality of the fit reported, it was not attempted in this work. Unavoidably, the use of more flexible linkers could imply the introduction of parameter distributions, such as the relative orientation between the g-tensors, the distance between the two electrons or the J exchange interaction.²⁷ This was clearly evidenced in our recent work on the biradical TEMTriPol-1³⁵ and must therefore be accounted for to obtain accurate simulations.

5. On the prediction of DNP polarization gain and build-up time

To test further the predictive capabilities of the simulation tool, we performed calculations using two models, introduced in our previous work.³³ These two models enable probing specifically various aspects of the DNP mechanism and the results and the comparisons to experimental data are given in Table 2. The first model, called “multi-nuclei”, enables the calculation of 2 electrons and N≥1 protons. It provides a method to account for the impact of multiple nuclei on the gain, the depolarization and more importantly on the nuclear polarization build-up time (T_B). The second model, called the “box” model, allows computing a large number of identical three-spin systems (2 electrons and 1 proton) in interaction. This enables probing the effect of PA’s concentration by including the “MAS induced” spectral diffusion generated by neighbouring biradicals.

Table 2.

∊_Depo, ∊_on/off and polarization build-up time T_B measured experimentally at 110 K and 8 kHz MAS frequency and simulated using similar input conditions for the box models (isolated and interacting), the multi-nuclei model, and the extrapolated approach. The calculations were performed for 10 mM AMUPol in glycerol-D₈/D₂O/H₂O (6/3/1 %v) and 15 mM TEKPol in CHCl₃/TBE/MeOH-D₄ (65/30/5 %v), where biradical concentration and nuclear spin concentration/relaxation properties are required. For the glycerol-D₈/D₂O/H₂O (6/3/1 %v) matrix, $T_{1,n}^{\mathrm{B}\mathrm{u}\mathrm{l}\mathrm{k}}=65$ s at 9.4 T³² and 76 s at 14.1 T⁷⁷, and the ratio ¹H/nitroxide = 476. For CHCl₃/TBE/MeOH-D₄ (65/30/5 %v), $T_{1,n}^{\mathrm{B}\mathrm{u}\mathrm{l}\mathrm{k}}=5.6$ s at 9.4 T, and the ratio ¹H/nitroxide = 437.

Biradical	Experiment ∊B/∊Depo/∊on/off	Simulation ∊B/∊Depo/∊on/off (Multi-nuclei)	Simulation ∊B/∊Depo/∊on/off (Multi-nuclei corrected)	Experimental TB (s)	Calculated TB (s)
AMUPol at 9.4 T	85 / 0.40 / 210	208 / 0.64 / 325	114/ 0.38/ 300	2.9±0.1	3.2
AMUPol at 14.1 T	70 / 0.55 / 128	147 / 0.71 / 207	83 / 0.5 / 170	5.2±0.2	5.2
TEKPol at 9.4 T	73 / 0.60 / 118	108 / 0.81 / 133	60 / 0.54 / 110	2.8±0.1	2.6

The multi-nuclei model

The “multi-nuclei” model, is designed to match the experimental proton density and the relative ratio between biradical and protons (see Table 2). More specifically, two types of protons are considered, local and bulk. Only the local protons have a hyperfine coupling (always greater than the MAS frequency). For all nuclei we assume that nuclear spin-lattice relaxation time depends on the hyperfine coupling strength.⁷⁵ For a given nucleus i, it can be written:

$$\frac{1}{{\mathit{T}}_{1,\mathit{i}}^{\mathit{n}}}\mathrm{ }=\frac{1}{{\mathit{T}}_{1,1}^{\mathit{n}}}{\left(\frac{{\mathit{A}}_{\mathit{a},1}^{}}{{\mathit{A}}_{\mathit{a},\mathit{i}}^{}}\right)}^2+\frac{1}{{\mathit{T}}_{1,\mathbf{B}\mathbf{u}\mathbf{l}\mathbf{k}}^{\mathit{n}}}$$ (1)

where $T_{\mathrm{1,1}}^{\mathrm{n}}$ represents the nuclear spin-lattice relaxation time of the closest (most strongly coupled) proton and $T_{1,\mathrm{B}\mathrm{u}\mathrm{l}\mathrm{k}}^{\mathrm{n}}$ the nuclear spin-lattice relaxation time measured in absence of doping. A_a,1 and A_a,i represent the hyperfine coupling between the electron and the i^th proton. More details can be found in refs [33,75].

Adjusting the nuclear relaxation time of strongly coupled protons

$T_{1,\mathrm{B}\mathrm{u}\mathrm{l}\mathrm{k}}^{\mathrm{n}}$ was measured for glycerol-D₈/D₂O/H₂O (6/3/1 v%) and CHCl₃/TBE/MeOH-D₄ (65/35/5 v%) at 9.4 T and ~110 K in absence of radical doping. The saturation-recovery build-up curve was fitted to a mono-exponential, and $T_{1,\mathrm{B}\mathrm{u}\mathrm{l}\mathrm{k}}^{\mathrm{n}}$ estimated to 65 s and 5.6 s for the aqueous and organic solvent matrices, respectively. At this point, there is one parameter that has not been evaluated yet, the nuclear spin-lattice relaxation time of the closest proton, $\mathrm{ }{T}_{1,1}^{\mathrm{n}}$ , since this is very challenging to determine experimentally.⁷⁶ Consequently, the spin-lattice relaxation time used in the simulations for the closest proton, $\mathrm{ }{T}_{1,1}^{\mathrm{n}}$ , was determined by fitting the sum of the simulated build-up curves (over all the protons), to match the experimental polarization build-up time (T_B), both in the AMUPol and TEKPol case. Significantly, $T_{1,1}^{\mathrm{n}}$ is extracted at around 0.1 s in both cases, even if $T_{1,\mathrm{B}\mathrm{u}\mathrm{l}\mathrm{k}}^{\mathrm{n}}$ and T_B are substantially different for 10 mM AMUPol in glycerol-D₈/D₂O/H₂O (6/3/1 v%) and for 15 mM TEKPol in CHCl₃/TBE/MeOH-D₄ (65/35/5 v%). The validity of this result is supported by the fact that the average distance to the closest proton is of the same order of magnitude in both AMUPol and TEKPol.

Simulating DNP efficiency without accounting for spectral spin diffusion and intermolecular CE

Using $T_{1,1}^{\mathrm{n}}$ = 0.1 s for both AMUPol and TEKPol, we can use Equation 1 to calculate $T_{1,i}^{\mathrm{n}}$ for all the other protons, and then compute, using the multi-nuclei model, the DNP enhancement factors (∊_B,∊_on/off), the depolarization factor (∊_depo) and the build-up time (T_B) for 10 mM AMUPol in glycerol-D₈/D₂O/H₂O (6/3/1 v%) and for 15 mM TEKPol in CHCl₃/TBE/MeOH-D₄ (65/35/5 v%). The simulation results can be found in Table 2 and are compared to experimental values. Systematically, the multi-nuclei model overestimates the DNP enhancement factor and underestimates the depolarization effect. Nevertheless, the relative trends are consistent with the experimental data.

AMUPol and TEKPol are two examples of very different situations. For 10 mM AMUPol in glycerol-D₈/D₂O/H₂O (6/3/1 v%), the DNP build-up time is ~ 2.9 s at 9.4 T, 100 K, and with a MAS frequency of 8 kHz. Since the nuclear spin lattice relaxation time in absence of radical doping is one order of magnitude longer, one can safely conclude that the nuclear spin-lattice relaxation time is not the limiting factor in this case. This can be highlighted by verifying that when $T_{1,\mathrm{B}\mathrm{u}\mathrm{l}\mathrm{k}}^{\mathrm{n}}$ ≥ 20 s, it has minimal effect on the DNP enhancement factor and build-up time (see Figure S5a). However, with 15 mM TEKPol in CHCl₃/TBE/MeOH-D₄ (65/35/5 v%), the DNP build-up time is similar to the nuclear spin-lattice relaxation in absence of doping (2.8 s and 5.6 s, respectively, at 9.4 T, 100 K, and with a MAS frequency of 8 kHz). The shorter $T_{1,\mathrm{B}\mathrm{u}\mathrm{l}\mathrm{k}}^{\mathrm{n}}$ in this case limits the overall DNP efficiency (as illustrated in Figure S5b). This is in agreement with previous theoretical predictions described in ref [33].

Using the box model to estimate the effect of electron spectral diffusion

Although the results presented in the previous paragraph (based on the multi-nuclei model) seem encouraging, there is still much room for improvement in the modelling of the DNP mechanism, especially to mimic the MAS-induced spectral diffusion (via the electron-electron intermolecular dipolar rotor events) and the contribution to the CE from the intermolecular electron-nuclei couplings. In other words, the multi-nuclei model does not account for the effect of the PA concentration on the DNP mechanism. A model that could account for both PA concentration and a realistic nuclear spin density is still to be developed, and beyond the scope of this article.

One can try to correct the values obtained by the multi-nuclei model to account for the presence of multi-electrons (“box model”). To that end, we propose to use the simplified three-spin system in a box (multiple copies of two electrons and one proton) and to estimate the impact of the presence of intermolecular dipolar interactions on the DNP efficiency. For this, we compute ∊_B, ∊_Depo, and ∊_on/off, either considering the presence of intermolecular interactions or not, in order to obtain a correction factor defined as follows:

$$R_n=\frac{{ϵ}_n^{\mathrm{b}\mathrm{o}\mathrm{x}\mathrm{ }\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}}{{ϵ}_n^{3\mathrm{ }\mathrm{s}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{ }\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}}$$

where n = B or Depo or On/Off.

The correction factors R_B/R_Depo/R_On/Off obtained are 0.55/0.58/0.95, 0.57/0.7/0.82 and 0.55/0.67/0.81 for 10 mM AMUPol in glycerol-D₈/D₂O/H₂O (6/3/1 v%) at 9.4 and 14.1 T, and 15 mM TEKPol in CHCl₃/TBE/MeOH-D₄ (65/35/5 v%) at 9.4 T respectively. These factors were used to correct the multi-nuclei model and account for the electron concentration effect. The results are shown in Table 2 and are comparable with the experimental values, highlighting that indeed the inter-PA interactions need to be accounted for to obtain better agreement with experiment.

6. Conclusions

In this work we have shown that MAS-DNP simulations allow reproducing bis-nitroxide DNP field profiles very accurately given that the radical structure and the EPR properties can be determined. This was demonstrated on AMUPol and TEKPol for which DFT and high-field EPR measurements were combined to obtain the g-tensors, their relative orientations, the electron-electron dipolar coupling, as well as the J exchange interaction.

This work highlights DFT’s prediction capabilities for biradical’s structure. It clearly confirms the presence of an exchange interaction of ~15 MHz and a dipolar coupling of ~35 MHz for AMUPol, as initially reported,^23,30 although it was a matter of debate⁷⁸ until recently.⁶⁸ For TEKPol, we estimate the dipolar interaction to 30 MHz while the J exchange interaction is negligible in the bTbK family.

In addition, pulsed high-field EPR measurements were performed at 240 GHz, which confirm the orientation dependence of the electron longitudinal relaxation time T_1,e in the 300 to 900 μs range as previously observed^27,62 and the short and flat dependency of the phase memory time T_m (estimated to 2.5 μs throughout the EPR line). We also prove in this work the critical impact of the T_1e orientation dependence to reproduce the relative ratio between the positive and negative maxima of the DNP field profile. Moreover, we show how the microwave B₁ field strength ω₁/2π, expected in the 0.1 to 1 MHz range, can be refined to ~0.35 MHz for our experimental setups by simulating the detailed shape of the DNP field profile. This is consistent with recent estimates extracted from high-frequency structural simulator calculations.^72,73

To further push the boundaries of the prediction capabilities, we used the previously developed “multi-nuclei” model to simulate compute ∊_B, ∊_Depo, ∊_on/off, and the corresponding polarization build-up times. The spin-lattice relaxation times of bulk protons $T_{1,n}^{\mathrm{B}\mathrm{u}\mathrm{l}\mathrm{k}}$ used in the simulations were estimated by measuring the ¹H nuclear spin-lattice relaxation times in absence of PA doping. The ¹H spin-lattice relaxation times of nuclei close to the PA (the ones experiencing the largest hyperfine couplings) were adjusted in order to obtain DNP build-up times T_B in agreement with experiments. This gave an estimation of the spin-lattice relaxation time of the closest ¹H for both AMUPol and TEKPol at 9.4 T and 100 K to be ~0.1 s. Finally, we introduce an approach to correct the ∊_B, ∊_Depo, ∊_on/off values obtained with the “multi-nuclei” model, while accounting for inter-PA effects, which improves the agreement with experiment.

This work highlights the ability of the MAS-DNP simulations described here to be quasi-predictive and further substantiates recent and on-going efforts towards using numerical simulations for in silico PA design.