Analysis of Spliceosome Dynamics by Maximum Likelihood Fitting of Dwell Time Distributions

Abstract

Colocalization single-molecule methods can provide a wealth of information concerning the ordering and dynamics of biomolecule assembly. These have been used extensively to study the pathways of spliceosome assembly in vitro. Key to these experiments is the measurement of binding times—either the dwell times of a multi-molecular interaction or times in between binding events. By analyzing hundreds of these times, many new insights into the kinetic pathways governing spliceosome assembly have been obtained. Collections of binding times are often plotted as histograms and can be fit to kinetic models using a variety of methods. Here, we describe the use of maximum likelihood methods to fit dwell time distributions without binning. In addition, we discuss several aspects of analyzing these distributions with histograms and pitfalls that can be encountered if improperly binned histograms are used. We have automated several aspects of maximum likelihood fitting of dwell time distributions in the AGATHA software package.

1. Introduction

The spliceosome is an extremely complex and highly dynamic molecular machine found in eukaryotes [1]. It carries out precursor mRNA (pre-mRNA) splicing by concerted removal of intronic sequences and ligation of the flanking exons. The splicing process requires the coordinated action of five small nuclear ribonucleoprotein particles (snRNPs): U1, U2, U4, U5 and U6. Each snRNP contains a uridine-rich small nuclear RNA (U snRNA) and several snRNP-specific proteins [2]. In addition to large-scale conformational rearrangements of the snRNPs, numerous other splicing factors assemble, rearrange and/or dissociate from the spliceosome during each step of splicing [2–5]. Single-molecule fluorescence microscopy methods such as single-molecule FRET (smFRET) and colocalization single-molecule spectroscopy (CoSMoS) have revealed the transient behaviors of the spliceosome that are often obscured by ensemble techniques. In fact, splicing was first discovered through single-molecule imaging of RNA/DNA hybrids using electron microscopy [6, 7]. Recent high resolution cryo-EM structures have revealed the overall structure, and detailed inner-workings of the several key states of the spliceosome [4–6]. The structural rearrangements observed in these different states have revolutionized our understanding of splicing mechanism as well as validated key single-molecule results concerning juxtaposition of the sites of splicing chemistry prior to 5’ splice site cleavage [8–11].

In addition to pre-mRNA splicing, CoSMoS and other colocalization approaches have been used to study many other multistep biochemical processes including transcription, translation, DNA replication, and actin filament branching [12–18]. In general, colocalization experiments involve observation of the binding and release of fluorescent molecules from a surface-tethered substrate. Often this is enabled by the use of spectrally distinguishable fluorophores (e.g., Cy3 and Cy5), which can be individually excited and detected [15]. This has allowed multiple fluorescent species to be followed simultaneously, providing unique insights into biomolecular assembly and disassembly pathways. Early work on the S. cerevisiae (yeast) splicing machinery revealed that spliceosomes assemble on pre-mRNA in a partially ordered pathway with multiple reversible steps, potentially identifying points of regulation [19, 20]. Critically, these experiments also revealed quantitative kinetic information about several discrete steps in splicing—something which was not possible using earlier approaches such as native gel electrophoresis of cellular splicing extracts.

In this article, we discuss and compare statistical methods that are used to obtain the fit parameters associated with CoSMoS data of spliceosome assembly. We also introduce the A GATHering of Analyses (AGATHA) software package that we have developed to facilitate maximum likelihood fitting of single-molecule data and its statistical analysis. We illustrate the use of AGATHA in fitting data related to assembly of splicing factors on RNAs; however, these maximum likelihood methods are generally useful and can be used to analyze single molecule data originating from many different types of experiments beyond pre-mRNA splicing.

2. Example Data and Initial Analysis

2.1. RNA Binding Dynamics of a Yeast Splicing Factor

In order to demonstrate the methods used in statistical analysis of binding times obtained from single-molecule experiments, we will use two recently published data sets describing the binding of the yeast splicing factor branchpoint bridging protein (BBP) to pre-mRNA substrates containing or lacking the branch site (BS) [21]. In these experiments, Larson et. al showed that the presence of a BS promotes longer binding of a fluorescently-tagged BBP molecule to a surface-immobilized RNA. CoSMoS experiments were performed using a custom built, micromirror TIRF microscope in which the laser excitation beams enter and exit through the objective. The workflow for constructing this microscope has already been published [22]. Pre-mRNAs, labeled with a red laser-excited Cy5 fluorophore, were first immobilized on a functionalized glass slide. Whole cell extract containing BBP protein labeled with a green-laser excited Dy549 fluorophore was then added. This experimental set-up for two color CoSMoS is schematically illustrated in Figure 1A. Individual fluorophores were visualized as discrete spots of intensity, allowing the locations of the RNA and splicing factors to be determined. Images were then recorded from the camera over time, creating movies of “red” immobilized RNAs and “green” dynamic BBP proteins. Detailed descriptions of the experimental set-up and data collection can be found elsewhere [19, 21–26].

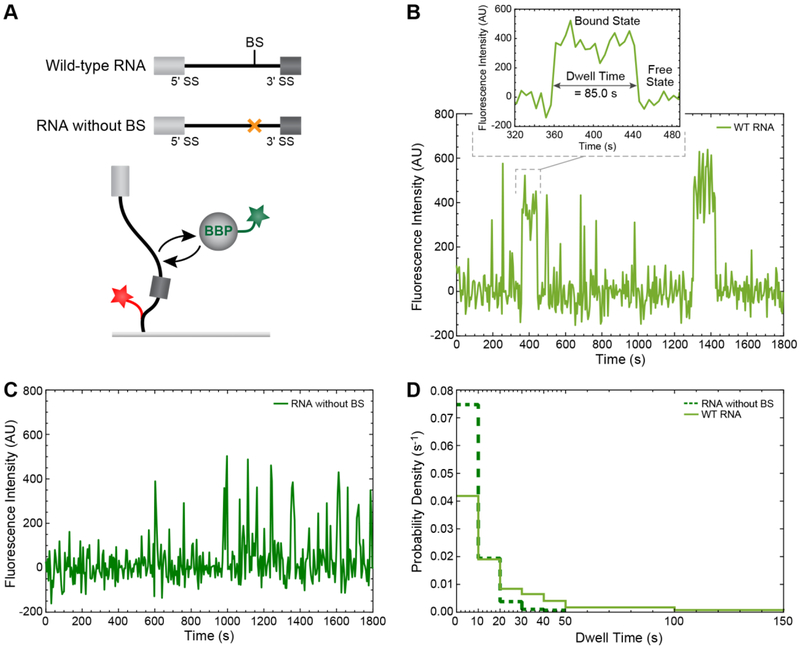
Figure 1.

Analysis of single-molecule binding dynamics of BBP on RNA substrates. (A) Cartoon schematic of the CoSMoS experiment described by Larson and Hoskins [21] in which green-labeled BBP binds to and dissociates from a surface-immobilized, red-labeled RNA substrate either containing (wild-type, WT) or lacking the BS sequence. (B) Single-molecule fluorescence intensity versus time plot showing multiple BBP binding events on a single WT RNA molecule. One of such binding event is magnified to highlight a single BBP dwell time. (C) Single-molecule fluorescence intensity versus time plot showing multiple BBP binding events on a single RNA molecule lacking the BS sequence. (D) Comparison between the probability density histograms of dwell times for BBP on either the WT RNA or the substrate lacking the BS.

2.2. Obtaining a List of Dwell Times from Movies of Single Molecules

In the above experiments with BBP, the fluorescence signal from the surface tethered pre-mRNAs was then used to define Areas Of Interest (AOIs). AOIs were then mapped from the >635 nm field of view (FOV) corresponding to the “red” pre-mRNA locations to the <635 nm FOV in which the “green” BBP was imaged [25]. This was then followed by pixel intensity integration over each AOI, which produced a BBP fluorescence intensity trajectory at each pre-mRNA location (Figure 1B). In this example, the peaks in fluorescence intensity were identified by changes in signal that exceeded a threshold value of 3.2σ_s, where σ_s represents the baseline noise of the fluorescence trajectory. In effect, the association/dissociation of BBP on an individual RNA corresponds to the appearance/disappearance of fluorescence peaks from the AOI. The details about mapping and spot discrimination methods that can be used to obtain the fluorescence intensity trajectories has been previously described [25].

Often a single AOI will show multiple binding events (cf. Figure 1B), and each binding event is characterized by its own binding or dwell time. The dwell times observed will depend on the biochemical properties of the system studied. For example, inspection of individual fluorescence trajectories of BBP binding to a pre-mRNA containing a BS reveals both short and long events (Figure 1B). However, when a pre-mRNA lacks a BS, fluorescence trajectories of BBP binding reveal primarily short events (Figure 1C). This is expected since BBP should most strongly associate with RNAs containing the 5’-UACUAAC-3’ BS sequence [27].

2.3. Plotting the Single-Molecule Data as a Distribution of Dwell Times

A single CoSMoS experiment can yield hundreds of dwell times derived from many different binding events occurring on many different molecules. It is often beneficial to first plot the dwell time distribution as a probability density (PD) histogram. In this method, dwell times are first binned, and the population in each bin (N_bin) is then divided by the product of the bin width (w) and total number of events [N_tot; PD = N_bin/(w × N_tot)]. The probability density histograms of dwell times for BBP on RNAs with or without a BS are compared in Figure 1D. The dwell time distribution for BBP binding on RNA that lacks a BS (dark green) is narrower (shifted towards shorter dwell times) than that obtained from BBP binding to RNA containing a BS (light green). This arises due to the scarcity of long-lived binding events in the absence of the BS. The simplest binding mechanism of BBP on pre-mRNA (R) without a BS can be described as a single-step process:

$$R+BBP\rightleftharpoons R.BBP$$ (1)

In contrast, the broader distribution of BBP dwell times on the wild-type RNA could be due to the presence of two or more populations of BBP-RNA complexes.

A more quantitative and theoretical analysis of the dwell time distributions can provide additional information about kinetic features of the BBP-RNA complexes. The probability density function (PDF) for the lifetime in an individual state can be described as an exponential distribution [28]. For mechanisms with multiple states, the probability density function is the sum of the exponential distributions [28]. A general expression for PDF with k states can be written as:

$$PDF(t)=\sum _{i=1}^k\frac{a_i}{{\tau }_i}{e}^{-\frac{t}{{\tau }_i}}\text{ for }t>0$$ (2)

where τ_i, and a_i, are the time constant and relative amplitude of the i^th state respectively, such that a_i satisfies the constraint ∑a_i = 1 It is of significant interest to know the characteristic time constants, τ_i, for each complex as they provide information about the interconversion of the complexes and their relative kinetic stabilities. The values of these time constants can be extracted by fitting an appropriate equation to the measured data as discussed below.

3. Methods for Fitting Distributions of Dwell Times

3.1. Obtaining the Fit Parameters and Associated Errors

The method of least squares is frequently used to estimate the best fit parameters. Although this approach is straightforward and powerful, it can have its pitfalls if not used carefully [29–32]. This is particularly apparent when used to fit data which are not normally distributed. An alternative approach is the Maximum Likelihood (ML) estimation [33, 34]. For a sufficiently large dataset, different methods should ideally yield the same estimates for the fit parameters. However, in practice, the extracted fit parameters can often depend on the chosen method. This will be illustrated in Section 3.3 by comparing the fit results obtained from two independent methods. For simplicity, we will focus the discussion below on fitting and error estimates of kinetic parameters using the ML approach since it is likely less familiar to most biochemists.

Using Equation (2), the probability density for observing the first data point, t₁, reads as

$$PDF\left(t_1\right)=\sum _{i=1}^k\frac{a_i}{{\tau }_i}{e}^{-\frac{t_1}{{\tau }_i}}$$ (3)

As the measurement of one dwell time is independent of any other dwell time observation within an experiment, the probability density for observing all the n measured data points, t₁, t₂…and, t_n can be written as a product of the individual probability densities. This total probability density defines the likelihood function (Lik (τ_i, a_i)):

$$Lik\left({\tau }_i,a_i\right)=\prod _{j=1}^n\left[\sum _{i=1}^k\frac{a_i}{{\tau }_i}{e}^{-\frac{t_j}{{\tau }_i}}\right]$$ (4)

In other words, the likelihood function characterizes the probability to observe a particular set of dwell time values obtained from an experiment. Maximizing the function, Lik (τ_i, a_i), with respect to the parameters τ_i and a_i will make the observed data most probable. Hence, the values of τ_i and a_i that yield a global maximum of Lik (τ_i, a_i), are the best fit parameters of the PDF to the experimentally observed distribution.

It is important to note that the experimental conditions set limits on the measured dwell times (t), t_m ≤ t ≤ t_x, such that nothing shorter than t_m can be measured in an experiment of duration t_x. The parameter t_m is often limited by the camera frame rate. These constraints on the dwell times calls for a conditional PDF instead of Equation (2), which can be defined as

$$PDF(t)=\frac{a}{\left(e^{-\frac{t_m}{\tau }}-e^{-\frac{t_x}{\tau }}\right)}\left(\frac{e^{-\frac{t}{\tau }}}{\tau }\right),wherea=1.$$ (5)

Similarly, one could obtain the conditional PDF for bi-exponential distribution,

$$PDF(t)={\left[a_1\left(e^{-\frac{t_m}{{\tau }_1}}-e^{-\frac{t_x}{{\tau }_1}}\right)+a_2\left(e^{-\frac{t_m}{{\tau }_2}}-e^{-\frac{t_x}{{\tau }_2}}\right)\right]}^{-1}\left(\frac{a_1}{{\tau }_1}{e}^{-\frac{t}{{\tau }_1}}+\frac{a_2}{{\tau }_2}{e}^{-\frac{t}{{\tau }_2}}\right),$$ (6)

with a₁ + a₂ = 1.

To obtain the best fit of Equation (5) to the dwell time distribution of BBP on RNA without a BS (Figure 1D), we maximize the logarithmic likelihood function:

$$L(\tau )=\ln (Lik(\tau ))=-n.\ln \left[e^{-\frac{t_m}{\tau }}-e^{-\frac{t_x}{\tau }}\right]-n.\text{ln}(\tau )+{\sum }_{j=1}^n\left(-\frac{t_1}{\tau }\right).$$ (7)

Optimizing the product of the probabilities (Equation 4) is often computationally inefficient since this product can yield a very small number. With increasing number of data points, this product can run out of precision very quickly due to the floating-point arithmetic used by computers. Therefore, it is better to maximize the log of the likelihood function as it converts the product of the individual probability densities to summation and preserves the fitting results.

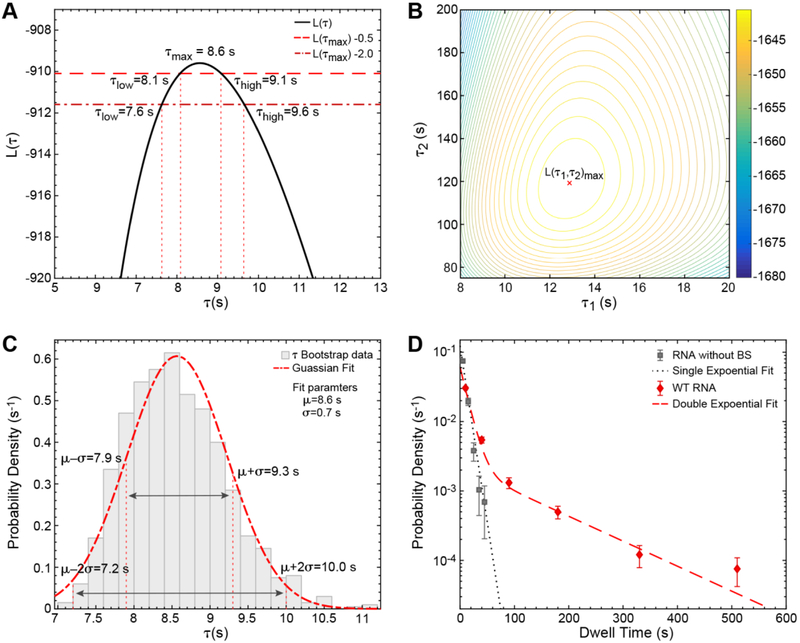
Figure 2A shows the plot between L(τ) vs τ in which L(τ) gets a maximum value of −909.6 at τ_max = 8.6s. This τ_max value is the ML estimate for the fit parameter τ for BBP on RNA without BS. In other words, this parameter indicates that BBP has a characteristic dwell time of 8.6 s when associating with RNAs lacking a BS sequence.

Figure 2.

Fitting and statistical analysis of BBP dwell time histograms. (A) The log likelihood function, L(τ), for BBP binding times on RNAs without a BS is plotted as a function of parameter τ. The τ low and high values, where the L(τ_max) −0.5 line intersects the L(τ) curve, are the 0.5 unit intervals: 8.1 s and 9.1 s. Similarly, the 2 unit limits are 7.6 s and 9.6 s. (B) Contour plot of the log likelihood function, L(τ₁, τ₂)versus τ₁ and τ₂ for a₁ = 0.74. L(τ₁,τ₂) corresponds to the double exponential PDF with dwell times of BBP on WT RNA. (C) Probability density histogram of the ML estimates of τ that are obtained from 1000 random samples (Nboot=1000) of the dwell time dataset for BBP on RNA lacking a BS via bootstrapping. The histogram was fit with a Gaussian distribution to obtain a mean value, μ = 8.6 s, and the standard deviation, σ = 0.7 s. (D) Probability density histograms of the dwell times for BBP are fit with either a single (RNA without BS, black) or double exponential (WT RNA, red) PDFs. Fit parameters and their respective error estimates for both data sets are given in Table 1.

Similarly, one could obtain the ML estimates for a₁, τ₁, a₂, and τ₂ of the double exponential PDF [Equation (6)], which is useful for describing the dwell time data set of BBP on WT RNA. In this case, the more complicated equation is necessary to correctly fit the appearance of both long and short dwell times in the data set when BBP binds RNAs containing a BS sequence. A contour plot of the logarithmic likelihood function, L(τ₁,τ₂) [corresponding to the double exponential PDF, Equation (6)], is plotted as a function of τ₁ and τ₂ by holding a₁ constant (Figure 2B). L(τ₁,τ₂) obtains a maximum value of −1639.5 at τ₁ = 12.9 s and τ₂ =119.3 s with the ML estimate for a₁ = 0.74.

Apart from estimating the optimized fit parameters, it is equally important to quantify the errors associated with the fit parameters. There are many possible ways to estimate the errors: a standard approach to assess the standard deviations corresponding to the parameters estimates is by finding the diagonal elements of the covariance matrix of Lik (θ_i) with respect to fit variables, θ_is [35]. Here, the covariance matrix can be written as C (θ) = I (θ)⁻¹, where

$$I\left({\theta }_i,{\theta }_j\right)=-{\left(\frac{{\partial }^{2}Lik(\theta )}{\partial {\theta }_i\partial {\theta }_j}\right)}_{{\theta }_{imax},{\theta }_{jmax}}$$ (8)

θ_imax, and θ_jmax are the ML estimates for θi, and θ_j respectively. For a single exponential distribution, it is straightforward from Equations (5) and (8) to obtain an analytical expression for standard deviation, $\sigma \approx {\tau }_{max}/\sqrt{n}$, where τ_max is the ML estimate of τ. With a total of 288 binding events/dwell times, and τ_max = 8.6 s. (data corresponding to Figure 2A) the standard deviation turns out to be ~0.5 s. It is more difficult to obtain the analytical expressions for the standard deviations associated with all parameters of higher order exponential distributions. As a result, one can approach these problems using numerical analysis.

Another way of estimating the error in fit parameters is by finding likelihood intervals. The likelihood intervals (i.e., the ranges for the fit parameters) are the values most probable within certain neighborhoods around the maxima [29]. For example, consider the line, L(τ_max) − m plotted against the likelihood curve. The points of intersection of these curves, τ_low and τ_high, will provide a good estimate for the uncertainty in τ_max (Figure 2A). The error estimate, in this particular case, depends solely on the value of m. The likelihood intervals for m = 0.5, and m =2 correspond to one and two standard deviation limits respectively [35]. For higher order exponential distributions, a similar procedure can be employed by estimating the error on one parameter while keeping the other parameters constant. Likelihood intervals estimates for a₁, τ₁ and τ₂ are shown in Table 1 for a distribution containing two exponential terms. Likelihood intervals estimates are relatively easy to obtain for a single exponential fit but can become laborious with increasing numbers of variables.

Table 1.

Comparison between the likelihood intervals and the bootstrap confidence intervals for single and double exponential fits.

RNA	Function	Parameter	ML estimate	Likelihood Intervals				Bootstrap Mean	Confidence Intervals
				m = 0.5 68%		m = 2 95%			σ 68%		2σ 95%
Without BS	Single	τ (s)	8.6	8.1	9.1	7.6	9.6	8.6	7.9	9.2	7.2	10.0
				−0.5	0.5	−0.9	1.1		−0.7	0.7	−1.4	1.4
WT RNA	Double	a1	0.74	0.70	0.77	0.67	0.79	0.74	0.69	0.78	0.65	0.82
				−0.03	0.03	−0.06	0.06		−0.04	0.04	−0.08	0.08
		τ1(s)	12.9	11.9	13.9	10.9	15.2	12.9	11.6	14.2	10.3	15.5
				1.0	1.0	−2.0	2.3		−1.3	1.3	−2.6	2.6
		τ2(s)	119.4	107.2	133.9	96.5	151.1	120.9	104.4	137.4	87.8	154.0
				−12.2	14.6	−22.9	31.6		−16.5	16.5	−33.1	33.1

In many cases, the statistical method of bootstrapping is advantageous over the aforementioned methods in estimating the errors of the fit parameters [36]. Bootstrapping is a resampling method in which a new data set is generated from the observed data by random sampling, with the new and original data sets being of the same size. Ideally, this resampling method preserves the actual distribution of the parameters present in the observed data set. An example of the bootstrap analysis is illustrated in Figure 2C, where 1000 data sets were simulated from the dwell times for BBP on RNA without a BS. The ML estimates for τ were obtained for all 1000 data sets. The distribution of ML estimates for τ was analyzed by plotting a probability density histogram and then fitting to a Gaussian distribution. The Gaussian fit yields a mean value of 8.6 s and standard deviation of 0.7 s for τ, which are comparable to the ML estimate and 0.5-unit likelihood intervals (Figure 2A). In a similar fashion, one could obtain the uncertainty in the estimates for a large number of parameters in a fit. A direct comparison of the error estimates for fit parameters obtained from the likelihood intervals, and the bootstrap analysis can be found in Table 1.

3.2. Determining the Goodness of the Fit

Although ML is a powerful technique, care should be taken in assessing the goodness of the fit to the unbinned data. This can be done by using statistical tests such as the likelihood ratio or Akaike Information Criterion (AIC) for model selection based on the likelihoods [37, 38]. For example, a log likelihood ratio test can identify if the dwell time distribution for BBP association with WT RNA is better described by single or double exponential PDFs. The MATLAB function Iratiotest efficiently implements this procedure and, in this example, results in rejection of the model based on a single exponential PDF. For fitting of data sets with unknown kinetic features, it is often advisable to begin fitting to a single exponential PDF. The log likelihood ratio test or AIC can then be used to test if the simplest model is sufficient or if more complicated PDFs are needed to model the data. Figure 2D shows good agreements between the data and the fit curves for BBP dwell times on RNAs with and without a BS.

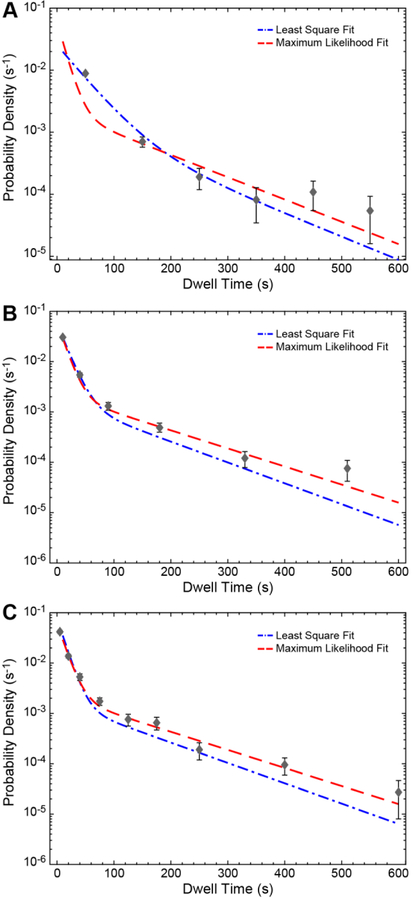
Critically, it is important to consider the histogram binning since one could easily bias the fit if the histogram is not binned properly. For example, we created a histogram with six bins of equal width (100 s each) for the dwell time data set of BBP binding to WT RNA along with the curve obtained using a ML fit of the unbinned data (Figure 3A). It is evident that the ML fit curve (red) deviates significantly from the equally binned histogram as well as the curve obtained from least squares fitting of the bin centers (blue line and black points). To correct this, one can construct an unequally binned histogram with narrow bin widths for shorter intervals. We have plotted the same ML curve along with unequally binned histograms of the same data set in Figures 3B and C. The agreement between the ML fit and the histogram gets better with increasing number of unequal bins.

Figure 3.

Bin size-dependent comparison between ML and least squares fits of dwell time distributions. The probability density histograms for the dwell times of BBP on WT RNA with (A) 6, equally-sized bin widths, (B) 6, variably-sized bind widths, and (C) 9, variably sized bin widths. Lines represent the fits to the bin centers (black points) using least squares methods (blue) or fits of the unbinned data using ML methods (red). For both methods, the fit parameters and their corresponding confidence intervals are given in Tables 1 and 2.

3.3. Comparison Between Maximum Likelihood and Least Square Fitting

The data plotted in Figure 3 also illustrate a potential pitfall of least squares fitting of dwell time distributions. In this case, the least squares fits were obtained using the curve fitting application of MATLAB (Table 2). With least squares fitting, it is possible to obtain ill-defined fit parameters with large standard deviations despite having reasonable R² or adjusted R² values. In this case, the least squares fitting is improved by increasing the number of bins and by using variable bin sizes. If the bin number is large, the least squares predictions for the parameters approach those obtained by ML estimates (compare parameters in Table 1 vs. Table 2). However, the least squares method results in broader confidence intervals as compared to the ML error estimates.

Table 2.

Analysis of the double exponential fit to the dwell time distribution for BBP on WT RNA using nonlinear least squares fitting of histogram bin centers.

No. of Bins	Bin Size	Parameter	Non Linear Least Square Fit	Confidence Intervals				R2/Adj R2	Corresponding Figure
				68%		95%
6	Equal	a1	0.91	−1.32	3.14	−5.06	6.88	0.9465/0.9108	3A
		τ1(s)	38.5	−29.2	106.1	−142.6	219.5
		τ2(s)	116.1	−2399	2631	−6617	6849
6	Variable	a1	0.82	0.74	0.91	0.59	1.06	0.9996/0.9994	3B
		τ1(s)	15.4	13.5	17.2	10.4	20.3
		τ2(s)	104.9	22.1	188.0	−116.7	326.5
9	Variable	a1	0.70	0.65	0.75	0.59	0.81	0.9992/0.9989	3C
		τ1(s)	12.4	11.6	13.2	10.6	14.2
		τ2(s)	107.4	69.3	145.5	21.4	193.5

Additionally, least square fits can be highly sensitive to user inputs for upper and lower bounds for the fit coefficients as well as sample size. To see the effect of the latter, we simulated data sets of different sizes with a₁ = 0.75, τ₁ = 10.0 s, and τ₂ = 100.0 s. As sample size increases, ML estimates gets very close to the input parameters with narrower confidence intervals (Table 3). However, increasing the number of bins with these large data sets does result in overestimated values of τ₂ in least squares fits (Table 3). This can be attributed to the fact that the least squares method is very sensitive to outliers, assumes the variables to be independent, and the error to be normal. In cases where error terms are not normal, the confidence intervals of the least square estimates are not reliable [24–26]. In our simulation, maximum likelihood outperforms the least squares method for typical “single molecule”-sized data sets of 100–1000 data points.

Table 3.

Dependence of fitting methods on sample size using simulated data with a double exponential PDF.

Data points	Number of Bins	Bin Size	Parameter	Maximum Likelihood Results*	Nonlinear Least Squares Results*	R2/Adj R2
100000**	1000	Equal (1 s/bin)	a1 = 0.75	0.74 (0.74–0.74)	0.72 (0.72–0.72)	0.0.9997/0.9997
			τ1 = 10 s	10.9 (10.9–10.9)	10.2 (10.1–10.2)
			τ2 = 100 s	101.8 (100.3–103.1)	123.4 (120.6–126.1)
10000**	1000	Equal (1 s/bin)	a1 = 0.75	0.75 (0.73–0.76)	0.73 (0.69–0.72)	0.0.9975/0.9975
			τ1 = 10 s	10.9 (10.5–11.3)	10.2 (10.1–10.2)
			τ2 = 100 s	102.7 (107.5–97.1)	122.0 (114.7–130.1)
10000*	15	Variable	a1 = 0.75	0.75 (0.73–0.76)	0.76 (0.74–0.79)	0.0.9999/0.9999
			τ1 = 10 s	10.9 (10.5–11.3)	10.8 (10.5–11.1)
			τ2 = 100 s	102.7 (107.5–97.1)	116.0 (80.5–151.5)
1000	100	Variable	a1 = 0.75	0.76 (0.72–0.80)	0.73 (0.67–0.81)	0.9951/0.9950
			τ1 = 10 s	9.5 (8.3–10.7)	10.4 (10.1–12.8)
			τ2 = 100 s	102.7 (85.7–119.7)	124.8 (88.3–161.4)
1000	10	Variable	a1 = 0.75	0.76 (0.72–0.80)	0.76 (0.72–0.80)	0.9999/0.9998
			τ1 = 10 s	9.5 (8.3–10.7)	11.08 (10.6–11.6)
			τ2 = 100 s	102.7 (85.7–119.7)	114.4 (60.9–167.9)
100	10	Variable	a1 = 0.75	0.79 (0.59–0.99)	0.68 (0.72–1.00)	0.9988/0.9982
			τ1 = 10 s	8.9 (3.3–14.5)	6.9 (9.8–14.1)
			τ2 = 100 s	90.7 (17.2–193.2)	50.0 (−3.9 to 103.9)

^*Intervals for each fitting method are shown in parentheses.

^**Maximum likelihood fitting results obtained using MEMLET software [34]. MEMLET is more efficient at processing large data sets (≥10000 data points) than AGATHA software.

4. Use of AGATHA Software for ML Fitting

Here, we introduce “AGATHA” (A GATHering of Analyses), a MATLAB-based software package that provides tools for the analysis of the dwell times obtained from CoSMoS experiments (https://github.com/hoskinslab/AGATHA). AGATHA includes a number of subprograms including those for ML analysis (Plotting Histogram), identifying patterns of signal appearance (Sequential Arrival, Simultaneous Arrival, and Short Counter), photobleaching analysis (Counting Photobleaching Steps), and data visualization (Two Color Plot). These programs are accessed via the AGATHA GUI (Figure 4). The Sequential Arrival and Simultaneous Arrival programs are useful for deducing pathways of signal appearance and disappearance in three color CoSMoS experiments (i.e., determining pathways of biomolecular assembly or disassembly [15]). These programs classify binding events into various categories depending upon times of signal appearance or disappearance. The Counting Photobleaching Steps program counts the number of bleaching steps present in a fluorescence intensity trace by fitting the data to a step function. This is useful for counting the number of fluorophores (biomolecules) present in a molecular assembly. Instruction manuals for each of these programs are found in their respective GUIs. Here, we restrict ourselves to the Plotting Histogram program as the others are beyond the scope of this article. We also note that Woody et. al have independently developed a similar program, MEMLET (MATLAB Enabled Maximum Likelihood Estimate Tools), that utilizes the ML approach to fit data by providing a variety of general or user defined PDFs [34].

Figure 4.

Screenshot of the startup screen for AGATHA software, a collection of programs designed to expedite analysis of dwell times and fluorescence intensity trajectories obtained from CoSMoS experiments.

4.1. Plotting Histograms

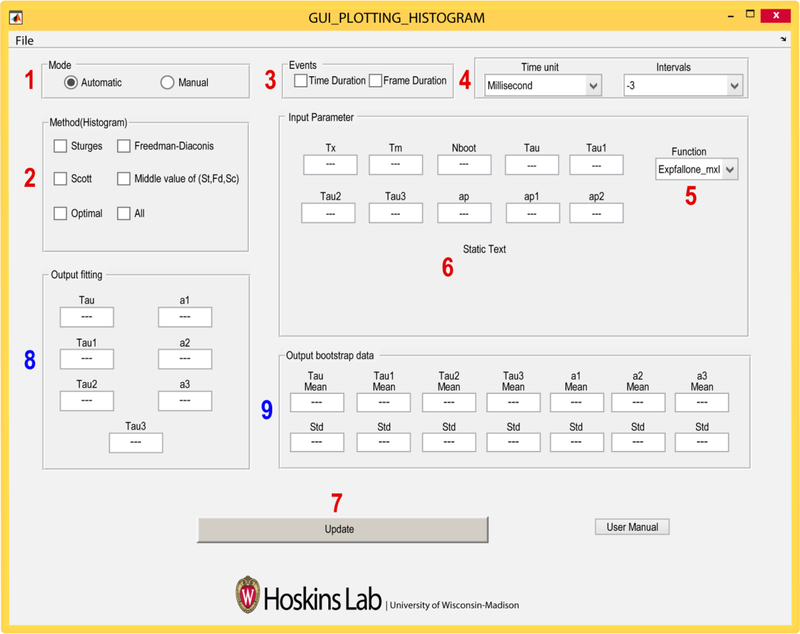
The Plotting Histogram program (PH) facilitates plotting of dwell time data using various methods for bin size selection as well as ML fitting of the unbinned data. PH calculates the appropriate number of bins from the chosen method (described below) and also can remove empty bins by combining neighboring bins. Along with the histogram, it displays the error in the counting statistics of each bin center by calculating the binomial distribution variance, ${\sigma }_{bin}^2$, as, ${\sigma }_{bin}=\sqrt{nP(1-P)}$, where n is the total number of the data points, and P is the probability of the binding event [39]. Finally, it returns the fit parameters and associated standard deviations by using ML and bootstrap analysis. AGATHA simplifies ML data analysis by requiring the user to supply the relevant inputs to entry widgets in the PH GUI (Figure 5, numbers 1–7). Fitting results are also displayed in widgets once the program has been run (Figure 5, numbers 8 and 9). Below we describe data entry and use of each of the widgets in the PH GUI.

Figure 5.

Screenshot of the Plotting Histogram GUI. Red numbers indicate widgets which require user input, and blue numbers indicate locations of the fitted parameters output. In addition, this program also outputs various histograms which are saved in a user-specified folder.

4.2. Instructions for Using the Plotting Histogram Program

1. Mode: In this widget, the user either instructs the software to automatically calculate the number of bins plotted in a histogram (Automatic) or the user can manually input the bin edges in increasing order (Manual).

2. Histogram: When Automatic is selected in widget 1, the user then selects one or more of the listed methods for calculating the number of bins in the histogram.

   • Sturges: According to the Sturges rule, the number of the bins for a histogram are estimated based on the range of the given data. This calculates the number of bins, m as m = (1 + log₂ (n)), where n is the total number of data points [28, 40]. It will perform poorly if the number of data points is less than 30 and the points are not normally distributed [41]. As dwell times often follow an exponential distribution (similar to Figure 3A), this method may fail to show an appropriate trend in the data.
   • Freedman-Diaconis: This method is less sensitive to outliers in a given data, and might be more suitable for data with heavy-tailed distributions [42]. It uses a bin width, h, as $h=IQR(X)/{(n)}^{1/3}$ where X is the dwell time data, n is number of data points, and IQR is the interquartile range of X.
   • Scott: This method works better if the data is mostly normally distributed. However, this rule is appropriate for other distributions as well. It calculates bin width, h, as $h=3.5*{\sigma }_X/{(n)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$, where σ_X is the standard deviation of the data set X, and n is number of data points [43].
   • Middle: This method make use of all three methods mentioned above, then choses the middle (median) value for bin numbers.
   • Optimal: An optimization principle is used to minimize the expected least squares loss function between the histogram and an unknown underlying density function [43]. The optimal bin width, h*, is obtained as a minimizer of the formula, (2M − V)/h², where M and V are mean and variance of the data points across bins with a width h. Optimal number of bins, m, are calculated as, m = (max(X) − min(X))/h*, where max(X) and min(X) are the maximum and minimum value of the given data set X. In our experience, this method is frequently used for plotting dwell time distributions obtained from CoSMoS experiments.
   • All: This selects all of the above methods and runs them independently.

3. Events: In this widget, the user specifies whether or not the dwell time data is reported in units of time or camera frames.

4. Time Units and Intervals: The time units (seconds or milliseconds) are selected within this widget as well as the interval type from the drop-down menu. AGATHA uses input interval files generated by the GLIMPSE and IMSCROLL programs (available at https://github.com/gelles-brandeis/CoSMoS_Analysis) [25]. In these programs the dwell times are classified as different types of intervals, each assigned an integer value between −3 and +3. Details about event classification have been previously described [25] and depend on whether or not the binding the event has been observed in its entirety as well as whether or not binding events or times between binding events are being analyzed.

5. Function: PH is equipped with single, double and triple exponential probability distributions for fitting the measured data. These functions as labelled as Expfallone_mxl, Expfalltwo_mxl, and Expfallthree_mxl, respectively. PH currently includes equations for processing up to third order PDFs but can be expanded to higher distributions if needed.

6. Input PH Parameters: The user should enter the experimentally-constrained times Tx (length of the experiment) and Tm (minimum time that can be resolved by the experiment) along with a number for Nboot (number of datasets to be simulated for bootstrap analysis which is the same as the number of iterations of bootstrap analysis). For example, Nboot=1000 was used for Figure 2C. For single exponential distributions, the user should enter an initial estimate for Tau [τ in Equation (5)]. For bi-exponential PDFs, the user gives initial guesses for Tau1, Tau2, and ap. The input value ap is converted to a₁ = 1/(1 + ap²) before maximizing the log likelihood in order to constrain between 0 and 1. Similarly, for tri-exponential distribution fit parameters are extended to Tau1, Tau2, Tau3, ap1 and ap2, and the a₁, a₂, and a₃ are deduced using equations a₁ = 1/(1 + ap1²), a₂ = (1 − a₁)/(1 + ap2²) and a₁ + a₂ + a₃ = 1. If the initial guesses are far off, the program may crash and fail to find a solution. In which case, new values can be chosen and the analysis rerun.

7. Update: Clicking the update button will ask the user to select the intervals file to be analyzed and to create an output folder for the results.

8. Output Fitting: The ML estimates for the fit parameters are returned here.

9. Output Bootstrap data: The mean and standard deviation of the fit parameter values are displayed after bootstrap analysis. The histograms before and after the fitting will be saved in the same directory with the same name as the input interval file. The program also saves the bootstrap results for all the fitting parameters.

5. Conclusion

AGATHA and MEMLET facilitate ML fitting of complex single molecule data with user-friendly capabilities and options that complement standard software programs. MATLAB’s DF tool application only provides a single exponential function for fitting and cannot fit probability density distributions for multiple exponential or user-defined PDFs. Both AGATHA and MEMLET are capable of fitting data with multi-exponential PDFs and provide estimates and errors for fitting parameters using ML and bootstrapping techniques. Additionally, MEMLET directly provides likelihood ratio model testing, allows the user to input any PDF, and can take text or MATLAB variable files as input. On the other hand, AGATHA is supplemented with various tools for histogram binning and error calculation. Current versions of AGATHA require input in IMSCROLL format [21]; however, these types of files can be easily constructed from any data set.

In conclusion, ML fitting of unbinned dwell or binding time data is often preferable compared to least squares fitting of binned data sets, which can be skewed based on how the histogram has been constructed. Implementation of ML methods in MATLAB can be laborious. Fortunately, this is greatly simplified by the AGATHA software.

Highlights.

• Single-molecule methods can measure discrete binding events between individual biomolecules

• Maximum likelihood fitting of unbinned binding data can be used to determine kinetic parameters

• AGATHA software automates many time-consuming steps in data fitting and histogram analysis