Abstract
Biotin (vitamin B7) is an enzyme cofactor required by organisms from all branches of life but synthesized only in microbes and plants. In the final step of biotin biosynthesis, a radical S-adenosyl-L-methionine (SAM) enzyme, biotin synthase (BioB), converts the substrate dethiobiotin to biotin through the stepwise formation of two C–S bonds. Previous electron paramagnetic resonance (EPR) spectroscopic studies identified a semi-stable intermediate in the formation of the first C–S bond as 9–mercaptodethiobiotin linked to a paramagnetic [2Fe–2S] cluster through one of its bridging sulfides. Herein, we report orientation-selected pulse EPR spectroscopic results that reveal hyperfine interactions between the [2Fe–2S] cluster and a number of magnetic nuclei (e.g., 57Fe, 15N, 13C and 2H) introduced in a site-specific manner via biosynthetic methods. Combining these results with quantum chemical modeling gives a structural model of the intermediate showing that C6, the target of the second hydrogen-atom abstraction, is now in close proximity to the nascent thioether sulfur and is ideally positioned for the second C–S bond forming event.
Keywords: Biotin, Biotin Synthase BioB, Radical SAM Enzyme, Orientation-selected ENDOR, Broken-symmetry DFT
Graphical Abstract
1. INTRODUCTION
Biotin, an essential human nutrient also called vitamin B7, is an enzyme cofactor required by most organisms and serves to deliver CO2 for use in a variety of metabolic reactions.1–2 Biotin is synthesized in microbes and plants through a semiconserved pathway (Figure 1). The penultimate biosynthetic product, dethiobiotin (DTB), is generated from L-alanine, pimeloyl coenzyme A or pimeloyl acyl carrier protein, CO2, and the amine group of S-adenosyl-L-methionine (SAM) by the biotin biosynthetic enzymes BioF, BioA and BioD.3 In the final step of biotin biosynthesis, DTB is converted to biotin through introduction of a sulfur atom bridging the C6 and C9 positions, a reaction catalyzed by a radical SAM enzyme known as biotin synthase (BioB).4–5
Figure 1. Biotin biosynthesis pathway.
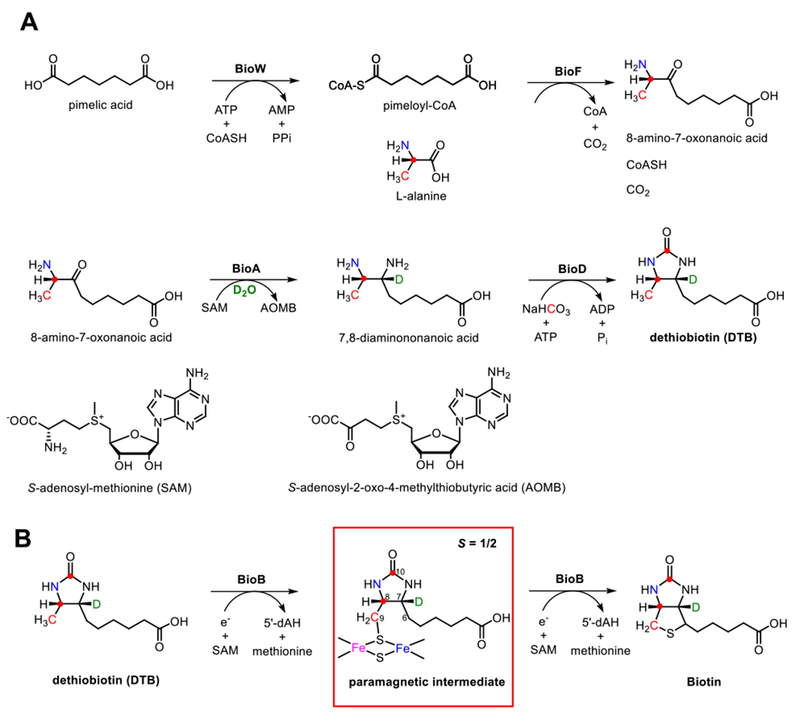
A, Biosynthesis of DTB from exogenous pimelic acid requires BioW, BioF, BioA and BioD enzymes along with appropriate substrate and cofactors; this pathway was exploited for in vitro biosynthesis of isotopically labeled DTB. In E. coli, pimeloyl acyl carrier protein is generated de novo by BioC, BioH, and fatty acid synthase and likely serves as a direct substrate for BioF. B, In the final step of biotin biosynthesis, the radical SAM enzyme BioB catalyzes the formation of biotin via two sequential hydrogen-atom abstractions from the substrate DTB leading to the sulfur incorporation. Isotopically-labeled nuclei investigated in this work are shown in color.
BioB exists as a homodimer (2 × 38.6 kDa) in solution.6 Each monomer contains a SAM-binding [4Fe–4S]RS (RS = radical SAM) cluster and an auxiliary [2Fe–2S] cluster; this latter cluster has a unique coordination environment consisting of one arginine (Arg260) and three cysteine (Cys97, Cys128 and Cys188) ligands.6 As illustrated in Figure 1B, BioB catalyzes the oxidative insertion of a sulfur atom between C9 and C6 positions of DTB, completing the thiophane ring of biotin in a two-step process. An early hypothesis suggested that the sulfur was sourced from a PLP-dependent cysteine desulfurase.7–8 However, BioB with Fe–S clusters reconstituted with 34S showed incorporation of the heavy-atom isotope into biotin,9 and biotin formation coincides with destruction of the [2Fe–2S] cluster,10–11 strongly suggesting that one of the cluster’s μ-sulfides is the true sulfur source.
The BioB-catalyzed reaction begins with reductive cleavage of the sulfonium C5′–S bond of SAM by the [4Fe–4S]RS cluster yielding a cluster-bound methionine and a 5′-deoxyadenosine radical (5′-dA•).12 The transient 5′-dA• radical abstracts a hydrogen atom from the C9 position of DTB to form a presumed dethiobiotinyl radical that is then quenched by a μ-sulfide of the auxiliary [2Fe–2S] cluster, generating 9-mercaptodethiobiotin (MDTB);13 this process is coupled with the transfer of an electron from the sulfide into one of the iron atoms, generating an S = 1/2 paramagnetic intermediate.5, 14 The corresponding electron paramagnetic resonance (EPR) spectrum consists of two species (they appear in an ≈2:1 ratio) that have similar g-values and relaxation behavior as reduced [2Fe–2S] clusters.5, 10, 14 The distinction between the two species is currently unknown; however, we note that only one species is observed when the paramagnetic intermediate is prepared using the Arg260Met mutant of BioB, suggesting that structural differences in the vicinity of Arg260 could play a role.5
In the second step, conversion of MDTB to biotin, a second 5′-dA• radical, generated from another equivalent of SAM, then abstracts a hydrogen atom from the C6 position of DTB. The resultant radical then attacks the sulfur again, closing the thiophane ring, yielding biotin and leading to disintegration of the resulting diferrous [2Fe–1S] cluster.4, 13
Leveraging a biosynthetic route to DTB (Figure 1A), we previously installed 13C (I = 1/2) into the BioB substrate DTB site-specifically at position C9. Using the corresponding 13C hyperfine interaction (HFI), we identified the nature of the paramagnetic intermediate as MDTB covalently coordinated to a still-intact [2Fe–2S] cluster via its newly acquired thiolate sulfur.14 We posited that C9 had formed a covalent C–S bond with the bridging sulfide, resulting in MDTB now being present as a bridging thiolate, and showed that anisotropic contribution to the HFI—which is sensitive to the distance between the magnetic 13C nucleus and the electron spin borne by the irons—was wholly consistent with this positioning. However, the detailed structure of the rest of the MDTB fragment in this intermediate state remains unknown.
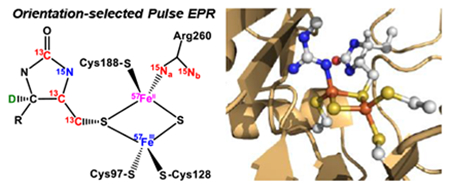
Therefore, in this work, we took further advantage of the biotin biosynthetic enzymes (BioW, BioF, BioA and BioD) to install magnetic isotopes (e.g., 15N, 13C and 2H) in site-selective positions throughout DTB. We then mapped the HFI tensors (A) of these nuclei onto the g-tensor of the net S = 1/2 [2Fe–2S] cluster using orientation-selected ENDOR15–17 (Electron Nuclear Double Resonance) and HYSCORE18 (Hyperfine Sublevel Correlation) spectroscopies. These HFI provide geometrical information—namely, the distance between the magnetic nuclei and the electron spin-carrying centers of the cluster. We have also selectively labeled the BioB enzyme with 57Fe in the auxiliary [2Fe–2S] cluster and with 15N in the terminal guanidino groups of arginine residues (i.e., guanidino-15N2–Arg).
Evaluating these spectroscopic results against quantum chemical models gives a consensus structural model of the paramagnetic intermediate in which C6, following hydrogen-atom abstraction by the second 5′-dA• radical, is ideally positioned to be quenched by the thiolate sulfur of the cluster-bound MDTB and to generate biotin. This EPR-derived structure of the paramagnetic intermediate not only provides more intimate details on the mechanism of BioB, but also reinforces the emerging concept that in order for RS enzymes to maintain control over their reactive intermediates, the active sites must be organized to selectively promote the desired reaction trajectory and to minimize all other potential side reactions.
2. MATERIALS AND METHODS
2.1. Production and purification of BioB.
Detailed descriptions of protein purification and assay protocols are provided in the supplementary information file and references provided therein; the following cursory description should be sufficient to understand how BioB samples were prepared for spectroscopic analysis.
2.1.1. Non-isotopically-labeled BioB.
BioB was overexpressed in E. coli BL21(DE3)pLysS harboring a modified pET21d plasmid (pJJ 15) that encodes E. coli BioB coupled to an N-terminal hexahistidine tag via a linker that contains a TEV protease recognition sequence.19 Cell growth at 37 °C and IPTG-induced expression at 25 °C were carried out in Luria broth containing 50 μM FeCb as previously described.19 Following cell lysis, purification from the soluble lysate followed standard metal ion-affinity column procedures using a Ni-NTA-agarose column (Qiagen) with elution using 200 mM imidazole, immediately followed by passage through a BioGel P2 desalting column (BioRad) to remove imidazole. Aerobic purification typically provides ~25 mg BioB per liter of culture and the resulting protein contains two [2Fe-2S]2+ clusters per BioB dimer, while the RS cluster site is empty, presumably due to oxidative degradation of this cluster during purification.19–20 The N-terminal fusion tag was not removed as we have previously shown that the presence of this tag has no effect on catalytic activity or UV/visible and EPR spectra.11, 19
2.1.2. Guanidino-15N2-arginine-labeled BioB.
Since Luria broth contains a variety of arginine-containing peptides, incorporation of isotopically-labeled arginine into overexpressed proteins requires the use of defined media. We chose to use a minimal media recipe that had previously been developed for overexpression of B12-dependent methionine synthase,21 in which glucose-M9 minimal media is supplemented with a mixture of amino acids, including in this case, arginine containing 15N in the terminal positions of the guanidine functional group (Cambridge Isotope Laboratories). We further enhanced label incorporation by blocking endogenous arginine biosynthesis through deletion of arginosuccinate lyase: we obtained the ΔargH strain JW3932 from the KEIO knockout strain collection22 (Coli Genetic Stock Center) and made the strain competent for protein expression by treating with the DE3 lysogenization kit (MilliporeSigma) and transforming with plasmid pJJ15.19 BioB was otherwise expressed and purified as described above. Isotope label incorporation was confirmed by MALDI-MS of peptides derived from a tryptic digest. BioB contains 20 Arg residues spread throughout the primary sequence, but only Arg260 and Arg95 are positioned near the EPR detectable [2Fe-2S]+ cluster.6
2.1.3. 57Fe-labeled BioB.
Since Luria broth contains a significant amount of natural abundance iron, we expressed 57Fe-labeled BioB in glucose-M9 minimal media supplemented with casamino acids and 10 μM 57FeCl3. Protein was expressed using strain pJJ15/BL21(DE3)pLysS and purified as described above. Prior studies using Mossbauer spectroscopy have confirmed that this aerobically purified protein contains 57Fe in the [2Fe-2S]2+ clusters and does not contain any detectable 57Fe bound at other sites.20 In situ reconstitution of the [4Fe-4S]RS2+ clusters with natural abundance Fe, as described in section 2.3 below, was also previously shown to proceed without exchange of the 57Fe label in the [2Fe-2S]2+ cluster.20
2.2. Biosynthesis of isotopically-labeled DTB.
We utilized a fully biosynthetic route to the production of DTB (as illustrated in Figure 1), using isotopically-labeled L-alanine (Cambridge Isotope Laboratories and MilliporeSigma) and unlabeled pimelic acid as precursors. The biotin biosynthetic enzymes B. spaericus BioW and E. coli BioF, BioA, and BioD were separately expressed and purified to >90% homogeneity. Pimeloyl CoA was produced by incubation of pimelic acid, coenzyme A, and ATP with BioW and purified using reverse-phase HPLC. DTB was then produced by incubation of pimeloyl CoA with L-alanine, SAM, ATP, and NaHCCb with BioF, BioA, and BioD and purified using reverse-phase HPLC. For incorporation of 2H at the C7 position, a mixture of the latter three enzymes was repeatedly concentrated and diluted in D2O, all of the substrates were lyophilized and redissolved in D2O, and the reaction was run in buffered D2O. For each labeled sample, isotope incorporation was confirmed by a combination of NMR (Figure S22-S26) and LCMS analysis, as appropriate for the respective isotope.
2.3. Generation of the paramagnetic intermediate.
The samples of the paramagnetic intermediate studied in this work were generated as follows:5, 14 The reaction was conducted under anaerobic conditions at 27 – 30 °C. Firstly, a buffered solution (100 mM Tris-HCl, 10 mM KC1, pH = 8.0) containing 300 μM BioB (monomer conc.), 10 mM DTT, 1 mM Na2S, 1 mM FeCl3, 10 μM flavodoxin, 5 μM ferredoxin(flavodoxin):NADP+ oxidoreductase, 2 mM NADPH and 300 μM DTB was prepared and incubated for 15 min. The reaction was then initiated by adding 300 μM SAM; after 30 – 60 min, the sample was transferred to an EPR tube, removed from the glove box and flash-frozen in liquid nitrogen. Generation of the paramagnetic intermediate was verified by X-band continuous-wave (CW) EPR spectroscopy.
2.4. EPR spectroscopy and analysis.
2.4.1. CW EPR spectroscopy.
X-band (9.38 GHz) CW EPR spectra were recorded on a Bruker (Billerica, MA) EleXsys E500 spectrometer equipped with a super-high Q resonator (ER4122SHQE). Cryogenic temperatures were achieved and controlled using an ESR900 liquid helium cryostat in conjunction with a temperature controller (Oxford Instruments ITC503) and a gas flow controller. CW EPR spectra of the paramagnetic intermediate were recorded at 40 K with microwave power as high as 100 mW in order to minimize the contribution from the flavin semiquinone radical which is easily saturated. These measurement conditions also minimized the contribution from the reduced [4Fe–4S]RS+ cluster (g-values of [2.044, 1.944, 1.914]23) due to its fast relaxation properties, although its contribution at lower temperatures was negligibly small (Figure 2). Simulations of the CW spectra and the following pulse EPR spectra were performed using EasySpin 5.1.10 toolbox24–25 within the Matlab 2014a software suite (The Mathworks Inc., Natick, MA).
Figure 2. EPR characterizations of the paramagnetic intermediate.
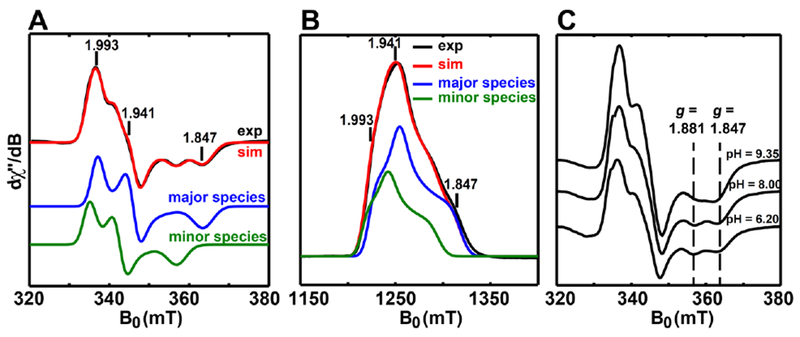
A, X-band (9.38 GHz) CW EPR spectra of the intermediate recorded at 40 K with 100 mW power. B, Q-band (34.0 GHz) electron spin-echo detected field swept EPR spectrum of the intermediate at 10 K. The pulse sequence was π/2-τ-π-τ-echo, with π/2 = 16 ns and τ = 300 ns. The black traces are experimental spectra, while the red traces are the simulated spectra involving the contributions from both the major component (64%, g-tensor = [1.993, 1.941, 1.847], blue traces) and the minor component (36%, g-tensor = [2.005, 1.960, 1.881], green traces). C, pH-dependence of X-band CW EPR spectra of the paramagnetic intermediate recorded at 40 K with 100 mW power. The buffer was 100 mM Tris-HCl, 10 mM KCl and 10 mM DTT, with pH = 6.20, 8.00 or 9.35.
2.4.2. Q-band pulse ENDOR spectroscopy.
Q-band (~34.0 GHz) pulse ENDOR experiments were performed on a Bruker Biospin EleXsys 580 spectrometer equipped with a 10 W amplifier and a R.A. Isaacson cylindrical TEon resonator in an Oxford CF935 cryostat. ENDOR measurements were performed at 10 K by employing the Mims pulse sequence (π/2-τ-π/2-RF-π/2-τ-echo) for small hyperfine couplings16 or Davies pulse sequence (π-RF-π/2-τ-π-τ-echo) for larger hyperfine couplings.17 ENDOR spectra were collected stochastically by randomly hopping the RF excitation frequency.26 Pulse sequences were programmed with the PulseSPEL programmer via the Xepr interface.
For a single molecular orientation with respect to the applied magnetic field, a nucleus (N) with nuclear spin of I = 1/2 (e.g., 13C, 15N, 1H and 57Fe) that is hyperfine coupled to an S = 1/2 electron spin will give rise to two ENDOR transitions appearing at positions that are a function of νN, the nuclear Larmor frequency, and A, the orientation-dependent HFI tensor.15 If the HFI is weak (when νN > A/2), the observed ENDOR transitions are centered at the νN of the nucleus and split by the HFI A, which applies to the cases of 15N-ENDOR (Figure 3D, 3E & 6C), 13C-ENDOR (Figure 5A-C), and 1H-ENDOR (Figure 4A) in this work. When the HFI is strong (νN < A/2), the observed ENDOR transitions are centered at half of the HFI A and split by 2 χ νN, which applies to the case of 57Fe-ENDOR (Figure 3A) in this work.
Figure 3. Orientation-selected Q-band ENDOR spectra of the paramagnetic intermediate with magnetic nuclei (57Fe and guanidino-15N2) incorporated in the BioB enzyme.
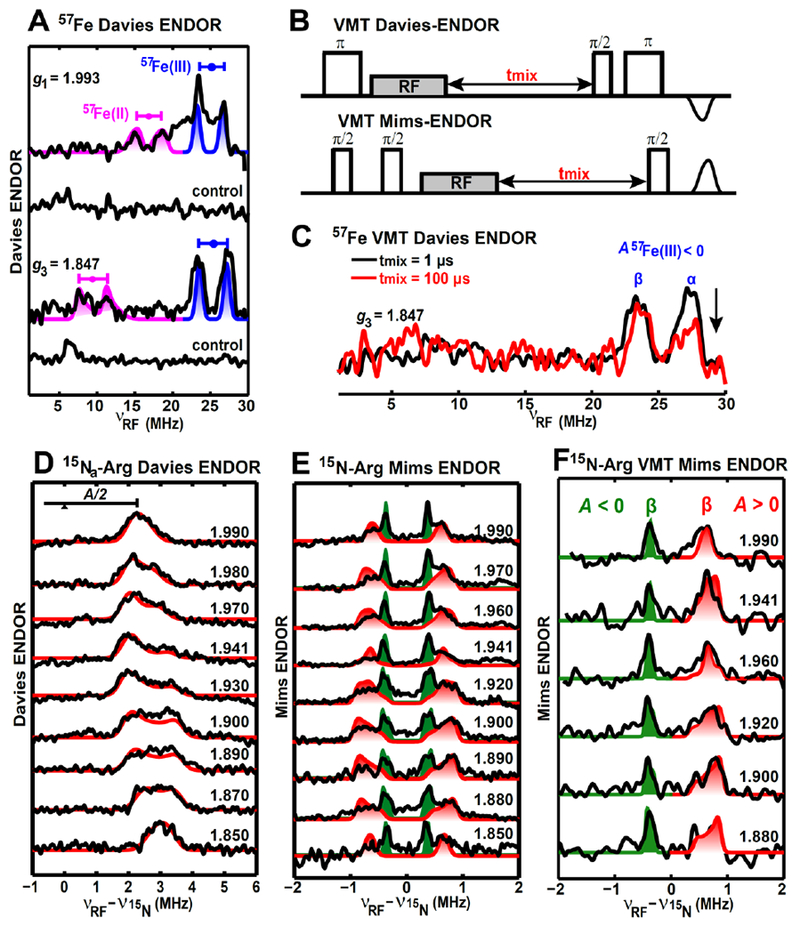
A, Q-band Davies-ENDOR spectra of the intermediate with 57Fe-enriched and natural-abundant (control sample) [2Fe–2S] cluster at two magnetic fields corresponding to g1 and g3 values. The g-tensor used for the simulations (same as follows) is g = [1.993, 1.941, 1.847], The hyperfine parameters for simulations are A(57Fe(III)) = [−50.0, −47.0, −51.0] MHz, Euler angle = [0, 15, 0]° and A(57Fe(II)) = [35.2, 16.5, 18.5] MHz, Euler angle = [0, 13, 0]°. B, Pulse sequences of the VMT Davies- and Mims-ENDOR. C, 57Fe VMT Davies-ENDOR spectra recorded at g3 = 1.847. D&E, Orientation-selected Q-band ENDOR spectra (D, Davies ENDOR, E, Mims ENDOR) of the intermediate with (guanidino-15N2)-arginine. Simulation parameters for two 15N from Arg260 (red traces and red shades) are A(15Na) = [3.65, 4.10, 7.23] MHz, Euler angle = [150, 35, 0]°, and A(15Nb) = [0.70, 1.28, 1.79] MHz, Euler angle = [0, 42, 0]°. Simulation parameters for the third 15N (green shades) are A = [−0.62, −0.74, −0.90] MHz, Euler angle = [100, 48, 0]°. F, Orientation-selected Q-band VMT Mims-ENDOR spectra of the intermediate with (guanidino-15N2)-arginine. Spectra were recorded with tmix =100 μs, and only the ENDOR transition corresponding to β electron spin manifold is detected, favoring us with more accurate simulations of the two 15N (15Nb and the third 15N) with opposite signs of hyperfine couplings.
All the experimental spectra are in black (except for the red trace shown in Figure C, which is also the experimental spectrum), while the simulated spectra are colored. Particular spectrometer settings for the ENDOR-spectra shown in Figure 3 were as follows: 8 K, 34.07 GHz, microwave inversion pulse π = 56 ns, π/2 = 12 ns, τ = 300 ns, and RF pulse = 50 μs for Figure A; 10 K, 34.06 GHz, microwave inversion pulse π = 80 ns, π/2 = 12 ns, τ = 300 ns, and RF pulse = 20 μs for Figure 3D; 10 K, 34.11 GHz, π/2 = 12 ns, τ = 240 ns, and RF pulse = 20 μs for Figure E. Figure C and Figure F have the same spectrometer settings as Figure A and Figure E, respectively, except for the mixing time tmix.
Figure 6. Orientation-selected Q-band Mims-ENDOR spectra of the paramagnetic intermediate with magnetic nuclei (2H7 and 15N1) from the substrate DTB.
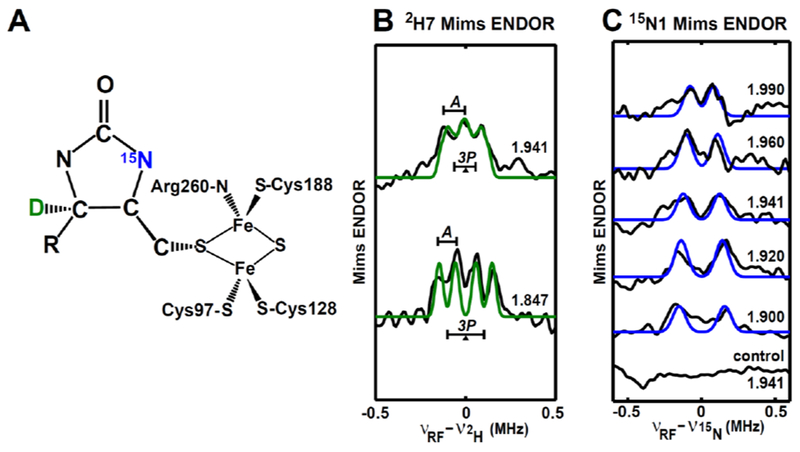
A, Depiction of the intermediate with the incorporated nuclei 2H7 marked in green, and 15N1 marked in blue. The geometry of the intermediate is adapted from the DFT model given in Figure 7A & Figure 8B. B, Mims-ENDOR spectra of 2H7-DTB-labled intermediate. C, Mims-ENDOR spectra of 15N1-DTB-labled intermediate.
Experimental parameters: 10 K, microwave pulse π/2 = 12 ns, τ = 240 ns for 2H7 and 300 ns for 15N1, RF pulse = 20 μs. Simulation parameters: g = [1.993, 1.941, 1.847]; A(15N1) = [−0.14, −0.25, −0.39] MHz, Euler angle = [0, 10, 0]°; A(2H7) = [0.03, 0.03, 0.09] MHz, P(2H7) = [−0.02, −0.08, 0.10] MHz, Euler angle = [0, 150, 0]°. All the experimental spectra are in black, while the simulated spectra are colored. The BioB enzyme used to generate the intermediate sample is natural abundant and (guanidino-15N2)-arginine enriched for 15N1-DTB-labeled and 2H7-DTB-labeled intermediate, respectively.
Figure 5. Orientation-selected Q-band Mims-ENDOR spectra of the paramagnetic intermediate with magnetic nuclei (13C9, 13C8 and 13C10) from the substrate DTB.
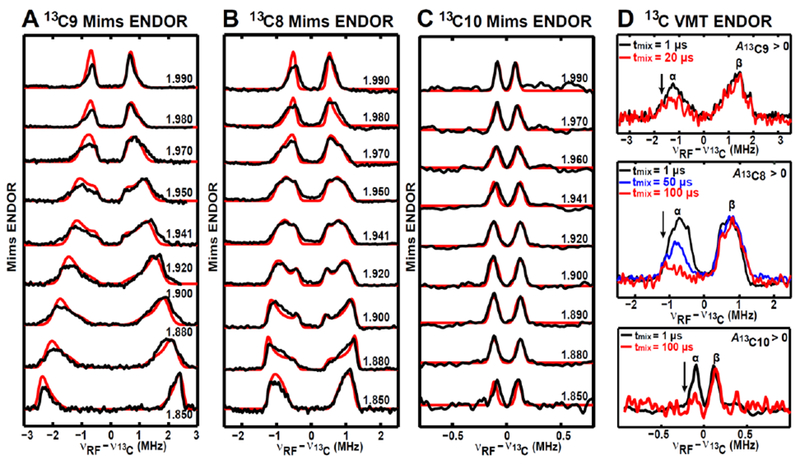
A, Mims-ENDOR spectra of 13C9-DTB-labled intermediate. B, Mims-ENDOR spectra of 13C8-DTB-labeled intermediate. C, Mims-ENDOR spectra of 13C10-DTB-labeled intermediate. D, 13C VMT-ENDOR spectra of the paramagnetic intermediate recorded at g = 1.941 and T = 10 K. The ENDOR transitions corresponding to β electron spin manifold in the spectra acquired by using various tmix are normalized, with the decreases in the ENDOR transitions corresponding to α spin manifold.
Experimental parameters: 10 K, microwave pulse π/2 = 12 ns, τ = 140 ns for 13C9, 240 ns for 13C8, 300 ns for 13C10, RF pulse = 30 μs. Simulation parameters: g = [1.993, 1.941, 1.847]; A(13C9) = [1.30, 0.85, 4.98] MHz, Euler angle = [90, 11, 100]°; A(13C8) = [1.00, 0.70, 2.60] MHz, Euler angle = [110, 36, 90]°; A(13C10) = [0.18, 0.14, 0.31] MHz, Euler angle = [70, 125, 10]°. All the experimental spectra are in black, while the simulated spectra are in red, except for the VMT ENDOR spectra in Figure D. The BioB enzymes used to generate these three intermediate samples are natural abundant.
Figure 4. Orientation-selected Q-band 1H-ENDOR (A) and X-band 1H-HYSCORE (B) spectra of the paramagnetic intermediate.
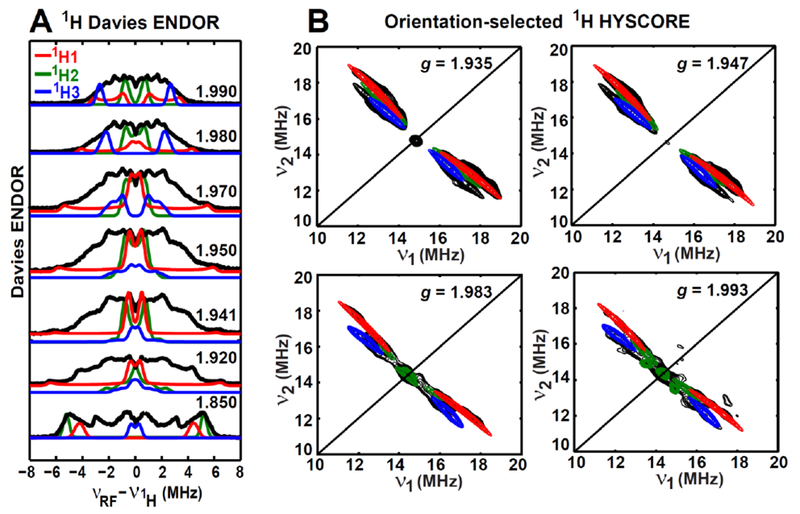
All the experimental spectra are in black, while the simulated spectra are colored as red, green and blue for 1H1, 1H2, and 1H3, respectively. Simulation parameters for the three β-protons are A(1H1) = [−1.07, −1.07, 13.86] MHz, Euler angle = [0, −36, 0]°; A(1H2) = [−1.70, −1.70, 10.05] MHz, Euler angle = [0, −5, 0]°; A(1H3) = [−0.65, −0.65, 5.84] MHz, Euler angle = [0, −95, 30]°.
Particular spectrometer settings for 1H-ENDOR are 10 K, 34.10 GHz, microwave inversion pulse π = 80 ns, π/2 = 12 ns, τ = 300 ns and RF pulse = 20 μs. Experimental parameters for X-band HYSCORE are as follows: temperature = 10 K, tπ/2 = 16 ns, tπ = 16 ns, and microwave frequency = 9.428 GHz, magnetic field = 348.0 mT, τ = 204 ns for g = 1.935; microwave frequency = 9.326 GHz, magnetic field = 342.1 mT, τ = 200 ns for g = 1.947; microwave frequency = 9.326 GHz, magnetic field = 336.0 mT, τ = 200 ns for g = 1.983; microwave frequency = 9.326 GHz, magnetic field = 334.3 mT, τ = 204 ns for g = 1.993. The time increment in both dimensions was 24 ns with 180 steps.
For nuclei (N) with nuclear spin of I = 1 (i.e., 2H in this work), the two ENDOR transitions are further split by the orientation-dependent nuclear quadrupole coupling tensor (P): ν± = |νN ± A/2 ± 3P/2|, The corresponding ENDOR transitions are ν± = νN ± A/2 ± 3P/2, giving a four-line pattern comprised of two sets of splitting. One splitting arises from the quadrupole splitting, 3P, with the definition of 3Pmax = 3e2Qq/2h27 The other splitting arises from the hyperfine coupling A. The quadrupole coupling tensor we report in this work is defined as [P1, P2, P3] = e2Qq/4I(2I-1)h[−1+η, −1−η, 2], with the asymmetry parameter η = (P1−P2)/P3 which is in the range from 0 to 1, corresponding to an axially symmetric and rhombic electric field gradient at the nucleus, respectively.
For Mims-ENDOR experiments,16 the ENDOR intensities are modulated by the response factor (R) which is a function of the hyperfine coupling A and the time interval (τ) between the first and the second π/2 microwave pulse in the three-pulse sequence: R ~ [1−cos(2πAτ)], When Aτ = n (n = 0, 1, 2, 3 …), this factor will be zero, corresponding to a minima in the ENDOR response, i.e., the hyperfine “suppression holes” in Mims-ENDOR spectra. This Mims-hole effect can be avoided by adjusting the τ value. This is why varying τ values of 140 ns, 240 ns and 300 ns were chosen for 13C9, 13C8 and 13C10 Mims-ENDOR experiments, respectively (see Figure 5A–C).
All the samples investigated in this work were frozen solutions of paramagnets with g-tensors that are significantly anisotropic as to be evident even at modest applied magnetic fields (≈350 mT). Thus, ENDOR/ESEEM/HYSCORE spectra must be obtained at the field positions across the whole EPR envelope to capture the full span of the HFI and to orient its tensor elements to the g tensor via a set of experimentally determined Euler angles (zyz convention).
A variable mixing-time (VMT) ENDOR experiment was conducted to determine the absolute sign of the HFI at a given field position (Figure 3C, 5D & S4).28 As shown in Figure 3B, the pulse sequence of VMT Davies-ENDOR is π-RF-tmix-π/2-τ-π-τ-echo, while the pulse sequence of VMT Mims-ENDOR is π/2-τ-π/2-RF-tmix-π/2-τ-echo. Various mixing-times tmix ranging from 1 μs to 100 μs were used and the default delay time for the microwave pulse after RF was 1 μs for the regular ENDOR experiment. For an S = 1/2, I = 1/2 spin system, as the mixing time tmix is increased to a length on the order of the electron-spin relaxation time, the ENDOR response corresponding to Ms = +1/2 (α) electron spin manifold decreases more rapidly than the response corresponding to Ms = −1/2 (β) manifold. By comparing the relative intensity of the ν+ (the high RF frequency peak) and ν− (the low RF frequency peak) ENDOR transitions for the ENDOR spectra acquired at different tmix, we can match each transition to their corresponding electron spin manifold and determine the sign of A.
2.4.3. X-band HYSCORE spectroscopy.
X-band HYSCORE spectra were recorded on the Bruker Biospin EleXsys 580 spectrometer with a split-ring (MS5) resonator at 10 K using the pulse sequence π/2-τ-π/2-t1-π-t2-π/2-τ-echo. The pulse length for inversion pulse (tπ) and the π/2 pulse (tπ/2) was 32 ns (or 16 ns, see figure captions) and 16 ns, respectively. Eight-step phase cycling was used. Time-domain spectra were baseline-corrected (third-order polynomial), apodized with a hamming window, zero-filled to eight-fold points, and fast Fourier-transformed to yield the frequency-domain spectra. Particular spectrometer settings are given in the corresponding figure captions. Field-dependent HYSCORE spectroscopy serves as a complementary method for us to decrease the uncertainties of simulations from ENDOR spectra and completely lock in the parameters of hyperfine tensors A (±0.01 MHz).
2.4.4. Hyperfine tensor analysis.
The hyperfine tensor A, describing the interaction between a magnetic nucleus and the electron spin, can be obtained from simulations of the orientation-selected ENDOR as well as HYSCORE spectra. The HFI tensor A is a sum of isotropic aiso and anisotropic Tdip contributions. The anisotropic contribution Tdip is composed of local (Tloc) and non-local (Tnon-ioc) interactions. Tloc arises from electron spin density in p-, d- or f- type orbital centered on the magnetic nucleus. Tnon-loc describes the through-space dipolar interaction between the nuclear spin and electron spin in orbitals centered on all other atoms.29
aiso arises from the probability of finding the unpaired electron at the nucleus. This can be due to overlap of the nucleus with a spin-carrying orbital of another atom, or from the spin being localized in an orbital centered on that nucleus. In this latter case, aiso and Tloc terms are related where aiso reflects the contribution of the 2s orbital to the 2spn hybrid orbital. Tloc arises from the 2p orbital contribution to the hybrid orbital. These two terms can be calculated through the following equations, when the isotropic hyperfine interactions aiso is dominant:30
| (eq. 1) |
| (eq. 2) |
where ρ is the spin density on nucleus (13C or 15N), a0 (3777 MHz for 13C, −2540 MHz for 15N)31 is the isotropic HFI for one electron in the 2s orbital of nucleus, and T0 (107 MHz for 13C, −77 MHz for 15N)31 is the anisotropic HFI for one electron in a 2p orbital of nucleus, n is equal to 3 for the case of 13C9, 13C8 or 15N1, but is equal to 2 for 13C10. Therefore, the corresponding Tloc values for 13C9, 13C8, 15N1, and 13C10 are calculated to be 0.20 MHz, 0.12 MHz, 0.02 MHz and 0.01 MHz, respectively. However, in general, as the Tloc may not be diagonal in the same coordinate frame which diagonalizes the Tnon-loc, the decomposition of the Tdip tensor (Tdip = Tnon-loc + Tloc) is not that simple.32 Therefore, we present the Tdip tensors from both EPR experiment and density functional theory (DFT)-predictions in Figure 8C, which involve small contributions from Tloc, except for 1H and 2H7.
Figure 8. Structural model of the paramagnetic intermediate.
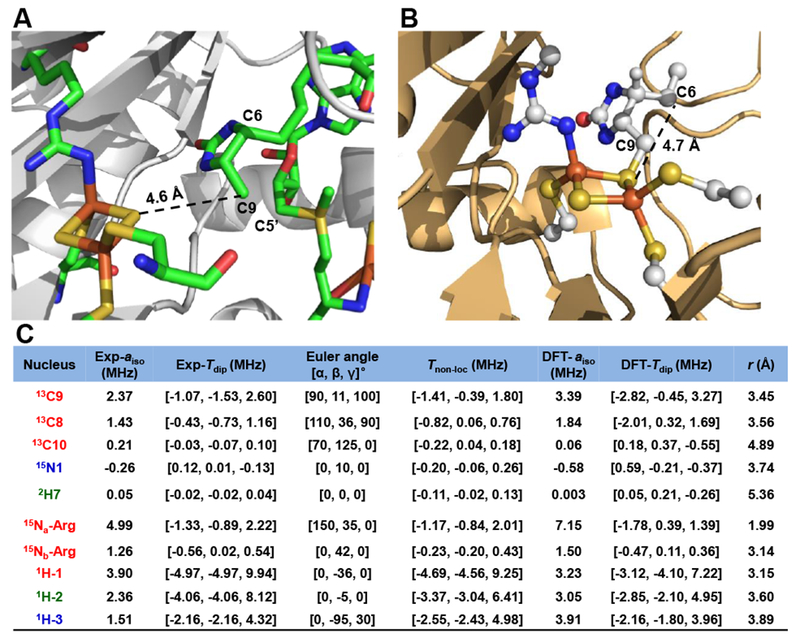
A, X-ray structure of the resting-state BioB with DTB and SAM bound (PDB: 1r30), adapted from reference 6. B, Structural model (model A) derived from quantum chemical modeling using broken-symmetry DFT. C, The hyperfine coupling tensors of the multiple nuclei in the intermediate. The uncertainty of the experimental extracted hyperfine parameters is ± 0.01 MHz. Tnon-loc is computed using Randall’s model33 with spin-projection factors calculated from the structure shown in B, with KA = 2.087 and KB = −1.087. Both Exp-Tdip and DFT-Tdip include small contributions of Tloc (except for 1H and 2H, see Materials and Methods for details). The distance r in the rightmost column is corresponding to the nucleus to the nearer iron center (ferric iron for three protons and ferrous iron for the other nuclei) in model A.
The Tnon-loc term is determined by the distance between the electron spin and nuclear spin, r, according to the basic point-dipole approximation model:
| (eq. 3) |
where ρ′ is the spin density residing on the single electron spin center. In our case, for the electron spin system containing two antiferromagnetically-coupled high spin irons (Fe(III), S = 5/2, and Fe(II), S = 2) centers, an extended point-dipole approximation model33 was employed to calculate the non-local anisotropic hyperfine couplings (Tnon-loc) of magnetic nuclei, based on the geometry either from the X-ray structure or from the DFT-optimized structures. Briefly, the through-space dipolar part of HFI tensor can be computed using the following equation adapted from Randall et al.,33:
| (eq. 4) |
where KA and KB are projection factors for spin center A and B, respectively, which are determined through the eq. 5a&b. TA (TB) are determined from the basic point-dipole approximation model assuming each spin center having 100% spin population, as shown in eq. 6. Γ is calculated through eq. 7.
| (eq. 5a) |
| (eq. 5b) |
where and SA = 5/2 (for FeIII), SB = 2 (for FeII) and S = 1/2.
| (eq. 6) |
| (eq. 7) |
Here, rA, rB, α and β are illustrated in Figure S1.
2.5. Density functional theory (DFT) computations.
2.5.1. Structural models.
We first constructed a model of the BioB auxiliary [2Fe–2S] cluster based on the coordinates from the X-ray structure of oxidized protein solved to 3.4 Å resolution (PDB: 1r30).6 Included in this model (~39 atoms in total) is the [2Fe–2S] cluster as well as four coordinating proteinaceous ligands: three thiolates (–SCH2CH3) representing cysteines and one guanidino group (–HNC(=NH)NHCH3) representing the arginine ligand. Similarly, we built structural models of exemplar [2Fe–2S] clusters from the all-cysteine coordinated ferredoxin class of proteins and the bis-cysteine, bis-histidine coordinated Rieske proteins using the X-ray crystal structure coordinates corresponding to the oxidized form of each (PDB: 1qt9 for ferredoxin;34 PDB: Iz01 for Rieske35). X-ray structures of the one-electron reduced ferredoxin and Rieske proteins are available and will be used to validate our DFT approach via comparisons to geometry-optimized structural models described below (PDB: 1czp for ferredoxin;34 PDB: 1z02 for Rieske35).
For the models of the paramagnetic intermediate (~59 atoms in total), we again started with the X-ray structure of BioB that has DTB and SAM bound (PDB: 1r30).6 In this structure of the oxidized protein, C9 of DTB is located ~4.6 Å (center-to-center) away from the nearer μ-sulfide of the [2Fe–2S] cluster. This distance was shortened to 1.8 Å, typical of a carbon-sulfur bond, by translating the [2FeÅ2S] cluster and DTB fragments toward one another (Figure S2). Models with different protonation states of the guanidino group were also considered and tested (see Figure 7, S15-S17).
Figure 7. Broken-symmetry DFT computed Löwdin spin distributions and HFI values over four models (A, B, C and D) of the paramagnetic intermediate.
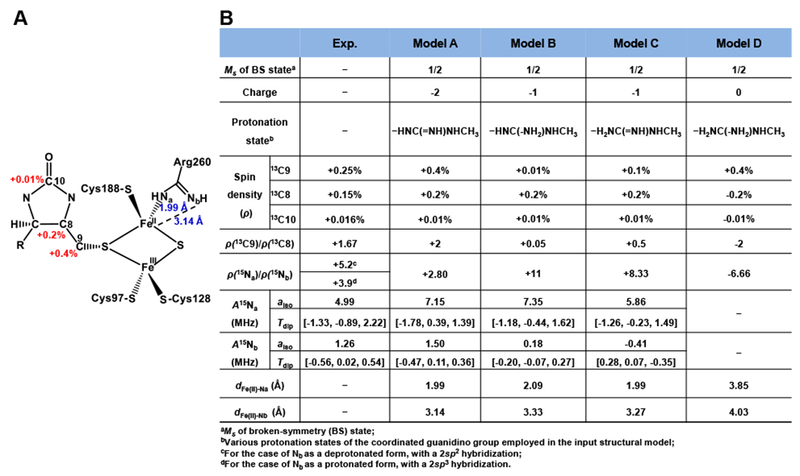
A, Depiction of the model A with Löwdin spin densities (red number) on three 13C nuclei (13C9, 13C8 and 13C10) and the bond distances (blue number) between guanidino nitrogens and Fe(II), also see Figure S15-S17 for details. B. The comparisons of spin densities and 15Na,b HFI values of four models with the experimental parameters. The spin-projection factors calculated from the structure are KA = 2.087, KB = −1.087 for model A, KA = 2.066, KB = −1.066 for model B, and KA = 2.019, KB = −1.019 for model C.
2.5.2. Geometry optimizations.
All calculations were carried out along the S = 1/2 potential energy surface using the broken-symmetry DFT (BS-DFT) methodology36–40 as implemented in the ORCA 3.0.3 quantum chemistry program.41 Unrestricted Kohn-Sham geometry optimizations were carried out using BP86 density functional42–43 along with the zero-order regular approximation (ZORA) to include the scalar relativistic effects.44–46 The segmented all-electron relativistically contracted (SARC) def2-SVP basis sets were used for the hydrogen, carbon and nitrogen atoms, while the def2-TZVP(-f) basis sets were used for all the other atoms (iron and sulfur).47 The calculations were sped up by employing the resolution of identity (RI) approximation along with the decontracted auxiliary basis set of def2-TZVP/J coulomb-fitting48 which is implemented in ORCA 3.0.3. Increased integration grids (Grid4) and tight SCF convergence were used throughout the calculations. Solvent effects have been taken into account with conductor-like screening model (COSMO) with a dielectric constant ε of 2049–51 (Note that the difference on the optimized structural level by using lower epsilon value 4.0 is very subtle. Lower epsilon value 4.0 also yields similar EPR parameters as that obtained by using 20, as shown in Table S2&S3.) To be noted, in order to ensure that the geometry of the [2Fe–2S] cluster is reasonable, four Cα atoms in the three thiolate-containing ligands and one guanidino-containing ligand are constrained to their crystallographic positions, as referenced from the case of geometry optimization of the [4Fe–4S] cluster in IspH enzyme.50–51 For optimizing the geometry of the paramagnetic intermediate, one additional constraint was applied by fixing the bond length between the C9 of DTB and the nearest μ-sulfide of [2Fe–2S] to 1.8 Å, which is typical for a C–S bond.
2.5.3. EPR parameters calculations.
The exchange-coupling constants J and the hyperfine coupling tensors were calculated for the optimized geometries using the BS-DFT methodology37–40 which employed the hybrid meta-GGA TPSSh functional52 with the chain-of-sphere (RIJCOSX) approximation53 and the same def2-TZVP(-f) basis sets and the decontracted auxiliary basis sets that were used in the geometry optimization. Calculations of the hyperfine tensors of 1H, 13C and 14/15N used the EPR-II basis. Increased integration grids (Grid4 and GridX4 in ORCA convention) and tight SCF convergence were used throughout the calculation of all EPR parameters. Initial broken symmetry guesses were constructed using the “flipspin” feature of ORCA 3.0.3. J (defined as H = −2JS1S2) was calculated by using the energy difference between the high-spin (HS) state and the BS state for a single geometry (HS state geometry in this work). The J values reported in this work is computed via Yamaguchi’s formula (eq. 8),54 which has been shown to be proper from strong coupling to weak coupling limit. Convergence to the correct BS states in all the calculations was confirmed via the calculated Löwdin spin populations.
| (eq. 8) |
In order to compare the DFT-predicted hyperfine coupling values (ABS-DFT) of BS states with the experimental values, we employed the method developed by Neese, et al.36, 55–56 for our intermediate model by using the following equation:
| (eq. 9) |
where Ms(BS) = 1/2, SA = 5/2 (for FeIII), SB = 2 (for FeII), KA and KB are the projection factors calculated through eq. 5a&b. Asite is the value which can be used to compare with the experimental value. The positive sign “+” is applied to all the atoms on the majority spin (α spin, for Fe(III) side), while the negative sign “–” is applied to all the atoms on the minority spin (β spin, for Fe(II) side). For the nuclei on the bridge (nuclei on DTB in our case), as they cannot be assigned directly to the single spin center, three methods were used by Cox, et al.57 to estimate the Asite for bridge nuclei: (i), using the BS-DFT predicted HFI values (ABS-DFT) directly, without further corrections; (ii), projecting the raw predicted HFI values to each spin center and then taking an average value, as shown by eq. 10; (iii), projecting the raw predicted HFI values to each spin center and then adding these two values, as shown by eq. 11.
| (eq. 10) |
| (eq. 11) |
Therefore, method (i) gives the largest hyperfine value, method (ii) gives the smallest hyperfine value Asite, while method (iii) yields a value in between. Although the absolute values of Asite vary with the method, the trend of the predicted hyperfine values for different nuclei, which correlate with their spin populations, is the most important information obtained from DFT. In this work, we choose method (iii) which yields the closest hyperfine values, as shown in Figure 8C.
3. RESULTS AND DISCUSSION
3.1. g-tensor of the paramagnetic intermediate.
Field-swept EPR spectra for all samples of the paramagnetic intermediate presented in this work are qualitatively similar. Each sample was analyzed using both X-band (9.38 GHz) and Q-band (34.32 GHz) EPR spectroscopy, with representative spectra shown in Figure 2A and Figure 2B, respectively. As previously reported,5, 10, 14 the EPR spectra are composed of signals from two species: a major component (64%, blue trace) with a rhombic g-tensor [1.993, 1.941, 1.847] with a gav value of 1.927—in the range of the values typical for reduced [2Fe–2S]+ clusters (see Table 1)—and a minor component (36%, green trace) with g-values = [2.005, 1.960, 1.881], As noted in the Introduction, only one species contributes to the spectrum (with g-values = [2.000, 1.947, 1.862]) when the intermediate is trapped using Arg260Met BioB.5 Clearly no labile protons exist on the methionine moiety, so one possible origin of the two components in the spectrum of the intermediate trapped by using WT BioB could be due to modest changes in the electronic structure of the [2Fe–2S] cluster caused by different protonation states of the guanidino group of the ligating Arg260 or by changes in the protonation states of the other amino acids in the vicinity of the [2Fe–2S]+ cluster, such as the remote Arg95 which is hydrogen-bonded to Arg260.6
Table 1.
g-tensor frames of reduced [2Fe–2S]+ (S = 1/2) cluster.
| Enzyme | gav | z-axis (Fe-Fe) | y-axis (S-S) | x-axis (normal) | Ref. |
|---|---|---|---|---|---|
| Ferredoxin | 1.965 (g1 > g2 > g3) | 2.051 | 1.887 | 1.958 | 68 |
| 1.966 (g1 > g2 > g3) | 2.052 | 1.887 | 1.961 | 68 | |
| Ferredoxin | 1.965 | 1.957 | 1.887 | 2.052 | 69 |
| Rieske | 191 (g1 > g2 > g3) | 1.80/1.90 | 1.90/1.80 | 2.02 | 70 |
| Rieske | 1.88 (g1 > g2 > g3) | 2.01 | 1.91 | 1.78 | 71 |
| Rieske | 1.901 | 1.79 | 2.024 | 1.89 | 72–73 |
| MitoNEET | 1.947 (g1 > g2 > g3) | 2.007 | 1.897 | 1.937 | 74 |
| BioB PIa | 1.927 (g1 > g2 > g3) | 1.993 | 1.847 | 1.941 | this work |
PI = paramagnetic intermediate.
To test this hypothesis, the EPR spectra of this paramagnetic intermediate prepared at different pH values were compared (Figure 2C). There is no discernable difference between the spectra for the pH 6.20 and 8.00 samples. However, when the pH is increased to 9.35, the proportion of the minor component (with g3-value = 1.881) diminishes, suggesting that the minor component arises from a species that is protonated relative to the species responsible for the major component (with lower g3-value = 1.847). In the computational section that follows (see section 3.4), we probe various protonation states of the guanidino group of Arg260 to see if these could account for the observed spectral changes.
One important note: in all the orientation-selected pulse EPR data presented below—especially for those samples in which a unique magnetic nucleus has been installed (e.g., 13C9, 13C8, 13C10, 2H7 and 15N1)—we observe peaks corresponding to only one class of that magnetic nucleus. These features are well-simulated using a single HFI tensor and the g-tensor for the major component, i.e., [1.993, 1.941, 1.847]. The reason that there is no observable distinct set of hyperfine couplings from the minor component could be that the hyperfine coupling interactions associated with the two species are sufficiently close to each other (as shown in Figure S3). Or the hyperfine coupling resulting from a different electronic structure of the minor species is too rhombic/inhomogeneous to be observed. In what follows we report the HFI tensors relative to the g-tensor of the major component and employ them to extract structural information of this transient intermediate.
3.2. Hyperfine interaction tensors of magnetic nuclei in the BioB enzyme.
To more precisely map out the unpaired electron spin distribution over the intermediate, we first acquired orientation-selected Q-band Davies-ENDOR spectra using BioB in which the [2Fe–2S] cluster was selectively-labeled with 57Fe (Figure 3A). We detected two doublets, each split by 2 × ν57Fe (Larmor frequency of 57Fe) and centered at A/2. Their orientation dependence is well-simulated with one rather isotropic HFI tensor of A = [−50.0, −47.0, −51.0] MHz and one anisotropic tensor of A = [+35.2, +16.5, +18.5] MHz. The magnitudes of these two 57Fe HFI tensors are typical for reduced [2Fe–2S]+ clusters (they are particularly similar to the ferredoxin cluster of Aquifex aeolicus Aae Fd4,58 see Table 2), where the isotropic tensor is assigned to the ferric site, and the more anisotropic one is assigned to the ferrous site. The negative sign of 57Fe(III) HFI was confirmed using a VMT Davies-ENDOR experiment, as shown in Figure 3C.28 As the mixing time tmix is increased from 1 μs (black trace) to 100 μs (red trace), the high RF frequency peak (ν+ = |νN − MsA|) of 57Fe(III) decreases, suggesting that the ν+ ENDOR transition is corresponding to the α electron spin manifold (Ms = +1/2), giving a negative hyperfine coupling A. As the signal intensity for 57Fe(II) is low, shown in Figure 3A, the corresponding VMT effect is too weak to be resolved. The positive sign for 57Fe(II) is assumed based on comparisons to ferredoxin Fd (Table 2).
Table 2.
57Fe hyperfine parameters of reduced [2Fe–2S]+ (S = 1/2) cluster.
| Enzyme | g1 | g2 | g3 | A (57Fe(II)) (MHz) | A (57Fe(III)) (MHz) | Ref. | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | A2 | A3 | β (°)f | A1 | A2 | A3 | β (°)f | |||||
| Ae Fd1a | 2.046 | 1.952 | 1.896 | 30 | 15 | 9 | 40 | −42 | −49 | −55 | 20 | 58 |
| Ae Fd4a | 2.005 | 1.948 | 1.917 | 32.5 | 24.0 | 11.0 | 10 | −42.5 | −50.0 | −56.5 | 15 | 58 |
| Ae Fd5a | 2.019 | 1.928 | 1.921 | 35.0 | 12.0 | 23.0 | α = 18g | −42.2 | −49.5 | −56.5 | 19 | 58 |
| PDOb | 2.01 | 1.91 | 1.70 | 33.0 | 13.0 | 14.0 | 0 | −43.0 | −55.0 | −50.0 | 0 | 71 |
| Tt Rieskec | 2.02 | 1.90 | 1.80 | 33 | 14 | 11 | 0 | −43 | −50 | −55 | 0 | 75 |
| Adrenodoxin | 2.02 | 1.935 | 1.93 | 35 | 24 | 17 | α = 30h | −43 | −56 | −50 | - | 76 |
| Putidaredoxin | 2.01 | 1.94 | 1.94 | 35 | 21 | 14 | - | −43 | −50 | −56 | - | 77 |
| Se-putidaredoxin | 2.04 | 1.98 | 1.93 | 34 | 17 | 14 | - | −40.5 | −48.2 | −52.3 | - | 77 |
| Algal ferredoxind | 2.05 | 1.96 | 1.89 | 36.5 | 15.0 | 13.0 | 0 | −42.0 | −50.0 | −51.6 | 0 | 78 |
| BioB PIe | 1.993 | 1.941 | 1.847 | 35.2 | 16.5 | 18.5 | 13 | −50.0 | −47.0 | −51.0 | 15 | this work |
Ae = Aquifex aeolicus.
PDO = phthalate dioxygenase.
Tt Rieske = Thermus thermophilus Rieske protein.
Algal ferredoxin from Synechococcus lividus.
PI = paramagnetic intermediate.
Euler angle of [α, β, γ]° with α = 0°, γ = 0°.
Euler angle of [18, 0, 0]°.
Euler angle of [30, 0, 0]°.
The correspondence of these 57Fe HFI tensors to those previously characterized in [2Fe–2S]+ clusters supports our prior hypothesis that the intermediate conserves the characteristics of a reduced [2Fe–2S]+ cluster,5, 14 i.e., after the hydrogen-atom abstraction from the C9 of DTB, the radical character of the dethiobiotinyl radical is transferred to the [2Fe–2S] cluster resulting in the EPR spectrum characteristic of antiferromagnetically exchange-coupled FeIIFeIII spin system (S = 1/2). Formally, one electron from the sulfur lone pair is donated to form the C–S bond with the dethiobiotinyl radical, and the other electron goes to reduce one of the irons.
We further employed orientation-selected Davies and Mims ENDOR to extract the HFI tensors of guanidino 15N-nitrogens of the Fe-coordinated Arg260 in this intermediate (Note that the ϵ and peptide nitrogens are not labeled in these samples, only the η1 and η2 nitrogen of each arginine are labeled.). As shown in Figure 3D and 3E, a strong HFI of A(15Na) = [+3.65, +4.10, +7.23] MHz (red traces with signals from only one electron spin manifold detected for strong coupled 15Na) and a relatively weak HFI of A(15Nb) = [+0.70, +1.28, +1.79] MHz are measured (red shaded doublets for 15Nb). The assignments of these ENDOR features to specific nitrogens of Arg260 were made based on previous analysis of the anisotropic HFI.14 The VMT-ENDOR spectra (Figure S4) show that both 15Na and 15Nb have positive aiso, suggesting that they both originate from the guanidino group of Arg260 and the spin density residing on Arg260 is negative (as the nuclear magneton of 15N is negative, see eq. 1). The negative spin density is reasonably delocalized from the ferrous site (β electron spin),59 providing direct evidence of Arg260 coordinating to the Fe(II) site in this intermediate (see Supplementary section 2.1). The strong HFI of 15Na is comparable to that of nitrogens covalently coordinated to iron (Table 3), suggesting that the guanidino group is bound to the ferrous site in a monodentate fashion, leaving the weak HFI arising from the remote 15Nb (dFe–Nb ≈ 3.14 Å from computational model A, vide infra). We also observe a third and more isotropic 15N HFI tensor of A = [−0.62, −0.74, −0.90] MHz (Figure 3E & 3F, green shades) that has a negative sign (Figure S4), as shown in the orientation-selected VMT 15N-Mims ENDOR spectra (Figure 3F), suggesting its different origin in comparison with 15Na,b from Arg260. This HFI can be decomposed to aiso = −0.75 MHz and T = −0.07 MHz. Using a simplistic single point-dipole interaction to account for the anisotropic hyperfine coupling T (as opposed to the extended point-dipole model applied to all the other nuclei in this work, eq. 4) reveals that this 15N nucleus is at least 4.8 Å away from the spin center. As only arginine residues are labeled with 15N in their guanidino groups, this additional 15N signal likely corresponds to the nearby guanidino group of Arg95. Our prior experiments using three-pulse ESEEM (Electron Spin Echo Envelope Modulation) spectroscopy to characterize 14N nuclei near the [2Fe–2S] cluster revealed 14N-modulations arising from the coordinated Arg260.5 However, the ESEEM spectrum of the intermediate generated using the Arg260Met BioB mutant showed residual 14N modulations, with the quadrupole parameters falling in the range of values typical for an arginine side chain.5 This combined with our current observation of a third set of 15N-ENDOR signals strongly suggests that the unaccounted for 14N-ESEEM signals arise from Arg95. These ENDOR results (Figure 3D & 3E) are fully consistent with orientation-selected 15N HYSCORE spectra (Figure S5), which are well-simulated with the same three 15N-HFI tensors derived from the ENDOR analysis.
Table 3.
Hyperfine parameters for 15N coordinated to Fe.
| System | g1 | g2 | g3 |
A(15N) (MHz) |
Euler angle [α, Β, γ]° | aiso (MHz) | T (MHz) | r15 N-M (Å) | Ref. | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | A2 | A3 | |||||||||
| 15Na-Arg | 1.993 | 1.941 | 1.847 | 3.65 | 4.10 | 7.23 | [150, 35, 0] | 4.99 | 0.67 | 1.99a | this work |
| 15Nb-Arg | 0.70 | 1.28 | 1.79 | [0, 42, 0] | 1.26 | 0.27 | 3.14a | this work | |||
| 15Nδ-His-1b | 2.008 | 1.91 | 1.79 | 4.8 | 4.8 | 8.4 | - | 6.0 | 1.2 | - | 79 |
| 15Nδ-His-2 | 6.5 | 6.5 | 10.4 | - | 7.8 | 1.3 | - | 79 | |||
| 15Nε-His | 0.25-0.4 | - | - | - | - | 79 | |||||
| 15Nδ-His-1c | 2.13 | 1.92 | 1.78 | 3 | 6.5 | 11.5 | - | 7 | 2.5 | - | 80 |
| 15Nδ-His-2 | 0 | 6 | 9 | - | 5 | 2.25 | - | 80 | |||
| 15Nε-His | ~0.20 | - | - | - | - | 80 | |||||
| 15Nδ-His-1d | 2.03 | 1.90 | 1.76 | 5.0 | 5.0 | 9.8 | - | 6.6 | 1.6 | - | 81 |
| 15Nδ-His-2 | 6.1 | 6.1 | 9.9 | - | 7.6 | 1.5 | - | 81 | |||
| 15Nε-His | 0.30-0.40 | - | - | - | - | 81 | |||||
| 15Nδ-His-1e | 2.01 | 1.93 | 1.76 | 4.6 | 5.4 | 8.1 | [0, 35, 0] | 6.0 | 1.1 | - | 82 |
| 15Nδ-His-2 | 6.4 | 7.0 | 9.8 | [0, 50, 0] | 7.7 | 1.1 | - | 82 | |||
| 15Nδ-His-1e | 2.01 | 1.91 | 1.70 | 5.4 | 5.4 | 8.4 | [0, 38, 0] | 6.4 | 1.0 | - | 71 |
| 15Nδ-His-2 | 6.3 | 6.7 | 10.2 | [0, 45, 0] | 7.7 | 1.2 | - | 71 | |||
| 15Nδ-Hisf | 2.005 | 1.937 | 1.895 | 6.9 | 6.9 | 10.2 | - | 8 | 1.1 | - | 83 |
| 15Nε-His | ~0.5 | - | - | - | - | 83 | |||||
| 15Nδ-Hisg | 2.007 | 1.937 | 1.897 | 7.4 | 7.5 | 11.4 | [105, 57, 54] | 8.77 | 1.32 | - | 74 |
| 15Nε-His | ~0.80 | - | - | - | - | 74 | |||||
| Hemeh | 5.97 | 5.97 | 2.0 | −13.86 | −9.65 | −10.06 | - | −11.19 | 1.33 | - | 84 |
| MoaAi | 2.063 | 1.897 | 1.897 | ~6.10 | - | - | - | ~1.94 | 85 | ||
| MoaA | ~0.50 | - | - | - | ~3.0 | 85 | |||||
| MoaA | ~0.20 | - | - | - | ~4.2 | 85 | |||||
| CPO-Naj | 2.32 | 2.16 | 1.95 | 4.6 | 4.1 | 3.7 | - | 4.1 | ~0.25 | - | 86 |
| CPO-Nb | 7.6 | 7.6 | 7.6 | - | 7.6 | ~0 | - | 86 | |||
| CPO-Nc | 8.7 | 7.9 | 7.3 | - | 7.9 | ~0.3 | - | 86 | |||
| CPO-Nd | 9.0 | 8.3 | 7.5 | - | 8.2 | ~0.4 | - | 86 | |||
| PFL-AEk | 2.01 | 1.88 | 1.87 | 9.7 | 6.0 | 3.5 | [0, 30, 0] | 6.4 | ~1.65 | - | 87-88 |
| LAMl | 2.00 | 1.90 | 1.85 | ~9.10 | - | - | - | - | 89 | ||
The distance is from 15Na,b-Arg260 to the ferrous of [2Fe-2S] cluster, based on the BS-DFT optimized geometry of model A of the paramagnetic intermediate.
Reiske type [2Fe-2S]+ cluster (at pH = 7) from hyperthermostable archaeal sulredoxin (SDX) from Sulfolobus tokodaii strain 7. 15Nδ-His-1 and 15Nδ-His-2 are two 15N direct coordinated to Fe, while 15Nε-His are the remote 15N of histidyl ligands.
Reiske type [2Fe-2S]+ cluster (at pH =13) from hyperthermostable archaeal sulredoxin (SDX) from Sulfolobus tokodaii strain 7.
Reiske type [2Fe-2S]+ cluster (at pH = 7) from bc1 complex of Rhodobacter sphaeroides.
Reiske type [2Fe-2S]+ cluster (at pH = 7) of Phthalate Dioxygenase (PDO) from Pseudomonas cepacia.
Rat mitoNEET type [2Fe-2S]+ cluster.
Human mitoNEET type [2Fe-2S]+ cluster.
Take an average of four histidine 15N of Heme.
Guanosine 5′-triphosphate (5′-GTP) binding to [4Fe-4S]+ cluster of MoaA.
Four pyrrole-nitrogen of chloroperoxidase (CPO).
15N-amino SAM binds to [4Fe-4S]+ cluster of pyruvate formate-lyase activating enzyme (PFL-AE) after SAM cleavage.
15N-amino SAM binds to [4Fe-4S]+ cluster of lysine 2,3-aminomutase (LAM) after SAM cleavage.
We also extracted three sets of axial-hyperfine tensors for β-protons coupled to the [2Fe–2S]+ cluster in this intermediate using the 1H-HYSCORE lineshape analysis method of Dikanov.60–61 Briefly, for a nuclear spin I = 1/2 coupled to an S = 1/2 electron spin, the contour lineshape (the ridge forming each cross-peak on a contour plot of HYSCORE spectra) of an axial hyperfine coupling is described by the following equation:
| (eq. 12) |
where , , νN is the nuclear Larmor frequency (14.82 MHz for 1H at 348.0 mT was used in this work). When we plot the HYSCORE spectra as να2 versus νβ2 (Figure S6), the contour line shape will be transformed into a straight line with the slope and intercept as Qα and Gα, respectively. Then we can extract the corresponding values of aiso and T for the axial HFI tensors. As the β-protons of cysteines coordinated to the ferrous site yield more rhombic HFI tensors,60–62 the three axial-HFI tensors we were able to extract (Figure S7) are reasonably assigned to the β-protons of cysteines coordinated to the ferric site with aiso > 0 and T > 0, (see Supplementary section 2.2, Figure S6-S8). We also rule out the two protons bound to C9 as their HFI are expected to be rhombic. Indeed, the DFT-predicted (model A, vide infra) HFI tensors for the two protons on C9 are very anisotropic: aiso = 3.86 MHz, Tdip = [−1.76, −8.45, 10.21] MHz and aiso = 2.15 MHz, Tdip = [−1.09, −4.30, 5.39] MHz.
Employing aiso and T values extracted from the HYSCORE data (Figure S7B), we were able to simulate the orientation-selected 1H Davies-ENDOR spectra (Figure 4A) with the following HFI tensors of A(1H) = [−1.07, −1.07, 13.86] MHz, Euler angle = [0, −36, 0]° and A(1H) = [−1.70, −1.70, 10.05] MHz, Euler angle = [0, −5, 0]° for 1H1 (red traces) and 1H2 (green traces), as their Tmax values are distinguishable from the spectra recorded at the magnetic fields corresponding to g = 1.920 and 1.850, respectively. For the HFI tensor of 1H3 (blue traces), we instead simulated the orientation-selected HYSCORE spectra first (blue contour in Figure 4B) by using A(1H3) = [−0.65, −0.65, 5.84] MHz, Euler angle = [0, −95, 30]°, as the corresponding Davies-ENDOR signals are overlapping with other proton signals. The Euler angles of the HFI tensors relative to the g tensor, as illustrated in Figure S8, were critical in assigning these three protons, with 1H1 and 1H2 from β-protons of Cysl28 and 1H3 from Cys97. To be noted, there is one remaining β-proton of Cys97, which is predicted to have a similar hyperfine coupling as that of 1H1 of Cys128 based on the DFT predications and the extended point-dipole33 calculations via eq. 4. This could be the reason why we only extracted three sets of axial-HFI tensors of β-protons in the paramagnetic intermediate. These three HFI tensors are similar to the cysteine β-protons of other reduced [2Fe-2S]+ clusters60–62 and are also consistent with our BS-DFT computational predications (vide infra).
Using the extended point-dipole model33 for antiferromagnetically exchange-coupled spin systems (see Materials and Methods), we were able to calculate the through-space dipolar couplings of 15Na, 15Nb, and three cysteine β-protons using the geometry of the reduced [2Fe–2S]+ cluster (without the MDTB ligand, vide infra) starting from the crystal structure coordinates but then optimized via the BS-DFT methodology, as listed in Table 4. The calculated dipolar hyperfine couplings for the reduced [2Fe–2S] cluster are close to the experimental values for this intermediate, indicating that the ligands of the [2Fe–2S] cluster are not disturbed dramatically from their positions after forming the paramagnetic intermediate, consistent with its behaving as a typical reduced [2Fe–2S]+ cluster (vide supra).
Table 4.
Extended point-dipole approximation analysis of the nuclei coupled to the reduced [2Fe-2S] cluster, in comparison with the experimental parameters of the paramagnetic intermediate.
| Nucleus | aiso (MHz)a | Exp-Tdip (MHz)a | Tnon-loc (MHz)b | Tnon-loc (MHz)c |
|---|---|---|---|---|
| 15Na | 4.99 | [−1.33, −0.89, 2.22] | [−1.12, 0.48, 1.60] | [−1.12, −0.86, 1.98] |
| 15Nb | 1.26 | [−0.56, 0.02, 0.54] | [−0.50, 0.18, 0.68] | [−0.14, −0.13, 0.27] |
| 1H1 | 3.90 | [−4.97, −4.97, 9.94] | [−5.34, −5.11, 10.45] | [−4.62, −4.56, 9.18] |
| 1H2 | 2.36 | [−4.06, −4.06, 8.12] | [−3.00, 2.60, 5.60] | [−3.28, −3.07, 6.35] |
| 1H3 | 1.51 | [−2.16, −2.16, 4.32] | [−2.49, −2.27, 4.77] | [−2.99, −2.82, 5.81] |
Experimental hyperfine parameters of the paramagnetic intermediate.
The calculated through-space dipolar hyperfine (eq. 4, with KA = 2.333, KB = −1.333) by using the coordinates of [2Fe-2S] cluster in BioB, adapted from the oxidized X-ray crystal structure (PDB:1r30).
The calculated through-space dipolar hyperfine (eq. 4, with KA = 2.088, KB = −1.088) by using the BS-DFT optimized geometry of the reduced [2Fe-2S] cluster in BioB, shown in Figure S13C&S14C.
3.3. Hyperfine interaction tensors of DTB-derived magnetic nuclei.
With most of the spin density of this intermediate localized on the [2Fe–2S] cluster, the spin delocalized onto the MDTB ligand is expected to be small. We then employed orientation-selected Mims ENDOR (Figure 5 & 6), complemented with HYSCORE (Figure S9-S12) to extract the HFI tensors of DTB-derived magnetic nuclei (13C9, 13C8, 13C10, 15N1 and 2H7). Labeling at 13C9 (Figure 5A) gives the largest HFI of A = [1.30, 0.85, 4.98] MHz, corresponding to aiso = 2.37 MHz and T = 1.31 MHz, which is comparable to the HFI (A = [1.8, 2.0, 5.1] MHz) of the carbon atom (C3) coordinated to the [4Fe–4S] cluster in the reaction intermediate of IspG.63 The aiso of 13C9 is larger than the values of β-13C of cysteines coordinated to the ferric site of other reduced [2Fe–2S]+ clusters64 (see Table 5). We also determined the absolute sign of 13C9 hyperfine coupling via VMT ENDOR experiment; as shown in Figure 5D, the positive HFI suggests it originates from through-bond spin delocalization.59 This large HFI as well as its positive sign indicates that C9 is covalently linked to the μ-sulfide of the [2Fe~2S]+ cluster with some positive spin density delocalized from the μ-sulfide. Indeed, we are able to estimate the spin density on 13C9 to be ca. 0.25% using eq. 1 (see Materials and Methods).
Table 5.
13Cβ-cysteine hyperfine parameters of reduced [2Fe–2S]+ (S = 1/2) cluster.
| Enzyme | g1 | g2 | g3 |
A (13C) (MHz) |
Euler angle [α, β, γ]° | 13Cβ-cysteine coordinated to | Ref. | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | A2 | A3 | aiso | T | |||||||
| FdxBa | 2.020 | 1.936 | 1.934 | 0 | −0.4 | 3.7 | 1.1 | 1.3 | [40, 81, 13] | ferric | 64 |
| −1.2 | −1.6 | 2.2 | −0.2 | 1.2 | [−30, −19, 82] | ferric | |||||
| 2.3 | 2.3 | 3.8 | 2.8 | 0.5 | [0, 50, 0] | ferrous | |||||
| 1.3 | 1.3 | 2.8 | 1.8 | 0.5 | [0, −60, 0] | ferrous | |||||
| TthNEETb | 2.009 | 1.932 | 1.896 | 0.2 | −0.2 | 3.6 | 1.2 | 1.2 | [54, 27, 64] | ferric | 64 |
| −1.3 | −1.7 | 2.7 | −0.1 | 1.4 | [53, −58, 59] | ferric | |||||
| 2.7 | 2.7 | 3.6 | 3.0 | 0.3 | [0, 20, 0] | ferrous | |||||
| ARFC | 2.022 | 1.901 | 1.804 | −0.4 | −0.6 | 3.4 | 0.8 | 1.3 | [−35, −59, 89] | ferric | 64 |
| −0.7 | −1.1 | 3.0 | 0.4 | 1.3 | [25, 53, 0] | ferric | |||||
| Ferredoxind | - | 0.76 - 1.20 | - | - | 90 | ||||||
| 1.90 - 2.10 | - | - | |||||||||
| 13C9e | 1.993 | 1.941 | 1.847 | 1.30 | 0.85 | 4.98 | 2.37 | 1.30 | [90, 11, 100] | - | this work |
FdxB = ferredoxin from Pseudomonas putida.
TthNEET = thermophile mitoNEET homologue from Thermus thermophilus.
ARF = archaeal Rieske from Sulfolobus solfataricus.
Ferredoxin from anabaena 7120 ferredoxin.
l3C9 of the BioB paramagnetic intermediate.
As expected, the more distant 13C nucleus at position C8 (Figure 5B) is less strongly coupled than C9, with HFI of A(13C8) = [1.00, 0.70, 2.60] MHz and aiso = 1.43 MHz (positive sign, Figure 5D), corresponding to approximately half the spin density of 13C9. The most distant 13C interaction we measured corresponding to C10 (Figure 5C), has a small HFI of A(l3C10) = [0.18, 0.14, 0.31] MHz with aiso = 0.21 MHz (positive sign, Figure 5D), which is among the smallest 13C HFI reported so far (Table S1), but still carries a positive spin density (ca. 0.016% via eq. 1) delocalized from the [2Fe–2S]+ cluster. It should be noted that the same absolute positive sign (Figure 5D) of HFI for these three 13C nuclei (13C9, 13C8 and 13C10) as well as their relative magnitude (corresponding to their spin densities) is an important metric for evaluating the computational models presented below (see Figure 7).
In addition, we were able to determine HFI tensors for 2H bound at the C7 position (Figure 6B) and 15N at N1 (Figure 6C), with A(2H7) = [0.03, 0.03, 0.09] MHz and A(15N1) = [−0.14, −0.25, −0.39] MHz. Their corresponding distances to the nearest Fe are approximately 5.36 Å and 3.74 Å for 2H7 and 15N1 (from computational model A, vide infra), respectively. We can also resolve a small nuclear quadrupole splitting (Figure 6B) of 2H7 with P(2H7) = [−0.02, −0.08, +0.10] MHz, resulting in a four-line pattern at g3 = 1.847 which shrinks to a three-line pattern at g2 = 1.941 where the hyperfine splitting is comparable to the quadrupole splitting.
3.4. Broken-symmetry DFT computational model.
These HFI tensors for magnetic nuclei from the BioB enzyme (Figure 3 & 4) and the substrate DTB (Figure 5 & 6) are now used to validate structural models of the transient [2Fe~2S]+-MDTB complex.
We first evaluated the reliability of our BS-DFT methodology by comparing the optimized geometries of two reduced [2Fe–2S]+ cluster models with their corresponding structures obtained from X-ray crystallography (PDB: 1czp for reduced ferredoxin;34 PDB: 1z02 for reduced Rieske protein35). The resultant geometries are indeed very similar to the X-ray structures of the reduced proteins (Figure S13 & S14)—especially in terms of Fe–S distance (−2.18 − 2.29 Å for ferredoxin and −2.17 – 2.25 Å for Rieske protein), Fe–Fe distance (−2.70 Å for ferredoxin and −2.62 Å for Rieske protein) and the Fe–S–Fe angle (−74° for ferredoxin and −72° for Rieske protein)—suggesting that the BS-DFT approach used in this work is reliable. We then applied this same methodology to model the auxiliary [2Fe–2S] cluster (without the MDTB ligand) in BioB. The initial BioB model was constructed using the coordinates from the X-ray structure of oxidized enzyme (PDB: 1r30, see Materials and Methods). The low crystallographic resolution (3.4 Å) portends the rather unreasonable [2Fe–2S] cluster (Figure S13) metrics: Fe-Fe distance (3.24 Å) and the Fe-S-Fe angle (93.4°).65–66 However, the BS-DFT geometry optimization yields a more reasonable geometry of the reduced [2Fe–2S] cluster, as shown in Figure S13, with the spin distribution, the exchange-coupling constant J (−93 cm−1) and the computed projection factors (KA = +2.088, KB = −1.088) typical for a reduced [2Fe–2S] cluster (Figure S14).62, 67
To develop a model of the paramagnetic intermediate, we began again with the X-ray structure of BioB which also has DTB and SAM bound in the active site (PDB: 1r30).6 We simply translated the DTB moiety closer to the [2Fe–2S] cluster, moving the C9 atom from its original position—4.6 Å away from the nearer μ-sulfide of the oxidized cluster—to now 1.8 Å, a typical length of a C–S bond (Figure S2, see Materials and Methods). We also considered four different protonation states of the coordinating guanidino group, as illustrated in Figure 7, S15-S17. Following geometry optimization, the models were each evaluated in terms of geometrical parameters (e.g., metal-ligand bond lengths) and predicted hyperfine parameters.
Placing four protons on the two η nitrogens of the guanidino group (model D) causes the ligand to dissociate, resulting in Fe⋯N internuclear distances (dFe-Na~3.85 Å and dFe-Nb −4.04 –) that are too long and thus incompatible with the relatively large anisotropic 15N HFI measured above. Models B and C each have three protons distributed over the guanidino group. The initial input geometries differed only in which of the nitrogens was doubly protonated (Figure 7). After geometry optimization, both models had the NH group ligating the Fe(II) ion. In model B, the NH2 group is distant from the iron whereas the NH2 group is situated in between the two iron ions in model C. Essentially, the two models are related to one another by a rocking of the guanidino group and transfer of the odd proton to the non-coordinating nitrogen. The DFT-predicted 15N HFI tensors for the coordinating nitrogen in models B and C (and model A, vide infra) are similar to one another and similar to the experimentally-determined HFI for the most strongly-coupled nitrogen. The predicted HFI tensor for the NH2 nitrogen is more discriminating. Model C yields a negative aiso for this 15N, which is inconsistent with the experimental data and likely results from its proximity to the high-spin Fe(III) ion. In contrast, model B yields a positive aiso for this 15N nucleus, but the magnitude is much less than we determined experimentally (0.18 vs 1.26 MHz), suggesting that protonation of the non-coordinating nitrogen of the guanidino group pushes it too far from the cluster (cf. dFe(II)-Nb values in Figure 7B). Model A, in which each η-nitrogen of the guanidino group has only one proton, predicts the 15N-HFI tensors which are in close agreement with our experimental findings; therefore, we prefer this protonation formulation of the [2Fe–2S] cluster ligand.
The predicted HFI for nuclei that are part of the MDTB ligand are also influenced by the protonation state of Arg260 as its optimized geometry relative to the [2Fe–2S] cluster varies between models A, B, and C (the spin density distribution differences are summarized in Figure S17). By comparing the predicted signs and relative magnitudes of the three 13C HFI that we have measurements for (13C9, 13C8, and 13C10), only model A is fully consistent with our experimental results (Figure 7).
As an intriguing aside, the DFT-predicted g3 value for models B and C is slightly larger than that predicted for model A (1.968 and 1.990 vs. 1.959). We are reminded that the minor species seen in EPR spectra of the BioB paramagnetic intermediate, which has g3-value = 1.881 > g3 = 1.847 of the major species, seems to grow in when the buffer is more acidic suggesting that it is more protonated relative to the major species (see Figure 2). Thus, the optimized geometry of models B and/or C might represent this minor component with the guanidino group in a protonated form.
Altogether, model A reasonably represents the major-component model of the observed paramagnetic intermediate, which has a deprotonated form of guanidino group –HNC(=NH)NHR. The corresponding DFT-predicted HFI tensors of the nuclei (13C, 15N, 2H and β-protons) in model A match well with those obtained from experiment, as shown in Figure 8. Especially, the DFT-predicted axial HFI tensors of β-protons of cysteines coordinated to the ferric site match well with our β-protons assignment by using Dikanov’s method (vide supra)60–61 This model conserves the electronic structure characteristics of a typical reduced [2Fe–2S]+ cluster with most of the spin density localized on the cluster. C9 of DTB has formed a bond to the bridging sulfur of this auxiliary cluster and sits in the plane bisecting the Fe–S–Fe angle with a C9-S-S angle of 129°. Notably, the Fe-S bonds of the [2Fe–2S] cluster gets slightly elongated in this model (Figure S18). Also, coordination of the C9 allows a small, positive spin density to delocalize onto the DTB moiety (Figure S18).
Most interestingly, C6, the target of the second hydrogen-atom abstraction, is now placed at a distance to the nearer μ-sulfide (rS⋯⋅C6 = 4.7 Å) similar to where C9 (rS⋯⋅C9 = 4.6 Å) was seen in the pre-reaction structure (Figure 8). This distance is slightly longer than the closest nonbonded distance predicted by van der Waals radii (~3.5 Å), suggesting that thermal or conformational motions are necessary to bring the transient DTB C9 radical into a reactive transition-state complex with the μ-sulfide, and likewise in the second step, the MDTB C6 radical with the reactive μ-thiolate. However, a C–S distance of 4.6 – 4.7 Å is sufficiently close to prevent other chemical species (e.g., amino acid side-chains, solvent components, etc.) from approaching the reactive carbon radicals. An emerging theme in the reaction mechanisms of radical SAM enzymes is that the radicals that are generated by hydrogen-atom abstraction via 5′-dA• must be within van der Waals control of their next target. Our model of the BioB radical intermediate is consistent with this hypothesis: once the second equivalent of SAM is cleaved to generate the 5′-dA• and this radical abstracts the hydrogen-atom from C6, it is essential to have MDTB C6 radical immediately quenched by the bridging thiolate sulfur. This action forms the second C–S bond, closes the thiophane ring, and completes biotin formation.
4. CONCLUSIONS
We have derived a structural model of a paramagnetic intermediate generated after the first hydrogen-atom abstraction in the biotin synthase radical SAM enzyme by combining orientation-selected EPR-derived hyperfine interaction tensors of a number of incorporated magnetic nuclei (e.g., 57Fe, 15N, 13C and 2H) with quantum chemical modeling. This reaction intermediate (model A), corresponding to the major EPR spectral component, with g3-value = 1.847, includes Arg260 as a deprotonated guanidino group –HNC(=NH)NHR, coordinated to the ferrous iron of the auxiliary [2Fe-2S] cluster as a monodentate ligand. The MDTB C9 is covalently coordinated to the auxiliary [2Fe–2S] cluster, which maintains the geometric and electronic structure characteristics of a typical reduced [2Fe–2S]+ cluster, with most of the spin density localized on the cluster and only a small positive spin density residing on the MDTB ligand via through-bond (C9 and μ-thiolate) spin delocalization. Most crucially in our model, C6, the target of the second hydrogen-atom abstraction, is now located in close proximity to the newly acquired thiolate sulfur, which likely reduces undesired side reactions and promotes thiophane ring formation in the final step of biotin synthesis.
Supplementary Material
ACKNOWLEDGMENT
We thank Julie D. Cramer for helping prepare the protein samples. The work was supported by the National Science Foundation (MCB 09-23829 to J.T.J.) and National Institutes of Health (GM104543, 1R35GM126961-01 to R.D.B.). The EPR spectrometers at the CalEPR facility used in this study were funded by the National Institutes of Health (S10-RR021075) and the NSF (CHE-1048671).
Footnotes
Supporting Information Available: Detailed descriptions of protein purification and assay protocols; VMT 15N Mims-ENDOR spectra; Orientation-selected HYSCORE spectra; Analysis of beta-protons; Geometries and spin distribution of the structural models of the paramagnetic intermediate; NMR spectra of DTB isotopologues; Cartesian coordinates of BS-DFT optimized geometry. This material is available free of charge via the Internet at http://pubs.acs.org.
REFERENCES
- 1.Depeint F; Bruce WR; Shangari N; Mehta R; O’Brien PJ, Mitochondrial function and toxicity: Role of the B vitamin family on mitochondrial energy metabolism. Chemico Biological Interactions 2006, 163 (1), 94–112. [DOI] [PubMed] [Google Scholar]
- 2.Waldrop GL; Holden HM; Maurice MS, The enzymes of biotin dependent CO2 metabolism: What structures reveal about their reaction mechanisms. Protein Science 2012, 21 (11), 1597–1619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Marquet A; Tse Sum Bui B; Florentin D, Biosynthesis of biotin and lipoic acid In Vitamins & Hormones, Academic Press: New York, 2001; Vol. 61, pp 51–101. [DOI] [PubMed] [Google Scholar]
- 4.Taylor AM; Farrar CE; Jarrett JT, 9-Mercaptodethiobiotin is formed as a competent catalytic intermediate by Escherichia coli biotin synthase. Biochemistry 2008, 47 (35), 9309–9317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Taylor AM; Stoll S; Britt RD; Jarrett JT, Reduction of the [2Fe–2S] cluster accompanies formation of the intermediate 9-Mercaptodethiobiotin in Escherichia coli biotin synthase. Biochemistry 2011, 50 (37), 7953–7963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Berkovitch F; Nicolet Y; Wan JT; Jarrett JT; Drennan CL, Crystal structure of biotin synthase, an S-adenosylmethionine-dependent radical enzyme. Science 2004, 303 (5654), 76–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ollagnier-de-Choudens S; Mullier E; Hewitson KS; Fontecave M, Biotin synthase is a pyridoxal phosphate-dependent cysteine desulfurase. Biochemistry 2002, 41, 9145–9152. [DOI] [PubMed] [Google Scholar]
- 8.Ollagnier-de-Choudens S; Mulliez E; Fontecave M, The PLP - dependent biotin synthase from Escherichia coli: mechanistic studies. FEBS Letters 2002, 532 (3), 465–468. [DOI] [PubMed] [Google Scholar]
- 9.Bui BTS; Florentin D; Fournier F; Ploux O; Mejean A; Marquet A, Biotin synthase mechanism: on the origin of sulphur. FEBS Letters 1998, 440 (1-2), 226–230. [DOI] [PubMed] [Google Scholar]
- 10.Jameson GNL; Cosper MM; Hernandez HL; Johnson MK; Huynh BH, Role of the [2Fe~2S] cluster in recombinant Escherichia coli biotin synthase. Biochemistry 2004, 43 (7), 2022–2031. [DOI] [PubMed] [Google Scholar]
- 11.Ugulava NB; Sacanell CJ; Jarrett JT, Spectroscopic changes during a single turnover of biotin synthase: destruction of a 2Fe-2S cluster accompanies sulfur insertion. Biochemistry 2001, 40 (28), 8352–8358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Escalettes F; Florentin D; Tse Sum Bui B; Lesage D; Marquet A, Biotin synthase mechanism: evidence for hydrogen transfer from the substrate into deoxyadenosine. J. Am. Chem. Soc 1999, 121 (15), 3571–3578. [Google Scholar]
- 13.Farrar CE; Siu KKW; Howell PL; Jarrett JT, Biotin synthase exhibits burst kinetics and multiple turnovers in the absence of inhibition by products and product-related biomolecules. Biochemistry 2010, 49 (46), 9985–9996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fugate CJ; Stich TA; Kim EG; Myers WK; Britt RD; Jarrett JT, 9-Mercaptodethiobiotin is generated as a ligand to the [2Fe–2S]+ cluster during the reaction catalyzed by biotin synthase from Escherichia coli. J. Am. Chem. Soc 2012, 134 (22), 9042–9045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hoffman BM, Electron nuclear double resonance (ENDOR) of metalloenzymes. Acc. Chem. Res 1991, 24 (6), 164–170. [Google Scholar]
- 16.Mims WB, Pulsed endor experiments. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 1965, 283 (1395), 452–457. [Google Scholar]
- 17.Davies ER, A new pulse endor technique. Phys. Lett 1974, 47 (1), 1–2. [Google Scholar]
- 18.Höfer P; Grupp A; Nebenführ H; Mehring M, Hyperfine sublevel correlation (hyscore) spectroscopy: a 2D ESR investigation of the squaric acid radical. Chem. Phys. Lett 1986, 132 (3), 279–282. [Google Scholar]
- 19.Ugulava NB; Gibney BR; Jarrett JT, Biotin synthase contains two distinct iron-sulfur cluster binding sites: chemical and spectroelectrochemical analysis of iron-sulfur cluster interconversions. Biochemistry 2001, 40 (28), 8343–8351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ugulava NB; Surerus KK; Jarrett JT, Evidence from Mossbauer spectroscopy for distinct [2Fe-2S]2+ and [4Fe-4S]2+ cluster binding sites in biotin synthase from Escherichia coli. J. Am. Chem. Soc 2002, 124 (31), 9050–9051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Banerjee RV; Johnston NF; Sobeski JK; Datta P; Matthews RG, Cloning and sequence analysis of the Escherichia coli metH gene encoding cobalamin-dependent methionine synthase and isolation of a tryptic fragment containing the cobalamin-binding domain. J. Biol. Chem 1989, 264 (23), 13888–95. [PubMed] [Google Scholar]
- 22.Baba T; Ara T; Hasegawa M; Takai Y; Okumura Y; Baba M; Datsenko KA; Tomita M; Wanner BF; Mori H, Construction of Escherichia coli K-12 in-frame, single-gene knockout mutants: the Keio collection. Mol. Syst. Biol 2006, 2, 2006 0008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Duin EC; Lafferty ME; Crouse BR; Allen RM; Sanyal I; Flint DH; Johnson MK, [2Fe-2S] to [4Fe-4S] cluster conversion in Escherichia coli biotin synthase. Biochemistry 1997, 36 (39), 11811–11820. [DOI] [PubMed] [Google Scholar]
- 24.Stoll S; Schweiger A, EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson 2006, 178 (1), 42–55. [DOI] [PubMed] [Google Scholar]
- 25.Stoll S; Britt RD, General and efficient simulation of pulse EPR spectra. Phys. Chem. Chem. Phys 2009, 11 (31), 6614–6625. [DOI] [PubMed] [Google Scholar]
- 26.Bruggemann W; Niklas JR, Stochastic ENDOR. J. Magn. Reson 1994, 108 (1), 25–29. [Google Scholar]
- 27.Abragam A; Bleaney B, In Electron Paramagnetic Resonance of Transition Ions. 2nd ed.; Dover Publications: New York, 1986. [Google Scholar]
- 28.Epel B; Manikandan P; Kroneck PMH; Goldfarb D, High-field ENDOR and the sign of the hyperfine coupling. Appl. Magn. Reson 2001, 21 (3), 287–297. [Google Scholar]
- 29.Schweiger A; Jeschke G, Principles of Pulse Electron Paramagnetic Resonance. Oxford University Press: New York, 2001. [Google Scholar]
- 30.Manikandan P; Choi E-Y; Hille R; Hoffman BM, 35 GHz ENDOR characterization of the “very rapid” signal of xanthine oxidase reacted with 2-Hydroxy-6-methylpurine (13C8): evidence against direct Mo–C8 interaction. J. Am. Chem. Soc 2001, 123 (11), 2658–2663. [DOI] [PubMed] [Google Scholar]
- 31.Morton JR; Preston KF, Atomic parameters for paramagnetic resonance data. J. Magn. Reson 1978, 30 (3), 577–582. [Google Scholar]
- 32.Willems J-P; Lee H-I; Burdi D; Doan PE; Stubbe J; Hoffman BM, Identification of the protonated oxygenic ligands of ribonucleotide reductase intermediate X by Q-Band 1,2H CW and Pulsed ENDOR. J. Am. Chem. Soc 1997, 119 (41), 9816–9824. [Google Scholar]
- 33.Randall DW; Gelasco A; Caudle MT; Pecoraro VL; Britt RD, ESE-ENDOR and ESEEM characterization of water and methanol ligation to a dinuclear Mn(III)Mn(IV) complex. J. Am. Chem. Soc 1997, 119(19), 4481–4491. [Google Scholar]
- 34.Morales R; Charon M-H; Hudry-Clergeon G; Pétillot Y; Norager S; Medina M; Frey M, Refined X-ray structures of the oxidized, at 1.3 Å, and reduced, at 1.17 Å, [2Fe–2S] ferredoxin from the cyanobacterium anabaena PCC7119 show redox-Linked conformational changes. Biochemistry 1999, 38 (48), 15764–15773. [DOI] [PubMed] [Google Scholar]
- 35.Martins BM; Svetlitchnaia T; Dobbek H, 2-oxoquinoline 8-monooxygenase oxygenase component: active site modulation by Rieske-[2Fe-2S] center oxidation/reduction. Structure 2005, 13 (5), 817–824. [DOI] [PubMed] [Google Scholar]
- 36.Sinnecker S; Neese F; Noodleman L; Lubitz W, Calculating the electron paramagnetic resonance parameters of exchange coupled transition metal complexes using broken symmetry density functional theory: application to a MnIII/MnIV model Compound. J. Am. Chem. Soc 2004, 126 (8), 2613–2622. [DOI] [PubMed] [Google Scholar]
- 37.Noodleman L; Davidson ER, Ligand spin polarization and antiferromagnetic coupling in transition metal dimers. Chem. Phys 1986, 109 (1), 131–143. [Google Scholar]
- 38.Noodleman L; Case DA, Density-Functional Theory of Spin Polarization and Spin Coupling in Iron—Sulfur Clusters In Advances in Inorganic Chemistry, Cammack R, Ed. Academic Press: San Diego, 1992; Vol. 38, pp 423–470. [Google Scholar]
- 39.Noodleman L, Valence bond description of antiferromagnetic coupling in transition metal dimers. J. Chem. Phys 1981, 74 (10), 5737–5743. [Google Scholar]
- 40.Neese F, Prediction of molecular properties and molecular spectroscopy with density functional theory: From fundamental theory to exchange-coupling. Coord. Chem. Rev 2009, 253 (5), 526–563. [Google Scholar]
- 41.Neese F, ORCA-an ab initio, Density Functional and Semiempirical Program Package. University of Bonn: Bonn, Germany, 2007; Vol. v 26–35. [Google Scholar]
- 42.Perdew JP, Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33 (12), 8822–8824. [DOI] [PubMed] [Google Scholar]
- 43.Becke AD, Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38 (6), 3098–3100. [DOI] [PubMed] [Google Scholar]
- 44.Lenthe E. v.; Ehlers A; Baerends E-J, Geometry optimizations in the zero order regular approximation for relativistic effects. J. Chem. Phys 1999, 110 (18), 8943–8953. [Google Scholar]
- 45.Lenthe E. v.; Baerends E-J; Snijders JG, Relativistic regular two - component Hamiltonians. J. Chem. Phys 1993, 99 (6), 4597–4610. [Google Scholar]
- 46.Wüllen C. v., Molecular density functional calculations in the regular relativistic approximation: Method, application to coinage metal diatomics, hydrides, fluorides and chlorides, and comparison with first-order relativistic calculations. J. Chem. Phys 1998, 109 (2), 392–399. [Google Scholar]
- 47.Pantazis DA; Chen X-Y; Landis CR; Neese F, All-electron scalar relativistic basis sets for third-row transition metal atoms. J. Chem. Theory Comput 2008, 4 (6), 908–919. [DOI] [PubMed] [Google Scholar]
- 48.Weigend F, Accurate coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys 2006, 8 (9), 1057–1065. [DOI] [PubMed] [Google Scholar]
- 49.Klamt A; Schuurmann G, COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc., Perkin Trans. 2. 1993, (5), 799–805. [Google Scholar]
- 50.Blachly PG; Sandala GM; Giammona DA; Bashford D; McCammon JA; Noodleman L, Broken-Symmetry DFT computations for the reaction pathway of IspH, an iron–sulfur enzyme in pathogenic bacteria. Inorg. Chem 2015, 54 (13), 6439–6461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Blachly PG; Sandala GM; Giammona DA; Liu T; Bashford D; McCammon JA; Noodleman L, Use of Broken-Symmetry Density Functional Theory to characterize the IspH oxidized state: implications for IspH mechanism and inhibition. J. Chem. Theory Comput 2014, 10 (9), 3871–3884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Staroverov VN; Scuseria GE; Tao J; Perdew JP, Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys 2003, 119 (23), 12129–12137. [DOI] [PubMed] [Google Scholar]
- 53.Neese F; Wennmohs F; Hansen A; Becker U, Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange. Chem. Phys 2009, 356 (1), 98–109. [Google Scholar]
- 54.Yamanaka S; Kawakami T; Nagao H; Yamaguchi K, Effective exchange integrals for open-shell species by density functional methods. Chem. Phys. Lett 1994, 231 (1), 25–33. [Google Scholar]
- 55.Pantazis DA; Krewald V; Orio M; Neese F, Theoretical magnetochemistry of dinuclear manganese complexes: broken symmetry density functional theory investigation on the influence of bridging motifs on structure and magnetism. Dalton Trans. 2010, 39 (20), 4959–4967. [DOI] [PubMed] [Google Scholar]
- 56.Cox N; Ames W; Epel B; Kulik LV; Rapatskiy L; Neese F; Messinger J; Wieghardt K; Lubitz W, Electronic structure of a weakly antiferromagnetically coupled MnIIMnIII model relevant to manganese proteins: a combined EPR, 55Mn-ENDOR, and DFT Study. Inorg. Chem 2011, 50 (17), 8238–8251. [DOI] [PubMed] [Google Scholar]
- 57.Rapatskiy L; Ames WM; Pérez-Navarro M; Savitsky A; Griese JJ; Weyhermüller T; Shafaat HS; Högbom M; Neese F; Pantazis DA; Cox N, Characterization of oxygen bridged manganese model complexes using multifrequency 17O-hyperfine EPR spectroscopies and density functional theory. J. Phys. Chem. B 2015, 119 (43), 13904–13921. [DOI] [PubMed] [Google Scholar]
- 58.Cutsail GE; Doan PE; Hoffman BM; Meyer J; Telser J, EPR and 57Fe ENDOR investigation of 2Fe ferredoxins from Aquifex aeolicus. J. Biol. Inorg. Chem 2012, 17 (8), 1137–1150. [DOI] [PubMed] [Google Scholar]
- 59.Cano J; Ruiz E; Alvarez S; Verdaguer M, Spin density distribution in transition metal complexes: some thoughts and hints. Comments Inorg. Chem 1998, 20 (1), 27–56. [Google Scholar]
- 60.Dikanov SA; Bowman MK, Determination of ligand conformation in reduced [2Fe-2S] ferredoxin from cysteine β-proton hyperfine couplings. J. Biol. Inorg. Chem 1998, 3 (1), 18–29. [Google Scholar]
- 61.Kolling DRJ; Samoilova RI; Shubin AA; Crofts AR; Dikanov SA, Proton environment of reduced rieske iron–sulfur cluster probed by two-dimensional ESEEM spectroscopy. J. Phys. Chem. A 2009, 113 (4), 653–667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Abdalla JAB; Bowen AM; Bell SG; Wong LL; Timmel CR; Harmer J, Characterisation of the paramagnetic [2Fe-2S]+ centre in palustrisredoxin-B (PuxB) from Rhodopseudomonas palustris CGA009: g-matrix determination and spin coupling analysis. Phys. Chem. Chem. Phys 2012, 14 (18), 6526–6537. [DOI] [PubMed] [Google Scholar]
- 63.Wang W; Wang K; Li J; Nellutla S; Smirnova TI; Oldfield E, An ENDOR and HYSCORE investigation of a reaction intermediate in IspG (GcpE) catalysis. J. Am. Chem. Soc 2011, 133 (22), 8400–8403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Taguchi AT; Miyajima-Nakano Y; Fukazawa R; Lin MT; Baldansuren A; Gennis RB; Hasegawa K; Kumasaka T; Dikanov SA; Iwasaki T, Unpaired electron spin density distribution across reduced [2Fe-2S] cluster ligands by 13Cβ-Cysteine Labeling. Inorg. Chem 2018, 57 (2), 741–746. [DOI] [PubMed] [Google Scholar]
- 65.Fuchs MGG; Meyer F; Ryde U, A combined computational and experimental investigation of the [2Fe-2S] cluster in biotin synthase. JBIC Journal of Biological Inorganic Chemistry 2010, 15 (2), 203–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Rana A; Dey S; Agrawal A; Dey A, Density functional theory calculations on the active site of biotin synthase: mechanism of S transfer from the Fe2S2 cluster and the role of 1st and 2nd sphere residues. JBIC Journal of Biological Inorganic Chemistry 2015, 20 (7), 1147–1162. [DOI] [PubMed] [Google Scholar]
- 67.Noodleman L; Baerends EJ, Electronic structure, magnetic properties, ESR, and optical spectra for 2-iron ferredoxin models by LCAO-Xα valence bond theory. J. Am. Chem. Soc 1984, 106 (8), 2316–2327. [Google Scholar]
- 68.Bertrand P; Gayda J-P, A theoretical interpretation of the variations of some physical parameters within the [2Fe-2S] ferredoxin group. Biochim. Biophys. Acta-Protein Structure 1979, 579 (1), 107–121. [DOI] [PubMed] [Google Scholar]
- 69.Gambarelli S; Mouesca J-M, Correlation between the magnetic g tensors and the local cysteine geometries for a series of Reduced [2Fe–2S] protein clusters. A quantum chemical density functional theory and structural analysis. Inorg. Chem 2004, 43 (4), 1441–1451. [DOI] [PubMed] [Google Scholar]
- 70.Bertrand P; Guigliarelli B; Gayda J-P; Peter B; Gibson JF, A ligand-field model to describe a new class of 2Fe-2S clusters in proteins and their synthetic analogues. Biochim. Biophys. Acta-Protein Structure and Molecular Enzymology 1985, 831 (2), 261–266. [Google Scholar]
- 71.Gurbiel RJ; Doan PE; Gassner GT; Macke TJ; Case DA; Ohnishi T; Fee JA; Ballou DP; Hoffman BM, Active site structure of Rieske-type proteins: electron nuclear double resonance studies of isotopically labeled phthalate dioxygenase from Pseudomonas cepacia and Rieske protein from Rhodobacter capsulatus and molecular modeling studies of a Rieske center. Biochemistry 1996, 35 (24), 7834–7845. [DOI] [PubMed] [Google Scholar]
- 72.Shubin AA; Dikanov SA, Variations of g-tensor principal values in reduced [2Fe–2S] cluster of iron-sulfur proteins. Appl. Magn. Reson 2006, 30 (3), 399–416. [Google Scholar]
- 73.Bowman MK; Berry EA; Roberts AG; Kramer DM, Orientation of the g-tensor axes of the Rieske subunit in the Cytochrome bcl complex. Biochemistry 2004, 43 (2), 430–436. [DOI] [PubMed] [Google Scholar]
- 74.Dicus MM; Conlan A; Nechushtai R; Jennings PA; Paddock ML; Britt RD; Stoll S, Binding of histidine in the (Cys)3(His)1-Coordinated [2Fe–2S] cluster of Human mitoNEET. J. Am. Chem. Soc 2010, 132 (6), 2037–2049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Fee JA; Findling KL; Yoshida T; Hille R; Tarr GE; Hearshen DO; Dunham WR; Day EP; Kent TA; Münck E, Purification and characterization of the Rieske iron-sulfur protein from Thermus thermophilus. Evidence for a [2Fe-2S] cluster having non-cysteine ligands. J. Biol. Chem 1984, 259 (1), 124–133. [PubMed] [Google Scholar]
- 76.Fritz J; Anderson R; Fee J; Palmer G; Sands RH; Tsibris JCM; Gunsalus LC; Orme-Johnson WH; Beinert H, The iron electron-nuclear double resonance (ENDOR) of two-iron ferredoxins from spinach, parsley, pig adrenal cortex and Pseudomonas putida. Biochim. Biophys. Acta-Bioenergetics 1971, 253 (1), 110–133. [DOI] [PubMed] [Google Scholar]
- 77.Muenck E; Debrunner PG; Tsibris JCM; Gunsalus IC, Moessbauer parameters of putidaredoxin and its selenium analog. Biochemistry 1972, 11 (5), 855–863. [DOI] [PubMed] [Google Scholar]
- 78.Anderson RE; Dunham WR; Sands RH; Bearden AJ; Crespi HL, On the nature of the iron sulfur cluster in a deuterated algal ferredoxin. Biochimica et Biophysica Acta (BBA) - Bioenergetics 1975, 408 (3), 306–318. [DOI] [PubMed] [Google Scholar]
- 79.Iwasaki T; Kounosu A; Uzawa T; Samoilova RI; Dikanov SA, Orientation-selected 15N-HYSCORE detection of weakly coupled nitrogens around the Archaeal Rieske [2Fe–2S] center. J. Am. Chem. Soc 2004, 126(43), 13902–13903. [DOI] [PubMed] [Google Scholar]
- 80.Iwasaki T; Kounosu A; Samoilova RI; Dikanov SA, 15N HYSCORE characterization of the fully deprotonated, reduced form of the Archaeal Rieske [2Fe–2S] center. J. Am. Chem. Soc 2006, 128 (7), 2170–2171. [DOI] [PubMed] [Google Scholar]
- 81.Dikanov SA; Kolling DRJ; Endeward B; Samoilova RI; Prisner TF; Nair SK; Crofts AR, Identification of hydrogen bonds to the Rieske cluster through the weakly coupled nitrogens detected by electron spin echo envelope modulation spectroscopy. J. Biol. Chem 2006, 281 (37), 27416–27425. [DOI] [PubMed] [Google Scholar]
- 82.Gurbiel RJ; Batie CJ; Sivaraja M; True AE; Fee JA; Hoffman BM; Ballou DP, Electron-nuclear double resonance spectroscopy of nitrogen-15-enriched phthalate dioxygenase from Pseudomonas cepacia proves that two histidines are coordinated to the [2Fe-2S] Rieske-type clusters. Biochemistry 1989, 28 (11), 4861–71. [DOI] [PubMed] [Google Scholar]
- 83.Iwasaki T; Samoilova RI; Kounosu A; Ohmori D; Dikanov SA, Continuous-wave and pulsed EPR characterization of the [2Fe–2S](Cys)3(His)1 cluster in Rat MitoNEET. J. Am. Chem. Soc 2009, 131 (38), 13659–13667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Scholes CP; Lapidot A; Mascarenhas R; Inubushi T; Isaacson RA; Feher G, Electron nuclear double resonance (ENDOR) from heme and histidine nitrogens in single crystals of aquometmyoglobin. J. Am. Chem. Soc 1982, 104 (10), 2724–2735. [Google Scholar]
- 85.Lees NS; Hänzelmann P; Hernandez HL; Subramanian S; Schindelin H; Johnson MK; Hoffman BM, ENDOR spectroscopy shows that guanine N1 Binds to [4Fe–4S] Cluster II of the S-Adenosylmethionine-dependent enzyme MoaA: mechanistic implications. J. Am. Chem. Soc 2009, 131 (26), 9184–9185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Lee H-I; Dexter AF; Fann Y-C; Lakner FJ; Hager LP; Hoffman BM, Structure of the modified Heme in allylbenzene-inactivated chloroperoxidase determined by Q-Band CW and pulsed ENDOR. J. Am. Chem. Soc 1997, 119 (17), 4059–4069. [Google Scholar]
- 87.Walsby CJ; Ortillo D; Broderick WE; Broderick JB; Hoffman BM, An anchoring role for FeS clusters: chelation of the amino acid moiety of S-adenosylmethionine to the unique iron site of the [4Fe–4S] cluster of pyruvate formate-lyase activating enzyme. J. Am. Chem. Soc 2002, 124 (38), 11270–11271. [DOI] [PubMed] [Google Scholar]
- 88.Walsby CJ; Ortillo D; Yang J; Nnyepi MR; Broderick WE; Hoffman BM; Broderick JB, Spectroscopic approaches to elucidating novel iron–sulfur chemistry in the “radical-SAM” protein superfamily. Inorg. Chem 2005, 44 (4), 727–741. [DOI] [PubMed] [Google Scholar]
- 89.Chen D; Walsby C; Hoffman BM; Frey PA, Coordination and mechanism of reversible cleavage of S-adenosylmethionine by the [4Fe-4S] center in Lysine 2,3-Aminomutase. J. Am. Chem. Soc 2003, 125 (39), 11788–11789. [DOI] [PubMed] [Google Scholar]
- 90.Houseman ALP; Oh BH; Kennedy MC; Fan C; Werst MM; Beinert H; Markley JL; Hoffman BM, Nitrogen-14,15, carbon-13, iron-57, and proton-deuterium Q-band ENDOR study of iron-sulfur proteins with clusters that have endogenous sulfur ligands. Biochemistry 1992, 31 (7), 2073–2080. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


