Abstract
We present a new optical coherence tomography (OCT) angiography method for imaging tissue microvasculature in vivo based on the characteristic frequency-domain flow signature in a short time series of a single voxel. The angiography signal is generated by Fourier transforming the OCT signal time series from a given voxel in multiple acquisitions and computing the average magnitude of non-zero (high-pass) frequency components. Larger temporal variations of the OCT signal caused by blood flow result in higher values of the average magnitude in the frequency domain compared to those from static tissue. Weighting of the signal by the inverse of the zero-frequency component (i.e., the sum of the OCT signal time series) improves vessel contrast in flow regions of low OCT signal. The method is demonstrated on a fabricated flow phantom and on human skin in vivo and, at only 5 time points per voxel, shows enhanced vessel contrast in comparison to conventional correlation mapping/speckle decorrelation and speckle variance methods.
1. Introduction
Angiography has provided a valuable means to investigate and assess the vasculature in normal and diseased tissue [1]. It has been performed using invasive, high-resolution (sub-micrometer) microscopy with 100 µm-1 mm field of view (FOV) and using non-invasive methods that have worse resolution but broader FOV, such as magnetic resonance imaging, computed tomography and position emission tomography [1–3]. Bridging these two extremes is an extension of optical coherence tomography (OCT) [4], optical coherence tomography angiography (OCTA), which offers label-free, non-invasive imaging of small blood vessels, including arterioles, capillaries and venules, at intermediate resolution and FOV [5]. Whereas OCT image contrast is determined by the level of backscattering in tissue, OCTA images the microvascular network via motion-induced changes in the OCT signal. OCTA achieves a resolution and FOV in the ranges of 2-20 μm and a few mm to ~20 mm, respectively [6], and an imaging depth limited to <1 mm, due to the strong scattering of OCT light in tissue. Thus, in vivo applications in humans focus mainly on transparent or superficial tissues, including the eye (largely the posterior retinal and choroidal microvasculature) [7–9], and the dermal skin [10,11].
OCTA has been widely applied in clinical ophthalmology with commercially available imaging systems [12,13]. It has also been used to study cutaneous microvasculature and its temporal alteration in normal human subjects and patients with cutaneous conditions, such as wounds and burn scars [11,14,15], psoriasis [16], and skin cancer [17,18]. The clinical applicability of OCTA imaging will likely be further improved by extending the FOV to image larger tissue areas [6], extending the imaging depth to visualize deeper vessels [19], improving the sensitivity of detection of the smallest vessels with low flow contrast [20], and improving the processing speeds to achieve real-time visualization.
OCTA identifies blood vessels by differences in the OCT signal versus time between that arising from moving scatterers in blood and that due to the surrounding largely static tissue. Such flow-induced differences are encoded in both the amplitude and phase of the complex OCT signal [5]. OCTA variants utilize one of: temporal changes in the OCT amplitude signal (e.g., speckle variance and correlation mapping/speckle decorrelation) [10,11,21–23]; the phase signal (e.g., Doppler OCT and phase variance) [24–26]; or the complex OCT signal (e.g., complex differential variance and OCT-based microangiography (OMAG)) [27–29].
Related methods that exploit the vasculature signature in the detected signal in the frequency domain, the main topic of interest here, have been explored for both velocimetry and angiography [30–33]. In early work on velocimetry, Barton et al. [30] analyzed the frequency content of the OCT intensity signal using a sliding window. The ratio of the highest to the lowest frequencies was used to determine flow velocities in cross-sectional images. Also for velocimetry, Szkulmowski et al. proposed a joint spectral and time domain method to process multiple OCT A-scan spectra (n = 40) acquired from the same locations, estimating flow velocities via independent Fourier transformations in time and in the optical frequency domain [31]. Szkulmowska et al. extended the method to three-dimensional (3D) velocimetry and angiography, and reduced the number of spectra acquired (n = 16) from each lateral location [32]. For angiography, Matveev et al. recently utilized the fast-changing OCT signal components to visualize vessel structures by Fourier transform of closely adjacent, but not co-located, complex A-scans (acquired at a density of 16,384 A-scans/mm) to extract the frequency spectrum. This was followed by high-pass filtering to eliminate the low frequency (static) components and inverse Fourier transformation to highlight the vessel structures [33]. The exceptionally high number of samples acquired within each B-scan practically limits the area that can be analyzed.
In this paper, we propose an alternative method that analyzes the frequency spectrum of the detected OCT signal taken from multiple acquisitions at a given voxel. The higher average magnitude of non-zero frequency components in the short-time series OCT signal intensity induced by the blood flow is used to identify vessels. Weighting by the OCT signal is incorporated to improve the contrast of blood vessels with low OCT signal and mitigate surface reflection artifacts. We characterize the method by studying the vessel contrast achieved from a flow phantom and from human skin tissue in vivo. We compare the short-time series OCTA method to commonly used intensity-based OCTA methods, including speckle decorrelation (correlation mapping) and speckle variance [11,21,34]. The results demonstrate, for a modest increase in acquisition times for a given A-scan rate, improved vessel contrast and visibility, in particular, for small vessels. Further, its simplicity lends itself to rapid calculation. These advantages suggest its potential for future applications.
2. Methods
2.1 Short-time series OCTA algorithm
The basic assumption underlying the method is that blood flow induces stronger non-zero frequency components in the OCT signal than those induced by the surrounding static tissue [31,33]. As with other OCTA methods, the method first requires the acquisition of co-located B-scans (i.e., B-scans from the same lateral location) at multiple time points, throughout an acquisition volume. The OCT intensity signal (i.e., the modulus of the complex amplitude of the OCT signal) at the same voxel locations comprises a discrete time series with the nth sample at location (x, y, z) denoted by:
| (1) |
where (x, y, z) is the voxel coordinate in the fast scanning, slow scanning and depth axes, respectively; I represents the OCT intensity signal as a function of the voxel coordinate with time point tn for n, an integer ranging from 1 to 2N + 1, where 2N + 1 is the total number of co-located B-scans (i.e., total number of time samples) acquired from the same lateral location; and T is the time interval between co-located B-scans.
The time series at each voxel in Eq. (1) is discrete Fourier transformed to obtain the complex frequency signal with the frequency components F denoted by:
| (2) |
where f0 is the interval between neighboring discrete frequencies, determined by 1/[(2N + 1)T]; and m is the index of the (two-sided) frequency components ranging from -N to N. The average magnitude of the complex frequency signal at non-zero frequencies is then calculated as
| (3) |
Alternatively, if many B-scans are acquired for analysis (i.e., 2N + 1 ≥ 29 for the scanning parameters used in this study), instead of a single frequency component, a narrow band centered on the zero-frequency component is excluded (i.e., high-pass filtered). This narrow band should be optimized for a particular tissue and setup, and will depend on the frequency spectrum recorded from static tissue. The optimization for human skin tissue, recorded using our system parameters, is shown in the Results section. However, there, we demonstrate that only a small number of co-located B-scans (~5) is required for practical imaging of the vessel network with our method. Thus, the elimination of only the zero-frequency component, as shown in Eq. (3), applies.
After Fourier transformation, voxels with low OCT signal intensity lead to a correspondingly low magnitude of the complex non-zero frequency components, even if there is flow. To enhance the flow detectability at low OCT signal levels, we incorporate weighting by the inverse of the OCT signal intensity (i.e., zero-frequency component scaled by the number of co-located B-scans), given by:
| (4) |
where is the mean OCT signal intensity and is the zero-frequency component of the 2N + 1 time samples at the same location. To avoid division by zero and over-emphasizing the signal in regions with excessive noise, is first averaged, and thresholded at an empirically chosen signal level of 16 dB above the noise floor to replace the low signal with the threshold. We used an averaging window of 3 × 3 pixels in the cross-sectional plane, approximately 1.4 and 1.9 times the lateral and axial resolutions, respectively. It is used both for our method and for the accompanying speckle decorrelation calculation, empirically chosen to improve the signal-to-noise ratio (SNR) of angiography without significantly degrading the imaging resolution. We assume that an odd number of co-located B-scans are acquired for each lateral location for simplicity, but even numbers are applicable as well. The vessel contrast created by Eq. (3) and the further improvement introduced by weighting according to Eq. (4) will be demonstrated and discussed in Section 3.
2.2 OCT scanning of flow phantom and human skin
OCT scans were acquired using a commercial spectral-domain scanner (an upgraded TELESTO II, Thorlabs Inc., USA) to demonstrate the short-time series OCTA method on both a flow phantom and in vivo on normal human skin. The system has a center wavelength of 1300 nm and provides an imaging resolution of 5.5 µm (in air) and 13 µm, respectively, axially and laterally (as defined by the vendor). The scanner was operated at 76 kHz (A-scan/s), below its maximum of 146 kHz. Scans were acquired in one of two modes: 2D scanning by acquiring 200 co-located B-scans from a single lateral location with a FOV of 6 × 3.6 mm (1024 × 1024 pixels) in x and z directions, respectively; and 3D scanning with a FOV of 6 × 1.8 × 3.6 mm in x, y and z directions. In 3D scanning mode, 240 lateral (y) locations were scanned with a set of 5 co-located B-scans acquired from each location, using the same pixel sizes in x and z directions as in the 2D mode. It took approximately 4 and 21 s to acquire a scan, respectively, in the 2D and 3D scanning modes. In addition, the time interval between B-scans was 17.8 ms (~56 B-scans/s) for both 2D and 3D modes, leading to a discrete frequency spectrum with components up to 28 Hz.
For comparison to short-time series OCTA, speckle variance in the same 3D scans was calculated over the 5 co-located B-scans using the method presented by Mariampillai et al. [21]. Speckle decorrelation was determined for each adjacent pair of co-located B-scans using the formula described in [15] with a window of 3 × 3 pixels in the fast scanning and depth axes. This led to 4 decorrelation B-scans from each lateral location, which were then averaged to generate a single enhanced decorrelation B-scan. In addition, the speckle decorrelation and speckle variance was weighted by the averaged and thresholded OCT signal at the corresponding pixels to reduce the noise [10]. The same threshold level used in short-time series OCTA was used here. The same lateral averaging window (3 × 3 pixels) was applied to the short-time series and speckle variance images to ensure a fair comparison.
Blood vessels were mainly compared over a depth range of 300 µm from the skin tissue surface (determined from the OCT depth scan by assuming an average refractive index of 1.4) to ensure sufficiently strong signals from all three methods. For each method, the maximum OCTA signal of each A-scan in this depth range was used to generate a projection image of vessels. For visualization, the same colormap was used in the projection and cross-sectional OCTA images. The lower and upper thresholds were set at, respectively, the 50% and 99.5% points of the cumulative distribution function of the OCTA signal in the image. These thresholds were empirically chosen to maximize the vessel contrast without loss of vessels with low signal. The thresholds were then used to normalize the vessel signal for each method to the same range (0-1). For quantification, each projection image was processed to measure the vessel area density, defined as the ratio of the total vessel area to the total tissue area in the thresholded vessel image. The threshold was set using Otsu’s method for each image [35]. This method assumes two classes of pixels (i.e., foreground and background pixels) following a bi-modal histogram to calculate the optimal threshold to separate the two classes of pixels. The vessel images were thresholded using the optimal threshold estimated by this method to determine the vessel area and density.
The silicone flow phantom was fabricated in house by mixing Elastosil P7676A and P7676B fluid (Wacker Chemie AG, Germany) with titanium dioxide in a 3D-printed plastic container [36]. The container was customized with two holes in the sidewalls to hold a small glass capillary (outer diameter: 80 µm; inner diameter: 50 µm) that mimicked a vessel orthogonal to the incident optical beam. After curing, the result was a capillary embedded in the silicone that mimicked the static tissue. The capillary was then connected to a syringe filled with a polystyrene microsphere suspension (nominally 0.5-µm or 2-µm diameter) to mimic the blood flow. The syringe was connected to a pump (Fusion 200, Chemyx Inc., USA) to introduce and control the flow speed. The scattering properties of the phantom were adjusted by tuning the ratio of titanium dioxide to Elastosil P7676A and P7676B so that the phantom had a signal attenuation that approximately matched the attenuation of normal human skin.
Human subjects (n = 4) were recruited for in vivo OCT scanning with ethics approval from the Human Research Ethics Committee of The University of Western Australia. Written consent was acquired from all subjects prior to OCT scanning of skin on the volar forearm, including one subject who had received laser treatment for wart removal. For this subject, one region from the treated area and one from the adjacent normal skin were selected for OCT imaging. To reduce bulk tissue motion during data acquisition, a spacer was attached to the skin surface to tightly couple the OCT probe and the skin tissue. A piece of thin metal with a center hole (5 mm in diameter) to image through was also attached to the skin as a fiducial marker to check for motion artifact [15,37]. We observed generally good vessel contrast and negligible vessel distortions, so no motion correction was performed. Further details on the imaging probe spacer and scanning setup can be found in [15]. The acquired scans from the phantom and skin tissue were then processed using the three OCTA methods and compared.
3. Results
This section firstly considers the contrast present in the short-time series OCTA method and its optimization by selecting the number of samples and incorporating signal weighting. The difference between short-time series implemented on the OCT intensity and on the complex signal is also shown. Results from the optimized short-time series OCTA method are then compared to those acquired from speckle decorrelation and speckle variance.
3.1 Vessel contrast
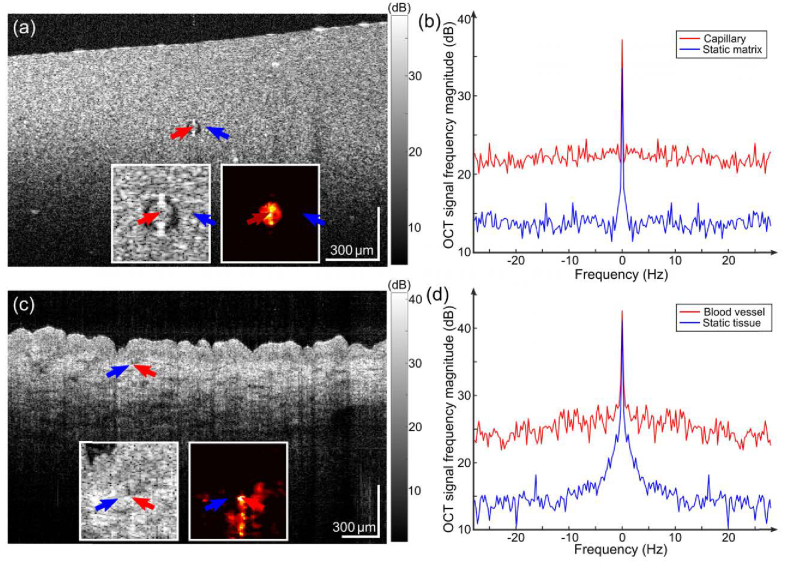
The blood vessel contrast in short-time series OCTA originates from the elevated non-zero frequency components induced by the moving scatterers in blood. An example of such contrast, obtained from an extended time series of 200 B-scans, is shown in Fig. 1(b), which plots the Fourier transform (magnitude) of the time series of the OCT intensity signal in the phantom scan in Fig. 1(a). The frequency spectra in red and blue are determined from, respectively, a region in the polystyrene microsphere flow in the capillary (red arrow) and in the adjacent static matrix (blue arrow), as indicated in Fig. 1(a). The insets in Fig. 1(a) magnify the vessel region (left) and the corresponding angiography signal (right).
Fig. 1.
Vessel contrast in time series OCTA. Single B-scans obtained from the flow phantom (a) and human skin (c). Arrows mark the locations for analysis in (b) and (d). Insets show the magnified OCT logarithmic intensity images (left) and the corresponding angiography images (right). Two-sided spectral density of the signal from 200 B-scans in the flow and static regions is shown in (b) for the phantom and (d) for human skin. Frequency spectra originating from the capillary flow and blood flow are given by the red trace; whereas, those from the static matrix and tissue are given by the blue trace. Scale bars: 300 µm in physical length.
The frequency spectrum of the OCT signal from the static matrix region in Fig. 1(b) (blue trace) is ~20 dB lower at ~1.1 Hz than its value at the peak and remains consistently low for frequencies above this. Whilst a similar sharp drop-off is observed in the capillary flow region (for flow speed 3 mm/s), the magnitude for frequencies at and above 1.1 Hz is much higher (Fig. 1(b), red trace) than in the static matrix.
Similar plots were obtained from in vivo skin, determined from 200 co-located B-scans, with a single B-scan shown in Fig. 1(c) and the spectral density shown in Fig. 1(d), indicating consistent contrast between blood vessels and static tissue. This contrast may be parameterized as the average magnitude of the non-zero (high-pass) frequencies using Eq. (3). In addition, Fig. 1(d) indicates that the contrast between flow and static tissue is present at frequencies higher than ~2 Hz, which is chosen as the cut-off for the calculation of average magnitude at high frequencies in Eq. (3). Note that the peak centered at zero frequency for the static tissue in skin (Fig. 1(d), blue trace) has a larger width than that of the static matrix in the phantom (Fig. 1(b), blue trace). This may be due to residual motion in the skin tissue, from the pulse (approximately 60-100 beats per minute) or from other sources. In the following sections, when only 5 co-located B-scans are acquired for analysis, the frequency interval is much larger (i.e., 11.2 Hz), requiring only removal of the zero-frequency component, as per Eq. (3), to achieve the desired high-pass filtering.
3.2 Choice of time series length
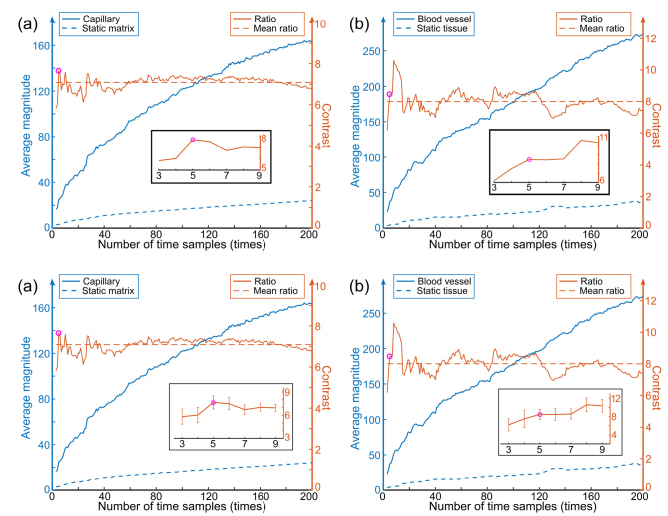
The frequency spectra shown in Fig. 1 are from acquisitions comprising 200 co-located B-scans, chosen to enable detailed analysis at a single lateral location. Such long acquisitions are not practical for clinical applications: a trade-off is needed to reduce the number of time samples whilst maintaining high vessel contrast. We investigated this trade-off, presented in Fig. 2, showing average magnitude and contrast obtained by calculating the average magnitude for frequencies above 2 Hz for the flow region (solid blue) and static tissue (dashed blue) comprising 3 × 3 pixels in the phantom (Fig. 2(a)) and skin tissue (Fig. 2(b)).
Fig. 2.
Vessel contrast in time series OCTA for varying numbers of time samples (i.e., co-located B-scans) in the phantom (a) and skin tissue (b). The average high-pass frequency magnitude versus number of time samples is shown for the flow (solid blue) and static tissue regions (dashed blue) with reference to the left vertical axis. Their ratio is shown by the solid orange plots with the mean value marked by the dashed orange line relative to the right vertical axis. Insets show the magnified traces of contrast for 3-9 samples. The magenta circles indicate the ratios for 5 samples.
The average magnitude increases, for both the flow regions in the capillary/blood vessels and for the static matrix/static tissue, versus the number of acquired co-located B-scans, as does the difference in the average magnitude between the flow and static regions. Notably, the ratio between the two (solid orange plots) peaks at around 5-10 co-located B-scans before it reaches a plateau (with local fluctuations). In Figs. 2(a) and (b), the dashed orange lines show the mean of all the ratios (n = 3 to 200), with a value in the range 7-8. The magenta circles show the ratio for 5 B-scans. This figure indicates that acquisition of ~5 co-located B-scans is sufficient to provide good vessel contrast with the short-time series method, further supported by the blood vessel imaging results in Section 3.5. Acquiring more co-located B-scans may be beneficial in some circumstances, but increases acquisition time and, thus, increases potential for motion artifact. In contrast, acquiring only 3 or 4 co-located B-scans still shows clear contrast for the specific vessel analyzed in Fig. 2(b), but can be problematic for vessels with lower contrast. We, therefore, chose to use 5 co-located B-scans from the same tissue location for the 3D imaging of the vessel network presented below.
3.3 Signal enhancement by weighting
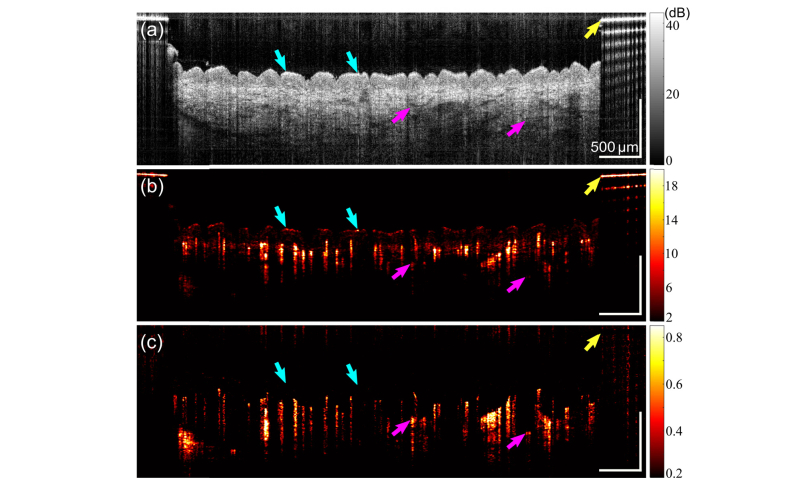
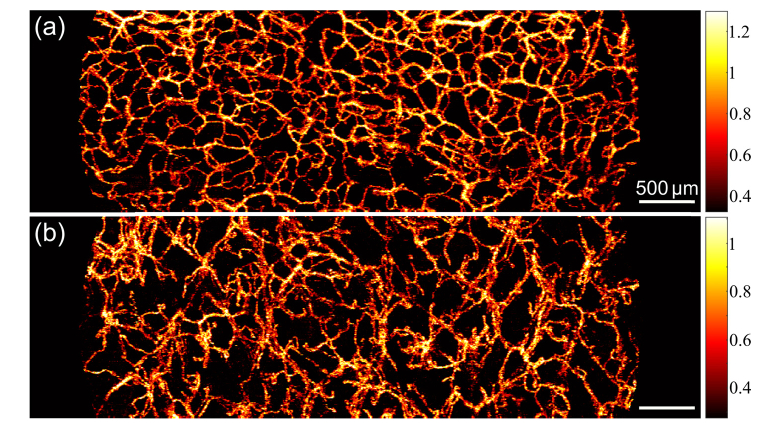
To enhance the vessel signal in the flow regions with low OCT signal (e.g., regions marked by magenta arrows in Fig. 3(a)), we further weight the average magnitude of non-zero frequencies by the inverse of the linear OCT signal intensity, as described by Eq. (4). The weighted image in Fig. 3(c) shows increased vessel signal (e.g., for vessels marked by the magenta arrows), compared to Fig. 3(b) before weighting. The level of improvement is better appreciated in the projection images, comprising vessels from the forearm skin surface to 300 µm deep, as shown in Fig. 4(b). Compared to the equivalent unweighted image in Fig. 4(a), the weighted image shows improved visibility in terms of vessel connectivity and the number of visible vessels. In addition, the weighting significantly suppresses the artificial vessel signals caused by strong surface reflections, as indicated by the cyan arrows in Fig. 3(b). Another positive effect is the removal of the very strong surface reflection at the metal fiducial maker surface indicated by the yellow arrows. Therefore, we incorporate this weighting into our method as an important step in optimizing the vessel image quality.
Fig. 3.
Cross-sectional OCT image (a) and vessel image in short-time series OCTA before (b) and after (c) weighting by the inverse of the mean OCT intensity signal. Arrows indicate the corresponding pixels in the three images at the tissue surface (cyan), blood vessels (magenta) and metal marker surface (yellow), respectively. Scale bars: 500 µm.
Fig. 4.
Projection of blood vessels by short-time series OCTA based on OCT intensity signal before (a) and after weighting (b), and the complex OCT signal with weighting (c). The projections display vessels to 300 µm deep from the skin surface. Scale bars: 500 µm.
3.4 Intensity vs. complex signal-based processing
As with other OCTA methods, it is possible to analyze either the intensity or the full complex OCT signal (i.e., intensity and phase). We applied the short-time series method to both cases in the same skin scans. A representative example is shown by the vessel projection images in Fig. 4. A comparison of Figs. 4(b) and (c) indicates that intensity and complex signal-based processing lead to very comparable detection of vessels. However, using the complex signal produces more motion artifacts (horizontal lines) evident in Fig. 4(c).
We used a customized imaging spacer and setup to minimize motion during data acquisition, which has previously been shown to be effective when used in combination with the speckle decorrelation method [15]. Whilst residual tissue motion is almost absent in Figs. 4(a) and (b), based on intensity only, it is still detectable as multiple horizontal lines in Fig. 4(c), due to the incorporation of the more motion-sensitive phase information. An additional motion correction algorithm would be required to mitigate such artifacts, if the complex signal was to be the basis of the method. To avoid this need, the short-time series OCTA results in the following section were calculated using the OCT intensity signal alone.
3.5 Comparison with speckle decorrelation and speckle variance
To further assess the performance of our OCTA method, we compared it to two commonly used intensity-based OCTA methods, speckle decorrelation (correlation mapping) and speckle variance, applied to sets of 5 co-located B-scans in 3D scans.
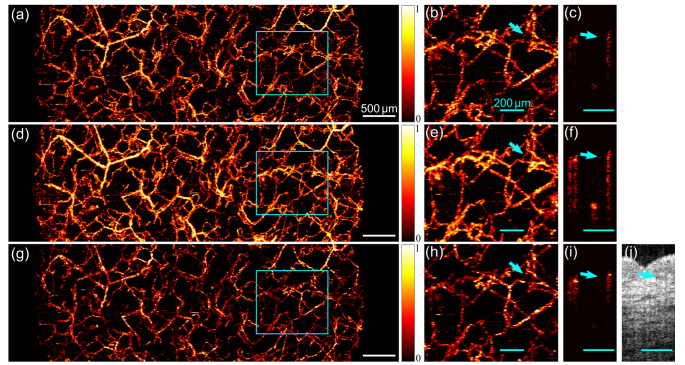
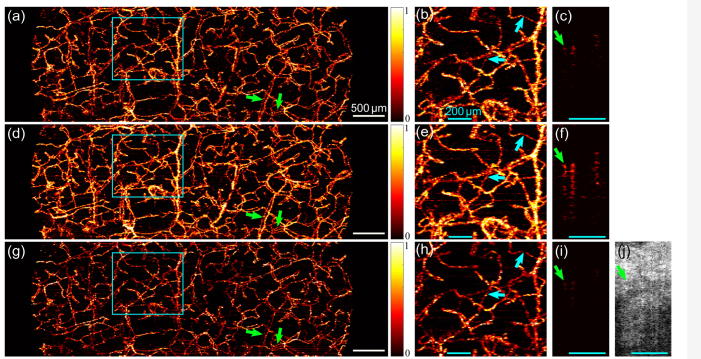
Figure 5 shows an example from forearm skin, projecting the blood vessels from the skin surface to 300 µm in depth. Vessel images generated by the short-time series method are in the middle row to allow ready comparison to images generated by speckle decorrelation (above) and speckle variance (below). In Fig. 5(d), the short-time series method provides visualization of the vessel network that is comparable to that of the speckle decorrelation (Fig. 5(a)) and speckle variance methods (Fig. 5(g)). Further examination indicates the improved contrast of the blood vessels in the short-time series projection image, observed as the enhanced connectivity and visibility of the vessels. One such example, taken from the outlined tissue regions in Fig. 5(d), is magnified in Fig. 5(e). In comparison to Figs. 5(b) and (h), obtained using speckle decorrelation and speckle variance, respectively, several vessel segments are more clearly observed, with a representative example marked by the arrows. The cross-sectional views of these marked vessels are shown, respectively, in Figs. 5(c), (f) and (i). Such improvement is further quantified by measuring the vessel area density, with an estimated accuracy of approximately 1%. This results in a superior area density of 28% for the short time-series image shown in Fig. 5(d), in comparison to 21% and 20% for speckle decorrelation and speckle variance, respectively. The higher density in the short-time-series method results from the improved vessel contrast, as shown in Fig. 5.
Fig. 5.
OCTA comparison case 1. Projection of blood vessels by speckle decorrelation (a), short-time series (d) and speckle variance (g). The outlined regions in (a), (d) and (g) are magnified in (b), (e) and (h), respectively. Vessels from the forearm skin are projected from the surface to 300 µm in depth. The arrows mark the same vessel segment in (b), (e) and (h) with the cross-sectional views in (c), (f) and (i), respectively. (j) OCT image (0-41 dB) corresponding to (c), (f) and (i). White scale bars: 500 µm. Cyan scale bars: 200 µm.
The consistent superiority of vessel contrast afforded by short-time series OCTA is observed in all human subjects (n = 4) in this study, with a further example shown in Fig. 6. The maximum intensity projection of the blood vessels, from the skin surface to 300 µm deep by the three methods, is visualized in Figs. 6(a), (d) and (g). This case also shows the superior vessel visibility provided by the short-time series method in Fig. 6(d), over speckle decorrelation (Fig. 6(a)) and speckle variance (Fig. 6(g)). The vessel contrast differences are highlighted by the corresponding magnified region in Figs. 6(b), (e) and (h), indicating the superior vessel signal strength and connections evident in the short-time series images, with specific instances marked by the cyan arrows. The measured vessel area density (27%), in this case, is higher than for speckle decorrelation (21%) and speckle variance (19%), consistent with the analysis of Fig. 5. Interestingly, this case shows several examples of parallel vessels in local regions in Figs. 6(a), (d) and (g) (e.g., the vessels marked by the green arrows). They are more readily observed in the short-time series images than in the images obtained by speckle decorrelation or speckle variance in the example cross-sectional views of the vessel marked by the left green arrow shown, respectively, in Figs. 6(c), (f) and (i). Another projection approach used in the literature is to take the mean OCTA vessel signal, instead of the maximum [5,38]. In this study, consistent vessel contrast differences among the three methods are observed in the mean projections as well (not shown).
Fig. 6.
OCTA comparison case 2. Projection of blood vessels by speckle decorrelation (a), short-time series (d) and speckle variance (g). The outlined regions in (a), (d) and (g) are magnified in (b), (e) and (h), respectively. Vessels from the forearm skin are projected from the surface to 300 µm in depth. The arrows in the projections mark the same vessel segments. Cross-sectional views of the vessel marked by the left green arrows in (a), (d) and (g) are shown in (c), (f) and (i), respectively. (j) OCT image (0-41 dB) corresponding to (c), (f) and (i). White scale bars: 500 µm. Cyan scale bars: 200 µm.
To further elucidate the contrast differences among the three methods, an experiment was performed to examine the OCTA signal in the phantom versus flow speed (9 values ranging from 0 to 2 mm/s). Figure 7 shows the resulting signal strength in the flow region, determined by subtracting the noise in the static region () from the original flow signal () and then normalizing the flow signals to their maximum after subtraction. The normalized signal is thus defined as: , where is the normalized OCTA signal shown in Fig. 7. All three methods show an increase of the signal strength with increasing flow speed of the microspheres (diameter: 2 µm), from the baseline signal due to Brownian motion at zero flow speed. The signals then all saturate at approximately 0.8-1.2 mm/s. Compared to speckle decorrelation and speckle variance, the short-time series method shows higher normalized signal in the low speed range. This observation is consistent with the improved contrast for small vessels seen in Figs. 5-6. In addition, the short-time series method shows the smallest dynamic range in the normalized signal in Fig. 7. This indicates a possible disadvantage for velocimetry (if required in future work), as compared to speckle decorrelation and speckle variance.
Fig. 7.
Normalized OCTA signal versus flow speed in the flow region of the phantom for short-time series (blue), speckle decorrelation (red) and speckle variance (black).
In addition to visualization of normal vessel networks, short-time series OCTA also shows good vessel contrast for the subject with a treated wart. The resulting vessel image is shown in Fig. 8(a) in comparison to the adjacent normal skin of the same subject in Fig. 8(b). The wart was removed with a laser ~16 years prior to OCT scanning. Comparison of the images generated by the three OCTA methods consistently shows the improved visualization by the short-time series method, for both the normal and treated skin regions (not shown). Though the treated region shows a very comparable skin color to the normal skin, the underlying microvasculature visualized by the short-times series method clearly reveals the morphological differences. For example, the treated region presents a network with more branches and a distinct honeycomb-like pattern (i.e., local loops), absent from the normal skin. The quantified vessel area density in the treated region (34%) is significantly higher than that in the normal skin (29%). Such visualization and the associated contrast demonstrate the potential of short-time series OCTA for future studies of various cutaneous conditions.
Fig. 8.
Short-time series OCTA imaging of a subject with a laser-treated wart. Projection of blood vessels from the surface to 300 µm in depth of the laser-treated area (a) and the adjacent normal skin (b). Scale bars: 500 µm.
Another important factor is the computation time, which can be limiting for applications requiring near-real-time or real-time imaging. Overall, speckle decorrelation is more time consuming than short-time series or speckle variance due to the requirement for window processing (not simply averaging) to generate the vessel signal. It took ~420 ms to calculate the decorrelation of a pair of B-scans (1024 × 1024 pixels per B-scan) using a 3 × 3 pixel window on an Intel Core i7-3820 processor with MATLAB R2016a (The MathWorks, Inc.). When a larger window is used for processing, the computation time increases significantly (e.g., 990 ms for a 5 × 5 pixel window). In contrast, data processing for the short-time series and speckle variance methods is much faster, taking ~64 ms and ~27 ms, respectively, to process each set of 5 co-located B-scans. This feature indicates the promise for future implementation of the short-time series on fast scanning OCT systems to enable in-procedure or even real-time visualization of microvasculature.
4. Discussion
The method proposed here takes a short time series of OCT B-scans acquired at the same location as an input, and performs a discrete Fourier transform to determine the frequency content in order to image blood vessels. The observed higher magnitudes at non-zero (high-pass) frequencies in the blood vessels (up to 28 Hz demonstrated here) create a clear contrast to distinguish blood vessels from surrounding static tissue. This method is easily applicable to OCT scans acquired using normal scanning parameters for imaging of the microvascular network. In case studies on human skin, short-time series OCTA shows moderately but consistently improved vessel contrast in comparison to speckle decorrelation and speckle variance, especially for the small vessels. Whilst the in vivo comparison was demonstrated on skin tissue, future application of short-time series OCTA to other tissues, such as the retina, will provide further characterization of the method.
Matveev et al. previously proposed an angiography method based upon frequency analysis of adjacent A-scans [33]. After removing the low frequencies via high-pass filtering, their final vessel signal is the fast-changing OCT signal built by inverse Fourier transformation of the filtered frequency signal. In comparison, our method directly uses the frequency spectrum to compute the vessel signal, normalizing the average of the non-zero frequency components by the average OCT signal. Additionally, their method detects more vessels by decreasing the threshold of the high-pass filter. However, when the threshold was decreased to 30 Hz, the static tissue shows an artificially high “vessel” signal, degrading the vessel image. In contrast, we used frequencies only up to 28 Hz without contrast degradation. Another difference is that we performed the analysis on a time series of co-located OCT B-scans, instead of neighboring A-scans. This eliminates the requirement for very high A-scan sampling density, but at the cost of a slightly higher number of co-located B-scans. In their method, phase alignment was required to correct for bulk tissue motion due to the use of the complex OCT signal. In contrast, we implemented the short-time series method on the OCT intensity signal alone, providing high vessel contrast without motion correction. These features of our method support simple data acquisition and computation, which is attractive for its ready application.
Mioseev et al. recently revised the original method by Matveev et al. to analyze adjacent B-scans along the slow scanning axis [39]. For reduced numbers of time samples (i.e., adjacent B-scans), they observed that high-pass filtering of short sequences in the frequency domain, using the method proposed by Matveev et al., leads to artifacts. To address this issue, they proposed the use of high-pass filtering with a finite impulse response filter in the signal domain (i.e., time domain). As a point of difference, our method calculates the vessel signal in the frequency domain and is not affected by such artifacts, even for as few as 5 time samples (i.e., 5 co-located B-scans). In addition, we chose to use co-located B-scans so as to avoid the degradation of vessel contrast due to the possibly corrupting spatial frequency-induced frequency content resulting from analyzing adjacent B-scans.
The number of co-located B-scans acquired from the same location is an important parameter for the practical implementation of the short-time series method. We chose 5 in this study so as to minimize the amount of collected data and corresponding total acquisition time, whilst still attaining a high vessel/static tissue contrast in skin. A very large number of co-located B-scans does not significantly improve the vessel contrast, as we showed. This is due to the simultaneous increase of the vessel signal in both the static tissue and the flow regions. In addition, extraneous motion can become a problem as the acquisition time lengthens. A smaller number of co-located B-scans, on the other hand, leads to slightly poorer vessel contrast, but can still visualize most vessels for even 3 or 4 co-located B-scans. When the minimum number (i.e., 2) is used, the formula in Eq. (3) is then equivalent to the simplified OMAG method that generates contrast by subtracting the intensity signal in two co-located B-scans [40]. This equivalence does not exist as more co-located B-scans are used, and which leads to superior vessel image quality, as compared to only 2 co-located B-scans (i.e., the subtraction method). The consistent optimization of this sampling parameter is as yet unverified and, thus, needs further investigation when applied to imaging microvasculature in other tissues, such as the retina.
One limitation of short-time series used in this study is the small detectable frequency range (i.e., up to 28 Hz), set by the B-scan time interval. Blood flow produces a characteristic peak typically in the kilohertz-frequency range [31], well outside the range accessed by our method. Increasing the OCT scanning speed to shorten the B-scan interval increases the maximum detectable frequency, but is limited by the fast-axis scanning speed of our system. Alternatively, reducing the sample density (i.e., the number of A-scans) in the B-scan can also improve this, but only slightly, as adequate sample density is needed to represent the vessels in the projection images. Thus, short-time series OCTA, as proposed in this study, is not suitable for velocimetry. In future, faster scanning systems may help address this [41].
5. Conclusions
We have presented a new method, short-time series OCTA, to perform imaging of tissue microvasculature in vivo. Our method uses the flow-induced signature in the frequency domain via Fourier transform of the time series of the OCT signal in five B-scans from the same lateral location. The angiography signal is computed as the average magnitude of the non-zero (high-pass) frequency components, clearly differentiating blood vessels and static tissue, as demonstrated in a flow phantom and in human skin in vivo. Weighting of the angiography signal by the inverse of the mean OCT signal demonstrated improved detection of blood vessels. We determined the practical minimum number of co-located B-scans needed for analysis, as well as confirming that implementation on the OCT intensity signal is practically superior to implementation on the complex signal without motion correction. The imaging performance of short-time series OCTA was assessed by comparison to the commonly used speckle decorrelation and speckle variance methods, showing consistently superior results, evidenced by improved visualization, especially for small vessels, and increased vasculature density of the human cutaneous microvascular network. Given the requirement for only normal sampling parameters, in combination with fast computing, this method should find application as an efficient and straightforward approach to OCTA in various biomedical applications to visualize the microvasculature in vivo.
Acknowledgements
The authors would like to thank Dr Karol Karnowski for discussions regarding data processing, Dr Danuta Sampson for advice in general, and Qingyun Li for assistance in OCT scanning. P. Gong was supported by a Healy Research Collaboration Award. This study was supported with funding from the Australian Research Council and the National Health and Medical Research Council.
Funding
Australian Research Council; National Health and Medical Research Council.
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References and links
- 1.McDonald D. M., Choyke P. L., “Imaging of angiogenesis: from microscope to clinic,” Nat. Med. 9(6), 713–725 (2003). 10.1038/nm0603-713 [DOI] [PubMed] [Google Scholar]
- 2.Fayad Z. A., Fuster V., Nikolaou K., Becker C., “Computed tomography and magnetic resonance imaging for noninvasive coronary angiography and plaque imaging: current and potential future concepts,” Circulation 106(15), 2026–2034 (2002). 10.1161/01.CIR.0000034392.34211.FC [DOI] [PubMed] [Google Scholar]
- 3.Danad I., Raijmakers P. G., Appelman Y. E., Harms H. J., de Haan S., van den Oever M. L. P., Heymans M. W., Tulevski I. I., van Kuijk C., Hoekstra O. S., Lammertsma A. A., Lubberink M., van Rossum A. C., Knaapen P., “Hybrid imaging using quantitative H215O PET and CT-based coronary angiography for the detection of coronary artery disease,” J. Nucl. Med. 54(1), 55–63 (2013). 10.2967/jnumed.112.104687 [DOI] [PubMed] [Google Scholar]
- 4.Drexler W., Fujimoto J. G., Optical Coherence Tomography: Technology and Applications (Springer International Publishing AG, Cham, 2015). [Google Scholar]
- 5.Chen C. L., Wang R. K., “Optical coherence tomography based angiography [Invited],” Biomed. Opt. Express 8(2), 1056–1082 (2017). 10.1364/BOE.8.001056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Xu J., Song S., Wei W., Wang R. K., “Wide field and highly sensitive angiography based on optical coherence tomography with akinetic swept source,” Biomed. Opt. Express 8(1), 420–435 (2016). 10.1364/BOE.8.000420 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Campbell J. P., Zhang M., Hwang T. S., Bailey S. T., Wilson D. J., Jia Y., Huang D., “Detailed vascular anatomy of the human retina by projection-resolved optical coherence tomography angiography,” Sci. Rep. 7(1), 42201 (2017). 10.1038/srep42201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gorczynska I., Migacz J. V., Zawadzki R. J., Capps A. G., Werner J. S., “Comparison of amplitude-decorrelation, speckle-variance and phase-variance OCT angiography methods for imaging the human retina and choroid,” Biomed. Opt. Express 7(3), 911–942 (2016). 10.1364/BOE.7.000911 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Leitgeb R. A., Werkmeister R. M., Blatter C., Schmetterer L., “Doppler optical coherence tomography,” Prog. Retin. Eye Res. 41, 26–43 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Enfield J., Jonathan E., Leahy M., “In vivo imaging of the microcirculation of the volar forearm using correlation mapping optical coherence tomography (cmOCT),” Biomed. Opt. Express 2(5), 1184–1193 (2011). 10.1364/BOE.2.001184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Liew Y. M., McLaughlin R. A., Gong P., Wood F. M., Sampson D. D., “In vivo assessment of human burn scars through automated quantification of vascularity using optical coherence tomography,” J. Biomed. Opt. 18(6), 061213 (2012). 10.1117/1.JBO.18.6.061213 [DOI] [PubMed] [Google Scholar]
- 12.Gao S. S., Jia Y., Zhang M., Su J. P., Liu G., Hwang T. S., Bailey S. T., Huang D., “Optical coherence tomography angiography,” Invest. Ophthalmol. Vis. Sci. 57(9), OCT27–OCT36 (2016). 10.1167/iovs.15-19043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Munk M. R., Giannakaki-Zimmermann H., Berger L., Huf W., Ebneter A., Wolf S., Zinkernagel M. S., “OCT-angiography: A qualitative and quantitative comparison of 4 OCT-A devices,” PLoS One 12(5), e0177059 (2017). 10.1371/journal.pone.0177059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gong P., Es’haghian S., Wood F. M., Sampson D. D., McLaughlin R. A., “Optical coherence tomography angiography for longitudinal monitoring of vascular changes in human cutaneous burns,” Exp. Dermatol. 25(9), 722–724 (2016). 10.1111/exd.13053 [DOI] [PubMed] [Google Scholar]
- 15.Gong P., Es’haghian S., Harms K. A., Murray A., Rea S., Kennedy B. F., Wood F. M., Sampson D. D., McLaughlin R. A., “Optical coherence tomography for longitudinal monitoring of vasculature in scars treated with laser fractionation,” J. Biophotonics 9(6), 626–636 (2016). 10.1002/jbio.201500157 [DOI] [PubMed] [Google Scholar]
- 16.Qin J., Jiang J., An L., Gareau D., Wang R. K., “In vivo volumetric imaging of microcirculation within human skin under psoriatic conditions using optical microangiography,” Lasers Surg. Med. 43(2), 122–129 (2011). 10.1002/lsm.20977 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ulrich M., Themstrup L., de Carvalho N., Manfredi M., Grana C., Ciardo S., Kästle R., Holmes J., Whitehead R., Jemec G. B. E., Pellacani G., Welzel J., “Dynamic optical coherence tomography in dermatology,” Dermatology (Basel) 232(3), 298–311 (2016). 10.1159/000444706 [DOI] [PubMed] [Google Scholar]
- 18.Schuh S., Holmes J., Ulrich M., Themstrup L., Jemec G. B. E., De Carvalho N., Pellacani G., Welzel J., “Imaging blood vessel morphology in skin: Dynamic optical coherence tomography as a novel potential diagnostic tool in dermatology,” Dermatol. Ther. (Heidelb.) 7(2), 187–202 (2017). 10.1007/s13555-017-0175-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Blatter C., Weingast J., Alex A., Grajciar B., Wieser W., Drexler W., Huber R., Leitgeb R. A., “In situ structural and microangiographic assessment of human skin lesions with high-speed OCT,” Biomed. Opt. Express 3(10), 2636–2646 (2012). 10.1364/BOE.3.002636 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.An D., Balaratnasingam C., Heisler M., Francke A., Ju M., McAllister I. L., Sarunic M., Yu D. Y., “Quantitative comparisons between optical coherence tomography angiography and matched histology in the human eye,” Exp. Eye Res. 170, 13–19 (2018). 10.1016/j.exer.2018.02.006 [DOI] [PubMed] [Google Scholar]
- 21.Mariampillai A., Standish B. A., Moriyama E. H., Khurana M., Munce N. R., Leung M. K. K., Jiang J., Cable A., Wilson B. C., Vitkin I. A., Yang V. X. D., “Speckle variance detection of microvasculature using swept-source optical coherence tomography,” Opt. Lett. 33(13), 1530–1532 (2008). 10.1364/OL.33.001530 [DOI] [PubMed] [Google Scholar]
- 22.Motaghiannezam R., Fraser S., “Logarithmic intensity and speckle-based motion contrast methods for human retinal vasculature visualization using swept source optical coherence tomography,” Biomed. Opt. Express 3(3), 503–521 (2012). 10.1364/BOE.3.000503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jia Y., Tan O., Tokayer J., Potsaid B., Wang Y., Liu J. J., Kraus M. F., Subhash H., Fujimoto J. G., Hornegger J., Huang D., “Split-spectrum amplitude-decorrelation angiography with optical coherence tomography,” Opt. Express 20(4), 4710–4725 (2012). 10.1364/OE.20.004710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mahmud M. S., Cadotte D. W., Vuong B., Sun C., Luk T. W. H., Mariampillai A., Yang V. X. D., “Review of speckle and phase variance optical coherence tomography to visualize microvascular networks,” J. Biomed. Opt. 18(5), 50901 (2013). 10.1117/1.JBO.18.5.050901 [DOI] [PubMed] [Google Scholar]
- 25.Zotter S., Pircher M., Torzicky T., Bonesi M., Götzinger E., Leitgeb R. A., Hitzenberger C. K., “Visualization of microvasculature by dual-beam phase-resolved Doppler optical coherence tomography,” Opt. Express 19(2), 1217–1227 (2011). 10.1364/OE.19.001217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Schwartz D. M., Fingler J., Kim D. Y., Zawadzki R. J., Morse L. S., Park S. S., Fraser S. E., Werner J. S., “Phase-variance optical coherence tomography: a technique for noninvasive angiography,” Ophthalmology 121(1), 180–187 (2014). 10.1016/j.ophtha.2013.09.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nam A. S., Chico-Calero I., Vakoc B. J., “Complex differential variance algorithm for optical coherence tomography angiography,” Biomed. Opt. Express 5(11), 3822–3832 (2014). 10.1364/BOE.5.003822 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ruminski D., Sikorski B. L., Bukowska D., Szkulmowski M., Krawiec K., Malukiewicz G., Bieganowski L., Wojtkowski M., “OCT angiography by absolute intensity difference applied to normal and diseased human retinas,” Biomed. Opt. Express 6(8), 2738–2754 (2015). 10.1364/BOE.6.002738 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wang R. K., Jacques S. L., Ma Z., Hurst S., Hanson S. R., Gruber A., “Three dimensional optical angiography,” Opt. Express 15(7), 4083–4097 (2007). 10.1364/OE.15.004083 [DOI] [PubMed] [Google Scholar]
- 30.Barton J., Stromski S., “Flow measurement without phase information in optical coherence tomography images,” Opt. Express 13(14), 5234–5239 (2005). 10.1364/OPEX.13.005234 [DOI] [PubMed] [Google Scholar]
- 31.Szkulmowski M., Szkulmowska A., Bajraszewski T., Kowalczyk A., Wojtkowski M., “Flow velocity estimation using joint Spectral and Time domain Optical Coherence Tomography,” Opt. Express 16(9), 6008–6025 (2008). 10.1364/OE.16.006008 [DOI] [PubMed] [Google Scholar]
- 32.Szkulmowska A., Szkulmowski M., Szlag D., Kowalczyk A., Wojtkowski M., “Three-dimensional quantitative imaging of retinal and choroidal blood flow velocity using joint Spectral and Time domain Optical Coherence Tomography,” Opt. Express 17(13), 10584–10598 (2009). 10.1364/OE.17.010584 [DOI] [PubMed] [Google Scholar]
- 33.Matveev L. A., Zaitsev V. Y., Gelikonov G. V., Matveyev A. L., Moiseev A. A., Ksenofontov S. Y., Gelikonov V. M., Sirotkina M. A., Gladkova N. D., Demidov V., Vitkin A., “Hybrid M-mode-like OCT imaging of three-dimensional microvasculature in vivo using reference-free processing of complex valued B-scans,” Opt. Lett. 40(7), 1472–1475 (2015). 10.1364/OL.40.001472 [DOI] [PubMed] [Google Scholar]
- 34.Jonathan E., Enfield J., Leahy M. J., “Correlation mapping method for generating microcirculation morphology from optical coherence tomography (OCT) intensity images,” J. Biophotonics 4(9), 583–587 (2011). [DOI] [PubMed] [Google Scholar]
- 35.Otsu N., “A threshold selection method from gray-level histograms,” IEEE Trans. Syst. Man Cybern. 9(1), 62–66 (1979). 10.1109/TSMC.1979.4310076 [DOI] [Google Scholar]
- 36.Es’haghian S., Kennedy K. M., Gong P., Sampson D. D., McLaughlin R. A., Kennedy B. F., “Optical palpation in vivo: imaging human skin lesions using mechanical contrast,” J. Biomed. Opt. 20(1), 16013 (2015). 10.1117/1.JBO.20.1.016013 [DOI] [PubMed] [Google Scholar]
- 37.Gong P., McLaughlin R. A., Liew Y. M., Munro P. R. T., Wood F. M., Sampson D. D., “Assessment of human burn scars with optical coherence tomography by imaging the attenuation coefficient of tissue after vascular masking,” J. Biomed. Opt. 19(2), 21111 (2013). 10.1117/1.JBO.19.2.021111 [DOI] [PubMed] [Google Scholar]
- 38.Zhang A., Zhang Q., Wang R. K., “Minimizing projection artifacts for accurate presentation of choroidal neovascularization in OCT micro-angiography,” Biomed. Opt. Express 6(10), 4130–4143 (2015). 10.1364/BOE.6.004130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Moiseev A., Ksenofontov S., Sirotkina M., Kiseleva E., Gorozhantseva M., Shakhova N., Matveev L., Zaitsev V., Matveyev A., Zagaynova E., Gelikonov V., Gladkova N., Vitkin A., Gelikonov G., “Optical coherence tomography-based angiography device with real-time angiography B-scans visualization and hand-held probe for everyday clinical use,” J. Biophotonics 11(10), e201700292 (2018), doi:. 10.1002/jbio.201700292 [DOI] [PubMed] [Google Scholar]
- 40.Choi W. J., Wang H., Wang R. K., “Optical coherence tomography microangiography for monitoring the response of vascular perfusion to external pressure on human skin tissue,” J. Biomed. Opt. 19(5), 056003 (2014). 10.1117/1.JBO.19.5.056003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Klein T., Wieser W., Reznicek L., Neubauer A., Kampik A., Huber R., “Multi-MHz retinal OCT,” Biomed. Opt. Express 4(10), 1890–1908 (2013). 10.1364/BOE.4.001890 [DOI] [PMC free article] [PubMed] [Google Scholar]