Optimal seed solver: optimizing seed selection in read mapping

Abstract

Motivation: Optimizing seed selection is an important problem in read mapping. The number of non-overlapping seeds a mapper selects determines the sensitivity of the mapper while the total frequency of all selected seeds determines the speed of the mapper. Modern seed-and-extend mappers usually select seeds with either an equal and fixed-length scheme or with an inflexible placement scheme, both of which limit the ability of the mapper in selecting less frequent seeds to speed up the mapping process. Therefore, it is crucial to develop a new algorithm that can adjust both the individual seed length and the seed placement, as well as derive less frequent seeds.

Results: We present the Optimal Seed Solver (OSS), a dynamic programming algorithm that discovers the least frequently-occurring set of x seeds in an L-base-pair read in $\mathcal{O}(x\times L)$ operations on average and in $\mathcal{O}(x\times L^2)$ operations in the worst case, while generating a maximum of $\mathcal{O}(L^2)$ seed frequency database lookups. We compare OSS against four state-of-the-art seed selection schemes and observe that OSS provides a 3-fold reduction in average seed frequency over the best previous seed selection optimizations.

Availability and implementation: We provide an implementation of the Optimal Seed Solver in C++ at: https://github.com/CMU-SAFARI/Optimal-Seed-Solver

Contact: hxin@cmu.edu, calkan@cs.bilkent.edu.tr or onur@cmu.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

The invention of high-throughput sequencing (HTS) platforms during the past decade triggered a revolution in the field of genomics. These platforms enable scientists to sequence mammalian-sized genomes in a matter of days, which have created new opportunities for biological research. For example, it is now possible to investigate human genome diversity between populations (1000 Genomes Project Consortium, 2010, 2012), find genomic variants likely to cause disease (Flannick etal., 2014; Ng etal., 2010), and study the genomes of ape species (Marques-Bonet etal., 2009; Prado-Martinez et al., 2013; Scally etal., 2012; Ventura etal., 2011) and ancient hominids (Green etal., 2010; Meyer etal., 2012; Reich etal., 2010) to better understand human evolution.

However, these new sequencing platforms drastically increase the computational burden of genome data analysis. First, billions of short DNA segments (called reads) are aligned to a long reference genome. Each read is aligned to one or more sites in the reference based on similarity with a process called read mapping (Flicek and Birney, 2009). Reads are matched to locations in the genome with a certain allowed number of errors: insertions, deletions, and substitutions (which usually constitute less than 5% of the read’s length). Matching strings approximately with a certain number of allowed errors is a difficult problem. As a result, read mapping constitutes a significant portion of the time spent during the analysis of genomic data.

Pigeonhole principle based seed-and-extend mappers are one kind of popular mappers that have been widely used to aid many biological applications (Green etal., 2010; Navin etal., 2011; Van Vlierberghe etal., 2010). In pigeonhole based seed-and-extend mappers such as mrFAST (Alkan etal., 2009; Xin etal., 2013), RazerS3 (Weese etal., 2012), GEM (Marco-Sola etal., 2012), SHRiMP (Rumble etal., 2009) and Hobbes (Ahmadi etal., 2011), each read is partitioned into one or more short segments called seeds. Here we define seeds as substrings of a read. This definition is different from the ‘spaced seeds’ definition (which can be a subsequence, rather than a substring)—a concept we will explain in the Related Works section. Seeds are used as indices into the reference genome to reduce the search space and speed up the mapping process. Since a seed is a substring of the read that contains it, every correct mapping for a read in the reference genome will also be mapped by the seed (assuming no errors in the seed). Therefore, mapping locations of the seeds generate a pool of potential mappings of the read. Mapping locations of seeds in the reference genome are pre-computed and stored in a seed database (usually implemented as a hash table or Burrows-Wheeler-transformation (BWT) (Burrows etal., 1994) with FM-indexing (Ferragina and Manzini, 2000)) and can be quickly retrieved through a database lookup.

When there are errors in a read, the read can still be correctly mapped as long as there exists one seed of the read that is error free. The error-free seed can be obtained by breaking the read into many non-overlapping seeds; in general, to tolerate e errors, a read is divided into e + 1 seeds, and based on the pigeonhole principle, at least one seed will be error free.

Alternatively, a mapper can use overlapping seeds. Such mappers follow the q-gram approach (Rasmussen etal., 2006) in order to achieve full mapping sensitivity (finding all valid mappings that have fewer errors than permitted) or simply select overlapping seeds without guaranteeing the full mapping sensitivity under the given error threshold (e.g. bowtie2 (Langmead and Salzberg, 2012), BWA-MEM (Li, 2013)). Compared to the pigeonhole principle (a special case of the q-gram approach), selecting overlapping seeds using the q-gram approach could generate longer, less frequent seeds. However, in order to guarantee full mapping sensitivity, this approach requires selecting a larger number of seeds, which may increase the total number of potential mappings, there by reducing the speed of a mapper. In this work, we focus on seed selection mechanisms based on the pigeonhole principle that provide full mapping sensitivity by selecting non-overlapping seeds.

For each selected non-overlapping seed, its locations are further verified using weighted edit-distance calculation mechanisms (such as Smith–Waterman (Smith and Waterman, 1981) and Needleman–Wunsch (Needleman and Wunsch, 1970) algorithms), to examine the similarity between the read and the reference at each potential mapping site. Locations that pass this final verification step (i.e. contain fewer than e substitutions, insertions and deletions) are valid mappings and are recorded by the mapper for use in later stages of genomic analysis.

Computing the edit-distance is an expensive operation and is the primary computation performed by most read mappers. In fact, speeding up this computation is the subject of many other works in this area of research, such as Shifted Hamming Distance (Xin etal., 2015), Gene Myers’ bit-vector algorithm (Myers, 1999) and SIMD implementations of edit-distance algorithms (Rognes, 2011; Szalkowski etal., 2008). To allow edits, mappers must divide reads into multiple seeds. Each seed increases the number of locations that must be verified. Furthermore, to divide a read into more seeds, the lengths of seeds must be reduced to make space for the increased number of seeds; shorter seeds occur more frequently in the genome which requires the mapper to verify even more potential mappings.

Therefore, the key to building a fast yet error tolerant mapper with high sensitivity is to select many seeds (to provide greater tolerance) while minimizing their frequency of occurrence (or simply frequency) in the genome to ensure fast operation. Our goal, in this work, is to lay a theoretically-solid foundation to enable techniques for optimal seed selection in current and future seed-and-extend mappers.

Selecting the optimal set of non-overlapping seeds (i.e. the least frequent set of seeds) from a read is difficult primarily because the associated search space (all valid choices of seeds) is large and it grows exponentially as the number of seeds increases. A seed can be selected at any position in the read with any length, as long as it does not overlap with other seeds. We observe that there is a significant advantage to selecting seeds with unequal lengths, as possible seeds of equal lengths can have drastically different levels of frequencies.

Our goal in this paper is to develop an inexpensive algorithm for seed-and-extend mappers based on the pigeonhole principle that derives the optimal placement and length of each seed in a read such that the overall sum of frequencies of all seeds is minimized.

This paper makes the following contributions:

• It examines the frequency distribution of seeds in the seed database and provides how often seeds of different frequencies are selected using a naïve seed selection scheme. We confirm the discovery of prior works (Kiełbasa etal., 2011) that frequencies are not evenly distributed among seeds and frequent seeds are selected more often under a naïve seed selection scheme. We further show that this phenomenon persists even when using longer seeds.

• It provides an implementation of an optimal seed finding algorithm, Optimal Seed Solver, which uses dynamic programming to efficiently find the least-frequent non-overlapping seeds of a given read. We prove that this algorithm always provides the least frequently-occurring set of seeds in a read.

• It provides a comparison of the Optimal Seed Solver and existing seed selection optimizations, including Adaptive Seeds Filter in the GEM mapper (Marco-Sola etal., 2012), Cheap K-mer Selection in FastHASH (Xin etal., 2013), Optimal Prefix Selection in the Hobbes mapper (Ahmadi etal., 2011) and spaced seeds in PatternHunter (Ma etal., 2002). We compare the complexity, memory traffic, and average frequency of selected seeds of Optimal Seed Solver with the above four state-of-the-art seed selection mechanisms. We show that the Optimal Seed Solver provides the least frequent set of seeds among all existing seed selection optimizations at reasonable complexity and memory traffic.

2 Motivation

To build a fast yet error tolerant mapper with high mapping coverage, reads need to be divided into multiple, infrequently occurring seeds. In this way, a mapper can find all correct mappings of the read (mappings with small edit-distances) while minimizing the number of edit-distance calculations that need to be performed. To achieve this goal, we have to overcome two major challenges: (i) seeds are short, in general, and therefore frequent in the genome; and (ii) the frequencies of different seeds vary significantly. We discuss each challenge in greater detail.

Assume a read has a length of L base-pairs (bp) and $x\%$ of it is erroneous (e.g. L = 80 and $x\%=5\%$ implies that there are 4 edits). To tolerate $x\%\times L$ errors in the read, we need to select $x\%\times L+1$ seeds, which renders a seed to be $L÷(x\%\times L+1)$-base-pair long on average. Given that the desired error rates for many mainstream mappers have been as large as 0.05, the average seed length of a hash-table based mapper is typically not greater than 16-bp (Alkan etal., 2009; Ahmadi etal., 2011; Marco-Sola et al., 2012; Rumble etal., 2009; Weese etal., 2012).

Seeds have two important properties: (i) the frequency of a seed is monotonically non-increasing with larger seed lengths and (ii) frequencies of different seeds typically differ (sometimes significantly) (Kiełbasa etal., 2011). Figure 1 shows the static distribution of frequencies of 10-bp to 15-bp fixed-length seeds from the human reference genome (GRCh37). This figure shows that the average seed frequency decreases with the increase in the seed length. With longer seeds, there are more patterns to index the reference genome. Thus each pattern, on average, is less frequent.

Fig. 1.

Frequency distribution of unique seeds in fixed-length seed (k-mers at varying ‘k’s) databases of human reference genome version 37. Each plot shows how many unique seeds there are at each frequency level. Notice that the trend in each plot is not a continuous line but is made of many discrete data points. Each data point denotes how many unique seeds there are at each frequency level

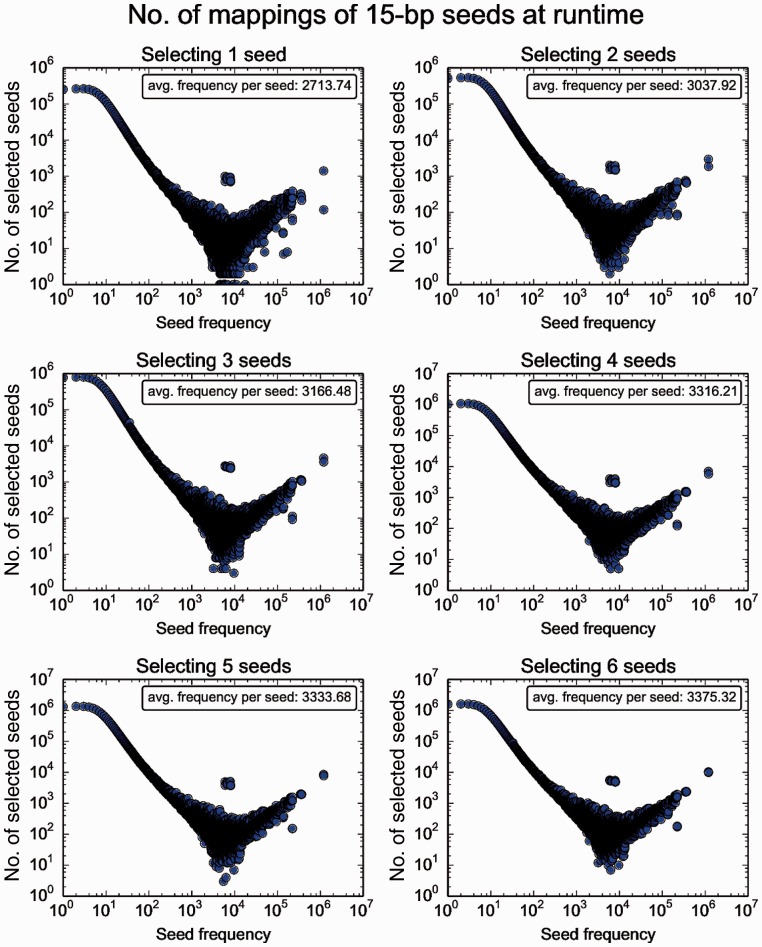
From Figure 1, we can also observe that the frequencies of seeds are not evenly distributed: for seeds with lengths between 10-bp to 15-bp, many seeds have frequencies below 100. As the figure shows, a high number of unique seeds, often over 10³, correspond to seed frequencies below 100. However, there are also a few seeds which have frequencies greater than 100K (note that such unique seeds are very few, usually 1 per each frequency). This explains why most plots in Figure 1 follow a bimodal distribution; except for 10-bp seeds and perhaps 11-bp seeds, where the frequency of seeds peaks at around 100. Although ultra-frequent seeds (seeds that appear more frequently than 10⁴ times) are few among all seeds, they are ubiquitous in the genome. As a result, for a randomly selected read, there is a high chance that the read contains one or more of such frequent seeds. This effect is best illustrated in Figure 2, which presents the numbers of frequencies of consecutively selected seeds, when we map over 4 million randomly selected 101-bp reads from the 1000 Genomes Project (1000 Genomes Project Consortium, 2010) to the human reference genome.

Fig. 2.

Frequency distribution of selected seeds at runtime by consecutively selecting 15-bp seeds from reads while mapping 4 031 354 101-bp reads from a real read set, ERR240726 from the 1000 Genomes Project, to human reference version 37, under different numbers of required seeds. Unlike Figure 1, which counts each unique seed only once, this figure records the overall distribution of frequencies over selected seeds while mapping a real read set. In this figure, upon selection, each seed contributes to the frequency counter individually (duplicating seeds will be counted multiple times by each selection)

Unlike in Figure 1, in which the average frequency of 15-bp unique seeds is 5.25, the average frequencies of selected seeds in Figure 2 are all greater than 2.7K. Furthermore, from Figure 2, we can observe that the ultra-frequent seeds are selected far more often than some of the less frequent seeds, as the selected seed count increases with seed frequencies higher than 10⁴ (as opposed to Fig. 1, where seed frequencies over 10⁴ usually have seed counts below 10). This observation suggests that the ultra-frequent seeds are surprisingly numerous in reads, especially considering how few ultra-frequent seed patterns there are in total in the seed database (and the plots in Figure 2 no longer follow a bimodal distribution as in Fig. 1). We call this phenomenon the frequent seed phenomenon. The frequent seed phenomenon is explained in previous works (Kiełbasa etal., 2011). To summarize, highly frequent seed patterns are ubiquitous in the genome, therefore they appear more often in randomly sampled reads, such as reads sampled from shotgun sequencing. Frequency distributions of other seed lengths are provided in the Supplementary Materials Section 1.1.

The key takeaway from Figures 1 and 2 is that although longer seeds on average are less frequent than shorter seeds, some seeds are still much more frequent than others and such more frequent seeds are very prevalent in real reads. Therefore, with a naïve seed selection mechanism (e.g. selecting seeds consecutively from a read), a mapper selects many frequent seeds, which increases the number of calls to the computationally expensive verification process during read mapping.

To reduce the total frequency of selected seeds, we need an intelligent seed selection mechanism to avoid using frequent patterns as seeds. More importantly, as there is a limited number of base-pairs in a read, we need to carefully choose the length of each seed. Extension of an infrequent seed does not necessarily provide much reduction in the total frequency of all seeds, but it will ‘consume’ base-pairs that could have been used to extend other more frequent seeds. Besides determining individual seed lengths, we should also intelligently select the position of each seed. If multiple seeds are selected from a small region of the read, as they are closely packed together, seeds are forced to keep short lengths, which could potentially increase their seed frequency. Thus, seed selection must be done carefully to minimize the total frequency of seed occurrence.

Based on the above observations, our goal in this paper is to develop an algorithm that can calculate both the length and the placement of each seed in the read such that, the total frequency of all seeds is minimized. We call such a set of seeds the optimal seeds of the read as they produce the minimum number of potential mappings to be verified while maintaining the sensitivity of the mapper. We call the sum of frequencies of the optimal seeds the optimal frequency of the read.

3 Methods

The biggest challenge in deriving the optimal seeds of a read is the large search space. If we allow a seed to be selected from an arbitrary location in the read with an arbitrary length, then from a read of length L, there can be $\frac{L\times (L+1)}{2}$ possibilities to extract a single seed. When there are multiple seeds, the search space grows exponentially since the position and length of each newly selected seed depend on the positions and lengths of all previously selected seeds. For x seeds, there can be as many as $\mathcal{O}(\frac{L^{2\times x}}{x!})$ seed selection schemes.

Below we propose Optimal Seed Solver (OSS), a dynamic programming algorithm that finds the optimal set of x seeds of a read in $\mathcal{O}(x\times L)$ operations on average and in $\mathcal{O}(x\times L^2)$ operations in the worst case scenario.

Although in theory a seed can have any length, in OSS, we assume the length of a seed is bounded by a range [S_min, S_max]. This bound is based on our observation that, in practice, neither very short seeds nor very long seeds are commonly selected as optimal seeds. Ultra-short seeds (<8-bp) are too frequent. Most seeds shorter than 8-bp have frequencies over 1000. Ultra-long seeds ‘consume’ too many base-pairs from the read, which shorten the lengths of other seeds and increase their frequencies. This often leads to higher total seed frequency. Furthermore, long seeds (e.g. 40-bp) are mostly either unique or non-existent in the reference genome (seed of 0 frequency is still useful in read mapping as it confirms there exist at least one error in it). Extending a unique or non-existent seed longer provides little benefit while ‘consuming’ extra base-pairs from the read.

Bounding seed lengths reduces the search space of optimal seeds. However, it is not essential to OSS. OSS can still work without seed length limitations (to lift the limitations, one can simply set S_min = 1 and $S_{\text{max}}=L$), at the cost of extra computation.

We describe our Optimal Seed Solver algorithm in three sections. First, we introduce the core algorithm of OSS (Section 3.1). Then we improve the algorithm with four optimizations (Section 3.2), optimal divider cascading, early divider termination, divider sprinting and optimal solution forwarding. Finally we explain the overall algorithm and provide the pseudo-code (Section 3.3).

3.1 The core algorithm

A naïve brute-force solution to find the optimal seeds of a read would systematically iterate through all possible combinations of seeds. We start by selecting the first seed by instantiating all possible positions and lengths of the seed. On top of each position and length of the first seed, we instantiate all possible positions and lengths of the second seed that is sampled after (to the right-hand side of) the first seed. We repeat this process for the rest of the seeds until we have sampled all seeds. For each combination of seeds, we calculate the total seed frequency and find the minimum total seed frequency among all combinations.

The key problem in the brute-force solution above is that it examines many obviously suboptimal combinations. For example, in Figure 3, there are two 2-seed combinations, S_A and S_B, extracted from the same read, R. Both combinations end at the same position, p, in R. We call S_A and S_Bseed subsets of the partial read R[1...p]. In this case, between S_A and S_B, S_B has a higher total seed frequency than S_A. For any number of seeds that is greater than 2, we know that in the final optimal solution of R, seeds before position p will not be exactly like S_B, since any seeds that are appended after S_B (e.g. ${S\prime }_{\text{B}}$ in Fig. 3) can also be appended after S_A (e.g. ${S\prime }_{\text{A}}$ in Fig. 3) and produce a smaller total seed frequency. In other words, compared to S_B, only S_A has the potential to be part of the optimal solution and worth appending more seeds after. In general, among two combinations that have equal numbers of seeds and end at the same position in the read, only the combination with the smaller total seed frequency has the potential of becoming part of a bigger optimal solution (with more seeds). Therefore, for a partial read and all combinations of subsets of seeds in this partial read, only the optimal subset of this partial read (with regard to different numbers of seeds) might be relevant to the optimal solution of the entire read. Any other suboptimal subsets of seeds of this partial read (with regard to different numbers of seeds) is guaranteed to not lead to the optimal solution and should be pruned.

Fig. 3.

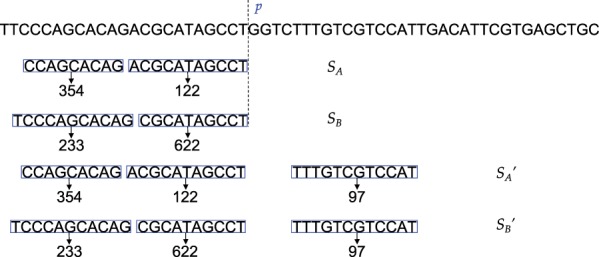
Example showing that a seed subset (S_B) that leads to a higher frequency than another subset (S_A) that ends at the same location (p) in the read must not be part of the optimal seed solution. In this figure, the total seed frequency of S_A is smaller than S_B. Both combinations can be extended by adding a third seed, making them $S_{\text{A}}\prime$ and $S_{\text{B}}\prime$ respectively. For any third seed, the total seed frequency of $S_{\text{B}}\prime$ must be greater than $S_{\text{A}}\prime$. Hence, S_B must not be part of any optimal solution

The above observation suggests that by summarizing the optimal solutions of partial reads under a smaller number of seeds, we can prune the search space of the optimal solution. Specifically, given m (with m < x) seeds and a substring U, only the optimal m seeds of U could be part of the optimal solution of the entire read. Any other suboptimal combinations of m seeds of U should be pruned.

Storing the optimal solutions of partial reads under a smaller number of seeds also helps speed up the computation of larger numbers of seeds. Assuming we have already calculated and stored the optimal frequency of m seeds of all substrings of R, to calculate the optimal $(m+1)$-seed solution of a substrings, we can i) iterate through a series of divisions of this substring; ii) calculate the seed frequency of each division using pre-calculated results and iii) find out the division that provides the minimum seed frequency. In each division, we divide the substring into two parts: We extract m seeds from the first part and 1 seed from the second part. The minimum total seed frequency of this division (or simply the ‘optimal frequency of the division’) is simply the sum of the optimal m-seed frequency of the first part and the optimal 1-seed frequency of the second part. As we already have both the optimal m-seed frequency of the first part and the 1-seed frequency of the second part pre-calculated and stored, the optimal frequency of this division can be computed with one addition and two lookups.

The optimal$(m+1)$-seed solution of this substring is simply the division that yields the minimum total frequency. Given that each seed requires at least S_min base-pairs, for a substring of length $L\prime$, there are in total $L\prime -(m+1)\times S_{\text{min}}$ possible divisions to be examined. This relationship can be summarized as a recurrence function in Equation 1, in which $\mathtt{\text{Opt}}(U,m)$ denotes the optimal m-seed frequency of substring U and u denotes the length of U.

$$\mathtt{\text{Opt}}(U,m+1)={\min }_i[\mathtt{\text{Opt}}(U[1:i-1],m)+\mathtt{\text{Opt}}(U[i:u],1)]$$ (1)

We can apply the same strategy to the entire read: to obtain the optimal x + 1 seeds from read R, we first examine all possible 2-part divisions of the read, which divide the read into a prefix and a suffix. For each division, we extract x seeds from the prefix, and 1 seed from the suffix. The optimal $(x+1)$-seed solution of the read is simply the division that provides the lowest total seed frequency. As we have discussed above, for a division to be optimal, its x-seed prefix and 1-seed suffix must also be optimal (this provides the minimum total seed frequency). By the same logic, to obtain the optimal x-seed solution of a prefix, we can further divide the prefix into an optimal $(x-1)$-seed prefix and an optimal 1-seed substring (which is no longer a suffix of the read). We can keep applying this prefix-division process until we have reached 1-seed prefixes. In other words, by progressively calculating the optimal solutions of all prefixes from 1 to x seeds, we can find the optimal $(x+1)$-seed solution of the read.

OSS implements the above strategy using a dynamic programming algorithm: to calculate the optimal $(x+1)$-seed solution of a read, R, OSS computes and stores optimal solutions of prefixes with fewer seeds through x iterations. In each iteration, OSS computes optimal solutions of prefixes with regard to a specific number of seeds. In the mth iteration ($m\le x$), OSS computes the optimal m-seed solutions of all prefixes of R, by re-using optimal solutions computed from the previous $(m-1)\text{th}$ iteration. For each prefix, OSS performs a series of divisions and finds the division that provides the minimum total frequency of m seeds. For each division, OSS computes the optimal m-seed frequency by summing up the optimal $(m-1)$-seed frequency of the first part and the 1-seed frequency of the second part. Both frequencies can be obtained from previous iterations. Overall, OSS starts from one seed and iterates to x seeds. Finally OSS computes the optimal $(x+1)$-seed solution of R by finding the optimal division of R and reuses results from the xth iteration.

3.2 Further optimizations

With the proposed dynamic programming algorithm, OSS can find the optimal $(x+1)$ seeds of a L-bp read in $\mathcal{O}(x\times L^2)$ operations: In each iteration, OSS examines $\mathcal{O}(L)$ prefixes (to be exact, $L-(x+1)\times S_{\text{min}}$) and for each prefix OSS inspects $\mathcal{O}(L)$ divisions (to be exact, $L\prime -i\times S_{\text{min}}$ divisions of an $L\prime$-bp prefix for the ith iteration). In total, there are $\mathcal{O}(L^2)$ divisions to be verified in an iteration.

To speed up OSS and reduce the average complexity of processing each iteration, we propose four optimizations: optimal divider cascading, early divider termination, divider sprinting and optimal solution forwarding. With all four optimizations, we empirically reduce the average complexity of processing an iteration to $\mathcal{O}(L)$. Below we describe the four optimizations in detail.

3.2.1 Optimal divider cascading

Until this point, our assumption is that optimal solutions of prefixes within an iteration are independent from each other: the optimal division (the division that provides the optimal frequency) of one prefix is independent from the optimal division of another prefix, thus they must be derived independently.

We observe that this assumption is not necessarily true as there exists a relationship between two prefixes of different lengths in the same iteration (under the same seed number): the first optimal divider (the optimal divider that is the closest towards the beginning of the read, if there exist multiple optimal divisions with the same total frequency) of the shorter prefix must be at the same or a closer position towards the beginning of the read, compared to the first optimal divider of the longer prefix. We call this phenomenon the optimal divider cascading, and it is depicted in Figure 4. The proof that the optimal divider cascading phenomenon always holds is provided in the Supplementary Materials Section 1.2.

Fig. 4.

All prefixes and their first optimal dividers in an iteration. We observe that the first optimal divider of a longer prefix is never more towards the beginning of the read than the first optimal divider of a shorter prefix

Based on the optimal divider cascading phenomenon, we know that for two prefixes in the same iteration, the first optimal divider of the shorter prefix must be no further than the first optimal divider of the longer prefix. With this relationship, we can reduce the search space of optimal dividers in each prefix by processing prefixes within an iteration from the longest to the shortest.

In each iteration, we start with the longest prefix of the read, which is the read itself. We examine all divisions of the read and find the first optimal divider of it. Then, we move to the next prefix of the length $|L-1|$. In this prefix, we only need to check dividers that are at the same or a prior position than the first optimal divider of the read. After processing the length $|L-1|$ prefix, we move to the length $|L-2|$ prefix, whose search space is further reduced to positions that are at the same or a closer position to the beginning of the read than the first optimal divider of the length $|L-1|$ prefix. This procedure is repeated until the shortest prefix in this iteration is processed.

3.2.2 Early divider termination

With optimal divider cascading, we are able to reduce the search space of the first optimal divider of a prefix and exclude positions that come after the first optimal divider of the previous, 1-bp longer prefix (recall that with optimal divider cascading OSS starts with the longest prefix and gradually moves to shorter prefixes). However, the search space is still large since any divider prior to the first optimal divider of the previous prefix could be the optimal divider. To further reduce the search space of dividers in a prefix, we propose the second optimization—early divider termination.

The goal of early divider termination is to reduce the number of dividers we examine for each prefix. The key idea of early divider termination is to find the early divider termination position in the target prefix, as we are moving the divider backward one base-pair at a time, where all dividers that are prior to the termination position are guaranteed to be suboptimal and can be excluded from the search space.

The key observation that early divider termination builds on is simple: The optimal frequency of a substring monotonically non-increases as the substring extends longer in the read (see Lemma 1 in Supplementary Materials Section 1.2 for the proof of this fact).

Based on the optimal divider cascading, we start at the position of the first optimal divider in the previous prefix. Then, we gradually move the divider towards the beginning (or simply move backward) and check the total seed frequency of the division after each move. During this process, the first part of the division gradually shrinks while the second part gradually grows, as we show in Figure 5. According to the Lemma 1 in the Supplementary Materials Section 1.2, the optimal frequency of the first part must be monotonically non-decreasing while the optimal frequency of the second part must be monotonically non-increasing.

Fig. 5.

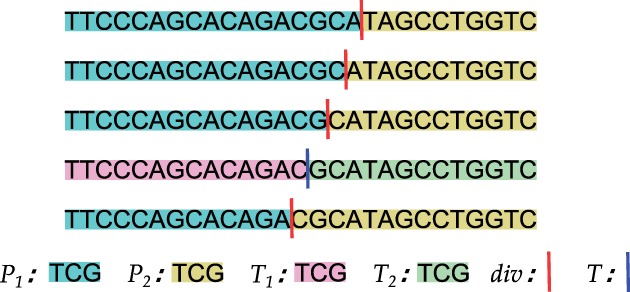
Moving a divider dividers in a prefix according to optimal divider cascading. The divider starts at the position of the previous prefix’s first optimal divider, then gradually moves towards the beginning of the prefix, until it reaches the termination position, T. P1 (in blue) and P2 (in yellow) are the first and the second part of each division, respectively. T1 (in pink) and T2 (in green) are the first and the second part of the termination division, respectively

For each position of the divider, let $\mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{P_2}$ denote the frequency of the second part (P₂, in yellow) and $\Delta \mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{P_1}$ denote the change of frequency of the first part (P₁, in blue) between current and the next move (the two moves are only 1 bp apart). Early divider termination suggests that: the divider should stop moving backward, whenever $|\Delta \mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{P_1}|>|\mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{P_2}|$. All dividers that are prior to this position are guaranteed to have greater total seed frequencies. We call this stopping position the termination position, and the division at this position—the termination division, denoted as T, and the above inequality that determines the termination position, the termination inequality ($|\Delta \mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{P_1}|>|\mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{P_2}|$). We name the first and the second part of T as T₁ and T₂ respectively.

For any divider D that comes prior to the termination position, compared to the termination division, T, its first part is shorter than the first part of the termination division ($|\Delta {\mathtt{\text{D}}}_1|<|\Delta {\mathtt{\text{T}}}_1|$) and its second part is longer. Hence the optimal frequency of its first part is greater $(\mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{D_1}\ge \mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{T_1})$ and the optimal frequency of its second part is smaller $(\mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{D_2}\le \mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{T_2})$. Let $|\Delta \mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{D_{1-}{T}_1}|$ denote the increase of the optimal frequency of the first part between current division D and termination division T and $|\Delta \mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{D_{2-}{T}_2}|$ denote the decrease of the second part. Based on Lemma 1, we have $|\Delta \mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{D_{1-}{T}_1}|\ge |\Delta \mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{T_1}|$. Since the frequency of a seed can be no smaller than 0, we also have $|\mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{T_2}|\ge |\Delta \mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{D_{2-}{T}_2}|$. Combining these two inequalities with the termination inequality, ($|\Delta \mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{T_1}|>|\mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{T_2}|$) we have $|\Delta \mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{D_{1-}{T}_1}|>|\Delta \mathtt{\text{FRE}}{\mathtt{\text{Q}}}_{D_{2-}{T}_2}|$. This suggests that compared to the termination division, the frequency increase of the first part of D must be greater than the frequency reduction of the second part. Hence, the overall optimal frequency of such a division must be greater than the optimal frequency of the termination division. Therefore, a division prior to the termination position cannot be optimal.

Using early divider termination, we can further reduce the search space of dividers within a prefix and exclude all positions that are prior to the termination position. Since the second part of the prefix hosts only one seed and frequencies of most seeds decrease to 1 after extending it to a length of over 20-bp, we observe that the termination position of a prefix is reached fairly quickly, only after a few moves. With both optimal divider cascading and early divider termination, from our experiments, we observe that we only need to verify 5.4 divisions on average (this data is obtained from mapping ERR240726 to human genome v37, under the error threshold of 5) for each prefix. To conclude, with both optimizations, we have reduced the average complexity of Optimal Seed Solver to $\mathcal{O}(x\times L)$.

3.2.3 Divider sprinting

According to optimal divider cascading and early divider termination, for each prefix, after inheriting the starting divider from the previous prefix, we gradually move the divider towards the beginning of the prefix, one base-pair at a time, until early divider termination is triggered. In each move, we check the optimal frequency of the two parts in the current division as well as the frequency increase of the first part compared to the previous division. We stop moving the divider when the frequency increase of the first part is greater than the optimal frequency of the second part.

We observe that it is unnecessary to always move the divider a single base-pair at a time and check for frequencies after each move. In the early divider termination method, the move terminates only when the frequency increase of the first part is greater than the optimal seed frequency in the second part. This suggests that when the frequency of the first part remains unchanged between moves, which produces no increase in frequency, we do not need to check the frequency of the second part as it will not trigger early termination. When multiple dividers in a region share the same first-part frequency, we only need to verify the last divider of this region and skip all the other dividers in the middle (an example is provided in the Supplementary Materials Section 1.4). The last divider always provides the least total seed frequency among all dividers in this region since it has the longest second part compared to other dividers (longer substring always provides less or equally frequent optimal seeds) while keeping its first-part frequency the same. We call this method divider sprinting.

3.2.4 Optimal solution forwarding

With optimal divider cascading, early divider termination and divider sprinting, we observe that the average number of divisions per prefix reduces from 5.4 (plain OSS) to 3.7. Nevertheless, for each prefix, we still need to examine at least two divisions (one for the inherited optimal division of the previous prefix and at least one more for early divider termination). We observe that some prefixes can also inherit the optimal solution of the previous prefix without verifying any divisions, as they share the same optimal divider with the previous prefix. Within an iteration, we recognize that there exist many prefixes that share the same second-part frequency with the previous prefix when divided by the previous prefix’s optimal divider. We conclude that such prefixes must also share the same optimal divider as well as the same optimal seed frequency with the previous prefix (detailed proof is provided in the Supplementary Materials Section 1.3). We call this optimal solution forwarding.

With optimal solution forwarding, for each incoming prefix, after inheriting the optimal divider from the previous prefix, we first test if the second-part frequency of the new prefix equals the second-part frequency of the previous prefix. If they are equal, then we can assert that the optimal divider of the previous prefix must also be the optimal divider of the new prefix and move on to the next read, without examining any divisions.

With optimal solution forwarding, we observe that the average number of division verifications per prefix reduces further to 0.95 from 5.4 (this data is obtained from mapping ERR240726 to human genome v37, under the error threshold of 5), providing a 5.68x potential speedup over OSS without any optimizations.

3.3 The full algorithm

Algorithm 1 and 2 show the full algorithm of the Optimal Seed Solver. Before calculating the optimal x-seed frequency of the read, R, we assume that we already have the optimal 1-seed frequency of any substring of R and it can be retrieved in a $\mathcal{O}(1)$-time lookup via the $optimalFreq(\text{substring})$ function (this assumption is valid only if seeds are stored in a large hash table. For seeds that are pre-processed by the Burrows-Wheeler transformation, OSS requires $\mathcal{O}(s)$ total steps in FM-indexing to obtain the frequency of the seed, where s is the length of the seed. In total, it requires $\mathcal{O}(L^3)$ total steps to index all possible seeds in the read, which potentially could generate $\mathcal{O}(L^3)$ memory accesses and $\mathcal{O}(L^3)$ cache misses in the worst case. Later in Supplementary Materials Section 1.6, we propose lock-step BWT, a mechanism that reduces the average number of cache misses per read to $\mathcal{O}(L)$, by imposing a minimum seed length requirement and by traversing all prefixes of the read in a lock-step fashion. Specifically, lock-step BWT organizes all prefixes together such that they extend the same base-pair in the read at the same time. Please refer to Supplementary Materials Section 1.6 for further details). It requires at most $\mathcal{O}(L^2)$ lookups to the seed database for all possible substrings of the read.

Let $firstOptDivider(\text{prefix})$ be the function to calculate the first optimal divider of a prefix. Then the optimal set of seeds can be calculated by filling a 2-D array, opt_data, of size $(x-1)\times L$. In this array, each element stores two data: an optimal seed frequency and a first optimal divider. The element at ith row and jth column stores the optimal i-seed frequency of the prefix $R[\mathrm{1...}j]$ which includes the optimal i-seed frequency of the prefix and the first optimal divider of the prefix. The optimal divider divides the prefix into an (i − 1)-seed prefix and an 1-seed substring.

Algorithm 1 provides the pseudo-code of optimalSeedSolver, which contains the core algorithm of OSS and the optimal divider cascading optimization; and Algorithm 2 provides the pseudo-code of firstOptDivider, which contains the early divider termination, the divider sprinting and the optimal solution forwarding optimizations.

To retrieve the starting and ending positions of each optimal seed, we can backtrack the 2-D array and backward induce the optimal dividers between optimal seeds. We start with the final optimal divider of the entire read, which divides the read into a (x – 1)-seed prefix and a suffix. Among them, the suffix makes the last (right most) optimal seed of the read. Then we examine the (x – 1)-seed prefix from the previous step and retrieve its optimal divider, which divides the prefix into an (x – 2)-seed prefix and a substring. Among the two, the substring makes the second last optimal seed of the read. This process is repeated until we have retrieved all x optimal seeds of the read. Further details as well as the pseudo-code of the backtracking process is provided in Supplementary Materials.

For better understanding, we provide a real example in Supplementary Materials Section 1.4 to show how Optimal Seed Solver operates.

4 Related works

The primary contribution of this work is a dynamic programming algorithm that derives the optimal non-overlapping seeds of a read in $\mathcal{O}(x\times L)$ operations on average. To our knowledge, this is the first work that finds the optimal seeds and the optimal frequency of a read. The most related prior works are optimizations to the seed selection mechanism which reduce the sum of seed frequencies of a read using greedy algorithms. We will compare to such methods shortly, both qualitatively (in this section) and quantitatively (in Section 5).

We first quickly distinguish OSS from other methods (Kucherov etal., 2014; Langmead and Salzberg, 2012; Li, 2013) which solve similar yet unrelated problems. These previous works either determine the number and length of erroneous seeds such that the total number of branches in backtracking is minimized for each seed (Kucherov etal., 2014) or simply select seeds and their locations through probabilistic methods without providing error tolerance guarantees (e.g. bowtie2 (Langmead and Salzberg, 2012) and BWA-MEM (Li, 2013)). By contrast, OSS finds the number and lengths of non-overlapping seeds such that the total frequency of all seeds is minimized. Former mechanisms are not designed for seed-and-extend based mappers that rely on non-overlapping seeds following the pigeonhole principle. In this paper, we only compare seed selection mechanisms that follow the pigeonhole principle.

Existing seed selection optimizations can be classified into three categories: (i) extending seed length, (ii) avoiding frequent seeds and (iii) rebalancing frequencies among seeds. Optimizations in the first category extend frequent seeds longer in order to reduce their frequencies. Optimizations in the second category sample seed positions in the read and reject positions that generate frequent seeds. Optimizations in the third category rebalance frequencies among seeds such that the average seed frequency at runtime is more consistent with the static average seed frequency of the seed table.

In the remainder of this section, we qualitatively compare the Optimal Seed Solver (OSS) to four state-of-the-art works selected from the above three categories. They are: Cheap K-mer Selection (CKS) in FastHASH (Xin etal., 2013), Optimal Prefix Selection (OPS) in the Hobbes mapper (Ahmadi etal., 2011), Adaptive Seeds Filter (ASF) in the GEM mapper (Marco-Sola etal., 2012) and spaced seeds in PatternHunter (Ma etal., 2002). (In this paper, we name the mapping strategies used in the the Hobbes and the GEM mappers, which were not given names in the original papers, as OPS and ASF, respectively.) Among the four prior works, ASF represents works from the first category; CKS and OPS represent works from the second category and spaced seeds represents works from the third category. Below we elaborate each of them in greater details.

The Adaptive Seeds Filter (ASF) (Marco-Sola et al., 2012) seeks to reduce the frequency of seeds by extending the lengths of the seeds. For a read, ASF starts the first seed at the very beginning of the read and keeps extending the seed until the seed frequency is below a pre-determined threshold, t. For each subsequent seed, ASF starts it from where the previous seed left off in the read, and repeats the extension process until the last seed is found. In this way, ASF aims to guarantee that all seeds have a frequency below t.

Compared to OSS, ASF has two major drawbacks. First, ASF assumes the least frequent set of seeds in a read has similar frequencies; hence, they share a common frequency threshold t. We observe that this is not always true. The optimal set of seeds often have very different frequencies. This is because some seeds do not provide much frequency reduction despite long extensions while other seeds yield significant frequency reductions only at certain extension lengths (the frequency reduction looks like a step function). By regulating all seeds with the same frequency threshold, ASF inefficiently distributes base-pairs among seeds. Second, ASF sets a fixed frequency threshold t for all reads, which often leads to under-utilization of base-pairs in reads. Different reads usually get different optimal thresholds (the threshold that provides the least frequent set of seeds under ASF for the read). For reads that contain frequent seeds, optimal thresholds are usually large (e.g. t > 1000), while for reads without frequent seeds, optimal thresholds are usually small (e.g. t < 100). Unfortunately, ASF can apply only a single threshold to all reads. If t is set to a large value to accommodate reads with frequent seeds, then for other reads, ASF extracts only short seeds even if there are many unused base-pairs. Otherwise if t is set to a small value, then frequent seeds consume many base-pairs and reads with frequent seeds have insufficient base-pairs to construct enough seeds to tolerate all errors. OSS, however, finds the least frequent set of seedsindividually for each read, which could contain highly variable seed frequencies.

Note that the method of selecting seeds consecutively starting at the beginning of a read does not always produce infrequent seeds. Although most seeds that are longer than 20-bp are either unique or non-existent in the reference, there are a few seeds that are still more frequent than 100 occurrences even at 40-bp (e.g. all ‘A’s). With a small S_max (e.g. $S_{\text{max}}\le 40$) and a small t ($t\le 50$), ASF cannot not guarantee that all selected seeds are less frequent than t. This is because ASF cannot extend a seed by more than S_max-bp, even if its frequency is still greater than t. If a seed starts at a position that yields a long and frequent seed, ASF will extend the seed to S_max and accept a seed frequency that is still greater than t.

Setting a static t for all reads further worsens the problem. Reads are drastically different. Some reads do not include any frequent short patterns (e.g. 10-bp patterns) while other reads have one to many highly frequent short patterns. Reads without frequent short patterns do not produce frequent seeds in ASF, unless t is set to be very large (e.g. $\ge 10\hspace{0.17em}000$) and as a result the selected seeds are very short (e.g. $\le 8$-bp). Reads with many frequent short patterns have a high possibility of producing longer seeds under medium-sized or small t’s (e.g. $\le 100$). For a batch of reads, if the global t is set to a small number, reads with many frequent short patterns will have a high chance of producing many long seeds that the read does not have enough length to support. If t is set to a large number, reads without any frequent short patterns will produce many short but still frequent seeds as ASF will stop extending a seed as soon as it is less frequent than t, even though the read could have had longer and less frequent seeds.

Cheap K-mer Selection (CKS) (Xin et al., 2013) aims to reduce seed frequencies by selecting seeds from a wider potential seed pool. For a fixed seed length k, CKS samples $\lfloor \frac{L}{k}\rfloor$ seed positions consecutively in a read, with each position apart from another by k-bp. Among the $\lfloor \frac{L}{k}\rfloor$ positions, it selects x seed positions that yield the least frequent seeds (assuming the mapper needs x seeds). In this way, it avoids using positions that generate frequent seeds.

CKS has low overhead. In total, CKS only needs $\lfloor \frac{L}{k}\rfloor$ lookups for seed frequencies followed by a sorting of $\lfloor \frac{L}{k}\rfloor$ seed frequencies. Although fast, CKS can provide only limited seed frequency reduction as it has a very limited pool to select seeds from. For instance, in a common mapping setting where the read length L is 100-bp and seed length k is 12, the read can be divided into at most $\lfloor \frac{100}{12}\rfloor =8$ positions. With only 8 potential positions to select from, CKS is forced to gradually select more frequent seeds under greater seed demands. To tolerate 5 errors in this read, CKS has to select 6 seeds out of 8 potential seed positions. This implies that CKS will select the 3rd most frequent seed out of 8 potential seeds. As we have shown in Figure 1, 12-bp seeds on average have a frequency over 172, and selecting the 3rd frequent position out of 8 potential seeds renders a high possibility of selecting a frequent seed which has a higher frequency than average.

Similar to CKS, Optimal Prefix Selection (OPS) (Ahmadi et al., 2011) also uses fixed length seeds. However, it allows a greater freedom of choosing seed positions. Unlike CKS, which only select seeds at positions that are multiples of the seed length k, OPS allows seeds to be selected from any position in the read, as long as seeds do not overlap.

Resembling our optimal seed finding algorithm, the basis of OPS is also a dynamic programming algorithm that implements a simpler recurrence function. The major difference between OPS and OSS is that OPS does not need to derive the optimal length of each seed, as the seed length is fixed to k-bp. This reduces the search space of optimal fixed-length seeds to a single dimension, i.e. only the seed placements. The worst case/average complexity of OPS is $\mathcal{O}(L\times x)$.

Compared to CKS, OPS is more complex and requires more seed frequency lookups. In return, OPS finds less frequent seeds, especially under large seed numbers. However, with a fixed seed length, OPS cannot find the optimal non-overlapping variable-length seeds.

Spaced seeds (Ma et al., 2002) aims to rebalance frequencies among patterns in the seed database. Rebalancing seeds reduces the frequent seed phenomenon which, in turn, reduces the average seed frequency in read mapping (in other words, it improves the sensitivity/selectivity ratio of seeds in read mapping (Egidi and Manzini, 2015)). Spaced seeds rebalance seeds by using different patterns that are hashed into the same hash value are considered as a single ‘spaced seed’. By carefully designing the hashing function, which extracts base-pairs only at selected positions from a longer (e.g. 18-bp) pattern, spaced seeds can group up frequent long patterns with infrequent long patterns and merge them into the new and more balanced spaced seeds, which have smaller frequency variations. At runtime, long raw seeds are selected consecutively in the reads, which are processed by the rebalancing hash function to generate spaced seeds.

Compared to OSS, spaced seeds has two disadvantages. First, the hash function cannot perfectly balance frequencies among all spaced seeds. After rebalancing, there is still a large disparity in seed frequency amongst seeds. Second, seed placement in spaced seeds is static, and does not accommodate for high frequency seeds. Therefore, positions that generate frequent seeds are not avoided which still give rise to the frequent seeds phenomenon.

5 Results

In this section, we compare the average case complexity, memory traffic and effectiveness of OSS against the four prior studies, ASF (Marco-Sola et al., 2012), CKS (Xin et al., 2013), OPS (Ahmadi et al., 2011) and spaced seeds (Ma et al., 2002) as well as the naïve mechanism, which selects fixed seeds consecutively. Memory traffic is measured by the number of required seed frequency lookups to map a single read. The effectiveness of a seed selection scheme is measured by the average seed frequency of mapping 4 031 354 101-bp reads from a real read set, ERR240726 from the 1000 Genomes Project, under different numbers of seeds.

We do not measure the execution time of each mechanism because different seed selection optimizations are combined with different seed database implementations. CKS, OPS and spaced seeds use hash tables for short, fixed-length seeds while ASF and OSS employs slower but more memory efficient BWT and FM-index for longer, variant-length seeds. However, this combination is inter-changeable. CKS and OPS can also work well with BWT and FM-index and ASF, OSS can also be combined with a large hash-table, given sufficient memory space. Besides, different existing implementations have their unique, implementation-specific seed database optimizations, which introduces more variations to the execution time. Due to these reasons, we only compare the complexity and memory traffic of each seed selection scheme, without measuring their runtime performance.

We benchmark each seed optimization scheme with multiple configurations. We benchmark ASF with multiple frequency thresholds, 5, 10, 100, 500 and 1000. If a read fails to provide enough seeds in ASF, due to having many long seeds under small thresholds, the read will be processed again in CKS with a fixed seed length of 12-bp. We benchmark CKS, OPS and the naïve under three fixed seed lengths, 12, 13 and 14. We benchmark spaced seeds with the default bit-mask provided in the PatternHunter’s paper (Ma etal., 2002), ‘110100110010101111’, which hashes 18-bp long seeds into 11-bp long signatures.

All seed selection mechanisms are benchmarked using an in-house seed database, which supports varying seed lengths between S_min = 10 and S_max = 30.

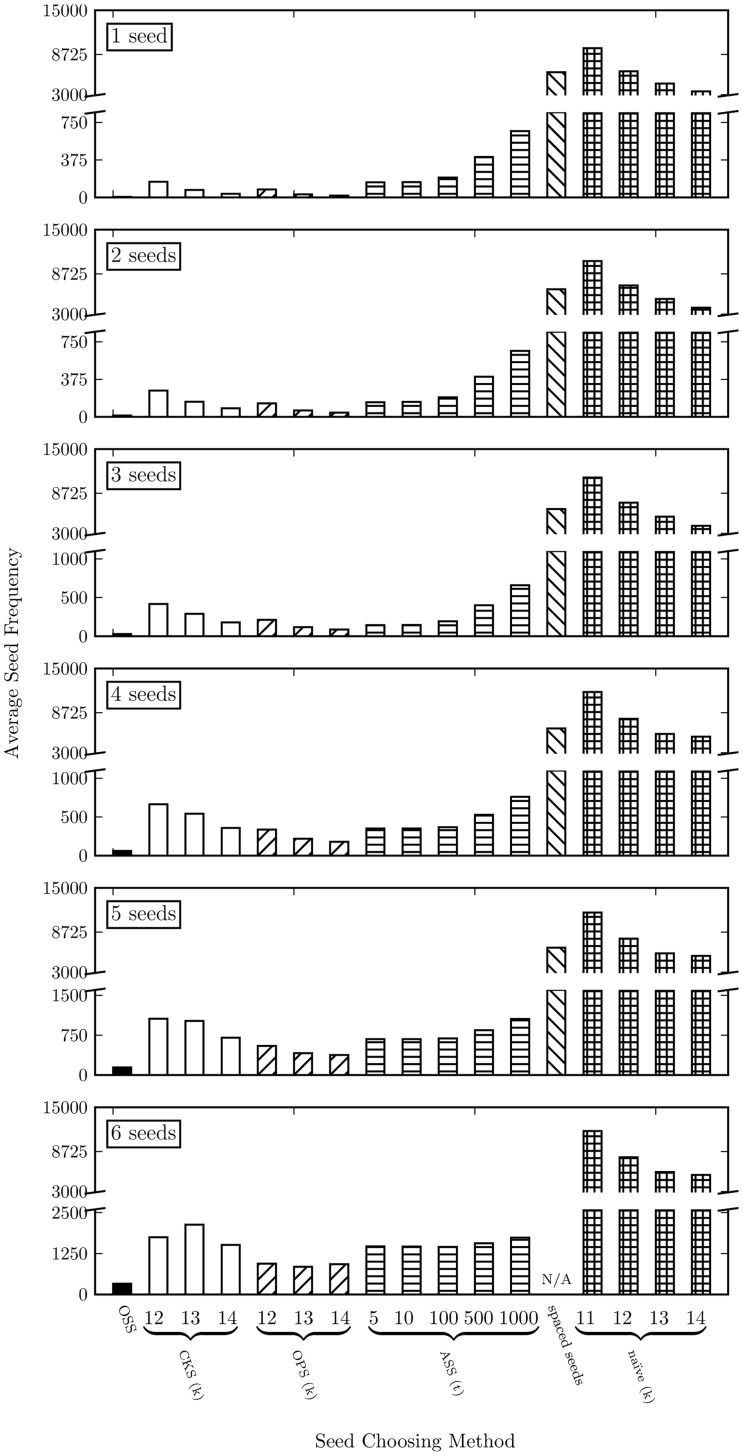
Table 1 summarizes the average-case complexity and memory traffic of each seed selection optimization. From the table, we can observe that OSS requires the most seed frequency lookups ($\mathcal{O}(L^2)$) with the worst average case complexity, ($\mathcal{O}(x\times L)$), which the same as that of OPS. Nonetheless, OSS is the most effective seed selection scheme, as Figure 6 shows. Among all seed selection optimizations, OSS provides the largest frequency reduction of seeds on average, achieving a 3x larger frequency reduction compared to the second best seed selection scheme, OPS.

Table 1.

An average case complexity and memory traffic comparison (measured by the number of seed-frequency lookups) of seed selection optimizations, including Optimal Seed Solver (OSS), Adaptive Seeds Filter (ASF), Cheap K-mer Selection (CKS), Optimal Prefix Selection (OPS), spaced seeds and naïve (selecting fixed-length seeds consecutively)

	Optimal Seed Solver	ASF	CKS	OPS	Spaced seeds	naïve
Empirical average case complexity	$\mathcal{O}(x\times L)$	$\mathcal{O}(x)$	$\mathcal{O}(x\times log\frac{L}{k})$	$\mathcal{O}(x\times L)$	$\mathcal{O}(x)$	$\mathcal{O}(x)$
Number of lookups	$\mathcal{O}(L^2)$	$\mathcal{O}(x)$	$\mathcal{O}(\frac{L}{k})$	$\mathcal{O}(L)$	$\mathcal{O}(x)$	$\mathcal{O}(x)$

Note that only OSS has different empirical average case complexity and worst case complexity. The average case and worst case complexity of other optimizations are equal. The empirical average-case complexity of OSS is derived from mapping a real read set, ERR240726, under variable number of errors.

Fig. 6.

Average seed frequency comparison among Optimal Seed Solver (OSS), Adaptive Seeds Filter (ASF), Cheap K-mer Selection (CKS), Optimal Prefix Selection (OPS), spaced seeds and naïve (selecting fixed length seeds consecutively). The results are gathered by mapping 4031354 101-bp reads from the read set ERR240726_1 from 1000 Genomes Project under different numbers of seeds (for better accuracy and error tolerance). In each figure, a smaller average seed frequency indicates a more effective seed selection mechanism

As shown in Figure 6, the average seed frequencies of OSS, CKS and OPS increase with larger seed numbers. This is expected, as there is less flexibility in seed placement with more seeds in a read. For OSS, more seeds also means shorter average seed length, which also contributes to greater average seed frequencies. For ASF, average seed frequencies remains similar for three or fewer seeds. When there are more than three seeds, the average seed frequencies increase with more seeds. This is because up to three seeds, all reads have enough base-pairs to accommodate all seeds, since the maximum seed length is S_max = 30. However, once beyond three seeds, reads start to fail in ASF (due to having insufficient base-pairs to accommodate all seeds) and the failed reads are passed to CKS instead. Therefore the increase after three seeds is mainly due to the increase in CKS. For t = 10 with six seeds, we observe from our experiment that 66.4% of total reads fail in ASF and are processed in CKS instead.

For CKS and OPS, the average seed frequency decreases with increasing seed length when the number of seeds is small (e.g.<4). When the number of seeds is large (e.g. 6), it is not obvious if greater seed lengths provide smaller average seed frequencies. In fact, for 6 seeds, the average seed frequency of OPS rises slightly when we increase the seed length from 13-bp to 14-bp. This is because, for small numbers of seeds, the read has plenty of space to arrange and accommodate the slightly longer seeds. Therefore, in this case, longer seeds reduce the average seed frequency. However, for large numbers of seeds, even a small increase in seed length will significantly decrease the flexibility in seed arrangement. In this case, the frequency reduction of longer seeds is surpassed by the frequency increase of reduced flexibility in seed arrangement. Moreover, the benefit of having longer seeds diminishes with greater seed lengths. Many seeds are already infrequent at 12-bp. Extending the infrequent seeds longer does not introduce much reduction in the total seed frequency. This result corroborates the urge of enabling flexibility in both individual seed length and seed placements.

Overall, OSS provides the least frequent seeds on average, achieving a 3x larger frequency reduction than the second best seed selection schemes, OPS.

6 Discussion

As shown in the Section 5, OSS requires $\mathcal{O}(L^2)$ seed-frequency lookups in order to derive the optimal solution of a read. For a non-trivial seed database implementation such as BWT with FM-index, this can be a time consuming process. For reads that generate equally frequent seeds in OSS and other seed selection mechanisms, OSS could be less beneficial as it generates more queries of seed frequencies to the seed database without reducing the total seed frequency. When such reads are prevalent (very unlikely), OSS might not be the ideal seeding mechanism. One workaround under this event is to combine OSS with other greedy seed selection algorithms (e.g. CKS, OPS). In such a configuration, OSS will only be invoked when greedy seed selection algorithms fail to deliver infrequent seeds. However, how to combine different seeding mechanisms is beyond the scope of this paper and will be explored in our future research.

The Optimal Seed Solver also revealed that there is still great potential in designing better greedy seed selection optimizations. From our experiment, we observe that the most effective greedy seed selection optimization still provides 3 × more frequent seeds on average than optimal. Better greedy algorithms that provide less frequent seeds without a large number of database lookups are also part of our future research.

7 Conclusion

Optimizing seed selection is an important problem in read mapping. The number of selected non-overlapping seeds defines the error tolerance of a mapper while the total frequency of all selected seeds in the reference genome determines the performance of the mapper. To build a fast yet error tolerant mapper, it is essential to select a large number of non-overlapping seeds while keeping each seed as infrequent as possible. In this paper, we confirmed the frequent seed phenomenon discovered in previous works (Kiełbasa etal., 2011), which suggests that in a naïve seed selection scheme, mappers tend to select frequent seeds from reads, even when using long seeds. To solve this problem, we proposed the Optimal Seed Solver (OSS), a dynamic-programming algorithm that finds the optimal set of seeds that has the minimum total frequency. We further introduced four optimizations to OSS: optimal divider cascading, early divider termination, divider sprinting and optimal solution forwarding. Using all four optimizations, we reduced the average-case complexity of OSS to $\mathcal{O}(x\times L)$, where x is the total number of seeds and L is the length of the read; and achieved a $\mathcal{O}(x\times L^2)$ worst-case complexity. We compared OSS to four prior studies, Adaptive Seeds Filter, Cheap K-mer Selection, Optimal Prefix Selection and spaced seeds and showed that OSS provided a 3-fold seed frequency reduction over the best previous seed selection scheme, Optimal Prefix Selection. We conclude that OSS is an efficient algorithm that can find the best set of seeds, which can potentially improve the performance of future read mappers.

Funding

This study is supported by two NIH grants (HG006004 to C. Alkan and O. Mutlu; and HG007104 to C. Kingsford) and a Marie Curie Career Integration Grant (PCIG-2011-303772) to C. Alkan under the Seventh Framework Programme. C. Alkan also acknowledges support from The Science Academy of Turkey, under the BAGEP program.

Conflict of Interest: none declared.